Relative performance of two-stage continual reassessment method in contrast to an optimal benchmark

Abstract

Background

The two-stage, likelihood-based continual reassessment method (CRM-L; O’Quigley and Shen [1]) entails the specification of a set of design parameters prior to the beginning of its use in a study. The impression of clinicians is that the success of model-based designs, such as CRM-L, depends upon some of the choices made in regard to these specifications, such as the choice of parametric dose-toxicity model and the initial guess of toxicity probabilities.

Purpose

In studying the efficiency and comparative performance of competing dose-finding designs for finite (typically small) samples, the non-parametric optimal benchmark (O’Quigley, Paoletti and Maccario [2]) is a useful tool. When comparing a dose-finding design to the optimal design, we are able to assess how much room there is for potential improvement.

Methods

The optimal method, based only on an assumption of monotonicity of the dose-toxicity function, is a valuable theoretical construct serving as a benchmark in theoretical studies, similar to that of a Cramer-Rao bound. We consider the performance of CRM-L under various design specifications and how it compares to the optimal design across a range of practical situations.

Results

Using simple recommendations for design specifications, the CRM-L will produce performances, in terms of identifying doses at and around the MTD, that are close to the optimal method on average over a broad group of dose-toxicity scenarios.

Limitations

Although the simulation settings vary the number of doses considered, the target toxicity rate and the sample size, the results here are presented for a small, though widely-used, set of two-stage CRM designs.

Conclusions

Based on simulations here, and many others not shown, CRM-L is almost as accurate, in many scenarios, as the (unknown and unavailable) optimal design. On average, there appears to be very little margin for improvement. Even if a finely tuned skeleton [3] offers some improvement over a simple skeleton, the improvement is necessarily very small.

1. Introduction

Numerous Phase 1 clinical trial designs have been proposed for identifying the maximum tolerated dose (MTD) from a discrete set of doses in which toxicity is described by a binary random variable. One important measure of performance of a particular design is its accuracy, which is reflected by the distribution of the dose selected as the MTD. For instance, suppose method A recommends the true MTD 45% of the time and method B 50%. One might conclude that method B is superior to method A. However, it is also important to consider how often a method recommends doses other than the true MTD. If method A recommended either the true MTD or a neighboring dose (MTD−1, MTD+1) in a large percentage of trials, while method B tended to recommend either the MTD or doses far from the MTD, then method A could be considered the better option. A necessary component of the evaluation process is to have some concept for how well a design can possibly perform. The nonparametric optimal design described by O’Quigley, Paoletti and Maccario [2] is a theoretical construction and therefore not applicable in a real trial. The authors [2] showed that it is not generally possible to do better than the optimal design on the basis of the observations themselves, so it can be used as an upper bound for the performance of any dose-finding scheme. To improve on the finite sample optimal design requires extraneous knowledge. Such knowledge could come from an informative prior distribution or possibly from the use of some parametric assumption, an assumption beyond the reasonable stipulation of monotonicity, and one that is necessarily strong and, in almost all practical cases, unverifiable.

O’Quigley, Pepe and Fisher [4] introduced the continual reassessment method (CRM) as an alternative to the traditional Up-and-Down escalation schemes reviewed by Storer [5]. In its original form the CRM is a Bayesian method based on the use of a simple working model and sequential updating of the dose-toxicity relationship to estimate the dose level at which to treat the next available patient.

In addition to the Bayesian approach, O’Quigley and Shen [1] outlined a two-stage likelihood based approach to the CRM (referred to as CRM-L). Suppose that we have a discrete set of k dose levels, {d₁,…, d_k}. The CRM-L begins by assuming a parameterizerd working model, denoted by ψ(d_i, a), for the true toxicity probability. The working model ψ(d_i, a) is monotonic in both dose level, d_i, and the parameter, a, for instance, the power model or logistic curve. The model ψ(d_i, a) is misspecified, meaning that the true mechanism generating the observations is different from the working model. After having included j subjects, we obtain an estimate, â_j, based on the maximum likelihood estimate (MLE) of a. Suppose, after the inclusion of j patients, the log-likelihood L_j(a) is maximized at a = â_j. Once â_j has been calculated, we can obtain an estimate of the probability of toxicity at each dose level via ψ(d_i, â_j), i = 1,…, k. On the basis of this formula, the dose given to the (j+1) th patient is determined. Specifically, for a target toxicity rate, θ, this dose is d_i = arg min_i |ψ(d_i, â_j)−θ|. The MTD is the recommended dose after the inclusion of a predetermined sample size of n patients.

O’Quigley and Shen [1] described the need for an initial escalation stage within the framework of sequential likelihood estimation, due to the fact that the likelihood equation fails to have a solution on the interior of the parameter space in the absence of some heterogeneity (at least one toxic and one non-toxic response) in the observed responses. They recommended including an initial stage utilizing traditional or non-traditional up-and-down schemes: that is, starting at the lowest available dose, three patients are treated and only if all three fail to experience a DLT do we escalate to a higher dose level. As soon as the first dose-limiting toxicity (DLT) is observed, the first stage is closed and the second stage is subsequently opened based on CRM modeling, using the data accumulated thus far in the trial. Even though the first stage is closed, the toxicity response information accrued by the initial scheme is retained and used in the second stage.

Some, although very little, evidence of the efficiency of the CRM-L was provided in O’Quigley, Paoletti and Maccario [2] and Paoletti, O’Quigley and Maccario [6] by comparing the performance of CRM-L to the optimal design. It has been established that the CRM has superior statistical properties to those of the traditional escalation schemes [7]. The papers of O’Quigley, Paoletti and Maccario [2] and Paoletti, O’Quigley and Maccario [6] compared the performance of the CRM-L to the optimal method for very few dose-toxicity scenarios. Model-based dose-finding designs, such as CRM-L, require some clinical, as well as statistical, specifications prior to its implementation. These specifications can vary from trial to trial, depending on the clinical objective and practical constraints of the study. In general, there is a perception among clinicians that the performance of model-based designs, and in particular the CRM, is sensitive to one or more of these specifications. An important question that arises is that of, having specified some CRM design, how well does it perform on average across some given class of true, unknown situations. The finite sample optimal method is a tool that can be used as a benchmark in answering this question. In this article, we demonstrate through extensive simulation, that recommended specification choices for the two-stage CRM produce results very close to the optimal benchmark on average across a broad range of scenarios. An accuracy index serves as a measure of design comparison of CRM-L’s performance to the optimal design. In Section 2, we provide a discussion of the design specifications recommended for implementing CRM-L. In Section 3, we give the details of the nonparametric optimal design. Section 4 provides simulation results comparing the CRM-L to the optimal design. Finally, in Section 5, we conclude with some discussion.

2. Specifications for the two-stage CRM

A CRM dose-finding design requires particular design specifications laid out prior to the beginning of the trial. These specifications involve both clinical and statistical components. The clinical elements of the design adhere to the clinical and practical goals of the trial and include the sample size, the target DLT rate and the number of dose levels. These parameters are usually specified by the clinician and are referred to by Cheung [8] as “clinician-input parameters.” Our goal here is not to provide a discussion of how these guidelines are chosen, but rather to assess the overall performance of the two-stage CRM relative to an optimal benchmark, given various choices of these clinical specifications. The statistical aspects of the CRM include the choice of initial guess of DLT probabilities, also known as the skeleton, the parameterized form of the working model and the initial escalation scheme used in the first stage. Below, we provide a brief review on the choice of each of these statistical design components. Once the specifications of the design (clinical and statistical) have been decided, the optimal benchmark can be used as a comparative measure of performance over an extensive range of situations. The primary objective of the simulation studies is to emphasize the limited room for improvement that exists, on average, by using practical recommendations for CRM design specifications, such as a one-parameter power model and a “reasonable” skeleton. It is possible to find a set of specifications, particularly a skeleton, that will lead the CRM-L to outperform the optimal method in specific dose-toxicity relations. Although a particular CRM-L design may appear superior to the optimal in a certain scenario, it will be inferior on average, and may even exhibit poor operating characteristics in many other scenarios. Although it is possible for CRM-L to outperform the optimal method in isolated cases, the optimal method can be considered a benchmark for overall performance across a set of toxicity scenarios.

2.1 Choice of parameterized working model

As previously mentioned, the CRM begins by assuming a parameterized working model, denoted by ψ(d_i, a), for the true DLT probability. Shen and O’Quigley [9] showed that a one-parameter model is sufficient to accurately estimate the DLT probability at a prespecified dose level in large samples, even in the presence of model misspecification. This one-parameter model is monotonic in both dose level, d_i, and the parameter, a. There are many choices possible for ψ but a commonly used function in CRM designs is the power model

$$\psi (d_i,a)={\alpha }_i^{exp(a)}$$ (1)

where α_i are the standardized units representing the discrete dose levels d_i. Here, 0 <α₁<…<α_k<1 and −∞< a<∞. This model is a simple choice that has demonstrated excellent operating characteristics in a wide variety of practical scenarios [1 – 3, 8, 10, 11]. O’Quigley, Pepe and Fisher [4] suggested that the α_i, i=1,…, k be chosen to reflect a priori assumptions about the DLT probabilities corresponding to each dose level. A physical interpretation of the d_i is not necessary so long as they represent a monotone increasing set, so they can simply be labeled by α_i. It should be noted that the working model is not expected to represent the entire dose-toxicity curve. It is sufficient that the parameterized working model be flexible enough to allow for estimation of the dose-toxicity curve at and around the MTD. With regards to maximum likelihood estimation, the α_i ‘s correspond to a class of invariant models characterized by a power transformation so that replacing α_i with another set, ${\alpha }_i^{\ast }={\alpha }_i^m$; m> 0 will result in identical operating characteristics. Therefore, it is difficult to attribute any real meaning to the α_i. The spacing between α_i values will have an impact on performance and we discuss this idea further in the following section. Paoletti and Kramar [10] provide a comprehensive comparison of various working model choices in the CRM. They conclude that a one-parameter model should be used in a non-Bayesian setting and recommend the use of the power model (1).

2.2 Choice of skeleton

Preferably, the skeleton values would be chosen in such a way that represents the clinician’s beliefs regarding the DLT probabilities at each dose level. Unfortunately, in practice, investigators have little or no information as to whether a selected skeleton is sensible due to the fact that the true dose-toxicity curve is unknown. Therefore, skeleton choice is to a large degree arbitrary. Fortunately, it has been shown by several authors [12, 13] that CRM designs are robust and efficient with the implementation of “reasonable” skeletons. O’Quigley and Zohar [13] define a “reasonable” skeleton as one that demonstrates good robustness properties in terms of its operating characteristics. It is relatively straightforward to have an intiutive idea about whether or not a skeleton is “reasonable.” For instance, the “unreasonable” skeleton α₁= 0.12, α₂= 0.20, α₃= 0.21, α₄= 0.22, α₅= 0.36 would have trouble distinguishing between levels 2, 3 and 4. Of course, it would be beneficial to have a more precise definition for “reasonable” and “unreasonable,” yet it is not easy to find a simple solution that works in all situations. We can rely on the algorithm of Lee and Cheung [3] to generate adequate spacing between skeleton values at neighboring doses, without having to rely on a clinician’s estimate at every dose level. In fact, the clinician can provide his or her opinion on which dose he or she believes to possess the target DLT rate. This would be the investigators belief of the prior MTD, ν. Using this information, the target DLT rate, θ, the number of doses, k, and a “spacing” measure, δ, referred to as the indifference interval half-width [3], we can generate skeleton values using the getprior function in R package dfcrm. (i.e. getprior(δ, θ, ν, k)).

2.3 Initial cohort size

The clinical motivation underlying a two-stage CRM is the desire of a clinician to be more conservative in escalation than the original CRM, which does not begin at the lowest level, but rather at a level believed by the investigator to be the MTD. Such a starting dose could possibly be more toxic than that which the clinicians are comfortable beginning the trial. Mathematically, with regards to pure-likelihood based designs like the two-stage CRM, the necessity of an initial stage was described by O’Quigley and Shen [1], since the likelihood fails to have a solution in the absence of at least one toxic and one non-toxic response. Therefore, in order to obtain this required heterogeneity in the observed responses, an initial escalation scheme, such as the standard 3+3 inclusion, could be implemented. The first cohort of patients is enrolled at the lowest dose, and if none experience a DLT, the next entered cohort is enrolled on the next highest level. This process continues until the first DLT is observed. Once some heterogeneity in the responses has been observed, the model-based second stage begins. Another specification for two-stage CRM is how rapidly to escalate in the early part of the trial, which is based on how many patients to include in each cohort of the initial escalation scheme. This could be done in groups of 1, 2, or 3 patients, and we include each of these various cohort sizes in our simulation results comparing two-stage CRM to the optimal benchmark.

Our objective here is not to contrast the advantages and disadvantages of implementing a particular set of these specifications over another. This has been undertaken in previously published literature on the CRM [9, 10, 12, 13]. Plus, some of these specifications will vary from trial to trial based purely on the preference of the clinical and statistical team, as well as other factors. The focus of this paper is to emphasize the idea that utilizing the simple set of recommended specifications for the CRM-L outlined in this section will result in operating characteristics close to that of the optimal method on average. In the next section, we define “close to optimal” in terms of the efficiency of CRM-L relative to the optimal benchmark.

3. Nonparametric optimal benchmark

Although the nonparametric optimal design outlined in O’Quigley et al. [2] is not useful as a practical design, it can be used as a benchmark for efficiency. A fundamental assumption for the optimal design is the notion that a patient who experiences a DLT at a particular dose level, would necessarily experience a DLT at any higher level. Similarly, if a patient tolerates a given dose level, he or she would also tolerate any lower level. These assumptions lead to the development of complete and partial information, ideas vital to the derivation of a nonparametric optimal design. It is worth keeping in mind that for drugs or treatments which fall outside of this prescription, the whole theory falls down so that, although very general and widely applicable, the nonparametric optimal design does not apply universally.

3.1 Partial information

During the course of a Phase 1 trial, each patient receives a dose and is observed for the presence or absence of toxicity only at that dose. Therefore, we can only observe information that is incomplete. For instance, consider a trial investigating six available dose levels. Suppose a patient is given dose level 4 and experiences a toxic reaction. The monotonicity assumption implies that a toxicity would necessarily be observed at dose levels 5 and 6. We will not have any information regarding whether the patient would have suffered a toxic response for any dose below level 4. Conversely, should dose 3 be deemed safe for an enrolled patient, then we can infer that he or she would experience a nontoxic outcome at dose levels 1 and 2. However, any information concerning whether the patient would have had a DLT had he or she been given any dose above level 3 is unknown. The following table illustrates partial information:

Dose Levels	1	2	3	4	5	6
DLT	*	*	*	1	1	1
DLT	0	0	0	*	*	*

3.2 Complete information

For each patient, if we knew the response at each available dose level, we would have complete information. In simulating trial data, we can generate each patient’s toxicity tolerance from which we can observe responses at all available dose levels. For example, suppose we have a patient that experiences a DLT from dose level 3. Complete information is summarized in the following table:

Dose levels	1	2	3	4	5	6
DLT	0	0	1	1	1	1

A random number, representing the toxicity tolerance of a patient, can be generated over (0,1) and compared to the probability of toxicity at each dose level. These random numbers can be drawn from a uniform (0,1) distribution U. Each patient j, j = 1,…, n has an outcome, u_j, generated from U. Based on these outcomes and the probability of toxicity, R(d₁),…, R(d_k) at each of the k doses, it can be determined whether a patient would see a DLT at any level. A patient will have a toxic outcome if treated at dose level i if u_i≤ R(d_i). Table 1 presents the complete toxicity vectors of 25 simulated patients for true toxicity probabilities R(d₁) = 0.04, R(d₂) = 0.07, R(d₃) = 0.20, R(d₄) = 0.35, R(d₅) = 0.55 and R(d₆) = 0.70. Patient 7 for instance has a toxicity tolerance of u₇= 0.238. Therefore, he or she will experience a non-toxic response at dose levels 1, 2, and 3 because u₇> R(d_i) for i=1, 2, 3, and suffer a toxic response at dose levels 4, 5, and 6 because u₇< R(d_i) for i=4, 5, and 6.

Table 1.

Simulated Phase 1 trial of complete information

Patient	Tolerance	Toxicity at dose level i
j	uj	1	2	3	4	5	6
1	0.004	1	1	1	1	1	1
2	0.751	0	0	0	0	0	0
3	0.563	0	0	0	0	0	1
4	0.429	0	0	0	0	1	1
5	0.198	0	0	1	1	1	1
6	0.995	0	0	0	0	0	0
7	0.238	0	0	0	1	1	1
8	0.509	0	0	0	0	1	1
9	0.381	0	0	0	0	1	1
10	0.053	0	1	1	1	1	1
11	0.005	1	1	1	1	1	1
12	0.883	0	0	0	0	0	0
13	0.944	0	0	0	0	0	0
14	0.579	0	0	0	0	0	1
15	0.241	0	0	0	1	1	1
16	0.840	0	0	0	0	0	0
17	0.080	0	0	1	1	1	1
18	0.267	0	0	0	1	1	1
19	0.688	0	0	0	0	0	1
20	0.297	0	0	0	1	1	1
21	0.196	0	0	1	1	1	1
22	0.962	0	0	0	0	0	1
23	0.578	0	0	0	0	0	1
24	0.432	0	0	0	0	1	1
25	0.657	0	0	0	0	0	1
	R̂(di)	0.08	0.12	0.24	0.40	0.56	0.80

The information in Table 1 is not obtainable from a trial due to the fact that we cannot, in reality, observe a patient’s toxicity tolerance. We can however simulate complete vectors of toxicity information and use them to estimate the toxicity probabilities by using the sample proportion of observed toxicities at each dose. That is, we can estimate R(d_i), i=1…, k from the sample proportions R̂(d_i) and use them to select the MTD as the dose that minimizes |R̂(d_i)−|θ. The last row of Table 1 gives the sample proportions of the simulated trial. After 25 patients, the recommended dose is level 3, with an estimated toxicity probability of 0.24, which is closest to a chosen target toxicity rate of 0.20. It can be shown that R̂(d_i) is an unbiased estimator of R(d_i) and that the variance of R̂(d_i) achieves the Cramer-Rao lower bound. In this sense, the design can be considered optimal.

3.3. Accuracy measure

One way to assess how well a method is performing is by simply observing in what percentage of trials a method is recommending the true MTD. This is referred to as the percentage of correct selection (PCS). A more thorough assessment will involve looking at the entire distribution of the selected doses in order to see how often a method recommends doses other than the correct one as the MTD. For instance, in order to adhere to certain ethical considerations presented by Phase 1 trials, it is appropriate to evaluate how often a method selects doses above the MTD (i.e. overly toxic doses). It is important to have some measure of accuracy that represents the distribution of doses selected as the MTD. Here, we rely on the accuracy index of Cheung [8] given by

$${\mathrm{A}}_n=1-k\times \frac{{\displaystyle \sum _{i=1}^k}{\rho }_i\times p_i}{{\displaystyle \sum _{i=1}^k}{\rho }_i}$$

where p_i= Pr(dose i is selected as the MTD) and ρ_i is a distance measure between the true probability of toxicity, R(d_i), at dose level i and the target toxicity rate θ. Examples of the distance measure include absolute distance, ρ_i=|R(d_i)−θ| or squared distance, ρ_i = (R(d_i)−θ². In this article, we restrict our attention to absolute distance. The distance measure is a description of the true dose-toxicity curve, with the denominator of A_n representing the extent to which the toxicity probabilities deviate from the target. Therefore, steeper curves will have larger values of ${\displaystyle \sum _{i=1}^k}{\rho }_i$ than will flatter curves. For instance, consider the two dose-toxicity curves given below, and suppose we are to target θ= 0.20.

	1	2	3	4	5	6
Curve 1	0.02	0.05	0.09	0.2	0.55	0.7
Curve 2	0.08	0.12	0.18	0.2	0.25	0.33

Using absolute distance as our distance measure, ρ₁= 0.18, ρ₂= 0.15, ρ₃= 0.11, ρ₄= 0.00, ρ₅= 0.35, ρ₆= 0.50 and Σ_iρ_i=1.29. Curve 2 is flatter around the MTD and has Σ_iρ_i = 0.40. This is a numerical reflection of the obvious fact that it is a more serious error for a method to select dose 5 under Curve 1 than under Curve 2. The p_i measures the proportion of times each dose level is selected as the MTD. For instance, given below is the recommendation distribution for 5000 runs of the optimal method when the target is 0.20 for Curve 1 above.

	1	2	3	4	5	6
True DLT Rates	0.02	0.05	0.09	0.20	0.55	0.70
Proportion MTD selection	0.00	0.03	0.18	0.76	0.03	0.00

In this case, p₁= 0.00, p₂= 0.03, p₃= 0.18, p₄= 0.76, p₅= 0.03, p₆= 0.00. The accuracy index, A_n, provides a numerical measure of the distribution of MTD recommendation. Its maximum value is 1 with larger values (close to 1) indicating that the method possesses high accuracy. In the next section, we will compute the accuracy measure for CRM-L designs in various situations and compare it to that of the non-parametric optimal design.

How well a method is performing relative to another can be quantified by efficiency. There are many ways to measure efficiency, some of which can be found in O’Quigley, Paoletti and Maccario [2], Paoletti et al. [6] and Cheung [8]. In Chapter 8 of Cheung [8], the author defines the efficiency of CRM designs in terms of the ratio of average PCS for CRM relative to the optimal method over several true scenarios. This definition of efficiency appears to be not fully satisfactory in that it solely considers PCS, which takes into account only what happens at the MTD, and ignores recommendation percentages at other levels. We define efficiency as the ratio of the accuracy index of CRM-L to that of the optimal design, which considers recommendation percentages across the entire dose range.

In a single dose-toxicity scenario considered in Paoletti et al. [6], CRM was seen to be 93% efficient relative to the optimal. Cheung [8] describes CRM designs as being “quite efficient” and “close to optimal” based on efficiency measures that are approximately 82% to 86% of the optimal benchmark. Here, we define “close” to optimal as achieving an efficiency measure larger than 90%, on average, over all scenarios considered. Although the notion of “close” is subjective, this threshold seems reasonable when considering the fact that CRM-L is making MTD recommendations based on partial information, while the optimal method benefits from complete information. Simulation results in the following section will demonstrate that, on average, across many scenarios, CRM-L is close to optimal.

4 Simulations

4.1 Set-up

In this section, we present simulation results in order to get an idea of how well the CRM-L is performing when compared to the optimal design. For each simulated trial using the optimal method, complete information was generated for a fixed sample size of n patients, from which the sample proportions R̂(d_i) were calculated. These values were used to select the MTD as the dose that minimizes |R̂(d_i)−θ| at the end of each trial. The distribution of MTD selection for the optimal method was calculated by tabulating the proportion of simulated trials in which dose i was selected as the MTD. The PCS is this proportion for the true MTD.

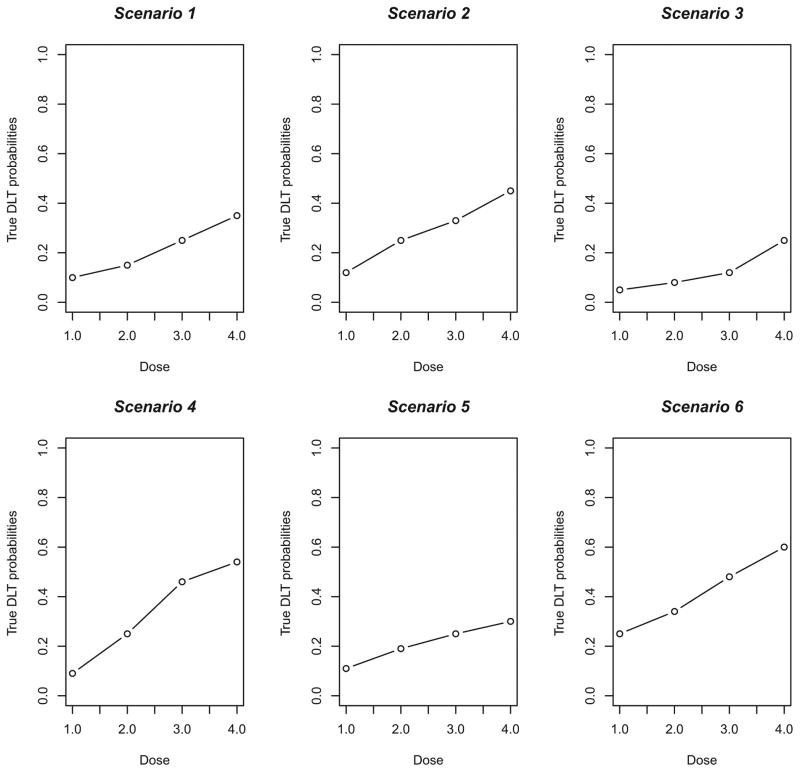
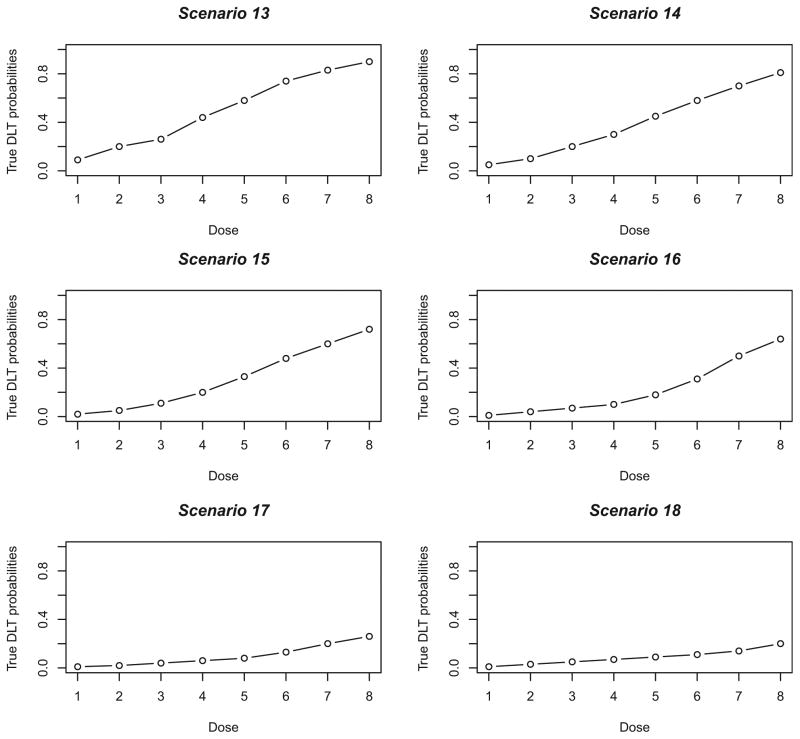
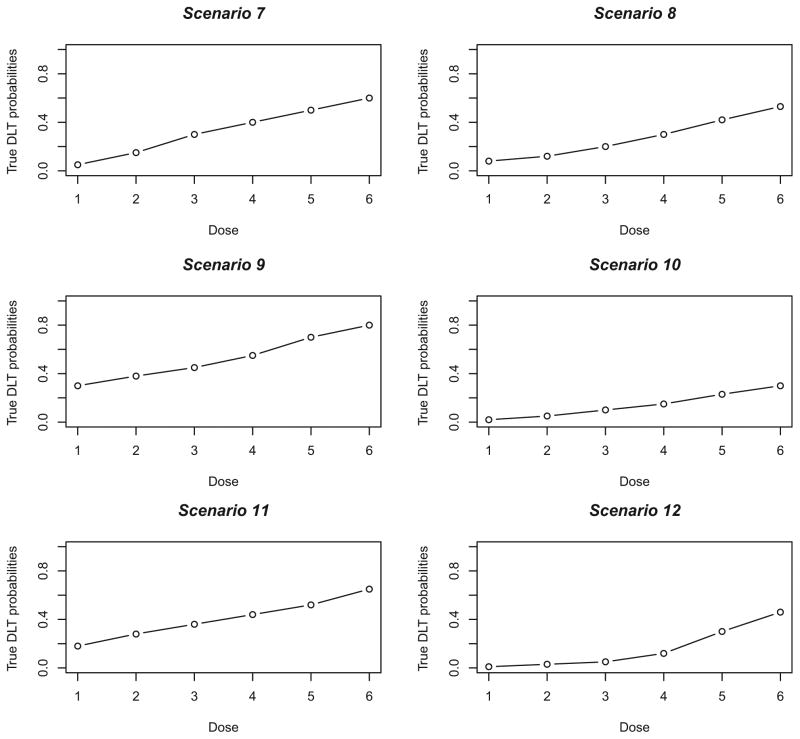
Obviously, it is not possible to look at all situations, but the true DLT probabilities chosen reflect a somewhat wide range of toxicity scenarios, in that there is a mixture of steep (i.e. Scenarios 4, 7), flat (i.e. Scenarios 5, 11, 13) and intermediate (i.e. Scenarios 2, 8, 14) dose-toxicity curves. We also varied the location of the MTD within the dose space, including curves (i.e. Scenarios 3, 6, 9, 10, 18) where the MTD is at the extremes (i.e. highest or lowest level). The true DLT probability scenarios are graphically represented in Figures 1 – 3. We present a variety of specifications for the clinician-input parameters by including various number of dose levels (k), sample sizes (n), target toxicity rates (θ) and initial cohort sizes in the first stage. Specifically, for Scenarios 1 – 6, k= 4 dose levels are being investigated, the target toxicity rate is θ= 0.25, the fixed sample size for each simulated trial is n= 20, and the initial cohort size is 3 patients. For Scenarios 7 – 12, there are k= 6 dose levels, the target toxicity rate is θ= 0.30, the fixed sample size for each simulated trial is n= 25 and the initial cohort size is 2 patients. Finally, for Scenarios 13 – 18, k= 8, θ= 0.20, n= 30, and initial cohort size is 1. In each simulated trial, escalation is restricted to no more than one level. For each scenario, 10,000 trials were simulated under the true toxicity probabilities given next to scenario number in Tables 3 – 5, with the true MTD indicated in bold type. Overall, the simulations study the operating characteristics, in relation to the optimal method, of two sets of specifications for CRM-L, as follows:

Figure 1.

True dose–toxicity curves for Scenarios 1–6.

DLT: dose-limited toxicity

Figure 3.

True dose–toxicity curves for Scenarios 13–18.

DLT: dose-limited toxicity.

Table 3.

Compared proportions of MTD recommendation and accuracy measure for the optimal design and CRM-L after 10,000 simulated trials. The true MTD is indicated in bold type. The target toxicity rate is 25% and the fixed sample size for each trial is 20 patients. First stage cohort size is 3.

Dose	1	2	3	4	A(n)
Scenario 1	0.10	0.15	0.25	0.35
CRM-L(A)	0.06	0.26	0.36	0.32	0.240
CRM-L(B)	0.07	0.26	0.39	0.28	0.266
Optimal	0.06	0.20	0.43	0.31	0.321
Scenario 2	0.12	0.25	0.33	0.45
CRM-L(A)	0.21	0.42	0.27	0.10	0.324
CRM-L(B)	0.20	0.43	0.28	0.09	0.351
Optimal	0.18	0.46	0.28	0.08	0.391
Scenario 3	0.05	0.08	0.12	0.25
CRM-L(A)	0.01	0.05	0.22	0.73	0.701
CRM-L(B)	0.00	0.05	0.24	0.70	0.671
Optimal	0.01	0.03	0.19	0.77	0.750
Scenario 4	0.09	0.25	0.46	0.54
CRM-L (A)	0.19	0.59	0.20	0.03	0.513
CRM-L (B)	0.18	0.59	0.21	0.02	0.523
Optimal	0.13	0.73	0.13	0.01	0.688
Scenario 5	0.11	0.19	0.25	0.30
CRM-L (A)	0.11	0.29	0.28	0.33	0.217
CRM-L (B)	0.11	0.30	0.31	0.28	0.243
Optimal	0.10	0.26	0.29	0.36	0.251
Scenario 6	0.25	0.34	0.48	0.60
CRM-L (A)	0.67	0.27	0.06	0.01	0.759
CRM-L (B)	0.66	0.27	0.06	0.00	0.758
Optimal	0.64	0.30	0.06	0.00	0.753

Avg. A(n): CRM-L (A) = 0.459; CRM-L(B) = 0.469; Optimal = 0.526

Table 5.

Compared proportions of MTD recommendation and accuracy measure for the optimal design and CRM-L after 10,000 simulated trials. The true MTD is indicated in bold type. The target toxicity rate is 20% and the fixed sample size for each trial is 30 patients. First stage cohort size is 1.

Dose	1	2	3	4	5	6	7	8	A(n)
Scenario 13	0.09	0.20	0.26	0.44	0.58	0.74	0.83	0.90
CRM-L (A)	0.19	0.49	0.28	0.04	0.00	0.00	0.00	0.00	0.858
CRM-L (B)	0.21	0.46	0.29	0.04	0.00	0.00	0.00	0.00	0.848
Optimal	0.14	0.48	0.35	0.03	0.00	0.00	0.00	0.00	0.868
Scenario 14	0.05	0.10	0.20	0.30	0.45	0.58	0.70	0.81
CRM-L (A)	0.02	0.23	0.49	0.24	0.02	0.00	0.00	0.00	0.788
CRM-L (B)	0.02	0.23	0.48	0.24	0.02	0.00	0.00	0.00	0.784
Optimal	0.01	0.15	0.55	0.28	0.01	0.00	0.00	0.00	0.818
Scenario 15	0.02	0.05	0.11	0.20	0.33	0.48	0.60	0.72
CRM-L (A)	0.00	0.03	0.25	0.51	0.20	0.01	0.00	0.00	0.744
CRM-L (B)	0.00	0.03	0.25	0.51	0.20	0.01	0.00	0.00	0.742
Optimal	0.00	0.01	0.19	0.58	0.22	0.01	0.00	0.00	0.778
Scenario 16	0.01	0.04	0.07	0.10	0.18	0.31	0.50	0.64
CRM-L (A)	0.00	0.00	0.04	0.20	0.49	0.26	0.02	0.00	0.627
CRM-L (B)	0.00	0.00	0.03	0.20	0.50	0.24	0.02	0.0	0.625
Optimal	0.00	0.00	0.02	0.11	0.55	0.31	0.01	0.00	0.664
Scenario 17	0.01	0.02	0.04	0.06	0.08	0.13	0.20	0.36
CRM-L (A)	0.00	0.00	0.01	0.03	0.09	0.26	0.46	0.15	0.546
CRM-L (B)	0.00	0.00	0.00	0.02	0.09	0.28	0.44	0.17	0.526
Optimal	0.00	0.00	0.00	0.01	0.04	0.22	0.58	0.17	0.635
Scenario 18	0.01	0.03	0.05	0.07	0.09	0.11	0.14	0.20
CRM-L (A)	0.00	0.00	0.01	0.04	0.08	0.13	0.25	0.48	0.619
CRM-L (B)	0.00	0.00	0.01	0.03	0.07	0.12	0.23	0.53	0.654
Optimal	0.00	0.00	0.00	0.01	0.03	0.08	0.21	0.66	0.769

Avg. A(n): CRM-L (A) = 0.697; CRM-L(B) = 0.696; Optimal = 0.755

• CRM-L (A) – The power model, $\psi (d_i,a)={\alpha }_i^{exp(a)}$, is used to model toxicity probabilities, using a “reasonable” skeleton, as defined in Section 2.2. For instance, in Scenarios 1 – 6, we used α₁ = 0.10, α₂ = 0.20, α₃ = 0.30 and α₄ = 0.40. The spacing of this skeleton was investigated in O’Quigley and Zohar [13] and exhibited good operating characteristics across a broad range of true dose-toxicity scenarios. We took a similar approach in Scenarios 7 – 18, adjusting for the number of dose levels being investigated. All skeleton values used in the simulation results are provided in Table 2.

• CRM-L (B) – Again, the power model is used to model DLT probabilities with a skeleton chosen according to the algorithm of Lee and Cheung [3]. These values were generated using the getprior function in R package dfcrm. (i.e. getprior(δ, θ, ν, k)). For Scenarios 1 – 6, we used getprior(0.06,0.25,2,4)).

Table 2.

Skeleton values for each CRM-L design considered under each of the 18 scenarios of true DLT probabilities.

Skeletons for Scenarios 1 – 6
Dose	1	2	3	4
CRM-L(A)	0.10	0.20	0.30	0.40
CRM-L(B)	0.14	0.25	0.38	0.50
Skeletons for Scenarios 7 – 12
Dose	1	2	3	4	5	6
CRM-L(A)	0.10	0.20	0.30	0.40	0.50	0.60
CRM-L(B)	0.10	0.15	0.22	0.30	0.38	0.46
Skeletons for Scenarios 13 – 18
Dose	1	2	3	4	5	6	7	8
CRM-L (A)	0.10	0.20	0.30	0.40	0.50	0.60	0.70	0.80
CRM-L (B)	0.03	0.07	0.13	0.20	0.29	0.38	0.47	0.55

All simulation results for the CRM-L designs were carried out using the crmsim function in R package dfcrm, while R code for the optimal method is available for download at www.faculty.virginia.edu/model-based_dose-finding.

4.2 Results

The simulation results assess how well the CRM-L designs and the nonparametric optimal design are performing in two ways. One is by simply observing the distribution of dose selection as the MTD. The second is measured by the accuracy index described in the previous section. Tables 3 – 5 compare the distribution of selected doses for the CRM-L designs and the optimal design, as well as provide the value of A_n. There are several scenarios (i.e. 5, 6, 10) in which at least one CRM-L design yields a PCS approximately equal to that of the optimal method. It is interesting to note, however, that in these scenarios, the CRM-L designs result in a different accuracy benchmark than that of the optimal design. This indicates that it matters what doses are being recommended by a method when it fails to correctly recommend the MTD. In Scenario 10, for example, CRM-L (A) selects the dose directly below the MTD, a dose with a DLT probability just 0.07 less than the target rate, 29% of the time, while the optimal does this 31% of the time. In other words, the optimal method missed more often on a dose that was closer to the target than did the CRM-L (A), which results in the different accuracy index values. Despite this fact, the accuracy indices of the CRM-L designs are quite close to that of the optimal, again indicating that the capacity for improvement of a design over the CRM-L is quite limited in these scenarios.

In other scenarios (1, 2, 3, 8, 9, 16), the CRM-L recommends results in a PCS very close (within 5%) to that of the optimal method. Specifically, in Scenario 1, the PCS is 39% and 43% for the better performing CRM-L design (CRM-L (B)) and the optimal method, respectively. The accuracy index for the CRM-L designs yielded values of 0.240 and 0.266, compared to 0.321 for the optimal method. In Scenarios 4, 12 and 18, the performance of the CRM-L diminishes relative to the optimal benchmark. The difference in recommendation proportions for the CRM-L and optimal design widens. In Scenario 4, CRM-L (A) and (B) recommend the true MTD in 59% of simulated trials, whereas the optimal method does so 73% of the time. Similarly, in Scenario 12, the recommendation percentages are 54% for the better performing CRM-L design and 71% for the optimal. These disparities are again reflected in measuring accuracy. Even in these cases where the CRM performs less well, it is recommending the MTD, or a neighboring dose (MTD−1 or MTD+1), in a large percentage of trials. For example, in Scenario 18, keeping in mind that the target rate is 0.20, CRM-L (B) recommends, as the MTD, doses with DLT probabilities between 0.14 and 0.20 in 76% of the trials.

4.3 Super-optimality

There are some scenarios (5 and 13) in which one or more of the CRM-L designs yield a higher PCS than the optimal. It should be noticed in these scenarios that, while the PCS may be higher for CRM-L designs, the accuracy indices are lower than the optimal after accounting for the entire MTD selection distribution. Scenarios 6 and 10 are the only situations of those investigated in which at least one CRM-L design is “super-optimal” in that it has a higher PCS and accuracy index than the optimal design. In this case, it is important to keep in mind that the optimal design is non-parametric. The CRM utilizes parametric assumptions, which could lead to information at one level providing information about all other levels. For instance, the working model and the true situation could be very similar or related by some power transformation. This is actually the case in Scenario 10. CRM-L (B) results in a PCS that is 7% higher than that of the optimal method. A closer examination of the skeleton of CRM-L (B) reveals that the true DLT probabilities in this scenario are approximately equal to the skeleton raised to the exp(0.46) power, meaning that a single value of the parameter a nearly exactly produces the true dose-toxicity curve at every level. This scenario provides evidence that improving on the finite sample optimal design requires extraneous knowledge. The knowledge in this case comes in the form of a strong parametric assumption that, in almost all practical cases, is unverifiable. It is also worth pointing out that this skeleton is part of the worse performing CRM-L design in Scenario 11, so that super-optimality is almost certainly very specific to certain scenarios, and cannot be broadened to a class of scenarios. This point is reflected in the average accuracy index values given at the bottom of each table. Although CRM-L is slightly super-optimal in Scenario 6, on average it is inferior to the optimal method across Scenarios 1 – 6, but not by much. The average accuracy index is approximately 0.53 for the optimal and 0.46 to 0.47 for the CRM-L. Similar conclusions can be made with regards to the other scenario sets as well. The “most” super-optimal case is CRM-L (B) in Scenario 10, yet overall in Scenarios 7–12, CRM-L (B) yields a lower accuracy index on average than CRM-L (A). In fact, CRM-L (B) has a lower accuracy index than CRM-L (A) in every scenario with the exception of the super-optimal Scenario 10.

Another case may be that a particular skeleton encourages experimentation at some level. For instance, consider a CRM-L design in which a skeleton of (0.0001, 0.20, 0.85, 0.90, 0.95, 0.99) is used, and suppose the target DLT rate is 0.20. This seems to be a very poor design, and will likely have poor operating characteristics if the true MTD is any dose other than level 2. If the true MTD is level 2, however, this design will probably do very well and, most likely, beat the optimal. This does not appear to be the case in any of the eighteen scenarios considered here, so we provide an example. Consider the two scenarios in Table 6 with 5 dose levels and a target DLT rate of = 0.θ 25. In both scenarios, we ran 10,000 simulated trials of n= 20 patients using the power model with two different skeletons. Skeleton 1 is (0.14, 0.30, 0.50, 0.66, 0.79) and Skeleton 2 is (0.10, 0.20, 0.30, 0.40, 0.50). Skeleton 1 is quite close to the true DLT probabilities at levels 1 and 2. Further, the gap between the skeleton at level 1 (0.14) and level 2 (0.30) and the gap between 0.30 and the skeleton at level 3 (0.50) is sufficiently large to cause the method to home in on level 2, which is closest to the target rate of 0.25. Consequently, Skeleton 1 produces a super-optimal PCS of 48% in Scenario 1. Skeleton 2 possesses reasonable spacing between adjacent levels and produces a PCS of 42%. Scenario 2 in Table 6 illustrates the idea that a super-optimal result should be taken as a “red-flag” rather than with the optimism of being a superior design. In Scenario 2, the MTD is now at the highest level, dose 5. Using the same two skeletons as Scenario 1, 10,000 simulated trials again produced a result close to that of the optimal (within 5%) with Skeleton 1, but performance significantly diminished with Skeleton 2. This result reiterates the fact that a super-optimal design in one scenario is not expected to be super-optimal across a range of scenarios. In fact, a design that is super-optimal will produce results well below what is optimal in other scenarios. This is again reflected in the average accuracy measure across the two scenarios. Although Skeleton 2 is super-optimal in Scenario 1, it possesses a lower overall mean accuracy index (0.578) than Skeleton 1 (0.629), with Skeleton 1 average index being close to optimal (0.662). Super-optimality is not an indication that the CRM-L design used in this scenario is a “better” design than the optimal. Rather, this should be considered an isolated case in which it is possible to beat the optimal.

Table 6.

Compared proportions of MTD recommendation and accuracy measure for the optimal design and CRM-L after 10,000 simulated trials. The true MTD is indicated in bold type. The target toxicity rate is 25% and the fixed sample size for each trial is 20 patients. First stage cohort size is 3.

Dose	1	2	3	4	5
Scenario 1	0.15	0.25	0.35	0.45	0.60	A(n)
Skeleton 1	0.27	0.42	0.22	0.08	0.01	0.543
Skeleton 2	0.28	0.48	0.20	0.04	0.00	0.627
Optimal	0.25	0.43	0.24	0.07	0.00	0.580
Scenario 2	0.01	0.05	0.10	0.15	0.25
Skeleton 1	0.00	0.01	0.07	0.27	0.66	0.714
Skeleton 2	0.00	0.02	0.16	0.37	0.45	0.529
Optimal	0.00	0.01	0.07	0.23	0.70	0.743

Avg. A(n): Skeleton 1 = 0.629; Skeleton 2 = 0.578; Optimal = 0.662

Assessing the overall performance of CRM-L across many practical situations indicates that it is close to optimal, on average, using simple parametric models and reasonable skeletons, even in the presence of model misspecification. The average accuracy index measure is 0.595 for CRM-L designs and 0.655 for the optimal. The efficiency of the CRM-L designs in terms of average accuracy index can be computed by 0.595/0.655 = 0.909, indicating that CRM-L is approximately 91% efficient in terms of its overall performance against the optimal, for sample sizes between 20 and 30 patients.

5 Conclusion

In this article, we compared the overall performance two-stage, likelihood-based continual reassessment method (CRM-L) with the nonparametric optimal method outlined by O’Quigley, Paoletti and Maccario [1] through extensive simulation. We have studied a wide variety of situations, and those presented here are very typical and have not been cherry picked in any way. A large number of other situations, and indeed (upon request) any specific situation, can be provided to any interested reader, or can be generated using the R code on the website provided in Section 4.1. The results presented here portray the CRM-L as a Phase 1 trial design upon which the capacity for improvement is limited on average across many scenarios, even for small samples. In literature on Phase 1 trial methods, higher PCS is often equated with better performance. The simulation results in this article show that the CRM-L may be exhibiting “better performance” with a PCS of 29% (Scenario 11) than with a PCS of 55% (Scenario 12), because it is closer to the performance of the optimal in the former case than in the latter. If the optimal can only achieve a PCS of 30%, and CRM-L achieves 29%, how can we expect better performance in this particular case, without incorporating some extraneous information that is not appropriate across a broad class of situations? As was previously noted, outperforming the optimal requires skeletons that strongly encourage experimentation at a particular level and/or strong parametric assumptions. Identifying a set of specifications that improves upon this 30% would likely have one of these two properties, hindering performance in other scenarios and ultimately being inferior to the optimal on average. Super-optimality should not be considered a reflection of exceptional design performance, but rather a warning that the chosen design is benefiting from extraneous knowledge that is not likely to produce good operating characteristics across a broad range of scenarios.

Figure 2.

True dose–toxicity curves for Scenarios 7–12.

DLT: dose-limited toxicity.

Table 4.

Compared proportions of MTD recommendation and accuracy measure for the optimal design and CRM-L after 10,000 simulated trials. The true MTD is indicated in bold type. The target toxicity rate is 30% and the fixed sample size for each trial is 25 patients. First stage cohort size is 2.

Dose	1	2	3	4	5	6	A(n)
Scenario 7	0.05	0.15	0.30	0.40	0.50	0.60
CRM-L (A)	0.00	0.16	0.46	0.28	0.09	0.01	0.564
CRM-L (B)	0.01	0.16	0.42	0.30	0.10	0.01	0.521
Optimal	0.00	0.18	0.55	0.23	0.05	0.00	0.641
Scenario 8	0.08	0.12	0.20	0.30	0.42	0.53
CRM-L (A)	0.00	0.05	0.24	0.42	0.24	0.05	0.482
CRM-L (B)	0.00	0.04	0.22	0.41	0.26	0.07	0.459
Optimal	0.00	0.03	0.25	0.47	0.21	0.03	0.552
Scenario 9	0.30	0.38	0.45	0.55	0.70	0.80
CRM-L (A)	0.63	0.26	0.10	0.01	0.00	0.00	0.829
CRM-L (B)	0.63	0.24	0.11	0.02	0.00	0.00	0.823
Optimal	0.65	0.25	0.09	0.01	0.00	0.00	0.842
Scenario 10	0.02	0.05	0.10	0.15	0.23	0.30
CRM-L (A)	0.00	0.00	0.01	0.10	0.29	0.59	0.758
CRM-L (B)	0.00	0.00	0.01	0.08	0.24	0.67	0.807
Optimal	0.00	0.00	0.01	0.08	0.31	0.60	0.771
Scenario 11	0.18	0.28	0.36	0.44	0.52	0.65
CRM-L (A)	0.19	0.38	0.27	0.12	0.03	0.00	0.534
CRM-L (B)	0.20	0.33	0.30	0.14	0.04	0.00	0.496
Optimal	0.20	0.40	0.27	0.10	0.02	0.00	0.546
Scenario 12	0.01	0.03	0.05	0.12	0.30	0.46
CRM-L (A)	0.00	0.00	0.00	0.14	0.54	0.32	0.598
CRM-L (B)	0.00	0.00	0.00	0.14	0.50	0.35	0.567
Optimal	0.00	0.00	0.00	0.12	0.71	0.17	0.745

Avg. A(n): CRM-L (A) = 0.628; CRM-L(B) = 0.612; Optimal = 0.684