Assessing the Goodness of Fit of Personal Risk Models

Abstract

We describe a flexible family of tests for evaluating the goodness of fit (calibration) of a pre-specified personal risk model to the outcomes observed in a longitudinal cohort. Such evaluation involves using the risk model to assign each subject an absolute risk of developing the outcome within a given time from cohort entry, and comparing subjects’ assigned risks with their observed outcomes. This comparison involves several issues. For example, subjects followed only for part of the risk period have unknown outcomes. Moreover existing tests do not reveal the reasons for poor model fit when it occurs, which can reflect misspecification of the model’s hazards for the competing risks of outcome development and death. To address these issues, we extend the model-specified hazards for outcome and death and use score statistics to test the null hypothesis that the extensions are unnecessary. Simulated cohort data applied to risk models whose outcome and mortality hazards agreed and disagreed with those generating the data show that the tests are sensitive to poor model fit, provide insight into the reasons for poor fit, and accommodate a wide range of model misspecification. We illustrate the methods by examining the calibration of two breast cancer risk models as applied to a cohort of participants in the Breast Cancer Family Registry. The methods can be implemented using the Risk Model Assessment Program (RMAP), an R package freely available at http://stanford.edu/~ggong/rmap/.

1. Introduction

Recent emphasis on personalized medicine has stimulated the development of models that specify an individual’s risk of a future adverse health outcome. Such a model uses the person’s covariates to calculate his/her hazard rates for future outcome development and death, and then combines these hazards into a probability of outcome development during a specified future risk period. Typically, clinical care (e.g., chemoprevention) decisions are based on short-term predictions (e.g., one-year, five-year, ten-year), with the length of the risk period short enough to allow useful assessment and comparison of a person’s risk for a future adverse outcome, given his/her risk factors at the time risk assessment. Longer projections (e.g. breast cancer risk by age 80 years for a woman who is currently aged 40 years) are less useful for two reasons. First, they require the assumption that her risk factors will not change during the extended future period. Second, validation of these predictions would require longitudinal follow-up of large numbers of subjects for long time periods, which often is infeasible.

For any given outcome and time period, the models differ in the personal risk factors they use, and how they handle the competing risk of death. For breast cancer within ten years, for example, the Breast Cancer Risk Assessment Tool (BCRAT) [1–3] uses US incidence and mortality hazards to assign a woman a probability of developing the disease before dying from other causes, while version 6 of the International Breast Cancer Intervention Study (IBIS) model [4] assigns her a probability of developing breast cancer under the assumption that her mortality rate during the period is zero. The risks assigned under these two assumptions can be expected to differ little for individuals with negligible death rates, but they can differ substantially for those with life-threatening comorbidities. In this case, the issue of primary concern for clinical decision-making is one’s risk of developing the outcome before dying from other causes.

Personal risk models need validation against longitudinal cohort data independent of that used to develop them. This paper focuses on model calibration (also called goodness of fit), which reflects how well the model-specified outcome probabilities agree with people’s subsequent observed outcomes. We need well-fitting models so that patients can rationally weigh the costs and benefits of preventive interventions in relation to an accurate assessment of their own risks. We also need to understand the reasons for poor fit, when it occurs. For example, a model’s poor fit may reflect its misspecification of mortality hazards among cohort members, whose health care access and lifestyles may differ from those of the population used for the model-specified death rates.

We assume that each individual in the population of interest has an unknown true probability μ of developing the outcome during the risk period. We wish to test the null hypothesis that each individual’s model-assigned risk r equals is/her true risks μ. Testing this hypothesis against longitudinal data from subjects randomly sampled from the population is straightforward when all subjects can be classified as outcome-positive (i.e., developed the outcome during the risk period) or outcome-negative (died without the outcome during the period or survived the period outcome-free). Then, using generalized linear models (GLMs) for binary data [5], we can take the response variable to be an indicator taking value one for outcome-positive subjects and zero otherwise, and model the expected value μ of this indicator as a function μ(η) of a linear predictor η = α + β^T z. Here μ(α) equals the model-specified outcome probability r, and z is a vector of covariates indicating patterns of possible poor model fit. Thus the null hypothesis that the model is well-calibrated becomes the hypothesis β = 0. Two commonly used link functions η(μ)are the logistic link

$$\eta =log\left[\mu /(1-\mu )\right]\text{with}\alpha =log\left[r/(1-r)\right],$$ (1)

and the complementary log-log link

$$\eta =log\left[-log(1-\mu )\right]\text{with}\alpha =log\left[-log(1-r)\right].$$ (2)

The GLM likelihood-based efficient score statistic for β = 0 has an asymptotic null distribution that is central chi-square.

However such GLMs cannot be used when some subjects are last observed alive and outcome-free before the risk period ends, since their outcome indicators are unknown. To deal with this problem, some investigators have simply deleted such censored subjects from the analysis. While this approach retains the simplicity of the GLMs, it can lead to severe upward bias in outcome probability estimates by excluding the time at risk of the censored subjects, who were outcome-free until last observed [6].

An alternative strategy is to partition subjects into K disjoint subgroups, and within each subgroup, obtain nonparametric estimates of the subjects’ true hazards for outcome and death during the period that starts from cohort entry and ends at a time t* years or months later. These estimates can then be used to obtain an estimate π̂_k of the mean outcome probability for comparison with the mean assigned risk r̄_k among subjects in subgroup k, and to obtain estimates ${\widehat{\sigma }}_k^2$ of the asymptotic variance of π̂_k, k = 1,…,K [6,7]. Model calibration can then be tested by comparing the statistic

$$X_K^2={\sum }_{k=1}^K\frac{{\left({\widehat{\pi }}_k-{\overline{r}}_k\right)}^2}{{\widehat{\sigma }}_k^2}$$ (3)

to a central chi-square distribution on K degrees of freedom (DF). In the absence of censoring, this test is similar to one proposed by Hosmer and Lemeshow [8] for goodness-of-fit of logistic regression models. Because of this similarity, we shall refer to the test statistic (3) as the Hosmer-Lemeshow (HL) statistic.

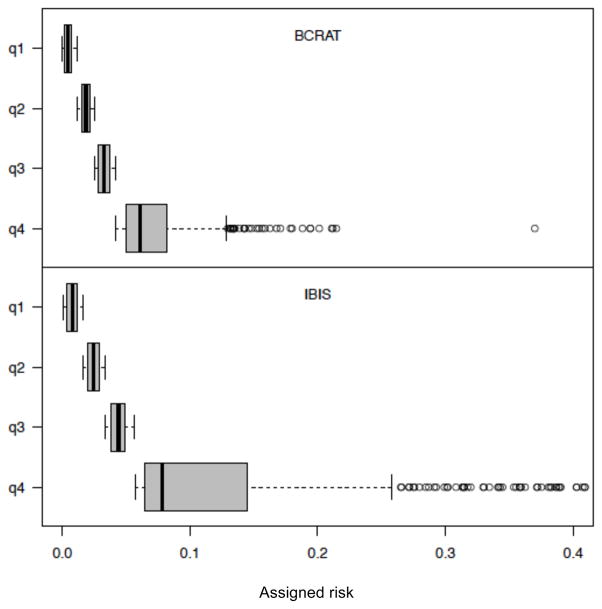
However there are disadvantages to this approach. First, the choice of subgroups is arbitrary, and for any choice of subgroups the distribution of risks within a subgroup can differ when different models are evaluated using the same cohort, or when different cohorts are used to assess the same model. Even when investigators use a common subgroup definition (such as quartiles of assigned risk), the quartile cut points vary across different models and different cohorts, which complicates model comparison. This problem is aggravated by the fact that estimating the event-specific hazards and the corresponding outcome probability can be too cumbersome for exploratory analysis involving different choices of subgroups. Finally, aggregating subjects into subgroups large enough for stable hazard estimation involves loss of information on model fit at the individual risk level, since some subgroups may contain subjects with substantially different risks. For example, Figure 1 shows box plots of the breast cancer risks assigned by the BCRAT and IBIS risk models to a subset of the NY BCFR data [9] for subgroups defined by quartiles of model-assigned risk. Because the risk distributions are right-skewed, the highest risk quartile spans a large range of risks, so that a summary calibration measure involves substantial information loss. Importantly, the accuracy of individual risks assigned to these high-risk women is often of greatest interest for planning preventive strategies.

Figure 1.

Box plots of BCRAT and IBIS risks as assigned to N = 1747 NY-BCFR subjects, within quartiles of assigned risk.

Here we propose a more flexible and informative way to evaluate model calibration in the presence of independent right-censoring. Specifically, we replace the single null hypothesis of agreement between true and assigned outcome probabilities for all individuals in the population by the joint null hypothesis that the model-specified event-specific hazards agree with the actual hazards governing events in the population during the risk period. We test this joint hypothesis by extending the model-specified hazards for outcome and death via a proportional hazards model. We then use the full (not partial) likelihood-based score statistics to test the null hypothesis that the regression coefficients in the extended hazards are zero. This approach, which builds on the work of Breslow [10], is analogous to the GLMs of equations (1,2) for binary data and enjoys their flexibility and exploratory advantages. In the absence of censoring, the extensions form a pair of GLMs for the binary outcome and death responses, with the exploratory covariates z contributing via a complementary log-log link of the form (2).

We begin by describing these score statistics and illustrating them with examples. We then report the results of simulations evaluating the size and power of the tests and comparing them to that of the HL test of equation (3). Finally, we illustrate the issues by evaluating the fit of risk models for a woman’s 10-year risk of breast cancer as applied to a subset of the participants in the New York Breast Cancer Family Registry (NY BCFR) cohort [9].

2. Methods

We wish to test the null hypothesis that the outcome and mortality hazards of a specific risk model agree with those of a given population, by comparing the model predictions with longitudinal data from a random sample of N subjects from the population. To do so, we use the risk model to assign each subject a probability r of developing the outcome of interest within t* months or years since cohort entry, based on his/her covariates ascertained at cohort entry. (See Appendix A for description of how the model assigns outcome probabilities.) To develop the proposed calibration tests, we expand the model’s hazards for outcome and death, and then test the null hypothesis that the unknown parameters in the expansions are zero, i.e., that the model fits the subjects’ survival data. Specifically, let z_ij denote the i^th subject’s values for a vector of covariates related to outcome (j=1) and death (j=2). These covariates may be risk factors, functions of the assigned risks such as multinomial subgroup indicators, or simply unit scalars z_ij = 1. We take the subject’s expanded hazard rates as

$${\lambda }_{ij}\left(t;z_i\right)={\lambda }_{ij}\left(t\right)e^{{\beta }_j^T{z}_{ij}},j=1,2,$$ (4)

where t is time since cohort entry, λ_ij(t) denotes the model-specified hazard for an event of type j, and β_j and z_ij are column vectors of dimension K. The subject’s observed data have the form (t_i, y_i1, y_i2) where t_i is the minimum of t^*, time of outcome development, time of death and time of censoring, and y_ij is an indicator assuming the value 1 if event j is observed at time t_i and zero otherwise, j = 1,2. Under the assumption that the censoring times are independent of times to outcome and death, the subject’s contribution to the likelihood function for β = (β₁, β₂) is

$$L_i(\beta )={\prod }_{j=1}^2{\left[{\lambda }_{ij}\left(t_i\right)e^{{\beta }_j^T{z}_{ij}}\right]}^{y_{ij}}{e}^{-{\mathrm{\Lambda }}_{ij}\left(t_i\right)e^{{\beta }_j^T{z}_{ij}}},j=1,2,i=1,\dots ,N,$$ (5)

where ${\mathrm{\Lambda }}_{ij}(t)={\int }_0^t{\lambda }_{ij}(u)du$ is the subject’s model-specified cumulative hazard. Note that L_i(β) is a full likelihood rather than a partial likelihood as defined by Cox [11]. Differentiating log L_i(β) with respect to β_j gives the subject’s contributions to the efficient score and null observed information for β_j as

$$U_{ij}=\frac{\partial }{\partial {\beta }_j}{\left[log{L}_i(\beta )\right]}_{{\beta }_j=0}=\left[y_{ij}-{\mathrm{\Lambda }}_{ij}\left(t_i\right)\right]z_{ij}\text{and}{V}_{ij}={\mathrm{\Lambda }}_{ij}\left(t_i\right)z_{ij}{z}_{ij}^T,j=1,2.$$ (6)

(Note that any time at risk of death after outcome occurrence is excluded from equation (6). This approach is appropriate because the mortality rates of outcome-positive and outcome-negative subjects may differ, and accounting for this difference would involve a more complex multi-state process for both the risk model(s) under evaluation and the evaluation itself. Moreover since the evaluation concerns model calibration within a short (e.g. five-year) time period, time at risk after this period is excluded.)

Equation (6) gives the score test statistic corresponding to events of type j as

$$T_j={U_j}^T{V}_j^{-1}{U}_j=\left({\sum }_{i=1}^N{U}_{ij}^T\right){\left({\sum }_{i=1}^N{V}_{ij}\right)}^{-1}\left({\sum }_{i=1}^N{U}_{ij}\right),j=1,2.$$ (7)

Under the null hypothesis that the model hazards are correctly specified for the population of interest, the outcome-based statistic T₁ and mortality-based statistic T₂ have asymptotic chi-square distributions on K DF. In addition, a summary test of agreement between total observed and predicted numbers of events (both outcomes and deaths) can be obtained by setting z_i1 = z_i2 = z_i for all subjects and β₁ = β₂ = β. This gives the combined test statistic

$$T_{+}={U_{+}}^T{V_{+}}^{-1}{U}_{+}=\left({\sum }_{i=1}^N{U}_{i+}^T\right){\left({\sum }_{i=1}^N{V}_{i+}\right)}^{-1}\left({\sum }_{i=1}^N{U}_{i+}\right),$$ (8)

where the subscript “+” denotes summation over the values j = 1,2. Calculating these test statistics requires extracting the model-specified cumulative hazards at arbitrary followup times t. If the model software does not provide this information, it can be approximated as described in Appendix B.

Regression models of the form (4) and their corresponding test statistics (7,8) provide a flexible framework that can be informative in evaluating model calibration. The investigator can vary the choice of regression model to examine different types of model fit, and the fit for various subgroups of subjects. The choice of regression model can help determine whether the model mis-specifies the outcome hazards, the mortality hazards, or both. In addition, the choice of covariate vector z can help determine population subgroups of individuals for whom the model fits poorly. The following examples illustrate the flexibility of the approach.

Example 1

The covariates might be scalar weights z_ij = w_ij determined by the subjects’ assigned risk or risk factors, to allow focus on those whose attributes are of particular interest. Then the test statistics (7) and (8) have the Poisson regression form

$$T_j=\frac{{\left(O_j-E_j\right)}^2}{E_j},\text{where}{O}_j={\sum }_{i=1}^N{w}_{ij}{y}_{ij}\text{and}{E}_j={\sum }_{i=1}^N{w}_{ij}{\mathrm{\Lambda }}_{ij}\left(t_i\right)$$ (9)

correspond to observed and expected counts of events of type j, j = 1,2,+. These test statistics have asymptotic null distributions that are chi-squared on one DF.

Example 2

We might choose as covariates a common vector z_i = (z_i1,…,z_iK)^T of indicators for membership in one of the K subgroups S₁,…,S_K in a partition of the subjects, as determined by personal risk factors or assigned risks. Then the test statistics (7) and (8) become

$$T_j={\sum }_{k=1}^K\frac{{\left[O_j(k)-E_j(k)\right]}^2}{E_j(k)},\text{with}{O}_j(k)={\sum }_{i\in S_k}{y}_{ij}\text{and}{E}_j(k)={\sum }_{i\in S_k}{\mathrm{\Lambda }}_{ij}\left(t_i\right)$$ (10)

denoting observed and expected counts of events of type j in subgroup k, k = 1,…,K, j = 1,2,+. The asymptotic null distributions of these test statistics are chi-squared on K DF. Subjects for whom the model fits poorly can be examined by plotting standardized residuals (SRs) of the

$${SR}_j(k)=\frac{O_j(k)-E_j(k)}{\sqrt{E_j(k)}},k=1,\dots ,K,j=1,2,+$$ (11)

form against subgroup-specific mean values of covariates or assigned risk. As we shall show in the application to breast cancer data, these SR plots allow visual inspection of model inadequacy and can help reveal the reasons for poor model fit.

We are currently implementing the methods in the Risk Model Assessment Program (RMAP), an R package freely available at http://stanford.edu/~ggong/rmap/.

3. Simulations

We used simulations to explore the performance of the proposed statistics and to examine the utility of residual plots for exploratory analyses. To do so, we considered the problem of evaluating a set of risk models using data from cohorts consisting of N = 1000 and N = 10,000 subjects randomly selected from a given population and followed for outcome occurrence or death during a ten-year period. The following is a brief description of how we generated and analyzed the data, and the summary measures we used to assess goodness of model fit.

3.1 Data generation

For each of the N subjects, we randomly and independently sampled times to censoring (j = 0), outcome (j = 1) and death (j = 2) according to independent exponential distributions with hazard parameters λ_j, j = 0,1,2. We then recorded the subject’s observed data as (t_i, y_i1, y_i2) where t_i = min(t_i0,t_i1,t_i2,t^*), with t^* = 10 years and t_ij denoting time to censoring (j = 0), outcome development (j = 1) and death (j = 2), and where y_ij takes value 1 if t_i = t_ij and zero otherwise, j = 1,2. We assumed that the hazard parameters governing the distributions of censoring and death do not vary across subjects, with λ₀ = 0.056 and λ₂ = 0.0042. We also assumed that the hazard parameters λ_i1 governing the distribution of times to outcome development are log normally distributed in the population, with log λ_i1 = c_i1 + c_i2. The covariate pairs (c_i1, c_i2) were sampled from a bivariate Gaussian distribution with parameters (μ, Σ), where μ = (−6.155,0.500) and Σ=diag(0.640,0.562). These parameter values were chosen to approximate those seen in the NY-BCFR data – they correspond to a 3% risk of death and a 4% mean risk of developing the outcome in the ten-year risk period, in the absence of competing risks.

3.2 Data analysis

We checked how well three risk models were calibrated to the population from which the data were generated. All three models assign risk according to Appendix Equation (A.1), but they differ with respect to their outcome and mortality hazards. The correct model specifies the same hazards used to generate the data. The biased outcome model specifies the correct mortality hazard, but its outcome hazard depends only on the first covariate c_i1. The biased mortality model specifies the correct outcome hazard, but misspecifies the mortality hazard as λ₂ = 0.0084 (twice the correct value).

For each of these three risk models, we evaluated the performance of 12 calibration tests corresponding to three choices of covariates z and four types of test statistic. The first covariate choice was the constant z_ij ≡ 1, which provides a test of overall agreement between observed and predicted numbers of events (outcomes and deaths). The resulting test statistic has a null asymptotic chi-square distribution on K=1 DF. (We also examined tests obtained using covariates z_ij = w_i = exp(|r_i − r̄|)/exp(r_max − r̄)), which weight a subject’s contribution in proportion to the distance between his/her assigned risk and the mean for all subjects, and found that this test performed similarly to the unweighted version). The remaining two covariate choices were indicators for membership in quintiles of assigned risk and in quintiles of the covariate c_i2 that is omitted from the biased outcome model. Here the resulting statistics have null asymptotic chi-square distributions on K=5 DF. The four types of test statistic were: 1) the HL statistic of equation (3); 2) the combined statistic T₊ (obtained by setting z_i1 = z_i2 and β₁ = β₂ = β); 3) the outcome-based statistic T₁(β₁ = β, β₂ = 0)); and 4) the mortality-based statistic T₂(β₁ = 0, β₂ = β). For each risk model and each test, we examined the proportion of 1600 replications in which the test statistic exceeded the 95^th percentile of its chi-square distribution. We also examined standardized residuals (SRs) to determine those subsets of subjects for whom the model fit poorly.

3.3 Simulation results

Table I shows the size and power of the 12 tests as applied to the correct, biased-outcome and biased mortality risk models. Several patterns are evident. For the correct risk model (column 1) the nominal and actual sizes of the tests agree well, with occasional exceptions for the HL test, which tends occasionally to incorrectly reject a well-calibrated model. However differences emerge when the risk model misspecifies the hazards. For the model that misspecifies the outcome hazard, the outcome-based test is most sensitive to poor fit, and the HL and combined tests show similar sensitivity, as measured by the statistical power of the test. In contrast, for the model that misspecifies the mortality hazard, the mortality-based and combined tests outperform the HL test.

Table I.

Size and Power^a of Tests for Risk Model Calibration using Simulated Cohorts of Size N

Test Statistic		Risk Model
		Correct outcome and death hazards	Biased outcome hazardb	Biased mortality hazardc
N = 1,000
Overall (zi=1)	$X_1^2$ (HL) d	0.049	0.966	0.049
	T+ (Combined)	0.054	0.849	0.884
	T1 (Outcome-based)	0.056	0.989	0.056
	T2 (Mortality-based)	0.053	0.058	0.991
Risk-stratifiede	$X_5^2$ (HL)	0.087	0.684	0.074
	T+ (Combined)	0.051	0.769	0.630
	T1 (Outcome-based)	0.052	0.963	0. 052
	T2 (Mortality-based)	0.056	0.057	0.907
Covariate-stratifiedf	$X_5^2$ (HL)	0.112	0.967	0.098
	T+ (Combined)	0.041	0.967	0.596
	T1 (Outcome-based)	0.065	0.999	0.065
	T2 (Mortality-based)	0.057	0.059	0.903
N = 10,000
Overall (zi=1)	$X_1^2$ (HL)	0.041	1.000	0.064
	T+ (Combined)	0.054	1.000	1.000
	T1 (Outcome-based)	0.048	1.000	0.048
	T2 (Mortality-based)	0.053	0.053	1.000
Risk-stratified	$X_5^2$ (HL)	0.071	1.000	0.064
	T+ (Combined)	0.042	1.000	1.000
	T1 (Outcome-based)	0.044	1.000	0.044
	T2 (Mortality-based)	0.038	0.053	1.000
Covariate-stratified	$X_5^2$ (HL)	0.061	1.000	0.056
	T+ (Combined)	0.054	1.000	1.000
	T1 (Outcome-based)	0.051	1.000	0.051
	T2 (Mortality-based)	0.046	0.046	1.000

^aproportion of 1600 replications in which T exceeded the 95^th percentile of a chi-square distribution with K degrees of freedom (K=1 for unweighted and weighted statistics; K = 5 for all others)

^bmodel omits covariate c₂ (see text)

^cmodel misspecifies the mortality rate as triple its correct value

^dgoodness-of-fit test of text equation (3)

^ein quintiles of assigned risk

^fin quintiles of covariate c₂ omitted by biased outcome model

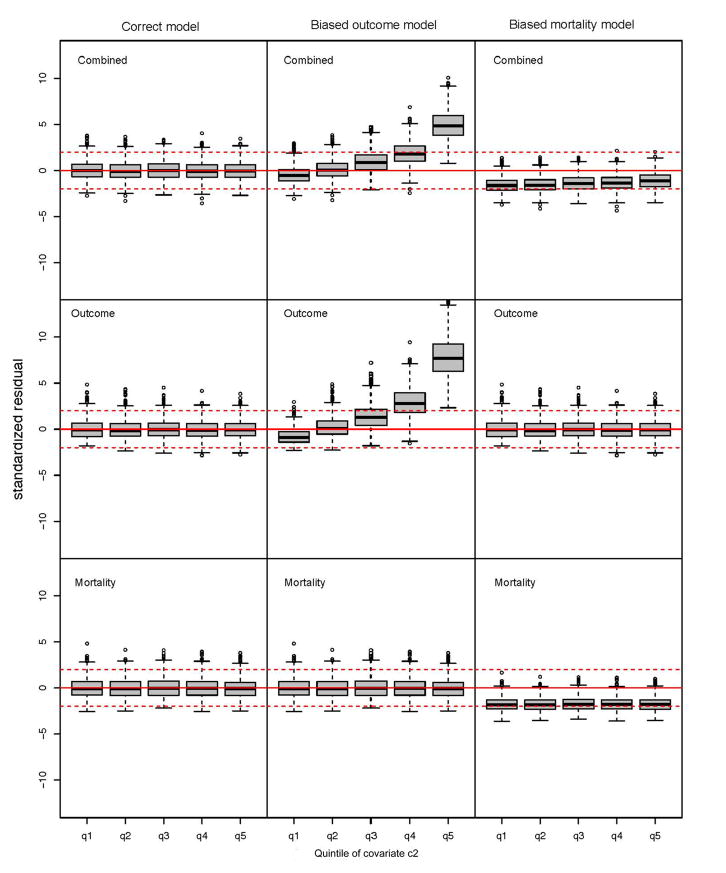
Figure 2 shows box plots of SRs obtained from the simulations involving N = 1000 subjects, with subjects classified in quintiles of the covariate c₂ that is omitted from the biased outcome model. The columns correspond to the three risk models (correct, biased outcome, biased mortality) and the rows correspond to the three tests (combined, outcome-based, mortality-based). These SRs are asymptotically standard normal deviates under the null hypothesis that the model is well-calibrated to the population from which the subjects were sampled. The first column of Figure 2 shows that the SRs for all three tests behave as expected when the correct model is applied to the data. In contrast, the second column (for the model that omits the covariate c₂) indicates that combined and outcome-based SRs show trends of increasing poor fit with increasing quintile of c₂, while the mortality-based SRs conform to their null expectation, as they should. These results suggest that we can use SR patterns to identify covariates whose addition to a risk model will improve model fit without having to construct an expanded model that includes the covariate of interest. Finally, the third column of Figure 2 shows that when the risk model overestimates the population mortality hazard, the SRs from both the combined and mortality-based tests are systematically negative, while those from the outcome-based test show the expected null behavior. These results suggest that examination of outcome- and mortality-specific SRs can reveal reasons for poor model fit, and a simple way to determine covariates whose addition to a risk model would substantially improve its calibration.

Figure 2.

Box plots of three types of standardized residuals corresponding to three risk models (A. correct model, B. biased outcome model, C. biased mortality model) as applied to simulated data from 1600 cohorts, each of size N = 1000 subjects. Each box plot in a panel corresponds to the residuals of subjects stratified by quintiles of the covariate c2. The three types of residuals are determined by the score test (combined, outcome-based, mortality-based).

4. Application To Cohort Data

We now use the proposed tests to evaluate how well the BCRAT and IBIS models predict the 10-year breast cancer risks of a cohort of women recruited and followed at the New York site of the Breast Cancer Family Registry (BCFR) [9,12]. Eligible subjects (N = 1857) were those who at cohort entry reported a family history of breast or ovarian cancer or a personal history of ovarian cancer but not breast cancer (see [9] for details). During the first ten years after cohort entry, 83 subjects developed breast cancer, 55 died without breast cancer, 989 were last observed alive and breast-cancer-free before 10 years, and 730 were alive and breast-cancer-free at ten years.

4.1 The risk models

We used each of the two risk models (BCRAT and IBIS) to calculate each subject’s ten-year cumulative hazards for outcome and death, and then used these cumulative hazards in the test statistics and SR plots. Both models assign 10-year breast cancer probabilities according to the Appendix formulae (A.1–A.3).

The BCRAT breast cancer hazard depends on a subject’s age at risk assessment, race, and other personal covariates such as age at menarche, age at first birth, number of affected first-degree female relatives, number of breast biopsies, and history of atypical hyperplasia. This empiric model specifies this hazard by combining race- and age-specific breast cancer incidence rates with hazard ratios determined from the estimated odds-ratios in a case-control study of breast cancer [1–3]. For the mortality hazards, the model uses all-cause mortality rates among US females, specific for age and race (white, nonwhite). We adapted the code and hazard rates of the BCRAT software (Breast Cancer Risk Assessment Tool) [13] to assign each subject values for her BCRAT cumulative hazards Λ_i1(t_i) for breast cancer (j = 1) and death (j = 2), as evaluated at her time t_i of last observation.

The IBIS breast cancer hazards depend on a two locus genetic model with one locus containing information on BRCA genes and the other locus containing information on a latent, dominantly acting low penetrance gene, plus nongenetic risk factors similar to but not identical with those used by BCRAT [4]. Version 6.0.0 of the IBIS risk evaluator specifies the mortality hazards as zero, although version 7.0.0 allows user-specified mortality hazards. To evaluate the proposed test statistics, we used the zero mortality hazards of Version 6.0.0, and checked how well the observed deaths in the cohort agree with this specification. (Note from equations (9,10) that the assumption of zero mortality hazards implies that all IBIS-based expected death counts are zero.) We first assigned each subject a ten-year risk r_i using the IBIS software available at the web link (IBIS Breast Cancer Risk Evaluation Tool) (IBIS risk evaluator – Version 6.0.0) [14]. We then approximated her cumulative breast cancer hazard Λ_i1(t_i) using Appendix equation (A.4) with r_i(t*) taken as her IBIS-assigned 10-year risk. We took her cumulative mortality hazard Λ_i2(t_i) = 0, and evaluated the accuracy of this assumption by taking the null variance of the mortality-based score statistic as

$$V_2={\sum }_{i=1}^N{V}_{i2}={\sum }_{i=1}^N{y}_{i2}{z}_{i2}{z}_{i2}^T.$$ (12)

Here y_i2 is an indicator assuming the value one if she died at time t_i and zero otherwise, and z_i2 = (z_i21,…,z_i24)^T is a vector of indicators for membership in one of the four quartiles of assigned risk.

4.2. Results

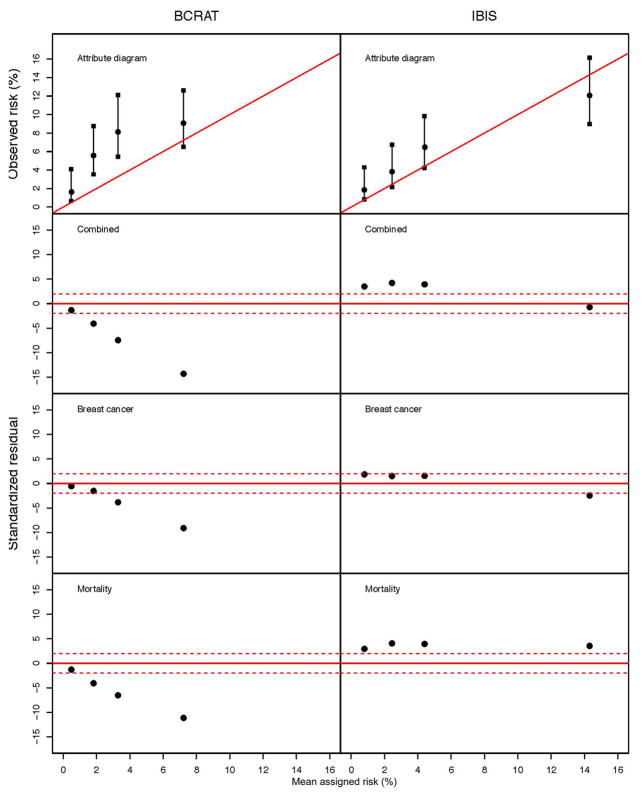
We estimated the cohort’s overall cumulative breast cancer risk during the 10-year period as 6.25% (95% confidence interval 5.02%–7.76%), using survival analysis that accommodates censoring and the competing risk of death [7]. This estimate significantly exceeds the mean risk of 3.20% assigned by the BCRAT model (P < 0.001), but agrees more closely with the risk of 5.49% assigned by IBIS (P = 0.98). The top panel of Figure 3 shows attribute diagrams (ADs) for the two models, based on quartiles of model-assigned risk. Under the null hypothesis that a model is well-calibrated, the points and confidence intervals of its AD should lie close to the diagonal line. The BCRAT AD shows that observed risks significantly exceed the mean assigned risks in the first three quartiles, while the results for IBIS show less discrepancy. The HL statistics of equation (3) support this conclusion, with values $X_4^2=19.28$ (P < 0.001) for BCRAT and $X_4^2=1.22$ (P = 0.27) for IBIS. These results suggest that the breast cancer risks assigned by BCRAT are too low for this cohort. However we shall see that the quartile-specific SRs for breast cancer and death offer a different interpretation.

Figure 3.

Attribute diagrams and plots of standardized residuals for BCRAT and IBIS models as applied to the NY-BCFR cohort by quartile of assigned risk.

Table II shows quartile-specific and overall counts of observed and expected breast cancers and deaths for the two models. Also shown are the quartile-specific SRs of (11) and the corresponding stratified calibration test statistics (10). These SRs are plotted in the lower three panels of Figure 3. The SRs of a well-calibrated model should lie within the band defined by the dashed lines in these panels. It is evident from both Table II and Figure 3 that the BCRAT-based expected counts for both breast cancer and death are too high compared to the cohort observations. This excess of BCRAT prediction over observation is particularly high for the deaths, indicating that the US mortality rates specified by BCRAT are substantially higher than those observed in this cohort. Thus the BCRAT underestimation of 10-year risk shown in the AD reflects the model’s overestimation of these competing death rates. In contrast to the negative BCRAT SRs, those for IBIS are largely positive, and show the statistically significant excess of observed (O = 55) vs. predicted (E = 0) deaths in Version 6.0.0 of the IBIS model.

Table II.

Calibration of BCRAT and IBIS Risk Models to the NY-BCFR Breast Cancer Cohort

		Quartile of Assigned Risk
		<25%	25–49%	50–74%	75%+	Total
Number of subjects
All		464	465	464	464	1857
BCRAT
Breast Cancer	Observed	5	19	25	34	83
	Expected	6.24	26.62	52.44	142.02	227.32
	SRa	−0.50	−1.48	−3.79	−9.06	98.89d
Deathb	Observed	7	13	21	14	55
	Expected	11.10	37.70	78.37	149.80	276.97
	SR	−1.23	−4.02	−6.48	−11.10	182.87d
Both Events	Observed	12	32	46	48	138
	Expected	17.33	64.32	130.81	291.83	504.29
	SR	−1.28	−4.03	−7.41	−14.27	276.42d
IBIS
Breast Cancer	Observed	6	13	22	42	83
	Expected	2.80	8.44	15.58	60.73	87.55
	SR	1.91	1.57	1.63	−2.40	14.53c
Death	Observed	9	17	16	13	55
	Expectede	0	0	0	0	0
	SRf	3	4.12	4.00	3.61	55.01d
Both Events	Observed	15	30	38	55	138
	Expected	2.80	8.44	15.58	60.73	87.55
	SRf	3.55	4.28	3.99	−0.67	47.29d

^aEntries for quartiles are standardized residuals $SR=(O-E)/\sqrt{E}$ and entries in Total column are test statistics $T={\sum }_{k=1}^4{\left(O_k-E_k\right)}^2/E_k$

^bwithin 10 years of followup

^cp< 0.01 based on ${\chi }_4^2$ distribution

^dp< 0.001 based on ${\chi }_4^2$ distribution

^efrom equation (10), all expected death counts for this model are zero, since Version 6.0.0 of the IBIS risk evaluator specifies mortality hazards equal to zero.

^fcalculated by using equation (12) to estimate the variance V₂ of an observed death count as the count itself.

These results should be interpreted with caution, for two reasons. First, in a cohort of this sample size (N = 1857 subjects), some SRs will have large absolute values purely by chance. Second, the ADs and SR plots are not directly comparable. On the one hand, an AD shows 10-year observed risks as calculated by cumulating the nonparametric hazard estimates for both types of event until 10 years after cohort entry. In contrast, the SRs are deviances between event counts as observed and as predicted at the subjects’ actual event times (which are typically less than 10 years). Despite these differences, the SRs provide useful information regarding the reasons for the poor model fit reflected in the overall test statistics and ADs.

The ease with which SRs can be plotted and evaluated allows flexibility in identifying population subgroups for which model calibration is poor. For example, we also plotted the model-specific SRs obtained by stratifying subjects by age at cohort entry, race/ethnicity, and number of blood relatives with breast or ovarian cancer (data not shown). These plots revealed subgroups for whom model fit was particularly poor. Identifying these subgroups and the reasons for the poor fit (outcome discrepancies, mortality discrepancies or both) can help identify specific needs for improvement in model performance.

5. Discussion

We have noted that evaluating the calibration of personal risk models for long-term adverse events is needed to help patients and their caregivers make rational decisions about preventive interventions with potential adverse side effects. Despite this need, evaluating model calibration has received less attention in the literature than evaluating risk model discrimination. We also have noted the complications of evaluating model calibration when some subjects cannot be followed for the full risk period, a common feature of large, long-term cohort subjects with staggered cohort entry. For this common situation, we have proposed simple and flexible efficient score tests that avoid some of the limitations of the commonly used HL test. We also have presented results of simulations showing that the score tests have good performance characteristics, and we have applied the tests to cohort data on ten-year risk of developing breast cancer.

The simulations and application to data show that in the presence of poor model fit, the score tests can help determine the reasons for the poor fit, and inform investigators about changes needed to improve fit. For example, plotting residuals corresponding to categories of a new marker can reveal how much adding the marker to a risk model is likely to improve its calibration. In addition, mortality-based residual plots can reveal model misspecification of death rates. This is an overlooked reason for poor model fit, often due to specification of population death rates that are higher than those of highly selected and well-educated participants in long-term cohort studies. By decomposing the calibration tests into components due to misspecification of the hazards for outcome and mortality, the methods provide leads to the reasons for discrepancies between observed and predicted outcomes.

Appendix

A. Assigning model risks

The risk model software uses the covariates of subject i at cohort entry to assign him/her an outcome probability

$$r_i=r\left(a_i\right)={\int }_{a_i}^{a_i+t^{\ast }}{h}_{i1}\left(u\right){\mathrm{e}}^{-\left[H_{i1}\left(u\right)+H_{i2}\left(u\right)\right]}du,$$ (A.1)

where a_i denotes the subject’s age at cohort entry, and h_ij(u) denotes the subject’s model-assigned hazard at age u with $H_{ij}(u)={\int }_0^u{h}_{ij}(v)dv$, for outcome development (j = 1) and death (j=2). It is convenient to transform these hazards from functions h_ij of age to functions λ_ij of time t since cohort entry, via the relation

$${\lambda }_{ij}\left(t\right)=h_{ij}\left(a_i+t\right)\text{and}{\mathrm{\Lambda }}_{ij}\left(t\right)=H_{ij}\left(a_i+t\right)-H_{ij}\left(a_i\right),0\le t\le t^{\ast },i=1,\dots ,N,j=1,2.$$ (A.2)

With this transformation, the subject’s model-assigned risk (4) can be written

$$r_i={\int }_0^{t^{\ast }}{\lambda }_{i1}\left(u\right)e^{-\left({\mathrm{\Lambda }}_{i1}+{\mathrm{\Lambda }}_{i2}\right)\left(u\right)}du.$$ (A.3)

B. Calculating model-specified cumulative hazards

Some online risk models may not provide the code needed to extract the model’s cumulative hazards for outcome and death at subjects’ last observation times, as needed to compute the test statistics. If the software allows user-specified mortality hazards, specifying these hazards as zero gives equation (6) as r_i(t_i) = 1 − e^{−Λ_i1(t_i)}, which then gives the cumulative outcome hazards as Λ_i1(t_i) = −log[1 − r_i(t_i)]. If the model software does not provide assigned risks r_i(t) at arbitrary followup times t but the outcome hazard rates can be assumed approximately constant in the risk period (0,t*), then Λ_i1(t_i) can be approximated as

$${\mathrm{\Lambda }}_{1i}\left(t_i\right)~\frac{t_i}{t^{\ast }}{\mathrm{\Lambda }}_{1i}\left(t_{\ast }\right)=-\frac{t_i}{t^{\ast }}ln\left[1-r_i\left(t^{\ast }\right)\right].$$ (A.4)