Improved Statistical Power of Alzheimer Clinical Trials by Item-Response Theory: Proof of Concept by Application to the Activities of Daily Living Scale

Abstract

Discovery of effective treatment for Alzheimer disease (AD) depends upon the availability of outcome measures that exhibit good sensitivity to rates of longitudinal decline on global functional performance. The Alzheimer’s Disease Cooperative Study-Activities of Daily Living inventory (ADCS-ADL) is a frequently used functional endpoint in clinical trials for AD that assesses patient functional ability on the basis of informant ratings of patient performance on a variety of everyday tasks. Previous research has shown that the items comprising the ADCS-ADL are sensitive to characteristic longitudinal trajectories in AD. However, standard procedures for combining information from individual items into an overall test score may not make full use of the information provided by informant responses. The current study explored an application of item-response theory (IRT) techniques to the calculation of test scores on the ADCS-ADL. Using data from 2 ADCS clinical trials on mild-to-moderate AD patients we found that IRT based scoring increased sensitivity to change in functional ability and improved prospective statistical power of the ADCS-ADL as an outcome measure in clinical trials.

Functional impairment, including disruptions in the ability to prepare food and drink, maintain good hygiene, converse with others, and perform everyday tasks such as shopping and taking out the garbage, is a critical component of the clinical presentation of Alzheimer disease (AD). The assessment of functional outcomes is a mandated coprimary endpoint, along with cognitive function, in clinical trials conducted to support applications for drug approval by the European Medicines Agency.¹ The Alzheimer’s Disease Cooperative Study (ADCS) has developed and validated functional activity of daily living (ADL) scales for measuring functional ability in cognitively normal elderly subjects (ADL-PI),² patients with mild cognitive impairment (ADL-MCI),² and persons with AD (ADCS-ADL). ³ The current paper deals specifically with the ADCS-ADL, using data from a study on the safety and efficacy of vitamin B supplementation in mild-to-moderate AD patients,⁴ and focuses on the standard procedure by which the instrument is scored.

The ADCS-ADL uses an ordinal scoring algorithm in which each response category for each question is assigned a numeric score, with zero indicating the lowest level of performance and higher numbers indicating better performance, with the highest scores indicating independent conduct of each ADL. Total scores for the administration of each test are calculated by adding up the scores associated with the endorsed response categories across all items. Galasko et al³ have demonstrated that the items comprising the ADCS-ADL have good individual sensitivity to functional decline in AD. However, these authors also provided evidence that the degree of sensitivity exhibited by ADCS-ADL items varies across the AD spectrum. In particular, whereas most items exhibited near-peak sensitivity to 12-month decline in patients with moderate AD (baseline mini-mental state examination (MMSE) 5 to 20), with sensitivity defined as the proportion of subjects who exhibited at least a 1-step decline, some items were relatively insensitive to decline across earlier stages of disease progression (MMSE>20), whereas others were comparably insensitive to decline across later stages (MMSE<5). As a result, overall test sensitivity, defined as the number of ADL items on which each subject exhibited at least a 1-step decline, was weaker in early and late stages than in intermediate stages of the disease.³

An alternative and potentially more optimal approach to quantifying ADL performance would be to utilize a scoring algorithm that explicitly accounts for heterogeneity in item scaling and sensitivity. One framework for doing so is item-response theory (IRT).⁵ The specific variant of IRT considered here is the Graded Response Model (GRM) of Samejima,⁶ which models ordinal-categorical item-response data by assuming: (1) a continuous linear regression relationship between a unidimensional latent ability variable and an observable performance variable; and (2) that the item-response categories that comprise the test are derived from a discretization of the observable performance variable at a set of fixed cutoff points. Critically, no a priori restrictions beyond strict ordinality are placed on the location or spacing of these fixed cutoff points, and hence the model is capable of accommodating considerable heterogeneity within and between items with respect to both the magnitude of decline in functional ability that is associated with a 1-step reduction on the ordinal-categorical rating scale for a given item, and the functional ability ranges to which sets or sequences of response categories are most sensitive.

The goal of the current research is to establish a proof of concept for the systematic application of latent variable modeling approaches to the analysis of item-response patterns on the ADCS-ADL in future clinical trials. Success in this endeavor will be assessed through an evaluation of the sensitivity to longitudinal functional decline exhibited by IRT-based estimates of functional ability on the ADCS-ADL, the benchmark being performance that is superior to that of ADL Total scores in this regard. Statistical power to detect treatment effects on longitudinal rates of change can be represented as a function of the accuracy that can be achieved in the estimation of the mean rate of change of the untreated study population,^7,8 making the implications of a demonstration of improved longitudinal sensitivity from IRT-based ability estimation both practical and far reaching.

METHODS

Data and Materials

The primary data set used for this study is derived from the ADCS homocysteine (HC) trial,⁴ which examined the effects of vitamin B supplementation on the rate of cognitive and functional decline in a sample of 409 mild-to-moderate AD patients (baseline MMSE 14 to 26; mean age at baseline, 76.3±8 y). The trial featured a nominal 18-month duration with observations scheduled every 6 months and an observed dropout rate of approximately 10% annually. Please see the original article⁴ for additional details of the study design and subject characteristics. No significant effect of treatment on the rate of decline was detected in the primary analysis. One participant’s 18-month data were excluded from all phases of the analysis because of excessive missing data at the item level. Data from 1 measurement occasion each for 2 additional subjects were excluded from the linear mixed-effects model analyses (see below) because of procedural errors in test administration discovered after the trial was closed.

Data from the ADCS docosahexaenoic acid (DHA) trial⁹ were utilized for validation purposes. This study also featured an 18-month duration with testing scheduled every 6 months and enrolled 402 mild-to-moderate AD patients (baseline MMSE 14 to 26; mean age at baseline, 76±8.7 y). Further details on this trial can be found in the original article.⁹

Statistical Analysis

The mathematical formulation of the unidimensional GRM incorporates 2 basic classes of parameters.⁶ The first of these consists of test parameters that describe the characteristics of the items and response categories that constitute the inventory. These can be thought of as functioning in a manner somewhat analogous to the rank-based scores that are assigned to each of the item-response categories and used in the calculation of ADL Total scores. These test parameters can be classified as: (1) difficulty parameters, which describe the locations of the cutoff points, or response category boundaries, on the functional performance scale; and (2) discrimination parameters, which indicate how well each item discriminates between relatively high-ability and low-ability subjects. Along with the test parameters, the GRM also incorporates subject-specific latent ability parameters that describe each individual’s underlying functional ability level. Estimates of these latent ability parameters, calculated from observed responses and from the previously determined test parameter estimates, serve as the IRT-based alternatives to ADL Total scores.

Test parameters for the ADCS-ADL were estimated using data from the last visit (month 18) for the subjects who completed the HC trial (n=343 after data were excluded for the subject noted above); estimation was by approximate marginal maximum likelihood, in which the distribution of the (unknown) ability parameters is integrated out of the likelihood before it is maximized with respect to the test parameters.^5,10 Eighteen-month data were chosen for this purpose because a broader range of ADL function was represented at this stage of the trial, and in particular because several of the items on the ADCS-ADL featured response categories that were not endorsed by any of the patient informants until the final observation. For the purposes of the IRT analysis, questions referencing the selection of clothes and getting dressed (labeled 6A and 6B, respectively, in the ADCS-ADL) were coded as separate items, resulting in a 24-item inventory. The model fit was assessed by examining χ² residuals for contingency table analyses of observed versus expected response category frequencies for all 2-item subsets and was judged to be acceptable (all χ² residuals ≤3.5¹⁰). Once training in the GRM model was complete, functional ability scores for each patient at each measurement occasion were calculated as empirical Bayesian model estimates.¹⁰ This procedure determines the estimate of the ability score for each test administration as the maximizer of the posterior distribution of the ability scores conditional on the observed responses for that test administration.⁵ The term “empirical” in this case references the fact that the posterior distribution is evaluated at the estimated, rather than at the true but unknown, values of the item parameters. The GRM fit, as well as the functional ability estimates, was based on the observed data with no imputation of missing data at the item level.

ADL Total scores were calculated following standard procedures, which for the ADCS-ADL results in a scoring range from 0 to 78, with missing items contributing zero points to the total score.

To compare the relative efficiency of IRT and ADL Total scores as outcome measures for a clinical trial, we estimated sample size requirements for future clinical trials assuming a linear mixed-effects model analysis as previously described.^7,8 Parameter estimates for sample size calculations were determined through a linear mixed-effects model with group-specific slopes and a common variance-covariance matrix fit to the HC trial data.⁴ Findings are reported both as the sample size per arm required to detect a 25% slowing of the mean rate of decline relative to placebo with power=0.8 and type I error rate=0.05, and in terms of the percentage reduction (%-Reduction) in the required sample size per arm achievable through the use of IRT scores as compared with ADL Total scores.

Two strategies for establishing the reliability and validity of the longitudinal modeling results comparing ADL Total and IRT scoring of the HC trial were pursued. First, to ascertain the significance of any observed advantage in statistical power, bootstrap 95% confidence intervals (95% CI) based on 10,000 bootstrap samples were calculated for %-Reduction estimates and other quantities of interest from the HC trial. Second, to ensure that the results of the longitudinal analyses could not be accounted for by the use of dependent training and testing data sets, we replicated the relative efficiency calculations using data from an independent data set. The GRM fit from the HC trial was used to calculate functional ability scores for ADCS-ADL data from the DHA trial; a linear mixed-effects model was fit to this independent data set as described above, and point estimates of the required sample size per arm and the %-Reduction from IRT scoring were calculated.

All analyses were performed using the statistical computing software R.¹¹ IRT analyses were conducted using the package “ltm,”¹⁰ and all longitudinal modeling was carried out with the package “lme4.”¹²

RESULTS

HC Trial Analyses

Estimated sample size requirements to detect a 25% attenuation of the mean rate of decline in treatment versus placebo are presented for a range of trial designs in Table 1 (statistical power=0.8, a 2-tailed hypothesis test with type I error rate=0.05, and equal allocation to treatment and placebo arms with no dropout). The IRT endpoint is consistently more efficient than the ADL Total score endpoint, with relative efficiency gains becoming more marked for longer trials. An 18-month trial with biannual observations using the IRT endpoint would require an estimated 15.0% fewer subjects compared with a comparably powered trial using the ADL Total score endpoint, and a 24-month trial using the IRT endpoint would require an estimated 19.8% fewer subjects than a comparable trial using the ADL Total score endpoint (Table 1). Bootstrap 95% CIs indicated that the %-Reduction from IRT scoring was significantly greater than zero in the 18-month (95% CI≈[1.3%, 26.7%]) and 24-month (95% CI≈[5%, 32.3%]) scenarios but not in the 12-month (95% CI≈[− 6.4%, 18.9%]) scenario.

TABLE 1.

Sample Size Requirements to Detect a Treatment Effect Using ADL Total Versus IRT Scoring, as Estimated From the Training (HC Trial) and Validation (DHA Trial) Data Sets

Trial Length (mo)	N/arm				%-Reduction
	HC		DHA
	ADL	IRT	ADL	IRT	HC	DHA
12	486	452	490	442	7.1%	9.8%
18	322	274	341	282	15%	17.4%
24	267	214	291	228	19.8%	21.7%

Both N/arm and %-Reduction assume no dropout and equal allocation.

ADL indicates activity of daily living; DHA, the Alzheimer’s Disease Cooperative Study (ADCS) docosahexaenoic acid trial; HC, the ADCS homocysteine trial on which the IRT model was trained; IRT, item-response theory; N/arm, sample size per arm, to detect a 25% reduction in the mean rate of decline, with observations every 6 months, power=0.8, 2-tailed significance level=0.05; %-Reduction, the percentage reduction in required sample size for IRT score versus ADL total scoring.

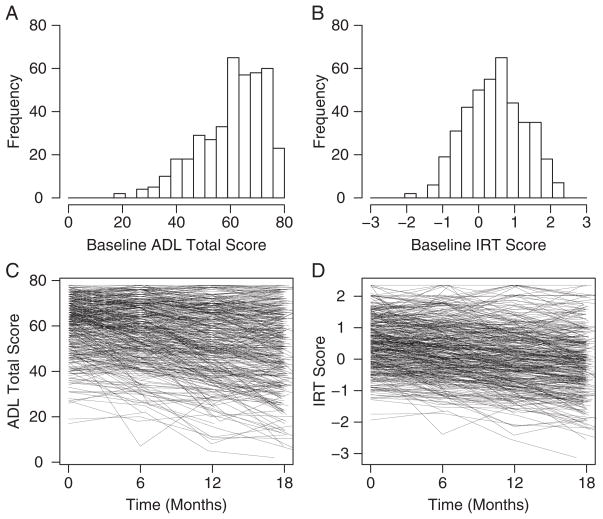
IRT scores tended to exhibit greater symmetry and approximate normality compared with ADL Total scores, particularly at the beginning of the trial. Histograms of baseline ADL Total and IRT scores depicting this difference are presented in Figures 1A and B. Reduced heterogeneity of the regression slope was also observed for IRT scores compared with ADL Total scores, as can be seen in the spaghetti plots in Figures 1C and D. The visual impression conveyed in these figures was also reflected in the parameter estimates from the linear mixed-effects model fits. Regression slope heterogeneity, characterized as the coefficient of variation (cv_Slp) formed by the estimated within-group SD of the subject-specific rates of decline from the mixed-effects model divided by the absolute value of the estimated placebo mean rate of decline, was 0.92 under ADL Total scoring and 0.78 under IRT scoring, reflecting greater consistency in subject-specific rates of decline relative to the mean rate of decline in the latter case. This difference has important implications for statistical power and sample size requirements, as discussed below.

FIGURE 1.

Homocysteine trial data; A, ADL Total scores at baseline; B, IRT scores at baseline; C, ADL Total scores against time-on-trial in months; D, IRT scores against time-on-trial in months. ADL indicates activity of daily living; IRT, item-response theory.

A second phenomenon seen in Figures 1C and D is a reduced tendency for IRT scores to remain near the instrument ceiling. This difference was also reflected in the estimated correlations (ρ_LME) of the random intercept and slope coefficients from the linear mixed-effects model fits. For ADL Total scores this correlation was estimated to be 0.31, whereas for IRT scores the estimate was 0.17 (boot-strap P-value<0.05). Thus, although ADCS-ADL performance was observed to decline at a slower rate for subjects who were relatively functionally intact at baseline than for subjects who were more impaired regardless of which scoring procedure was used, the trend was more pronounced under ADL Total scoring, as suggested by the figures.

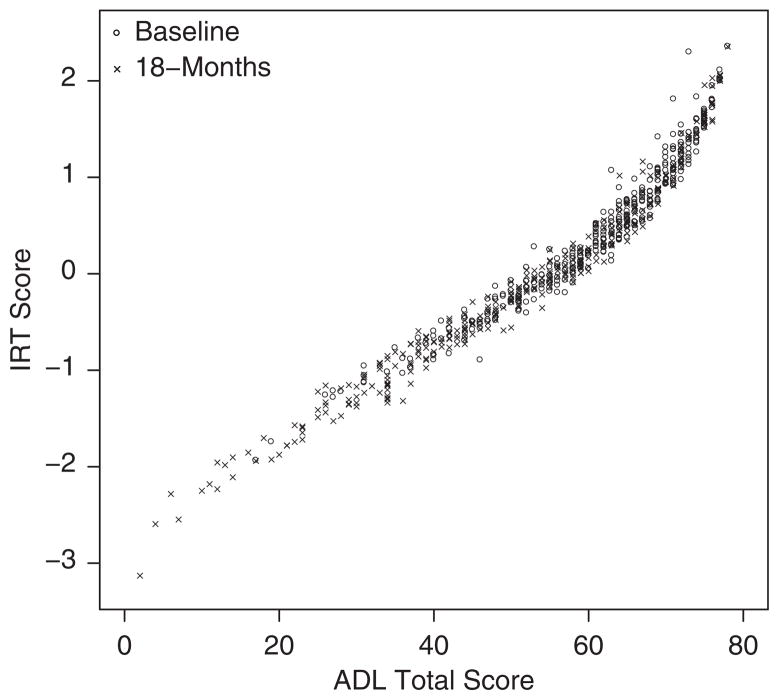
Another perspective on the phenomenon described above is offered in Figure 2, which plots IRT scores against ADL Total scores at baseline and 18-month observation times for the n=342 patients with valid 18-month data. ADL Total and IRT scores were strongly correlated, Spearman’s ρ=0.98 (0.99) at baseline (18 months), and in addition were linearly related through the intermediate range of the instrument. However, the IRT scoring procedure effectively stretched the tails of the scoring range relative to the ADL Total scoring procedure. This tail-stretching effect of IRT scoring is at the heart of the differences in distributional shape, as evident in Figures 1A and B, and of the longitudinal phenomenon noted in connection with Figures 1C and D. As we argue in the Discussion section, it is also responsible for the observed sensitivity differences between the 2 scoring procedures.

FIGURE 2.

IRT scores against ADL Total scores at baseline and 18-month observation times for n = 342 trial participants who completed the HC trial and were included in linear mixed-effects model analyses. ADL indicates activity of daily living; HC trial, homocysteine trial; IRT, item-response theory.

DHA Trial Validation Analyses

Sample size per arm and %-Reduction estimates for the DHA trial data are presented along with results from the HC trial in Table 1. Sample size estimates informed by data from each of the 2 trials were comparable, with %-Reduction estimates from the DHA trial slightly more favorable toward IRT scoring than estimates from the HC trial. The stronger estimated correlation between the random intercept and slope coefficients was also replicated, with ρ_LME=0.37 for ADL Total scores and ρ_LME=0.2 for IRT scores in the DHA trial.

DISCUSSION

The IRT scoring procedure was associated with improved longitudinal sensitivity and statistical power to detect a difference in the rate of decline in treatment versus control, as reflected in the lower estimated sample size requirements for IRT relative to ADL Total scores. Furthermore, the efficiency advantage enjoyed by the IRT scoring procedure was most pronounced in relatively longer trials. We have used sample size calculations assuming a linear mixed-effects model analysis to demonstrate the potential gain in efficiency achieved by using IRT score as an outcome in clinical trials, but this finding does not depend on this particular analysis plan. For example, comparable relative efficiency estimates are obtained using power calculations assuming an analysis plan comparing mean change from baseline (data not shown).

The reductions in the required sample size per arm reflect improved signal-to-noise characteristics of the IRT score, which exhibits a larger placebo mean rate of decline relative to the variability in subject-specific rates of decline (equivalently, a smaller cv_Slp, as reported in the Results section). The extended scoring range afforded by the IRT analysis (Fig. 2), and previously reported evidence that the ADCS-ADL is more sensitive to decline in moderate than in mild AD patients,³ suggests that the superior performance of the IRT scoring procedure owes primarily to improved resolution of the variability in rates of decline in functional ability among mildly demented patients. ADL Total scores, in contrast, may have been less sensitive to decline in relatively functionally intact patients because of a ceiling effect within this range of function. Nonuniform calibration of this sort would be expected to produce simultaneous attenuation of the detectable mean rate of decline and inflation of within-group variability in patient-specific rates of decline, the net result being a loss of statistical power, as was observed. The higher estimated correlations of random intercept and slope coefficients under ADL Total as compared with IRT scoring are also consistent with this hypothesis.

Several characteristics of these results and the methods by which they were achieved are in order. First, we note that the sample size of the HC trial proved somewhat restrictive, primarily because of the low frequencies of response observed for several of the item-response categories on the test. This lack of sampling density necessitated the use of 18-month data for IRT model training. In consideration of the sample size we reported bootstrap CIs for the estimated improvement in efficiency by IRT scoring conditional on the estimated parameters from the original GRM fit. The CIs supported the significance of the %-Reduction results for trials 18 months or longer. Validation of the results with an independent test data set was also accomplished by applying the GRM fit for the HC trial to the DHA data. Furthermore, to ensure that low response frequencies in boundary categories—that is, categories representing either unimpaired or fully impaired functional performance—did not predispose the analysis to an over-estimation of the rate of functional decline, a sensitivity analysis was performed in which the HC trial data were reanalyzed after collapsing over boundary categories with response rates <5% (recoding was required for 2 items). The efficiency of the IRT scoring procedure was unaffected by this change. We note, however, that these efforts do not address the inevitable uncertainty in the estimates of the GRM test parameters. Replication of these findings and more precise estimation of test parameters with a larger sample will therefore be necessary before the IRT endpoint can be implemented in actual clinical trials.

A second consideration concerns the assumption made by the GRM that observable responses are determined by a unidimensional latent trait. This assumption is central to many of the most commonly used IRT models⁵ but is rarely satisfied in practice and is almost certainly not completely accurate in the present case. As a first step in exploring alternatives to ADL Total scoring we argue that this simplification is justifiable, as it is consistent with the unidimensionality assumption implicit in the additive procedure by which standard ADL Total scores are calculated. Furthermore, as reported in the Methods section, diagnostic checks provided some indication that violations of model assumptions were not severe. In the final analysis, our view is that the value in latent variable modeling approaches like the one described here depends less on the question of whether the chosen model is perfectly accurate than on the question of whether the model can provide a useful and reliable approximation that can better serve the ultimate goal of supporting drug and therapeutic discovery for the treatment of AD.

CONCLUSIONS

We have shown that the application of IRT estimation procedures to the analysis of ADCS-ADL can lead to increases in the statistical power to detect treatment effects on the mean rate of decline in mild-to-moderate AD patients. These results provide a proof of concept for the application of latent variable modeling techniques to the analysis of ordinal-categorical outcome measures in AD as a means of improving the efficiency of clinical trials. It is hoped that this report will further stimulate applied research in this area.