Testing for Efficacy in Adaptive Clinical Trials with Enrichment

Abstract

Adaptive design of clinical trials has attracted considerable interest because of its potential of reducing costs and saving time in the clinical development process. In this paper, we consider the problem of assessing the effectiveness of a test treatment over a control by a two-arm randomized clinical trial in a potentially heterogenous patient population. In particular, we study enrichment designs that use accumulating data from a clinical trial to adaptively determine patient subpopulation in which the treatment effect is eventually assessed. A hypothesis testing procedure and a lower confidence limit are presented for the treatment effect in the selected patient subgroups. The performances of the new methods are compared with existing approaches through a simulation study.

1. Introduction

We consider the problem of assessing the effectiveness of a test treatment over a control by a two-arm randomized clinical trial in a potentially heterogenous patient population. It is assumed that, prior to the treatment initiation, the study population may be divided into k mutually exclusive subgroups according to some baseline covariates, such as age, gender, cancer stage, genomic biomarker [1], and genomic signature [2]. When patient subgroups respond to treatment differently, a two-stage design with enrichment uses accumulating data to adaptively determine patient subpopulation in which the treatment effect is eventually assessed as well as adaptively estimate sample size. In other words, the adaptive design with enrichment, also called enrichment design, allows the changes in enrolled population based on the interim analysis results.

The enrichment design attempts to reduce costs in drug research and development (R&D) by targeting from the original heterogenous study population a patient subpopulation that might optimally benefits from the treatment. In a 2003 study based on the R&D costs of 68 randomly selected new drugs at 10 companies, DiMasi et al. [3] claimed that pharmaceutical companies spent, on average, 802 million US dollars to develop a new drug. Some health economists estimate that the current cost of drug development is between $1.3 billion and $1.7 billion for each drug, but there is much debate about those figures [4]. Regardless, most experts agree that the R&D cost in the drug industry, especially the cost of clinical trials, is rising significantly. Enrichment design might effectively reduce the cost since it minimizes the possibility of recruiting patient subpopulations whose responses to the treatment are sufficiently low to the rest of the trial. Thus, it may require less subjects to test the treatment efficacy and save time in the development process. Furthermore, it may increase probability of success since the large treatment effect in the enriched patient subpopulation will be more likely to be detected, resulting in more chances for drug approval.

Since the main interest of most enrichment designs is to select the “best” patient subpopulation in which the treatment superiority is evaluated using all data at the end of the trial, it is very important to develop good selection rules and construct valid yet efficient hypothesis testing procedure. There are several previous work addressing these issues with a two-stage deign [5, 6, 7, 8, 9]. Follmann [5] proposed an enrichment rule based on the difference in the treatment effect estimates across patient subgroups at the first stage and developed two final test statistics for homogeneous and heterogenous study population, respectively. Under both conditions, the Type I error rate were well controlled regardless of adaption at the second stage. However, he only focused on the global null hypothesis but not the one corresponding to the enriched subpopulation. Russek-Cohen and Simon [6] presented a two-stage adaptive procedure by applying a test for subpopulation through treatment by group interaction in the decision rule at the end of the first stage. Although their design was effective in many scenarios, the subgroup with smaller treatment benefit or even no benefit went to a second stage in some scenarios. Moreover, they do not have theoretical proof for Type I error rate control. Authors in last three articles proposed testing procedures based on the weighted combination of z-statistics from both stages and allowed to test null hypothesis for overall patient population and the enriched subpopulation simultaneously. All of them proved strong control of Type I error rate in their designs. To be specific, Wang et al [7] presented a rich range of enrichment designs using the conditional power as the criterion in decision rules at the end of the first stage, with considerations of sample size re-estimation and futility stopping. The enrichment design was found to have higher power than standard method in a couple of enrichment scenarios. Wang et al [8] and Rosenblum and Van der Laan [9] allowed changes to the population enrolled by a class of decision rules based on the first stage test statistics. Rosenblum and Van der Laan [9] showed that their enrichment designs were more powerful than the fixed design except the scenarios where the treatment efficacy were similar in subpopulations and than designs by Wang et al [8] in detecting the treatment effect for overall patient population. However, they did not consider adapting sample size at the second stage. In addition, they showed Type I error rate control only when there are two mutually exclusive subgroups.

In this paper, we develop statistical methods for adaptive enrichment designs that involves study population with k ≥ 2 mutually exclusive patients subgroups. We focus on testing the treatment efficacy only for the selected subpopulation and propose a new hypothesis testing procedure which differs from Rosenblum and Van der Laan's method but also strongly control the Type I error rate regardless of the enrichment rules. In addition, we propose a lower confidence limit for the treatment effect in the selected patient subpopulation, which is a good start for statistical estimation of treatment effect that rarely was mentioned in the previous works. Furthermore, we explore the impact of the new method on probability of success and the expected net present value (NPV), related to combinations of enrichment rules, testing procedures, and sample size re-estimation. Rosenblum and Van der Laan's method is included in the primary comparisons.

The organization of the rest of this paper is as follows. In section 2, we present the new statistical test procedure and lower confidence limit, as well as other possible test procedures. In section 3, simulation studies are conducted to compare performance of enrichment designs in a few scenarios. The enrichment rules, simulation setups, and results are given in order. Finally, we concludes with some discussions in Section 4.

2. Two-stage combination test

2.1. Basic formulation

Denote by P the entire study population consisting of mutually exclusive patient subgroups P_i, i = 1, ..., k. In the first stage, 2n₁ subjects from each subgroup are equally randomized to the new and control treatment. We observe the following outcomes:

$$X_{tij}={\theta }_{ti}+{∊}_{tij},t=1,2;i=1,\dots ,k;j=1,\dots ,n_1;$$ (1)

where t = 1 for new treatment and t = 2 for control, $\overrightarrow{\theta }=({\theta }_{11},{\theta }_{12},\dots ,{\theta }_{1k};{\theta }_{21},{\theta }_{22},\dots ,{\theta }_{2k})$ are mean responses, and ε_tij ~ N(0, σ²) are independent errors with σ² assumed to be known for simplicity. Furthermore, we assume that the larger the mean, the better the outcome measures.

Depending on the results of the first stage, the study may continue only with selected patient subgroup(s) in the second stage. More specifically, if we let G_s, s = 1, ..., 2^k – 1, be all possible non-empty subsets of {1, 2, . . . , k}, then the study may continue with one of these subpopulations. The subpopulation selected will be denoted by G_τ, which can be determined based on first stage data as well as external information. In the second stage, 2N₂ subjects are equally randomized to the new and control treatment from each subgroup i that belongs to subpopulation G_τ. In this paper, we allow the second stage sample size, N₂, to be re-estimated based on interim analysis; and let n₂ be the pre-planned sample size per subgroup. We denote by Y_tij the jth observation from subgroup i with tth treatment at the second stage.

Our main interest is to determine whether the test treatment is superior (and by how much) to the control in the selected subpopulation ${\bigcup }_{i\in G_{\tau }}$ P_i, referred to as population G_τ when there is no ambiguity. If we let |G_s| denote the number of elements in set G_s and define

$${\Delta }_s=\sum _{i\in G_s}({\theta }_{1i}-{\theta }_{2i})∕\mid G_s\mid ;\text{and}{H}_{0,s}=\{{\Delta }_s\le 0\},$$ (2)

then the family of null hypothesis of interest is {H_0,s, 1 ≤ s ≤ 2^k – 1}. The main parameter of interest is Δ_τ, and the null hypothesis of particular interest is H_0,τ : Δ_τ ≤ 0. It is worthy to note that this null hypothesis is implied by the intersection hypothesis $H_{0,\tau }^{\ast }={\bigcap }_{i\in G_{\tau }}\{{\theta }_{1i}\le {\theta }_{2i}\}$, in other words, $H_{0,\tau }^{\ast }\subseteq H_{0,\tau }$.

2.2. Statistical test procedure and lower confidence limit

In this section, we describe a statistical procedure to test hypothesis H_0,τ and provide a lower confidence limit for Δ_τ. From the first stage data, a two-sample z-statistic can be constructed for each non-empty subpopulation G_s:

$$Z_s=\sum _{i\in G_s}\sum _{j=1}^{n_1}(X_{1ij}-X_{2ij})∕(\sqrt{2n_1\mid G_s}\mid \sigma )=\sqrt{\mid G_s\mid n_1}({\stackrel{‒}{X}}_{1s}-{\stackrel{‒}{X}}_{2s})∕\left(\sqrt{2}\sigma \right),$$ (3)

where X̄_1s and X̄_2s are sample means within population G_s for the treatment and control groups, respectively. In addition, we let $W_s=\sqrt{\mid G_s\mid n_1}({\stackrel{‒}{X}}_{1s}-{\stackrel{‒}{X}}_{2s}-{\Delta }_s)∕\left(\sqrt{2}\sigma \right)$. Similarly, from the second stage data, we can derive a two-sample z-statistic:

$$T_2=\sum _{i\in G_{\tau }}\sum _{j=1}^{N_2}(Y_{1ij}-Y_{2ij})∕\left(\sqrt{2N_2\mid G_{\tau }\mid }\sigma \right)=\sqrt{\mid G_{\tau }\mid N_2}({\stackrel{‒}{Y}}_{1\tau }-{\stackrel{‒}{Y}}_{2\tau })∕\left(\sqrt{2}\sigma \right).$$ (4)

where Ȳ_1τ and Ȳ_2τ are sample means.

We propose to conduct hypothesis test of H_0,τ based on weighted combination of Z_τ and T₂, i.e., using the final statistic

$$T={\omega }_1{Z}_{\tau }+{\omega }_2{T}_2,$$ (5)

where the weights are pre-specified, for example, ${\omega }_1=\sqrt{n_1∕(n_1+n_2)}$ and ${\omega }_2=\sqrt{n_2∕(n_1+n_2)}$ may be used.

To derive the critical value for the rejection region, we first note that (W₁, W₂, . . . , W_2^k–1) follows a multivariate normal distribution with mean zero and known covariance matrix, and the distribution does not depend on the unknown parameter $\overrightarrow{\theta }$. Hence, the distribution function of W = max_{1≤s≤2^k–1} W_s, denoted by H, is also independent of $\overrightarrow{\theta }$. Therefore, for any given significance level α, we may define the critical value c_α as follows.

Definition 1

Let W and Z be two independent random variables such that W follows distribution H and Z follows standard normal. We let c_α be the unique value such that

$$pr({\omega }_{1}W+{\omega }_{2}Z\ge c_{\alpha })=\alpha .$$ (6)

In other words, c_α satisfies that $\int \Phi \{(c_{\alpha }-{\omega }_{1}w)∕{\omega }_2\}dH\left(w\right)=\int H\{(c_{\alpha }-{\omega }_{2}z)∕{\omega }_1\}d\Phi \left(z\right)=1-\alpha$, where Φ is the cumulative distribution function of standard normal. It is worthy to point out that the critical value c_α is the (1 – α)^th quantile of the distribution of the final statistic T under the global null hypothesis. Thus, based on simulated values of T from this global null distribution, c_α can be easily calculated. We emphasize that c_α only depends on the sample sizes from the first stage and the prespecified combination weights, i.e., it is independent of the unknown mean parameters.

Now we are ready to state our first main result regarding strong control of familywise error rate, which is defined as the probability of wrongly rejecting any true null hypothesis among the family {H_0,s, 1 ≤ s ≤ 2^k – 1}. In our testing situation, this equals the probability that the selected subpopulation non-positive treatment effect and its corresponding null hypothesis is rejected, i.e., ${\sum }_{s=1}^{2^k-1}I({\Delta }_s\le 0){\mathrm{pr}}_{\overrightarrow{\theta }}(\tau =s,T\ge c_{\alpha })$.

Theorem 1

To test the hypothesis H_0,τ : Δ_τ ≤ 0 versus H_1,τ : Δ_τ > 0, the rejection region {T ≥ c_α} strongly control Type I error rate at level α.

Our second main result provides a lower confidence limit (LCL) for Δ_τ, the treatment effect in the selected patient subpopulation.

Theorem 2

If we define

$${\Delta }_L=\frac{n_1({\stackrel{‒}{X}}_{1\tau }-{\stackrel{‒}{X}}_{2\tau })+\sqrt{n_2{N}_2}({\stackrel{‒}{Y}}_{1\tau }-{\stackrel{‒}{Y}}_{2\tau })}{n_1+\sqrt{n_2{N}_2}}-c_{\alpha }\sigma \frac{\sqrt{2(n_1+n_2)∕\mid G_{\tau }\mid }}{(n_1+\sqrt{n_2{N}_2})},$$ (7)

then we have $p{r}_{\overrightarrow{\theta }}({\Delta }_{\tau }>{\Delta }_L)\ge 1-\alpha ,\forall \overrightarrow{\theta }$. In other words, Δ_L provides a LCL for Δ_τ with at least 1 – α coverage probability.

Note that, when there is no sample size re-estimation (i.e., n₂ = N₂), the lower confidence limit is very similar to the z-interval, with the only difference being replacing normal critical value by c_α.

The key to prove Theorem 1 is the fact that Z_τ is stochastically smaller than W under the null hypothesis, and the key to prove Theorem 2 is that W_τ is stochastically smaller than W. These properties are similar to the stochastic ordering results for designs with treatment selection [10, 11]. All the proofs are given in Appendix I.

2.3. Other test procedures

From now on, without loss of generality, we denote by G₁ the subset that select the entire population, i.e., G₁ = {1, 2, ..., k}. Rosenblum and Van der Laan [9] proposed the rejection region {ω₁Z₁ + ω₂T₂ ≥ Φ^–1 (α)}, where Φ is the cumulative distribution function of standard normal. Note that the test statistic is weighted combination of z-statistic for the entire population from the first stage and the z-statistic for the selected subpopulation from the second stage, and the threshold is the usual normal critical value. They have shown that the procedure guarantees strong control of familywise Type I error rate at level α if there is no sample size re-estimation and the trial only involves two subgroups (i.e., k = 2); however, it is unknown whether the result remains true when k > 2. In the simulation section, we refer to this test procedure as RV-method.

In addition, we have the following closed test for the family of hypotheses $H_{0,s}^{\ast }:{\bigcap }_{i\in G_s}\{{\theta }_{1i}\le {\theta }_{2i}\},1\le s\le 2^k-1$, which is closed because every intersection is still in the family. For any given s, we define an α-level individual test of $H_{0,s}^{\ast }$ with rejection region

$$R_s=\{\begin{array}{cc}\{{\omega }_1{Z}_s+{\omega }_2{T}_2\ge {\Phi }^{-1}\left(\alpha \right)\},\hfill & \text{if}{G}_{\tau }\subseteq G_s;\hfill \\ \{{\omega }_1{Z}_s+{\omega }_2{T}_2^{\left(s\right)}\ge {\Phi }^{-1}\left(\alpha \right)\},\hfill & \text{if}{G}_s\subset G_{\tau },\hfill \end{array}\phantom{\}}$$ (8)

where $T_2^{\left(s\right)}$ is the z-statistics restricted to subpopulation G_s when the second stage experiment is conducted in a larger population G_τ. Finally, $H_{0,s}^{\ast }$ is rejected with rejection region ${\bigcap }_{i:G_s\subseteq G_i}{R}_i$, i.e., when all G_i satisfying $G_s\subseteq G_i$ are rejected by individual tests.

Remark 1

Note that, in order to reject $H_{0,s}^{\ast }$ by the above closed test, G₁ has to be rejected; therefore this closed test procedure is uniformly dominated by the RV-method. Consequently, this closed test is not included in the simulation study.

2.4. Designs with early termination

For ethical and economical reasons, a clinical trial may be terminated early if the interim analysis shows that the test treatment is not even marginally better than the control, or it is clearly superior to the control. More specifically, we let (d₀, d₁, d₂) be any given constants such that

$$\mathrm{pr}\{(W\ge d_1)\cup (W\ge d_0,{\omega }_{1}W+{\omega }_{2}Z\ge d_2)\}=\alpha ,$$

where W and Z are two independent random variables such that W follows distribution H and Z follows standard normal. One would stop the trial for futility if W_τ < d₀ or for superiority if W_τ ≥ d₁; otherwise, one would continue to the second stage and claim superiority of the test treatment if ω₁W_τ + ω₂T₂ ≥ d₂. We state without proof that the above procedure strongly control the Type I error rate. Furthermore, the lower confidence limit can be obtained as follows:

$${\stackrel{‒}{\Delta }}_L=\{\begin{array}{cc}{L}_1,\hfill & M=1;\hfill \\ \max \{L_1,\min (L_0,L_2)\},\hfill & M=2,\hfill \end{array}\phantom{\}}$$ (9)

where M is the random stage at which recruitment is stopped, and lower limits L₀, L₁ and L₂ are defined as $L_0=({\stackrel{‒}{X}}_{1\tau }-{\stackrel{‒}{X}}_{2\tau })-d_0\sqrt{2∕\left(\mid G_{\tau }\mid n_1\right)}\sigma$, $L_1=({\stackrel{‒}{X}}_{1\tau }-{\stackrel{‒}{X}}_{2\tau })-d_1\sqrt{2∕\left(\mid G_{\tau }\mid n_1\right)}\sigma$, and $L_2=\frac{n_1({\stackrel{‒}{X}}_{1\tau }-{\stackrel{‒}{X}}_{2\tau })+\sqrt{n_2{N}_2}({\stackrel{‒}{Y}}_{1\tau }-{\stackrel{‒}{Y}}_{2\tau })}{n_1+\sqrt{n_2{N}_2}}-d_2\sigma \frac{\sqrt{2(n_1+n_2)∕\mid G_{\tau }\mid }}{(n_1+\sqrt{n_2{N}_2})}$.

3. Simulation results

3.1. Enrichment procedures

We consider two enrichment procedures for selecting subpopulation ${\bigcup }_{i\in G_{\tau }}$ at the second stage by assessing the interim data at the end of the first stage. One is based on the conditional power search (CPS) [12]. Here, based on the postulated effect size, we evaluate conditional power, which is the probability of rejecting the null hypothesis at the end of the trial given that the hypothetical trend follows the true effect size [7]. The other is called greedy search (GS) that is mainly based on the two-sample z-statistics.

To improve study power for better treatment effect evaluation, we allow sample size re-estimation for the second stage. That is, the total sample size at the second stage may be increased from the original $N_2^{\left(1\right)}=2\mid G_{\tau }\mid n_2$ up to $N_2^{\left(2\right)}=2\mid G_{\tau }\mid N_2$ with a few discrete choices. For simplicity, we allow futility rules for terminating a trial but exclude any possibility of early stopping for efficacy at the end of the first stage.

The CPS procedure is as follows. Let CP_m(G_s) be the conditional power evaluated at the postulated effect size Δ_s for the patient subpopulation G_s with second stage sample size $N_2^{\left(m\right)}$, m = 1, 2. First, we consider G₁ which includes all patients subgroups. If CP₁(G₁) ≥ 0.8, then no patient enrichment occurs and the trial will be continued with the entire patient population using the original sample size $N_2^{\left(1\right)}$. Otherwise, if CP₂(G₁) ≥ 0.8, then no patient enrichment occurs and the trial will be continued with the entire patient population using the adjusted sample size. Otherwise, the subgroup P_i with the smallest z-statistics is excluded. If at least one of conditional powers corresponding to the subpopulation that includes all remaining subgroups is no less than 0.8, the selection stops. The trial will be continued with the selected subpopulation using the smallest sample size of those achieving 80% conditional power in the second stage. Otherwise, the subgroup with the smallest z-statistics among the remaining P_i's will be excluded, and the selection proceeds. We repeat the same procedure until no more P_i can be excluded, i.e., all CP(G_s)'s are less than 0.8. Then the trial will be continued with the original eligibility criteria and sample size $N_2^{\left(1\right)}$, provided that the conditional power is at least 0.2. Otherwise, the trial will be terminated for futility.

Greedy search is straightforward and only based on the mutually exclusive patient subgroups P_i, i = 1, ..., k. First, we calculate the z-statistics for all P_i's. The one with the largest z-statistics will be selected as G_τ and enriched at the second stage. The conditional power is used to determine if adaptive sample size is needed. If at lease one CP_m(G_τ) ≥ 0.8, then G_τ will be enriched with the smallest sample size of of those achieving 80% conditional power; otherwise, it will be enriched with the total sample size of $N_2^{\left(2\right)}$.

With the above enrichment rules, the treatment effect in the selected subpopulation G_τ will be tested using all cumulative data at the end of the trial. Probability of trial success of G_s is the probability that G_s is selected and claimed significant. And the expected NPV of the trial, E(NPV), is the summation over G_s, s = 1, ..., 2^k – 1, the products of potential net revenue and the probability of success of G_s, minus the initial investment. Equivalently, E(NPV), can be calculated using the summation over subgroups P_i, i = 1, ..., k, the products of potential net revenue and the probability of success of P_i, minus the initial investment.

3.2. Simulation setup

We conduct a simulation study to compare the power and the expected NPV regarding to the following characteristics, the types of design (adaptive vs standard fixed), selection rules (CPS vs GS), test methods (RV-method vs new method as defined in Theorem 1), and sample size re-estimation (yes vs no).

The choice of simulation parameters is as follows. We assume σ = 1 without loss of generality. The total sample size is set at 200 patients (100 at each stage), which ensures 80% power to test a mean difference of 0.4 with one-sided test at 0.025 level. The second stage sample size may be increased to 200 or 300.

We consider k=3 mutually exclusive patient subgroups {P₁, P₂, P₃} with subgroup effect sizes (δ₁, δ₂, δ₃), where δ_i = θ_1i – θ_2i, i = 1, 2, 3. The overall effect size for the entire study population is δ₀ = (δ₁ + δ₂ + δ₃)/3. We consider nine groups of mean patterns for (δ₁, δ₂, δ₃): (–δ/2, –δ/2, δ), (–δ/2, δ/4, δ), (–δ/2, δ, δ), (0, 0, δ), (0, δ/2, δ), (0, δ, δ), and (δ/2, δ/2, δ), (δ/2, 3δ/4, δ), (δ/2, δ, δ), with δ equaling 0.4 and 0.6. Also, we include the last 6 patterns with δ satisfying δ₀ = (δ₁ + δ₂ + δ₃)/3 = 0.4 (excluding the first three mean patterns where the effect size of P₃ is extremely large when δ₀ = 0.4). In addition, we consider the global null hypothesis with (δ₁, δ₂, δ₃) = (0, 0, 0). Thus, a total of 25 scenarios of effect parameters are considered for each simulation setup, and 20,000 trials are run for each scenario. The estimated probability of success of G_s is the proportion of simulated trials where G_s is selected and claimed significant. The estimated overall power is the percentage of simulated trials with claimed significance.

To estimate the expected NPV, we predetermine the initial investment and the parameters for revenues over time. On one hand, parameters for the initial investment include: initial trial setup ($100k); cost of site setup ($15K per site for 20 sites); patient cost ($7K per patient); approval fee by FDA ($50K); manufacturing gear-up ($5M). Note that the costs here are only related to the clinical trial under consideration, but do not include investments on other compounds that do not make to the trial stage and the costs of research and development on this drug before the trial. Because the excluded costs remain the same for all trial designs we compare, we should have valid differences in pairwise comparisons. On the other hand, the revenue for the trial is generated using a model considered by Bolognese and Patel (see their 2012 ASA Biopharmaceutics Section webinar titled “Designing adaptive drug development programs for phases 2 and 3 in neuropathic pain”). The main parameters include: (1) the effective patent life (3, 7, 10, 13 years); (2) slope between 1-5 yeas, denoted by a, which are determined by the 5^th year net revenue of $0, $0.25B, $0.5B, $0.75B, $1.5B, corresponding to five categories of effect sizes (≤0.2, 0.2-0.5, 0.5-0.8, 0.8-1.5, >1.5); (3) slope after 5^th year (denoted by b) and decay parameter for period after patent expiration (denoted by c), which we set as (0.15a, 1), (0.3a ,0.5), and a third one where both b and c depend on treatment efficacy. We also assume a total of 20 years for the proposed drug and a discount rate of 0.1 per year. For example, when the patent life is 7 years, the effect size is 1.0, b=0.3a and c=0.5, the revenues at the tth year before discount is

$$R\left(t\right)=\{\begin{array}{cc}0.15t,\hfill & t\le 5,\hfill \\ 0.75+0.045(t-5),\hfill & 5<t\le 7,\hfill \\ 0.84exp(-0.5(t-7)),\hfill & 7<t\le 20.\hfill \end{array}\phantom{\}}$$ (10)

For each combination of trial characteristics (including types of design, selection and testing rules, presence of sample size re-estimation, and patterns for subgroup effect sizes) and cost scenario, the expected NPV is calculated based on average NPV over 20,000 simulated trials. For each simulated trial, the revenue is earned only if the trial resulted in a rejection of null hypothesis (claiming that the selected subpopulation has positive treatment effect) and the amount depends on the number of selected subgroups and their effect sizes (part 2 of the Bolognese and Patel model described above).

3.3. Results

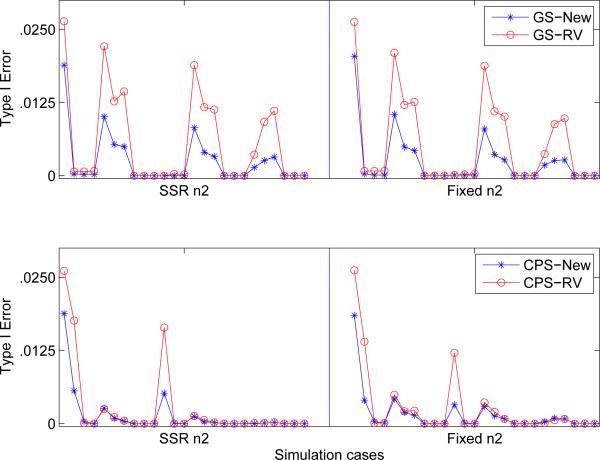
Figure 1 displays the Type I error rate comparison in designs using RV-method and the new test procedure as defined in Theorem 1. The critical values for the new method is 2.4360, which is determined by simulation. As expected, the new method strongly control Type I error rate, and is conservative in many cases. It appears that RV-method also controls the Type I error rate, but there is no formal proof that the result holds in general.

Figure 1.

Comparison of Type I error in two-stage enrichment designs under 25 simulation scenarios (see text) for the RV-method and New-method. The top two graphs are based on greedy search (GS) of enrichment subpopulation, while the bottom two are based on conditional power search (CPS). SSR stands sample size re-estimation and “Fixed” represent fixed 2nd stage sample size.

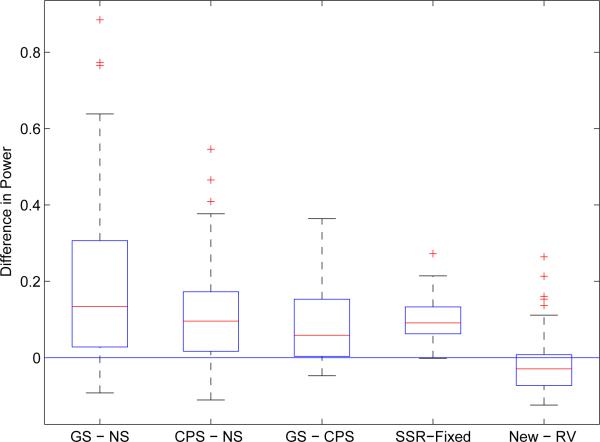
Figure 2 shows five pairwise power comparisons from perspectives of enrichment rules, sample size determination, and statistical test methods. For each factor, pairwise difference was evaluated for each combination of the other design characteristics. It is found that the adaptive design with enrichment is more powerful than the standard fixed design without enrichment. The average power improvement could be around 0.19 and 0.11 in designs with GS and CPS, respectively. Moreover, The powers tend to be higher in the adaptive designs with GS than with CPS (0.08 average improvement), and in designs with sample size re-estimation than with fixed sample size (0.09 average improvement). In addition, there are also power differences between two test methods. Specifically, the new method is superior to RV-method in the scenarios where effect sizes are heteromerous among the mutually exclusive patient subgroups, such as (–δ/2, δ/4, δ) and (0, 0, δ); while the RV-method tends to perform better when the treatment effects are nearly equal among subgroups.

Figure 2.

Pairwise power comparison between types of enrichment rules (the three boxplots on the left), sample size determination methods (the fourth boxplot), and statistical test methods (the last boxplot). GS stands for greedy search of enrichment subpopulation; NS for no search; and CPS for conditional power search. SSR stands sample size re-estimation and “Fixed” represent fixed 2nd stage sample size. Each boxplot is generated based on pairwise difference regarding the factor, considering all possible combinations of other design characteristics. For example, the comparison between GS and NS includes power differences for 100 simulation cases (25 each for RV method with SSR; RV method with fixed sample size; new method with SSR; and new method with fixed sample size).

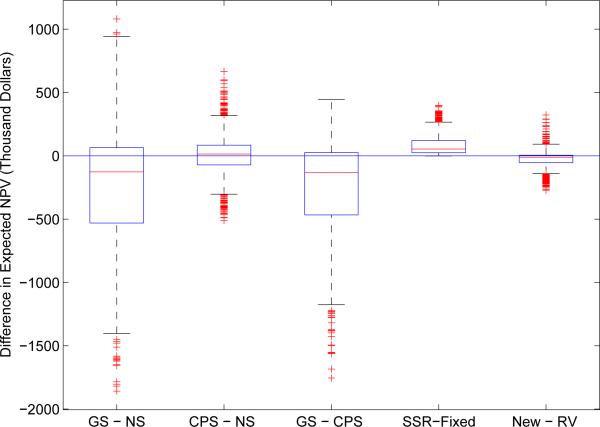
Similar pairwise comparisons are presented in Figure 3 for the expected NPV. The NPV in the adaptive design with CPS and the standard fixed design are close, while a lower NPV is found in the adaptive design with GS mainly because it tends to select a smaller subpopulation. Furthermore, the benefit does not differ too much between adaptive designs with and without sample size re-estimation; with a slight edge in favor of the former. Furthermore, we found that the RV-method might lead to higher NPV when the patients subgroups have similar effect sizes, such as (δ/2, 3δ/4, δ) and (δ/2, δ, δ); and this finding is consistent with power comparison.

Figure 3.

Pairwise comparison of the expected net present value (NPV) between types of enrichment rules (the three boxplots on the left), sample size determination methods (the fourth boxplot), and statistical test methods (the last boxplot). The boxplots are constructed and arranged similar to Figure 2.

4. Discussion

We have presented a hypothesis testing procedure for assessing the effectiveness of a treatment over a control by a two-arm randomized clinical trial in a potentially heterogenous patient population. This procedure has been shown to strongly control the Type I error rate at α level, regardless of enrichment rules and sample size adaption. In addition, we have provided a lower confidence limit for the treatment effect in the selected subpopulation following an adaptive clinical trial with enrichment. Similar to test procedure, the confidence limit is valid under flexible enrichment rules and sample size re-estimation.

Simulation results point out that adaptive design with enrichment may offer big power improvement. This is particularly prominent for designs with GS enrichment because the enrollment at the rest of trial is restricted to the promising patient subgroup selected based on the “best” performance at the end of the first stage. However, GS enrichment tends to perform poorly in the expected NPV. In particular, when the treatment effects in subgroups appear similar, the GS enrichment suffers big NPV loss because it eliminates the possibility of marketing the new treatment to those subgroups that are almost equally beneficial as the selected subgroup. We suggest that, if an adaptive trial with GS enrichment claimed significance, it should be followed by a trial including all potentially beneficial subgroups to increase the expected NPV.

In our work, we calculate the conditional power based on the postulated effect size, assuming that the true effect size remains stable in the course of the trial. However, it is common that there is no good estimate of true treatment effect before a clinical trial. Thus, it would be of great interest to investigate power and the expected NPV performances when the conditional power is obtained based on the observed effect size from the actual interim data, which assumes that the observed treatment effect estimate is true in the population.

Finally, even though the new hypothesis testing procedure and lower confidence limit are derived with error variance σ² assumed to be known, the results can be readily extended to the case with unknown common variance. In this case, the critical value in definition (6) needs to be modified to include sample variance in the probability calculation.

Appendix

Proof of Theorem 1

The event of Type I error can be expressed as

$$\begin{array}{cc}\hfill E=& \bigcup _{1\le s\le 2^k-1,{\Delta }_s\le 0}\{\tau =s,{\omega }_1{Z}_s+{\omega }_2{T}_2\ge c_{\alpha }\}\hfill \\ \hfill =& \bigcup _{1\le s\le 2^k-1,{\Delta }_s\le 0}\{\tau =s,{\omega }_1{W}_s+{\omega }_2{T}_2\ge c_{\alpha }-{\omega }_1\sqrt{{\mid G\mid }_s{n}_1∕2}\sigma {\Delta }_s\}.\hfill \end{array}$$ (11)

It is easy to check that

$$\begin{array}{cc}\hfill E& \subseteq \bigcup _{1\le s\le 2^k-1,{\Delta }_s\le 0}\{\tau =s,{\omega }_1{W}_s+{\omega }_2{T}_2\ge c_{\alpha }\}\hfill \\ \hfill & \subseteq \bigcup _{1\le s\le 2^k-1,{\Delta }_s\le 0}\{\tau =s,{\omega }_{1}W+{\omega }_2{T}_2\ge c_{\alpha }\}\hfill \\ \hfill & \subseteq \{{\omega }_{1}W+{\omega }_2{T}_2\ge c_{\alpha }\}.\hfill \end{array}$$ (12)

Consequently, Theorem 1 follows from the fact that, conditioned on the first stage data (given N₂), T₂ follows standard normal distribution.

Proof of Theorem 2

By definition of Δ_L, we have

$${\Delta }_L-{\Delta }_{\tau }=\frac{n_1({\stackrel{‒}{X}}_{1\tau }-{\stackrel{‒}{X}}_{2\tau }-{\Delta }_{\tau })+\sqrt{n_2{N}_2}({\stackrel{‒}{Y}}_{1\tau }-{\stackrel{‒}{Y}}_{2\tau }-{\Delta }_{\tau })}{n_1+\sqrt{n_2{N}_2}}-c_{\alpha }\sigma \frac{\sqrt{2(n_1+n_2)∕\mid G_{\tau }\mid }}{(n_1+\sqrt{n_2{N}_2}}.$$ (13)

Therefore, the event {Δ_L < Δ_τ} is equivalent to

$$\{n_1({\stackrel{‒}{X}}_{1\tau }-{\stackrel{‒}{X}}_{2\tau }-{\Delta }_{\tau })+\sqrt{n_2{N}_2}({\stackrel{‒}{Y}}_{1\tau }-{\stackrel{‒}{Y}}_{2\tau }-{\Delta }_{\tau })<c_{\alpha }\sigma \sqrt{2(n_1+n_2)∕\mid G_{\tau }\mid }\}=\{{\omega }_1{W}_{\tau }+{\omega }_2{T}_2<c_{\alpha }\}.$$ (14)

Note that ${\mathrm{pr}}_{\overrightarrow{\theta }}({\omega }_1{W}_{\tau }+{\omega }_2{T}_2<c_{\alpha })\ge {\mathrm{pr}}_{\overrightarrow{\theta }}({\omega }_{1}W+{\omega }_2{T}_2<c_{\alpha })=1-\alpha$. The proof is complete.