Abstract
Purpose
To develop high-resolution electrical properties tomography (EPT) methods and investigate a gradient-based EPT (gEPT) approach which aims to reconstruct the electrical properties (EP), including conductivity and permittivity, of an imaged sample from experimentally measured B1 maps with improved boundary reconstruction and robustness against measurement noise.
Theory and Methods
Using a multi-channel transmit/receive stripline head coil, with acquired B1 maps for each coil element, by assuming negligible Bz component compared to transverse B1 components, a theory describing the relationship between B1 field, EP value and their spatial gradient has been proposed. The final EP images were obtained through spatial integration over the reconstructed EP gradient. Numerical simulation, physical phantom and in vivo human experiments at 7 T have been conducted to evaluate the performance of the proposed methods.
Results
Reconstruction results were compared with target EP values in both simulations and phantom experiments. Human experimental results were compared with EP values in literature. Satisfactory agreement was observed with improved boundary reconstruction. Importantly, the proposed gEPT method proved to be more robust against noise when compared to previously described non-gradient-based EPT approaches.
Conclusion
The proposed gEPT approach holds promises to improve EP mapping quality by recovering the boundary information and enhancing robustness against noise.
Keywords: EPT, electrical properties, B1 mapping, gradient
INTRODUCTION
Electrical properties (EP) of biological tissues, which consist of electrical conductivity and permittivity, depend on the frequency of the externally applied electromagnetic field and vary as a function of the relative intracellular and extracellular fluid volumes, the ionic concentrations, and the cellular membrane permeability (1,2). Both electrical conductivity and permittivity can be affected by various pathological conditions; ex vivo experimental results have shown that cancerous tissues have significantly different EP values as compared with normal tissues over a wide electromagnetic frequency spectrum, e.g., >200% for breast cancer and >100% for bladder cancer at radio and microwave frequencies (3–5). A study examining the impedance spectroscopy of different tissue groups (6) indicated that electrical-property–based contrast could help differentiate malignant and benign tissues, which can be challenging with anatomy-based imaging modalities, such as MRI, CT and ultrasound. It is therefore anticipated that accurate EP imaging might have the potential of providing valuable information for cancer diagnosis and disease progression monitoring (7).
In the past decades, a number of efforts have been made in an attempt to map EP distributions in vivo. Recently, electrical properties tomography (EPT) has gained considerable interest as a non-invasive in-vivo imaging approach to simultaneously map conductivity and permittivity at the Larmor frequency of protons using MRI scanners (8–11). Among related techniques, electrical impedance tomography (EIT) (12,13) requires mounting electrode and injecting current into the sample and provides limited spatial resolution due to insufficient number of detecting electrodes and the ill-posed nature of the inverse problem. Magnetic resonance electrical impedance tomography (MREIT) (14) utilizes an MRI scanner to detect the magnetic field induced by the probing current, providing high spatial resolution but with safety-concerning current density to reach sufficient signal to noise ratio (SNR). Both EIT and MREIT could be challenged by the shielding effect to make electrical current penetrate through non-conductive medium (such as the skull) (15). Magneto-acoustic tomography with magnetic induction (MAT-MI) holds promises of high spatial resolution, but no in vivo results have been reported so far (15–18). EPT detects the EP distribution by exploring the radiofrequency (RF) field commonly used in MRI, with high spatial resolution, high penetration depth and eliminated need of current inject. Scanning is conducted similar to existing MRI imaging techniques, making it applicable for clinical application.
In the meantime, EP values at the operating Larmor frequency are a key factor in quantifying local specific absorption rate (SAR) (19). At high (3T) and ultra-high (≥7 T) field magnetic field pstrength, SAR is a safety concern in MR examinations and becomes a significant limiting factor in MRI. Knowing EP distribution could help deduce the applied radiofrequency electric fields and allow for fast, subject-specific SAR estimation. Using this SAR information as a constraint to design RF pulses could enhance flexible management of tissue heating, which in turn would contribute to further optimize the use of high-field and ultra-high-field MR scanners, helping benefit from the intrinsically higher SNR and contrast to noise ratios obtained as the main magnetic field increases (20)
The concept of imaging EP based on measured MR signals was initially introduced by Haacke et al. (8). Wen (9) later pointed out that the distribution of the RF field in high-field MRI directly relates with the conductivity and permittivity distribution in the sample, and could be explained by an electromagnetic wave equation—the homogeneous Helmholtz equation. From then on, this equation has been utilized in the majority of EPT studies (10,21–25).
Biological tissues may exhibit rapid spatial changes in EP due to their complicated structures. Such rapid spatial variation in EP has been a challenge to existing EPT approaches as most of them are based upon the homogenous formula. Derived from Maxwell’s equations, several algorithms trying to tackle the boundary issue have been proposed, either based on the inhomogeneous Helmholtz equations (Eq. 1) (21,26,27) or utilizing the continuous nature of Gauss’s Law for magnetism (21). However, in vivo applications reported so far making use of these algorithms often result in EP maps suffering inconstant fidelity and fairly large variance, due to either high computational demand of the numerical solution or the inherently high sensitivity of such EPT algorithms to measurement noise (10).
In the present study, a new gradient-based EPT (gEPT) approach is proposed, in which the spatial gradient of EP are explicitly considered in the algorithm and utilized to reconstruct EP maps through spatial integration. Simulation studies, phantom validation and in vivo human experiments have been conducted at 7 T to investigate the gEPT algorithm, with a special focus on its enhanced boundary reconstruction and robustness against noise contamination in the context of highly refined structural details that characterize real life experiments.
THEORY
A schematic diagram of the gEPT approach is shown in Fig. 1. A multi-channel transceiver RF array coil is utilized for RF power transmission and MR signal reception. The spatial gradient of EP is derived using the magnitude and relative phase of multiple transmit and receive B1 fields from the multiple channels. The final EP maps are reconstructed via spatial integration on the obtained gradient field.
FIG. 1.
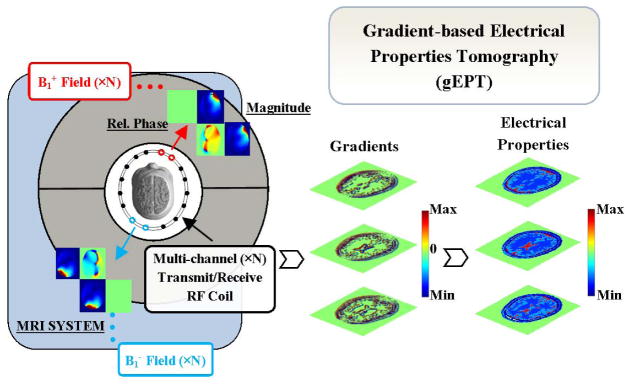
Schematic diagram of the gradient-based electrical properties tomography using a multi-channel transceiver radiofrequency array coil.
Central Equations
Inside an MRI scanner, the RF field usually operates centered closely to the Larmor frequency of the nuclei of interest, and therefore, this field can be treated as a time-harmonic field. Combining the time-harmonic Ampere’s Law and Faraday’s Law in Maxwell’s equations, we can derive the following core equation underlying the EPT theory (11,27,28):
| [1] |
where B is the magnetic field vector in the Cartesian coordinate, r denotes position, ω the Larmor angular frequency for protons, εc (r) = ε(r) − iσ(r)/ω the complex permittivity, σ the conductivity, ε the permittivity, and μ0 the magnetic permeability of free space, respectively. Here, ε is measured in units of ε0—the permittivity of free space. For simplicity, the spatial coordinate variable r will not be mentioned in the rest of this paper.
As shown in Appendix A, Equation 1 can be further transformed into the expression of transmit ( ) (26,29) and receive ( ) B1 fields, which are the B1 field components in the positively and negatively rotating coordinates, respectively.
| [2] |
| [3] |
Here, g denotes ∇lnεc, the gradient field of the natural logarithm of εc. Although Bz is not directly measurable in MRI, in this study, we assumed the contribution of the derivatives of Bz could be ignored compared to those of B1+ or B1−, given the structure of the microstrip array RF coil that we used (21,30). We verified the validity of this assumption in numerical simulations of both phantom and realistic head model as shown in Fig. 2d–e.
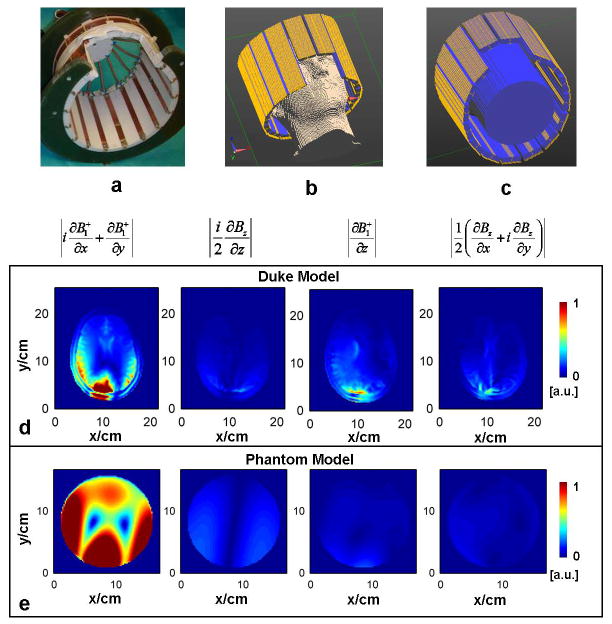
FIG. 2.
a: Photograph of the sixteen-channel RF coil used in experiments. b: Simulation setup of the coil and a head model. c: Simulation setup of the coil and a cylindrical phantom model. d and e: The relative magnitude of derivative components related to B1+ or Bz in a slice near the middle of the RF coil in the z-axis of the Duke head (d) and of a homogeneous phantom model (e), respectively.
After the removal of Bz-related terms, defining g+ ≡ gx + igy and g− ≡ gx − igy, Eq. 2 and 3 can be rewritten as
| [4(a)] |
| [4(b)] |
Solution to the Central Equations
Magnitude of and relative phase of both and can be measured directly in MRI. Although the measured magnitude of is usually coupled with the proton density, we utilized two different approaches to separate it from the magnitude of , one for phantom compartments with uniform proton density and one for heterogeneous human brain tissues. For each of Eq. 4(a) and 4(b), taking the magnitude and relative phase of the B1 field as known information, Eq. 4 can be expressed as a function of several unknowns: , g±, gz, ε, σ and , where represents the absolute phase of a chosen transmit or receive reference channel (see details in Eqs. A6 and A7 in Appendix A). Equations 4(a) and 4(b) can be transformed into linear equations by combining the nonlinear or linearly dependent items as shown in Eqs. A6 and A7. Using a transceiver RF array coil with Nch channels, for any individual voxel in the image domain we will have a number of 2×Nch Eqs. A.6 and A.7 for either transmit or receive . From this set of equations, g+ and g− were derived by fitting |B1| and ϕr from Nch transmit and receive channels to achieve minimum sum of square errors. To improve the reliability of the result, this procedure was repeated using each of the Nch transmit or receive channels as a reference channel. Weighted by the magnitude of the local B1 field of the corresponding reference channel, the resulting Nch sets of g+ and g on the same voxel were combined to yield the final g+ and g, which were transformed into gx and gy.
Once the gradient ∇lnεc is obtained, with the additional information of a small number of S seed points to provide initial value, final maps of the electrical properties were reconstructed using a 2D finite-difference method (31).
MATERIALS AND METHODS
Computer Simulation
Simulation Setup
Electromagnetic simulation was performed based on the finite-difference time-domain (FDTD) method in software SEMCAD (Schmid & Partner Engineering AG, Zurich, Swizerland). A 16-channel microstrip array coil (Fig. 2 a) (32), which is used in the experimental part of the study, was numerically modeled and loaded with either the Duke head model of the Virtual Family (Fig. 2 b) (33) or a head-sized phantom (Fig. 2 c) (diameter of 15 cm and height of 20 cm) with the average electrical properties of the brain (σ = 0.55 Sm−1 and ε = 52 ε0) at 298 MHz (Larmor frequency of proton at 7 T). For each coil element, the complex magnetic field at 298 MHz was simulated with a voxel size of 2×2×2 mm3. Target EP maps, which were calculated using the simulated magnetic and electric fields based on Maxwell’s equations, were employed as a ground truth to evaluate the performance of the gEPT algorithm.
Evaluating Accuracy and Noise Robustness of gEPT Based on Simulation
Using the proposed gEPT, estimated EP maps were calculated using simulated magnitude and relative phase Δϕ± maps of the 16 coil elements. A comparison was made between gEPT and the conventional EPT approach based on the homogeneous Helmholtz equation and utilizing multiple transmit/receive RF channels (23,30). To derive εc using the latter, simulated and absolute phase ϕ+ maps of the 16 channels (absolute ϕ+ phase maps cannot be experimentally measured), were utilized to create 16 instances of equations , from which εc was calculated by minimizing the sum of the squares of the residual errors of the 16 equations.
Relative error (RE) and correlation coefficient (CC) were employed as metrics to evaluate reconstructions. For a specific spatial distribution of quantity q, the RE and CC are defined as
| [5] |
where L is the total number of reconstructed voxels and subscript r denotes reconstructed value. Because of technical challenges to acquire reliable B1 information in structures surrounding the brain, such as skull, subcutaneous tissues and skin, we only included three soft tissues (grey matter, white matter and cerebrospinal fluid) to evaluate EP reconstruction within the brain.
In order to account for thermal noise present in actual MRI measurements, we further investigated the behavior of gEPT under noise contamination by adding Gaussian white noise, whose variance was 1/50th of the magnitude of the simulated B1 field (SNR=50, determined to match experimental data), to the real and imagery parts of simulated B1 data in both Duke head and homogeneous phantom model. A comparison was carried out between gEPT and aforementioned Helmholtz-based approach in the phantom model in identical noise-contaminated B1 simulation data smoothed with a Gaussian filter.
Experiments
Experiments were carried out on a 7 T whole body MRI scanner (Siemens, Erlangen, Germany). A 16-channel microstrip array RF coil (32), shown in Fig. 2a, was utilized for all experiments, powered by 16×1kW amplifiers (CPC, Hauppauge, NY, USA) controlled by a remotely operated 16-channel RF phase/amplitude gain unit. As previously described in more details (21,34), global SAR was continuously monitored, with a maximum upper limit, based on International Standard IEC 60601-2-33 2010, determined from the ratio between peak local SAR and global SAR derived from electromagnetic model of the 16-channel coil loaded with a human head.
B1-mapping Protocols
Using a previously proposed hybrid B1-mapping technique consisting of a series of MRI sequences (21,35–37), the magnitude , proton density biased magnitude , and relative phase and were collected for the 16 transmit and receive channels. First of all, a 3D flip angle (FA) map was measured using the Actual Flip Angle technique (AFI) (38), all channels transmitting together with a large nominal FA of 90° (phantom experiments) or 60° (in-vivo experiments). To obtain and for each individual channel, a series of low FA 2D GRE (gradient-recalled echo, nominal FA=10°) images were acquired with one channel transmitting at a time and all channels receiving together. The raw data from the low FA GRE was converted to after being normalized by the measured 3D FA map (36). The proton density weighted magnitude and of receive B1 field were acquired via another series of 2D GRE images obtained with all channels transmitting together (using the same B1 excitation configuration as the 3D AFI), with a long TR of 10s (≫ T1) and with a large nominal FA the same as that of 3D AFI to reach high SNR, normalized by the sine of the corresponding 3D FA map (37).
Phantom Setup and Experiment
A three-compartment 3D phantom, as shown in Fig. 6e, was built out of different saline gel solutions. The EP values of the three compartments of the phantom were σ=0.34, 0.71 and 1.12 Sm−1 and ε=77, 61 and 65 ε0 at the frequency of 298 MHz, respectively, measured with an Agilent 85070D dielectric probe kit and an Agilent E4991A network analyzer (Agilent, Santa Clara, CA, USA). The three solutions consisted of distilled water, NaCl, Sucrose, CuSO4·5H2O and Gelatin in the mass ratio of 100:0.12:0:0.025:3, 100:2.54:73.97:0.025:3 and 100:2.5:49.92:0.025:3, respectively.
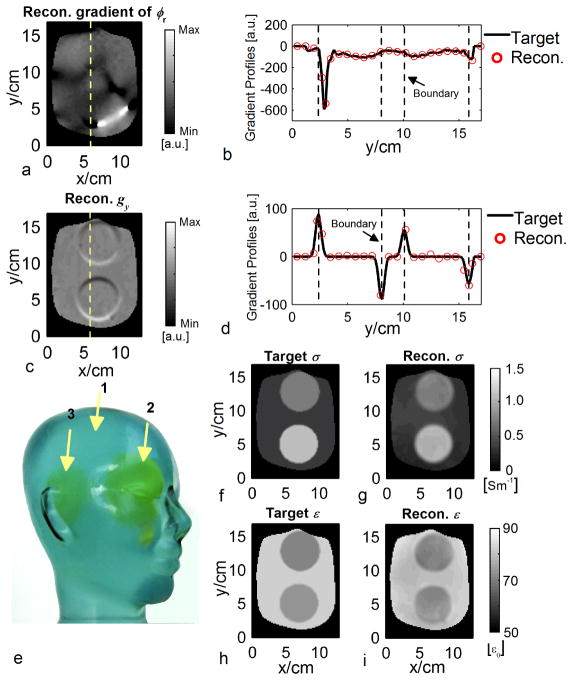
FIG. 6.
Physical phantom results. a: Reconstructed images of ∂ϕr1,6/∂y. ϕr1,6: relative phase between channel #6 and #1. b: Profiles of reconstructed ∂ϕr1,6/∂y and the MRI measurement as the target along the dashed line in a. c: Reconstructed images of imagery part of gy. d: Profiles of reconstructed imagery part of gy and the probe measurement as the target along the dashed line in c. e: Photograph of the phantom. Arrows indicate the interior components. f and h: The target images of σ and ε, respectively. g and i: The reconstructed images of σ and ε using gEPT, respectively.
The phantom was positioned at the isocenter of the coil with its “nose” facing up. Two separate B1 shimming combinations were performed, one tending to reproduce a circularly polarized CP mode with |B1+| maximized at the center of the phantom and another one tending to reproduce a so-called CP2+ mode (39) with |B1+| maximized in a peripheral ring; this strategy, somehow similar to the TIAMO approach (39), helped to circumvent dark spots that were virtually impossible to avoid in individual B1 shimming configurations due to the overall high relative permittivity of the phantom (~77 in majority of the volume). Two full sets of B1-mapping sequences were conducted using the two B1 shimming configurations described above. For each shimming configuration, the 3D AFI images were acquired with TE/TR1/TR2 = 3.23/20/120 ms and two averages in 18 mins; the small FA 2D GRE images with TE/TR = 3.3/76 ms, nominal FA of 12°, and ten averages in 28 mins; the large FA 2D GRE images with TE/TR = 3.1/10000 ms and two averages in 42 mins. These acquisitions were performed in a total number of twelve 3-mm thick slices centered on the phantom center along the z-direction, with a spatial resolution of 1.5×1.5 mm2 within slices in a FOV of 288×189 mm2.
Prior to EP reconstruction, the data were smoothed using a Gaussian filter with a kernel size of 5×5×3 voxels and standard deviation (SD) of 1.2×1.2×0.8 voxels to reduce noise, with a resulting effective voxel size of 4.8×4.8×6.4 mm3 (see Appendix B for definition). In order to remove the proton density from the acquired maps, the phantom was segmented utilizing a priori knowledge of the spherical shape and location of its compartments, and within individual compartment a uniform ρ was assigned so as to maximize continuity of the resulting magnitude map of across compartment boundaries. Utilizing two sets of B1 fields measured under the two B1 shimming settings, two maps of g were calculated and merged based on the respective AFI maps. Three voxels in compartment #1 were chosen as seed points.
In Vivo Human Experiments
We studied two healthy human subjects, with signed consent forms approved by the Institutional Review Board at the University of Minnesota, using the proposed gEPT to generate EP maps in the brain in vivo. In contrast to the phantom experiment, a single B1 shimming configuration, approaching a CP mode, was sufficient to collect B1 maps in the human head without excessively weak |B1+| areas. The 3D AFI images were acquired with TE/TR1/TR2 = 3.23/20/120 ms and one average in 9 mins; the small FA 2D GRE images with TE/TR = 3.3/76 ms, nominal FA of 10°, and ten averages in 28 mins; the large FA 2D GRE images with TE/TR = 3.1/10000 ms and one average in 21 mins. A total of twelve axial slices of B1 field data were acquired with a voxel size of 1.5×1.5×5mm3 with a FOV of 288×189 mm2. A Gaussian filter with kernel size of 5×5×3 voxels and SD of 1.2×1.2×0.8 voxels was used to remove high-frequency noise in the B1 data with a resulting effective voxel size of 4.8×4.8×10.7 mm3. Using a left-right symmetrical RF array coil loaded with an approximately symmetrical normal human head, proton density ρ was estimated based on the left-right mirroring symmetry previously reported of where i and j indicate sixteen transmit and receive channels, respectively (21,35).
RESULTS
Simulations
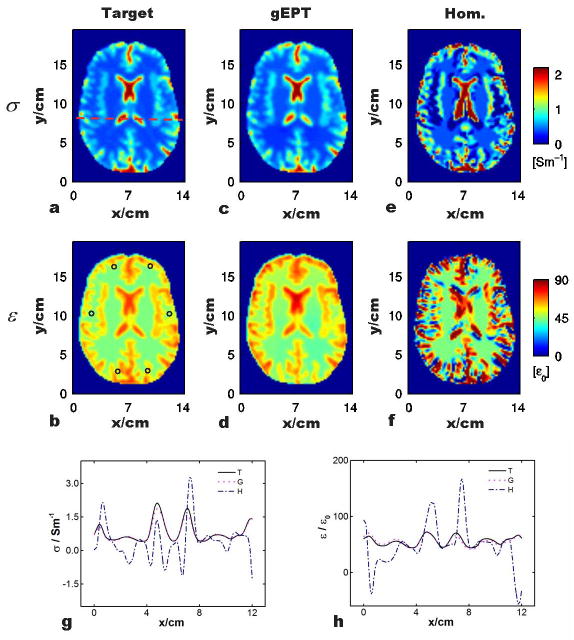
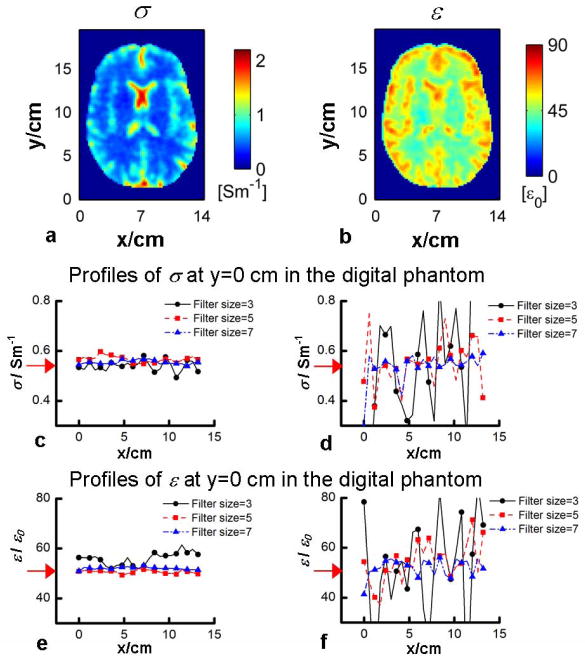
Fig. 3a–b shows the target electrical properties in a transverse slice of the Duke head model. As marked in Fig. 3b (circles), six seed points were selected evenly distributed around the periphery of the brain region for gEPT reconstruction. Fig. 3c–d shows the results of reconstructed σ and ε in the same slice using the proposed gEPT under noise-free condition. Profiles of the results, along the dash line shown in Fig. 3a, are shown in Fig. 3g–h for a closer comparison to the target values. In general, it can be seen in Fig. 3c–d that the detailed structural information present in the target maps was accurately reproduced in the reconstructed maps of σ and ε using gEPT; in Fig 3g–h, the reconstruction profiles closely follow those of target values. Within the brain region, the overall RE and CC of the reconstruction are RE=8.5%/CC=0.98 for σ reconstruction, and RE=7.6%/CC=0.90 for ε reconstruction, respectively. In contrast, as shown in Fig. 3e–f as well as in the profiles in Fig. 3g–h, results using the homogeneous Helmholtz equation exhibit substantial errors near the boundaries with RE=99.7%/CC=0.38 for σ reconstruction and RE=58.0%/CC=0.25 for ε reconstruction, respectively. The reconstruction performance of using gEPT under noise situation (SNR=50) based on the Duke head model is depicted in Fig. 4a–b. A 3D Gaussian filter, with a kernel size of 3 voxels and SD of 0.8 voxels in all three directions, was utilized to smooth the data before gEPT reconstruction. As can be seen in Fig. 4a–b, the resulting maps using gEPT show consistency in comparison with the target images in Fig. 3a–b. Overall RE=15.7% and CC=0.96 for the reconstructed σ, and RE=10.2% and CC=0.80 for the reconstructed ε were achieved, respectively, with the results for individual tissues summarized in Table 1. Note the slightly smoothed patterns of the reconstructed EP maps, especially the permittivity, that we attributed to the use of the smoothing filter.
FIG. 3.
Comparison of the reconstructed electrical properties based on gEPT and homogeneous Helmholtz equation, respectively, with respect to the target values. a and b: Target σ and σ. ‘o’: location of seed points. c and d: Reconstruction using gEPT. e and f: Reconstruction based on homogeneous equation. g and h: Profiles of the reconstructed σ and ε using the two methods along the red dash line as shown in (a). ‘T’: target, ‘G’: gEPT and ‘H’: homogeneous Helmholtz equation.
FIG. 4.
a and b: Reconstruction of the electrical properties of the Duke head model using gEPT when SNR=50. Reconstruction of the electrical properties using gEPT (c and e) or based on the Helmholtz equation (d and f) in the homogeneous phantom model when SNR=50 and different Gaussian filter was applied. Red arrows indicate the true target EP values of the phantom model.
TABLE 1.
Relative errors and correlation coefficients of EP reconstruction using gEPT in the Duke head model based on various assumptions when SNR=50.
| REs | SNR=50 without Bz | SNR=50 without Bz Estimated PD | SNR=50 with Bz | ||||
|---|---|---|---|---|---|---|---|
| GM | σ | 13.6% | 13.6% | 13.4% | |||
| ε | 9.3% | 11.3% | 6.3% | ||||
|
| |||||||
| WM | σ | 12.2% | 11.6% | 11.7% | |||
| ε | 8.4% | 10.6% | 8.2% | ||||
|
| |||||||
| CSF | σ | 19.1% | 19.3% | 18.7% | |||
| ε | 16.2% | 14.9% | 6.6% | ||||
|
| |||||||
| Total (REs/CCs) | σ | 15.7% | 0.96 | 15.7% | 0.96 | 15.3% | 0.96 |
| ε | 10.2% | 0.80 | 11.6% | 0.82 | 7.1% | 0.90 | |
For the numerical homogeneous phantom study, Gaussian filters of different sizes were utilized to smooth the noise-contaminated B1 data (SNR=50), including 3-, 5- and 7-voxel kernels with corresponding SD of 0.8, 1.2 and 1.6 voxels. Using gEPT, a voxel in the center of the slice of interest was used as the seed point. The results shown in Fig. 4c–f indicate that, compared to the Helmholtz-based approach (even though the latter is free of boundary errors in this homogeneous phantom model), gEPT is more robust against measurement noise, and does not require the use of strong Gaussian filter with large kernel size and/or SD value to reduce the noise level. Using gEPT, no significant accumulation of noise-induced error was observed as the distance increases from the central seed point.
As can be observed in Fig. 2, in the center slice of the Duke head or of the phantom model, the component related to the x- and y-direction derivatives of B1+ is the dominant one among the coefficients of Eq. 2, and similar observations can be made for the receive B1 field. It was thus considered reasonable to ignore Bz-related components to calculate the solution of Eq. 2 and 3. In order to further evaluate the impact of omitting these components, gEPT based reconstructions were performed while also using Bz, obtained from simulations, with SNR=50. As can be seen in Table 1, the corresponding conductivity results were similar to those obtained without Bz, both for individual tissue and overall brain, while the corresponding permittivity results slightly deteriorated.
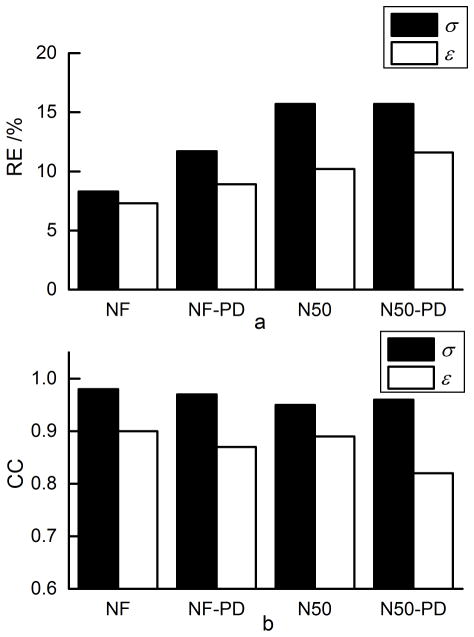
The impact of empirically estimating proton density in Duke head based on the symmetrical assumption on the gEPT performance is shown in Table 1 and Fig. 5. As can be seen, in the most realistic scenario, i.e. with unknown proton density and added measurement noise, the RE for σ and ε were 15.7% and 11.6%, and CC 0.96 and 0.82, respectively. In comparison with the noise-free situation, the effect of empirical proton density estimation was not as significant as the effect of measurement noise.
FIG. 5.
Summary of RE and CC of gEPT under different conditions. “NF”: noise-free with no proton density bias. “NF-PD”: noise-free with proton density estimated by symmetry assumption. “N50”: noisy condition SNR=50 with no proton density bias. “N50-PD”: noisy condition SNR=50 with proton density estimated by symmetry assumption. a: RE. b: CC.
Phantom Studies
The estimated proton densities were 1.00, 0.64 and 0.74 for the three compartments of the phantom used (Fig. 6e), respectively. In Fig. 6, examples of the extracted gradient of relative phase ϕr1,6 (between channel #6 and #1) and g are compared to the target values, showing high accuracy even in the vicinity of the boundaries where EPT algorithms based on the homogeneous Helmholtz equation typically tend to fail. Three voxels within component #1, one located at the iso-center and two near the circumference, were chosen as the seed points to provide EP information using their probe-measured values. The reconstructed EP maps are shown in Fig. 6g–i and summarized as σ=0.34±0.07, 0.71±0.08, and 0.97±0.13 Sm−1/ε=75.6±2.7, 63.3±5.3 and 64.3±3.2 ε0 for the corresponding components of the phantom, respectively, depicting large agreement compared with measurements using the dielectric probe.
In Vivo Human Experiments
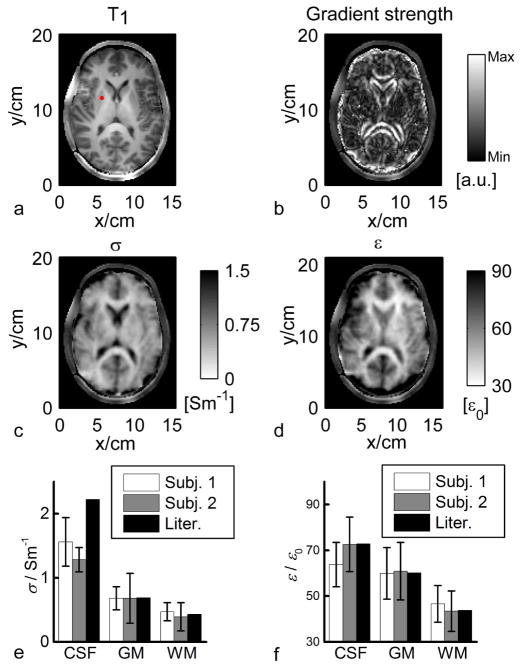
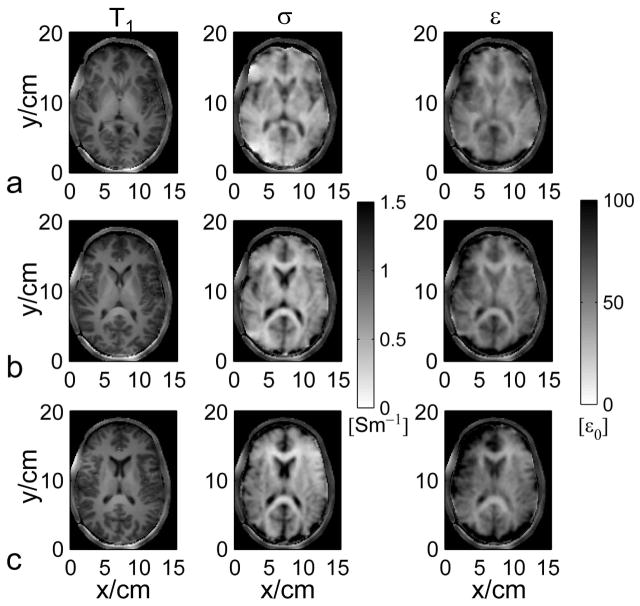
Figure 7 shows in vivo results in two healthy human subjects. As indicated by the red dot in Fig. 7a, one seed point within the right putamen was used to provide the initial EP information, assigned with σ and ε of grey matter based on previously reported ex vivo measurement (40). In the brain, transverse slice #6 was chosen to illustrate the results of gEPT because it is the closest to the middle of the RF coil along z-direction, where Bz variations are expected to be the smallest and thus can be ignored. From subject #1, magnitude of the extracted ∇lnεc (real part) is shown in Fig. 7b, as well as the estimated σ and ε in Fig. 7c and d, respectively. When comparing Fig. 7a (T1w image) with Fig. 7b (gradient strength derived from measured B1 maps), one can appreciate the spatial correspondence between contours of anatomical structures (ventricles, gyri/sulci) and local high values of estimated gradient. Likewise, the conductivity and permittivity maps shown in Figs. 7c and d restitute with remarkable accuracy the spatial distribution of white matter, grey matter and ventricles, as well as the curvature of the cortex. Importantly, EP imaging results from two more adjacent slices further confirm these observations, as shown in Fig. 8, as structural variations from one slice to another identified on T1w images can be followed on corresponding EP maps as well. As anticipated, errors arise at the periphery of the brain when approaching the vicinity of the skull as almost no MR signal is detected in bones with standard MR sequence so that no reliable B1 information could be collected. Using a segmentation of the brain tissues obtained with the T1w image, the statistics (mean±SD) for three types of tissues, grey matter (GM), white matter (WM) and cerebrospinal fluid (CSF) on slice #6 of the two subjects were summarized in Fig. 7e and f in comparison with literature-reported values (40). Note the high consistency between the gEPT reconstructed values and ex vivo measurements. One exception concerns the mean conductivity of CSF, which is lower than the literature value. Factors, such as partial volume effect (large difference between conductivity of CSF and surrounding tissues) or the weaker average magnitude of B1 for each coil element at the center of the brain, with reduced SNR, could contribute to the drop in value of the mean reconstructed conductivity in CSF.
FIG. 7.
In vivo experimental results in humans. a: T1-weighted image. The red dot indicates the seed point. b: Reconstructed magnitude image of the real part of ∇lnεc. c: Reconstructed σ. d: Reconstructed ε. e and f: Summary of the reconstruction results of σ and ε of the two human subjects with reference to the literature values.
FIG. 8.
a–c: The reconstructed electrical properties in three transverse slices in the brain of human subject #1 using gEPT with respect to the T1-weighted images.
DISCUSSION
The fundamental novelty in our proposed gEPT approach consists in recognizing and explicitly utilizing the fact that the gradient g bears the necessary information to reconstruct EP boundaries. Although in vivo EPT in the human brain have been reported, at different magnetic fields (1.5, 3 and 7 T) and with different RF coil designs (21,23,25,41), it is our understanding that these maps still suffer from significant deviations in EP values especially near tissue boundaries as a result of the homogeneous Helmholtz equation (28). In the proposed gEPT method, measurable information of both B1+ and B1− fields from a multi-channel transceiver RF coil was acquired and utilized to solve our central equations, and the derived gradient field g was explicitly employed to reconstruct EP maps. We believe that our results (see Figs. 7 and 8) demonstrate a substantial improvement in the quality of EP maps obtained in vivo on human brain imaging. In attempting to address the boundary issue, an adaptive-filter approach has been proposed and in vivo results have been acquired (42). However, it can be challenging to sustain its fidelity in small inhomogeneous regions because its effectiveness heavily relies on the accuracy of a pre-segmentation of imaged objects.
Another merit of our proposed gEPT algorithm comes from the inherent low-pass filtering property (noise reduction) of integration on the gradient g while most other studies obtained EP maps directly through differentiation on B1 fields without explicitly utilizing g information. MR signals are by nature contaminated with noise. Some insight into the high sensitivity of conventional non-gradient-based EPT to measurement noise can be gained by looking at both the homogeneous and inhomogeneous Helmholtz equations: it can be seen that the Laplacian operator will amplify errors that then propagate linearly into the complex permittivity εc, and its derivative g. Although a strong spatial filter can attenuate measurement noise without significantly distorting the B1 field, subsequent EP reconstruction will significantly be affected by such smoothing procedure, especially for the Helmholtz equation-based methods (28). As shown in Fig. 4c–f in a homogeneous phantom model, with gEPT, the employed integration method over g largely suppresses the amplification of noise-related errors that are still observed with the Helmholtz equation-based method, which is free of boundary errors in the homogeneous model. In this study, the gEPT method which only utilizes the derived g separately from εc in the central equation, has been shown with largely improved imaging performance. Nonetheless, it is anticipated that utilizing information carried in both εc and g may further improve robustness and reliability of the reconstruction.
The increased performance of gEPT against measurement noise will in return contribute to improved boundary reconstruction by eliminating the use of strong spatial filter on B1 field, so that B1-maps could be exploited at higher spatial resolution. As a result, significant improvement in EP map quality may be obtained in vivo (Fig. 7 and 8). In the current study, additional factors relating with the use of high B0 field (7 T) may contribute to the robust performance of gEPT even in the presence of measurement noise, such as enhanced curvature of RF field caused by shortened wavelength and boosted SNR of MR signal; likewise, redundant transmit and receive B1 information resulting from the use of multiple RF channels may give an advantage to our approach. In the future, it will be worth investigating different integration methods to reconstruct EP from its gradient g, such as the 2-D layer potential technique utilized in MREIT (43) and MAT-MI (44).
The assumptions made to establish the central equation are prone to two main sources of errors. The first source of error comes from the elimination of Bz, a quantity that cannot be measured with existing MR techniques. Using the microstrip RF coil with a uniform geometry along the z-direction, it was demonstrated that only minimum Bz-related components are expected in a group of transverse slices positioned at the middle of the coil along the z-axis as shown in Fig. 2 d–e; it was further shown in Table 1, using noise-contaminated B1 data, that when actually including Bz (as known), the improvement of gEPT was not significant compared to the case eliminating Bz. Besides, the assumption that Bz can be ignored has been adopted in previous EPT studies (21,30) and is supported by simulation results using EM modeling (45). Note however that the current implementation of the gEPT algorithm has been demonstrated only for experimental configurations where the aforementioned assumptions can be made; further work will be needed to investigate the applicability of gEPT algorithm to coil structures and/or anatomical targets that do not meet these criteria.
Another modeling error comes from the method of proton density estimation utilized in receive B1 magnitude mapping. Till now, there has been no direct technique in proton density imaging at UHF; the previously reported approach (21,35), which is based on the symmetrical assumption between the transmit and receive B1 field, has been employed in this study. As shown in Fig. 5, when using a left-right symmetric RF coil and an approximately symmetric normal human head model, the left-right symmetry assumption between the summations of the magnitude of transmit and receive B1 fields performs as a feasible alternative to extract proton density for the purpose of gEPT. In practice, asymmetrical experimental conditions, such as shifted object position from the symmetric axis or unbalanced gains of RF signal in different receive channels, need to be accounted for to minimize errors from less accurate proton density estimation. The symmetry assumption can also be prone to inaccuracies if the imaged sample presents noticeably asymmetrical EP distribution.
A full framework describing EPT without resorting to any assumption has been proposed in another study (27). Although this general theory may provide a formalism to extract missing components, e.g. Bz and proton density, it remains to be demonstrated how this theoretical approach could be fully translated into experimental settings. With our proposed method we were able to demonstrate in-vivo EP maps carrying a remarkable accuracy of tissue’s electrical properties that include a depiction of underlying anatomical structures (white and grey matter, ventricles) without significant deterioration due to either measurement noise or boundary artifact while utilizing standard MR imaging sequences.
As explained in the Methods section, some seed point(s) with known EP values is (are) needed to convert the estimated gradient into absolute EP maps. Evaluation in numerical simulation indicated that the performance of gEPT is fairly stable regarding to variable seed point locations and errors in the assigned EP value of chosen seed points (results not shown here). As one would expect, the more seed points are utilized, the more reliable and stable results can be achieved. For future in vivo application, the EP values of a few seed points could be obtained from brain regions expected to exhibit relatively smooth local EP distribution (i.e. no sharp boundaries), identified on standard anatomical MR images (e.g. large white matter bundles). In these locations, homogeneous-Helmholtz-based EPT methods could be utilized to measure absolute EP values in these seed points, even though these methods would likely fail in the vast fraction of brain tissues presenting sharp EP boundaries. It is worth emphasizing that more advanced algorithms could advantageously combine the advantage of gEPT together with those of other EPT algorithms for a more integrated approach and improved performance.
CONCLUSION
In summary, we have developed a novel gradient-based MR electrical properties tomography (gEPT) approach, and demonstrated significant improvement of in vivo EP maps of the human brain with gEPT, especially with regard to boundary reconstruction and robustness against noise. The current gEPT implementation has been specifically designed for coil structures and anatomical targets that satisfy specific assumptions about the unknown B1 components. Further work will be needed to investigate the applicability of gEPT to other configurations that do not satisfy these criteria. By generating more accurate and more stable in vivo EP maps, the gEPT method promises to help develop a more significant role of EPT in the investigation of fundamental aspects of tissues, clinical diagnosis and SAR prediction.
Acknowledgments
We thank Mr. Leo Mariappan for useful discussions. This work was supported in part by NIH R21 EB017069, R01 EB006433, R01 EY023101, U01 HL117664, R21 EB014353, R21 EB009138, T32 EB008389, P30 NS076408, P41 EB015894, 2R01 EB006835, 2R01 EB007327, S10 RR26783, NSF CBET-1264782, DGE-1069104, and WM KECK Foundation.
APPENDIX A: DERIVING THE CENTRAL EQUATIONS
Deriving Eq. 2 and 3 From Eq. 1
Following the rule of cross product and curl operation, Equation 1 can be rewritten as
| [A1] |
In the rotating frame, the effective transmit and receive B1 field components can be expressed via the combination of the Cartesian B1 components (46) as
| [A2] |
Utilizing Gauss’s Law for Magnetism ∇ · B = 0, it gives us
| [A3] |
Adding the first two identities in Eq. A1 with coefficients of (1, i) or (1, −i), we can further transform Eq. 1 into Eq. 2 and 3, respectively, by utilizing the identities in Eq. A2 and A3.
Solving the Central Equation Using the Magnitudes and Relative Phases of and From Multiple Channels
Equation 4(a) was chosen as an example to illustrate the steps to derive g+ using multiple channels of magnitude and relative phase of the transmit B1 field. For the purpose of simplicity, the ‘+’ sign attached in g+ and B1+ was removed in Eq. 4(a). Expanding the Laplacian and gradient operation on the complex B1 field B1 = |B1|eiϕ, we have
| [A4] |
| [A5] |
where ϕ ≡ ϕ0 + ϕr denotes the spatial phase of the complex B1 field, ϕ0 the phase of a designated reference channel and ϕr the relative phase of the given channel. Substituting ϕ with ϕ0 + ϕr and separating the real and imaginary parts in Eq. 4(a), we will obtain
| [A6] |
and
| [A7] |
where ε′ ≡ ε/ε0, ε″ ≡ −σ/(ωε0), c ≡ ω2μ0ε0, ℜ or ℑ denotes the real or imagery part of a complex number, respectively. For each voxel in the image, Eqs. A6 and A7 can be transformed into a set of linear equations utilizing magnitude and relative phase information from multiple channels. Note that, as shown in Eqs. A6 and A7, several channel-independent unknown items which are either nonlinear or dependent on each other were grouped into one component. The obtained linear equations were solved by least-square method to provide g+.
APPENDIX B: DEFINATION OF EFFECTIVE VOXEL SIZE
A 1D Gaussian filter is defined as
| [B1] |
where x is distance and σs the standard deviation of the filter, both in unit of voxels. The spatial frequency response of the filter [B1] is given by
| [B2] |
where f is spatial frequency and σf σf = 1/2πσs the standard deviation of the frequency response of the filter, in unit of 1/voxel. Defining the cut-off frequency fc where the power spectrum drops to half, we have
| [B3] |
The effective voxel size after smoothing is perceived as the necessary voxel size to preserve the cut-off frequency. Based on the sampling theorem, the effective voxel size after filtering is the smaller of and filter’s kernel size.
For a 3D Gaussian filter, similar analysis can be applied on its each direction.
References
- 1.Gabriel C, Gabriel S, Corthout E. The dielectric properties of biological tissues: I. Literature survey. Phys Med Biol. 1996;41:2231–2249. doi: 10.1088/0031-9155/41/11/001. [DOI] [PubMed] [Google Scholar]
- 2.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys Med Biol. 1996;41:2251–2269. doi: 10.1088/0031-9155/41/11/002. [DOI] [PubMed] [Google Scholar]
- 3.Surowiec AJ, Stuchly SS, Barr JR, Swarup A. Dielectric properties of breast carcinoma and the surrounding tissues. IEEE Trans Biomed Eng. 1988;35:257–263. doi: 10.1109/10.1374. [DOI] [PubMed] [Google Scholar]
- 4.Jossinet J, Schmitt M. A Review of Parameters for the Bioelectrical Characterization of Breast Tissue. Ann N Y Acad Sci. 1999;873:30–41. doi: 10.1111/j.1749-6632.1999.tb09446.x. [DOI] [PubMed] [Google Scholar]
- 5.Wilkinson BA, Smallwood RH, Keshtar A, Lee JA, Hamdy FC. Electrical Impedance Spectroscopy and the Diagnosis of Bladder Pathology: A Pilot Study. J Urol. 2002;168:1563–1567. doi: 10.1016/S0022-5347(05)64521-1. [DOI] [PubMed] [Google Scholar]
- 6.Jossinet J. The impedivity of freshly excised human breast tissue. Physiol Meas. 1998;19:61–75. doi: 10.1088/0967-3334/19/1/006. [DOI] [PubMed] [Google Scholar]
- 7.Swarup A, Stuchly SS, Surowiec A. Dielectric properties of mouse MCA1 fibrosarcoma at different stages of development. Bioelectromagnetics. 1991;12:1–8. doi: 10.1002/bem.2250120102. [DOI] [PubMed] [Google Scholar]
- 8.Haacke EM, Petropoulos LS, Nilges EW, Wu DH. Extraction of conductivity and permittivity using magnetic resonance imaging. Phys Med Biol. 1991;36:723–734. [Google Scholar]
- 9.Wen H. Noninvasive quantitative mapping of conductivity and dielectric distributions using RF wave propagation effects in high-field MRI. Proc. SPIE 5030, Medical Imaging: Physics of Medical Imaging; San Diego, CA, USA. 2003. pp. 471–477. [Google Scholar]
- 10.Katscher U, Voigt T, Findeklee C, Vernickel P, Nehrke K, Dossel O. Determination of Electric Conductivity and Local SAR Via B1 Mapping. IEEE Trans Med Imag. 2009;28:1365–1374. doi: 10.1109/TMI.2009.2015757. [DOI] [PubMed] [Google Scholar]
- 11.Zhang X, Zhu S, He B. Imaging Electric Properties of Biological Tissues by RF Field Mapping in MRI. IEEE Trans Med Imag. 2010;29:474–481. doi: 10.1109/TMI.2009.2036843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Metherall P, Barber DC, Smallwood RH, Brown BH. Three-dimensional electrical impedance tomography. Nature. 1996;380:509–512. doi: 10.1038/380509a0. [DOI] [PubMed] [Google Scholar]
- 13.Paulson K, Lionheart W, Pidcock M. Optimal experiments in electrical impedance tomography. IEEE Trans Med Imag. 1993;12:681–686. doi: 10.1109/42.251118. [DOI] [PubMed] [Google Scholar]
- 14.Woo EJ, Seo JK. Magnetic resonance electrical impedance tomography (MREIT) for high-resolution conductivity imaging. Physiol Meas. 2008;29:R1–26. doi: 10.1088/0967-3334/29/10/R01. [DOI] [PubMed] [Google Scholar]
- 15.Xu Y, He B. Magnetoacoustic tomography with magnetic induction (MAT-MI) Phys Med Biol. 2005;50:5175–5187. doi: 10.1088/0031-9155/50/21/015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li X, Xu Y, He B. Imaging Electrical Impedance From Acoustic Measurements by Means of Magnetoacoustic Tomography With Magnetic Induction (MAT-MI) IEEE Trans Biomed Eng. 2007;54:323–330. doi: 10.1109/TBME.2006.883827. [DOI] [PubMed] [Google Scholar]
- 17.Hu G, Cressman E, He B. Magnetoacoustic imaging of human liver tumor with magnetic induction. Appl Phys Let. 2011;98:23703. doi: 10.1063/1.3543630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mariappan L, He B. Magnetoacoustic Tomography with Magnetic Induction: Bioimepedance reconstruction through vector source imaging. IEEE Trans Med Imag. 2013;32:619–627. doi: 10.1109/TMI.2013.2239656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Collins CM, Liu W, Wang J, Gruetter R, Vaughan JT, Ugurbil K, Smith MB. Temperature and SAR calculations for a human head within volume and surface coils at 64 and 300 MHz. J Magn Reson Imaging. 2004;19:650–656. doi: 10.1002/jmri.20041. [DOI] [PubMed] [Google Scholar]
- 20.Uđurbil K, Adriany G, Andersen P, et al. Ultrahigh field magnetic resonance imaging and spectroscopy. Magn Reson Imaging. 2003;21:1263–1281. doi: 10.1016/j.mri.2003.08.027. [DOI] [PubMed] [Google Scholar]
- 21.Zhang X, Van de Moortele P-F, Schmitter S, He B. Complex B1 mapping and electrical properties imaging of the human brain using a 16-channel transceiver coil at 7T. Magn Reson Med. 2013;69:1285–1296. doi: 10.1002/mrm.24358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu J, Zhang X, Van de Moortele P-F, Schmitter S, He B. Determining electrical properties based on B(1) fields measured in an MR scanner using a multi-channel transmit/receive coil: a general approach. Phys Med Biol. 2013;58:4395–4408. doi: 10.1088/0031-9155/58/13/4395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sodickson D, Alon L, Deniz C, et al. Local Maxwell Tomography Using Transmit-Receive Coil Arrays for Contact-Free Mapping of Tissue Electrical Properties and Determination of Absolute RF Phase. Proceedings of the 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012. p. 387. [Google Scholar]
- 24.Van Lier AL, Brunner DO, Pruessmann KP, Klomp DWJ, Luijten PR, Lagendijk JJW, van den Berg CAT. B 1+ Phase mapping at 7 T and its application for in vivo electrical conductivity mapping. Magn Reson Med. 2012;67:552–561. doi: 10.1002/mrm.22995. [DOI] [PubMed] [Google Scholar]
- 25.Voigt T, Katscher U, Doessel O. Quantitative conductivity and permittivity imaging of the human brain using electric properties tomography. Magn Reson Med. 2011;66:456–466. doi: 10.1002/mrm.22832. [DOI] [PubMed] [Google Scholar]
- 26.Liu J, Zhang X, He B. Imaging Electrical Properties of Human Head with Tumor Using Multi-channel Transceiver Coil at UHF: A Simulation Study. Proceedings of the 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012. p. 3486. [Google Scholar]
- 27.Sodickson D, Alon L, Deniz C, Ben-Eliezer N, Cloos M, Sodickson L, Collins CM, Wiggins G, Novikov D. Generalized Local Maxwell Tomography for Mapping of Electrical Property Gradients and Tensors. Proceedings of the 21th Annual Meeting of ISMRM; Salt Lake City, USA. 2013. p. 4175. [Google Scholar]
- 28.Seo JK, Kim M-O, Lee J, Choi N, Woo EJ, Kim HJ, Kwon OI, Kim D-H. Error analysis of nonconstant admittivity for MR-based electric property imaging. IEEE Trans Med Imaging. 2012;31:430–437. doi: 10.1109/TMI.2011.2171000. [DOI] [PubMed] [Google Scholar]
- 29.Zhang X, Schmitter S, Van de Moortele P-F, Liu J, He B. From Complex B1 Mapping to Local SAR Estimation for Human Brain MR Imaging Using Multi-channel Transceiver Coil at 7T. IEEE Trans Med Imaging. 2013;32:1058–1067. doi: 10.1109/TMI.2013.2251653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Katscher U, Findeklee C, Voigt T. B1-based specific energy absorption rate determination for nonquadrature radiofrequency excitation. Magn Reson Med. 2012;68:1911–1918. doi: 10.1002/mrm.24215. [DOI] [PubMed] [Google Scholar]
- 31.Iserles A. A first course in the numerical analysis of differential equations. 2. Cambridge, UK; New York: Cambridge University Press; 2009. [Google Scholar]
- 32.Adriany G, Van de Moortele P-F, Ritter J, Moeller S, Auerbach EJ, Akgün C, Snyder CJ, Vaughan T, Uğurbil K. A geometrically adjustable 16-channel transmit/receive transmission line array for improved RF efficiency and parallel imaging performance at 7 Tesla. Magn Reson Med. 2008;59:590–597. doi: 10.1002/mrm.21488. [DOI] [PubMed] [Google Scholar]
- 33.Christ A, Kainz W, Hahn EG, et al. The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2010;55:N23. doi: 10.1088/0031-9155/55/2/N01. [DOI] [PubMed] [Google Scholar]
- 34.Metzger GJ, van de Moortele P-F, Akgun C, et al. Performance of external and internal coil configurations for prostate investigations at 7 T. Magn Reson Med. 2010;64:1625–1639. doi: 10.1002/mrm.22552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Van de Moortele P-F, Ugurbil K. Very Fast Multi Channel B1 Calibration at High Field in the Small Flip Angle Regime. Proceedings of the 17th Annual Meeting of ISMRM; Hawaii, USA. 2009. p. 367. [Google Scholar]
- 36.Van de Moortele P-F, Snyder C, DelaBarre L, Adriany G, Vaughan T, Ugurbil K. Calibration Tools for RF Shim at Very High Field with Multiple Element RF Coils: from Ultra Fast Local Relative Phase to Absolute Magnitude B1+ Mapping. Proceedings of the 15th Annual Meeting of ISMRM; Berlin, Germany. 2007. p. 1676. [Google Scholar]
- 37.Van de Moortele P-F, Akgun C, Adriany G, Moeller S, Ritter J, Collins CM, Smith MB, Vaughan JT, Uğurbil K. B1 destructive interferences and spatial phase patterns at 7 T with a head transceiver array coil. Magn Reson Med. 2005;54:1503–1518. doi: 10.1002/mrm.20708. [DOI] [PubMed] [Google Scholar]
- 38.Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007;57:192–200. doi: 10.1002/mrm.21120. [DOI] [PubMed] [Google Scholar]
- 39.Orzada S, Johst S, Maderwald S, Bitz AK, Solbach K, Ladd ME. Mitigation of B1(+) inhomogeneity on single-channel transmit systems with TIAMO. Magn Reson Med. 2013;70:290–294. doi: 10.1002/mrm.24453. [DOI] [PubMed] [Google Scholar]
- 40.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys Med Biol. 1996;41:2271–2293. doi: 10.1088/0031-9155/41/11/003. [DOI] [PubMed] [Google Scholar]
- 41.Van Lier ALHMW, Raaijmakers A, Voigt T, Lagendijk JJW, Luijten PR, Katscher U, van den Berg CAT. Electrical Properties Tomography in the Human Brain at 1.5, 3, and 7T: A Comparison Study. Magn Reson Med. 2013 doi: 10.1002/mrm.24637. [DOI] [PubMed] [Google Scholar]
- 42.Huhndorf M, Stehning C, Rohr A, Helle M, Katscher U, Jansen O. Systematic Brain Tumor Conductivity Study with Optimized EPT Sequence and Reconstruction Algorithm. Proceedings of the 21th Annual Meeting of ISMRM; Salt Lake City, USA. 2013. p. 3626. [Google Scholar]
- 43.Oh SH, Lee BI, Woo EJ, Lee SY, Cho MH, Kwon O, Seo JK. Conductivity and current density image reconstruction using harmonic Bz algorithm in magnetic resonance electrical impedance tomography. Phys Med Biol. 2003;48:3101–3116. doi: 10.1088/0031-9155/48/19/001. [DOI] [PubMed] [Google Scholar]
- 44.Li X, He B. Multi-excitation magnetoacoustic tomography with magnetic induction for bioimpedance imaging. IEEE Trans Med Imag. 2010;29:1759–1767. doi: 10.1109/TMI.2010.2052063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang B, Sodickson DK, Lattanzi R, Duan Q, Stoeckel B, Wiggins GC. Whole body traveling wave magnetic resonance imaging at high field strength: homogeneity, efficiency, and energy deposition as compared with traditional excitation mechanisms. Magn Reson Med. 2012;67:1183–1193. doi: 10.1002/mrm.23107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hoult DI. The principle of reciprocity in signal strength calculations—A mathematical guide. Concepts Magn Reson. 2000;12:173–187. [Google Scholar]