Seamless Phase I/II Adaptive Design For Oncology Trials of Molecularly Targeted Agents

Abstract

In dose-finding trials of chemotherapeutic agents, the goal of identifying the maximum tolerated dose is usually determined by considering information on toxicity only, with the assumption that the highest safe dose also provides the most promising outlook for efficacy. Trials of molecularly targeted agents challenge accepted dose-finding methods because minimal toxicity may arise over all doses under consideration and higher doses may not result in greater response. In this article, we propose a new early-phase method for trials investigating targeted agents. We provide simulation results illustrating the operating characteristics of our design.

1 Introduction

1.1 Background

In general, the primary objective of Phase I clinical trials is to identify the maximum tolerated dose (MTD) of the agent or agents being investigated. In a subsequent Phase II trial, the agent is evaluated for efficacy at the recommended dose (MTD). In oncology trials of chemotherapeutic agents, identification of the MTD is usually determined by considering dose-limiting toxicity (DLT) information only, with the assumption that the MTD is the highest dose that satisfies some safety requirement, so that it provides the most promising outlook for efficacy. Numerous Phase I designs have been proposed for identifying the MTD from a discrete set of doses in which toxicity is described as a binary outcome (Storer, 1989; O’Quigley, Pepe, and Fisher, 1990; Ji, et al., 2010; among many others) or an ordinal outcome (Yuan, Chappell, Bailey, 2007; Van Meter, Garrett-Mayer, and Bandyopadhyay, 2011; Iasonos, Zohar, and O’Quigley, 2011; among others). Usually, Phase I and Phase II trials are performed independently, without formally sharing information across the separate phases. There has been a recent shift in the paradigm of drug development in oncology to integrate Phase I and Phase II trials so that drug development process may be accelerated, while potentially reducing costs (Yin, 2012). To this end, several published Phase I/II methods have extended dose-finding methodology to allow for the modeling of both toxicity and efficacy (O’Quigley, Hughes, and Fenton, 2001; Braun, 2002; Thall and Cook, 2004; Yin, Li and Ji, 2006; among others). Each of these designs, as well as the one we propose in this current work, is referred to by Federov and Leonov (2013) as a “best intention” (BI) design, meaning that it aims to allocate patients in the current trial to the “best” treatment based on the current knowledge available. We distinguish these designs from “optimal” designs in the area of dose-finding that seek to maximize global information about dose-response curves in order optimize doses for future patients. In addition to the detailed discussion provided by Federov and Leonov (2013), we refer any reader interested in this type of design to Dragalin and Federov (2006) and Whitehead et al. (2006), among many others.

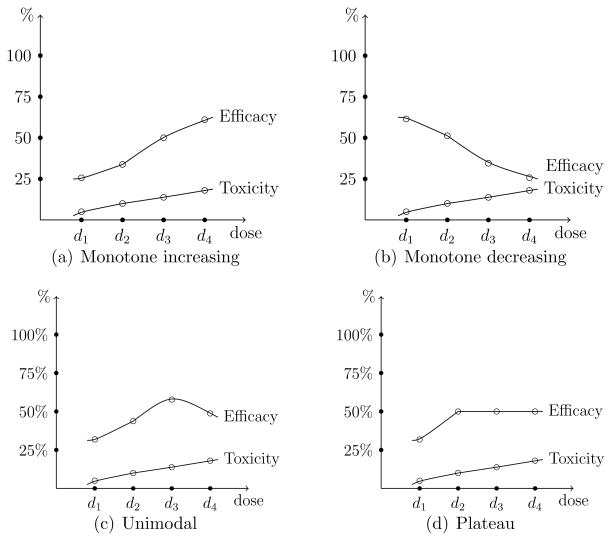
In general, the design of Phase I trials is driven by the assumption of monotone increasing dose-toxicity and dose-efficacy relationships. By contrast, many molecularly targeted agents (MTA’s) are essentially considered safe and higher doses do not necessarily produce greater efficacious response. Dose-efficacy relationships may exhibit non-monotone patterns, such as increasing at low doses and either decreasing or plateauing at higher levels, as displayed in Figure 1. Therefore, the goal of the trial shifts to identifying the optimal biological dose (OBD), which is defined as the dose with acceptable toxicity that maximizes efficacious response. Despite the emergence of molecularly targeted agents in oncology drug development, there are relatively few statistical methods for designing Phase I trials of these agents (Mandrekar, Qin, and Sargent, 2010). Assuming minimal toxicity over the therapeutic dose range, Hunsberger et al. (2005) described two practical Phase I designs for identifying the OBD for molecularly targeted agents. Zhang, Sargent and Mandrekar (2006) introduced a trinomial continual reassessment method (TriCRM) that utilizes a continuation ratio to model toxicity and efficacy simultaneously. Mandrekar, Cui, and Sargent (2007) extended this method to account for combinations for two agents. Polley and Cheung (2008) outlined a two-stage design for finding the OBD that implements a futility interim analysis. Recently, Hoering, LeBlanc, and Crowley (2011) and Hoering et al. (2013) proposed methods for early phase trials of targeted agents that uses a traditional dose-finding method to find the MTD in Phase I, and then subsequently allocates patients in Phase II to the MTD (Hoering et al., 2011) or a small set of doses at and around the MTD (Hoering et al., 2013) based on a randomization scheme.

Figure 1.

Possible dose-toxicity and dose-efficacy relationships for molecularly targetd agents.

In this article, we outline a method for identifying the OBD that combines features of the continual reassessment method (CRM; O’Quigley et al., 1990) and order restricted inference (Robertson, Wright, and Dykstra, 1988). The existing methods in this area take a fixed set of admissible doses from the Phase I portion into the Phase II portion of the study in order to assess efficacy. For instance, the design of Hoering et al. (2013) uses a 3+3 design in the Phase I portion to locate the MTD. However, if the OBD is not close to the MTD, a design that targets the MTD may fail to accurately locate the most efficacious dose. Moreover, the statistical limitations of the 3+3 design have been discussed at length in the literature (Garrett-Mayer, 2006; Iasonos et al., 2008; Ji and Wang, 2013; among others). We contrast this approach with the one we propose here in that, throughout the duration of the trial, we continuously monitor safety data in order to adaptively update our set of acceptable doses with which to make allocation decisions based on efficacy. The rest of the paper is organized as follows. We finish this section by outlining our overall strategy and providing a motivating example for this work. In Section 2, we outline the statistical models and inference used in the proposed design. In Section 3, we describe the dose-finding algorithm and in Section 4 we report simulation findings illustrating the operating characteristics of the design. Finally, we conclude with some discussion.

1.2 Locating the OBD

As previously noted, the assumption of monotonicity with regards to dose-toxicity relationships is usually appropriate for MTA’s, yet this assumption for dose-efficacy curves may fail. For these types of therapies, dose-efficacy curves could follow a non-monotone pattern, such as a unimodal or plateau relationship. In general, suppose a trial is investigating a set, = {d₁, …, d_I}, of I doses and that the probability of efficacious response at dose d_i is denoted π_E(d_i). In the presence of unimodal (including monotone increasing and monotone decreasing) or plateau dose-efficacy relationships, the primary objective of the trial is to find the optimal dose, d_ν ∈ 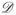, defined such that

$${\pi }_E(d_1)\le \cdots \le {\pi }_E(d_{\nu })\ge \cdots \ge {\pi }_E(d_I).$$ (1)

In other words, π_E(d_ν) corresponds to the dose d_ν where the peak of the unimodal relationship occurs, or where the dose-efficacy curve begins to plateau. Using the terminology of Hwang and Peddada (1994), π_E(d_ν) is said to be a nodal parameter (or a node) in that it is known that π_E(d_ν) ≥ π_E(d_i) for all i ≠ ν. Order restriction (1) is referred to as an umbrella ordering with the node of the umbrella occurring at d_ν. For instance, if the node occurs at the highest dose, we have a monotone increasing dose-efficacy relationship. In actuality, we do not know where in the dose range this node occurs and we must account for this uncertainty. The node could occur at any of the I available dose levels, with non-decreasing efficacy probabilities for doses before the node and non-increasing efficacy probabilities for doses after the node. The strategy we propose is to use this information to formulate a set of possible dose-efficacy relationships and make progress by appealing to Bayesian model choice, in order to account for the uncertainty surrounding the shape of the true dose-efficacy curve.

In locating the OBD, accepted early-phase designs are challenged by the use of non-traditional endpoints that accompany cytostatic agents. The potential growth of targeted therapies will be driven by the need to define suitable measures of biologic effect and finding ways to incorporate them into early-phase designs. Although the relationship between clinical outcome and biologic activity may not be clear, it is generally assumed that the absence of targeted effect will accompany a lack of clinical efficacy. Before a targeted agent can be taken into large-scale trials to test for clinical efficacy, early-phase trials are needed to establish that the therapy can produce a biologic activity with the potential to translate to clinical benefit. Protocol-specific endpoints give the investigator a measure of targeted effect that serves as a driving factor in early-phase trial design.

Parulekar and Eisenhauer (2004) and Korn (2004) provide a discussion of the challenges presented by non-toxicity endpoints in Phase I trial design of targeted agents. Unlike cytotoxic agents, the effects of these agents will likely be cytostatic, which will require measures of anti-tumor activity other than those used as traditional endpoints, such as tumor shrinkage. Surrogate markers of efficacy, such as measurement of target inhibition or pharmacokentic endpoints, will be necessary. Incorporation of these endpoints can be challenging due to the fact that (1) it may be difficult to define the desired biological effect, and (2) once defined, these endpoints may lack reliable, validated assays, making them practically difficult to measure. For the methods proposed in this article, we make the assumption that a surrogate efficacy endpoint is defined and able to be measured in order to find the OBD.

1.3 A motivating example

As an example, we describe the Phase I trial of Gerber et al. (2011) that assessed the safety and pharmacokinetcs of a vascular targeting agent, bavituximab, in patients with advanced solid tumors. The trial investigated four dose levels (0.1, 0.3, 1, 3 mg/kg) and the goal of the study was to dose escalate to the predicted biologically effective dose, rather than the MTD, because for monoclonal antibodies, the MTD may not correspond to optimal efficacy. Any of the four dose levels could be the node of the unimodal or plateau dose-efficacy curve, corresponding to the optimal dose. These four possible dose-efficacy relationships are provided in Table 1. There are other possibilities, in addition to those in Table 1, that could be considered for inclusion into this subset of possible relationships. For example, for a unimodal curve with node at d₃, another possibility is given by π_E(d₁) ≤ π_E(d₄) ≤ π_E(d₂) ≤ π_E(d₃). This notion of formulating a subset of possible curves has been undertaken by other authors (Conaway, Dunbar, and Peddada, 2004; Wages, Conaway, and O’Quigley, 2011) within the context dose-finding in drug combinations. These papers assessed the possible loss of information in only using a subset of relationships and they found that, in general, using a subset did not drastically reduce the performance of their methods. An important idea to this approach is that we do not need to identify the “correct” relationship at every dose level. We just need one which is “close” to correct, in that it is correct in specifying the node (optimal dose) of the umbrella ordering.

Table 1.

Possible dose-efficacy relationships for I = 4 dose levels.

Shape of relationship	Location of node	Possible Dose-efficacy relationship
Unimodal or plateau	d1	πE(d4) ≤ πE(d3) ≤ πE(d2) ≤ πE(d1)
Unimodal or plateau	d2	πE(d1) ≤ πE(d3) ≤ πE(d4) ≤ πE(d2)
Unimodal or plateau	d3	πE(d1) ≤ πE(d2) ≤ πE(d4) ≤ πE(d3)
Unimodal	d4	πE(d1) ≤ πE(d2) ≤ πE(d3) ≤ πE(d4)

2 Methods

Consider a trial investigating a set of I doses, 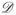= {d₁, …, d_I}. Toxicity and efficacy are modeled as binary endpoints so that, for each subject j, we measure

$$Y_j=\{\begin{array}{ll}0\hfill & \text{if}\text{no}\text{toxicity},\hfill \\ 1\hfill & \text{if}\text{toxicity}\hfill \end{array}{Z}_j=\{\begin{array}{ll}0\hfill & \text{if}\text{no}\text{response},\hfill \\ 1\hfill & \text{if}\text{response.}\hfill \end{array}$$

The dose for the jth entered patient, X_j, j = 1, …, n can be thought of as random, taking values x_j ∈ .

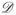2.1 Modeling toxicity with CRM

The CRM was introduced as an alternative to the traditional escalation schemes reviewed by Storer (1989). The details of CRM are provided by O’Quigley et al. (1990), so we only briefly recall them here. In its original form the CRM is a Bayesian method that uses sequential updating of dose-toxicity information to estimate the dose level at which to treat the next available patient. The method begins by assuming a functional dose-toxicity curve, F(d_i, β), that is monotonic in both dose level, d_i, and the parameter, β, in order to model the DLT probabilities, π_T(d_i), at each dose i; i = 1, …, I. For instance, the power model, $F(d_i,\beta )=p_i^{exp(\beta )}$, is common to CRM literature, where 0 < p₁ < ··· < p_I < 1 are the standardized units (skeleton) representing the discrete dose levels d_i. The p_i are also referred to as a working model. After having included j subjects, we have toxicity data in the form Ω_j = {(x₁, y₁), …, (x_j, y_j)}, and we can generate an estimate, β̂_j, based on the posterior mean of β. Using β̂_j, we can obtain an estimate of the DLT probability at each dose level via π̂_T(d_i) = F(d_i, β̂_j), i = 1, …, I, from which the dose recommended for the (j + 1) th patient is determined. Specifically, for target DLT rate, ϕ_T, this dose is d_i = arg min_i |F(d_i, β̂_j) − ϕ_T|. The MTD is the recommended dose after the inclusion of some predetermined sample size of N patients is exhausted or a stopping rule takes effect. In the bivariate extension of the CRM that we describe in this article, instead of using the DLT probability estimates, π̂_T(d_i), to determine the recommended dose for the next patient, we will use them in defining a set of acceptable doses with regards to safety. To this end, ϕ_T will be redefined from a target DLT probability to a maximum acceptable toxicity rate that will guide the definition of safe doses.

2.2 Models and inference for efficacy

Suppose now that, instead of utilizing a single working model as we did with toxicity, we make use of some class of working models and model selection techniques in order to allow for more flexibility in modeling the dose-efficacy relationship. This class of skeletons would correspond to various possible dose-toxicity relationships (Table 1). The models and inference for efficacy are based on specifying both a unimodal and plateau skeleton for each of the possible dose-efficacy relationships. For instance, if the node is located at d₂, we identify a skeleton that (1) peaks at d₂ and decreases after d₂, and another that (2) begins to plateau at d₂ and remains constant after d₂. Using Table 1 as a guide, in general, we need to specify K = 2 × I − 1 working models; I unimodal skeletons, with nodes at each of the I doses, and I − 1 plateau skeletons, with nodes at each of the first I − 1 doses. The dose-efficacy relationship does not plateau at dose level d_I, so only one working model with node at d_I is needed. For a particular skeleton, k; k = 1, …, K, we model π_E(d_i), the true probability of efficacious response at d_i by

$${\pi }_E(d_i)=Pr(Z_j=1\mid d_i)\approx G_k(d_i,\theta )=q_{ik}^{exp(\theta )}k=1,\dots ,K,$$

for a class of working dose-efficacy models, G_k(d_i, θ) and θ ∈ Θ. Like toxicity, for efficacy we appeal to the simple power model, which has shown itself to work well in practice. Here, Θ = (−∞, ∞) and 0 < q_1k < ··· < q_Ik < 1 is the skeleton of model k. Further, we may wish to take account of any prior information concerning the plausibility of each model and so introduce τ(k) = {τ(1), …, τ(K)}, where τ(k) ≥ 0 and where Σ_k τ(k) = 1. Even when there is no prior information available on the possible skeletons we can formally proceed in the same way by specifying a discrete uniform for τ(k). After inclusion of the first j patients into the trial, we have efficacy data in the form of 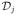= {(x₁, z₁), …, (x_j, z_j)}. Under working model k, we obtain an estimate, θ̂_jk, for the parameter θ. In the Bayesian framework, we assign a prior probability distribution h(θ) for the parameter θ of each model, and a prior probability τ(k) to each possible skeleton. For each model, we utilize a Normal prior with mean 0 and variance 1.34 on θ so that h(θ) = 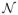(0, 1.34) (O’Quigley and Shen, 1996). In order to establish running estimates of the probability of efficacy at the available doses, we need an expression for the likelihood for the parameter θ. After inclusion of the first j patients into the study, the likelihood under model k is given by

$$L_k(\theta \mid {\mathcal{D}}_j)=\prod _{\ell =1}^j{\{G_k(x_{\ell },\theta )\}}^{z_{\ell }}{\{1-G_k(x_{\ell },\theta )\}}^{(1-z_{\ell })}$$ (2)

which, for each skeleton, can be used in order to generate a summary value, θ̂_jk, for θ. Given the set 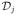and the likelihood, the posterior density for θ is given by

$$P_k(\theta \mid {\mathcal{D}}_j)=\frac{L_k(\theta \mid {\mathcal{D}}_j)h(\theta )}{{\int }_{\mathrm{\Theta }}{L}_k(\theta \mid {\mathcal{D}}_j)h(\theta )d\theta }.$$

This information can be used to establish posterior model probabilities given the data as

$$w(k\mid {\mathcal{D}}_j)=\frac{{\tau }^{(k)}{\int }_{\mathrm{\Theta }}{L}_k(\theta \mid {\mathcal{D}}_j)h(\theta )d\theta }{{\displaystyle \sum _{k=1}^K}{\tau }^{(k)}{\int }_{\mathrm{\Theta }}{L}_k(\theta \mid {\mathcal{D}}_j)h(\theta )d\theta }.$$

The prior model probabilities, τ(k), are updated by the efficacy response data, 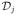. It is expected that the more the data support model k, the greater its posterior probability will be. Thus, we appeal to sequential Bayesian model choice in order to guide allocation decisions. Each time a new patient is to be enrolled, we choose a single skeleton, k^*, with the largest posterior probability such that

$$k^{\ast }=arg\underset{k}{max}w(k\mid {\mathcal{D}}_j),k=1,\dots ,K.$$

We then utilize G_k^*(d_i, θ) to generate efficacy probability estimates at each dose. Beginning with the prior for θ and having included the jth subject, we can compute the posterior probability of a response for d_i so that

$${\widehat{\pi }}_E(d_i)=G_{k^{\ast }}(d_i,{\widehat{\theta }}_{j{k}^{\ast }});{\widehat{\theta }}_{j{k}^{\ast }}={\int }_{\mathrm{\Theta }}\theta P_k(\theta \mid {\mathcal{D}}_j)d\theta .$$

The efficacy probability estimates, π̂_E(d_i), are used to make decisions regarding dose allocation as described in Section 3.

3 Dose-finding Algorithm

Overall, we are going to allocate each entered patient to the dose estimated to be the most efficacious, among those with acceptable toxicity. After obtaining the DLT probability estimates, π̂_T(d_i), for each dose, we are going to first restrict our attention to those doses with estimated probabilities less than a maximum acceptable toxicity rate, ϕ_T. In general, after j entered patients, we define the set of “acceptable” doses as

$${\mathcal{A}}_j=\{d_i:{\widehat{\pi }}_T(d_i)\le {\varphi }_T;i=1,\dots ,I\}.$$

We then allocate the next entered patient to a dose in 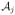based upon estimated efficacy probabilities, π̂_E(d_i). By incorporating an acceptable set, 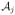, we exclude overly toxic doses. After each cohort inclusion the acceptable set is redefined based on the current DLT probability estimates, so it is possible, once more data has been observed, for 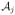to include a dose that was previously excluded when a limited amount of data existed. The allocation algorithm depends upon the amount of data that has been observed so far in the trial. If a limited amount of data exists, we will rely on an adaptive randomization phase to allocate future patients to acceptable doses. In the latter portion of the trial, when a sufficient amount of data has been observed, we will utilize a maximization phase in which we allocate according to the most efficacious treatment among the set of acceptable doses.

3.1 Adaptive randomization (AR) phase

Early in the trial, there may not be enough data to rely entirely on maximization of estimated efficacy probabilities within 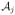to accurately assign patients to the most efficacious dose with acceptable toxicity. There may be doses in 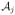that have never been tried and information on these can only ever be obtained through experimentation. Added randomization allows for information to be obtained on competing doses and prevents the method from getting “stuck” on a dose that has been tried early in the trial. Therefore, we do not rely entirely on the maximization of estimated efficacy probabilities for guidance as to the most appropriate treatment but rather implement adaptive randomization (AR) to obtain information more broadly. Based on the estimated efficacy probabilities, π̂_E(d_i), for doses in 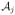, calculate a randomization probability R_i,

$$R_i=\frac{{\widehat{\pi }}_E(d_i)}{{\displaystyle \sum _{d_i\in {\mathcal{A}}_j}}{\widehat{\pi }}_E(d_i)}$$

and randomize the next patient or cohort of patients to dose d_i with probability R_i. We are going to rely on this randomization algorithm for a subset of n_R patients in order to allow information to accumulate on untried doses, before switching to a phase in which we simply allocate according to the maximum estimated efficacy probability among the acceptable doses. The number of patients on which to implement the AR phase may vary from trial to trial. In some cases, clinician/statistician teams may choose to set n_R according to their personal preference. Some may favor randomization for the entirety of the study, while others may choose not to randomize any patients and treat according to which dose the data indicates is the most efficacious. We found that the method exhibits good performance, in terms of choosing desirable doses, when at least some randomization is employed. It is difficult to make a definitive recommendation for n_R, since it is not feasible to determine at what exact value that performance is optimized across a broad range of situations. Optimal performance may depend upon many factors, including the number of dose levels, the true dose-toxicity/efficacy curves, and the maximum sample size N. In the simulations below, we explore performance of our method under various values of n_R. The results will demonstrate that our method, across a wide range of scenarios, is fairly robust to this choice. The size of the AR phase can be expanded or contracted according to the desire of the clinician/statistician team and operating characteristics will be relatively unaffected. As a general rule of thumb, adaptively randomizing for half of the maximum sample size seems to work well in a wide variety of scenarios.

3.2 Maximization phase

Upon completion of the AR phase, the trial design switches to a maximization phase in which maximized efficacy probability estimates guide allocation. Among the doses contained in 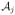, we allocate the (j + 1)th patient cohort to the dose x_j+1 according to the estimated efficacy probabilities, π̂_E(d_i), such that

$$x_{j+1}=arg\underset{d_i\in {\mathcal{A}}_j}{max}{\widehat{\pi }}_E(d_i)$$

Continuing in this way, the OBD is the recommended dose d_i = x_N+1 for the hypothetical (N + 1)th patient after the inclusion of the maximum sample size of N patients or some stopping rule takes effect.

3.3 Starting the trial

In order to get the trial underway, we will choose the efficacy skeleton with the largest prior probability, τ(k), among the working models being considered. If several, or all, of the working models have the same maximum prior probability, then we will choose at random from these skeletons. Given the starting skeleton, k^*, for efficacy, the starting dose, x₁ ∈ 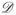, is then chosen. Specifically, based on the toxicity skeleton, p_i, we define the acceptable set, a priori, to be

$${\mathcal{A}}_j=\{d_i:p_i\le {\varphi }_T;i=1,\dots ,I\}.$$

Based on the efficacy skeleton, q_ik^*, for doses in 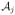, we calculate the randomization probability R_i,

$$R_i=\frac{q_{i{k}^{\ast }}}{{\displaystyle \sum _{d_i\in {\mathcal{A}}_j}}{q}_{i{k}^{\ast }}}$$

and randomize the first patient or cohort of patients to dose x₁ = d_i with probability R_i.

3.4 Ending the trial

Safety

Investigators will want some measure by which to stop the trial in the presence of undesirable toxicity. At any point in the trial, we can calculate an exact binomial confidence interval for toxicity ( ${\pi }_T^{-}(d_1),{\pi }_T^{+}(d_1)$) at the lowest dose, d₁. The value of ${\pi }_T^{-}(d_1)$ provides a lower bound for the probability of toxicity at d₁, above which we are 95% confident that the true toxicity probability for d₁ falls. We want to compare this lower bound to our maximum acceptable toxicity rate, ϕ_T. If our lower bound exceeds this threshold, we can be confident that the new treatment has too high of a DLT rate to warrant continuing the trial. Therefore, if ${\pi }_T^{-}(d_1)>{\varphi }_T$, stop the trial for safety and no treatment is identified as the OBD.

Futility

If the new treatment is no better than the current standard of care, we would also like for the trial to be terminated. After j inclusions, we calculate an exact binomial confidence interval for efficacy ( ${\pi }_E^{-}(x_j),{\pi }_E^{+}(x_j)$) at the current dose, x_j. The value of ${\pi }_E^{+}(x_j)$ provides an upper bound for the probability of efficacy at the current treatment, below which we are 95% confident that the true efficacy probability for that dose falls. We want to compare this upper bound to some futility threshold, ϕ_E, that represents the efficacy response rate for some current standard of care. If our upper bound fails to reach this threshold, we can be confident that the new treatment does not have a sufficient enough response rate to warrant continuing the trial. Therefore, if ${\pi }_E^{+}(x_j)<{\varphi }_E$, stop the trial for futility and no treatment is identified as the OBD. This stopping rule will only be assessed in the maximization phase, not the AR phase, so that here j ≥ n_R. The reason for this is that the upper bound will be calculated on the current treatment, which is based on the maximum estimated efficacy probability. We can be confident that if the maximum of the estimated probabilities did not reach the futility threshold, then none of the other acceptable toxicity doses would reach it, since they are presumed to have lower efficacy than the selected treatment. In the AR phase, when we randomize, there may exist a more efficacious treatment in the set 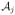that was not selected purely because of randomization. Consequently, another treatment may have reached the futility threshold had it been selected, so we would not want to stop the trial in this case.

4 Numerical results

4.1 Simulation setting

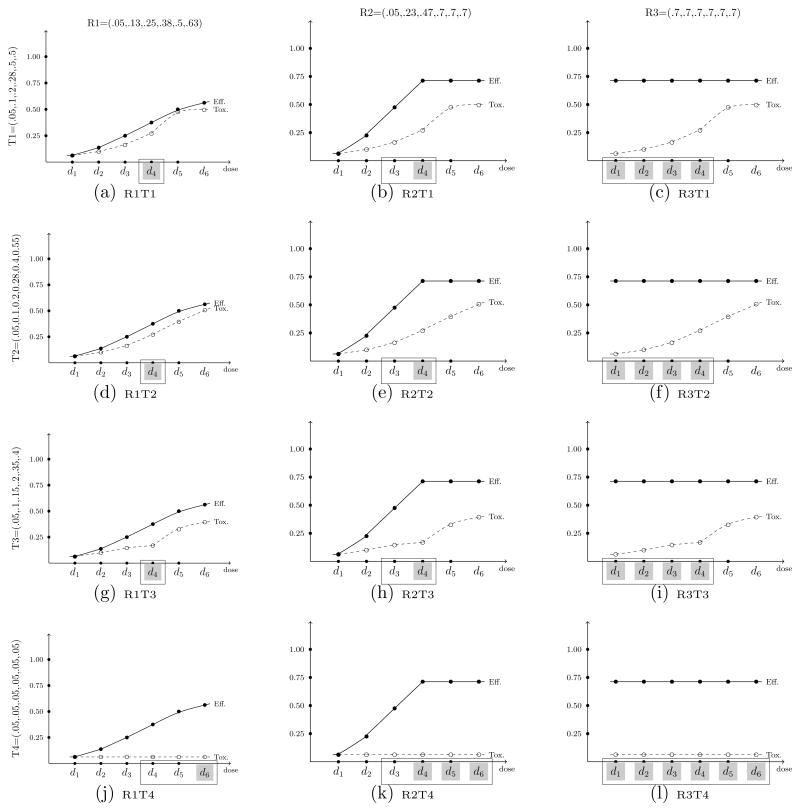
For the first set of simulated results contained in this section, we compare the performance of the proposed approach with that of Hoering et al. (2013) for identifying the OBD in a trial investigating I = 6 dose levels. Throughout the simulation results, we denote the method of Hoering et al. (2013) as HMLC, and our proposed method as WT. The comparison assesses the performance of each method over the twelve true toxicity/efficacy scenarios contained in their paper, which are provided in Figure 2. True toxicity probabilities are denoted T1 through T4, while true efficacy probabilities are denoted R1 through R3. In each set of 1000 simulated trials, the maximum sample size was set to N = 64. The Phase II portion of Hoering et al. (2013) randomized n₂ = 48 patients to three doses levels (arms); (1) the recommended dose (RD) from Phase I, (2) the dose level immediately above the RD (RD+1), and (3) the dose level immediately below the RD (RD−1). For response, the authors test competing hypotheses H₀ : p = 0.05 vs. H₁ : p = 0.30. The Phase I sample sizes for the Hoering et al. (2013) method are reported in Table 1 of Hoering et al. (2011), with a minimum sample size of n₁ = 16. Therefore, we thought a justifiable total sample size for comparison was N = 16 + 48 = 64. For our proposed method, the size of the AR phase was set equal to one quarter the total sample size so that n_R = 16. In a subsequent section, we investigated the impact of various sizes, n_R, of the AR phase on operating characteristics.

Figure 2.

A set of twelve true (toxicity, efficacy) scenarios. True toxicity probabilities are denoted T1 through T4, while true efficacy probabilities are denoted R1 through R3. The good doses are indicated with a □, while the best doses are shaded in gray.

The proposed design embodies characteristics of the CRM so we can utilize these features in specifying design parameters. The toxicity probabilities were modeled via the power model given in Section 2.1 with skeleton values p_i = {0.01, 0.08, 0.15, 0.22, 0.29, 0.36}. It has been shown (O’Quigley and Zohar, 2010) that CRM designs are robust and efficient with the implementation of “reasonable” skeletons. Simply defined, a reasonable skeleton is one in which there is adequate spacing between adjacent values. This skeleton also reflects the idea that, for MTA’s, it is often assumed that there is minimal toxicity over the dose range. For efficacy, probabilities were modeled via the class of power models in Section 2.2, using K = 2 × I − 1 = 11 skeletons that correspond to the possible dose-efficacy relationship. The six sets of values used for the unimodal relationships were:

• 1q_i1 = {0.60, 0.50, 0.40, 0.30, 0.20, 0.10}
• 2q_i2 = {0.50, 0.60, 0.50, 0.40, 0.30, 0.20}
• 3q_i3 = {0.40, 0.50, 0.60, 0.50, 0.40, 0.30}
• 4q_i4 = {0.30, 0.40, 0.50, 0.60, 0.50, 0.40}
• 5q_i5 = {0.20, 0.30, 0.40, 0.50, 0.60, 0.50}
• 6q_i6 = {0.10, 0.20, 0.30, 0.40, 0.50, 0.60}.

The five sets of values for the plateau relationships were:

• 7q_i7 = {0.20, 0.30, 0.40, 0.50, 0.60, 0.60}
• 8q_i8 = {0.30, 0.40, 0.50, 0.60, 0.60, 0.60}
• 9q_i9 = {0.40, 0.50, 0.60, 0.60, 0.60, 0.60}
• 10q_i,10 = {0.50, 0.60, 0.60, 0.60, 0.60, 0.60}
• 11q_i,11 = {0.60, 0.60, 0.60, 0.60, 0.60, 0.60}

We assumed, a priori, that each of these eleven models was equally likely and set τ(k) = 1/11.

Another design parameter that must addressed is the association between toxicity and efficacy responses. The models and inference presented in Section 2 estimate toxicity and efficacy probabilities independently, ignoring an association parameter, ψ. In order to provide a justifiable comparison to Hoering et al. (2013), as well as to illustrate our method’s robustness to the misspecification of an association parameter, we generated correlated binary outcomes using the function ranBin2 in R package binarySimCLF (R Core Team). The log odds ratio specification used to generate the data was set to ψ = 4.6 to match that used by Hoering et al. In each set of 1000 simulations, in order to define the acceptable set 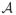, the maximum acceptable toxicity rate was specified to be ϕ_T = 0.33 and the minimum efficacy threshold to be ϕ_E = 0.05. Again, these values were chosen in order to present results in a setting mimicking that of Hoering et al. (2013). For each scenario, using the definitions of Hoering et al., the best dose is defined as the level that maximizes efficacy while assuring safety, and a good dose is defined as a level where efficacy is above predefined boundary while maintaining safety. In Figure 2, the best doses are indicated with gray shading, while good doses are indicated with a □.

4.2 Operating characteristics

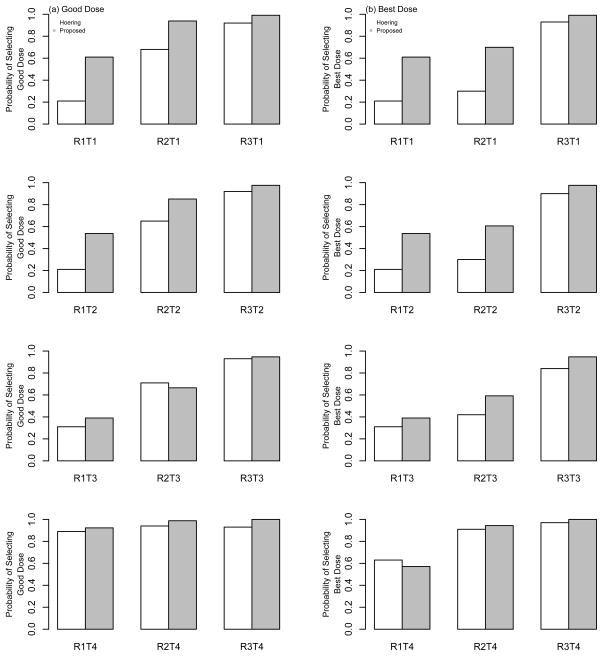
The results of the comparison are summarized in Table 2 and Figure 3, with each bar in the figure representing the proportion of simulated trials that each method selected a good dose [Figure 3(a)] and the best dose [Figure 3(b)]. Overall, the results indicate a superior performance for the proposed method over that of Hoering et al. (2013). The left column of Figure 2 and the first four rows of Table 2 represent cases in which the dose-efficacy curves have monotone increasing probabilities. In the first three of these scenarios (R1T1, R1T2, and R1T3), d₄ is the only good and best dose. WT outperforms HMLC in these scenarios by selection percentages of 40%, 34% and 8%, respectively. In R1T4, the toxicity probabilities plateau at a value of 0.05 across the dose range, so the highest dose, d₆, is considered the best dose. The HMLC method selects the best dose as the OBD in 63% of simulated trials, compared to 57% by the WT method. The next four rows of Table 2 and the middle colum of Figure 2 illustrate situations in which the dose-efficacy curves increase until dose d₄ and remain constant after d₄ (plateau). Again, in terms of selecting both good and best doses, WT improves upon the selection percentages of HMLC in most cases (R2T1, R2T2, R2T4), by as much as 30 to 40% in some scenarios. HMLC performs slightly better in selecting a good dose in R2T3, doing so in 71% of trials compared to 67% by WT. Finally, in the last four rows of Table 2 and the right column of Figure 2, most of the doses are considered to be best/good doses, so, as expected, both methods produce high selection percentages in these cases. The WT method does perform slightly better in these last four scenarios, yielding selection percentages that range from 3% to 10% higher than those produced by HMLC.

Table 2.

Operating characteristics of the proposed design and Hoering et al. (2013). Overall probability of selecting a best or good dose level as the OBD after 1000 simulation runs with a maximum sample size of N = 64 patients.

Efficacy Scenario	Toxicity Scenario	Best Dose Level	Good Dose Level	Probability of Picking Best Dose with Our Proposed Design	Probability of Picking Good Dose with Our Proposed Design	Probability of Picking Best Dose with Hoering et al. Design	Probability of Picking Good Dose with Hoering et al. Design
R1	T1	4	4	0.61	0.61	0.21	0.21
R1	T2	4	4	0.54	0.54	0.20	0.20
R1	T3	4	4	0.39	0.39	0.31	0.31
R1	T4	6	4–6	0.57	0.92	0.63	0.89
R2	T1	4	3, 4	0.70	0.94	0.30	0.68
R2	T2	4	3, 4	0.61	0.85	0.30	0.65
R2	T3	4	3, 4	0.59	0.67	0.42	0.71
R2	T4	4–6	3–6	0.94	0.99	0.91	0.94
R3	T1	1–4	1–4	0.99	0.99	0.93	0.93
R3	T2	1–4	1–4	0.98	0.98	0.90	0.90
R3	T3	1–4	1–4	0.95	0.95	0.84	0.85
R3	T4	1–6	1–6	1.00	1.00	0.97	0.97

Figure 3.

Operating characteristics of the proposed design and Hoering et al. (2013). Each bar represents the proportion of times that each method recommended (a) good doses and (b) best doses as the OBD at the conclusion of a simulated Phase I/II trial with a maximum sample size of N = 64 patients.

We feel that this improved performance by the WT across the 12 scenarios considered here can mostly be attributed to the HMLC’s use of a Phase I portion to identify an MTD. This may not be appropriate for MTA’s, due to the uncertainty surrounding the shape of the dose-efficacy curve. If the MTD-based Phase I portion does not identify doses around the OBD, then the Phase II portion could possibly be randomizing to incorrect doses. In contrast, throughout the duration of the trial, our method continuously monitors toxicity and efficacy data to identify a set of safe doses, within which we allocate to a dose with high efficacy. This allows for the adaptive updating of the doses being considered after each patient inclusion, rather than restricting attention to two or three doses after a Phase I component designed to find the MTD. Overall, the strong showing of our method against published work in the area in extensive simulation studies makes us feel confident in recommending it as a viable alternative in Phase I/II trials of MTA’s.

4.3 Sensitivity analysis

In this set of simulations, we investigated the sensitivity of our proposed method to the design specifications over a class of five true (toxicity, efficacy) scenarios. The analysis assesses the effect of changing (1) the number of dose levels, (2) the true value of the association parameter ψ, (3) the size of the AR phase n_R, and (4) the maximum sample size N. We also investigated the sensitivity of the proposed methods to the choice of both toxicity and efficacy skeletons, but we exclude these results for the sake of brevity. As expected, since our method leans upon the CRM, it is robust to skeleton choice, so long as “reasonable” skeletons are chosen (O’Quigley and Zohar, 2010). We are happy to share these results with any interested reader.

We ran simulations using outcomes generated from the three fixed values of ψ; ψ = {−2, 0, −2}. The maximum sample size for each simulated trial was set to N = 48, and we varied the size of the AR phase; i.e. n_R = {12, 24, 36, 48}. The toxicity probabilities were modeled via the power model given in Section 2.1 with skeleton values p_i = {0.01, 0.08, 0.15, 0.22, 0.29}. For efficacy, probabilities were modeled via the class of power models in Section 2.2, using K = 2 × I − 1 = 9 skeletons. The nine sets of values used were: q_i1 = {0.30, 0.40, 0.50, 0.60, 0.70}, q_i2 = {0.40, 0.50, 0.60, 0.70, 0.60}, q_i3 = {0.50, 0.60, 0.70, 0.60, 0.50}, q_i4 = {0.60, 0.70, 0.60, 0.50, 0.40}, q_i5 = [0.70, 0.60, 0.50, 0.40, 0.30}, q_i6 = {0.70, 0.70, 0.70, 0.70, 0.70}, q_i7 = {0.60, 0.70, 0.70, 0.70, 0.70}, q_i8 = {0.50, 0.60, 0.70, 0.70, 0.70} and q_i9 = {0.40, 0.50, 0.60, 0.70, 0.70}. We assumed, a priori, that each of these nine skeletons is equally likley and set τ(k) = 1/9.

The previous set of true scenarios (Figure 2) investigated monotone increasing (R1) and plateau (R2, R3) dose-efficacy curves. The set of true scenarios for the sensitivity analysis assess performance for unimodal relationships. Table 3 reports the percentage of trials in which each dose was selected as the optimal dose at the end of each trial, and the average trial size for each of the Scenarios 1–4. The true (toxicity, efficacy) probabilities for each dose are given next to the number of the scenario. In Scenario 1, all doses are safe and the peak of the unimodal curve occurs at dose d₃. In Scenario 2, all but the highest dose are safe, and the OBD occurs at d₂. In Scenario 3, again all but d₆ are safe and the OBD occurs at dose d₅. Finally, in Scenario 4, all doses are safe and there exists a monotone decreasing dose-efficacy curve with the OBD at d₁. In each set of 1000 simulations, the maximum acceptable toxicity rate was specified to be ϕ_T = 0.33 and the efficacy threshold ϕ_E = 0.20.

Table 3.

Selection percentages for each dose under the proposed method for various design specifications. The maximum sample size for each simulated trial was N = 48 patients. The OBD in each scenario is indicated in bold-type.

Scenario 1	True (toxicity, efficacy) probability
	(0.01, 0.30)	(0.05, 0.50)	(0.10, 0.60)	(0.15, 0.40)	(0.20, 0.25)
ψ = 0; nR = 12	0.069	0.321	0.515	0.078	0.017
ψ = 0; nR = 24	0.049	0.327	0.567	0.053	0.004
ψ = 0; nR = 36	0.042	0.305	0.593	0.058	0.002
ψ = 0; nR = 48	0.062	0.285	0.587	0.060	0.006
ψ = −2; nR = 12	0.082	0.315	0.513	0.077	0.013
ψ = 2; nR = 12	0.063	0.303	0.512	0.107	0.015
Scenario 2	(0.02, 0.38)	(0.06, 0.50)	(0.12, 0.40)	(0.30, 0.30)	(0.40, 0.25)
ψ = 0; nR = 12	0.253	0.481	0.211	0.050	0.005
ψ = 0; nR = 24	0.241	0.538	0.182	0.034	0.005
ψ = 0; nR = 36	0.255	0.542	0.180	0.021	0.002
ψ = 0; nR = 48	0.265	0.537	0.158	0.035	0.005
ψ = −2; nR = 12	0.227	0.512	0.205	0.051	0.005
ψ = 2; nR = 12	0.250	0.468	0.206	0.064	0.012
Scenario 3	(0.03, 0.25)	(0.09, 0.35)	(0.16, 0.48)	(0.28, 0.65)	(0.42, 0.52)
ψ = 0; nR = 12	0.098	0.124	0.278	0.474	0.026
ψ = 0; nR = 24	0.061	0.095	0.271	0.540	0.033
ψ = 0; nR = 36	0.048	0.082	0.266	0.561	0.043
ψ = 0; nR = 48	0.061	0.061	0.215	0.539	0.124
ψ = −2; nR = 12	0.078	0.130	0.297	0.455	0.040
ψ = 2; nR = 12	0.073	0.118	0.256	0.526	0.027
Scenario 4	(0.02, 0.68)	(0.05, 0.56)	(0.07, 0.49)	(0.09, 0.40)	(0.11, 0.33)
ψ = 0; nR = 12	0.627	0.211	0.115	0.034	0.013
ψ = 0; nR = 24	0.672	0.230	0.084	0.009	0.005
ψ = 0; nR = 36	0.713	0.206	0.069	0.011	0.001
ψ = 0; nR = 48	0.748	0.183	0.055	0.011	0.003
ψ = −2; nR = 12	0.644	0.214	0.094	0.031	0.017
ψ = 2; nR = 12	0.622	0.216	0.099	0.045	0.018

Examination of Table 3 reveals strong performance for our method in these scenarios, recommending the OBD in a large percentage of trials (≈ 50 – 70%) after N = 48 patients. The results in Table 3 also demonstrate the robustness of our method to the association between efficacy and toxicity. The performance of WT is practically unchanged for all values of ψ, given that n_R remains unchanged. Therefore, even in the presence of correlated binary outcomes, the fact that our method ignores any association between toxicity and efficacy in estimating probabilities does not affect its operating characteristics. In general, the selection percentages remain fairly consistent for n_R = 12, 24, 36, and 48. All percentages in each scenario are within 10% of one another, so the chosen size of the AR phase does not drastically alter performance. These simulations represent only a small set of situations. More study, under a broader range of scenarios, may provide more insight into the general behavior of n_R.

5 Discussion

In this article, we have outlined a new Phase I/II design that accounts for the both toxicity and efficacy of molecularly targeted agents. The simulation results demonstrated the method’s ability to effectively recommend the OBD, defined by acceptable toxicity and high efficacy, in a high percentage of trials with manageable sample sizes. The method we propose in this work is a bivariate extension of the CRM, leaning upon properties of order restricted inference utilized in the partial order CRM (POCRM; Wages et al., 2011). This approach falls into a broader class of extended model-based designs that utilize multiple non-monotonic skeletons, which increases the ability of CRM designs to handle more complex dose-finding problems (O’Quigley and Conaway, 2011). This class of design is developed within the framework of CRM, with the added step of Bayesian model choice to account for the multiple models. Therefore, many of the features associated with CRM design specifications, such as one-parameter models and “reasonable skeletons” (O’Quigley and Zohar, 2010), can be employed in these extended designs.

The proposed design is most appropriate when both binary toxicity and binary efficacy endpoints can be observed in a reasonably similar time-frame. In some practical situations, this may not be possible due to the fact that efficacy may occur much later than toxicity. This would create a situation where we would be estimating DLT probabilities based on more patient observations than efficacy probabilities. Since we are ignoring their association in modeling these responses, we can fit the likelihood for each response based on different amounts of data, and simply utilize the efficacy data we have available, even though it may be less than that of the toxicity data. This idea requires further study and we are exploring modifications to the proposed methodology to handle such practical issues. Along these same lines, incorporating time-to-event outcomes may be an effective extension of the method as a means of handling delayed response.