Abstract
Purpose
Two-point fat-water separation methods are increasingly being used for chest and abdominal MRI and have recently been introduced for use in MR angiography of the lower extremities. With these methods, flowing spins can accumulate unintended phase shifts between the echo times. The purpose of this study is to demonstrate that these phase shifts can lead to inaccurate signals in the water and fat images.
Methods
In vitro experiments were conducted at 1.5 T and 3.0 T using a stenosis-mimicking phantom and a computer-controlled pump to image a range of physiologically relevant velocities.
Results
In the phantom images acquired using bipolar readout gradients, fat-water signal inaccuracies were visible in regions of flow, with increasing severity as the flow rate was increased. Additionally, similar effects were observed in regions of high flow in clinical chest and liver exams. In the phantom images, the effect was eliminated by using a dual-pass method without bipolar readout gradients.
Conclusion
When using fat-water separation methods with bipolar readout gradients, phase shifts caused by the motion of spins can lead to signal inaccuracies in the fat and water images. These artifacts can be mitigated by employing approaches that do not use bipolar readout gradients.
Keywords: two-point fat-water separation, non-subtractive MRA, flow artifacts, chemical shift separation
Introduction
Two-point (1–3) fat-water chemical-shift-encoded “Dixon” MRI recently has been used for MR angiography (MRA) of the lower extremities (4,5). Fat-water-separated contrast-enhanced (CE) MRA methods, unlike conventional methods (6,7), do not require subtraction of a pre-contrast mask image from post-contrast images. This is because the vascular signal appears in the water-only images, whereas the bright signal from fat appears in the fat-only images. With these methods, maximum intensity projection (MIP) processing of the water-only images yields angiograms without the need for subtraction of a pre-contrast mask. There are multiple motivations for using a subtraction-free CE-MRA method as an alternative to the standard subtraction-based methods, including: i) lower sensitivity to artifacts caused by involuntary patient motion between pre- and post-contrast acquisitions, ii) shorter overall imaging time and iii) higher signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) (8).
Apart from emerging applications in peripheral MRA, two-point fat-water separation methods are routinely used in applications for imaging other body parts as well. For example, at our institution, these methods frequently are used for post-contrast evaluation of the liver during delayed-venous or hepatobiliary phases. These methods also are used alongside conventional MRA techniques for evaluation of chest-wall lesions in patients with known or suspected pulmonary embolus.
Recent application of fat-water separation methods in peripheral and abdominal MRA have increased the need to better understand and characterize the behavior of fat-water separation artifacts related to flow. Flow has been previously mentioned in the literature as a potential cause of artifacts in fat-water imaging (9). In the work described here, a flow-related artifact in fat-water imaging is systematically investigated. This artifact results when uncompensated phase accrued by moving water spins is misinterpreted by the reconstruction algorithm (due to deviations from the signal model), and a fraction of the signal that should appear in the water image is inappropriately allocated to the fat image for voxels that contain the moving water spins.
Since this artifact manifests as an inappropriate allocation of signal in the water and fat images (a fraction of the moving-water signal appears in the fat images), and in order to distinguish it from the well-known fat-water swaps caused by errors in determining the dominant species in a given voxel, this artifact will be referred to as a signal “misallocation” artifact.
To produce fat-water-separated images, various strategies can be used to acquire images with the requisite two echo times, including: i) dual-pass strategies, where each echo is acquired in a separate TR, and a positive-amplitude readout gradient is used with each echo, ii) fly-back strategies, where both echoes are acquired in the same TR and a positive-amplitude readout gradient is used with each echo, but there is a large negative-amplitude re-winder gradient in between, and iii) bipolar strategies, where both echoes are acquired in the same TR and one echo is acquired with a positive-amplitude readout gradient, and the other echo is acquired with a negative-amplitude readout gradient. Dual-pass strategies require long scanning times and fly-back strategies restrict in-plane resolution, given the required echo spacing and the time needed for the re-winder gradient lobe. Bipolar strategies permit good sampling efficiency and allow for relatively long readout times, but they suffer from a number of phase errors. A host of methods have been developed to address some of these phase errors in fat-water-separated MRI (10–14).
It is well known that bipolar gradients are flow sensitizing since they induce a phase shift in moving spins proportional to the velocity of the spins. In phase contrast imaging, this velocity sensitivity is used intentionally to encode flow information. However, in fat-water separation methods, flow-induced phase shifts can be a source for undesired misallocations of signals between fat and water images. The purpose of this work is to investigate the effects of flow-induced phase shifts in two-point fat-water separation imaging. The effect is described theoretically and examples are shown in images acquired from a controlled flow phantom and from clinical patients.
Theory
Even though two-point chemical shift methods with flexible choice of echo times have been introduced previously (13,15), in this theoretical description we assume the echo times are chosen such that fat and water are exactly in-phase and out-of-phase at the two echo times. For a voxel containing both fat and water, the complex in-phase and out-of-phase signals then can be written as:
| [1] |
and
| [2] |
where W is the magnitude of the water signal, F is the magnitude of the fat signal, and φin_phase and φout_of_phase are terms modeling the phase at each echo from sources other than chemical shift (including contributions related to coil sensitivity, field inhomogeneity and magnetic susceptibility).
Spins moving with a constant velocity during the application of a readout gradient accumulate a phase shift that is proportional to the first moment of the gradient at the echo time, which can be described by the following equation:
| [3] |
where γ is the gyromagnetic ratio of the proton, M1 is the first moment of the readout gradient at each echo time and V is the velocity of flowing spins along the readout direction.
In physiological applications, it is reasonable to assume that voxels that contain flowing blood can be modelled as containing only moving water (i.e. no fat). Thus, in the presence of flow, the signal from the in-phase and out-of-phase echoes can be written as:
| [4] |
| [5] |
In principle, two-point chemical shift fat-water separation can be performed based on the in-phase and out-of-phase magnitude images. However, as discussed in (9) the practical implementation often involves complex value calculations and an estimation of a smoothed field map. As a first step in the reconstruction algorithm, the phases of the two echo images are demodulated using the phase of the in-phase image. Therefore, it can be assumed that the in-phase image has zero phase. A low-pass-filtered field estimation is then used to remove the phase contributions in the out-of-phase image due to inhomogeneities in the main magnetic field. Therefore, only phase variations associated with the flow remain uncorrected. These flow-induced phase differences can be written as:
| [6] |
The reconstructed water and fat signals can be calculated as:
| [7] |
| [8] |
This relationship predicts that the fraction of water signal misallocated to the fat image increases rapidly with increasing phase shift between the first and second echo times and complete misallocation of the water signal into the fat image occurs when the flow-induced phase difference is equal to 180°.
Methods
A stenosis-mimicking phantom (diameter = 12 mm narrowed to 4 mm) was filled with Gadolinium-doped water and was placed in a water bath to minimize magnetic susceptibility effects. A bottle of vegetable oil was placed adjacent to the stenosis phantom (outside the water bath) to provide a reference fat signal. A computer-controlled pump (Shelley Medical Imaging Technologies, London, Ontario) was used to produce flow rates ranging from 0–12 mL/s at 1 mL/s increments. Using a conservation-of-mass estimation, it can be calculated that these flow rates correspond to velocities from 0–11 cm/s through the larger portion of the tube and 0–95 cm/s through the stenotic narrowing. These velocities were chosen to span the range of those expected to be encountered physiologically.
Data acquisition was performed on two different clinical MRI systems: a wide-bore 1.5T scanner and a 3.0T scanner (Optima MR450w and Discovery MR750, respectively, GE Healthcare, Waukesha, WI). A commercially-available dual-echo spoiled gradient-recalled-echo (3) pulse sequence was used for two-point fat-water-separated imaging. Imaging parameters on the 1.5T system were selected to be similar to those used for clinical chest MRI exams at our institution, and included: coronal slab excitation, FOV = 44 cm (S/I) × 44 cm (R/L) × 23 cm (A/P), with 320 × 256 × 76 matrix size for an acquired spatial resolution of 1.4 mm (R/L) × 1.7 mm (A/P) × 3.0 mm (S/I), interpolated to 0.86 mm × 0.86 mm × 1.5 mm through zero-filling. Other parameters included TR/TE1/TE2 = 6.6/2.1/4.2 ms, flip angle = 12°, bandwidth = ± 90.9 kHz. Imaging parameters on the 3.0T system were selected to be similar to those used for clinical contrast-enhanced peripheral MRA exams at our institution, and included: coronal slab excitation, FOV = 44 cm (S/I) × 35 cm (R/L) × 23 cm (A/P), with 320 × 204 × 76 matrix size for an acquired spatial resolution of 1.4 mm (R/L) × 1.7 mm (A/P) × 3.0 mm (S/I), interpolated to 0.86 mm × 0.86 mm × 1.5 mm through zero-filling. Other parameters included TR/TE1/TE2 = 4.1/1.3/2.4 ms, flip angle = 12°, bandwidth = ± 250.0 kHz. Readout gradient waveforms generated on the scanner were recorded and were transferred to an offline computer for calculation of the gradient moments using MATLAB (The Mathworks, Natick, MA). Table 1 summarizes the imaging parameters used as well as the first moments of the readout gradients at each echo time for both field strengths.
Table 1.
The requisite longer echo spacing at 1.5T versus 3.0T increases the relative difference in the first moments at the two echo times for these two field strengths. This table shows some of the imaging parameters that were used in this study, as well as the associated first moments of the readout gradients at the two echo times. Note that acquiring partial echoes compared to full echoes can make ΔM1 smaller or larger.
| Field Strength | RBW | TE1/TE2 | M1(TE1) | M1(TE2) | ΔM1 | |
|---|---|---|---|---|---|---|
| 1.5 T | Full Echo | ± 90.9 kHz | 2.1 / 4.2 ms | 0.40 G(ms)2/cm | −0.85 G(ms)2/cm | − 1.26 G(ms)2/cm |
| Partial Echo | ± 90.9 kHz | 2.1 / 4.2 ms | 0.80 G(ms)2/cm | −0.14 G(ms)2/cm | − 0.93 G(ms)2/cm | |
|
| ||||||
| 3.0 T | Full Echo | ± 250 kHz | 1.3 / 2.4 ms | 0.65 G(ms)2/cm | −0.05 G(ms)2/cm | −0.70 G(ms)2/cm |
| Partial Echo | ± 250 kHz | 1.1 / 2.2 ms | 0.34 G(ms)2/cm | −0.47 G(ms)2/cm | −0.80 G(ms)2/cm | |
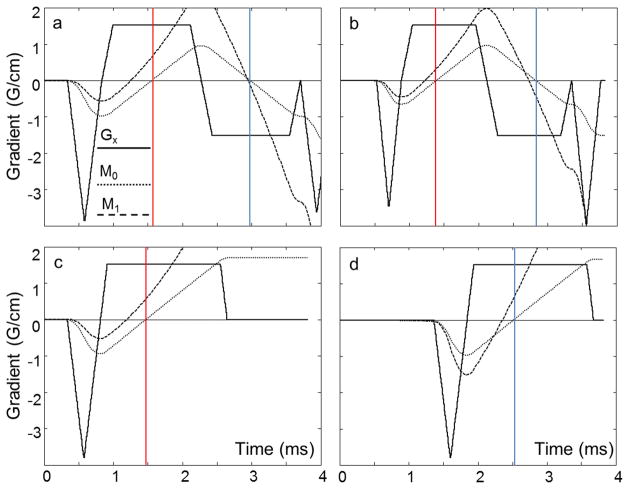
At each flow rate, imaging was performed using both a single-pass, bipolar readout gradient strategy and a dual-pass, unipolar readout gradient strategy. Figure 1 shows gradient waveforms for two bipolar acquisitions; one with full-echo (a) and one with partial-echo (b) readouts. Figure 1(c) and (d) show gradient waveforms for partial-echo readouts for two consecutive TRs of the dual-pass acquisition. For Figure 1(a) and (b), note that the first moment of the readout gradient, M1, is different at the two echo times (denoted by the colored lines) when using a bipolar readout gradient. Note also that, although the M1 values at each of the echo times are different for the full-echo and partial-echo acquisitions, ΔM1 does not change substantially in this example. For Figure 1(c) and (d), it is mathematically straightforward to show that the M1 values at the two echo times are equal when using the dual-pass strategy.
FIG 1.
A bipolar readout gradient has different first moment (M1) values at the first and second echo times, causing flow-induced phase shifts, which lead to fat-water signal misallocations in Dixon fat-water separation methods. The M1 values (dashed line) can be changed by acquiring full echoes (a) instead of partial echoes (b), however, the difference between first moments at the two echo times (ΔM1) remains relatively constant for a wide range of imaging parameters. If a dual-pass, unipolar acquisition is used, where each echo is acquired in a separate TR (c and d), gradient first moment values will be equal at the two echo times (ΔM1 = 0) creating no flow-induced phase shifts, and therefore no fat-water signal misallocations.
For the stenosis-mimicking phantom, in order to determine the velocity range for which the assumption of laminar flow held true, the Reynolds numbers were calculated for the different flow rates using the following equation:
| [9] |
where Q is the flow rate, D is diameter of the tube, v is the viscosity of the water, and A is the cross-sectional area of the tube. Reynolds numbers higher than 2040 were considered to indicate turbulent flow (16).
In order to characterize the amount of water signal from the flowing spins that was misallocated to the fat image, rectangular regions of interest (ROIs) were placed on the fat images. The ROIs measured 3 pixels wide by 34 pixels long, and included the stenosis and a contiguous area downstream of it. The average value measured in the ROI was normalized against an ROI placed on the stationary oil bottle to provide the amount of signal misallocated to the fat image. This signal value was plotted against the flow rate both for the single pass, bipolar readout method and for the dual-pass, unipolar readout method.
Images from two human subjects referred for chest and abdominal 1.5T MRI at our institution were included with IRB approval. In vivo imaging parameters for the chest MRI exam were identical to those used for the phantom experiment at 1.5T. In vivo imaging parameters for the abdominal MRI exam included: axial excitation, FOV = 40 cm (S/I) × 32 cm (R/L) × 30 cm (A/P), with 320 × 192 × 100 matrix size for an acquired spatial resolution of 1.25 mm (R/L) × 2.1 mm (A/P) × 3.0 mm (S/I), interpolated to 0.78 mm × 0.78 mm × 1.5 mm through zero-filling. Other parameters included TR/TE1/TE2 = 6.6/2.1/4.2 ms, flip angle = 12°, bandwidth = ± 90.9 kHz.
Results
As shown in Figure 2, when the stenosis-mimicking phantom was imaged using bipolar readout gradients, incorrect mapping of water signal into the fat images became increasingly visible as the flow rate was increased, which was manifest as an increase in both the area and the intensity of the misallocated signal. As the signal at the site of the narrowing is mapped into the fat image, it may create the illusion of an exaggerated stenosis. Using Equation [9] with literature values of water viscosity at room temperature (v = 10−6 m2/s) the flow was considered to become turbulent through the narrowed region of the stenosis-mimicking phantom for flow rates exceeding 6.4 mL/s.
FIG 2.
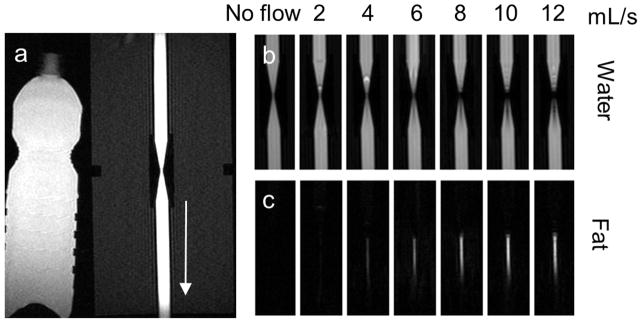
When a bipolar readout gradient is used, increasing the velocity of flowing spins leads to more fat-water signal misallocations (incorrect mapping of water signal into the fat image.) Water images (b) and fat images (c) from a flow phantom experiment at 3.0T show the increasing signal misallocations as the flow increases from 0 to 12 mL/s through a tube containing a narrowing. The arrow in (a) shows the direction of flow. Note that the region of misallocated signal artifact in the fat image increases in both area and intensity as the flow increases.
Incorrect mapping of water signal into the fat image can be mitigated if a dual-pass, unipolar acquisition is used, as shown in Figure 3, which compares images acquired using a single pass, bipolar readout method (a-d), and a dual pass, unipolar readout method (e-h) with the pump set at a flow rate of 8 mL/s (corresponding to 64 cm/s maximum velocity through the narrowing) at 1.5 T. Figure 3(a–b) shows the magnitude in-phase (from TE2) and out-of-phase (from TE1) images and the reconstructed water and fat images (c–d) acquired using a single-pass, bipolar readout gradient acquisition. Figure 3(e–h) shows similar images acquired using a dual-pass, unipolar readout gradient acquisition. The scan time for the dual-pass, unipolar readout gradient acquisition was 80% longer than the single-pass, bipolar readout gradient acquisition. Figure 3(i) shows the average misallocated signal intensity in the fat image for both single-pass, bipolar and dual-pass, unipolar acquisitions for a range of flow rates. Note that the artifact intensifies as the flow is increased in the single-pass, bipolar acquisition but remains unchanged in the dual-pass, unipolar acquisition.
FIG 3.
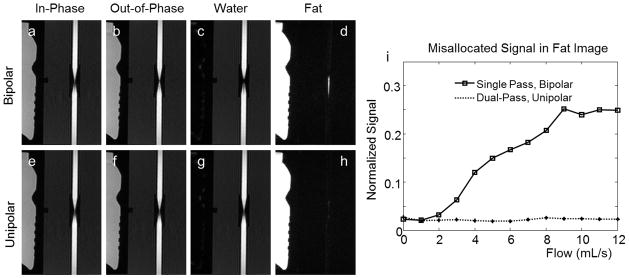
Flow-induced fat-water signal misallocations can be mitigated using a dual-pass, unipolar readout method rather than a single pass, bipolar readout method. Fat-water signal misallocation artifacts are related to unwanted phase that accrues between the in-phase and the out-of-phase echoes. Note that the in-phase and out-of-phase echo images both in the single pass, bipolar readout acquisition (a and b) and in the dual-pass, unipolar readout acquisition (e and f) show minimal flow-induced artifacts. Fat-water signal misallocations are visible when a bipolar readout is used (c and d) but no fat-water signal misallocations are visible when each echo is acquired in a separate TR in a dual-pass, unipolar acquisition (g and h). Imaging was performed at 1.5 T. ROIs placed on the fat images acquired at the different flow rates show that the average signal intensity increases with flow rate in images acquired using the bipolar acquisition but remain constant in images acquired using the dual-pass, unipolar acquisition (i).
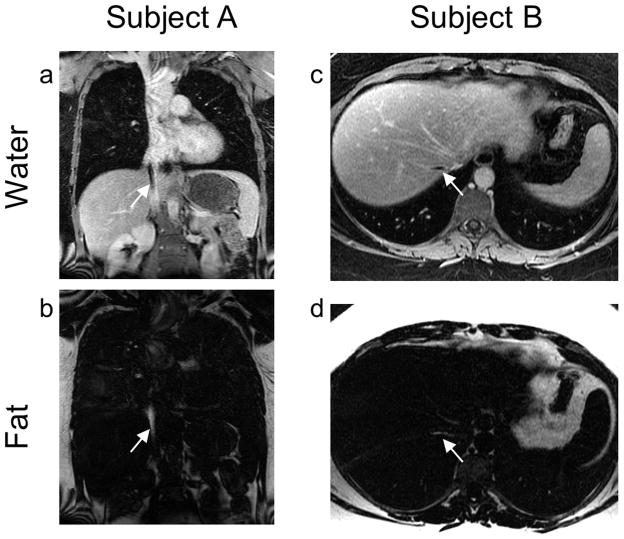
Figure 4(a) and (b) show clinical chest images of a subject (female, 25 years old) demonstrating flow-induced fat-water signal misallocation in the inferior vena cava (IVC) (arrows). Figure 4(c) and (d) show clinical liver images of another subject (female, 30 years old) demonstrating severe flow-induced fat-water signal misallocation in the right hepatic vein (arrows). Note that in both cases the artifacts occurred in regions of flow aligned along the direction of the readout gradient (S/I in Figure 4a, b and R/L in Figure 4c, d).
FIG 4.
Flow-induced fat-water signal misallocations may occur in vivo when spins flow along the readout direction. Two such instances are shown here. In Subject A, the readout direction is Superior/Inferior in this coronal acquisition, and in Subject B, the readout direction is Right/Left in this axial acquisition. Note the dark spot (arrow) in the water image from Subject A resembling an IVC clot and the dark spot (arrow) in the water image from Subject B resembling a hepatic vein thrombus similar to that found in patients with Budd-Chiari syndrome. The bright signal missing from the water images is clearly seen in the fat images (arrows). A Gadolinium-based Contrast Agent (GBCA) was administered prior to acquisition of these fat-water-separated images.
Discussion
In this study, the effects of flow-induced phase shifts on two-point fat-water-separated MRI were investigated using a stenosis-mimicking flow phantom. It is known that when two echoes are encoded using bipolar readout gradients, velocity-dependent phase shifts will accrue between the two echoes. This phase shift will be proportional to the flow rate and the first moments of the bipolar readout gradients at the echo times. Only the special case of two-point fat-water separation is discussed in this note. However, flow-induced phase can result in misallocation artifacts and inaccuracies in three- (or higher)–point methods too depending on the frequency response curve of those methods (17). Flow-induced effects should be considered when multi-echo sequences are used for fat-water-separated imaging in the presence of high flow rates such as when evaluating blood vessels in lower extremities using newly-proposed non-subtractive MRA methods (4). Further, it is important to recognize this signal misallocation artifact in order to avoid misdiagnosis of arterial stenosis or occlusion in the lower extremities, an IVC clot in the chest, or a hepatic vein thrombus resembling Budd-Chiari syndrome in the liver. Such artifacts can occur in vessels containing flow that is oriented along the readout direction.
Multiple solutions can be imagined to lower the risk of generating flow-induced signal misallocations. For example, flow-induced signal misallocation artifacts can be mitigated by avoiding the use of bipolar readout gradients and acquiring each echo in a separate TR using a dual-pass, unipolar acquisition. These artifacts can also be reduced if the readout gradients are specifically designed to minimize the difference between M1 at the out-of-phase and in-phase echo times. In this study, ΔM1 values were measured for readout gradients that employed a range of receiver bandwidths for both full-echo and fractional-echo acquisitions. Using fly-back gradients with nulled first moments at the echo times can also eliminate these artifacts but would result in significantly shortened readout duration given the in-phase and out-of-phase echo time restrictions.
The time between out-of-phase and in-phase echoes is twice as long at 1.5 T compared to 3.0 T. Using similar readout gradient strengths, longer echo spacing leads to larger ΔM1 values at 1.5 T compared to 3.0 T, as is evident in Table 1. This means that images acquired at 1.5 T may be more susceptible to flow-induced signal misallocation artifacts compared to images acquired at 3.0 T.
Several authors have previously studied the effects of chemical shift on phase-contrast MRI (18,19). In this work, we have explored another relationship between flow and chemical shift. We have shown that when flow-induced phase shifts are large (i.e. large difference between first moments of the readout gradients at the first and second echo times) fat-water signal allocation may be inaccurate.
When two-point methods are used for primarily non-vascular applications (including in abdominal and chest MRI) the increased imaging time associated with using dual-pass, unipolar readout gradient methods can lead to breath-holding times longer than what is clinically acceptable. Therefore, we speculate that use of single-pass, bipolar readout gradient methods remains advantageous. However, it is important that radiologists are aware of this artifact and are encouraged to examine fat images and single-echo images if signal anomalies are observed in vasculature. On the other hand, when two-point methods are used for MRA of the lower extremities, it would be unrealistic to expect a full examination of the entire vascular tree in the fat images as well as the water images. Dual-pass, unipolar readout gradient acquisition can be one solution to address this signal misallocation artifact. Further investigation is necessary to find other solutions with less of a scan time penalty.
This study has several limitations. First, the flow pattern used in the phantom experiments did not necessarily fully represent flow patterns found in vivo. In the phantom experiments, a constant flow was used, while physiological flow is often pulsatile. Physiological pulsatility may influence the effect of this flow-induced signal misallocation artifact. Some effects of flow pulsatility on two-point fat-water MRI have been reported previously (20), however, a more comprehensive study of pulsatility effects on fat-water separation may be necessary.
Another limitation of this study is that the stenosis-mimicking phantom that was used to achieve velocities high enough to represent those likely found in vivo leads to complex flow patterns beyond the stenosis, making accurate identification of the velocities in the post-stenotic region difficult. These two effects together make it difficult to directly correlate the amount of signal misallocation to the velocity of the flowing spins. Additionally, turbulent and complex flow can lead to intra-voxel dephasing that in turn leads to signal loss. Intra-voxel dephasing becomes more dominant than fat-water signal misallocation artifacts as the velocity is increased in the experimental set-up used in this study, and can complicate interpretation of the two effects. Using a more viscous fluid instead of Gd-doped water will lower the turbulence; however, care must be taken not to introduce additional chemical-shift components into the experiment by using a fluid with a complicated NMR spectrum.
Furthermore, a rigorous study is necessary to systematically investigate the clinical implications of flow-induced signal misallocations for different applications of fat-water separation methods.
In conclusion, this study has shown that flow-induced phase shifts in fat-water separation techniques that use bipolar readout gradients can lead to incorrect mapping of a fraction of the water signal to fat images. While the bipolar acquisition strategy has advantages in terms of short acquisition time, it is important to consider its potential to confound the evaluation of blood vessels by enhancing the severity of stenoses or creating the appearance of intravascular clot. This study also has shown that methods that use dual-pass, unipolar readout gradients are useful for mitigating these flow-induced signal misallocation effects.
Acknowledgments
The authors would like to thank Alejandro Roldan, Kevin Johnson, Leonardo Rivera and Oliver Wieben for their help with the phantom study and Scott Nagle and Peter Bannas for their assistance with reviewing clinical images. We also acknowledge the support of the NIH (R01 DK083380 and R01 DK088925).
References
- 1.Dixon WT. Simple proton spectroscopic imaging. Radiology. 1984;153:189–194. doi: 10.1148/radiology.153.1.6089263. [DOI] [PubMed] [Google Scholar]
- 2.Berglund J, Ahlström H, Johansson L, Kullberg J. Two-point dixon method with flexible echo times. Magnetic Resonance in Medicine. 2011;65:994–1004. doi: 10.1002/mrm.22679. [DOI] [PubMed] [Google Scholar]
- 3.Ma J. Breath-hold water and fat imaging using a dual-echo two-point dixon technique with an efficient and robust phase-correction algorithm. Magnetic Resonance in Medicine. 2004;52:415–419. doi: 10.1002/mrm.20146. [DOI] [PubMed] [Google Scholar]
- 4.Leiner T, Habets J, Versluis B, Geerts L, Alberts E, Blanken N, Hendrikse J, Vonken E-J, Eggers H. Subtractionless first-pass single contrast medium dose peripheral MR angiography using two-point Dixon fat suppression. European radiology. 2013:1–8. doi: 10.1007/s00330-013-2833-y. [DOI] [PubMed] [Google Scholar]
- 5.Michaely HJ, Attenberger UI, Dietrich O, Schmitt P, Nael K, Kramer H, Reiser MF, Schoenberg SO, Walz M. Feasibility of gadofosveset-enhanced steady-state magnetic resonance angiography of the peripheral vessels at 3 Tesla with Dixon fat saturation. Investigative radiology. 2008;43:635–641. doi: 10.1097/RLI.0b013e31817ee53a. [DOI] [PubMed] [Google Scholar]
- 6.Korosec FR, Frayne R, Grist TM, Mistretta CA. Time-resolved contrast-enhanced 3D MR angiography. Magnetic Resonance in Medicine. 1996;36:345–351. doi: 10.1002/mrm.1910360304. [DOI] [PubMed] [Google Scholar]
- 7.Meaney JFM, Ridgway JP, Chakraverty S, Robertson I, Kessel D, Radjenovic A, Kouwenhoven M, Kassner A, Smith MA. Stepping-Table Gadolinium- enhanced Digital Subtraction MR Angiography of the Aorta and Lower Extremity Arteries: Preliminary Experience. Radiology. 1999;211:59–67. doi: 10.1148/radiology.211.1.r99ap1859. [DOI] [PubMed] [Google Scholar]
- 8.Stinson EG, Trzasko JD, Riederer SJ. SNR and CNR Performance Comparison in Dixon- vs. Subtraction-type Contrast Enhanced MR Angiography; 2013 April; Salt Lake City, Utah, USA. p. 4458. [Google Scholar]
- 9.Eggers H, Börnert P. Chemical shift encoding-based water–fat separation methods. Journal of Magnetic Resonance Imaging. 2014 doi: 10.1002/jmri.24568. [DOI] [PubMed] [Google Scholar]
- 10.Ma J, Slavens Z, Sun W, Bayram E, Estowski L, Hwang K-P, Akao J, Vu AT. Linear phase-error correction for improved water and fat separation in dual-echo dixon techniques. Magnetic Resonance in Medicine. 2008;60:1250–1255. doi: 10.1002/mrm.21747. [DOI] [PubMed] [Google Scholar]
- 11.Lu W, Yu H, Shimakawa A, Alley M, Reeder SB, Hargreaves BA. Water–fat separation with bipolar multiecho sequences. Magnetic Resonance in Medicine. 2008;60:198–209. doi: 10.1002/mrm.21583. [DOI] [PubMed] [Google Scholar]
- 12.Yu H, Shimakawa A, McKenzie CA, Lu W, Reeder SB, Hinks RS, Brittain JH. Phase and amplitude correction for multi-echo water–fat separation with bipolar acquisitions. Journal of Magnetic Resonance Imaging. 2010;31:1264–1271. doi: 10.1002/jmri.22111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Eggers H, Brendel B, Duijndam A, Herigault G. Dual-echo Dixon imaging with flexible choice of echo times. Magnetic Resonance in Medicine. 2011;65:96–107. doi: 10.1002/mrm.22578. [DOI] [PubMed] [Google Scholar]
- 14.Peterson P, Månsson S. Fat quantification using multiecho sequences with bipolar gradients: Investigation of accuracy and noise performance. Magnetic Resonance in Medicine. 2014;71:219–229. doi: 10.1002/mrm.24657. [DOI] [PubMed] [Google Scholar]
- 15.Xiang Q-S. Two-point water-fat imaging with partially-opposed-phase (POP) acquisition: An asymmetric Dixon method. Magnetic Resonance in Medicine. 2006;56:572–584. doi: 10.1002/mrm.20984. [DOI] [PubMed] [Google Scholar]
- 16.Avila K, Moxey D, de Lozar A, Avila M, Barkley D, Hof B. The Onset of Turbulence in Pipe Flow. Science. 2011;333:192–196. doi: 10.1126/science.1203223. [DOI] [PubMed] [Google Scholar]
- 17.Brodsky EK, Chebrolu VV, Block WF, Reeder SB. Frequency response of multipoint chemical shift-based spectral decomposition. Journal of Magnetic Resonance Imaging. 2010;32:943–952. doi: 10.1002/jmri.22308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Middione MJ, Ennis DB. Chemical shift-induced phase errors in phase-contrast MRI. Magnetic Resonance in Medicine. 2013;69:391–401. doi: 10.1002/mrm.24262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johnson KM, Wieben O, Samsonov AA. Phase-contrast velocimetry with simultaneous fat/water separation. Magnetic Resonance in Medicine. 2010;63:1564–1574. doi: 10.1002/mrm.22355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Eggers H, Boernert P, Leiner T. Suppression of High Intensity Flow Artifacts in Subtractionless First-Pass Peripheral Angiography with Dual-Echo Dixon Imaging. Proceedings 21st Scientific Meeting, International Society for Magnetic Resonance in Medicine; Salt Lake City, Utah, USA. 2013. p. 0310. [Google Scholar]