Pathway-guided Identification of Gene-Gene Interactions

Summary

Assessing gene-gene interactions (GxG) at the gene level can permit examination of epistasis at biologically functional units with amplified interaction signals from marker-marker pairs. Current gene-based GxG methods tend to be designed for studying interactions among two or a few genes. For complex traits, it is often common to have a list of many candidate genes to explore GxG. In this work, we propose a pathway-guided approach based on penalized regression for detecting interactions among genes. Specifically, we apply the principal component analysis to summarize the multi-SNP genotypes and SNP-SNP interaction between a gene pair, and to identify important main and interaction effects using an L1 penalty, which incorporates adaptive weights based on biological guidance and trait supervision. Our approach aims to combine the advantages of biological guidance and data adaptiveness, and yields credible findings that have both biological and statistical support and may be likely to shed insights in order to formulate biological hypotheses for further cellular and molecular studies. The proposed approach can be used to explore the gene-gene interactions with a list of many candidate genes and is applicable even when sample size is smaller than the number of predictors studied. We evaluate the utility of the pathway-guided penalized GxG regression using simulation and real data analysis. The numerical studies suggest improved performance over methods not utilizing pathway and trait guidance.

Introduction

The focus of genetic association studies for complex diseases has been gradually shifting from assessing the main genetic effect to assessing interaction effects among genes (Cordell, 2009). Complex diseases, such as hypertension, cancer, diabetes, and psychiatric disorders are believed to have a polygenic basis and gene-gene interaction (GxG) may play significant roles in disease etiology (Lin et al., 2013; Pillai et al., 2013; Koh-Tan et al., 2013; Howson et al., 2012; Ziyab et al., 2013). Understanding GxG may also help to uncover missing heritability (Marchini et al., 2005; Evans et al., 2006) and to explain inconsistent findings from main-effect analyses (Hirschhorn et al., 2002).

GxG can be defined from a biological view or a statistical view. The biological GxG refers to the physical interactions between biomolecules such as DNA, RNA or protein at the cellular level (Cordell, 2002). The statistical GxG refers to a deviation from additive main effects of genes on a relevant scale. Although there were debates about the relationship between the two, evidence has shown that the statistical GxG and the biological GxG can converge to the same scientific process (Bush et al., 2009). Differences in biological epistasis among individuals give rise to statistical epistasis, and hence statistical analyses can be used to infer the presence of gene-gene interactions (Moore & Williams, 2005). For example, Bridges (1919) used a statistical model to identify genes with interaction effects on Drosophila eye color (Bridges, 1919), and the corresponding biological mechanism that depicts how these genes influence biological pathways was understood many years later (Lloyd et al., 1998). In this work, we propose a pathway-guided and trait-supervised procedure to further facilitate the detection of statistical GxG, and hope it can eventually lead to better understanding of biological epistasis and disease etiology.

Many methods have been proposed to detect GxG, such as logic regression (Kooperberg et al., 2001), classification/regression tress (CART), multivariate adaptive regression splines (MARS) (Cook et al., 2004), and methods building upon principals of multifactor dimensionality reduction (MDR) (Ritchie et al., 2003; Lou et al., 2007; Lou et al., 2008; Jestinah et al., 2011; Gui et al., 2013). These methods have shown promising performances in detecting the interaction effects important to complex diseases or traits. (Ritchie, 2011; Steen, 2012; Dennis et al., 2011; Mackay, 2014). However, most of these methods considered interactions among SNPs instead of interactions among genes. There are several advantages to assessing GxG at the gene level instead of at the SNP level. First, genes are the basic units in the biological mechanism and SNPs within a gene tend to work together (Lehne et al., 2010; Kostem, et al. 2011). Hence gene-level results can be more biologically insightful, easier to interpret, and more informative in revealing underlying mechanisms. Second, modeling multi-SNP information also incorporates linkage disequilibrium (LD) among SNPs in any downstream analysis such as association tests (He et al., 2011). Third, the polygenic nature of complex diseases suggests moderate effect sizes for individual variants. Aggregating SNP effects at the gene level can amplify the signals and make them more detectable; it can also overcome etiological heterogeneity across individuals where the increased risk of different individuals is caused by different variants of the same gene. Finally, by using appropriate dimension reduction to summarize multi-SNP information, gene-level GxG methods are able to use fewer degrees of freedom, which further helps to improve power over SNP-level analyses. For these reasons, several gene-level methods for GxG have been proposed, such as the Turkey 1-df method (Chatterjee et al., 2006), principal component (PC) analysis and the partial least square (PLS) based model (Wang et al., 2009), kernel-based regressions (Larson & Schaid, 2013), and the nonparametric test based method (Aschard et al., 2013). These studies suggested that gene-level methods have higher power in detecting GxG than traditional SNP-SNP strategies, especially when the causal SNPs are not directly genotyped.

Most of the methods available for studying GxG interactions are for two or a few genes. However, for complex traits, it is often common to have a list of many candidate genes in order to explore GxG. Even with a moderate size gene set, there can be a huge number of GxG terms even at the gene level; e.g., a set of 10 genes would lead to 45 pairwise GxG interaction terms. Directly modeling all GxG interactions would be inefficient due to computational challenge and lack of power. The solution is to reduce the search space of GxG by filtering out potentially unimportant genes (Ritchie, 2011). In current practice, the GxG search space is reduced either in a trait-supervised fashion or by using prior biological information.

To reduce the GxG search space supervised by the trait information, one would first apply main-effect association tests on each gene/SNP to remove unimportant ones and then model interactions among the remaining ones (Wu et al., 2010). Two interaction mechanisms for Amyotrophic Lateral Sclerosis (ALS) have been identified by this method (Sha et al., 2009). However, filtering out genes/SNPs through main-effect screening would have low power if the causal genes only have strong interaction effects but no main effects. To improve on this method, several non-parametric methods were proposed to perform more effective filtering, such as the ReliefF (Robnik-Sikonja & Kononenko, 2003) and Tuned ReliefF (TuRF) methods (Moore & White, 2007), which use the nearest neighbors method to find the important genes. The nearest neighbor of an individual is the one which has the highest genetic similarity with the target individual at the focused genes. If the gene is important to the trait, the nearest neighbor pair tends to have similar traits. ReliefF sums up all the weighted trait differences to test whether one gene is important to the trait. These methods can successfully reduce the search space by eliminating unimportant genes/SNPs and retaining important ones that may be missed by main-effect screening (Cordell, 2009).

Another way to reduce GxG search space is to use biological knowledge or prior knowledge as a filter (Ritchie, 2011), such as Biofilter (Bush et al., 2009). Biofilter builds the list of important genes based on databases such as the Kyoto Encyclopedia of Genes and Genomes (KEGG), Protein interaction database (PID) and Biocarta (http://www.biocarta.com). Its underlying rationale is that if the interactions among a group of genes are supported by more biological evidence, the corresponding statistical finding for GxG is more credible. Biofilter uses an implication index, which is the number of databases supporting a focused GxG, to quantify the strength of biological support. If no database provides support to the focused GxG, it would be removed from the search space. Recent studies have shown that Biofilter can effectively reduce the GxG search space and result in biologically meaningful GxG findings (Pendergrass et al., 2013; Turner et al., 2011; Bush et al., 2011).

Statistical analyses coupled with biological guidance can lead to credible findings that have both biological and statistical support and that may be more likely to shed insight on the formation of follow-up biological hypotheses for further cellular and molecular studies. However, directly filtering out genes without incorporating trait information can be too arbitrary, especially when the prior knowledge is not trait-specific. In this paper, we propose a penalized method that incorporates biological guidance and trait supervision to detect GxG at the gene level. Specifically, we apply PC analysis to summarize the multi-SNP genotypes and SNP-SNP interaction between a gene pair, and to identify important main and interaction effects using an L1 penalty, which incorporates adaptive weights based on association strength and trait-specific pathway supports. We demonstrate the utility of pathway-guided penalized regression for GxG identification using simulation and real data analysis.

Methods

For individual i, let Y_i be the trait value and G_m,i be the multi-marker genotype vector of the l_m markers in gene m. Given the genotypes of genes s and t, s ≠ t, the interaction design vector between the two genes is denoted by H_st,i = G_s,i ⊗ G_t,i, where ⊗ is the Kronecker product. Also define genotype design matrix G_m = [G_m,₁, ··· G_m,N]^T, interaction design vector H_st = [H_st,1, ··· H_st,N]^T and trait vector Y = [Y₁, ··· Y_N]^T, where N is the sample size. Finally assume that there are M genes, and the total number of GxG among these genes is q = M(M − 1)/2.

Obtaining gene-level genetic information

We first summarize the multi-SNP information at gene level for the main-effect design matrix and the interaction-effect design matrix by a PC analysis. To fix the idea, we only use the first PC, but the model can be straightforwardly extended to include multiple PCs. The PCs are obtained by standardizing the design matrix of all individuals. We use X_1,m to denote the first PC obtained from genotype design matrix G_m and use X_2,st to denote the PC obtained from the interaction design matrix H_st. Note that one can summarize the information of gene-gene interaction using X_1,s · X_1,t. Doing so can bypass the need to compute and decompose the large matrix H_st. However, we found that X_1,s · X_1,t may not be able to capture much of the variability of H_st (Table 1) because X_1,s and X_1,t are obtained by maximizing the information captured in the main effect G_s and G_t, respectively. Obtaining PCs from the interaction design matrix H_st helps to capture a higher proportion of variability (Table 1). More details are given under the result section of Simulation II.

Table 1.

False positive rate and proportion of variance explained by PCs using different summarizing strategies by different gene size under Simulation II with random support and quantitative traits. The genes are classified into small size (1~33 SNPs), medium size (34~67 SNPs) and large size (68~102 SNPs), hence there are six categories for the gene pairs: SS, SM, SL, MM, ML and LL. “PC1_SNP×SNP” indicates the first PC from the interaction design matrix and “PC1_geneS×PC1_geneT” indicates the cross product of the PCs for gene S and for gene T.

Size of Gene Pairs			SS	SM	SL	MM	ML	LL
Average Number of SNP× SNP Terms			84	443	923	2289	4800	9996
Proportion of variance explained		PC1SNP×SNP	0.40	0.26	0.19	0.15	0.10	0.05
		PC1geneS×PC1geneT	0.32	0.16	0.05	0.07	0.02	0.008
False Positive Rate	No size weight*	PC1SNP×SNP	0.002	0.004	0.005	0.01	0.038	0.083
		PC1geneS×PC1geneT	0.003	0.006	0.034	0.023	0.076	0.100
	With size weight**	PC1SNP×SNP	0.003	0.005	0.005	0.009	0.025	0.058
		PC1geneS×PC1geneT	0.004	0.008	0.036	0.021	0.053	0.073

^*“No size weight” indicates setting ω_size = 1; ω_effect and ω_path are set as proposed.

^**“With size weight” indicates setting ω_size as proposed; ; ω_effect and ω_path are set as proposed.

Variable selection guided by pathway supports

We use the following generalized linear model (GLM) to assess the main and interaction effects of genes:

$$g(\mu )=\sum _{m=1}^M{X}_{1,m}{\gamma }_m+\sum _{\ell =1}^q{X}_{2,\ell }{\beta }_{\ell }=X_1\gamma +X_2\beta ,$$

where g(·) is the link function, μ =E(Y|X) is the conditional mean trait value given covariates X₁ and X₂ with X₁ = [X_1,1, ···, X_1,M] being the PCs of M genes and X₂ = [X_2,1, ··· X_2,q] being the PCs of q = M(M − 1)]/2 GxG terms. Parameter γ is the main effect vector with γ = [γ₁, ···, γ_M]^T, and β is the interaction effect vector with β = [β₁, ··· β_q]^T. For quantitative traits, we set g(μ) = μ, i.e., the identify link function. For binary traits, we set g(μ) = log(μ/(1−μ)), i.e., the logit link function, which is commonly used in practice.

To detect important terms, we estimate γ and β by minimizing the following penalized log-likelihood

$$-logL(\gamma ,\beta ;Y,X_1,X_2)+{\lambda }_1{\sum }_{m=1}^M{\omega }_{1,m}\mid {\gamma }_m\mid +{\lambda }_2{\sum }_{\ell =1}^q{\omega }_{2,\ell }\mid {\beta }_{\ell }\mid ,$$ (1)

where L(γ,β; Y, X₁, X₂) is the likelihood function of γ and β; ω_1,m’s and ω_2,ℓ’s are the weights for main effects and interaction effects, respectively; λ₁ and λ₂ are the tuning parameters of main effects and interaction effects, respectively. The weights (either the weight for main effect ω₁ or interaction effect ω₂) are constructed based on three components: weights based on gene size (denoted by ω_size), weights based on pathway supports (denoted by ω_path) and weights based on effect size on the trait (denoted by ω_effect). That is, the overall weight is ω_m = ω_size,m · ω_path,m · ω_effect,m.

Weights for gene size ω_size

In gene-set association analysis, it has been noted that larger genes (i.e., genes with more SNPs) are more likely to be chosen as significant (Wang et al., 2010). Although here we summarized the gene information into the first PC, our results indicated that large genes tended to be selected if no penalty was imposed on large genes (e.g., we obtained higher false positive rates (FPR) for larger genes when ω _size =1, as can be seen in Fig. 1). This is probably related to the observation that the variation captured by the first PC decreases as the gene size increases (e.g., Table 1). On the other hand, incorporating gene size in the penalty weights can make false positives (FPs) less concentrated in the category of pairs of large genes. We note that while conventionally, gene size refers to the number of SNPs in a gene, in our work, gene size refers to the number of columns in the corresponding design matrix, e.g., G_m or H_ℓ. Specifically, we set ω_size,m = 1+(s_m − min{s_i})/(max{s_i}− min{s_i}), where for main effect, s_m is the number of columns of G_m and for interaction effect, s_m is the number of columns of H_m. To coordinate ω_size with other weights (i.e., ω_path and ω_effect) and to avoid ω_size dominating other weights, we consider the rescaled s_m − min{s_i} and divide it by max{s_i} − min{s_i} so that ω_size is between 1 (no size weight) and 2 (maximum size weight). In other words, the maximum penalty from gene size is bounded at 2 times the minimum penalty.

Figure 1.

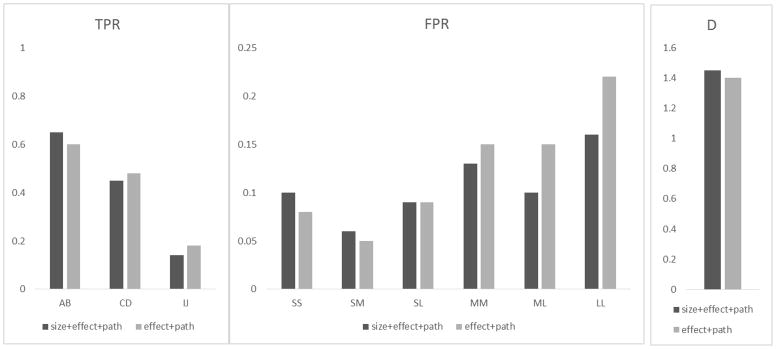
The true positive rate (TPR), false positive rate (FPR) and D statistic (D = log TPR − log FPR) for detecting GxG gene pairs in Simulation I with two types of ω_size: (1) ω_size,m = 1 (i.e., no size weights), represented by the light gray bar, and (2) ${\omega }_{\mathit{size},m}=1+\frac{s_m-{min}_m{s}_m}{{max}_m{s}_m-{min}_m{s}_m}$ where s_m is the gene size, represented by the dark gray bar. The x-axis represents the gene labels in the TPR plot and represents the gene sizes in the FPR plot, i.e., S/M/L for small/medium/large genes.

Weights for pathway support ω_path

We use weight ω_path to incorporate the strength of pathway support. We focus only on biological evidence relevant to the trait of interest (e.g., via PubMed search) and quantify the support strength by the number of pathways that support the interaction among certain gene pairs. Define N_path as the total number of pathways related to the trait and n_ℓ is the number of sources supporting the ℓth gene-gene pair. We set ω_path,ℓ = 1 − n_ℓ/(2N_path)so that a gene pair with greater pathway support receives less penalty. Because our focus is on GxG effects, we set ω_path,m =1 for main effect terms. The value of ω_path is between 0.5 and 1 to avoid the dominance of one weight over the other.

Weight for effect size ω_effect

Weight ω_effect is the adaptive weight (Zou, 2006) that inversely weighs each effect term by an initial estimate of the effect size, i.e., ${\omega }_{\mathit{effect},m}=1/\mid \stackrel{\sim }{{\gamma }_m}\mid$ for the main effect terms and ${\omega }_{\mathit{effect},\ell }=1/\mid \stackrel{\sim }{{\beta }_{\ell }}\mid$ for interaction terms. As a result, important terms receive a smaller penalty and tend to be retained in the selecting process while unimportant terms receive a larger penalty and are more likely to be eliminated. We use the iterative L1 penalty method (i.e., the multi-step adaptive lasso of Buhlmann and Meier (2008)) to obtain the initial estimates $\stackrel{\sim }{{\gamma }_m}$ and $\stackrel{\sim }{{\beta }_{\ell }}$. Specifically, $\stackrel{\sim }{{\gamma }_m}$ and $\stackrel{\sim }{{\beta }_{\ell }}$ are obtained by minimizing:

$$-logL(\beta ,\gamma ;Y,X_1,X_2)+{\lambda }_1^{\ast }{\sum }_{m=1}^M\frac{\left|{\gamma }_m^{(t)}\right|}{\left|{\gamma }_m^{(t-1)}\right|}+{\lambda }_2^{\ast }{\sum }_{\ell =1}^q\frac{\left|{\beta }_{\ell }^{(t)}\right|}{\mid {\beta }_{\ell }^{(t-1)}\mid },$$ (2)

where ${\gamma }_m^{(t)}$ and ${\beta }_{\ell }^{(t)}$ are the estimate for the m-th main effect and ℓ-th interaction effect in the t-th iterative. The difference between Equations (1) and (2) is that in Equation (2), the adaptive weights of the current iteration are the estimates from the previous iteration. The iteration continues until γ_m and β_ℓ converge for all m and ℓ. Using a penalized estimator method allows us to obtain the initial estimates even when the sample size is smaller than the total number of variables, and the iterative procedure yields more accurate estimates (Li & Sillanpaa, 2012). The estimates for some (potentially unimportant) variables can be 0 with the L1 penalty. When that occurs, we set $\stackrel{\sim }{{\gamma }_m}=min({min}_{{\beta }_k>0}{\gamma }_k,{10}^{-3})$ and use similar treatment for $\stackrel{\sim }{{\beta }_{\ell }}$ as well.

Computing tuning parameters

For a given value of (λ₁, λ₂), we compute the L1-reguralized estimates of γ_m and β_ℓ, and calculate the Bayesian information criterion (BIC) = − 2 log L(γ̂, β̂; Y, X₁, X₂) + k log N for the corresponding model, where k is the number of terms retained in the model. The (λ₁, λ₂) that gives the smallest BIC is used to obtain the final model. We use BIC to tune λ₁ and λ₂ because our goal is to select the true model structure and BIC has the consistency property in model selection (French et al., 2006; Guo & Lin, 2009; Hastie et al., 2009; Lake et al., 2003).

Simulation

We use simulation to evaluate the performance of the proposed method and the impact of different choices of weights. We performed two sets of simulation. Simulation I was based on a well-controlled hypothetical dataset with the sample size much larger than the number of predictors. It aimed to determine the optimal forms of the weights and to enable us to understand the impact of different weight specifications. Simulation II was based on the Wellcome Trust Case-Control Consortium (2007) data for Crohn’s disease with the sample size smaller than the number of predictors. It aimed to evaluate the utility of the proposed approaches under realistic settings.

Simulation I

Design of Simulation I

In Simulation I, we generated 11 genes with different sizes (Table 2. The genes were labeled as gene A to gene K, and the number of SNPs in each gene was randomly determined from a uniform (1, 100) distribution. The minor allele frequency (MAF) of a SNP was randomly determined from a uniform (0.1, 0.5) distribution. The SNPs within each gene were sorted by their MAF and only the middle 50% were used as causal SNPs. In our simulation, genes with ≤30 SNPs were labeled as small (S), genes with ≥70 SNPs were labeled as large (L), and genes with 30 ~ 70 SNPs (exclusively) were labeled as medium-sized genes (M). We considered six categories of gene-gene pairs: SS, SM, SL, MM, ML and LL.

Table 2.

In Simulation I, 11 genes are generated; the number of SNPs in each gene ranges from 7 to 99.

Gene ID	A	B	C	D	E	F	G	H	I	J	K
Number of SNPs	42	7	48	77	46	20	31	99	84	72	14

We generated trait value Y_i from Model (3) below, where we assumed that gene F has the main causal effect and there exist causal interaction effects between genes A and B (i.e., two small genes), between genes C and D (i.e., a small gene and a large gene), and between genes I and J (i.e., two large genes):

$$Y_i=({\sum }_{l\in \{\mathit{casual}\mathit{SNPs}\}}{G}_{F,li}){\varphi }_F+{\sum }_{st\in \{AB,CD,IJ\}}\left({\sum }_{k,k^{\prime }\in \mathit{casual}\mathit{SNPs}}{G}_{s,ki}·G_{t,k^{\prime }i}\right){\zeta }_{st}+e_i,$$ (3)

where G_m,li is the genotype of SNP l in gene m for subject i and e_i is generated from Normal(0,1). Coefficients ϕ_F, ζ_AB, ζ_CD and ζ_IJ are effect size; in the simulation, we used a common value for these coefficients and the common value was determined so that the partial R² explained by interactions was around 30%. The partial R² of the interaction effect is defined as $R^2=(R_{12}^2-R_1^2)/(1-R_1^2)$, where $R_{12}^2$ is the R-square value for Model (3) containing both main and interaction effects, and $R_1^2$ is the R-square value for Model (3) containing only main effects (i.e., ζ_st =0 for all s and t). The total number of relevant pathways was 20. In each replication, we simulated 1500 individuals and performed 200 replications per scenario.

To assess the impact of a weight type, we performed the analyses under two conditions: (a) setting the corresponding weight type as 1 (i.e., neutral weights) and (b) incorporating the proposed weight type. For example, to assess the impact of ω_path, we examine the performance of (a) using ω_size + ω_effect (a) vs. the performance of (b) using ω_size + ω_path + ω_effect. For each condition, we computed the true positive rate (TPR) of detecting the causal GxG gene pairs. We also computed the FPR among the non-causal gene pairs. Finally, we calculated the D statistic (Athanasiou, 2011), which is defined as D =log TPR − log FPR and is commonly used as an omnibus index to integrate TPR and FPR. Higher D indicates better performance of the method.

Results of Simulation I

Assessment of ω_size (Figure 1)

When evaluating ω_size, we set the number of pathways supporting each interaction pairs as 20, 10, and 0 for A×B (MS gene pair), C×D (ML gene pair) and I×J (LL gene pair), respectively. We considered ω_size,m = 1 (i.e., no gene size weights) and ω_size,m = 1+(s_m − min{s_i})/(max{s_i} − min{s_i}), where, s_m is the number of columns in the design matrix. The results indicated that without penalizing the gene size, the FPRs for large genes were substantially larger than the FPRs for small genes, e.g., the FPRs of LL pairs were higher relative to MM pairs and to ML pairs. By setting ω_size as proposed, the FPRs became less clustered in the large gene pairs, i.e., the FPRs in LL, ML and MM pairs decreased, the FPRs for SL pairs remained similar, and the FPRs for gene pairs not involving large genes (e.g., SS and SM) increased slightly. For TPR, we observed that the TPR deceased as the gene size increased, which is because ζ_AB, ζ_CD and ζ_IJ were set to be the same and the number of pathway supports happen to decrease as gene size increases. By comparing the TPR with and without ω_size, we see that the TPR increased slightly for A×B (MS pair), and decreased slightly for C×D (ML pair) and for I×J (LL pair). This is because ω_size encouraged the model to select smaller terms, although the differences were small. According to the D statistic, adding a size penalty always increases the overall performance.

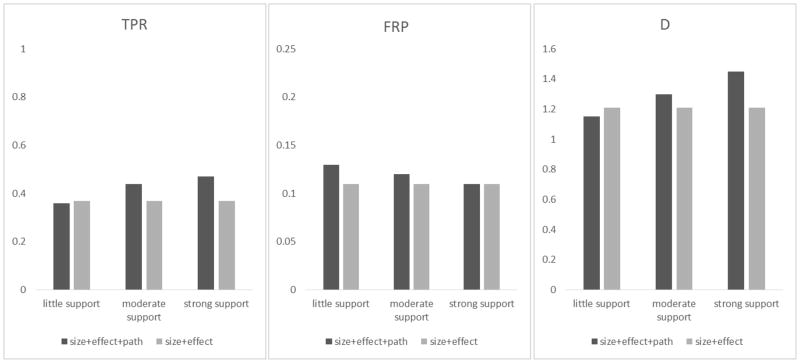
Assessment of ω_path (Figure 2)

Figure 2.

The true positive rate (TPR), false positive rate (FPR) and D statistic (D=log TPR − log FPR) for detecting GxG gene pairs in Simulation I under three different scenarios, i.e., causal gene pairs with little, moderate and strong pathway supports (as detailed in Table 3). In each scenario, the dark gray bars represent the results of incorporating pathway support (i.e., setting ω_path as proposed) and the light gray bars represent the results of no pathway support (i.e., setting ω_path =1).

Our proposed weight for pathway support has a general form of ${\omega }_{\mathit{path},\ell }=1-\frac{1}{2}\times \frac{n_{\ell }}{N_{\mathit{path}}}$ for GxG term ℓ, and is ranged between $\frac{1}{2}$ to 1. In other words, the maximum amount of penalty reduction from pathway support is set to be half. Note that ω_path actually encourages gene pairs with pathway support to be selected more frequently. When evaluating ω_path, we set the number of pathways supporting each interaction according to Table 3, where we considered three scenarios, i.e., all causal interactions with little, moderate, or strong pathway support. Figure 2 suggests that for the scenarios of moderate and strong support, incorporating w_path has little impact on FPR but can boost TPR. For the little support scenario, incorporating w_path (which relatively discourages the selection of gene pairs with little support) did not cause too much reduction in TPR. However, there is a slight increase in FPR in the little and moderate support scenarios compared to using the null pathway weight. This is likely because under those two scenarios, the majority of the pathway supports are assigned to the null GxG gene pairs (i.e., the last column of Table 3). Overall, it is worth incorporating the pathway weights --- the gain in the D statistic caused by ω_path in moderate and strong supports is substantially more than the loss in little supports, and the scenario of little support might occur less frequently in reality.

Table 3.

The biological supports under four scenarios. Each scenario contains 20 pathways. The differences between scenarios are the number of pathways supporting the causal GxG.

Scenarios	Number of pathways supporting GxG of a gene pair				Total # of pathway supportsb	% for causal gene pairs (1 − a/b)
	Causal GxG gene pairs			Non-causal GxG gene pairs (52 pairs)a
	A×B	C×D	I×J
Little support	2	1	0	92	95	3%
Moderate support	11	10	9	166	196	18%
Strong support	20	19	18	160	177	48%

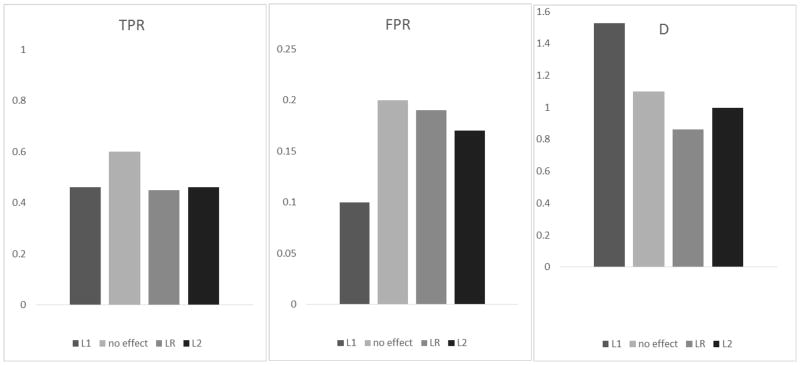
Assessment of ω_effect (Figure 3)

Figure 3.

The true positive rate (TPR), false positive rate (FPR) and D statistic (D =log TPR − log FPR) for detecting GxG gene pairs in Simulation I using ω_effect calculated by different methods: (from left to right) iterative L1 penalty regression (L1); ω_effect =1 (no effect weight); linear regression (LR); and L2 penalty regression (L2).

When evaluating ω _effect, we set the number of pathways supporting each interaction pair as 20, 10, and 0 for A×B, C×D and I×J, respectively. We compared the performance of four different ways to obtain the adaptive weights: (1) using the effect estimates from the iterative L1 penalty (L1), (2) using ω_effect =1 (null weights), (3) using the effect estimates from linear regression (LR), and (4) using the effect estimates from penalized L2 regression (L2). The other two weights, i.e., w_path and w_size, were specified using the proposed form. Figure 3 suggests that a null weight can lead to high TPR and high FPR and can result in a low D value. All three estimating methods yielded similar TPRs but different FPRs. The iterative L1 penalty method had the smallest FPR and was the best choice among the methods. In contrast, the linear regression had the worst performance, and it is infeasible when the number of variables exceeds the number of samples. The L2 penalty method had an FPR slightly smaller than that of the linear regression method.

Simulation II

Design of Simulation II

In Simulation II, we used the data for Crohn’s disease from the Wellcome Trust Case-Control Consortium (WTCCC) (2007) to simulate genotypes. Wang et al. (2010) reported two important pathways for Crohn’s disease: (1) the IL-12 and STAT4 pathway which contains 12 genes, and (2) the T cell receptor pathway which contains 67 genes. In total there are 76 genes under considerations: three genes in both pathways, nine genes only in the IL-12 and STAT4 pathway, and 64 genes only in the T cell receptor pathway. We computed the number of pathway supports for gene pair ℓ, n_ℓ, which is the number of pathways that contain the gene pair. Among the $\left(\begin{array}{c}76\\ 2\end{array}\right)=2850$ gene pairs, there are $\left(\begin{array}{c}3\\ 2\end{array}\right)=3$ gene pairs that have 2 pathway support (i.e., n_ℓ=2); 9×64=576 gene pairs has 0 pathway supports (i.e., n_ℓ=0); and the remaining 2850−3−576=2271 gene pairs with 1 pathway support. Different from Biofilter, we kept those gene pairs with 0 pathway supports in the model but with higher penalty; thus the selection procedure is more likely to drop them unless the data support their importance.

We simulated 200 replicated datasets with 1500 subjects per replications. We assigned two genes as causal main-effect genes and another 10 gene pairs (different from the causal main-effect genes) with causal interaction effects. We sorted the SNPs within a causal gene by their MAFs and used the middle 50% SNPs as causal. To generate phenotype, we set

$$\begin{array}{l}\mathit{g}({\mathit{\mu }}_{\mathit{i}})=\\ \mathit{\alpha }+{\sum }_{\mathit{m}=\mathbf{1}}^{\mathbf{2}}\left({\sum }_{\mathit{l}\in \{\mathit{casual}\mathit{SNPs}\}}{\mathit{G}}_{\mathit{m},\mathit{li}}\right){\mathit{\varphi }}_{\mathit{m}}+\\ {\sum }_{\mathit{s},\mathit{t}\in \{\mathbf{01}\mathit{casual}\mathit{gene}\mathit{pairs}\}}\left({\sum }_{\mathit{k},{\mathit{k}}^{\prime }\in \{\mathit{casual}\mathit{SNPs}\}}{\mathit{G}}_{\mathit{s},\mathit{ki}}·{\mathit{G}}_{\mathit{t},{\mathit{k}}^{\prime }\mathit{i}}\right){\mathit{\zeta }}_{\mathit{st}},\end{array}$$ (4)

where G_m,li∈{0,1,2} is the genotype of the causal SNP l in gene m. For quantitative trait, we set g(μ_i)= μ_i and generated Y_i from N(μ_i,1)with α=0 and the values of ϕ’s and ζ’s such that the partial R² contributed from the interaction effects was around 30%. For binary trait we set $\mathit{g}({\mathit{\mu }}_{\mathit{i}})=\mathit{log}(\frac{{\mathit{\mu }}_{\mathit{i}}}{\mathbf{1}-{\mathit{\mu }}_{\mathit{i}}})$ and generated Y_i from Bernoulli(μ_i). Parameter α was set to make the prevalence around 7%. Similar to quantitative traits, the values of ϕ’s and ζ’s were determined so that the partial R² from the interaction effects was around 30%. For binary traits, we used Nagelkerke R² (Nagelkerke, 1991) which is defined as $\{\mathbf{1}-{\left(\frac{-\mathbf{2}{\mathit{L}}_{\mathbf{1}}}{-\mathbf{2}{\mathit{L}}_{\mathbf{12}}}\right)}^{\frac{\mathbf{2}}{\mathit{N}}}\}/\left\{\mathbf{1}-{(-\mathbf{2}{\mathit{L}}_{\mathbf{1}})}^{\frac{\mathbf{2}}{\mathit{N}}}\right\}$, where L₁₂ is the log-likelihood of the logistic regressions containing both main and interaction effects, and L₁ is that of the logistic regression containing only main effects. For each replication, we oversampled cases so as to obtain a balanced case-control sample (i.e., 750 cases and 750 controls).

We considered three scenarios as listed in Table 4 by carefully selecting 10 interactive gene pairs to evaluate the performance of the proposed procedure. Its performance was benchmarked against the penalized regression with only gene-size weight. In the “no support” scenario, most of the causal gene pairs were with 0 pathway support. In “random support” scenario, we randomly selected 10 gene pairs as causals. In the “strong support” scenario, which was the opposite of the “no support” scenario, the 10 causal gene pairs were selected from those with strong pathway support. For each scenario, we computed the TPR across the 10 gene pairs, the FPR across the non-causal gene pairs, and the D statistics.

Table 4.

Different level of biological supports among the 10 gene pairs considered in Simulation II. No Support: the causal gene pairs do not have much pathway support; Random: the causal gene pairs that are randomly selected; Strong support: the causal gene pairs have strong pathway support.

# of supporting pathways	2 Pathways	1 Pathway	0 Pathway
Scenario
1. No Support	0	2	8
2. Random Support	1	7	2
3. Strong Support	3	6	1

Results of Simulation II

With the real data based Simulation II, we first examined the performance of different weighting schemes for quantitative traits (Figure 4) and binary traits (Figure 5). We also evaluated the performance of different PC strategies for summarizing the interaction information of a gene pair (Figure 6 and Table 1). Finally, we explored the possible reasons of high FDRs for large genes (Table1).

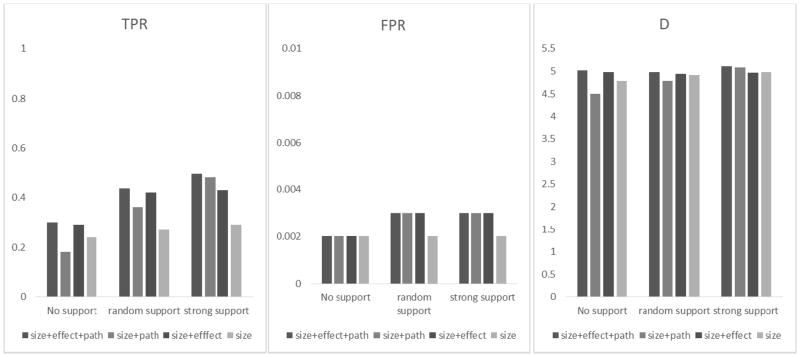
Figure 4.

Results of different weighting schemes for Simulation II based on Crohn’s disease with quantitative phenotypes. True positive rate (TPR), false positive rate (FPR) and the D statistic (D = log TPR − log FPR) for detecting GxG gene pairs were obtained from three different scenarios as defined in Table 4, i.e., the causal gene pairs do not have much pathway support (no support), have strong pathway support (strong support), and the causal gene pairs that are randomly selected (random support). Given a certain scenario, the bars (from left to right) represent the results of using all weights (i.e., size-effect-and-pathway), size-and-pathway, size-and-effect, and size only.

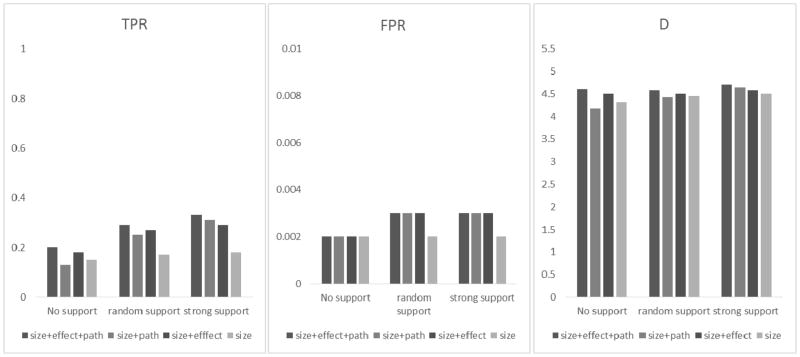
Figure 5.

Results of different weighting schemes for Simulation II based on Crohn’s disease with binary phenotypes. True positive rate (TPR), false positive rate (FPR) and the D statistic (D = log TPR − log FPR) for detecting GxG gene pairs were obtained from under three different scenarios as defined in Table 4, i.e., the causal gene pairs do not have much pathway support (no support), have strong pathway support (strong support), and the causal gene pairs that are randomly selected (random support). Given a certain scenario, the bars (from left to right) represent the results of using all weights (i.e., size-effect-and-pathway), size-and-pathway, size-and-effect, and size only.

Figure 6.

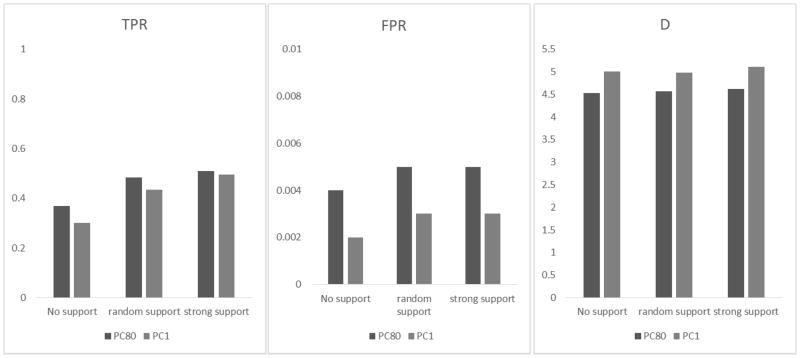
Results of PC80 vs. PC1 based on Simulation II with quantitative phenotypes. The setting is the same as Figure 4 except that all weights (i.e., size-effect-and-pathway) are used in PC80 and PC1. True positive rate (TPR), false positive rate (FPR) and the D statistic (D = log TPR − log FPR) for detecting GxG gene pairs were obtained from under three different scenarios as defined in Table 4, i.e., the causal gene pairs do not have much pathway support (no support), have strong pathway support (strong support), and the causal gene pairs that are randomly selected (random support).

Evaluating different weighting schemes

Figures 4 (for quantitative traits) and 5 (for binary traits) show the results of using different weights (i.e., ω_size + ω_effect + ω_path, ω_size + ω_path, ω_size + ω_effect, and ω_size) under different scenarios of pathway supports. In both figures, we see that the values of TPR and D from ω_size + ω_effect + ω_path were much larger than the baseline TPR/D that used ω_size only. Across different scenarios, the effect weights played a relatively substantial role under the scenarios of no support and random support (i.e., the pathway support is randomly given to 10 gene pairs). That is, for the TPR and D statistics under the panels of no support and random support, there is a big gap between Column 1 (ω_size + ω_effect + ω_path) and Column 2 (ω_size + ω_path), while the gap is small between Column 1 and Column 3 (ω_size + ω_effect). On the other hand, when the pathway support is strong (strong support), the gap between Column 1 and Column 2 becomes much smaller than the gap between Column 1 and Column 3, indicating a strong role from the pathway weight when pathway support exists.

We see that under the scenarios of random support and strong support, adding ω_path into the model helps to boost TPR and D (i.e., TPR/D of ω_size + ω_path are higher than those of ω_size). However, under the scenario of no support, adding ω_path reduces the TPR and D statistics. Nevertheless, we see that such loss can be avoided by incorporating ω_effect. Across all scenarios, we see adding ω_effect always helps to boost TPR and D (i.e., TPR/D from ω_size + ω_effect are greater than those from ω_size only). For binary traits (Fig. 5), the results are similar to the quantitative traits. While FPRs were also retained around 0.002~0.003, the TPRs were smaller, at about 70% of the TPRs for the quantitative traits. This is not unexpected because binary trait values contained less information than quantitative trait values.

Evaluating different PC strategies for summarizing interaction information

Under the setting of Figure 4 (i.e., Simulation II, quantitative traits), we evaluated the performance of using the first PC (referred to as PC1) and using the top few PCs that explained 80% of variation (referred to as PC80). Because there are multiple PCs for a gene pair in PC80, we use group lasso (Yang and Zou, 2014) to select important gene pairs by setting a group as a gene pair. The results are shown in Figure 6. We observe that PC80 had higher TPR than PC1; yet it also had higher FPR than PC1. The resulting D statistics are lower for PC80 than that of PC1. The results are not unexpected: although PC80 captured more information than PC1, the number of variables in PC80 also increased dramatically. On average, the number of interaction terms increased from ~3K for PC1 to ~35K for PC80. The relative performance of PC1 and PC80 seems to reflect a tradeoff between the degrees of freedom spent and the information captured with a moderate sample size (N =1500).

By focusing on the random support scenario, we compared the proportion of interaction information captured by PCs from the interaction design matrix (referred to as PC1_SNP×SNP) to that captured by the product of PCs that summarize the information of each gene (referred to as PC1_geneS×PC1_geneT). The proportion of variations in the interaction design matrix, H_st, captured by its first PC is $\frac{\mathit{var}(PC{1}_{\mathit{SNP}\times \mathit{SNP}})}{\text{total}\text{variation}\text{of}{H}_{st}}$. The proportion of variations in H_st captured by the PC product is $\frac{\mathit{var}(PC{1}_{\mathit{geneS}}\times PC{1}_{\mathit{geneT}})}{\text{total}\text{variation}\text{of}{H}_{st}}$. The results are summarized in Table 1, from which we see that PC1_SNP×SNP captured higher amount of variation than PC1_geneS×PC1_geneT, and the difference increases as gene size increases. We also observed that the FPRs of PC1_SNP×SNP were smaller than those of PC1_geneS×PC1_geneT, which is not unexpected because when the amount of information retained in the PCs became less, it became harder for the proposed algorithm to separate the noise from the signals.

Evaluating FDRs of different gene-pair sizes

Using the scenario of random support in Figure 4, we further examined the FPRs of different gene sizes when using the size weight (i.e., setting ω_size as proposed) and when not using the size weight (i.e., setting ω_size =1). The genes are classified into small size (1~33 SNPs), medium size (34~67 SNPs) and large size (68~102 SNPs), hence there are six size-categories for the gene pairs: SS, SM, SL, MM, ML and LL. From Table 1, we see that when setting ω_size =1, the FPR increased as the gene size increased, which again is probably due to the fact that the variation captured by the first PC decreases as the gene size increases. When the amount of variations captured by the PCs became smaller, the information content that can be used to detect GxG signals became less and may result in higher FPRs for large genes. When setting ω_size as proposed, the FDRs for gene pairs with non-large sizes stayed similar, but the FDRs for gene pairs involving large genes were reduced.

Real Data Analysis

Crohn’s disease, also known as Crohn syndrome and regional enteritis, is a type of inflammatory bowel disease that may affect any parts of the gastrointestinal tract from mouth to anus, causing a wide variety of symptoms. Crohn’s disease is a complex genetic disease and many studies have been carried out to find the genetic factors responsible (Holmans et al., 2009).

We applied our approach to the WTCCC genome-wide association dataset for Crohn’s disease (CD) (Wellcome Trust Case-Control Consortium, 2007). The data contains 2005 cases and 3004 controls, and each individual had 469,557 SNPs genotyped by Affymetrix. We focused our analysis on the two important pathways to Crohn’s disease (Wang et al., 2010), the IL-12 and STAT4 pathway and the T cell receptor pathway. As mentioned in the design of Simulation II, there were 76 genes from the two pathways with three genes involved in both pathways, nine genes only in the IL-12 and STAT4 pathway, and 64 genes only in the T cell receptor pathway. We extracted the SNPs of the 76 genes and removed SNPs with MAF smaller than 1%. We performed the analysis using the proposed method (i.e., incorporate all weights) and the benchmark method (only incorporate gene-size weight in the penalty). The significant genes and gene pairs are listed in Table 5. For GxG effects, we also listed the number of supporting pathways. For the proposed method, many significant gene pairs identified contain the GRB2 gene. GRB2 has been found to be significant in Crohn’s disease (Lee et al., 2011, Vaughan et al., 2013); it encodes the protein GRB2, which is an adaptor protein involved in signal transduction and cell communication. Compared to the proposed method, the benchmark methods found two more GxG pairs with 0 pathway support and did not detect four of the GxG pairs with pathway support. Such results agreed with the simulation study in the sense that the proposed method may discourage the detection of GxG with no pathway support when the data suggested so.

Table 5.

List of significant main-effect genes and GxG gene pairs identified by the proposed method and the benchmark method. (“--” means not found by the corresponding method.)

	Gene Names	# of pathways supporting the gene/gene pair
		ωpath + ωeffect + ωsize	ωsize
Main effect	GRB2	1	1
	IL12B	1	1
	PPP3CA	1	--
GxG effect	AKT3&GRB2	1	1
	CD247&IL12B	1	1
	CD4&FYN	1	1
	CHP&GRB2	1	1
	FYN&IKBKB	1	--
	GRB2&GSK3B	1	--
	GRB2&MAP3K14	1	--
	GRB2&NCK2	1	--
	ETV5&PPP3CA	0	0
	CHP&IL12B	--	0
	IL18R1&RASGRP1	--	0

Discussion

In this work, we proposed a pathway-guided approach for detecting interactions among genes. We constructed a weighted L1 penalty to select the important gene effect and gene-gene interactions; the weights were based on the number of pathways supportive of the effects as well as the estimated effect size. The numerical studies suggested an improved performance over the methods without using the guidance from pathway support and effect strength. The proposed approach can be used to explore gene-gene interactions with a list of candidate genes and is applicable even when sample size is smaller than the number of predictors studied. Although in theory the proposed method can handle an arbitrary number of genes, the number of GxG interactions increases exponentially with the number of genes. Therefore, our approach would be more suitable for studying GxG effects among a list of pre-selected genes, such as genes from certain relevant pathways, rather than for whole genome analysis.

Our approach aims to combine the advantages of biological guidance and trait supervision in association detections; we achieve this by formulating these two strategies that are commonly used for reducing the GxG search space as the prior weights so as to regularize the GxG detection (as opposed to using these criteria as “filters”). Our results suggested that both types of weights are necessary, i.e., both ω_path and ω_effect were necessary to obtain a robust D gain for the proposed method across different scenarios. Using ω_path would increase the TPR for the causal GxG interactions which have strong pathway support. However, it may also decrease the TPR for those GxG effects with little or no pathway support. For these scenarios, incorporating ω_effect gives the power to identify novel GxG effects even for those with no known biological supports, i.e., it minimizes the TPR reduction and sometimes even boosts the TPR because it encourages pairs with non-zero GxG effects to be selected in the model.

When constructing our algorithm, we intended to use biological knowledge to guide, instead of force, the detection of interactions. We used three strategies to assure this goal. First, we incorporated the biological knowledge as prior information instead of as a filter in the statistical inference. Second, we constrained the range of ω_path between 0.5 and 1 so that ω_path did not overwhelm other weights and yet could still encourage the algorithm to select the gene pair when the data are consistent with this prior information. Finally, we also used the data-adaptive weight based on the empirical effect size to safeguard the validity of the findings if inappropriate biological knowledge is used. The practice of using pathway knowledge to guide variable selection is based on the presumption that the pathway knowledge can reflect the underlying biological mechanisms. However, it is likely that the pathway structures depend on phenotypes and hence the “canonical” pathway information would only represent the status of healthy controls. From this point of view, treating the biological information as prior knowledge and performing data adaptive selection can provide robustness against vague information and can minimize false positive and false negative findings.

In reality, different pathways often have substantial overlaps, and our method intends to make use of such overlapping. Specifically, we treat these overlapping pathways as separate pathways, and then for a given gene pair ℓ, we obtain n_ℓ, the number of pathways that contain gene pair ℓ. The rationale is that a gene pair that is involved in multiple pathways tends to be more biologically important and has a higher chance of interaction. On the other hand, such pathway support is only incorporated as prior information, which will encourage our algorithm to select the gene pair only if the data are consistent with it. In addition, we also incorporate the adaptive weight based on the empirical effect size to guide the variable selection, which provides another layer of safeguard. When calculating n_ℓ, one should use the pathway information from the same “level”. For example, in KEGG, pathways are labeled with different levels; the energy metabolism pathway is one of the pathways at the top level. The energy pathway contains several lower-level pathways, such as the carbon fixation pathway and the nitrogen metabolism pathway. Each of the lower level pathways contains pathways of even lower level. It would not be appropriate to treat pathways of different levels equally when counting n_ℓ because one pathway can merely be a subset of the other pathway.

Prior biological information (such as Biofilter) is often available at the gene or the higher pathway level. Hence one of the advantages to study interaction at gene level is that the prior knowledge and the effect assessment are aligned at the same level (genes). However, the corresponding findings are also limited at gene-level resolution. Therefore, a complete GxG study may require two steps; first performing a gene-level screening using the methods as proposed to identify interactive gene pairs, and then using those approaches that can provide the SNP×SNP level of resolution to follow up on the significant gene pairs and comprehend the sources of gene-level signals.

In our method, we summarize the information of gene-gene interaction using the PCs. Alternatively, Wang et al. (2009) apply PLS to summarize the gene information at gene level, which aims to maximize both the SNP-SNP correlation and the SNP-trait correlation. Performance of GxG tests using leading components from PLS was shown to be superior to using PCs from PCA (Wang et al., 2009). However, because PLS components were formed by maximizing their correlations with trait values, the corresponding GxG terms tend to stay significant even with no true interaction effects. Besides using PCA vs. PLS, our method also differs from Wang et al. (2009) in two other aspects. First, Wang et al. (2009) capture the GxG effect of a gene pair by the product of the leading PLS components, while our work captures the GxG effect by the PCs of the interaction design matrix. Second, Wang et al (2009) performed hypothesis testing to select important gene pairs, while we use penalized likelihood estimation with biological weights from pathway support and adaptive weights from effect sizes.

In this paper, we only used the pathway membership in the variable selection process. There exist other types of information, such as pathway structure, the regulation relationship between genes, protein interaction, RNA networking or metabolite information, which can provide valuable guidance in the exploration of gene-gene interaction in a large search space. Further study will be required to appropriately formulate biological knowledge from multiple resources into the most appropriate statistical model in order to lead to efficient variable selection.