Emergence of Complex Wave Patterns in Primate Cerebral Cortex

Abstract

Slow brain rhythms are attributed to near-simultaneous (synchronous) changes in activity in neuron populations in the brain. Because they are slow and widespread, synchronous rhythms have not been considered crucial for information processing in the waking state. Here we adapted methods from turbulence physics to analyze δ-band (1–4 Hz) rhythms in local field potential (LFP) activity, in multielectrode recordings from cerebral cortex in anesthetized marmoset monkeys. We found that synchrony contributes only a small fraction (less than one-fourth) to the local spatiotemporal structure of δ-band signals. Rather, δ-band activity is dominated by propagating plane waves and spatiotemporal structures, which we call complex waves. Complex waves are manifest at submillimeter spatial scales, and millisecond-range temporal scales. We show that complex waves can be characterized by their relation to phase singularities within local nerve cell networks. We validate the biological relevance of complex waves by showing that nerve cell spike rates are higher in presence of complex waves than in the presence of synchrony and that there are nonrandom patterns of evolution from one type of complex wave to another. We conclude that slow brain rhythms predominantly indicate spatiotemporally organized activity in local nerve cell circuits, not synchronous activity within and across brain regions.

Introduction

Complex spatiotemporal patterns emerge from physical and biological systems, ranging from bacterial colonies to turbulent fluids and the collective motion of fish or birds (Hussain, 1986; Vicsek and Zaferis, 2012). These patterns emerge over a wide range of spatial and temporal scales. The brain likewise shows coherent activity at multiple spatial and temporal scales, and it is customary to link the spatial and temporal scales of brain rhythms (Buzsáki and Draguhn, 2004). For example, neurologists attribute slow-wave EEG signals to widespread synchronized activity in the cerebral cortex (Binnie et al., 2003). By contrast, cognitive events in conscious brains are linked to high-frequency brain oscillations in local nerve circuits (Buzsáki and Draguhn, 2004). Brain activity can show local spatiotemporal order as planar propagating or spiral waves (Rubino et al., 2006; Huang et al., 2010; Sato et al., 2012), but the relevance of these patterns remains unclear because we lack a methodological framework that can quantify and compare them.

Here, we measured local field potentials (LFPs) in the visual cortex of anesthetized marmoset monkeys. We adapt physical theories of turbulence to quantify the complex wave patterns and their dynamics. We show the brain displays a rich variety of activity whereby synchrony and planar propagating waves are interspersed by complex wave patterns that radiate from, converge to, or spiral around phase singularities in the LFP field. The complex waves influence spiking activity: high spike rates are associated with complex waves rather than synchrony and plane waves. The rich repertoire of wave patterns revealed by our experiments may enable the brain to coordinate distributed neural activity in a flexible and dynamic way.

Materials and Methods

Recordings were made from the middle temporal (MT) area of three adult male marmosets (Callithrix jacchus). Procedures conformed to the Australian National Health and Medical Research Council code of practice for the use and care of animals and were approved by institutional committee at the University of Sydney. Details of preparation are given previously (McDonald et al., 2014). Anesthesia and analgesia were maintained by intravenous sufentanil infusion (6–30 μg kg⁻¹ h⁻¹) and inspired 70:30 mix of N₂O and carbogen. The animal viewed a uniform gray field presented on a cathode-ray-tube monitor (Sony G500, refreshed at 100 Hz, viewing distance 45 cm, mean luminance 45–55 cd/m²). Data were recorded using multielectrode arrays (10 × 10 electrodes, 1.5 mm length, electrode spacing 400 μm, Blackrock Microsystems). Recording surface insertion depth was targeted to 1 mm. Recording duration ranged from 5 to 25 min; in total, 52 min of recording were analyzed. The LFP sample frequency was 1024 Hz; spike sample frequency was 24 kHz. δ-Band of LFP (1–4 Hz) was extracted by applying an eighth-order Butterworth filter forwards and backwards in time to prevent phase distortion. The Hilbert transform was applied to this filtered signal for each (x, y) channel to extract instantaneous amplitude A(x, y, t) and phase φ(x, y, t) (Le Van Quyen et al., 2001). Single-cell and multicell activity was classified offline using commercial (Plexon) and in-house software written in MATLAB (MathWorks), as described previously (Solomon et al., 2014). Activity of 71 single cells (mean spike rate 2.0 Hz) was analyzed.

Phase velocity field (PVF).

Previous Hilbert phase-based methods for LFP analysis were restricted to analyzing spatial phase gradients at single time points (Rubino et al., 2006; Muller et al., 2014). Here, we introduce the PVF, which simultaneously characterizes spatial and temporal change. The PVF was calculated by adapting optical flow techniques (Horn and Schunck, 1981). We assume that contours of phase move continuously between frames, giving a phase constancy restraint as follows:

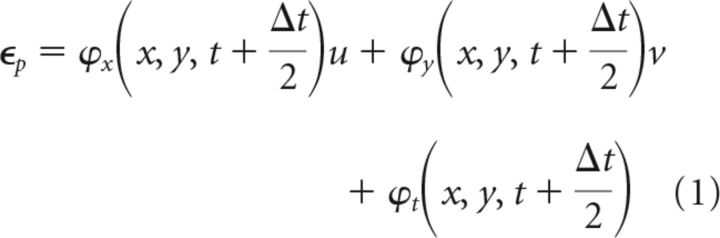where u and v denote the x- and y-components of phase velocity, Δt (∼1 ms) is the sampling period, and subscripts denote partial derivatives. Velocity components u and v were calculated by minimizing errors in ϵ_P and the departure from smoothness ϵ_S (Horn and Schunck, 1981) where:

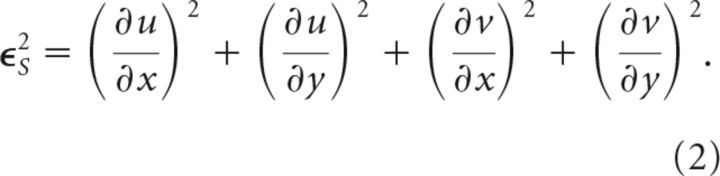The total error is given by the following:

where α is a weighting factor and σ_S and σ_P are penalizer functions. We used α = 20 as the weighting factor and the Charbonnier penalty, σ_S(x²) = σ_P(x²) = 2 $\sqrt{x^2+{\beta }^2}$ with β = 0.01, as a penalizer function. Phase velocity components u and v that minimize Equation 3 were found by minimizing the corresponding Euler–Lagrange equations (Bruhn et al., 2005). Partial derivatives were calculated using circular statistics (Batschelet, 1981). Derivatives at array edges and near reference channels (n = 4) and inactive electrodes (n < 4) were interpolated using centered or forward difference approximations.

Identification of plane waves and synchrony.

We defined synchronous activity as the time (seconds) where the average magnitude of the PVF was 1 SD or more below the mean across the recording epoch. Plane waves were detected using the order parameter defined as average normalized phase velocity $\overline{v_{\varphi }}$ (Vicsek and Zaferis, 2012):

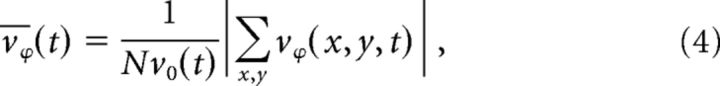where N is the number of vectors in the PVF (here N = 100), v₀ is the average velocity magnitude over all units, and v_ϕ is the phase velocity v_ϕ(x,y,t) = (u(x,y,t), v(x,y,t)). Normalized phase velocity $\overline{v_{\varphi }}$ ranges from 0 to 1, with $\overline{v_{\varphi }}$ → 1 as velocity vectors align to a single direction. Threshold $\overline{v_{\varphi }}$ ≥ 0.85 was chosen to identify plane waves; variation of this value from 0.8 to 0.9 did not substantially change the results.

Identification of complex wave patterns.

Complex waves are organized around points with zero velocity (critical points, phase singularity points) in the PVF (Perry and Chong, 1987). Critical points were identified as intersections of the two bilinearly interpolated null clines of the PVF (i.e., curves of zero velocity in the x- or y-direction). Each critical point was classified using the eigenvalues of the Jacobian matrix estimated at the corners of the four-electrode cell containing the critical point as follows:

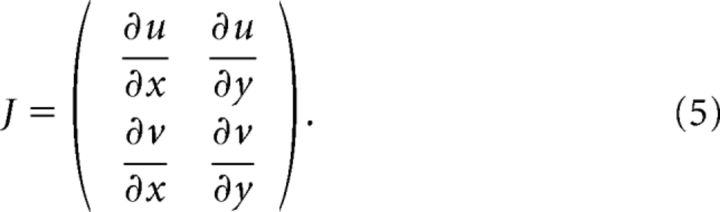Eigenvalues were bilinearly interpolated to estimate the Jacobian at the critical point (Perry and Chong, 1987). Each critical point was classified, based on the trace (τ) and determinant (Δ) of the Jacobian, as a node (Δ > 0 and τ² > 4Δ), focus (Δ > 0 and τ² < 4Δ), or saddle (Δ < 0). Patterns were further classified as stable (τ < 0) or unstable (τ > 0).

To estimate the size of complex waves, the winding number (Poincaré index) was calculated for 2 × 2 and 4 × 4 squares of electrodes centered on the critical point. Spiral and node patterns have winding numbers of 1; saddles have −1 for all squares. Spiral-in and spiral-out patterns were required to show coherent positive or negative curl (MATLAB curl function) within at least two recording sites of the critical point. Nodes occupied an equivalent region of positive or negative divergence (MATLAB divergence function). Critical points within two recording sites of recording area boundary were rejected.

The centers of complex waves were identified by critical points that persisted for at least 10 ms. A critical point at v_ϕ(x₁, y₁, t) was considered to have persisted if there was another critical point at v_ϕ(x₂, y₂, t + Δt) of the same type, where Δt ≤ 5 ms and the distance between (x₁, y₁) and (x₂, y₂) was <1 grid space (400 μm).

Determining motif dynamic in pattern evolution.

Each recording was classified into a symbolic array indicating the dominant wave type (or lack of any classified structure) at each time step (see Fig. 3B). Unclassified sequences <70 ms duration were discarded, and consecutive symbols were reduced to a single instance. A motif-tracking algorithm (Wilson et al., 2008) was used to count the number of occurrences of single transitions (motifs with a length of 2) and longer sequences (length 3–20). Motifs containing an unclassified state were discarded. For single transitions, expected probabilities were calculated by the following:

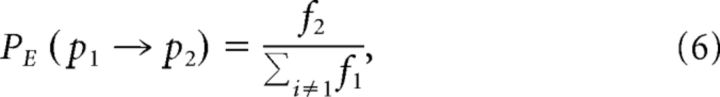where P_E(p₁ → p₂) is the expected probability of transitioning from pattern 1 to pattern 2 and f_i is the observed frequency of pattern i. For longer motifs, the expected frequencies were calculated by the following:

where F_E(p₁ → p₂ → … → p_n) is the expected frequency of the motif consisting of patterns p₁ to p_n and P_O(p_i → p_j) is the observed probability of transition from p_i to p_j. Significance of motifs was qualitatively measured using the Z-score (Milo et al., 2002) defined as follows:

where F₀ is the observed frequency and SD denotes standard deviation.

Figure 3.

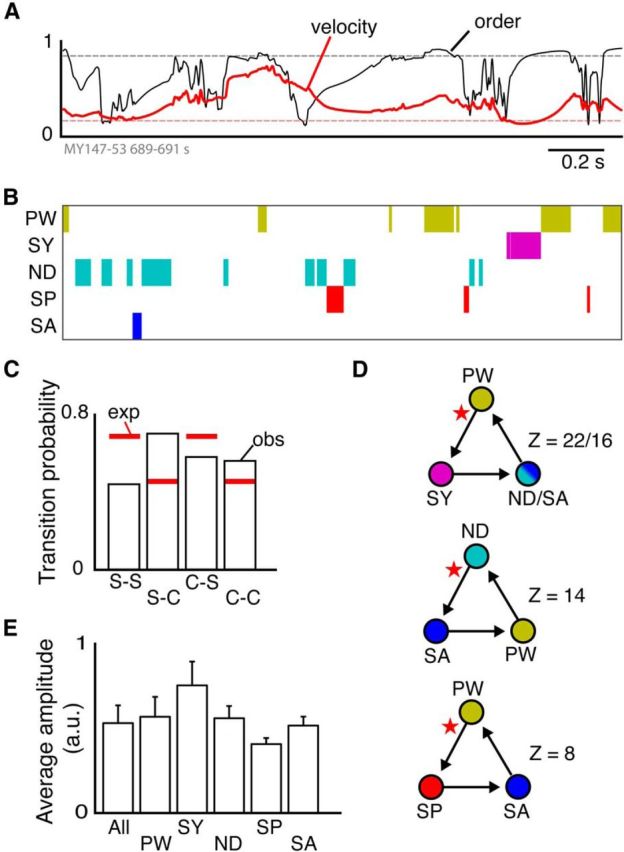
Classification of complex waves. A, Fluctuation of order parameter (thin black line) and average velocity magnitude (red) of PVF over 2 s. Dashed lines indicate order parameter and velocity thresholds. B, Raster plot of classified patterns over the same time period as in A. C, Expected (red lines) and observed probability (black bars) of transitions between simple (S) waves (plane waves, synchrony) and complex waves (C). D, Representation of most significant temporal motifs. Circles represent structure types. Arrows indicate temporal transitions. Star symbols indicate first transition. Z-score indicates deviation from expected transition probability. E, Average δ-band signal amplitude (arbitrary units) during different pattern types. Error bars indicate SEM between recordings. PW, Plane wave; SY, synchrony; ND, node (source, sink); SP, spiral (spiral-in, spiral-out); SA, saddle.

Comparison with spiking activity.

Local relation of LFP phase to single-cell spiking activity was calculated by taking the instantaneous phase at each electrode position for each spike, pooled across electrodes and animals. Global relation was calculated as average phase across the recording area. As control, the analysis was repeated with spikes randomly shuffled in time. Firing rates were calculated by averaging the instantaneous spike rate with a 50 ms sliding window. Spike rates were Z-scored within each channel then averaged across channels.

Spike rate variability.

Fano factor (F_W) for time window W was calculated from single-unit spiking activity using the following:

where S_W is the number of spikes in window W. Average Fano factor across a recording was obtained by averaging F_W over all nonoverlapping windows W of length t_w. Fano factors were averaged over cells and recordings to give the average for window sizes t_w logarithmically spaced from 10 ms to 1 s as follows:

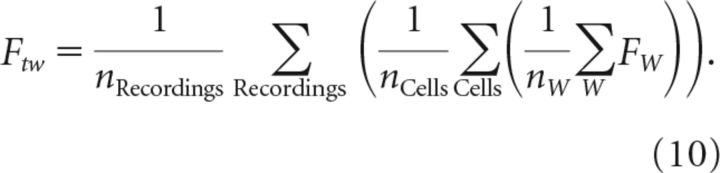To calculate Fano factor during the activity of individual patterns, time steps where the target pattern was not active were deleted. Differences were quantified with a two-sample Kolmogorov–Smirnov (KS) test on the sets of F_tw across windows.

Surrogate data.

We generated surrogate LFP data as follows. The phase values for each frequency component f of the discrete Fourier transformed signal were shifted by adding a random value ψ(f) chosen uniformly in the range 0–2π. The same random value ψ(f) was applied at all electrodes. Phase at each f was then shifted by an additional random variable θ_i(f), which is normally distributed (mean 0, SD π/4) and calculated independently for each electrode i. Inverse Fourier transform was then applied. Surrogate data produced in this way preserve autocorrelations but reduce the cross-correlation structure by, on average, 50% between electrodes (Prichard and Theiler, 1994).

Results

We recorded spiking activity and LFPs from MT with a 10 × 10 array of electrodes while the animal viewed a spatially uniform screen (Fig. 1A). As expected, LFP power spectra showed dominance of slow rhythms, with mean frequency between 1 and 2 Hz (Fig. 1B). We bandpass filtered the δ-band (1–4 Hz) signal (Fig. 1C, red curve) and computed instantaneous δ-phase at each electrode using the Hilbert transform (Le Van Quyen et al., 2001) (Fig. 1D). Phase measurements were collated across electrodes to create spatial phase maps (Fig. 1E). The maps evolved in a complex way over time and space, alternating between coherent and seemingly chaotic activity. We analyzed the dynamics of these maps using the PVF (see Materials and Methods), which enables objective analysis of the patterns visible to naked eye inspection of the raw data (Fig. 1D–F).

Figure 1.

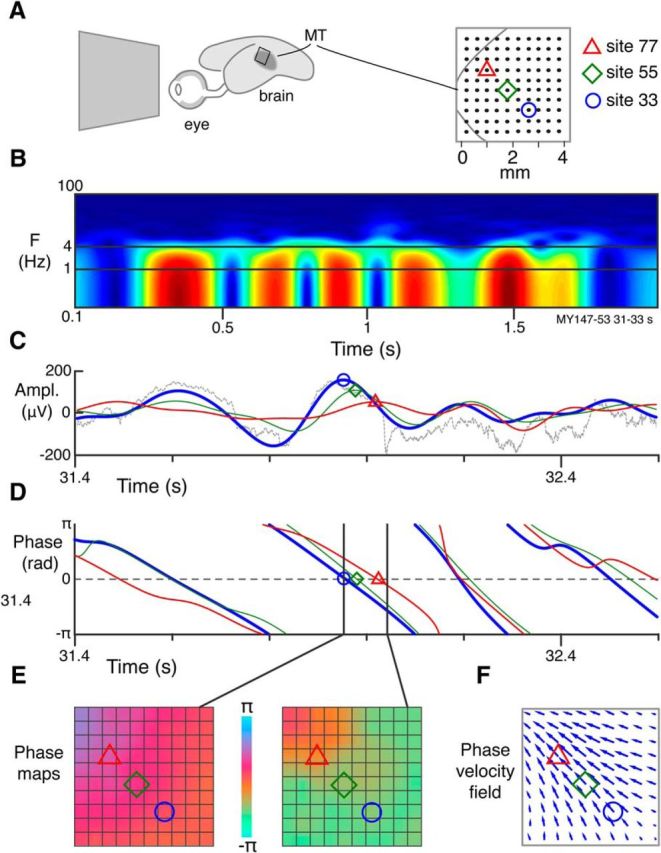
Extraction of PVFs from LFP recordings. A, Representation of marmoset eye and brain showing approximate position of MT area and position of electrode array. Magnified view of electrode array at right shows estimated border of MT and electrode spacing. Three recording sites are indicated. B, Normalized time-power spectrum of LFP recorded from site 33 over 2 s. Warmer colors represent higher root-mean-squared power. C, Bandpass (1–4 Hz) filtered LFP amplitude recorded over 1 s from the three sites shown in A. Thin gray line indicates raw trace for site 33. D, Instantaneous phase of the filtered LFP for the three indicated sites. Symbol positions represent how discontinuities at ±π occur at minima in the LFP signal; zeros occur at maxima. Thin gray line indicates raw trace for site 33. E, Single-channel phase signals are combined to give 2D phase maps at each recorded time step. Phase maps are bilinearly interpolated over reference (n = 4) and inactive channels (n = 3). F, PVFs are calculated between consecutive phase maps. PVFs are typically calculated between maps separated by 1 ms; more temporally separated maps are presented here for display purposes.

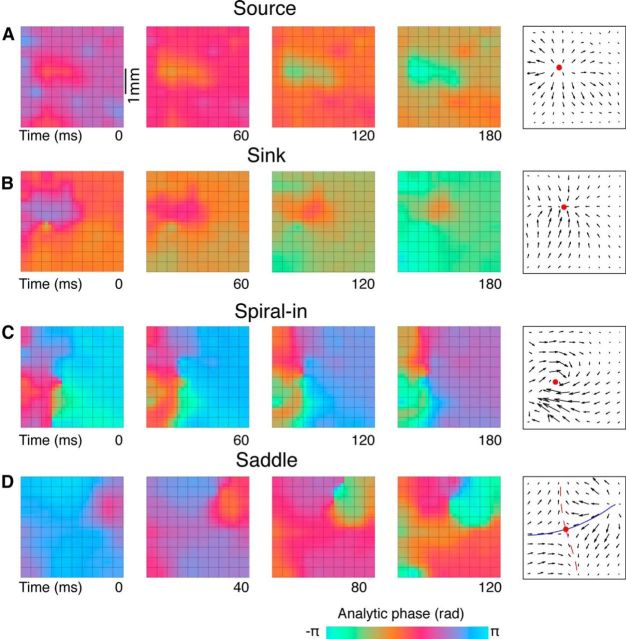
The PVF readily identifies the synchronous activity and traveling plane waves identified in previous work (Fig. 1E,F), and additionally reveals a repertoire of more complex spatiotemporal patterns (Fig. 2). We use the term complex waves to refer to these patterns (see Materials and Methods). Complex waves are organized around an apex point in the phase map, which in other physical systems is referred to as a phase singularity or “critical point” (Perry and Chong, 1987). Four variants of complex waves are distinguished. In the first type (source), phase diverges from a critical point and propagates radially outward (Fig. 2A). In the second type (sink), phase converges to a critical point (Fig. 2B). In the third and fourth types, phase rotates toward (spiral-in) or away from (spiral-out) the critical point, creating pinwheel patterns in the phase map (Fig. 2C). Saddle structures were also observed where the phase map curves down in one direction and up in another (Fig. 2D). In each case, the critical point typically drifted around (or out of) the recording area over the course of tens to hundreds of milliseconds.

Figure 2.

Examples of complex waves. Color maps show successive frames of instantaneous phase maps. Quiver plots show PVFs at a single time step within the patterns. Filled circles represent critical points. A, Phase expands from a source point. B, Phase contracts toward a sink point. C, Phase rotates around a central singularity in a spiral wave. D, Phase moves toward a central point (from bottom-left and top-right) and away from the central point (to top-left and bottom-right) in a saddle pattern. These stable (blue, solid) and unstable (red, dashed) directions are shown as lines on the PVF.

Isolated descriptions of spiral waves, sources, and sinks were previously made in anesthetized (Huang et al., 2010) and waking animals (Freeman and Barrie, 2000; Mohajerani et al., 2013; Muller et al., 2014), but lack of methodological framework has prevented quantitative analysis and obscured their prevalence. Here, we applied the PVF to classify complex brain waves, by adapting critical point theory from turbulence physics (see Materials and Methods). The PVF also allows objective identification of plane waves and synchrony by defining velocity and order parameters (Fig. 3A; see Materials and Methods). Approximately half (44%) of the phase map time series could be classified automatically using these combined criteria (Fig. 3B). The EEG frequency range we analyzed (δ-band) is customarily described as “synchronized EEG,” yet we found less than one-fourth of the classified time series comprised synchronous activity (19.4%). Rather, plane waves were the dominant pattern (60.0%), with complex waves making up the remaining classified time (20.6%). Moreover, complex waves are likely more common than our analysis suggests: inspection of the unclassified parts of the time series showed that they usually contained more than one complex wave.

To ensure that the complex brain waves are not simply induced by our analysis methods, we generated surrogate datasets that preserve autocorrelation in the original signals but reduce the cross-correlation structure (see Materials and Methods). The duration, fraction, and frequency of complex brain waves were significantly reduced in these surrogate data (p < 0.01, KS test; p < 0.05, post hoc Wilcoxon rank sum comparisons). These results rule out the possibility that complex waves are artifacts of the analyses.

Are complex brain waves isolated events, or are they linked to each other? We reasoned that, if complex brain waves occur randomly, the transition probability from one complex wave to another should follow their overall frequency of occurrence. Instead, we found that transitions between simple waves (synchrony and plane waves) occur less frequently than expected, and transitions from simple waves to complex waves (nodes, spirals, and saddles) occur more frequently than expected (Fig. 3C). All differences were significant (p < 0.01, KS test; p < 0.05, post hoc Wilcoxon rank sum comparisons). To understand better these transitions, we created symbolic arrays from the classified wave patterns and interrogated the array for 3-pattern temporal motifs (see Materials and Methods). This analysis revealed that complex waves typically intersperse simple plane waves (Fig. 3D), as predicted by physical modeling studies (van Hecke et al., 1999). Intuitively, for example, transition from a plane wave traveling in one direction to a plane wave traveling in a different direction will involve a pattern with a phase singularity.

We next asked how complex waves are related to the amplitude of the δ-band LFP signal. This analysis (Fig. 3E) shows that synchrony is associated with high δ-band amplitude (averaged across the recording array), whereas complex waves are associated with low average δ-band amplitude. This result reconciles our findings with the conventional view that high amplitude δ-band EEG signal is caused by synchronized cortical activity. The new insight gained by our analysis is that low amplitude δ-band EEG signal does not signify incoherence or quiescence of cortical activity. Rather, low-amplitude δ-EEG signifies complex waves in local cortical circuits.

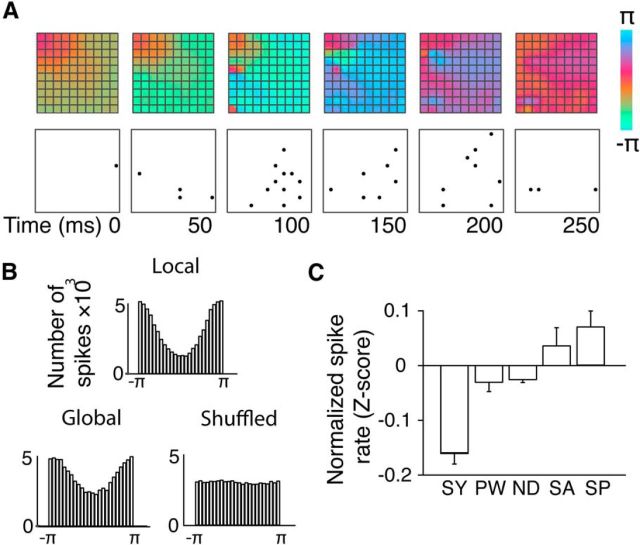
Do complex waves influence neural spike activity? We related the classified wave patterns to simultaneously recorded spike activity at each recording point (Fig. 4A). As expected (Destexhe et al., 1999), spikes were weakly entrained to the phase of δ-band LFP signals at the recording site, with spike probability highest where the local phase was close to ±π (blue/green in color maps of Figs. 1, 2, and 4). Entrainment was diminished if phase was averaged across the recording area and obliterated if spikes were compared with surrogate data (Fig. 4B; see Materials and Methods). Crucially, spike rates were highest near the position and time of spirals and saddles (p < 0.05, Wilcoxon rank sum comparisons) and lowest in the presence of synchrony (Fig. 4C; p < 0.05, Wilcoxon rank sum comparisons). In complex patterns, spike rates were weakly (r = −0.02), but significantly (p < 0.01) correlated with distance from the critical point (MATLAB corrcoef function), indicating that the effect of complex patterns is distributed across the spatial extent of the pattern. The presence of complex waves in δ-band activity explains a small but significant proportion of total variance in average firing rate (ω² = 2%, ANOVA with symbolic pattern array) in the frequency range we analyzed. Similar structures in higher frequency bands are expected to bring additional explanatory power, given the known influences of high-frequency LFPs on brain spiking activity (Buzsáki and Draguhn, 2004; Einevoll et al., 2013). We conclude that switches between complex waves and synchrony influence the temporal structure of cortical spiking activity.

Figure 4.

Relation of coherent structures to spiking activity. A, Snapshots of phase maps and corresponding (multiunit) spiking activity. Spikes (black circles) are common near phase π and rare near phase 0. B, Histograms of phase values during (single-unit) spikes for phase obtained at the same electrode as a spike (Local), for average phase across the recording array (Global), and for local phase with spikes shuffled in time (Shuffled). C, Average normalized (Z-scored) firing rate of single cells in classified coherent structures. PW, Plane wave; SY, synchrony; ND, node (source/sink); SP, spiral (in/out); SA, saddle. Error bars indicate SEM.

Complex waves show preferential switching and temporal motifs Fig. 3C,D); this switching might contribute to the high variability in resting spike rate in cortical neurons (Churchland et al., 2010). We estimated variability using the Fano factor (variance/mean of spike counts; see Materials and Methods) for individual neurons. The Fano factor averaged across the entire recording epoch (i.e., across many switches between synchrony and complex wave patterns) was significantly higher than the Fano factor calculated during individual patterns (3.1 ± 0.10 vs 1.88 ± 0.03, mean ± SEM; n = 100, p < 0.01, KS test). Furthermore, the Fano factor calculated within 100 ms of pattern transition points was higher than during individual patterns (2.04 ± 0.03, p < 0.05, KS test). Together, these results suggest that complex waves are an important part of the relationship between LFPs and the spiking activity of cortical neurons.

Discussion

Our results show that spontaneous slow rhythms in LFP activity in an anesthetized brain form a continuum from simple to complex wave patterns. Simple wave structures (plane waves and synchrony) are usually separated by complex waves that form around phase singularities (spiral waves, sources, sinks, and saddles). The temporal evolution of simple and complex waves echoes the previously described motif organization in cortical circuits, whereby spontaneous cortical activity recapitulates previous stimulus-evoked activity (Mohajerani et al., 2013) and represents a potential mechanism for the brain to process information in a distributed and dynamic way (Gong and van Leeuwen, 2009).

A fundamental question in neuroscience concerns the relation between the spiking of individual nerve cells and the synaptic activity that dominates LFPs (Einevoll et al., 2013). Our analysis showed that spikes are weakly phase locked to δ-band oscillations in LFPs and that the complex waves differentially influence nerve cell activity: spike rates were highest in the presence of spirals and saddles and lowest in the presence of synchrony (Fig. 4). Further, we found that high resting state variability, a prominent feature of cortical nerve cells (Churchland et al., 2010), is influenced by switches between simple and complex wave patterns.

We conclude that, to gain improved understanding of the relation of nerve cell spikes to LFPs, the fine spatiotemporal dynamics of the LFP should be taken into consideration. Our turbulence-based approach allows the required objective analysis and can be easily applied to study how other LFP frequency bands influence cortical spike rates. It will also be of interest to relate complex wave activity to the phenomena of “up” and “down” states, and to apply our method to other neural signals in waking as well as anesthetized brains.