The Spiral Staircase: Tonotopic Microstructure and Cochlear Tuning

Abstract

Although usually assumed to be smooth and continuous, mammalian cochlear frequency-position maps are predicted to manifest a staircase-like structure comprising plateaus of nearly constant characteristic frequency separated by abrupt discontinuities. The height and width of the stair steps are determined by parameters of cochlear frequency tuning and vary with location in the cochlea. The step height is approximately equal to the bandwidth of the auditory filter (critical band), and the step width matches that of the spatial excitation pattern produced by a low-level pure tone. Stepwise tonotopy is an emergent property arising from wave reflection and interference within the cochlea, the same mechanisms responsible for the microstructure of the hearing threshold. Possible relationships between the microstructure of the cochlear map and the tiered tonotopy observed in the inferior colliculus are explored.

Introduction

The cochlear tonotopic map relates the local characteristic frequency (CF) to position within the cochlea. In many animals, including humans, the CF, defined as the frequency of maximum sensitivity (minimum threshold) at low sound levels, is thought to vary quasiexponentially with position, with higher frequencies mapping to the base of the cochlear spiral and lower frequencies to the apex (von Békésy, 1960). The form of the tonotopic map is known most reliably from labeling studies in which auditory-nerve fibers of known CF are injected with dye and their dendrites traced back to their sites of origin within the cochlea (Liberman, 1982; Müller, 1996, 2005, 2010; Manley et al., 1999). Because neural tracing experiments generally yield no more than a handful of labeled fibers from any one ear, tonotopic maps are estimated by fitting smooth mathematical functions to sparse data pooled across individuals. Although such measurements reveal the overall form of the map, they cannot resolve possible fine structure. Here, I combine computational modeling with otoacoustic and basilar-membrane (BM) measurements to argue that although cochlear maps in sensitive ears appear exponential over distances spanning multiple octaves, on smaller scales they manifest a regular staircase-like structure, with segments of nearly constant CF punctuated by sharp transitions.

Materials and Methods

BM transfer functions were computed using an active, transmission-line model of the cochlea based on the “double-pole” form of the BM admittance obtained by Zweig (1991). Parameter values and other details of the implementation have been described previously (Shera and Cooper, 2013). Briefly, the model was driven at the basal (stapes) end by a Thévenin equivalent pressure whose source impedance could be adjusted to produce any desired value of stapes reflectance. Intensity dependence was simulated using a series of linear models whose overall gain was varied parametrically with intensity by moving the poles of the BM admittance along lines in the complex frequency plane perpendicular to the real frequency axis (Shera, 2001b). To generate reflection-source otoacoustic emissions [stimulus-frequency otoacoustic emissions (SFOAEs)], the basic model was augmented with small, irregular spatial variations in the gain of the cochlear amplifier. This micromechanical irregularity was introduced by jittering the poles of the BM admittance with position using random numbers drawn from a zero-mean Gaussian distribution with an SD of a few percent (Zweig and Shera, 1995). Different ears were simulated by fixing the smooth model parameters but varying the pattern of micromechanical irregularities (i.e., by using different seed values for the pseudorandom number generator).

Figure 1 illustrates the effect of micromechanical jittering on the model BM impedance and, more relevant here, on the corresponding complex wave number of the traveling wave. Whereas the real part of the wave number (the propagation function, κ) determines the spatial period (wave length) of the wave, the imaginary part of the wave number (the gain function, γ) controls wave amplification. In regions of positive γ (i.e., basal to the wave peak, where the real part of the BM impedance is negative), the traveling wave is amplified by forces operating within the organ of Corti; in regions of negative γ, the wave power is attenuated. The model propagation and gain functions have the same qualitative form as those derived from chinchilla data (Shera, 2007). Because the irregularities introduced by jittering the admittance poles are small, densely distributed, and include the spatial-frequency components necessary to produce coherent reflection (Zweig and Shera, 1995), the principal effect of the jittering is to scatter the forward-traveling wave, causing the cochlear model to emit sound. These results depend on neither the exact form of the model nor its precise parameter values; qualitatively similar effects are seen in other active models of the mammalian cochlea (Talmadge et al., 1998; de Boer and Nuttall, 2006; Choi et al., 2008; Ku et al., 2008; Epp et al., 2010; Verhulst et al., 2012; Neely and Rasetshwane, 2015).

Figure 1.

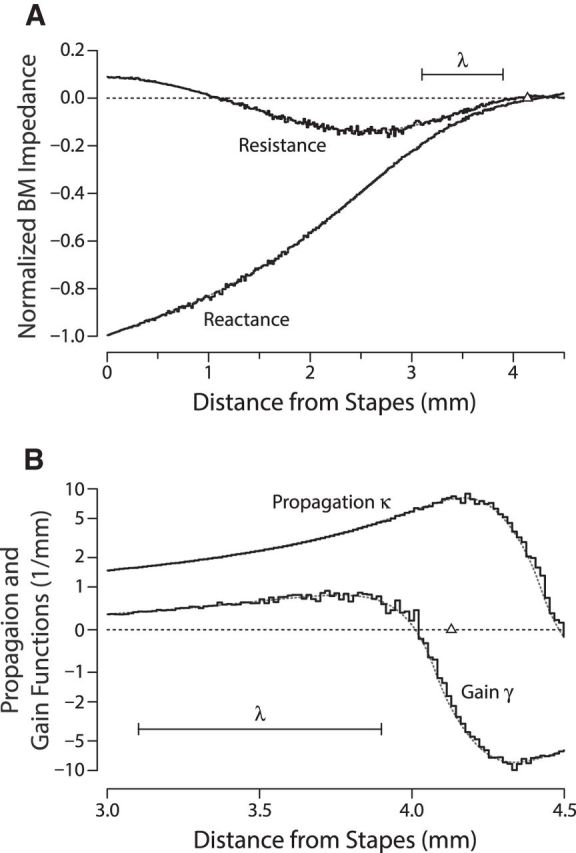
Effect of micromechanical irregularities on the BM impedance and complex wave number of the traveling wave. A, Real and imaginary parts (resistance and reactance, respectively) of the model BM impedance versus cochlear location at a fixed stimulus frequency (∼8.5 kHz). The impedance is shown normalized by its magnitude at the base (x = 0). B, Real and imaginary parts (propagation and gain functions, κ and γ, respectively) of the corresponding wave number in the region near the peak of the traveling wave. In each panel, values are shown for models both with (irregular solid line) and without (smooth gray dotted line) micromechanical irregularities introduced by jittering the poles of the BM admittance randomly with position. The triangle along the abscissa (Δ) marks the location of the peak of the traveling-wave envelope, and the scale bar (λ) indicates the size of the wavelength at this location. Note that the scales along the two abscissas differ: A shows the BM impedance throughout the basal region, whereas B zooms in and shows the wave number near the wave peak where the principal scattering occurs. To facilitate representation of the small perturbations in gain, the scale along the y-axis in B has been made linear for |y| < 1 and logarithmic elsewhere.

Results

BM interference patterns

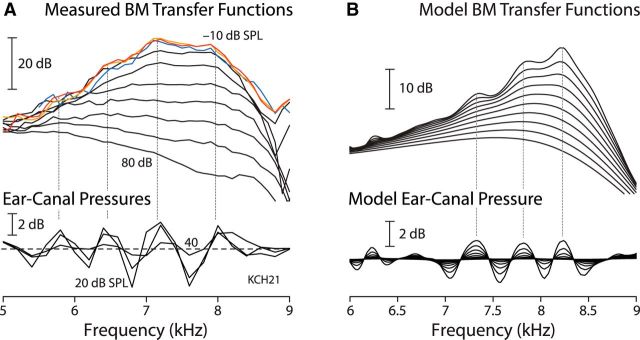
Fine structure in the tonotopic map follows from interference patterns evident in the motion of the BM. At sound levels near the threshold of hearing, BM frequency responses exhibit a quasiperiodic rippling present in both the magnitude and the phase of the mechanical transfer function (Rhode, 2007; Shera and Cooper, 2013). As illustrated in Figure 2A, the pattern of spectral ripples measured in BM motion appears tightly correlated with ripples measured simultaneously in ear-canal pressure as the frequency of the tonal stimulus is varied. Similar correspondence of ripple spacing was found in all nine (of 14) animals in which both BM and ear-canal ripples were measured (Shera and Cooper, 2013). Both sets of ripples decrease with increasing sound intensity and disappear entirely postmortem.

Figure 2.

Spectral ripples in BM transfer functions and ear-canal pressure. A, Isostimulus BM velocity transfer functions (top) and normalized ear-canal pressures (bottom) measured in a sensitive chinchilla. BM data were recorded from −10 to 80 dB SPL in 10 dB steps. For clarity, transfer functions in the linear regime where the curves overlap and the ripples are largest are shown in color [(−10, 0, 10) dB SPL ↔ (red, orange, blue), respectively]. Ear-canal pressures were measured at 20, 30, and/or 40 dB SPL probe levels and then normalized by the stimulus amplitude. Dotted vertical lines mark the approximate locations of the peaks in ear-canal pressure and show that the ripples in the BM transfer functions and ear-canal pressures are highly correlated. B, BM velocity and ear-canal pressure transfer functions computed using active cochlear models containing mechanical irregularities in the BM admittance. Intensity dependence was simulated using a family of linear models with the same pattern of irregularities but differing in overall amplifier gain. The model reproduces the observed equality of spacings between the BM and ear-canal ripple peaks. In the model, the two interference patterns can be shifted relative to one another slightly by modifying phase shifts associated with middle-ear transmission and reflection. Adapted from Shera and Cooper (2013).

The close correspondence between the ear-canal and BM rippling patterns—in particular, the spacing between their peaks—suggests that they originate through common mechanisms. The ear-canal rippling pattern is known to result from the alternating constructive and destructive interference between the stimulus pressure and a delayed echo at the same frequency—an SFOAE—evoked from the cochlea (Kemp and Chum, 1980; Zwicker and Schloth, 1984; Shera and Zweig, 1993). The strong empirical correlation between the acoustic and mechanical rippling patterns therefore suggests that BM motion is also modulated by wave interference effects related to the production and propagation of otoacoustic emissions (Shera, 2001a; de Boer and Nuttall, 2006; Shera and Cooper, 2013).

Model simulations performed using an active model of cochlear mechanics support the otoacoustic origins of BM rippling (Shera, 2001a; Shera and Cooper, 2013). To generate SFOAEs, we augmented the model with densely distributed micromechanical irregularities in the BM admittance, as suggested by coherent-reflection theory (Zweig and Shera, 1995; Shera et al., 2008). Figure 2B shows model BM transfer functions and corresponding ear-canal pressures normalized by stimulus amplitude. To simulate the dependence on stimulus intensity, we employed a series of linear models differing in the overall gain of the cochlear amplifier (Shera, 2001b). Ripples resembling those in the data (Fig. 2A) are clearly evident in the model responses. As in the data, ripple amplitudes are largest at low stimulus levels, where the amplifier gain is greatest.

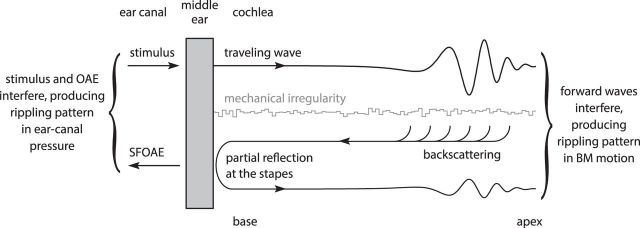
Analysis of the model demonstrates that the ripples depend on wave backscattering due to the presence of micromechanical irregularities in the organ of Corti. As illustrated in Figure 3, ear-canal ripples result when backscattered waves transmitted through the middle ear interfere with the applied stimulus pressure. BM ripples arise when the backscattered waves undergo partial reflection at the stapes due to the impedance mismatch present at the cochlear boundary with the middle ear. Reflection at the stapes launches a secondary forward-traveling wave that combines with the primary wave produced by the stimulus. Frequency-dependent phase differences between the two forward waves then create the rippling interference pattern measurable on the BM. Simulations performed to explore the dependence on model parameters corroborate the role of multiple internal reflection (Shera and Cooper, 2013). For example, the ripples measured on the BM—but not those in the ear canal—decrease when the stapes reflection coefficient is reduced by modifying the impedance of the middle ear. Both ear-canal and BM ripples disappear altogether when the micromechanical irregularities that scatter the forward-traveling wave are removed. Unlike the resultant spectral ripples, which vary smoothly and quasiperiodically with frequency, the irregularities introduced into the model vary randomly with position (Fig. 1). The irregularities simulate erratic spatial variations in the micromechanics, such as disorganization in the number and arrangement of outer hair cells (Engström et al., 1966; Bredberg, 1968; Wright, 1984; Lonsbury-Martin et al., 1988; Hilger et al., 1995), intrinsic to the biological cochlea.

Figure 3.

Wave reflection mechanisms that produce interference ripples in both ear-canal pressure and BM motion. The figure shows a schematic representation of the ear canal, middle ear, and cochlea. Distributed micromechanical irregularities (gray squiggle) scatter the forward-traveling wave launched by the ear-canal stimulus. The multiple backscattered wavelets combine to form a net reverse-traveling wave, which is then partially reflected at the stapes (where it produces a secondary forward-traveling wave that interferes with the primary wave) and partially transmitted to the ear canal (where it produces an otoacoustic emission that interferes with the stimulus pressure). Adapted from Shera and Cooper (2013).

Ripple effects on cochlear signal processing

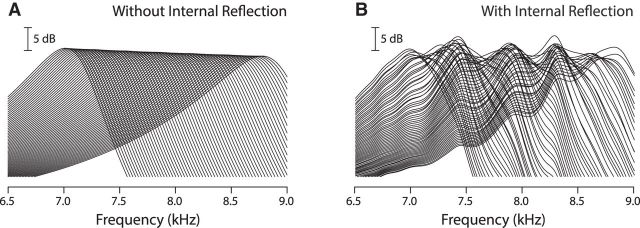
Multiple internal reflections have important consequences for the cochlea's analysis and representation of sound. Figure 4 illustrates how wave interference alters BM frequency responses computed at multiple, equally spaced locations along the cochlea. By adding ripples to the transfer functions, internal reflections alter the mechanical sensitivity, modifying the shape and spatial variation of the response. These transformations result in the generation of threshold and tonotopic microstructure.

Figure 4.

BM transfer functions computed at 64 equispaced locations in two different models. A, Transfer functions in a “smooth” model without micromechanical irregularity. The CFs span the range 7–9 kHz, representing a distance of ∼1 mm along the chinchilla BM; frequency responses were computed at intervals approximately corresponding to the width of two inner hair cells. B, Transfer functions computed at the same spatial locations as in A but using an “irregular” model in which small, micromechanical irregularities and an impedance mismatch at the stapes give rise to multiple internal reflection.

Sensitivity and threshold microstructure

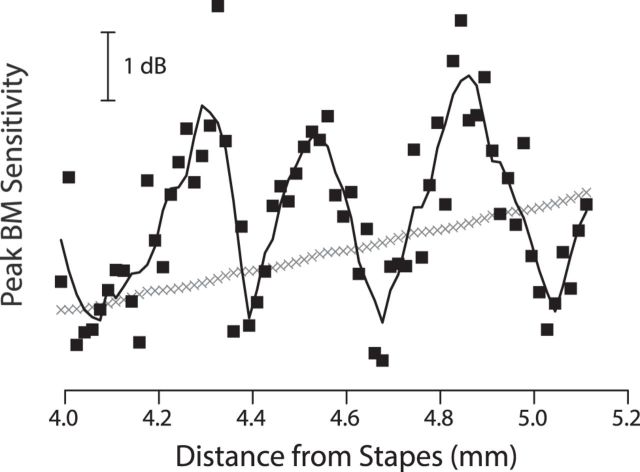
Perhaps the most conspicuous effect of the ripples is to change the maximum mechanical sensitivity (i.e., the height of the transfer function). For example, at the measurement location probed by the chinchilla data of Figure 2, the ripples increase the peak vibration amplitude by several decibels. The magnitude and sign of the change in peak sensitivity vary with location, and the pattern can be most readily explored in the model. Figure 5 illustrates the predicted spatial variation in peak sensitivity by plotting the maximum value of the transfer function versus cochlear location for each of the two models (smooth and irregular) employed in Figure 4. Whereas peak sensitivity varies only slowly in the smooth model, the presence of micromechanical irregularity introduces both a stochastic variation, due to the irregularity in the local BM admittance, and an emergent, quasiperiodic oscillation arising from multiple internal reflection. The variations in mechanical sensitivity shown here imply the existence of corresponding variations in BM “threshold” (i.e., in the stimulus pressure needed to produce a criterion BM velocity), with threshold minima occurring at frequencies of maximum sensitivity. Thus, the predicted quasiperiodic variation in model BM sensitivity constitutes a cochlear mechanical analog of what Elliott (1958) dubbed “a ripple effect in the audiogram,” the well known microstructure of the behavioral hearing threshold curve (Elliott, 1958; Thomas, 1975). Similar results have been reported using other computational models (Epp et al., 2010). The microstructure of the hearing threshold curve provides compelling psychophysical evidence that the sort of wave interference effects discussed here modulate the firing patterns of the auditory nerve (Kemp, 1979; Long, 1984; Zwicker and Schloth, 1984).

Figure 5.

Sensitivity microstructure created by multiple internal reflection. Peak BM sensitivity versus cochlear location for models with and without multiple internal reflection. Sensitivities were computed from the two families of equispaced transfer functions shown in Figure 4. Results for the mechanically smooth model (without internal reflection) are shown using gray symbols (×); those for the irregular model are shown using black squares (■). A local trend computed using a Savitzky–Golay smoothing filter is superposed to guide the eye.

Tonotopic microstructure

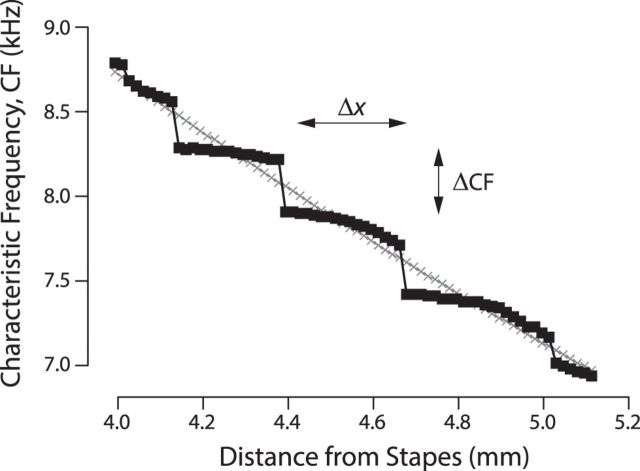
Less obviously, the interference ripples change not only the peak mechanical sensitivity at each location but also the frequency at which it occurs. In other words, multiple internal reflections modify the local CF. In the chinchilla data of Figure 2A, for example, the ripples act to decrease the CF by ∼400 Hz. Just as with the change in sensitivity, both the sign and magnitude of the change in CF depend on location, and the pattern can be explored in the model. The two families of equispaced transfer functions shown in Figure 4 demonstrate that although the CFs change uniformly with position in the smooth model, in the micromechanically irregular model the CFs appear to cluster around certain preferred values, corresponding to ripple peaks. Consequently, the tonotopic map obtained from these transfer functions remains exponential on the largest scales but manifests a local, staircase-like structure consisting of plateaus of nearly constant CF alternating with sudden jumps (Fig. 6). The inclination of the steps, and thus the salience of the staircase pattern, depends on the ripple amplitude: the larger the BM ripples, the flatter (more horizontal) the steps. In the model, the amplitude of the BM ripples depends on cochlear sensitivity and round-trip amplifier gain, on the degree and distribution of micromechanical irregularities, and on the amount of wave reflection at the stapes. It is important to emphasize that stepwise tonotopy is an emergent feature; no mechanical parameter of the model, such as BM stiffness, manifests a comparable stepwise variation with position.

Figure 6.

Tonotopic microstructure created by multiple internal reflection. CF versus cochlear location for models with and without multiple internal reflection. CFs were computed from the two families of equispaced transfer functions shown in Figure 4. Results for the mechanically smooth model (without internal reflection) are shown using gray symbols (×); those for the irregular model are shown using black squares (■). Double-headed arrows indicate the approximate width (Δx) and height (ΔCF) of the stair steps.

Variability of the microstructures

Figures 5 and 6 give predicted tonotopic and sensitivity microstructures for one “ear” (i.e., for a single model realization of the micromechanical irregularities). Figure 7 provides a sense of the variability by showing microstructures obtained using three additional random patterns (all other model parameters were held fixed). Although the introduction of irregularities invariably produces BM ripples and their associated microstructures, quantitative details, such as the inclination of the stair steps, the locations of sensitivity maxima, and the depth (or peak-to-peak variation) of the fine structure, all vary idiosyncratically from ear to ear, just as actual emission spectra and threshold microstructures do in human subjects. Many of these features can also be varied in more predictable fashion by changing the model parameters held constant in the simulations. For example, whereas boosting the overall gain of the cochlear amplifier generally increases the depth of the sensitivity microstructure and sharpens up the steps of the staircase, decreasing the impedance mismatch at the stapes has the opposite effect. Finally, although the operations needed to rigorously predict hearing thresholds measured psychophysically from BM mechanical sensitivities computed at a single point are more complicated than simply flipping the latter upside down on a log scale (Epp et al., 2010), it is interesting to note that sensitivity curves with large peak-to-peak variations (Fig. 7, bottom, red curve) tend to manifest relatively sharp peaks separated by broad valleys. This is precisely the pattern expected from human behavioral data: threshold curves in subjects with pronounced fine structure typically exhibit deep threshold minima separated by broad maxima (Long, 1984; Zwicker and Schloth, 1984).

Figure 7.

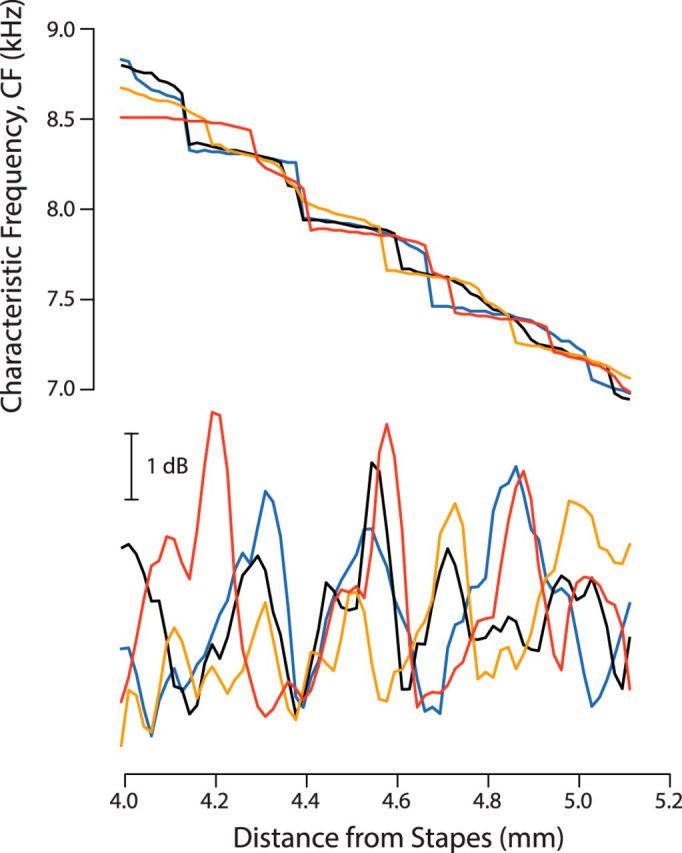
Tonotopic and sensitivity microstructures in four different “ears.” The two panels show BM CF (top) and peak mechanical sensitivity (bottom) versus cochlear location computed in four models identical in every way except for the random pattern of micromechanical irregularities. Different ears are shown using different colors; the results from Figures 5 and 6 are included for comparison (blue lines).

The staircase and cochlear tuning

Simple arguments yield approximate expressions for the height and width of the stair steps while elucidating their relationship to cochlear frequency selectivity. In a nutshell, the model predicts that the steps are determined by round-trip traveling-wave delay (i.e., emission latency) and its functional correlate, the sharpness of cochlear tuning. Whereas the step height is approximately equal to the equivalent rectangular bandwidth (ERB) of the auditory filters, the step width is approximately equal to the width of the spatial excitation pattern. Thus, the steps are expected to vary with location in the cochlea, becoming taller and narrower as one ascends the spiral staircase from apex to base.

We can make these qualitative comments more precise by noting that the model of Figure 3 implies that both threshold and tonotopic microstructures arise through a common mechanism, the modification of BM frequency responses by rippling patterns arising from wave reflection and interference, and their features are therefore strongly correlated. For example, the model predicts that the height of the tonotopic steps (ΔCF) matches the frequency spacing between adjacent threshold minima (Δf). Behavioral and otoacoustic measurements corroborate model predictions that the threshold spacing Δf, like the modal interval between neighboring spontaneous emissions, is largely determined by SFOAE latency (Zwicker and Schloth, 1984; Zweig and Shera, 1995; Talmadge et al., 1998; Shera, 2003; Bergevin et al., 2012). Since SFOAE phase (φ) changes by one cycle between consecutive ripple peaks (threshold minima), the threshold spacing Δf is determined by the local phase slope. In particular, Δf satisfies |φ̄′|Δf ≅ 2π, where the prime denotes the frequency derivative and the diacritical bar indicates a local average over the interval. Thus, Equation 1 follows:

where τ(f) = −φ′/2π is the local SFOAE phase-gradient (or group) delay at frequency f [and τ̄(f) its local trend or average]. Therefore, the model predicts that the step heights ΔCF vary inversely with SFOAE latency.

Because SFOAE latencies vary from species to species, from ear to ear, and from frequency to frequency within an ear, so also do the step heights, ΔCF. In particular, predicted step heights are smaller both at low frequencies (where delays are longer than at high frequencies) and in humans compared with small laboratory animals (where delays are shorter). In addition, SFOAE latency is an intrinsically irregular function of frequency whose fine structure and local trend vary idiosyncratically from ear to ear (Shera and Guinan, 2003; Kalluri and Shera, 2013). Thus, the step heights are also expected to vary somewhat irregularly, both across frequency and between subjects. The coherent-reflection model traces these irregularities of delay to the micromechanical irregularities involved in emission generation (Zweig and Shera, 1995).

Compelling evidence indicates that SFOAE group delay trends are connected to the bandwidth of cochlear frequency tuning (Shera et al., 2002, 2010; Joris et al., 2011), especially in the basal part of the cochlea (i.e., CF ≳ 1 kHz in humans). Relationships between tuning and group delay are expected from filter theory, with sharper tuning generally requiring proportionally longer delay. The empirical covariation of SFOAE latency and cochlear tuning is summarized by the so-called “tuning ratio,” defined as r = Q_ERB(CF)/N_SFOAE(f)|_f=CF. In this equation, Q_ERB (CF) and N_SFOAE(f) represent trend lines computed from pooled data that characterize the frequency dependence of cochlear tuning and otoacoustic delay in a particular species. More precisely, the value Q_ERB CF/ERB, where ERB is the equivalent rectangular bandwidth or critical band (Fletcher, 1938), quantifies the sharpness of tuning, and the dimensionless delay N_SFOAE ≡ f · τ̄ represents the SFOAE latency trend, measured in periods of the stimulus frequency (Shera et al., 2010).

Combining the equations involving τ̄ yields an estimate for the typical step height and its variation with frequency: ΔCF ≅ r · ERB. Neural, behavioral, and otoacoustic measurements indicate that the tuning ratio has a nearly invariant form in a wide variety of mammalian species, including cat, guinea pig, chinchilla, rhesus monkey, and human (Shera et al., 2010; Joris et al., 2011). In particular, r ∼ 1 throughout much of the cochlea, including the entire basal half (Shera et al., 2010). Thus, ΔCF ∼ ERB so that the step height approximates the critical band in these regions.

The width of individual steps, Δx, can be estimated from their height using the traditional, exponential approximation to the cochlear map. One finds that Δx ≅ (ΔCF/CF)l, where l is the space constant of the “smoothed” cochlear map (i.e., the distance over which the CF would change by a factor of e if BM rippling were absent). By local scaling, the distance (ERB/CF)l equals the equivalent rectangular spread (ERS) of the excitation pattern (Shera et al., 2010). Thus, the typical step width Δx ≅ r · ERS, which reduces to Δx ∼ ERS throughout much of the cochlea.

Discussion

The cochlear mapping between frequency and position is usually assumed to be smooth and continuous at all stimulus intensities. The measurements and modeling reported here, however, suggest that at low levels the mammalian cochlea actually manifests a tiered tonotopy whose step height and width are determined by the bandwidths of cochlear frequency tuning, as reflected in otoacoustic emission latencies. Unlike nonuniformities in the cochlear map conjectured previously (Wilson, 1980; Temchin and Ruggero, 2014), the staircase-like form predicted by the model is not a static structural feature that mirrors some corresponding pattern in cochlear anatomy or material properties. Rather, the staircase arises dynamically, as an emergent property, via the same mechanisms responsible for the microstructure of the hearing threshold.

Although the evidence for tonotopic microstructure presented here is indirect and grounded in computational modeling, the physics of the model identifies staircase-like tonotopy as the all but inevitable consequence of processes long recognized in cochlear mechanics: the internal reflection and interference of cochlear traveling waves. Tonotopic microstructure is thus the natural, albeit previously overlooked, concomitant of such familiar phenomena as stimulus-frequency otoacoustic emissions, BM rippling patterns, and threshold microstructure. Direct evidence for the spiral staircase requires high-resolution measurement of the cochlear map, or some segment thereof, in individual ears. Although intracellular labeling studies are problematic for this application due to their sparse yield, measurements of mechanical transfer functions at multiple, closely spaced locations along the BM (Ren, 2002; Lee et al., 2015) should prove more feasible, provided they can be performed without compromising cochlear sensitivity through surgery or other trauma.

Because ripple amplitudes decrease with increasing stimulus intensity and may be entirely absent in ears with certain types of hearing impairment (e.g., damage to the outer hair cells), the model predicts that the staircase will be most prominent in sensitive ears at sound levels near threshold in quiet (assuming sufficient reflection at the cochlea–middle ear boundary). For similar reasons, one might expect tonotopic microstructure to have little role in hearing at sound intensities where mechanical suppression and compression greatly reduce SFOAE magnitudes relative to the stimulus, decreasing the amplitude of BM ripples. Indeed, the influence of threshold microstructure on loudness perception is generally limited to sound intensities <40 dB SPL (Mauermann et al., 2004). However, as with threshold microstructure, much depends on the spectrotemporal structure of the ongoing sound and the dynamical response it evokes within the cochlea. For example, behavioral measurements reveal that fine structure in masked thresholds persists to moderate sound levels when thresholds are elevated by nonsimultaneous (rather than suppressive) masking (Long, 1984). Unfortunately, obtaining clear psychophysical evidence for tonotopic microstructure in humans is hindered both by the existence of multiple coding strategies for sound frequency (i.e., temporal as well as place codes) and by the confound of threshold microstructure, which the model identifies as the inevitable concomitant. For subjects predicted to exhibit tiered tonotopy on the basis of their thresholds, changes in stimulus frequency at low sound levels are necessarily accompanied by changes in audibility.

By modulating the firing patterns of the auditory nerve, both threshold and tonotopic microstructures may shape—and/or be shaped by—the development and maturation of the central auditory system. Noteworthy in this regard are reports that fine-grained mapping studies in both cats and rats find a discontinuous, stepwise progression of CFs along the main tonotopic axis of the central nucleus of the inferior colliculus (CNIC; Schreiner and Langner, 1997; Malmierca et al., 2008). The CNIC maps appear strikingly similar to the cochlear staircase shown in Figure 6 (cf. Schreiner and Langner, 1997, their Fig. 1). Furthermore, the mean step heights and their variation with CF match estimates of psychophysical and neural critical bands (Schreiner and Langner, 1997), just as predicted here for the cochlear map.

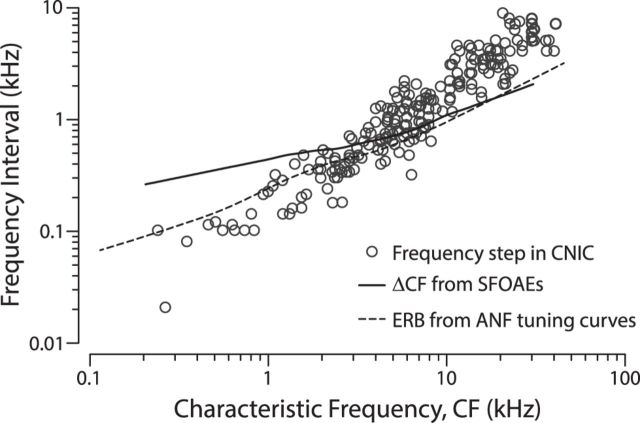
To explore structural similarities between the peripheral and central staircases, Figure 8 compares step heights for the CNIC map in cats (Schreiner and Langner, 1997) with predictions for the modal cochlear step size obtained from measurements of cat SFOAE phase-gradient delay (Shera and Guinan, 2003) using Equation 1. A dashed trend line showing the ERB computed from cat auditory-nerve tuning curves is superposed for comparison (Shera et al., 2010). Although the match among the curves is imperfect, detailed comparisons are necessarily clouded by reliance on data obtained from different animals in different laboratories using different stimuli and sound levels. In addition, the data compared involve three distinct measurement paradigms, each harboring its own potential sources of systematic error. For example, at low frequencies the measured SFOAE latencies may be biased downwards (predicted step height biased upwards) by the suppression paradigm used to extract the emissions (Shera et al., 2008). In addition, determination of the step size along the main (dorsal-ventral) tonotopic axis in the CNIC is complicated by the existence of shallower (and smoother) gradients in other directions (Schreiner and Langner, 1997).

Figure 8.

Tiered tonotopy in the cat. Open circles (○) show frequency step heights versus CF obtained from high-resolution tonotopic maps of the CNIC (data from Schreiner and Langner, 1997, their Fig. 2c). The solid line gives the expected trend for the mode of the step heights for the cat cochlear map estimated using Equation 1 from measurements of SFOAE delay obtained at 40 dB SPL (Shera and Guinan, 2003). The dashed line shows a trend line fit to ERBs computed from neural tuning curves measured in cat auditory nerve fibers (Shera et al., 2010).

Despite these complications, the overall correspondence between the predicted cochlear and measured CNIC stair steps, together with their mutual correlation with the critical band, remains intriguing. Given the different types of data being compared, there was little prior reason to suspect that the curves might lie anywhere close to one another, let alone enjoy overlapping numerical values and exhibit approximately the same frequency dependence. These unexpected similarities prompt one to ask whether the cochlear and collicular staircases might be causally connected. Several hypotheses come to mind.

According to the first hypothesis, the staircase in the inferior colliculus might be inherited dynamically from the cochlea via ascending projections. If so, the model predicts that the staircase seen in the CNIC would become less pronounced if the map were remeasured at higher sound levels where BM ripple amplitudes are smaller. In addition, because round-trip SFOAE phase shifts and delays, and thus the predicted step heights, are not identical in the two ears (e.g., due to intercochlear variations in the pattern of micromechanical irregularities; Fig. 7), the dynamical hypothesis predicts that details of the inferior colliculus staircase will generally depend on whether it is measured using ipsilateral or contralateral acoustic stimulation. Although their comparison is limited to but a single example, Schreiner and Langner (1997) report that “the CF values obtained by stimulation of either ear are largely the same,” a result at variance with this prediction. Additional data, supplemented with ear-canal measurements of SFOAE latency, would provide more definitive tests.

According to the second hypothesis, the tiered tonotopy emerging from the cochlea might shape the development of the inferior colliculus map, whose tonotopy then becomes hardwired soon after the onset of hearing. This scenario provides a compelling cochlear mechanical explanation for the functional and anatomical correlations with the critical band seen in the CNIC (Schreiner and Langner, 1997; Malmierca et al., 2008). Supporting this hypothesis are studies documenting the role of prenatal and postnatal auditory-nerve firing patterns in shaping the tonotopic organization of the auditory brainstem (Sanes and Takács, 1993; Leake et al., 2006; Clause et al., 2014). In addition, compared with emission measurements in adult ears, those in the ears of human newborns report larger and more numerous spontaneous otoacoustic emissions (Kok et al., 1993; Abdala, 1996) and increased reflection-source otoacoustic emissions (Abdala and Dhar, 2012), perhaps due to a transient hyperactivity of the immature cochlear amplifier (Mills and Rubel, 1996) and/or increased reflection at the cochlear boundary with the middle ear (Abdala and Keefe, 2006; Dhar and Abdala, 2007). These findings suggest that threshold and tonotopic microstructures are likely to be enhanced in the developing and newborn cochlea.

According to the third hypothesis, the causality runs in reverse and cochlear frequency selectivity and delay are fine-tuned during development via descending projections from the inferior colliculus mediated by efferent synapses in the cochlea. Supporting this hypothesis are measurements in neonatal cats showing that cochlear de-efferentation achieved by sectioning the olivocochlear bundle disrupts the normal development of auditory-nerve fiber thresholds and tuning (Walsh et al., 1998).

None of these hypotheses are mutually exclusive; all warrant further investigation. Finally, the evident similarities between the staircase maps in the cochlea and midbrain might not arise primarily through direct causal interactions, but via mutual, independent correlations with the critical band.