Efficient Adaptively Weighted Analysis of Secondary Phenotypes in Case-control Genome-wide Association Studies

Summary

We propose and compare methods of analysis for detecting associations between genotypes of a single nucleotide polymorphism (SNP) and a dichotomous secondary phenotype (X), when the data arise from a case-control study of a primary dichotomous phenotype (D), which is not rare. We considered both a dichotomous genotype (G) as in recessive or dominant models, and an additive genetic model based on the number of minor alleles present. To estimate the log odds ratio, β₁, relating X to G in the general population, one needs to understand the conditional distribution [D∣X,G], in the general population. For the most general model, [D∣X,G], one needs external data on P(D=1) to estimate β₁. We show that for this “full model”, maximum likelihood (FM) corresponds to a previously proposed weighted logistic regression (WL) approach if G is dichotomous. For the additive model, WL yields results numerically close, but not identical, to those of the maximum likelihood, FM. Efficiency can be gained by assuming that [D∣X,G] is a logistic model with no interaction between X and G (the “reduced model”). However, the resulting maximum likelihood (FM) can be misleading in the presence of interactions. We therefore propose an adaptively weighted approach (AW) that captures the efficiency of RM but is robust to the occasional SNP that might interact with the secondary phenotype to affect risk of the primary disease. We study the robustness of FM, WL, RM and AW to misspecification of P(D=1). In principle, one should be able to estimate β₁ without external information on P(D=1) under the reduced model. However, our simulations show that the resulting inference is unreliable. Therefore, in practice one needs to introduce external information on P(D=1), even in the absence of interactions between X and G.

Introduction

Genome-wide association studies (GWAS) usually measure hundreds of thousands of single nucleotide polymorphisms (SNPs) on thousands of subjects with a primary disease (cases) and without the primary disease (controls). Often data on other characteristics (“secondary phenotypes”) of cases and controls are available, and researchers wish to study the association between a secondary phenotype and SNPs by taking advantage of the valuable data already collected for the primary disease. However, the case-control study sample is not representative of the entire population, for which the associations between secondary phenotype and SNPs are desired. Ignoring the ascertainment in the case-control study design in secondary analysis can induce biased estimates of association and false positive significance tests, as described in Jiang et al. (2006), Lin and Zeng (2009), Richardson et al. (2007), Monsees et al. (2009) and Wang and Shete (2011).

Li, Gail, Berndt and Chatterjee (LGBC) (2010) studied methods for testing for associations between a SNP from a case-control GWAS and a secondary phenotype in the special case that the primary disease in the GWAS was rare. LGBC assumed that the secondary phenotype (X = 0 or 1) and SNP genotype (G=0 or 1) were binary (as for dominant or recessive genetic models), and the primary disease status indicator D=0 or 1, according as the primary disease was absent or present. The aim was estimation of the log odds ratio relating X and G in the general population based on

$$\mathrm{logit}(P(X=1\mid G))={\beta }_0+{\beta }_{1}G.$$ (1)

To take account of the case-control sampling, one must consider the model

$$P(D=1\mid G,X)=\frac{\exp ({\mathrm{\delta }}_0+{\mathrm{\delta }}_{1}G+{\mathrm{\delta }}_{2}X+{\mathrm{\delta }}_{12}GX)}{1+\exp ({\mathrm{\delta }}_0+{\mathrm{\delta }}_{1}G+{\mathrm{\delta }}_{2}X+{\mathrm{\delta }}_{12}GX)}.$$ (2)

For a rare primary disease, the denominator of (2) disappears from the likelihoods, simplifying the analysis. LGBC showed that under the general model (2) and for a rare primary disease, maximum likelihood estimation of β₁ is equivalent to analyzing data from the controls alone. If one assumes, as in Lin and Zeng (2009) that δ₁₂ = 0 in equation (2), then a much more efficient estimate of β₁ is obtained, whose variance is only very slightly smaller than obtained by taking a weighted average of estimates from cases and from controls, which we call the efficient weighted estimate (see LGBC). However, these estimates were biased and led to above nominal hypothesis test sizes if in fact δ₁₂ ≠ 0. Therefore LGBC proposed an adaptively weighted estimator that put more weight on the control only estimate when the data suggested δ₁₂ ≠ 0 and put more weight on the efficient weighted estimate when there was little evidence that δ₁₂ ≠ 0.

We now consider the case when the primary disease condition is not rare, as might arise in GWAS of visual acuity, or elevated blood pressure. Such data might arise, for example, from a hospital-based case-control study. In a hypertension clinic, a sample of cases might be selected for genome-wide scanning and compared to a sample of patients without hypertension. Such a study would not yield information on the probability of hypertension in the general population. A cohort study might yield a large number of subjects with diminished visual acuity. Genome scans might be performed on some members of the cohort with diminished visual acuity and some members without diminished visual acuity. In this context, the probability of diminished visual acuity, P(D=1), could be estimated from the cohort information. We compare the adaptively weighted to other methods for a disease that is not rare, and we treat both dichotomous models for G and additive models in which G represents the number of minor alleles.

For a disease that is not rare, estimates of the other parameters in models (1) and (2) apart from β₁ can be very unstable and lead to invalid inferences for secondary phenotypes unless the disease prevalence is known (Lin and Zeng 2009). Thus one needs to assume that P(D=1) is known, in which case β₁ can be estimated by maximum likelihood under equations (1) and (2) to yield β̂_1FM. Here FM stands for full model. Under this assumption, or assuming that the sampling fractions for cases and controls are known, an apparently simpler estimate can be obtained by reweighting the log-likelihood corresponding to equation (1) to obtain a weighted estimate β̂_1WL (Monsees 2009). This estimate had been obtained earlier as a consequence of weighted logistic regression (Richardson et al 2007). We prove in this paper that β̂_1WL is in fact the maximum likelihood estimate (MLE), β̂_1FM under the dichotomous genetic model. In simulations, we find that β̂_1WL is numerically very near but not equal to β̂_1FM for the additive genetic model.

Efficiency can be improved over β̂_1FM if one is willing to assume δ₁₂ = 0 and known P(D =1). In fact, Lin and Zeng (2009) studied this case. We denote the corresponding MLE β̂_1RM, which is more efficient than β̂_1FM. Here RM stands for “reduced model.” However, β̂_1RM can be misleading if δ₁₂ ≠ 0. Therefore, we developed an adaptive estimate β̂_1AW that puts more weight on β̂_1FM when there is evidence that δ₁₂ ≠ 0 and more weight on β̂_1RM when there is less evidence that δ₁₂ ≠ 0.

In principle, one should be able to estimate β₁ when δ₁₂ =0 by MLE without knowing P(D=1), as discussed in Lin and Zeng (2009). The corresponding estimate is denoted as β̂_1RMU in this paper. A potential advantage of β̂_1RMU is that it does not require specification of P(D=1), whereas β̂_1WL, β̂_1FM, β̂_1RM, and β̂_1AW do. Our numerical studies show for δ₁₂ = 0, that β̂_1RMU yields unbiased estimates of β₁, but estimates of the variance of β̂_1RMU from the information matrix can be too small, which leads to hypothesis tests with size above nominal levels. Moreover, when δ₁₂ ≠ 0, β̂_1RMU can be seriously misleading, just as can β̂_1RM. Therefore, methods based on external knowledge of P(D =1) are needed in practice, and we study the robustness of the estimators β̂_1WL, β̂_1FM, β̂_1RM, and β̂_1AW to misspecification of P(D=1). We compare these estimators for studying associations with a preselected candidate SNP and for discovering a SNP associated with X among all the SNPs studied in the GWAS data.

In the next section, we describe the methods in more details for a common primary common disease. In Section 3, we present results of analyses and numerical studies. We discuss these results in Section 4 and defer most technical details to the Appendix.

Methods

We first consider the important scenario of an unmatched case-control study with dichotomous genotype G and secondary phenotype X, but where the primary disease is not rare. We extend all the methods to the additive genetic model at the end of this section. The data for dichotomous G can be represented as a 2 by 4 array (Table I). Let r₀ = (r₀₀₀, r₀₀₁, r₀₁₀, r₀₁₁) and r₁ = (r₁₀₀, r₁₀₁, r₁₁₀, r₁₁₁) denote the case and control cell frequency vectors, respectively, and let n₀ and n₁ be the numbers of controls and cases selected respectively. In the table r_dgx represents the cell counts for D = d, G = g and X =x.

Table I.

Data for an unmatched case-control study with dichotomous genotype and phenotype

	G=0		G=1
	X=0	X=1	X=0	X=1	Total
D=0	r000	r001	r010	r011	n0
D=1	r100	r101	r110	r111	n1

Weighted Logistic Regression Method

Jiang et al. (2006) and Richardson et al. (2007) proposed a weighted logistic regression method that can be used to estimate the association between genotype and secondary phenotype. Monsees et al. (2009) studied this method through simulations in GWAS that assumed δ₁₂ =0. Defining weights that are inversely proportional to the sampling fractions w_i = P(D = i)/n_i w_i = P(D = i) /n_i for cases (i=1) and controls (i=0), one can construct a weighted pseudo-log likelihood from the data in Table I as

$$\begin{array}{ccc}{l}_w& =& \sum _{i=0}^1{w}_i\sum _{j=1}^{n_i}\log (P(X_{\mathit{ij}}\mid G_{\mathit{ij}}))=\sum _{x=0}^1\sum _{g=0}^1(w_0{r}_{0\mathit{gx}}+w_1{r}_{1\mathit{gx}})\frac{\exp [({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}g)x]}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}g)}\\ & =& w_0(r_{000}\log (\frac{1}{1+\exp ({\mathrm{\beta }}_0)})+r_{010}\log (\frac{1}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_1)})+\\ & & r_{001}\log (\frac{\exp ({\mathrm{\beta }}_0)}{1+\exp ({\mathrm{\beta }}_0)})+r_{011}\log (\frac{\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_1)}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_1)}))+\\ & & w_1(r_{100}\log (\frac{1}{1+\exp ({\mathrm{\beta }}_0)})+r_{110}\log (\frac{1}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_1)})+\\ & & r_{101}\log (\frac{\exp ({\mathrm{\beta }}_0)}{1+\exp ({\mathrm{\beta }}_0)})+r_{111}\log (\frac{\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_1)}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_1)})).\end{array}$$ (3)

Maximizing (3), one obtains the estimate of β₁,

$${\widehat{\beta }}_{1\mathit{WL}}=\log \left(\frac{w_0{r}_{011}+w_1{r}_{111}}{w_0{r}_{010}+w_1{r}_{110}}\frac{w_0{r}_{000}+w_1{r}_{100}}{w_0{r}_{001}+w_1{r}_{101}}\right)$$ (4)

The justification for equation (4) is that the corresponding score equations obtained by differentiation of (3) with respect to β₀ and β₁ have expectation zero in the entire population, even though the data were obtained from a stratified (on D) random sample from the population. Thus equation (4) is unbiased for β₁. This approach requires no modeling of the primary disease probability as in equation (2) and is therefore robust to a possible non-zero interaction δ₁₂ between X and G (see Section 3). We address how efficient β̂_1WL is compared to maximum likelihood when the weights are known, which we assume hereafter. Because we usually need to estimate P(D=1) from external data, we also study the sensitivity of various estimates to misspecification of P(D=1).

Maximum Likelihood

Jiang et.al. (2006) discuss efficient semi-parametric likelihood methods for secondary phenotype analysis in case-control studies. Lin and Zeng (2009) investigate this method for secondary phenotypes in GWAS. Their method is based on the retrospective likelihood

$$\begin{array}{cc}& L=\prod _{i=0}^1\prod _{j=1}^{n_i}P(X_{\mathit{ij}},G_{\mathit{ij}}\mid D_{\mathit{ij}}=i)\\ =& \prod _{i=0}^1\prod _{j=1}^{n_i}P(D_{\mathit{ij}}=i\mid X_{\mathit{ij}},G_{\mathit{ij}})P(X_{\mathit{ij}}\mid G_{\mathit{ij}})P(G_{\mathit{ij}})/P(D_{\mathit{ij}}=i)\end{array}$$ (5)

where i=0,1 indexes the primary disease status and j=1,…,n_i indexes the subjects with D=i. For binary genotype and secondary phenotype as in Table I, equation (5) can be rewritten as

$${\prod _{d=0}^1\prod _{g=0}^1\prod _{x=0}^1\left(\frac{P(D=d\mid X=x,G=g)P(X=x\mid G=g)P(G=g)}{P(D=d)}\right)}^{r_{\mathit{dgx}}}$$ (6)

In most of the paper we assume that the disease prevalence P(D = 1) is known, and we let PG₀ = P(G = 0) and PG₁ = P(G = 1) = 1 − PG₀. Maximizing (6) is equivalent to maximizing

$${\prod _{d=0}^1\prod _{g=0}^1\prod _{x=0}^1\left(P(D=d\mid X=x,G=g)\frac{\exp (x({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}g))}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}g)}P{G}_g\right)}^{r_{\mathit{dgx}}}$$ (7)

subject to the constraint $\sum _{x=0}^1\sum _{g=0}^{1}P(D=1\mid X=x,G=g)\frac{\exp (x({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}g))}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}g)}P{G}_g=P(D=1)$.

Depending on which disease model is used, one can obtain two different MLE estimates of β₁ from (7). If model (2) is used, there will be 7 unknown parameters θ_FM = {β₀, β₁, δ₀, δ₁, δ₂, δ₁₂, PG₀} in the likelihood (7). Their MLE estimates are denoted as θ̂_FM. If δ₁₂ =0 is assumed in model (2), there will be 6 unknown parameters θ_RM = {β₀, β₁, δ₀, δ₁, δ₂, PG₀} in the likelihood (7), and we denote the corresponding MLE estimates by θ̂_RM. One might anticipate that β̂_1RM is more efficient than β̂_1FM, and numerical studies in Results confirm this. Lin and Zeng (2009) also estimated β₁ from (6) without assuming that P(D = 1) is known by setting δ₁₂ =0. We study the properties of their estimator and denote it by β̂_1RMU.

Adaptively Weighted Estimate

To capture the efficiency of β̂_1RM while avoiding the bias in this estimate that results when δ₁₂ ≠ 0, we propose an estimator, as in LGBC, that adaptively combines β̂_1FM and β̂_1RM as

$${\widehat{\beta }}_{1\mathit{AW}}=\frac{{\widehat{\delta }}_{12\mathit{FM}}^2}{{\widehat{\delta }}_{12\mathit{FM}}^2+{\widehat{\sigma }}_{\mathit{FM}}^2}{\widehat{\beta }}_{1\mathit{FM}}+\frac{{\widehat{\sigma }}_{\mathit{FM}}^2}{{\widehat{\delta }}_{12\mathit{FM}}^2+{\widehat{\sigma }}_{\mathit{FM}}^2}{\widehat{\beta }}_{1\mathit{RM}}.$$ (8)

In this equation, ${\widehat{\mathrm{\delta }}}_{12\mathit{FM}}^2$ is the MLE estimate of interaction in the full model, and ${\widehat{\mathrm{\sigma }}}_{\mathit{FM}}^2$ is the estimated variance of β̂_1FM. This new method strikes a balance between bias and efficiency. It puts more weight on the efficient β̂_1RM when ${\widehat{\mathrm{\delta }}}_{12\mathit{FM}}^2$ is small compared to ${\widehat{\sigma }}_{\mathit{FM}}^2$ and more weight on the less efficient β̂_1FM when ${\widehat{\mathrm{\delta }}}_{12\mathit{FM}}^2$ is large compared to ${\widehat{\sigma }}_{\mathit{FM}}^2$, which indicates that there is an interaction between the effects of secondary phenotype and genotype on the risk of primary disease.

Additive Genetic Model

When an additive genetic model is assumed for the genotype G, we use G={0,1,2} to denote the number of minor alleles in the SNP genotype. The data can be represented in a 2 by 6 array in which controls with frequency vector r₀ = (r₀₀₀, r₀₀₁, r₀₁₀, r₀₁₁, r₀₂₀, r₀₂₁) and cases with frequency vector r₁ = (r₁₀₀, r₁₀₁, r₁₁₀, r₁₁₁, r₁₂₀, r₁₂₁) are in separate rows, similar to Table I. We assume Hardy-Weinberg equilibrium and express PG₀ = P(G = 0) = (1 − p)², PG₁ = P(G = 1) = 2p(1− p) and PG₂ = P(G = 2) = p², where p is the unknown minor allele frequency (MAF). From these data, one can obtain the pseudo-log likelihood for weighted logistic regression method as in (3) and the retrospective likelihood for the maximum likelihood methods as in (5) (6) and (7) where the disease prevalence is assumed known. The adaptively weighted estimate β̂_1AW is computed from the MLE estimates β̂_1FM, ${\widehat{\mathrm{\delta }}}_{12\mathit{FM}}^2$ and β̂_1RM from equation (8).

Under the additive genetic model, β̂_1WL cannot be written explicitly, and iterative numerical methods are needed. We used SAS PROC SURVEYLOGISTIC, which also yields a correct variance estimate. Under model (2), 7 unknown parameters θ_FM = {β₀, β₁, δ₀, δ₁, δ₂, δ₁₂, p} appear in the likelihood (7), and the corresponding MLE is θ̂_FM. If δ₁₂ = 0 in model (2), there are 6 unknown parameters θ_RM = {β₀, β₁, δ₀, δ₁, δ₂, p}, and we denote the corresponding MLE by θ̂_RM.

Results

Analytic findings

For dichotomous G, the MLE β̂_1FM can be expressed in closed form as a function of r_ijk and P(D = 1) (see Appendix). This proves β̂_1FM = β̂_1WL. Thus the weighted logistic estimate is fully efficient under the full disease model (2). However, numerical calculations based on the Fisher information and simulation studies described later show that β̂_1FM is considerably less efficient than β̂_1RM, which is based on the additional assumption δ₁₂ = 0. If P(D = 1) ≈ 0 P(D = 1) ≈ 0, the estimate β̂_1WL = β̂_1FM in equation (4) reduces to the log odds ratio in control subjects only. LGBC had previously shown that for a rare primary disease, β̂_1FM is the log odds ratio in controls only, but the new results show that β̂_1FM = β̂_1WL whether the disease is rare or not. For the additive genetic model, simulations indicate that β̂_1WL is numerically close, but not identical, to β̂_1FM. Therefore, in what follows we usually present data for β̂_1FM and not fo β̂_1WL.

The Appendix outlines algorithms to estimate β̂_1RM for the case where P(D = 1) is known and β̂_1RMU for the case where P(D = 1) is not known. Following re-parameterization, these estimates are closed form functions of certain cell probabilities. However, iterative methods are needed to estimate those cell probabilities. A variance estimate for β̂_1AW is given in the Appendix that takes the variability of β̂_1FM, β̂_1RM, and δ̂_12FM into account. We refer to procedures such as hypothesis tests or confidence interval estimation that are associated with β̂_1WL, β̂_1FM, β̂_1RM, β̂_1AW, and β̂_1RMU respectively as WL, FM, RM, AW, and RMU procedures.

Simulations to compare estimates and tests for a pre-selected SNP

First we consider the case of a pre-selected SNP, as might arise in a candidate gene study. We used Monte Carlo simulation to evaluate the performance of different estimators and procedures for a pre-selected SNP under the dichotomous genetic model. The simulation results for the additive genetic model are quite similar to those for the dichotomous genetic model and are briefly summarized at the end of this section. For dichotomous G, we fixed the probabilities in the general population of carrying one or two alleles of interest (G =1) as P(G = 1) = 0.3. We set β₀ = 0 and let β₁ = 0 and 0.25 under the null and alternative hypotheses. For the disease model, we set δ₁ = 0 and δ₂ = log(1.5), varied the value δ₁₂ from -1.5 to 1.5, and choose the value of δ₀ to yield a disease prevalence P(D=1) of 0.10 or 0.30. For each set of simulation parameters, the conditional distributions of X and G given D were determined, and we generated 10,000 datasets with 1000 cases and 1000 controls from two independent quadrinomial distributions, [X,G∣D], corresponding to the case (D=1) and control (D=0) populations. We obtained estimates β̂_1FM, β̂_1RM, β̂_1AW, and β̂_1RMU, together with their estimated variances from the corresponding information matrices for β̂_1FM, β̂_1RM, and β̂_1RMU. The variances of β̂_1AW was calculated as in the Appendix from Taylor series expansion. Wald statistics, calculated as the squared estimate divided by its estimated variance, led to rejection of the null hypothesis for values exceeding 3.84, the 95^th percentile of the chi-squared distribution with one degree-of-freedom. In order to study the robustness of our procedures to misspecification of P(D =1), we used values 0.11 and 0.12 instead of the correct P(D =1)= 0.10, and 0.32 and 0.34, instead of the correct P(D =1)= 0.30.

Figure 1 gives the sizes of the various procedures for testing H₀: β₁ = 0 for true primary disease probability 10% (panels A, B, C) and 30% (panels D, E, F) for the dichotomous genetic model. Correct specification of the primary disease probability corresponds to panels A and D, and the effects of misspecification are shown in the middle and right columns. Consider first the case where P(D =1) is correctly specified. Then the FM and AW tests have nominal size across the range of values of δ₁₂ both for P(D =1) values of 10% and 30%. As expected, the RM test has nominal size when δ₁₂ =0, but not otherwise. The RMU procedure, which does not require specifying P(D =1) has above nominal size not only when δ₁₂ ≠ 0, as expected, but also when δ₁₂ = 0. This is because estimates of the standard error of variance of β̂_1RMU are skewed, and many are very small (Figure 2, panel B), leading to many rejections even for small values of β̂_1RMU, as shown by the red dots in panel D of Figure 2. In contrast, at δ₁₂ = 0, the size of the RM procedure is nominal (Figure 1, panels A, D) and the corresponding estimates of the standard errors of estimates of β̂_1RM are not skewed (Figure 2, panels A, C). These findings are confirmed by Table II, where the size of RMU is seen to be near 0.10 at δ₁₂ = 0. We conclude that only the FM and AW procedures should be used in general, but that the RM procedure has proper size at δ₁₂ =0. The RMU procedure should not be used, because it does not control size, even for a pre-selected SNP. Therefore we do not present results for the RMU method in the following simulations. Separate simulations show that even with only 200 cases and 200 controls, FM and AW tests have nominal size (unreported data). Other simulations yielded similar results with δ₁ = log(1.5) and P(X=1)=0.5 (unreported data). The previous conclusions are robust to misspecification of P(D =1) when the true probability is 10% (Figure 1, panels B, C). When P(D =1)=30%, the FM and AW procedures have near nominal size with misspecified values of P(D =1) for values of δ₁₂ in the range -0.5 to 0.5. Outside this range, overestimating P(D =1) results in some elevation in size above nominal levels (Figure 1, panels E, F).

Figure 1.

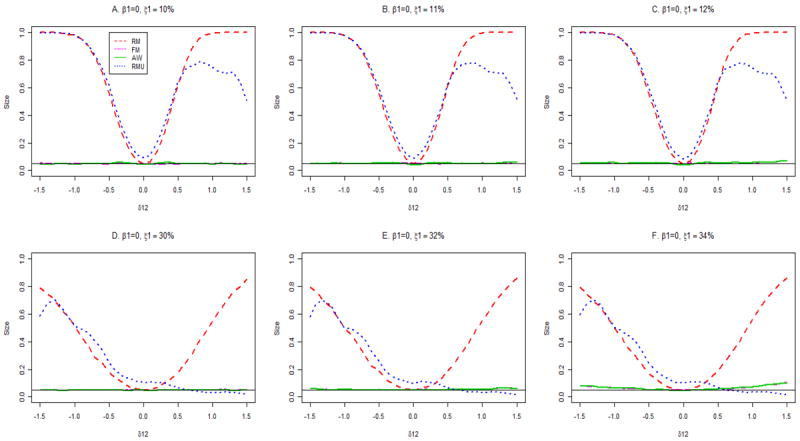
Type I error rates of association tests at the 5% nominal significance level. The true disease rate is 10% for panels A, B and C, and 30% for panels D, E and F.

Figure 2.

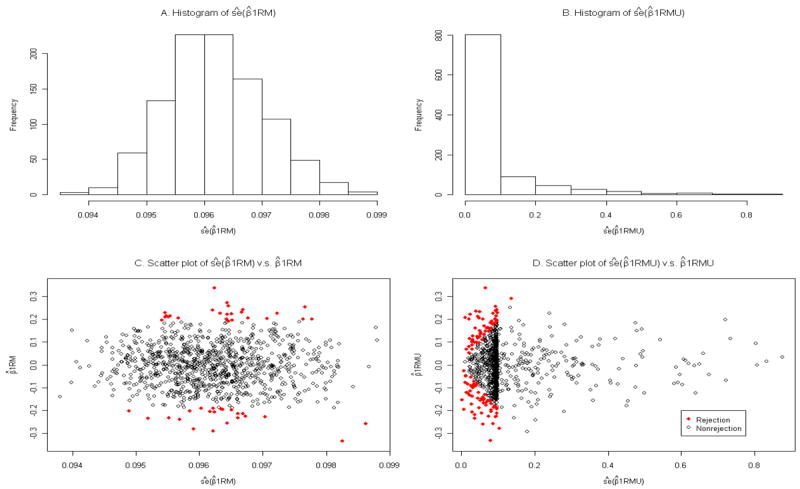
Simulation results for the estimated standard errors of β̂_IRM and β̂_1RMU. The results are for β₁ = 0, δ₁₂ = 0, and the primary disease probability is 30%, based on 1000 replicates. The panels A and B present histograms of the estimated standard errors (ŝe) of β̂_1RM and β̂_1RMU, and panels C and D contain scatter plots of β̂_1RM versus its estimated standard error and β̂_1RMU versus its estimated standard error, respectively. The red solid dots indicate the rejections of the null hypothesis for the Wald test with α = 0.05. The type one error is 0.047 for the RM and 0.113 for the RMU.

Table II.

Type I error and power for a pre-selected SNP and for several values of δ₁₂

	Primary disease probability = 10%					Primary disease probability = 30%
	β1 = 0; Size*
	δ12 = −0.5	δ12 = −0.3	δ12 = 0	δ12 = 0.3	δ12 = 0.5	δ12 = −0.5	δ12 = −0.3	δ12 = 0	δ12 = 0.3	δ12 = 0.5
FM	0.047	0.050	0.051	0.047	0.047	0.049	0.052	0.051	0.055	0.051
AW	0.051	0.060	0.045	0.058	0.051	0.049	0.052	0.051	0.056	0.052
RM	0.561	0.254	0.052	0.270	0.618	0.177	0.101	0.050	0.103	0.178
RMU	0.612	0.303	0.094	0.330	0.639	0.246	0.151	0.102	0.100	0.065
	β1 = 0.25; Power*
	δ12 = –0.5	δ12 = –0.3	δ12 = 0	δ12 = 0.3	δ12 = 0.5	δ12 = –0.5	δ12 = –0.3	δ12 = 0	δ12 = 0.3	δ12 = 0.5
FM	0.511	0.521	0.515	0.528	0.526	0.669	0.671	0.662	0.681	0.673
AW	0.452	0.455	0.571	0.561	0.547	0.647	0.648	0.672	0.697	0.683
RM	0.080	0.255	0.750	0.978	0.999	0.338	0.504	0.729	0.896	0.957
RMU	0.127	0.316	0.783	0.919	0.904	0.441	0.568	0.669	0.468	0.218

^*Based on 10,000 independent simulations for each column of four estimates. Analyses use the correct primary disease probability.

Figure 3 presents the power for the FM and AW procedures. Results are also given for the RM procedure, although the power should be ignored for RM except when δ₁₂ =0, because the size is otherwise not controlled for the RM procedure. At δ₁₂ =0, the RM procedure has higher power than the AW procedure, which has higher power than the FM procedure, both for P(D =1) =10% and P(D =1)=30% (Figure 3, panels A, D). These relationships are shown clearly in Table II. This is not surprising, because RM, and to a lesser extent, AW, take advantage of the assumption that δ₁₂ =0. For P(D =1)=10%, the power of AW exceeds that of FM for δ₁₂ > -0.2, but is less than that of FM for δ₁₂ < -0.2 (Figure 3, panel A). Note that AW is more efficient than FM in the region |δ₁₂|<0.2 that surrounds δ₁₂ = 0. This property of AW leads to higher power for AW than FM in simulations for GWAS in the next section.

Figure 3.

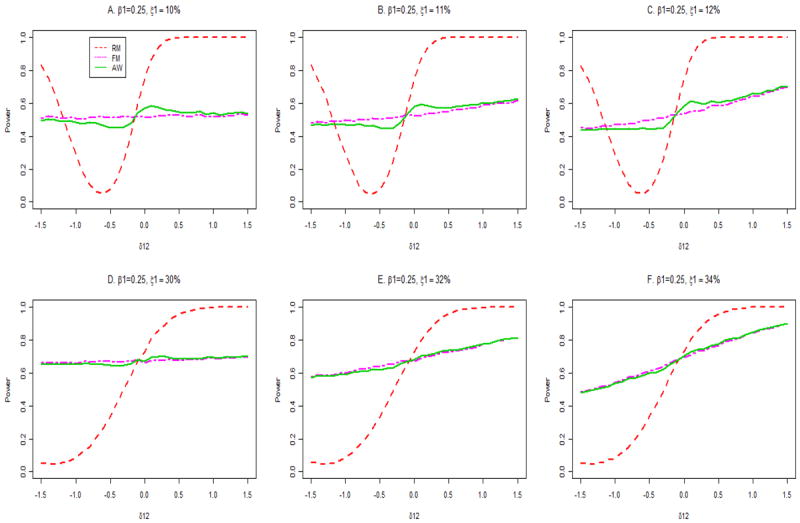
Powers of association tests at the alternatie β₁ = 0.25. The true disease probability is 10% for panels A, B and C and 30% for panels D, E and F.

For P(D=1)=30%, a similar pattern is seen, but the absolute differences in power between the FM and AW procedures is small (Figure 3, panel D). For P(D =1)=10%, the powers of the FM and AW procedures are not greatly changed by misspecification of P(D =1) (Figure 3, panels B, C). In contrast, for P(D =1)=30%, overestimation of P(D =1) changes the power appreciably for values of δ₁₂ away from 0 (Figure 3, panels E, F); in part these changes reflect increases in size above nominal levels (Figure 1, panels E, F).

Figures 4 and 5 show the biases (panels A, B, C), coverage probabilities of 95% confidence intervals for β₁ (panels D, E, F), and mean squared errors (MSE; panels G, H, I) for true disease probabilities, P(D =1), of 10% (Figure 4) and 30% (Figure 5) when β₁= 0.25. When the correct disease probability is used (panels A, D, G), the estimates β̂_1FM and β̂_1AW are unbiased, have the same small MSE, and are associated with nominal confidence interval coverage across the range of values of δ₁₂, both for P(D =1)=10% (Figure 4) and 30% (Figure 5). In contrast, β̂_1RM is severely biased and has sub-nominal confidence interval coverage and inflated MSE for values of δ₁₂ away from 0. The good performance of FM and AW persist in the presence of misspecification of P(D =1) when P(D =1) = 10% (Figure 4, middle and right columns). However, when P(D =1) = 30%, the FM and AW procedures yield slightly biased estimates of β₁ and slightly sub-nominal coverage of confidence intervals for large or small values of δ₁₂ if P(D =1) is misspecified (Figure 5, panels C, F).

Figure 4.

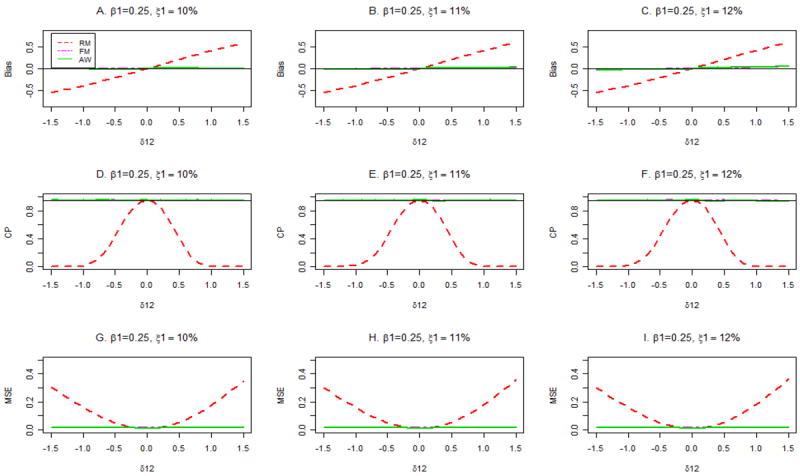
Bias, coverage probabilities (CP) of 95% confidence intervals and mean squared errors (MSE) for different estimators with assumed primary disease probabilities ξ₁ =10%, 11% and 12%. The true primary disease probability is 10%, and β₁ = 0.25.

Figure 5.

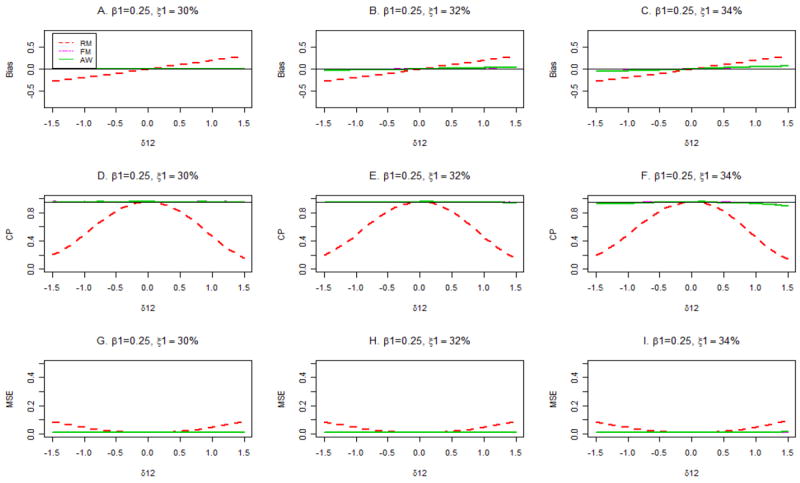
Bias, coverage probabilities (CP) of 95% confidence intervals and mean squared errors (MSE) for different estimators with assumed primary disease probabilities ξ₁ =30%, 33% and 36%. The true primary disease probability is 30%, and β₁ = 0.25.

For the additive genetic model, we fixed the minor allele frequency at p=0.4, from which we have P(G = 0) = 0.36, P (G = 1) = 0.48 and P (G = 2) = 0.16. We set β₀ = 0.1 and let β₁ = 0 and 0.1 under the null and alternative hypotheses. For the disease model, we set δ₁ = log(2) and δ₂ = log(1.5), varied the value δ₁₂ from -0.5 to 0.5, and choose the value of δ₀ to yield a disease prevalence P (D=1) of 0.10 or 0.30. The comparisons among FM, RM and AW methods were very similar to those for dichotomous G with respect to estimation and testing for a pre-selected SNP (data not shown).

Genome-wide Size and Power

In this section we investigate the size and power of different methods to discover SNPs associated with the secondary phenotype in a GWAS. Assuming there were N = 500,000 independent SNP genotypes, we controlled the experiment-wise significance by setting α = 0.05/(5×10⁵) = 10^-7. It may be reasonable to suppose that δ₁₂ = 0 for a large proportion of SNPs. As in LGBC, we assume that 99% of SNPs have δ₁₂ = 0, and 1% of SNPs have δ₁₂ independently distributed as N(0, (log(2)/2)²), which implies that about 95% of nonzero δ₁₂ values are in the interval [-log(2), log(2)]. We evaluated the genome-wide type I error and power (β₁ = 0 and 0.25 for dichotomous G and β₁ = 0 and 0.1 for the additive genetic model) of Wald tests analytically by averaging over the mixture distribution of δ₁₂ (see LGBC, 2010). Briefly, we computed the conditional power given δ₁₂ from the non-central chi-square distribution with non-centrality determined by {β₀, β₀, δ₁, δ₁₂, PG₁(or p), P(D = 1)} with the same parameter values as in simulations for pre-selected SNPs. We then averaged this conditional power over the distribution of δ₁₂.

For dichotomous G, the genome-wide type I error and power for different methods are presented in Table III for numbers of cases (n₁) and controls (n₀) each equal to 1000, 5000 or 10,000. The genome-wide type I error is always above nominal 0.05 level and usually equals 1.0 for the RM procedure, indicating that this test should not be used even if only a small proportion of SNPs have δ₁₂ ≠ 0. Both FM and AW have near nominal genome-wide type I error. However, for sample sizes n₁ = n₀ = 5000 or 10,000, the power of AW greatly exceeds that of FM when the true primary disease rate=10%. For example, when n₁ = n₀ = 5000, the power of AW is 70%, while that of FM is only 20%. Thus, substantial power gains can be achieved with AW. This power difference is smaller, but not negligible, when the primary disease probability is 30% (Table III). Misspecification of the primary disease probability has little effect on the size and power of the AW and FM procedures.

Table III.

Genome-wide type I error and power with genome-wide significance 0.05 level when δ₁₂ is from a mixture distribution^a for binary genetic model.

	True primary disease probability = 10%						True primary disease probability =30%
	β1 = 0; Genome wide sizeb			β1 = 0.25; Powerb			β1 = 0; Genome wide sizeb			β1 = 0.25; Powerb
n0= n1c	1000	5000	10,000	1000	5000	10,000	1000	5000	10,000	1000	5000	10,000
	Assumed primary disease probability = 10%						Assumed primary disease probability = 30%
RM	1.000	1.000	1.000	0.004	0.703	0.996	0.104	1.000	1.000	0.003	0.677	0.997
FM	0.049	0.049	0.049	0.000	0.199	0.844	0.049	0.049	0.049	0.002	0.511	0.988
AW	0.049	0.049	0.049	0.003	0.699	0.997	0.049	0.049	0.049	0.003	0.676	0.998
	Assumed primary disease probability = 11%						Assumed primary disease probability = 32%
RM	1.000	1.000	1.000	0.004	0.703	0.996	0.109	1.000	1.000	0.003	0.677	0.997
FM	0.049	0.049	0.049	0.000	0.206	0.853	0.049	0.049	0.049	0.002	0.541	0.991
AW	0.049	0.049	0.049	0.003	0.700	0.997	0.049	0.049	0.049	0.003	0.677	0.998
	Assumed primary disease probability = 12%						Assumed primary disease probability = 34%
RM	1.000	1.000	1.000	0.004	0.703	0.996	0.110	1.000	1.000	0.003	0.677	0.997
FM	0.049	0.049	0.049	0.000	0.214	0.861	0.049	0.049	0.054	0.002	0.569	0.993
AW	0.049	0.049	0.049	0.003	0.700	0.997	0.049	0.049	0.055	0.003	0.677	0.998

^aThe δ₁₂ comes from a mixture distribution. With probability 0.99, δ₁₂ =0. With probability 0.01, δ₁₂ has a normal distribution with mean 0 and variance (log(2)/2)².

^bBased on 10,000 independent simulations for each column of three estimates.

^cThere are n₁ cases and n₀ controls in the case-control study.

Qualitatively similar conclusions hold for the additive genetic model (Table IV), which also shows that FM and WL perform very similarly. In particular, the size of RM greatly exceeds nominal levels and should be avoided. AW, FM and WL have nominal size, but AW is more powerful than FM or WL, especially for P(D=1)=10%, but also for for P(D =1)=30%. Data in Table IV also indicate that these conclusions are robust to moderate misspecification of for P(D =1), where the relative error is around 10%.

Table IV.

Genome-wide type I error and power with genome-wide significance 0.05 level when δ₁₂ is from a mixture distribution^a for additive genetic model.

	True primary disease probability = 10%						True primary disease probability =30%
	β1 = 0; Genome wide sizeb			β1 = 0.15; Powerb			β1 = 0; Genome wide sizeb			β1 = 0.15; Powerb
n0= n1c	1000	5000	10,000	1000	5000	10,000	1000	5000	10,000	1000	5000	10,000
	Assumed primary disease probability = 10%						Assumed primary disease probability = 30%
RM	1.000	1.000	1.000	0.002	0.429	0.971	0.527	1.000	1.000	0.001	0.442	0.975
FM	0.049	0.049	0.049	0.000	0.103	0.661	0.049	0.049	0.049	0.001	0.312	0.935
WL	0.049	0.049	0.049	0.000	0.100	0.653	0.049	0.049	0.049	0.001	0.305	0.931
AW	0.049	0.049	0.049	0.001	0.425	0.971	0.049	0.049	0.049	0.001	0.440	0.977
	Assumed primary disease probability = 11%						Assumed primary disease probability = 32%
RM	1.000	1.000	1.000	0.002	0.461	0.977	0.701	1.000	1.000	0.002	0.466	0.979
FM	0.049	0.052	0.055	0.000	0.122	0.712	0.049	0.052	0.056	0.001	0.356	0.954
WL	0.049	0.051	0.054	0.000	0.119	0.705	0.049	0.052	0.056	0.001	0.351	0.952
AW	0.050	0.053	0.058	0.001	0.457	0.978	0.050	0.052	0.057	0.002	0.465	0.981
	Assumed primary disease probability = 12%						Assumed primary disease probability = 34%
RM	1.000	1.000	1.000	0.002	0.492	0.982	0.996	1.000	1.000	0.002	0.488	0.982
FM	0.051	0.062	0.083	0.000	0.145	0.760	0.051	0.067	0.130	0.001	0.399	0.967
WL	0.051	0.060	0.077	0.000	0.141	0.752	0.051	0.069	0.139	0.001	0.395	0.966
AW	0.052	0.068	0.097	0.002	0.488	0.983	0.051	0.069	0.132	0.002	0.488	0.984

^aThe δ₁₂ comes from a mixture distribution. With probability 0.99, δ₁₂ =0. With probability 0.01, δ₁₂ has a normal distribution with mean 0 and variance (log(2)/2)².

^bBased on 10,000 independent simulations for each column of three estimates.

^cThere are n₁ cases and n₀ controls in the case-control study.

Discussion

In this paper we studied analyses of secondary dichotomous phenotypes for data from a case-control study of a primary disease that is not rare. We treated both dichotomous (dominant or recessive) and additive genetic models. Using external information on the probability of the primary disease in the population, we developed an adaptive procedure, AW, and compared it with the previously published FM, WL, RM and RMU methods to analyze secondary phenotypes. We found that when the primary disease is fairly common (10%), AW has good properties both for inference on a pre-specified SNP and for discovery of SNP associations in a GWAS. In particular, it is more powerful in a GWAS than its chief competitors, FM and WL, which perform similarly. AM performs well whether or not an interaction δ₁₂ between the secondary phenotype and the SNP genotype affects the risk of the primary disease. AW is also robust to misspecification of the probability of the primary disease in the general population, except when P(D=1) is large and |δ₁₂| is large. When the primary disease is common (30%), the performance of AW is similar to that of FM and WL, although AW still has a slight power advantage in GWAS. With a common primary disease, one may prefer to use WL, because it is easy to compute and has previously been used and studied. For dichotomous G, we showed theoretically that the weighted logistic methods proposed by Richardson et al. (2007) and Monsees et al. (2009) are equivalent to maximum likelihood, which we call FM, for a primary disease model in which there is no restriction on δ₁₂ but in which the probability of the primary disease is known. For the additive genetic model, WL yields numerical estimates close to but not identical to FM.

The maximum likelihood procedure that assumes δ₁₂ =0 and that requires external information on the probability of the primary disease, which we call RM, is the most efficient method when δ₁₂ =0, but it does not control size when δ₁₂ ≠ 0 and can be very misleading. A maximum likelihood procedure that assumes δ₁₂ =0 and that does not require external information on the probability of the primary disease (Lin and Zeng; 2009), which we call RMU, does not control size even when δ₁₂ =0 and should be avoided. The problem arises because under the null hypothesis β₁ = 0 and assuming δ₁₂ =0, other parameter estimates are biased and unstable, leading to incorrect estimates of the information matrix and underestimates of the standard error of β̂_1RMU. Lin and Zeng (2009) alluded to this instability, and their publically available software at http://www.bios.unc.edu/~lin/software/SPREG/ requires knowing P(D=1). Thus, for a dichotomous secondary phenotype, there seems to be no practical alternative to obtaining information on the probability of the primary disease and using it in procedures like AW, WL and FM. When there is substantial uncertainty concerning the probability of the primary disease, sensitivity analyses may be helpful. It is encouraging; however, that AW and FM are rather robust to misspecification of this probability for the dichotomous genetic model; and are robust to the moderate misspecification (10% relative error) of this probability for the additive genetic model.

If case-control data for a common primary disease arise in a nested case-control study within a cohort, the cohort information will provide a direct estimate of the probability of the primary disease. Our unreported simulations demonstrate that very similar inference for the secondary endpoint is obtained from AW and FM procedures whether one assumes that the probability of the primary disease is known or whether one instead inserts the estimate from the cohort data.

Wang and Shete (2011) used a series of estimating equations to solve for the parameters in the reduced model, which in our notation are θ = {β₀, β₁, δ₀, δ₁, δ₂, PG₀}. Their assumptions include: (1) δ₁₂ =0; and (2) both the probability of the primary disease, P(D=1), and the probability of the secondary phenotype, P(X=1), are known. More work is needed to determine how robust their procedures are to violations of these assumptions and to assess their efficiency compared to maximum likelihood procedures. However, it is likely that violation of the assumption δ₁₂ =0 can induce misleading results, as for the maximum likelihood procedures RM and RMU.

Several topics warrant additional research, including extensions of the models to allow for covariates and for continuous secondary phenotypes. If only a few covariates are needed, the methods of the present paper can be used within strata defined by the covariates.

Appendices

Derivation of β̂_1FM

Under equations (1) and (2), we need to estimate 7 parameters: θ_FM = {β₀, β₁, δ₀, δ₁, δ₂, δ₁₂, PG₀} by maximizing the likelihood (7). In the Appendices, we denote P(D = 1) ≡ ξ₁. In order to avoid complicated calculations, we take the logarithm of (7) and change the variables first. By letting

$$p_{\mathit{ijk}}=P(D=i,G=j,X=k)=\frac{\exp (i({\mathrm{\delta }}_0+{\mathrm{\delta }}_{1}j+{\mathrm{\delta }}_{2}k+{\mathrm{\delta }}_{12}\mathit{jk}))}{1+\exp ({\mathrm{\delta }}_0+{\mathrm{\delta }}_{1}j+{\mathrm{\delta }}_{2}k+{\mathrm{\delta }}_{12}\mathit{jk})}\frac{\exp (k({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}j))}{1+\exp ({\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}j)}P{G}_j;i,j,k=0,1,$$ (A1)

and with the constraints $\sum _{i,j,k=0}^1{p}_{\mathit{ijk}}=1$ and $\sum _{j,k=0}^1{p}_{1\mathit{jk}}={\mathrm{\xi }}_1$, we have the equivalent log-likelihood,

$$\begin{array}{c}{\stackrel{\sim }{l}}_{\mathit{FM}}=r_{000}\log (1-{\mathrm{\xi }}_1-p_{001}-p_{010}-p_{011})+r_{010}\log (p_{010})+r_{001}\log (p_{001})+r_{011}\log (p_{011})+\\ +r_{100}\log (p_{100})+r_{110}\log (p_{110})+r_{101}\log (p_{101})+r_{111}\log ({\mathrm{\xi }}_1-p_{100}-p_{110}-p_{101})\end{array}$$ (A2)

which has six parameters ϕ_FM = (p₀₁₀, p₀₀₁, p₀₁₁, p₁₀₀, p₁₁₀, p₁₀₁). Using the standard maximization technique, we have the following estimates: ${\widehat{p}}_{001}=\frac{(1-{\xi }_1)r_{001}}{n_0}$, ${\widehat{p}}_{010}=\frac{(1-{\xi }_1)r_{010}}{n_0}$, ${\widehat{p}}_{011}=\frac{(1-{\xi }_1)r_{011}}{n_0}$, ${\widehat{p}}_{100}=\frac{{\xi }_1{r}_{100}}{n_1}$, ${\widehat{p}}_{101}=\frac{{\xi }_1{r}_{101}}{n_1}$, and ${\widehat{p}}_{110}=\frac{{\xi }_1{r}_{110}}{n_1}$. Solving for the original parameters using (A1), we obtain

$$\begin{array}{l}{\widehat{\mathrm{\delta }}}_{0\mathit{FM}}=\log (\frac{{\widehat{p}}_{100}}{{\widehat{p}}_{000}})=\log (\frac{{\mathrm{\xi }}_1}{1-{\mathrm{\xi }}_1}\frac{r_{100}}{r_{000}}\frac{n_0}{n_1}),{\widehat{\mathrm{\delta }}}_{1\mathit{FM}}=\log (\frac{{\widehat{p}}_{110}}{{\widehat{p}}_{010}}\frac{{\widehat{p}}_{000}}{{\widehat{p}}_{100}})=\log (\frac{r_{110}}{r_{010}}\frac{r_{000}}{r_{100}}),\\ {\widehat{\mathrm{\delta }}}_{2\mathit{FM}}=\log (\frac{{\widehat{p}}_{101}}{{\widehat{p}}_{001}}\frac{{\widehat{p}}_{000}}{{\widehat{p}}_{100}})=\log (\frac{r_{101}}{r_{001}}\frac{r_{000}}{r_{100}}),{\widehat{\mathrm{\delta }}}_{12\mathit{FM}}=\log (\frac{{\widehat{p}}_{111}}{{\widehat{p}}_{011}}\frac{{\widehat{p}}_{010}}{{\widehat{p}}_{110}}\frac{{\widehat{p}}_{001}}{{\widehat{p}}_{101}}\frac{{\widehat{p}}_{100}}{{\widehat{p}}_{000}})=\log (\frac{r_{111}}{r_{011}}\frac{r_{010}}{r_{110}}\frac{r_{001}}{r_{101}}\frac{r_{100}}{r_{000}}),\\ P{\widehat{G}}_{0\mathit{FM}}=={\widehat{p}}_{100}+{\widehat{p}}_{101}+{\widehat{p}}_{000}+{\widehat{p}}_{001}=\frac{{\mathrm{\xi }}_1(r_{100}+r_{101})}{n_1}+\frac{{\mathrm{\xi }}_0(r_{000}+r_{001})}{n_0},\\ {\widehat{\mathrm{\beta }}}_{0\mathit{FM}}=\log (\frac{{\widehat{p}}_{101}+{\widehat{p}}_{001}}{{\widehat{p}}_{100}+{\widehat{p}}_{000}})=\log (\frac{{\mathrm{\xi }}_1{r}_{101}{n}_0+(1-{\mathrm{\xi }}_1)r_{001}{n}_1}{{\mathrm{\xi }}_1{r}_{100}{n}_0+{(1-{\mathrm{\xi }}_1)}_1{r}_{000}{n}_1}),\mathrm{and}\\ {\widehat{\mathrm{\beta }}}_{1\mathit{FM}}=\log (\frac{({\widehat{p}}_{111}+{\widehat{p}}_{011})({\widehat{p}}_{100}+{\widehat{p}}_{000})}{({\widehat{p}}_{110}+{\widehat{p}}_{010})({\widehat{p}}_{101}+{\widehat{p}}_{001})})=\log (\frac{{\mathrm{\xi }}_1{r}_{111}{n}_0+(1-{\mathrm{\xi }}_1)r_{011}{n}_1}{{\mathrm{\xi }}_1{r}_{110}{n}_0+{(1-{\mathrm{\xi }}_1)}_1{r}_{010}{n}_1}\frac{{\mathrm{\xi }}_1{r}_{100}{n}_0+{(1-{\mathrm{\xi }}_1)}_1{r}_{000}{n}_1}{{\mathrm{\xi }}_1{r}_{101}{n}_0+(1-{\mathrm{\xi }}_1)r_{001}{n}_1}),\end{array}$$

where ${\widehat{p}}_{111}={\mathrm{\xi }}_1-{\widehat{p}}_{100}-{\widehat{p}}_{110}-{\widehat{p}}_{101}=\frac{{\mathrm{\xi }}_1{r}_{111}}{n_1}·{\widehat{p}}_{000}=1-{\mathrm{\xi }}_1-{\widehat{p}}_{001}-{\widehat{p}}_{010}-{\widehat{p}}_{011}=\frac{(1-{\mathrm{\xi }}_1)r_{000}}{n_0}$

Proof of β̂_1FM = β̂_1W

With w_i = P(D = i)/n_i = ξ_i/n_i, ${\widehat{\mathrm{\beta }}}_{1W}=\log \left(\frac{w_0{r}_{011}+w_1{r}_{111}}{w_0{r}_{010}+w_1{r}_{110}}·\frac{w_0{r}_{000}+w_1{r}_{100}}{w_0{r}_{001}+w_1{r}_{101}}\right)={\widehat{\mathrm{\beta }}}_{1\mathit{FM}}$.

Derivation of β̂_1RM with known disease rate when δ₁₂ = 0

Assuming δ₁₂ = 0 we have the reduced disease model logit (P(D = 1 ∣ G, X)) = δ₀ + δ₁G + δ₂X. Including the parameters in equation (1), we need to estimate 6 parameters θ_RM = {β₀, β₁, δ₀, δ₁, δ₂, PG₀}. To do this we maximize the likelihood (6). As in (A1), we reparameterize first. By letting P_ijk = P (D = i, X = j, G = k); i,j,k = 0, 1 and incorporating the constraints $\sum _{i,j,k=0}^1{p}_{\mathit{ijk}}=1$ and $\sum _{j,k=0}^1{p}_{1\mathit{jk}}={\mathrm{\xi }}_1$, we obtain

$$\begin{array}{l}{\stackrel{\sim }{l}}_{\mathit{RM}}=r_{000}\log (1-{\mathrm{\xi }}_1-p_{001}-p_{010}-p_{011})+r_{010}\log (p_{010})+r_{001}\log (p_{001})+r_{011}\log (p_{011})+\\ +r_{100}\log (p_{100})+r_{110}\log (p_{110})+r_{101}\log (\frac{p_{001}{p}_{010}{p}_{100}({\mathrm{\xi }}_1-p_{100}-p_{110})}{p_{110}{p}_{011}(1-{\mathrm{\xi }}_1-p_{001}-p_{010}-p_{011})+p_{001}{p}_{010}{p}_{100}})\\ +r_{111}\log (\frac{p_{110}{p}_{011}(1-{\mathrm{\xi }}_1-p_{001}-p_{010}-p_{011})({\mathrm{\xi }}_1-p_{100}-p_{110})}{p_{110}{p}_{011}(1-{\mathrm{\xi }}_1-p_{001}-p_{010}-p_{011})+p_{001}{p}_{010}{p}_{100}})\end{array}$$ (A3)

which has only five parameters ϕ_RM = (p₀₁₀, p₀₀₁, p₀₁₁, p₁₀₀, p₁₁₀). Using the SAS procedure PROC NLPTR, we obtained the maximum likelihood estimators ϕ̂_RM Re-expressing our results in terms of the original parameters, we have ${\widehat{\mathrm{\delta }}}_{0\mathit{RM}}=\log (\frac{{\widehat{p}}_{100}}{{\widehat{p}}_{000}})$, ${\widehat{\mathrm{\delta }}}_{1\mathit{RM}}=\log (\frac{{\widehat{p}}_{110}}{{\widehat{p}}_{010}}\frac{{\widehat{p}}_{000}}{{\widehat{p}}_{100}})$,

$$\begin{array}{l}{\widehat{\mathrm{\delta }}}_{2\mathit{RM}}=\log (\frac{{\widehat{p}}_{101}}{{\widehat{p}}_{001}}\frac{{\widehat{p}}_{000}}{{\widehat{p}}_{100}}),P{\widehat{G}}_{0\mathit{RM}}={\widehat{p}}_{100}+{\widehat{p}}_{101}+{\widehat{p}}_{000}+{\widehat{p}}_{001},{\widehat{\mathrm{\beta }}}_{0\mathit{RM}}=\log (\frac{{\widehat{p}}_{101}+{\widehat{p}}_{001}}{{\widehat{p}}_{100}+{\widehat{p}}_{000}}),\\ {\widehat{\mathrm{\beta }}}_{1\mathit{RM}}=\log (\frac{({\widehat{p}}_{111}+{\widehat{p}}_{011})({\widehat{p}}_{100}+{\widehat{p}}_{000})}{({\widehat{p}}_{110}+{\widehat{p}}_{010})({\widehat{p}}_{101}+{\widehat{p}}_{001})}),\end{array}$$

where p̂₀₀₀ = 1 − ξ₁ − p̂₀₀₁ − p̂₀₁₀ − p̂₀₁₁, ${\widehat{p}}_{101}=\frac{{\widehat{p}}_{001}{\widehat{p}}_{010}{\widehat{p}}_{100}({\xi }_1-{\widehat{p}}_{100}-{\widehat{p}}_{110})}{{\widehat{p}}_{110}{\widehat{p}}_{011}(1-{\xi }_1-{\widehat{p}}_{001}-{\widehat{p}}_{010}-{\widehat{p}}_{011})+{\widehat{p}}_{001}{\widehat{p}}_{010}{\widehat{p}}_{100}}$, and ${\widehat{p}}_{111}=\frac{{\widehat{p}}_{110}{\widehat{p}}_{011}(1-{\xi }_1-{\widehat{p}}_{001}-{\widehat{p}}_{010}-{\widehat{p}}_{011})({\xi }_1-{\widehat{p}}_{100}-{\widehat{p}}_{110})}{{\widehat{p}}_{110}{\widehat{p}}_{011}(1-{\xi }_1-{\widehat{p}}_{001}-{\widehat{p}}_{010}-{\widehat{p}}_{011})+{\widehat{p}}_{001}{\widehat{p}}_{010}{\widehat{p}}_{100}}$.

Derivation of β̂_1RMU with unknown disease rate when δ₁₂ = 0

As in Lin and Zeng (2009), we can obtain the estimate of β₁ without knowing the disease rate. Using the general retrospective likelihood (6), we express the log likelihood with new set of parameters P_ijk = P (D = i, X = j, G = k); i,j,k = 0, 1 as follows:

$$\begin{array}{lll}{\stackrel{\sim }{l}}_{\mathit{RMU}}& =& r_{000}\log (p_{000})+r_{010}\log (p_{010})+r_{001}\log (p_{001})+r_{011}\log (p_{011})+r_{100}\log (p_{100})+r_{110}\log (p_{110})\\ & +& r_{101}\log (\frac{p_{001}{p}_{010}{p}_{100}({\xi }_1-p_{100}-p_{110})}{p_{110}{p}_{011}{p}_{000}+p_{001}{p}_{010}{p}_{100}})+r_{111}\log (\frac{p_{110}{p}_{011}{p}_{000}({\xi }_1-p_{100}-p_{110})}{p_{110}{p}_{011}{p}_{000}+p_{001}{p}_{010}{p}_{100}})\\ & -& n_0\log (p_{000}+p_{001}+p_{010}+p_{011})-n_1\log (1-p_{000}-p_{001}-p_{010}-p_{011})\end{array}$$

which has only six parameters ϕ_RMU = (p₀₀₀, p₀₁₀, p₀₀₁, p₀₁₁, p₁₀₀, p₁₁₀). Using the SAS procedure PROC NLPTR, we obtained the maximum likelihood estimators ϕ̂_RMU. In terms of the original parameters, we have

$$\begin{array}{l}{\widehat{\mathrm{\delta }}}_{0\mathit{RMU}}=\log (\frac{{\widehat{p}}_{100}}{{\widehat{p}}_{000}}),{\widehat{\mathrm{\delta }}}_{1\mathit{RMU}}=\log (\frac{{\widehat{p}}_{110}}{{\widehat{p}}_{010}}\frac{{\widehat{p}}_{000}}{{\widehat{p}}_{100}}),\\ {\widehat{\mathrm{\delta }}}_{2\mathit{RMU}}=\log (\frac{{\widehat{p}}_{101}}{{\widehat{p}}_{001}}\frac{{\widehat{p}}_{000}}{{\widehat{p}}_{100}}),P{\widehat{G}}_{0\mathit{RMU}}={\widehat{p}}_{100}+{\widehat{p}}_{101}+{\widehat{p}}_{000}+{\widehat{p}}_{001},{\widehat{\mathrm{\beta }}}_{0\mathit{RMU}}=\log (\frac{{\widehat{p}}_{101}+{\widehat{p}}_{001}}{{\widehat{p}}_{100}+{\widehat{p}}_{000}}),\mathrm{and}\\ {\widehat{\mathrm{\beta }}}_{1\mathit{RMU}}=\log (\frac{({\widehat{p}}_{111}+{\widehat{p}}_{011})({\widehat{p}}_{100}+{\widehat{p}}_{000})}{({\widehat{p}}_{110}+{\widehat{p}}_{010})({\widehat{p}}_{101}+{\widehat{p}}_{001})}),\end{array}$$

where ${\widehat{p}}_{101}=\frac{{\widehat{p}}_{001}{\widehat{p}}_{010}{\widehat{p}}_{100}({\xi }_1-{\widehat{p}}_{100}-{\widehat{p}}_{110})}{{\widehat{p}}_{110}{\widehat{p}}_{011}(1-{\xi }_1-{\widehat{p}}_{001}-{\widehat{p}}_{010}-{\widehat{p}}_{011})+{\widehat{p}}_{001}{\widehat{p}}_{010}{\widehat{p}}_{100}}$ and ${\widehat{p}}_{111}=\frac{{\widehat{p}}_{110}{\widehat{p}}_{011}(1-{\xi }_1-{\widehat{p}}_{001}-{\widehat{p}}_{010}-{\widehat{p}}_{011})({\xi }_1-{\widehat{p}}_{100}-{\widehat{p}}_{110})}{{\widehat{p}}_{110}{\widehat{p}}_{011}(1-{\xi }_1-{\widehat{p}}_{001}-{\widehat{p}}_{010}-{\widehat{p}}_{011})+{\widehat{p}}_{001}{\widehat{p}}_{010}{\widehat{p}}_{100}}$.

Variance estimator of β̂_1AW

Ignoring the variability of the variance estimator of ${\widehat{\mathrm{\beta }}}_{1\mathit{FM}}:{\widehat{\mathrm{\sigma }}}_{\mathit{FM}}^2$, we identify the adaptively weighted estimator as a function of (β̂_1FM, δ̂_12FM, β̂_1RM) and we have

$${\widehat{\mathrm{\beta }}}_{1\mathit{AW}}=g({\widehat{\mathrm{\beta }}}_{1\mathit{FM}},{\widehat{\mathrm{\delta }}}_{12\mathit{FM}},{\widehat{\mathrm{\beta }}}_{1\mathit{RM}})=\frac{{\widehat{\mathrm{\delta }}}_{12\mathit{FM}}^2}{{\widehat{\mathrm{\delta }}}_{12\mathit{FM}}^2+{\widehat{\sigma }}_{\mathit{FM}}^2}{\widehat{\mathrm{\beta }}}_{1\mathit{FM}}+\frac{{\widehat{\mathrm{\sigma }}}_{\mathit{FM}}^2}{{\widehat{\mathrm{\delta }}}_{12\mathit{FM}}^2+{\widehat{\mathrm{\sigma }}}_{\mathit{FM}}^2}{\widehat{\mathrm{\beta }}}_{1\mathit{RM}}.$$ (A4)

In order to derive the variance estimator of β̂_1AW, we first obtain the joint asymptotic distribution of the MLE estimators (β̂_1FM, δ̂_12FM, β̂_1RM). ϕ̂_FM and ϕ̂_RM are MLE estimates of (A2) and (A3) using the full disease model and the reduced disease model respectively. Let I_ϕFM (6 × 6) and I_ϕRM (5 × 5) denote the observed information matrices for likelihood with the full (A2) and reduced (A3) model respectively. Then, asymptotically,

$$\left(\begin{array}{l}{\widehat{\mathrm{\beta }}}_{1\mathit{FM}}-{\mathrm{\beta }}_{1F}\\ {\widehat{\mathrm{\delta }}}_{12\mathit{RM}}-{\mathrm{\delta }}_{12F}\\ {\widehat{\mathrm{\beta }}}_{1\mathit{RM}}-{\mathrm{\beta }}_{1R}\end{array}\right)=\left(\begin{array}{l}-{(\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{FM}}({\widehat{\mathrm{\varphi }}}_{\mathit{FM}}))}^T{I}_{\mathrm{\varphi }\mathit{FM}}^{-1}{U}_{\mathrm{\varphi }\mathit{FM}}+O_p(n^{-1/2})\\ -{(\nabla {\widehat{\mathrm{\delta }}}_{12\mathit{FM}}({\widehat{\mathrm{\varphi }}}_{\mathit{FM}}))}^T{I}_{\mathrm{\varphi }\mathit{FM}}^{-1}{U}_{\mathrm{\varphi }\mathit{FM}}+O_p(n^{-1/2})\\ -{(\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{RM}}({\widehat{\mathrm{\varphi }}}_{\mathit{RM}}))}^T{I}_{\mathrm{\varphi }\mathit{RM}}^{-1}{U}_{\mathrm{\varphi }\mathit{RM}}+O_p(n^{-1/2})\end{array}\right)$$

where U_ϕFM and U_ϕRM denote the score functions for ϕ_FM and ϕ_RM respectively and n denotes the total sample size. ∇β̂_1FM (ϕ̂_FM), ∇δ̂_12FM (ϕ̂_FM) and ∇β̂_1RM (ϕ̂_RM) are the gradient matrices of β̂_1FM, δ̂_12FM, and β̂_1RM with respect to ϕ_FM and ϕ_RM, evaluated at v ϕ̂_FM and ϕ̂_RM.

Then using the delta method, we have variance estimator of β̂_1AW given by

$${\widehat{\mathrm{\sigma }}}_{\mathit{AW}}^2={\{g^{\prime }({\widehat{\mathrm{\beta }}}_{1\mathit{FM}},{\widehat{\mathrm{\delta }}}_{12\mathit{FM}},{\widehat{\mathrm{\beta }}}_{1\mathit{RM}})\}}^T{\sum }_{\mathit{ML}}{g}^{\prime }({\widehat{\mathrm{\beta }}}_{1\mathit{FM}},{\widehat{\mathrm{\delta }}}_{12\mathit{FM}},{\widehat{\mathrm{\beta }}}_{1\mathit{RM}}),$$

where g′ is the gradient matrix of g (A4) with respect to (β̂_1FM, δ̂_12FM, β̂_1RM) and Σ_ML is the asymptotic variance-covariance matrix of (β̂_1FM, δ̂_12FM, β̂_1RM). We partition Σ_ML as

$${\sum }_{\mathit{ML}}=\left(\begin{array}{cc}{\sum }_{12•12}& {\sum }_{12•3}\\ {\sum }_{3•12}& {\sum }_{33}\end{array}\right)$$

where

$$\begin{array}{l}{\sum }_{12•12}={(\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{FM}}({\widehat{\mathrm{\varphi }}}_{\mathit{FM}}),\nabla {\widehat{\mathrm{\delta }}}_{12\mathit{FM}}({\widehat{\mathrm{\varphi }}}_{\mathit{FM}}))}^T{I}_{\mathrm{\varphi }\mathit{FM}}^{-1}(\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{FM}}({\widehat{\mathrm{\varphi }}}_{\mathit{FM}}),\nabla {\widehat{\mathrm{\delta }}}_{12\mathit{FM}}({\widehat{\mathrm{\varphi }}}_{\mathit{FM}})),\\ {\sum }_{33}={(\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{RM}}({\widehat{\mathrm{\varphi }}}_{\mathit{RM}}))}^T{I}_{\mathrm{\varphi }\mathit{RM}}^{-1}\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{RM}}({\widehat{\mathrm{\varphi }}}_{\mathit{RM}}),\\ \mathrm{and}{\sum }_{12•3}={\sum }_{3•12}=\left(\begin{array}{c}{(\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{FM}}({\widehat{\mathrm{\phi }}}_{\mathit{FM}}))}^T{I}_{\mathrm{\phi }\mathit{FM}}^{-1}\mathrm{E}(U_{\mathrm{\phi }\mathit{FM}}{U}_{\mathrm{\phi }\mathit{RM}}^T)I_{\mathrm{\phi }\mathit{RM}}^{-1}\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{RM}}({\widehat{\mathrm{\phi }}}_{\mathit{RM}})\\ {(\nabla {\widehat{\mathrm{\delta }}}_{12\mathit{FM}}({\widehat{\mathrm{\phi }}}_{\mathit{FM}}))}^T{I}_{\mathrm{\phi }\mathit{FM}}^{-1}\mathrm{E}(U_{\mathrm{\phi }\mathit{FM}}{U}_{\mathrm{\phi }\mathit{RM}}^T)I_{\mathrm{\phi }\mathit{RM}}^{-1}\nabla {\widehat{\mathrm{\beta }}}_{1\mathit{RM}}({\widehat{\mathrm{\phi }}}_{\mathit{RM}})\end{array}\right).\end{array}$$