A primer to frequent itemset mining for bioinformatics

Abstract

Over the past two decades, pattern mining techniques have become an integral part of many bioinformatics solutions. Frequent itemset mining is a popular group of pattern mining techniques designed to identify elements that frequently co-occur. An archetypical example is the identification of products that often end up together in the same shopping basket in supermarket transactions. A number of algorithms have been developed to address variations of this computationally non-trivial problem. Frequent itemset mining techniques are able to efficiently capture the characteristics of (complex) data and succinctly summarize it. Owing to these and other interesting properties, these techniques have proven their value in biological data analysis. Nevertheless, information about the bioinformatics applications of these techniques remains scattered. In this primer, we introduce frequent itemset mining and their derived association rules for life scientists. We give an overview of various algorithms, and illustrate how they can be used in several real-life bioinformatics application domains. We end with a discussion of the future potential and open challenges for frequent itemset mining in the life sciences.

INTRODUCTION

High-throughput molecular analysis techniques nowadays yield datasets with a size and complexity at which they are no longer directly interpretable by humans. In recent years, pattern mining methods have become indispensable for life scientists to narrow down the search for relevant new knowledge instead of getting lost in the wealth of information. The term ‘pattern mining' covers a wide variety of techniques that are all designed to transform complex datasets into something more manageable. In this introductory article, we focus on a group of techniques referred to as ‘frequent itemset mining'.

Frequent itemset mining methods were developed to identify elements that often co-occur in a dataset. The archetypical usage case is the market basket problem [1], in which frequent itemset mining techniques are applied to discover which items are often bought together by customers (referred to as ‘patterns'). An example of an interesting pattern could be that beer and chips frequently co-occur in the same supermarket basket (also termed a ‘transaction'). This type of information can be of great interest for shopkeepers. For example, they could decide to place these items further apart, so the customer will follow a longer route through the store. Additionally, the pattern mining results may reveal other items that may be of use for the target population, which could then be suggestively placed in between the two co-occurring items to increase overall sales. Despite the seeming simplicity of the problem, the number of possible frequent itemsets rapidly explodes with larger datasets, making a brute-force search intractable. Nevertheless, more efficient algorithms have been developed to tackle this computationally demanding problem.

The application of frequent itemset mining is not restricted to market basket analysis. These techniques have proven their value in a wide range of knowledge extraction problems. In bioinformatics, typical applications include the interpretation of gene expression data [2], annotations [3], protein interaction networks [4] and biomolecular localization prediction [5]. Frequent itemset mining is typically used in bioinformatics to identify biologically relevant patterns that can be interpreted in a biological context.

The algorithms that have been developed for market basket type problems can often be readily applied to bioinformatics problems, as long as the biological problem is properly translated into the transactional input that the algorithms can accept. Equivalent to finding items that are often purchased together, a biological question may be to identify frequently co-occurring protein domains in a set of proteins. In this example, each protein represents a single transaction, equivalent to the market basket, with the domains being the items, equivalent to the products. The same class of algorithms can be applied to both of these analogous problems. In other cases, the conversion of biological data can be more challenging, due to for example the complex structure of many biological datasets, their often stochastic nature, the presence of missing values and scaling issues.

Methods to extract relevant frequent itemsets from transactional data have been extensively studied, and many efficient algorithms are available. They offer several advantages over other pattern detection methods, including the computational efficiency of the search and the intuitive interpretability of the extracted patterns. Frequent itemsets can furthermore be converted into rules that can be used in various downstream applications. A key factor that often hampers their application in bioinformatics lies not in the extraction of patterns itself, but rather in how they are subsequently ranked and filtered. For example, the most commonly used algorithm (Apriori [6]) is notorious for the redundancy in the itemsets it generates, and the number of patterns it finds rapidly explodes unless parameters are stringently controlled. Various metrics that define the interestingness of a pattern (support, lift, maximal entropy, etc) for subsequent ranking and filtering of retrieved patterns have been studied at theoretical and experimental level. Nevertheless, biological questions often require the definition of special task-specific interestingness metrics, in which (biological) domain knowledge is formalized.

The goal of this primer is to first explain the central concepts of frequent itemset mining and association rule generation. We then introduce a number of representative and popular algorithms and software frameworks. To conclude, we give an overview of successful bioinformatics applications and highlight the future challenges and opportunities in the use of these techniques for biological data interpretation.

DEFINITIONS

Some key terms used in frequent itemset mining have already been mentioned in the introduction. In this section, we explain and formalize these expressions to introduce the basic concepts of frequent itemset mining. A more in-depth introduction can be found in [7] and [8].

Frequent itemsets

Let be the set of all possible items. A subset X = {i₁ , … , i_k} ⊆ is called an itemset, or a k-itemset if it contains k items.

A transaction over is a pair T = (tid, I), where tid is the transaction identifier and I is an itemset.

A set of transactions over 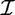can be termed as a transaction database 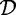over 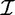. We omit 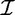whenever it is clear from the context.

The support of an itemset X is the number of transactions that contain the itemset X:

An itemset is called frequent if its support is no less than a given minimal support threshold σ, with 0 ≤ σ ≤ |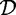|. The collection of frequent itemsets in 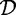with respect to σ is denoted by:

Frequent itemset mining is concerned with finding the set of itemsets 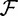. Note that items can be any kind of attribute–value pairs; thus, they can also represent the absence of an item i₂ in presence of another item i₁ (negative occurrences) [9].

Association rules

Additionally, we can perform association rule mining. An association rule is an expression of the form X ⇒ Y, where X and Y are itemsets, and X ∩ Y = Ø. Such a rule expresses the association that if a transaction contains all items in X, then that transaction also contains all items in Y. X is called the body or antecedent, and Y is called the head or consequent of the rule.

The support of an association rule X ⇒ Y, is the support of X ∪ Y:

The confidence of an association rule X ⇒ Y is the conditional probability of having Y contained in a transaction, given that X is contained in that transaction:

The rule is called confident if its confidence exceeds a given minimal confidence threshold γ, with 0 ≤ γ ≤ 1. The collection of frequent and confident association rules in 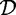with respect to σ and γ is denoted by:

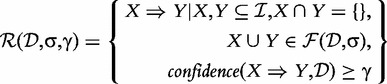Association rule mining is concerned with finding the set of association rules 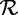. Note that itemset mining is actually a special case of association rule mining. Every frequent itemset represents the trivial rule X ⇒ {}, which has the same support as the support of X and holds with 100% confidence. Association rule mining is typically the step conducted after the actual itemset mining, as the rules can be derived from the itemsets.

This notion of association rules is very general, and much research has been invested into constraint-association rule mining, which can efficiently limit the search to rules that satisfy constraints, such as rules having a negative consequent [10].

Interestingness measures

Some examples of interestingness measures have already been introduced, in particular the support and confidence measures. Additionally, several other interestingness measures have been proposed [11], with some potentially being better suited to handle large biological databases (e.g. [12]). However, support and confidence remain the two most widely used constraints.

Support is an important measure because a rule that has low support may occur simply by chance. Confidence, on the other hand, measures the reliability of the inference made by a rule.

Other frequently used measures include lift and coverage. The lift of an association rule X ⇒ Y is the ratio of the observed support for this association rule, to the expected support if X and Y were independent:

The coverage of an association rule X ⇒ Y measures how often the rule is applicable in the transaction database:

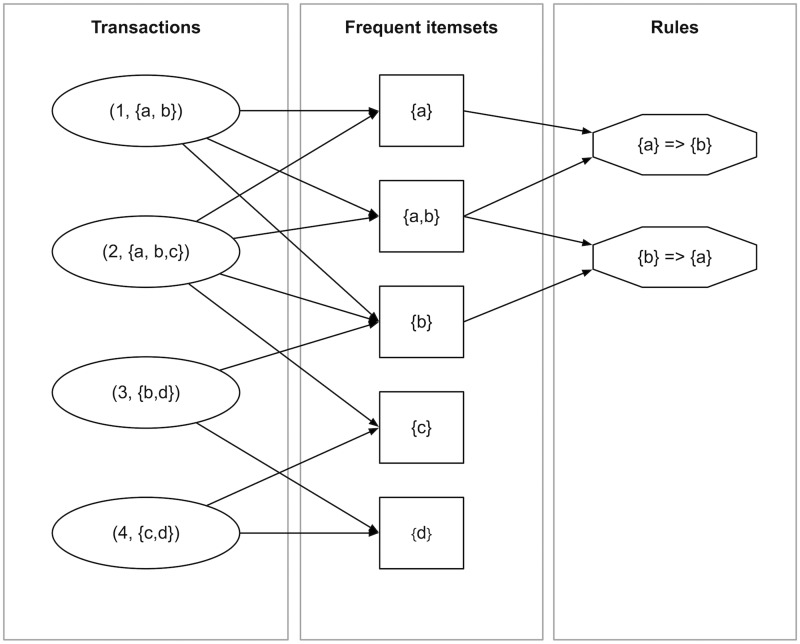
We can illustrate these definitions with a representative toy example. Figure 1 shows how association rules are generated out of transactions. The transactions are shown in circular boxes on the left. These transactions each support some (frequent) itemsets. The frequent itemsets with respect to a minimal support threshold of 2 are shown in squared boxes (itemsets with a lower support are omitted). Equivalently, association rules can be generated out of the frequent itemsets. The frequent and confident association rules with a support threshold of 2 and a confidence threshold of 50% are shown in octagonal boxes. Edges between the frequent itemsets and the association rules indicate which itemsets have been used to generate the association rules. Additionally, Table 1 presents an overview of interestingness measures for these association rules.

Figure 1:

Toy example to demonstrate how frequent itemsets and association rules can be derived from a series of transactions. Transactions are indicated by circular boxes, and are labeled as (tid, I), where tid is the transaction identifier and I = {i₁, … , i_k} is an itemset containing the items i₁ to i_k. Frequent itemsets are represented as a squared box, and association rules are shown as an octagonal box.

Table 1:

Measures related to the itemsets and association rules presented in Figure 1

Rule	Support	Confidence	Lift	Coverage
{a} ⇒ {b}	2	100%	33%	2
{b} ⇒ {a}	2	66%	33%	3

ALGORITHMS AND IMPLEMENTATIONS

Problem statement

A brute-force approach for association rule mining is to compute the support and confidence for every possible rule. This method is prohibitively expensive because the search space is exponential to the number of items occurring in the database. More specifically, for a set of items 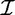, 2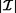 itemsets and 3 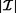association rules can be generated [6]. Therefore, a common strategy is to divide the problem into two subtasks. First, all frequent itemsets are generated, after which all frequent and confident association rules are generated. Figure 1 illustrates these two subtasks intuitively. In the next section, we further elaborate on the algorithmic approaches to tackle both subtasks.

Algorithms for itemset and association rule mining

In the first subtask, all frequent itemsets are generated. Most algorithms for general itemset mining can be characterized based on two properties: their traversal of the search space, and their computation of support. In general, all itemset mining algorithms repeatedly generate relatively small collections of candidate frequent itemsets, count their supports and remove all itemsets that turn out to be infrequent. The most important property, also called the Apriori Property, is that all supersets of an infrequent itemset must also be infrequent. Hence, many itemsets can be pruned from the search space when one of their subsets is known to be infrequent.

Essentially, the search space traversal will be either a depth-first traversal of all candidate itemsets or a breadth-first traversal. In a breadth-first traversal, all itemsets of size k are iteratively generated, starting with k = 1. In a depth-first traversal, a recursive divide and conquer principle is followed. More specifically, for a selected item i, first, all frequent itemsets containing i are generated, after which all frequent itemsets not containing i are generated.

The chosen traversal strategy is typically closely connected to the size of the database and the computation of the support of all candidate itemsets. If the data do not fit in main (fast) memory, the supports are counted by considering all transactions one by one, testing for every candidate itemset whether it is contained in that transaction. Here, a breadth-first approach is typically used, such as in the standard Apriori [6] algorithm. However, many optimizations already exist for this algorithm, partitioning or sampling the data in such a way that they do fit in memory. In that case, a depth-first search is typically used. The support of an itemset is then computed by simply storing for each item the ids of transactions it is contained in, counting the size of the intersection of these sets for each item in the itemset. For example, this strategy is used in Eclat [13].

Again, a plethora of optimizations and variations exist, of which frequent pattern (FP)-growth [14] is one of the most common. It combines a depth-first search with a compressed memory-resident database.

After the generation of all frequent itemsets, the second subtask consists of the computation of all frequent and confident association rules. Essentially, each frequent itemset is divided into two parts, an antecedent and a consequent, for every possible combination, and the corresponding confidences are then computed.

Software for frequent itemset mining

A detailed discussion of each itemset mining algorithm is beyond the scope of this review. However, Table 2 presents, summarizes and compares some important characteristics of commonly used methods and provides a reference to software implementations when available.

Table 2:

Overview of popular frequent itemset mining algorithms and implementations

Algorithm	Itemsets, subgraphs or rules	Context	License	Publication	Additional information or implementations
Anets	All (apriori), various threshold measures	Annotation mining	GNU GPL	16	http://sourceforge.net/projects/anets
AGM	All (apriori)	Subgraph mining	/	57	/
Apriori (Borgelt)	All	/	GNU GPL	6, 94	http://www.borgelt.net/apriori.html
Apriori (Goethals)	All	/	Research only	6	http://adrem.ua.ac.be/∼goethals/software/
ARIA	All (apriori), various verifications	Annotation mining	/	15	http://pedant.gsf.de/ARIA/index.htm
Carpenter	Closed	Quantitative omics profiles	GNU GPL	29	http://www.borgelt.net/carpenter.html
CBA	All (apriori)	Classifiers	/	67	/
CMAR	All (FP-growth)	Classifiers	/	68	/
Cobbler	Closed	Quantitative omics profiles	/	40	/
CODENSE	Coherent dense subgraphs	Subgraph mining	Research only	62	http://zhoulab.usc.edu/CODENSE/
COLL	All (apriori), chi-squared threshold pruning	Annotation mining	Open source	3	http://datadryad.org/resource/doi:10.5061/dryad.nr353
COPS	All (FP-tree), score threshold	Biclustering	Contact authors	18	http://www.cos.uni-heidelberg.de/index.php/n.ha
CPAR	All	Classifiers	/	69	/
CPMine	All (eclat), machine learning	Structural patterns	/	22	/
DeBi	Maximal	Biclustering	Creative Commons 2.0	29	http://www.molgen.mpg.de/∼serin/debi/main.html
Distiller	Closed	Quantitative omics profiles	Academic use only	49	http://homes.esat.kuleuven.be/∼kmarchal/Supplementary_Information_Lemmens_2008/startPage.html
Eclat (Borgelt)	All	/	GNU GPL	13, 94	http://www.borgelt.net/eclat.html
FESP	Emerging patterns	Classifiers	/	92, 93	/
Farmer	Closed	Quantitative omics profiles	Research only	41	http://www.sgi.com/tech/mlc/
FSG	/	Subgraph mining	/	58	/
FPGrowth	All	/	GNU GPL	14	/
GenMax	Maximal	Quantitative omics profiles	Research only	36	http://www.cs.rpi.edu/∼zaki/www-new/pmwiki.php/ Software/Software
GenMiner	Closed	Quantitative omics profiles	Research only	46	http://keia.i3s.unice.fr/?Logiciels_et_Implémentations___GenMiner
gSpan	All	Subgraph mining	Internal research only	59	http://www.cs.ucsb.edu/∼xyan/software/gSpan.htm
KRIMP	Minimal descriptive length	Future work		83	http://adrem.ua.ac.be/∼jvreeken/prj/krimp/
MAFIA	Maximal	/	Contact authors	95	http://sourceforge.net/projects/himalaya-tools/files/
MAGO	Multilevel association rules	Quantitative omics profiles	/	47	/
MaxConf	Closed	Quantitative omics profiles	Research only	96	https://bitbucket.org/tara/fpm/src/5813e782542b?at=default
MaxMiner	Maximal	Quantitative omics profiles	/	35	/
Min-Ex	δ-free itemsets	Quantitative omics profiles	/	32	/
MULE	Maximal frequent connected subgraph	Subgraph mining	Research only	4	http://compbio.case.edu/koyuturk/software/mule/
NetCAR	Maximal frequent connected subgraph	Classifiers	Research only	77	http://bioinformatics.oxfordjournals.org/content/24/13/1523.long
PathFinder	Large	Subgraph mining	/	64	/
REMMAR	Shortest distance thresholding	Quantitative omics profiles	Research only	48	http://websystem.csie.ncku.edu.tw/REMMAR_Program.rar
TD-Close	Closed	Quantitative omics profiles	/	42	/
TopKRGs	Top-k	Quantitative omics profiles	/	43	/

Several implementations presented in Table 2 can be run as stand-alone software. Additionally, data mining frameworks that allow frequent itemset mining exist for practical use, often with a graphical user interface and interactivity features. Table 3 shows a number of popular software frameworks, including their license and their corresponding references (when available).

Table 3:

Overview of software frameworks for frequent itemset mining

Application name	Description	License	Publication	Available from
Arules	FIM toolbox in R	GNU GPL-2	84	http://cran.r-project.org/web/packages/arules/index.html
ARtool	FIM toolbox for binary databases	GNU GPL	97	http://www.cs.umb.edu/∼laur/ARtool/
KNIME Desktop	Data analytics platform	GNU GPL	98	http://www.knime.org/
MIME	Interactive FIM toolbox	Research only	99	http://adrem.ua.ac.be/mime
Orange	Data analytics platform	GNU GPL-3	100	http://orange.biolab.si/
PyFIM	Python library	GNU LPL	94	http://www.borgelt.net/pyfim.html
Rapidminer	Data analytics platform	AGPL-3	101	http://rapid-i.com/
SPMF	FIM toolbox	GNU GPL-3	/	http://www.philippe-fournier-viger.com/spmf/index.php
Weka	Machine learning library	GNU GPL	102	http://www.cs.waikato.ac.nz/ml/weka/

BIOINFORMATICS APPLICATIONS

Frequent itemset mining can be used to tackle a broad range of bioinformatics problems. For the purpose of providing a representative overview of potential applications, we discuss six bioinformatics subdomains in which these techniques have been successfully used.

Frequent annotation mining

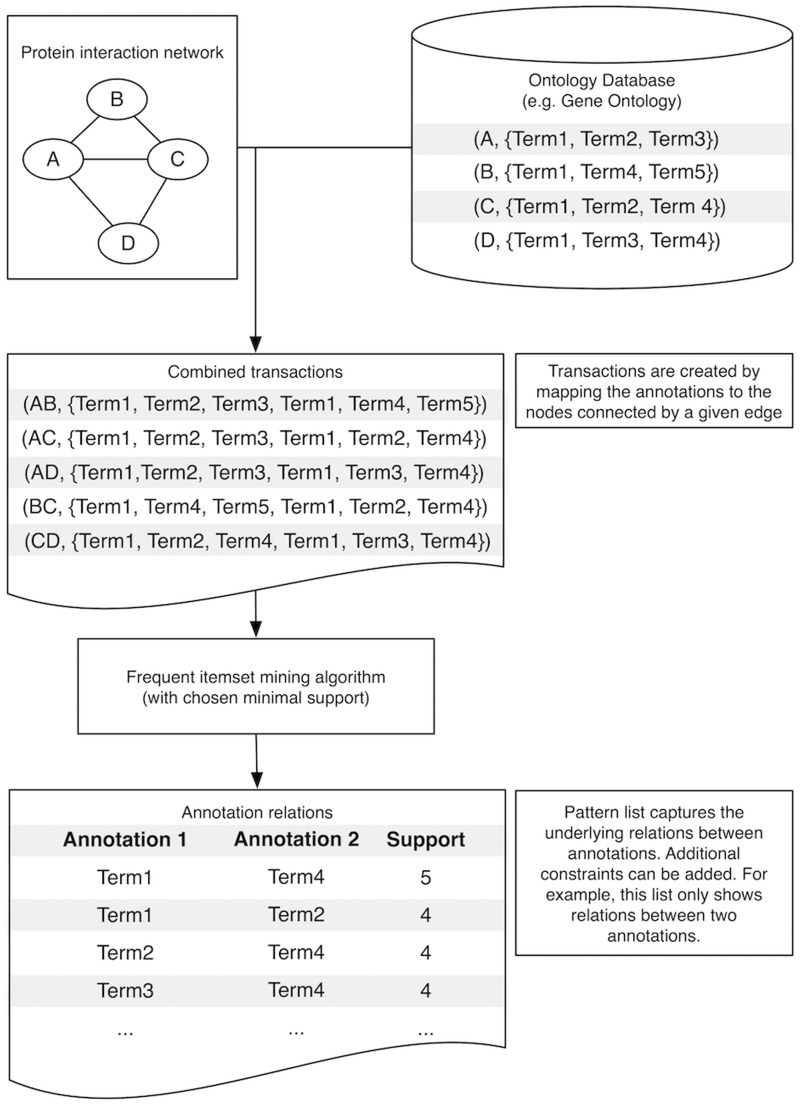
Annotations of a molecular entity (such as a gene) describe certain properties (e.g. function or localization) by means of terms of a controlled vocabulary. They are crucial in many bioinformatics workflows. A useful application of frequent itemset mining is the prediction of novel annotations. Patterns of frequently co-occurring annotations derived with frequent itemset mining techniques can play an essential role in that task. Co-occurrence of annotations can be defined strictly, with each biomolecule corresponding to a transaction and each annotation term as an item. However, it can also be defined in terms of neighborhood, e.g. by considering which annotations frequently co-occur over pairs of biomolecules that undergo a physicochemical interaction (e.g. protein interactions). Figure 2 shows such an example of how frequent itemset mining can be used to extract co-occurring annotations from a network of annotated and interacting biomolecules. Derived associations could then be used to improve the unsupervised annotation of biomolecules [15].

Figure 2:

Mining for frequent co-occurrences in annotations. Annotations can be mapped to biological entities, such as interactions between biological molecules. As such, each transaction is composed of the transaction identifier (represents the interaction between both partners) and the items (the annotations corresponding to each of the biomolecules). Frequent itemset miners can then be used to uncover patterns of often co-occurring annotations and several interestingness measures can be computed (e.g. support). This information can then be interpreted by the researcher or used to create weighted protein networks [16].

Frequent itemset mining can also be used to identify relationships between various existing ontologies. For example, cross-ontology association rule mining can connect the biological process, cellular compartment and protein function subtrees within the Gene Ontology [3].

There are, however, some specific challenges in frequent annotation mining. Annotations will only frequently co-occur if the items are frequent, regardless of the hierarchical structure of the ontology. Inconsistencies in the level of specificity of the annotations of individual biomolecules can result in an apparently lower frequency in individual annotation terms, potentially leaving interesting patterns undetected. A solution for this problem is the explicit integration of the annotation structure into association networks [16].

Structural motif discovery

Structural patterns or motifs are frequently occurring combinations of structural properties in biomolecules (such as molecular sequences). Although these features are omnipresent and extremely diverse, the underlying conservation typically points to a functionally important role. As a consequence, motif discovery is an important and widely explored topic in bioinformatics. When structural features are transformed into transactions, frequent itemset mining can be used to discover combinations of structural features that occur more frequently than expected. Examples of frequent itemset mining-based motif discovery include transcription factor binding motifs [17, 18], splicing patterns [19], combinatorial patterns involved in histone modification [20] and even spatial motifs [21, 22]. Additional constraints can be used to mine for specific patterns, such as the spacing between the motifs in a sequence [23], the spatial proximity of amino acids in a 3D structure [24] and peptide binding to the major histocompatibility complex [25].

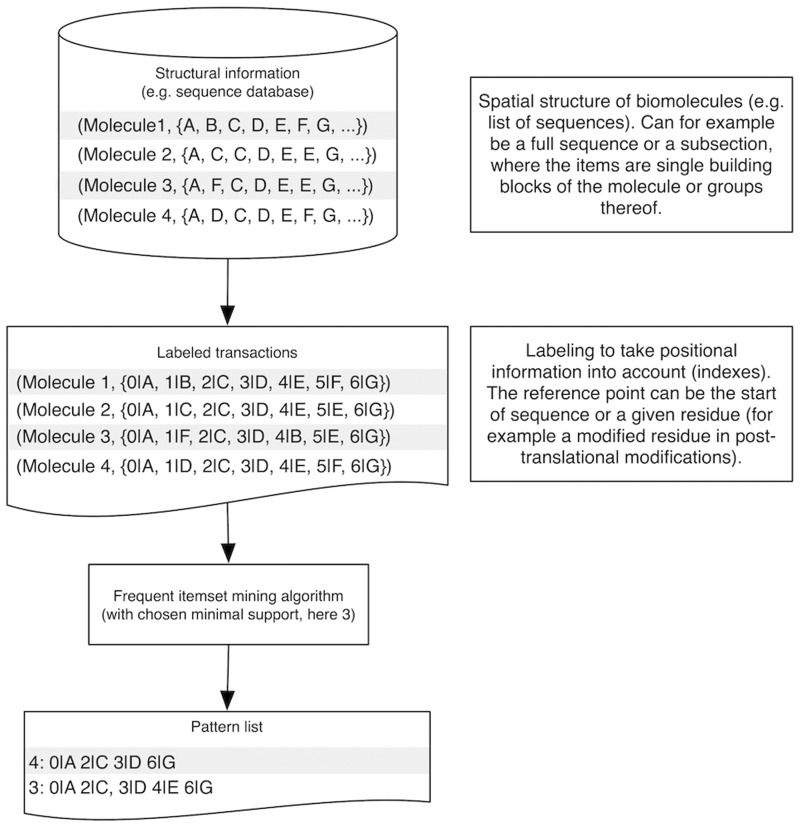
A simplified example of structural mining is the discovery of motifs in sequences surrounding a specific site, e.g. for a class of known post-translational modifications, as demonstrated in Figure 3. Biological sequences with the site of interest can be retrieved from public repositories and aligned with the common site as the central anchor point. All surrounding residues can then be given indexes to capture positional information relative to the site of interest. Each of these short sequence stretches can be considered as a transaction and the whole as a transaction database that can be mined for patterns. The resulting patterns indicate a degree of conservation and may be used to discriminate between classes.

Figure 3:

Visualization of structural pattern mining. Here the biological sequence of a domain on a biomolecule is processed with frequent itemset mining algorithms to identify conserved motifs. These motifs incorporate the underlying dependencies between the items in the form of the support value or other quality measures.

Frequent itemset mining has also been applied to aid in the alignment of 3D structures. For example, the Sequence Order Independent aLignment (SOIL) algorithm [26] uses frequent itemset mining to find subsets of amino acids that often spatially co-occur. Using frequent itemset mining in this case speeds up the protein structure alignment. This top-K itemset-based approach was competitive with other alignment methods and allowed for a more restrictive similarity measurement.

Pattern detection in quantitative ‘omics' profiles

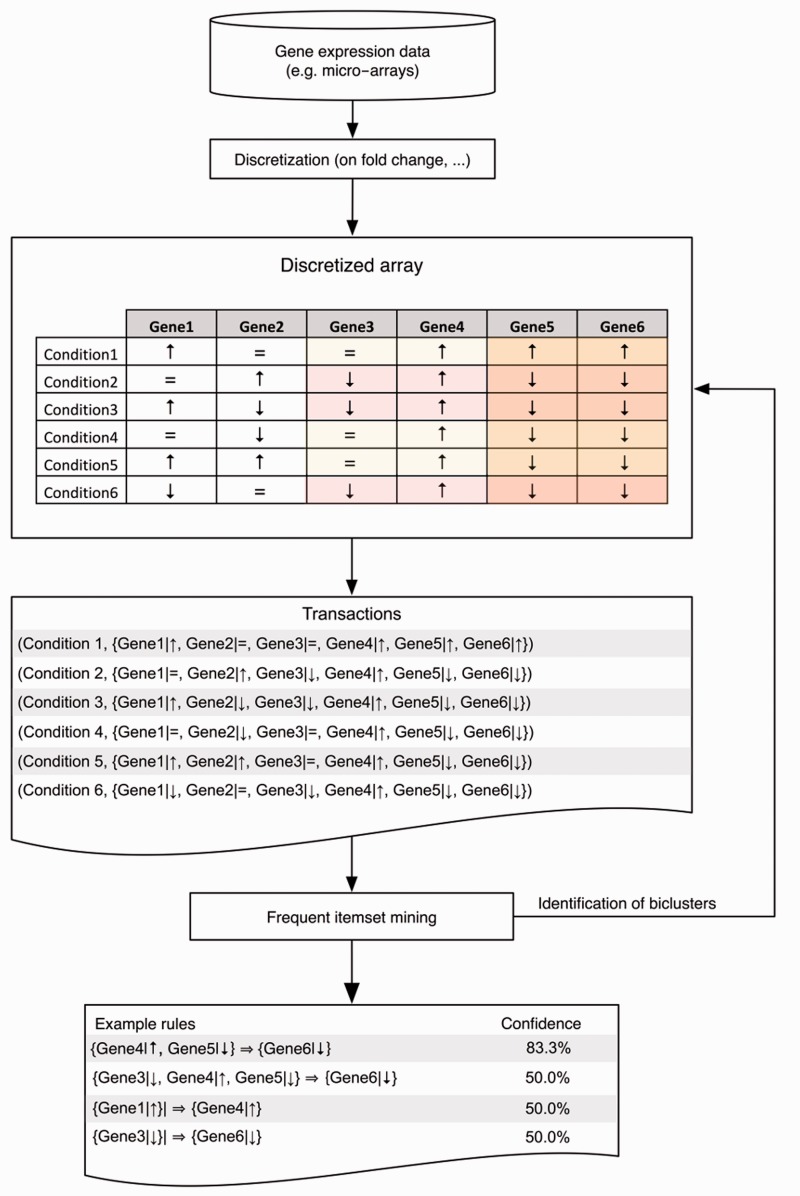
Association rule mining has been extensively used for the analysis of quantitative molecular profiles. A popular application is biclustering, which is the discovery of sets of submatrices within a larger matrix. The stereotypical use case of biclustering in bioinformatics is the analysis of co-expressed genes (with measured expression values) from a dataset under a (sub)set of conditions. High-throughput techniques for genome-wide expression profiling have resulted in the availability of many gene expression matrices [27]. However, the analysis thereof is confounded by the size of the data. Studying gene co-expression often requires a condition selection strategy, as even genes under influence of a common regulator are not necessarily co-regulated under all conditions. The dimensionality of this problem rapidly limits the applicability of standard clustering approaches. An elegant solution is frequent itemset mining. The problem is then translated into the discovery of associations between the expression values of genes and (optionally) additional data sources [28]. While biclustering is not exclusively a frequent itemset mining problem, frequent itemset mining-based algorithms have been shown to perform equally or superior to various other methods [29]. For example, they have proven their value in the elucidation of disease mode-of-actions such as for HIV-1 [30] and exploration of protein complexes in cell lysates with blue native gel electrophoresis [31]. Before frequent itemset mining-based biclustering, continuous values are typically discretized [28], e.g. to a binary (up and down) or ternary (up, down and unchanged) format. Frequent itemset mining is applied to this converted dataset, so that each condition can be considered as a transaction containing all measured genes and their regulation direction. The problem is thus reduced to finding frequently occurring sets of genes with a specific regulation pattern [28]. A toy example is shown in Figure 4.

Figure 4:

From expression matrix to bicluster. Gene expression data are converted into a matrix and discretized into a regulation category. In this figure, there are three groups: up, down or unchanged. This matrix can then be formatted into a suitable format for frequent itemset miners (transactional layout) to generate biclusters or rules.

For more than a decade, association rule mining has been used to identify relationships in gene expression data [32, 33]. However, algorithms such as Apriori [6] have limitations: they tend to detect a large number of redundant patterns and suffer from poor scaling. These limitations have been partially addressed using post-processing methods [34] or by the introduction of modified algorithms. For example, the redundancy in itemsets can be decreased by ignoring irrelevant rules [34] or by limiting the search space to certain itemset classes, such as maximal itemsets [35, 36] or the highest scoring itemsets (top-K) [37]. Furthermore, the need for a discretization step can be circumvented, e.g. by using quantitative association rules based on half-spaces [38]. In addition, various row-enumeration strategies were found to be highly successful to find correlations in micro-array data [39–43]. Each of these methods has its advantages and issues, but makes distinct assumptions at the start. For example, some methods search for closed itemsets [39, 40], whereas others only consider the top-K results [43]. The itemset type also affects the analysis of the significance of the discovered patterns. For example, maximal itemset mining leads to a drastically reduced number of patterns but also results in the loss of information on the relative importance of the itemset subsets in relation to the dataset. As such, the support of the maximal itemset can be very close to the minimal threshold, while the relations between various items in this itemset are frequent. When in doubt, less restrictive methods such as closed itemset mining should also be explored.

The need to reduce the (often large) number of patterns to those that actually matter has led to a new generation of techniques that focus on biological importance, instead of pure database characteristics. Several methods take an integrative approach, in which correlations between co-regulated genes and external sources of information are considered. Most common are the incorporation of gene or pathway annotations [44, 45], regulatory network evidence, expression data or combinations thereof [2, 46–49]. However, defining the biological interestingness is still not trivial, and various derived measures have been proposed [50].

Frequent itemset-based exploration of single-nucleotide polymorphisms

Frequent itemset mining has also been used to identify strong associations between allelic combinations associated with diseases. An FP-based method was found to be suitable for the detection of strong interactive effects [51]. More recently, a scalable Apriori-based approach to identify discriminative patterns between high-order single-nucleotide polymorphisms (SNPs) and disease phenotypes was proposed [52]. Another method based on Apriori separates the search within the set attributes from the search between the set attributes, resulting in rules that were shown to be consistent with literature [53].

Millions of SNPs exist, with many of these showing correlated genotypes. This has led to the search for so-called tag SNPs that are subsets sufficient to infer the other SNPs from. Common methods suffer from various problems with larger chromosomes, thus becoming very memory-intensive and time-consuming [54]. FastTagger [54] incorporated frequent itemset mining to overcome several of these problems.

Subgraph mining in molecular networks

Network analysis is highly relevant for biological research. By understanding the functional interactions between processes and molecules ongoing in living organisms, a much deeper understanding of the organismal response can be obtained. It is nowadays a popular task in systems biology to identify biologically relevant subgraphs in these networks, e.g. to reveal underlying regulatory principles.

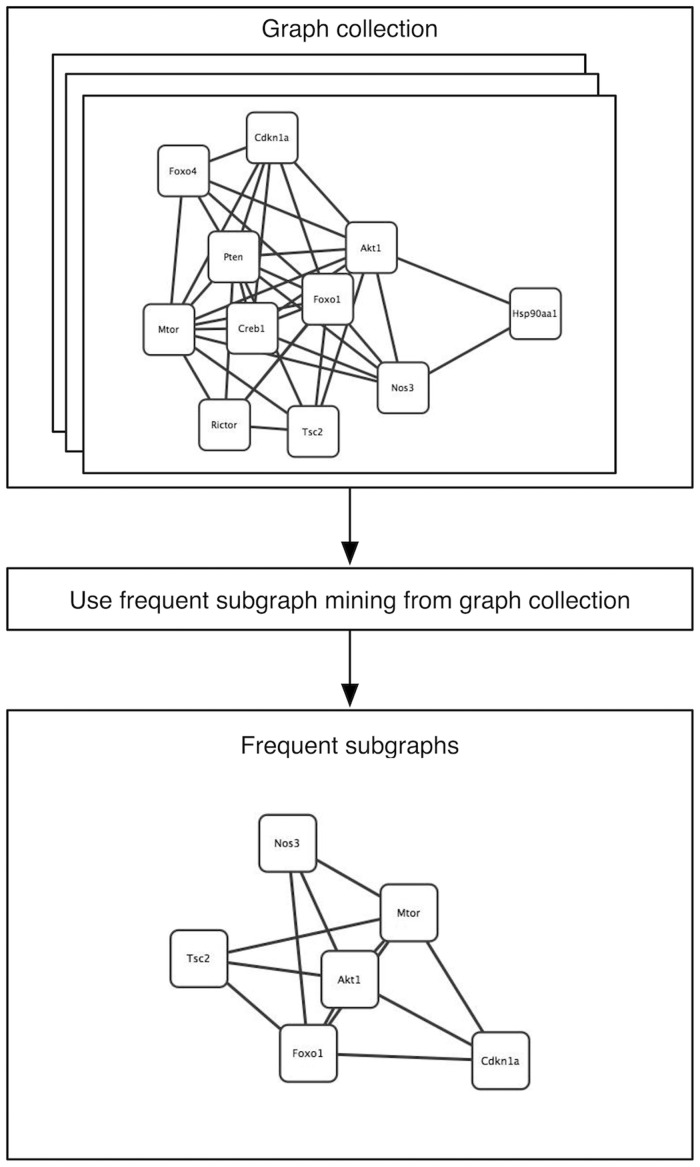
Finding structures in networks has been a long-standing question in data mining and has inspired the creation of several subgraph mining algorithms, some of which are based on frequent itemset mining. A major distinction between different approaches can be made according to whether subgraphs are searched in a single graph or in multiple graphs (Figure 5). Although algorithms to query a single biological network for its frequent subgraphs exist [55, 56], the most common and straightforward applications deal with multiple graphs. Traditional methods started as Apriori-based frequent substructure miners [57, 58]. These methods search for frequent subgraphs across multiple graphs instead in a way equivalent to searching frequent itemsets in a dataset of transactions. Although the core algorithm remains the same, the interestingness measures need to be retooled to the graph field. For example, support can be redefined as the number of graphs in the dataset containing a given subgraph. Non-Apriori-derived methods are often based on pattern growth. They iteratively attempt to add edges in every direction to frequent subgraphs, simulating a ‘grow out’ process [59–61].

Figure 5:

Gene interaction networks in mouse, human and rat as derived from String [12]. Frequent edges among these interaction networks can be extracted and presented as a frequent subgraph. Conserved subgraphs can have universal functional importance within the studied species.

The aforementioned methods are all capable of identifying substructures in a dataset, but biological networks pose additional challenges for conventional network mining approaches. Memory limitations are for example a typical issue [4]. The massive size of biological networks requires the use of heuristics to reduce the possible pattern space without information loss. Common approaches include the collapse of the different graphs to be analyzed into one or more summary graphs [62], which can then be mined for coherent dense subgraphs. Another approach is the reduction of each graph individually by collapsing nodes with identical labels into a single node [4]. Both methods can reduce noise and increase functional coherence of the patterns. To further reduce false patterns due to noise, weights can be added to the edges based on the reliability of the relation (e.g. based on experimental reproducibility) [63], or complementary types of experimental evidence (e.g. expression profiles, subcellular localization and sequence information) can be integrated [64].

Molecular interactions can also be represented as a transactional database for use with regular frequent itemset mining tools, where each edge is considered a transaction. For example, a protein-protein interaction (PPI) network can be converted into a set of transactions to detect rules that provide novel insights into the functional annotation of the network [65]. In a related analysis [66], additional features (e.g. subcellular localization information, motifs, various annotation types) were added to the items present in the transactions before rule mining.

Frequent itemsets for classification

Patterns and, in particular, association rules can be used as a foundation to construct a classifier. Several popular implementations exist [67–69]. They all rely on the philosophy that if attributes frequently appear together, there must be an underlying relation between them and this relation can be used for classification.

Machine learning techniques such as support vector machines (SVM) [70] largely function as a black box. The underlying models are often not interpretable in regard to the predictions they make. Association rule-based classifiers overcome this problem. They are more transparent about the reasoning behind their predictions, as they provide knowledge-based explanative rules and thus serve as a ‘white-box’ model [71]. Association rule-based classifiers have achieved accuracies equivalent to traditional SVM methods for common biological problems [71]. This transparency has enabled a range of studies that used frequent itemset mining to generate rules for classification [72–74].

Generating rules for classification is not a trivial task. Normally, a transactional database layout is used for mining and rules for classification are of the form X ⇒ C_i, with X being an itemset of observables and C_i being the class label. Thus, the data need to be transformed, so that each item represents a pair of attribute and value, together with a class label (e.g. P53, downregulated ⇒ cancer). A common example is the classification of sample types (e.g. tumor and healthy) with gene expression data [37, 72, 73]. For this purpose, expression values are discretized, and association rules are generated from maximal itemsets [72]. Furthermore, any other discrete or discretizable feature can be used, from cell properties [74] to protein–protein interactions [75]. Typically, only the rules that exceed a defined minimal support and confidence will be used for classification.

The combination of association rule mining with other classification methods, such as SVMs, can significantly increase their accuracy [76]. Association rule-based methods are also still being improved, e.g. by incorporation of a phylogenetic co-occurrence graph [77] or by speeding up rule detection with an ANT-based optimization [78].

FUTURE DIRECTIONS

Frequent itemset mining techniques can be powerful and elegant tools to extract meaningful patterns from biological data. Nevertheless, we would like to highlight some remaining challenges. Addressing these challenges would benefit further adoption of frequent itemset mining approaches by the bioinformatics community.

First, the definition of interestingness is very dependent on the biological problem at hand, and there are no simple guidelines to develop an appropriate interestingness metric for a new problem. Existing measures such as support, lift, coverage, occupancy [79] and entropy [80] give information about the dataset, but are not guaranteed to identify biologically relevant patterns. Another measure is the minimum improvement constraint [81], which only retains associations that have stronger correlations than their generalizations. This method rejects many unproductive and redundant rules [82]. In addition, support-based measures prioritize patterns that occur more often, but these patterns can be biologically trivial. For example, the detection of a frequent co-occurrence of the ATP-binding domain and a kinase domain while mining kinase structures offers little novel insight, whereas more interesting co-occurring domains will receive a much lower score. There is a clear need for measures that quantify biological interestingness.

A second challenge lies in the definition of a threshold that patterns need to exceed before they are considered frequent. If set too low, the number of patterns explodes, making proper interpretation impossible. If the threshold is too high, interesting less-frequent patterns might be missed. Methods such as Top-K mining avoid the problem of defining the lower threshold entirely [82].

A third problem is related to the heuristics used by the algorithms. Calculating all possible itemsets or association rules is not computationally efficient for large datasets and rarely useful for life sciences. Furthermore, generating all possible patterns often results in lists mostly comprising redundant patterns. Various heuristics have been proposed to more efficiently traverse the solution space and better capture the characteristics of the dataset in the shape of informative patterns. For example, Krimp [83] tries to find the best compression for a dataset and top-K mining identifies the top K scoring itemsets. Nevertheless, these theoretically elegant heuristics do not necessarily reflect biological foundations.

Another aspect that is relevant for the bioinformatics community, but has not yet been fully explored, is the visualization of patterns. In general, table-based, matrix-based and graph-based visualization methods exist. Commonly known examples are arulesviz [84], FPViz [85] and WiFIsViz [86], which are all available as R packages. Although these visualizations allow deeper understanding of the data, there is room for future work.

Last but not least, pattern mining and association rule discovery is vulnerable to false discoveries, as it searches the entire sample space for frequent co-occurrences. Owing to the massive scale, it is prone to find relations that are true in the sample set, but do not necessarily hold any relation to the actual underlying process in the dataset and may identify uninteresting rules, with many type I errors [82]. Several solutions to these problems have been proposed, of which the most popular can be attributed to two families: family-wise error rate, such as the Bonferroni correction, and false discovery rate [87]. Owing to the difficulties inherent to family-wise error rate, control of the false discovery rate has become increasingly popular. Some examples of false discovery rate methods are the Benjamini–Liu [88] and Benjamini–Hochberg [89] procedures. Various permutation-based and holdout approaches also exist [90]. Shrinkage estimates and Bayesian smoothing have also been proposed to limit overestimation of measures, such as support, and to reduce type I errors [82].

Key Points.

• Frequent itemset mining (and derived association rule mining) is a group of pattern mining techniques designed to identify elements that frequently co-occur, like sets of products that often end up together in the supermarket basket.

• Owing to the straightforward interpretability of the resulting patterns, frequent itemset mining techniques are powerful tools to extract relevant knowledge from complex biological data.

• The flexibility of frequent itemset mining techniques is demonstrated by the diverse range of bioinformatics problems they have been applied to, including annotation mining, structural motif discovery, subgraph detection, SNP analysis and biclustering of expression profiles. Furthermore, they can be used as input to construct classifiers.

FUNDING

This work was supported by the Research Foundation-Flanders (FWO) [grant number: G.0903.13N]; the agency for Innovation by Science and Technology (IWT) [grant number 120025]; and the University of Antwerp [BOF docpro to S.N.; BOF ID to T.N.V.].

Biographies

Stefan Naulaerts is a PhD student in bioinformatics at the University of Antwerp. He works on the integration and mining of ‘omics’ data, often using frequent itemset mining.

Pieter Meysman is a post-doctoral researcher in bioinformatics at the University of Antwerp. His research focuses on the application of data mining algorithms for pattern discovery in transcriptomics and evolutionary genomics.

Wout Bittremieux is a PhD student in bioinformatics at the University of Antwerp. His research focuses on using data mining techniques in mass spectrometry-based proteomics.

Trung Nghia Vu is a final year PhD student at the University of Antwerp. His research interests include data mining on mass spectrometry-based proteomics and metabolomics data.

Wim Vanden Berghe is Professor in Epigenetics at the University of Antwerp. His research interest focuses on nutritional and phytomedicinal epigenetic mechanisms in cancer, neuroinflammation and cardiovascular diseases.

Bart Goethals is a professor in data mining at the University of Antwerp. His research focuses on data mining, data science and big data analytics. He has won several awards in the data mining field.

Kris Laukens is coordinator of the biomedical informatics research center and professor at the University of Antwerp. His research lies in the application of data mining to complex life science data.