On the principle of ion selectivity in Na⁺/H⁺-coupled membrane proteins: Experimental and theoretical studies of an ATP synthase rotor

Significance

The biological function of many membrane proteins requires a continuous energy supply. Differences in the electrochemical potential of Na⁺ and H⁺ across membranes, resulting from the metabolism of cellular nutrients or light harvesting, are the most prominent source of energy, aside from ATP. To harness this electrochemical energy, membrane proteins capture Na⁺ or H⁺ from their environment and couple their functional mechanisms to the translocation of these ions from one side of the membrane to the other. Here, we use experimental and computer simulation methods to investigate the structural and energetic factors that enable a crucial membrane enzyme, the ATP synthase, to selectively recognize Na⁺ or H⁺. We envisage that these insights will apply to other classes of membrane proteins too.

Abstract

Numerous membrane transporters and enzymes couple their mechanisms to the permeation of Na⁺ or H⁺, thereby harnessing the energy stored in the form of transmembrane electrochemical potential gradients to sustain their activities. The molecular and environmental factors that control and modulate the ion specificity of most of these systems are, however, poorly understood. Here, we use isothermal titration calorimetry to determine the Na⁺/H⁺ selectivity of the ion-driven membrane rotor of an F-type ATP synthase. Consistent with earlier theoretical predictions, we find that this rotor is significantly H⁺ selective, although not sufficiently to be functionally coupled to H⁺, owing to the large excess of Na⁺ in physiological settings. The functional Na⁺ specificity of this ATP synthase thus results from two opposing factors, namely its inherent chemical selectivity and the relative availability of the coupling ion. Further theoretical studies of this membrane rotor, and of two others with a much stronger and a slightly weaker H⁺ selectivity, indicate that, although the inherent selectivity of their ion-binding sites is largely set by the balance of polar and hydrophobic groups flanking a conserved carboxylic side chain, subtle variations in their structure and conformational dynamics, for a similar chemical makeup, can also have a significant contribution. We propose that the principle of ion selectivity outlined here may provide a rationale for the differentiation of Na⁺- and H⁺-coupled systems in other families of membrane transporters and enzymes.

Gradients in the electrochemical potential of H⁺ or Na⁺ across biological membranes sustain a wide range of essential cellular process. The resulting proton or sodium motive forces (pmf, smf) are the predominant energy source for secondary-active membrane transporters, which mediate the uptake of many substances required by the cell (1–3), and also enable pathogenic bacteria to protect themselves from human-made antibiotics and other toxic compounds (4–6). Downhill membrane permeation of Na⁺ and H⁺ across the membrane also powers the ATP synthase (7), which produces most of cellular ATP, and energizes the rotation of bacterial flagella (8). Thus, the importance of this mode of energy transduction in cells cannot be overstated. Nevertheless, little is known about the factors that control and modulate the specificity for Na⁺ or H⁺ in most of these processes.

It seems clear, although, that there is no correlation between function type and ion specificity; that is, the same process in different species can be coupled to either Na⁺ or H⁺ (2, 5–7, 9–11). Organism-specific environmental factors, such as temperature or pH, also do not provide a consistent rationale; for example, ATP synthases from thermoalkaliphilic bacteria use a H⁺ gradient despite the scarcity of H⁺ and the potentially greater degree of H⁺ leakage across the membrane at high temperatures, compared with Na⁺ (12, 13). Indeed, pmf- and smf-driven systems are often found within the same organism, and sometimes with the same or similar function; for example, malate uptake in Bacillus subtilis is mediated by the H⁺-coupled symporter CimH (14) and by the Na⁺-coupled MaeN (15). Moreover, specific membrane transporters and enzymes are sometimes coupled to both Na⁺ and H⁺, either concurrently (using multiple binding sites), such as the multidrug efflux pump NorM of Vibrio cholera (16) and the Methanosarcina acetivorans ATP synthase (17), or alternately (using a single binding site), such as the Escherichia coli melibiose permease (18) and some membrane-integral pyrophosphatases (19).

At the molecular level, the architecture of pmf- and smf-driven membrane proteins within the same family has consistently been found to be largely conserved (20–28). Thus, it appears as if the Na⁺ or H⁺ specificity of these systems is dictated by localized variations in their amino acid sequence, rather than by major structural or mechanistic adaptations. This conclusion leads to an intriguing dilemma. Under most physiological conditions, the concentration of Na⁺ exceeds that of protons by many orders of magnitude (for example, a millionfold in mitochondria, or a billionfold in alkaline environments). Thus, in membrane-protein families with members that are driven by the smf or the pmf, the latter must have evolved amino acid adaptions that result in an extreme H⁺ selectivity, so as to counter the large Na⁺ concentration excess. Conversely, specific coupling to the smf would not actually require a strong Na⁺ selectivity; weak H⁺ selectivity or nonselectivity would be sufficient for Na⁺-coupling, physiologically. How can variation changes at the amino acid level result in such extreme variations in the H⁺ selectivity of a protein structure, spanning 10 or more orders of magnitude?

In previous theoretical studies, we have addressed this question for the family of ion-motive ATPases (17, 29, 30), which comprises eukaryotic and prokaryotic ATP synthases, as well as vacuolar ion pumps. In these multicomponent enzymes, a membrane-embedded substructure known as the rotor ring can revolve around its axis, relative to the rest of the protein’s membrane domain. This rotational motion enables the ring to capture Na⁺ or H⁺ ions as they enter the protein via an access channel, and to shuttle them to a separate exit channel, in a sequential manner. Because the entry and exit channels are not colinear, there is a strict correspondence between the direction of ion permeation and the sense of rotation of the ring (which in turn determines the type of activity of the catalytic sector of the enzyme, i.e., ATP synthesis or hydrolysis).

The principle of ion selectivity emerging from the abovementioned computational studies posits that rotor rings are universally H⁺ selective, owing to the fact that ion binding is consistently mediated by a conserved carboxylic side chain (the intrinsic H⁺/Na⁺ selectivity of a carboxylic group in solution is 10,000-fold), and that this inherent H⁺ selectivity is enhanced or suppressed by multiple orders of magnitude, depending on the balance between hydrophobic and polar groups lining the ion-binding sites (aside from the key carboxyl side chain); geometric factors may additionally fine-tune the selectivity of these sites, for a given chemical composition.

In this study, we challenge the validity of this theory through experimental measurements and further computational analyses. Specifically, we set out to experimentally determine the thermodynamic ion selectivity of a rotor ring from a Na⁺-driven ATP synthase, and to compare this ring with others physiologically driven by either Na⁺ or H⁺. We find that the results of this analysis are qualitatively and quantitatively consistent with the theory of ion selectivity proposed previously, and provide novel insights into the influence of conformational factors.

Results

Na⁺ Binds to the Ilyobacter tartaricus c-Ring, but Not K⁺ or Cs⁺.

To begin to assess the ion specificity of the c-ring from the I. tartaricus ATP synthase, comparative calorimetric measurements were made for Na⁺, K⁺, and Cs⁺. Under conditions in which the initial Na⁺ concentration was small but not specifically optimized (30–50 μM), sequential additions of NaCl aliquots to a detergent-solubilized (n-octyl-β-d-glucopyranoside) c-ring sample, up to a total concentration of ∼3 mM, resulted in a series of large but progressively diminishing signals in a pattern that indicates an exothermic binding process (Fig. S1A). Saturation was observed at ∼1 mM NaCl (at pH ∼6.5), after which the signals continued to be significant and decayed more slowly (Fig. S1A). An equivalent titration of the buffer solution lacking the protein resulted in a pattern that is highly similar to that measured for the protein sample after saturation (Fig. S1A). These data thus indicate that the isothermal titration calorimetry (ITC) signals obtained for the c-ring sample before saturation reflect Na⁺ binding to the protein, whereas those recorded after saturation primarily reflect the heat of dilution of the NaCl aliquots.

To verify that the signals measured for the protein solution represent Na⁺ binding to a selective site in the protein, analogous titrations were carried out with KCl and with CsCl (up to a final concentration of 8 and 3 mM, respectively). In contrast to the results obtained with NaCl, the signals measured for the protein sample and for the buffer solution were highly similar, in both cases. That is, the measured signals reflect the heat of dilution of the KCl/CsCl aliquots throughout the entire titration (Fig. S2). We conclude, therefore, that neither K⁺ nor Cs⁺ (nor Cl⁻) bind to the I. tartaricus c-ring.

Consistent with this conclusion, titration with NaCl in the presence and in the absence of CsCl in the protein solution produced similar signal patterns before saturation (Fig. S1B). After saturation, the patterns differ, in that the heat of dilution of the injected NaCl aliquots is minimal for the sample containing CsCl, owing to the fact that the ionic strength of the protein solution is largely preset (Fig. S1B). These conditions are advantageous, as they enhance the extent to which the heat signals measured throughout the titration reflect Na⁺ binding to the protein.

Na⁺ Binds to the Functional Ion-Binding Sites in the c-Ring.

The functional ion-binding sites in the c-subunit rings of all rotary ATPases are located along the outer circumference of the structure, approximately halfway across the transmembrane region (21, 23, 31–35). The amino acid composition of these binding sites varies across species, but invariably they feature at least one carboxylic side chain (most commonly glutamate). In rotary ATPases that are physiologically coupled to the H⁺ gradient, this conserved side chain enables H⁺ binding to the c-ring through protonation (36, 37); in enzymes coupled to Na⁺, as in I. tartaricus, the carboxylate group coordinates the bound Na⁺ directly (21, 33, 35). Carboxylic amino acids are, however, often found elsewhere in the c-subunits, usually at either side of the transmembrane region. For example, each of the c-subunits in the I. tartaricus ring has four additional aspartate/glutamate residues, flanked by other polar side chains. Therefore, it would be legitimate to question whether the signals observed in our ITC experiments represent nonspecific Na⁺ binding to the protein, rather than to the functional binding sites.

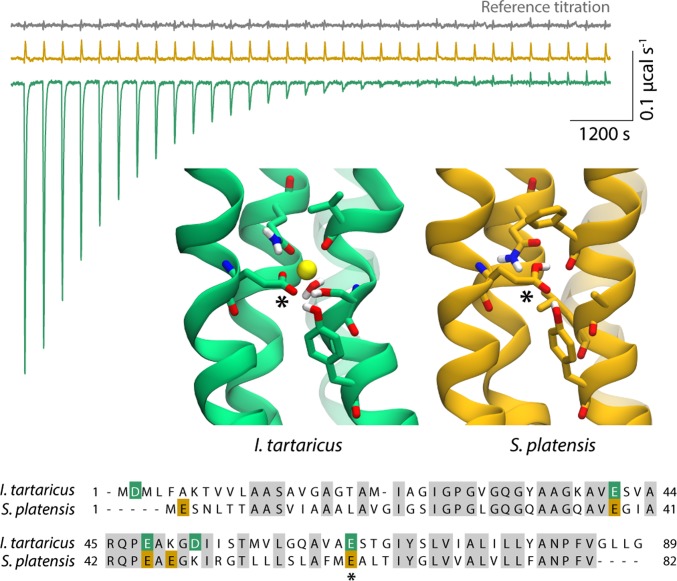
To address this question, we compared the ITC results obtained for the I. tartaricus c-ring, under optimized conditions (e.g., initial [Na⁺] < 10 μM), with analogous measurements for the c-ring of the Spirulina platensis ATP synthase. These two c-rings have the same number of Glu/Asp side chains, and these are in similar positions in the structure (Fig. 1) (21, 23). However, the S. platensis c-ring is strongly selective for H⁺ over Na⁺, owing to the specific amino acid composition of its ion-binding sites. Indeed, labeling of the S. platensis c-ring with N,N′-dicyclohexylcarbodiimide (DCCD), which specifically reacts with the protonated form of the conserved glutamate (38), cannot be inhibited by Na⁺, even if the concentration of Na⁺ exceeds that of H⁺ by a billionfold (29). We reasoned, therefore, that if the ITC signals measured for the I. tartaricus c-ring reflect nonspecific Na⁺ binding, similar signals ought to be detected for the S. platensis c-ring. The experimental data, however, reveal no evidence of Na⁺ binding to the S. platensis c-ring (Fig. 1), which demonstrates that the exothermic signals obtained for the I. tartaricus c-ring originate from Na⁺ binding to the functional sites in the core of the transmembrane domain.

Fig. 1.

Specific binding of Na⁺ to the I. tartaricus c-ring. Representative ITC experiment in which the I. tartaricus (green) and S. platensis (yellow) c-rings are titrated with NaCl at pH 6.5. The reference titration of the buffer in the absence of either protein (gray) is also provided. The Inset shows the atomic structures of the ion-binding sites in the I. tartaricus and S. platensis c-rings, in the Na⁺- and H⁺-bound states, respectively (21, 23, 49). A sequence alignment of the c-subunits in these two organisms highlights the location of all Asp/Glu side chains, including those in the functional ion-binding sites (*).

ITC Signals Reflect Na⁺ Competition with H⁺.

All c-rings known to be physiologically coupled to transmembrane Na⁺ gradients can also bind H⁺, although functional coupling to H⁺ (i.e., catalytic activity) has been observed typically only in in vitro conditions where the concentration of Na⁺ is sufficiently low, e.g., less than 50 μM at pH 7 (39). [Thus, far, only the ATP synthase from Methanosarcina acetivorans has been observed to mediate Na⁺ and H⁺ permeation concurrently in physiological conditions (17).] Nevertheless, DCCD-labeling assays of Na⁺-coupled c-rings have clearly demonstrated that a competition between H⁺ and Na⁺ exists in a broader concentration range (40, 41). It should be noted, however, that the irreversible nature of the DCCD-labeling reaction precludes a proper thermodynamic analysis of this competition using this biochemical approach.

We reasoned, therefore, that ITC signals detected in titrations of the I. tartaricus c-ring (Fig. 1), in which the initial Na⁺ concentration in the protein sample is less than 10 μM, ought to reflect Na⁺ binding to sites that are either initially occupied by H⁺ or empty, i.e., the progressive displacement of an equilibrium in which Na⁺ and H⁺ compete for the same binding sites. To determine whether this is the case, we carried out NaCl titrations of protein samples prepared at pH values ranging from 5.5 to 7.5. Note that SDS/PAGE gels demonstrate that the oligomeric state of the native protein (c₁₁) is maintained at pH values as low as 4.5, despite the very low amounts of Na⁺ (42), consistent with the notion that the ring binding sites are preloaded with H⁺ (Fig. S3).

These experiments showed the pH dependence that would be expected for a competition process, i.e., the Na⁺ signals measured in the titrations are systematically weaker if the pH of the protein sample (and the injected solution) is lowered. Note this effect is not due to differences in, e.g., the concentration of Na⁺ or protein in this measurements; the corresponding binding isotherms, i.e., the heat released per injection normalized with respect to all relevant concentrations (denoted by Δq), are increasingly shallower as the H⁺ concentration is raised (Fig. 2).

Fig. 2.

Competitive binding of Na⁺ and H⁺ to the I. tartaricus c-ring. The Insets show representative NaCl titrations of the I. tartaricus c-ring at similar protein concentrations and three different pH values (the error in the pH represents the different values measured in the dialysis buffer before ITC experiment and in the protein solution after titration). The heat signals released per injection normalized with respect to all relevant concentrations (black circles) can be fitted by a Wiseman isotherm (Eq. 1) (black curve) (43, 44), from which the apparent dissociation constant, K_d^app, and apparent enthalpy, ΔH_o, can be derived.

To quantify the competition between Na⁺ and H⁺ in terms of dissociation constants, the isotherms measured at different pH values must be fitted to theoretical curves from a plausible binding model and analyzed globally. Here, we assumed a model in which each of the 11 identical binding sites in the I. tartaricus c-ring bind Na⁺ in a one-step reaction and in an independent manner. Such process can be described by the so-called Wiseman isotherm as follows (43, 44):

$$\mathrm{\Delta }\mathit{q}\mathrm{=}\frac{{\mathit{Q}}_{\mathrm{obs}}}{{\left[{\text{Na}}^{\mathrm{+}}\right]}_{\text{i}}}\mathrm{=}\mathrm{\Delta }{\mathit{H}}^{\text{o}}{\mathit{V}}_{\text{o}}\left[\frac{1}{2}\mathrm{+}\frac{1\mathrm{-}\left({\left[\mathrm{N}{\mathrm{a}}^{\mathrm{+}}\right]}_{\text{s}}/\left[\text{P}\right]\right)\mathrm{-}\left(1/c\right)}{2\sqrt{{\left(1\mathrm{+}\left({\left[{\text{Na}}^{\mathrm{+}}\right]}_{\text{s}}/\left[\text{P}\right]\right)+\left(1/\mathit{c}\right)\right)}^2\mathrm{-}4{\left[{\text{Na}}^{\mathrm{+}}\right]}_{\text{s}}/\left[\text{P}\right]}}\right],$$ [1]

where Q_obs refers to the integrated heat signals measured for the protein sample (after subtracting those obtained from a reference titration of the buffer), ΔH^o is the apparent enthalpy of Na⁺ binding (i.e., at a given pH), and V_o is the effective volume of the calorimeter cell; [Na⁺]_i is the Na⁺ concentration of the injected solution, and [P] and [Na⁺]_s are the concentrations of protein (i.e., c-subunit) and of accumulated Na⁺ in the calorimeter cell, respectively. The dimensionless parameter c is defined as follows:

$$c\mathrm{=}\frac{\mathit{n}\left[\text{P}\right]}{{\mathit{K}}_{\text{d}}^{\text{app}}\left({\text{Na}}^{+}\right)},$$ [2]

where n is the number of Na⁺ ions that bind to each c-subunit, and K_d^app (Na⁺) is the apparent dissociation constant at a given pH.

The value of c determines the shape of the binding isotherm (43). Large c values (c > 1,000) reflect very strong binding, which result in quasirectangular isotherms from which n and ΔH^o, but not K_d, may be derived from fitting. If c ranges instead from 1 to 1,000, the binding isotherm has a sigmoidal shape, and n, K_d, and ΔH^o can be determined independently. The isotherms measured for the I. tartaricus ring, however, appear to correspond to c < 1, i.e., they are not sufficiently sigmoidal to permit a determination of all three parameters reliably. Small c values typically require that the protein concentration used in the ITC experiment be increased (which is challenging for detergent-solubilized membrane proteins), so as to compensate for the weak binding. Fortunately, the crystal structure of the I. tartaricus c-ring makes clear that n = 1, i.e., only one ion (Na⁺ or H⁺) binds to each of the 11 binding sites in ring; in cases such as this where the binding stoichiometry is known, the K_d can be determined with confidence also for small c values, if the protein and the titrant concentrations are also well characterized (44, 45).

Specifically, the apparent K_d^app (Na⁺) obtained from Na⁺ titrations of the I. tartaricus c-ring in a Hepes–tetramethylammonium hydroxide (TMAOH) buffer at pH 7.0 is ∼0.340 mM (Fig. 2, Left). Comparable values were obtained for imidazole/HCl and phosphoric acid/TMAOH, at the same pH, which demonstrates that the buffer molecules do not interact directly with the c-ring binding sites (Fig. S4). Note, however, that the apparent enthalpy of Na⁺ binding becomes more negative as the ionization enthalpy of the buffer is increased. Because the c-ring lacks histidine residues, this correlation confirms that the measured ITC signals primarily reflect the displacement of H⁺ bound to the c-ring by Na⁺, and the subsequent binding of the released protons to the buffer molecules. Consistent with these results, the apparent K_d^app (Na⁺) at pH ∼6.5 increases up to 0.76 and 0.74 mM (using Hepes-TMAOH and Mes-TMAOH, respectively), and that measured at pH ∼5.6 (using Mes-TMAOH) increases further, to 3.0 mM (Fig. 2, Center and Right). It is therefore clear that this trend reflects the competition of Na⁺ and H⁺ for the same binding sites in the c-ring.

The I. tartaricus c-Ring Is H⁺ Selective, but Physiologically Coupled to Na⁺.

Because Na⁺ and H⁺ compete for the same binding site, the absolute dissociation constants for both ions under the experimental conditions might be derived from the following classical expression:

$$K_{\text{a}}^{\text{app}}\left({\text{Na}}^{\mathrm{+}}\right)\mathrm{=}\frac{{\mathit{K}}_{\text{a}}\left({\text{Na}}^{\mathrm{+}}\right)}{1\mathrm{+}\left[{\text{H}}^{\mathrm{+}}\right]{\mathit{K}}_{\text{a}}\left({\text{H}}^{\mathrm{+}}\right)},$$ [3]

where K_a = 1/K_d. This expression can be rewritten as convenient linear relationship between K_d^app (Na⁺) and [H⁺] as follows:

$$K_{\text{d}}^{\text{app}}\left({\text{Na}}^{+}\right)\mathrm{=}{\mathit{K}}_{\mathrm{d}}\left({\text{Na}}^{+}\right)\left[1+\frac{\left[{\text{H}}^{+}\right]}{{\mathit{K}}_{\mathrm{d}}\left({\text{H}}^{+}\right)}\right].$$ [4]

The y-axis intercept of a plot of K_d^app (Na⁺) versus [H⁺] (i.e., [H⁺] = 0) is therefore the absolute dissociation constant for Na⁺, whereas the negative of the x-axis intercept [i.e., [Na⁺] = 0 and thus K_d^app (Na⁺) = 0] is the absolute dissociation constant for H⁺.

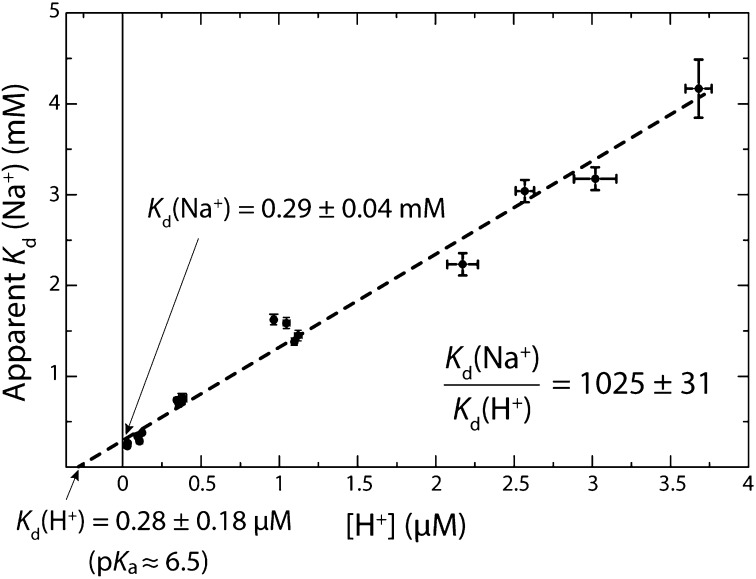
Fig. 3 shows such a plot for a series of ITC titrations carried out at five different pH values, between 5.5 and 7.5, along with a linear regression of the data. The resulting absolute dissociation constants under these experimental conditions are K_d(Na⁺) = 0.29 ± 0.04 mM and K_d(H⁺) = 0.28 ± 0.18 μM. The ion selectivity of this c-ring, defined as the ratio between the dissociation constants for Na⁺ and H⁺, is therefore 1,025 ± 31 (Fig. 3). That is, the c-ring of the I. tartaricus ATP synthase is H⁺ selective, as had been anticipated by previous theoretical studies (29). This proton selectivity, however, is much smaller than the ratio of Na⁺ to H⁺ concentrations under physiological conditions, namely 10⁵ to 10⁷ (46), which explains why the enzyme is coupled to a smf, rather than to a pmf.

Fig. 3.

Determination of absolute dissociation constants for Na⁺ and H⁺. The values of the apparent K_d(Na⁺) obtained from the ITC titrations of the I. tartaricus c-ring are plotted against the H⁺ concentration (pH) of each experiment (Eq. 4). The error bars on each measurement reflect the uncertainty in the apparent K_d deduced from the fitting of the Wiseman isotherm to the normalized experimental data, and the variation in the pH before (dialysis buffer) and after (protein solution) the ITC experiment. The absolute dissociation constants, K_d(Na⁺) and K_d(H⁺), and the selectivity, K_d(Na⁺)/K_d(H⁺) correspond to the X/Y intercepts and the slope of the linear fit, respectively. The errors in these values reflect the statistical error of the regression.

The c-Ring Confers Ion Specificity to the Enzyme.

To the best of our knowledge, the results reported here constitute the first quantitative determination of the ion selectivity of an F-type ATP synthase c-ring. Before this work, however, ²²Na⁺ binding assays at various pH values were used to determine the selectivity of the K-ring of the V-type rotary ATPase from Enterococcus hirae (47), whose physiological function is to extrude Na⁺ ions across the cytoplasmic membrane, driven by ATP hydrolysis (48). The architecture of the rotor rings from E. hirae and I. tartaricus is similar, in that both are homomeric assemblies of identical subunits, and feature a series of ion-binding sites along their outer circumference, approximately halfway across the transmembrane region (21, 31). However, the E. hirae ring consists of 10 K-subunits, rather than 11, and each of these subunits consists of four transmembrane helices, rather than two. Furthermore, the ion-binding sites in the E. hirae ring are located only within each K-subunit, and not at their interfaces, as in the I. tartaricus c-ring. Therefore, the 10 Na⁺ ions bound to the E. hirae ring are more sparsely distributed that the 11 ions bound to the I. tartaricus ring.

The absolute dissociation constants measured for the E. hirae ring are K_d(H⁺) = 3.5 μM (pK_a = 5.5) and K_d(Na⁺) = 12 μM (47). That is, the E. hirae ring is weakly H⁺ selective (3.5-fold), which under physiological conditions translates into a strong specificity for Na⁺. The stronger H⁺ selectivity of the I. tartaricus c-ring therefore results from a weaker affinity for Na⁺ (0.29 mM) compounded with a stronger affinity for H⁺ (0.28 μM). It is important to note that the K_d(Na⁺) value determined here for the isolated I. tartaricus c-ring is in excellent agreement with K_m(Na⁺) values determined in assays of the Na⁺-dependent ATPase activity of the full-length enzyme, in pH conditions where the competition with H⁺ is likely to be minimal (0.23–0.27 mM at pH 8.0–9.2) (39). Furthermore, the ratio between the K_d(Na⁺) values of I. tartaricus and E. hirae rotor rings is in line with the ratio between the K_m(Na⁺) values determined for these two enzymes, in comparable pH conditions (39, 48). This correspondence between absolute and relative K_d(Na⁺) and K_m(Na⁺) values underscores the central premise of this study, namely that the thermodynamic ion specificity of this class of enzymes is predominantly conferred by the rotor ring, rather than by, e.g., the adjacent subunit a, despite the involvement of the latter in facilitating access to the c-ring ion-binding sites from the surrounding solution.

Measured Selectivity Values Validate Existing Theoretical Framework.

As mentioned in the Introduction, previous theoretical studies based on of a range of experimental structures and computer-generated models have led us to formulate the structural basis for the principle of ion selectivity of the rotor ring, and enabled us to rationalize the strikingly broad spectrum of selectivity values that seem to occur in nature, which spans a least 10 orders of magnitude (17, 29, 30). The rotor rings of E. hirae and I. tartaricus are on the same end of that broad spectrum, but the difference in their ion selectivity is nevertheless significant. The availability of a quantitative experimental measurement of this difference presents an opportunity to assess the validity of the specific thermodynamic framework and computer simulation methods used in those theoretical studies.

To this end, we recomputed and compared the H⁺/Na⁺ selectivity of the E. hirae and I. tartaricus rings as previously described, i.e., through alchemical free-energy calculations based on molecular dynamics (MD) simulations of each c-ring embedded in a phospholipid membrane (29). The protocol followed here differs from that reported earlier only in that the number of intermediates and the length of the simulations were increased, so as to improve the precision of the calculations. In addition, we considered two plausible forms of the H⁺-bound state of the I. tartaricus c-ring, namely one in which the water molecule that is known to co-coordinate the ion in the Na⁺-bound state (49) remains in the site upon H⁺ binding, or model a, and another in which it does not, or model b (note that such ambiguity does not exist for E. hirae). Independent analysis of models a and b provides a two-pronged test: not only calculated and experimental values of the relative ion selectivity of E. hirae and I. tartaricus ought to be in agreement, but that agreement ought to be found only if the most probable form of the I. tartaricus H⁺-bound state, according to the same free-energy calculations, is considered.

The results of these calculations are summarized in Fig. 4A. When model a is considered, the calculated H⁺/Na⁺ selectivity of the I. tartaricus c-ring is 3.6 ± 0.6 kcal/mol greater compared with that calculated for E. hirae, whereas for model b the difference in selectivity is reduced to 2.0 ± 0.6 kcal/mol. From comparison of these two values, it can be deduced that the binding free energy of the water molecule to the H⁺-bound sites in the I. tartaricus c-ring is 1.6 kcal/mol (SI Materials and Methods). This value translates into a dissociation constant of ∼69 mM, which implies a 99.88% occupancy, given that the bulk concentration of water is 55.5 M. Thus, from a computational standpoint, it is clear that a water molecule contributes to coordinate both Na⁺ and H⁺ in the I. tartaricus binding sites. More importantly, the relative selectivity value of 3.6 ± 0.6 kcal/mol obtained in this most probable case, i.e., model a, is in very good agreement with the value derived from the experimental dissociation constants, i.e., 3.4 kcal/mol. In our view, this cross-consistency between computations of experiments validates the framework used in our previous theoretical studies of the selectivity of ATP synthase rotor rings, and by extension, the general principle of ion selectivity derived from those studies.

Fig. 4.

Computational analysis of the relative ion selectivity of the I. tartaricus and E. hirae c-rings. (A) Calculated values of the free energy of H⁺/Na⁺ selectivity (ΔG_sel) for the I. tartaricus and E. hirae c-rings (gray bars), compared with that previously reported for S. platensis (29). Note that all calculated values are shifted uniformly, so that the value for E. hirae matches the experimental measurement (47) and serves as the reference for this comparative analysis. The experimental and calculated values of the difference in the free energy of selectivity (ΔΔG_sel) between the I. tartaricus the E. hirae c-rings are indicated. Two alternative models of the I. tartaricus H⁺-bound state (a and b) were considered (Results). (B) Breakdown of the calculated value of the difference in the ion selectivity (ΔΔG) between the I. tartaricus the E. hirae c-rings [“total (FEP)” and “total (TI)”] into local and nonlocal contributions (SI Materials and Methods). The local contributions (“binding site”) comprise all of the ion–protein and protein–protein interactions within an ion-binding site, i.e., involving Q32, V63, E65, S66, T67, Y70, and a structural water molecule in I. tartaricus (Fig. 5A), and L61, T64, Q65, Y68, Q110, and E139 in E. hirae (Fig. 5A). Nonlocal contributions (“rest”) include all interactions between the binding site (as defined above) and the rest of the system (e.g., other regions in the protein, other binding sites, the lipid membrane, etc.).

Local Conformational Dynamics Fine-Tune the Ion Selectivity.

In the broad spectrum of ion selectivity values across the rotary ATPase family, the 300-fold difference between the c-rings of E. hirae and I. tartaricus can be thought as a fine-tuning. The structural basis for this fine-tuning is, however, not apparent, given the similarity in the chemical composition of the ion-binding sites in these two rings (Fig. 5A). Both feature the characteristic glutamate residue that permits ion binding (E139/E65), in addition to a very similar set of polar side chains and backbone groups (21, 31). There are only two substitutions from E. hirae to I. tartaricus, namely T64 to S66 and Q65 to T67. The shorter side chain of T67 cannot coordinate the bound ion, but the position of the carboxamide group of Q65 in E. hirae is instead occupied by a water molecule in I. tartaricus (49), as mentioned in the previous section.

Fig. 5.

Structural basis for the difference in ion selectivity of the I. tartaricus and E. hirae c-rings. (A) Close-up of the structure of the ion-binding sites in the I. tartaricus and E. hirae c-rings, in the Na⁺-bound state. The figures show representative configurations observed in MD simulations, extracted from a clustering analysis. The residues involved in Na⁺ coordination in each case are highlighted. Note these residues form a well-defined network of H-bonds (omitted for clarity). The primary mode of Na⁺ coordination in both cases is one in which the conserved carboxylic side chain (E65/E139) interacts with Na⁺ in a monodentate configuration. However, a bidentate mode is also feasible in E. hirae, for an equivalent H-bonding network. (B) Probability of the monodentate and bidentate modes of Na⁺ coordination, from simulations of the I. tartaricus and E. hirae c-rings. The Na⁺ coordination number N was quantified using the function n = Σ_i [1 − (r_i/r₀)³⁰] [1 − (r_i/r₀)⁶⁰]⁻¹, where r_i denotes the distances between the Na⁺ ion and the six nearest oxygen atoms in the site, and r₀ = 2.75 Å. In the I. tartaricus ring, the six oxygen atoms are E65:O_ε1, E65:O_ε2, Q32:O_ε1, V63:O, S66:O_γ, and W:O; in the E. hirae ring, the corresponding atoms are E139:O_ε1, E139:O_ε2, Q110:O_ε1, L61:O, T64:O_γ, and Q65:O_ε1.

Because the calculated difference in the free energies of H⁺/Na⁺ selectivity of the E. hirae and I. tartaricus rings is consistent the experimental value, we reasoned that it ought to be possible to extract the structural basis for this difference from a posteriori analysis of the MD trajectories from which the calculated free-energy values are derived. To first evaluate whether the difference in the ion selectivity of these two rings is due to local or nonlocal factors, we decomposed the calculated free-energy difference into two contributions (SI Materials and Methods): that due to the interactions within each of the binding sites (i.e., ions, protein, and water), and that due to remote interactions with (and within) the rest of the system (i.e., protein, lipids, solvent). As mentioned, the transmembrane topologies of the individual subunits in the E. hirae and I. tartaricus rings differ, as do their stoichiometry and the distribution of ion-binding sites along their circumference, so it is conceivable that nonlocal factors have an effect. Nevertheless, we found that most of the change in the free energy of ion selectivity between these two rings arises from differences within the binding sites (Fig. 4B).

To identify these local factors, we analyzed and compared the geometry and dynamics of the ion coordination sphere for either Na⁺ or H⁺ in the two rings. This analysis revealed significant differences that would explain the computed (and measured) change in ion selectivity. For example, a subtle but clear difference between the Na⁺-bound states is that the ion coordination number in E. hirae varies dynamically between five and six, owing to the fact that E139 can coordinate the Na⁺ ion either in a monodentate or a bidentate configuration (Fig. 5). By contrast, the Na⁺-coordination number in I. tartaricus is exclusively five (Fig. 5). In E. hirae, the monodentate mode is also the most probable (consistent with the X-ray structure), but the population of the bidentate configuration (or intermediates thereof) is nevertheless significant (Fig. 5B), and as a result the electrostatic stabilization of the Na⁺-bound state is greater (Fig. S5 A–D). It is worth noting that comparison of these two coordination modes in the E. hirae ring reveals no differences in the network of H-bonding interactions between the side-chain and backbone groups that participate in the Na⁺-coordination sphere (Fig. 5 and Fig. S5 E and F); i.e., the bidentate mode does not occur at the expense of protein–protein interactions. Thus, despite the fact that monodentate modes in I. tartaricus and E. hirae are large identical (Table S1), the possibility of a higher Na⁺ coordination number in E. hirae would explain its stronger affinity for Na⁺.

To rationalize the origin of this difference, we compared the distances between the four helices that flank the ion-binding sites in either ring, at equivalent positions across the transmembrane span. This analysis reveals that the two inner helices are further apart in E. hirae than in I. tartaricus, by 0.7 Å on average (Fig. S6), most likely due to the enrichment of glycine residues in the latter; indeed, mutation of these glycine residues in the I. tartaricus c-subunit results in c-rings with an increased subunit stoichiometry (50). Because in addition the E. hirae ring consists of 20 transmembrane hairpins, rather than the 11 seen in I. tartaricus, the curvature of the E. hirae ring (i.e., the reciprocal of the radius) is smaller, and therefore it is expected that the distance between the outer helices flanking the ion-binding sites is shorter (Fig. S6). Indeed, the simulations show that the spacing between the outer helices in E. hirae is 0.4 Å smaller than I. tartaricus, on average. This shift implies that the H-bonding interaction network involving E65/E139 in one of the outer helices and S66/T64 and Y70/Y68 in the adjacent helix (Fig. 5) is more compact in E. hirae than in I. tartaricus; thus, the former can accommodate a bidentate Na⁺-coordination mode without disrupting the abovementioned H-bonding network, whereas apparently the latter cannot.

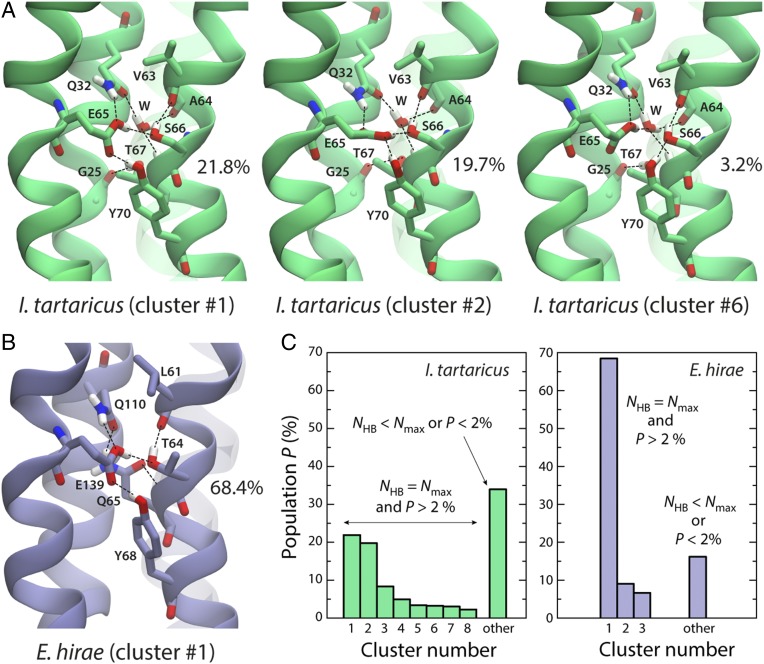
The different compactness of the ion-binding site in the E. hirae and I. tartaricus rings also appears to explain the difference between the energetics of the H⁺-bound states. In both rings, substitution of Na⁺ by H⁺ leads to a rearrangement of the binding sites so as to maximize the number of hydrogen bonds, including that donated by the protonated E139/E65 (Fig. 6). However, whereas in the E. hirae ring this is achieved primarily by a single configuration (Fig. 6 B and C), a variety of distinct configurations of comparable statistical weight can be identified in I. tartaricus, which interexchange rapidly (Fig. 6 A and C). Therefore, despite that fact that the most populated configurations in E. hirae and I. tartaricus are highly similar (i.e., clusters #1 in Fig. 6; Table S1), binding of H⁺ to the I. tartaricus ring would be more favorable for entropic reasons.

Fig. 6.

Structural basis for the difference in ion selectivity of the I. tartaricus and E. hirae c-rings. (A and B) Close-up of the structure of the ion-binding sites in (A) the I. tartaricus and (B) E. hirae c-rings, in the H⁺-bound state. The H⁺ binds covalently to E65/E139 and the hydrogen bond network within the binding site reconfigures relative to the Na⁺-bound state (dashed lines). The figures show representative configurations observed in MD simulations, obtained through a clustering analysis based on all putative hydrogen-bonding interactions within each of the binding sites involving the protonated E65/E139 (see below). This analysis shows that, whereas E. hirae features one primary configuration (B), a variety of seemingly equivalent configurations coexist in I. tartaricus (A). (C) Summary of the clustering analysis. P denotes the probability of each cluster, and N_HB denotes the total number of hydrogen bonds in the binding site (not only those formed by E65/E139), the maximum value of which is N_max (eight for I. tartaricus and six for E. hirae). For a given c-ring, clusters with the same value of N_HB are equivalent energetically; the greater the number of these energetically equivalent clusters, the larger the entropy of the H⁺-bound state. The cluster analysis was carried out using METAGUI (66, 67). For I. tartaricus, the distances considered were E65:O_ε1 − S66:O_γ, E65:O_ε2 − S66:O_γ, E65:O_ε1 − Q32:N_ε2, E65:O_ε2 − Q32:N_ε2, E65:O_ε1 − Y70:O_H, E65:O_ε2 − Y70:O_H, and E65:O_ε2 − W:O; the analogous distances in E. hirae are E139:O_ε1 − T64:O_γ, E139:O_ε2 − T64:O_γ, E139:O_ε1 − Q110:N_ε2, E139:O_ε2 − Q110:N_ε2, E139:O_ε1 − Y68:O_H, E139:O_ε2 − Y68:O_H, and E139:O_ε2 − Q65:O_ε1.

Taken together, these subtle but noticeable differences in the conformational dynamics of the ion-binding sites in the E. hirae and I. tartaricus rings, both in the Na⁺- and H⁺-bound states, would explain the greater H⁺ selectivity of the latter.

Discussion and Conclusions

In this work, we set out to experimentally determine the thermodynamic ion selectivity of the ATP synthase c-ring from the anaerobe Ilyobacter tartaricus, and to rationalize its origins at the structural level. Because this rotor ring is physiologically driven by Na⁺ but may also be coupled to H⁺ in the absence of Na⁺, we reasoned that this analysis ought to provide insights into the molecular and environmental factors that control the ion specificity of this class of enzymes, and possibly also other types of membrane proteins driven by either the pmf or the smf. To this end, we established an ITC assay designed to specifically probe the energetics of exchange between the H⁺- and Na⁺-bound forms of the protein complex.

As would be expected for a competition process, the apparent dissociation constants for Na⁺ were found to increase linearly with the proton concentration of the buffer solution (i.e., lower pH values); furthermore, a negative correlation was found between the apparent enthalpy of Na⁺ binding and the deprotonation enthalpy of the buffer. Thus, the ITC experiment directly probes the relative binding energetics of two competing ions. Owing to this competition, however, the apparent Na⁺ binding affinities are weaker than what is required to concurrently determine the binding stoichiometry (n) and the thermodynamic binding parameters from analysis of the ITC data alone. Nevertheless, it is evident from the X-ray structure of the I. tartaricus c-ring that only one ion may reside in each of the 11 identical binding sites in the protein, and therefore it can safely be assumed that n = 1 per c-subunit. Note that similar a priori assumptions have been made in previous ITC studies of Cl⁻/H⁺ and Na⁺/H⁺ antiporters on the basis on structural information (51–53). Reassuringly, ITC studies of membrane proteins in which the binding stoichiometry could be actually determined, for example those of substrate binding to the Glt_Ph symporter, confirmed the n value deduced from crystal structures (54).

A clear conclusion from our ITC measurements is that the I. tartaricus c-ring is markedly H⁺ selective; Na⁺ binding, at equivalent concentrations of both ions, is about 300 times less probable. In typical physiological settings, however, the concentration of Na⁺ is at least a million times larger than that of H⁺; thus, our results actually imply a strong Na⁺ specificity in vivo, consistent with earlier functional and structural analyses of this enzyme and its c-ring (21, 39). Interestingly, the value of the absolute K_d (Na⁺) deduced from a global analysis of the ITC data (0.29 mM) is in excellent agreement with the K_m (Na⁺) value (0.23 mM) deduced from activity assays of the complete enzyme at pH 9.2 (i.e., no H⁺ competition is expected) (39). Likewise, the pH dependence of the inhibition of the enzyme by DCCD, in Na⁺-free conditions, suggests a pK_a value of 6.7 (55), which is also in excellent agreement with the value of 6.5 deduced from our ITC measurements. These results are evidence of the notion that the c-ring is the element that confers ion specificity to the enzyme (29, 55), and strongly indicate that the microenvironment of the c-ring binding sites in our experimental conditions is akin to that in which ion binding and release occur in the operating rotor. In our experiment, the c-ring is isolated and solubilized in 1% octyl-glucoside, a detergent with a short alkyl-chain that most probably allows water to hydrate the ion-binding sites (34, 38). Likewise, in the complete enzyme the c-ring sites that bind and/or release ions at any given time are only those exposed to the noncontiguous aqueous channels that traverse the protein complex, whereas those exposed to the hydrophobic core of the lipid membrane do not (on the molecular timescale). It appears, therefore, that the K_d (Na⁺) and K_d (H⁺) measurements reported here fortuitously represent a mechanistically relevant environment. Consistent with this notion, the rate constants for DCCD labeling of c-rings isolated in 1% octyl-glucoside were found to be very similar to those measured in the context of the complete enzyme, reconstituted in proteoliposomes (55). For completeness, however, it would be of interest to consider alternative c-ring preparations that provide a purely hydrophobic environment more akin to the lipid membrane, to verify the notion that the c-ring binding sites exposed to the membrane in the operating enzyme do not release the bound ions (38). The absolute affinities for both Na⁺ and H⁺ under such conditions should logically be considerably greater, because the empty form of the binding sites would be much more energetically penalized. It would also be of interest to assess whether other components of the membrane domain of the enzyme, in particular subunit a, contribute to its physiological ion specificity, for example by examining hybrid constructs of Na⁺- and H⁺-dependent ATP synthases.

The determination of the selectivity of the I. tartaricus c-ring has enabled us to challenge a previously proposed theoretical framework, based on MD simulations, with which we have compared and rationalized the functional specificity of different rotary ATPases (17, 29, 30, 33). The quantitative agreement between computational and experimental results obtained here validates that approach and therefore substantiates the principle of ion selectivity derived from it. This principle posits that all rotary ATPases select H⁺ over Na⁺, in a broad spectrum that spans 10 or more orders of magnitude. The extreme H⁺ selectivity of the c-rings in alkaliphiles or mitochondria (which cannot be rationalized in terms of the size of the ion) ensures dependable coupling to the pmf despite the enormous excess of Na⁺ in physiological settings. The mild H⁺ selectivity of the I. tartaricus c-ring, by contrast, enables its ATP synthase to use the smf produced by metabolic decarboxylation reactions, precisely due to the resulting Na⁺ concentration excess. ATP synthases in the middle of this spectrum, such as that in Methanosarcina acetivorans, are concurrently coupled to H⁺ and Na⁺, as both ion types compete in physiological conditions for the multiple (and identical) binding sites in the ring (17). At the structural level, we have proposed that the inherent H⁺ selectivity of all rotor rings is conferred by the strictly conserved carboxylate side chain in their ion-binding sites, and that this inherent H⁺ selectivity is gradually weakened or enhanced through localized structural and chemical adaptations (17, 29, 30). Specifically, in enzymes coupled to Na⁺, the H⁺ selectivity of the key carboxyl side chain is countered by the presence of multiple polar groups able to coordinate a Na⁺ ion, whereas in H⁺-coupled c-rings the opposite is accomplished through hydrophobic substitutions. Interestingly, the incorporation of water molecules into a binding site, so as to stabilize one of the ion-bound states but not the other is observed to further enhance or suppress its H⁺ selectivity (17, 37). Additional ITC experiments for mutagenized forms of the c-ring binding sites would be of interest to further assess the notion that the selectivity of these sites is ultimately set by the balance of hydrophobic and polar groups neighboring the conserved carboxyl side chain. That said, it should be noted that the effect of single-point hydrophobic mutations in the binding site of the I. tartaricus c-ring (S66A, Y70F) has been already qualitatively demonstrated through assays of Na⁺ protection against DCCD labeling of E65 as a function of pH (40, 41). These experiments clearly show that the protective effect of Na⁺ is diminished in the mutants relative to the wild type. Consistent with these observations, H⁺ transport assays for the F_o domain of the Na⁺-dependent ATP synthase from Propionigenium modestum (a very close homolog of the I. tartaricus enzyme) have shown that hydrophobic substitutions in the c-ring binding sites (S66A, Q32I) markedly diminish the extent to which Na⁺ inhibits ATP-driven H⁺ transport (56), i.e., the enzyme is more H⁺ selective, consistent with our theory. Here, we show that subtle variations in the geometry and conformational dynamics of two ion-binding sites of similar chemical makeup can also contribute to differentiating their Na⁺/H⁺ selectivity, by as much as two orders of magnitude. Factors such as the configurational entropy of one of the ion-bound states or the existence of subpopulations with an enhanced ion coordination number are, however, not immediately apparent in crystal structures, but can be readily inspected through computer simulations.

We believe that the principle of ion selectivity outlined above may well apply to other classes of membrane proteins that depend on electrochemical gradients of Na⁺ or H⁺ to sustain their function. Coordinating glutamate and aspartate residues are a common feature of systems coupled to Na⁺ (28, 57, 58). However, it is likely that some of these systems are actually H⁺ selective, like the Na⁺-dependent ATP synthases; given that a large excess of Na⁺ over H⁺ is a feature of many natural environments, there is no evolutionary pressure to create binding sites that are highly Na⁺ selective. This intrinsic H⁺ selectivity would explain, for example, the observation that Na⁺-dependent pyrophosphates are coupled to H⁺ under low Na⁺ concentrations (although still 1,000 times greater than that of H⁺) (19). Moreover, whereas Na⁺ coordination typically requires five to six ligands, proton binding requires only an ionizable side chain and a hydrogen bond acceptor, and therefore one or two hydrophobic substitutions in a Na⁺ site may result in H⁺-coupling, as observed among ATP synthases. The melibiose carrier family is a case in point. In Escherichia coli, MelB is strongly Na⁺ dependent, whereas in Klebsiella pneumonia this carrier is driven by H⁺. The substitution of an asparagine by alanine in the cation-binding site of the E. coli protein, however, results in cotransport of H⁺ and melibiose and diminished Na⁺ stimulation (59). Accordingly, the opposite mutation in the K. pneumonia MelB causes sugar transport to be coupled to Na⁺ uptake (60). It appears, therefore, that the principle of Na⁺/H⁺ selectivity described here may indeed apply to other important membrane transporters and enzymes, aside from rotary ATPases.

Materials and Methods

Protein Purification and Sample Preparation.

The ATP synthase was purified from I. tartaricus cells as described previously (39). To isolate the c-ring from the ATP synthase, the complex was disrupted with N-lauroylsarcosine, and all subunits except the c-ring were precipitated with ammonium sulfate, as described elsewhere (55). After centrifugation, the supernatant containing the c-ring was collected and dialyzed (1:500) (molecular mass cutoff of 6,000 Da; Spectra/Por; Spectrumlabs) against 5 mM ammonium acetate and 10 mM Tris⋅HCl, at pH 8, to remove the detergent and reduce the Na⁺ content. After two to three exchanges of the dialysis buffer, the sample was precipitated by titrating the buffer with acetic acid, thus lowering the pH to 4.5. The resulting Na⁺ concentration in the supernatant, i.e., in the c-ring sample, was ∼30–50 μM (see below). The material collected by centrifugation was dissolved in the ITC buffer (see below) and equilibrated by dialysis (molecular mass cutoff of 12,000–14,000 Da; Spectra/Por; Spectrumlabs). The resulting samples were analyzed by SDS/PAGE with and without trichloracetic acid treatment (61). The c-ring from the S. platensis ATP synthase was isolated as described previously (23).

Determination of Protein Concentrations.

Protein concentrations were determined using the BCA assay (Pierce Chemicals), following the manufacturer’s procedure. A c-ring sample whose concentration had been determined by amino acid analysis was used as a calibration standard. A calibrated scale was obtained by diluting that c-ring sample in the ITC buffer used at pH 6. The c-subunit concentration in the protein solutions used in the ITC measurements varied from 0.01 to 0.03 mM.

Control of pH and Na⁺ Concentration.

Before every ITC titration, the pH of the dialysis buffer and of the titrant solution was determined, and was then compared with the pH of the titrated protein sample. In all cases, the pH values of the three solutions were within 0.05 units; thus, both the solution in the cell and in the syringe of the calorimeter are pH matched and the pH values do not change during the Na⁺ titration of the c-ring. The residual Na⁺ contamination of the last dialysis buffer used during the preparation of all protein samples was quantified using atomic absorption spectroscopy (PerkinElmer Life Sciences), and in all cases it was found to be less than 10 μM, i.e., at pH 7 the Na⁺ occupancy of the c-ring binding sites before the titration should be about 1%. The specific values measured at the beginning of each titration were explicitly considered in the derivation of the binding isotherms, and therefore in the determination of K_d and ∆H values.

Isothermal Titration Calorimetry.

All measurements were made at 25 °C on a VP-ITC calorimeter (MicroCal). Before the measurements, the protein was solubilized in 1% (wt/vol) n-octyl-β-d-glucopyranoside (OG), and both the solubilized protein and the titrant were centrifuged to obtain homogenous solutions. For each titration, the Na⁺ concentration in the last dialysis buffer was measured using an atomic absorption spectrometer AAnalyst 100 (PerkinElmer Life Sciences). The pH values of the dialysis buffer and of the injected and protein solutions were also measured for each ITC measurement. The buffers used were 10 mM Mes-TMAOH at pH 5.5 and pH 6.5; 10 mM Hepes-TMAOH at pH 6.5; and 10 mM Hepes-TMAOH, 10 mM imidazole-HCl, and 10 mM phosphoric acid-TMAOH at pH 7.0. The injection syringe contained the same buffer and detergent used in the protein solution, plus 15–60 mM NaCl, depending on the pH. CsCl was added to the protein and injected solutions to ensure their total ionic strength (including buffers) was equivalent, namely 60 mM. The titrations were performed under constant stirring (307 rpm), using injections of 7 μL (except the first injection, which was 4 μL). To ensure equilibration, 6-min intervals were allowed between injections. Identical reference titrations were carried out in the absence of the c-ring to determine the effect of NaCl dilution. The protein samples were dialyzed after each titration and reused; no difference between fresh and reused samples was observed. SDS/PAGE was used to verify the integrity of the c-ring complex after the ITC measurements.

MicroCal Origin was used to analyze the titration data and calculate the binding isotherms, and to introduce the necessary corrections to account for displaced-volume effects and for the trace amounts of Na⁺ in the protein sample at the beginning of each titration. To evaluate the latter, the residual Na⁺ concentration in the last dialysis buffer, denoted by [Na⁺]_free, was measured for each sample as described above. For each titration of that sample, the apparent dissociation constant K_d^app(Na⁺) was obtained by fitting the Weisman isotherm (Eq. 1) to the uncorrected data. The fraction of Na⁺ bound to the protein at the start of that titration could be then estimated to be [Na⁺]_bound = [P] (1 + K_d^app(Na⁺)/[Na⁺]_free)⁻¹, where [P] is the c-subunit concentration. The total value of the initial Na⁺ concentration, i.e., the sum of [Na⁺]_free and [Na⁺]_bound (less than 10 μM), was then used to adjust the molar ratios [Na]_s/[P] associated with each of the injections, and the Weisman isotherm was corrected by refitting to the adjusted data. Typically, the adjustments in the molar ratios are ∼20% for the first injection (which is routinely eliminated from the evaluation), and about ∼6% for the second; after the fifth injection, the adjustments are lower than 2%.

All-Atom MD Simulations and Free-Energy Calculations.

All MD simulations were carried out with NAMD 2.7/2.9 (62) using the CHARMM27/CMAP forcefield (63, 64), at constant temperature (298 K), constant pressure (1 atm), and constant membrane area, and with periodic boundary conditions. Electrostatic interactions were calculated using particle mesh Ewald with a 12-Å real-space cutoff; van der Waals interactions were also cutoff at 12 Å. The two simulation systems, i.e., the c-rings from the E. hirae V-type ATPase (31) and from the I. tartaricus F-type ATP synthase (21), embedded in hydrated 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) bilayers, were prepared with GRIFFIN (65), followed by a series of restrained (10 ns) and unrestrained (10–50 ns) simulations carried out to gradually equilibrate the protein–lipid interface and the ion–protein complex. In total, the systems include ∼210,000 atoms (540 lipid and ∼38,500 water molecules) and ∼100,000 atoms (237 lipid and ∼18,000 water molecules), respectively (Fig. S7). All binding sites in both c-rings were initially occupied with Na⁺. The total charge of both molecular systems is zero; 10 Cl⁻ ions were added to the E. hirae system to counter the net charge of the protein.

The free-energy perturbation (FEP) method was used to calculate the relative Na⁺/H⁺ selectivity of the two c-rings; the configurations obtained at the end of the unrestrained simulations were used as input. In these FEP/MD calculations, one of the bound Na⁺ ions and the coordinating carboxylate group (Cγ, Cδ, Oε₁, Oε₂ atoms) are gradually transformed into a protonated carboxyl group (Cγ′, Cδ′, Oε₁′, Oε₂′, Hε₂′), while the rest of the system adjusts accordingly. (The uncoupled Na⁺ ion was confined to the binding site using flat-bottom distance restraints to Cδ, Oε₁, and Oε₂, offset by 3.3 Å; note this value encompasses the full width of the probability distributions of these distances in the coupled state; Table S1.) These calculations were carried out in the forward (Na⁺ to H⁺) and backward (H⁺ to Na⁺) directions, using 51 intermediate simulations of 2 ns each, including 0.4 ns for initial equilibration. The free energy of this transformation, ΔG_site, is related to the free energy of selectivity of the binding site, ΔG_sel, by the following expression (29):

$$\begin{array}{c}\mathrm{\Delta }{\mathit{G}}_{\text{sel}}\left({\text{Na}}^{+}\to {\text{H}}^{+}\right)\mathrm{=-}{\mathit{k}}_{\text{B}}\mathit{T}\log \frac{{\mathit{K}}_{\text{d}}\left({\text{Na}}^{\mathrm{+}}\right)}{{\mathit{K}}_{\text{d}}\left({\text{H}}^{\mathrm{+}}\right)}\\ \mathrm{=}\mathrm{\Delta }{\mathit{G}}_{\text{site}}\left(\text{E}\mathrm{:}{{\rm N}\mathrm{a}}^{+}\to \text{E}\mathrm{:}{\text{H}}^{+}\right)\mathrm{-}\mathrm{\Delta }{\mathit{G}}_{\text{hyd}}\left(\text{E}\mathrm{:}{{\rm N}\mathrm{a}}^{+}\to \text{E}\mathrm{:}{\text{H}}^{+}\right),\end{array}$$ [5]

where K_d(Na⁺) and K_d(H⁺) are the dissociation constants of each ion and ΔG_hyd is the difference in the binding free energy of H⁺ and Na⁺ to a carboxyl group in water. It follows that the difference in the ion selectivity of two different c-rings is as follows:

$$\mathrm{\Delta }\mathrm{\Delta }{\mathit{G}}_{\text{sel}}\left({\text{Na}}^{+}\to {\text{H}}^{+}\right)\mathrm{=}\mathrm{\Delta }\mathrm{\Delta }{\mathit{G}}_{\text{site}}\left(\text{E}\mathrm{:{\rm N}}{\mathrm{a}}^{+}\to \text{E}\mathrm{:}{\text{H}}^{+}\right).$$ [6]

Note that differences in the local environment of the binding sites in the experiment and in simulation preclude a clearcut comparison of measured and calculated values of the Na⁺/H⁺ selectivity. By contrast, measured and calculated values of the difference in the ion selectivity of two binding sites ought to be directly comparable; provided that the two experiments and the two simulations are carried in similar conditions, environment-dependent factors are likely to be comparable for both binding sites and thus have a negligible influence on ΔΔG_sel.