Noninvasive in vivo imaging reveals differences between tectorial membrane and basilar membrane traveling waves in the mouse cochlea

Significance

The membranes within the cochlea vibrate in response to sound. However, measuring these vibrations to study the sense of hearing has been a technological challenge because invasive techniques have been required. Herein, we describe a new technique capable of depth-resolved displacement measurements in 3D space with picometer sensitivity within the unopened mouse cochlea. We used this technique to make, to our knowledge, the first measurements of the tectorial membrane, the structure that overlies the sensory hair cell stereociliary bundles, within a healthy cochlea. We found that the tectorial membrane sustains traveling wave propagation differently than the more commonly measured basilar membrane. This finding provides a clearer understanding of the mechanical stimulus at the level of the inner hair cell responsible for non-linear sound encoding.

Abstract

Sound is encoded within the auditory portion of the inner ear, the cochlea, after propagating down its length as a traveling wave. For over half a century, vibratory measurements to study cochlear traveling waves have been made using invasive approaches such as laser Doppler vibrometry. Although these studies have provided critical information regarding the nonlinear processes within the living cochlea that increase the amplitude of vibration and sharpen frequency tuning, the data have typically been limited to point measurements of basilar membrane vibration. In addition, opening the cochlea may alter its function and affect the findings. Here we describe volumetric optical coherence tomography vibrometry, a technique that overcomes these limitations by providing depth-resolved displacement measurements at 200 kHz inside a 3D volume of tissue with picometer sensitivity. We studied the mouse cochlea by imaging noninvasively through the surrounding bone to measure sound-induced vibrations of the sensory structures in vivo, and report, to our knowledge, the first measures of tectorial membrane vibration within the unopened cochlea. We found that the tectorial membrane sustains traveling wave propagation. Compared with basilar membrane traveling waves, tectorial membrane traveling waves have larger dynamic ranges, sharper frequency tuning, and apically shifted positions of peak vibration. These findings explain discrepancies between previously published basilar membrane vibration and auditory nerve single unit data. Because the tectorial membrane directly overlies the inner hair cell stereociliary bundles, these data provide the most accurate characterization of the stimulus shaping the afferent auditory response available to date.

Biomechanical properties directly relate to the physiological function of many tissues. The most popular techniques to measure tissue biomechanics, laser Doppler vibrometry (LDV) and atomic force microscopy, are limited to surface measurements. However, measurements made from the surface of a tissue may not adequately predict what is happening inside. The accurate measurement of subsurface displacements is particularly important when studying tissues composed of multiple layers of cells and extracellular matrix, each with different mechanical properties. The difficulty in measuring displacements deep in tissue with high sensitivity is particularly problematic for studies of the auditory portion of the inner ear, the cochlea, where a bony shell surrounds fluid-filled chambers that encompass the sensory tissues of the organ of Corti. Sound-induced vibrations of the organ of Corti stimulate transduction by sensory hair cells, which transmit the information to the auditory nerve. To measure the high-frequency, subnanometer vibrations in the cochlea, most in vivo studies of cochlear mechanics have opened the surrounding bone, placed a reflective glass bead on the undersurface of the organ of Corti, and then measured sound-evoked movements of the bead using LDV (1, 2). Opening the cochlea allows the light to enter and leave the interior of the cochlea, but can alter the vibratory pattern due to pressure changes, temperature changes, or mechanical trauma (3–6). Together, this large body of work has revealed how sound pressure waves, conveyed into the fluids of the inner ear by the middle ear ossicles, propagate longitudinally up the length of the basilar membrane (BM) in the form of a traveling wave (7). In addition, outer hair cells (OHCs) produce force to amplify and sharpen the traveling wave, a process termed cochlear amplification (2, 8). Cochlear amplification develops within the complex, interlocking, 3D structure of the organ of Corti (9–11).

Despite the critical role of cochlear amplification in creating the normal sense of hearing, the mechanical properties of the organ of Corti structures other than the BM have been essentially unstudied in vivo because of their inaccessibility to LDV. However, some recordings have been made from the top surface of the organ of Corti in the guinea pig cochlear apex using LDV (12–14). More recently, optical coherence tomography (OCT) has been used to study how regions within the organ of Corti other than the BM vibrate because it permits depth-resolved measurements inside tissue (15–18). These data have indicated that this complex structure does not vibrate as a rigid body (19, 20). However, the time-domain OCT and spectral-domain OCT systems used to date have been limited by slow data acquisition speed and a noise floor that is higher than that of LDV.

Herein, we report a new approach, volumetric optical coherence tomography vibrometry (VOCTV, pronounced “voctive”), which provides a practical method for depth-resolved displacement measurements with sensitivity and speed comparable to LDV. We prove the usefulness of this technique by directly measuring, to our knowledge for the first time, traveling wave propagation within the cochlea of living mice over a 3D volume of tissue by noninvasively imaging through the bony shell that surrounds the cochlea. We used this technique to measure vibration of the tectorial membrane (TM), the structure that overlies the hair cell stereociliary bundles, and compared its vibratory response to that of its commonly measured counterpart, the BM. The vibratory pattern of the TM is important to understand because this structure lies directly above the inner hair cell stereociliary bundles and thus is critical for shaping the afferent auditory response. We show that the ability of VOCTV to measure subsurface biomechanics within an organ permits physiologic investigations of organized multicellular tissues with complex biomechanics and greatly extends the ability to understand cochlear physiology.

Results

VOCTV was implemented using swept-source OCT with a 200-kHz sweep rate 1,310-nm center wavelength source. For vibrometry in particular, swept-source OCT provides a number of advantages over spectrometer-based OCT. The sweep rate is faster than the frame rate of commercially available OCT spectrometers, enabling the measurement of higher frequency signals. In addition, the long coherence length (>100 mm) improves the signal roll-off compared with typical spectrometer-based systems, providing the ability to image with negligible signal loss with depth. The coherence length is an inverse function of the linewidth of the laser. Because the swept-source laser has a very narrow instantaneous linewidth, the coherence length is long. The coherence length should not be confused with the axial resolution, which is a function of the wavelength range of the sweep. Another benefit of this approach is that swept-source OCT is compatible with balanced detection which strongly suppresses common mode noise including a component of excess intensity noise (21) while also canceling DC and autocorrelation artifacts.

VOCTV, however, required two key modifications beyond that necessary for routine swept-source OCT to achieve high vibrational sensitivity at high speed (Fig. 1A). First, one must correct for phase jitter caused by wavelength instability inherent to swept-laser sources and asynchrony between the source and sample clocks (22), as both factors impede measurement of subnanometer displacements. Using a phase reference from a nonvibrating structure within the scan can work in some situations (23). However, we completely eliminated phase jitter by calibrating the spectral interferograms every sweep using the phase of the Hilbert transform of the spectral interferograms from a Mach–Zehnder interferometer with a fixed optical delay that were simultaneously acquired. Second, because of the large amount of data inherent to the 4D data set collected with VOCTV, the amount of processing time can limit its usefulness for in vivo experiments. Real-time processing of large amounts of OCT data can be effectively performed using multiple GPUs (24). However, our swept-source OCT approach permitted pipelining, in which wavelength-by-wavelength processing could be performed during the laser sweep in real-time. Thus, we inserted a field-programmable gate array (FPGA) after the digitizer to perform linearization in the k-domain, real-time spectral-calibration, and Fourier analysis to generate the depth-resolved complex data for each axial line (A-line). In addition, hardware processing was beneficial because the length of time that each step takes was defined and consistent, thus guaranteeing that FPGA processing would enable continuous streaming of processed complex OCT A-lines. To reduce the bottleneck of data transfer to the CPU, we restricted the axial range of the A-line that was sent from the FPGA to only include a user-selectable region of interest. This strategy reduced the number of data points from 1,024 to ∼300, which increased the complex OCT A-line transfer speed to the CPU by ∼3×.

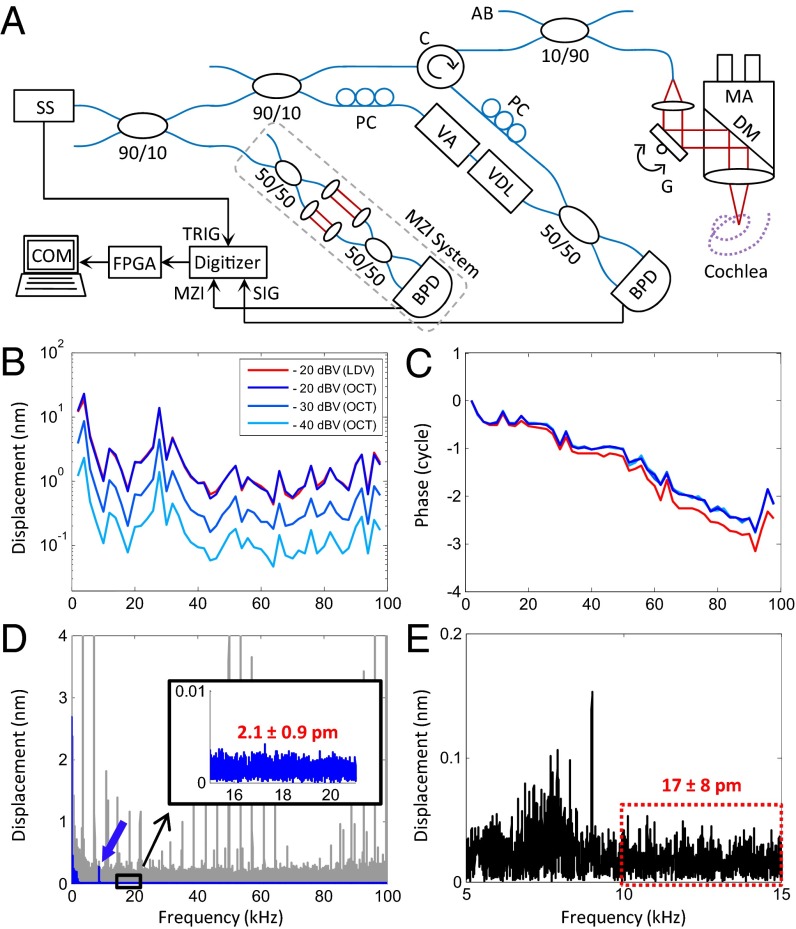
Fig. 1.

Schematic and characteristics of the VOCTV system. (A) System schematic: AB, aiming beam; BPD, balanced photodetector; C, circulator; COM, computer; DM, dichroic mirror; FPGA, Field-programmable gate array; G, 2D galvanometer; MA, microscopic adaptor; MZI, MZI signal; PC, polarization controller; SIG, OCT signal; SS, swept source; TRIG, sweep trigger; VA, variable attenuator; VDL, variable delay line. (B and C) Magnitude and phase of a vibrating piezo using OCT (blue) and LDV (red). The input voltage was varied from −40 to −20 dBV (dB relative to 1 V) in 10-dB increments. (D) Vibration magnitude of the piezo using a 9-kHz stimulus, 150-ms duration, and −40 dBV input voltage. Noise floor is high before phase calibration and exhibits large harmonic noise peaks (gray) that obscure the real measurement (blue), which is revealed after phase calibration. Postcalibration, the noise floor (Inset) closely approaches the SNR-limited theoretical value (1.7 ± 0.9 pm). (E) The vibration magnitude of the basilar membrane in a live mouse using a pure tone stimulus of 9 kHz, 3-dB SPL (sound pressure level), played for 150 ms. The noise floor in vivo was 17 ± 8 pm.

The frequency response of VOCTV was assessed using a piezoelectric actuator and found to be similar to LDV up to the Nyquist frequency of 100 kHz (Fig. 1 B and C). A frequency-dependent roll-off in the magnitude that matched theoretical predictions based on the sweep-rate and duty-cycle of the laser and a phase lead consistent with a fixed time delay were found and accounted for during data processing (Fig. S1). Because we sought to use VOCTV to measure displacements at known stimulus frequencies, we assessed the noise floor of the system in the frequency domain. Both the SNR of the voxel under study in the image and the recording length influence the noise floor, therefore we exclusively used a 150-ms recording time and specify the SNR for each measurement. No averaging was performed. From the piezo (SNR 59 dB), the noise floor was 2.1 ± 0.9 pm (mean ± SD; Fig. 1D). From a mirror (SNR 110 dB), the calculated noise floor was 4.8 ± 2.5 fm, close to the theoretical shot noise limit of 3.8 ± 2.0 fm (SNR 112 dB). Specific to our application, the noise floor of the mouse cochlea in vivo was 17 ± 8 pm at the basilar membrane (SNR 40 dB; Fig. 1E). This noise floor was low enough to enable the detection of vibrations in response to a 3-dB sound pressure level (SPL) pure tone stimulus, which is so barely audible that it is not typically used experimentally. These measurements validate the exceptional sensitivity of VOCTV and its appropriateness for in vivo vibrometry.

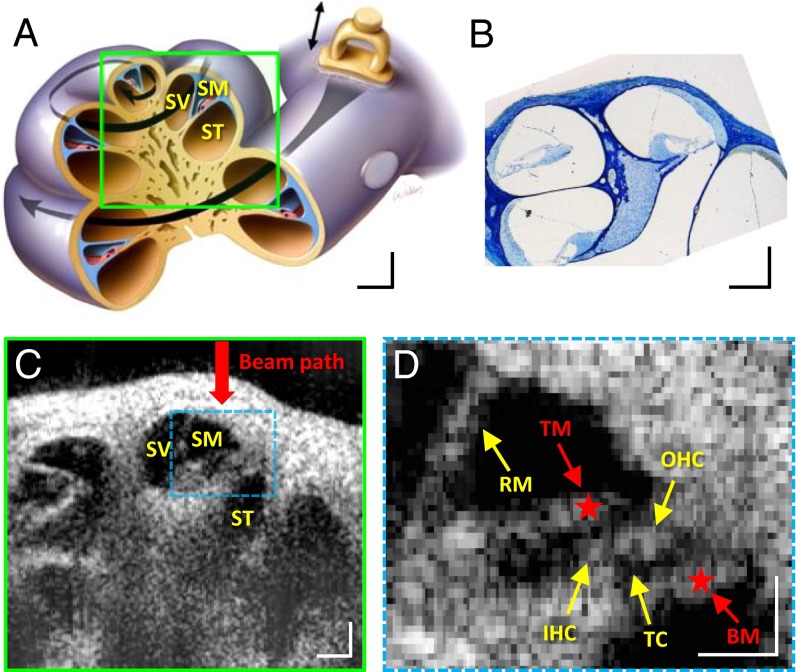
We scanned a cross-section of the mouse cochlea in vivo and generated anatomic images (Fig. 2). VOCTV enabled imaging through the otic capsule bone to noninvasively study the interior of the cochlea. Different cochlear turns, the three fluid-filled chambers that compose each turn, and the key structures of the organ of Corti were visualized. Thus, the resolution of the anatomic image was adequate to accurately localize the structures within the organ of Corti whose biomechanical properties are important to hearing.

Fig. 2.

Images of mouse cochlea in the apical turn. (A–C) Illustration (A), histological image (B), and cross-sectional OCT image (C) of the mouse cochlea. (D) Enlarged and frame-averaged image of the organ of Corti. Many structures within the organ of Corti are visible. BM, basilar membrane; IHC, inner hair cells; OHC, outer hair cells; RM, Reissner’s membrane; SM, scala media; ST, scala tympani; SV, scala vestibule; TC, tunnel of Corti; TM, tectorial membrane. Red stars highlight the measurement locations for the data in Fig 3 A–D. (Scale bars: 100 μm × 100 μm.)

The anatomic images were used to perform targeted vibrometry of the BM and TM. We investigated the BM because it is the most commonly studied structure and the TM because it stimulates the hair cell stereociliary bundles to elicit sound transduction. Because of its low scattering coefficient and inaccessibility, vibration of the TM has never before been measured in vivo noninvasively. We positioned the beam to the region of interest, played a pure tone into the ear canal of the anesthetized mouse, and collected the phase of the complex OCT signal at every voxel along the A-line over time. We then selected one voxel at the depth of interest and converted its interferometric phase into a measurement of the displacement magnitude and phase (relative to the sound stimulus) by Fourier transformation with zero-padding and Hanning windowing (25). The stimulus frequency and intensity were swept from 2 to 11 kHz and from 10 to 80 dB SPL, respectively, to obtain a series of vibratory response curves. We varied the stimulus duration from 20 to 100 ms, using longer durations for lower intensity stimuli to lower the noise floor and shorter durations for higher intensity stimuli to maximize the speed of data collection. The time required to measure a full series of curves at one x–y position was ∼2 min.

With this protocol, we measured the vibratory response from both the BM and the TM from the same cochlear cross-section (i.e., from the same longitudinal location along the cochlear duct) (Fig. 3 A and B). We then measured the vibration of the middle ear ossicular chain and normalized the responses of the BM and TM (Fig. 3 C and D). In some mice, we performed these measurements at four different locations along the length of the cochlea (Fig. S2). Consistent with the tonotopic gradient along the length of the cochlea, the characteristic frequency (defined as the frequency where the vibratory response is maximal for 10 dB SPL stimuli) depended on the location and was lower at the more apical locations. The phase of the BM and TM, normalized to that of ossicular chain, demonstrated a progressive phase lag as the sound frequency was increased, consistent with traveling wave propagation.

Fig. 3.

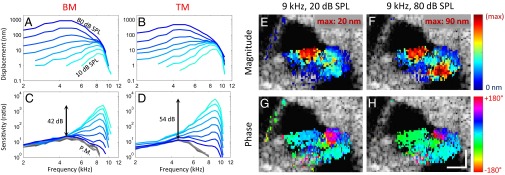
Vibration measurement of the organ of Corti. (A and B) Displacement measurements of the BM and TM. Each line corresponds to the displacement magnitude to sound stimuli ranging from 10- to 80-dB SPL in steps of 10 dB. (C and D) The displacement of the BM and TM divided by the displacement of the middle ear ossicular chain (sensitivity). In living mice, the BM and TM demonstrated nonlinear gain, with larger movements relative to the ossicular chain in response to lower intensity sounds. The postmortem sensitivities from the same mouse are shown in gray. The sensitivities overlapped at all tested sound intensities (30- to 80-dB SPL), indicating linearity. (E–H) Pseudocolored vibration magnitude (E and F) and phase (G and H) response to low intensity (E and G) and high intensity (F and H) sound stimuli at the characteristic frequency. The magnitude plots were normalized to the peak magnitudes in each image (20 nm and 90 nm). Vibrations below the noise floor threshold (mean + 3SD) were not plotted over the anatomic image. The phase at the center of the basilar membrane was set to 0° and the phase of all other voxels were referenced to it. (Scale bars: 100 μm × 100 μm.)

The vibratory responses of both the BM and TM demonstrated three key properties associated with cochlear amplification (26, 27), although there were important differences between the two structures in the degree of the effects (Table 1). First, both structures demonstrated gain, defined as the ratio of the peak vibrational sensitivity in living to dead mice. The gain was nonlinear, with larger relative displacements at low sound intensity levels. However, this effect was greater for the TM than for the BM. For example, TM displacement was about twice BM displacement in response to a 10-dB SPL sound stimulus. In contrast, at high sound intensities TM displacement was about half BM displacement. Second, both the BM and TM demonstrated sharper frequency tuning as the stimulus level was decreased. However, TM tuning was sharper than BM tuning, which we quantified by calculating the Q_10dB values using the vibrational magnitudes evoked by 10-dB SPL stimuli (the bandwidth 10 dB down from the peak magnitude was divided by the characteristic frequency). Third, the frequency at which the peak vibratory magnitude occurred in both the BM and the TM shifted to higher frequencies as the intensity was lowered. However, the amount of shift was ∼340 Hz greater in the TM compared with the BM. Together, the greater nonlinearities in the TM vibratory responses indicate that the TM is more affected by OHC force production than is the BM during the process of cochlear amplification.

Table 1.

Comparison between the vibratory characteristics of the BM and the TM

Measurement	Basilar membrane	Tectorial membrane	P value
Maximum displacement at 10-dB SPL, nm	4.66 ± 1.67	11.25 ± 3.43	<0.0001
Maximum displacement ratio between BM and TM at 10-dB SPL	DBM_10dB	DBM_10dB × (2.46 ± 0.33)	<0.0001
Maximum displacement at 80-dB SPL, nm	923 ± 168	472 ± 75	<0.0001
Maximum displacement ratio between BM and TM at 80-dB SPL	DBM_80dB	DBM_80dB × (0.52 ± 0.12)	<0.0001
Gain, dB	38.6 ± 4.4	53.0 ± 4.4	<0.0001
Q10dB of responses to tones presented at 10-dB SPL	3.69 ± 0.79	4.19 ± 0.78	<0.0001
CF, kHz	CFBM	CFBM + (0.34 ± 0.15)	<0.0001

All statistics are expressed as mean ± SD. n = 13 locations from eight mice. When measuring Q_10dB and CF, the 10-dB curves were fitted to fifth-order polynomials for interpolation purposes.

We then extended our measurement protocol to acquire 2D cross-sectional data by scanning the beam radially across the cochlear duct and recording from all voxels in the image. We applied a pure-tone sound stimulus at the characteristic frequency for that location (9 kHz) using either a low or high intensity (20- or 80-dB SPL, respectively). Vibratory responses 3SD above the mean noise floor were superimposed upon the anatomic images using pseudocolor (Fig. 3 E–H); magnitudes were linearly scaled to use the full pseudocolor range, and the phase of the basilar membrane was set to 0° with every other voxel referenced to it. As expected, the organ of Corti demonstrated sound-induced vibrations, whereas the surrounding otic capsule bone and bony core of the cochlea did not. Consistent with the previous measurements, BM displacements were larger than TM displacements at 80-dB SPL, whereas TM displacements were larger than BM displacements at 20-dB SPL. We also found differential motions between organ of Corti structures. For example, the phase of the TM led the BM at 20-dB SPL yet lagged the BM at 80-dB SPL. In addition, the lateral compartment of the organ of Corti (Hensen, Claudius, and Boettcher cells; pink region in Fig. 3 G and H) led the BM by ∼135° (19). These data provide clear in vivo evidence that the organ of Corti does not vibrate as a rigid body, but instead has complex mechanics.

Lastly, we used VOCTV to measure a 3D volume of tissue by scanning the beam both radially and longitudinally over the cochlear duct during the presentation of a 7.5-kHz sound stimulus at 20- and 40-dB SPL. To focus our analysis, we segmented the data (Fig. S3) and studied only the BM and TM. The vibratory pattern was reconstructed as a surface map in 3D space, using color to encode the amplitude of the response. Comparing the spatial patterns of vibration at a single time point for three different viewpoints emphasizes differences in the peak amplitude and peak position (Fig. 4 A–F). In addition, we plotted the magnitude and phase data en face (Fig. 4 G–J). Longitudinally, the location of the peaks in both structures shifted basally as the stimulus intensity was increased from 20- to 40-dB SPL, consistent with the known frequency-shift linked to the degree of cochlear amplification. However, at both intensities the location of peak TM vibration was more apical than the location of peak BM vibration. Radially, the peak TM vibrations occurred at the free edge, whereas in the BM they appeared near the midpoint. This result is consistent with the anatomy of these two structures, where the TM is medially fixed at the spiral limbus whereas the BM is fixed at both sides. The phase plots reveal that there were progressive phase lags along the length of the BM and TM, consistent with traveling wave propagation. We then reconstructed the propagation of the BM and TM traveling waves in 1D at three time points (Fig. S4) as well as in 3D throughout multiple phase cycles to create a movie (Movies S1 and S2). These visualizations highlight the ∼2× greater displacement magnitude and apically shifted peak position of the TM compared with the BM.

Fig. 4.

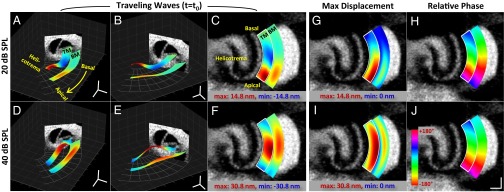
Traveling wave on the TM and BM along the length of cochlea at two different sound intensities. (A–F) Traveling waves shown from three different viewpoints. Images represent the peak magnitude response of the TM and BM membranes to a 7.5-kHz input sound at single time point. The displacement is exaggerated by 4,000× for clearer visualization. The range of the scaled JET colormap was set to the displacement range of the TM. (G–J) En face images of the magnitude (G and I) and the phase (H and J) of the vibration on the BM and the TM. The magnitude is scaled from zero to the maximum displacement of the TM and the phase is referenced to the phase of the BM at the basal-most spot. (Scale bars: 100 μm × 100 μm.)

Discussion

Optical coherence tomography has revolutionized in vivo tissue imaging (28–30). However, its widespread use in vibrometry has been limited for several reasons, including the vast quantity of data that must be acquired and processed very fast to make high frequency measurements, speed limitations inherent to spectrometer-based OCT, phase noise within the system, and difficulty in obtaining reliable and convincing anatomic images in vivo to localize the vibratory measurements (31). Here, we describe VOCTV, a technique which overcomes all these issues by combining swept-source technology, phase stabilization routines, and FPGA processing to provide high sampling and throughput rates with high sensitivity inside tissue. Thus, the ability to make noninvasive subsurface displacement measurements within biological tissues with a sensitivity smaller than atomic radii (30–300 PM) is now practical for in vivo use. We have demonstrated its suitability for extensive physiological studies of the mouse cochlea with 1D, 2D, and 3D measurements. Benefits of this approach are that it overcomes the need to either open the bone that protects the cochlea (32–35) or limit studies to only that region of the cochlea visible through the round window membrane (36, 37). The ability to image through the bone permit a wide range of experimental paradigms that were not previously possible, such as measuring BM and TM traveling waves as we show here.

The reliability of VOCTV for animal studies is another strong advantage over LDV. Nearly every experimental animal used for cochlear mechanics studies with VOCTV provides consistent data, whereas the rate of successful experimental outcomes with LDV is generally accepted to range from 5% to 50%. This is because of the ability of VOCTV to image deep into tissue, in our case, even peering through the bone surrounding the cochlea. However, there are limitations of this technique. The deeper the structure lies within tissue, the more the light is attenuated, which results in a higher noise floor. Also, the displacement measurement from one voxel is essentially an averaged motion of all structures within the point-spread function. Crosstalk occurs between nearby voxels when their point-spread functions overlap, degrading accuracy (38). To minimize this effect, we actively control the side-bands of our point spread function by conditioning the source spectral profile to resemble a Hanning window thus reducing side-lobes at the price of a slight reduction in axial resolution. Lastly, it should be pointed out that the vibrational measurements only reflect the vector component of motion parallel to the incident laser beam. Thus, measurements from different angles would be needed to recover the complete 3D vector of motion. This limitation is of particular importance when studying the TM, as it likely has a radial component of motion that defines how it stimulates the sensory hair cell stereocilia. As our measurements were not made directly perpendicular to the BM, the vibrational data presented in this manuscript should be interpreted as the vector sum of the transverse and radial motion.

This technology will clearly be important for studies of the auditory system because although inner hair cells furnish the majority of the afferent auditory input (39), nearly all in vivo cochlear mechanics measurements come from the BM. Using VOCTV, we get closer to the level of the inner hair cell by reporting, to our knowledge, the first direct, noninvasive measures of TM motion. Thus, VOCTV provides a unique and unparalleled way to measure the mechanical basis of sound transduction within the cochlea. We found that the TM supports traveling wave propagation, confirming ex vivo predictions (40). Compared with the BM, the TM has a larger dynamic range, sharper frequency selectivity, and a more apical position of maximal vibration. These differences explain discrepancies between single-unit auditory nerve recordings and basilar membrane vibratory responses. For example, simultaneous measures of auditory nerve responses and BM vibration in chinchilla have demonstrated that the auditory nerve does not respond as well as the BM vibration at low frequencies (41). However, this can now be explained by the larger dynamic range of the TM, which reduces the response to higher-intensity, lower-frequency stimuli. Another example is that the tonotopic frequency map of the cochlea based upon auditory nerve recordings is apically shifted compared with the map based upon BM vibratory responses and damage patterns after noise exposure (42, 43). The apically shifted TM response we measured may explain at least part of this difference.

Together, these findings support the concept that micromechanical interactions within the organ of Corti that have been previously unmeasurable modulate the stimulus to the inner hair cells, and affect the neural code of hearing. Modeling efforts have demonstrated how differential motion between two parallel structures could lead to sharp frequency tuning (44–46). The differences between the TM and the BM traveling waves that we measured strongly support this concept.

Methods

Animal Preparation.

The study protocol was approved by the Stanford IACUC. Wild-type CBA adult mice (ages P28–P42) of either sex were used. Each mouse was anesthetized with ketamine/xylazine, and its left middle ear bulla was surgically opened to access to the apex of the cochlea without disturbing the otic capsule bone. After performing all of the desired experiments in the living mouse, the animal was killed by anesthesia overdose so as not to move the head. Further measurements were made postmortem. Finally, vibration measurements were made from the middle ear ossicular chain.

Hardware.

The OCT system was custom-built and comprised a broadband swept-source with a center wavelength of 1,310 nm and 200-kHz sweep rate (MEMS-VCSEL, Thorlabs), 100-nm bandwidth, dual-balanced photodetector (WL-BPD600MA, Wieserlabs), and an 800-MHz digitizer (NI-5772, National Instruments). An adaptor was built to attach the sample arm to the bottom of a dissecting microscope (Zeiss Stemi-2000). A 2D galvo mirror (OIM101, Optics In Motion) was used to guide the beam, and a dichroic mirror permitted visualization through the oculars while simultaneously performing imaging. A 75-mm focal length objective lens was used. The spatial resolution of our system was measured to be 9.8 µm laterally, assessed by visually discriminating separate lines on an Air Force target, and 15 µm axially in air, assessed as the full-width, half-maximum reflection from a mirror. For all experiments, the power on the sample was 16 mW.

Phase Stabilization Software and FPGA Processing.

OCT using a swept wavelength source experiences drifts and jumps in the OCT phase signal even with a stationary sample when the digitizer clock and laser sweep trigger are not synchronized (22). Wavelength calibration was performed on every sweep to achieve high phase stability for phase measurements. This calibration was performed by collecting the signal from a Mach–Zehnder interferometer (MZI) with a fixed optical pathlength difference simultaneously with the OCT signal through the second channel of the digitizer. The unwrapped phase of the Hilbert transform of a band-pass filtered MZI signal was used to identify indices to linearize the OCT signal in wavenumber (i.e., resampling). To mitigate the error of the discrete time Hilbert transform in the beginning and in the end, we discarded the first and last 10 data points of the Hilbert phase results. Phase drifts and jumps were effectively removed by the calibration procedure, and the noise floor was close to shot-noise limited value (Fig. 1D).

This processing algorithm was complex, requiring both calibration and interpolation in k-space. We performed this using an FPGA (NI-7966R, National Instruments) that was directly connected to the digitizer. Use of the FPGA allowed for a high degree of parallelism. It could also execute a user-defined pipeline with precise timing, which was critical to maintain high-speed data collection. The FPGA also permitted us to restrict the data transferred to the host to the depth region selected by the user (i.e., an area of the cochlea), which provided a significant speed-up as a result of the reduced amount of data transferred across the bus.

All processing up to and including the first FFT was done on the FPGA, providing the depth-resolved reflectivity profile (an A-line). The complex-valued FFT in the defined region of interest were transferred to the host. To get the vibratory response, the interferometric phase for a given depth was calculated and then processed in software by unwrapping in time, followed by a second FFT with zero-padding and Hanning windowing. A full series of response curves from a single voxel covering 20 frequencies and 8 intensities could be collected and processed in ∼2 min. 2D and 3D vibratory maps using a sound stimulus at one frequency and one intensity took 1–2 min and 10–20 min, respectively, depending on number of x–y positions sampled and the signal-to-noise ratio of the OCT signal. Lower sound intensities required longer measurement times because a longer duration sound was necessary to achieve a low noise floor.

Vibration data from any given voxel were not analyzed if the anatomic image intensity of that voxel was <3SD of the noise floor of the background intensity or if the vibration magnitude at the stimulus frequency was below a threshold set at the mean + 3SD of the noise floor measured at nearby frequencies. This ensured a >99.4% measurement validity based on Rician distribution of magnitude data (47). The data collection software, including the FPGA routine, was coded in Labview (National Instruments) and the analysis software was coded in MATLAB (Mathworks). Throughout the manuscript, positive phase indicates a lead and negative phase indicates a lag.

Stimulus Generation.

Sound stimuli were synthesized in software, output by a speaker, and carried through a tube to enter the ear canal of the mouse as described (48–50). The sound waveforms were sent through a DAQ (NI-6363, National Instruments) and triggered by the sweep trigger from the laser to synchronize the sound output with the data collection.