Segmentations of MRI Images of the Female Pelvic Floor: A Study of Inter- and Intra-reader Reliability

Abstract

Purpose

To describe the inter- and intra-operator reliability of segmentations of female pelvic floor structures.

Materials and Methods

Three segmentation specialists were asked to segment out the female pelvic structures in 20 MR datasets on three separate occasions. The STAPLE algorithm was used to compute inter- and intra-segmenter agreement of each organ in each dataset. STAPLE computed the sensitivity, specificity, and positive predictive values (PPV) for inter- and intra-segmenter repeatability. These parameters were analyzed using intra-class correlation analysis. Correlation of organ volume to PPV and sensitivity was also computed.

Results

Mean PPV of the segmented organs ranged from 0.82 to 0.99, and sensitivity ranged from 33 to 96%. Intra-class correlation ranged from 0.07 to 0.98 across segmenters. Pearson correlation of volume to sensitivity were significant across organs, ranging from 0.54 to 0.91. Organs with significant correlation of PPV to volume were bladder (−0.69), levator ani (−0.68), and coccyx (−0.63).

Conclusion

Undirected manual segmentation of the pelvic floor organs are adequate for locating the organs, but poor at defining structural boundaries.

Qualitative and quantitative differences in the three-dimensional (3D) depiction of pelvic floor anatomy of asymptomatic nulliparous (1,2) and symptomatic women (3) have been reported. The transformation of two dimensional (2D) magnetic resonance imaging (MRI) data, obtained from thin-section images, to a 3D rendering is accomplished by manual segmentation, that is, serial outlining of each anatomic structure to be displayed in the 3D rendering. Subsequently, a series of advanced imaging processing techniques based on triangle decimation and the marching cubes algorithm is applied to form 3D objects that can be given color and opacity, and can be rotated and manipulated in space (4,5). The volume of any given 3D structure can be readily calculated, using voxel size information from the original MR scan.

Image-based 3D reconstruction has proven to be a useful research technique for localizing and measuring the volume of tumors in the brain, kidneys and bladder (5–8). In several pelvic floor imaging studies, 3D renderings have been used to measure the volume of the levator ani in healthy women and those with incontinence, prolapse and other measures of pelvic floor dysfunction (1,3,6). In another study, 3D renderings were used to quantify diminished levator ani muscle mass in women with pelvic floor dysfunction (9).

It is hypothesized that evaluation of 3D renderings may improve understanding of anatomical and pathophysiologic changes in women with pelvic floor disorders, However, the research utility of such comparisons depends on a standardized and reproducible technique for creating and measuring the 3D renderings (4).

The purpose of the present analysis is to evaluate the inter- and intra-observer reliability of the segmentation technique used to generate the 3D renderings, applied to the bony and soft tissue structures of the female pelvis, as derived from MR images obtained using a standardized protocol.

MATERIALS AND METHODS

Source images for this study were acquired from a large cohort of well-characterized women in a multi-center trial, the Childbirth And Pelvic Symptoms study of the Pelvic Floor Disorders Network (10). Data acquisition was prospectively acquired following IRB approval at sites associated with six network clinical sites and the Data Coordination Center. This study is HIPAA-compliant and informed consent was obtained from all participants. Two hundred MR data sets were obtained from a multicenter study comparing 2D MRI studies from newly primiparous women at 6–12 months postpartum. Eighty-eight of the women sustained an advanced perineal tear during vaginal delivery, 81 delivered vaginally without an advanced perineal tear, and 31 delivered by cesarean section before labor.

Imaging parameters were standardized across study centers in the original protocol to minimize the effect of imaging variations on the final measurements. The source MR images of the pelvis were obtained in the axial plane, using a 1.5 Tesla (T) magnet and a surface coil. Source imaging parameters were: T2 Turbo SE axial images with repetition time (TR) 5000 ms, echo time (TE) 132 ms, field of view (FOV) 200 cm, slice thickness 3 mm/interleaved, no gap, flip angle 180°, matrix 270 × 256.

Twenty of the reconstructed MR data sets were randomly chosen from the study group. The proportions of datasets from cesarean and vaginal delivery with and without advanced tears were similar to the larger group. Three segmentation specialists (readers) were asked to segment out the bony and soft tissue pelvic structures from each of the 20 MR datasets, each on 3 separate occasions using the 3DSlicer software (11) (www.slicer.org). Two of the readers were fellowship trained urogynecologists both trained by a body radiologist to interpret female pelvic MR images, and the third was a computer scientist, also trained in the interpretation of female pelvic MR images. All were very familiar with female pelvic MRI anatomy, and each had several years experience in segmentation of female pelvic floor structures. The source MRI data-sets were shuffled, and delivered to the individual readers in random order, such that each reader was unable to identify the dataset being segmented. Segmentation was performed on a Windows^™ based computer workstation, with an advanced graphics processor, and a 20-inch hi resolution color LCD monitor, and pen-based graphics tablet. The 3DSlicer software was loaded, which allows for multiplane visualization of the grayscale MR images. Segmentation was performed on the axial images, with real-time visual feedback from the coronal and sagittal planes.

Before performing the segmentations for study analysis, a dedicated 1-day training session was completed, in which the extent of each structure was demonstrated on a sample MRI dataset. The readers agreed on the general location and extent of each organ, using the sample MRI dataset, before proceeding to segment the study datasets. The organs selected for segmentation and analysis were pelvic bones, symphysis, coccyx, obturator internus, levator ani, vagina, rectum, urethra, and bladder. For each organ, therefore, there would be 9 segmentations (3 per reader, times 3 readers), and 20 datasets, for a total of 180 segmentations per organ. In cases where the organs could not reliably identified, an individual reader had the option of choosing not to segment that organ.

IMAGE ANALYSIS

Upon completion of all segmentations, a specialized algorithm, known as the STAPLE algorithm (12), was applied to determine the inter- and intra-reader agreement in the segmentation of each organ on each dataset. The STAPLE algorithm estimates a consensus (reference) segmentation and quantitative performance evaluation from a collection of segmentations. We assume that there is an underlying unknown reference standard segmentation, which each expert would agree on and is trying to generate when labeling the image. Each expert generates a segmentation by labeling the image according to their interpretation of the MRI, on a slice by slice basis. We assume the expert may make some random errors in labeling voxels, and as a consequence, repeated segmentations by the same expert are not always the same. We characterize the quality of each expert segmentation by the probability that the label the expert gives to a voxel matches the underlying reference standard segmentation. When we consider each segmented structure by itself, the probability that the expert labels the structure when the reference standard also labels the structure, is well-known as the sensitivity.

Because this measure depends on the size of a structure, it is also helpful to characterize performance in a manner that does not depend on how much of the image is occupied by the structure, and this is described by the probability that the label of the reference standard segmentation matches the segmentation label provided by the expert. When we consider each segmented structure by itself, this probability is the well-known positive predictive value, and in general is called the posterior probability value.

For each dataset, STAPLE computes a “consensus” reference standard, based on the voxels included in each segmentation for a specific organ. This “true” reference standard is then used to evaluate the voxels in each individual segmentation of that organ to look for agreement. This technique is applied to each organ for each dataset. For an intra-reader analysis, STAPLE was used to compute the consensus (reference) from the three segmentations of each organ performed by an individual reader, for a single dataset, and compares each of the three segmentations against that consensus. For an inter-reader analysis, STAPLE computes the consensus from all of the segmentations in that dataset, and then compares each individual segmentation against that consensus to determine the agreement for each organ of that dataset.

Statistical Analysis

For each organ of each dataset, the STAPLE algorithm reports on the sensitivity, specificity, and positive predictive values of the intra- and inter-reader variability. These parameters are explained as follows.

STAPLE compares the voxels in the individual segmentations to the voxels in the probabilistic “true” reference standard, and measures classification accuracy rates. If a voxel is selected in the individual segmentation, and selected also in the “true” reference standard segmentation, this is considered agreement. If a voxel is un-selected in the individual segmentation, and un-selected also in the “true” reference standard segmentation, this is also considered agreement. If a voxel is present in the individual and absent in the reference segmentations, this is considered non-agreement.

If we denote the reader segmentation decision as D and the “true” organ present as L, then STAPLE estimates the following performance rates: Pr(D = d|L = l), and Pr(L = l|D = d). For the present conventional binary segmentation problem, where each voxel is labeled either 0 or 1, we interpret Pr(D = 1|L = 1) as sensitivity (i.e., reader and consensus agree that voxel is present), Pr(D = 0|L = 0) as specificity (i.e., reader and consensus agree that voxel is absent), and Pr(L = 1|D = 1) (the posterior probability that the true label is 1 when the rater has decided the label is 1) as positive predictive value.

Next, we compared the volumes between the readers for each organ to look for divergences between readers. Volumes are reported in cubic millimeters.

Finally, to quantify the reliability of the volume, we calculated a measure of reliability known as the intra-class correlation (ICC) (13). ICC can be conceptualized as the ratio of variance between images to total variance; this ratio is high when the volumes from the segmentations of each image clusters in a narrow range compared with the range over which all the images are measured. A high ICC value indicates good reliability, in terms of volume agreement. Both good within-reader and between-reader reliability are required to assure good reproducibility. To study within-reader, between-reader, and overall reproducibility, for each organ, we calculated ICC for the volumes of the 3 segmentations from each reader separately and the ICC for the volumes of all the 9 segmentations. Because measurements are being repeated on the same image set, a high correlation between readers was expected; therefore, we set a threshold for the ICC of 0.85 to be considered reliable and a lower limit of 0.7 to be considered acceptable.

The rationale for reporting sensitivity and positive predictive value as the performance parameters is as follows: Consider sensitivity as the rate of correct detection of the organ, and specificity as the rate of correct detection of the region outside the organ. Sensitivity is reduced by failing to correctly label a part of the organ, and specificity is reduced by incorrectly labeling the region outside the organ. Consider the predictive value as the rate at which the true label of a voxel matches the label provided by the rater. The PPV is near 1 when the individual segmentation of an organ is contained within the consensus reference standard region of the organ, with possibly a small overlap at the edges. For example, if we examine the three graphs in the Figure 1, where the red (heavy) rectangle is the consensus area and the light rectangle is the predicted area, for A the PPV is high, for B it is 1 and for C it is low. However, none of the three predictions is close to the consensus. Another way of thinking of this is that if the readers use different criteria to identify the edges of an organ so that one lies within the other (such as, concentric circles), to the extent that the consensus includes the largest circle, all the PPVs will be 1; if the consensus is within the largest circle then the smaller circles will have a PPV of 1 and the largest will have a PPV equal to the percent of coverage that the consensus has relative to the largest circle, which is likely to be high.

Figure 1.

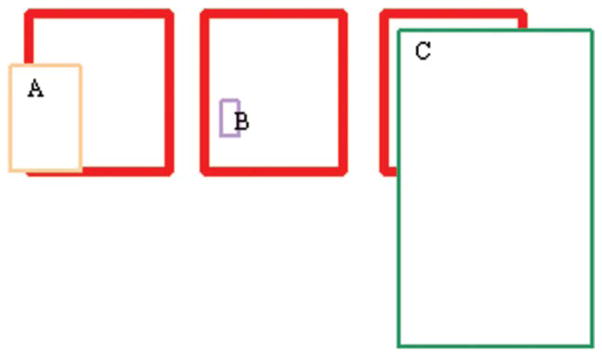
Three cases of high (A,B) and low (C) PPV, with varying sensitivities. The heavy red box represents the consensus segmentation, and A, B, C boxes represent individual segmentations compared against the consensus. The sensitivities vary from low (B) to medium (A) despite high PPV, and a high sensitivity is noted in (C), despite a low relatively low PPV.

If on the other hand, we use sensitivity as the criterion, then we would like the prediction by a reader to cover a large percent of the consensus area. In the above diagram, the sensitivity would be high for C and low for A and B. Therefore, we see that there is a difference between whether we measure the prediction within the consensus or the consensus within the prediction.

Therefore, a high PPV and low sensitivity indicates that the segmenters identified the organs within the same region (high PPV) but did not agree on the location of the organ boundaries (low sensitivity).

In addition, it is common to use both sensitivity and specificity to give complete information on an association between a test and disease. However, in this study, because the volume of background is much larger than that of any single organ, the specificity for any segmentation will be close to 1. Therefore, calculating specificity has little meaning for quantifying the quality of any of the segmentations, and this parameter is not considered further.

Furthermore, large differences in volume between readers are indicative of disagreement on the landmarks defining the organ. When there is a large difference, then the smaller volume has a greater chance of being embedded in the consensus (because the consensus is computed from all the predictions), i.e., a higher PPV, and a larger volume has a greater chance of covering the consensus, i.e., a higher sensitivity. Therefore, we also computed the correlation between PPV and volume and between sensitivity and volume to demonstrate these relationships. The volumes for each image were standardized before computation of the correlations.

Good agreement relies on both agreement on volume and position of each organ. For the segmentations to agree, the volumes of all the segmentations must have small variability within each image, i.e., if the volumes have high variability, the segmentations must have low reliability.

Large differences in volume between readers would be indicative of disagreement on the landmarks defining the organ, either within the slice planes or across the range of slices chosen for segmentation. When there is a large difference, then the smaller volume has a greater chance of being embedded in the consensus (because the consensus is computed from all the predictions), i.e., a higher PPV, and a larger volume has a greater chance of covering the consensus, i.e., a higher sensitivity.

RESULTS

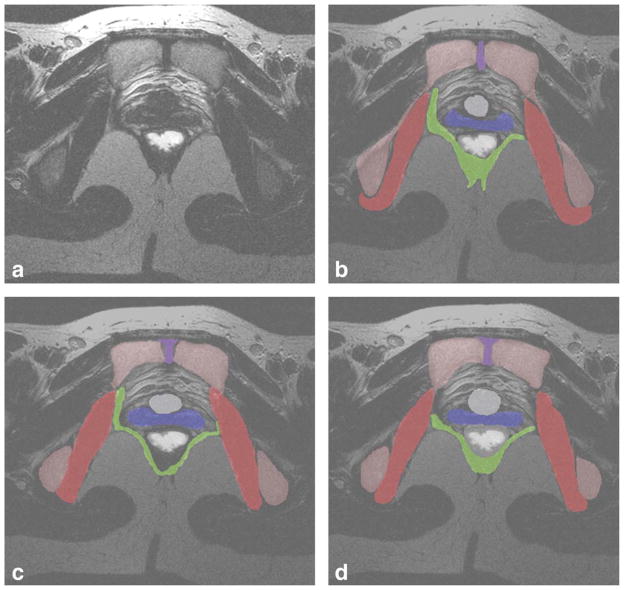
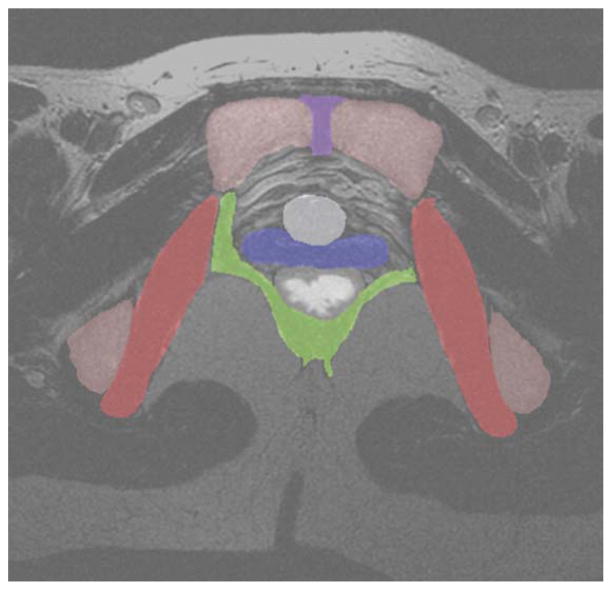
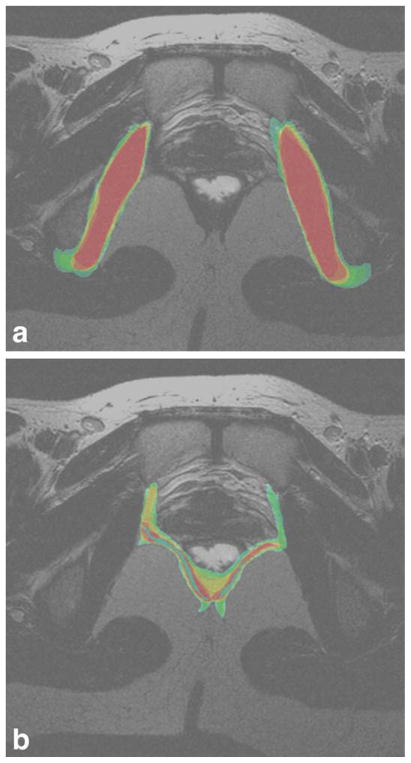
A sample MRI slice, taken at the level of the bladder neck is given in Figure 2a. Examples of individual segmentations of all organs from each of the 3 readers is given in Figure 2b–d. The consensus segmentation for this slice is given in Figure 3. The distribution of the average segmentation is given in Figure 4a, which demonstrated a structure with relatively high sensitivity and PPV (i.e., obturator internus muscle). Figure 4b demonstrates the distribution of the average segmentation for a structure with a relatively low sensitivity, but high PPV (i.e., levator ani).

Figure 2.

a–d: A sample T2-weighted axial MRI slice, taken at the level of the bladder neck is given in Figure 2a. Example individual segmentations of all organs from each of the three readers is given in Figure 2b–d. Legend: red, obturator internus; green, levator ani; blue, vagina; white, rectum; gray, bladder neck; violet, symphysis; pink, pelvic bones.

Figure 3.

The T2-weighted axial MRI slice from Figure 1, shaded with the consensus segmentation of each organ as computed by STAPLE. Legend: red, obturator internus; green, levator ani; blue, vagina; white, rectum; gray, bladder neck; violet, symphysis; pink, pelvic bones.

Figure 4.

a,b: The distribution of average overlap is given in Figure 3a for a structure with high agreement (the obturator internus), and Figure 3b for a structure with low agreement (levator ani). In these figures, areas in red indicate areas of complete agreement among all nine segmentations for that slice. Orange indicates a region of less agreement, with decreasing agreement in the order yellow, green, and blue, which indicates the least agreement.

Table 1 presents the PPV and sensitivity for each of the measures. The PPV is high, but sensitivity is low for almost all organs except the bladder.

Table 1.

Summary of Sensitivity and PPV by Segmenter and by Organ

Organ	Segmenter	N	Sensitivity				PPV
			Mean	Std Dev	Minimum	Maximum	Mean	Std Dev	Minimum	Maximum
Background	1	56	0.99	0.00	0.99	1.00	0.98	0.01	0.94	0.99
	2	56	1.00	0.00	1.00	1.00	0.98	0.01	0.96	0.99
	3	57	1.00	0.00	1.00	1.00	0.97	0.01	0.93	0.98
Bones	1	55	0.78	0.06	0.62	0.86	0.87	0.11	0.58	0.95
	2	56	0.78	0.04	0.71	0.85	0.95	0.03	0.87	1.00
	3	57	0.57	0.08	0.46	0.75	0.94	0.13	0.00	1.00
Vagina	1	53	0.50	0.12	0.29	0.67	0.93	0.20	0.00	1.00
	2	56	0.78	0.10	0.56	0.91	0.91	0.08	0.61	1.00
	3	57	0.68	0.14	0.41	0.85	0.95	0.03	0.84	1.00
Obturator	1	53	0.86	0.02	0.82	0.89	0.87	0.22	0.00	0.97
	2	56	0.83	0.03	0.76	0.88	0.89	0.22	0.00	0.99
	3	57	0.69	0.09	0.51	0.88	0.91	0.22	0.00	0.98
Urethra	1	54	0.59	0.09	0.41	0.74	0.93	0.23	0.00	1.00
	2	56	0.78	0.08	0.60	0.88	0.89	0.22	0.00	1.00
	3	57	0.79	0.08	0.67	0.92	0.89	0.21	0.00	1.00
Bladder	1	54	0.96	0.03	0.89	0.99	0.91	0.06	0.69	1.00
	2	56	0.80	0.14	0.55	0.97	0.99	0.01	0.97	1.00
	3	57	0.78	0.20	0.43	0.98	0.99	0.04	0.73	1.00
Rectum	1	54	0.87	0.09	0.63	0.99	0.89	0.24	0.00	1.00
	2	56	0.84	0.13	0.45	0.95	0.90	0.22	0.00	1.00
	3	57	0.59	0.24	0.19	0.95	0.96	0.05	0.82	1.00
Levator	1	53	0.77	0.07	0.64	0.88	0.82	0.10	0.59	1.00
	2	56	0.49	0.08	0.40	0.66	0.95	0.04	0.82	1.00
	3	57	0.33	0.06	0.23	0.42	0.91	0.05	0.73	1.00
Coccyx	1	49	0.57	0.18	0.24	0.85	0.91	0.12	0.39	1.00
	2	55	0.76	0.09	0.63	0.90	0.83	0.16	0.43	1.00
	3	57	0.53	0.14	0.23	0.70	0.95	0.06	0.78	1.00
Symphysis	1	52	0.43	0.15	0.24	0.74	0.85	0.25	0.00	1.00
	2	56	0.77	0.10	0.50	0.92	0.89	0.09	0.53	1.00
	3	57	0.54	0.11	0.34	0.80	0.94	0.07	0.58	1.00

Table 2 shows the correlation between sensitivity and volume and PPV and volume. Sensitivity is positively related to volume for all measures. For all measures, PPV is negatively related to volume. Large differences in volume is noted between readers, in the setting of high PPV.

Table 2.

Correlation Between Volume and PPV, Correlation Between Volume and Sensitivity

Organ	PPV		Sensitivity
	Pearson correlation	P value	Pearson correlation	P value
Background	−0.80	<0.0001	0.66	<0.0001
Bones	−0.23	0.0024	0.91	<0.0001
Vagina	−0.18	0.021	0.89	<0.0001
Obturator	−0.060	0.044	0.77	<0.0001
Urethra	−0.094	0.23	0.91	<0.0001
Bladder	−0.69	<0.0001	0.54	<0.0001
Rectum	−0.071	0.34	0.80	<0.0001
Levator	−0.68	<0.0001	0.97	<0.0001
Coccyx	−0.63	<0.0001	0.82	<0.0001
Symphysis	−0.17	0.029	0.88	<0.0001

Comparison between the volumes between the readers for each organ is given in Table 3. Note that for each organ, except background, there is at least one reader that diverges from the other two.

Table 3.

Mean Organ Volume by Segmenter and by Organ

Analysis Variable: volume (in cubic millimeters)
Organ	Segmenter	N	Mean	Std dev	Minimum	Maximum
Background	1	56	4200379.64	788086.56	1997880.25	5335986.33
	2	56	4216916.97	761854.19	2022996.83	5118986.21
	3	57	4299626.27	779117.89	2058588.87	5278183.59
Bones	1	55	141922.28	31881.84	96148.22	244373.23
	2	56	134448.17	27816.51	84977.42	205251.48
	3	57	90387.13	19187.19	61301.27	136153.22
Vagina	1	53	18851.85	5558.59	10050.66	37374.21
	2	56	31603.58	7655.83	19515.38	48037.02
	3	57	22495.96	5770.48	9528.81	37916.83
Obturator	1	53	90319.22	15280.40	55538.18	119129.64
	2	56	91642.50	16696.26	64063.11	128875.84
	3	57	69520.14	13578.65	40735.12	106832.80
Urethra	1	54	2938.96	855.03	1361.39	5586.59
	2	56	4693.17	1081.66	2735.60	8148.15
	3	57	4492.98	1237.58	2375.34	9201.00
Bladder	1	54	59557.60	42188.52	18881.84	149519.50
	2	56	48426.12	40981.13	7575.07	133086.78
	3	57	48883.96	41384.21	7902.83	131879.88
Rectum	1	54	46127.94	18164.27	11983.34	101299.10
	2	56	44799.67	16398.30	20278.88	84292.22
	3	57	35387.47	16302.28	9902.34	81114.26
Levator	1	53	38981.40	10953.01	16492.31	75933.84
	2	56	21537.35	4613.26	12391.69	30590.97
	3	57	16926.42	4948.43	10210.90	29563.06
Coccyx	1	49	1646.27	758.81	311.28	4025.13
	2	55	3589.47	1400.38	1137.08	6781.79
	3	57	1508.64	419.03	560.76	2625.29
Symphysis	1	52	1617.89	738.63	293.43	3834.72
	2	56	3122.21	970.95	1654.40	6941.53
	3	57	2350.76	848.44	1083.98	4960.33

The calculated ICC for the volumes of the three segmentations from each reader, and the separately calculated ICC for the volumes of all the nine segmentations are shown in Table 4. This table shows that most of the organs have very poor overall ICC values, except for bladder. For those organs with overall low volume reproducibility, within segmenter ICCs for all the organs are also poor for at least one segmenter. In addition, the overall ICC for an organ is always lower, sometimes much lower, than the smallest within-reader ICCs for that specific organ.

Table 4.

Intra-class Correlation for Organ Volumes

Organ	3 Readings for segmenter 1	3 Readings for segmenter 2	3 Readings for segmenter 3	9 Readings for all segmenters
Background	0.99	0.9997	0.999	0.99
Bones	0.56	0.96	0.73	0.37
Vagina	0.63	0.72	0.53	0.31
Obturator	0.70	0.94	0.78	0.51
Urethra	0.42	0.80	0.71	0.37
Bladder	0.99	0.997	0.996	0.98
Rectum	0.29	0.57	0.41	0.24
Levator	0.64	0.80	0.39	0.16
Coccyx	0.14	0.54	0.28	0.07
Symphysis	0.05	0.75	0.58	0.24

DISCUSSION

Sensitivity is low for almost all organs except the bladder, despite the high PPV. This indicates that the readers identified the organs within the region of the consensus (high PPV) but did not agree on the location of the organ boundaries. (low sensitivity). This is demonstrated in Figure 4a,b, where the distributions of segmentations for the obturator internus (Fig. 4a) and levator ani (Fig. 4b) are shown, respectively. In these figures, the red areas indicate areas of complete segmentation overlap across all segmentations from each reader. Decreasing overlap is indicated by orange colored regions, followed by yellow, green, and blue. For the obturator internus (mean sensitivity range, 0.69–0.86; mean PPV range, 0.87–0.91; Fig. 4a), the area of complete agreement (red) occupies a very large area of the widest (green) segmentation boundary, indicating relatively close boundary agreement across segmentations. However, for the levator ani (mean sensitivity range, 0.33–0.77; mean PPV range, 0.82–0.91; Fig. 4b), the area of complete overlap (red) is substantially smaller than the area of the widest (green) segmentation boundary, indicating high disagreement between readers regarding the location of the organ boundaries.

It should be noted that the bladder is well defined on the study images because it contains urine, which is MR opaque, making it easier to reliably identify. This would explain the high sensitivity and PPV for the bladder. For the other organs, the readers were not constrained in the range of image slices on which they were asked to identify the organs of interest. Variations in the range of slices segmented by a reader would affect the total segmented volume for a given organ, thus affect the ICC among and between readers. The extent of slice range variability was not investigated in the present study.

Sensitivity is positively related to volume for all measures; that is, the greater the volume the more likely it is to include the consensus. PPV is negatively related to volume: that is, the greater the volume the lower the overlap between the measured organ and the consensus.

The large differences in volume between readers, in the presence of high PPV indicate that readers are segmenting within the consensus boundary of the organ, but are disagreeing on the location of the organ boundaries.

Comparison between the volumes between the readers for each organ is given in Table 3. Note that for each organ, except background, there is at least one reader that diverges from the other two. Because the PPV is large, the divergent reader is very likely segmenting “within” the consensus volume, but probably segmenting on less (or more) slices than the others.

Most of the organs have very poor overall ICC values, i.e., poor overall volume reproducibility, except for bladder. As noted previously, due to its opacity, the bladder is easier to reliably identify, which likely accounts for its relatively high volume reproducibility. For the other organs, segmented slice range variability likely contributed to the poor overall volume reproducibility.

The relatively high positive predictive values seen in our study suggest that readers are able to correctly identify the core of each organ, but the low sensitivities mean that there is disagreement regarding the location of the structural borders. Unsurprisingly, the sensitivity (or ability to locate a structure) increased with the structure’s volume. However, the large variation in volumes (and the low overall ICC) within the setting of high PPV suggests difficulty in agreeing on the organ boundaries,. accounting for the relatively low reproducibility in the present series.

In conclusion, The present results show that the manual segmentation process introduces variability into the reconstruction of 3D images from 2D source data.

The present findings suggest that undirected manual segmentation methods are adequate for locating structures of interest, but may be inadequate for defining structural boundaries, at least regarding female pelvic floor organs, identified by non-radiologists. It is notable that the present study did not attempt to define a “bounding box” volume to constrain the readers when they were segmenting out the individual organs. It is possible that constraining the readers to look only inside a specific bounding box might have produced improved results, but this possibility was not investigated in the present work. It is also possible that reduction in segmentation variability may be achieved using automatic segmentation algorithms, and this is an area for future work. It is also possible that different results might be obtained if the readers were all specialists in female pelvic floor radiology. These possibilities remain to be investigated further.