Orbitofrontal Cortex Is Required for Optimal Waiting Based on Decision Confidence

SUMMARY

Confidence judgments are a central example of metacognition—knowledge about one’s own cognitive processes. According to this metacognitive view, confidence reports are generated by a second-order monitoring process based on the quality of internal representations about beliefs. Although neural correlates of decision confidence have been recently identified in humans and other animals, it is not well understood whether there are brain areas specifically important for confidence monitoring. To address this issue, we designed a postdecision temporal wagering task in which rats expressed choice confidence by the amount of time they were willing to wait for reward. We found that orbitofrontal cortex inactivation disrupts waiting-based confidence reports without affecting decision accuracy. Furthermore, we show that a normative model can quantitatively account for waiting times based on the computation of decision confidence. These results establish an anatomical locus for a metacognitive report, confidence judgment, distinct from the processes required for perceptual decisions.

INTRODUCTION

If you are asked to report your confidence in a decision—how certain you are that you made the correct choice—you can readily answer. What is the neural basis for this ability? Early behavioral studies considered confidence judgments as a type of metacognitive process related to self-awareness. These studies established that several species besides humans are capable of confidence judgments but that some, such as rats, may not be (Flavell, 1979; Hampton, 2001; Smith et al., 2003; Metcalfe, 2008). Against this backdrop of behavioral results, a recent line of studies identified single neuron correlates of decision confidence across species, in the brains of rats and monkeys (Kepecs et al., 2008; Kiani and Shadlen, 2009; Middlebrooks and Sommer, 2012; Komura et al., 2013), as well as functional correlates in humans (Lau and Passingham, 2006; Fleming et al., 2010; Rolls et al., 2010a, 2010b; Yokoyama et al., 2010; De Martino et al., 2013). However, it is still not well understood where and how choice confidence is computed or how it is made accessible to an overt behavioral report. These issues are particularly interesting because they relate to the definition of meta-cognition and awareness.

A mechanistic interpretation of metacognitive theories implies that a second-order brain circuit reads first-order representations of a separate circuit and transforms them into a second-order representation, such as a decision variable for confidence (Kepecs et al., 2008; Kiani and Shadlen, 2009; Insabato et al., 2010; Middlebrooks and Sommer, 2012; Komura et al., 2013). The representation of decision confidence in specific brain regions implies that lesions of such brain areas might affect the behavioral manifestation of decision confidence without changing other aspects of the choice behavior. In contrast, theoretical studies suggest that because confidence estimation is central to statistical inference, it ought to play a fundamental role in probabilistic or Bayesian neural computations of all kinds (Zemel et al., 1998; Ma et al., 2006; Moreno-Bote, 2010; Rao, 2010). This view suggests that the computations of choice and confidence are mixed within the same neural circuits and hence representations of confidence might not be explicit or anatomically segregated (Higham, 2007). Consistent with these ideas, data from primates show that neurons in parietal cortex that represent a perceptual decision also encode the confidence associated with that decision (Kiani and Shadlen, 2009).

Here we pursued the hypothesis that orbitofrontal cortex (OFC) is causally required for confidence reporting independent of perceptual decision making. This hypothesis was based on two lines of evidence. First, previously we found that rat OFC contains an explicit representation of decision confidence (Kepecs et al., 2008). Second, OFC has been implicated in goal-directed or intentional decisions that require the evaluation of predicted outcomes (Padoa-Schioppa and Assad, 2006; Wallis, 2007; Rolls and Grabenhorst, 2008; Schoenbaum et al., 2009; Kennerley et al., 2011; Morrison et al., 2011; Jones et al., 2012). Because reporting confidence requires performing an action based on a predicted outcome, an intact OFC may be required for adaptive adjustment of the behavior according to decision confidence. At the same time, OFC is probably not involved in most perceptual decisions.

Studying confidence reports in animals requires a clear behavioral readout of confidence. Gambling on the outcome of a decision generates an observable wager that can quantitatively index confidence (Persaud et al., 2007; Middlebrooks and Sommer, 2012). Appropriate wagering requires an evaluation of decision confidence that can be distinguished from random betting using a computational approach (Kepecs et al., 2008; Fleming and Dolan, 2010; Fleming et al., 2010; De Martino et al., 2013; Kepecs and Mainen, 2012). Therefore to evaluate whether OFC is required for confidence reports of perceptual decisions, we designed a gambling task for rats with continuous wagers based on their willingness to wait for delayed reward, interpreted the wagers within a theoretical framework for statistical confidence, and used inactivation methods to probe the role of OFC in waiting-based confidence judgments.

RESULTS

A Postdecision Wagering Task

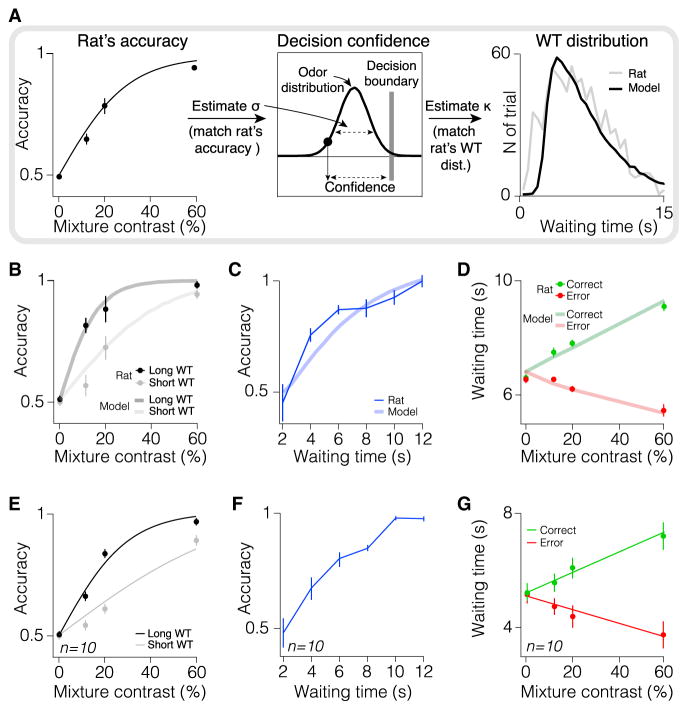
To study confidence in perceptual decisions, we used an extensively studied odor categorization task that allowed us to systematically vary the difficulty and hence confidence in a decision (Uchida and Mainen, 2003; Kepecs et al., 2008). Upon entry into a central odor port, rats (N = 10) received an olfactory stimulus (binary mixture of 2-octanol stereoisomers) and responded to the left or right choice ports based on the dominant odor component (Figure 1A, see Experimental Procedures). Trials with different odor-mixture ratios (20:80, 40:60, 44:56, and 50:50 mixtures and their conjugates, 80:20, etc.) were randomly interleaved. Rats achieved high performance for easy stimuli (larger mixture ratios), but were challenged by more difficult discriminations (Figure 1B). The perceptual accuracy was stable across several sessions of testing (Figure 1B). As previously reported (Uchida and Mainen, 2003; Zariwala et al., 2013), reaction times, as measured by the duration animals were sampling the odor before moving to the choice port, showed little sensitivity to odor-mixture ratio (Figure 1C; Figure S1 available online).

Figure 1. Postdecision Wagering Task Using Temporal Wagers.

(A) Schematic of the behavioral paradigm. To start a trial, rats entered the central odor port and after a pseudorandom delay of 0.2–0.5 s, a mixture of odors was delivered. Rats responded by moving to the left or right choice port, where a drop of water was delivered after a 0.5–8 s waiting period for correct decision (exponentially distributed with a decay constant of 1.5 after a 0.5 s offset and 8 s maximum). In a small fraction of correct choice trials, water rewards were omitted. Trials of different odor-mixture ratios were randomly interleaved independent of rats’ performance in the previous trials. While waiting for reward, animals were required to keep their snouts inside the choice port, which was continuously monitored using infrared photo-beams. Failure to break the photo-beam resulted in error.

(B) Behavioral performance and psychometric function of an example rat. Each thin line represents logistic fit (see Experimental Procedures) to the behavioral data collected in a single test session. Dots represent behavioral performance averaged across all trials of all test sessions. Thick gray line represents logistic fit to the average performance data shown with black dots. Error bars represent ±SEM across trials.

(C) Odor sampling duration (the duration animals were sampling the odor before moving to the choice port) as a function of odor mixture contrast in an example rat. Thin lines represent odor sampling duration in each of test sessions. Thick line represents the data averaged across all trials of all test sessions.

(D) The timing of reward delivery (blue, see Experimental Procedures) and the distribution of waiting times at the reward ports of all test sessions for one example rat (black). Waiting times were measured for all the error trials and fraction of correct trials (i.e., reward omission trials).

An ideal confidence-reporting task requires a report of choice and the confidence associated with that choice in the same trial (Kepecs and Mainen, 2012; Middlebrooks and Sommer, 2012). Lacking this, it is difficult to rule out alternative mechanisms, a limitation of opt-out tasks (Smith et al., 2008; Kepecs, 2013). In addition, a continuous, rather than discrete, behavioral measure of confidence might enable stronger inferences about the underlying mechanisms (Schurger and Sher, 2008; Kepecs and Mainen, 2012). To allow rats to wager on the likelihood that their decision was correct, we delayed reward delivery and measured the time animals were willing to wait at the choice ports (Figures 1A and 1D). Reward delay was drawn from an exponential distribution (decay constant, τ = 1.5, see Experimental Procedures) to generate a relatively constant level of reward expectancy over a range of delays (i.e., flat hazard rate; Janssen and Shadlen, 2005; Zariwala et al., 2013). Incorrect choices were not explicitly signaled and hence rats eventually left the choice ports to initiate a new trial. To measure waiting time (WT) for correct choices, we introduced a small fraction of catch trials (10%–15%) for which rewards were omitted. Therefore, in this novel postdecision wagering paradigm, each trial resulted in a binary choice as well as a graded wager, WT, for all incorrect trials and a fraction of correct trials.

Derivation of Optimal Confidence-Based Temporal Wagering

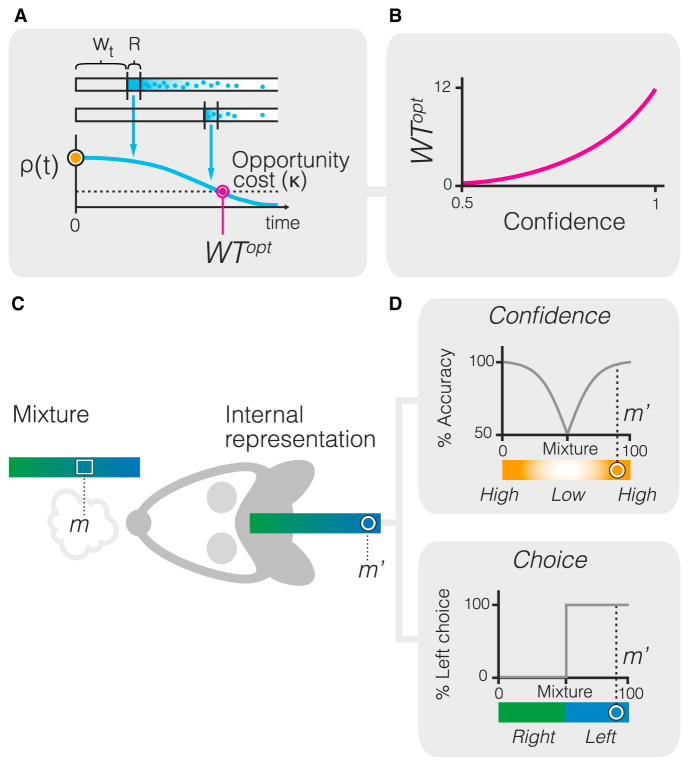
To maximize reward, an ideal observer should wait until the relative expected value of waiting for reward drops below the expected value of leaving. Because reward size is constant from trial-to-trial but depends on being correct, the subjective expected value of staying varies from trial-to-trial with the level of decision confidence. To derive the normative waiting time, we assumed that the observer arrives at the reward port with a specific internal expectation about how likely it is to receive the reward, reflecting its decision confidence, which we denoted by the variable C. Assume that the observer has spent time t in the port without receiving a reward. The observer then faces the decision whether to spend the next interval, from t to t + dt inside the reward port or leave and initiate a new trial. This decision should be based on the reward hazard function—the probability of getting reward at the next moment given that no reward has been received until now (Figure 2A). This probability can be computed through Bayes’ theorem. Let us denote as W_t the event that waiting until time t was not rewarded, and R the event that reward arrives at the next moment, from t to t + dt. The reward expectation (hazard) function can be expressed as the conditional probability P(R|W_t):

$$P(R\mid W_t)=\frac{P(W_t\mid R)P(R)}{P(W_t)}.$$ (Equation 1)

Figure 2. A Computational Framework for Estimating Waiting Time Based on Decision Confidence.

(A) The optimal waiting time can be estimated by comparing the rate of reward expectation ρ(t) and the opportunity cost, κ. While waiting for a reward, the agent faces this decision at each moment in time. If the expected rate of reward falls below the opportunity cost, the observer should abort the trial and initiate a new trial. The rate of reward expectation ρ(t) is the probability that a reward will arrive at the next moment (denoted as event R), given that the agent did not yet receive reward (denoted as event W)

(B) The model predicts that WT^opt monotonically increases with the level of decision confidence, C.

(C) In each trial, the stimulus is defined as the percentage of one of the components in the odor mixture (m) and the internal representation of the stimulus (m′) is a noisy read-out of the external stimulus.

(D) Choice in each trial is computed by comparing the value of m′ and the decision boundary (b = 50%), thus a step function of m′. Decision confidence, is a function of the distance between the internal representation of stimulus m′ and the decision boundary, as defined by Equation 7.

Notice that by definition the probability of waiting without reward given that reward arrives in the next moment, P(W_t|R), is 1. The probability of being rewarded at the next moment, P(R), depends on the subject’s estimate of the time of reward delivery. We denote the experimenter-defined temporal distribution of reward during the anticipation period as P_rew(t), a distribution that was kept fixed during testing (see Figure 1D, blue curve). Then the probability of getting rewarded at the next moment is given by:

$$P(R)=P_{\text{trial}}\times P_{\text{rew}}(t)dt,$$ (Equation 2)

where P_trial is the expectation of being rewarded in the current trial for the given choice. Because we are describing the reasoning of the ideal observer, the expectation to be rewarded should be based on the internal representation of response accuracy, which means that P_trial can be associated with the decision confidence, i.e., P_trial = C. The probability of waiting until time t without reward can be evaluated as 1 − P(W̄_t), i.e., as one minus the probability of being rewarded during that time

$$P(W_t)=1-C\underset{0}{\overset{t}{\int }}{P}_{\text{rew}}(t^{\prime })d{t}^{\prime }.$$ (Equation 3)

From these equations, we can compute the probability of being rewarded within time interval from t to t + dt under the condition that the reward was not delivered before that

$$\frac{P(R\mid W_t)}{dt}\equiv \rho (t)=\frac{C·P_{\text{rew}}(t)}{1-C\underset{0}{\overset{t}{\int }}{P}_{\text{rew}}(t^{\prime })d{t}^{\prime }}.$$ (Equation 4)

Here ρ(t) is the rate of reward expected by the observer within the next time interval, which is the reward expectation per unit time. Since, in our experiments, P_rew(t) = exp(−t/τ)/τ, we obtain the reward hazard as a function of decision confidence

$$\rho (t)=\frac{1}{\tau }\frac{{Ce}^{-t/\tau }}{1-C+{Ce}^{-t/\tau }}.$$ (Equation 5)

To obtain the optimal waiting time, the rate of reward expectation ρ(t) should be compared to the average reward rate for the session, κ, representing the value of leaving or opportunity cost. Indeed, if ρ(t)<κ, i.e., when the expected rate of reward falls below the opportunity cost, the observer should leave the port and initiate a new trial (Figure 2A). The optimal waiting time, WT^opt, can therefore be obtained from the equation $\rho ({WT}^{\text{opt}})=\kappa$, where ρ(t) is given by Equation 5, whereas κ is a parameter similar across trials. From this equation, the optimal waiting time is a function of the decision confidence, C (Figure S2):

$${WT}^{\text{opt}}=\tau ln\left(\frac{C}{1-C}\frac{1-\kappa \tau }{kt}\right).$$ (Equation 6)

Here C is decision confidence variable from trial to trial, whereas κ is the opportunity cost (a constant). Opportunity cost is expected to be smaller than 1/τ, because otherwise the ideal observer would not have an incentive to go to the reward port. Thus, the product κτ is less than one. This derivation reveals that WT^opt monotonically increases with confidence levels, consistent with intuition (Figure 2B and Figure S2). The equation predicts that when κ>C/τ, then WT is zero; meaning that in very low confidence trials or when the opportunity cost is large, it is not worth for the observer to wait inside the reward port. Thus in these cases the animal should abort the trial as quickly as possible.

To model decision confidence, we used a signal detection theory framework where each choice and its associated confidence could be estimated by comparing the sampled stimulus and the decision boundary. We modeled the stimulus as the percentage of one of the components in the odor mixture henceforth denoted by m and defined a noisy read-out of that as the internal representation of the stimulus m′ (Figure 2C; see Experimental Procedures). In each trial, the values of m′ exceeding the decision boundary (b = 50%) result in a response to the right, whereas the values m′<50% produce a left response (Figure 2D). The distance between the internal representation of stimulus m′ and boundary provides an estimate of decision confidence, C (Figure 2D). Specifically, decision confidence in our approach is defined as the probability of making the correct decision C = C(m′) (see Experimental Procedures). It is not difficult to see that for a simple decision task described here, the probability of being correct is

$$C(m^{\prime })=\frac{1}{2}\left[1+\text{erf}\left(-\frac{\mid m^{\prime }-b\mid }{\sigma \sqrt{2}}\right)\right],$$ (Equation 7)

where σ is the SD of overall sensory and internal noise distribution. Thus confidence, C, is an internal metric about the probability of choice correctness. Because the internal representation of the stimulus m′ varies from trial to trial even if the stimulus mixture m is fixed, response accuracy becomes coupled with decision confidence. Because C = C(m′) is an internal variable, it is not available for direct measurement but it could be assessed through the time spent by the observer in the reward port as described above (Equation 6). Notably, decision confidence with similar properties could also be derived from other decision frameworks based on Bayes’ rule, integration of evidence, and attractor models (Kepecs and Mainen, 2012).

Rats’ Behavior Is Consistent with the Normative Temporal Wagering Model

We used this computational framework to examine whether rats’ WTs could be used as a trial-by-trial proxy of decision confidence. To do so, we fitted our model to rats’ behavior (Figure 3). Starting from the rat’s psychometric curve, we estimated the overall choice uncertainty (SD of the overall sensory and internal noise distribution, σ, see Experimental Procedures for details of fitting). We then used the estimated σ to calculate the intermediate variable, decision confidence (C), for each trial (Figure 3A, middle). We then fitted a single free parameter, the opportunity cost, κ, that minimized the difference between rat’s and the model’s WT distribution (Figure 3A, right). Although this model fit the mean WTs for each condition well, to fit to the full WT distribution we also assumed that rat’s estimation of elapsed time carries uncertainty. Specifically, previous studies have shown that the SD of time estimates scales with elapsed time; referred to as “scalar timing” (Gibbon, 1977; Gibbon et al., 1997; Janssen and Shadlen, 2005). Therefore, for the fitting, the model’s WT distribution was blurred with a normal distribution whose SD was proportional to the elapsed time (Figure 3A, right; see Experimental Procedures). As expected from Equation 6, following this fitting, the WTs showed a monotonic relationship with the estimated confidence levels (Figure 2B), demonstrating that WTs in the task could be viewed as a trial-by-trial proxy for decision confidence.

Figure 3. Postdecision Waiting Time Report Follows Decision Confidence.

(A) Fitting the computational model to the behavioral data. Two parameters need to be estimated. First, the SD of the sensory and internal noise distribution (σ), which was used to calculate model’s trial by trial choice and confidence. Second, the opportunity cost (κ), which, alongside confidence and reward delay distribution (Equation 6) was used to calculate model’s WT. (Left and Middle) Estimating the model’s noise from rat’s psychometric curve; σ was estimated, which could minimize the difference between rat’s and model’s psychometric curves. The estimated σ was used to estimate the confidence associated with a choice in each trial. (Right) The opportunity cost, κ, was estimated by minimizing the difference between the rat’s and the model’s WT distributions. Following the fitting, the model’s WT distribution closely overlapped rat’s WT distribution. See Experimental Procedures for details of fitting.

(B–D) Predictions of the model and behavioral data from example rat. The model produces testable predictions about the relationship between confidence, perceptual accuracy, stimulus difficulty, and trial outcome. The predictions of the model closely match the behavioral data. In each image, thick lines represent the predictions of the model (with parameters optimized to fit rat’s accuracy curve and overall WT distribution) and behavioral data are shown as mean ± SEM across trials. (B) The model predicts that decisions with longer WT have higher accuracy (thick lines). Lines show model’s psychometric curves separated based on WT. Dark gray thick line represents long WT (defined as above 70^th percentile), light gray thick line represents short WT (shorter than 70^th percentile). Dots show rat’s perceptual accuracy separated based on WT. Black dots represent long WT trials (defined as above 70^th percentile) and gray dots indicate short WT trials (shorter than 70^th percentile). Logistic psychometric fits, used for the slope comparison, are not shown. (C) In the model, WT predicts choice accuracy (thick line). Consistent with this prediction, rat’s decision accuracy increases with longer WT (thin line). (D) The model predicts that waiting time varies with stimulus difficulty in opposing directions depending on choice correctness (thick lines; correct: green, error: red) and rat’s WTs are consistent with this prediction. Dots show mean WT of the example rat as a function of odor mixture contrast and trial outcome (correct, green; error, red).

(E–G) As in (B)–(D) averaged across 10 rats (mean ± SEM across rats). In (E), black and gray lines represent logistic fit on the accuracy data in long and short WT trials, respectively (see Experimental Procedures). In (G), lines represent linear fits on the rats’ WT data.

This model yields specific predictions about how WT, as a proxy for decision confidence, relates to other experimentally controlled and monitored variables. First, decisions in trials with longer WT are expected to have higher accuracy (Figure 3B, thick lines) for any given stimulus difficulty. Consistent with this prediction, when we separated behavioral trials into long and short WT, choice accuracy in trials with intermediate odor mixture contrast showed significant dependency on WT (Figures 3B and 3E, p < 0.05, Mann-Whitney U test across trials in 10/10 rats; and p < 0.05, Mann-Whitney U test across rats). The slope of the rats’ psychometric functions was also steeper for long WT trials (p < 0.05 in 10/10 rats; and p < 0.001 across rats, bootstrap test, see Experimental Procedures). Second, WT is expected to predict choice accuracy (Figure 3C, thick line). Consistent with this prediction, we found that animals’ WT-conditioned accuracy function (see Experimental Procedures) monotonically increased with longer WT, ranging from chance level to near-perfect performance (Figures 3C and 3F). Third, WT is expected to vary with stimulus difficulty in opposite directions depending on choice correctness (Figure 3D, thick lines). Indeed, we found that rats’ mean WTs varied with stimulus difficulty, and this relationship was opposing for correct and error trials (Figures 3D and 3G). For all these predictions, the model with parameters optimized to fit the rats’ overall WT distributions (Figure 3A) showed a striking match to their behavioral data, as can be seen in Figures 3B–3D. These properties further established WT as a good trial-by-trial proxy of C and suggest that it can serve as an implicit report of decision confidence.

We also examined the effects of trial history on the stability and confidence-dependence of WT. We found that the mean WT was stable from the beginning to the end of a session (Figures S3A and S3B, p > 0.3, Mann-Whitney U test across trials in 10/10 rats; and p = 0.86, Mann-Whitney U test across rats). We observed a small but systematic effect of the outcome of the previous trial (correct/error) and the WT of the previous trial (short/long) on absolute WT. Rats tended to wait longer for reward following trials with correct outcome as well as after trials with long WT. These effects did not reach significance when averaging across rats (Figure S3A, p > 0.10, Mann-Whitney U test across rats), but were significant in many individual rats (Figures S3C and S3D, p < 0.05, Mann-Whitney U test across trials in 7/10 rats for the effect of previous outcome, and 5/10 rats for the effect of previous WT). These patterns of modulation would be expected if the distribution of temporal reward expectancies, P_rew(t), was updated based on the reinforcement history. At the same time, these effects did not lead to significant changes to the C-dependence of WT (Figures S3E–S3P, p > 0.10, ANOVA across rats, see Experimental Procedures).

Inactivation of Orbitofrontal Cortex Impairs Confidence-Based Waiting Times but Not Choice Accuracy

Next, we pharmacologically inactivated OFC and examined decision performance and C-dependent waiting times. Rats were first trained in the task described above. After reaching criterion performance levels, we implanted dual cannulae bilaterally in lateral and ventrolateral parts of OFC (Figures 4A and S4; see Experimental Procedures). Following recovery, on alternate testing days rats (n = 4) received intra-OFC infusion of either the GABA-A agonist muscimol for silencing neural activity or a saline solution or no injection. Because we found no differences in accuracy, reaction time and WT between saline and no injection sessions (p > 0.10, Mann-Whitney U test across trials in four of four rats; and p > 0.10 Mann-Whitney U test across rats), we combined these as the control condition. We found that OFC inactivation did not change sensory discrimination performance (Figures 4B and S5A), odor sampling duration, or movement time (Figures S5D–S5I), establishing that it is not required for perceptual decisions (accuracy: p > 0.10, bootstrap test on the slope of the psychometric functions in four of four rats; and p > 0.60, ANOVA across rats; reaction time: p > 0.10, ANOVA across trials in two of four rats (p = 0.01 in other two rats); and p > 0.20, ANOVA across rats; see Experimental Procedures). Moreover, average WT was not affected by OFC inactivation (Figures 4C and S5C; p > 0.20, Mann-Whitney U test across trials in three of four rats (p = 0.01 in the fourth rat); and p > 0.80, Mann-Whitney U test across rats). However, while psychometric functions of the short and long WT trials had significantly different slopes in the control condition, this difference was negligible in the inactivation condition (Figure 4D; p < 0.05 in four of four rats; and p < 0.01 across rats, bootstrap test on the slope differences). Moreover, we found that the dependence of WT on stimulus difficulty and outcome was significantly reduced (Figure 4E; p < 0.01, bootstrap test on the slope of the fitted lines in four of four rats; and p < 0.01, ANOVA across rats, see Experimental Procedures) without a concomitant change in the mean WT. In addition, accuracy as a function of WT flattened (Figure 4F; p < 0.05, Mann-Whitney U test for selected time bins across trials in three of four rats; and p < 0.05; Mann-Whitney U test for selected time bins across rats), establishing that WT became a worse predictor of performance.

Figure 4. OFC Inactivation Disrupts Confidence-Dependent Waiting Time but Not Decision Accuracy.

(A) Schematic for cannulae implants and anatomical locations of confirmed inactivation sites across rats. See Figure S4 for examples of histology sections.

(B) Decision accuracy as a function of odor mixture contrast for control (saline and no injection combined) and muscimol conditions for the example rat (top) and averaged across rats (bottom). Lines are logistic fits to the data (see Experimental Procedures). In all images, error bars are ±SEM across trials or across rats. Cannulae implantation itself had no effect on the decision accuracy (Figure S6).

(C) Mean waiting times for control and muscimol conditions for the example rat (top) and averaged across rats (bottom).

(D) Psychometric functions separated based on WT in the control and muscimol conditions for the example rat (top) and averaged across rats (bottom). Black and gray dots represent long WT (above 70^th percentile) and short WT (shorter than 70^th percentile) control trials, respectively. Red and pink dots represent long WT (above 70^th percentile) and short WT (shorter than 70^th percentile) muscimol trials, respectively. Lines represent logistic fit on the accuracy data (see Experimental Procedures).

(E) Mean normalized WT plotted as a function of odor mixture contrast and trial outcome for control and averaged across rats (bottom). To combine WTs across different sessions of each rat and across rats, normalized WTs were used. For this normalization, the WT in each trial was divided by mean WT of all trials of the session (see Experimental Procedures). Lines are linear fit to the data. Asterisks indicate significant differences (p < 0.05) between individual data points. Cannulae implantation itself had no effect on the WT pattern (Figure S6). See Figure 6 for effect of muscimol on WT patterns in rats with cannulae positioned outside OFC.

(F) Decision accuracy as a function of z-scored waiting time (see Experimental Procedures) for control and muscimol conditions for the example rat (top) and averaged across rats (bottom).

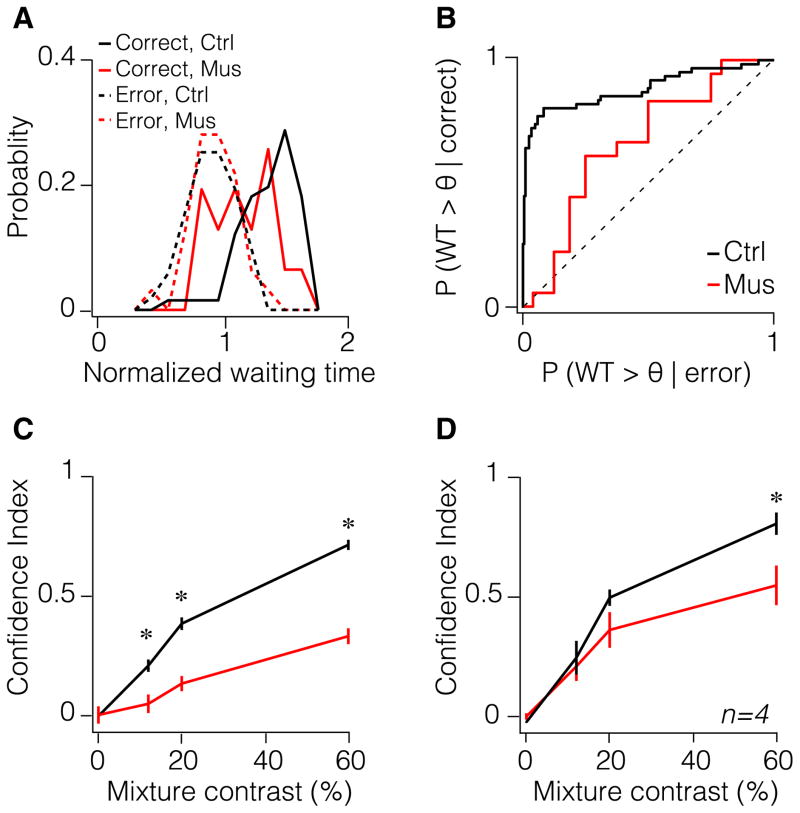
The previous analyses only considered the mean WT patterns and not their variance and distribution. Therefore we next evaluated how well a subject’s waiting time report conformed to its actual decision accuracy using type-II receiver operating characteristic (ROC) analysis (Kepecs et al., 2008; Fleming et al., 2010; Rounis et al., 2010; Figures 5A and 5B; see Experimental Procedures). This confidence-reporting index (CRI) systematically varied as a function of stimulus difficulty (Figures 5C and 5D; p < 0.01, ANOVA across trials in four of four rats) as expected and was significantly reduced by OFC inactivation (Figures 5C, 5D, and S5B; p < 0.01, ANOVA across trials in four of four rats; and p < 0.05, ANOVA across rats).

Figure 5. OFC Inactivation Reduces the Accuracy of Confidence Report.

(A) Probability distribution of normalized WTs for error and correct (reward omission) trials in control and muscimol conditions shown for 60% odor mixture contrast for the example rat.

(B) ROC curve computed from probability distributions in (A), as threshold, θ, varied. A rescaled value for the area under this ROC curve is used as the confidence-reporting index (CRI) (see Experimental Procedures).

(C) CRI as a function of odor mixture contrast for control and muscimol conditions for the example rat. Error bars are bootstrapped estimates.

(D) CRI as a function of odor mixture contrast for control and muscimol conditions averaged across rats. Error bars are ±SEM across rats.

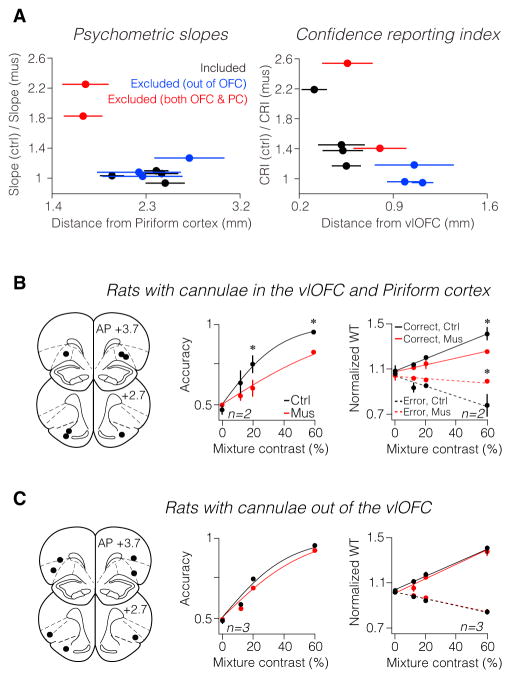
Finally, we considered the specificity of these results to the ventrolateral portion of OFC (vlOFC). Out of nine implanted rats, we initially excluded five rats from our previous analyses in which histological examination showed that some of the four cannulae were positioned either too lateral to vlOFC or too ventral reaching the piriform cortex (Figure S4). To quantify the relationship between the position of cannulae and the behavioral effects, we measured the position of the cannulae relative to the centers of the vlOFC and the piriform cortex (see Experimental Procedures for details). We then examined confidence reports and perceptual accuracy as a function of the average distance of cannulae relative to the OFC and piriform cortex (Figure 6A). The perceptual accuracy of rats with cannulae close to the piriform cortex was attenuated by muscimol inactivation, suggesting an important role for the piriform region in our odor-guided decision task (Figure 6B; p < 0.05 in two of two rats, bootstrap test on the slope differences). On the other hand, when cannulae were positioned very laterally, outside vlOFC, we did not observe any effects of inactivation on either perceptual accuracy or the WT pattern (Figure 6C; p > 0.2 in three of three rats, bootstrap test on the slope differences). These results specifically implicate the vlOFC in confidence reporting.

Figure 6. Observed Behavioral Effects Are Specific to Ventrolateral OFC Inactivation.

(A) Behavioral effects as a function of cannula location. (Left) Psychometric slope ratios for each rat as a function of cannulae distance from the piriform cortex (PC). (Right) CRI ratios for each rat as a function of cannula distance from the vlOFC. Each dot indicates the average distance measured for each rat (averaged across all visible cannulae tracks). Error bars are SEM across measurements.

(B) Rats with cannulae both in the vlOFC and piriform cortex (n = 2). (Left) Schematic of cannulae positions. (Middle) Rats’ psychometric functions. (Right) Rats’ WT pattern. Asterisks indicate significant differences (p < 0.05) between individual data points.

(C) The same as (B) for rats with cannulae out of the vlOFC (n = 3). Compare behavioral effects shown in (B) and (C) with effects shown in Figures 4B and E.

DISCUSSION

Confidence judgments are usually studied using explicit self-reports in humans and are taken at face value. To study nonhuman animals, a different approach is required. We introduced a new postdecision gambling task that makes confidence reports valuable for animals and allows experimenters to collect choices and confidence reports from the same trials (Kepecs and Mainen, 2008; Middlebrooks and Sommer, 2012). This is an advantage compared to opt-out tasks in which animals are presented with a third choice that provides a guaranteed but smaller reward. Opt-out choices may be made in epochs when the attentional or motivational state of an animal is reduced, so that if an animal is monitoring these state changes, it could prefer to opt out of the perceptual decision. For these reasons, opt-out designs are not ideal for studying decision confidence because in these tasks each trial only provides either a perceptual or an opt-out choice, making it difficult to rule out behavioral mechanisms that do not require uncertainty monitoring. The time investment gambling task described here had fundamental similarity to the restart task we previously used in which rats could abort the current trial to restart a new trial (Kepecs et al., 2008). However, the restart task provided only a binary measure of decision confidence (i.e., stay or restart). Consequently, another feature of current task design is that WTs served as continuous wagers (instead of binary bets). This is preferable to mitigate the problem of finding the optimal payoff matrix for binary bets that depends on animals’ internal costs and valuations (Clifford et al., 2008; Schurger and Sher, 2008; Middlebrooks and Sommer, 2011).

To establish that WTs could serve as indices of confidence, we compared rats’ WT patterns to a normative model of decision confidence. First, we showed that the optimal time to wait depends monotonically on the initial reward probability for each trial (Figure 2). In perceptual decisions, reward probability can be estimated based on the confidence associated with a decision. Second, we derived three predictions for decision confidence and compared these to WTs. As expected for a proxy of confidence, we found that WTs (1) correlated with the slope of psychometric functions, (2) predicted decision accuracy, and (3) showed a characteristic dependence on signal-to-noise ratio and outcome (Figure 3). This allowed us to interpret our findings in the context of a normative model rather than a semantic definition of confidence. From a computational standpoint, the observed WTs could only be explained by models in which the variable P(correct|evidence), i.e. confidence, is taken into consideration. Rats’ WTs are determined not only by decision confidence, but also by estimated reward delivery time and other reinforcement-related factors (Figure S3). Nevertheless, the accurate computation of such reward expectation is only possible by incorporating confidence information.

Inactivation of the vlOFC disrupted the confidence-dependence of WTs without a change in decision accuracy or mean WT (Figures 4, 5, and 6). These results provide evidence that an intact OFC is necessary for reporting confidence but not for perceptual decision making under uncertainty. Beyond establishing an anatomical locus for confidence judgments, the results also show that confidence reporting and the computation of perceptual decisions are at least in part distinct processes localized to different brain regions. From this perspective, our findings reinforce recent observations regarding the role of pulvinar in the representation of perceptual confidence (Komura et al., 2013). Using an opt-out task, these authors showed that inactivation of pulvinar increases monkeys’ opt-out choices in the wagering task without affecting perceptual categorization. However, for reasons discussed above, this experimental design could not rule out alternative possibilities. For instance, pulvinar inactivation could cause either lower risk-taking propensity or reduced attention, both leading to an increased opt-out behavior (Kepecs, 2013).

Our findings leave open the question of whether OFC locally computes confidence or instead receives confidence signals from other areas (Kiani and Shadlen, 2009; Insabato et al., 2010; Rolls et al., 2010a, 2010b; Komura et al., 2013) but we consider it likely that choice and confidence are computed together and represented in regions important for perceptual decision making and then relayed to OFC. In this scenario, OFC might act as a central region for monitoring confidence level, alongside other reward-related variables, regardless of perceptual modality. Neuronal signals related to metacognitive monitoring have been observed in several subregions of the frontal cortex (Lau and Passingham, 2006; Persaud et al., 2007; Kepecs et al., 2008; Tsujimoto et al., 2010; Fleming et al., 2010; Rolls et al., 2010a, 2010b; Yokoyama et al., 2010; De Martino et al., 2013; Middlebrooks and Sommer, 2012; So and Stuphorn, 2012), as well as in parietal cortex (Kiani and Shadlen, 2009) and thalamic nuclei such as pulvinar (Komura et al., 2013), suggesting that metacognitive representations may be widespread in the brain. Our results suggest that OFC may integrate distinct sources of information, and similar to its role in value-based decisions, may provide outcome predictions based on confidence monitoring processes.

Previous findings have implicated OFC in representing reward expectations (Schoenbaum and Roesch, 2005; Wallis, 2007; Rolls and Grabenhorst, 2008) and in goal-directed behavior across species (Wallis, 2007; Rolls and Grabenhorst, 2008; Schoenbaum et al., 2009; Morrison and Salzman, 2011). Because decision confidence is also critical for computing the value of the current decision outcome (Hare et al., 2008), our results are consistent with a role for OFC in outcome valuation. OFC lesions are also known to impair the devaluation of reward outcomes, reversal learning, and increase impulsivity (Bechara et al., 2000; Schoenbaum et al., 2002; Berlin et al., 2004; Wallis, 2007; Rolls and Grabenhorst, 2008; Rudebeck and Murray, 2008; Burke et al., 2009; Schoenbaum et al., 2009; Noonan et al., 2010; Walton et al., 2010; Mar et al., 2011), all of which reflect a compromise in the relative potency of explicitly imagined outcomes, as opposed to routine habits, in driving decisions (Balleine, 2011). These are consistent with our observations that OFC inactivation only affected WT wagering behavior and not well-learned decisions. Inactivation of OFC might have impaired general reward expectations and the motivation to wait for the reward (Noonan et al., 2010; Mar et al., 2011). However, WT after OFC inactivation was only reduced for correct trials, and increased for incorrect trials (Figure 4), suggesting that a disruption of reward expectation could not by itself account for the data. The fact that OFC inactivation did not affect the mean WT suggests that the animals’ ability to estimate the elapsed time remained intact. Moreover, rats’ movement times were not different between the muscimol and control sessions (Figure S5) and were not different when comparing pre- and postcannulae implantation (Figure S6), implying that the observed behavioral patterns could neither be attributed to the inactivation nor to the lesion of motor-related structures along the cannulae walls. The observation that following OFC inactivation rats failed to adjust their WT based on the decision is consistent with the broader notion that an intact OFC is necessary for some aspects of reward-maximizing choice behavior (Wallis, 2007; Padoa-Schioppa, 2011). Confidence is also a form of uncertainty; therefore, our results are broadly consistent with observations demonstrating that OFC is involved in representing uncertainty and risk in humans (Critchley et al., 2001; Hsu et al., 2005; Tobler et al., 2007; Fleming et al., 2010; Rolls et al., 2010a; De Martino et al., 2013), monkeys (O’Neill and Schultz, 2010), and rats (Kepecs et al., 2008; Roitman and Roitman, 2010).

In summary, our results support the view that OFC is particularly important for reward-based behaviors when values are inferred, for instance using model-based reinforcement learning algorithms (Daw and Doya, 2006; Hampton et al., 2006; McDannald et al., 2011; Jones et al., 2012; Wilson et al., 2014), rather than when values are stored based on previous experiences. This is because, the estimation of decision confidence is an example of the computation of an inferred value based on a hidden belief state. Consequently, the role of OFC in confidence monitoring can be viewed as a second-order and metacognitive process that fits into the broader conception that OFC is critical for making on-the-fly predictions about behaviorally important outcomes.

EXPERIMENTAL PROCEDURES

Subjects

Ten male Long-Evans rats were used for the experiments. Data from all rats were used for the quantification of confidence reporting behavior. Nine rats underwent the cannulae implantation surgery and based on anatomical localizations of implanted cannulae (Figures 6 and S4), data collected from four rats were used for investigating the effect of OFC inactivation on the confidence reporting behavior.

Rats were motivated by water restriction and had unlimited access to food. All procedures involving animals were carried out in accordance with NIH standards and were approved by the Cold Spring Harbor Laboratory Institutional Animal Care and Use Committee.

Behavior

Behavioral Task and Training

The apparatus has been described previously (Uchida and Mainen, 2003; Kepecs et al., 2008). Rats self-initiated each experimental trial by introducing their snout into the central port where odor was delivered. After a variable delay, drawn from a uniform random distribution of 0.2–0.5 s, a binary mixture of two pure odorants, S(+)-2-octanol and R(−)-2-octanol, was delivered at one of seven concentration ratios (80:20, 60:40, 56:44, 50:50, 44:56, 40:60, 20:80 creating odor mixture contrast of 0%, 12%, 20%, and 60%) in pseudorandom order within a session. After a variable odor sampling time up to 0.7 s, rats responded by withdrawing from the central port, which terminated the delivery of odor and moved to the left or right choice port. Choices were rewarded according to the dominant component of the mixture, that is, at the left port for mixtures A/B > 50/50 and at the right port for A/B < 50/50. For trials with 50/50 odor mixture, the reward was randomly assigned to one of the choice ports. A variable reward delay period after entry into the choice port was introduced. For correct choices, reward was delivered between at least 0.5 s after entry into the choice port and up to 8 s. The reward delay was drawn from an exponential distribution with decay constant equal to 1.5 (Figure 1D) resulting in a relatively constant level of reward expectancy over a range of delays (i.e., flat hazard rate). In a small fraction of correct choice trials distributed pseudorandomly throughout the behavioral session (10%–15% of correct trials), rewards were omitted. These reward omission trials were distributed to never occur on the consecutive trials. Because the rat spends time consuming the water in the rewarded correct trials, we used the reward omission trials to measure WT in the correct trials.

To perform the task described above, rats went through a multistep training procedure typically lasting 6–8 weeks starting with imperative trials, moving to choice trials and gradually introducing choice trials with low odor mixture contrast.

Surgery and Inactivation Procedures

Surgery

All surgical procedures were carried out under aseptic conditions. Anesthesia was initiated with inhalation of 2.5% isoflurane (Vetland) and retained with intraperitoneal injections of ketamine (50 mg/kg) and medetomidine (0.4 mg/kg), After craniotomy, dual guide cannulae (26-gauge Plastics One) were stereotactically implanted in each hemisphere targeted 1.5 mm above OFC (AP+3.2, ML±3.2, DV+2.8 from dura and AP+4.1, ML±2.8, DV+1.8 from dura). Dual stainless steel stylets were inserted into the guide cannulae to ensure patency (protruding 0.5 mm below the tip of the guide cannulae).

Pharmacological Inactivation

Temporary inactivation was achieved via localized injections of γ-aminobutyric acid (GABA_A) receptor agonist muscimol (Sigma Aldrich) under light anesthesia induced by 2% isoflurane (for about 6 min during which hindleg reflex never disappeared over the course of infusion). On each testing day, the stylets were replaced with dual injector cannulae (33-gauge, Plastics One) protruding 1.5 mm below the tip of guide cannulae. One minute after proper placement of the injectors, muscimol (0.05 μg in 0.4 μl) or sterile saline (0.9%; 0.4 μl) was injected over a 5 min period. Fluid was infused via 0.38 mm diameter polyethylene tubing (Intramedic) attached to the injector on one end and to a 2 μl Hamilton syringe (Hamilton) on the other end. The syringe was driven with a syringe pump (Harvard Apparatus).

Injections were monitored by observing the movement of a small air bubble in the tubing to confirm that fluid was moving. After infusions were complete, the injector cannulae were left in place for 2 min and then replaced with stylets to maintain cannulae patency. Behavioral testing began about 30 min after infusion. It has been shown that the maximal extent of muscimol spread, using this procedure, was 1.5–2 mm within 10–20 min of injection (Martin and Ghez, 1999).

Histology

Once experiments were complete, rats were deeply anesthetized and then transcardially perfused with 4% paraformaldehyde. Brains were removed, postfixed, and coronal sections of 50 μm were made using a fixed-tissue vibratome (VT1000S, Leica Instruments). Only animals in which at least three of the four cannulae were located within the lateral and ventrolateral portions of OFC were included in our analysis. We determined that four of nine implanted animals had correct cannulae positions while the others extended either ventrally into the piriform cortex or caudally into the striatum (Figures 6 and S4).

Computational Model

Confidence Estimation Model

To predict the expected patterns of decision confidence, we used a simple model for two-alternative decisions. We used a signal detection theory framework where each choice and its associated confidence could be estimated by comparing the sampled stimulus and the decision boundary. The boundary was fixed at 50%. In this framework, the choice in each trial is computed by comparing stimulus and boundary. We modeled the stimulus as the percentage of one of the components in the mixture henceforth denoted by m. The internal representation of the stimulus m′ is different from the actual value m:

$$m^{\prime }=m+\xi .$$ (Equation 8)

Here ξ is the Gaussian variable with zero mean and the SD of σ: $p(\xi )=e^{-{\xi }^2/2{\sigma }^3}/\sqrt{2\pi {\sigma }^2}$. The origin of noise ξ is 2-fold: it may be contributed by the external uncertainties in the stimulus as well as the internal sources of error. From fits to experimental data, we obtained an estimate of σ ≈ 18%, i.e., internal and external sources of noise in their strength are equivalent to approximately 18% of the fraction of one components in the mixture. In each trial, it is assumed that the value of the internal representation of the stimulus determines the response of the observer. The values of m′ exceeding the decision boundary b = 50% result in response to the right, while the values m′<50% produce a left response. For a given external stimulus m, the fraction of right responses i.e., the psychometric function is given by

$$P(m)=\frac{1}{2}\left[1+\text{erf}\left(-\frac{m-b}{\sigma \sqrt{2}}\right)\right].$$ (Equation 9)

In each trial, the distance between the internal representation of stimulus m′ and boundary provides an estimate of decision confidence, C. Decision confidence in our approach is defined as the probability of making the correct decision C = C(m′). Decision confidence, however, is a function of the internal representation of the stimulus m′, which is different from the external value (Equation 8). It is not difficult to see that for a simple decision task, the probability of being correct could be estimated using Equation 7.

It is important that, in each individual trial, the same internal representation of the stimulus m′ that determines response (response to the right occurs when m′≥50%) is used to evaluate the decision confidence through Equation 7. The internal representation of the stimulus m′ varies from trial to trial even if the stimulus mixture m is fixed. Response accuracy therefore becomes coupled with decision confidence. Because C = C(m′) is an internal variable, it is not available for direct measurement. Instead, it could be assessed through the time spent by the observer in the reward port. In the computational model, we used Equation 6 describing an ideal observer. Note that Equation 6 predicts that there are only two conditions when WT goes to infinity (i.e., waiting never terminates): when the opportunity cost, κ, is zero (waiting has no cost) or when a rat is completely confident about its choice C = 1. However, there is always some reward to be gained in future trials and because of reward omission trials, a rat cannot be completely certain of reward; hence, WT is always finite.

Fitting the Model to Behavioral Data

To fit our model to rats’ behavioral data, we estimated two parameters. First, the width of the total noisy distribution (σ, made up of sensory and internal noise) used to calculate model’s trial by trial choice and confidence. Second, opportunity cost (κ) which, alongside confidence and reward delay distribution (Equation 6) is used to calculate model’s WT. Parameter estimation was done using a maximum likelihood method, implemented using MATLAB’s fminsearch function. To avoid local minima, we re-ran fminsearch 1,000 times using random starting parameter values and selected the set of parameter estimates with the smallest mean squared error.

Starting from rat’s psychometric curve, we estimated one parameter (σ) that minimized the mean squared error of choice predictions. We then used the estimated σ to calculate the intermediate variable, decision confidence (C), in each trial (Figure 3A, middle) and subsequently estimated one other parameter, κ (Equation 6), which could minimize the difference between rat’s and the model’s WT distribution (Figure 3A, right). Although this model fit the mean WTs per condition well, to fit to the entire WT distribution we also assumed “scalar timing.” In other words, we assumed that a rat’s estimation of elapsed time carries uncertainty and in particular that the SD scales with elapsed time (Gibbon, 1977; Gibbon et al., 1997; Janssen and Shadlen, 2005). This implies that a time t is perceived at time t ± σ(t), where

$$\sigma (t)=\varphi ·t,$$ (Equation 10)

where ϕ is the coefficient of variation or Weber fraction (Gibbon, 1977). Consistent with previous findings, we set ϕ = 0.3 (Gibbon et al., 1997; Janssen and Shadlen, 2005). Therefore, for the fitting, the model’s WT distribution was blurred with a normal distribution whose SD was proportional to the elapsed time (Figure 3A, right). Lines in Figures 3B–3D show predictions of the model with parameters optimized to fit rat’s accuracy curve and WT distribution.

Analysis of Behavioral Data

We collected 68,243 trials from ten rats as following: 24,032 control trials (saline injection or no injection) and 11,106 muscimol trials from four rats (79 sessions, in average 445 trials per session per rat, minimum trial per session = 295, maximum trial per session = 654, minimum session per rat = 15, maximum session per rat = 29). These data were included in analysis of confidence-related WTs as well as the muscimol experiment; 23,473 control trials and 9,632 muscimol trials from six rats (five of them implanted, 81 sessions, in average 408 trials per session per rat, minimum trial per session = 281, maximum trial per session = 701, minimum session per rat = 12, maximum session per rat = 18). Due to incorrect position of cannulae revealed by histological examination (Figure S4), these data were only used in the analysis of confidence-related WTs and in Figure 6.

In general, we used nonparametric Mann-Whitney U test for single comparisons and one or two-way ANOVA, post-hoc test adjusted, for multiple comparisons. Bootstrap test used for the comparing fit parameters in Figures 3E and 4B–4E) and for comparisons shown in Figures 5C and S5B. For statistical analysis across rats, averaged data for each rat was used. However, the large number of trials collected for each rat also enabled us to examine the significance of behavioral effects for each subject separately. For such analyses on single rats, statistical tests were performed across all trials collected for each animal. Asterisks in figures illustrate statistically significant (p < 0.05) differences for individual data points using Mann-Whitney U test (bootstrap test was used for Figure 5C). Filled/empty markers in scatter plots indicate significant/nonsignificant differences tested using Mann-Whitney U test (bootstrap test was used for Figure S5B). Unless stated otherwise, error bars in figures indicate SEM across trials for individual animals or across rats for the population data.

Perceptual Accuracy and Reaction Time Data

For illustration proposes only, we fit behavioral choice data (probability of choosing left port) as a function of odor concentration (%A) to a logistic function of the following form (Figure 1B):

$$\mathit{Accuracy}=\frac{1}{1+e^{-(\alpha +\beta \times \mathit{Odor}\mathit{mixture})}},$$ (Equation 11)

where α is a measure of choice bias and β reflects perceptual sensitivity.

We fit behavioral accuracy data as a function of odor mixture contrast to a logistic function of the following form (Figures 3E, 4B, and 4D):

$$\mathit{Accuracy}=\frac{1}{1+e^{-(\beta \times \mathit{Odor}\mathit{Contrast})}},$$ (Equation 12)

where β reflects perceptual sensitivity (i.e., psychometric slope), with higher values implying increased sensitivity.

Waiting Time Data

WT data exhibited small variation across sessions and subjects. Therefore, for each rat the WTs of each session were normalized to the mean of the WT of that session (normalized WT). Other possible ways to normalize the data (normalization to the median WT of the session or normalization to the mean/median of the WT for odor mixture contrast = 0) resulted in very similar findings. For illustration proposes, nonnormalized WT data were used in Figure 3.

For Figure 4F, z-scored WT (Equation 13) was used to compute the conditioned accuracy graphs (see below). However, using normalized WT (instead of z-scored waiting time) showed comparable results.

$${\mathit{ZscoredWT}}_{\text{trial}}=\frac{{WT}_{\text{trial}}-\mu ({WT}_{\text{session}})}{\sigma ({WT}_{\text{session}})}$$ (Equation 13)

We fit WT data as a function of odor mixture contrast and trial outcome to a linear function of the following form (Figures 3G and 4E):

$$\mathit{NormalizedWT}=\alpha +(\pm \beta \times \mathit{Odor}\mathit{contrast}),$$ (Equation 14)

where β indicates the slope of change in the normalized WT as a function of the odor mixture contrast and its sign (−/+) indicates error/correct outcomes, respectively.

WT-Conditioned Accuracy Measures

To estimate rats’ decision accuracy as a function of WT, we assumed that WTs for correctly performed reward omission trials (which were pseudorandomly distributed) were a good representative for the distribution of all correctly performed trials. Therefore, the z-scored WT data (Equation 13) were expanded to all correct trials (taking into account the odor stimulus identity) and WT-conditioned accuracy functions were computed (Figure 4F). For illustration purposes unnormalized WT data was used for the similar analysis shown in Figures 3C and 3F.

Confidence-Reporting Index

An objective measure of confidence reporting ability can be computed based on the type II ROC curve, which quantifies how well a subject’s confidence report conforms to its actual decision accuracy. For each animal for each of the experimental conditions (muscimol versus control) the probability distribution of the normalized WT for the error trials and correct trials were first computed (Figure 5A). The ROC was then generated for each of the experimental conditions (Figure 5B), which indicates P (WT > θ | correct) as a function of P (WT > θ | error), where θ refers to the threshold that was varied to construct the ROC curve. The CRI is the rescaled measure of the area under the ROC curve, so that values close to zero indicate poor confidence and values close to 1 indicate perfect decision confidence (Figures 5C, 5D, 6A, S3N–S3P, and S5B).

Effects of Trial History on Waiting Time and Confidence Reporting Measures

Apart from decision confidence, the waiting time at the choice ports also depends on when an animal is expecting the reward delivery. We were interested to determine the extent to which WT pattern and CRI, our measures of confidence report, were affected by trial history. Figures S3E–S3G show an example rat in which none of the mentioned parameters affected its mean WT. Consequently, the WT patterns are overlapping. Figures S3H–S3J show an example rat in which outcome as well as WT of previous trial affected its absolute WT. As a result, whereas WT patterns show a general shift, the confidence-dependent WT patterns are robust. When averaging across rats, WT as a function of odor mixture contrast and outcome did not vary between the beginning and end of a session, after correct and error trials or after long and short WTs (Figures S3K–S3M; p > 0.10, ANOVA across rats). Similarly, CRI as a function of odor mixture contrast did not vary between the beginning and end of a session, after correct and error trials, or after long and short WTs (Figures S3N–S3P; p > 0.20, ANOVA across rats).