Abstract
Stark shift on a superconducting qubit in circuit quantum electrodynamics (QED) has been used to construct universal quantum entangling gates on superconducting resonators in previous works. It is a second-order coupling effect between the resonator and the qubit in the dispersive regime, which leads to a slow state-selective rotation on the qubit. Here, we present two proposals to construct the fast universal quantum gates on superconducting resonators in a microwave-photon quantum processor composed of multiple superconducting resonators coupled to a superconducting transmon qutrit, that is, the controlled-phase (c-phase) gate on two microwave-photon resonators and the controlled-controlled phase (cc-phase) gates on three resonators, resorting to quantum resonance operations, without any drive field. Compared with previous works, our universal quantum gates have the higher fidelities and shorter operation times in theory. The numerical simulation shows that the fidelity of our c-phase gate is 99.57% within about 38.1 ns and that of our cc-phase gate is 99.25% within about 73.3 ns.
Quantum computation and quantum information processing have attached much attention1 in recent years. A quantum computer can factor an n-bit integer exponentially faster than the best known classical algorithms and it can run the famous quantum search algorithm, sometimes known as Grover's algorithm, which enables this search method to be speed up substantially, requiring only 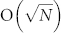 operations, faster than the classical one which requires O(N) operations1. Universal quantum gates are the key elements in a universal quantum computer, especially the controlled-phase (c-phase) gate or its equivalent gate – the controlled-not (CNOT) gate. C-phase gates (or CNOT gates) assisted by single-qubit rotations can construct a universal quantum computing. Compared to the synthesis with universal two-qubit entangling gates and single-qubit gates, the direct implementation of a universal three-qubit quantum gate [controlled-controlled-phase (cc-phase) or controlled-controlled-not (Toffoli) gate] is more economic and simpler as it requires at least six CNOT gates2 to synthesize a Toffoli gate which is equivalent to a cc-phase gate. By far, there are some interesting physical systems used for the construction of universal quantum gates, such as photons3,4,5,6,7,8,9, nuclear magnetic resonance10,11,12,13,14, quantum dots15,16,17,18,19,20,21,22, diamond nitrogen-vacancy center23,24,25, and cavity quantum electrodynamics (QED)26,27.
operations, faster than the classical one which requires O(N) operations1. Universal quantum gates are the key elements in a universal quantum computer, especially the controlled-phase (c-phase) gate or its equivalent gate – the controlled-not (CNOT) gate. C-phase gates (or CNOT gates) assisted by single-qubit rotations can construct a universal quantum computing. Compared to the synthesis with universal two-qubit entangling gates and single-qubit gates, the direct implementation of a universal three-qubit quantum gate [controlled-controlled-phase (cc-phase) or controlled-controlled-not (Toffoli) gate] is more economic and simpler as it requires at least six CNOT gates2 to synthesize a Toffoli gate which is equivalent to a cc-phase gate. By far, there are some interesting physical systems used for the construction of universal quantum gates, such as photons3,4,5,6,7,8,9, nuclear magnetic resonance10,11,12,13,14, quantum dots15,16,17,18,19,20,21,22, diamond nitrogen-vacancy center23,24,25, and cavity quantum electrodynamics (QED)26,27.
Circuit QED, composed of superconducting Josephson junctions (act as the artificial atoms) and a superconducting resonator (acts as a cavity and quantum bus)28,29,30,31,32,33,34, is a promising implementation of cavity QED and it has the excellent features of the good scalability and the long coherence time. It has been used to realize the strong and even ultra-strong coupling between a resonator and a superconducting qubit28,35, and complete some basic tasks of the quantum computation on the superconducting qubits. For example, DiCarlo et al.36 demonstrated the c-phase gate on two transmon qubits assisted by circuit QED in 2009. In 2014, Chow et al.37 experimentally implemented a strand of a scalable fault-tolerant quantum computing fabric. In 2012, Fedorov et al.38 implementated a Toffoli gate and Reed et al.39 realized the three-qubit quantum error correction with superconducting circuits. In 2014, Barends et al.40 realized the c-phase gate on every two adjacent Xmon qubits with a high fidelity in a five-Xmon-qubit system assisted by circuit QED. DiCarlo et al.41 prepared and measured the three-qubit entanglement in circuit QED in 2010, and Steffen et al.42 realized the full deterministic quantum teleportation with feed-forward in a chip-based superconducting circuit architecture in 2013.
In a high-quality resonator, a microwave photon always has the longer life time than that of a superconducting qubit43, which makes the resonator a good candidate for quantum information processing based on the basis of Fock states. With a superconducting qubit coupled to a resonator, Hofheinz et al.44 realized the generation of a Fock state in 2008. In the same year, Wang et al.45 realized the measurement of the decay of Fock States. Hofheinz et al.46 demonstrated the synthesis of an arbitrary superposition of Fock states in 2009. With two qubits coupled to three resonators, Merkel and Wilhelm47 proposed a scheme for the generation of the entangled NOON state on two resonator qudits (with d levels) in 2010. In 2011, Wang et al.48 demonstrated in experiment the generation of the entangled NOON state on two resonators. With a qubit coupled to two resonators, Johnson et al.49 realized the single microwave-photon non-demolition detection in 2010 and Strauch50 exploited the all-resonant method to control the quantum state of superconducting resonators and gave some theoretic schemes for Fock state synthesis, qudit logic operations, and synthesis of NOON states in 2012. With a qubit coupled to multiple resonators, Yang et al. proposed a theoretic scheme for the generation of the entangled Greenberger-Horne-Zeilinger state on resonators based on the Fock states51 in 2012 and entangled coherent states of four microwave resonators52 in 2013.
Besides the entanglement generation for quantum information processing, resonator qudits can also be used for quantum computation, that is, universal quantum logic gates53,54,55. In 2011, Strauch53 gave an interesting scheme to construct the quantum entangling gates on the two resonator qudits based on the arbitrary Fock states, by using the two-order coupling effect of the number-state-dependent interaction between a superconducting qubit and a resonator in the dispersive regime, discovered by Schuster et al.56 in 2007. The operation time of his c-phase gate on two resonator qudits with the basis of the Fock states |0〉r and |1〉r is 150 ns. In a processor with one two-energy-level charge qubit coupled to multiple resonators, Wu et al.54 presented an effective scheme to construct the c-phase gate on two resonators with the number-state-dependent interaction between the qubit and two resonators in 2012. Its operation time is 125 ns. In a similar processor, we gave a scheme for the construction of the c-phase gate (cc-phase gate) on two (three) resonator qubits55 (only working under the subspace of Fock states {|0〉r, |1〉r}), by combining the number-state-dependent selective rotation between a superconducting transmon qutrit (just the three lowest energy levels are considered) and a resonator (two resonators) and the resonance operation on the rest resonator and the qutrit in 2014. The fidelity of our c-phase (cc-phase) gate can reach 99.5% (92.9%) within 93 (124.6) ns in theory, without considering the decoherence and the dephasing rates of the qutrit and the decay rate of the microwave-photon resonators.
In this paper, we exploit the all-resonance-based quantum operations on a qutrit and resonators to design two schemes for the construction of the c-phase and the cc-phase gates on resonators in a processor composed of multiple microwave-photon resonators coupled to a transmon qutrit far different from the previous works for the c-phase and cc-phase gates on resonators based on the second-order couplings between the qubit and the resonators53,54,55. Our simulation shows that the fidelity of our c-phase gate on two microwave-photon resonators approaches 99.57% within the operation time of about 38.1 ns and that of our cc-phase gate on three resonators is 99.25% within about 73.3 ns. Our all-resonance-based universal quantum gates on microwave-photon resonators without classical drive field are much faster than those in similar previous works53,54,55.
Results
All-resonance-based c-phase gate on two resonator qubits
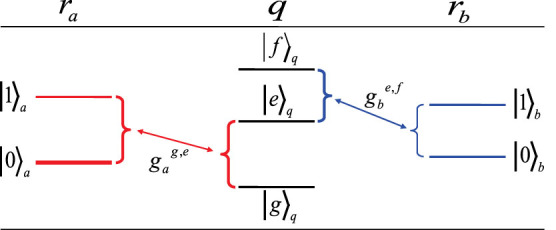
Let us consider the quantum system composed of two high-quality superconducting resonators coupled to a transmon qutrit with the three lowest energy levels, i.e., the ground state |g〉q, the excited state |e〉q, and the second excited state |f〉q, shown in Fig. 1. In the interaction picture, the Hamiltonian of the system is ( ):
):
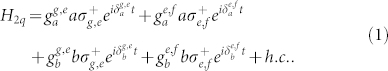 |
Here, 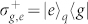 and
and 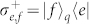 are the creation operators for the transitions of the qutrit |g〉q → |e〉q and |e〉q → |f〉q, respectively. a+ and b+ are the creation operators of the resonators ra and rb (labeled as a and b in subscripts), respectively.
are the creation operators for the transitions of the qutrit |g〉q → |e〉q and |e〉q → |f〉q, respectively. a+ and b+ are the creation operators of the resonators ra and rb (labeled as a and b in subscripts), respectively. 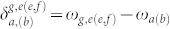 and ωg,e(e,f) = Ee(f) − Eg(e). Ei is the energy for the level |i〉q of the qutrit. ωa and ωb are the transition frequencies of the resonators a and b, respectively.
and ωg,e(e,f) = Ee(f) − Eg(e). Ei is the energy for the level |i〉q of the qutrit. ωa and ωb are the transition frequencies of the resonators a and b, respectively. 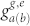 and
and 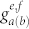 are the coupling strengths between the resonator ra (rb) and the qutrit q with these two transitions. Tuning the transition frequencies of the transmon qutrit and the coupling strength between the transmon qutrit and each resonator57,58,59, one can turn on and off the interaction between the qutrit and each resonator effectively60.
are the coupling strengths between the resonator ra (rb) and the qutrit q with these two transitions. Tuning the transition frequencies of the transmon qutrit and the coupling strength between the transmon qutrit and each resonator57,58,59, one can turn on and off the interaction between the qutrit and each resonator effectively60.
Figure 1.
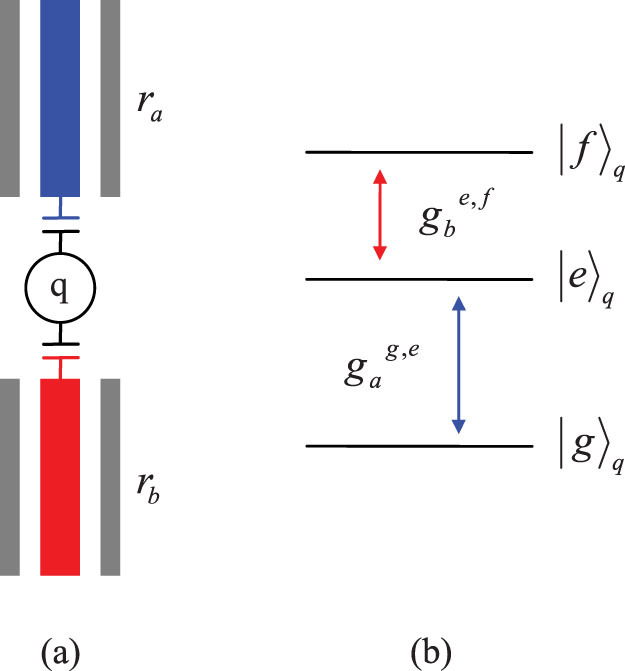
(a) The schematic diagram for our c-phase gate on two microwave-photon resontors in circuit QED. It contains two high-quality superconducting resonators (ra and rb) capacitively coupled to a superconducting quantum interferometer device (SQUID) which acts as a superconducting transmon qutrit (q), whose transition frequency can be tuned by the external magnetic flux. (b) The schematic diagram for the three lowest energy levels of the qutrit with small anharmonicity. 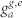 is the coupling strength between ra and the qutrit with the transition |g〉q ↔ |e〉q.
is the coupling strength between ra and the qutrit with the transition |g〉q ↔ |e〉q. 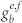 is the coupling strength between rb and the qutrit with the transition |e〉q ↔ |f〉q.
is the coupling strength between rb and the qutrit with the transition |e〉q ↔ |f〉q.
Let us suppose that the general initial state of the system is
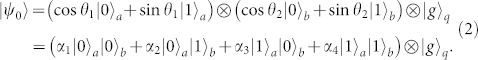 |
Here, α1 = cosθ1cosθ2, α2 = cosθ1sinθ2, α3 = sinθ1cosθ2, and α4 = sinθ1sinθ2. The all-resonance-based c-phase gate on two microwave-photon resonators can be constructed with three steps, shown in Fig. 2. We describe them in detail as follows.
Figure 2. The principle and the steps of our c-phase gate on ra and rb with all-resonance operations.
Step i), by tuning off the interaction between the transmon qutrit and rb, and resonating ra and the two lowest energy levels |g〉q and |e〉q of the qutrit (ωa = ωg,e) with the operation time of 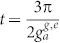 , the state of the system can be evolved into
, the state of the system can be evolved into
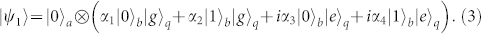 |
Step ii), by turning off the interaction between the qutrit and ra, and resonating rb and the two energy levels |e〉q and |f〉q of the qutrit (ωb = ωe,f) with the operation time of 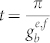 , the state of the system can evolve from |ψ1〉 into
, the state of the system can evolve from |ψ1〉 into
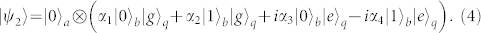 |
Step iii), by turning off the interaction between the qutrit and rb, and resonating ra and the energy levels |g〉q and |e〉q of the qutrit with the operation time of 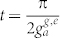 , one can get the final state of the system as
, one can get the final state of the system as
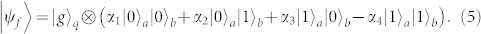 |
This is just the c-phase gate operation on the resonators ra and rb, which indicates that a π phase shift takes place only if there is one microwave photon in each resonator.
If the operation time in step i) is taken to 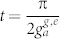 , one can get the final state of the system as
, one can get the final state of the system as
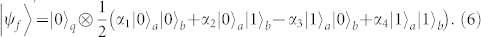 |
This is just the result of another c-phase gate operation on the resonators ra and rb, which indicates that the π phase shift happens only if there is one microwave photon in ra and no microwave photon in rb.
To show the feasibility of the resonance processes for constructing our c-phase gate, we numerically simulate its fidelity and operation time with the feasible experiential parameters. The evolution of the system composed of these two resonators and the transmon qutrit can be described by the master equation28,61
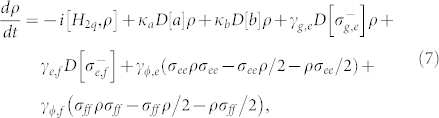 |
where D[L]ρ = (2LρL+ − L+Lρ − ρL+L)/2 with 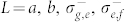 . σee = |e〉q〈e| and σff = |f〉q〈f|. κa (κb) is the decay rate of the resonator ra (rb), γg,e (γe,f) is the energy relaxation rate of the qutrit with the transition |e〉 → |g〉 (|f〉 − |e〉), and γϕ,e and γϕ,f are the dephasing rates of the levels |e〉 and |f〉 of the qutrit, respectively. For simplicity, the parameters for our numerical simulation are chosen as:
. σee = |e〉q〈e| and σff = |f〉q〈f|. κa (κb) is the decay rate of the resonator ra (rb), γg,e (γe,f) is the energy relaxation rate of the qutrit with the transition |e〉 → |g〉 (|f〉 − |e〉), and γϕ,e and γϕ,f are the dephasing rates of the levels |e〉 and |f〉 of the qutrit, respectively. For simplicity, the parameters for our numerical simulation are chosen as: 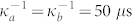 ,
, 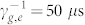 ,
, 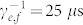 ,
, 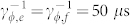 , ωa/(2π) = 5.5 GHz, and ωb/(2π) = 7.0 GHz. In the first step, we chose ωg,e/(2π) = 5.5 GHz, ωe,f/(2π) = 4.7 GHz,
, ωa/(2π) = 5.5 GHz, and ωb/(2π) = 7.0 GHz. In the first step, we chose ωg,e/(2π) = 5.5 GHz, ωe,f/(2π) = 4.7 GHz, 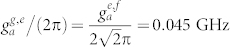 , and
, and 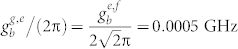 . In the second step, ωg,e/(2π) = 7.8 GHz, ωe,f/(2π) = 7.0 GHz,
. In the second step, ωg,e/(2π) = 7.8 GHz, ωe,f/(2π) = 7.0 GHz, 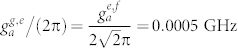 , and
, and 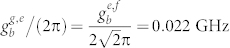 . The parameters in the third step are the same as those in the first step. It worth noticing that the long coherence time of the transmon qubit with 50 μs, the high quality factor of a 1D superconducting resonator with above 106, and the tunable coupling strength of a charge qubit and a resonator with from 200 KHz to 43 MHz have been realized in experiments59,62,63. For superconducting qutrits, the typical transition frequency between two neighboring levels is from 1 GHz to 20 GHz64,65.
. The parameters in the third step are the same as those in the first step. It worth noticing that the long coherence time of the transmon qubit with 50 μs, the high quality factor of a 1D superconducting resonator with above 106, and the tunable coupling strength of a charge qubit and a resonator with from 200 KHz to 43 MHz have been realized in experiments59,62,63. For superconducting qutrits, the typical transition frequency between two neighboring levels is from 1 GHz to 20 GHz64,65.
The fidelity of our c-phase gate is defined as
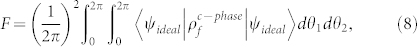 |
where |ψideal〉 is the final state |ψf〉 of the system composed of the resonator qubits ra and rb after an ideal c-phase gate operation is performed with the initial state |ψ0〉, which is obtained by not taking the dissipation and dephasing into account. 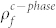 is the realistic density operator after our c-phase gate operation on the initial state |ψ0〉. Our simulation shows that the fidelity of our c-phase gate is 99.57% within the operation time of about 38.1 ns. Taking
is the realistic density operator after our c-phase gate operation on the initial state |ψ0〉. Our simulation shows that the fidelity of our c-phase gate is 99.57% within the operation time of about 38.1 ns. Taking 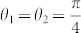 as an example, the density operators of the initial state and the final state are shown in Fig. 3 (a) and (b), respectively.
as an example, the density operators of the initial state and the final state are shown in Fig. 3 (a) and (b), respectively.
Figure 3.
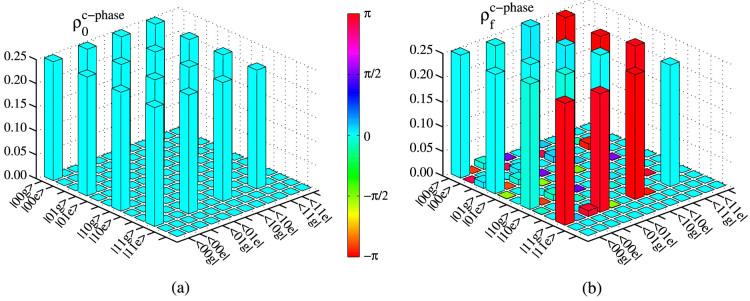
(a) The density operator ρ0 of the initial state |ψ0〉 of the quantum system composed of the two resonator qudits and the superconducting qutrit for constructing our c-phase gate. (b) The density operator 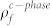 . Here we take
. Here we take 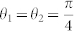 .
.
In fact, by using the resonance operations, one can also construct the swap gate on two resonator qubits simply with our device by the five steps shown in Tab. 1.
Table 1. The steps for constructing the SWAP gate on ra and rb with all-resonance operations.
| Step | Coupling | Time | Transition |
|---|---|---|---|
| i) | 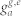 |
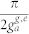 |
|0〉a, |1〉a → |g〉q, |e〉q |
| ii) | 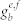 |
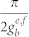 |
|0〉b, |1〉b → |e〉q, |f〉q |
| iii) | 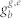 |
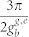 |
|0〉b, |1〉b → |g〉q, |e〉q |
| iv) | 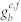 |
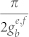 |
|0〉b, |1〉b → |e〉q, |f〉q |
| v) | 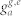 |
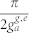 |
|0〉a, |1〉a → |g〉q, |e〉q |
Cc-phase gate on superconducting resonators
Our cc-phase gate is used to perform a minus phase manipulation on the three resonator qubits only if the resonators ra, rb, and rc are in the state |1〉a|1〉b|0〉c.
Our device for the cc-phase gate on the three high-quality superconducting resonators ra, rb, and rc which are coupled to the transmon qutrit q is shown in Fig. 4. In the interaction picture, the Hamiltonian of the whole system composed of the three resonators and the qutrit is:
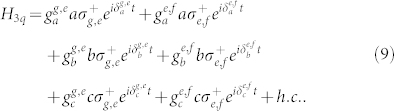 |
Suppose that the initial state of the system is
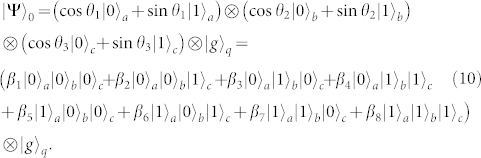 |
Here, β1 = cosθ1cosθ2cosθ3, β2 = cosθ1cosθ2sinθ3, β3 = cosθ1sinθ2cosθ3, β4 = cosθ1sinθ2sinθ3, β5 = sinθ1cosθ2cosθ3, β6 = sinθ1cosθ2sinθ3, β7 = sinθ1sinθ2cosθ3, and β8 = sinθ1sinθ2sinθ3. The cc-phase gate on three resonator qubits can be constructed with nine resonance operations between the qutrit and the resonators. The detailed steps are described as follows.
Figure 4. The schematic diagram for our cc-phase gate on three microwave-photon resonators with all-resonance operations in circuit QED.
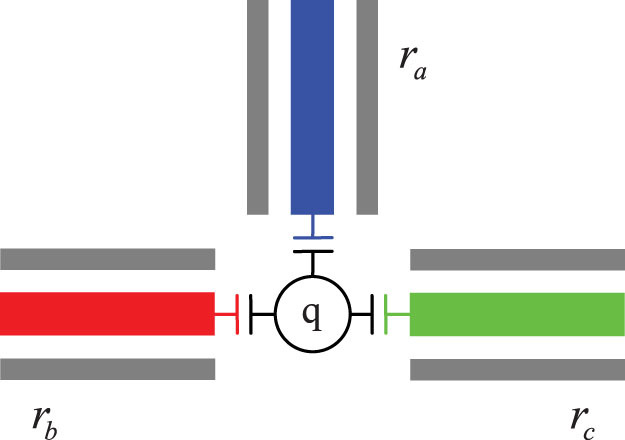
ra, rb, and rc are three high-quality resonators and they are capacitively coupled to the transmon qutrit q.
First, turning off the interaction between q and rb and that between q and rc, and resonating ra and q with the transition |g〉q ↔ |e〉q (ωa = ωg,e), the state of the whole system becomes
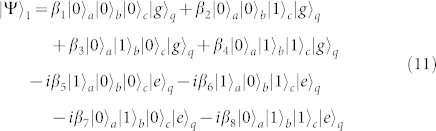 |
after the interaction time of 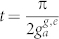 .
.
Second, turning off the interaction between q and ra and that between q and rc, and tuning the frequency of rb or q to make ωb = ωe,f, one can complete the resonance manipulation on rb and q with the transition |e〉q ↔ |f〉q. The state of the whole system can be changed into
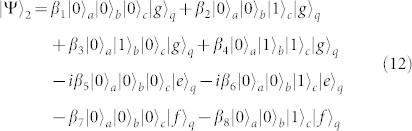 |
after the operation time of 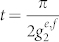 .
.
Third, repeating the same operation as the one in the first step, the state of the whole system can be evolved into
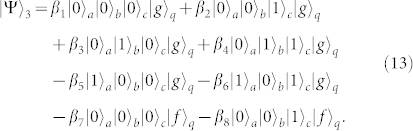 |
Fourth, turning off the interaction between q and rb and that between q and rc, and resonating ra and q with the transition |e〉q ↔ |f〉q, the state of the whole system evolves from |Ψ〉3 into
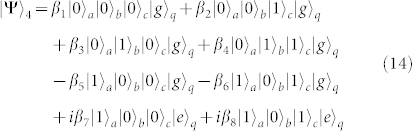 |
after the operation time of 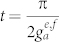 .
.
Fifth, turning off the interaction between q and ra and that between q and rb, and resonating rc and q with the transition |e〉q ↔ |f〉q (ωc = ωe,f), the state becomes
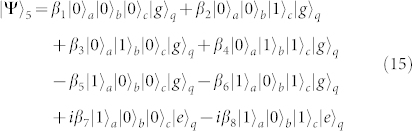 |
after the operation time of 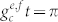 .
.
Sixth, repeating the fourth step, the state of the whole system becomes
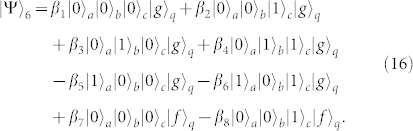 |
Seventh, taking the same manipulation as the one in the first step, the system is in the state
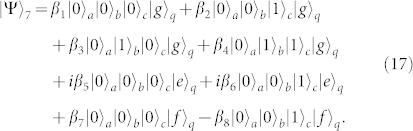 |
Eighth, repeating the second step, the state of the system evolves from |Ψ〉7 into
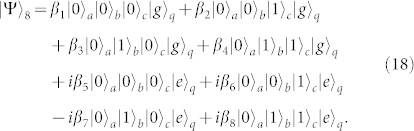 |
Ninth, repeating the first step, one can get the final state of the whole system as follows
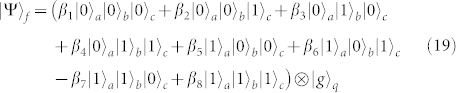 |
This is just the result of our cc-phase gate on the three microwave-photon resonators.
The evolution of the system composed of three resonators coupled to the transmon qutrit can be described by the master equation
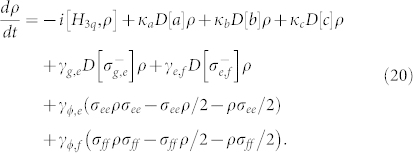 |
Here κc is the decay rate of the resonator rc. In our simulation for the fidelity of our cc-phase gate, the parameters of the system are chosen as: ωa/(2π) = 5.5 GHz, ωb/(2π) = 7.0 GHz, ωc/(2π) = 8.0 GHz, 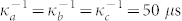 , and ωg,e/(2π) − ωe,f/(2π) = 800 MHz. The energy relaxation rates and the dephasing rates of the transmon qutrit are chosen the same as those in the construction of our c-phase gate. The details for the parameters chosen in each step for the simulation of our cc-phase gate are shown in Table 2.
, and ωg,e/(2π) − ωe,f/(2π) = 800 MHz. The energy relaxation rates and the dephasing rates of the transmon qutrit are chosen the same as those in the construction of our c-phase gate. The details for the parameters chosen in each step for the simulation of our cc-phase gate are shown in Table 2.
Table 2. The parameters for constructing the cc-phase gate on ra, rb, and rc.
| Step | ωg,e/(2π) (GHZ) |
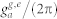 (MHZ) (MHZ) |
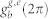 (MHZ) (MHZ) |
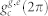 (MHZ) (MHZ) |
|---|---|---|---|---|
| i) | 5.5 | 45 | 0.5 | 0.5 |
| ii) | 7.8 | 0.5 | 28 | 0.5 |
| iii) | 5.5 | 27 | 0.5 | 0.5 |
| iv) | 6.3 | 24 | 0.5 | 0.5 |
| v) | 8.8 | 0.5 | 0.5 | 20 |
| vi) | 6.3 | 29 | 0.5 | 0.5 |
| vii) | 5.5 | 27 | 0.5 | 0.5 |
| viii) | 7.8 | 0.5 | 28 | 0.5 |
| ix) | 5.5 | 45 | 0.5 | 0.5 |
Let us define the fidelity of our cc-phase gate as
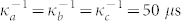 |
where |ψideal〉 is the final state |Ψ〉f of the system composed of three resonator qubits ra, rb, and rc after an ideal cc-phase gate operation when the initial state of the system is |Ψ〉0, without considering the dissipation and the dephasing. 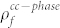 is the realistic density operator after our cc-phase gate operation on the initial state |Ψ〉0. We numerically simulate the fidelity of our cc-phase gate, by taking the dissipation and the dephasing into account. The fidelity of our cc-phase gate is 99.25% within the operation time of about 73.3 ns.
is the realistic density operator after our cc-phase gate operation on the initial state |Ψ〉0. We numerically simulate the fidelity of our cc-phase gate, by taking the dissipation and the dephasing into account. The fidelity of our cc-phase gate is 99.25% within the operation time of about 73.3 ns.
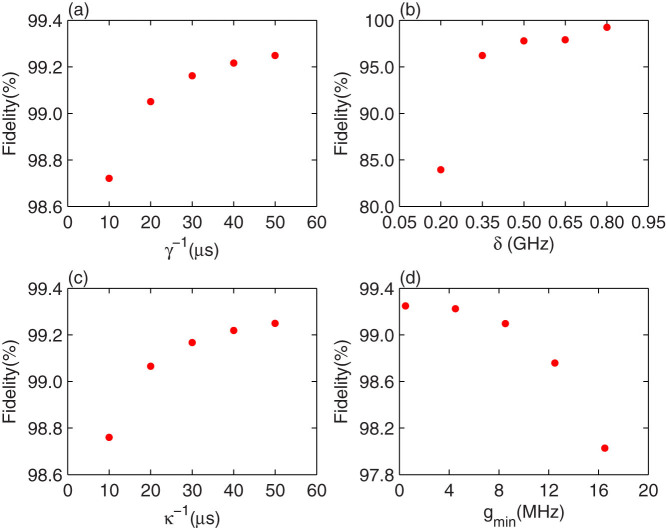
In a realistic experiment, the energy relaxation rate γ and the anharmonicity δ = ωg,e − ωe,f of the qutrit, the decay rate κ of the resonator, and the minimum value of tunable coupling strength gmin influence the fidelity of our cc-phase gate. Their effects are shown in Fig. 5 (a)–(d) in which we simulate the fidelity of the gate by varying a single parameter and fixing the other parameters. In Fig. 5 (b), although the fidelity of the cc-phase gate is reduced obviously when the anharmonicity of the qutrit becomes small, it can in principle be improved by taking a smaller coupling strength for the resonance operation.
Figure 5. The fidelity of the cc-phase gate varying with the parameters:
(a) the energy relaxation rate of the qutrit γ, (b) the anharmonicity δ = ωg,e − ωe,f, (c) the decay rate of resonators with κa = κb = κc ≡ κ, and (d) the minimum value of tunable coupling strength gmin. Here 2γe,f = γg,e = γϕ,e = γϕ,f ≡ γ for (a)–(d). Except for the variable in (a)–(d), the other parameters for these simulations are shown in Table 2.
Discussion
The number-state-dependent interaction between a superconducting qubit and resonator qudits is an important nonlinear effect which has been used to construct the quantum entangled states and quantum logic gates on resonator qudits in the previous works53,54,55,66. This effect is a useful second-order coupling between the qubit and the resonator in the dispersive regime, which indicates a slow operation of the state-dependent selective rotation on the qubit with a drive field. In contrary, our gates are achieved by using the quantum resonance operation only, which is not the high-order coupling item of the qubit and the resonator, and has been realized for generating the Fock states in a superconducting resonator with a high fidelity44. All-resonance-based quantum operations make our universal quantum gates on microwave-photon resonators have a shorter operation time, compared with those in previous works55. Moreover, our gates have a higher fidelity than those in the latter if we take the decoherence of the qubit and the decay of the resonators into account. Although there are nine steps in constructing our cc-phase gate on three resonators, compared with the three steps in constructing our c-phase gate, the total period of the resonance operations in our cc-phase gate is not much longer than the one in our c-phase gate.
In our simulations, the quantum errors from the preparation of the initial states of Eqs. (2) and (10) are not considered. Single-qubit operations on a qubit40 have been realized with the error smaller than 10−4 and it can be depressed to much small67. That is to say, the error from single-qubit operations has only a negligible influence on the results of the fidelities of our fast universal quantum gates. There are several methods which can help us to turn on and off the resonance interaction between a superconducting qutrit and a resonator, such as tuning the frequency of the qutrit, tuning the frequency of the resonator, or tuning their coupling strength. In experiment, a tunable coupling superconducting device has been realized59,68. The coupling strength between a phase qubit and a lumped element resonator68 can be tuned from 0 MHz to 100 MHz. The coupling strength between a charge qubit and a resonator59 can be tuned from 200 KHz to 43 MHz. Tuning the frequency of a high quality resonator has also been realized69. The frequency of a 1D superconducting resonator with the quality of 104 can be tuned with a range of 740 MHz. The frequency of a transmon qubit70 can be tuned in a range of about 2.5 GHz. In the system composed of several resonators coupled to a superconducting qutrit, by tuning the frequency of the qutrit only to complete the resonance operation between the qutrit and the resonators with a high fidelity, one should take small coupling strengths between them, which leads to a long-time operation61. By using the tunable resonator or tunable coupling strength only to turn on and off the interaction, the fast high-fidelity resonance operation requires a much larger tunable range. Here, we tune the frequency of the qutrit and the coupling strengths between the qutrit and each resonator to turn on and off their resonance interactions to achieve our fast universal gates. The coupling strengths are chosen much smaller than the anharmonicity of the transmon qutrit, which helps us to treat the qutrit as a qubit70 during the resonance operations without considering the effect from the third excited energy level of the qutrit. To implement our gates in experiment with a high fidelity, one should also apply a magnetic flux with fast tunability. On one hand, it can tune the frequency of the qutrit instantaneously to get the high-fidelity resonance operation71. On the other hand, it can help us to get a fast tunable coupling strength between the qutrit and the resonator59,68.
In summary, we have proposed two schemes for the construction of universal quantum gates on resonator qubits in the processor composed of multiple high-quality microwave-photon resonators coupled to a transmon qutrit, including the c-phase and cc-phase gates. Different from the ones in the previous works based on the dispersive coupling effect of the number-state-dependent interaction between a superconducting qubit and the resonator qubits55, our gates are achieved by all-resonance quantum operations and they have the advantages of higher fidelities and shorter operation times. With the optimal feasible parameters, our numerical simulations show that the fidelity of our c-phase gate approaches 99.57% within the operation time of 38.1 ns and that of our cc-phase gate is 99.25% within 73.3 ns, not resorting to drive fields.
Methods
Quantum resonance operation
Quantum resonance operation is the key element for the construction of our all-resonance-based universal quantum gates on microwave-photon resonators. In a system composed of a two-energy-level qubit coupled to a cavity, the Hamiltonian of the system is (in the interaction picture)72
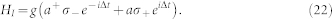 |
Here Δ = ωc − ωq and ωc is the frequency of the cavity. The Hamiltonian HI describes the state transfer between the qubit and the cavity. In the system, the unitary time-evolution operation is given by 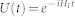 , which can be expanded at the exact resonances between the qubit and the cavity (Δ = 0) as72
, which can be expanded at the exact resonances between the qubit and the cavity (Δ = 0) as72
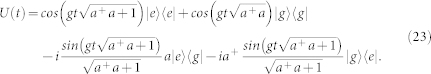 |
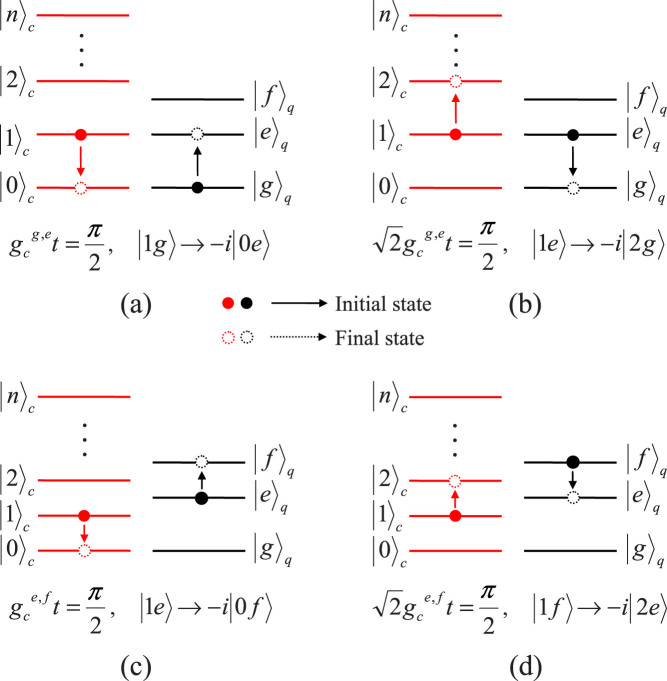
In our work, the resonance interactions take place between a three-energy-level qutrit and a single-model cavity field. To keep the resonance operation between the cavity and the qutrit with the wanted transition |g〉 ↔ |e〉 or |e〉 ↔ |f〉, one should take a small coupling strength between the qutrit and the cavity, compared with the anharmonicity of the qutrit, to avoid the off-resonance interaction between the cavity and the qutrit with the unwanted transition. The details of the state evolution of the system composed of a qutrit and a cavity are described in Fig. 6 (in which we give all the resonance processes used in this work only). In the quantum resonance operation between the cavity and the qutrit in the transmission between the energy levels |g〉 and |e〉, the evolution |1g〉 → −i|0e〉 (|0e〉 → −i|1g〉) is completed with 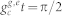 , shown in Fig. 6 (a). With
, shown in Fig. 6 (a). With 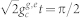 , the evolution |1e〉 → −i|2g〉 (|2g〉 → −i|1e〉) can be achieved, shown in Fig. 6 (b). In the quantum resonance operation between the cavity and the qutrit in the transmission between the energy levels |e〉 and |f〉, the evolution |1e〉 → −i|0f〉 (|0f〉 → −i|1e〉) is completed with
, the evolution |1e〉 → −i|2g〉 (|2g〉 → −i|1e〉) can be achieved, shown in Fig. 6 (b). In the quantum resonance operation between the cavity and the qutrit in the transmission between the energy levels |e〉 and |f〉, the evolution |1e〉 → −i|0f〉 (|0f〉 → −i|1e〉) is completed with 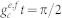 , shown in Fig. 6 (c). With
, shown in Fig. 6 (c). With 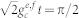 , the evolution |1f〉 → −i|2e〉 (|2e〉 → −i|1f〉) can be achieved, shown in Fig. 6 (d).
, the evolution |1f〉 → −i|2e〉 (|2e〉 → −i|1f〉) can be achieved, shown in Fig. 6 (d).
Figure 6. Schematic diagram for the resonance processes between a single-model cavity field and a qutrit.
|n〉c is the Fock state of the cavity. t is the operation time of the resonance processing.
Author Contributions
M.H. and M.J. completed the calculation and prepared the figures. M.H. and F.G. wrote the main manuscript text. F.G. supervised the whole project. All authors reviewed the manuscript.
Acknowledgments
This work was supported by the National Natural Science Foundation of China under Grant Nos. 11174039 and 11474026, and NECT-11-0031.
References
- Nielsen M. A. & Chuang I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, England, 2000). [Google Scholar]
- Shende V. V. & Markov I. L. On the CNOT-cost of Toffoli gates. Quantum Inf. Comput. 9, 461–486 (2009). [Google Scholar]
- Knill E., Laflamme R. & Milburn G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001). [DOI] [PubMed] [Google Scholar]
- O'Brien J. L. et al. Demonstration of an all-optical quantum controlled-NOT gate. Nature 426, 264–267 (2003). [DOI] [PubMed] [Google Scholar]
- Ren B. C., Wei H. R. & Deng F. G. Deterministic photonic spatial-polarization hyper-controlled-not gate assisted by a quantum dot inside a one-side optical microcavity. Laser Phys. Lett. 10, 095202 (2013). [Google Scholar]
- Ren B. C. & Deng F. G. Hyper-parallel photonic quantum computation with coupled quantum dots. Sci. Rep. 4, 4623 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren B. C. & Deng F. G. Universal hyper-parallel hybrid photonic quantum gates with dipole-induced transparency in the weak-coupling regime. arXiv 1411.0274 (2014). [Google Scholar]
- Nemoto K. & Munro W. J. Nearly deterministic linear optical controlled-NOT gate. Phys. Rev. Lett. 93, 250502 (2004). [DOI] [PubMed] [Google Scholar]
- Wei H. R. & Deng F. G. Scalable photonic quantum computing assisted by quantum-dot spin in double-sided optical microcavity. Opt. Express 21, 17671–17685 (2013). [DOI] [PubMed] [Google Scholar]
- Gershenfeld N. A. & Chuang I. L. Bulk spin-resonance quantum computation. Science 275, 350–356 (1997). [DOI] [PubMed] [Google Scholar]
- Jones J. A., Mosca M. & Hansen R. H. Implementation of a quantum search algorithm on a quantum computer. Nature 393, 344–346 (1998). [Google Scholar]
- Long G. L. & Xiao L. Experimental realization of a fetching algorithm in a 7-qubit NMR spin Liouville space computer. J. Chem. Phys. 119, 8473–8481 (2003). [Google Scholar]
- Feng G., Xu G. & Long G. Experimental realization of nonadiabatic Holonomic quantum computation. Phys. Rev. Lett. 110, 190501 (2013). [DOI] [PubMed] [Google Scholar]
- Long G. L. & Xiao L. Parallel quantum computing in a single ensemble quantum computer. Phys. Rev. A 69, 052303 (2004). [Google Scholar]
- Li X. et al. An all-optical quantum gate in a semiconductor quantum dot. Science 301, 809–811 (2003). [DOI] [PubMed] [Google Scholar]
- Hu C. Y., Young A., O'Brien J. L., Munro W. J. & Rarity J. G. Giant optical Faraday rotation induced by a single-electron spin in a quantum dot: applications to entangling remote spins via a single photon. Phys. Rev. B 78, 085307 (2008). [Google Scholar]
- Hu C. Y., Munro W. J. & Rarity J. G. Deterministic photon entangler using a charged quantum dot inside a microcavity. Phys. Rev. B 78, 125318 (2008). [Google Scholar]
- Wei H. R. & Deng F. G. Universal quantum gates for hybrid systems assisted by quantum dots inside double-sided optical microcavities. Phys. Rev. A 87, 022305 (2013). [Google Scholar]
- Wang H. F., Zhu A. D., Zhang S. & Yeon K. H. Optically controlled phase gate and teleportation of a controlled-NOT gate for spin qubits in a quantum-dot-microcavity coupled system. Phys. Rev. A 87, 062337 (2013). [Google Scholar]
- Wei H. R. & Deng F. G. Universal quantum gates on electron-spin qubits with quantum dots inside single-side optical microcavities. Opt. Express 22, 593–607 (2014). [DOI] [PubMed] [Google Scholar]
- Bonato C. et al. CNOT and Bell-state analysis in the weak-coupling cavity QED regime. Phys. Rev. Lett. 104, 160503 (2010). [DOI] [PubMed] [Google Scholar]
- Xu G. F., Zhang J., Tong D. M., Sjöqvist E. & Kwek L. C. Nonadiabatic holonomic quantum computation in decoherence-free subspaces. Phys. Rev. Lett. 109, 170501 (2012). [DOI] [PubMed] [Google Scholar]
- Togan E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010). [DOI] [PubMed] [Google Scholar]
- Wei H. R. & Deng F. G. Compact quantum gates on electron-spin qubits assisted by diamond nitrogen-vacancy centers inside cavities. Phys. Rev. A 88, 042323 (2013). [Google Scholar]
- Neumann P. et al. Quantum register based on coupled electron spins in a room-temperature solid. Nat. Phys. 6, 249–253 (2010). [Google Scholar]
- Duan L. M. & Kimble H. J. Scalable photonic quantum computation through cavity-assisted interactions. Phys. Rev. Lett. 92, 127902 (2004). [DOI] [PubMed] [Google Scholar]
-
Koshino K., Ishizaka S. & Nakamura Y.
Deterministic photon-photon
 gate using a Λ system. Phys. Rev. A
82, 010301(R) (2010). [Google Scholar]
gate using a Λ system. Phys. Rev. A
82, 010301(R) (2010). [Google Scholar] - Blais A., Huang R. S., Wallraff A., Girvin S. M. & Schoelkopf R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004). [Google Scholar]
- Wallraff A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004). [DOI] [PubMed] [Google Scholar]
- Blais A. et al. Quantum-information processing with circuit quantum electrodynamics. Phys. Rev. A 75, 032329 (2007). [Google Scholar]
- Cao Y., Huo W. Y., Ai Q. & Long G. L. Theory of degenerate three-wave mixing using circuit QED in solid-state circuits. Phys. Rev. A 84, 053846 (2011). [Google Scholar]
- Johansson J. R., Johansson G., Wilson C. M. & Nori F. Dynamical casimir effect in a superconducting coplanar waveguide. Phys. Rev. Lett. 103, 147003 (2009). [DOI] [PubMed] [Google Scholar]
- Ong F. R. et al. Circuit QED with a nonlinear resonator: ac-Stark shift and dephasing. Phys. Rev. Lett. 106, 167002 (2011). [DOI] [PubMed] [Google Scholar]
- Rigetti C. et al. Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Phys. Rev. B 86, 100506(R) (2012). [Google Scholar]
- Díaz P. F. et al. Observation of the Bloch-Siegert shift in a qubit-oscillator system in the ultrastrong coupling regime. Phys. Rev. Lett. 105, 237001 (2010). [DOI] [PubMed] [Google Scholar]
- DiCarlo L. et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240–244 (2009). [DOI] [PubMed] [Google Scholar]
- Chow J. M. et al. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nat. commun. 5, 4015 (2014). [DOI] [PubMed] [Google Scholar]
- Fedorov A. et al. Implementation of a Toffoli gate with superconducting circuits. Nature 481, 170–172 (2012). [DOI] [PubMed] [Google Scholar]
- Reed M. D. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382–385 (2012). [DOI] [PubMed] [Google Scholar]
- Barends R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014). [DOI] [PubMed] [Google Scholar]
- DiCarlo L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010). [DOI] [PubMed] [Google Scholar]
- Steffen L. et al. Deterministic quantum teleportation with feed-forward in a solid state system. Nature 500, 319–322 (2013). [DOI] [PubMed] [Google Scholar]
- Devoret M. H. & Schoelkopf R. J. Superconducting circuits for quantum information: An outlook. Science 339, 1169–1174 (2013). [DOI] [PubMed] [Google Scholar]
- Hofheinz M. et al. Generation of Fock states in a superconducting quantum circuit. Nature 454, 310–314 (2008). [DOI] [PubMed] [Google Scholar]
- Wang H. et al. Measurement of the decay of Fock states in a superconducting quantum circuit. Phys. Rev. Lett. 101, 240401 (2008). [DOI] [PubMed] [Google Scholar]
- Hofheinz M. et al. Synthesizing arbitrary quantum states in a superconducting resonator. Nature 459, 546–549 (2009). [DOI] [PubMed] [Google Scholar]
- Merkel S. T. & Wilhelm F. K. Generation and detection of NOON states in superconducting circuits. New J. Phys. 12, 093036 (2010). [Google Scholar]
- Wang H. et al. Deterministic entanglement of photons in two superconducting microwave resonators. Phys. Rev. Lett. 106, 060401 (2011). [DOI] [PubMed] [Google Scholar]
- Johnson B. R. et al. Quantum non-demolition detection of single microwave photons in a circuit. Nat. Phys. 6, 663–667 (2010). [Google Scholar]
- Strauch F. W. All-resonant control of superconducting resonators. Phys. Rev. Lett. 109, 210501 (2012). [DOI] [PubMed] [Google Scholar]
- Yang C. P., Su Q. P. & Han S. Y. Generation of Greenberger-Horne-Zeilinger entangled states of photons in multiple cavities via a superconducting qutrit or an atom through resonant interaction. Phys. Rev. A 86, 022329 (2012). [Google Scholar]
- Yang C. P., Su Q. P., Zheng S. B. & Han S. Y. Generating entanglement between microwave photons and qubits in multiple cavities coupled by a superconducting qutrit. Phys. Rev. A 87, 022320 (2013). [Google Scholar]
- Strauch F. W. Quantum logic gates for superconducting resonator qudits. Phys. Rev. A 84, 052313 (2011). [Google Scholar]
- Wu C. W. et al. Scalable one-way quantum computer using on-chip resonator qubits. Phys. Rev. A 85, 042301 (2012). [Google Scholar]
- Hua M., Tao M. J. & Deng F. G. Universal quantum gates on microwave photons assisted by circuit quantum electrodynamics. Phys. Rev. A 90, 012328 (2014). [Google Scholar]
- Schuster D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007). [DOI] [PubMed] [Google Scholar]
- Laloy A. P. et al. Tunable resonators for quantum circuits. J. Low Temp. Phys. 151, 1034–1042 (2008). [Google Scholar]
- Harris R. et al. Sign- and magnitude-tunable coupler for superconducting flux qubits. Phys. Rev. Lett. 98, 177001 (2007). [Google Scholar]
- Srinivasan S. J., Hoffman A. J., Gambetta J. M. & Houck A. A. Tunable coupling in circuit quantum electrodynamics using a superconducting charge qubit with a V-shaped energy level diagram. Phys. Rev. Lett. 106, 083601 (2011). [DOI] [PubMed] [Google Scholar]
- Strauch F. W., Onyango D., Jacobs K. & Simmonds R. W. Entangled-state synthesis for superconducting resonators. Phys. Rev. A 85, 022335 (2012). [Google Scholar]
- Su Q. P., Yang C. P. & Zheng S. B. Fast and simple scheme for generating NOON states of photons in circuit QED. Sci. Rep. 4, 3898 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang J. B. et al. Improved superconducting qubit coherence using titanium nitride. Appl. Phys. Lett. 103, 012602 (2013). [Google Scholar]
- Megrant A. et al. Planar superconducting resonators with internal quality factors above one million. Appl. Phys. Lett. 100, 113510 (2012). [Google Scholar]
- Xiang Z. L., Ashhab S., You J. Q. & Nori F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623 (2013). [Google Scholar]
- Hoi I. C. et al. Demonstration of a single-photon router in the microwave regime. Phys. Rev. Lett. 107, 073601 (2011). [DOI] [PubMed] [Google Scholar]
- Strauch F. W., Jacobs K. & Simmonds R. W. Arbitrary control of entanglement between two superconducting resonators. Phys. Rev. Lett. 105, 050501 (2010). [DOI] [PubMed] [Google Scholar]
- Motzoi F., Gambetta J. M., Rebentrost P. & Wilhelm F. K. Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 103, 110501 (2009). [DOI] [PubMed] [Google Scholar]
- Allman M. S. et al. Rf-SQUID-mediated coherent tunable coupling between a superconducting phase qubit and a lumped-element resonator. Phys. Rev. Lett. 104, 177004 (2010). [DOI] [PubMed] [Google Scholar]
- Sandberg M. et al. Tuning the field in a microwave resonator faster than the photon lifetime. Appl. Phys. Lett. 92, 203501 (2008). [Google Scholar]
- Schreier J. A. et al. Suppressing charge noise decoherence in superconducting charge qubits. Phys. Rev. B 77, 180502(R) (2008). [Google Scholar]
- Houck A. A. et al. Generating single microwave photons in a circuit. Nature 449, 328–331 (2007). [DOI] [PubMed] [Google Scholar]
- Scully M. O. & Zubairy M. S. Quantum Optics (Cambridge University, Cambridge, 1997). [Google Scholar]