Estimation of mean response via effective balancing score

Summary

We introduce effective balancing scores for estimation of the mean response under a missing at random mechanism. Unlike conventional balancing scores, the effective balancing scores are constructed via dimension reduction free of model specification. Three types of effective balancing scores are introduced: those that carry the covariate information about the missingness, the response, or both. They lead to consistent estimation with little or no loss in efficiency. Compared to existing estimators, the effective balancing score based estimator relieves the burden of model specification and is the most robust. It is a near-automatic procedure which is most appealing when high dimensional covariates are involved. We investigate both the asymptotic and the numerical properties, and demonstrate the proposed method in a study on Human Immunodeficiency Virus disease.

1. Introduction

In social and medical studies, the primary interest is usually the mean response, the estimation of which can be complicated by missing observations due to nonresponse, drop out or death. The data observed are triplets {(Y_i, δ_i, X_i), i = 1, ···, n}, where Y_i is the response, δ_i = 1 if Y_i is observed and δ_i = 0 if Y_i is missing, and X_i is the vector of covariates and always observed. Under the missing at random mechanism (Rosenbaum & Rubin, 1983); that is, Pr(δ = 1 | X, Y) = Pr(δ = 1 | X), estimation of E(Y) is mostly developed using the parametric form of the missingness pattern π(X) = Pr(δ = 1 | X) or the response pattern m(X) = E(Y | X). Important methods include regression estimation (Rubin, 1987; Schafer, 1997), inverse propensity score estimation (Horvitz & Thompson, 1952), augmented inverse propensity weighting estimation (Robins et al., 1994), and their modified versions such as D’Agostino (1998), Scharfstein et al. (1999), Little & An (2004), Vartivarian & Little (2008), and Cao et al. (2009). A review of most methods can be found in Lunceford & Davidian (2004) and Kang & Schafer (2007). Consistency and efficiency of these estimators rely on correct model specification. Even for the “doubly robust” estimators, either π(X) or m(X) needs to be correctly specified for consistency and both correctly specified for efficiency (Robins & Rotnitzky, 1995; Hahn, 1998). When X ∈ ℝ^p is high dimensional, model specification is challenging: it is hard for a parametric model to be sufficiently flexible to capture all the important nonlinear and interaction effects yet parsimonious enough to maintain reasonable efficiency.

One family of estimators are built upon the balancing score. According to Rosenbaum & Rubin (1983), a balancing score b(X) has the property E(Y | b(X)) = E(Y | b(X), δ = 1). Therefore, E(Y) can be estimated via b(X) over the complete cases {(Y_i, δ_i, X_i) : δ_i = 1}. The most well known balancing scores include the propensity score (Rosenbaum & Rubin, 1983) and the prognostic score (Hansen, 2008). The mean response can be estimated via the balancing score by such nonparametric approaches as stratification (Rosenbaum & Rubin, 1983) and nonparametric regression (Cheng, 1994). Of course, the naive balancing score is X. However, estimation using X as a balancing score is subject to the curse of dimensionality when X ∈ ℝ^p is high dimensional (Abadie & Imbens, 2006).

Balancing scores have been estimated through parametric modeling. In comparison to the other estimators, balancing score based estimators are less sensitive to model misspecification, largely due to the nonparametric approaches to utilize the balancing score (Rosenbaum, 2002). One important property of the balancing score based estimator, which has rarely been utilized, is that full parametric modeling is actually unnecessary. For example, if π(x) = f{b(x)} for some function b(X) and unknown function f, then E(Y) can be estimated via b(X) through stratification or nonparametric regression as subjects with similar values in b(X) have similar values in π(X). Provided that we can find such a function b(X), there is no need for the full parametric form of π(X).

In this work, we introduce the effective balancing score. Like the propensity score and the prognostic score, the effective balancing score creates a conditional balance between the subjects with response observed and the subjects with response missing. Unlike the conventional balancing scores, estimation of the effective balancing score is free of model specification via the technique of dimension reduction (Li, 1991; Cook & Weisberg, 1991; Cook & Li, 2002; Li & Zhu, 2007; Li & Wang, 2007). The effective balancing score carries all X information about the missingness or the response in the sense δ ⊥ X | S or Y ⊥ X | S, where S stands for the effective balancing score and ⊥ stands for conditional independence. It thus leads to consistent estimation of E(Y) with little or no loss in efficiency. As a parsimonious summary of X, the effective balancing score is of dimension much smaller than p. Compared with existing methods, the effective balancing score based estimator has the following advantages: (1) It relieves the burden of model specification and is the most robust with potentially optimal efficiency; (2) Through the technique of dimension reduction, the effective balancing score is of low dimension which enables the effective use of stratification and nonparametric regression; (3) It avoids the shortcoming of inverse propensity weighting, i.e., instability caused by estimates of π(X) that are close to zero.

2. Effective balancing score

2·1. Effective balancing score

Let be the response from X ∈ ℝ^p. Usually relates to X through only a few linear combinations; that is, $\mathcal{R}\perp X\mid ({\beta }_1^{\prime }X,\cdots ,{\beta }_K^{\prime }X)$ with β_k ∈ ℝ^p : k = 1, ···, K distinctive vectors. Let B = (β₁, ···, β_K) with β₁, ···, β_K orthonormal and K the smallest dimension to satisfy the conditional independence, then B is a basis of the central dimension-reduction space with K the structural dimension (Cook, 1994). The columns of B are arranged in descending order of importance; that is, λ₁ ≥ λ₂ ≥ ··· ≥ λ_K > 0 where λ_k measures the amount of X information carried by ${\beta }_k^{\prime }X$ and is explained in §3.2. In general, K is much smaller than p. If we let S = B′X, then S ∈ ℝ^K is a parsimonious summary of X: it is of lower dimension than X but carries all X information about 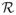. In this paper, we refer to B = (β₁, ···, β_K) as the effective directions.

Let 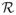= δ and B_δ be the effective directions of 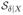, then

$$\delta \perp X\mid B_{\delta }^{\prime }X,$$ (1)

and we refer to $S_{\delta }=B_{\delta }^{\prime }X$ as the effective propensity score.

Let 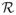= Y and denote B_Y as the effective directions of 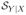, then

$$Y\perp X\mid B_Y^{\prime }X.$$ (2)

Obviously, $B_Y^{\prime }X$ is a prognostic score satisfying the definition of Hansen (2008). We refer to $S_Y=B_Y^{\prime }X$ as the effective prognostic score.

Each effective score creates the conditional balance

$$Y\perp \delta \mid S,$$ (3)

where S is either S_δ or S_Y. For S = S_δ, (3) follows similarly as in Theorem 3 of Rosenbaum & Rubin (1983). For S = S_Y,

$$Pr(\delta =1\mid Y,S)=E\{E(\delta \mid Y,X)\mid Y,S\}=E\{E(\delta \mid X)\mid Y,S\}=E\{E(\delta \mid X)\mid S\},$$

where the second equation is due to missingness at random and the last equation to (2). Since the last expectation is E(δ | S) = Pr(δ = 1 | S), (3) follows. It is immediate from (3) that both effective scores are balancing scores.

Example 1

Suppose Y | X is normal with mean m(X) = X₁ + exp(X₂ + X₃) + X₁X₄ and variance ${\sigma }^2(X)=X_1^2+X_4^2$, with the probability of observing Y as $\pi (X)=\text{expit}(0.1X_1^2+X_2+X_3)$. Then, the prognostic score is {m(X), σ²(X)} and the propensity score is π(X). The effective prognostic score is { $(X_2+X_3)/\sqrt{2},X_1,X_4$} and the effective propensity score is { $(X_2+X_3)/\sqrt{2},X_1$}.

The effective balancing scores may have higher dimensions than their conventional counterparts. However, estimation of the propensity score and the prognostic score requires correct model specification and is subject to the challenges discussed in §1. The effective balancing scores, on the other hand, can be obtained without model specification.

We can also let 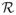= (δ, Y) be a bivariate response. Denote B_d as the effective directions for 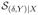, then

$$\delta \perp X\mid B_d^{\prime }X\text{and}Y\perp X\mid B_d^{\prime }X.$$ (4)

In other words, $B_d^{\prime }X$ carries all X information about both δ and Y, and creates both propensity balance and prognostics balance. We refer to $S_d=B_d^{\prime }X$ as the effective double balancing score. In Example 1, $S_d=\{(X_2+X_3)/\sqrt{2},X_1,X_4\}$ is the same as S_Y.

Remark 1

As shown by (1) and (2), so long as either independence in (4) holds, S_d is a balancing score satisfying the conditional balance (3). It is for this reason that we refer to S_d as the effective double balancing score.

In summary, both the effective prognostic score and the effective double balancing score have the properties

$$Y\perp \delta \mid S\text{and}Y\perp X\mid S.$$

The first property implies E(Y | S) = E(Y | S, δ = 1), which ensures unbiased estimation of E(Y) via S from the complete cases. The second property implies that S carries all X information about the response, which ensures efficient estimation of E(Y) via S. The effective propensity score possesses only the first property and is not as efficient as the other two. We will show in §3 and §4 that S_d can improve over S_Y under certain situations. Without loss of generality, we assume E(X) = 0 and cov(X) = I_p the identity matrix.

2·2. Estimation of effective balancing score

To find the effective balancing scores is to find the effective directions: the effective directions of 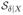for the effective propensity score and the effective directions of 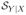for the effective prognostic score. For the effective double balancing score, we need the effective directions of .

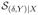Remark 2

Under missingness at random, there is the relationship 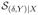= 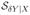for continuous response Y. The effective directions of 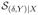can be estimated through the univariate response δY. A similar approach applies if Y is categorical. See Appendix 1.

There are many dimension reduction methods for estimating the effective directions. The most fundamental methods are the sliced inverse regression (Li, 1991) and the sliced average variance estimation (Cook & Weisberg, 1991). Both methods are developed under the linearity condition; that is, E(X | B′X) is a linear function of B′X. Many new methods have been developed to improve over these two. To improve estimation efficiency, there are the likelihood based methods of Cook (2007), Cook & Forzani (2008) and Cook & Forzani (2009). To relax the distribution assumption, Li & Dong (2009) and Dong & Li (2010) proposed methods to remove the linearity condition, and Ma & Zhu (2012) successfully applied a semiparametric approach to eliminate all distributional assumptions. These methods lead to root-n consistent estimates under proper conditions. As to be shown in Theorem 2, the proposed estimation of E(Y) requires only the effective direction estimates to be root-n consistent. In this work, we adopt the fitted principal component method of Cook (2007) in the numerical studies unless stated otherwise. More information about these dimension reduction methods is given in §6.

Remark 3

Under missingness at random, there is the relationship

$${\mathcal{S}}_{(\delta ,Y)\mid X}=\text{span}({\mathcal{S}}_{\delta \mid X},{\mathcal{S}}_{Y\mid X})$$

following Chiaromonte et al. (2002). That is, the effective directions of 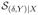include both the effective directions of 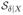and the effective directions of .

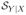In addition to the method in Remark 2, Remark 3 suggests a pooling method for the effective directions of 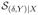. Since δ and Y are mostly related, there is likely overlap between 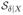and 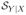. Therefore, the pooling method needs to be followed by such a method as Gram-Schmidt’s orthogonolization to remove redundancy.

3. Mean response estimation via effective balancing score

In this section, let S stand for the effective balancing score and B the matrix of effective directions. We first consider B as known and later investigate the impact from the estimation of B. As S = B′X consists of linear combinations of X, it is always observed. As B has columns of orthonormal vectors, S has the identity covariance matrix. Since S carries all X information about the missingness or the response, we can use S ∈ ℝ^K instead of X ∈ ℝ^p for the estimation of E(Y) through stratification or nonparametric regression. In this work, we focus on nonparametric regression.

3·1. Nonparametric regression via effective balancing score

Let m(S) = E(Y | S) be the conditional mean response given the effective balancing score, then E(Y) = E{m(S)} can be estimated through the estimation of m(S). To obviate model specification, we estimate m(·) by nonparametric kernel regression (Silverman, 1986)

$$\widehat{m}(s)=\sum _{i=1}^n{\delta }_i{y}_i{\mathcal{K}}_H(s_i-s)/\sum _{i=1}^n{\delta }_i{\mathcal{K}}_H(s_i-s),$$ (5)

where S_i = B′X_i, 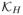(u) = det(H)⁻¹ 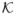(H⁻¹u) for u = (u₁, ···, u_K) with H the bandwidth matrix and 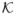(·) the kernel function. Since S has identity covariance, we take H = h_nI_K with h_n a scalar bandwidth (Härdle et al., 2004). We then estimate E(Y) by

$$\widehat{\mu }=n^{-1}\sum _{i=1}^n\widehat{m}(s_i).$$ (6)

We refer to μ̂ as the nonparametric regression via effective balancing score estimator, or briefly the nonparametric balancing score estimator. By the result of Devroye & Wagner (1980), m̂(s) converges in probability to E(δY | s)/E(δ | s). It is immediate from (3) that E(δY | s) = E(δ | s)E(Y | s). Therefore, m̂(s) converges in probability to m(s), and consequently (6) to μ = E(Y).

Theorem 1

Under the regularity conditions, the nonparametric balancing score estimator μ̂ is asymptotically normally distributed. If as n → ∞, h_n → 0 and ${nh}_n^K\to \infty$, then

$$n^{1/2}(\widehat{\mu }-\mu )\to N(0,{\sigma }^2)$$

with

$${\sigma }^2=var(Y)+E[\{\pi {(S)}^{-1}-1\}var(Y\mid S)].$$

where π(S) = E(δ | S).

For S = S_Y or S = S_d, due to (2) and (4), we have Y ⊥ X | S and thus var(Y | S) = var(Y | X). It follows that

$${\sigma }^2=var(Y)+E\left[\{\pi {(X)}^{-1}-1\}var(Y\mid X)\right],$$

, which is the optimal efficiency for the semiparametric estimators of E(Y), see Hahn (1998). This means that the nonparametric balancing score estimation via S_Y or S_d is both consistent and optimally efficient. For S = S_δ, as var(Y | S) ≥ var(Y | X), the optimal efficiency may not be reached.

Theorem 2

With B replaced by its root-n consistent estimate B̂, the nonparametric balancing score estimators have the same asymptotic properties as in Theorem 1.

Proof of Theorem 1 and 2 are given in the Appendix. Due to Theorem 2, we will use S_δ, S_Y, and S_d for the effective balancing scores whether B is known or estimated.

3·2. Dimension of effective balancing score

To determine the dimension of the effective balancing score is to determine K, the number of effective directions. A simple approach is the sequential permutation test of Cook & Yin (2001).

The dimension of the effective balancing score affects performance of the proposed estimator through nonparametric regression (5). Following Theorem 1, the impact from nonparametric regression is asymptotically negligible for h_n ~ n ^−α with 0 < α < 1/K. For larger K, selection of h_n is more constrained as α falls in a narrower range. More specifically, nonparametric regression introduces bias $h_n^2\mathcal{B}$ and variance ${(n^2{h}_n^K)}^{-1}\mathcal{V}$ to μ̂, see Appendix 2. The mean squared error of μ̂ is minimized at h_opt ~ n ^−2/(K+4). At h_opt, the asymptotic variance is n ⁻¹ σ² + n ^−8/(K+4) 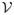. If K ≤ 3, μ̂ is root-n consistent and the variance from nonparametric regression is asymptotically negligible. If K = 4, μ̂ is root-n consistent but the variance from nonparametric regression is not asymptotically negligible. If K > 4, μ̂ converges slower than n^−1/2. Ideally, we would like S of dimension no more than 3 to reach the minimum mean squared error, root-n consistency, and negligible impact from nonparametric regression. Note that without dimension reduction; that is, S = X ∈ ℝ^p, the proposed estimator reduces to the nonparametric regression estimation of Cheng (1994) which can perform poorly for large p.

We compare the three effective balancing scores. The effective double balancing score and effective prognostic score improve over the effective propensity score, as S_Y and S_d lead to more efficient estimation than S_δ as shown by Theorem 1. The effective double balancing score can improve over the effective prognostic score when 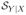is more than three-dimensional but 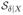is less than three-dimensional. Here is a hypothetical example. Suppose 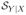has 5 effective directions, 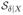has one effective direction, and B_d = (B_δ, B_Y) has the effective propensity direction B_δ as the most important. To maintain conditional balance (3), S_Y needs to be of dimension 5. For S_d, we can use only the first three components: while the first component ensures conditional balance and thus consistency, the other two components enhance efficiency.

We can use $S^{\ast }=({\beta }_1^{\prime }X,{\beta }_2^{\prime }X,{\beta }_3^{\prime }X)$ in case of K > 3, which shows generally good performance in numerical studies. Most dimension reduction methods estimate β_k’s as the eigenvectors of a kernel matrix, and the corresponding eigenvalue λ_k reflects the amount of X information carried by ${\beta }_k^{\prime }X$, see §6. When the first three components carry enough X information in the sense that (λ₁ + λ₂ + λ₃)/(λ₁ + ···, λ_K) is no less than 0.90, S* leads to good estimation. We refer to S^* as the dimension further reduced effective score. If K > 3 and the first three components carry a low percentage of X information, which rarely happens in practice, we can use generalized additive modeling for the estimation of E(Y | S). That is, instead of the multivariate kernel regression (5), E(Y | S) is estimated through the additive model $Y=g_1({\beta }_1^{\prime }X)+\cdots +g_K({\beta }_K^{\prime }X)+\epsilon$, where each g_k is nonparametric and estimated by smoothing on a single coordinate, see Hastie & Tibshirani (1986). Though the generalized additive model is a bit restrictive by assuming the additivity, it relieves the curse of dimensionality that hinders multivariate kernel regression when K is big.

3·3. Estimation procedure

• Step 1. Estimate the effective directions B and determine the dimension K;

• Step 2. If K ≤ 3, compute the effective balancing score S = B̂′X; if K > 3, let $S^{\ast }=({\beta }_1^{\prime }X,{\beta }_2^{\prime }X,{\beta }_3^{\prime }X)$ be the dimension further reduced effective score;

• Step 3. Estimate E(Y) by nonparametric regression via the effective balancing score S or the dimension further reduced effective score S^*.

For bandwidth selection, the optimal bandwidth is h_opt ~ n^−2/(K+4) which minimizes the mean squared error of μ̂ and can be estimated by the plug in method (Fan & Marron, 1992), see Appendix 2. This optimal bandwidth is smaller than the conventional bandwidth h_n ~ n ^−1/(K+4), which is optimal for the estimation of conditional mean m(S) (Härdle et al., 2004). At the conventional bandwidth, though the proposed estimator does not attain the minimal mean squared error, the bias and variance from nonparametric regression are asymptotically negligible. Therefore, when the sample size is large, we can use the conventional bandwidth which is easier to determine (Sheather & Jones, 1991).

For variance estimation, we can use the asymptotic variance formula in Theorem 1. The asymptotic variance leaves out the negligible terms; that is, the variability introduced by the estimation of the effective directions and the nonparametric regression of m(S). We recommend bootstrap for variance estimation: bootstrap n samples from the original triplets {(Y_i, X_i, δ_i) : i = 1, ···, n} with replacement; compute the nonparametric balancing score estimate μ̂^(b) over the bootstrapped data {(Y_i, X_i, δ_i)^(b) : i = 1, ···, n}; repeat these two steps many times and use the sample variance of μ̂^(b) as the estimate of var(μ̂). The bootstrap estimate includes all sources of variation.

4. Numerical Studies

We investigate the numerical performance of the proposed estimators: μ̂_δ uses the effective propensity score, μ̂_Y uses the effective prognostic score, and μ̂_d uses the effective double balancing score. Also computed are the commonly used model based estimators: the parametric regression estimation μ̂_reg, the inverse propensity weighted estimator μ̂_ipw, and the augmented inverse propensity weighted estimator μ̂_aipw. In the model based estimations, we use linear regression for m(X) and linear logistic regression for π(X). In all simulations, 200 datasets with n = 200 or n = 1000 are used.

In simulation 1, X = (X₁, ···, X₁₀) has components of independent N(0, 1), π = expit(X₁) and Y = 3X₁ + 5X₂ + ε with ε of independent N(0, 1). Estimation results are in Table 1. With m(X) linear and π(X) logistic linear, both working models are correct for the model based estimations. We see the nonparametric balancing score estimators have comparable performance to the model based estimators. Due to adoption of the nonparametric procedures, additional bias and variation are introduced to the proposed estimators. However, the additional bias and variation diminish as sample size gets large. The estimators μ̂_Y and μ̂_d reach the optimal efficiency, and μ̂_δ is less efficient. The last observation agrees with the discussion following Theorem 1.

Table 1.

Results for simulation 1: Monte Carlo bias (Bias), standard deviation (SD), root mean squared error (RMSE), and the estimated standard deviation (ESD) and coverage percentage (CP) of the 95% confidence interval from bootstrap with 200 replications.

		μ̂δ	μ̂Y	μ̂d	μ̂reg	μ̂ipw	μ̂aipw
n = 200	Bias	0.04	0.09	0.09	−0.04	0.00	−0.03
	SD	0.57	0.43	0.45	0.42	0.58	0.43
	RMSE	0.57	0.44	0.46	0.43	0.58	0.43
	ESD	0.63	0.45	0.48	0.43	0.61	0.43
	CP	96.5	94.0	95.5	95.0	95.0	95.0
n = 1000	Bias	0.02	0.04	0.05	0.00	0.02	0.00
	SD	0.23	0.20	0.19	0.19	0.23	0.19
	RMSE	0.23	0.20	0.20	0.19	0.23	0.19
	ESD	0.24	0.20	0.20	0.19	0.24	0.19
	CP	96.5	96.0	95.5	96.5	96.0	95.5

In simulation 2, X = (X₁, ···, X₁₀) has components of independent N(0, 1), π = expit{exp(X₂)} and $Y=(X_1+X_3)-10X_2^4+5exp(X_4+X_5)-X_3(X_4+X_5)+\epsilon$ with ε of independent N(0, 1). Estimation results are in Table 2. As m(X) is nonlinear and π(X) is log-logistic, the working models are incorrect and we see large bias in the model based estimators. The nonparametric balancing score estimators show negligible bias and good efficiency.

Table 2.

Results for simulation 2: Monte Carlo bias (Bias), standard deviation (SD), root mean squared error (RMSE), and the estimated standard deviation (ESD) and coverage percentage (CP) of the 95% confidence interval from bootstrap with 200 replications.

		μ̂δ	μ̂Y	μ̂d	μ̂reg	μ̂ipw	μ̂aipw
n = 200	Bias	0.08	0.14	0.06	3.12	−7.72	−7.39
	SD	8.80	8.47	7.91	8.98	24.45	23.83
	RMSE	8.80	8.47	7.91	9.50	25.64	24.95
	ESD	9.20	8.85	8.35	7.45	12.69	16.96
	CP	93.5	92.0	92.5	78.0	93.5	94.0
n = 1000	Bias	0.06	0.11	0.04	1.91	−10.74	−10.88
	SD	3.86	3.38	3.32	4.06	10.67	10.45
	RMSE	3.86	3.38	3.32	4.49	15.14	15.09
	ESD	3.83	3.67	3.56	3.91	7.49	7.52
	CP	95.0	95.5	95.0	88.0	80.5	82.0

In this simulation, 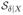has one effective direction, 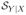has four effective directions, and 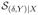has four effective directions. For μ̂_Y and μ̂_d, we use only the first three components of the estimated S_Y and S_d. Among its first three components, S_d has X₂ as information conveyer for δ and the other two components as primary information conveyers for Y. Therefore, the dimension reduced score $S_d^{\ast }$ still maintains the conditional balance (3) and leads to consistent estimate with good efficiency. For S_Y, its first three components carry around 93% X information about Y. The dimension reduced score $S_Y^{\ast }$ does not maintain the conditional balance, but it conveys enough X information for the proposed estimation: μ̂_Y has much smaller bias and is more stable than the model based estimators. This simulation also shows that μ̂_d can outperform μ̂_δ and μ̂_Y : it outperforms the former in efficiency and the latter in consistency.

Dimension reduction methods are mostly developed under certain distributional assumptions. It is thus worth investigating robustness of the proposed estimation to the distribution assumptions under which the effective directions are estimated. For this purpose, we have the following simulation. In simulation 3, Z₁, ···, Z₄ are independent N(0, 1), π = expit(−Z₁ + 0.5Z₂−0.25Z₃−0.1Z₄), and Y = 210 + 4Z₁ + 2Z₂ + 2Z₃ + Z₄ + ε. Suppose the covariates actually observed are X₁ = exp(Z₁/2), X₂ = Z₂/(1 + exp(Z₁)), X₃ = (Z₁Z₃/25 + 0.6)³, X₄ = (Z₃ + Z₄ + 20)², X₅ = X₃X₄, and X₆, ···, X₁₀ of independent uniform (0, 1). This setup mimics that of Kang & Schafer (2007). Here we use the sliced inverse regression to estimate the effective directions, even though X does not satisfy the linearity condition, to explore robustness.

Estimation results are in Table 3. Here we see that the proposed estimation is quite robust to mild violation of the linearity condition. This is not surprising, as sliced inverse regression is not sensitive to the linearity condition (Li, 1991). The effective balancing scores are all 4-dimensional, and we use the dimension reduced effective scores in the proposed estimation. Though the dimension reduced effective scores lose some X information, the proposed estimators still outperform the model based estimators. The inverse propensity weighting estimator μ̂_ipw has huge bias and variability, demonstrating the instability associated with inverse propensity weighting. The doubly robust estimator μ̂_aipw has poor performance, exemplifying the drawback of doubly robust estimators whose performance relies on model specification.

Table 3.

Results for simulation 3: Monte Carlo bias (Bias), standard deviation (SD), root mean squared error (RMSE).

		μ̂δ	μ̂Y	μ̂d	μ̂reg	μ̂ipw	μ̂aipw
n = 200	Bias	−0.17	0.08	−0.12	0.33	247.21	−2.70
	SD	0.50	0.42	0.42	0.46	184.3	3.21
	RMSE	0.53	0.43	0.44	0.57	308.35	4.20
n = 1000	Bias	−0.14	0.07	−0.09	0.27	261.72	−4.38
	SD	0.20	0.19	0.19	0.23	110.06	6.48
	RMSE	0.24	0.2	0.21	0.35	283.92	7.82

In summary, the proposed estimators have comparable performance to the model based estimators when the parametric models are correctly specified, and outperform the model based estimators otherwise. The proposed estimators also show roughly root-n consistency. When the effective balancing score is more than three dimensional, its first three components lead to good estimate.

5. Application

We demonstrate the proposed estimation by an Human Immunodeficiency Virus study, where 820 infected patients received combination antiretroviral therapy and had baseline characteristics measured prior to therapy, see Matthews et al. (2011). The baseline characteristics included weight, body mass index, age, CD4 counts, HIV viral load, hemoglobin, platelet, SGPT, and albumin. We are interested in the CD4 counts 96 weeks post therapy. Due to drop out and death, around 50% patients were lost to follow-up at 96 weeks. It is plausible to assume missing at random; that is, whether a patient stayed in the study depended on his/her baseline characteristics. In this study, X is the vector of baseline characteristics and Y is the CD4 counts at 96 weeks. Our interest is the mean CD4 count E(Y).

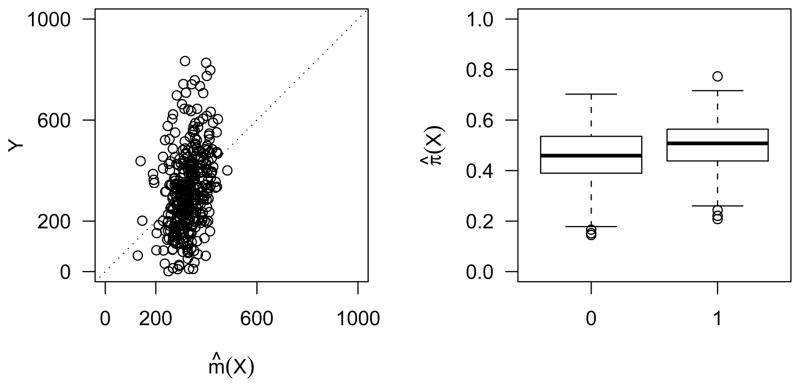
We first fit the response pattern m(X) = E(Y | X) by linear regression and the propensity score π(X) = Pr(δ = 1 | X) by linear logistic regression. Figure 1 shows poor fit of m̂(X) and π̂(X). With X of dimension 9, it is nearly impossible to try out all possible higher order terms for m(X) and π(X). This casts doubt on the reliability of model based estimators. We turn to the effective balancing scores for the estimation of E(Y).

Fig. 1.

Parametric fit to the response and the missingness. On the left is the observed response versus the fitted response from linear regression. On the right is the box plot of the fitted propensity score from linear logistic regression: 0 for the subjects with Y missing and 1 for the subjects with Y observed.

The estimates of E(Y) are in Table 4, where the standard deviations are estimated by bootstrap with 200 replications. In the proposed estimation, the effective propensity score S_δ; is 1-dimensional, the effective prognostic score S_Y and the effective double balancing score S_d are 2-dimensional, where the dimensions are determined by the sequential permutation test (Cook & Yin, 2001).

Table 4.

Estimates of mean CD4 counts at 96 weeks: the proposed estimator μ̂_δ, μ̂_Y, and μ̂_d, the inverse propensity weighting estimator μ̂_ipw, the regression estimator μ̂_reg, and the augmented inverse propensity weighting estimator μ̂_aipw.

	μ̂δ	μ̂Y	μ̂d	μ̂reg	μ̂ipw	μ̂aipw
Estimate	322.7	323.3	323.0	322.4	680.6	328.5
SD	8.6	8.8	8.8	8.4	33.2	8.9

Diagnostic analysis indicates overlapping of 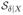and 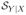. More specifically, the first effective direction of 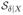and that of 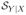are close, both close to the first effective direction of 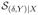. As the first effective direction of 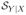conveys about 70% X information about Y, the three nonparametric balancing score estimates are quite close. The inverse propensity weighting estimator π̂_ipw shows big bias and variability due to the poor fit of π̂(X) and the sensitivity associated with inverse weighting. In spite of the poor fit of m̂(X), the regression estimator μ̂_reg seems to have little bias. This is because the bias of μ̂_reg is $n^{-1}{\sum }_{i=1}^n\{\widehat{m}(X_i)-m(X_i)\}$, and averaging over the samples can sometimes mitigate the point-wise bias in m̂(X).

6. Discussion

Most dimension reduction methods recover B = (β₁, ···, β_K) as the eigenvectors of a kernel matrix. The sliced inverse regression takes cov{E(X | 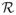)} as the kernel matrix and the sliced average variance estimation uses E[{I − cov(X | 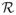)}²], both estimated through slicing the response 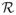. The eigenvectors corresponding to the K largest eigenvalues are the estimates. Both methods give root-n consistent estimates under the linearity condition, which is satisfied if X has an elliptically symmetric distribution. The sliced average variance additionally assumes cov(X | B′X) to be constant.

The principal fitted component method of Cook (2007) is an extension of the sliced inverse regression. The method first finds a basis function F_y = {f₁(y), ···, f_r(y)} for the inverse regression X | Y, and then estimates the effective directions through P_F X, the projection of X onto the subspace spanned by F_y. Though derived from normal likelihood function, the method is not tied to normality. It has “double robustness” in the sense that root-n consistency is attained under either normality or F_y is well correlated to E(X | Y). Appropriate selection of F_y allows more effective utilization of the inverse regression information than the sliced inverse regression. Approaches for finding F_y include the inverse response plot of X versus Y (Cook, 1998), spline basis, and inverse slicing. When the inverse regression X | Y has isotropic errors, estimates of β₁, ···, β_K are simply the K largest eigenvectors of cov(P_F X). Cook (2007), Cook & Forzani (2008) and Cook & Forzani (2009) give details about this method under various scenarios. Ding & Cook (2013) further extends this method to matrix-valued covariates.

Recently, Ma & Zhu (2012) proposed the semiparametric dimension reduction method. It is the only method that requires no distributional assumptions for root-n consistency. The estimation of B = (β₁, ···, β_K) is from an estimating equation derived from a semiparametric influence function. By appropriately defining the terms in the influence function, this semiparametric method includes many dimension reduction methods as special cases. For example, one estimating equation takes the form

$$E([E(X\mid Y)-E\{E(X\mid Y)\mid B^{T}X\}]{\{X-E(X\mid B^{T}X)\}}^T)=0,$$

which reduces to the sliced inverse regression under the linearity condition. Consistency is achieved if either E(· | Y) or E(· | B^T X) is correctly specified, and nonparametric regression is proposed for estimating the two conditional means to circumvent model specification. This method can also handle categorial covariates so long as at least one covariate is continuous. This is a powerful method for dimension reduction but involves intensive computation.

As mentioned in §2, any root-n consistent dimension reduction method is good for finding the effective directions in the proposed method. We can pick a method of our convenience so long as the distributional assumptions are satisfied.

Appendix

Appendix 1. Proof for =

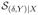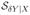
Denote B_d as the basis for 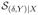and B_d* as the basis for 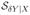. From (4),

$$\delta \perp X\mid B_d^{\prime }X,Y\perp X\mid B_d^{\prime }X.$$

It follows that $\delta Y\perp X\mid B_d^{\prime }X$ and ⊂ .

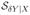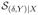Note that

$$Pr(\delta =0\mid X)=Pr(\delta Y=0\mid X)-Pr(Y=0,\delta =1\mid X)=Pr(\delta Y=0\mid X),$$

where the second equation is due to Pr(Y = 0 | X) = 0 for Y continuous. Since B_d* is the basis for 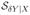, the right hand side of the above equation is a function of $B_{d\ast }^{\prime }X$. Thus $\delta \perp X\mid B_{d\ast }^{\prime }X$ and ⊂ .

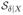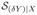Note that

$$\begin{array}{l}Pr(Y\le y,\delta =1\mid X)=Pr(\delta Y\le y\mid X)-Pr(\delta =0\mid X)I(y\le 0),\text{and}\\ Pr(Y\le y,\delta =1\mid X)=Pr(Y\le y\mid X)Pr(\delta =1\mid X).\end{array}$$

The second equation is true due to missing at random. In the above equations, Pr(δY ≤ y | X) is a function of $B_{d\ast }^{\prime }X$ as B_d* is the basis for 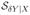, Pr(δ = 0 | X) and Pr(δ = 1 | X) are functions of $B_{d\ast }^{\prime }X$ as 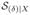⊂ 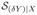. Therefore, Pr(Y ≤ y | X) is a function of $B_{d\ast }^{\prime }X$. It follows that $Y\perp X\mid B_{d\ast }^{\prime }X$ and ⊂ .

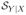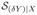As 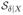⊂ 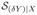and 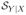⊂ 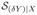, it follows from Remark 2 that ⊂ .

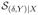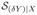If Y is categorical, we can perform a shift transformation Y* = Y + c such that Y* > 0. It follows that = = .

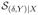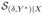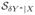Appendix 2. Proof of Theorem 1

Theorem 1 is developed under the following regularity conditions:

1. The kernel function satisfies: ∫u 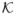(u)du = 0, ∫ uu^T 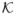(u)du = 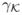I₂, and ∫ 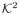(u)du = 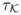, with 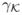< ∞ and < ∞.

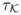2. π(x) is bounded away from 0.

3. The density of x is bounded away from 0.

We write n^1/2(μ̂ − μ) as

$$n^{1/2}(\widehat{\mu }-\mu )=n^{1/2}{A}_n+n^{1/2}{B}_n+n^{1/2}{C}_n,$$

with

$$\begin{array}{l}{A}_n=n^{-1}\sum _{i=1}^{n}m(S_i)-\mu ,\\ B_n=n^{-1}\sum _{i=1}^{n}E\{\widehat{m}(S_i)-m(S_i)\mid {\mathcal{O}}_i\},\\ C_n=n^{-1}\sum _{i=1}^n\widehat{m}(S_i)-m(S_i)-E\{\widehat{m}(S_i)-m(S_i)\mid {\mathcal{O}}_i\},\end{array}$$

where 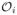= {(X_j, Y_j, δ_j) : j ≠ i}. It is obvious that n^1/2A_n converges in distribution to N (0, var{m(S)}).

By (5),

$$\widehat{m}(S_i)=n^{-1}\sum _{j=1}^n{\delta }_j{Y}_j{\mathcal{K}}_H(S_i-S_j)/n^{-1}\sum _{j=1}^n{\delta }_j{\mathcal{K}}_H(S_i-S_j),$$

with $n^{-1}{\sum }_{j=1}^n{\delta }_j{\mathcal{K}}_H(S_i-S_j)=\pi (S_i)f(S_i)+o_p(1)$ and f(s) the density of S. It follows that

$$B_n=n^{-1}\sum _{j=1}^n{\delta }_{j}E[\frac{{\mathcal{K}}_H(S_i-S_j)\{Y_j-m(S_i)\}}{\pi (S_i)f(S_i)}\mid {\mathcal{O}}_i]\{1+o_p(1)\}.$$

Similar to the argument for Theorem 2.1 of Cheng (1994), it can be shown that $\sqrt{n}(B_n-B_n^{\ast })=o_p(1)$ with

$$B_n^{\ast }=n^{-1}\sum _{j=1}^n{\delta }_j\frac{Y_j-m(S_j)}{\pi (S_j)}.$$

Due to conditional independence (3), $n^{1/2}{B}_n^{\ast }$ converges in distribution to N (0, E{var(Y | S)/π(S)}).

For C_n, E(C_n) = 0 and $nE(C_n^2)\le E[{\{\widehat{m}(S)-m(S)\}}^2]=O({\{\text{tr}(H{H}^T)\}}^2+{\{ndet(H)\}}^{-1})$, thus C_n = o_p(n^−1/2). As A_n and $B_n^{\ast }$ are independent, n^1/2(μ̂ − μ) is asymptotically normal of mean 0 and variance var{m(S)} + E{var(Y | S)/π(S)}.

Following Ruppert & Wand (1994), the negligible terms involving H are

$$\begin{array}{ll}\hfill E(B_n)& =E\{\widehat{m}(S)-m(S)\}=\frac{1}{2}\text{tr}\{H^T{\mathrm{\Delta }}_m(S)H\},\\ \hfill n\{var(C_n)\}& =E[{\{\widehat{m}(S)-m(S)\}}^2]={\{ndet(H)\}}^{-1}E[var(Y\mid S){\{f(S)\pi (S)\}}^{-1}]{\tau }_{\mathcal{K}}.\end{array}$$

With H = h_nI_K, $E(B_n)=h_n^2\mathcal{B}$ and $n\{var(C_n)\}={({nh}_n^K)}^{-1}\mathcal{V}$,

$$\begin{array}{ll}\hfill \mathcal{B}& =\frac{1}{2}\text{tr}\{{\mathrm{\Delta }}_m(S)\},\\ \hfill \mathcal{V}& =E[var(Y\mid S){\{f(S)\pi (S)\}}^{-1}]{\tau }_{\mathcal{K}}.\end{array}$$

In the above expressions, ${\mathrm{\Delta }}_m(S)=E\{{\mathscr{H}}_m(S)+2{\nabla }_m^T(S){\nabla }_{\pi f}/\pi f(S)\}{\gamma }_{\mathcal{K}}$, where ∇_m(s) and 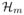(s) stand for the gradient and the Hessian matrix of m(s), respectively, ∇_πf/πf(s) = {π(s)∇_f (s) + ∇_π(s)f(s)}/{π(s)/{π(s)f(s)} with ∇_π(s) and ∇_f (s) the gradients of π(s) and f (s), respectively.

The mean squared error is

$$E\{{(\widehat{\mu }-\mu )}^2\}=h_n^4{\mathcal{B}}^2+{(n^2{h}_n)}^{-K}\mathcal{V}+n^{-1}{\sigma }^2.$$

The optimal bandwidth, which minimizes the mean squared error, is

$$h_{\mathit{opt}}={\{K\mathcal{V}/(4{\mathcal{B}}^2)\}}^{1/(K+4)}{n}^{-2/(K+4)},$$

which can be estimated by the plug-in method.

Appendix 3. Proof of Theorem 2

Denote the proposed estimator under B̂, the root-n estimate of B, as $\widehat{\widehat{\mu }}$ which is given as in (6) except that

$$\widehat{m}(S_i)=n^{-1}\sum _{j=1}^n{\delta }_j{Y}_j{\mathcal{K}}_H({\widehat{S}}_i-{\widehat{S}}_j)/n^{-1}\sum _{j=1}^n{\delta }_j{\mathcal{K}}_H({\widehat{S}}_i-{\widehat{S}}_j),$$

with Ŝ = B̂X.

The difference between $\widehat{\widehat{\mu }}$ and μ̂ comes from that between 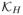(S_i − S_j) and ${\mathcal{K}}_H({\widehat{S}}_i-\widehat{S_j})$. With H = h_nI_K, ${\mathcal{K}}_H(S_i-S_j)=h_n^{-K}\mathcal{K}\{(S_i-S_j)/h_n\}$ and ${\mathcal{K}}_H({\widehat{S}}_i-{\widehat{S}}_j)=h_n^{-K}\mathcal{K}\{({\widehat{S}}_i-\widehat{S_j})/h_n\}$. The latter can be further written as

$$h_n^{-K}\mathcal{K}\left(\frac{S_i-S_j}{h_n}+\frac{(\widehat{B}-B)(X_i-X_j)}{h_n}\right),$$

At optimal bandwidth h_n ~ n^−2/(K+4) and B̂ − B = O_p(n^−1/2), the second term inside the kernel function is O{n^−K/(2K+8)} = o_p(n^−1/2). It follows that $\sqrt{n}(\widehat{\widehat{\mu }}-\widehat{\mu })~o_p(1)$, and $\widehat{\widehat{\mu }}$ is asymptotically equivalent to μ̂.