Water Permeation Drives Tumor Cell Migration in Confined Microenvironments

SUMMARY

Cell migration is a critical process for diverse (patho) physiological phenomena. Intriguingly, cell migration through physically confined spaces can persist even when typical hallmarks of 2D planar migration, such as actin polymerization and myosin II-mediated contractility, are inhibited. Here, we present an integrated experimental and theoretical approach (“Osmotic Engine Model”) and demonstrate that directed water permeation is a major mechanism of cell migration in confined microenvironments. Using microfluidic and imaging techniques along with mathematical modeling, we show that tumor cells confined in a narrow channel establish a polarized distribution of Na⁺/H⁺ pumps and aquaporins in the cell membrane, which creates a net inflow of water and ions at the cell leading edge and a net outflow of water and ions at the trailing edge, leading to net cell displacement. Collectively, this study presents an alternate mechanism of cell migration in confinement that depends on cell-volume regulation via water permeation.

INTRODUCTION

Cell migration is a fundamental phenomenon that underlies diverse physiological and pathological processes such as tissue morphogenesis, immune response, and cancer metastasis. Much of what we know about the mechanisms of cell migration stems from in vitro studies with 2D substrates (Friedl and Alexander, 2011; Mogilner and Oster, 1996; Pollard and Borisy, 2003). The classical model of cell migration along 2D planar surfaces is characterized by cycles of actin polymerization-driven lamellipodial protrusion, integrin-dependent adhesion, myosin II-mediated contraction, and de-adhesion at the trailing edge. Although 2D migration is relevant in certain processes, such as neutrophil migration along the endothelium or epithelial cell wound healing, most 2D assays fail to recapitulate the physiological tissue environment encountered in vivo (Wirtz et al., 2011).

Cells often migrate in vivo within 3D extracellular matrices (ECMs). Cells also migrate through 3D longitudinal tracks with bordering 2D interfaces (i.e., channels). These channels are formed between the connective tissue and the basement membrane of muscle, nerve, and epithelium (Friedl and Alexander, 2011). 3D longitudinal channels are also formed between adjacent bundled collagen fibers in fibrillar interstitial tissues. Importantly, cells have been reported to migrate through such 3D channels in vivo (Alexander et al., 2008). The cross-sectional areas (Wolf et al., 2009) of pores/channels encountered in vivo range from 10 to >300 μm², suggesting that cells migrating in vivo experience varying degrees of physical confinement. Mounting evidence suggests that physical confinement alters cell migration mechanisms (Balzer et al., 2012; Konstantopoulos et al., 2013; Pathak and Kumar, 2012; Stroka et al., 2013).

To isolate the effect of physical confinement that tumor cells experience as they migrate through the ECM microtracks in vivo, we have developed a chemotaxis-based microfluidic device containing microchannels of varying cross-sectional areas (Balzer et al., 2012; Tong et al., 2012). Migration of cells through wide microchannels (width by height = 50 × 10 μm²) recapitulates the earmarks of 2D cell motility and depends on actin polymerization and myosin II-mediated contractility. However, metastatic breast cancer cells migrate through narrow (3 × 10 μm²) microchannels even when actin polymerization, Rho/ROCK- or myosin II-dependent contractility, or β1-integrin function are inhibited (Balzer et al., 2012). Here, we present an actin- and myosin-independent mechanism of cell migration that is based on water permeation and active and passive ion transport in confined spaces.

Ion channels and aquaporins (AQPs) have previously been implicated in 2D cell migration (Papadopoulos et al., 2008; Schwab et al., 2007). However, their specific molecular roles during migration are not well understood. Cytoskeletal components regulate the activity of ion channels (Dreval et al., 2005; Grunnet et al., 2002; Mazzochi et al., 2006), and as a result, volume regulation via these ion pumps requires an intact cytoskeleton. For example, the sodium hydrogen exchanger-1 (NHE-1) is known to physically interact with the actin cytoskeleton (Goss et al., 1994; Grinstein et al., 1993; Wakabayashi et al., 1992). Pharmacological inhibition of NHE-1 restrains leukocyte chemotaxis (Ritter et al., 1998) and the migration speeds of endothelial and epithelial cells (Klein et al., 2000). AQPs, transmembrane proteins that allow transport of water molecules across the cell membrane, are also involved in cell migration. Specifically, aquaporin 5 (AQP5) is overexpressed in lung and breast tumor cells and facilitates 2D migration of these cells (Chae et al., 2008; Jung et al., 2011), presumably by regulating water influx to facilitate protrusions by actin polymerization (Papadopoulos et al., 2008) and/or by stabilizing microtubules (Sidhaye et al., 2012). AQPs have been identified as potential targets for cancer therapeutic development, but like ion channels, their contribution to 2D versus confined migration is not well understood.

Here, we present an integrated experimental and theoretical approach showing that water permeation is a major mechanism of cell migration in confined microenvironments. We have termed this mode of migration the “Osmotic Engine Model,” which is dependent on cell-volume regulation and the fluxes of ions and water into and out of the cell. Specifically, the polarized cell inside a narrow channel establishes a spatial gradient of ion channels and pumps in the cell membrane, creating a net inflow of water and ions at the cell leading edge and a net outflow of water and ions at the trailing edge. This leads to net cell displacement even when actin polymerization is inhibited. Because water flow is driven by osmotic pressure differences across the membrane (Lang et al., 1998), we hypothesized that external osmotic shocks at the leading and/or trailing edges of cells would have a strong influence on cell migration. Our Osmotic Engine Model predicts all key results pertinent to the application of osmotic shocks, which we have verified experimentally using a novel microfluidic device combined with cell engineering and microscopy techniques. Collectively, this study presents an alternate mechanism of migration in confined spaces that cells may exploit when actin polymerization is inhibited.

RESULTS

Role of Na⁺/H⁺ Exchangers and AQP5 in Migration through Confined Spaces

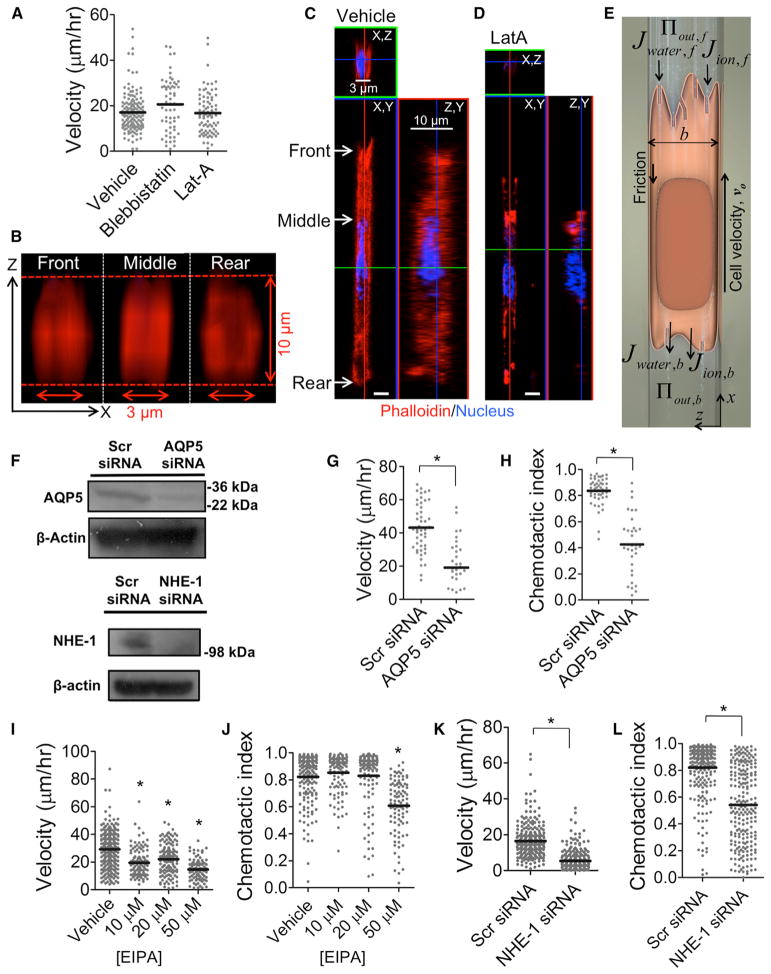
We have recently demonstrated (Balzer et al., 2012) and herein confirmed that confined migration of human metastatic MDA-MB-231 breast cancer cells persists even after actin polymerization or myosin II-mediated contractility is blocked (Figures S1A and S1B available online). We also validated these observations with mouse S180 sarcoma cells. We found no change in migration velocity for S180 cells treated with 50 μM blebbistatin or 2 μM latrunculin-A (Lat-A) relative to appropriate vehicle controls (Figure 1A), thereby confirming that neither myosin II-mediated contractility nor actin polymerization is required for migration in narrow channels. Actin filament disruption in Lat-A-treated S180 cells was confirmed via immunofluorescence microscopy by staining cells with Alexa-tagged phalloidin (Figures 1B–1D). Thus, we sought to develop an integrated theoretical and experimental approach to understand the mechanism by which tumor cells move through narrow channels even in the absence of actin polymerization and myosin II-mediated contractility.

Figure 1. Migration in Confined Spaces Requires AQPs and Na⁺/H⁺ Exchangers but Not Actin Polymerization.

(A) S180 cell velocity in the presence of 50 μM blebbistatin or 2 μM latrunculin-A (Lat-A). Each data point represents average velocity of one cell over the course of 2 hr. Horizontal bars indicate mean.

(B) Front, middle, and rear (X, Z) plane reconstructions of the actin cytoskeleton for the cell in (C).

(C) Vehicle control- or (D) Lat-A-treated S180 cells were stained for actin by phalloidin-Alexa 568, and cross-sections of confocal images are shown. White scale bars represent 3 μm.

(E) Schematic of the Osmotic Engine Model, based on water permeation through the cell membrane at leading and trailing edges.

(F) Immunoblots indicating knock down of AQP5 in MDA-MB-231 cells and NHE-1 in S180 cells.

(G and H) Velocity (G) and chemotactic index (H) of scramble control and AQP5-depleted MDA-MB-231 cells.

(I and J) Velocity (I) and chemotactic index (J) of S180 cells treated with increasing concentrations of EIPA.

(K and L) Velocity (K) and chemotactic index (L) of scramble control and NHE-1 siRNA-transfected S180 cells.

*p < 0.05 in comparison with control by Student’s t test. All migration experiments were performed in 3 μm-wide channels. See also Figure S1.

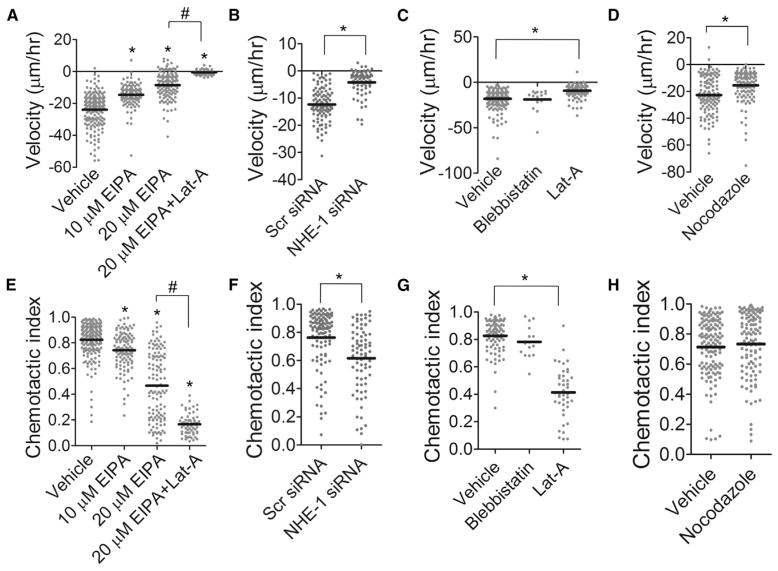
Here we propose an Osmotic Engine Model that predicts that confined migration depends on the activity of transmembrane proteins responsible for water and ion flux through the cell membrane and does not directly require actin polymerization or actomyosin contractility. In this model, the polarized cell inside a confining channel establishes a spatial gradient of ion channels and pumps in the cell membrane, which results in a net inflow of water at the leading edge and a net outflow of water at the trailing edge (Figure 1E). We therefore examined the potential contributions of specific ion pumps and AQPs to confined cell migration. Although AQP1, AQP3, and AQP5 have been implicated in cancer, AQP5 expression is 3-fold higher than that of AQP1 and AQP3 in S180 (Figures S1E and S1F) and MDA-MB-231 cells (data not shown), thereby justifying our focus on AQP5. Knockdown of AQP5 in human MDA-MB-231 breast cancer cells, as confirmed via immunoblotting (Figure 1F), markedly suppressed cell migration velocity and chemotactic index in narrow channels (Figures 1G and 1H). We next chose to focus on Na⁺/H⁺ pumps, due to their established role in cell migration and volume regulation (Schwab, 2001; Schwab et al., 2012). Inhibition of Na⁺/H⁺ channels via the use of 5-(N-ethyl-N-isopropyl)amiloride (EIPA) reduced cell migration velocity and chemotactic index in a dose-dependent manner for both S180 (Figures 1I and 1J) and MDA-MB-231 cells (Figure S1C). The inhibitory effects of EIPA on cell migration were also observed in wide channels (Figure S1D). Of all Na⁺/H⁺ exchangers that are localized on the plasma membrane, NHE-1, -2, and -4 have been implicated in cancer (Beltran et al., 2008). Because the expression of NHE-1 on S180 cells is 5-fold higher than that of NHE-2 and -4 (Figures S1E and S1G), we examined its contribution to migration in confined spaces. Knockdown of NHE-1, as confirmed by immunoblotting (Figure 1F), reduced cell migration velocity and chemotactic index. This effect was comparable to that seen with the highest dose of the pharmacological inhibitor EIPA (50 μM) (Figures 1K and 1L), thereby suggesting the dominant role of NHE-1 among other Na⁺/H⁺ exchangers in migration through confined spaces. Collectively, these data reveal that NHE-1 and AQP5 regulate 2D and confined migration.

Theoretical Basis of the Osmotic Engine Model

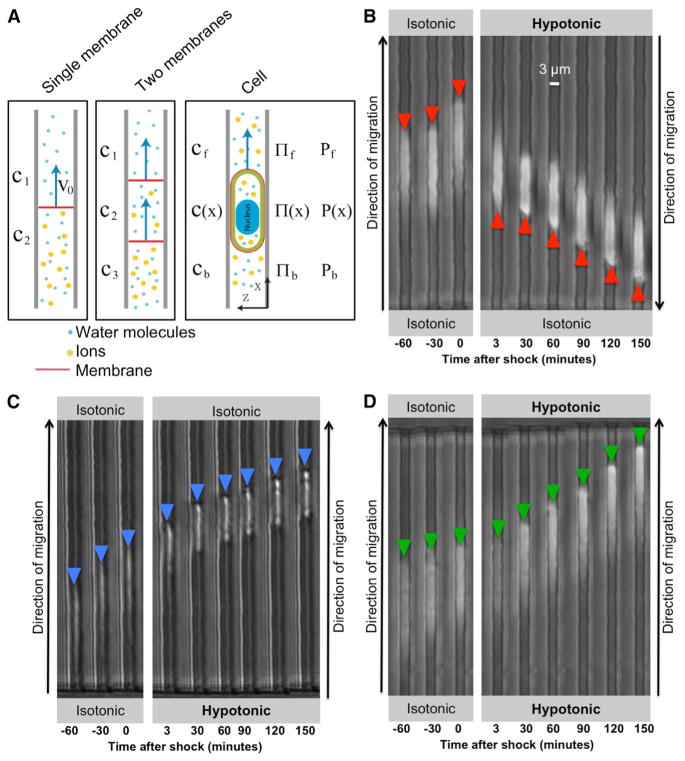
The physics behind the Osmotic Engine Model is based on forces driving water flow across the membrane (Figure 2A) (Jiang and Sun, 2013). The water flow across a semipermeable membrane (permeable to water but not permeable to ions) is driven by the chemical potential difference across the surface, ΔΨ = (ΔP − ΔΠ), where ΔP is the hydrostatic pressure difference and ΔΠ is the osmotic pressure difference. At equilibrium, the chemical potential is zero when the hydrostatic pressure difference exactly balances the osmotic pressure difference. Water is directly permeable to membranes, but AQP channels can further increase water permeability. In addition, eukaryotic cells have many different types of passive channels and active ion pumps that regulate the flow of ions and small solutes across the cell membrane (Figure 2A). Therefore, the cell can actively control the osmotic pressure difference, ΔΠ_, as ΔΠ = Π_in − Π_out = RT(c_in − c_out), where c_in and c_out are ion concentrations inside and outside of the cell, respectively. By establishing polarized distributions of AQPs, passive ion channels, and active ion pumps, the cell can direct the water flow at the leading and trailing edges, which leads to overall translocation of the cell. Detailed descriptions of the physics are given in the Extended Experimental Procedures, and Table S1 contains a list of all parameters. Here we outline some essential features of the model.

Figure 2. Localized Osmotic Shocks Influence Cell Migration in Confined Spaces.

(A) Schematics showing the movement of a moveable semipermeable membrane, a vesicle enclosed by a semipermeable membrane, and a cell driven by osmotic pressure difference (see Extended Experimental Procedures for further explanation).

(B–D) Also shown are phase-contrast image sequences of S180 cells before shock and after (B) a hypotonic shock at the leading edge, (C) a hypotonic shock at the trailing edge, or (D) a hypotonic shock at both the leading and trailing edges. Hypotonic shock = 165 mOsm/l.

See also Figure S2 and Movie S1.

To begin, we consider water fluxes at the front (leading edge) and back (trailing edge) (Figure 2A):

$$\begin{array}{l}{J}_{\mathit{water},f}=-{\alpha }_f\mathrm{\Delta }{\mathit{\Psi }}_f\hfill \\ J_{\mathit{water},b}=-{\alpha }_b\mathrm{\Delta }{\mathit{\Psi }}_b\hfill \end{array},$$ (1)

where (f,b) denotes the leading and trailing edges of the migrating cell, respectively, α_f and α_b are permeation constants related to the polarized distribution of AQPs at the front and back, and ΔΨ_f and ΔΨ_b are the water chemical potential differences across the membrane at the two edges. The water chemical potential is related to the hydrostatic (ΔP = P_in − P_out) and osmotic pressure (ΔΠ = Π_in − Π_out) differences across the membrane. From the net volume change, we have:

$$\frac{dL}{dt}=(J_{\mathit{water},f}+J_{\mathit{water},b}),$$ (2)

where L is the length (proportional to volume) of the cell. Importantly, by introducing FITC-dextran into the upper inlets of the device, we have experimentally verified that the cells completely occlude the channels (Figures S1H–S1J). The change in ion content is as follows:

$$\frac{dn}{dt}=S(J_{in,f}+J_{\mathit{out},f}+J_{in,b}+J_{\mathit{out},b}),$$ (3)

where n is the number of solutes in the cell; n is related to c_in by n = ∫ c_in·Sdx. S is the channel cross-sectional area, and the ionic fluxes at the leading and trailing edges (J_in,f, J_out,f, J_in,b, and J_out,b) are given by Equations S4 and S5 in the Extended Experimental Procedures. If the cell is polarized, the flux parameters (α, β, γ, ΔΠ_c) introduced in the Extended Experimental Procedures would be different at the front and back, leading to different fluxes of ions and water at the leading and trailing edges. Net cell movement is achieved through control of the fluxes of ions and water at the leading and trailing edges. Here, we assume that the flux parameters are constants; thus, we do not consider possible dynamics in polarization of the cell, though this may be explored in future work.

The movement of the cell is resisted by friction between the cell cortex and cell cytoplasm, plus the friction between the cell membrane and channel walls. Therefore, the tension, T, in the cell membrane and cortex balances these frictional forces:

$$\frac{\partial T}{\partial x}=\left(\frac{6\eta }{b}+{\eta }_w\right)v_0.$$ (4)

Here, η is the viscous drag coefficient of the cytoplasm, ξ_w is the friction coefficient between the cell and the channel wall, and v_o is the velocity of the cell relative to the channel walls. If we regard the cortex as an elastic layer, then T = σh_, where σ is the cortical stress and h is the cortical thickness.

Because there are different ion and water fluxes at the leading and trailing edges, the hydrostatic pressure and ion concentration inside the cell are not uniform. These quantities can be modeled using the Stokes equation and the diffusion equation, respectively:

$$\begin{array}{c}\nabla P=\eta {\nabla }^2\mathbf{v}\\ \frac{\partial c}{\partial t}+\mathbf{v}·\nabla c-D{\nabla }^{2}c\end{array},$$ (5)

where v is the cytoplasmic flow field, c is the cytoplasmic solute concentration, D is the diffusion constant, and P is the hydrostatic pressure of the cytoplasm. Given the flux boundary conditions, these equations can be solved if we assume that the concentration field equilibrates to steady state rapidly. The net average cytoplasmic velocity at steady state, $\overline{v}=1/b{\int }_0^{b}v(z)dz$, should be zero. Therefore, solving the cytoplasmic velocity equation will determine the average velocity and the velocity of migrating cells. This set of equations closes the problem and provides a simple model of cell migration driven by fluid permeation. Thus, the cell migration speed is

$$v_0=\frac{b^{2}h\alpha \{2D({\mathit{\Pi }}_{\mathit{out},b}-{\mathit{\Pi }}_{\mathit{out},f})+\mathit{LRT}[\gamma (\mathrm{\Delta }{\mathit{\Pi }}_{c,f}-\mathrm{\Delta }{\mathit{\Pi }}_{c,b})+\beta ({\sigma }_{c,f}-{\sigma }_{c,b})]\}}{6{bL}^{2}RT\alpha \beta \eta +12hL\alpha \eta (2D+\mathit{LRT}\gamma )+b^2[4Dh+\mathit{LRT}(2h\gamma +L\alpha \beta {\zeta }_w)]}.$$ (6)

The derivation and explanation of this analytical expression and the various terms are given in detail in the Extended Experimental Procedures, and parameters are listed in Table S1. Note that the cell velocity is only a function of the current cell length, L, which is proportional to cell volume. Also, the velocity is independent of the constitutive relation of the cell cortex or any active stress in the cortex. Therefore, the content of the cortex is unimportant, and the cortex simply balances the tension from frictional force. This model predicts that actin and myosin have no direct influence on the overall cell velocity. However, actin and myosin activity will influence the steady-state volume of the cell. The volume of the cell does influence migration velocity in Equation 5, but this influence is generally weak within the parameter regimes considered (see below).

Osmotic Shocks Regulate Cell Migration Speed and Direction

If cells migrate in narrow channels using the osmotic engine mechanism, we would expect that the application of an osmotic shock influences cell motility even in the case where cell polarization remains unchanged. If the osmotic pressure outside the cell’s leading edge (Π_out,f) decreases, or if the osmotic pressure outside the cell’s trailing edge (Π_out,b) increases, the sign of the cell migration velocity could change, as suggested by Equation 6. Notice that ΔΠ_c is proportional to Π_out, as explained in the Extended Experimental Procedures. Thus, the model predicts that application of a hypotonic shock at the leading edge or a hypertonic shock at the trailing edge of the cell may reverse the direction of cell migration. Although these results are not intuitive, they are testable with our microchannel device, which provides the ability to modulate the extracellular osmolarity distinctly at either the leading or trailing edge of the cells migrating through narrow channels (Figures S2A–S2C). To vary extracellular osmolarity, we added either deionized, filtered water or xylose to the culture medium to create hypotonic (85–328 mOsm/l) or hypertonic (375–615 mOsm/l) solutions, respectively (Figure S2D). Osmolarity was measured with an osmometer.

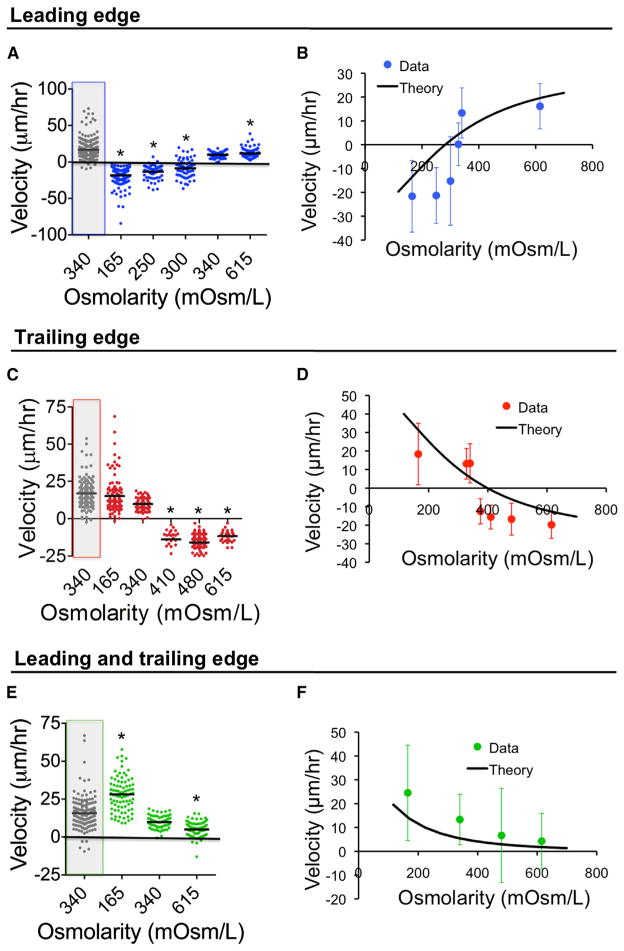
Using phase-contrast time-lapse microscopy, we tracked the migration of cells through narrow channels in an isotonic medium (340 mOsm/l) using FBS (10%) as a chemoattractant. As shown in Figure 2B and Movie S1, prior to the application of an osmotic shock, S180 cells migrated toward the chemoattractant (from bottom to top). At time t = 0, the medium at the top of the chamber (i.e., leading edge of the migrating cell) was changed to hypotonic (165 mOsm/l) and still contained 10% FBS, whereas an isotonic solution was maintained at the bottom of the chamber (Figure 2B). This osmotic shock caused a rapid reversal in cell migration direction (Figures 2B and 3A). The speed of migration in the opposite direction decreased progressively as the osmolarity of the medium approached isotonicity (Figure 3A). We confirmed that ~99% of cells remained viable throughout the full osmotic range, as assessed by the trypan blue exclusion assay (not shown). Most importantly, our experimental results agreed well with the theoretical predictions (Figure 3B).

Figure 3. The Osmotic Engine Model Predicts Cell-Velocity Patterns in Response to Osmotic Shocks.

S180 cell velocity as a function of osmotic shock at the (A) leading edge, (C) trailing edge, or (E) both leading and trailing edges. In (A), (C), and (E), gray boxes indicate migration velocity before shock, whereas data with white background represent an osmotic shock (or media change only, in the case of 340 mOsm/l control). *p < 0.05 in comparison with control (340 mOsm/l postshock) by Student’s t test. All migration experiments were performed in 3 μm-wide channels. Theoretical predictions using one set of parameters are also shown for velocity as a function of osmotic shock at the (B) leading edge, (D) trailing edge, or (F) both leading and trailing edges. Data points in (B), (D), and (F) represent mean ± SD. See also Figure S3.

The application of a hypotonic shock at the trailing edges of cells had no significant effect on migration direction (Figures 2C and 3C and Movie S1). Interestingly, a hypotonic shock at the cell trailing edge had similar effects as a hypertonic shock at the cell leading edge (Figures 3A–3D). Likewise, a hypertonic shock at the trailing edge reversed migration direction (Figures 3C and 3D) as did a hypotonic shock at the leading edge (Figures 3A and 3B). Finally, when cells were shocked at both the leading and trailing edges with either hypotonic or hypertonic media, there was no change in direction of migration (Figures 2D, 3E, and 3F and Movie S1). In all cases, the average speed of migration during the first 30 min after osmotic shock was a function of the osmolarity, and all sets of data agree well with the quantitative predictions of the model (Figures 3B, 3D, and 3F). It should be noted that we used the same set of parameters (Table S1) for all fittings in this paper. Similar qualitative observations were made using MDA-MB-231 cells (Figures S3A–S3C) and human CH2879 chondrosarcoma cells (Figures S3D–S3F), though their sensitivities to osmotic shock vary between cell lines.

Cells Shrink in Response to Polarized Hypotonic Shock in Narrow Channels

Cell-volume regulation is dependent on water flux across the cell membrane, which is driven by osmotic pressure gradients (Lang et al., 1998). When a detached cell is abruptly suspended in a hypotonic medium, it typically responds by initially swelling due to water influx in order to equilibrate intracellular and extracellular osmotic pressure, followed by regulatory volume decrease through release of ions, which brings the cell nearly back to its original volume (Stewart et al., 2011; Wehner et al., 2003). Indeed, we confirmed these results and observed an osmolarity-dependent increase in average cell volume several minutes after placing the cells into a hypotonic medium (Figures S4A and S4B).

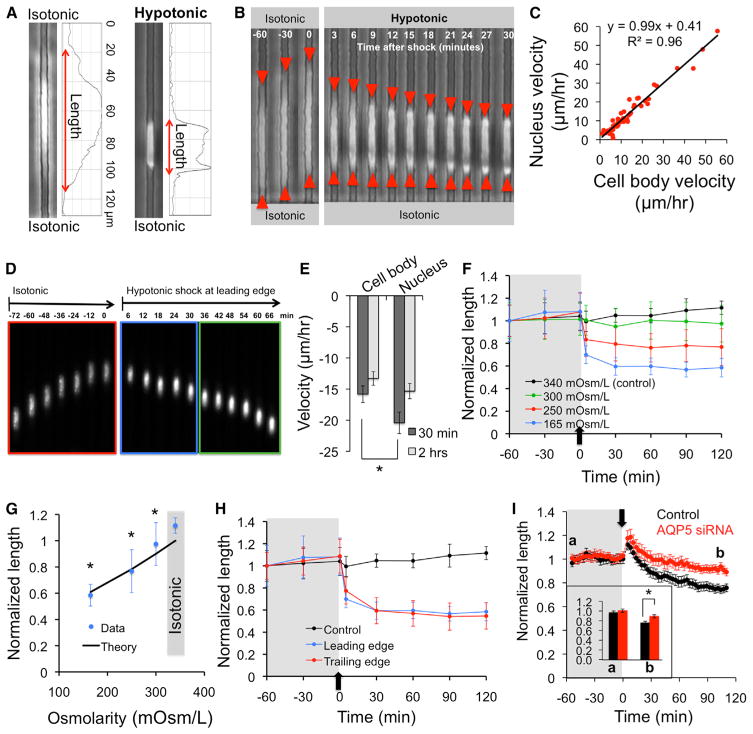
Interestingly, our model predicts a counterintuitive overall decrease in cell length (and volume) following a hypotonic shock at either end of the cell within a confining microchannel. We thus experimentally quantified cell length as a function of time before and after osmotic shock. Because S180 cells completely occupied the cross-sectional area of the narrow microchannels as indicated by the lack of FITC-dextran flow around the cell (Figures S1H–S1J), cell length multiplied by the width and height of the microchannels provides an estimate of cell volume (with an estimated error of 10% accounting for cell protrusions) inside the channel. We then combined phase-contrast imaging with quantitative image analysis to measure the length (and thus the volume) of cells live during migration within the confining channels before and after an osmotic shock (Figure 4A). Notably, after a hypotonic shock at the leading edge, we observed a significant osmolarity-dependent decrease in cell length that did not recover, even 2 hr after the onset of shock (Figures 4B and 4F). Cell body and nucleus velocity were highly correlated during migration in isotonic media (Figure 4C); however, the nucleus traveled faster than the cell body during the first 30 min after a hypotonic shock at the leading edge, whereas no difference was noted after 2 hr (Figures 4D and 4E). During the first 30 min, the displacement of the cell centroid was primarily due to cell shrinkage at the preshock leading edge and was accompanied by little to no displacement of the “new” leading edge (Figure 4B). This resulted in repositioning of the nucleus and faster nucleus velocity at 30 min postshock (Figures 4D and 4E). The nucleus velocity matched that of the cell body at later time points (Figure 4E) when the cell length reached an equilibrium (Figure 4F), as discussed below (Figure 5D). Decreases in cell length were also measured for cells migrating within an even more physically restrictive microchannel (width by height = 3 × 6 μm²) (Figure S4C); these results confirmed that observed decreases in cell length following osmotic shock were not simply due to cell rounding (i.e., increases in cross-sectional area) within the channels but were due to actual changes in cell volume. In accord with theoretical predictions, the equilibrium cell length decreased with decreasing osmolarity at the leading edge (Figure 4G). A similar decrease in cell length was also observed for cells hypotonically shocked at the trailing edge (Figure 4H). Collectively, our results indicate that application of a hypotonic shock at either the leading or trailing edge causes cell shrinkage. An explanation for this phenomenon is described in the Extended Experimental Procedures. We verified these observations with MDA-MB-231 cells (Figure 4I). Most importantly, AQP5 depletion significantly suppressed the cell volume decrease induced by a hypotonic shock in MDA-MB-231 cells (Figure 4I).

Figure 4. Hypotonic Shocks Produce a Nonintuitive Decrease in Cell Volume during Migration in Confined Spaces.

(A) S180 cell length was computed based on the plot profiles of phase-contrast images.

(B) Phase-contrast sequence indicating the decrease in S180 cell length, mostly from the original leading edge, following a hypotonic shock (165 mOsm/l) at the leading edge.

(C) Nucleus versus cell-body velocity for S180 cells before osmotic shock.

(D and E) Fluorescence images of nucleus translocation in S180 cells (D) and velocities (computed over first 30 min or 2 hr) of cell body and nucleus (E) after a hypotonic shock at the leading edge. Bars indicate mean ± SEM, *p < 0.05.

(F) S180 cell length normalized to initial value (at t = −60 min, preshock) as a function of time before and after various hypotonic shocks at the leading edge.

(G) Normalized lengths of S180 cells at equilibrium (t = 120 min) following a hypotonic shock at the leading edge, overlaid with the theoretical prediction.

(H) Normalized S180 cell length as a function of time before and after a hypotonic (165 mOsm/l) shock at the leading or trailing edge.

(I) Normalized control and AQP5-depleted MDA-MB-231 cell length as a function of time before and after a hypotonic (165 mOsm/l) shock at the leading edge. Data points represent mean ± SD. *p < 0.05 in comparison with (G) isotonic case or (I) scramble control by Student’s t test. All migration experiments were performed in 3 μm-wide channels. See also Figure S4.

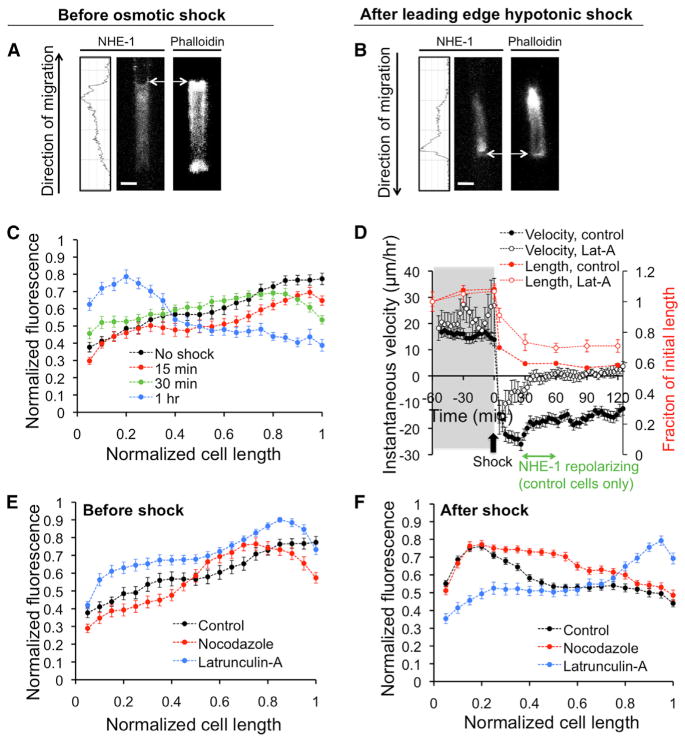
Figure 5. NHE-1 Polarizes to the Leading Edges of Cells Migrating in Confinement.

(A and B) Confocal images and corresponding NHE-1 plot profiles of S180 cells stained for NHE-1 or for actin by phalloidin-Alexa 488, (A) in isotonic medium or (B) after a hypotonic shock at the leading edge. White scale bars represent 3 μm, whereas white arrows point to cell’s leading edge.

(C) Normalized NHE-1 fluorescence intensity (to maximum value for each cell) as a function of the normalized cell length (to maximum cell length), for isotonic conditions, or at various time points following a hypotonic shock at the leading edges of S180 cells.

(D) Instantaneous velocity (primary y axis) and normalized cell length (secondary y axis) as a function of time before and after a hypotonic shock at the leading edge of control and Lat-A-treated S180 cells. Data points represent mean ± SEM of at least 150 cells. The time during which NHE-1 repolarizes in control cells, according to (C), is indicated in green in this panel.

(E and F) Also shown are plots of normalized fluorescence intensity as a function of normalized cell length for control-, nocodazole-, or Lat-A-treated S180 cells (E) in isotonic conditions or (F) after a hypotonic shock at the leading edge.

In (C), (E), and (F), data points represent mean ± SEM of at least 30 cells. All experiments were performed in 3 μm-wide channels. Hypotonic shock = 165 mOsm/l. See also Figure S5.

Cell Volume Is Inversely Correlated with Migration Speed before and after Osmotic Shock

The model predicts that cell migration velocity weakly depends on cell volume inside the microchannel (Figure S4). In general, there existed a wide distribution of volumes within a suspended cell population (Figure S4B), which led to a wide distribution of lengths within the population of cells confined in the microchannels (Figures S4D–S4F). Consistent with theoretical predictions, we observed a weak but significant negative correlation (p < 0.05) between the magnitude of S180 cell speed and volume during preshock migration (Figure S4D), as well as after a hypotonic shock at either the leading edge (Figure S4E) or trailing edge (Figure S4F). We also observed a wide distribution in cell speeds (Figures S4D–S4F), in accord with the heterogeneity of cell size. Thus, smaller cells migrated faster within the microchannels.

NHE-1 and AQP5 Polarize to the Leading Edges of Cells Migrating in Narrow Channels

According to the model, the cell migration velocity is zero if the flux parameters (α, β, γ, ΔΠ_c) are uniform throughout the cell. A nonzero velocity can be achieved if these parameters are different at the leading and trailing edges, presumably because of cell polarization. We thus determined whether cells migrating in confinement displayed a polarization of ion pumps and AQPs. We focused on NHE-1 due to its dominant role in S180 migration through confined spaces (Figures 1K and 1L). Confocal microscopy of NHE-1-immunostained S180 cells revealed a polarized distribution of NHE-1 at the cell leading edge during migration in an isotonic medium (Figures 5A and 5C). Importantly, application of a hypotonic shock at the top of the chamber induced reversal of cell migration direction (Figure 2B) and repolarization of NHE-1 to the new leading edge (same as preshock trailing edge) (Figures 5B and 5C). NHE-1 repolarization did not occur immediately but rather required 30–60 min after the application of the osmotic shock (Figure 5C). Similar observations for the NHE-1 spatial distribution before and after an osmotic shock were made for MDA-MB-231 cells (Figures S5A–S5C). It is noteworthy that not only NHE-1 but also AQP5 polarized to the leading edges of MDA-MB-231 cells preshock and repolarized to the new leading edges after a hypotonic shock at the top of the chamber (Figures S5D–S5F). NHE-1 in cells on a 2D planar surface was more uniformly distributed, with intense staining at both cell ends (Figures S5G and S5H).

It is worth noting that the Osmotic Engine Model applies to the time regime prior to ion channel or AQP repolarization, as the permeation constants (α, β, γ) do not change as a function of osmotic shock in the model. Because NHE-1 did not repolarize during the first 30 min after a 165 mOsm/l shock at the leading edge (Figure 5C), we considered the average experimental cell velocity during only the first 30 min postshock (Figures 3B, 3D, and 3F) rather than the overall cell velocity for the entire 2 hr duration that included repolarization of NHE-1 (Figures 3A, 3C, and 3E). Interestingly, cells experienced a migration surge in the opposite direction during the first 30 min postshock, according to a plot of instantaneous velocity versus time (Figure 5D). This surge correlated with the time course of the cells’ volume decrease postshock (Figures 4B and 5D). These changes in velocity and cell volume are at the heart of the Osmotic Engine Model, where the cell quickly expels water from the original leading edge, propelling the cell in the opposite direction.

NHE-1, AQP5, and Actin Polymerization Are Involved in Cell Migration Response to Hypotonic Shock at Leading Edge

We next investigated the role of the cytoskeleton in establishing NHE-1 polarity in S180 cells. Before osmotic shock, NHE-1 polarized to the leading edges of cells migrating in confined channels even in the presence of nocodazole or Lat-A (Figure 5E), suggesting that the NHE-1 gradient is established during the initial stages of cell entry into narrow channels. Interestingly, after application of a hypotonic shock at the top chamber, Lat-A, but not nocodazole, treatment inhibited the repolarization of NHE-1 to the new leading edge (Figure 5F), indicating that actin polymerization plays a key role in repolarization.

Because NHE-1 and AQP5 are involved in confined cell migration (Figures 1 and S1), we next evaluated whether disruption of these proteins affected cell migration velocity after a hypotonic shock at the leading edge. Using a trypan blue assay, we first verified that cell viability remained above 95% for the drug concentrations (e.g., Lat-A and EIPA) and osmolarities used in our experiments (data not shown). Following a hypotonic shock at the leading edge, S180 cell migration speed (in the opposite direction) and chemotactic index in 3 μm channels decreased with increasing EIPA doses (Figures 6A and 6E) or after knockdown of NHE-1 (Figures 6B and 6F). Furthermore, combinatorial treatment with 20 μM EIPA and 2 μM Lat-A nearly completely abrogated cell migration postshock (Figure 6A). Treatment with 10 μM EIPA or knockdown of AQP5 reduced the fraction of MDA-MB-231 cells that reversed direction after a 165 mOsm/l shock at the leading edge (Figures S6A and S6B).

Figure 6. Cell Migration in Confinement after an Osmotic Shock Depends on an Interplay between Na⁺/H⁺ Exchangers and Actin Polymerization.

(A–D) Velocity for (A) EIPA- or EIPA+Lat-A-, (B) NHE-1 siRNA-, (C) blebbistatin- or Lat-A-, and (D) nocodazole-treated S180 cells migrating in 3 μm channels.

(E–H) Also shown is the chemotactic index for (E) EIPA- or EIPA+Lat-A-, (F) NHE-1 siRNA-, (G) blebbistatin- or Lat-A, and (H) nocodazole-treated S180 cells. *p < 0.05 in comparison with control by ANOVA followed by Tukey test (A and E) or Student’s t test (B, C, D, F, G, and H). #p < 0.05 between groups indicated. All migration experiments were performed in 3 μm-wide channels. See also Figure S6.

Though Lat-A did not affect S180 cell migration velocity before osmotic shock, we did observe a reduction in the speed (Figure 6C) and chemotactic index (Figure 6G) of cells in the opposite direction after a hypotonic shock at the leading edge. In particular, Lat-A-treated cells still experienced the first “fast” phase of migration postshock, but the speed quickly decreased to a steady-state value close to zero within 30 min postshock (Figure 5D). Thus, although actin is not required in directionally persistent confined migration, it is critically involved during a response to osmotic shock in confined microenvironments, which also agrees with the fact that NHE-1 did not repolarize in Lat-A-treated S180 cells after a hypotonic shock at the leading edge (Figure 5F). Meanwhile, blebbistatin had no effect on cell velocity or chemotactic index postshock (Figures 6C and 6G). Nocodazole reduced cell migration speed postshock (Figure 6D) without affecting the chemotactic index (Figure 6H), though the decrease in migration speed was less drastic in comparison with before shock (Figures S6C and S6D). To rule out the possibility of cell migration being driven by a pressure gradient within the microfluidic device, we demonstrated that cell migration persists even in the absence of fluid flow from inlets to outlets (Figure S6E), and that a lack of the FBS chemoattractant drastically reduces cell migration velocity (Figure S6E) and chemotactic index (Figure S6F).

DISCUSSION

We recently demonstrated that actin polymerization and myosin II-mediated contractility may not be required for some cells in confined migration (Balzer et al., 2012). Here, we present an alternative mechanism for migration through confined spaces that is based on a net inflow of water at the cell leading edge and a net outflow of water at the trailing edge. A rigorous theoretical framework of the Osmotic Engine Model is consistent with all experimental data pertinent to the application of osmotic shocks in cells migrating inside physically constricted spaces. Our major observations aligning the theory and experiments are the following: (1) volume-regulating ion pumps and AQPs are involved in migration through confined spaces; (2) ion pumps and AQPs polarize to the leading edges of confined cells; (3) cells reverse direction when hypotonically shocked at the leading edges or hypertonically shocked at the trailing edges; (4) migration direction does not change when cells are hypotonically shocked at the trailing edges or hypertonically shocked at the leading edges; (5) cell volume decreases upon hypotonic shock in confinement; and (6) cell migration speed is weakly correlated with cell volume. Our model qualitatively predicts many nonintuitive results by capturing the key physics behind cell migration in confined spaces. This is an illustration of why theory is needed to explain complex biological phenomena. Our current model does not account for all possible ions, channels, and AQPs; a full model will require charged ions and consideration of voltages across the cell membrane.

The Osmotic Engine Model predicts that a nonzero cell velocity can be achieved in confined spaces as a result of (1) different extracellular osmolarities at the cell’s leading and/or trailing edges and/or (2) spatial polarization of ion channels and AQPs along the longitudinal cell axis. During chemoattractant-driven migration in isotonic media, NHE-1 and AQP5 are polarized at the leading edge (i.e., both γ and α have distinct values at the front and rear of the cell), resulting in a positive velocity. During the first 30 min after a hypotonic shock at the leading edge, the extracellular osmolarity at the postshock leading edge is higher than that of the trailing edge (i.e., Π_out and ΔΠ_c are different at the front and rear of the cell). This difference enables cell migration in the opposite direction away from the chemoattractant, and it can occur even though NHE-1 and AQP5 have not yet repolarized during the first 30 min postshock. In other words, because ΔΠ_c is proportional to Π_out,, the model correctly predicts that a hypotonic shock at the leading edge results in a reversal of cell direction. These theoretical and experimental observations illustrate that the differences in osmolarity at the leading and trailing edges of the cell can “override” the lack of spatial polarization of the ion pumps and AQPs to the leading edge. At later time points (t > 30 min postshock), redistribution of NHE-1 and AQP5 at the new leading edge occurs. The slight decrease in cell-body velocity noted at t > 30 min postshock may be attributed to the presence of the adverse chemoattractant gradient. Ion-pump and AQP polarization are key for migration in confined spaces possibly due to the geometrical constraints of cells squeezed into a longitudinal channel, where the cell width is much shorter than the length compared to the 2D case (Hung et al., 2013). As a result, water influx and efflux are directed along a single axis along the length of the confined cell, allowing water permeation to be a major mechanism driving cell migration within the microchannel. A similar mechanism is not possible on 2D planar surfaces without actin polymerization to guide the protrusions. In vivo, cells likely employ a combination of migration mechanisms, with water permeation being one of them, especially in 3D longitudinal tracks created by anatomical structures.

The decrease in volume observed after application of a hypotonic shock at the leading edge in microchannels is presumably due to water expulsion at the preshock leading edge, which drives the cell in the opposite direction. Indeed, AQP5 depletion suppresses both the fraction of cells reversing direction as well as the decrease in cell volume induced by the application of a hypotonic shock. The reversal of cell migration does not require actin within the first 30 min after osmotic shock, as predicted by the model, though our Lat-A experiments show that actin polymerization is necessary to establish the repolarization of NHE-1 following an osmotic shock. Note that Lat-A may also perturb ion-channel function.

Polarization of ion channels is typically associated with axonal trafficking in neurons (Chung et al., 2006). However, the role of ion channels and AQPs in cell migration has been largely under-appreciated, even on 2D planar surfaces, where water permeation facilitates actin polymerization and volume regulation (Papadopoulos et al., 2008). Furthermore, a mechanism that directly requires ion-channel and AQP polarization and activity without the need for actin polymerization has never been put forth. Previous theoretical models have considered water transport only while neglecting active and passive transport of ions as well as the mechanics of the cell cortex (Jaeger et al., 1999) or have considered cytoskeletal dynamics without accounting for water or ion-channel activity (Taber et al., 2011). Theoretical models have also shown that fluid flow can be driven by two chemically reacting molecular species and osmotic effects (Atzberger et al., 2009), and that a body immersed in a very viscous fluid can swim by drawing in and expelling fluid at different locations along its cell surface (Spagnolie and Lauga, 2010); however, these models have not identified the mechanism governing the fluid flow. Recent experimental work has suggested that neutrophil-like cells migrating in confined spaces push water ahead, generating a hydraulic pressure (Prentice-Mott et al., 2013). It has also been proposed that actin polymerization upsets the local cellular osmotic pressure equilibrium, and the resulting unbalanced osmotic force drives cell protrusion (Oster and Perelson, 1987). In addition, recent studies have shown that significant pressure gradients and fluid flow can occur in cells, presumably through myosin-dependent contraction (Charras et al., 2005; Iwasaki and Wang, 2008; Keren et al., 2009; Mitchison et al., 2008). In particular, NHE-1 activity has been proposed to influence cell swelling and hydrostatic pressure gradients in order to facilitate local protrusions (Mitchison et al., 2008). Importantly and uniquely, our model based on water and ion-channel polarization can explain the actin- and myosin II-independent migration that occurs in narrow channels.

Although our model qualitatively predicts all trends in S180 and CH2879 cell migration pertinent to osmotic shocks, it does not completely predict migration behavior of MDA-MB-231 cells. Although MDA-MB-231 cells can still migrate in the absence of actin polymerization, the decrease in migration speed suggests that there may be an actin-driven component. Meanwhile, inhibition of actin polymerization in S180 or CH2879 cells does not affect migration speed during normal migration. Thus, our model is most applicable to and correctly predicts behavior in S180 cells, which migrate independently of actin polymerization; however, water permeation also plays a critical role in migration and volume regulation of MDA-MB-231 cells.

Ion channels may become polarized to the leading edge by vesicular transport along microtubules, in accompaniment with actin polymerization, through diffusion, or by some other unknown mechanism. For example, microtubule transport facilitates delivery of post-Golgi carriers (Yadav et al., 2009), recycling endosomes (Palamidessi et al., 2008), and mRNA (Mingle et al., 2005) to the cell’s protruding edge. The fact that inhibition of microtubule polymerization by nocodazole reduced migration speed before and after osmotic shock indicates that microtubules are indeed involved in confined cell migration. However, nocodazole did not interfere with NHE-1 polarization before shock or repolarization after osmotic shock, suggesting that microtubules are not responsible for setting up NHE-1 gradients within cells. Rather, actin polymerization is likely accountable, as Lat-A prevented repolarization of NHE-1 upon osmotic shock at the leading edge. Therefore, our data suggest that actin polymerization helps the cell to establish initial ion-channel and AQP polarization, but once that is completed, the major mechanism for migration is water permeation rather than actin polymerization. The specific mechanism by which actin polymerization drives NHE-1 repolarization could be the focus of future work.

In conclusion, we have put forth an alternative mechanism in which a confined cell establishes a spatial gradient of ion channels and pumps in the cell membrane, creating a net inflow of water at the cell leading edge and a net outflow of water at the trailing edge, which leads to net cell displacement even when actin polymerization is inhibited. We demonstrated theoretically and experimentally that a nonzero velocity can be achieved in confined cells as a result of either (1) different extracellular osmolarities at the cell’s leading and trailing edges or (2) different numbers of ion channels and AQPs at the cell’s leading and trailing edges. This model may be relevant during in vivo situations where cells migrate through existing tracks in the extracellular space. Due to the pronounced role of Na⁺/H⁺ ion channels and AQPs in tumor cell migration, our model may be exploited for future development of cancer therapeutics.

EXPERIMENTAL PROCEDURES

Experimental Methods

Standard lithography was used to create the microchannel device as previously described in detail (Balzer et al., 2012; Tong et al., 2012). Control or small interfering RNA (siRNA)-treated S180, MDA-MB-231, or CH2879 cells in vehicle control or drug-containing media were added to the cell inlet port of the microchannel device and allowed to migrate into the 3 μm-wide channels in response to a 10% FBS chemoattractant gradient. Cells were then imaged for at least 1 hr using phase-contrast time-lapse microscopy. Then, the media in the appropriate inlets were replaced with (drug- or vehicle-containing) isotonic, hypotonic, or hypertonic media (Figures S2A–S2C) to produce an osmotic shock. In all experiments, the uppermost inlet contained 10% FBS. Phase-contrast time-lapse images were captured again at 3 min intervals for 2 hr.

Cell x,y position within the microchannel was identified as the midpoint between the poles of the cell body (using phase-contrast images) or the nucleus (using fluorescence images of Hoechst-stained cells) and tracked as a function of time. Cell velocity, chemotactic index, and length were computed as a function of time using a custom-written Matlab program. Instantaneous cell velocity was calculated by dividing each interval displacement by the time interval (3 min), and the mean velocity for a given cell was computed by averaging instantaneous velocities for all time intervals before or after osmotic shock. Chemotactic index was calculated by dividing the end-to-end displacement by the total path length of the cell. Thus, completely directed cell migration resulted in a chemotactic index equal to 1. Cell lengths were measured using the phase-contrast image sequences and the “plot profile” tool in ImageJ to determine the leading and trailing edges of the cell. These measurements were verified by confocal microscopy.

In select experiments, cells were fixed, permeabilized, blocked for non-specific binding, immunostained for target proteins (NHE-1 and AQP5), and quantitatively analyzed. Statistical significance was determined with a Student’s t test or analysis of variance (ANOVA) as appropriate. At least three independent trials were conducted for each experiment, and all data in this article represent the mean ± SEM or SD (as indicated) of pooled data from all experiments. A detailed description of the experimental methods is given in the Extended Experimental Procedures.

Theoretical Methods

The theoretical approach is based on an analysis of hydrostatic and osmotic forces governing water permeation across the cell membrane. In our model, we consider the kinetics of water, kinetics and diffusion of ions, flow of the cell cytoplasm, and mechanics of the cell cortex. Parameters used in our model are listed in Table S1. The detailed theoretical methods and results are described in the Extended Experimental Procedures.