Principal Component Regression and Linear Mixed Model in Association Analysis of Structured Samples: Competitors or Complements?

Abstract

Genome-wide association studies (GWAS) have been established as a major tool to identify genetic variants associated with complex traits, such as common diseases. However, GWAS may suffer from false positives and false negatives due to confounding population structures, including known or unknown relatedness. Another important issue is unmeasured environmental risk factors. Among many methods for adjusting for population structures, two approaches stand out: one is principal component regression (PCR) based on principal component analysis (PCA), which is perhaps most popular due to its early appearance, simplicity and general effectiveness; the other is based on a linear mixed model (LMM) that has emerged recently as perhaps the most flexible and effective, especially for samples with complex structures as in model organisms. As shown previously, the PCR approach can be regarded as an approximation to a LMM; such an approximation depends on the number of the top principal components (PCs) used, the choice of which is often difficult in practice. Hence, in the presence of population structure, the LMM appears to outperform the PCR method. However, due to the different treatments of fixed versus random effects in the two approaches, we show an advantage of PCR over LMM: in the presence of an unknown but spatially confined environmental confounder (e.g. environmental pollution or life style), the PCs may be able to implicitly and effectively adjust for the confounder while the LMM cannot. Accordingly, to adjust for both population structures and non-genetic confounders, we propose a hybrid method combining the use and thus strengths of PCR and LMM. We use real genotype data and simulated phenotypes to confirm the above points, and establish the superior performance of the hybrid method across all scenarios.

Introduction

Genome-wide association studies (GWAS) are the current gold standard in identifying genetic variants associated with complex traits. In practice, genetic correlations among subjects can arise from population heterogeneity, familial relatedness, or cryptic relatedness, all of which are regarded as population structures in a broad sense in this paper. Furthermore, due to the observational nature of GWAS, unknown environmental and non-genetic risk factors may arise as confounders. Failure to account for these correlations and confounders can produce both false positives and false negatives in GWAS.

When population structure acts like a confounder in GWAS, it is also called population stratification. Population stratification occurs most frequently in the case-control study design, where different ancestral populations have varying disease risks and different distributions of genetic variants. Many methods have been proposed, such as genomic control (GC) [Devlin and Roeder, 2004], structured association [Pritchard et al., 2000] and other mixture model-based methods [Zhang et al., 2002; Zhu et al., 2002], and genetic matching and stratification [Epstein et al., 2007; Guan et al., 2009]. The most appealing and widely used method is perhaps principal component regression (PCR) based on principal component analysis (PCA) of a large number of genetic variants across the genome [Price et al., 2006; Patterson et al., 2006; Zhao et al., 2007]. It includes a few top principal components (PCs) as covariates in a regression model, and has proven competent. The top PCs also offer a way to visualize the spatial locations of subjects, though this may be over-interpreted [Novembre and Stephens, 2008; Wang et al., 2012], and its assumption of linear PC effects can be violated, resulting in biased estimation of association [Lin and Zeng, 2011]. To account for more complex population structures, including familial correlations or cryptic relatedness, linear mixed models (LMMs) have emerged recently as most promising [Yu et al., 2005; Zhao et al., 2007]. Later it was found that if the identity-by-state (IBS) matrix is used, the additional modeling for population structure can be redundant [Malosetti et al., 2007; Zhao et al., 2007]. To overcome the computing bottleneck, several fast algorithms have been developed for LMM, including efficient mixed-model association (EMMA) [Kang et al., 2008] and its expedited version EMMAX [Kang et al., 2010], and genome-wide efficient mixed-model association (GEMMA) [Zhou and Stephens, 2012]. EMMA and GEMMA offer exact calculations, while EMMAX is an approximate method in estimating the variance components by ignoring the effects of the genetic variant of interest. Kang et al. (2010), by using the 1966 Northern Finland Birth Cohort (NFBC66) and the Wellcome Trust Case Control Consortium (WTCCC), showed that EMMAX can better control inflated false positives than PCR in GWAS. On the other hand, Wu et al. (2011) reported some simulated data showing that EMMAX could be “anticonservative” while PCR seemed to perform best. Wang and Peng (2013) offered some theoretical and numerical properties of the two methods.

Given the popularity of PCR and the emerging promise of LMM, in view of these discrepant comparisons between the two methods, it is natural to ask which one is preferred in practice. To address this important question, we aim to point out their connections and differences. Based on singular value decomposition, Hoffman (2013) showed that the PCR method can be regarded as an approximation to a LMM; here we use probabilistic PCA [Tipping and Bishop, 1999] to confirm this connection. As expected, the degree of the approximation depends on the number of the top PCs used, the choice of which however is difficult in practice. This connection offers a theoretical explanation on why LMM performed better than PCR in several real studies in presence of severe population stratification. This may give an impression that LMM can completely replace PCR, which however is not true. Due to the use of the fixed effects in PCR and random effects in LMM, there are other implications from model fitting. First, as is well known, when a larger number of PCs are used in PCR to better approximate a LMM, due to an increasing number of parameters to be estimated, the PCR method will lose power. Second, more importantly and perhaps surprisingly, we show that in the presence of unknown environmental (and non-genetic) confounders, PCR may outperform LMM. The reason is that, because PCs can represent geographical locations of human populations, use of the PCs may be able to adjust for environmental confounders that are spatially distributed. Hence, to account for both population stratification and unknown environmental confounders, we propose using a hybrid method combining PCR and LMM. We use a real genotype dataset to confirm the above points.

Methods

Suppose Y = (Y₁, …, Y_n)^T is the quantitative trait vector for n subjects, and $g^{\ast }={(g_1^{\ast },g_2^{\ast },\dots ,g_n^{\ast })}^T$ is the genotype score vector of a single nucleotide polymorphism (SNP) of interest, where $g_i^{\ast }=0,1,2$ is the minor allele count for the i^th subject. We have g = (g₁, …, g_n)^T as the normalized genetic scores with $g_i=(g_i^{\ast }-2p_0)/\sqrt{p_0(1-p_0)}$, where p₀ is the minor allele frequency (MAF) of the SNP.

LMM and PCR methods

A linear mixed model (LMM) accounting for population structure is

$$Y={\alpha }_0\mathbf{1}+g{\alpha }_1+u+\epsilon ,$$ (1)

where α₀ is the intercept, 1 is a vector of all 1’s, $u~N(0,{\sigma }_g^{2}K)$ is the so-called polygenic effect, K is a similarity matrix measuring the similarity or relatedness between any two subjects, and ε ~ N(0, σ²I) is the error term. ${\sigma }_g^2$ is the polygenic variance and σ² is the individual variance. The marginal covariance of Y is $var(Y)=\mathrm{\Omega }={\sigma }_g^{2}K+{\sigma }^{2}I$. The goal of an association analysis is to test the null hypothesis H₀: α₁ = 0.

The PCR model is

$$Y={\gamma }_0\mathbf{1}+g{\gamma }_1+Z{\gamma }_2+\epsilon$$ (2)

where γ₀ is the intercept, and Z is the matrix with each column as one of a few top PCs constructed by PCA from a large number of genetic variants, or more generally, as a few top eigen vectors of a similarity matrix measuring similarities among the subjects based on the genetic variants (Lee et al., 2009). ε ~ N(0, σ²I) is the error term. The goal of an association analysis is to test the null hypothesis H₀: γ₁ = 0.

A connection between PCR and LMM

In the LMM (1), we can regard the polygenic effect u as a collapsed effect of many genetic variants, say X^* with p genetic variants. X = (X_ij) is the matrix after normalizing X^*: for each SNP j of subject i, $X_{ij}=(X_{ij}^{\ast }-2p_j)/\sqrt{p_j(1-p_j)}$ with p_j as the MAF of SNP j. Then the LMM can be written as

$$Y={\alpha }_0\mathbf{1}+g{\alpha }_1+\sum _{j=1}^p{X}_{.j}{\eta }_j+\delta ={\alpha }_0\mathbf{1}+g{\alpha }_1+X\eta +\delta ,$$

where X._j = (X_1j, …, X_nj)^T, $\eta ~N(0,{\sigma }_g^{2}I)$ and δ ~ N (0, σ²I). Note that in the LMM, K = XX^T/p, the covariance matrix, can be used to measure the similarities among the n subjects. In probabilistic PCA [Tipping and Bishop, 1999], similar to factor analysis, each X._j is modeled to be independently and identically distributed as

$$X_{.j}\mid {\zeta }_j~N(W{\zeta }_j+{\zeta }_{\mathbf{0}},{\sigma }_x^{2}I),{\zeta }_j~N(0,I).$$

Since each SNP X._j is already centered at 0, we can simply take ζ₀ = 0. With any chosen number of columns for W, say q, the maximum likelihood estimator (MLE) of W is

$$\widehat{W}=U_q{({\mathrm{\Lambda }}_q-{\sigma }_x^{2}I)}^{1/2}R,$$

where U_q is a matrix with columns as the top q eigenvectors of the similarity or sample covariance matrix K = XX^T/p, and Λ_q is a diagonal matrix with q corresponding eigenvalues λ_j’s of K, and R is an arbitrary orthogonal rotation matrix. Since the scaling of the PCs has no effect in regression while for simplicity we can ignore rotation (i.e. choose R = I), we can take Ŵ= U_q; in other words,Ŵ contains the top q PCs based on X. Taking ζ = (ζ₁, …, ζ_p) and denoting ε_x as the corresponding matrix for the error term in the probabilistic PCA model, we approximate the LMM as

$$Y={\alpha }_0\mathbf{1}+g{\alpha }_1+(\widehat{W}\zeta +{\epsilon }_x)\eta +\delta ={\gamma }_0\mathbf{1}+g{\alpha }_1+\widehat{W}{\gamma }_2+\epsilon ,$$

where γ₀ = α₀, γ₂ = ζη and ε = ε_xη + δ. If q is the number of the top PCs that we use in PCR, Ŵ is Z in Equation (2). Hence the above approximate LMM reduces to the PCR model in Equation (2). Note however that in the PCR model γ₂ is treated as a fixed (i.e. non-random) effect, while in the LMM u (or γ₂) is random; this difference has important implications in later analysis.

The above derivation is for K = XX^T/p. For other K, e.g. calculated as the IBS matrix, due to its positive semi-definiteness as (a part of) the covariance matrix for the random effect u, we can have a decomposition K = AA^T/p_A, where A is a n × p_A matrix. Denote the jth column of A as A._j. Now replace the X._j by A._j and then proceed as before, e.g. by assuming $A_{.j}\mid {\zeta }_j~N(W{\zeta }_j+{\zeta }_{\mathbf{0}},{\sigma }_x^{2}I)$ and ζ_j ~ N (0, I), we can reach the same PCR model as an approximation to the LMM, where the PCs are generalized to the eigenvectors of any symmetric and positive semi-definite similarity matrix K [Lee et al., 2009; Zhang et al., 2013]. Hence our above conclusion holds for any positive semi-definite similarity matrix K.

Hoffman (2013) obtained the same connection based on the close relationship between PCA and singular value decomposition. Here our derivation is based on the probabilistic PCA formulation, which offers a statistical interpretation of the top PCs (or eigen-vectors) as the MLEs.

An environmental confounder

In observational studies like GWAS, unobserved environmental and non-genetic factors may arise as confounders, which may not be fully captured by the similarity matrix K estimated from genetic variants (Mathieson and McVean, 2012). A model with both a sample structure u and an environmental confounder μ is

$$Y={\alpha }_0\mathbf{1}+\mu +g{\alpha }_1+u+\delta ={\alpha }_0\mathbf{1}+D\theta +g{\alpha }_1+u+\delta ,$$ (3)

where μ = (θ₁, …θ₁, …θ_k, …θ_k)^T, $D=\text{diag}\{{({{\mathbf{1}}_{{\mathbf{n}}_{\mathbf{1}}}}^T,{{\mathbf{1}}_{{\mathbf{n}}_{\mathbf{2}}}}^T,\dots {{\mathbf{1}}_{{\mathbf{n}}_{\mathbf{k}}}}^T)}^T\}$, θ = (θ₁, θ₂, ···, θ_k)^T, 1_nj is a vector of all 1’s of length n_j, the number of samples in cluster j, and diag{a} is a matrix with vector a on the diagonal and all other elements 0. Here we assume that the samples are ordered into clusters with each cluster containing the samples sharing the same environmental risk; this assumption is not necessary, but only for simplicity and concreteness of presentation.

Now suppose θ_h ~ f (.), h = 1, …, k, where f (.) is the unknown distribution density of θ_h with variance ${\sigma }_{\theta }^2$. Then

$$var(Y)=D{D}^T{\sigma }_{\theta }^2+{\sigma }_g^{2}K+{\sigma }^{2}I={\sigma }_g^2\left(\frac{{\sigma }_{\theta }^2}{{\sigma }_g^2}D{D}^T+K+\frac{{\sigma }^2}{{\sigma }_g^2}I\right),$$

and $D{D}^T=\text{diag}(\mathbf{1}{\mathbf{1}}_{{\mathbf{n}}_{\mathbf{1}}}^{\mathbf{T}},\mathbf{1}{\mathbf{1}}_{{\mathbf{n}}_{\mathbf{2}}}^{\mathbf{T}},\dots \mathbf{1}{\mathbf{1}}_{{\mathbf{n}}_{\mathbf{k}}}^{\mathbf{T}})$. One potential issue with EMMAX or GEMMA is their only using K to model the covariance among the samples. Due to the commonality of the human genomes, the K matrix has a more “smooth” structure that may not approximate well a block diagonal matrix like DD^T (or other more general matrix induced by environmental confounders). Consequently, with a relatively large σ_θ, using K alone may fail to capture the phenotype covariance structure, leading to a lack of fit of the standard LMM (1).

On the other hand, if μ can be well approximated by a linear combination of the top PCs, say μ ≈ Zρ, then the PCR model is approximated by

$$Y={\gamma }_0\mathbf{1}+Z\rho +Z{\gamma }_2+g{\alpha }_1+\epsilon ={\gamma }_0\mathbf{1}+Z(\rho +{\gamma }_2)+g{\alpha }_1+\epsilon ,$$

which can be well fitted by the standard PCR model (2). In practice, this assumption of μ ≈ Zρ may be plausible if environmental confounders are spatially distributed, because the top PCs of genetic variants can represent geographic coordinates [Wang et al., 2012].

A hybrid model

As discussed, neither the (standard) LMM nor PCR is a complete winner in adjusting for both population structure and environmental confounders, but with different advantages. Hence we propose a hybrid model including both a few PCs and a random effect:

$$y={\gamma }_0\mathbf{1}+g{\gamma }_1+Z\rho +u+\delta ,$$ (4)

where Z is the top q PCs from the similarity matrix K, and $u~N(0,{\sigma }_g^{2}K)$, δ ~ N (0, σ²I). The PCs aim to capture a major part of population structure and environmental confounders, while the random effect account for the remaining and more subtle effects of population structure.

Since the PCs are extracted from the similarity matrix K, there may be some concerns on the repeated use of K for both the PCs and random effect. As an alternative, we can also use K₂ as the similarity matrix for u, where K₂ is a “residual” matrix of K after excluding the covariance explained by the top q PCs in Z. That is, by eigen decomposition we have

$$K=Q\mathrm{\Lambda }{Q}^T=(Q_1,Q_2)\text{diag}\{{\mathrm{\Lambda }}_1,{\mathrm{\Lambda }}_2\}{(Q_1,Q_2)}^T,$$

where Q is the eigenvectors and Λ is the eigenvalues, Q₁ is the top q PCs that we include in Z, Λ₁ is the corresponding eigenvalues of the top PCs. Q₂ is the remaining eigenvectors and Λ₂ is the corresponding eigenvalues. We use $K_2=Q_2{\mathrm{\Lambda }}_2{Q}_2^T$ in place of K as an alternative. It turns out that the restricted likelihoods of these two hybrid models are exactly the same (see the proof in an appendix), so will be their estimation and inference. Therefore, in the hybrid model the random effect (either u or u₂) is only used to capture the “residual” effects of the PCs.

The hybrid model has been used to account for population structure alone [Zhao et al., 2007], differing from our goal here to adjust for both population structure and environmental confounders, which has been largely neglected in the literature. In particular, several new studies [Lippert et al., 2013; Yang et al., 2014; Tucker et al., 2014] focused on the advantages and disadvantages of the PCR and LMM methods exclusively for population structures; in contrast, as a main contribution here, we explicitly separate out the effects of population structures (i.e. genetic confounders) and environmental confounders, based on which we illuminate the respective advantages (and disadvantages) of the PCR and LMM approaches.

Data

We used the genotype data with a familial structure to illustrate our points. The data was drawn from the Type 2 Diabetes Genetic Exploration by Next-generation Sequencing in Ethnic Samples (T2D-GENES) Consortium Project 2. It consisted of whole genome sequence data of 959 samples from 20 pedigrees from the San Antonio Family Studies (SAFS), with each family containing 22 to 86 family members. We first pruned all the common variants (CVs) by PLINK [Purcell et al., 2007] with a sliding window of size 50, a moving step 5 and r² ≤ 0.05. We randomly selected 31544 pruned CVs with MAF ≥0.05 from the autosomes, and use them to estimate the similarity matrix K; both the covariance matrix and IBS matrix were calculated, however, due to the increasing popularity of the IBS matrix in LMM for its better performance [Kang et al., 2008], we show the results with the IBS matrix.

We also used simulated phenotypes in simulations and a quantitative phenotype from the T2D-GENES data in example data analysis.

Results

Simulations

We simulated quantitative traits following the sample structure shown in estimated IBS matrix from the data, with or without an environmental risk, under both null and alternative hypotheses. We compared the LMM, implemented in EMMAX [Kang et al., 2008] and GEMMA [Zhou and Stephens, 2012], PCR [Patterson et al., 2006] and the hybrid method, with respect to their ability to correct for inflated type I errors as well as their power performance. We applied the F-test in EMMAX, and the Wald tests in GEMMA, the PCR model and hybrid model respectively. As a benchmark, we also applied the ordinary least squares (OLS) (i.e. assuming K = I in the LMM) with the t-test.

In the presence of only population structure

For the purpose of controlling Type I error and the inflation factor λ [Devlin and Roeder, 2004], we used model (1) with α₁ = 0 to simulate Y’s under the null hypothesis; to compare the power, we used model (1) with a genetic effect α₁ ≠ 0. We set α₀ = 5, and the vector u was sampled from $N(0,{\sigma }_g^{2}K)$, ε ~ N(0, σ²I). ${\sigma }_g^2$ was the polygenic variance, and K was the IBS matrix estimated from the T2D-GENES data. We randomly selected 11133 pruned CVs to be tested. For the PCR and hybrid methods, we included the top 20 PCs unless specified otherwise. For all the tests the nominal significance level was 0.05.

Under the null hypothesis (Table 1), as ${\sigma }_g^2$ increased, PCR gradually failed to control the Type I error rate and λ while EMMAX and GEMMA behaved well. For example, for ${\sigma }_g^2=90$ and σ² = 10, PCR had a severely inflated Type I error rate of 0.110 (and inflated λ = 1.493 > 1), while EMMAX and GEMMA had their type I errors around 0.05 (and λ ≈ 1). If we gradually increased the number of PCs for the scenario ${\sigma }_g^2=90$, σ² = 10, both the Type I error and λ were reduced notably; however, even with the top 100 PCs used, the Type I error was still around 0.070 and λ around 1.18.

Table 1.

Association testing under H₀ in the presence of only population structure based on the T2D-GENES genotype data.

set-up		EMMAX	GEMMA	PCR(20)	hybrid	OLS
${\sigma }_g^2=10$, σ2 = 90	Type I error	0.050	0.051	0.053	0.050	0.055
	λ	0.992	1.004	1.025	0.980	1.025
${\sigma }_g^2=60$, σ2 = 40	Type I error	0.051	0.052	0.073	0.053	0.095
	λ	1.041	1.044	1.185	1.029	1.363
${\sigma }_g^2=90$, σ2 = 10	Type I error	0.050	0.051	0.109	0.050	0.153
	λ	1.000	1.003	1.465	1.011	1.828

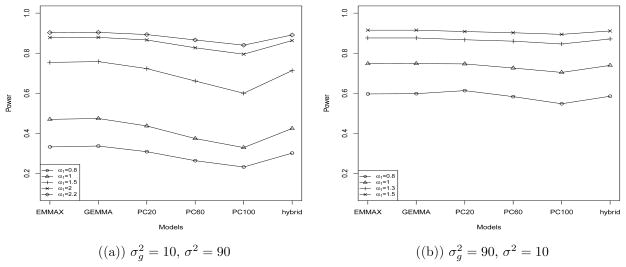
Figure 1 shows the power comparison with different genetic effect α₁. GEMMA usually had the highest power, which however was very close to that of PCR and of the hybrid model, especially as ${\sigma }_g^2$ increased. The power of the hybrid method was slightly lower than EMMAX and GEMMA, and was close to that of PCR with 20 PCs. For example, when ${\sigma }_g^2=10$ with α₁ = 1.5, the power was 0.754 for EMMAX, 0.758 for GEMMA, 0.723 for PCR with 20 PCs and 0.600 with 100 PCs, and 0.713 for the hybrid method; for ${\sigma }_g^2=90$, the power for the methods was 0.915, 0.915, 0.908, 0.894 and 0.911, respectively.

Figure 1.

Power of the association tests based on a simulated trait and the T2D-GENES genotype data.

In the presence of an environmental confounder

We considered a scenario with both population structure and an environmental confounder. We assumed that 496 samples in 8 families were from the same spatial area thus sharing the same environmental risk while the remaining in another cluster. For illustration, we selected 10000 SNPs that were significantly associated with the clustering assignment and were to be tested in association analysis. We saw that EMMAX and GEMMA had gradually increasing Type I errors as the environmental effect |θ_j| became larger, due to the inadequacy of the genetic similarity matrix to capture the environmental confounder. The hybrid method was consistently the best performer. For example, when |θ_j| = 4, while GEMMA had a Type I error rate of 0.109 (λ=1.645), PCR of 0.067 (λ=1.151) with 100 PCs, the hybrid method with 20 PCs could reduce it to 0.061 (λ=1.158), and further if more PCs were used. Here PCR also worked fine with 100 PCs mainly because ${\sigma }_g^2$ was not so big; when we increased ${\sigma }_g^2$ to 90, PCR lost its efficacy even with 100 PCs (Type I error =0.081 and λ=1.269) while the hybrid method could still control the Type I error rate to be 0.0618 (and λ=1.102) with only top 20 PCs.

Example

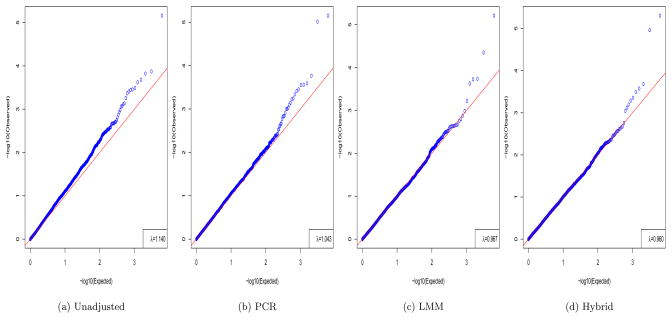
We conducted an association analysis with the systolic blood pressure (SBP) at the baseline as the quantitative phenotype in the T2D-GENES data. The genotype data used were the same as before. In particular, we used the IBS matrix as the similarity matrix K; the use of the covariance matrix as K performed worse (not shown). All the methods included subject gender, smoking status and age as covariates. As shown in Figure 2, no adjustment for population structure (i.e. OLS) led to severely inflated false positives with an inflation factor λ of 1.14, since it failed to correct for within-family correlations in the data. In contrast, PCR with the top 20 PCs could largely control the inflated false positives, while the GEMMA implementation of LMM had a slight advantage over PCR with a λ closer to 1; furthermore, there were fewer more significant p-values (< 0.001) resulting from the LMM than those from PCR. The good performance of LMM also suggested the non-existence or negligible effects of environmental confounders (that could not be adjusted by genetic similarity matrix K), possibly due to all study subjects were from the San Antonio area and thus there was a lack of environmental heterogeneity. It is reassuring to see that the hybrid method controlled the false positives as well as LMM, and at the same time, gave a few more p-values < 0.001.

Figure 2.

Q-Q plots of the p-values in the association tests for the SBP in the T2D-GENES data.

Discussion

As obtained in Hoffman (2013) but based on an alternative derivation, we have confirmed a close connection between PCR and LMM in association analysis of structured samples. This connection suggests both theoretical and practical advantages of the LMM method over PCR in presence of severe population stratification. In particular, the choice of how many PCs to use in PCR is difficult; too few PCs may cause inflated Type I errors while too many lead to power loss. It appears being increasingly accepted to take the LMM as a general and feasible model for population structure, from which the connection between the two methods also offers an explanation on why PCR often performs well if the population structure is not sufficiently complex or subtle. For example, when we used the European and African samples from the 1000 Genomes Project data, PCR with 20 PCs performed as well as the LMM method (not shown). A challenge however is how to tell whether a PCR model is adequate or not when compared to a LMM. In this regard, it seems that one should always use LMM over PCR. Most importantly, we have also pointed out a weakness of the LMM method in the presence of unknown environmental confounders that can arise from GWAS. Accordingly we have proposed a hybrid method, which performed consistently well across all scenarios in our study. In particular, the hybrid method can be easily implemented in any existing framework of fitting LMMs, such as in the EMMAX or GEMMA package. Therefore, we recommend the use of the hybrid method.

Table 2.

Association testing with a sample structure and environmental factor, and ${\sigma }_g^2=60$, σ² = 40 based on the T2D-GENES genotype data. 959 samples were artificially assigned into 2 clusters.

		EMMAX	GEMMA	PCR					hybrid	OLS
				20	40	60	80	100
θ1 = −1, θ2 = 1	Type I	0.057	0.059	0.081	0.067	0.065	0.061	0.059	0.052	0.152
	λ	1.133	1.146	1.302	1.218	1.152	1.125	1.097	1.076	1.947
θ1 = −2, θ2 = 2	Type I	0.073	0.075	0.092	0.070	0.068	0.062	0.061	0.053	0.288
	λ	1.279	1.299	1.381	1.237	1.175	1.139	1.113	1.093	3.823
θ1 = −4, θ2 = 4	Type I	0.107	0.109	0.136	0.083	0.077	0.070	0.067	0.061a	0.626
	λ	1.629	1.645	1.769	1.334	1.275	1.208	1.151	1.158a	11.976

^aFor PC#=40, 60, 80, 100, Type I errors=0.056, 0.055, 0.053, 0.051 and λ =1.111, 1.060, 1.062, 1.063 respectively.

Appendix: Proof of the equivalence between the two hybrid models

In the hybrid model (4), the random effect is assumed as $u~N(0,{\sigma }_g^{2}K)$. An alternative model is

$$Y=g\beta +Z\gamma +u_2+\epsilon ,$$ (5)

where $u_2~N(0,{\sigma }_g^2{K}_2)$ and others are the same as in model (4). Note that $K_2=Q_2\mathrm{\Lambda }{Q}_2^T$ is the “residual” similarity matrix after excluding the covariance explained by the top k PCs. Both K and K₂ are assumed known and we only need to estimate ${\sigma }_g^2$, σ² and the fixed effects.

The restricted maximum likelihood (REML) estimation and inference of β proceed using the likelihood on a linear transformation Y^* = AY such that Y^* does not depend on the fixed effects. One way to achieve this is, suppose X = (Z, g) = (Q₁, g), then A = I − P_x = I − X(X^TX)⁻¹X^T which is the projection matrix onto the orthogonal column space of X. After the projection, Model (4) becomes

$$Y^{\ast }=(I-P_x)u+(1-P_x)\epsilon$$ (6)

and Model (5) becomes

$$Y^{\ast }=(I-P_x)u_2+(I-P_x)\epsilon .$$ (7)

The only difference between equation (6) and (7) is (I − P_x)u and (I − P_x)u₂. And we have

$$\begin{array}{l}var((I-P_x)u)=(I-P_x){\sigma }_g^{2}K(I-P_x)={\sigma }_g^2(I-P_x)Q\mathrm{\Lambda }{Q}^T(I-P_x)\\ ={\sigma }_g^2(I-P_x)(Q_1,Q_2)\mathrm{\Lambda }{(Q_1,Q_2)}^T(I-P_x).\end{array}$$

Recall that I − P_x is the projection onto the orthogonal space of X, so we have (I − P_x)Q₁ = (I − P_x)X(I, 0)^T = 0, and

$$(I-P_x)(Q_1,Q_2)\mathrm{\Lambda }{(Q_1,Q_2)}^T(I-P_x)=(I-P_x)Q_2\mathrm{\Lambda }{Q}_2^T(I-P_x),$$

leading to

$$var((I-P_x)u_2)=(I-P_x){\sigma }_g^2{K}_2(I-P_x)={\sigma }_g^2(I-P_x)Q_2{\mathrm{\Lambda }}_2{Q}_2^T(I-P_x).$$

Thus the two models (6) and (7) are equivalent, implying that the REML estimation and inference for the original two hybrid models are equivalent too.