LEAP: Biomarker Inference Through Learning and Evaluating Association Patterns

Abstract

Single nucleotide polymorphism (SNP) high-dimensional datasets are available due to Genome Wide Association Studies (GWAS). Such data provide researchers opportunities to investigate the complex genetic basis of diseases. Much of genetic risk might be due to undiscovered epistatic interactions, which are interactions in which several genes combined affect disease. Research aimed at discovering interacting SNPs from GWAS datasets proceeded in two directions. First, tools were developed to evaluate candidate interactions. Second, algorithms were developed to search over the space of candidate interactions. Another problem when learning interacting SNPs, which has not received much attention, is evaluating how likely it is that the learned SNPs are associated with the disease. A complete system should provide this information as well. We develop such a system. Our system, called LEAP, includes a new heuristic search algorithm for learning interacting SNPs, and a Bayesian network based algorithm for computing the probability of their association.

We evaluated the performance of LEAP using 100 1000 SNP simulated datasets, each of which contains 15 SNPs involved in interactions. When learning interacting SNPs from these datasets, LEAP outperformed 7 others methods. Furthermore, only SNPs involved in interactions were found to be probable. We also used LEAP to analyze real Alzheimer's disease and breast cancer GWAS datasets. We obtained interesting and new results from the Alzheimer's dataset, but limited results from the breast cancer dataset.

We conclude that our results support that LEAP is a useful tool for extracting candidate interacting SNPs from high-dimensional datasets and determining their probability.

Introduction

The advancement of high-throughput technologies has provided us with unprecedented abundant data resources. For example, we have accumulated a vast amount of SNP datasets as a result of Genome Wide Association Studies (GWAS) using high-throughput technologies. A single nucleotide polymorphism (SNP) results when a nucleotide that is typically present at a specific location on the genomic sequence is replaced by another nucleotide [1]. These high dimensional GWAS datasets can concern over a million SNPs, and we expect to have more and higher dimension SNP datasets though ever improving next generation and third generation technologies. Whole genome sequencing could produce datasets with hundreds of millions of SNPs [2]. Such studies provide researchers unprecedented opportunities to investigate the complex genetic basis of diseases. By looking at single-locus associations, researchers have identified over 150 risk loci associated with 60 common diseases and traits [3-6].

However, it is likely that the discovery of loci with significant main effects may reveal only a small fraction of the undiscovered genetic risk of many common diseases [7-10]. That is, much of genetic risk might be due to undiscovered epistatic interactions, which are interactions in which several genes combined affect disease. Biologically, epistasis is believed to occur when the effect of one gene is modified by one or more other genes. Statistically, epistasis refers to an interaction between multiple loci such that the net effect on phenotype cannot be predicted by simply combining the effects of the individual loci. The individual loci may exhibit weak marginal effects, or perhaps they may exhibit none. There is already concrete evidence that epistatic interactions may play an important role in the genetic basis of common diseases [11].

We illustrate the notion of epistasis with no marginal effect with the following example. Suppose we have two genes and disease G₁, and G₂, disease D, and the alleles of G₁ are A and a, whereas those of G₂ are B and b.Suppose further that we have the probabilities (relative frequencies in the population) in the following table:

	AA (.25)	Aa (.5)	aa (.25)
BB (.25)	0.0	0.1	0.0
Bb (.5)	0.1	0.0	0.1
bb (.25)	0.0	0.1	0.0

If we assume that G₁ and G₂ mix independently in the population (no linkage), we then have that

$$\begin{array}{cc}\hfill P(D=yes)\mid AA)=& 0.0\times .25+0.1\times 0.5+0.0\times .25=.05\hfill \\ \hfill P(D=yes)\mid Aa)=& 0.1\times .25+0.0\times 0.5+0.1\times .25=.05\hfill \\ \hfill P(D=yes)\mid aa)=& 0.0\times .25+0.1\times 0.5+0.0\times .25=.05\hfill \end{array}$$

So, if we look at G₁ alone no statistical correlation with D will be observed. The same is true if we look at G₂ alone. However, as can be seen from the above table, the combinations AABb, AaBB, Aabb, and aaBb make disease D probable. Therefore, we say that both G₁ and G₂ exhibit no marginal effect, even though the two genes together affect disease. By changing the probabilities in the previous example slightly, we can obtain a situation in which there is a slight marginal effect.

Realizing the importance of discovering gene-gene interactions from genomic data, researchers have recently addressed this endeavor. Research proceeded in two directions. First, it was realized that standard techniques such as linear regression may not work well at learning interacting loci because both the predictors and the target are discrete. So other techniques were explored. One well-known technique is Multifactor Dimensionality Reduction (MDR) [12]. MDR combines two or more variables into a single variable (hence leading to dimensionality reduction); this changes the representation space of the data and facilitates the detection of nonlinear interactions among the variables. MDR has been successfully applied to detect epistatically interacting loci in hypertension [13], sporadic breast cancer [14], and type II diabetes [15]. Bayesian network scoring criteria were specifically developed to score models containing discrete random variables. So, Jiang et al. [16] evaluated the performance of 22 Bayesian network scoring criteria and MDR when learning two interacting SNPs with no marginal effects. Using 28,000 simulated datasets and a real Alzheimer's GWAS dataset, they found that several of the Bayesian network scoring criteria performed substantially better than other scores and MDR. The BN scores that performed best were ones that computed the BDeu score, which is the probability of the data given the model (See the Methods Section).

Another difficulty when learning interacting SNPs from high-dimensional datasets concerns the curse of dimensionality. For example, if we only investigated all 0, 1, 2, 3 and 4-SNP combinations when there are 500,000 SNPs, we would need to investigate 2.604 ×10²¹ interactions. Therefore, researchers worked on developing heuristic search methods that investigate multiple loci. Traditional techniques such as logistic regression (LOR) [17], logistic regression with an interaction term (LRIT) [18], penalized logistic regression [19] and Lasso [20,21] were applied to the task. Other techniques include full interaction modeling (FM) [22], using information gain (IG) [23,24], SNP Harvester (SH) [25], permutation testing [26,27], the use of ReliefF [28,29], random forests [30], predictive rule inference [31], a variational Bayes algorithm [32], Bayesian epistasis association mapping (BEAM) [33,34], maximum entropy conditional probability modeling (MECPM) [35], a Markov blanket method [36], and an ensemble-based method that uses boosting [37]. These techniques all score SNP combinations in some way; however the scoring criterion is embedded in the methodology.

All of these methods require some marginal effect to detect interacting SNPs. Many of the methods proceed in stages, using the first stage to identify promising SNPs, which in some way are investigated further in the second stage. However, Evans et al. [38] conclude that it is preferable to perform an exhaustive two-locus search across the genome rather than either of the two-stage procedures that we examined. Otherwise, investigators risk discarding significant loci that only exhibit small effects at the margins.

An exhaustive search is not possible when there are several million SNPs. So some researchers turned their efforts to reducing the search space based on ancillary knowledge. Oh et al. [39] performed a two-stage application of MDR. The first stage is a within-gene search in which all combinations of SNPs allocated to the same gene are investigated. Briggs et al. [40] identified promising regions harboring epistatic candidates by looking for concordance in affected sibling pairs. Jiang et al. [41] investigated all 2-loci combinations where one of the loci was previously known to be associated with the disease. Perhaps the most promising technique for reducing the search space is to restrict the search space for candidate gene sets by using knowledge about molecular pathways [42].

However, once the search space is reduced, we can still be left with a large number of SNPs, prohibiting an exhaustive search of even the pruned dataset. Furthermore, in an agnostic study we are searching for possible interactions for which we have no previous knowledge. Therefore, a multi-stage technique that can effectively locate interacting SNPs without an exhaustive search is still critical.

Another difficulty when learning interacting SNPs, which has not received as much attention, is evaluating how likely it is that the learned SNPs actually are associated with the disease. A complete system should provide this information as well. Based on our previous research, in this paper we develop such a system. We previously developed a heuristic search algorithm called multiple beam search (MBS) [43], and a Bayesian method for computing the posterior probability of a multiple SNP-phenotype association called the Bayesian network posterior probability (BNPP) [41]. We built on these previous results. Namely, we develop a new heuristic search algorithm that uses the best BDeu score identified in [16] and MBS [43] to learn SNPs possibly associated with the disease, and then we use the BNPP [41] to evaluate the probability of that association. The complete system is called LEAP.

Chen et al. [44] compared seven of the methods for learning interacting SNPs using datasets developed from models of epistatic interaction in which there were some marginal effects. Those methods are MDR, FM, IG, BEAM, SH, LOR, and MECPM (See above for these initialisms). We evaluate LEAP using datasets used in these comparisons. We also apply LEAP to real breast cancer and late onset Alzheimer's disease (LOAD) GWAS datasets.

Methods

The method we develop is based on Bayesian networks. So, first we review them.

Bayesian Networks

Bayesian networks [45-48] are increasingly being used for uncertain reasoning and machine learning in many domains including biomedical informatics [49-54]. A Bayesian network (BN) consists of a directed acyclic graph (DAG) G = (V, E), whose nodeset V contains random variables and whose edges E represent relationships among the random variables, and a conditional probability distribution of each node X ∈V given each combination of values of its parents. Often the DAG is a causal DAG, which is a DAG containing the edge X → Y only if is a direct cause of Y [45].

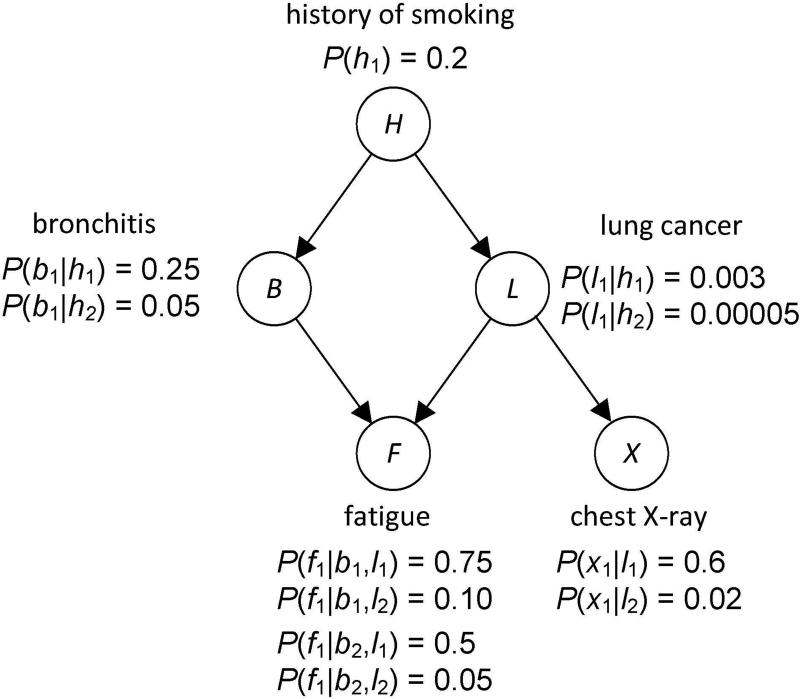
Figure 1 shows a causal BN modeling the relationships among a small subset of variables related to respiratory diseases. The value h₁ means the patient has a smoking history and the value h₂ means the patient does not. The other values have similar meaning.

Figure 1.

A BN modeling the relationships among a small subset of variables related to respiratory diseases is shown.

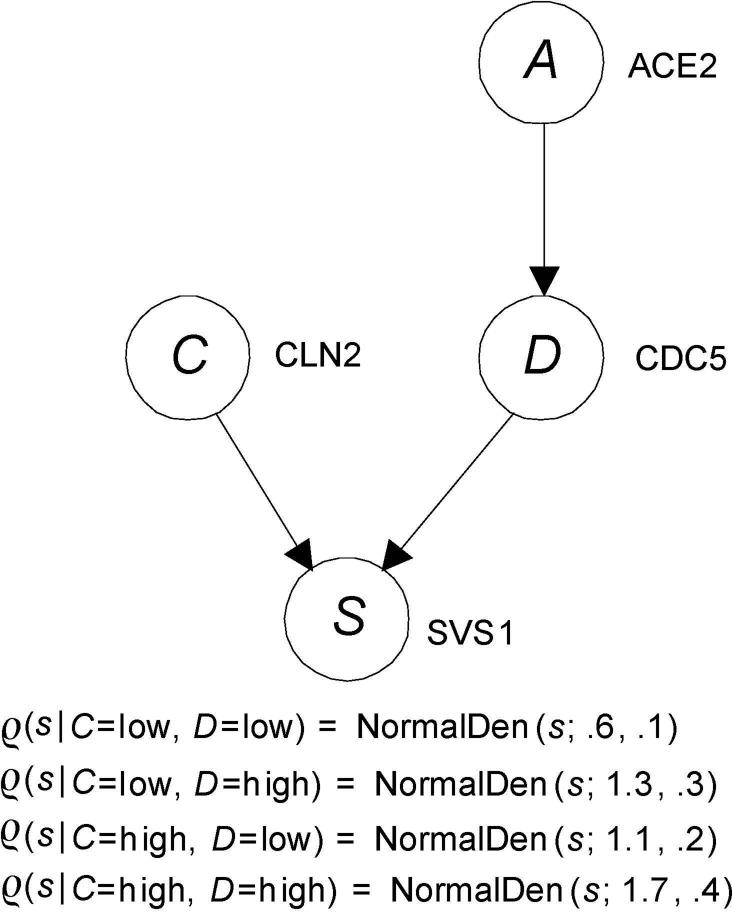
The probability distributions in Bayesian network can be discrete, continuous, or a hybrid combination of the two. Figure 2 shows an example modeling a small gene regulatory network in which the probability distributions are continuous.

Figure 2.

A BN modeling a small gene regulatory network with continuous probability distributions is shown. Only the conditional probability distribution of the leaf is given.

Using a BN, we can determine conditional probabilities of interest with a BN inference algorithm [45]. For example, using the BN in Figure 1, if a patient has a smoking history (h₁), and fatigue (x₁), a positive chest X-ray (f₁), we can determine the probability of the individual having lung cancer. That is, we can compute P(l₁ | h₁, x₁, f₁). Algorithms for exact inference in BNs have been developed [45]. However, the problem of doing inference in BNs is NP-hard [55]. So, approximation algorithms are often employed [45].

The task of learning a BN from data concerns learning both the parameters in a BN and the structure (called a DAG model). Specifically, a DAG model consists of a DAG G =(V, E)where V is a set of random variables, and a parameter set Θ whose members determine conditional probability distributions for G, but without specific numerical assignments to the parameters. The task of learning a unique DAG model from data is called model selection. As an example, if we had data on a large number of individuals and the values of the variables in Figure 1, we might be able to learn the DAG in Figure 1 from data.

In the score-based structure learning approach, we assign a score to a DAG based on how well the DAG fits the data. Cooper and Herskovits [56] developed the Bayesian score, which is the probability of the given the DAG. This score uses a Dirichlet distribution to represent prior belief for each conditional probability distribution in and contains hyperparameters representing these beliefs. The score is as follows:

$$scor{e}_{Bayes}(G:Data)=P(Data\mid G)=\prod _{i=1}^n\prod _{j=1}^{q_i}\frac{\Gamma \left({\sum }_{k=1}^{r_i}{a}_{ijk}\right)}{\Gamma ({\sum }_{k=1}^{r_i}{a}_{ijk}+{\sum }_{k=1}^{r_i}{s}_{ijk}}\prod _{k=1}^{r_i}\frac{\Gamma (a_{ijk}+s_{ijk})}{\Gamma \left(a_{ijk}\right)},$$ (1)

where r_i is the number of states of X_i, q_i is the number of different instantiations of the parents of X_i, ijk a is the ascertained prior belief concerning the number of times X_i took its k th value when the parents of X_i had their j th instantiation, and s_ijk is the number of times in the data that X_i took its k th value when the parents of X_i had their j th instantiation. The parameters a_ijk are known as hyperparameters.

When using the Bayesian score we often determine the values of the hyperparameters a_ijk from a single parameter α called the prior equivalent sample size [57]. If we want to use a prior equivalent sample size α and represent a prior uniform distribution for each variable in the network, for all i, j, and k we set a_ijk =α/ r_iq_i. In this case Equation 1 is as follows:

$$scor{e}_{\alpha }(G:Data)=P(Data\mid G)=\prod _{i=1}^n\prod _{j=1}^{q_i}\frac{\Gamma \zeta (\alpha \mid q_i)}{\Gamma (\alpha ∕q_i+{\sum }_{k=1}^{r_i}{s}_{ijk})}\prod _{k=1}^{r_i}\frac{\Gamma (\alpha ∕r_i{q}_i+s_{ijk})}{\Gamma (\alpha ∕r_i{q}_i)}.$$ (2)

To learn a DAG from data we can score all DAGs using the Bayesian score and then choose the highest scoring DAG. However, if the number of variables is not small, the number of candidate DAGs is forbiddingly large. Furthermore, the BN model selection problem has been shown to be NP-hard [58]. So heuristic algorithms have been developed to search over the space of DAGs during learning [45].

Problem of Learning Causal Predictors from High-Dimensional Data

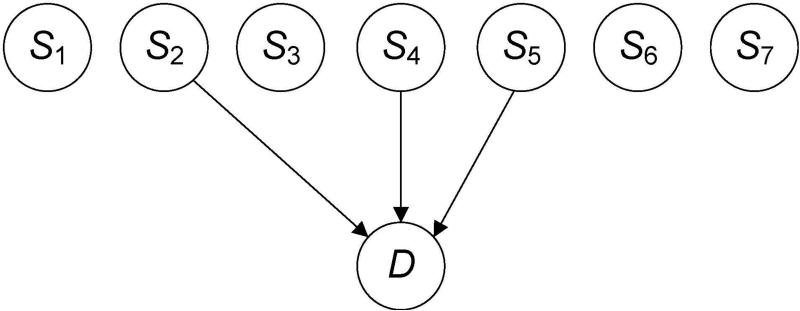
The general problem we are addressing concerns the case where we have a set A of n possible predictors of a target, where each predictor is either causative of the target (e.g., a SNP that causes a disease), or is a surrogate for a cause (e.g., a SNP that is in linkage equilibrium with a causative SNP). Our task is to learn the k predictors that are associated with the target. For the sake of focus, we will assume the predictors are SNPs and the target is a disease. Figure 3 shows a BN illustrating a problem instance and a solution. In this example, there are n = 7 possible predictors, and k = 3 predictors in the solution. The predictors are S₂, S₄, and S₅.

Figure 3.

There are n = 7 SNPs in the set A of candidate causal SNPs, and k = 3 of them are associated with D.

If each SNP has a strong effect by itself on disease D, the problem is easily solved simply computing the correlation of each SNP with D. However, if we have interactions with small marginal effects (such as epistasis) this is not possible, and the problem becomes very challenging. This is the problem with which we are concerned.

The solution to the problem is straightforward if n is very small and we have a large amount of data. We simply score all 2ⁿ DAG models, where each model has edges from the SNPs in one of the subsets of A to D, and choose the highest scoring model. However, there are two problems that we encounter if n is not very small. The first occurs even when n is not large. We discuss each in turn.

Suppose that n is not large but also that it is not very small. For example, let n = 20. Then we have 2²⁰ = 1,048,576 models, which means the number of possible models does not pose a problem. However, if each variables has 3 possible values (as in a SNP), in the model consisting of 20 parents there are 3²⁰ = 3.48×10⁹ combinations of values of the parents of D. We would almost never have a large enough dataset to provide sufficient data for each of these combinations, and, even if we did, the computation time of the BDeu score would usually be prohibitive. So, we cannot score all one million models.

An initial attempt at a solution would be to score all models that we can score, For example, we could score all 1, 2, 3, and 4-SNP models. However, we can't simply take the highest scoring model. Perhaps the solution consists of the first, third, and fifth highest scoring models. The BNPP, which is developed in the next subsection, addresses this problem.

The second problem is the curse of dimensionality which we have already mentioned. If n is large, we cannot investigate all possible models or even all 1, 2, 3, and 4-SNP models. So, we need a heuristic algorithm to search over the space of models. REGAL, which is developed after the BNPP, is such an algorithm.

BNPP

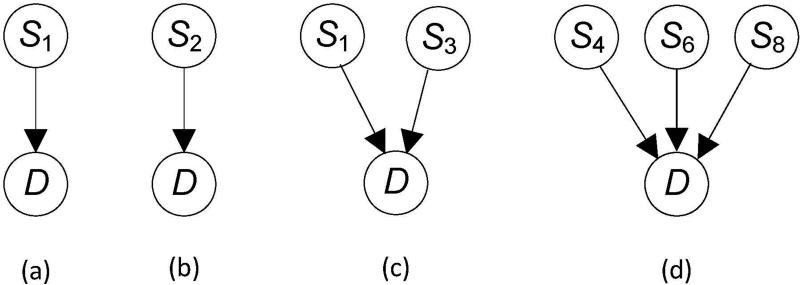
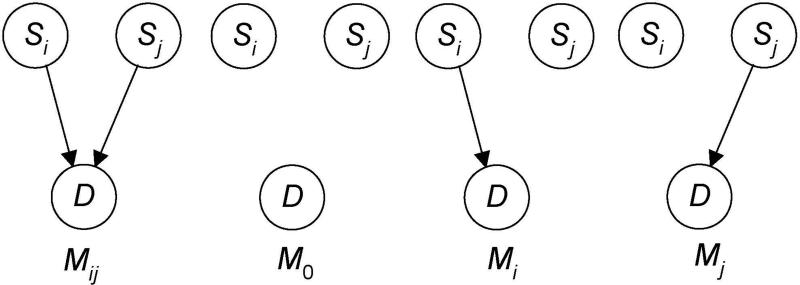
We call the model where the SNPs in some subset of A have edges to D an association pattern. Examples of such patterns appear in Figure 4. The first two represent that a single SNP by itself is associated with the disease, the third one represents that two SNPs together are associated with the disease, and the fourth one represents that three SNPs together are associated with the disease. It is important to recognize that, for example, the pattern in Figure 4 (c) does not entail that and S₁ and S₃ are interacting to affect D. Each could be affecting it separately.

Figure 4.

Association patterns with one, two, and three SNPs are shown.

If we can determine that a given association pattern is highly probably, then we can conclude that the SNPs in the pattern are probably associated with the disease. So, our goal is to compute the posterior probability of an association pattern M given Data. We can do that using Bayes' Theorem as follows:

$$P(M\mid Data)=\frac{P(Data\mid M)P\left(M\right)}{P\left(Data\right)}.$$ (3)

The P(Data | M) term can be computed using the BDeu score (Equation 2) with a particular choice of α. The P(M) term is the prior probability of M. We discuss the assessment of this probability at the end of this subsection. The posterior probability in Equation 3 is called the Bayesian Network Posterior Probability (BNPP), and was originally developed in [41]. Next we show how to compute the BNPP.

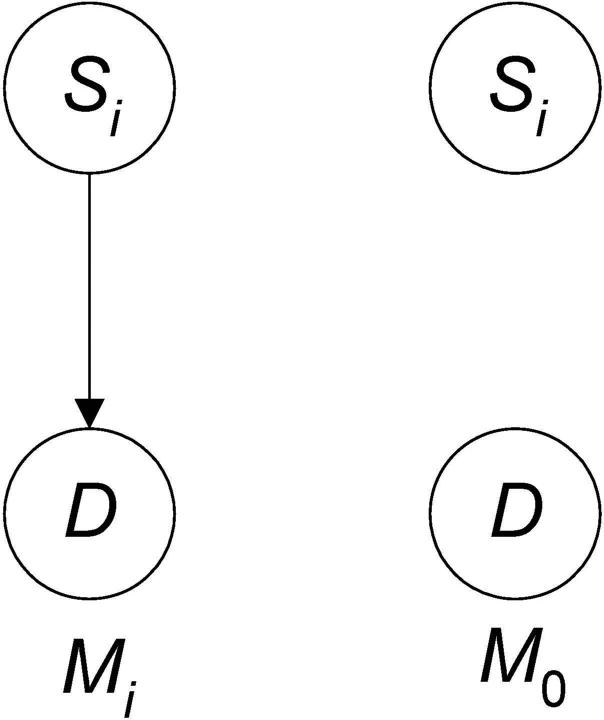
Consider first a 1-SNP pattern. Let M_i be the model that S_i all by itself is associated with D and M₀ be the model that it is not (see Figure 5). Then the posterior probability of M_i is given by

$$P(M_i\mid Data)=\frac{P(Data\mid M_i)P\left(M_i\right)}{P(Data\mid M_i)P\left(M_i\right)+P(Data\mid M_0)P\left(M_0\right)}.$$

Note that the model in Figure 5 is not just that S_i is associated with the disease, but rather that it is associated all by itself. That is, if S_i was involved in an epistatic interaction with no marginal effects, the model would be false.

Figure 5.

The model that S_i is associated with D all by itself is on the left and the model that it is not is on the right.

Figure 6 shows the model M_ij that S_i and S_j together are associated with D (without needing other interacting SNPs). This model includes the possibility that there is epistasis with no marginal effects, as well as the possibility that each SNP by itself is associated with D. The three competing models are on the right. The model denoted as M_i is not the same as the model M_i in Figure 5. Model M_i in Figure 6 represents that S_j is not associated with _D either by itself (other than possibly through S_i) or together with S_i; the model M_i in Figure 5 says nothing about S_j.

Figure 6.

The model that S_i and S_j together are associated with D is on left; the three competing models are on the right.

The number and complexity of the competing models increases with the size of the model. However, we need not identify all the competing models because Jiang et al. [41] developed a recursive algorithm for computing P(Data) for an arbitrary number of SNPs, which is the denominator in the formula for the posterior probability of a model. If there are j SNPs in the model, every subset of the j SNPs determines a competing model; so the likelihoods for 2^j models are computed. However, since ordinarily there are at most 5 SNPs in a model, this computation is feasible.

A challenge in many Bayesian analyses is the assessment of prior probabilities. Our application is no exception. Researchers in the Wellcome Trust Case Control Consortium [59] assessed that there are 1,000,000 regions of correlated SNPs in the genome and an expectation of 10 regions having an effect on phenotype. They therefore assign a prior probability of 0.00001 that a SNP is associated with a given disease. However, they note that other plausible estimates may vary from this prior probability by an order of magnitude or so in either direction. Using similar assumptions, Wacholder et al. [60] arrive at a prior probability between 0.0001 and 0.00001 that a randomly select nonsynonomous variant is associated with a complex disease. Based on these analyses, in an agnostic search we assume that each individual SNP has between a 0.0001 and a 0.00001 prior probability of being associated with a given disease. Using this assumption, Jiang et al. [41], obtained the lower and upper prior probabilities shown in Table I. These are the priors used in the studies in this paper. See [41] for further discussion of how they were derived. Wakefield [61] points out that “as more genome-wide association studies are carried out lower bounds on π₁ = 1−π₀ will be obtained from the confirmed ‘hits’ - it is a lower bound since clearly many non-null SNPs for which we have low power of detection will be missed.” We agree that in time additional results will help us to refine our assessment of priors.

Table I.

Lower and upper prior probabilities used to compute the BNPP are shown. They are developed in [41].

Model	Lower Prior Probability	Upper Prior Probability
1-SNP	1.0 × 10–6	1.0 × 10–5
2-SNP	6.0 × 10–12	6.0 × 10–10
3-SNP	5.6 × 10–17	5.6 × 10–14
4-SNP	6.96 × 10–22	6.96 × 10–18

To determine the probable causal SNPs we compute the BNPP of all 1, 2, 3, 4,..., and m-SNP models up to some computational feasible limit m. If a SNP appears in a probable model, it is probably a causal SNP. Note that if a SNP is in an (m+1)-SNP or higher interaction with no marginal interactions, it would not be found. Note further that the fact that a model is probable does not mean that it represents an interaction. If S_i and S_j each independently causes D, the model represented by the association pattern containing S_i and S_j will be probable. However, interacting SNPs are likely to be discovered in some discovered association pattern because together they should have a highly likelihood.

REGAL

Next we address the situation where n is so large that we cannot investigate all 1, 2, 3, 4, and m-SNP association patterns. Greedy Equivalent Search (GES) [62] learns from data a DAG model representing the generative probability distribution. Briefly, the algorithm starts with the empty DAG and greedily adds the edge to the DAG that increases the score the most until no edge increases the score. Then it greedily deletes the edge from the DAG such that the deletion increases the score the most until no deletion decreases the score. In the case of learning association patterns, it would first find the 1-SNP pattern with the highest score. Then it would repeatedly add SNPs that increased the score; finally, it would repeatedly delete SNPs that increased the score.

The GES algorithm will find the most concise DAG representing the probability distribution for a sufficiently large dataset if the composition property is satisfied [45], but this property is not satisfied in the case of pure, strict epistatic interactions [43]. One approach to addressing this problem is to do greedy search starting with every 1-SNP pattern rather than just the single highest scoring 1-SNP pattern. We called this algorithm Extended Greedy Approach to Learning (EGAL). If there are many SNPs, it is not computationally feasible to do a search starting with every 1-SNP pattern. So we first filter the SNPs by choosing the SNPs in the k highest scoring 1-SNP patterns with the following instruction:

Determine the set of Best _ SNPs of SNPs in the k highest scoring 1-SNP patterns;

An algorithm for EGAL follows. In this algorithm by score(A_i) we mean the BDeu score (Equation 2) of the association pattern containing the SNPs in A_i.

Algorithm EGAL

for each SNP SNP_i ∈ Best _ SNPs

A_i = {SNP_i};

do

if adding any SNP to A_i increases score(A_i)

add the SNP to A_i that increases score (A_i) the most;

while adding some SNP to A_i increases score (A_i)

do

if deleting any SNP from A_i increases score (A_i) the most

delete the SNP from A_i that increases score (A_i) the most;

while deleting some SNP from A_i increases score (A_i);

endfor;

report highest scoring set A_i taken over all i.

A difficulty with EGAL is that if there are several high-scoring SNPs, they may be the SNPs added to every 1-SNP pattern. So, two interacting SNPs could be missed. Our next algorithm repeatedly runs EGAL, and after each iteration removes the SNPs in the highest scoring pattern. We could do t iterations, or we could stop when the highest score is less than some threshold. We call this algorithm Repeated Extended Greedy Approach to Learning (REGAL). The following is the algorithm:

Algorithm REGAL

Learned _ SNPs =φ

Determine the set Best _ SNPs of SNPs in k highest scoring 1-SNP patterns;

repeat times

Using EGAL determine the highest scoring pattern M

obtained from SNPs in Best _ SNPs;

Insert the SNPs in M at the end of Learned _ SNPs;

Remove SNPs in M from Best _ SNPs;

endrepeat;

The output of REGAL is a set of SNPs called Learned _ SNPs which are candidates for being associated with the disease. The SNPs are ranked by the order in which they were discovered.

LEAP

Our complete system Learning and Evaluating Association Patterns (LEAP) combines REGAL and the BNPP. It first uses REGAL to heuristically search for a set of SNPs that are candidates for being associated with the disease. It then employs the BNPP to compute the probability of association patterns using SNPs in this subset. The following is an algorithm for LEAP. LEAP also computes the BNPP of all 1-SNP patterns since it is computationally feasible to do so.

Algorithm LEAP

Learn a set Learned _ SNPs of candidate SNPs using REGAL;

Compute the BNPP of all 1, 2, 3, 4,..., m-SNP patterns consisting of all

subsets of Learned _ SNPs;

Compute the BNPP of all 1-SNP patterns;

Report the association patterns ordered by the posterior probabilities.

The output of LEAP will be a set of association patterns, ordered by their posterior probabilities.

Results

We performed experiments evaluating LEAP using both simulated and real datasets. In all our experiments we used α=9 in the BDeu score, k = 1000 and t = 5 in REGAL, and m = 4 in the BNPP. All experiments were run using a Dell PowerEdge R515 which has an AMD Opteron™ 4276HE, 2.6GHz, 8C, Turbo CORE, 8M L2/ 8M L3, 1600Mhz Max Mem single processor and an additional AMD Opteron™ 4276HE, 2.6GHz, 8C, Turbo CORE, 8M L2/ 8M L3, 1600Mhz Max Mem processor.

Simulated Datasets

Chen et al. [44] generated 100 datasets based on two 2-SNP interactions, two 3-SNP interactions, and one 5-SNP interaction, making a total of 15 causative SNPs. The effects of the interactions were combined using a Noisy-OR model [45]. Each dataset concerned 1000 total SNPs, and contained 1000 cases and 1000 controls.

Using these datasets, we evaluate the two components, of LEAP, namely REGAL and the BNPP. We discuss each of these evaluations next.

REGAL Evaluation

REGAL performs the same task as other methods that learn association patterns¹ from data. That is, it learns a sequence of association patterns. Chen et al. [44] compared seven of these methods using the 100 1000 SNP simulated datasets discussed above. Those methods are MDR, FM, IG, BEAM, SH, LOR, and MECPM (See the Introduction Section for these initialisms). We compared REGAL's performance to the performance results Chen et al. [44] obtained for these 7 methods.

The methods were evaluated using the following power definition, which measures the frequency with which the interacting SNPs are ranked among the first K SNPs. For M interacting SNPs, the power is as follows:

$$Power\left(K\right)=\frac{1}{R\times M}\sum _{i=1}^R{x}_K\left(i\right)$$

where x_K (i) is the number of interacting SNPs appearing in the first K SNPs for the ith dataset, and R is the number of datasets. In our comparison experiments using the 100 1000 SNP datasets M = 15 and R = 100.

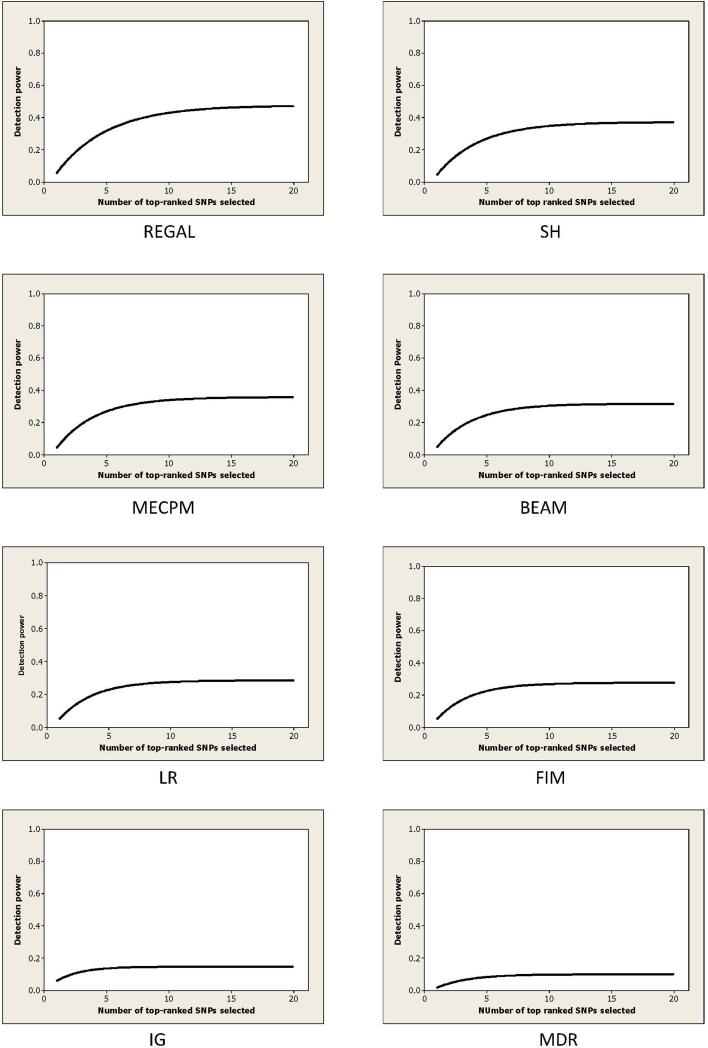
Figure 7 shows the results up to K = 20 for all 8 methods. REGAL exhibited the best performance according to this power measure.

Figure 7.

The detection power of 8 methods for the 15 SNPs when analyzing the 100 1000 SNP datasets is shown. The results for all methods other than REGAL were obtained from [41].

BNPP Evaluation

Next we discuss the results of applying the BNPP to the simulated datasets. Since no other method performs a task similar to the BNPP, we do not offer any comparison to other methods.

Recall that REGAL produces a set of SNPs called Learned _ SNPs. The BNPP then computes the posterior probability of all 1, 2, 3, and 4-SNP association patterns using SNPs in Learned _ SNPs, and also the posterior probability of all 1-SNP association patterns. Table II shows the output of the BNPP for one of the 100 1000 SNP datasets. We used the lower prior probabilities in Table I when calculating the BNPP. The SNPs labeled S1 through S15 are the ones involved in interactions. We call these SNPs the causal SNPs and the other 985 SNPs non-causal SNPs. Notice that many patterns containing causal SNPs have probability 1, and the first pattern containing a non-causal SNP has probability 0.0003. From these results, we can conclude that the probability is 1.0 that SNPs S6, S12, and S13 are associated with D, the probability is at least 0.992 that S8 is associated with D, the probability is at least 0.0004 that S11 is associated with D, and the probability is at least 0.0003 that S5 and S6 are each associated with D. So we have learned with high probability that four SNPs are associated with D.

Table II.

Sample output of the BNPP. For one of the 100 1000 SNP datasets, the most probable model up to the first model not including a causal SNP is shown. The posterior probabilities were computed using the BNPP and the lower prior probabilities in Table 1.

Causal Model	Posterior Probability
S6	1.0
S12	1.0
S13	1.0
S6, S12	1.0
S6, S13	1.0
S12, S13	1.0
S6, S12, S13	1.0
S6, S8	0.992
S6, S8, S13	0.980
S6, S8, S12	0.923
S6, S8, S12, S13	0.403
S6, S11	0.0004
S5, S6	0.0003
S6, S8, S31	0.0003

Note that, in general, we cannot conclude interactions from the BNPP analysis regardless of the order in which we learn patterns. One of the interactions used to generate the data is {S12,S13}, and this association pattern has probability 1. However, S12 and S13 each have probability 1 by themselves. Therefore, the association pattern consisting of both of them would also have probability 1 regardless of whether they are interacting or are independently affecting the disease. This means we cannot conclude from our analysis that S12 and S13 probably interact. Another interaction used to generate the data is {S6,S7,S8}. The pattern {S6,S8} has probability 0.992, while the probability of S6 by itself is only about 0.000001 (this is not shown in Table II). Therefore, we can conclude that S6 and S8 probably interact to affect D. So, sometimes with additional analysis we can learn interactions from the BNPP analysis.

Table III summarizes the information in Table II, taken over all 100 datasets. The average probability of the highest scoring model containing non-causal SNPs is only 0.055, whereas the average probability of the models preceding it is much higher at 0.772. However, this result does not fully illuminate the low probability of models containing non-causal SNPs. To further illustrate the low probability of models containing non-causal SNPs, Table IV shows true positive rates and false positive rates at three thresholds. If we require that a SNP be in a model with probability 1, we will identify almost 1/4 of the causal SNPs while never making a mistake. If we require that it be in a model with probability at least 0.006, we will identify almost 1/3 of the causal SNPs, while rarely making a mistake.

Table III.

Based on all the 100 1000 SNP datasets, the average probability of the most probable (best) model containing non-causal SNPs appears in Column 1. The average probability of the models preceding that model appears in Column 2. Column 3 shows the average total number of distinct SNPs in all the models preceding that model. The posterior probabilities were computed using the BNPP and the lower prior probabilities in Table 1.

Avg. Prob. of Best Model Containing Non-Causal SNPs	Avg. Prob. of Models Preceding Best Model Containing Non-Causal SNPs	Avg. Number of Causal SNPs in Models Preceding Best Model Containing Non-Causal SNPs
0.055 ± 0.219	0.772 ± 0.392	5.6 ± 1.075

Table IV.

Based on all 100 1000 SNP datasets, the true positive rate (sensitivity) and false =positive rate (1-specificity) at several thresholds are shown.

Threshold	True Positive Rate	False Positive Rate
1.0	0.234	0
0.5	0.273	0.00005
0.006	0.321	0.0001

Real Datasets

Reiman et al. [63] developed a GWAS late onset Alzheimer's disease (LOAD) data set that concerns data on 312,260 SNPs and contained records on 859 cases and 552 controls. Hunter et al. [64] conducted a GWAS concerning 546,646 SNPs and breast cancer as part of the National Cancer Institute Cancer Genetic Markers of Susceptibility (CGEMS) Project. The dataset consists of 1145 cases and 1142 controls. BRCA1 and BRCA2 are not included in this dataset because they are too rare to qualify. Furthermore, the study is in postmenopausal women, and these genes are known to be risk factors in premenopausal women. See http://cgems.cancer.gov/ concerning this dataset. We applied LEAP to both these real GWAS datasets.

LOAD Results

Table V shows the lower and upper posterior probabilities for the 10 most probable patterns learned from the LOAD dataset. We discuss each pattern in turn.

Table V.

Using the BNP and the low and high probabilities shown in Table 1, the posterior probabilities of the 10 most probable association patterns learned from the LOAD dataset are shown. The ranking in the far right column is according to the likelihood computed using the BDeu score.

	Model	Posterior Probability	Previous Load Assoc.	Rank of Lower Ranking SNP
1	APOE	(1.0, 1.0)	yes	1
2	rs41377151 (APOC1)	(1.0, 1.0)	yes	2
3	rs6784615 (NISCH)	(0.071, 0.434)	yes	3
4	APOE, rs6784615 (NISCH)	(0.041, 0.349)	yes	3
5	rs41377151 (APOC1), rs7355646	(0.035, 0.291)	no	1000
6	rs10824310 (PRKG1)	(0.034, 0.259)	yes	4
7	rs4356530	(0.024, 0.199)	yes	5
8	rs41377151 (APOC1), rs17126808 (PSD3)	(0.018, 0.163)	yes	18
9	rs41377151 (APOC1), rs16842422	(0.017, 0.152)	yes	26
10	rs41377151 (APOC1), rs383407	(0.015, 0.139)	no	56

The pattern containing only the APOE gene has posterior probability equal to 1.0. This gene is known to be the single most important risk factor for LOAD [63]. The pattern containing only SNP rs41377151 also has posterior probability equal to 1.0. This SNP is on the APOC1 gene, which is in strong linkage disequilibrium with APOE and for which previous studies have indicated that they predict LOAD equally well [65]. APOE and rs41377151, when considered together, had posterior probabilities of 1.25×10−4 and 1.25×10⁻⁵ for the lower and upper priors respectively. This result indicates that the model containing both loci is incorrect, and therefore that the two loci identify the same single causal mechanism of LOAD.

The third most probable pattern is the pattern containing only SNP rs6784615; it has upper posterior probability equal to 0.434. This SNP is on the NISCH gene, and previous research has associated this gene with LOAD [66]. The fourth most probable pattern contains APOE and rs6784615. Since these loci each individually have fairly high probability, this is not an indication of an interaction.

The fifth most probable contains SNP rs41377151 (APOC1) and SNP rs7355646; it has an upper posterior probably equal to 0.291. The pattern containing only SNP rs7355646 ranked 1000^th by likelihood and had an upper posterior probability equal to 6.84 ×10⁻⁵, which is of the same order of magnitude as its prior probability. Furthermore, no previous study has associated this SNP with LOAD. So this result is indicative of a possible interaction, and is a discovery first obtained in this study.

The sixth most probable pattern contains only SNP rs10824310, and previous research has linked this SNP to LOAD [67]. The seventh pattern contains only SNP rs4356530; this SNP has also been previously linked to LOAD [66].

The eighth most probable pattern contains SNP rs41377151 (APOC1) and SNP rs17126808, which is on the PSD3 gene. This SNP's likelihood ranks 18^th and its upper posterior probability is equal to 0. 027. Furthermore, previous research has linked this SNP to LOAD [68]. So this may not be indicative of an interaction. Similarly, the ninth most probable pattern contains SNP rs41377151 (APOC1) and SNP rs16842422. This SNP's likelihood ranks 26^th, its upper posterior probability is equal to 0. 019, and previous research has linked this SNP to LOAD [66]. So this also may not be indicative of an interaction.

Finally, the tenth most probable pattern contains SNP rs41377151 (APOC1) and SNP rs383407. This SNP's likelihood ranks 56^th, its upper posterior probability is equal to 0.003, and no research has linked this SNP to LOAD. So this may be indicative of an interaction, and is a finding first obtained in this study.

Breast Cancer Results

Table VI shows the 10 most probable patterns for the breast cancer datasets. The results are far less extensive for this dataset. The most probable models are all 1-SNP patterns, and no model has a high posterior probability. The model containing SNP rs10510126 has posterior probability equal to 0.03, which is substantially higher than that of the other models. Hunter et al. [64] also found this SNP to be most significant based on this dataset.

Table VI.

Using the BNP and the low and high probabilities shown in Table 1, the posterior probabilities of the 10 most probable association patterns learned from the breast cancer dataset are shown.

	Model	Posterior Probability	Previous BC Assoc.
1	rs10510126	(0.003, 0.03)	no
2	rs2107349	(0.0008, 0.008)	yes
3	rs17157903	(0.0007, 0.007)	yes
4	rs2420946 (FGFR2)	(0.0004, 0.004)	yes
5	rs12505080	0.0004, 0.004)	no
6	rs1219648 (FGFR2)	0.0004, 0.004)	yes
7	rs197275	0.0004, 0.004)	no
8	rs873811	0.0004, 0.004)	no
9	rs20779967	0.0004, 0.004)	no
10	rs7696175	0.0004, 0.004)	yes

Studies indicate thousands of genes may be associated with breast cancer [69]. So perhaps no single gene or small group of genes has a large posterior probability, which is what our results indicate.

Discussion

We developed LEAP, which learns probable SNP patterns associated with a disease from high-dimensional genomic datasets. LEAP consists of two components: REGAL, which mines likely SNPs from the datasets; and the BNPP which computes the posterior probability of patterns containing the mined SNPs. We compared REGAL to 7 other methods using genomic datasets, and in these comparisons REGAL performed best. We applied LEAP to real LOAD and breast cancer datasets. In the case of the LOAD dataset, we obtained a number of results substantiating previous findings, and two new results peculiar to this study. In the case of the breast cancer dataset we did not obtain extensive results. We conjecture that this may be due to the fact that thousands of loci affect breast cancer, and that no small group of loci has a very significant affect. In future research, we can run LEAP on this dataset using the first 10,000 SNPs and doing greedy search beyond 5 SNPs. This should take months, but could reveal more from the breast cancer dataset.

In general, our method does not determine whether a learned association pattern is an interaction. The most telling example of this appears in Table II where SNPs S12 and S13 each individually have probability one and the SNPs together have probability 1. However, sometimes a results can indicate an interaction. That is, if two SNPs together have high probability, and one of them individually does not have it, it is likely to be an interaction. An example of this is the pattern containing SNPs rs41377151 and rs7355646 in Table V.

However, once we learn an association pattern, we can investigate whether any of the SNPs in the association pattern interact using the information gain technique described in [70]. For example, if we want to investigate whether SNPs S1 and S2 interact, we compute information gain IG(S1; S2; D), which is as follows:

$$IG(S1;S2;D)=I(S1,S2;D)-I(S1;D)-I(S2;S).$$

where

$$I(S1;D)=H\left(D\right)-H(D\mid S1).$$

H(D) is the entropy of D, which is the measure of the uncertainty in D, and H(D|S1) is the conditional entropy of D given knowledge of SNP S1. If IG(S1; S2; D) is large, then an interaction is indicated because the two SNPs provide more information together than they do individually.