Linear Free Energy Relationships in RNA Transesterification: Theoretical Models to Aid Experimental Interpretations

Abstract

RNA cleavage transesterification is of fundamental reaction in biology that is catalyzed by both protein and RNA enzymes. In this work, a series of RNA transesterification model reactions with a wide range of leaving groups are investigated with density-functional calculations in an aqueous solvation environment in order to study linear free energy relationships (LFERs) and their connection to transition state structure and bonding. Overall, results obtained from the polarizable continuum solvation model with UAKS radii produce the best linear correlations and closest overall agreement with experimental results. Reactions with a poor leaving group are predicted to proceed via a stepwise mechanism with a late transition state that is rate controlling. As leaving group becomes more acidic and labile, the barriers of both early and late transition states decrease. LFERs for each transition state are computed, with the late transition state barrier showing greater sensitivity to leaving group pK_a. For sufficiently enhanced leaving groups, the reaction mechanism transits to a concerted mechanism characterized by a single early transition state. Further linear relationships were derived for bond lengths and bond orders as a function of leaving group pK_a and rate constant values that can be used for prediction. This work provides important benchmark linear free energy data that allows a molecular-level characterization of the structure and bonding of the transition states for this important class of phosphoryl transfer reactions. The relations reported herein can be used to aid in the interpretation of data obtained from experimental studies of non-catalytic and catalytic mechanisms.

Introduction

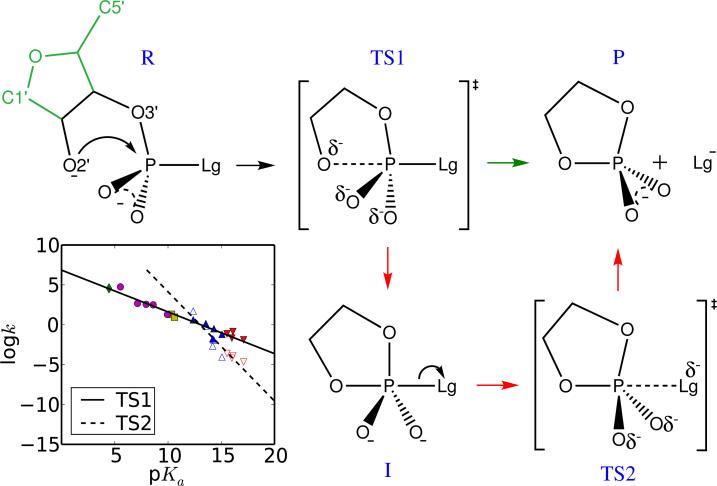
Cleavage of the phosphodiester bond of RNA¹ is a fundamental phosphoryl transfer reaction in biology² that is catalyzed by both protein enzymes such as RNase A,^3–5 and RNA enzymes such as the class of small self-cleaving nucleolytic ribozymes^6,7 that include the hammerhead,^8–10 hairpin,^11,12 hepatitis delta virus,^13–16 varkud satellite^17–19 and glmS^20–23 ribozymes. The first step in this reaction involves a cleavage transesterification whereby the 2^′-OH position on the RNA ribose ring becomes activated, and makes an in-line attack on the adjacent phosphate, proceeding through a pentavalent transition state or intermediate, and resulting in a 2^′,3^′-cyclic phosphate and a cleaved 5^′-leaving group (Scheme 1). Consequently, there is great interest in understanding the mechanisms whereby proteins and RNA enzymes are able to catalyze this reaction.

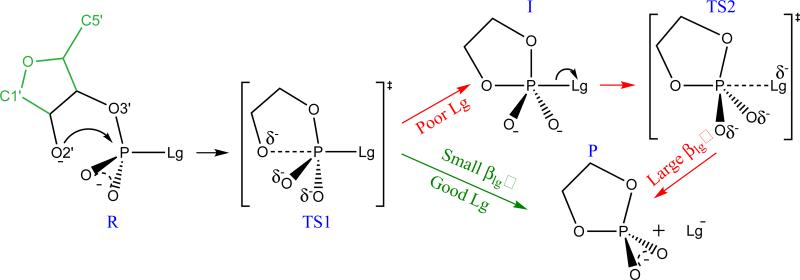
Scheme 1.

The mechanisms of RNA transesterification model reactions with different leaving groups (Lg⁻). R, TS1, I, TS2 and P stand for reactant, early transition state, intermediate, late transition state and product, respectively. Comparison of the RNA numbering scheme is shown in the leftmost frame (RNA atoms that are not present in the model reactions are indicated in green).

A powerful experimental method to study catalytic mechanism is to examine linear free energy relationships (LFERs) that provide insight into the nature of the transition state through examination of the sensitivity of the reaction rate constant (or equilibrium constant) to chemical modifications at key positions such as the nucleophile and leaving group.^24–32 For example, Brønsted coefficients have been utilized to estimate effective charge developed on the leaving group in the transition states and measure the effect of leaving group on the reaction rates.^29,33–37 The Leffler index^29,38–41 serves as an indicator of the extent of bond formation and bond fission in the transition state, and to locate its position along reaction coordinate. In this way, LFERs are used to make qualitative inferences about the nature of the transition state geometry, bonding and charge distribution.

The goal of this work is to establish a quantitative connection between LFER data and molecular structure and bonding relevant for RNA cleavage transesterification reactions. Toward this end, we have performed density-functional calculations for a set of RNA transesterification model reactions illustrated in Scheme 1, with different leaving groups shown in Scheme 2. The results are compared with available experimental data, and provide a detailed atomic level picture of mechanism. Further, relationships are established that allow prediction of bond lengths and bond orders in the rate controlling transition states that can be used to aid in the quantitative interpretation of LFERs in enzymes and ribozymes.

Scheme 2.

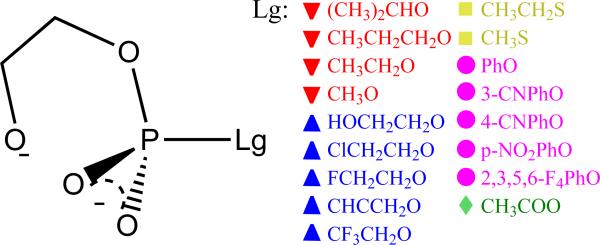
2-hydroxyethyl phosphate diester with various leaving groups (Lg⁻), color/shape coded into the following five general classes: alkoxide (red/down triangle), hetero-alkoxide (blue/up triangle), alkanethiolate (yellow/square), aryloxide (purple/circle) and carboxylate (green/diamond) anions.

Computational Methods

To explore the in-line mechanisms of RNA transesterification model reactions and analyze linear free energy relationships, stationary points (minima and transition states) along the reaction coordinate for the in-line mechanisms were identified using GAUSSIAN09⁴² suite of programs with the M06-2X⁴³ density-functional model and an ultrafine numerical integration grid (pruned from 99/590 radial/angular points). Geometry optimizations were carried out with the 6-31++G(d,p) basis set with default convergence criteria. Frequency analysis at the same theoretical level were performed to establish the nature of all the stationary points and to allow evaluation of thermodynamic quantities. Reaction pathways were verified with intrinsic reaction path calculations. Electronic energies for optimized geometries were further refined by single point calculation using the 6-311++G(3df,2p) basis set. This protocol for geometry optimization and energy refinement is designated herein by the abbreviated notation M06-2X/6-311++G(3df,2p)//M06-2X/6-31++G(d,p). Thermodynamic properties at 298.15K were obtained from the theoretical calculations using standard statistical mechanical expressions for separable vibrational, rotational and translational contributions in the canonical ensemble⁴⁴ and have been described in detail elsewhere.⁴⁵

Bond orders for bonds in the transition states were investigated using Natural Bond Order (NBO) analysis^46,47 at the same level of theory and basis set as for the geometry optimization. Calculated Wiberg bond orders are normalized by dividing 0.64, the Wiberg bond order calculated for a bridging P-O single bond in dimethyl phosphate (taken to be a fully formed P-O single bond).

Solvent effects are important in phosphoryl transfer reactions⁴⁸ and were examined using the same geometry optimization/energy refinement protocol, M06-2X/6-311++G(3df,2p)//M06-2X/6-31++G(d,p), as for the gas phase calculations, but with solvation effects included self-consistently and with full geometry optimization using the polarizable continuum model (PCM)^49,50 with two different sets of solvation radii (UFF⁵¹ and UAKS⁵²). The UFF radii is the default used in the Gaussian PCM solvation model, whereas the UAKS radii were optimized for use with Kohn-Sham density functional calculations at the PBE0/6-31G(d) level of theory.⁴² Our experience has been that the UAKS radii are generally reliable for stationary points that are stable minima, and fairly transferable to density-functional models that give similar densities (including the M06-2X functional used here, see for example references 53, 54). A limitation of the model in its current form, however, is that the radii do not necessarily adjust smoothly along the reaction path, and are not necessarily reliable for all transition states or transient intermediates. During the calculation, the default UAKS radii in the intermediates differed from those in the transition states. In order to make these radii consistent, we used an averaging strategy⁴⁸ whereby the radii of oxygen atoms connected to phosphorus in the intermediates were set to the average radii of oxygen atoms of the leaving group and nucleophile in the nearyby transition states. (see Supporting Information for details).

Results and Discussion

A series of RNA transesterification model reactions (Scheme 1) are herein studied with 17 different leaving groups (Scheme 2) that fall into the following five general classes: 1) alkoxide, 2) hetero-alkoxide, 3) alkanethiolate, 4) aryloxide and 5) carboxylate anions, and range from electron-donating poor leaving groups to electron-withdrawing enhanced leaving groups. In all of the model reactions studied here, the first step involves the association of the nucleophile - an intramolecular process that initiates formation of a five membered ring involving a pentavalent phosphorane species. There are two formal associative mechanisms that lead to the same products: a concerted mechanism that proceeds through a single transition state, and a stepwise mechanism that proceeds through two transition states that are separated by an intermediate. A concerted mechanism is described as either synchronous (having similar degrees of bonding to the nucleophile and leaving group in the transition state) or asynchronus (having differing degrees of bonding to the nucleophile and leaving group in the transition state). For either stepwise mechanisms or concerted asynchronus mechanisms, the transition states can further be designated as either “early” or “late”, depending on where along the reaction coordinate they occur. We denote a transition state as being “early” if it is characterized by a small degree of bond formation/cleavage with the nucleophile/leaving group, respectively. Conversely, a “late” transition state involves a nearly fully formed bond with the nucleophile and a nearly cleaved bond with the leaving group. For the “enhanced” leaving groups (with pK_a values less than ≈ 13) considered here, the mechanisms are concerted asynchronous and proceed through an early transition state (TS1). Alternatively, for relatively poor leaving groups (with pK_a values greater than ≈ 13) the mechanisms are stepwise and proceed through both early and late transition states (TS1 and TS2, respectively) separated by a shallow metastable intermediate (I). As described in detail below, early and late refer to the location of the transition state along a reaction coordinate that involves the difference in leaving group and nucleophile distances with the reactive phosphorus (negative and positive reaction coordinate values indicate early and late transition states, respectively).

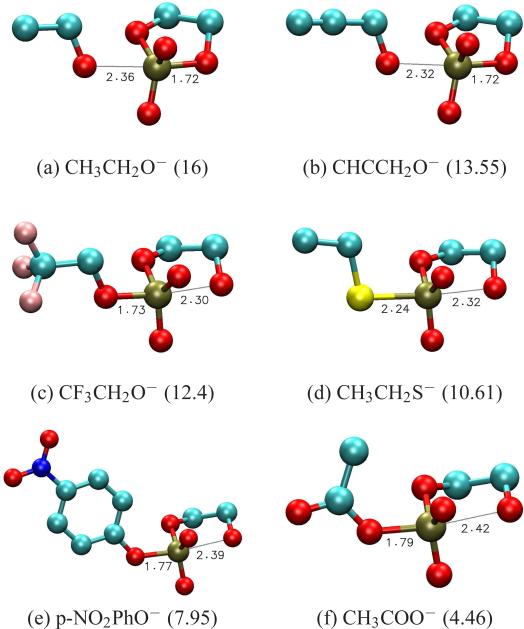
Representative examples of rate-limiting transition states for each of these leaving group classes are presented in Figure 1. Free energies of transition states, intermediates and products relative to reactants of model reactions, calculated using both UFF and UAKS solvation radii, are listed in Table 1 along with experimental pK_as of the leaving group conjugate acids in water at 25°C. Activation free energies for rate-limiting transition states of model reactions calculated at 25° and 80° are presented in Table 3 together with available experimental barriers.

Figure 1.

Structures of representative rate-limiting transition states for model reactions. Leaving groups (Lg⁻) and the pK_as associated with their conjugate acids (LgH) are indicated immediately below the structures.

Table 1.

Free energies (kcal/mol) of transition states (ΔG^≠), intermediates (ΔG_i) and products (ΔG) relative to reactants in RNA transesterification model reactions (Scheme 1) with different leaving groups as well as their experimental pK_as in water at 25°C.

	UFF				UAKS				Expt. pKa
Leaving Group	$\Delta G_1^{\ne }$	Δ Gi	$\Delta G_2^{\ne }$	Δ G	$\Delta G_1^{\ne }$	Δ Gi	$\Delta G_2^{\ne }$	Δ G
(CH3)2CHO–	20.26	20.25	25.96	−1.56	20.03	17.66	23.82	−10.95	17.1
CH3CH2CH2O–	18.94	19.11	24.26	−1.40	18.61	15.61	22.73	−9.40	16.1
CH3CH2O–	20.25	20.19	25.84	−0.04	19.73	16.80	23.17	−7.55	16
CH3O–	18.96	19.07	24.43	−0.59	19.00	15.94	22.36	−6.51	15.54
HOCH2CH2O–	18.25	16.61	19.64	−6.44	19.10	17.01	22.99	−12.68	15.07
ClCH2CH2O–	17.23	16.03	18.55	−6.94	18.13	15.44	20.08	−19.23	14.31
FCH2CH2O–	17.72	16.52	20.11	−5.52	19.88	5.67	21.08	−17.44	14.2
CHCCH2O–	16.85	15.27	17.75	−7.40	17.27	13.85	17.66	−16.66	13.55
CF3CH2O–	15.87	12.49	13.59	−11.28	16.62	11.91	15.11	−21.17	12.37
CH3CH2S–	14.42	· · ·	· · ·	−33.36	16.17	· · ·	· · ·	−30.04	10.61
CH3S–	14.94	· · ·	· · ·	−32.68	15.67	· · ·	· · ·	−29.45	10.33
PhO–	14.76	· · ·	· · ·	−23.07	15.70	· · ·	· · ·	−23.59	9.95
3-CNPhO–	13.87	· · ·	· · ·	−26.92	14.05	· · ·	· · ·	−28.18	8.61
4-CNPhO–	12.62	· · ·	· · ·	−30.50	13.96	· · ·	· · ·	−29.78	7.95
p-NO2PhO–	11.99	· · ·	· · ·	−32.69	13.80	· · ·	· · ·	−30.65	7.14
2,3,5,6-F4PhO–	10.96	· · ·	· · ·	−36.10	10.97	· · ·	· · ·	−37.23	5.53
CH3COO–	11.91	· · ·	· · ·	−32.87	11.22	· · ·	· · ·	−34.95	4.46

$\Delta G_1^{\ne }$ and $\Delta G_2^{\ne }$ are free energy barriers of early and late transition states (TS1 and TS2), respectively. All the experimental pK_as are taken from IUPAC chemical data series (No. 23),⁷¹ except those of ethylene glycol and 2,3,5,6-tetrafluorophenol, which are taken from the CRC Handbook⁷² and Bourne et al.,⁷³ respectively. The pK_a values of ethylene glycol and acetic acid have been corrected for statistical factors by adding log(p/q), where p and q are the number of reactive positions available in the acid and in the base, respectively.^58,74

Table 3.

Calculated and estimated experimental activation free energies ΔG^≠ (kcal/mol) for RNA transesterification model reactions with different leaving groups (Scheme 1). Experimental estimates were obtained from reaction rate constants using the Eyring equation.⁷⁷

	Calc. ΔG≠				Expt.a ΔG≠
	UFF		UAKS		PRPpOR	UpOR	UpOR	GpOR
Leaving Group	25°C	80°C	25°C	80°C	80°C	25°C	65°C	35°C
(CH3)2CHO–	25.96	26.36	23.82	24.15	30.76	26.01	-	-
CH3CH2CH2O–	24.26	24.52	22.73	23.00	-	-	-	-
CH3CH2O–	25.84	26.37	23.17	23.56	28.55	23.37	25.30	-
CH3O–	24.43	24.75	22.36	22.67	27.09	-	-	-
HOCH2CH2O–	19.64	20.10	22.99	23.52	26.66	-	-	-
ClCH2CH2O–	18.55	18.92	20.08	20.67	-	20.64	-	-
FCH2CH2O–	20.11	20.51	21.08	21.75	-	-	-	-
CHCCH2O–	17.75	18.23	17.66	18.11	-	-	-	-
CF3CH2O–	15.87	16.37	16.62	17.14	-	-	-	-
CH3CH2S–	14.42	14.64	16.17	16.46	-	-	-	-
CH3S–	14.94	15.32	15.67	15.94	-	-	-	-
PhO–	14.76	15.14	15.70	16.24	22.62	15.98	-	24.22
3-CNPhO–	13.87	14.42	14.05	14.53	-	-	-	-
4-CNPhO–	12.62	13.03	13.96	14.55	-	-	-	-
p-NO2PhO–	11.99	12.41	13.80	14.50	20.12	13.46	-	22.81
2,3,5,6-F4PhO–	10.96	11.38	10.97	11.39	-	-		-
CH3COO–	11.91	12.31	11.22	11.58	-	-	-	-

^aExperimental model systems are for the cyclization reaction of 2-hydroxypropyl phosphate (PRP-pOR),⁵⁸ uridine 3′-phosphate (UpOR)^33,56,75 and guanosine 3′-phosphate (GpOR).⁷⁶

In this work, we consider three following Brønsted-type correlations^24,25

$${\beta }_{lg}^1=\partial log{k}^1∕\partial \mathrm{p}{K}_{\mathrm{a}}$$ (1)

$${\beta }_{lg}^2=\partial log{k}^2∕\partial \mathrm{p}{K}_{\mathrm{a}}$$ (2)

$${\beta }_{eq}=\partial log{K}_{eq}∕\partial \mathrm{p}{K}_{\mathrm{a}}$$ (3)

where k¹ and k² are the rate constants estimated from the free energy barriers for TS1 and TS2, respectively, K_eq is the equilibrium constant estimated from the reaction free energy, and pK_a refers to the leaving group conjugate acid (LgH). Also of interest is the so-called Leffler index³⁸ (α_fission) which is defined as a ratio between the Brønsted correlations as

$${\alpha }_{fission}=\partial \log k∕\partial \log K_{eq}={\beta }_{lg}∕{\beta }_{eq}$$ (4)

where β_lg and k are the Brønsted correlation and the rate constant, respectively, for the rate-controlling transition state.

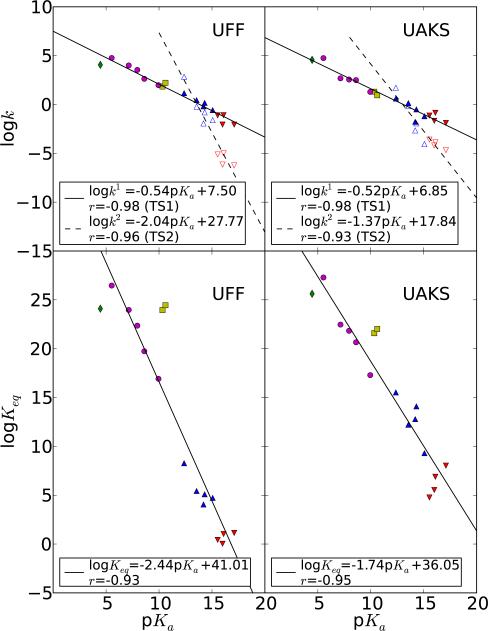
The calculated Brønsted correlations ${\beta }_{lg}^1$, ${\beta }_{lg}^2$ and β_eq are plotted in Figure 2 for both UFF and UAKS solvation radii. The β_lg values from available experiments are summarized in Table 2, together with our calculated β_lg at 25° and 80° for comparison. Finally, we examine correlations between bond lengths or bond orders and logk or pK_a values in Figures 3 and 4, respectively. All quantitative correlation relationships have been collected and are compiled in a single table (Table 4) for reference.

Figure 2.

Linear free energy relationships between calculated logarithmic rate constants (logk¹ and logk²) and experimental pK_as of leaving groups (top) and between calculated logarithmic equilibrium constants (logK_eq) and experimental pK s of leaving 1 a groups (bottom). k and k² are calculated rate constants for early and late transition states (TS1 and TS2), respectively. Rate constants are obtained from density-functional calculations with PCM solvation model and UFF (left) and UAKS (right) radii. Red down triangle, blue up triangle, yellow square, purple round and green diamond symbols correspond to alkyl, hetero-alkyl, thio, phenyl and acid leaving groups, respectively. Filled and empty symbols stand for TS1 and TS2, respectively. Regression parameters for logk¹, logk² and logK_eq are given as well as linear correlation coefficient for r.

Table 2.

Brønsted coefficients, β_lg, from experiments and calculation. The experimental coefficients, ${\beta }_{lg}^1$ and ${\beta }_{lg}^2$ were measured for transesterification reactions with aryl and alkyl leaving groups, respectively. The calculated coefficients, ${\beta }_{lg}^1$ and ${\beta }_{lg}^2$ were determined from theoretical rates derived from early and late transition states (TS1 and TS2), respectively, of the series of model reactions described in Scheme 1-2.

	Model System	${\beta }_{lg}^1$	${\beta }_{lg}^2$	β eq	Temp (°C)	Ref./Model
Expt.	Uridine 3′-phosphate	−0.54	−1.28	· · ·	25	33,56
	Uridine 3′-phosphate	−0.52	−1.34	· · ·	25	55
	Uridine 3′-phosphate	· · ·	−1.10	· · ·	65	75
	2-hydroxypropyl phosphatea	−0.52	−1.09	· · ·	80	58,55
	Guanosine 3′-phosphate	−0.38	· · ·	· · ·	35	76
	Phosphono monoanion	· · ·	· · ·	−1.74	25	57
Calc.	2-hydroxyethyl phosphate	−0.54	−2.04	−2.44	25	UFF
	2-hydroxyethyl phosphate	−0.54	−2.03	−2.44	80	UFF
	2-hydroxyethyl phosphate	−0.52	−1.37	−1.74	25	UAKS
	2-hydroxyethyl phosphate	−0.52	−1.32	−1.74	80	UAKS

^aLinear Brønsted correlation coefficients (${\beta }_{lg}^1$ and ${\beta }_{lg}^2$) were calculated from limited data⁵⁸ using adjusted pK_a values,⁵⁵ and may not be statistically reliable.

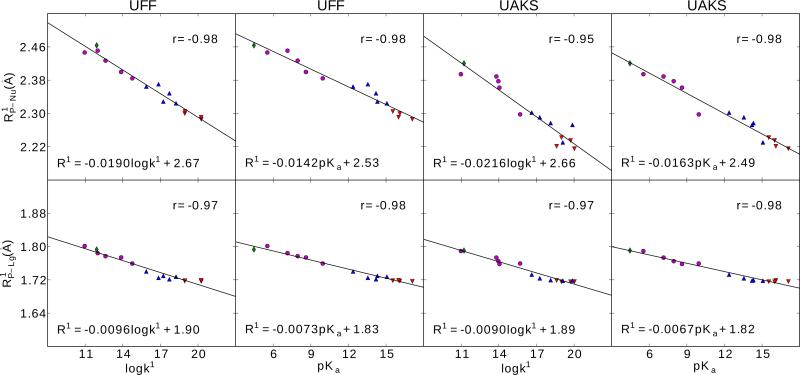
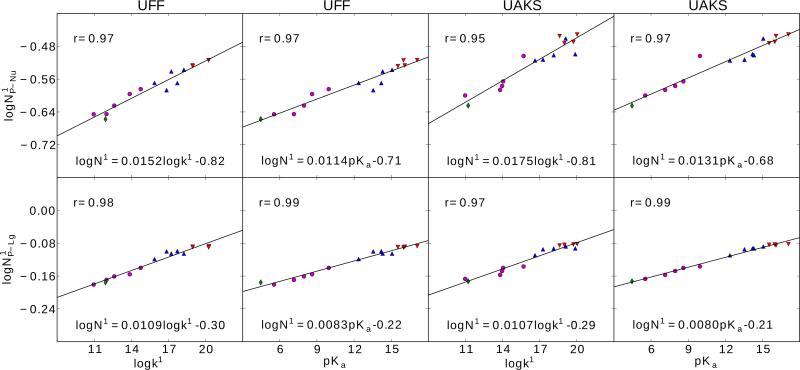
Figure 3.

Linear relationships between bond lengths ($R_{\mathrm{P}-\mathrm{Nu}}^1$ and $R_{\mathrm{P}-\mathrm{Lg}}^1$ P-Nu P-Lg, Å) of early transition states (TS1) and the corresponding calculated rate constants (logk¹) and experimental pK_as of leaving groups. The calculation were performed using density-functional method with PCM solvation model and UFF (left) and UAKS (right) radii. Red down triangle, blue up triangle, purple round and green diamond symbols correspond to alkyl, hetero-alkyl, phenyl and acid leaving groups, respectively. Regression parameters for R¹ are given as well as linear correlation coefficient for r.

Figure 4.

Linear relationships between logarithmic bond orders ($\log N_{\mathrm{P}-\mathrm{Nu}}^1$ and $\log N_{\mathrm{P}-\mathrm{Lg}}^1$) of early transition states (TS1) and the corresponding rate constants (logk¹) and experimental pK_as of leaving groups. The calculation were performed using density-functional method with PCM solvation model and UFF (left) and UAKS (right) radii. Red down triangle, blue up triangle, purple round and green diamond symbols correspond to alkyl, hetero-alkyl, phenyl and acid leaving groups, respectively. Regression parameters for logN¹ are given as well as linear correlation coefficient for r.

Table 4.

All the linear relationships discovered in RNA transesterification model reactions.

Model	y	x	m	b	r
UFF	logk1	pKa	−0.54	7.50	−0.98
	logk2	pKa	−2.04	27.77	−0.96
	logKeq	pKa	−2.44	41.01	−0.93
	$R_{\mathrm{P}-\mathrm{Nu}}^1$	logk1	−0.0190	2.67	−0.98
	$R_{\mathrm{P}-\mathrm{Nu}}^1$	pKa	−0.0142	2.53	−0.98
	$R_{\mathrm{P}-\mathrm{Lg}}^1$	logk1	−0.0096	1.90	−0.97
	$R_{\mathrm{P}-\mathrm{Lg}}^1$	pKa	−0.0073	1.83	−0.98
	$N_{\mathrm{P}-\mathrm{Nu}}^1$	logk1	0.0152	−0.82	0.97
	$N_{\mathrm{P}-\mathrm{Nu}}^1$	pKa	0.0114	−0.71	0.97
	$N_{\mathrm{P}-\mathrm{Lg}}^1$	logk1	0.0109	−0.30	0.98
	$N_{\mathrm{P}-\mathrm{Lg}}^1$	pKa	0.0083	−0.22	0.99
UAKS	logk1	pKa	−0.52	6.85	−0.98
	logk2	pKa	−1.37	17.84	−0.93
	logKeq	pKa	−1.74	36.05	−0.95
	$R_{\mathrm{P}-\mathrm{Nu}}^1$	logk1	−0.0216	2.66	−0.95
	$R_{\mathrm{P}-\mathrm{Nu}}^1$	pKa	−0.0163	2.50	−0.98
	$R_{\mathrm{P}-\mathrm{Lg}}^1$	logk1	−0.0090	1.89	−0.97
	$R_{\mathrm{P}-\mathrm{Lg}}^1$	pKa	−0.0067	1.82	−0.98
	$N_{\mathrm{P}-\mathrm{Nu}}^1$	logk1	0.0175	−0.81	0.95
	$N_{\mathrm{P}-\mathrm{Nu}}^1$	pKa	0.0131	−0.68	0.97
	$N_{\mathrm{P}-\mathrm{Lg}}^1$	logk1	0.0107	−0.29	0.97
	$N_{\mathrm{P}-\mathrm{Lg}}^1$	pKa	0.0080	−0.21	0.99

These linear relationships are characterized by a linear equation, y=mx+b, together with the corresponding correlation coefficients, r. The unit of bond length R is Angstrom (Å).

Experimental Reference Data

Several model reactions with various aryl and alkyl leaving groups have been investigated experimentally at different temperatures to analyze LFERs of RNA transesterification; the measured Brønsted coefficients are shown in Table 2. Lönnberg et al.⁵⁵ analyzed original measured kinetic data^33,56 of uridine 3^′-phosphate diester cleavage and derived a non-linear Brønsted correlation with a convex break at pK_a of 12.58; two significantly different Brønsted values (${\beta }_{lg}^1$ and ${\beta }_{lg}^2$) of -0.52 and -1.34 were obtained for model reactions with aryl and alkyl leaving groups, respectively. The reference β_eq value of -1.74 is taken from phosphoryl transfer of phosphono monoanion;⁵⁷ the β_eq value has been widely used as an estimation for β_eq of RNA transesterification model reactions.^2,33

It should be mentioned that the experimental model system in Table 2 that is closest in structure to the system examined in the present computational work is 2-hydroxypropyl phosphate diester.⁵⁸ This data was analyzed⁵⁵ by fitting to a non-linear Brønsted correlation model, although the authors note that the data was not sufficient to obtain definitive Brønsted parameters. Nonetheless, the break in the Brønsted plot appears to occur at a higher pK_a value than that measured for uridine 3^′-phosphate diester cleavage^33,56 and predicted from the present calculations on a very similar model system.

Comparison of Brønsted Coefficients

Calculated and experimental activation free energies for rate-limiting transition states are listed in Table 3. The barrier differences between UFF and UAKS calculations are on average 0.25±1.58 and 0.29±1.66 kcal/mol at 25°C and 80°C, respectively. UFF and UAKS barriers are on average 5.05±2.46 and 5.13±1.43 kcal/mol lower than experimental values at 80° for cyclization of 2-hydroxypropyl phosphate diesters. The calculated barriers are generally closer to the experimental values for the transesterification of uridine 3^′-phosphates (mean signed error of 0.47±1.80 and 0.58±0.96 kcal/mol for UFF and UAKS radii, respectively).

Linear relationships between calculated logarithmic rate constants for each transition state (TS1 and TS2) and the experimental pK_a of leaving groups are illustrated in Figure 2. Linear correlations from both UFF and UAKS solvation radii were overall similar, with correlation coefficients ranging in magnitude between 0.93 and 0.98. The ${\beta }_{lg}^1$ values predicted by UFF and UAKS (-0.54 and -0.52, respectively) are in close agreement with each other, whereas the ${\beta }_{lg}^2$ (-2.04 and -1.37, respectively) and β_eq (-2.44 and -1.74, respectively) values show greater variation. As expected, the ${\beta }_{lg}^2$ values are considerably greater than for ${\beta }_{lg}^1$, illustrating the increased sensitivity of the late transition state TS2 to nature of the leaving group. The sulfur-containing leaving groups appear as outliers for fits of logK_eq, particularly for the UFF model, due largely to overstabilization of the thiolate anion in solution by these models.

The LFER results from the UAKS radii are in excellent agreement with available experimental values for similar reactions. Calculated and experimental values for ${\beta }_{lg}^1$, ${\beta }_{lg}^2$ and β_eq are compared in Table 2. The ${\beta }_{lg}^1$ value for predicted by both UFF and UAKS (-0.54 and -0.52, respectively) are in close agreement with experimental value (-0.52) for the hydroxide-ion catalyzed transesterifications of uridine 3^′-phosphates with good leaving groups.⁵⁵ The ${\beta }_{lg}^2$ value predicted from the UAKS radii (-1.37), also agrees well with the experimental value of -1.34 for uridine 3^′-phosphates with poor leaving groups.⁵⁵ The UAKS value for β_eq (-1.74) is in excellent agreement with the value measured for the phosphono monoanion transfer reaction.⁵⁷

Another important quantity to analyze is the break point in the LFERs corresponding to TS1 and TS2 derive; i.e., the intersection of the fitted lines for ${\beta }_{lg}^1$ and ${\beta }_{lg}^2$. The break point predicted from the calculation with UAKS radii is 12.98, which is close to the analogous experimentally predicted value of 12.58.⁵⁵ The calculated value also falls within the range of the experimental pK_a values for the 2^′-hydroxyl group in uridine 3^′-phosphate ethyl ester (12.85),⁵⁹ and for the 2^′-hydroxyl group in chimeric oligonucleotide (13.1).⁶⁰

Overall, the UFF radii are in poorer quantitative agreement with experiment. This is not terribly surprising since the UAKS model radii were optimized to reproduce solvation free energies when used with density functional methods, having been developed using PBE0/6-31G(d) parameterization level.⁴² Nonetheless, the very close alignment of the UAKS results with experiments provides support for the supposition that one can use this model as a basis from which to determine reaction mechanism, and make a quantitative connection between experimental data and transition state geometry and bonding. These connections will be the focus of the following sections.

Reaction Mechanism

The results in Figures 1 and 2 illustrate that leaving groups have strong impact on the mechanisms of model reactions. Table 1 lists the calculated relative free energies of transition states, intermediates and products relative to reactants for both UAKS and UFF radii models, as well as the experimental pK_a values for the leaving groups.

The pK_a values listed in the table and discussed herein correspond to the equilibrium

$$\mathrm{LgH}\left(aq\right)\rightleftharpoons {\mathrm{Lg}}^{-}\left(aq\right)+{\mathrm{H}}^{+}\left(aq\right)$$ (5)

where the leaving group anion is Lg⁻(aq). Consequently, decreasing pK_a indicates a shift in the equilibrium so as to favor the state where the Lg-H bond is broken leading to the Lg⁻(aq) species. Decreasing leaving group pK_a is thus expected to be correlated with the transesterification reaction free energy, since the reaction product involves a similar state whereby a Lg-P bond is broken leading to the Lg⁻(aq) species. Indeed, we observe that the reaction free energies in Table 1, ΔG, generally trend toward more negative values with decreasing leaving group pK_a. Stability of the anion leaving group depends on its ability to electronically withdraw electron density up to a full -1 charge, and its solvation free energy. Hence, high pK_a values correspond to poor leaving groups, and low pK_a values correspond to good (enhanced) leaving groups.

As is typical for phosphoryl transfer reactions of phosphate diesters,² all of the transition states predicted here are associative in nature, meaning that the approach of the nucleophile to the phosphorus generally precedes cleavage of the bond to the leaving group. For the purposes of discussion, therefore, we introduce a coordinate, ζ , that describes the overall reaction progression as the difference in leaving group and nucleophile bond distances to phosphorus, i.e., ζ = R_P−Lg−R_P−Nu. With this definition of reaction coordinate, ζ for reactant and product states would have large negative and positive values, respectively. Referring to Scheme 1, the ζ value for the “early” transition state (TS1) would have a small negative value, whereas the “late” transition state (TS2) would have a small positive ζ value, and the intermediate (I) would have a near zero value. Here by “large”, “small” and “near zero” we mean that magnitudes are roughly greater than 1 Å, between 1 and 0.5 Å, and less than 0.5 Å, respectively.

If the reaction is native transesterification where the nucleophile and leaving group have similar pK_a values, the reaction will proceed through both an early and a late transition states, separated by a shallow, metastable intermediate.⁶¹ For a dianionic transition state, the intermediate is high in energy,⁶² and not sufficiently long lived⁵⁵ to undergo pseudorotation.^63,64 The UAKS results shown in Table 1 which are in good agreement with available experimental data indicate that the barriers to decomposition of the intermediates are fairly small (on average 3.00±0.58 kcal/mol). For reactions involving leaving groups that have comparable pK_a values to that of the nucleophile, the two transition states are expected to be somewhat similar in energy. However, the endocyclic bond between the nucleophile and phosphorus must also take into account some degree of strain energy to form a five-membered ring in the pentavalent transition state, although this is expected to be quite small. More significant is that cleavage of the exocyclic bond results in a considerably more strained tetravalent phosphorus species which is higher in energy. These effects have been discussed in detail elsewhere.^65–67 In addition to ring strain, differential solvation effects^62,68,69 of the acyclic reactant and cyclic product states also play a role. The overall result, for this series of reactions, is that for stepwise mechanisms (e.g., with poor leaving groups having high pK_a values), cleavage of the exocyclic bond (TS2) is typically rate controlling except the case that trifluoroethoxide serves as a leaving group where the barrier of TS1 is just slightly higher than that of TS2 by 1.51 kcal/mol. It should be noted that the present series of model reactions differ from native RNA transesterification reactions in that 1) the nucleophile of the former (a primary alcohol) has a higher pK_a value than the secondary 2^′OH group of the latter, and 2) the strain energy of ring formation is expected to differ due to coupling of the second ribose ring in the case of RNA.

The trends in reactivity modeled by the LFERs, and the ultimate shift in mechanism from a stepwise pathway involving a rate-controlling late (TS2) transition state to a concerted pathway with a single early (TS1) transition state, can be easily understood through consideration of the Hammond effect.^24,70 As the pK_a of the leaving group decreases, the reaction equilibrium favors the product state that contains the solvated anionic leaving group. As a consequence, the TS2 barrier height becomes lower, and shifts away from the products (i.e., toward less positive ζ values). Since chemical modification of the leaving group has a direct and profound effect on the stability of the exocyclic chemical bond to phosphorus, the cleavage of which is characteristic of the rate-controlling TS2, we expect ${\beta }_{lg}^2$ to have a large magnitude, indicating that the reaction rate is highly sensitive to modifications of the leaving group.

At some point, as the pK_a of the leaving group becomes lower, the shift and lowering of TS2 is such that it becomes only a decaying shoulder in the reaction profile and ultimately vanishes. This causes the reaction to revert to a single-step mechanism with only an early transition state (TS1) corresponding to formation of the endocyclic bond between the nucleophile and phosphorus. At this point a convex break point in the LFERs occurs, and for reactions involving leaving groups with pK_a values lower than the break point, the value of ${\beta }_{lg}^1$ is smaller in magnitude than ${\beta }_{lg}^2$, reflecting a diminished sensitivity to variation of the leaving group. Indeed, the ${\beta }_{lg}^2$ is more than 2.5 times larger than ${\beta }_{lg}^1$, which suggests Brønsted coefficients are useful indexes to identify mechanisms of RNA transesterification reactions. The mechanism predicted from our calculations is consistent with the interpretation of experimental data of Davis et al.³³ and Kosonen et al.⁵⁶ on transesterification of uridine 3^′-phosphate diesters. The computational results presented here indicate, for the series of model reactions considered, sufficiently enhanced leaving groups lead to concerted mechanisms that all proceed through a single early TS, and LFER analysis predicts a β_lg value with a small magnitude. For less enhanced and poor leaving groups, mechanisms are stepwise, and in almost all cases the rate-controlling transition state is late, leading to a large negative β_lg value.

Further support for the supposition that the rate-limiting transition states for transesterification of uridine 3^′-phosphate diesters with good leaving groups should be early (TS1) is given by calculation of the Leffler index,^2,38 α_fission. The α_fission = β_lg/β_eq=0.30, where the β_lg value of -0.52 is used.⁵⁵ The α_fission value is consistent with the average bond order of breaking P-Lg bond in early transition state from calculation with UAKS radii, 0.31.

Transition State Structure and Bonding

Experimental measurement of LFERs provides insight into mechanism, and qualitative inferences can be made with regard to characterization of the transition state. Theoretical calculations, on the other hand, can provide detailed information about the structure and bonding in the transition state. Of course, in order for this detailed information to be useful, the theoretical models must be sufficiently validated with respect to experiment. We have demonstrated that the present electronic structure calculations and PCM solvation model with UAKS radii agree well with available experiments on similar RNA transesterification model reactions. Consequently, we may proceed to derive relations that allow the prediction of structure and bonding in the transition state based on these results.

Calculated bond length (R) and bond order (N) results for the forming (P-Nu) bond and breaking (P-Lg) bond for both TS1 and TS2 are listed in Supporting Information. Linear relationships have been identified between these bond quantities and the calculated logarithmic rate constants or experimental leaving group pK_a values. These correlations are illustrated in Figures 3-4 and the regression values, along with linear correlation coefficients, are listed in Table 4 and can be used for prediction. Analogous correlations for TS2 were not evident from the calculations. Nonetheless, we were able to reasonably relate the bond lengths and bond orders in the transition states for this reaction with a simple 3-parameter exponential model:

$$N\left(R\right)=A{e}^{(B-R)∕C}$$ (6)

where R is the P-Nu or P-Lg bond length (Å) in the transition state, and the fitted parameters are A=0.94, B=1.64 Å and C=0.56 Å. This relation allows one to infer transition state bonding from geometry or visa versa. Plots of these relations are given in Supporting Information. The rich bonding information for the rating-limiting transition state is not otherwise quantitatively interpretable from Leffler indices.²

Conclusions

Herein a series of RNA transesterification model reactions with a wide range of leaving groups have been investigated with density-functional calculations in an aqueous solvation environment modeled with two different sets of solvation radii (UFF and UAKS). Linear free energy relationships are derived from the calculations for both early and late transition states. Results using the UAKS radii agree closely with available experiments, and provide a model from which quantitative information about transition state structure and bonding can be derived. Depending on the nature of the leaving group, reactions may proceed via a stepwise mechanism that passes through both an early and late transition states separated by a transient intermediate, or through a single early transition state. Brønsted correlations, ${\beta }_{lg}^1$ and ${\beta }_{lg}^2$ can be used to distinguish these two mechanisms. Further correlations are derived that connect transition state bond lengths and bond orders with experimental reaction rate constants and leaving group pK_a values, and between transition state bond lengths and bond orders. Together, these results provide models from which to aid in the interpretation of experimental LFER data, and make predictions about RNA cleavage transesterification reactions catalyzed by proteins and RNA enzymes.

Figure 5.

For Table of Contents Only. Depending on the nature of the leaving group, reactions may proceed via a stepwise mechanism or through a single early TS1. Brønsted correlations can be used to distinguish these two mechanisms.