Abstract
Because of the time and expense required to obtain clinical outcomes of interest, such as functional limitations or death, clinical trials often focus the effects of treatment on earlier and more easily obtained surrogate markers. Preliminary work to define surrogates focused on the fraction of a treatment effect “explained” by a marker in a regression model, but as notions of causality have been formalized in the statistical setting, formal definitions of high-quality surrogate markers have been developed in the causal inference framework, using either the “causal effect” or “causal association” settings. In the causal effect setting, high-quality surrogate markers have a large fraction of the total treatment effect explained by the effect of the treatment on the marker net of the treatment on the outcome. In the causal association setting, high-quality surrogate markers have large treatment effects on the outcome when there are large treatment effects on the marker, and small effects on the outcome when there are small effects on the marker. A particularly important feature of a surrogate marker is that the direction of a treatment effect be the same for both the marker and the outcome. Settings in which the marker and outcome are positively associated but the marker and outcome have beneficial and harmful or harmful and beneficial treatment effects, respectively, have been referred to as “surrogate paradoxes”. If this outcome always occurs, it is not problematic; however, as correlations among the outcome, marker, and their treatment effects weaken, it may occur for some trials and not for others, leading to potentially incorrect conclusions, and real-life examples that shortened thousands of lives are unfortunately available. We propose measures for assessing the risk of the surrogate paradox using the meta-analytic causal association framework, which allows us to focus on the probability that a given treatment will yield treatment effect in different directions between the marker and the outcome, and to determine the size of a beneficial effect of the treatment on the marker required to minimize the risk of a harmful effect of the treatment on the outcome. We provide simulations and consider two applications.
Keywords: Causal inference: Surrogate marker, Surrogate paradox
1. Introduction
In order to reduce costs and speed clinical research, determining good surrogate markers for clinical outcomes is of increasing interest. “Good” surrogate markers essentially allow one to understand how a given treatment would impact an outcome, but in a less expensive and more timely fashion. Examples include CD4 counts in blood as a marker for AIDS morbidity and mortality, blood pressure as a marker for risk of heart attack, and tumor progression as a marker for survival in cancer. Prentice (1989) provided one of the first formalized approaches. He suggested that good surrogates would have the property of being highly related to the outcome, and, when put into a regression model with treatment, would eliminate the coefficient associated with the treatment. When formulated in a causal inference setting, a shortcoming of this approach is that it implicitly assumes no confounders between the marker and the outcome, which cannot be guaranteed in most settings even if treatment is randomized, since the marker is observed post-treatment. Hence, two major approaches have been developed to assess surrogates in a causal framework, termed by Joffe and Greene (2009) “causal effects” (Lauritzen, 2004) and “causal association” (Frangakis and Rubin (2002)). In the causal effects paradigm, the treatment and surrogate marker are considered to be separately manipulable, allowing the total effect of the treatment to be decomposed into direct effects (holding the marker constant and changing treatment) and indirect effects (holding the treatment constant and changing the marker) to be assessed. In this setting, good surrogates leave little direct effect of the treatment. The causal association approach assumes only a manipulable treatment, finessing the issue of post-randomization of the marker by conditioning on the joint counterfactual distribution of the marker under both treatment and control. Here a good surrogate shows little effect of the treatment on the outcome when the marker is not affected by the treatment, with the treatment effect on the outcome closely tracking the treatment effect on the marker away from 0. Both the causal effects and causal association paradigms require assumptions to make progress, since their general models are unidentified. An alternative causal association approach, termed “meta-analytic” by Buyse and others (2000) and applicable only when multiple trials are available, assesses surrogacy in a fashion similar to the causal association framework, but can be identified from observable data only in randomized trials.
There are examples where use of a surrogate marker to assess treatment effect in advance of an outcome have been deleterious to health. Fleming and DeMets (1996) discuss the development of drugs to reduce ventricular arrhythmias, which were associated with cardiac-related deaths. Post-approval randomized trials showed these drugs, while effectively reducing premature ventricular beats, were nonetheless associated with substantially increased risk of death. This concept was formalized as the “surrogacy paradox” by Chen and others (2007a, b, c), who pointed out that it is possible for situations to exist in which the treatment has beneficial effect on the surrogate, the surrogate is positively associated with the outcome, yet the overall effect of the treatment on the outcome may be harmful. Chen and others pointed out that surrogates that met criteria for surrogacy under either the causal association paradigm or under the causal effects paradigm might still suffer from the surrogate paradox. Chen and others (2007a, b, c) and Ju and Geng (2010) also discussed under what conditions the surrogacy paradox could be avoided, focusing on the causal effect paradigm. VanderWeele (2013) discussed these manuscripts and concluded that the surrogate paradox can occur when one or more of the following three conditions occur: (i) a direct effect between the treatment and the outcome running in the opposite direction of the indirect effect between the treatment and outcome through the surrogate; (ii) confounding between the surrogate and outcome; and (iii) what he terms “lack of transitivity”, in which the treatment does not change the surrogate for all the same persons for whom the surrogate changes the outcome. Vanderweele notes that the “meta-analytic” approach to assess surrogacy may provide the most effective means of assessing the surrogacy paradox, as it requires fewer assumptions than the other causal analytic methods, and it focuses on quantities that more directly assess the surrogate paradox, namely “transportability” across different treatment settings. Because there now truly is repetition at the level of the trial, the nature of the association can be used to gauge the possibility of paradoxes.
We consider the issue of the surrogate paradox in the setting in which we have multiple clinical trials available where both the outcome and the surrogate marker of interest have been measured. This allows us to consider surrogacy assessment using the “meta-analytic” approach, first described in Buyse and others (2000) and developed further, which views surrogacy assessment primarily from a predictive perspective, namely that of predicting a trial-level treatment effect on an outcome given a trial-level treatment effect on a surrogate. The quality of a surrogates is assessed by the degree of correlation between the trial-level treatment effects on markers and outcomes; however, high correlations do not preclude the possibility of a surrogate paradox. Thus, our goal here is somewhat different—namely to assess probabilities that future trials could produce qualitative interactions between treatment effects on the marker and the outcome, either unconditionally or conditional on having observed the treatment effects on the marker. Specifically, we develop measures for four scenarios:
Predicting the probability that the true treatment effects for the outcome and marker will be in opposite directions in a new (
 ) trial “drawn” from the population of trials from which the
) trial “drawn” from the population of trials from which the 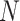 trials that make up the meta-analysis have also been “sampled”.
trials that make up the meta-analysis have also been “sampled”.Predicting the probability that the true treatment effects for the outcome will be harmful given that the true treatment effect on the marker is beneficial, again in a new (
 ) trial “drawn” from the population of trials from which the
) trial “drawn” from the population of trials from which the 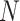 trials that make up the meta-analysis have also been “sampled”.
trials that make up the meta-analysis have also been “sampled”.Predicting the probability that the true treatment effect for the outcome will be in the opposite direction of the true treatment effect for the marker when some data (typically marker, but also possibly including outcome) have already been collected in the new (
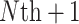 ) trial.
) trial.Estimating the size of the observed treatment effect on the marker required to preclude the possibility of a harmful true treatment effect on the outcome at a given level of probability (e.g. 0.95), either for a future (
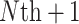 ) trial without data, or for a trial in which some data for the marker under both treatment arms has been collected.
) trial without data, or for a trial in which some data for the marker under both treatment arms has been collected.
Scenario (1) assesses the probability that the (causal) treatment effect of the marker and the outcome will be in different directions in the population of trials that informs the meta-analysis, while scenario (2) assesses the probability of the specifically higher risk situation that the marker would suggest the treatment is beneficial when in fact it is harmful with respect to the true outcome of interest. Scenario (3) focuses on the situation in which a specific trial is of interest, where typically a substantial amount of marker data and no or very little outcome data have been collected. If no trial data have been collected, Scenario (4) is similar to the first two scenarios in that a population measure is of interest, but one that focuses on assessing the level at which a beneficial observed marker effect might essentially put to rest concerns that a harmful treatment effect on the outcome is plausible; if trial data have been collected, it is more similar to Scenario (3) in which marker data only have been collected, but one that again focuses on assessing the degree to which harmful treatment effect on the outcome can be excluded.
Implicit in this development is the concept of “population” of trials with well-defined treatment and control conditions for each trial with the same specific outcome and marker for all trials, from which the “sample” of trials that make up meta-analysis is drawn. In some cases, this population might be restricted to a narrow range of treatment and control conditions, in other cases it might be a broad variety of different treatments with a common outcome and marker. Inference resulting from the methods developed below needs to be interpreted in light of these implied population structures. For this manuscript, we assume that the outcome and the marker have a hierarchical bivariate normal (BVN) distribution; extensions are considered in the discussion.
Few, if any, measures have been proposed to assess the risk surrogate paradox (Elliott and others, in discussion of VanderWeele, 2013). We believe our discussion below proposes sensible measures that are generalizable using the meta-analytic framework.
2. Estimating the probability that an outcome and marker will have opposite treatment effects in a new trial
First we summarize the development of the meta-analytic approach to surrogate marker assessment as described in Buyse and others (2000). Let  be the surrogate marker measure for the
be the surrogate marker measure for the  th subject,
th subject,  , in the
, in the 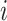 th trial,
th trial, 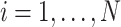 ,
, 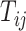 be the equivalent outcome measure, and
be the equivalent outcome measure, and 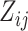 be the indicator for treatment arm (1 for treatment, 0 for control):
be the indicator for treatment arm (1 for treatment, 0 for control):
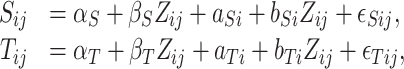 |
where the residual errors follow a BVN distribution:
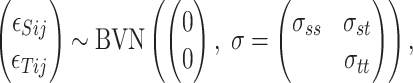 |
and the random trial-level effects follow a 4D multivariate normal (MVN) distribution:
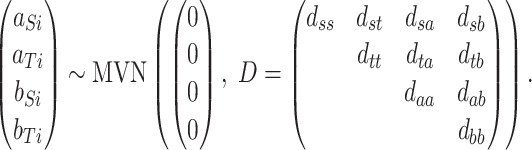 |
The causal effect of the treatment on the surrogate marker is given by the contrast of the value of the marker that would be observed under treatment,  , with the value that would be observed under control,
, with the value that would be observed under control, 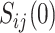 . Hence, the expected effect of the treatment on the surrogate marker within a given trial
. Hence, the expected effect of the treatment on the surrogate marker within a given trial 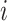 is given by
is given by 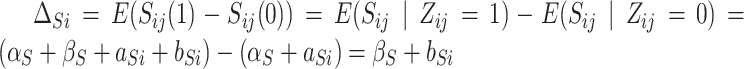 , where the second equality derives from randomization, which ensures
, where the second equality derives from randomization, which ensures 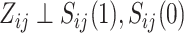 . Similarly, the expected effect of the treatment on the outcome is
. Similarly, the expected effect of the treatment on the outcome is  . Thus, we can consider
. Thus, we can consider 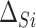 and
and  to be random effects, with a (marginal) BVN distribution:
to be random effects, with a (marginal) BVN distribution:
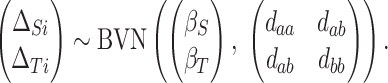 |
(2.1) |
Buyse and others suggest a “trial-level” measure of surrogacy given by proportion of variance in the total effect explained by the trial-level random effects associated with the surrogate:
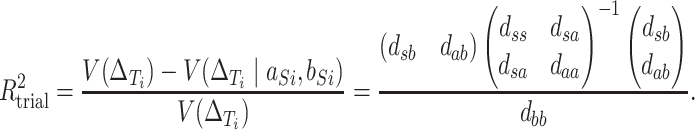 |
This formulation provides a convenient platform to measure surrogate paradox risk in several ways. First, assuming without loss of generality that the qualitative effects of the treatment (“beneficial” versus “harmful”) on the marker and outcome are in the same direction, with positive effects beneficial and negative effects harmful, we consider the probability that the 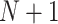 th trial will yield treatment effects on the marker and outcome in the same direction:
th trial will yield treatment effects on the marker and outcome in the same direction: 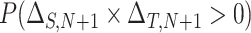 . This probability is given by
. This probability is given by
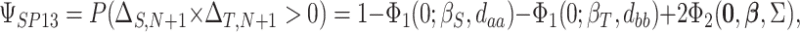 |
(2.2) |
where the subscript 13 in 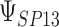 refers to the first and third quadrants of the Cartesian plane,
refers to the first and third quadrants of the Cartesian plane, 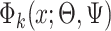 is the cumulative distribution function of a
is the cumulative distribution function of a  -variate normal distribution with mean
-variate normal distribution with mean 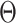 and variance
and variance  evaluated at
evaluated at 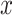 ,
,  , and
, and 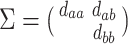 .
.
2.1. Maximum likelihood estimation
We can obtain inference about 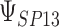 using mixed-model best linear unbiased estimators and predictors. Let
using mixed-model best linear unbiased estimators and predictors. Let  constitute the surrogate marker and outcome for each subject,
constitute the surrogate marker and outcome for each subject, 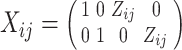 be the fixed effect matrix associated with the parameters
be the fixed effect matrix associated with the parameters 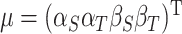 , and similarly the random effects matrix associated with
, and similarly the random effects matrix associated with 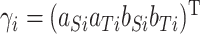 . We then obtain
. We then obtain 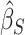 and
and 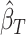 as the third and fourth elements of the maximum likelihood (ML) or restricted ML (REML) estimator of
as the third and fourth elements of the maximum likelihood (ML) or restricted ML (REML) estimator of 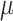 and similarly
and similarly 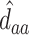 ,
,  ,
, 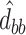 as the lower right corner of the ML or REML estimator of
as the lower right corner of the ML or REML estimator of 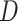 in the model
in the model
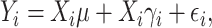 |
where 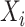 consists of the stacked elements of
consists of the stacked elements of 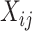 ,
, 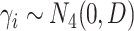 , and
, and  , and
, and 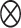 is the Kronecker product operator on two matricies. We then obtain
is the Kronecker product operator on two matricies. We then obtain
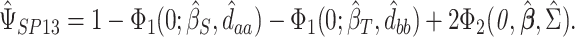 |
The variance of 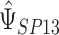 can be obtained via the Delta Method; details are provided in Section 1 of supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org).
can be obtained via the Delta Method; details are provided in Section 1 of supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org).
2.2. Bayesian estimation
Alternatively, a fully Bayesian approach can be employed that does not rely on asymptotic approximations for the variance by placing priors on 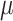 ,
, 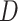 , and
, and 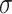 , obtaining draws via a Markov chain Monte Carlo chain, and transforming them via (2.2) to obtain the posterior distribution of
, obtaining draws via a Markov chain Monte Carlo chain, and transforming them via (2.2) to obtain the posterior distribution of  ,
, 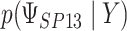 . Specifically, we assume an MVN prior for the fixed effects such that
. Specifically, we assume an MVN prior for the fixed effects such that 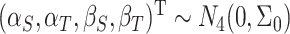 , and Wishart priors for the covariance matrices such that
, and Wishart priors for the covariance matrices such that 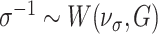 and
and  . A Gibbs sampling routine is then used to obtain draws from the posterior distributions of the parameters; conditional posterior distributions are described in Section 2 of supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org).
. A Gibbs sampling routine is then used to obtain draws from the posterior distributions of the parameters; conditional posterior distributions are described in Section 2 of supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org).
3. Estimating the probability that the treatment effects for the outcome will be harmful given that the treatment effect on the marker is beneficial
A second measure of surrogacy paradox risk targets the particularly dangerous situation where the surrogate marker suggests that the treatment will be beneficial, but in reality it is harmful: situations corresponding 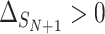 ,
, 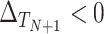 The probability that the
The probability that the 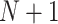 th trial will lie outside this quadrant, i.e. that
th trial will lie outside this quadrant, i.e. that  ,
,  or
or 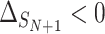 is given by
is given by
 |
(3.1) |
Either a frequentist or a Bayesian approach can be utilized as described for inference about 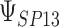 .
.
To get a sense of these measures, Figure 1 shows contour plots and associated measures of 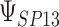 and
and 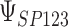 for four different scenarios. Scenario (a) corresponds to a reasonably strong correlation between surrogate marker and outcome effects, with some modest risk of marker/outcome treatment effect reversal because the treatment effects on the surrogate tend to be stronger than the treatment effects on the outcome. An example of this might be a setting in which the surrogate marker is taken as the outcome of interest measured early in the trial. Scenario (b) is similar to (a), but with a stronger treatment effect for the outcome, reducing the risk of the more dangerous reversal (beneficial marker effect but harmful outcome effect). Such an example might occur when part of the treatment effect on the outcome follows a pathway not through the marker, as in the case where we have specific surrogate biomarker, but the final effect of treatment on the outcome (e.g. survival) involves pathways not measured by this biomarker. Scenario (c) shows a very strong marker/outcome correlation, but because there is a small treatment effect size, the paradox risk is not eliminated. Such an example might often be reflected in studies of cardiovascular disease, where treatment effects tend to be small but highly correlated surrogate markers are often available. Finally, (d) shows a much weaker marker/outcome correlation, but the large effect size essentially eliminates paradox risk. These types of settings might be seen in trials of some solid tumors with targeted therapies, where large treatment effects might occur, but only relatively weak surrogates are available.
for four different scenarios. Scenario (a) corresponds to a reasonably strong correlation between surrogate marker and outcome effects, with some modest risk of marker/outcome treatment effect reversal because the treatment effects on the surrogate tend to be stronger than the treatment effects on the outcome. An example of this might be a setting in which the surrogate marker is taken as the outcome of interest measured early in the trial. Scenario (b) is similar to (a), but with a stronger treatment effect for the outcome, reducing the risk of the more dangerous reversal (beneficial marker effect but harmful outcome effect). Such an example might occur when part of the treatment effect on the outcome follows a pathway not through the marker, as in the case where we have specific surrogate biomarker, but the final effect of treatment on the outcome (e.g. survival) involves pathways not measured by this biomarker. Scenario (c) shows a very strong marker/outcome correlation, but because there is a small treatment effect size, the paradox risk is not eliminated. Such an example might often be reflected in studies of cardiovascular disease, where treatment effects tend to be small but highly correlated surrogate markers are often available. Finally, (d) shows a much weaker marker/outcome correlation, but the large effect size essentially eliminates paradox risk. These types of settings might be seen in trials of some solid tumors with targeted therapies, where large treatment effects might occur, but only relatively weak surrogates are available.
Fig. 1.
(a)  ,
, 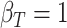 ,
,  ,
,  ,
, 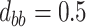 ,
, 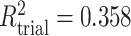 ,
,  ,
, 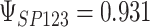 ; (b)
; (b) 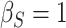 ,
, 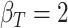 ,
, 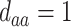 ,
, 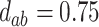 ,
, 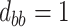 ,
, 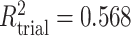 ,
, 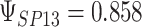 ,
, 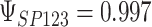 ; (c)
; (c) 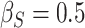 ,
,  ,
, 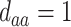 ,
, 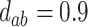 ,
, 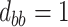 ,
, 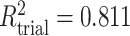 ,
, 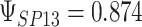 ,
, 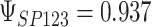 ; (d)
; (d) 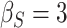 ,
,  ,
, 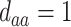 ,
, 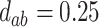 ,
, 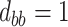 ,
, 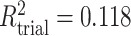 ,
, 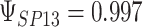 ,
, 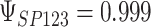 . Contour lines represent equal bivariate PDFs at levels of 0.02, except for (c), where contour lines represent an equal bivariate PDF at levels of 0.05.
. Contour lines represent equal bivariate PDFs at levels of 0.02, except for (c), where contour lines represent an equal bivariate PDF at levels of 0.05.
4. Estimating the probability that an outcome and marker will have opposite treatment effects in a new trial when partial data have been collected
The above discussion has focused on a population-level quantity than can also be viewed as providing inference about a future trial about which we have no collected data. If instead we have such data for the 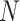 th trial and wish to condition on the observed
th trial and wish to condition on the observed 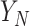 , we obtain the following for the random effect
, we obtain the following for the random effect  :
:
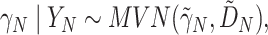 |
(4.1) |
where 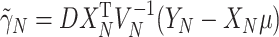 for
for  and
and  (This follows from considering the joint distribution of
(This follows from considering the joint distribution of  ,
, 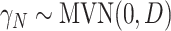 , and
, and 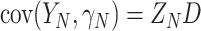 .) Our trial-level distribution of interest is obtained as
.) Our trial-level distribution of interest is obtained as
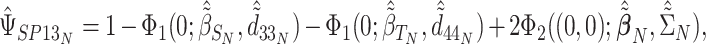 |
where  for
for 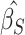 corresponding to the third element of the ML/REML estimate of
corresponding to the third element of the ML/REML estimate of 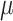 and
and 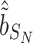 corresponding to third element of the ML/REML estimate of
corresponding to third element of the ML/REML estimate of 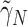 ,
,  for
for 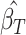 corresponding to fourth element of the ML/REML estimate of
corresponding to fourth element of the ML/REML estimate of 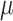 and
and 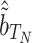 corresponding to fourth element of the ML/REML estimate of
corresponding to fourth element of the ML/REML estimate of  ,
, 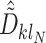 corresponding to the
corresponding to the 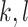 element of the ML/REML estimator of
element of the ML/REML estimator of 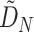 , and
, and 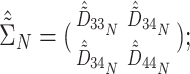 and similarly for
and similarly for 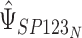 . Typically, the focus will be on
. Typically, the focus will be on 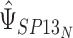 , where limited information will be available for
, where limited information will be available for 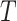 . However, this should not pose a barrier to estimation, since the mixed model can be estimated by replacing
. However, this should not pose a barrier to estimation, since the mixed model can be estimated by replacing 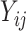 with
with  and
and 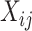 , with row vector
, with row vector 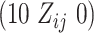 for elements lacking
for elements lacking 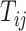 .
.
5. Estimating the size of the beneficial treatment effect on the marker required to preclude a harmful treatment effect on the outcome
Here our goal in our fourth proposed surrogacy paradox measure is to determine what is the minimum observed beneficial treatment effect for a marker than can reduce the probability that the true treatment effect for the outcome is harmful. Let 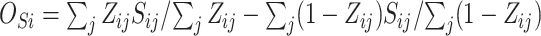 be the difference between the observed surrogate marker means under treatment and control. The joint distribution of true treatment effect on the outcome and observed treatment effect on the surrogate marker is given by
be the difference between the observed surrogate marker means under treatment and control. The joint distribution of true treatment effect on the outcome and observed treatment effect on the surrogate marker is given by
 |
(5.1) |
where  ,
, 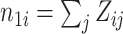 , and
, and 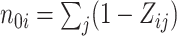 . Thus, the distribution of true treatment effect on the outcome
. Thus, the distribution of true treatment effect on the outcome 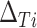 conditional on a given observed treatment effect on the surrogate marker
conditional on a given observed treatment effect on the surrogate marker 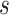 is distributed as
is distributed as
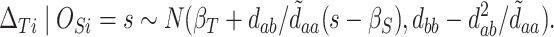 |
(5.2) |
Thus,
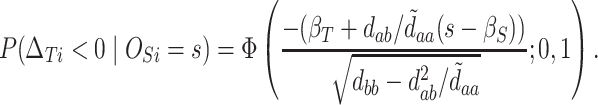 |
(5.3) |
At this point, the analysis can go one of two ways. If we have actually collected data to determine 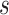 and want to compute the probability
and want to compute the probability 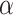 that the true effect in the outcome for the trial will be non-negative, we can compute directly from (5.3), replacing the values in (5.3) with their estimates
that the true effect in the outcome for the trial will be non-negative, we can compute directly from (5.3), replacing the values in (5.3) with their estimates 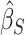 ,
, 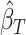 ,
,  ,
, 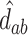 , and
, and 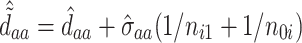 to determine
to determine 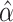 . Alternatively, we might want to determine the value of
. Alternatively, we might want to determine the value of 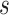 that will ensure that the probability that
that will ensure that the probability that 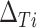 is negative is less than or equal to
is negative is less than or equal to 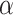 , or
, or 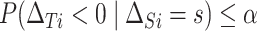 . A bit of algebra shows this requires
. A bit of algebra shows this requires
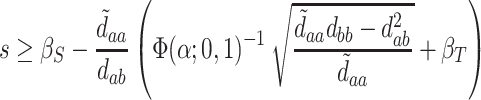 |
(5.4) |
(We assume that  and
and 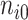 are known values for the study design). Again, replacing the values in (5.4) with their estimates and the greater than or equal to sign with equality yields
are known values for the study design). Again, replacing the values in (5.4) with their estimates and the greater than or equal to sign with equality yields 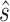 , the value of
, the value of 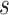 that would have to be observed to ensure that the true treatment effect in the outcome will be non-negative with at least probability
that would have to be observed to ensure that the true treatment effect in the outcome will be non-negative with at least probability  . We note that
. We note that 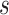 is related to the surrogacy threshold measure of Burzykowski and Buyse (2006), with the difference being that the threshold
is related to the surrogacy threshold measure of Burzykowski and Buyse (2006), with the difference being that the threshold 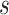 is computed conditional on the observed surrogate data only, with the goal being to estimate a specific observed treatment effect on a surrogate that is associated with a given risk of treatment reversal in a specific trial, whereas the surrogacy threshold measure conditions on latent trial-level effects to obtain a population-level measure of surrogate value. We use the Delta Method to obtain confidence intervals for
is computed conditional on the observed surrogate data only, with the goal being to estimate a specific observed treatment effect on a surrogate that is associated with a given risk of treatment reversal in a specific trial, whereas the surrogacy threshold measure conditions on latent trial-level effects to obtain a population-level measure of surrogate value. We use the Delta Method to obtain confidence intervals for 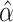 and
and 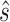 . Section 3 of supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org) provides details.
. Section 3 of supplementary material available at Biostatistics online (http://www.biostatistics.oxfordjournals.org) provides details.
6. Simulations
We perform simulations under the four surrogacy scenarios depicted in Figure 1 to examine the bias, efficiency, and coverage rates of the proposed estimators. All of the scenarios assume  ,
, 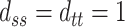 ,
, 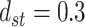 , and
, and 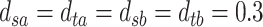 . The resulting
. The resulting  values are given in Figure 1.
values are given in Figure 1.
For each of the four scenarios, we generate 500 data sets from a meta-analysis with either 10, 40, or 100 trials, each trial with 150 subjects randomized to each treatment arm. The MIXED procedure in SAS is used to obtain point estimates and standard errors for 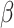 ,
, 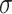 , and
, and 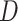 for each data set. Data sets with estimates of
for each data set. Data sets with estimates of 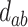 that were less than 0.1 were discarded in order to obtain more stable estimates of the quantities of interest; this situation was uncommon in all settings except Scenario (d), where the relatively weak surrogate marker lead to 35% of the simulations being rejected with 10 trials and 19% with 40 trials. Table 1 contains the point estimates, empirical standard errors and coverage rates of
that were less than 0.1 were discarded in order to obtain more stable estimates of the quantities of interest; this situation was uncommon in all settings except Scenario (d), where the relatively weak surrogate marker lead to 35% of the simulations being rejected with 10 trials and 19% with 40 trials. Table 1 contains the point estimates, empirical standard errors and coverage rates of 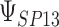 ,
, 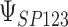 , and the value of
, and the value of 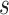 such that
such that 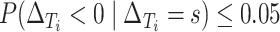 . There is some bias in the estimation of these quantities using only 10 trials, and the coverage rates are below nominal, similar to results observed in small meta-analytic sample settings in Li and Taylor (2010). In particular, Scenario (a), a “typical” setting for a moderately effective surrogate underestimated
. There is some bias in the estimation of these quantities using only 10 trials, and the coverage rates are below nominal, similar to results observed in small meta-analytic sample settings in Li and Taylor (2010). In particular, Scenario (a), a “typical” setting for a moderately effective surrogate underestimated 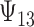 to a modest degree; proportionately, the estimate of
to a modest degree; proportionately, the estimate of 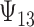 was downwardly biased more severely in Scenario (d), the low-correlation/large treatment effect setting, although as a practical matter is was still correctly estimated in excess of 0.99. Estimation of
was downwardly biased more severely in Scenario (d), the low-correlation/large treatment effect setting, although as a practical matter is was still correctly estimated in excess of 0.99. Estimation of 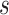 was more substantially downwardly biased as well, in all scenarios except (d), which was estimated very poorly. Nominal coverage was substantially below 95% for all estimators. When the number of trials is increased to 40, there is little bias in the estimates, although coverage remained somewhat downwardly biased. The bias was effectively zero when 100 trials are used, with nearly all of the estimates obtaining nominal coverage.
was more substantially downwardly biased as well, in all scenarios except (d), which was estimated very poorly. Nominal coverage was substantially below 95% for all estimators. When the number of trials is increased to 40, there is little bias in the estimates, although coverage remained somewhat downwardly biased. The bias was effectively zero when 100 trials are used, with nearly all of the estimates obtaining nominal coverage.
Table 1.
Simulation results
| 10 trials |
40 trials |
100 trials |
||||||
|---|---|---|---|---|---|---|---|---|
| Scenario | Quantity | True value | Estimate (SE) | Coverage | Estimate (SE) | Coverage | Estimate (SE) | Coverage |
a
|
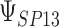 |
0.918 | 0.909 (0.05) | 0.91 | 0.917 (0.03) | 0.93 | 0.918 (0.02) | 0.93 |
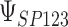 |
0.931 | 0.926 (0.05) | 0.86 | 0.931 (0.03) | 0.90 | 0.931 (0.02) | 0.93 | |
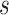 |
1.97 | 1.73 (0.93) | 0.94 | 1.90 (0.46) | 0.96 | 1.95 (0.28) | 0.95 | |
b
|
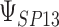 |
0.858 | 0.867 (0.08) | 0.84 | 0.859 (0.04) | 0.92 | 0.859 (0.02) | 0.95 |
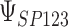 |
0.997 | 0.996 (0.007) | 0.69 | 0.997 (0.003) | 0.80 | 0.997 (0.002) | 0.91 | |
 |
-0.22 | -0.52 (0.86) | 0.95 | -0.29 (0.32) | 0.95 | -0.23 (0.18) | 0.95 | |
c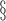
|
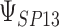 |
0.874 | 0.876 (0.05) | 0.91 | 0.875 (0.02) | 0.93 | 0.874 (0.01) | 0.94 |
 |
0.937 | 0.938 (0.04) | 0.84 | 0.938 (0.02) | 0.93 | 0.937 (0.01) | 0.96 | |
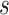 |
0.77 | 0.69 (0.27) | 0.86 | 0.74 (0.12) | 0.94 | 0.76 (0.08) | 0.96 | |
| d¶ | 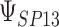 |
0.997 | 0.993 (0.01) | 0.86 | 0.996 (0.004) | 0.92 | 0.997 (0.002) | 0.92 |
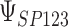 |
0.999 | 0.996 (0.007) | 0.76 | 0.998 (0.002) | 0.90 | 0.998 (0.001) | 0.92 | |
 |
-2.70 | -2.20 (4.37) | 0.76 | -2.61 (2.78) | 0.86 | -3.18 (2.29) | 0.93 | |
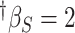 ,
, 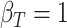 ,
,  ,
, 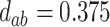 ,
, 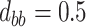 .
.
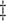
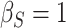 ,
, 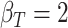 ,
, 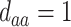 ,
, 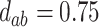 ,
, 
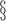
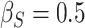 ,
, 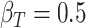 ,
,  ,
,  ,
,  .
.
¶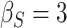 ,
, 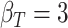 ,
, 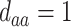 ,
,  ,
, 
Thus, in small samples, there may be some underestimation of the probability that the true treatment effects for the outcome and marker will be in the same direction—a conservative result—while the size of the beneficial treatment effect on the marker required to preclude the possibility of a harmful treatment effect on the outcome may be underestimated as well, which would be anti-conservative. In moderate to large meta-analyses, however, the proposed measures of the surrogacy paradox will be well-estimated when the normal approximations hold.
7. Applications
7.1. Early measures of intraocular pressure as a surrogate in glaucoma treatment
We illustrate the use of the proposed metrics in detecting the presence of the surrogate paradox using data from the Collaborative Initial Glaucoma Treatment Study (CIGTS) (Musch and others, 1999). This study was a multicenter randomized clinical trial comparing the effects of surgery versus a drug on the reduction of intraocular pressure (IOP) in glaucoma patients. A total of 607 patients were enrolled in the study, with 307 randomized to the drug arm. IOP was measured at 3 month intervals. We consider the measurement of IOP (recorded in mmHg) at 18 months after beginning treatment as a surrogate marker for IOP at 96 months. We take the trials to correspond to the 14 centers at which the study was conducted. Missing data (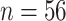 in marker [14 under control and 32 under treatment] and
in marker [14 under control and 32 under treatment] and 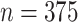 in outcome [178 under control and 197 under treatment]) are imputed via a linear mixed model with a random effect for trial, a quadratic trend for time, an effect for treatment, and an interaction between time and treatment. (Because the examples are for illustration, single imputation is used; a more complete analysis would multiply imputed the data to correctly account for the uncertainty in the imputed data.) The
in outcome [178 under control and 197 under treatment]) are imputed via a linear mixed model with a random effect for trial, a quadratic trend for time, an effect for treatment, and an interaction between time and treatment. (Because the examples are for illustration, single imputation is used; a more complete analysis would multiply imputed the data to correctly account for the uncertainty in the imputed data.) The  measure of surrogacy is 0.491, indicating that 18-month IOP is a marker of moderate quality for 96-month IOP.
measure of surrogacy is 0.491, indicating that 18-month IOP is a marker of moderate quality for 96-month IOP.
Figure 2 provides a plot of the treatment effect on reduction in IOP at 12 months and the treatment effect on reduction in IOP at 96 months for the 14 trials considered, with the size of each circle scaled to represent the size of the trial. The plot shows that in 13 of the 14 trials, the treatment caused a reduction in IOP in both the surrogate and final outcome; in the other trial, the treatment has a harmful effect (increase in IOP) on both the maker and the outcome, although the effect is not statistically significant at the trial level. Using an REML approach, the estimates and 95% confidence intervals of quantities of interest to evaluate the presence of the surrogate paradox are 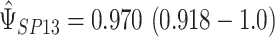 and
and  , indicating a small but non-trivial probability of the presence of the surrogate paradox when using early treatment IOP as a surrogate for later treatment IOP. For a new randomized trial with 150 subjects on each treatment arm, the smallest values of the treatment effect on
, indicating a small but non-trivial probability of the presence of the surrogate paradox when using early treatment IOP as a surrogate for later treatment IOP. For a new randomized trial with 150 subjects on each treatment arm, the smallest values of the treatment effect on 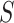 in which the probability of a beneficial treatment effect on
in which the probability of a beneficial treatment effect on 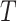 (i.e. the surrogate paradox is present) is
(i.e. the surrogate paradox is present) is 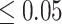 or
or 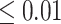 are 0.91 and 5.28 mmHg, respectively, which encompass the range of treatment effects on the surrogate marker observed across the 14 trials.
are 0.91 and 5.28 mmHg, respectively, which encompass the range of treatment effects on the surrogate marker observed across the 14 trials.
Fig. 2.

(a) Observed treatment effect on reduction in IOP at 12 months (surrogate endpoint) and treatment effect on reduction in IOP at 96 months (true endpoint) for 14 trials from the CIGTS study. (b) 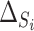 and
and 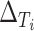 for 14 trials from the CIGTS study.
for 14 trials from the CIGTS study.
We also consider a Bayesian approach, assuming an MVN prior for the fixed effects such that 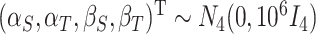 , and Wishart priors for the inverse of the covariance matrices either of the form
, and Wishart priors for the inverse of the covariance matrices either of the form 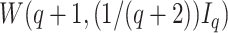 where
where 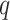 is the length of the associated random vector (2 for
is the length of the associated random vector (2 for 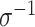 , 4 for
, 4 for 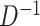 ) (Li and Taylor, 2010), or
) (Li and Taylor, 2010), or 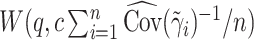 , where
, where 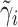 is the OLS estimator of
is the OLS estimator of  and
and 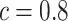 is chosen to make this prior somewhat “flatter” relative to Li and Taylor (Kass and Natarajan, 2006). Use of the Li and Taylor prior resulted in a posterior mean for
is chosen to make this prior somewhat “flatter” relative to Li and Taylor (Kass and Natarajan, 2006). Use of the Li and Taylor prior resulted in a posterior mean for 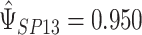 with a 95% credible interval (CI) of
with a 95% credible interval (CI) of  , a posterior mean for
, a posterior mean for 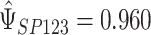 with a 95% CI of
with a 95% CI of 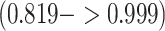 , and estimates of
, and estimates of 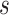 from
from 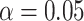 and
and 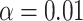 of 2.04 and 3.55 mmHg, respectively. Use of the Kass and Natarajan yielded a posterior mean for
of 2.04 and 3.55 mmHg, respectively. Use of the Kass and Natarajan yielded a posterior mean for 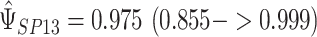 ; a posterior mean for
; a posterior mean for  ; and estimates of
; and estimates of  from
from 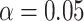 and
and  of 0.59 and 1.77 mmHg.
of 0.59 and 1.77 mmHg.
7.2. Blood pressure as a surrogate for hypertension
We provide a second illustration of the use of the proposed metrics in detecting the presence of the surrogate paradox using data from the Trial of Preventing Hypertension (TROPHY) (Julius and others, 2006). This study was a multicenter randomized trial which compared the effects of 2 years of treatment with candesartan versus standard of care on the incidence of hypertension in patients with prehypertension. Information on blood pressure and hypertension status were obtained at baseline, 1 and 3 months post-randomization and then every 3 months until month 24. The primary endpoint of the original study was development of hypertension. Here we consider the continuous measure of the average of systolic pressure and diastolic pressure at 12 months, and evaluate the average of systolic pressure and diastolic pressure at 1 month as a surrogate marker. Due to the development of hypertension (at which point patients changed their treatment regiment), there was some missing data in the 1- and 12-month blood pressure measurements (approximately 2% and 20% missing, respectively). Missing values were singly imputed using SAS PROC MI (SAS Institute, Inc., Cary, NC, USA). The imputation model included baseline measurements of age, race, weight, body-mass index, systolic and diastolic blood pressures, total cholesterol, high density lipoprotein cholesterol (HDL), low density lipoprotein cholesterol (LDL), HDL:LDL ratio, triglycerides, fasting glucose, total insulin, and creatine and was stratified by treatment and gender. The imputation model for the missing 12-month values also included all blood pressure measurements up to the 12-month time point.
A total of 772 patients from 69 centers were included in the original analysis. Prior to our analysis, seven centers with patients in only one treatment arm were removed. The remaining data consisted of 764 patients from 62 centers, with 389 randomized to the treatment group. The centers range in size from 2 patients to 46 patients. The left panel of Figure 3(a) provides a plot of the treatment effect on blood pressure reduction at 1 month and the treatment effect on blood pressure reduction at 12 months for the 62 centers considered, with the size of each circle scaled to represent the size of the center. The plot shows that in all but four of the trials, there was a beneficial effect of the treatment on the surrogate and in all but seven trials there was a beneficial effect of the treatment on the final outcome. There was a significant treatment effect on 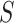 in 18 trials and a significant treatment effect on
in 18 trials and a significant treatment effect on 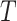 in 12 trials. As the estimate of the between trial covariance matrix,
in 12 trials. As the estimate of the between trial covariance matrix,  , is non-positive definite when estimated using REML estimation, only the Bayesian estimation procedure is applied. The same LT and KN priors as described in the IOP analysis were used (Li and Taylor, 2010; Kass and Natarajan, 2006). Figure 3(b) provides a plot of the fixed effect estimates plus the random effect estimates for the treatment effect on
, is non-positive definite when estimated using REML estimation, only the Bayesian estimation procedure is applied. The same LT and KN priors as described in the IOP analysis were used (Li and Taylor, 2010; Kass and Natarajan, 2006). Figure 3(b) provides a plot of the fixed effect estimates plus the random effect estimates for the treatment effect on 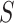 and
and 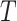 (
(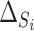 and
and 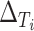 , respectively) for the 62 trials. Using the LT priors, the posterior means and 95% CI of these quantities are
, respectively) for the 62 trials. Using the LT priors, the posterior means and 95% CI of these quantities are  (95% CI: 0.995, 1) and
(95% CI: 0.995, 1) and  (95% CI: 0.998, 1), indicating very little probability of the presence of the surrogate paradox in this scenario. For a trial with 300 subjects, the smallest values of the treatment effect on
(95% CI: 0.998, 1), indicating very little probability of the presence of the surrogate paradox in this scenario. For a trial with 300 subjects, the smallest values of the treatment effect on 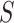 in which the probability of a harmful treatment effect on
in which the probability of a harmful treatment effect on 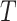 is
is 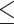 0.05 or
0.05 or 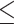 0.01 are
0.01 are  3.7 and
3.7 and  1.3, respectively. Use of the KN priors yields posterior means and 95% CIs of 0.975
1.3, respectively. Use of the KN priors yields posterior means and 95% CIs of 0.975  for
for 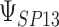 , 0
, 0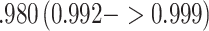 for
for 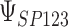 , and values of
, and values of  of 1.77 and 5.06 for
of 1.77 and 5.06 for 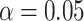 and 0.01, respectively.
and 0.01, respectively.
Fig. 3.

(a) Observed treatment effect on average of systolic and diastolic blood pressure at 1 month (surrogate endpoint) and treatment effect on average of systolic and diastolic blood pressure at 12 months (true endpoint) for 62 trials from the TROPHY study. (b) 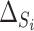 and
and 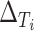 for 62 trials from the TROPHY study.
for 62 trials from the TROPHY study.
8. Discussion
For reasons of cost and time, finding good surrogate markers for outcomes is of great interest in clinical research. However, as Baker and Kramer (2003) note, use of surrogates is made difficult in settings where multiple complex pathways run from treatment to outcome. Surrogate markers that lie on only one of these pathways, and treatments that may affect multiple pathways, can lead to situations where markers can be misleading when considered in new settings. Methods to assess the risk of surrogate paradox can be an important tool to protect against failures that put health at risk. To our knowledge, this is one of the first manuscripts to attempt to quantify this risk using sensible measures that can easily be fit using existing mixed-model methodology. We consider both frequentist and Bayesian methods. Asymptotically, the two approaches yield similar results, although with small numbers of trials, there is some modest sensitivity to the use of priors for covariance matricies with diagonal matrix scales, as illustrated by our first (IOP) example. While such priors are useful for stabilizing covariance matrix estimates and allowing estimation when ML methods fail to converge, they will usually increase the surrogate paradox measure risks, as they weaken the correlation between the treatment effects on the marker and the treatment effects on the outcome. They will also tend to stabilize the surrogate paradox threshold measures for a given trial. The practitioner will have to decide if the tradeoffs in stability or ability to fit the model are worth the use of priors, and may wish to consider several priors to understand the sensitivity of the results to their choice, as we have done.
Several extensions are possible for this work. One option, following Burzykowski and others (2004), replaces the BVN assumption in the first stage of the model with a copula model, allowing for a larger range of marginal distributions to be considered. Another alternative replaces the first level of the hierarchical model with subdomains such as age, baseline biomarkers, or other baseline measures to assess whether there are subsets of the population for whom the surrogate marker effects may be misleading for the outcome of interest. As noted by a reviewer, such use of baseline covariates to identify treatment by covariate interactions assists not only in the identification of subsets of the population at risk for misleading conclusions when relying on a surrogate marker, but may provide evidence of covariate-specific surrogates more generally.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
This research was supported by the National Cancer Institute Grant R01CA-129102.
Supplementary Material
Acknowledgement
The authors thank two anonymous reviewers whose suggestions improved the manuscript. Conflict of Interest: None declared.
References
- Baker S. G., Kramer B. S. (2006). A perfect correlate does not a surrogate make. BMJ Medical Research Methodology 3, 16–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burzykowski T., Buyse M. (2006). Surrogate threshold effect: an alternative measure for meta-analytic surrogate endpoint validation. Pharmaceutical Statistics 5, 173–186. [DOI] [PubMed] [Google Scholar]
- Burzykowski T., Molenberghs G., Buyse M. (2004). The validation of surrogate end points by using data from randomized clinical trials: a case-study in advanced colorectal cancer. Journal of the Royal Statistical Society A167, 103–124. [Google Scholar]
- Buyse M., Molenberghs G., Burzykowski T., Renard D., Geys H. (2000). The validation of surrogate endpoints in meta-analyses of randomized experiments. Biostatistics 1, 49–67. [DOI] [PubMed] [Google Scholar]
- Chen H., Geng Z., Jia J. (2007a). Criteria for surrogate end points. Journal of the Royal Statistical Society B69, 919–932. [Google Scholar]
- Chen H., Geng Z., Jia J. (2007b). Surrogate end points in clinical trials: are we being misled? Annals of Internal Medicine 125, 605–613. [DOI] [PubMed] [Google Scholar]
- Chen H., Geng Z., Jia J. (2007c). Principal stratification in causal inference. Biometrics 58, 21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming T.T., DeMets D.L. (1996) . Surrogate end points in clinical trials: are we being mislead? Annals of Internal Medicine, 125, 605–613. [DOI] [PubMed] [Google Scholar]
- Frangakis C.E., Rubin D.B. (2002). Principal stratification in causal inference. Biometrics, 58, 21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joffe M. M., Greene T. (2009). Related causal frameworks for surrogate outcomes. Biometrics 65, 530–538. [DOI] [PubMed] [Google Scholar]
- Ju C., Geng Z. (2010). Criteria for surrogate end points based on causal distributions. Journal of the Royal Statistical Society B72, 129–142. [Google Scholar]
- Julius S., Nesbitt S. D., Egan B. M., Weber M. A., Michelson E. L., Kaciroti N., Black H. R., Grimm R. H., Messerli F. H., Oparil S., Schork M. A. (2006). Feasibility of treating prehypertension with an angiotensin-receptor blocker. New England Journal of Medicine 354, 1685–1697. [DOI] [PubMed] [Google Scholar]
- Kass R. E., Natarajan R. (2006). A default conjugate prior for variance components in generalized linear mixed models (comment on article by Browne and Draper). Bayesian Analysis 1, 535–542. [Google Scholar]
- Lauritzen S. L. (2004). Discussion of causality. Scandinavian Journal of Statistics 31, 189–193. [Google Scholar]
- Li Y., Taylor J. M. G. (2010). Predicting treatment effects using biomarker data in a meta-analysis of clinical trials. Statistics in Medicine 29, 1875–1889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musch D. C., Lichter P. R., Guire K. E., Standardi C. L.CIGTS Investigators. (1999). The collaborative initial glaucoma treatment study (CIGTS): study design, methods and baseline characteristics of enrolled patients. Ophthalmology 106, 653–662. [DOI] [PubMed] [Google Scholar]
- Prentice R. L. (1989). Surrogate endpoints in clinical trials: definition and operational criteria. Statistics in Medicine 8, 431–440. [DOI] [PubMed] [Google Scholar]
- VanderWeele T. J. (2013). Surrogate measures and consistent surrogates. Biometrics 69, 561–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



