New classification of lingual arch form in normal occlusion using three dimensional virtual models

Abstract

Objective

The purposes of this study were 1) to classify lingual dental arch form types based on the lingual bracket points and 2) to provide a new lingual arch form template based on this classification for clinical application through the analysis of three-dimensional virtual models of normal occlusion sample.

Methods

Maxillary and mandibular casts of 115 young adults with normal occlusion were scanned in their occluded positions and lingual bracket points were digitized on the virtual models by using Rapidform 2006 software. Sixty-eight cases (dataset 1) were used in K-means cluster analysis to classify arch forms with intercanine, interpremolar and intermolar widths and width/depth ratios as determinants. The best-fit curves of the mean arch forms were generated. The remaining cases (dataset 2) were mapped into the obtained clusters and a multivariate test was performed to assess the differences between the clusters.

Results

Four-cluster classification demonstrated maximum intercluster distance. Wide, narrow, tapering, and ovoid types were described according to the intercanine and intermolar widths and their best-fit curves were depicted. No significant differences in arch depths existed among the clusters. Strong to moderate correlations were found between maxillary and mandibular arch widths.

Conclusions

Lingual arch forms have been classified into 4 types based on their anterior and posterior dimensions. A template of the 4 arch forms has been depicted. Three-dimensional analysis of the lingual bracket points provides more accurate identification of arch form and, consequently, archwire selection.

INTRODUCTION

The shape of the mandibular dental arch is an important element in diagnosis and treatment planning. As arch form configuration is a key requirement for stable treatment results, correct identification of arch form is essential during the diagnostic phase, especially given the popularity of superelastic archwires.1,2,3,4

There is no single ideal arch form that meets all treatment goals due to the inevitable variations between individuals.5,6,7 Mandibular arch forms have been classified by various mathematical and statistical methods.8,9,10,11,12,13,14,15,16 For example, Raberin et al.17 classified the mandibular arch into 5 ideal forms by K-means cluster analysis. However, most of the researchers selected landmarks on incisal edges and cusp tips, which may not appropriately represent arch forms.

The validity of three-dimensional (3D) virtual models has been confirmed in several studies.18,19,20,21 Nevertheless, few studies have used this technology to evaluate dental arch forms.20,22,23 Given the substantial overlap in the identification of mandibular arch forms, a revised template based on facial axis (FA) points has been suggested.22 Recently, Bayome et al.24 proposed a clinical classification of dental arch forms by using FA points derived from 3D models.

A previous study evaluated the morphologic characteristics of lingual arch form in a limited sample size.25 Although the average arch form of a normal occlusion sample was provided, a classification of the lingual arch forms according to shape or size has not been attempted. Lombardo et al.26 classified lingual arch forms into three groups according to the x- and y-values of each tooth. Such two-dimensional evaluation has inherent errors in landmark identification and addresses size but not shape. Therefore, a classification that overcomes these limitations is required.

The purposes of this study were 1) to classify lingual dental arch form types based on the lingual bracket points and 2) to provide a new lingual arch form template based on this classification for clinical application through the analysis of 3D virtual models of normal occlusion sample.

MATERIALS AND METHODS

The sample consisted of 115 young adults with normal occlusion (64 males and 51 females) selected from a database of 15,621 Korean subjects. The subjects' age ranged from 20 to 30 years, with a mean of 23.5 years. The inclusion criteria were as follows:

• Angle's Class I molar and canine relationships

• 0° < ANB < 4°

• 0 mm < overbite and overjet < 4 mm

• Minor tooth size - arch length discrepancy (< 3 mm crowding, < 1 mm spacing)

• Flat or slight curve of Spee (< 2 mm)

• Absence of crossbite or dental midline deviation

• Permanent dentition with normal tooth size and shape, except third molars

• No previous orthodontic treatment

• No restorations involving contact areas, cusp tips, incisal edges, or facial surfaces

The institutional review board of The Catholic University of Korea (MC12SSSI0083) approved the study.

Mandibular and maxillary casts were placed in the occluded relationship and scanned with a 3D laser scanner (Orapix KOD-300; Orapix Co., Ltd, Seoul, Korea), set at 20-µm resolution. Lingual bracket points, which are the points on the lingual surface of the teeth on which the lingual brackets are centered, were digitized on each tooth of the upper and lower virtual models using Rapidform 2006 software (INUS Technology, Inc., Seoul, Korea; Figure 1).

Figure 1. Lingual bracket points (red dots) on the three-dimensional virtual models. Arch dimensions were measured from these points. A, intercanine width; B, intercanine depth; C, interpremolar width; D, interpremolar depth; E, intermolar width; F, intermolar depth.

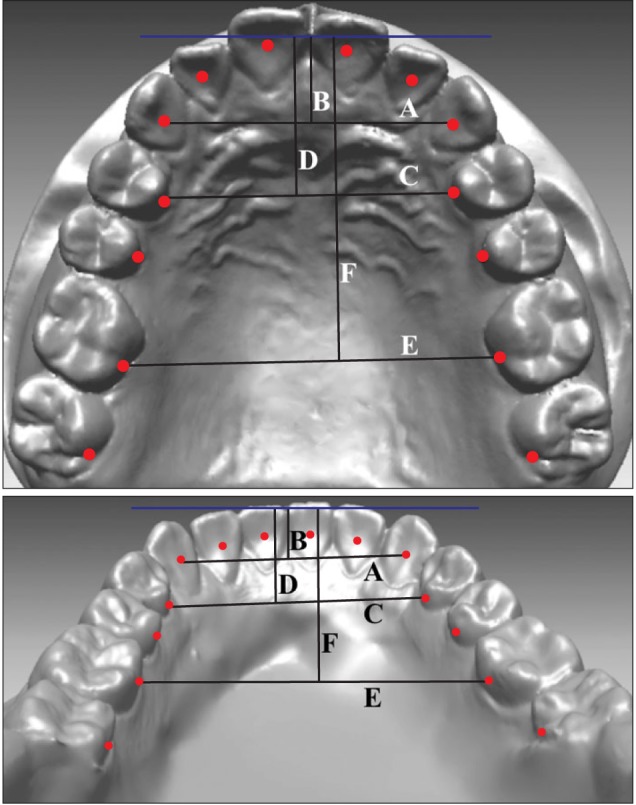
The contact point between the mandibular central incisors was set as the origin point. The transverse and anteroposterior directions were set as the x-axis and y-axis, respectively; the plane perpendicular to these axes was set as the z-axis. For reorientation of casts, the original x-axis of each cast was adjusted so that the mean inclination of Line A (line connecting the right and left contact points between the first and second premolars) and Line B (straight line connecting the right and left contact point between the second premolars and the first molars) became parallel to the original x-axis. The difference in z-axis values between the teeth was very small in each case so they were nullified for simplification of the mathematical calculations.

Six linear measurements and three ratios were evaluated per each upper and lower arch form (Table 1 and Figure 1). Ten randomly selected cases were reprocessed 2 weeks later to assess intraoperator reliability. Intraclass correlation coefficient (ICC) test revealed high reliability between the two assessments (ICC > 0.8).

Table 1. Definitions.

W/D, Width/depth.

The 115 casts were divided randomly into 2 datasets: Dataset 1 (68 cases) was used to classify arch forms, and dataset 2 (47 cases) was used to examine the differences between clusters for validation purposes. K-means cluster analysis was performed with dataset 1 to classify the samples into arch form types using SPSS (SPSS ver. 16.0.2.1; SPSS Inc., Chicago, IL, USA). Clustering was based on mandibular intercanine, interpremolar, and intermolar widths and width/depth ratios. Potential classifications into three to nine groups were run through the software. After inspecting the distributions in each classification and homogeneity of group sizes, the classification that demonstrated highly significant intergroup differences in the six parameters was chosen. Chi-square test was applied to evaluate the frequency distribution of the clusters and association between clusters and gender. Then, a multivariate test with Bonferroni adjustment for multiple comparisons was performed to evaluate the properties of the clusters.

The mean arch form of each cluster was calculated from the x- and y-coordinates of the lingual bracket points of each subject in the group. The mean coordinates of each point were inputted into a mathematical program (MATLAB 7.5 [R2007b]; MathWorks, Inc., Natick, MA, USA) to draw the best-fit curve that represented the mean arch form, using different types of polynomial equations.

Subsequently, dataset 2 was mapped into the same space and assigned to the 4 clusters already constructed. A multivariate test with Bonferroni adjustment for multiple comparisons was performed to validate the clustering. Then, members of both datasets in each cluster were combined and MATLAB was used to draw the arch forms. The mandibular arch forms were superimposed on the origin point and differences between arch forms were evaluated for clinical significance and application.

Pearson correlation analysis was applied to assess the relationship between maxillary and mandibular arch form variables.

RESULTS

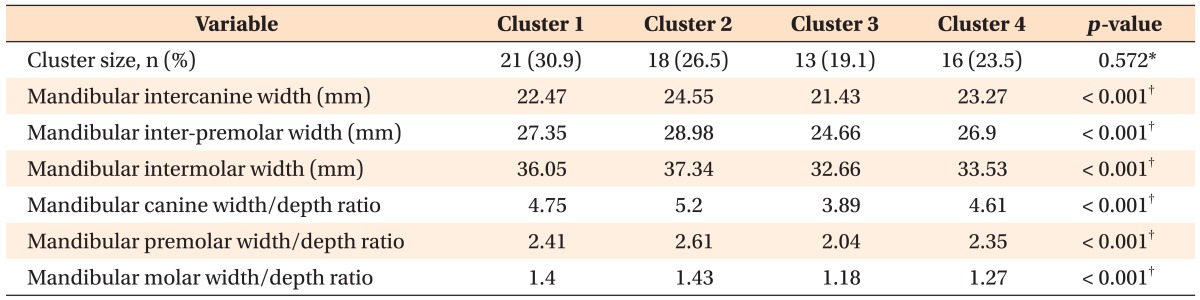
K-means cluster analysis was performed seven times to classify dataset 1 into three to nine clusters. The classification into 4 clusters showed the maximum intercluster distance in the 6 parameters and had the most homogeneous cluster size. Table 2 demonstrates the mean arch form dimensions of the four clusters. Chi-square test revealed an even frequency distribution of the subjects between the clusters (p = 0.572), and no significant association was noted between gender and clusters (p = 0.304).

Table 2. The Final centers of clusters and their frequency distribution.

^*Chi-square test.

^†Analysis of variance (ANOVA). ANOVA test was used only for descriptive purposes, because the clusters were chosen to maximize differences.

Table 3 compares the arch dimensions of the 4 cluster groups using dataset 2. In the mandible, the intercanine and intermolar depths showed significant differences (p = 0.025 and 0.015, respectively). However, there was no significant difference in the premolar depth. In the maxilla, all the dimensions except intercanine and interpremolar depths were significantly different between the clusters.

Table 3. Comparison of arch dimensions among the arch form groups.

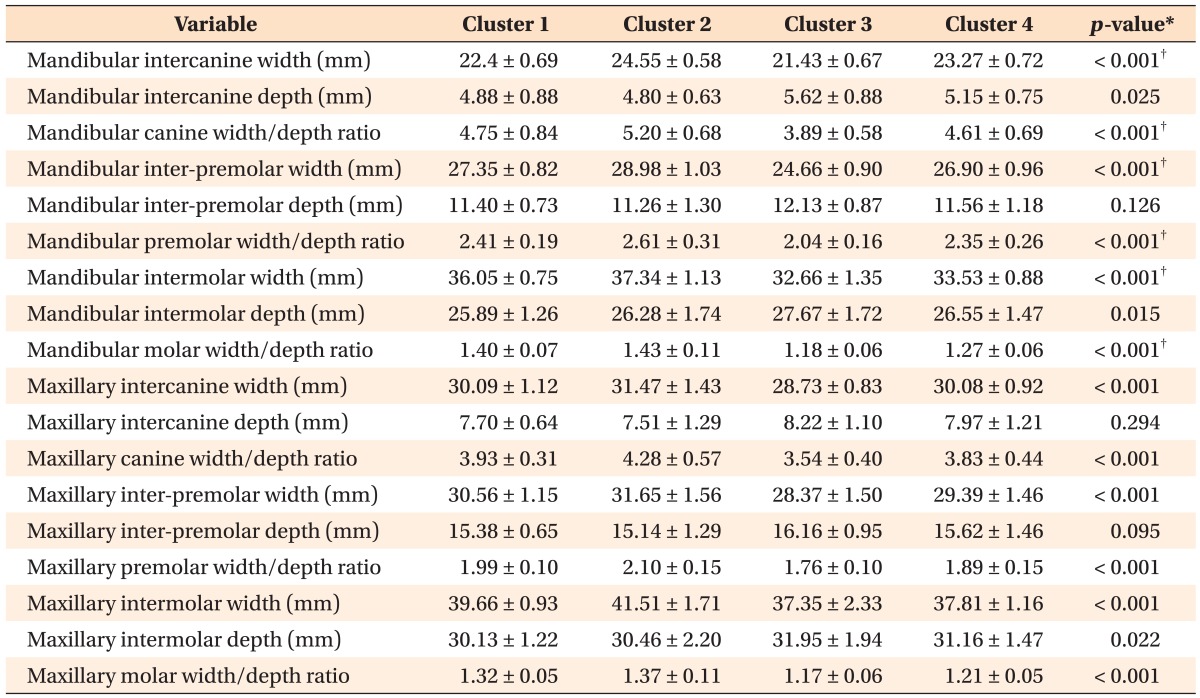
^*Analysis of variance (ANOVA).

^†ANOVA tests should be used only for descriptive purposes because the clusters have been chosen to maximize the differences among clusters.

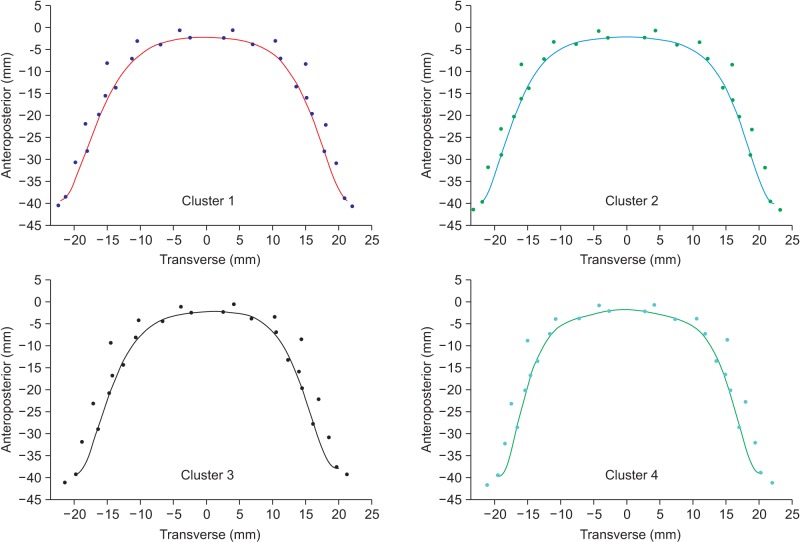
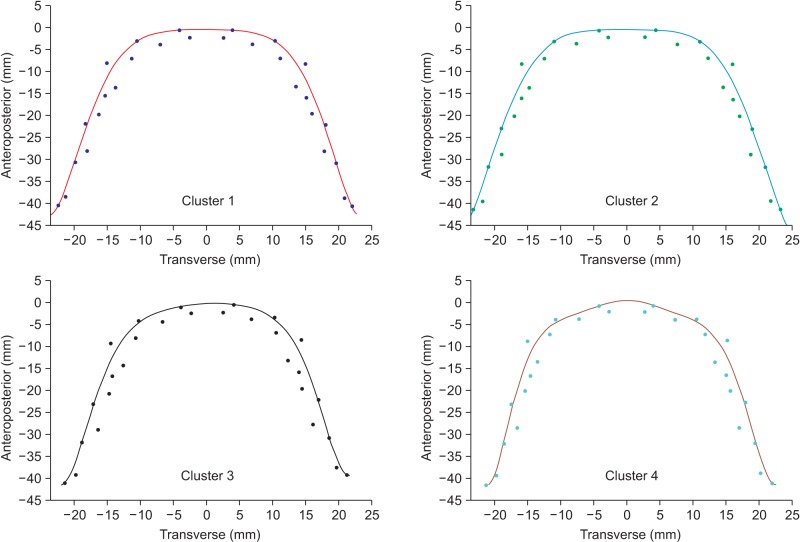
Figure 2 depicts the superimposition of the best-fit curves of the mandibular arches of the 4 clusters at the origin point. Cluster 2 (wide type) has broad intercanine and intermolar widths; Cluster 3 (narrow type) illustrates narrow intercanine and intermolar widths; Cluster 1 (tapering type) demonstrates broad intermolar width and narrow intercanine width; Cluster 4 (ovoid type) shows relatively narrow intermolar width and broad intercanine width. Figure 3 presents the suggested mandibular template of the 4 arch forms in 1:1 size. However, the best-fit curves of the maxillary arch forms had a high sum of square error (SSE) due to the position of the canines (Figure 4).

Figure 2. Superimposition of the best-fit curves of the mandibular arch clusters.

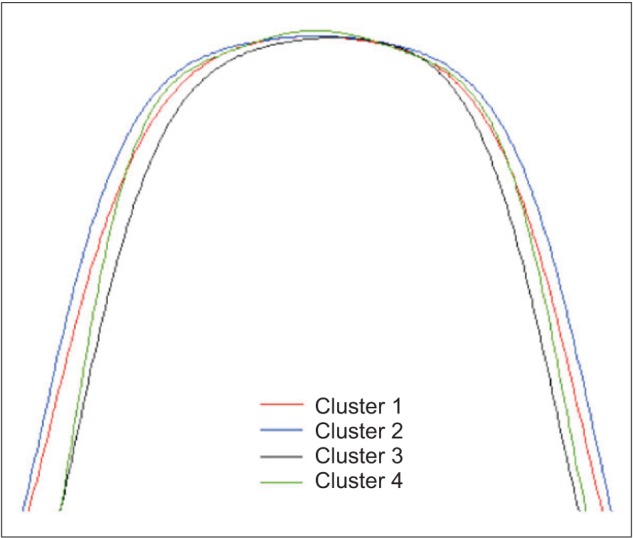
Figure 3. Template of mandibular lingual arch forms.

Figure 4. Template of maxillary lingual arch forms.

Table 4 shows the correlations between maxillary and mandibular arch form variables. The maxillary and mandibular arch widths showed strong to moderate correlations between each other. Likewise, the arch depths of the upper and lower jaw were correlated.

Table 4. Correlations between the maxillary and mandibular arch form dimensions.

IM, Intermolar; IP, interpremolar; IC, intercanine; W, width; D, depth.

Pearson correlation coefficients (r).

^*p < 0.05, ^†p < 0.01, and ^‡p < 0.001.

DISCUSSION

Currently, there is an enormous and growing interest in invisible braces due to the increased numbers of adult patients and social pressures in today's society. Despite improvements to the lingual orthodontic protocol, some patients experience discomfort and dysfunction.27,28 These problems could be minimized by selecting the most appropriate arch form. Therefore, it is necessary to have a classification for lingual arch forms that corresponds with the different groups of patients.

The existing arch wire templates lack good fit to the average dental arches and have substantial overlap among their classifications, thus several arch form classifications derived from FA points have been reported.2,22,24,29 Therefore, the aim of this study was to introduce a new improved classification system of arch form based on the lingual bracket points to improve clinical application of lingual preformed arch wires.

Recently, customized orthodontic treatment has recently gained recognition because of the wide variation between individuals. As a result, cluster analysis has gained popularity in biomedical science as it considers both individual variation and better control of the outliers.

In our study, a new, four-type classification of lingual arch form was found that considers size and shape. The classification was based on mandibular widths and width/depth ratios which were reported to be important for the stability of the treatment outcomes and represents the curvature of each segment of the arch.1,2,3 The validity of using the six parameters as determinants in K-means cluster analysis was tested. Several variables were added as determinants in different combinations, but the clustering membership and homogeneity showed no significant changes. Meanwhile, removing any of those six variables led to different results. Also, the significant strong and moderate correlations found between the maxillary and mandibular parameters supported the inclusion of the mandibular parameters as the only clustering factors. Hence, this classification considered both the shape and the size of the dental arch.

Our results support previous findings that there is no single, ideal arch form appropriate for all patients.2,17,24,29 The 4-cluster classification developed in our study might be more practical due to the difficulty in customizing superelastic archwires.

The narrow group had the narrowest intercanine and intermolar widths in both arches. The width/depth ratios of this group were somewhat similar to those of the narrow cluster of Lombardo et al.26 The remaining three groups in our results had larger arch widths and ratios but smaller intercanine depth and similar intermolar depth to all the forms proposed by Lombardo et al.26 These differences may be explained by differences in ethnicity and research methods.

There was no significant association between gender and arch form. This gender homogeneity is consistent with the findings of Raberin et al.17 This study could have been improved by using a larger sample, which might have also revealed rare arch forms.

Several studies recommended the use of fourth- or sixth-degree polynomial curves to represent the labial dental arch.2,8,13,14,15,30 In our study, several levels of polynomial equations were applied: the ninth-degree polynomial equation showed the least SSE and, hence, better fit; the resultant curves are smooth enough for clinical purposes.

The description of the maxillary arch shapes might not be sufficiently accurate for clinical use because of the high SSE even with the ninth-degree polynomial equation. Further studies are recommended to evaluate the maxillary arch by combining two mathematical equations: one for the anterior segment and the other for the posterior area. Clinically, the maxillary archwire can be assessed by excluding the canines from the arch curve equation and then adding them as an offset bend to the archwire.

Additional studies are warranted to evaluate lingual arch forms according to Angle's classification. Studies of the long-term stability of treatment outcomes based on the proposed classification are also recommended.

CONCLUSION

A new classification of lingual arch form has been identified that considers arch size and shape. Wide, narrow, tapering, and ovoid types were described according to the intercanine and intermolar widths.

A new template of these arch forms was introduced for more efficient identification of patient arch forms. This 4-type template might be more practical for clinical choice of mandibular lingual superelastic wires.