Abstract
The measurement of ionizing radiation (IR) is a crucial issue in different areas of interest, from environmental safety and industrial monitoring to aerospace and medicine. Optical fiber sensors have recently proven good candidates as radiation dosimeters. Here we investigate the effect of IR on germanosilicate optical fibers. A piece of Ge-doped fiber enclosed between two fiber Bragg gratings (FBGs) is irradiated with gamma radiation generated by a 6 MV medical linear accelerator. With respect to other FBG-based IR dosimeters, here the sensor is only the bare fiber without any special internal structure. A near infrared laser is frequency locked to the cavity modes for high resolution measurement of radiation induced effects on the fiber optical parameters. In particular, we observe a variation of the fiber thermo-optic response with the radiation dose delivered, as expected from the interaction with Ge defect centers, and demonstrate a detection limit of 360 mGy. This method can have an impact in those contexts where low radiation doses have to be measured both in small volumes or over large areas, such as radiation therapy and radiation protection, while bare optical fibers are cheap and disposable.
Keywords: ionizing radiation, optical fiber sensors, optical resonators, optical materials
1. Introduction
In the last decades, there has been a growing need for detection and quantification of IR in different contexts, such as environmental safety, industrial processes monitoring, radiation protection and medicine. In this regard, radiation dosimetry plays a central role to quantify the absorbed energy and thus assess radiation effects. When IR is applied in medical settings, the main issue is the measurement of the amount of radiation that is actually delivered to the patient [1]. The need for accurate dosimetry is greatest in radiation therapy for cancer. One of the aspects of an efficient treatment of cancer is the calibration of the clinical accelerator machines (reference dosimetry), but also accurate radiation beam shaping and measurement of dose delivered to the patient (relative and in vivo dosimetry) must be taken into account [2–5]. A number of physical and chemical devices based on liquids, solids and gases are currently available to detect IR and measure the released dose. Ionization chambers, silicon diodes, thermoluminescence devices, MOSFETs, diamond detectors and films are currently adopted as reference, relative and in vivo dosimeters [6–9]. However, among the above mentioned sensors, none meet the major requirements of an ideal dosimeter, which should be small in size but highly sensitive. The sensing element should only minimally perturb the radiation field and always measure the total absorbed dose. Moreover, immunity to environmental conditions and external interferences are desirable. Air-filled ionization chambers (sensitive volumes 0.6 cm3), for instance, have been the standard detectors for radiotherapy dosimetry, but they are not always suitable when high dose gradients (small fields), high dose-per-pulse, time-dose variance, and non-uniform beam distributions occur [10]. Volume averaging and lack of electronic equilibrium, which require a sufficiently large region of beam uniformity around the detector, complicate the use of ionization chambers in applications requiring high spatial resolution. A higher spatial resolution can be obtained with solid state detectors like diodes or diamonds due to their high sensitivity, and accordingly they can be realized with smaller dimensions (10−4–10−3 cm3). Liquid-filled ionization chambers with reduced sizes (0.002 cm3) have been also introduced in high precision radiation dosimetry. Liquid filled ionization chambers, like solid state detectors, combine a very small volume with a relatively high response, but further studies on the underlying theories for recombination effects are still needed for them to become a feasible option.
Recently, a considerable effort has been spent to demonstrate the feasibility of optical fiber sensing for application in radiation environments, although only a few experimental proofs have been provided on this subject [11]. So far, conventional FBG sensors, which have been successfully used for temperature, strain, and pressure monitoring [12], have been proposed for IR detection. FBG-based dosimeters transmit dose information through the fiber. Consequently, these sensors are immune to electromagnetic interference, which is usually a serious issue for electronic dosimeters. The ability to remotely monitor radiation is an additional advantage, as the sensor can be placed at a long distance from the readout electronics. Also, optical fiber sensors can be multiplexed so that a single reading unit can control several sensors. Thanks to their mechanical nature and very small size, fibers lend themselves to the realization of miniature radiation detectors with different geometries without perturbing the dose measurement. Optical sensors are generally based on either internal generation of light caused by radiation-matter interaction or changes of intrinsic physical-chemical properties of the material itself [13]. Most existing optical fiber-based dosimeters are extrinsic sensors. In this case, the role of fibers is primarily to transmit light from a thermoluminescent solid, a diode or a scintillating medium [13–15]. Recently, doped optical fibers have also been investigated as radioluminescent dosimeters [16,17]. The main drawback of such a system relies in the so-called “stem effect”, i.e., unwanted light contribution deriving from Cerenkov radiation generated in the fiber, which affects the reliability of dose measurements. There are also a few studies that demonstrate radiation-induced attenuation within a fiber. One of the underlying mechanisms is the creation of defect centers by interaction of high-energy photons with OH and Ge, naturally present in silica optical fibers, as well as with added dopants. The effects of ionizing radiation have been found to be sufficient to induce losses much greater than intrinsic fiber loss (∼dB/km) from the visible to the near-infrared spectral range, even at low/moderate doses (in the range 1–10 Gy) [18–20]. In all these cases, the interaction with IR can be quantified by measurements of the transmitted light intensity. Besides the increase in optical transmission loss, a correlated change of average refractive index also occurs in the optical waveguide, which can be exploited to extract the desired information with very high resolution [21,22]. Refractive sensing has the advantage of overcoming typical issues related to radiation power measurements, as well as systematic deviations due to fiber instability (bending, stress, degradation, etc.) that also limit repeatability and long-distance transmission for remote readout.
In a previous work [22] we demonstrated that a stand-alone phase-shifted FBG grating can be efficiently used as a passive dosimeter. In particular, we exploited the fact that after exposure to IR there is a change of both the refractive index and thermo-optic response of the fiber grating itself. In this article, after a review of theoretical models and phenomenology related to radiation induced effects on Ge-doped optical fiber, we show that an optical fiber resonator formed by two identical FBGs as end mirrors may serve as a high sensitivity detector for low dose IR measurements. In particular, as sensing region we use a portion of the Ge-doped fiber enclosed between the two FBGs, which are not exposed to IR but are only used as cavity reflectors. After irradiation, we observe a variation of the overall cavity thermo-optic response, which is directly related to the dose delivered to the fiber. In order to measure the thermo-optic response, we frequency lock a laser to the cavity and then monitor the wavelength shift of its resonance modes with the temperature. We demonstrate a detection limit of 360 mGy.
2. Phenomenology and Structural Models of Radio-Induced Point Defects in Ge Doped Optical Fiber
Exposure to IR creates damage to the structure of the irradiated material. Many authors have published on this subject and identified the physical and chemical mechanisms that induce effects on the silicon dioxide network [23–27]. Different types of structural models have been proposed to explain the photosensitivity of Ge doped silica. The first class of such models is termed “color center model” and is based on the generation or the conversion of point defects. The defects cause an alteration of the spectroscopic properties of vitreous silica, with occurrence of absorption bands that, through the Kramers-Kronig relations, provide an explanation for the refractive index variation [25,28]. Other authors propose models predicting “compaction effects” as the origin of the refractive index variations and they describe this variation through the Lorentz-Lorentz relation [29,30]. There are also some models that mix the color centers and the compaction effects models [31]. In this case, the conversion of a type of defect into another involves a large network reorganization, which originates the densification and, as a consequence, the refractive index variation.
The point defects are generated through two mechanisms named knock-on and radiolysis processes. The knock-on process consists in the impact between the bullet and an atom of the glass network which absorbs sufficient kinetic energy to move from its original position. In the case of silica, in order to create a defect through a knock-on, an energy of 10 eV is necessary for an oxygen atom and 20 eV for a silicon atom, the Si-O bond energy being about 5 eV. The radiolysis process consists in the ionization and electronic excitations induced by photons, which later may lead to the formation of point defects. Most of the electron-hole pairs generated by the radiolysis process give rise to luminescence through their recombination, while the remaining pairs interact with phonons and may cause the displacement of some atoms from their original position or can break some bonds [32]. The presence of impurities of Ge-atoms facilitates the formation of defects in the silica matrix: since the energy of the Ge-O bond (∼3.6 eV [33]) is lower than that of the Si-O bond, the breaking of these bonds is more probable with respect to that of the Si-O [34]. Many researchers have studied Ge-doped silica samples by investigating paramagnetic defects through electron paramagnetic resonance spectroscopy [24–27,35–37]. Diamagnetic defects can also be directly investigated by photoluminescence (PL) or cathodoluminescence spectroscopy [38,39]. The point defects are classified into intrinsic defects when the atomic species constituting the material are involved (O or Si atoms), or extrinsic defects when chemically different atoms such as Ge atoms are involved.
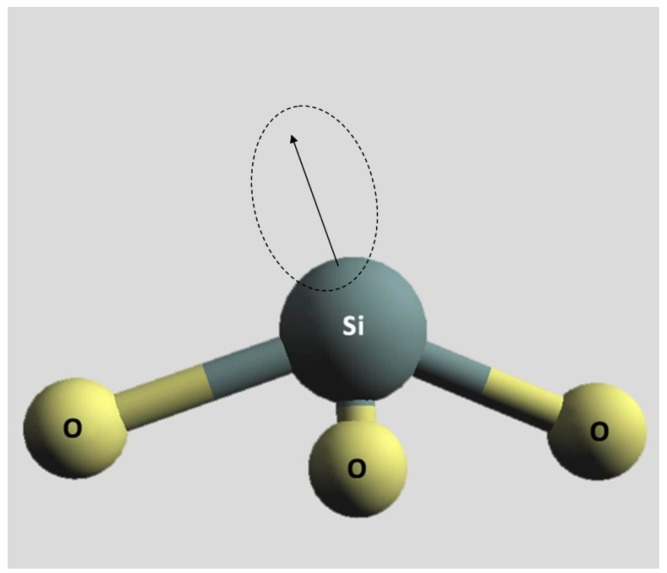
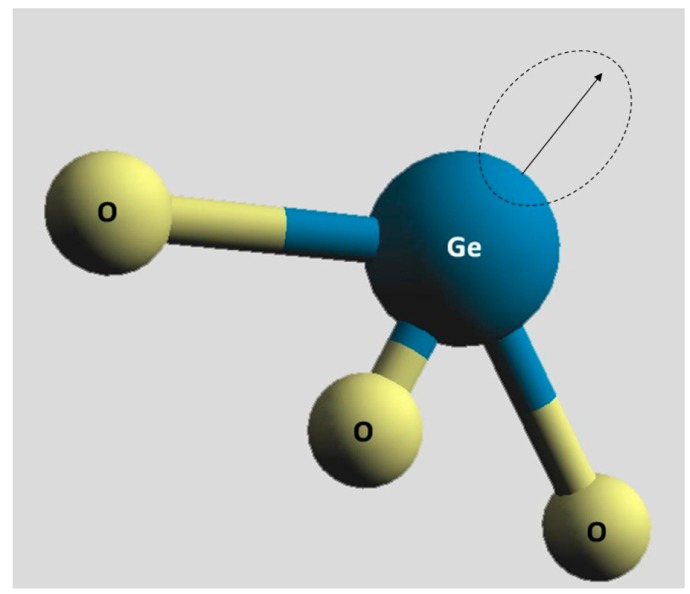
There are several intrinsic defects in Ge doped silica. The E′-center, which is generally denoted by the symbol ≡Si•, where the three parallel lines represent three oxygen separate bonds to one silicon atom and the dot denotes the unpaired electron (Figure 1). The oxygen-deficiency center (ODC) which is a neutral oxygen vacancy (Neutral Oxygen Vacancy–NOV), and can be divided into: the relaxed neutral oxygen vacancy ODC(I), denoted as ≡Si—Si≡, the unrelaxed neutral oxygen vacancy, denoted as ≡Si⋯Si≡, and the twofold coordinated silicon (Silicon Lone Pair Center–SLPC), denoted as =Si•• ODC(II). The non-bridging oxygen hole center (NBOHC), denoted as ≡Si–O•, which can be visualized as the oxygen part of a broken bond. The peroxy bridge (POL), denoted as ≡Si–O–O–Si≡, which is formed by oxygens in excess which create oxygen-oxygen bonds. The peroxy radical (POR) denoted as ≡Si–O–O•, which shows a paramagnetic defect with a O–O bond in the silica structure and the presence of interstitial oxygen atoms. There are also various extrinsic defects: the GeE′, denoted as ≡Ge•, which is structurally identical to the E′ center apart from substitution of Si with Ge (Figure 2): the two fold coordinated Germanium (GeODC(II)) or Germanium Lone Pair Center (GLPC), denoted as =Ge•• and the neutral oxygen vacancy (NOV), denoted as ≡Ge⋯Si≡; the Ge(1) and Ge(2) (Germanium Electron Center), denoted as ≡GeO4•, which are electron traps constituted by an electron trapped on a tetracoordinated Ge atom with a Si or Ge atom in the adjacent tetrahedron, respectively. A more comprehensive review of both the nature and the molecular structure of radiation-induced point defects in pure and doped glassy silica can be found in [27,36,37].
Figure 1.
Schematic illustration of a generic E′-center.
Figure 2.
Schematic illustration of a generic GeE′-center.
3. Experimental Section and Results
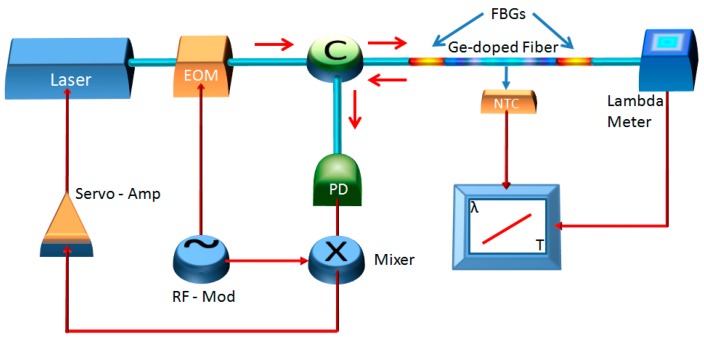
The detection method relies on the measurement of the thermo-optic response variation of a short length of Ge-doped optical fiber after exposure to IR. With respect to wavelength shift measurements, which are usually affected by environmental noise, such as thermal drifts and mechanical instabilities, the measurement of the thermo-optic response is substantially immune to these perturbations [22]. The sensing region (2-cm long) is enclosed between two FBGs. The FBGs form an optical cavity which is interrogated by a near-infrared laser. The laser is frequency locked to a cavity mode using a Pound-Drever-Hall scheme [40]. By scanning the fiber temperature and monitoring the laser wavelength, the thermo-optic response is retrieved. The experimental apparatus is shown in Figure 3.
Figure 3.
Experimental apparatus scheme. A DFB laser emitting at 1560 nm is frequency locked to an optical fiber cavity made by two FBGs. Variations of the thermo-optic response of the optical fiber forming the cavity are measured by scanning the temperature and measuring the wavelength of the light resonating into the cavity. EOM: Electro-optic modulator; C: Optical fiber circulator; PD: Photodiode; RF-Mod: Radio frequency modulation; NTC: Negative temperature coefficient resistor; Servo-Amp: Filtering and amplifying.
A 10 mW DFB Er-fiber laser emitting around 1560 nm (Koheras Adjustik TM, Birkerød, Denmark) is phase modulated at 72 MHz by an all-fiber electro-optic modulator. After modulation two sidebands are generated and overlapped to the laser carrier. This triplet enters the first port of a fiber circulator and then injects the FBG-cavity. When the cavity is on resonance, the sidebands are reflected back by the first FBG and interfere with the carrier resonating into the cavity.
The whole reflected field beam exits the second port of the circulator and is detected by a fast (2 GHz) InGaAs photodetector. The detector signal is demodulated with the 72 MHz modulation signal in a radiofrequency mixer, yielding an error signal, centered around the cavity mode, which is filtered and amplified by a servo system. The servo signal is finally fed back to the laser current, in order to lock its frequency to a cavity mode.
The FBG cavity is inserted into a thermally controlled chamber whose temperature is finely changed around the ambient value (25 °C), the fiber temperature being monitored by a negative temperature coefficient (NTC) resistor placed in contact with the fiber. The cavity transmitted light is collected by a high resolution lambda-meter that measures the center wavelength of the resonating cavity mode in real-time.
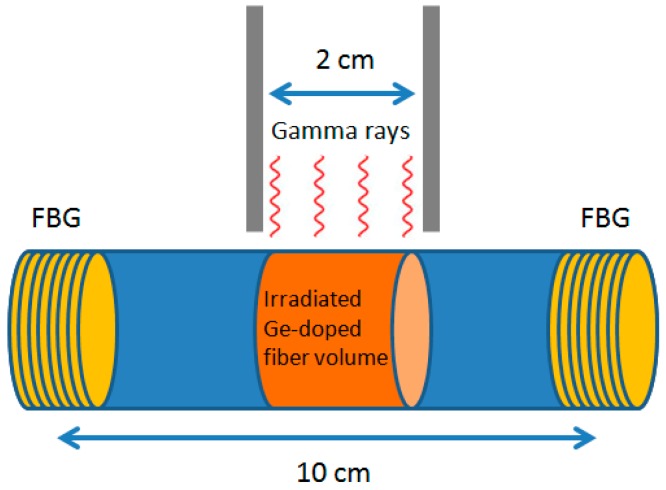
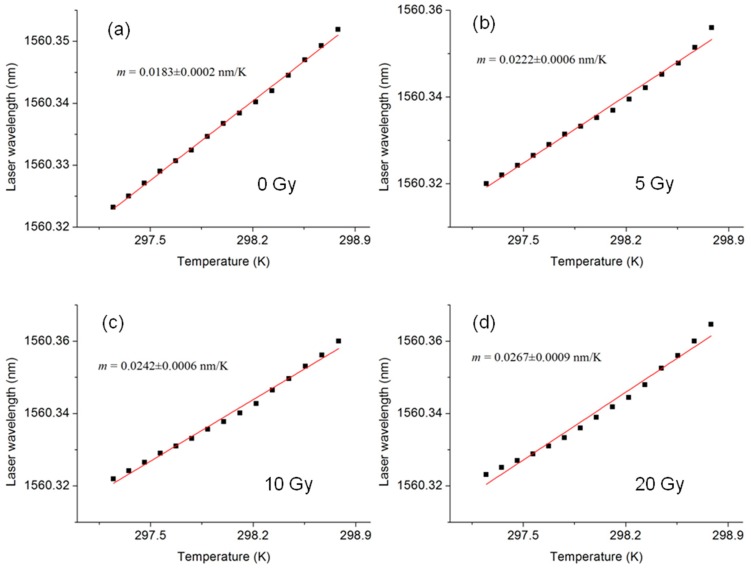
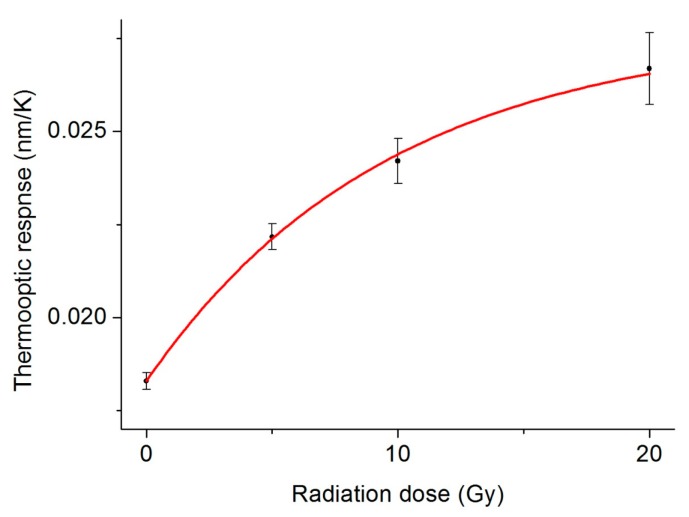
The fiber thermo-optic response was measured before irradiation and after exposure to gamma rays generated by a clinical linear accelerator (average energy 1.6 MeV) with consecutive doses of 5 Gy, 10 Gy and 20 Gy (Figure 4). The fiber was placed into a phantom made of Polymethylmethacrylate (PMMA), which is a good water-equivalent material. Figure 5a shows a graph of the cavity mode wavelength as function of the fiber temperature before irradiation. The data points are well approximated by a line whose angular coefficient m is the cavity thermo-optic coefficient. From a linear fit of the curve we obtain m = 0.0183 ± 2 × 10−4 nm/K. Figure 5b–d show the thermo-optic response measured after each dose, where a dependence of the slope of the curves on the dose is evident. In particular, the thermo-optic response for doses of 5 Gy, 10 Gy and 20 Gy were respectively 0.0222 ± 0.0006 nm/K, 0.0242 ± 0.0006 nm/K and 0.0267 ± 0.0009 nm/K. In Figure 6, the value of the thermo-optic response versus the dose delivered to the fiber is plotted. The curve exhibits an exponential behavior, showing the beginning of sensor saturation for doses above 10 Gy. From a single exponential fit, we obtain a saturation constant of about 9.6 Gy. Approximating the start of the exponential curve with a straight line, we obtain a linear trend with an angular coefficient of 0.0011 nm/K/Gy. Dividing this coefficient by the average value of the uncertainty on the single measurement of the thermo-optic response (0.0004 nm/K) we obtain a final detection limit of 360 mGy.
Figure 4.
Irradiation of a Ge-doped optical fiber enclosed between two FBGs with gamma rays from a 6 MV clinical linear accelerator (photon average energy 1.6 MeV).
Figure 5.
Wavelength of the laser locked to a cavity mode as function of the fiber temperature before irradiation (a) and after exposure to consecutive doses of 5 Gy, 10 Gy and 20 Gy (b–d). By a linear fit of the curves, we obtain the thermo-optic coefficient for each dose.
Figure 6.
Thermo-optic response versus the dose delivered to the fiber. Saturation of the sensor response starts for doses higher than 10 Gy.
These results show that the sensor can be used in those contexts where high sensitivity in small volumes is required, but at the cost of a limited dose range. The most appropriate field of application would be medical dosimetry, where doses on the order of 1 Gy or less are typically involved in radiotherapy treatments.
4. Conclusions
In this work, we investigated the effects of IR on standard SMF28TM Ge-doped fibers. A piece of fiber, enclosed between two FBGs, was irradiated with gamma rays from a clinical accelerator. We observed a change of the fiber thermo-optics response with the dose. We demonstrated that exploiting this effect the Ge-doped fiber can be used as IR sensor, obtaining a detection limit of 360 mGy. The experiment has been performed with a 2-cm long fiber, but, in principle, longer fibers can be used to increase the irradiated length and thus the sensitivity. For example, a 1-m long fiber could easily be arranged in a spiral over a surface of few cm2, leading to a detection limit of few mGy. As proof of principle we have chosen commercial Ge-doped fibers, but also other dopants could be considered. A systematic analysis of fiber materials and dopants, in order to further improve the system performance and sensitivity, will be the subject of a future work.
It is worth noting that the FBG optical cavity built around the fiber served only for measuring the thermo-optic response variations of the fiber, the FBGs being not irradiated at all. Thus, this configuration opens the way to a new class of very sensitive, cheap and disposable dosimeters based on doped fibers. The fiber could just be irradiated alone and then placed within a fiber cavity made up of two FBGs or a fiber-loop. In addition, dosimeters based on this method could be used both in small volumes or over large areas. The sensitive fiber could reach harsh and hardly accessible regions in a minimally invasive manner, such as in medical settings or industrial equipment. On the contrary, a grid of fibers could be placed over large areas, embedded in large structures or underground, e.g., in environmental monitoring and radio-protection applications.
Acknowledgments
The authors acknowledge support by Italian Ministry for Education and Research (MIUR) with the project FIRB RBFR10Q0PT_001 “DROPS”. The authors acknowledge Gianluca Notariale and Andrea Finizio for technical support and Giuseppe Palma for helpful discussions.
Author Contributions
S.A., L.C. and G.G. conceived and designed the experiments; S.A., A.G. and V.D. performed the experiment; S.A., V.D., L.C., P.D.N. and G.G. analyzed the data; V.D., R.P. and R.L. contributed reagents/materials/analysis tools; S.A., V.D., L.C., P.D.N. and G.G. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Radiation Quantities and Units. ICRU; Bethesda, MD, USA: 1980. International Commission on Radiation Units and Measurements (ICRU) ICRU Report 33. [Google Scholar]
- 2.Webb S. The Physics of Three-Dimensional Radiation Therapy—Advances in Technology. IOP Publishing Ltd.; Bristol, UK: 1997. [Google Scholar]
- 3.Intensity Modulated radiation Collaborative Working Group, Intensity-modulated radiotherapy. Current status and issues of interest. Int. J. Radiat. Oncol. Biol. Phys. 2001;51:880–914. doi: 10.1016/s0360-3016(01)01749-7. [DOI] [PubMed] [Google Scholar]
- 4.Sánchez-Doblado F., Andreo P., Capote R., Leal A., Perucha M., Arráns R., Núñez L., Mainegra E., Lagares J.I., Carrasco E. Ionization chamber dosimetry of small photon fields: A Monte Carlo study on stopping-power ratios for radiosurgery and IMRT beams. Phys. Med. Biol. 2003;48:2081–2099. doi: 10.1088/0031-9155/48/14/304. [DOI] [PubMed] [Google Scholar]
- 5.Aspradakis M.M., Lambert G.D., Steele A. Elements of commissioning step-and-shoot IMRT: Delivery equipment and planning system issues posed by small segment dimensions and small monitor units. Med. Dosim. 2005;30:233–242. doi: 10.1016/j.meddos.2005.08.005. [DOI] [PubMed] [Google Scholar]
- 6.Khan F. The Physics of Radiation Therapy. 2nd ed. Williams and Wilkins; Baltimore, MD, USA: 1992. [Google Scholar]
- 7.Bucciolini M., Buonamici F.B., Mazzocchi S., De Angelis C., Onori S., Cirrone G.A. Diamond detector versus silicon diode and ion chamber in photon beams of different energy and field size. Med. Phys. 2003;30:2149–2154. doi: 10.1118/1.1591431. [DOI] [PubMed] [Google Scholar]
- 8.Laub W., Wong T. The volume effect of detectors in the dosimetry of small fields used in IMRT. Med. Phys. 2003;30:341–347. doi: 10.1118/1.1544678. [DOI] [PubMed] [Google Scholar]
- 9.Chuang C.F., Verhey L.J., Xia P. Investigation of the use of MOSFET for clinical IMRT dosimetric verification. Med. Phys. 2002;29:1109–1115. doi: 10.1118/1.1481520. [DOI] [PubMed] [Google Scholar]
- 10.Cella L., Liuzzi R., Salvatore M. The Italian affair: The employment of parallel-plate ionization chambers, for dose measurements in high dose-per-pulse IORT electron beams. Med. Phys. 2010;37:2918–2924. doi: 10.1118/1.3432601. [DOI] [PubMed] [Google Scholar]
- 11.O’Keefe A., Fitzpatrick C., Lewis E., Al-Shamma’a A.I. A review of optical fibre radiation dosimeters. Sens. Rev. 2008;28:136–142. [Google Scholar]
- 12.Rao Y.J. In-fiber Bragg grating sensors. Meas. Sci. Technol. 1997;8:355–375. [Google Scholar]
- 13.Huston A.L., Justus B.L., Falkenstein P.L., Miller R.W., Ning H., Altemus R. Remote optical dosimetry. Nucl. Instr. Meth. Phys. Res. B. 2001;184:55–67. [Google Scholar]
- 14.Friebele E.J., Long K.J., Gingerich M.E. Radiation damage in single-mode optical-fiber waveguides. Appl. Opt. 1983;22:1754–57. doi: 10.1364/ao.22.001754. [DOI] [PubMed] [Google Scholar]
- 15.Vedda A., Chiodini N., di Martino D., Fasoli M., Keffer S., Lauria A., Martini M., Moretti F., Spinolo G., Nikl M., et al. Ce3+-doped fibers for remote radiation dosimetry. Appl. Phys. Lett. 2004;85:6356–6358. [Google Scholar]
- 16.Mones E., Veronese I., Vedda A., Loi G., Fasoli M., Moretti F., Chiodini N., Cannillo B., Brambilla M. Ce-doped optical fibre as radioluminescent dosimeter in radiotherapy. Radiat. Meas. 2008;43:888–892. [Google Scholar]
- 17.Aznar M., Andersen C.E., Bøtter-Jensen L., Bäck S.A., Mattsson S., Kjaer-Kristoffersen F., Medin J. Real-time optical-fibre luminescence dosimetry for radiotherapy. Phys. Med. Biol. 2004;49:1655–1669. doi: 10.1088/0031-9155/49/9/005. [DOI] [PubMed] [Google Scholar]
- 18.Friebele E.J., Schultz P.C., Gingerich M.E. Compositional effects of the radiation response of Ge-doped silica-core optical fiber waveguides. Appl. Opt. 1980;19:2910–2916. doi: 10.1364/AO.19.002910. [DOI] [PubMed] [Google Scholar]
- 19.Lu P., Bao X., Brown K., Kulkarni N. Gamma-induced attenuation in normal single-mode and multimode, Ge-doped and P-doped optical fibers: A fiber optic dosimeter for low dose levels. Can. J. Phys. 2000;78:89–97. [Google Scholar]
- 20.Krebber K., Henschel H., Weinand U. Fibre Bragg gratings as high dose radiation sensors? Meas. Sci. Tech. 2006;17:1095–1102. [Google Scholar]
- 21.Gagliardi G., Salza M., Avino S., Ferraro P., De Natale P. Probing the Ultimate Limit of Fiber-optic Strain Sensing. Science. 2010;330:1081–1084. doi: 10.1126/science.1195818. [DOI] [PubMed] [Google Scholar]
- 22.Avino S., D’Avino V., Giorgini A., Pacelli R., Liuzzi R., Cella L., De Natale P., Gagliardi G. Detecting ionizing radiation with optical fibers down to biomedical doses. Appl. Phys. Lett. 2013;103 doi: 10.1063/1.4826934. [DOI] [Google Scholar]
- 23.Eoin P., Robertson J. Theory of defects in vitreous silicon dioxide. Phys. Rev. B. 1983;27:3780–3795. [Google Scholar]
- 24.Neustruev V.B. Colour centres in germanosilicate glass and optical fibres. J. Phys. Condens. Matter. 1994;6:6901–6936. [Google Scholar]
- 25.Skuja L. Optically active oxygen-deficiency-related centers in amorphous silicon dioxide. J. Non-Cryst. Sol. 1998;239:16–48. [Google Scholar]
- 26.Medjahdi K., Boukenter A., Ouerdane Y., Messina F., Cannas M. Ultraviolet-induced paramagnetic centers and absorption changes in Ge-doped optical fibers. Opt. Express. 2006;14:5885–5894. doi: 10.1364/oe.14.005885. [DOI] [PubMed] [Google Scholar]
- 27.Roushdey S. Defect related luminescence in silicon dioxide network: A review. In: Basu S., editor. Crystalline Silicon—Properties and Uses. InTech; Rijeka, Croatia: 2011. pp. 135–172. [Google Scholar]
- 28.Jani M.G., Halliburton L.E. Point defects in neutron-irradiated quartz. J. Appl. Phys. 1984;56:942–946. [Google Scholar]
- 29.Piao F., Oldham W.G., Haller E.E. The mechanism of radiation-induced compaction in vitreous silica. J. Non-Cryst. Sol. 2000;276:61–71. [Google Scholar]
- 30.Buscarino G., Agnello S., Gelardi F.M., Boscaino R. The role of impurities in the irradiation induced densification of amorphous SiO2. J. Phys. Condens. Matter. 2010;22 doi: 10.1088/0953-8984/22/25/255403. [DOI] [PubMed] [Google Scholar]
- 31.Takahashi M., Ichii K., Tokuda Y., Uchino T., Yoko T., Nishii J., Fujiwara T. Photochemical reaction of divalent-germanium center in germanosilicate glasses under intense near-ultraviolet laser excitation: Origin of 5.7 eV band and site selective excitation of divalent-germanium center. J. Appl. Phys. 2002;92:3442–3446. [Google Scholar]
- 32.Ying L.T. Overview of the Sensitivity of Ge- and Al-doped Silicon Dioxide Optical Fibres to Ionizing Radiation. Mal. J. Fund. Appl. Sci. 2012;8:219–223. [Google Scholar]
- 33.Araujo R. Oxygen vacancies in silica and germania glasses. J. Non-Cryst. Sol. 1996;197:164–169. [Google Scholar]
- 34.Pacchioni G., Ieranò G. Ab initio formation energies of point defects in pure and Ge-doped SiO2. Phys. Rev. B. 1997;56:7304–7312. [Google Scholar]
- 35.Friebele E.J., Griscom D.L., Sigel G.H. Defect centers in a germanium-doped silica-core optical fiber. J. Appl. Phys. 1974;45:3424–3428. [Google Scholar]
- 36.Griscom D.L. A Minireview of the Natures of Radiation-Induced Point Defects in Pure and Doped Silica Glasses and Their Visible/Near-IR Absorption Bands, with Emphasis on Self-Trapped Holes and How They Can Be Controlled. Hindawi Pub. Corp. Phys. Res. Int. 2013 doi: 10.1155/2013/379041. [DOI] [Google Scholar]
- 37.Griscom D.L. Trapped-electron centers in pure and doped glassy silica: A review and synthesis. J. Non-Cryst. Sol. 2011;357:1945–1962. [Google Scholar]
- 38.Salh R. Concentration and Annealing Effects on Luminescence Properties of Ion-Implanted Silica Layers. Hindawi. Pub. Corp. J. Atom. Mol. Opt. Phys. 2011 doi: 10.1155/2011/326368. [DOI] [Google Scholar]
- 39.Kalceff M.A., Phillips M.R. Cathodoluminescence microcharacterization of the defect structure of quartz. Phys. Rev. B. 1995;52:3122–3134. doi: 10.1103/physrevb.52.3122. [DOI] [PubMed] [Google Scholar]
- 40.Drever R.W.P., Hall J.L., Kowalski F.V., Hough J., Ford G.M., Munley A.J., Ward H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B. 1983;31:97–105. [Google Scholar]