Extension of Nakagawa & Schielzeth's R²_GLMM to random slopes models

Abstract

1. Nakagawa & Schielzeth extended the widely used goodness-of-fit statistic R² to apply to generalized linear mixed models (GLMMs). However, their R²_GLMM method is restricted to models with the simplest random effects structure, known as random intercepts models. It is not applicable to another common random effects structure, random slopes models.

2. I show that R²_GLMM can be extended to random slopes models using a simple formula that is straightforward to implement in statistical software. This extension substantially widens the potential application of R²_GLMM.

Introduction

The coefficient of determination, R², is a widely used statistic for assessing the goodness-of-fit, on a scale from 0 to 1, of a linear regression model (LM). It is defined as the proportion of variance in the response variable that is explained by the explanatory variables or, equivalently, the proportional reduction in unexplained variance. Unexplained variance can be viewed as variance in model prediction error, so R² can also be defined in terms of reduction in prediction error variance. Insofar as it is justifiable to make the leap from ‘prediction’ to ‘understanding’, R² can be intuitively interpreted as a measure of how much better we understand a system once we have measured and modelled some of its components.

R² has been extended to apply to generalized linear models (GLMs) (Maddala 1983) and linear mixed effects models (LMMs) (Snijders & Bosker 1994) [reviewed by (Nakagawa & Schielzeth 2013)]. Nakagawa & Schielzeth (2013) proposed a further generalization of R² to generalized linear mixed effects models (GLMMs), a useful advance given the ubiquity of GLMMs for data analysis in ecology and evolution (Bolker et al. 2009). A function to estimate this R²_GLMM statistic, r.squaredGLMM, has been included in the MuMIn package (Bartoń 2014) for the R statistical software (R Core Team 2014). However, Nakagawa and Schielzeth's R²_GLMM formula is applicable to only a subset of GLMMs known as random intercepts models. Random intercepts models are used to model clustered observations, for example, where multiple observations are taken on each of a sample of individuals. Correlations between clustered observations within individuals are accounted for by allowing each subject to have a different intercept representing the deviation of that subject from the global intercept. Random intercepts are typically modelled as being sampled from a normal distribution with mean zero and a variance parameter that is estimated from the data. Although random intercepts are probably the most popular random effects models in ecology and evolution, other random effect specifications are also common, in particular random slopes models, where not only the intercept but also the slope of the regression line is allowed to vary between individuals. Random intercepts and slopes are typically modelled as normally distributed deviations from the global intercept and slope, respectively. For example, random slopes models, under the name of ‘random regression’ models, are used to investigate individual variation in response to different environments (Nussey, Wilson & Brommer 2007). The aim of this article is to show how Nakagawa and Schielzeth's R²_GLMM can be further extended to encompass random slopes models.

Nakagawa and Schielzeth's R²_GLMM

Nakagawa & Schielzeth (2013) defined two R² statistics for GLMMs, marginal and conditional R²_GLMM, that allow separation of the contributions of fixed and random effects to explaining variation in the responses. Marginal R²_GLMM gauges the variance explained by the fixed effects as a proportion of the sum of all the variance components:

eqn 1

where is the variance attributable to the fixed effects, is the variance of the lth of u random effects, is the variance due to additive dispersion and is the distribution-specific variance. The residual variance, , is defined as for the purposes of this manuscript but see Nakagawa & Schielzeth (2013) for an alternative definition of dispersion. Conditional R² additionally includes in the numerator the variance explained by the random effects:

eqn 2

It is the definition of the random effect variances, the , that requires generalization to allow R²_{GLMM (m)} and R²_{GLMM (c)} to be extended beyond random intercepts models. In Nakagawa and Schielzeth's formula, is simply the variance of the l th random intercept. This formula is correct for random intercept models because each observation has the same random effect variance. However, in other random effects specifications, the random effect variance can differ between observations, and, as pointed out by Nakagawa and Schielzeth, this causes difficulties in computing a single random effect variance component.

Extension of R²_GLMM to random slopes models

Consider the simplest and most familiar random slopes GLMM, a LMM with a single random intercept and a single random slope:

eqn 3

eqn 4

eqn 5

eqn 6

where Y_ij and x_ij are, respectively, the response and predictor values (covariates) for the ith observation on the jth individual. Random deviation of the jth individual from the fixed global intercept, β₀, is represented by α_0j, while random deviation from the fixed global slope, β₁, is represented by α_1j. Because intercepts and slopes are typically correlated, three parameters are required to model the random effect, which are represented by the covariance matrix Σ. The leading diagonal of Σ consists of the random intercept variance, , and the random slope variance, , while the off-diagonal element is the covariance, σ_α0α1, between the random intercept and random slope. Finally, ɛ_ij is the residual of the ith observation on the jth individual and is the residual variance. For LMMs, , so that .

The difficulty of defining for this model arises from the dependence of the random effect variance component on x_ij, which implies that cannot be defined from Σ alone, but requires input from the x_ij. An observation-specific random effect variance, , can be defined, given x_ij, as

eqn 7

showing the dependence of on x_ij. For example, when x_ij = 0 (i.e. at the intercept),

eqn 8

while when x_ij = 1,

eqn 9

(Snijders & Bosker 2012). In the most extreme case where the x_ij values are unique, there will be as many random effect variances as observations. The first step to estimating the random effect variance component is to estimate each . The random effect portion of the model, α_0j + α_1jx_ij, can then be viewed as a mixture of n normal distributions with a common mean of zero but up to n different variances, where n is the number of observations. When the mean is constant, the variance of a mixture is simply the mean of the individual variances (Behboodian 1970). The mean random effect variance is therefore

x eqn 9

A simple and general formula for given any value of x_ij can be derived as follows. For any random effects specification, let Z be the design matrix of the random effects of a GLMM with n rows and k columns corresponding to the k random effects, and Σ the covariance matrix of the random effects of dimension k. For example, in the simple random slopes model in equations 3-6, the first column of Z is a vector of ones corresponding to the random intercept, while the second is the predictor variable, the x_ij. The vector of observation-level random effect variances is the leading diagonal of the n × n matrix ZΣZ′, where Z′ is the transpose of Z (Laird & Ware 1982). The mean random effect variance, , is the mean of this vector, that is,

eqn 11

where the Tr denotes the trace operation, which sums the leading diagonal. An index notation version of the matrix notation equation 11 is contained within equation 20 of Snijders & Bosker (1994). The advantage of the matrix version is computational simplicity. Equation 11 gives the same results as Nakagawa & Schielzeth's method for random intercepts models but can also be used for random slopes models as well as models with no intercept. An estimate of for use in Equations 1 and 2 can be easily computed from the estimated covariance matrix of the lth random effect. Examples of the application of this procedure to estimating R²_GLMM from random slopes GLMMs using R are provided as Data S1.

The Supplementary R code also illustrates a simplified method of estimating the term β₀ in equation A6 of Nakagawa & Schielzeth (2013), which approximates 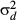for a Poisson GLMM. Rather than refit the model after centring or dropping the covariates as recommended, β₀ can be more easily estimated by taking the mean of , the linear predictor, where X is the design matrix for the fixed effects and is the vector of fixed effect estimates.

These extensions to R²_GLMM have been incorporated into the r.squaredGLMM function in version 1.10.0 of the MuMIn package (Bartoń 2014).

Discussion

The extension described above allows both marginal and conditional R²_GLMM to be estimated from a random slopes model, obviating the need to approximate R²_GLMM from the corresponding random intercepts model as recommended by Nakagawa & Schielzeth (2013). It is clearly preferable to estimate R²_GLMM from the correct model given that there is no computational cost but is the improvement in either marginal or conditional R²_GLMM likely to be substantial? Nakagawa & Schielzeth (2013) suggest that marginal and condition R²_GLMM will usually be very similar when approximated from a random intercepts fit, and Snijders & Bosker (2012) make a similar claim for their related R²₁ and R²₂ statistics. Not surprisingly, the gain in accuracy in both R²_GLMM statistics will depend on how well the random intercepts model approximates the random slopes model. The accuracy of the marginal R²_GLMM approximation will depend on the accuracy of the global slope (or slopes) estimate from the random intercepts model, because the scale of the global slope (or slopes) estimate determines (Nakagawa & Schielzeth 2013), which in turn determines marginal R²_GLMM. For balanced data, where the numbers of observations and the covariate distributions are balanced between groups, this approximation should be good, so the estimates of the global slope and marginal R²_GLMM are likely to be very similar under both models. However, unbalanced data are common in ecology, for example where sampling strategies are constrained in space by variable access to sampling sites or in time by fluctuating resources, and in such cases the improvement in marginal R²_GLMM could be considerable. For example, if one individual (or site, etc.) yields an unusually large number of observations, the global slope estimate will be biased towards that individual in a random intercepts model but not in a random slopes model. Examples of both scenarios are given in the Supplementary R code (Data S1).

Improvement in conditional R²_GLMM is easier to predict and explain. Regardless of the adequacy of the marginal R²_GLMM approximation, if the random slopes model fits substantially better than the random intercepts model, it should have lower residual variance (or less overdispersion, in the context of overdispersed Poisson or binomial GLMMs) and therefore higher conditional R²_GLMM.

This extension will apply to other statistics that incorporate a random effects variance component calculated from a random slopes model, including the intraclass correlation coefficient (ICC), which gauges variance between groups (e.g. individuals or sites) as a proportion of the total variance. ICC can be used to measure intraindividual repeatability, also known as consistency, and has been applied widely in ecology and evolutionary biology (Nakagawa & Schielzeth 2010). Like R², ICC has also been generalized to random intercepts GLMMs by Nakagawa & Schielzeth (2010), but not to random slopes GLMMs. Equation 11 could also be applied to calculating repeatability (Nakagawa & Schielzeth 2010) by fixing a column of Z to a single value. For example, age dependence in phenotypic consistency could be investigated by estimating ICC conditioned on a range of ages.

In conclusion, the extension of R²_GLMM to random slopes GLMMs substantially widens the range of models to which this useful measure can be applied.

Data accessibility

R scripts: uploaded as online supporting information.

Supporting Information

Additional Supporting Information may be found in the online version of this article.

Data S1

R code illustrating the calculation of R²_GLMM.