Detailed Characterization of a Nanosecond-Lived Excited State: X-ray and Theoretical Investigation of the Quintet State in Photoexcited [Fe(terpy)₂]²⁺

Abstract

Theoretical predictions show that depending on the populations of the Fe 3d_xy, 3d_xz, and 3d_yz orbitals two possible quintet states can exist for the high-spin state of the photoswitchable model system [Fe(terpy)₂]²⁺. The differences in the structure and molecular properties of these ⁵B₂ and ⁵E quintets are very small and pose a substantial challenge for experiments to resolve them. Yet for a better understanding of the physics of this system, which can lead to the design of novel molecules with enhanced photoswitching performance, it is vital to determine which high-spin state is reached in the transitions that follow the light excitation. The quintet state can be prepared with a short laser pulse and can be studied with cutting-edge time-resolved X-ray techniques. Here we report on the application of an extended set of X-ray spectroscopy and scattering techniques applied to investigate the quintet state of [Fe(terpy)₂]²⁺ 80 ps after light excitation. High-quality X-ray absorption, nonresonant emission, and resonant emission spectra as well as X-ray diffuse scattering data clearly reflect the formation of the high-spin state of the [Fe(terpy)₂]²⁺ molecule; moreover, extended X-ray absorption fine structure spectroscopy resolves the Fe–ligand bond-length variations with unprecedented bond-length accuracy in time-resolved experiments. With ab initio calculations we determine why, in contrast to most related systems, one configurational mode is insufficient for the description of the low-spin (LS)–high-spin (HS) transition. We identify the electronic structure origin of the differences between the two possible quintet modes, and finally, we unambiguously identify the formed quintet state as ⁵E, in agreement with our theoretical expectations.

Introduction

Switchable molecular compounds have significant potential as very high-density devices in the areas of data storage systems, molecular switching, and display devices.¹⁻³ Promising candidates include transition metal compounds, in particular octahedral Fe^II complexes, which can exist either in a low-spin (LS) or a high-spin (HS) state, depending on parameters such as temperature or pressure.⁴ Light can also induce a spin-state transition in many of these compounds,^5,6 where the resulting HS state can often be stabilized under certain conditions, typically at low temperatures, thus creating a molecular switch in the “on’ position. In order to improve on the performance of these systems, it is essential to characterize the HS state thoroughly, particularly in compounds where some sort of anomaly occurs; understanding how we can modify the properties and the stability of the excited HS state can lead to developments toward applications at room temperature.

The full dynamics of the LS–HS switching has long been described by a simple and rather complete theoretical framework, suggested by A. Hauser and co-workers.⁷⁻⁹ This theory describes the transitions along a single configurational coordinate (SCC), typically the breathing mode of the molecule (i.e., a symmetric stretching along the Fe–ligand bonds), which was found to be valid for all complexes with monodentate, bidentate, and often even polydentate ligands. However, experiments^10,11 and theory^11,12 suggested that the tridentate [Fe(terpy)₂]²⁺ (terpy: 2,2′:6′,2″-terpyridine) molecule behaves differently in several respects, the most important being that the SCC model for the HS–LS transition fails,^11,12 and the switching mechanism involves (at least) two vibrational modes (configuration coordinates). In addition to this anomaly, the nature of the HS state was unclear. Due to the axial compression exerted by the terpy ligands, the symmetry is lowered, and thus the octahedral ⁵T₂ is split into two quintet states of different symmetry with terms ⁵B₂ and ⁵E. These states differ in the configuration of the t_2g subshell and the molecular geometry, particularly the Fe–N bond lengths. A very recent extended X-ray absorption fine structure (EXAFS) study made an attempt to determine the structure of the populated quintet state, but instead of resolving the structure it could only address its distortion due to limited signal-to-noise conditions.¹³ On the basis of this it was concluded that the structure for the ⁵E is in somewhat better agreement with the experimental data than that of the ⁵B₂, although this proposed structure contradicts the energetics arising from the density functional theory (DFT) models applied by these authors, which suggest ⁵B₂ as the more stable quintet state.

In this paper, we revisit the electronic and molecular structure of the quintet state of [Fe(terpy)₂]²⁺ in aqueous solution with advanced experimental and theoretical techniques. We investigate the reasons for and the consequences of the failure of the SCC model (and thus the necessity for a description with two modes) in the molecular geometry and electronic structure. By combining X-ray absorption and emission spectroscopies (XAS and XES, respectively) and X-ray diffuse scattering (XDS) in a single pump–probe setup at the megahertz (MHz) repetition rate,¹⁴ we acquire simultaneously time-resolved structural and electronic structural data with unprecedented quality in the picosecond time domain. We prepare the quintet state of [Fe(terpy)₂]²⁺ with intense, 10 ps, green (532 nm) laser pulses leading to metal-to-ligand charge-transfer (MLCT) excitations that subsequently relax into the HS state on a subpicosecond time scale. We exploit XES and XAS X-ray probes to identify the formation of the quintet state and determine its lifetime; we also employ resonant X-ray emission spectroscopy (RXES) at the 1s → 3d excitations to gain further insights into the 3d states. With EXAFS and XDS we determine the structure of the molecule in the quintet state and its surrounding solvent cage. The results are compared to those obtained on photoexcited [Fe(bipy)₃]²⁺, which has been characterized by a wide range of experimental and theoretical techniques^{11,12,14−27} and which follows the SCC model (the formation of its photoinduced quintet state was shown to be accompanied by a 0.2 Å elongation of all Fe–N bonds).^11,18,20 Moreover, it has served to calibrate coarsely the arsenal of different X-ray tools used in this work.¹⁴ Indeed, optical tools to date suffer from the clear identification of the excited state in such compounds, as this requires an unambiguous observable. The UV–vis range is quite useful in detecting ultrafast changes, but the overlapping bands due to different excited states hampered in most cases a clear identification of the excited-state electronic and (even more) molecular structure. The X-ray tools employed here seek to fill this knowledge gap, and exploiting laser-pump–X-ray probe techniques at MHz repetition rates allows us to gain new insights into both the electronic and geometric structure changes due to its unprecedented signal quality, as we demonstrate in this work.

Experimental and Computational Methods

Experimental Details

The laser-pump X-ray-probe experiments were performed at sector 7ID-D of the Advanced Photon Source (APS) and at beamline ID26 of the European Synchrotron Radiation Facility (ESRF). Both setups utilized amplified laser systems with adjustable repetition rates in the MHz range, thus increasing the duty cycle of the pump–probe studies by orders of magnitude compared to others that use conventional amplified laser systems with kilohertz (kHz) rates. The experimental strategy combined different time-domain X-ray tools into one single setup, which enabled simultaneous measurements of X-ray diffuse scattering (XDS) together with nonresonant X-ray emission spectroscopy (XES)¹⁴ and also variants of X-ray absorption spectroscopy (XAS): (i) high-energy-resolution fluorescence detection (HERFD)^28,29 and (ii) total fluorescence yield (TFY) XAS. The former was possible owing to the implementation of a secondary X-ray crystal spectrometer that energy-resolved the emitted fluorescence. This spectrometer also permitted us to record resonant XES (RXES) to better resolve the 1s pre-edge and thus exploit the improved sensitivity to the 3d orbitals (details further below). Time-resolved XDS was recorded in the forward direction up to a Q-value of around 4 Å^–1 with a MHz-gateable, single-photon-counting area detector. This strategy of combined tools had been implemented and tested on the photoinduced spin transition of aqueous [Fe(bipy)₃]²⁺.^14,25 The present study applied this strategy and advanced setup to obtain complementary information about [Fe(terpy)₂]²⁺, whose investigation is supported by the analysis of the [Fe(bipy)₃]²⁺ data. The experiments at 7ID-D (APS) utilized 24-bunch mode (in top-up mode with a constant 102 mA ring current) with a 6.52 MHz X-ray pulse repetition rate. X-rays were monochromatized with a diamond (111) double-crystal monochromator. An amplified laser system (Duetto from Time-Bandwidth) generating 10 ps pulses at its second harmonic, 532 nm, was used for laser excitation. It was synchronized to the storage ring radio frequency system and operated at a repetition rate of 3.26 MHz, half that of the X-ray rate. The time delay between laser and X-ray pulses could be electronically adjusted in step sizes of 5 ps minimum duration. Details of this time-resolved setup are given in refs (14) and (30). The X-ray beam was focused by a pair of Kirkpatrick–Baez mirrors to 8 × 7 μm², (H × V) on the sample, and the laser beam overlapped this spot with a larger spot size (100 × 80 μm², H × V). The sample consisted of a free-flowing liquid jet of 13 mM aqueous [Fe(terpy)₂]²⁺ solution (total volume 200 mL). The liquid near the nozzle output was a flat sheet, with thickness 0.1 mm, which was oriented at about 45° to both laser and X-ray beams. This geometry permitted simultaneous recording of XDS data (collected in forward scattering direction) and XES data (collected sideways at 90° scattering angle, along the X-ray polarization vector, via the analyzer crystal). For these measurements the incident X-ray probing energy was tuned to 8.2 keV, far above the Fe K edge. The XDS experiments were performed with a Pilatus 100 K detector gated and synchronized to the bunch frequency as described in our previous MHz work.¹⁴ Following masking, azimuthal integration, and scaling, difference signals were constructed and averaged for each time delay and then corrected for multiple-pump–pulse contributions as described in ref (14). Considering the jet speed (6 m/s), the 80 μm spot illuminated by the laser travels only about 2 μm before the next laser pulse arrives 307 ns later. Therefore, it is obvious that the same sample volume is hit many times in such a high repetition rate experiment. Nevertheless, the studied [Fe(terpy)₂]²⁺ complex is very stable, and no degradation was found in any of the signals with exposure. The lifetime of the excited state is 2 orders of magnitude shorter than the separation between the X-ray pulses; therefore, the spectroscopic data are not affected by the previous excitation pulses. On the other hand, the energy transfer to the solvent leads to a temperature increase in the water, which affects the X-ray scattering data. This has been circumvented by using the scattering signal recorded at a Δt = −200 ps time delay as the background. The increased solvent temperature due to the previous laser shots is present in this water signal, and thus it serves as an appropriate reference, as explained in detail in our previous work on [Fe(bipy)₃]²⁺.¹⁴

The Kα XES, (1s2p) RXES, and HERFD-XAS data were collected using a 10 cm diameter, spherically bent (R = 1 m), single-crystal Ge(440) wafer analyzer that focused fluorescence onto a MHz-gated scintillator coupled to a photomultiplier. A bent Si(531) crystal with similar dimensions was used to record the Kβ spectra; the energy resolution was 1 eV for both setups. For recording HERFD-XANES (X-ray absorption near-edge structure), the selected emission energy was kept constant (at the maximum of the Kα₁ line), while in the case of RXES both the energy of the incident beam (Ω) and the fluorescence energy (ω) were scanned. The recorded RXES intensity is displayed on a 2D map with one axis being the incident energy and the other their difference, the energy transfer (Ω–ω).³¹ At the APS RXES data were obtained on aqueous [Fe(terpy)₂]²⁺, while at the ESRF RXES data were taken on aqueous [Fe(bipy)₃]²⁺. The experiments at ID26 (ESRF) utilized 16-bunch mode (no top-up, with decaying ring currents from 90 to 60 mA) with an X-ray repetition rate of 5.68 MHz. Laser excitation was made possible by moving our amplified femtosecond MHz laser system (Tangerine, Amplitude Systèmes) from the European XFEL to ID26. It was synchronized to one-fourth of the 16-bunch repetition rate (1.42 MHz) and to the storage ring. The laser-X-ray time delay was adjusted electronically similarly to what is done at APS. Here we focused on recording RXES planes around the pre-edge of photoexcited aqueous [Fe(bipy)₃]²⁺ (10 mM). The incident radiation was monochromatized by a cryogenically cooled Si(111) fixed-exit double-crystal monochromator. In contrast to the APS measurements, the X-ray (and thus laser) spot size on the sample was much larger (0.6 × 0.1 mm², H × V). Nevertheless the fractional excited-state population was not dramatically lower than at APS due to four times larger average laser power used and to the wavelength of the Tangerine at its second harmonic, 515 nm, which is absorbed more readily by [Fe(bipy)₃]²⁺ than 532 nm due to a larger laser cross section. X-ray emission was analyzed via four spherically bent Ge(440) crystal analyzers oriented nearly orthogonal to the X-ray beam (and along its polarization vector). In addition, the dispersed X-ray emission was directed above the sample to an avalanche photodiode (Si with effective thickness 0.1 mm and 10 × 10 mm² surface area). This vertical arrangement of Rowland circles allowed improvement of the overall energy resolution. The sample consisted of the same liquid sheet as described for the APS setup.

Theoretical Methods

In order to investigate the electronic structure of the quintet states of [Fe(terpy)₂]²⁺ we carried out DFT calculations using the ORCA2.8 program package^32,33 with the gradient-corrected (GGA) BP86 exchange-correlation functional^34,35 and the hybrid B3LYP* functional³⁶ in combination with the TZVP basis set. This approach has been proven to be rather accurate for the description of spin-state transitions in several Fe^II complexes.¹² The geometries of the ¹A₁, ⁵B₂, and ⁵E states were fully optimized with the BP86/TZVP method and then utilized as input for the simulation of the XDS data and for the calculations of XANES. To verify that the optimized molecular geometries corresponded to true minima on the potential energy surface, vibrational frequencies were calculated as second derivatives of the electronic energy. They were found to be positive for the ¹A₁ and ⁵E states confirming that these geometries corresponded to true minima. However, two negative and degenerate frequencies were found for the ⁵B₂ state. Since this could indicate that the obtained ⁵B₂ structure is a transition state, we performed single-point computations along the problematic normal modes as tests. We found that the potential well was rather flat around the minimum in these dimensions which can lead to a numerical error, resulting in negative frequencies. On the basis of this additional result, we concluded that the ⁵B₂ geometry also corresponds to a true minimum.

In order to be able to compare the strengths of the Fe–N bonds in the different electronic states, the Mayer bond order indices, which quantify bond strengths utilizing the actual computed wave function of the molecule,³⁷⁻³⁹ were calculated.

The ⁵E state of [Fe(terpy)₂]²⁺ with D_2d symmetry is susceptible to the Jahn–Teller (JT) effect. To estimate the contribution of this effect, geometry optimizations were repeated with the BP86/TZP method, by applying D_2d and C₂ point group symmetries with the ADF2013.01 code.^40,41 (Note that in C₂ symmetry the correct notation for the JT-distorted ⁵E state would be ⁵B, as seen in the correlation table in the Supporting Information (SI). However, in order to avoid possible confusion between ⁵B and ⁵B₂ term symbols, we decided to keep the ⁵E notation throughout this paper.) Potential energies of excited states have been calculated using time-dependent DFT (TD-DFT) at the B3LYP*/TZVP level, which was found to perform well for describing spin-state switching for a series of Fe^II compounds.¹² Since the ability of DFT to provide accurate spin-state energetics of Fe^II complexes is limited,^12,42 the ⁵B₂ and ⁵E potentials have been evaluated with an ab initio multireference second-order perturbation theory, the CASPT2 method (Complete Active Space Second-Order Perturbation Theory). These computations were performed with the MOLCAS7.6 program package,⁴³⁻⁴⁵ and their detailed description is given elsewhere.¹² The potentials were calculated along two different lines, one which connects the ¹A₁ and ⁵E minima and the other the ⁵B₂ and ⁵E minima. The ⁵B₂–⁵E line is almost orthogonal to the ¹A₁–⁵E line (cf. Figure 9).

Figure 9.

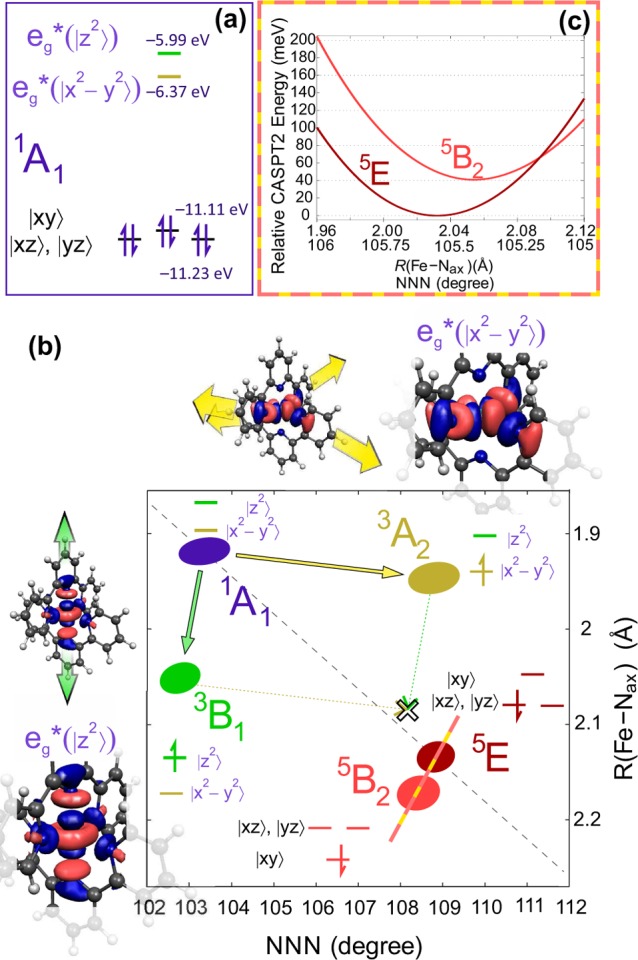
(a) Simplified molecular-orbital diagram for the singlet ground state of [Fe(terpy)₂]²⁺. (b) Schematic representation of the minima for the lowest singlet, lowest two triplet, and quintet states of their potential energy surfaces, along with the filling pattern of their unevenly filled t_2g or e_g^* spin orbitals, which are most relevant to their description. On the side, surface plots present the graphical representation of the two e_g antibonding orbitals of the ¹A₁ together with the structural changes when these antibonding orbitals are populated. The different directions of the expansions and the constraints on the ligand geometry suggest an explanation for the origin of the two modes. A hollow cross indicates the position reached in this configuration space when the coordinate changes at populating the e_g^*-type orbitals are added to approximate the transition to the quintet state. (c) CASPT2 potential curves of the two possible HS (⁵E and ⁵B₂) states of [Fe(terpy)₂]²⁺ along the line connecting their minima, extracted from the potential energy surface of ref (12). Their spin-up e_g orbitals are both populated, and their electronic structure differs only in which of the three t_2g-like nonbonding orbitals are filled with a spin-down electron.

A first-principles approach based on DFT in the generalized gradient approximation (GGA) was adopted to model the X-ray absorption near-edge spectra.⁴⁶ The Fe K-edge XANES was calculated in two steps: first the charge density with a 1s core-hole on the absorbing atom was computed, and then the XANES spectrum was calculated for the electric dipole (1s → p) transitions only, using the broadening parameters given in ref (47). These two steps were performed with the PWscf⁴⁸ and XSpectra⁴⁹ packages, respectively, of the Quantum ESPRESSO suite of codes.⁵⁰ These codes use plane-wave basis sets, pseudopotentials, and periodic boundary conditions; the [Fe(terpy)₂]²⁺ molecule was included in a cubic cell large enough to avoid interactions between molecules belonging to neighboring cells.^51,52 A 110 Ry cutoff energy was used for the plane-wave expansion; the charge density with a core-hole on the iron atom was determined at the Γ point; and a 2 × 2 × 2 Monkhorst–Pack grid was chosen for the calculation of the XAS spectrum of the LS ground state (3 × 3 × 3 for the photoinduced HS state). Spin-polarized calculations were performed in the case of the photoinduced HS state (S = 2). Norm-conserving pseudopotentials⁵³ in the Kleinman–Bylander⁵⁴ form were used, and the parameters for their generation are given in ref (52).

The absorption cross-section of RXES is given by the Kramers–Heisenberg equation⁵⁵ and can be simulated using multiplet calculations based on the Ligand Field Multiplet (LFM) theory.⁵⁵ The 1s2p RXES process for [Fe(terpy)₂]²⁺ was modeled assuming electric quadrupole transitions from the initial state 1s²2p⁶3d⁶ to the intermediate state 1s¹2p⁶3d⁷, followed by an electric dipole emission to the final state 1s²2p⁵3d⁷. The individual absorption and emission transition matrix elements were first calculated using the method developed by Thole,⁵⁶ in the framework established by Cowan⁵⁷ and Butler,⁵⁸ and then combined in a postprocessing step. Details about these calculations can be found in refs (55), (59), (60), and (61). The calculations were performed assuming an octahedral approximation (D_4h symmetry), with a crystal field parameter 10Dq = 2.0 eV for the LS state and 1.3 eV for the HS state; the transition lines were then convolved with a Gaussian, accounting for (some of) the experimental broadening (0.3 eV) and a Lorentzian accounting for the core-hole lifetime broadening (1.2 eV for the intermediate state and 0.2 eV for the final state). The Slater integrals that describe the electronic interactions were scaled down to 80% of their atomic values to account for covalency.

Results and Discussion

Formation and Decay of the Quintet State

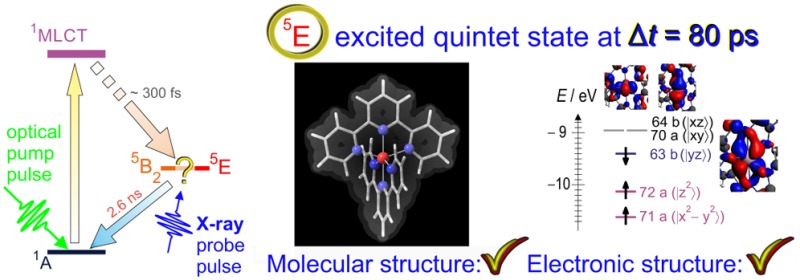
Potential energy surfaces (PESs) are the key to understanding the photophysics and photochemistry of molecular systems. It has been found recently that the PES of Fe^II or Ru^II compounds with a MN₆ core (M = Fe or Ru) can be described reasonably well using DFT and TD-DFT,^12,62,63 providing a means to qualitatively examine the de-excitation mechanism.⁶³ Therefore, we have completed our previous calculations¹² on [Fe(terpy)₂]²⁺ by adding the potential energies for the singlet and triplet metal-to-ligand charge transfer (MLCT) states. The most relevant ones of them are plotted together in Figure 1 with those of the lowest singlet and quintet as well as three of the triplet metal-centered states, along a combined coordinate based on the R(Fe–N_ax) bond length and the NNN angle of the donor atoms of the terpy ligands. This coordinate connects the LS and HS (⁵E) minima, which was found to be relevant to the description of this system.^11,12 The potential energy curves show very similar structure and crossings to those of [Fe(bipy)₃]²⁺.^12,26 Therefore, similar de-excitation pathways for both complexes after the excitation into the ¹MLCT may be expected. Although the metal-centered quintet (⁵E) crosses the ^1,3MLCT band somewhat close to its minimum, the coupling between these states was found negligible in a recent theoretical work on [Fe(bipy)₃]²⁺, and it was suggested that the system relaxes via the metal-centered triplet states before the intersystem crossing to the quintet.²⁶ This theoretical expectation has been proven experimentally very recently by femtosecond-resolved XES.²⁷ In [Fe(terpy)₂]²⁺ de-excitation via the triplet states seems highly likely given that the potential curve of the ³B₁ state crosses the ³MLCT band at its minimum. Strong coupling between them would make relaxation to this metal-centered triplet state rapid. Verification of this de-excitation pathway in [Fe(terpy)₂]²⁺ requires more involved theoretical or experimental evidence; moreover, one should keep in mind that the true triplet minima do not lie on this combined coordinate, as will be obvious in the final section of this discussion. Nevertheless, based on the mentioned crossing and the almost identical structure of potential energy curves to those of [Fe(bipy)₃]²⁺, the system is very likely to follow a decay path that includes triplets. A possible sequence is indicated by the arrows in Figure 1. From the intermediate lifetimes determined for [Fe(bipy)₃]^2+26,27 it is understood that relaxation to the quintet state takes place on the subpicosecond time scale, and based on the similarities and the possibly even better positioned triplet states, one can assume this is true for [Fe(terpy)₂]²⁺ as well.

Figure 1.

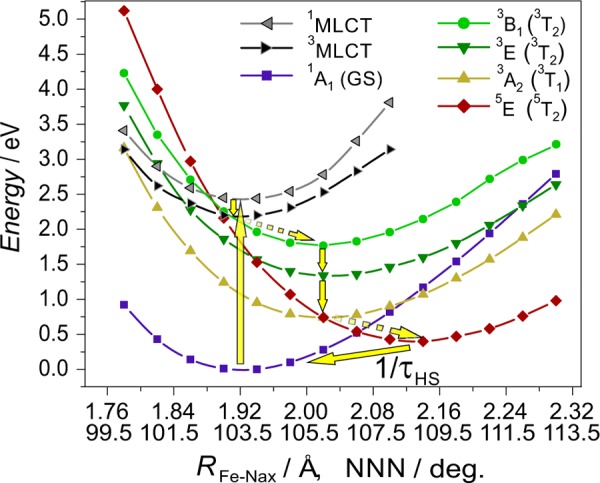
DFT (¹A₁, ³A₂, and ⁵E) and TD-DFT (¹MLCT, ³MLCT, ³B₁, and ³E) potential energy structure of [Fe(terpy)₂]²⁺ along the line connecting the ¹A₁ and ⁵E minima; arrows indicate a possible chain of transitions for the full photocycle. The octahedral parent term symbols are also given in parentheses to aid the identification of the metal-centered states. (As the curves for the ⁵E and ⁵B₂ states on this scale would almost coincide, for clarity only the first one is plotted. Also, in order to keep the figure relatively simple, from each of the ¹MLCT, the ³MLCT, and the metal-centered singlet states, only the lowest-lying ones are plotted. Note also that the arrows are only schematic representations of the transitions, particularly between parallel curves, as they cannot represent the coupling by the other vibrational modes between the connected states.)

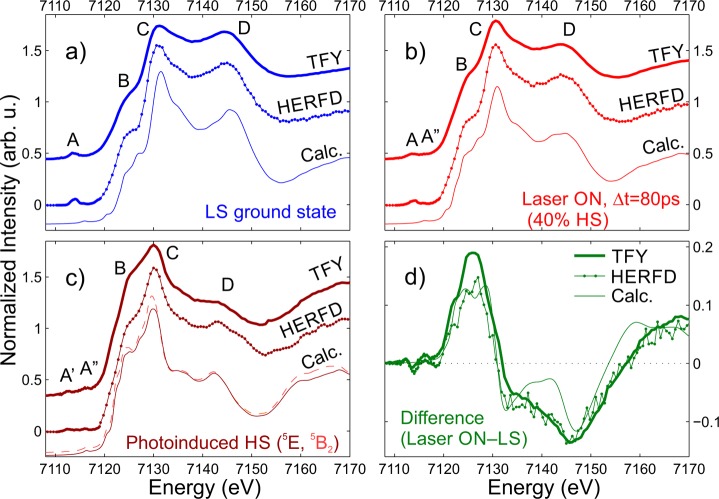
Having argued that the photocycle of [Fe(terpy)₂]²⁺ in many respects resembles that of [Fe(bipy)₃]²⁺, it is evident that experimental studies of the subpicosecond processes leading to the HS (quintet) state can only be achieved with femtosecond-resolved techniques. The lower temporal resolution synchrotron studies presented here probe the system after it has already reached the HS quintet state and as it decays back to the LS ground state. In order to verify the formation of the HS species and quantify its yield, XAS and XES spectra of an aqueous solution of [Fe(terpy)₂]²⁺ were taken before and 80 ps after light excitation. The TFY-XANES spectra (Figure 2a) show significant light-induced variations, the largest ones being the intensity increase of the 7125 eV B feature and the intensity decrease of the 7142 eV D feature. These changes are similar to those observed for the thoroughly studied [Fe(bipy)₃]²⁺ complex,^14,16,20 thus confirming the formation of the photoinduced HS state. In the XES spectra (Figure 2b,c), for both the Kα and Kβ emission lines the spectral variations associated with the formation of the photoinduced HS state are evident and fully consistent with previous studies.^14,24,25,64 The variations of both the Kα and the Kβ spectra are essentially identical to those of the [Fe(bipy)₃]²⁺ complex¹⁴ which is expected since the XES line shapes of 3d transition metal ions reflect practically only the spin state. The first coordination shells of Fe in both complexes are distorted octahedra, and XES spectra are not sensitive to the other relevant differences in symmetry.

Figure 2.

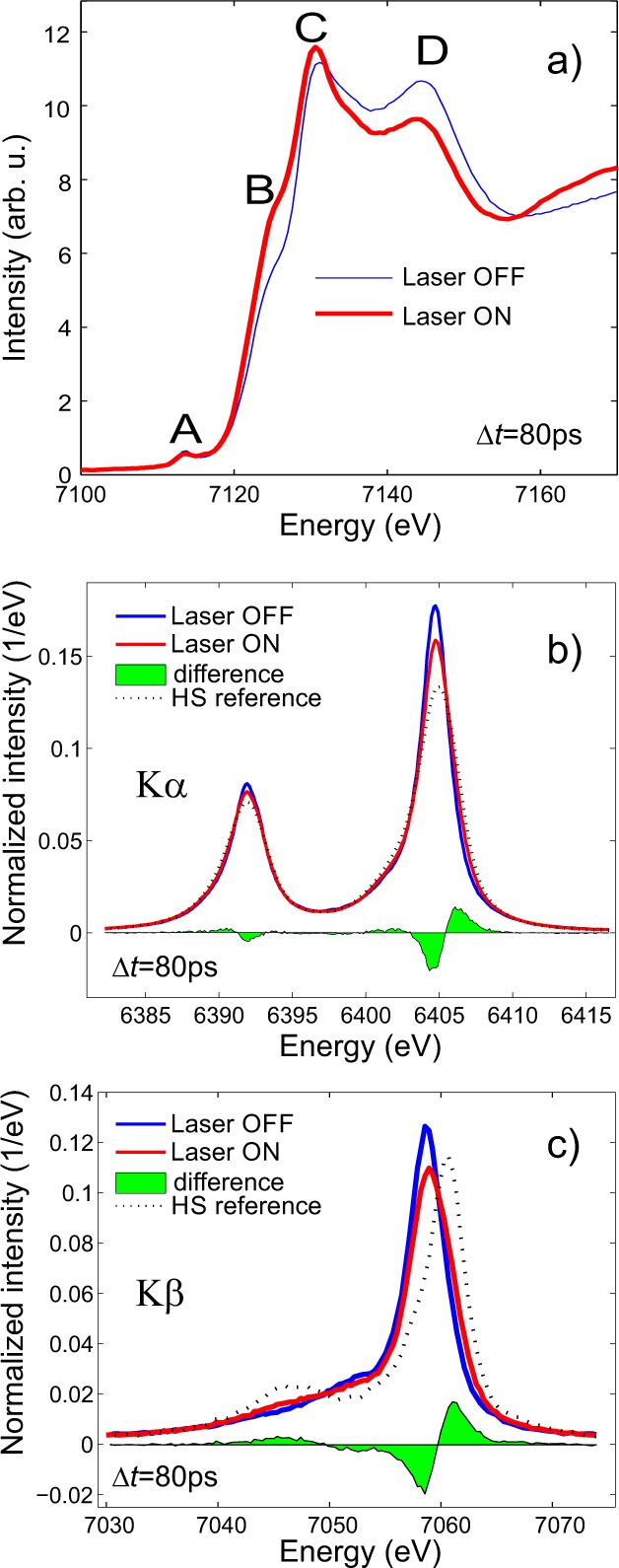
Fe K-edge TFY-XANES (a), Kα (b), and Kβ (c) X-ray emission spectra of a 13 mM aqueous solution of [Fe(terpy)₂]²⁺, with (red line) and without (blue line) laser excitation, with a time delay Δt = 80 ps for the laser-excited data. The evolution of the intensity of the B and D features, as well as the changes in the emission lines, are the signature of a change from the LS to HS configuration. The photoinduced HS fraction can be determined from XES by comparing the spectra to LS/HS references and was found to be γ = 40%.

The laser ON XAS and XES spectra (Figure 2, red line) represent the laser-excited state of the [Fe(terpy)₂]²⁺ complex, which is a combination of both LS and HS contributions. To infer the photoinduced HS fraction (γ), we used an approach that utilizes XES spectral differences between LS and HS references, referred to as the integrated absolute difference (IAD) approach.^14,25,64 The typical photoinduced HS fraction observed during our experiments at 80 ps delay was found to be γ = 40%, although at high laser power 60% could also be achieved.

The formation and decay of the photoinduced HS state can be followed by monitoring the intensity of an appropriate spectral or scattering feature at different time delays (Δt). From the XANES of [Fe(terpy)₂]²⁺ the intensity of the B feature at 7125 eV (which presents the largest variation at the spin-state transition) was used for this purpose; its time evolution is displayed in Figure 3. The corresponding fit of the kinetics uses a model consisting of an exponential decay and a broadening by a Gaussian pulse, which is described in the SI. The lifetime of the photoinduced HS state is τ_HS^XAS = 2.61 ± 0.01 ns. This value is fully consistent with the lifetime of τ_HS = 2.54 ± 0.13 ns obtained with the optical probe for aqueous [Fe(terpy)₂]²⁺.⁶⁵

Figure 3.

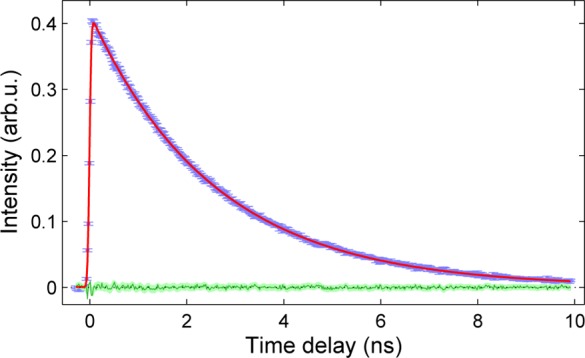
Time evolution of the intensity of the 7125 eV (B) feature of the [Fe(terpy)₂]²⁺ XANES spectrum (Figure 2a), reflecting a quintet lifetime of τ_HS = 2.61 ± 0.01 ns.

Structure of the Photoinduced Quintet State

Having verified the formation of the HS state and determined its lifetime, we make an attempt at determining its structure. The theoretical molecular geometry is available from DFT calculations,^11,12 and the ground state matches excellently the available experimental data, as can be seen in Table 1. For the possible quintet structures, the DFT models are very similar to each other; their corresponding Fe–N bond lengths differ at the few picometer level. This presents a great challenge to the experimental efforts that aim to determine the difference in order to identify which HS state is populated. The most distinct difference between the possible quintet states is the anisotropic distribution of Fe–N bond lengths in the first coordination shell, which is present in the case of the ⁵E quintet (leading to small but appreciable differences between axial and equatorial bonds), whereas it is lifted in the ⁵B₂ state. As will be shown in the following section, the very high quality of the picosecond EXAFS spectra presented here was decisive to resolve these very small structural variations and provide unambiguous assignment of the quintet structure.

Table 1. Most Relevant Structural and Bonding Parameters of the LS and HS States of [Fe(terpy)₂]^2+a.

	LS (1A1)		HS (5E)	HS (5B2)
	exptl66	calculated
R(Fe–Nax)	1.891(5) Å	1.886 Å	2.103 Å	2.159 Å
R(Fe–Neq)	1.988(10) Å	1.985 Å	2.198 Å	2.187 Å
NNN angle	102.8(3)°	102.6°	108.4°	107.2°
BFeNax	-	0.65	0.39	0.33
BFeNeq	-	0.60	0.34	0.34

^aThe experimental data are taken from ref (66). The calculations were carried out at the DFT BP86/TZVP level (for the ⁵E at the (relaxed) JT-distorted geometry). BAB denotes the Mayer bond order index, a powerful parameter quantifying the strength of chemical bonds between atoms A and B (based on MO coefficients and overlaps).^37,39,67

Resolving the Quintet Structure with EXAFS Spectroscopy

We have measured the EXAFS spectra of the [Fe(terpy)₂]²⁺ complex in its ground LS and photoexcited HS state (at a time delay of 80 ps) with outstanding statistical quality. The spectra allowed us to verify experimentally the DFT-predicted molecular geometries for both spin states. Moreover, the bond length accuracy of the HS spectrum, unprecedented in time-resolved experiments, permitted us to determine with high confidence which of the two possible quintet states (⁵E and ⁵B₂) is populated after the light excitation.

The conventional curve-fitting approach of Fourier-transformed EXAFS spectra with standard software packages⁶⁸ has been used. A detailed description of EXAFS data reduction procedures, fitting approach, and methods used for statistical evaluation of fit errors is available in the SI.

The Fourier-transformed (FT) EXAFS spectrum of the LS ground state is shown in Figure 4a together with the fit function. In this case we have started with the DFT-optimized ¹A₁ geometry as input structure and refined it during the fitting process. The inset in Figure 4a shows the corresponding k²-weighted EXAFS spectrum in k-space together with the fit curve. (The spectra in this figure appear shifted, as they have not been phase corrected.) The first peak observed in the FT-EXAFS spectrum in Figure 4a corresponds to the first coordination shell, which contains solely contributions from single-scattering paths involving axial and equatorial N atoms (N_ax and N_eq, respectively) and the central Fe atom. The peaks in the range between 2 and 4 Å correspond to the second and further coordination shells around the Fe^II ion, as well as multiple scattering paths from the first coordination shell. In the theoretical structure of the LS singlet state, the molecule is axially compressed. This leads to an anisotropic distribution of Fe–N bond lengths in the first coordination shell, with the axial Fe–N bonds about 0.1 Å smaller than the equatorial ones (cf. Table 1). The obtained EXAFS fit is in full agreement with this prediction, and we can unambiguously distinguish between the shorter axial Fe–N_ax bonds and the expanded equatorial bonds. The refined experimental bond lengths are R(Fe–N_ax) = 1.874 ± 0.004 Å and R(Fe–N_eq) = 1.969 ± 0.004 Å, in very good agreement with the DFT-calculated bond lengths listed in Table 1.

Figure 4.

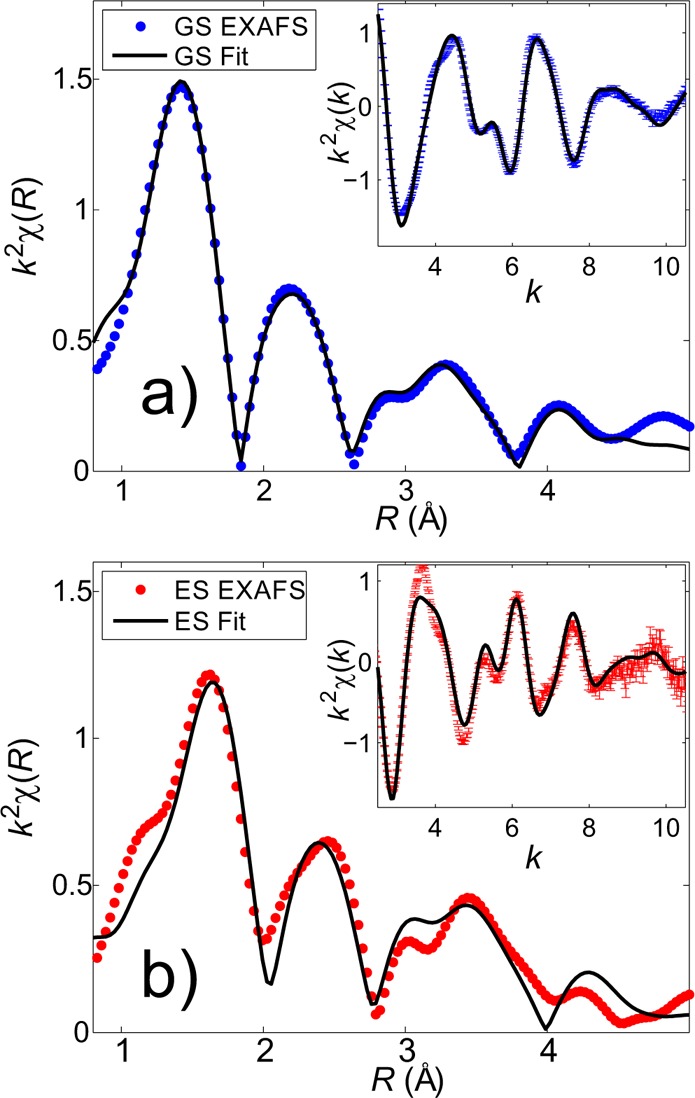
(a) EXAFS of [Fe(terpy)₂]²⁺ in the ground state; the fitted bond lengths are R(Fe–N_ax) = 1.874 ± 0.004 Å and R(Fe–N_eq) = 1.969 ± 0.004 Å. (b) EXAFS spectrum of the photoexcited quintet state of [Fe(terpy)₂]²⁺; the fitted bond lengths are R(Fe–N_ax) = 2.08 ± 0.02 Å and R(Fe–N_eq) = 2.20 ± 0.01 Å.

The EXAFS spectrum of the photoexcited [Fe(terpy)₂]²⁺ molecule measured at 80 ps time delay is presented in Figure 4b. The spectrum was obtained using the data reduction method described in the SI. The expected elongation of Fe–N bonds (together with the expansion of outer-lying coordination shells) is clearly visible from the shift of all main peaks present in the FT spectrum toward higher R-values. Similarly to Figure 4a, the inset shows the photoexcited EXAFS spectrum in k-space with the corresponding best-fit result.

To ensure an unbiased determination of the excited-state structure, a range of starting parameters was used that covered the structures of the two proposed quintet states (using the corresponding theoretical models) as initial guesses. As derived from the DFT, the anisotropy affecting the Fe–N bond lengths is preserved in the HS excited state only for the ⁵E structure, whereas the structure of the ⁵B₂ state has fairly similar Fe–N bond lengths for all six N atoms. Independent of the initial guess, in all cases the fit converged to a structure with substantially distinct Fe–N_ax and Fe–N_eq bonds lengths, clearly indicating that the anisotropic bond distribution is preserved in the photoexcited state and that we can distinguish between the two possible excited states. Furthermore, a rigorous statistical evaluation of the fit results based on χ²-analysis is discussed in detail in the SI and undoubtedly excludes the ⁵B₂ quintet state due to the lack of any substantial differences between its Fe–N bonds within the first coordination shell and supports the ⁵E quintet state as the only possible structural model of the HS state. The refined Fe–N bond lengths are R(Fe–N_ax) = 2.08 ± 0.02 Å and R(Fe–N_eq) = 2.20 ± 0.01 Å, in excellent agreement with the theoretical model for the ⁵E state (cf. Table 1), which allows us to unambiguously assign its structure to the dynamically measured HS state.

It is worth mentioning that the inclusion of outer coordination shells (beyond Fe–N single scattering contributions in the 1–2 Å range in Figure 4) was possible given the superior EXAFS data quality obtained in the experiment for both the LS ground and photoexcited HS state spectra. In both cases, the statistical goodness of the fit, evaluated using the χ² test (see the SI for more details), significantly improved when extending beyond the first coordination shell and also by taking into account some of the multiple scattering contributions from outer-lying C atoms. For both LS and HS spectra, only very minor changes to the second and third coordination shells of DFT-optimized geometries were needed for fits to converge to minimum χ² values (further details can be found in the SI).

Structural Information from XDS

The X-ray scattering signal from a (dilute) solution usually contains only a very small contribution from the solute. However, calculating the difference signal ΔS(Q, Δt) = S(Q, Δt) – S(Q, −∞) effectively removes the otherwise dominating, but almost constant, scattering signal from the solvent. This procedure thus highlights the scattering signature of the structural dynamics of the solute and its environment, the solvent cage, and the structural changes in the surrounding bulk solvent. The analysis approach applied here is fully analogous to the one presented in ref (14), where the analogous [Fe(bipy)₃]²⁺ compound was investigated.

Such difference signals acquired at six time delays from Δt = 100 ps to Δt = 25 ns measured on the [Fe(terpy)₂]²⁺ solution are shown in Figure 5a. Qualitatively, the characteristic negative feature around Q = 0.8–1.2 Å^–1 corresponds to the immediate (on the 100 ps time scale) appearance of the bond-elongated HS structure, and the oscillatory feature around Q = 2.2 Å^–1 arises from temperature (T) and density (ρ) changes in the bulk solvent, as described in detail in ref (14) for the [Fe(bipy)₃]²⁺ complex and in ref (69) for the PtPOP complex. Figure 5b shows the experimental signal ΔS(Q, Δt = 1 ns) as well as two simulated signals ΔS_model = γ × ΔS_Solute+Cage + ΔT × ΔS_ΔT + Δρ × ΔS_Δρ, where γ is the photoexcitation fraction and ΔS_Solute+Cage has been calculated for each of the two proposed HS structures ⁵E and ⁵B₂. The ΔT × ΔS_ΔT and Δρ × ΔS_Δρ contributions describe the changes in scattering due to bulk-solvent heating and density changes, respectively, and are determined in a separate experiment.^70,71 Figure 5c displays each of these three contributions to the model difference signal at Δt = 1 ns, where the magnitudes of the individual contributions are comparable. Separate fits were carried out for each time delay and for both putative HS states, yielding essentially similar results.

Figure 5.

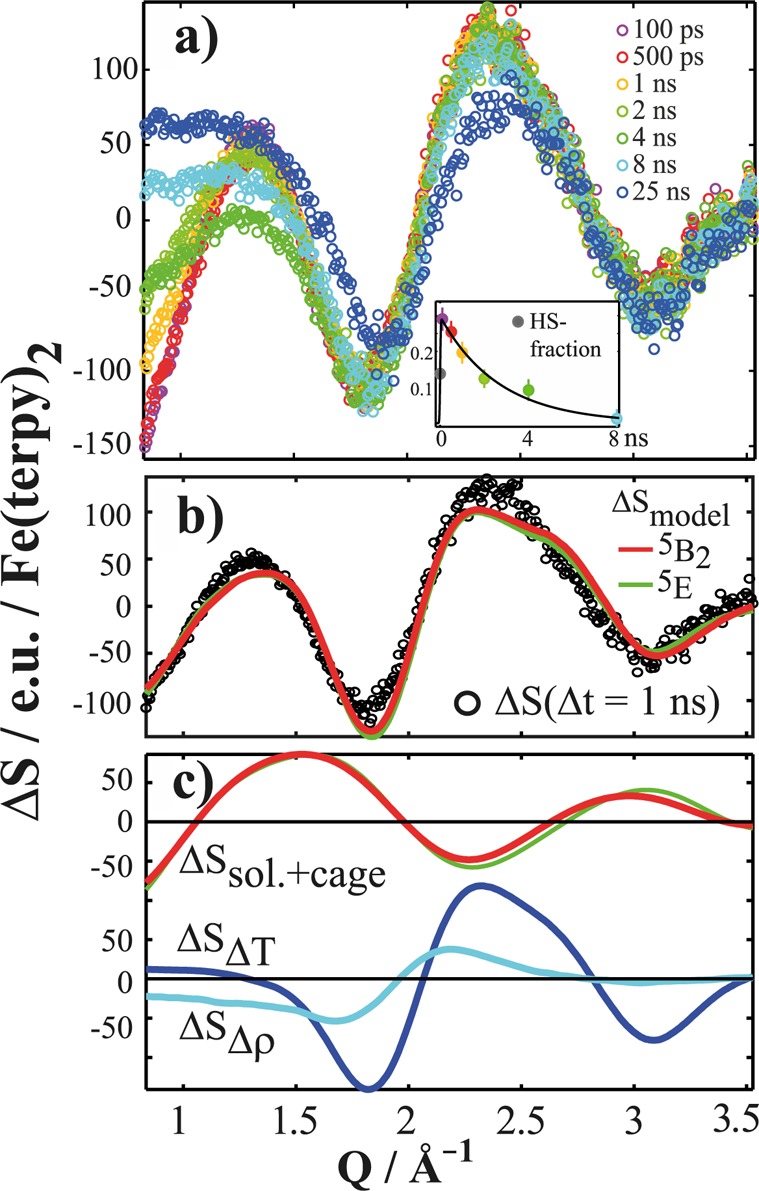
(a) Set of difference scattering signals ΔS(Q, Δt) acquired for [Fe(terpy)₂]²⁺, color-coded according to time delay. The inset shows the evolution of the HS fraction obtained from the magnitude of the solute-related contribution to the difference scattering signal as a function of time delay. (b) ΔS(Q, Δt = 1 ns) (black circles) and the best-fit simulated difference signal for both of the suggested HS structures (red = ⁵B₂, green = ⁵E). (c) Each of the three contributions to the simulated difference signal, with the two solute-related difference signals again shown in red (⁵B₂) and green (⁵E). Bulk solvent contributions are shown in light Δρ × ΔS_Δρ and dark blue ΔT × ΔS_ΔT.

The time evolution of the magnitude of γ, the photoexcited fraction for the HS state, is shown in the inset of Figure 5a. Fitting γ in analogy with the fit of the XAS signal described above, we find τ_HS^XDS = 2.7 ± 1.5 ns, which is in reasonable agreement with the XAS-derived value; the larger uncertainty arises from the fewer time-domain data points in the XDS data set. The time evolution of ΔT and Δρ reflects the dynamics of the energy transfer to the solvent. In general, they follow what was observed in the analysis of [Fe(bipy)₃]²⁺,¹⁴ although the density increase is somewhat smaller in magnitude in the present case (∼0.1 vs ∼0.4 kg·m^–3) and is at the limit of detection. The temperature increase is also observed to be lower (∼0.3 vs ∼0.6 °C), in agreement with the lower concentration of excited-state solutes depositing energy to the solvent through the nonradiative decay processes. Finally, it is evident from Figure 5b that the expected difference signals for the two putative structures are very similar and that they fit the acquired data almost equally well.

In conclusion, the XDS results confirm the plausibility of the DFT structural models, but the present data set does not allow us to recognize the tiny differences of the quintet structures in the variations of the solute signal. Moreover, the time evolution of ΔT and Δρ provides invaluable insights into the solvent dynamics around the excited solute.

Structure and Electronic Structure from XANES

K-edge XANES relates to the p-projected unoccupied electronic density of states of the absorbing atom. Since this is largely influenced by the coordination and bonding, this technique is usually rather sensitive to structural changes around the absorbing atom. For the laser-induced quintet state of [Fe(terpy)₂]²⁺, the population of the antibonding e_g^* orbitals leads to dramatic rearrangements in the molecular and electronic structure which, as has been shown in Figure 2a, are clearly evident in the near-edge region. The structural differences between the two quintet states, however, are considerably smaller, and distinguishing them with XANES is more challenging. Yet the electronic structure of the ⁵E and ⁵B₂ states differs, and one expects that this would yield differences in their XANES spectra. With the objective of obtaining further insights into the nature of the quintet state while at the same time assessing the capabilities of XANES to reveal electronic and structural information when very small changes are involved, we compare experimental XANES spectra with theoretical spectra obtained from DFT calculations.

The experimental XANES spectra of the ground and laser-excited (Δt = 80 ps) states were recorded in both TFY and HERFD (taken at the maximum of the Kα₁ peak) modes. These spectra are shown in Figure 6. HERFD-XANES usually leads to improvement in the energy resolution when compared to the conventional detection modes.²⁸ In the current experiment, although the HERFD spectra appear somewhat sharper and better resolved, the effect is not dramatic. This can be explained by the fact that the relatively broad energy resolution of the spectrometer (∼0.8 eV) could not improve too much further on the good resolution obtained already in the TFY-XANES due to the narrow energy bandwidth of the incident beam (∼0.5 eV).

Figure 6.

Experimental and calculated Fe K-edge XANES spectra of (molecular) [Fe(terpy)₂]²⁺. With the experimental data, both detection modes (TFY: thick lines and HERFD: dotted lines) are presented; for the theoretical spectrum (thin line), only the electric dipole contribution is plotted. (a) LS ground state; the theoretical spectrum was calculated using the ¹A₁ structure. (b) Partially excited [Fe(terpy)₂]²⁺ (Laser ON, Δt = 80 ps); the theoretical spectrum was constructed as a linear combination of the calculated LS (60%) and HS (40%) spectra. (Given the similarity of the two theoretical HS spectra, the reconstruction was done only for the ⁵E structure for clarity.) (c) Photoinduced HS state of [Fe(terpy)₂]²⁺; the plot shows the experimental spectra reconstructed from the laser ON and LS measurements (utilizing the population from XES) and the theoretical spectra calculated for both possible HS states, ⁵E (thin line) and ⁵B₂ (dashed line). (d) Transient XANES obtained as the difference of the laser ON–LS (ground state) spectra.

Theoretical modeling of K-edge XANES based on the single electron picture has became reliable, and its combination with experiment grew a powerful tool in electronic structure analysis.^52,72−74 The theoretical spectra were obtained with such a well-established, reliable approach that takes into account the 1s core hole, utilizing the Quantum ESPRESSO program packages.⁵⁰ Electric dipole transitions from the 1s state to the unoccupied p-states were calculated, and DFT (BP86/TZVP) optimized structures for the LS and HS states were utilized. Comparing first the spectra of the LS ground state in Figure 6a it is clear that the DFT-derived spectrum agrees very well with the experiment. The energy positions and the relative intensities of the major spectral features, labeled B, C, and D, are well reproduced, including the high-energy shoulder of peak C (which is resolved only in HERFD-XANES). The pre-edge peak labeled A consists of mostly quadrupolar transitions and so is not expected to be properly accounted for by the current electric dipole calculation.

Comparisons to the laser-excited (Δt = 80 ps) experimental spectra are shown in Figure 6b, c, and d. In Figure 6b the measured laser ON spectra, which contain a mixture of LS ground state and HS excited state contributions, are compared with a superposition of LS and HS theoretical spectra. Here the calculated HS component arises solely from the ⁵E state. The proportion of HS contribution is taken to be 40% based on the excitation fraction derived from the XES measurement. The calculated spectrum is seen to again reproduce the key spectral features, peaks B, C, and D. For a comparison that is independent of the LS and HS population fractions, the differences between the laser ON spectra and the LS ground state spectra are shown in Figure 6d. Here the theoretical HS–LS difference, which has been scaled to match the intensity of the measured curves, can be seen to mimic the shape of the experimental difference spectra. The agreement in both of these comparisons validates the compatibility of the DFT calculated HS state structure with the experimental observations.

To test whether XANES could distinguish between the two possible HS states and perhaps confirm the EXAFS assignment, theoretical spectra for the ⁵E and ⁵B₂ states were compared to experimental spectra for the HS state that have been reconstructed from the laser ON spectra assuming a 40% HS state fraction. These are shown in Figure 6c. The calculated spectra are seen to be very similar, making a definitive assignment of the experimental spectra to one or the other state difficult. Comparing the ratio of the B and C peak intensities obtained in HERFD and in the calculations, one could be tempted to interpret it as supporting the ⁵E model to be closer to the experiment. However, the C:D peak intensity ratios might lead to the opposite conclusion, which warns us that this approach might be very far-stretched, as the calculated intensities are apparently not accurate enough for such conclusions in the present case.

The primary electronic structure differences between the ⁵E and ⁵B₂ quintets manifest themselves in the occupation of the 3d orbitals, which brings us to the discussion of the variation of the experimental pre-edge region (peaks A, A′, and A″) upon excitation. This part of the spectrum stems from 1s → 3d transitions. Being sensitive to the occupation of the 3d orbitals, this shall provide further information on the electronic structure. Indeed, as is evident from Figure 6, this region shows large variations after excitation. However, in conventional XANES these peaks are usually weak and overlapping, and they are also partly obscured by the tail of the main K edge; therefore, they are often poorly resolved. In order to overcome these difficulties and obtain better resolved spectra, we have recorded 1s2p_3/2 RXES, the combination of XANES in the preedge region, and the (1s2p) XES around the Kα₁ peak. This is presented in the next section.

Resolving the XANES Pre-Edges with RXES: Further Insights into the 3d Electron States

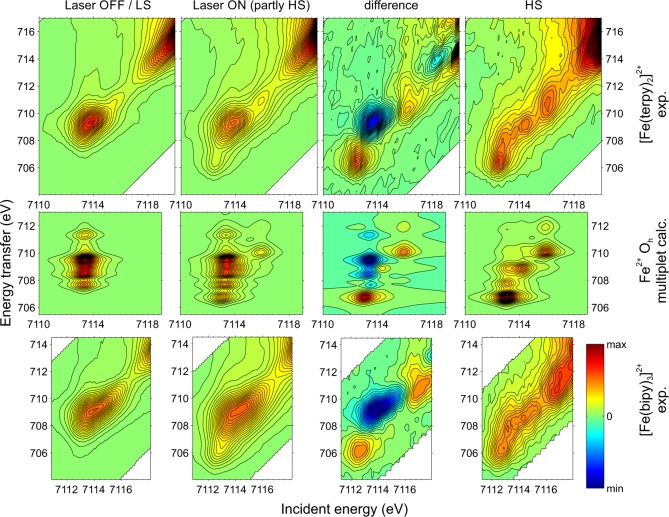
Exploring the pre-edge region of 1s XAS with RXES can reveal more details about the 3d-related part of the electronic structure. We performed 1s2p RXES on light-excited [Fe(terpy)₂]²⁺ at a time delay of Δt = 80 ps. These data are plotted in the top row of Figure 7 next to the ground-state spectrum. The difference between the light-excited and ground-state spectra is shown along with the (fully converted) HS spectrum that was reconstructed from the difference spectrum assuming the population obtained from XES.

Figure 7.

Experimental Fe 1s2p RXES spectra, from aqueous solutions of [Fe(terpy)₂]²⁺ (top row) and [Fe(bipy)₃]²⁺ (bottom row), showing the ground state, the laser-excited state at 80 ps time delay, their difference, and the reconstructed HS spectra. The theoretical spectra (middle row) were obtained from ligand-field multiplet calculations in an approximate O_h local symmetry, and there the “Laser ON (partly HS)” panel was constructed by the superposition of 40% HS and 60% LS. The spectral intensity is plotted above the plane spanned by the incident energy and the difference between the incident and emitted energy, the energy transfer. The energy scaling is equal for both axes and identical for all the plots in order to aid the comparison.

Fe^II in (close-to) octahedral environments is expected to have a single pre-edge resonance when in the LS state and three resonances when in the HS state.^55,75 This has been confirmed in several experiments including 1s2p RXES of an Fe^II compound at thermal spin-state switching.⁶⁴ These resonances are clearly present in the spectra in Figure 7, and the increase in resolution and information content with respect to XANES is evident when these features are compared to peaks A, A′, and A″ in Figure 6. Calculated RXES spectra are shown in the middle row of Figure 7. While a single-electron approach usually cannot give an accurate description for 1s2p RXES spectra, multiplet theory can do that for both LS and HS states.⁵⁵ For octahedral complexes the nature of the pre-edge transitions is electric quadrupolar due to symmetry reasons. The FeN₆ cores in [Fe(terpy)₂]²⁺ and [Fe(bipy)₃]²⁺ are distorted octahedra but at a level of distortion that makes the quadrupolar description sufficient to model the spectra. The calculations assumed LS and HS Fe^II ions in octahedral crystal fields, and the results reproduced the single LS and three HS resonances as can be seen in Figure 7. Multiplet interactions in the RXES final state of the ground-state system lead to small intensity peaks that appear vertically, at different energy transfer values, in the plotted RXES spectra. In the measured LS spectrum the expected (vertical) multiplet structure is weak but obviously present near the single resonance at around 7113.5 eV. In addition, a diagonal feature is observed (at ca. Ω = 7115.5 eV incident energy, Ω–ω = 710.5 eV energy transfer) which is not present in the calculation. This feature must reflect a p-type contribution as a result of orbital mixing (i.e., covalency). In fact, this mixing is expected to bring in a dipolar character, which is seen in the XANES-calculated dipolar contribution to the pre-edges in Figure 6. Upon laser excitation two more peaks (at ca. Ω = 7113 eV, Ω–ω = 706 eV, and ca. Ω = 7116 eV, Ω–ω = 711 eV) appear, while the intensity of the main peak drops. The difference of these spectra together with the known HS population allows us to reconstruct the 1s2p RXES spectrum of the HS state of [Fe(terpy)₂]²⁺, which shows a striking similarity to the calculated one.

We have also studied the 1s2p RXES spectra of the benchmark system [Fe(bipy)₃]²⁺ which has a somewhat different symmetry (D₃) and less geometrical constraints from the ligands as they are bidentate. The measured spectra are shown in the bottom row of Figure 7. Despite the somewhat worse energy resolution caused by a twice-larger incident bandwidth, it is apparent that the spectra are very similar to those of the [Fe(terpy)₂]²⁺. The almost identical difference spectra indicate that the nature of the variations in the two complexes are essentially the same.

The crystal field multiplet calculations nicely reproduce the overall spectral shapes and the difference spectra. Intra-atomic electron–electron interactions together with a crystal-field splitting are therefore the main contributions to the spectra. The calculations neglect orbital mixing effects and only consider electric quadrupole transitions; as a result spectral features may be missing on the high-energy side, and the spectral intensities cannot be fully reproduced.

The chemical sensitivity of the K absorption pre-edge is very different from the main edge. While the main edge spectral shape is dominated by the coordination shells, the pre-edge reflects electron–electron interactions within the d-shell as well as crystal-field effects and orbital mixing. The striking similarity of the difference spectra in the two compounds shows that intra-atomic d–d interactions in the HS state dominate the spectral shape. The 1s2p RXES planes thus visualize the dramatic change of the electronic levels when the molecules are in their short-lived photoexcited state. However, the reasonably good description by the multiplet calculations, an ionic approach utilizing O_h symmetry, points toward the need for more involved calculations. Distinguishing between ⁵E and ⁵B₂ in RXES would require full multiplet calculations including dipole and quadrupole transitions with molecular wave functions that describe the whole complex. This is currently not possible with sufficient accuracy. Angular-dependent RXES could help to identify the exact 3d configuration in single crystals;⁷⁶ however, this is hardly possible in solution.

Theoretical Insights into the Electronic Structure

Although the [Fe(terpy)₂]²⁺ molecule has already been investigated theoretically,^11,12 a few details relevant to the characteristics of the quintet states have been overlooked or at least not discussed in due detail. These include the relation between the structural differences and the occupation of the 3d orbitals in the two quintet states ⁵E and ⁵B₂, the effects of the Jahn–Teller (JT) distortion on the ⁵E, and the electronic structure origin of the two modes needed to describe the spin-state transition. Furthermore, the previous results raise disturbing questions: is it hopeless to distinguish the electronic structure differences of two possible quintets with X-ray spectroscopy? Why is the ⁵E state populated when almost all DFT calculations predict ⁵B₂ as being more stable? Here we complement the referred works by performing the necessary analysis using TD-DFT and CASPT2 and provide answers to all of the above-mentioned issues.

In order to unveil the variations in the electronic structure that cause the structural and bonding differences between the ⁵E and ⁵B₂ states, we compare the relevant molecular orbitals (MOs) obtained with spin-unrestricted DFT. To examine this in detail, in Figure 8 we present the highest occupied and the lowest unoccupied (Kohn–Sham) MOs. (A more extended version of this MO diagram is plotted in the SI.) Not surprisingly, these orbitals at the HOMO–LUMO gap have substantial Fe 3d character. The most interesting and relevant molecular orbitals at the gap are those with a dominant contribution from the atomic Fe d_xy, d_xz, and d_yz orbitals of β spin (i.e., spin down). Only one spin-down electron is available for these three orbitals. Which of these orbitals the electron occupies determines the atomic and electronic structural differences.

Figure 8.

Diagram of the spin-unrestricted KS molecular orbitals for the quintet states of [Fe(terpy)₂]²⁺ for ⁵E, and both the highly symmetric (D_2d) and the Jahn–Teller distorted (C₂) form is also shown. (Note that in a rigorous description the latter should be denoted as ⁵B in C₂ symmetry.) The energy levels (top) as well as the 3D representation (bottom) of the most relevant MOs of the ⁵B₂ and ⁵E states with relevant 3d character are shown.

In the simplest approximation of ligand-field theory, the Fe d_xy, d_xz, and d_yz atomic orbitals are nonbonding. However, this is altered in such a covalent molecule where the atomic orbtials are mixed to some extent with ligand orbitals. In the bottom of Figure 8 3D representations show the actual composition of these MOs for the ⁵B₂ state. Here the 5b₁ orbital is populated, which still has nonbonding d_xy character; the atomic orbital contribution (mixing coefficient) for the Fe d_xy is 84.2%, while those for all nitrogen orbitals are below 1%. Nevertheless, it is apparent that the d_xz and d_yz orbitals are mixed with in-phase p-type orbitals from the axial nitrogens (58.5% Fe(3d), 6.24% N(p)). The resulting 2-fold-degenerate 32e pair of MOs have a (π-)bonding character. However, this has no effect on the properties of the ⁵B₂ state since these MOs are unoccupied. In the ⁵E state (when constraining the symmetry to D_2d as in ref (11)), the energy order of the 5b₁ and 32e orbitals is swapped, and the 32e orbital pair is populated by a single electron. These orbitals bond to the axial nitrogens, as we just discussed, which shortens the Fe–N_ax bond lengths. (This orbital mixing and the corresponding charge transfer to the ligand via the bonding is usually referred to as backbonding or back-donation.)

Without constraints on the symmetry, the JT effect removes the degeneracy of the 32e orbitals in the ⁵E state and lowers the symmetry to C₂. The highest occupied orbital becomes the 63b, which has the main contribution from the Fe d_yz atomic orbital, and thus the backbonding to the axial nitrogens remains effective. The enhanced axial bonding is clearly reflected in the Mayer bond order indices^37,39,67 reported in Table 1 and provides a natural explanation for the geometry differences of the quintet states. Moreover, the energies of the levels of the quintet MOs become strikingly similar after applying the JT distortion to the ⁵E; the frontier orbitals have almost identical energies. The LUMO pair 64b and 70a (|xz⟩,|xy⟩) mimics the 32e (|xz⟩,|xy⟩) pair of ⁵B₂, and the even higher-energy unoccupied orbitals show high resemblance for the ⁵B₂ and ⁵E (C₂) states (see SI). Such similarities of the electronic structure readily explain why the presented spectroscopy data are so similar for the two quintet states.

The question remains why the ⁵E state is populated, contradicting most DFT results that favor the ⁵B₂ state as more stable.^11,13 The energy difference between the quintet states is rather small, and on such a scale the DFT calculations show a large scatter that depends on the choice of the exchange-correlation functional.¹² Therefore, we have performed CASPT2 calculations that provide more accurate energy differences. As can be seen in Figure 9(b), the two quintet minima are separated along a line that is almost orthogonal to the line connecting the LS and quintet states. The energy difference and the relative location of the potential wells belonging to the ⁵E and the ⁵B₂ states are best appreciated along this coordinate. This is plotted in Figure 9(c). The energy difference is 41 meV with the ⁵E state lower in energy. Moreover, as the ⁵E state is expected to split due to the Jahn–Teller effect, we can expect the energy to be even lower. (Note that the JT effect only affects the angle between the planes of the two terpy ligands, which changes by 4°, while the bond lengths and other angles stay practically the same.¹²) The combination of the energy difference from CASPT2 and the JT energy lowering obtained from DFT suggests that the distorted ⁵E can be as much as 150 meV lower in energy than the ⁵B₂ state. As the transfer to the quintet(s) takes place in the first picosecond after light excitation and the measurements are performed at a delay ≥80 ps by which time the excess energy is transferred to the solvent, we expect to find the system in the ⁵E, the more stable quintet state. Yet, since geometry optimization is practically impossible at the CASPT2 level on a such a large system with numerous electrons, one should keep in mind that this expectation might be biased.

Finally, we address the origin of the breakdown of the SCC model. In most octahedral Fe^II compounds that undergo spin-state transitions a single configuration coordinate is sufficient as a reaction coordinate, typically the breathing mode of the molecule which is proportional to the metal–ligand distance. This has been exploited in a very successful quantitative approach proposed by A. Hauser that describes well the HS–LS relaxation times for most complexes but not [Fe(terpy)₂]²⁺.^10,11 Given the slower than expected relaxations (and apparently higher barrier) found for [Fe(terpy)₂]²⁺ in different matrices, it was suggested that the SCC-based model is not applicable to this tridentate complex, and the involvement of an extra mode, probably the ligand bending measured by the NNN angle, is required, which increases the barrier height. Many details of this have not been brought to light; in a recent paper we found that the NNN angle of the ligand and the R(Fe–N_ax) bond lengths are promising candidates to describe the reaction coordinates.¹²

Starting with the description of the electronic structure of the ¹A₁ ground state, which has no unpaired electrons, we note that the spin-resctricted KS MOs have identical energies for α and β electrons, as is observed on the frontier orbitals of this state in Figure 9a. The tridentate terpyridine has geometrical constraints as the N atoms of its three linked pyridine rings in this planar ligand cannot take up ideal octahedral positions around the Fe center. Due to this, the energy of the molecular orbitals that have a dominant contribution from the 3d orbitals will have a relevant split in energy, depending on whether they are oriented parallel or orthogonal to the molecular axis that goes through the nitrogens of the central pyridine rings and the Fe^II ion. This splitting is small for the d_xy, d_xz, and d_yz nonbonding or weakly backbonding orbitals but high for the d_z²- and d_x²-y²-based orbitals, which originate from the octahedral e_g^* antibonding orbitals as seen in Figure 9a. In addition to the geometrical constraints, the backbonding between the axial N and the Fe contributes to the axial distortion of the molecule as well. The stronger bonding along the axis is again clearly identified in the Mayer bond order indices, as seen in Table 1.

To reach the quintet states, both antibonding e_g^* orbitals need to be populated with a spin-up electron. However, it is revealing to examine what would happen to the molecular geometry if only one of these orbitals is populated. The e_g(|x²–y²⟩) MO is based on the Fe d_x²–y² atomic orbital mixed with p-orbitals of the four equatorial nitrogens; therefore, populating this antibonding orbital causes an expansion in the molecule in this direction, opening up the NNN angle of the ligand, without affecting the axial R(Fe–N_ax) bond length. Indeed, the transition to the ³A₂ state is almost perfectly described by the NNN opening, as can be seen in Figure 9. This suggests that the opening of the NNN angle of the ligands is one of the relevant modes needed for the LS–HS transition. The e_g^*|z²⟩ antibonding orbital has large mixing of the Fe d_z² with the p-orbitals of the axial N atoms and smaller mixing with those of the equatorial N atoms. Therefore, the population of this MO leads to an increase in the lengths of the Fe–N_ax bonds and a smaller weakening of the equatorial Fe–N_eq bonds. This results in the increase of the axial R(Fe–N_ax) bond length without substantial effect on the NNN angle of the ligands because the pull on the side rings at the equatorial nitrogens by the iron caused by axial elongation is compensated by the simultaneous weakening of the Fe–N_eq bonds. This change corresponds to the second coordinate needed for the transition.^11,12 The optimized geometry of the triplet with the populated d_z²-based orbital, ³B₁, differs from that of the ground state almost only in R(Fe–N_ax), as shown in Figure 9. (Note that the geometry optimization of the ³B₁ could only be obtained by forcing the occupation of the e_g|z²⟩ MO with a symmetry constraint on the orbital populations.) Consequently, we can identify that these population changes combined with the geometrical constraints of the terpy ligand explain the need for the two-mode description of the switching and the breakdown of the SCC model in this molecule. The validity of relating the two necessary configuration coordinates to electronic structure effects is further supported if we add up the two vectors pointing from the singlet ground state to the triplet states in this coordinate system. Each of these vectors represent the structural variations caused by adding one electron to an e_g^* orbital. Therefore, we can expect that their sum approximates well the real quintet geometry, if the relation between structure and orbital population variations is valid. The resulting position (marked by a hollow cross in Figure 9) lies indeed fairly close to the actual positions found for the quintet states with the geometry optimizations. The mismatch is comparable to the distance between the ⁵E and ⁵B₂ states, which differ in the populations of t_2g-like orbitals. Accordingly, the two modes based on the opening of the NNN angle and the variation of the R(Fe–N_ax) bond lengths grasp rather well the main structural changes, and these seem to clearly correlate with the populations of the e_g-like orbitals. However, remaining smaller-scale variations in the electronic structure are also reflected in the molecular structure. Consequently, further refinement of these modes or involvement of further ones is needed to obtain a complete and fully satisfactory description of this system.

Conclusions

The challengingly small differences in the molecular geometry and electronic structure of the ⁵B₂ and ⁵E quintets were addressed utilizing a variety of time-resolved X-ray techniques. The minuscule explorable differences provided a demanding testing ground for the techniques, enabling assessment of their ability to discern small changes that occur in short-lived transient states. The formation and decay of the high-spin state was followed with all applied techniques. XANES, XES, and RXES spectra, despite their high quality and clear variations, could not reveal which of the two quintets is realized. XDS, which captured both the light-induced conversion to HS and the behavior of the solvent in the vicinity of the molecule, was also unable to distinguish between the two quintets. Excellent quality EXAFS spectra were able to resolve the bond-length variations accurately, leading to unambiguous identification of ⁵E as the formed quintet state which is in agreement with our theoretical predictions. Applying theoretical calculations (DFT, TD-DFT, and CASPT2), we were able to explain the electronic structure origin of the differences in the properties of the two possible quintet states. We identified that back-bonding in the ⁵E state is responsible for the structural differences between the quintet states. We revealed why the ⁵E state is the more stable one and also checked how this state varies upon the Jahn–Teller effect. The failure of spectroscopy to distinguish the quintets was readily explained by the striking similarity of their molecular orbital diagrams. Finally, we determined why one configurational coordinate is not sufficient for the description of the LS–HS transition in [Fe(terpy)₂]²⁺.

Due to the anomalous behavior of [Fe(terpy)₂]²⁺ among Fe^II complexes that undergo photoinduced LS to HS transitions, the identification of the quintet state produced after light excitation represents a milestone. Our work should inspire studies of the dynamics on the way to the quintet state, during the first picosecond after light excitation, using X-ray free electron lasers. This will lead to a more complete understanding of the photocycle of this system, which can motivate the design of novel molecules with better photoswitching performance.

Supporting Information Available

Further details on the relation between the states in the different symmetry groups, the lifetime fitting, the EXAFS analysis, and the calculated molecular orbital diagrams. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^⬢ Université Paris-Sud, ICMMO UMR CNRS 8182, Equipe de Chimie Inorganique, 91405 Orsay, France.

The authors declare no competing financial interest.