Abstract
Intensity discrimination Weber fractions (WFs) measured for short, high-frequency tones in quiet are larger at mid levels than at lower or higher levels. The source of this “mid-level hump” is a matter of debate. One theory is that the mid-level hump reflects basilar-membrane compression, and that WFs decrease at higher levels due to spread-of-excitation cues. To test this theory, Experiment 1 measured the mid-level hump and growth-of-masking functions to estimate the basilar membrane input/output (I/O) function in the same listeners. Results showed the initial rise in WFs could be accounted for by the change in I/O function slope, but there was additional unexplained variability in WFs. Previously, Plack [(1998). J. Acoust. Soc. Am. 103(5), 2530–2538] showed that long-duration notched noise (NN) presented with the tone reduced the mid-level hump even with a temporal gap in the NN. Plack concluded the results were consistent with central profile analysis. However, simultaneous, forward, and backward NN were not examined separately, which may independently test peripheral and central mechanisms of the NN. Experiment 2 measured WFs at the mid-level hump in the presence of NN and narrowband noise of different durations and temporal positions relative to the tone. Results varied across subjects, but were consistent with more peripheral mechanisms.
I. INTRODUCTION
An important characteristic of the auditory system, and indeed, any sensory system, is the ability to represent changes in intensity with a high degree of sensitivity across a wide range of intensities. The auditory mechanisms that may play a role in maintaining a wide dynamic range—either limiting or aiding this ability—are not fully known. The dynamic range of the auditory system can be assessed behaviorally using an intensity discrimination paradigm. In a typical intensity discrimination experiment, a stimulus called a pedestal or standard is presented in two or three temporal intervals and an increment in intensity is added to the pedestal in one of the intervals. The size of the increment is adjusted to find the listener's intensity discrimination limen for the pedestal stimulus—or, the detected change in level corresponding to a pre-defined accuracy. The intensity discrimination limen can be expressed in terms of the Weber fraction (WF) in decibels, or 10 log (ΔI/I), where I represents the pedestal intensity and ΔI is the increment intensity corresponding to a pre-defined accuracy.
A. The mid-level hump
Under certain stimulus conditions, intensity discrimination abilities can appear nonmonotonic as a function of pedestal level. If intensity discrimination is measured for short, high-frequency tones in quiet, WFs are poorer for mid-level [∼50 dB sound pressure level (SPL)] tones than for lower- or higher-level tones (Carlyon and Moore, 1984; Plack and Viemeister, 1992). This nonmonotonic effect for tones in quiet has been called the “mid-level hump.” A “bump” in intensity discrimination can also occur when WFs are measured for a pedestal tone occurring 100 ms after an intense forward masker (∼90 dB SPL) (Zeng et al., 1991). Under these stimulus conditions, the poorer WFs at mid pedestal levels than at lower or higher levels has been called the “Zeng Bump.” The mid-level hump for tones in quiet was specifically examined in the present study.
There are a number of proposed explanations for the mid-level hump for tones in quiet, each targeting different levels of the auditory system. One such account, the referential coding hypothesis, proposes a central origin of the mid-level hump. According to this view, listeners may use internal perceptual referents to judge intensity changes (Braida et al., 1984; Plack et al., 1995; Plack, 1998). At mid levels, the reference points of quiet threshold and loudness discomfort level are perceptually distant, so performance worsens. However, it is not clear how the referential coding hypothesis may account for the fact that the mid-level hump is reduced or absent for low-frequency, long-duration tones in quiet (e.g., Carlyon and Moore, 1984).
Alternative explanations of the mid-level hump rely on more peripheral mechanisms occurring at the level of, or even peripheral to, the auditory nerve. Carlyon and Moore (1984) proposed that the mid-level hump may reflect a gap in the auditory nerve (AN) fiber coding ranges of high and low spontaneous rate (SR) fibers. However, as discussed in Heinz et al. (2001), this explanation is untenable in light of physiological data. Specifically, the mid-level hump occurs for pedestal levels far lower than where the transition from high to low SR fibers occurs (80−90 dB SPL). Additionally, because of the existence of medium SR fibers (Liberman, 1978) there is in actuality no coding gap between high and low SR fibers.
Oxenham and Moore (1995) proposed that the mid-level hump may arise due to the increased variance in AN fiber firing rate at mid levels for short tones. The onset of a stimulus is associated with a higher number of neural firings, and there is larger overall AN firing variance associated with a higher number of neural firings (Young and Barta, 1986). Additionally, the onset response is greater at mid levels in high SR fibers (Rhode and Smith, 1985). Thus, short stimuli at mid levels tend to be associated with greater AN firing variance which may lead to poorer discrimination performance, and ultimately the mid-level hump.
Another explanation of the mid-level hump is that it reflects the mid-level onset of basilar-membrane compression (von Klitzing and Kohlrausch, 1994; Heinz et al., 2001). In the region of compression, the internal intensity difference between the pedestal and pedestal + increment is effectively reduced, which could result in higher discrimination limens. Using an analytical model of the auditory periphery, Heinz et al. (2001) reported a mid-level hump in predicted discrimination limens at higher frequencies. In their model, the mid-level hump was a direct result of physiologically-supported strong compression occurring at high frequencies. At levels above the mid-level hump, discrimination limens decreased again because basilar-membrane spread-of-excitation allowed for information regarding level changes to extend beyond the nonlinear regions at/near the characteristic frequency (CF) into linear off-CF channels. With the lower levels of excitation in the off-CF channels, the high SR AN fibers (with steeper rate level function slopes) dominated the response, leading to improved predicted discrimination abilities. In other words, spread-of-excitation cues, which grow more linearly away from the CF channel, may help counteract the limitations for intensity discrimination posed by compression. No previous studies have compared WFs in the context of the mid-level hump and a behavioral estimate of basilar-membrane compression in the same listeners. Such a comparison may lend further support to the basilar-membrane compression explanation of the mid-level hump. Experiment 1 of the present study examined the relationship between the mid-level hump and an estimate of the basilar membrane input/output (I/O) function.
B. The effect of notched noise on the mid-level hump
In an attempt to restrict spread-of-excitation cues, some previous studies have used a notched noise (NN) surrounding the pedestal frequency. When NN is gated on and off with the pedestal, WFs become larger at mid-levels, and thus the mid-level hump increases (Carlyon and Moore, 1984; Oxenham and Moore, 1995). In other studies, when a simultaneous NN is gated on 50 ms prior to the pedestal onset, the mid-level hump can be reduced or eliminated because WFs decrease at mid-levels (Plack and Viemeister, 1992; Plack, 1998). Plack (1998) also showed that the NN did not need to be simultaneous with the pedestal to confer a benefit—a temporal gap in the long NN around the pedestal also led to a reduction of the mid-level hump.
As with the mid-level hump itself, the source of the mid-level hump reduction with NN is also a matter of debate. Plack (1998) theorized that WF improvements at the mid-level hump with long NN were a result of profile analysis. As with the referential coding hypothesis, profile analysis refers to listeners' use of context when detecting changes in intensity. However, whereas referential coding refers to listeners' use of cross-time referents for components within the same frequency critical band, profile analysis refers to listeners' use of cross-frequency referents (Green et al., 1983). The latter is most relevant for a tone in the presence of a NN because listeners may be able to cue into a change in spectral shape occurring when an increment is added to the pedestal in the presence of NN by comparing the outputs of different auditory filters. Plack (1998) examined the effect of nonsimultaneous NN on the pedestal (by using a temporal gap in the NN), but he did not examine the effects of other temporal configurations of the NN on the WF at the mid-level hump (e.g., backward NN). Although profile analysis typically refers to cross-frequency comparisons of simultaneous components, Plack (1998) argued that the limited temporal resolution of the auditory system—modeled by a central temporal window (e.g., Moore et al., 1988)—could mean that nonsimultaneous stimuli in close temporal proximity would be effectively simultaneous. In other words, with short enough delays, profile analysis should be possible regardless of whether the NN is presented simultaneously with, before or after the pedestal. In contrast, more peripheral mechanisms (described below) should depend on the NN temporal position. Thus, NN temporal position relative to the pedestal provides an avenue for distinguishing central and peripheral influences on intensity discrimination abilities.
More peripherally, the NN may induce energetic masking within the pedestal frequency channel (Plack and Viemeister, 1992). The precise definition of energetic masking (e.g., its underlying component processes) is itself a matter of debate. There may be numerous underlying physiological processes that all contribute to energetic masking that could lead to different predictions of the effect of NN of different durations and temporal relationships to the pedestal on the mid-level hump. Possible peripheral influences are discussed below.
The NN, when simultaneous with the pedestal, may suppress the response to the pedestal (Plack and Viemeister, 1992). Two-tone suppression occurs nearly instantaneously and can effectively shift the dynamic ranges of AN fibers to higher sound levels, such that a given fiber can respond dynamically to levels where it was saturated in quiet (Geisler and Sinex, 1980; Costalupes et al., 1984). At the level of the basilar membrane, two-tone suppression acts to reduce the low-level basilar membrane response and reduce compression (Ruggero et al., 1992). Thus, if the mid-level hump reflects basilar-membrane compression, WFs at the mid-level hump could be improved by suppression. However, the nearly instantaneous suppressive mechanism does not explain why the mid-level hump is only decreased in long NN. Also inconsistent with a suppressive mechanism are the results of Plack (1998) showing that the mid-level hump is also reduced by nonsimultaneous NN, where suppression could not be acting.
The NN may also induce neural adaptation. Neural adaptation refers to the decrease in auditory nerve fiber firing rate to a stimulus over the course of sound stimulation, which can occur over a time course of about 150 ms (Smith and Zwislocki, 1975). This gives rise to a distinct difference in spike rate at the onset versus the later temporal portions of a stimulus. For a tone presented simultaneously with but delayed from the onset of a noise, the rate-level function (RLF) shows a dynamic range shift (thought to be due to suppression), but is also compressed and shallower due to neural adaptation (Costalupes et al., 1984). That is, there is less change in firing rate with level. Neural adaptation persists after stimulus offset (Smith, 1977), and thus the noise and tone do not need to be simultaneous in order for the RLF for the tone to be compressed (Kawase and Liberman, 1993). In the context of intensity discrimination performance in NN, a NN presented at least a few milliseconds prior to the pedestal onset may adapt the response to the pedestal if the noise falls within the pedestal's critical band. The resulting shallower RLF could mean poorer discrimination performance. Oxenham and Moore (1995) proposed a different influence of adaptation on intensity discrimination performance. They theorized that when the pedestal is gated at the onset of the NN there is greater variability in firing due to the AN onset response. When the pedestal is delayed from the onset of a NN, there may be reduced variability in firing to the NN due to neural adaptation. The authors suggested that the NN may be a less effective intensity referent in the onset condition where there is greater AN firing variability. According to this explanation, as a result of adaptation, WFs would improve if the pedestal was delayed from the onset of the NN.
Another possible mechanism evoked by the long NN is the medial olivocochlear reflex (MOCR). The MOCR is a bilateral, sound-evoked reflex involving fibers originating in the medial olivary complex which synapse at the base of the outer hair cells (OHCs) (Guinan, 2006). Eliciting the MOCR reduces the gain of the cochlear amplifier. As a result, the basilar-membrane response at low levels at or near CF is reduced and the range over which compression acts is reduced (Russell and Murugasu, 1997; Guinan, 2006; Cooper and Guinan, 2006). From the perspective of intensity discrimination abilities, this decrease in compression may be beneficial if the mid-level hump reflects a limitation of compression. The MOCR is relatively slow-acting, with the most rapid effects beginning 25 ms after elicitor onset followed by a gradual growth and decay of effect with a time constant of approximately 70 ms (Kim et al., 2001; James et al., 2005; Backus and Guinan, 2006). Thus, in experiments where the NN is gated on 50 ms prior to the pedestal, it is possible that the MOCR was elicited by the NN and had sufficient time to “build up” by the time of the pedestal onset. Experiment 2 of the present study explored the mechanisms of NN on the mid-level hump.
II. EXPERIMENT 1: LINKING THE MID-LEVEL HUMP FOR TONES IN QUIET TO GROWTH-OF-MASKING FUNCTIONS
A. Rationale
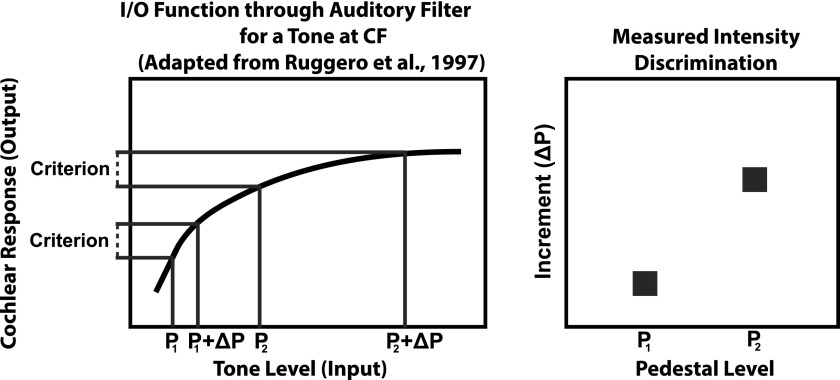
One hypothesis regarding the source of the mid-level hump for tones in quiet is that it is a reflection of basilar-membrane compression (Heinz et al., 2001). If this is true, then there should be a relationship between the slope of the basilar-membrane I/O function and the measured WFs up to and including the mid-level hump. In the present study, the I/O function was estimated using off-frequency, forward growth-of-masking (GOM) functions (e.g., Oxenham and Plack, 1997). There were a few assumptions inherent in linking WFs up to the mid-level hump and GOM functions. First, it was assumed that the listener would detect changes in the pedestal level using an auditory filter centered at the pedestal frequency (6 kHz, in this case). However, this assumption may only be valid for lower pedestal levels before spread-of-excitation cues prove beneficial (Florentine and Buus, 1981). Second, it was assumed that the listener would detect the increment added to the pedestal at a constant criterion pedestal + increment to pedestal ratio at the output of the auditory filter (see left panel of Fig. 1). That is, it was assumed there would be no variance associated with the decision variable or the sensitivity at the auditory filter output across the dynamic range. In the compressive region of the basilar-membrane I/O function, the size of the increment (and corresponding WF) would need to be much greater in order to maintain a constant criterion ratio at the output of the filter (see right panel of Fig. 1). At higher levels, where spread-of-excitation cues begin to dominate, the criterion ratio may be based on some combination of outputs across auditory filters (Florentine and Buus, 1981). As a result, the influence of compression on WFs may diminish at higher levels (Heinz et al., 2001). Third, it was assumed that the GOM function measured for a 6-kHz signal would be an accurate representation of the basilar-membrane I/O function associated with the 6-kHz filter. This last assumption relies on the power-spectrum model of masking. If the GOM function reflects the I/O function through a filter centered at 6 kHz, and WFs reflect intensity discrimination abilities through this filter, then there should be a relationship between the slope of the I/O function corresponding to a particular signal level and the WF for a tone of that level. This should be a negative relationship such that shallower estimates of I/O function slope are associated with higher/poorer WFs.
FIG. 1.
A schematic of the hypothesized relationship between the basilar membrane input/output function and intensity discrimination abilities. The left panel shows a schematic of an I/O function (in black). Dark gray lines show the Pedestal + Increment (P+ΔP) level yielding a criterion output ratio to the pedestal (P) at two input P levels. For the higher P level, the increment size needs to be much larger to maintain the same criterion output response because it falls in the region of compression.
B. Methods
1. Participants
Ten listeners (ages 18−37; 6 female) participated in this study. All were within normal limits bilaterally on measures of pure-tone audiometry (thresholds less than or equal to 15 dB hearing level (HL) for pure tones at 0.25−8 kHz), acoustic immittance, and distortion-product otoacoustic emissions. The right ear of each listener was tested in the experiments described below.
2. Stimuli
a. Growth-of-Masking functions.
The signal was a 6-kHz, 6-ms pure tone with 3-ms cos2 onset and offset ramps (no steady-state portion). Threshold for this signal in quiet was measured prior to the measurement of GOM functions. For GOM, the forward masker was a 3.6-kHz, 20-ms pure tone including 5-ms cos2 onset and offset ramps (10 ms steady-state). The signal onset immediately followed masker offset, with no temporal overlap. The basilar membrane response to the 3.6-kHz masker was assumed to be approximately linear at the 6-kHz CF place. A linear response to the masker at the signal frequency CF can be more certain with larger signal to masker frequency ratios. However, a more complete GOM function within the output limits of equipment is better achieved with maskers closer to the signal frequency. The signal-to-masker frequency ratio used here has been reported to produce a linear masker response for a 4-kHz signal (Jennings and Strickland, 2012; Yasin et al., 2013). To restrict the use of spread-of-excitation cues so as to obtain a more accurate estimate of compression, high-pass noise with a cutoff frequency of 1.2 × signal frequency was present in all GOM trials (Nelson et al., 2001). Its spectrum level was 50 dB below the signal level. The noise began 50 ms prior to masker onset and ended 50 ms after signal offset, including 5-ms cos2 onset and offset ramps.
The 6-ms signal duration was used for two reasons. First, this short signal allowed for the measurement of masked thresholds over a greater range of signal levels so that a more complete GOM function could be obtained. Maskers become less effective as signal durations become longer and as a result, a higher masker level is needed to mask a given signal level. This effectively shifts the GOM function vertically on a plot of signal levels (abscissa) vs masker levels (ordinate) (Oxenham and Plack, 1997). However, with this upward shift, a “ceiling” of maximum possible masker levels is quickly reached due to equipment output limitations. The maximum output of the equipment in this study was 93.7 dB SPL. Second, the short signal duration was used because the combined duration of the signal and forward masker was approximately within the estimated 25-ms MOCR delay (Backus and Guinan, 2006). This allows for the measurement of GOM without the influence (or with minimal influence) of the MOCR (Jennings et al., 2009; Roverud and Strickland, 2010).
b. Intensity discrimination.
The pedestal was a 6-kHz, 30-ms pure tone including 5-ms cos2 onset and offset ramps. Pedestal levels from 20 to 80 dB SPL in 5−10 dB steps were used. Quiet threshold for this pedestal tone was measured prior to measuring WFs. No high-pass noise was present in any trials or conditions. As discussed previously, a 6-ms signal rather than a 30-ms one was used in the GOM experiment in order to measure a more complete GOM function and to avoid influence of the MOCR with the combined masker and signal duration. A 30-ms pedestal (rather than a 6-ms one) was used to measure WFs for two reasons. First, a longer pedestal duration with a more tone-like quality aided listeners in distinguishing it from the background noise used in Experiment 2. Second, pedestal durations of approximately 30 ms have been used in previous studies examining the effect of noise on the mid-level hump (Carlyon and Moore, 1984; Oxenham and Moore, 1995; Plack and Viemeister, 1992; Plack, 1998). Using the 30-ms duration allows for more direct comparison of results across studies. Nizami (2006) examined the effect of pedestal duration on the mid-level hump. A 6-ms pedestal duration was not examined in that study. However, for 10 - and 30-ms pedestals, the shape of the intensity discrimination function was similar, only shifted vertically on the ordinate of a plot of pedestal level (abscissa) vs discrimination limen (ordinate).
3. Procedures
Stimuli were generated digitally at a sampling rate of 44.1 kHz using a Matlab program, delivered to a Lynx II XLR sound card, passed through a headphone buffer (TDT HB6), and delivered through the right ER-2 insert earphone. The ER-2 earphones have a flat frequency response at the eardrum from 250 to 8000 Hz. Listeners were seated in front of a computer screen in a double-walled, sound-attenuating booth, with insert earphones in the right and left ears and stimuli were presented to the right ear. Thresholds and WFs were measured using an adaptively tracking, three-interval forced choice procedure with a 500-ms interstimulus interval. To help demarcate each trial, a 50-ms silent buffer padded the beginning of the first interval and end of the last interval of each trial. Sound presentation intervals were visually indicated on the computer screen. Following the presentation of each three-interval trial, the listener selected the interval that was judged to contain the signal (for GOM functions and quiet threshold) or the incremented interval (for WFs) using a computer interface. Visual feedback was then presented for 250 ms indicating if the response was correct or incorrect. Thus, the temporal interval between the third presentation interval of one trial and the first presentation interval of the subsequent trial was equal to: 50-ms end buffer + subject response time + 250-ms visual feedback + 50-ms front buffer. At the end of a block of trials, the subject was shown the threshold track, as well as the mean threshold or WF and standard deviation resulting from that run. The subject recorded these values on a sheet of paper and selected a button on the computer screen to commence the subsequent run. The subject-recorded values were crosschecked with the digital file after each session. Each session was 1−1.5 h in duration.
a. Growth-of-masking functions.
For measurement of the signal threshold in quiet, the signal was presented in one randomly-selected interval on a given trial. The other two intervals contained silence. For measurement of GOM thresholds, the masker and high-pass noise were presented in each of the three intervals, and the signal was presented in one randomly selected interval. For some blocks of trials, the masker level was fixed and the signal level was varied to find threshold. In other blocks of trials, the signal level was fixed and the masker level was varied to find threshold. To maximize data collection efficiency, conditions were determined and pre-loaded in the computer program prior to each session. As the slopes of the I/O function near threshold and in the compressive region are not known a priori, the appropriate range and increments in fixed stimulus levels are not known. For a given step size, a range of fixed masker levels provides more detail about the steep slope of each listener's I/O function near quiet threshold and a range of fixed signal levels provides more detail about the shallow slope in the compressive region. Thus, conditions were set up for the subject in blocks with a range of both fixed masker and fixed signal levels in 5-dB steps. For signal-varied blocks, the signal level was increased following an incorrect subject response and decreased following two consecutive correct responses. For masker-varied blocks, the masker level was decreased following an incorrect response and increased following two consecutive correct responses. These tracking rules converge on 70.7% correct (Levitt, 1971). Signal and masker level step sizes were 5 dB for the first three level reversals. The step size was reduced to 2 dB for all subsequent reversals. The tracking program terminated after 12 total level reversals, and threshold was calculated as the average of the last eight level reversals.
b. Intensity discrimination.
The pedestal was presented in each of the three intervals and its intensity (I) was held constant throughout the run. An increment in intensity (ΔI) was added to the pedestal in a randomly selected interval in a given trial. A two-down, one-up adaptive tracking rule was used to adjust the size of the increment throughout the run. The increment size was increased following one incorrect subject response and decreased following two consecutive correct responses. The size of the increment, expressed as 10 log (ΔI/I), was increased or decreased in 5-dB steps for the first three reversals and 2-dB steps for the following reversals. The run was terminated after 12 total reversals, and the WF was the average of the last eight reversals.
For half of the participants, GOM functions were measured in a series of sessions first followed by WFs in later sessions. For the other half of the participants, GOM functions and WFs were measured in separate sessions in reverse order. During each session, each condition was run twice in a row. Generally, conditions with lower pedestal levels or lower fixed masker/signal levels were run first and levels increased across the session. In the collection of both GOM functions and WFs, there were no formal training sessions. However, GOM and WF conditions were each run in subsequent sessions until performance stabilized. For some participants, performance stabilized within four runs of a given condition, while for others, as many as 16 runs were required for performance to stabilize. For most subjects and conditions, additional thresholds and WFs were collected beyond apparent performance stabilization for further verification. Thresholds and WFs reported in this study are averages across runs. Any WFs or GOM thresholds in earlier runs that differed from the average of subsequent runs by 5 dB or more were excluded from the average. The GOM thresholds reported in the results are the average of between two and six run thresholds. The WFs reported are the average of between two and 12 runs. A greater number of averaged runs were used for subjects and conditions where variability appeared to persist (and thus more of these conditions were run), but where earlier runs did not fit the exclusion criterion described above.
C. Results
1. GOM function results
The GOM functions for all ten listeners are shown in Fig. 2. An averaged GOM function is also shown. This averaged function consists of thresholds for fixed signal and masker levels for which the majority of subjects had data points. Each GOM function was fitted with a 3rd-order polynomial function, as has been done in previous studies to characterize the I/O function (Plack and Arifianto, 2010), and the parameters of the fits were used in the analysis,
| (1) |
The polynomial fits to most data above quiet threshold are shown in Fig. 2 as the solid gray lines (teal online). For each subject, a, b, and c estimates are shown within each panel. Note that there is intersubject variability in the parameter estimates and in the form of these estimated functions, which is consistent with other psychophysical (e.g., Yasin et al., 2013) and physiological (e.g., Ruggero et al., 1997) studies in which I/O functions have been measured. For S1, S7, S8, and S9, masked thresholds were obtained very near quiet threshold and showed steep roll off. Thresholds at these low masker levels were not included in the fits. This was done for the following reasons. First, including the steep roll off data points led to poorer fits in the compressive region—a potentially important region in the analysis of WFs at the mid-level hump (described below). Second, the points were thought to primarily reflect internal noise, which dominates near quiet threshold. Internal noise is not a property of the underlying I/O function at the signal frequency on the basilar membrane, which has a linear slope at low levels with no steep roll off (Ruggero et al., 1997). Rather, internal noise is thought to be a manifestation of internal physiological noise, possibly at the neural transduction processing stage or later, which acts as an additional masker and adds to the intensity of the external masker stimulus (Humes and Jesteadt, 1989). As such, it represents a detection limitation for the stimulus used to measure GOM behaviorally. In the present study, the quiet thresholds for the pedestal used to measure WFs were lower (shown in Fig. 3) than thresholds for the signal used to measure GOM (Fig. 2) because of the difference in durations used for these stimuli. Thus, even if internal noise should be used in the analysis, it would dominate at lower stimulus levels for the pedestal stimulus than is shown in the GOM data. The dotted lines beyond the data range in Fig. 2 show fit extrapolations that were used in the analysis. Extrapolations were used in order for the I/O function fits to cover the level range of WFs up to the level of the mid-level hump.
FIG. 2.
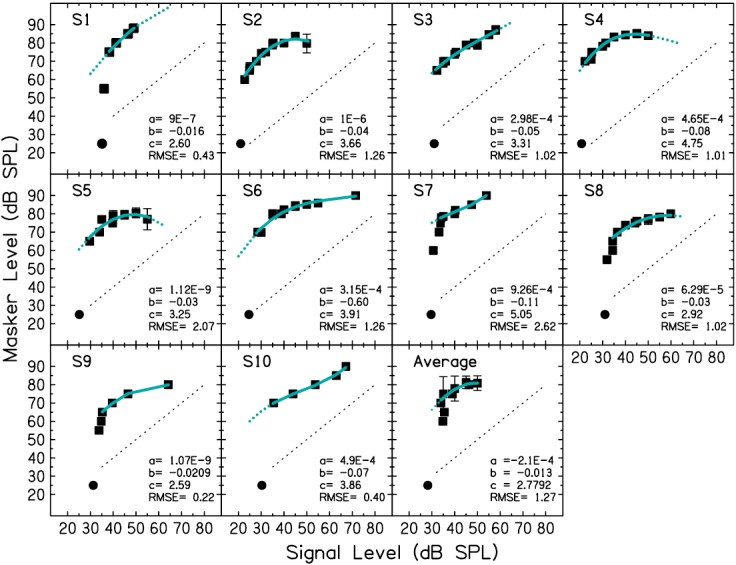
(Color online) GOM functions for 10 subjects and an average function for levels for which the majority of subjects had data points. The circle shows quiet threshold for the signal, placed arbitrarily at a masker level of 25 dB SPL. The solid gray line (teal online) shows the fit with a 3rd order polynomial function. The dotted gray lines (teal online) extending beyond the data show the extrapolations of the polynomial fit that were used in the Analysis. The parameters of the polynomial fits (a, b, and c) and root mean squared error (RMSE) of the fits are shown inset in each panel. The dotted black line in each panel shows for reference a linear function with a slope of 1 and an intercept of 0.
FIG. 3.
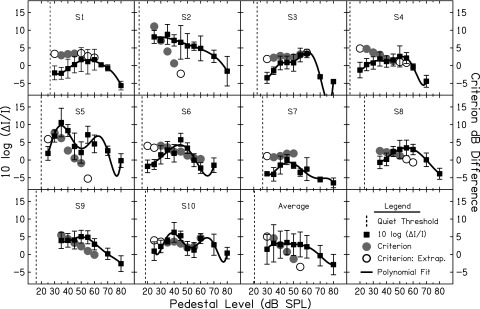
WFs for a 6-kHz, 30-ms pedestal as a function of pedestal level (black squares). The solid black line shows polynomial fits to the WF data (4th, 5th, or 6th order polynomials for each subject). The vertical dashed line shows quiet threshold for the pedestal tone. The circles (and right axis) show the criterion dB differences calculated from the estimated I/O function of each listener in the Analysis. The open circles show criterion calculations that were based on extrapolations of the I/O function fits. The filled gray circles show criterion dB differences that were not based on extrapolations.
2. Intensity discrimination results
The WFs across a range of pedestal levels are shown for each listener as the filled squares in Fig. 3. Averaged WFs across listeners are also shown at pedestal levels for which the majority of subjects had data points. The solid lines in Fig. 3 show polynomial function fits to the WF data. The lowest order polynomial that produced a good fit to the data was selected based on visual inspection and a small decrease (<0.5 dB) in root mean squared (RMS) error for higher-order polynomials. A similar procedure was used by Florentine et al. (1996) to fit loudness function data. The circles (and right axis) show the calculated criterion dB differences for a range of WFs based on the polynomial GOM data fits. These criterion differences will be described and discussed in Sec. II D. Consistent with previous literature, a mid-level hump is observed in the WFs (filled squares) for nearly all listeners. However, there is variability in both the location and breadth of the hump across individuals. Across subjects, the peak WF occurs between 35 and 60 dB SPL. For some subjects, the mid-level hump is quite broad and spans at least three signal levels (S1, S3, S4, S8, and S9), whereas for others, the mid-level hump is more “peaked” (S5, S6, S7, and S10). The data for S2 shows virtually no mid-level hump. Rather, WFs gradually decrease with increasing pedestal level. For listeners with more peaked mid-level humps, there is evidence of a “double hump.” The WFs of S5 and S10 show a clear double hump, and a slight double hump is present for S6 and S7. These double humps remained despite many repetitions of these conditions. Small double humps in intensity discrimination limens have been observed in some previous studies (Nizami et al., 2001; Nizami, 2006).
D. Analysis
It is apparent from the WF functions in Fig. 3 that there is variability among subjects in the level at which the mid-level hump occurs, the poorest WF at the mid-level hump, and how broad the peak of the mid-level hump is. What will be assessed in the Analysis is whether the variability in these WF characteristics can be at least partially explained by the variability in the estimated I/O function characteristics (Fig. 2).
1. Criterion dB differences
Based on the second assumption discussed in the Rationale section, the difference between the Pedestal + Increment (P + ΔP) and Pedestal (P) represented by each WF (the decision variable) should be constant once the change in slope across the I/O function is considered. The criterion P + ΔP to P ratio for each participant at each level was determined from the polynomial function fit to each subject's GOM data. First, the P + ΔP level represented by each WF was calculated. In other words, the decibel level of I + ΔI corresponding to each WF was determined. For example, for S6 the WF for a 30 dB SPL pedestal was 1.46, which corresponds to a P + ΔP level of 33.80 dB SPL. Next, Lout of the P and P + ΔP levels were calculated using Eq. (1). Using the parameters of the polynomial fit for S6, the output of 30 dB SPL and 33.80 dB SPL is 72.09 and 76.14 dB, respectively. This results in a criterion output difference of 4.05 dB. If it is correct to assume that listeners use a constant criterion P + ΔP to P ratio, then the dB difference in Lout should remain constant within each listener as long as information through the 6-kHz filter is used.
In many cases, because different tone durations were used in the collection of WFs and GOM, thresholds and lower-level limits of these data sets differed. For example, for S10, a WF was obtained with a 25 dB SPL (30-ms) pedestal. However, GOM data do not extend below 30 dB SPL (with the 6-ms signal) due to the difference in thresholds. Additionally, for many subjects, in measuring GOM data, masker thresholds corresponding to signal levels higher than 50−60 dB SPL could not be obtained due to the upper-level limit of the equipment. In these cases, where there was not GOM data corresponding to the pedestal levels up to the mid-level hump, the criterion dB difference calculations were based on extrapolations of the polynomial fit. Criterion dB difference calculations that were based on extrapolations are shown as the open circles in Fig. 3. Calculations based on fits within the GOM data range are shown as the filled gray circles. Criterion dB differences were calculated up to levels corresponding to the mid-level hump and beyond only if there was GOM data at those levels. Criterion dB differences for the averaged WFs were calculated using the averaged GOM data in Fig. 2.
In Fig. 3, the criterion dB differences at each WF are essentially constant up to the level of the mid-level hump for seven out of the ten listeners (S1, S3, S5, S6, S7, S8, and S10). This is consistent with the assumption that a constant criterion P + ΔP to P ratio was used at the output of the 6-kHz auditory filter. For S5, S6, and S10, criterion dB differences could be calculated beyond the mid-level hump without extrapolation (except for one level for S5). At levels beyond the mid-level hump for these listeners, the symbols in Fig. 3 begin to deviate from the constant dB difference, and generally decrease. For S2, S4, and S9 the criterion dB differences decreased across pedestal levels and did not remain constant.
The decrease in criterion dB differences beyond the mid-level hump or beginning at levels lower than the mid-level hump (S2, S4, and S9) resembles the “near-miss to Weber's law” commonly observed for longer-duration, lower-frequency tones in quiet (e.g., Viemeister, 1988). The near-miss to Weber's law—or the decrease in WFs with increasing pedestal levels—has been attributed to the use of spread-of-excitation cues in previous studies (Florentine and Buus, 1981; Heinz et al., 2001). As such, the decrease in criterion dB differences with increasing pedestal level may not necessarily violate the assumption that listeners are using a constant ratio across all levels. Rather, it may reflect the increasing influence of information in linear off-frequency channels with increasing pedestal levels. The criterion dB difference calculations at the 6-kHz place become invalid when this occurs because the assumption that the listener detects energy only through the 6-kHz auditory filter is violated. If this interpretation is correct, it may indicate that information in off-frequency channels contributed to WFs even below the mid-level hump for S2, S4, and S9. It follows that the WFs at the mid-level hump may have been even greater for these listeners had information away from the 6-kHz filter not been used. In the case of S2, spread-of-excitation cues may have eliminated the initial rise in WFs altogether.
A common result across all subjects' criterion dB differences is that the mid-level hump was eliminated once the I/O function slope was taken into account. Specifically, the initial rise in WFs (giving rise to the mid-level hump) was not present in the criterion dB differences. Instead, dB differences were either flat or decreased much like the near-miss to Weber's law. Overall, the results are consistent with the idea that the mid-level hump arises as a result of basilar-membrane compression, a peripheral process. However, there is additional remaining variability in overall criterion dB differences and the change in criterion dB differences with increasing pedestal level across subjects that the estimated I/O functions do not explain.
2. Correlation analysis
As was mentioned in Sec. I, a more central explanation of the mid-level hump is the referential coding hypothesis. According to this hypothesis, the mid-level hump occurs because the pedestal level is perceptually distant from the referent level anchors of absolute threshold and loudness discomfort level. If this is the case, it may be expected that there would be a positive relationship between quiet threshold for the 30-ms tone and the pedestal level of the mid-level hump. That is, the mid-level hump may occur at some constant level distance from quiet threshold. In actuality, the difference between the pedestal level of the mid-level hump (defined as the peak in the polynomial function fits in Fig. 3) and quiet threshold for the tone (dashed line in Fig. 3) ranged from 15.13 to 39.5 dB across listeners. The difference between the mid-level hump defined as the peak WF value and quiet threshold ranged from 15.1 to 37.5 dB across listeners. There appeared to be a positive relationship between quiet threshold and the mid-level hump as defined as the peak of the polynomial function fit (r = 0.46, p = 0.179, n = 10) and between quiet threshold and the mid-level hump as defined as the peak WF (r = 0.52, p = 0.126, n = 10), but neither was statistically significant. However, it should be noted that these correlation coefficients were calculated for a small number of data points (n = 10), and thus should be interpreted with caution.
In contrast, the WF function may reflect a change in slope of the basilar-membrane I/O function. Analyses were performed which examined the relationship between the slopes of the polynomial function fits to the GOM data across levels and the WF functions within each listener. For each listener, the derivative (slope) of the polynomial function fit to GOM data was determined for signal levels corresponding to the P + ΔP level at each WF. As was the case with calculations of criterion dB differences, at some levels, derivatives were based on polynomial fit extrapolations.
Figure 4 shows the relationship for each listener between the WFs and the derivatives at levels corresponding to each P + ΔP level. If the premises presented in the Rationale section are correct, then WFs should be negatively associated with the I/O function slopes at these levels, but only as long as the I/O function through the 6-kHz filter is used. As pedestal level increases, the likelihood that linear off-CF regions contribute to WFs increases and WFs themselves should decrease (Heinz et al., 2001). Once the WFs are dominated by spread-of-excitation cues, it is no longer appropriate to assume that the 6-kHz I/O function is linked to WFs. To minimize the possibility of including invalid data points in the analysis, WFs at higher pedestal levels were excluded. It is not possible to determine precisely when (and if) spread-of-excitation cues begin to dominate for each listener from the data. For this reason, an additional assumption was made that the decrease in WFs at levels higher than the mid-level hump primarily reflected the use of information away from CF. The WFs at higher pedestal levels than the mid-level hump for which WFs were statistically significantly lower than the mid-level hump WF (as determined by a one-sided Student's t test) were not included in the correlations in Fig. 4. However, as was discussed earlier with regards to the criterion dB differences in Fig. 3, the use of spread-of-excitation cues may possibly begin at levels even lower than the mid-level hump for some listeners.
FIG. 4.
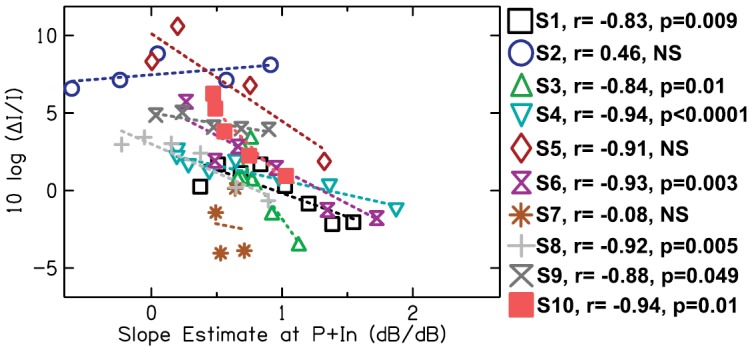
(Color online) The relationship between the I/O function slope estimates at levels corresponding to the pedestal + increment levels in WFs up to the mid-level hump and WFs up to the mid-level hump for 10 listeners. The symbol legend to the right of the figure also shows Pearson correlation coefficients of the regression (dotted lines) and p-values for each subject.
In spite of this possible spread-of-excitation cues complication, for most listeners, there was a negative relationship between WFs up to the mid-level hump and I/O function slope at the level corresponding to the P + ΔP for each WF. In other words, shallower slopes in the estimated I/O function were associated with higher (poorer) WFs for most listeners. For seven out of 10 subjects, the negative correlation was statistically significant. Although a negative trend is apparent for S5, it was not statistically significant possibly due to the small number of data points. For S2, the correlation was not significant, but a slight positive association is apparent. For this listener, the criterion dB differences shown in Fig. 3 did not appear constant for any two pedestal levels. If the interpretation of that data was correct—that the decreasing criterion dB differences reflected the increasing use of information away from CF—then it may not have been correct to assume a relationship between the WFs and the estimated I/O function at 6 kHz for this listener (shown in Fig. 4). In a similar sense, for S4 and S9, criterion dB differences in Fig. 3 showed a negative trend. Again, if it can be interpreted that this reflects some influence of off-frequency listening even below the mid-level hump, then this may explain the weaker/shallower relationship shown in Fig. 4 for these two listeners.
It is apparent in Fig. 4 that there are differences across listeners in WFs overall that are not explained by I/O function slope. The WFs for S7 are lower overall, whereas the WFs for S2 and S5 are higher overall. As noted above, these three listeners do not show statistically significant correlations—although, for S5, it may be a reflection of too few data points. The shifts in overall WFs along the ordinate in Fig. 4 may reflect differences in criteria among listeners (a more “central” influence on intensity discrimination abilities). In support of this idea, criterion dB differences shown in Fig. 3 at the lowest pedestal level (which would be least likely to be influenced by spread-of-excitation cues) are higher for listeners with higher WFs and lower for listeners with lower WFs.
E. Discussion
1. Summary and interpretation of results
The results and analyses lend support to the idea that the mid-level hump is (at least partially) a reflection of basilar-membrane compression. First, the initial rise of the mid-level hump was accounted for once each listener's estimated I/O function slope was used to calculate the criterion dB difference (circles in Fig. 3). Second, there was a significant negative correlation for most listeners between WFs with increasing pedestal level (giving rise to the mid-level hump) and the slope of the estimated I/O function (Fig. 4).
There were remaining differences across listeners in WFs that the estimate of the I/O function did not explain, which suggests additional factors contributing to WFs. First, there were differences across subjects in overall WFs that remained in calculated criterion dB differences. The output criterion at the lowest pedestal level (circle at lowest level in Fig. 3) varied across listeners, which may reflect differences in the “efficiency of use” of information at CF, a central source of variability. Second, there was variability across subjects in the rate of change in criterion dB difference across pedestal level (circles in Fig. 3). One interpretation is that this reflected differences across subjects in terms of when information away from the CF auditory filter (i.e., spread-of-excitation cues) began to dominate in WFs. The source of this variability could possibly be intersubject differences in the rate of broadening of excitation with increasing level, a peripheral source of variability driven by aspects of the cochlear amplifier (Ruggero et al., 1997). Alternatively, the variability could reflect intersubject differences in the use of spread-of-excitation cues, a central source of variability.
2. Methodological issues
All of the analyses in this experiment were based on the assumption that GOM functions are accurate representations of the I/O functions at the signal frequency place. There are some criticisms of the GOM method (cf. Plack et al., 2004). Additionally, even with the short signal duration used, a limited range of GOM thresholds were obtained because of the upper level limit of the equipment. As such, the calculations of criterion dB difference (Fig. 3) and correlations between WFs and I/O function slope (Fig. 4) included some points based on fit extrapolations. These extrapolations may have been inaccurate representations of the actual I/O functions at low and high levels.
The correlation analyses examined WFs up to the mid-level hump. However, for S2, S5, and S7, there were very few data points below the mid-level hump. These were also the listeners who did not show statistically significant correlations. By extending the duration of the pedestal, it may be possible to obtain WFs at lower pedestal levels (because threshold for this tone decreases). However, with longer pedestal durations, the size of the mid-level hump decreases (Carlyon and Moore, 1984) and there may be increasing influence of the MOCR.
It was assumed that GOM functions measured with a 6-ms signal would reflect the same underlying I/O function as would be measured using a 30-ms signal. The shorter signal was used in order to obtain more GOM data points within the upper-level limit of the equipment and to avoid influence of the sluggish MOCR—the combined 20-ms masker and 6-ms signal duration was approximately within the MOCR delay. A 30-ms pedestal was used to measure WFs to help distinguish the pedestal from the noise in subsequent experiments and to facilitate comparison among studies. It was assumed based on previous data (Nizami, 2006) that the WF function would be similar for 6-ms and 30-ms pedestals, only shifted vertically. However, additional research may be necessary to confirm these assumptions.
III. EXPERIMENT 2: INTENSITY DISCRIMINATION IN SIMULTANEOUS, FORWARD, AND BACKWARD NOISE
A. Rationale
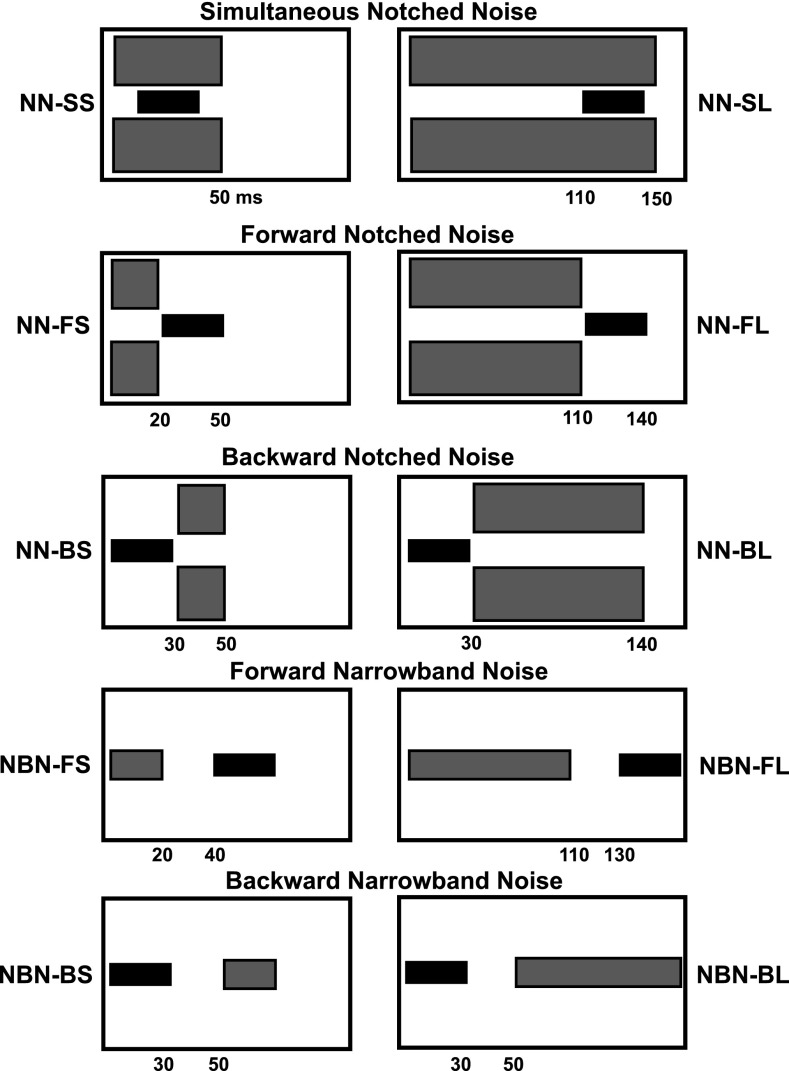
Previous studies have shown that a NN intended to restrict the use of spread-of-excitation cues can reduce or eliminate the mid-level hump (Plack and Viemeister, 1992; Plack, 1998). As discussed in the Introduction, there are a number of proposed mechanisms for the NN effect on WFs at the mid-level hump. Plack (1998) concluded that the improvement in WFs at the mid-level hump with NN was consistent with the use of profile analysis, a central mechanism. If this is the case, then the temporal relationship between the NN and pedestal should play little role and the NN should remain beneficial regardless of whether the NN occurs before, during, or after the pedestal. In contrast, any contributing peripheral mechanisms should depend on the NN duration and temporal relationship of NN and pedestal. In the present experiment, the WF at the mid-level hump was measured with NN of different temporal positions relative to the pedestal (simultaneous, forward, and backward), of different durations (“short,” and “long”), and of different levels.
Short and long, forward and backward narrowband noise (NBN) conditions were also examined in the present study. This was done to assess the possible peripheral influence (e.g., the MOCR) of masker components within the pedestal frequency channel and to test for a referential coding mechanism. Plack (1998) found no effect of a simultaneous NBN on WFs. However, only a simultaneous NBN was used and the effects of forward and backward NBN were not examined in that study.
B. Methods
1. Participants
Six participants from Experiment 1 also participated in Experiment 2: S1, S5, S6, S7, S8, and S10. Due to time constraints, the other four listeners from Experiment 1 could not participate.
2. Stimuli
Intensity discrimination was measured for the pedestal in different conditions of NN and NBN. The pedestal was a 6-kHz pure tone. The duration was 30 ms including 5-ms cos2 onset/offset ramps. The pedestal level was fixed at or near the mid-level hump for each listener (see peak WFs in Fig. 3). This was based on the findings from Plack (1998) demonstrating that the largest change in WF with NN occurred at the mid-level hump. The mid-level humps for S1 and S8 were relatively broad and spanned to higher pedestal levels. For these two listeners, the pedestal was fixed at the lower-level end of the mid-level hump.
The NN in the present study was a broadband noise 0.25−8 kHz, with a notch bandwidth of 1 kHz centered at 6 kHz. This notch bandwidth is wider than the 674 Hz-wide critical band for an auditory filter at 6 kHz (Glasberg and Moore, 1990). The same 1-kHz notch width was used in Plack and Viemeister (1992) and Plack (1998). In those two previous studies, the NN began 50 ms before pedestal onset and ended 50 ms after pedestal offset. In the present study, short and long simultaneous, forward, and backward NN conditions were examined. The durations and temporal characteristics of the NN are described in each section below. The temporal characteristics of all conditions are shown in Fig. 5. In each condition, NN level was systematically varied from −10 to 20 dB spectrum level. In previous studies, the NN was fixed at either 30 dB spectrum level below the pedestal (Plack and Viemeister, 1992) or 40 dB spectrum level below the pedestal (Plack, 1998). In the present study, with the fixed pedestal levels for each subject, the range of NN levels used included spectrum levels 40 and 30 dB below the pedestal. In some conditions, a NBN masker was used instead of a NN. The NBN frequency content spanned from 5.5 to 6.5 kHz. The NBN level was systematically varied from -10 to 20 dB spectrum level.
FIG. 5.
Schematic of the spectral and temporal characteristics of the conditions used in Experiment 2. The pedestal is in black, while the noise is in gray. The numerical values below each panel depict onsets and offsets of stimuli (in ms) relative to the onset of the first stimulus in the condition.
a. Simultaneous NN conditions.
The simultaneous NN was either short or long. In the short simultaneous notched noise condition (NN-SS), the NN was 50 ms including 5-ms cos2 onset/offset ramps. The pedestal's onset was 10 ms from the onset of the NN and thus was in the temporal center of the NN. Previous studies using short NN (Carlyon and Moore, 1984; Oxenham and Moore, 1995) gated the pedestal and NN on and off together. The 10-ms onset delay used in the present study meant that the onset response of the NN was avoided and that the initial rapid neural adaptation should have already occurred even in the short NN condition (Smith and Zwislocki, 1975). As such, it was assumed that there would only be small differences across all conditions (described below) in the amount of neural adaptation. Other possible mechanisms operating in the NN-SS condition include suppression and/or profile analysis. As was mentioned previously, the MOCR has an approximately 25-ms onset delay followed by a gradual effect buildup with a 70-ms time constant (Backus and Guinan, 2006). Thus it was assumed there would be little MOCR effect in this condition, although a small MOCR effect for the final 15 ms of the pedestal cannot be ruled out. In the long simultaneous notched noise condition (NN-SL), the NN was 150 ms including 5-ms cos2 ramps. The NN onset was 110 ms prior to pedestal onset. It was assumed that the primary difference in the NN-SL condition was that the MOCR would play a role in this condition.
b. Forward NN conditions.
In the forward NN conditions, there was no temporal overlap of the NN and the pedestal. As such, these conditions avoid the influence of suppression. Any neural adaptation from the NN for the pedestal may also be diminished relative to a simultaneous condition. The forward NN was either short or long. In the short forward notched noise condition (NN-FS), the NN was 20 ms including 5-ms cos2 ramps. There was no delay between NN offset and pedestal onset at the zero voltage points. Due to the short duration, this condition should have minimal influence of the MOCR because of its sluggish time course. However, it was assumed that profile analysis cues should still be available. In the long forward notched noise condition (NN-FL), the NN was 110 ms including 5-ms cos2 ramps. There was no delay between NN offset and pedestal onset at the zero voltage points. With the long-duration NN, the MOCR may play a role in this condition. Profile analysis cues should be available in this condition, as well.
c. Backward NN conditions.
In the backward NN conditions, the NN onset began immediately after pedestal offset at the zero-voltage points. It was theorized that there would be no peripheral influence of the NN on the pedestal. Again, the NN was either short or long. The short backward notched noise condition (NN-BS) included a NN that was 20 ms including 5-ms cos2 ramps. The long backward notched noise condition (NN-BL) included a NN that was 110 ms including 5-ms cos2 ramps. These conditions mirror the temporal characteristics of the forward NN conditions, only the influence of the NN is assumed to be more central (reflects the use of profile analysis only).
d. Forward NBN conditions.
Previous studies have reported considerable confusion effects with forward NBN maskers (Neff, 1986), and that delay between NBN masker and target is an effective method for reducing these effects (Neff, 1985). To avoid confusion for the NBN and pedestal in the present study, the NBN offset was 20 ms prior to pedestal onset at the zero-voltage points. This masker-pedestal delay also minimizes the influence of neural adaptation. The NBN was either short or long. The short NBN was 20 ms including 5-ms cos2 ramps (the NBN-FS condition). The duration of the NBN and the duration of the delay combined is 40 ms, longer than the MOCR onset delay. Thus, there may be some MOCR influence in this condition. The long NBN was 110 ms including 5-ms cos2 ramps (the NBN-FL condition). The combined NBN duration and delay duration equal 130 ms. It was assumed that a larger MOCR effect would be observed with the long NBN because there would be more time for the MOCR effect to build up by the onset of the pedestal. It has been shown in previous physiological studies that the magnitude of the MOCR effect decreases with decreasing elicitor bandwidth (Lilaonitkul and Guinan, 2009). Thus, while the NBN may elicit the MOCR, it may elicit a smaller effect than the wider-band NN. In both the NBN-FS and NBN-FL conditions, it was assumed that referential coding would be a possible mechanism.
e. Backward NBN conditions.
The backward NBN conditions shown in the fifth row of Fig. 5 mirror the forward NBN conditions, only the NBN onset occurs 20 ms after the pedestal offset. The backward short narrowband noise condition (NBN-BS) used the same masker duration as the NBN-FS condition. The backward long narrowband noise condition (NBN-BL) used the same masker duration as the NBN-FL condition. The backward conditions were used to test the influence of referential coding alone.
3. Procedures
The same equipment and general procedures described in Experiment 1 were used in Experiment 2. In the present experiment, the pedestal tone and noise stimuli were presented in all three temporal intervals of a three-interval, forced choice procedure. The intensity of the noise and pedestal was held constant throughout the run. An increment was added to the pedestal in one temporal interval, and WFs were measured for the pedestal tone. In a given block of trials, all other stimulus characteristics (e.g., noise duration, level) were held constant throughout the run. As in Experiment 1, during each experimental session each condition was run twice in succession, and noise-level conditions increased across the session.
Detection thresholds were also measured for the same conditions as WFs to determine the level of the noise that would affect audibility of the fixed-level pedestal tone. The signal level was fixed at the fixed pedestal level for each subject and the NN or NBN masker level was varied to find threshold. During preliminary data collection, it became clear that masked thresholds could only be obtained in the simultaneous NN conditions. Masker thresholds could not be measured in the forward and backward NN or NBN conditions because, with the fixed tone levels in the experiment, the masker levels required to mask the signal exceeded the maximum level output of the equipment. Unfortunately, due time constraints, no masked thresholds could be measured for S1and S5. The exclusion criteria used in Experiment 1 were also used in Experiment 2. Thresholds and WFs reported in the results are based on the average of between two and six runs.
C. Results and analysis
1. Intensity discrimination for a tone in simultaneous NN
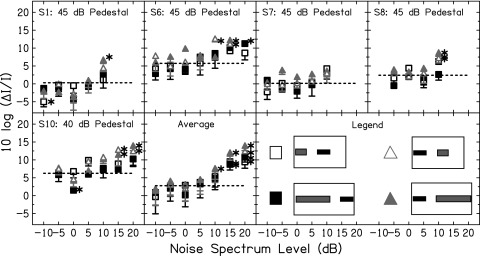
Figure 6 shows WFs in the simultaneous NN conditions (conditions depicted in row 1 of Fig. 5). The fixed pedestal levels are indicated at the top of each panel. The dashed horizontal line shows the WF in quiet for the fixed pedestal (taken from Fig. 3). Symbols that fall below this dashed line indicate a decrease in the WF at the mid-level hump when NN was presented. Within each subject, a Dunnett's pairwise comparison test was performed to assess whether the WF in each NN condition was statistically significantly different from the WF in quiet. The Dunnett's test corrects for multiple comparisons of each condition against a baseline or control. The number of comparisons in the present study was equal to the number of data points within each panel. The WFs statistically significantly different from WF in quiet are indicated by the asterisks in Fig. 6.
FIG. 6.
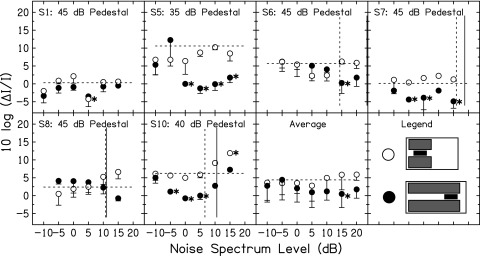
Intensity discrimination results in the simultaneous NN conditions for six listeners and for the average across listeners. For clarity, only the lower portion of the error bars is plotted. Subject number and fixed pedestal level are shown at the top of each panel. The symbol legend is in the bottom right panel. The horizontal dashed lines show WF in quiet (no NN). The asterisks show WFs in NN that were statistically significantly different from the WF in quiet. Vertical lines show masked thresholds for the tone in NN. The dashed vertical line shows threshold in the short NN, while the solid vertical line shows threshold in the long NN. Due to time constraints, these thresholds could not be measured for S1 and S5.
For S5, S6, S7, S10 and the averaged data, the long NN (NN-SL) led to a reduction in WF at the mid-level hump, but the short NN (NN-SS) did not. For S1 and S6 there were some reductions in WFs in the NN-SS condition, but these did not reach statistical significance. For S6 there was a smaller difference between the lowest WF in the NN-SS condition and the lowest WF in the NN-SL condition. The hypothesized difference between the NN-SS and NN-SL conditions is that the MOCR may play a (larger) role in the NN-SL condition. Thus, the MOCR may be a mechanism that contributed to the decreased WFs in these four listeners.
The data of S6, S7, and S10 also showed differences between threshold in the NN-SL condition and threshold in the NN-SS condition (solid vs dashed vertical lines). Due to time constraints, these thresholds could not be measured for S5. The difference in threshold between the NN-SL and NN-SS conditions is a measure of classical “overshoot” described in many previous studies (e.g., Zwicker, 1965; Strickland, 2001, 2004). It has been suggested that overshoot (the improvement in threshold for a signal when it is delayed from the onset of a noise) is the result of cochlear amplifier gain reduction with preceding sound. Support for this comes from studies demonstrating that overshoot is reduced by temporary (Champlin and McFadden, 1989; McFadden and Champlin, 1990) or permanent (Bacon and Takahashi, 1992; Strickland and Krishnan, 2005) hearing loss. A mechanism of this reduction in gain with sound may be the MOCR (Strickland, 2001). The present study suggests that listeners displaying overshoot in detection thresholds also displayed “overshoot” in WFs. However, due to the fact that thresholds were not measured in all listeners, this cannot be confirmed.
The results of S6, S7, and S10 go against a neural adaptation or suppression mechanism of WF improvement. Specifically, if these mechanisms contributed to the WF improvement, it would be expected that the short and long NN should be equally effective at reducing WFs at levels where they produce equal excitation. At no noise level for these subjects did the NN-SS condition produce the same magnitude of WF reduction as the NN-SL condition. For S1, the NN-SL and NN-SS conditions led to a similar reduction in WF at one level. The reduction with NN-SS was statistically significant. For this listener, the primary effect of the simultaneous NN may be neural adaptation or suppression, with little MOCR influence.
For S8, there appears to be a reduction in WF in the NN-SL condition with 15 dB spectrum level noise, although this was not statistically significantly different from WF in quiet. However, the vertical lines indicate that the noise masked the pedestal in both conditions at this level. Thus, WFs with a 15 dB spectrum level noise do not reflect intensity discrimination per se. To the left of the vertical lines, there was no statistically significant effect of the NN on WF for this subject. This subject also did not display overshoot.
2. Intensity discrimination for a tone with forward NN
Figure 7 shows WFs in the forward NN conditions (conditions depicted in row 2 of Fig. 5). As with the simultaneous NN conditions in Fig. 6, the WFs which are statistically significantly different from the WF in quiet (as determined by within-subject Dunnett's tests) are indicated by the asterisks.
FIG. 7.
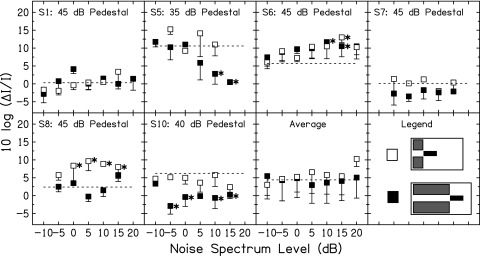
Intensity discrimination results in the forward NN conditions for six listeners and for the average across listeners. Subject number and fixed pedestal level are shown at the top of each panel. The symbol legend is in the bottom right panel. The dashed lines show WF in quiet (no NN). The asterisks show WFs in NN that were statistically significantly different from WF in quiet.
The forward NN led to decreased WFs for S5, S7, and S10, but only when the NN was long. The decreases in WFs for S7 failed to reach statistical significance, however. Listeners S5, S7, and S10 were the same listeners who showed a large, consistent difference between short and long simultaneous NN (NN-SS vs NN-SL). Thus, for S5, S7, and S10, the NN needed to be long, but did not need to be simultaneous with the pedestal, in order to result in a decrease in the WF at the mid-level hump. This is consistent with an MOCR mechanism of improving WFs. Even so, the pattern of results still appeared to differ between the forward and simultaneous NN conditions for these listeners. This may indicate an interaction of the suppression and MOCR mechanisms in the simultaneous NN conditions that did not occur in the forward NN condition.
For S6, forward NN led to increased WFs at the mid-level hump. This suggests that the results with simultaneous NN in Fig. 6 were more consistent with a suppression mechanism because the NN needed to be simultaneous with the pedestal in order to lead to an improvement in the WF. The NN-SS condition in Fig. 6 did show some reductions in WFs but they were not statistically significant.
For S1, the forward NN did not lead to significant improvements, regardless of its duration. This indicates that, for this listener, the NN needed to be simultaneous with the pedestal in order to lead to an improvement in the WF at the mid-level hump. This coupled with the fact that the duration of the NN did not play a role with simultaneous or forward NN, suggests that the MOCR did not play a significant role for this participant. The pattern of results is more consistent with a NN mechanism of suppression.
For S8, there was a slight improvement with NN-FL at one noise spectrum level. This improvement was not statistically significant. Generally, the long forward NN condition did not lead to changes in the WF at the mid-level hump. The NN-FS condition, however, led to poorer WFs. It is unclear what mechanism may be responsible for this effect. One possible explanation may be that the forward NN, when short, proved to be distracting or confusing. This may also be the underlying cause for the poorer WFs in the presence of forward NN of both durations that occurred for S6.
3. Intensity discrimination for a tone with backward NN
Figure 8 shows WFs with backward NN (conditions depicted in row 3 of Fig. 5). As in Figs. 6 and 7, the WFs that were statistically significantly different from WF in quiet are indicated by the asterisks. There were no statistically significant improvements in WFs with backward NN. For S5, the NN-BS condition led to a slight (nonsignificant) improvement WF at the lowest noise level tested. For S10, the NN-BL condition led to a decreased WF at the two lowest noise levels, however, these were not statistically significant improvements. For all other levels and all other subjects and averaged data, the backward NN led to no change or an increase of the WF at the mid-level hump. If it can be assumed that profile analysis can be used with a backward NN, the present results suggest profile analysis played little role in the improvement of WFs at the mid-level hump.
FIG. 8.
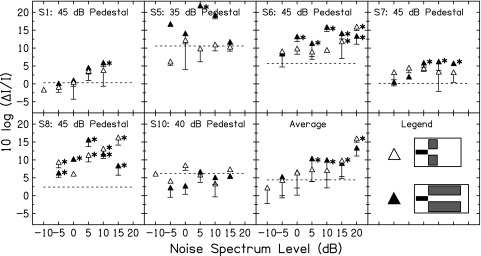
Intensity discrimination results in the backward NN conditions for six listeners and for the average across listeners. Subject number and fixed pedestal level are shown at the top of each panel. The symbol legend is in the bottom right panel. The dashed lines show WF in quiet (no NN). The asterisks show WFs in NN that were statistically significantly different from WF in quiet.
A repeated-measures mixed-model analysis of variance was performed for all NN data across conditions. The main factors were NN type (no NN, simultaneous, forward, and backward NN); NN duration (short or long); and NN level (ranging from −10 to 20 dB spectrum level). Subject and all interactions involving subject were considered random in the model. The dependent variable was WF. The main effect of NN type was statistically significant, F(2,10) = 12.71, p = 0.002. The main effect of NN duration was marginally significant, F(1,5) = 6.28, p = 0.054. NN level was not a statistically significant factor. There was a significant interaction of NN type × NN level, F(12,39) = 2.80, p = 0.007. There were no significant interactions of NN type × NN duration or NN duration × NN level. A three-way interaction of NN type × duration × level was approaching but did not reach statistical significance, F(12,39) = 1.90, p = 0.064. Generally these results indicate that WFs differed across NN type (no NN, simultaneous, forward, and backward NN), but that this depended on the level of the NN. This can be observed by comparing the “Average” panels across Figs. 6, 7, and 8. Differences in averaged WFs across simultaneous, forward and backward NN conditions are greater at higher noise levels.
4. Intensity discrimination for a tone with NBN
Figure 9 shows WFs in forward and backward NBN conditions. Due to time constraints, S5 did not participate in this part of the experiment. The asterisks indicate WFs in NBN that were statistically significantly different from quiet (as determined by a Dunnett's test). Only two small improvements in WFs occurred at the lowest levels for S1 and S10. For S1, this occurred at a very low level in the NBN-FS condition. The results of S10 showed a significant improvement in WF with a 0 dB spectrum level noise in the NBN-FL condition. At this spectrum noise level, a long forward NN led to a reduced WF, as well (see results for S10 in Fig. 7). However, it should be noted that for the same spectrum levels, the overall noise level in the pedestal channel is higher for the NBN that for the NN. For most listeners, and in the average results, high-level forward and backward NBN led to increased WFs.
FIG. 9.
Intensity discrimination results in forward and backward NBN conditions for five listeners and for the average across listeners. Subject number and fixed pedestal level are shown at the top of each panel. The symbol legend is at the bottom right of the figure. The dashed lines show WF in quiet. Asterisks indicate WFs with NBN that were statistically significantly different from WF in quiet.
A repeated-measures mixed-model analysis of variance was performed for all NBN data across conditions. The main factors were NBN type (no NBN, forward, and backward NBN); NBN duration (short or long); and NBN level (ranging from −10 to 20 dB spectrum level). Subject and all interactions involving subject were considered random in the model. The dependent variable was WF. The main effect of NBN type was significant, F(1,4) = 44.01, p = 0.003. As seen in the averaged data of Fig. 9, this appears to be driven by the difference between the no NBN condition and the NBN conditions. The main effect of NBN duration was not significant. NBN level was highly significant, F(6,15) = 26.55, p < 0.0001. There were no significant interactions.
Overall, while the long forward NN led to WF decreases for some subjects (Fig. 8), the long forward NBN generally did not (Fig. 9). However, only two listeners tested in the NBN conditions showed any WF decreases with the forward NN. If it can be assumed the benefit in the NN-FL condition was a result of activity of the MOCR, the small decreases (or lack thereof) in the NBN-FL condition suggest the MOCR was not as effective with a NBN. This result is consistent with physiological data indicating that the MOCR is more effective with wideband than with narrowband stimuli (Lilaonitkul and Guinan, 2009). Both forward and backward NBN resulted in poorer WFs at higher levels. The backward NBN results were presumed to reflect the central influence of the noise on WFs, although the influence was to make WFs larger. The NBN masker used in this experiment exhibited slower inherent envelope fluctuations than were present in the wider bandwidth NN. It is possible that these slow fluctuations in the NBN proved distracting to listeners or made the NBN a less reliable referent. Further explorations with the NBN conditions possibly using low-noise noise (Kohlrausch et al., 1997) may be needed to determine what influence this difference in envelope fluctuations may have had on WFs.
D. Discussion
1. Summary and interpretation of results
There was variability among listeners in the effect of the NN on the WF at the mid-level hump. For two listeners (S1 and S6) the NN needed to be simultaneous with the pedestal in order to reduce the WF at the mid-level hump. The duration of the NN had little effect on WF reduction. Forward and backward NN had either no effect or led to poorer WFs. This result is consistent with a mechanism of suppression. For three listeners (S5, S7, and S10), WF at the mid-level hump was reduced with simultaneous or forward NN and the NN needed to be longer in duration in order to reduce the WF. This result is consistent with an MOCR mechanism. For one subject (S8), simultaneous NN had no effect on WFs at the mid-level hump, while forward and backward NN resulted in poorer/larger WFs. The poorer performance in the presence of forward and backward NN suggests possibly some form of central interference or confusion. The intersubject variability in the influence of a presumed MOCR-induced mechanism or a suppressive mechanism on WFs is consistent with previous literature. Specifically, previous studies have reported high intersubject variability in the measured magnitude (Guinan et al., 2003) and timing (Hill et al., 1997; Backus and Guinan, 2006) of the MOCR, and large intersubject variability in the magnitude of measured suppression (e.g., Wright, 1996; Dubno and Ahlstrom, 2001).
It was assumed profile analysis cues would be available in simultaneous, forward and backward NN configurations. As such, the temporal position of the pedestal should not have played a role, as long as participants were able to gain a sense of the spectral profile within each interval. In the present study, backward NN had either no effect or led to poorer/increased WFs across listeners. These results are counter to a beneficial profile analysis mechanism. The finding that backward NBN led to increased rather than decreased WFs supports the idea that referential coding may not have played a beneficial role for intensity discrimination in these conditions either. Thus, while central factors may have influenced WFs in this experiment, it did not appear to be in a beneficial sense at least for the subjects and conditions examined in the present study.
As was discussed in Plack (1998), profile analysis generally refers to cross-frequency comparisons of simultaneous stimuli, but the limited temporal resolution of the auditory system may mean that temporally proximal nonsimultaneous stimuli can be effectively simultaneous. The limited temporal resolution of the auditory system has been represented as a temporal integration process by the temporal window model (TWM). The temporal window is asymmetric with a shorter/faster time constant for the “backward” component (3.5 ms) and a longer time constant for the “forward” component (weighted sum of 4.6 ms and 16.6 ms time constants) (Oxenham, 2001). Thus, the TWM may predict that the backward NN used in the present study was “less effectively simultaneous” than the forward NN. However, if the temporal window is centered over the pedestal as Plack (1998) assumed, there may be very little predicted integration with even the forward NN because the pedestal in the present study was 30 ms (rather than 6 ms as in Plack, 1998). Additionally, as the time constants in the TWM are derived from behavioral results, it is possible that the forward component reflects peripheral processes (e.g., neural adaptation) as well as central integration. Further research is needed to resolve this point.
2. Comparison to previous intensity discrimination work
Plack (1998) found that a simultaneous NN and a NN with a temporal gap surrounding the pedestal eliminated the mid-level hump for all three participants tested in that study. This is at least qualitatively similar to the results in the current study for S5, S7, and S10. However, the present study examined an additional condition which showed that the decrease in the mid-level hump WF with nonsimultaneous NN occurred with the forward NN components and not with the backward NN components. Plack's finding that the NN need not be simultaneous with the pedestal in order to reduce the mid-level hump is inconsistent with the results in the present study for S1, S6, and S8. For S1 and S6, the NN did need to be simultaneous in order to reduce the WF at the mid-level hump. For S8, WFs did not decrease significantly in any NN condition. One explanation for this inconsistency could be that the listeners tested in the Plack study were not fully representative of the variation that can be found among normal-hearing listeners.
Other studies examining the effect of NN on the mid-level hump have also shown results inconsistent with those of the present study and of Plack (1998). In Oxenham and Moore (1995), WFs at the mid-level hump were measured for a pedestal presented in the temporal center of a simultaneous 400-ms NN. In the three listeners tested, this longer NN did not lead to any reductions in WFs at the mid-level hump. Rather, WFs remained essentially equal to or even greater than those measured in quiet. The results of Oxenham and Moore (1995) appear consistent with the results of only S8 in the present study and are not consistent with those of Plack (1998). However, there were some methodological differences in the Oxenham and Moore study including a longer NN, a wider notch width (1300 Hz), and a 6.5-kHz signal rather than a 6-kHz pedestal frequency. Carlyon and Moore (1984) showed that gating the NN on and off with the pedestal led to significantly increased WFs at the mid-level hump. This is most similar to the NN-SS condition in the present study, where no significant changes in WFs relative to a pedestal in quiet condition were observed. Carlyon and Moore used a notch width of 1300 Hz, while the present study used a 1000-Hz wide noise. Additionally, in Carlyon and Moore, the NN was gated with the pedestal while the present study used a 10-ms pedestal onset delay. Further research is needed to determine the source of these inconsistent results.
Previously, Plack and Viemeister (1992) examined the influence of long simultaneous NN on the mid-level hump that occurs in quiet, but also in the context of the Zeng Bump. The Zeng Bump refers to poorer intensity discrimination abilities at mid levels for a tone occurring 100 ms after an intense forward masker. The long NN not only reduced the mid-level hump, but also the Zeng Bump. Plack (1998) and Plack and Viemeister (1992) both theorized that the decrease in the mid-level hump with NN was related to the decrease in the Zeng Bump with NN. However, the results of the present study provide evidence that these two effects (the mid-level hump and the Zeng bump) may be influenced by different mechanisms. Whereas the results of the present study are consistent with peripheral mechanisms leading to decreased WFs at the mid-level hump, previous studies have shown that WFs measured in the context of the Zeng Bump may be altered via more central mechanisms. Specifically, the Zeng Bump can be decreased by altering the perceived spatial separation of the masker and pedestal by manipulating masker interaural time difference while leaving the peripheral representations intact (Oberfeld et al., 2012, 2014) or by presenting a noise burst after the pedestal (Plack et al., 1995). In the present study, neither backward NN nor backward NBN led to decreased WFs at the mid-level hump. One explanation for these discrepant results is that there may be different mechanisms involved in these two “severe departures from Weber's Law.”
IV. SUMMARY AND CONCLUSIONS
In Sec. I, a number of possible sources of the mid-level hump were discussed, both peripheral and central. The central referential coding hypothesis proposes that WFs increase at mid levels in quiet due to the lack of a perceptual referent or anchor, and decrease with the presentation of noise because it provides a within-interval referent. In the present study, it was assumed that, if this were the case, the beneficial effects of the noise would occur regardless of whether the temporal position of the noise was simultaneous, forward, or backward relative to the pedestal. Two noise types were used as potential referents—a NN, which may provide a perceptual referent via profile analysis, and a NBN, which may provide a perceptual referent via referential coding (Plack, 1998). In the present study, the presentation of NN or NBN within the same temporal interval in a backward condition (Experiment 2) did not lead to any significant WF decreases. Rather, WFs increased at higher noise levels. Significant WF decreases were only observed with simultaneous or forward noise stimuli.
In Experiment 1, there was a relationship between the initial rise in each subject's WFs and the decreasing slope of each subject's estimated I/O function. This along with the previous findings of Heinz et al. (2001) support that the mid-level hump at least partly reflects a limitation posed by basilar-membrane compression, a peripheral source. Heinz et al. (2001) predicted the mid-level hump in intensity discrimination using an analytical model of the auditory periphery because of strong cochlear compression at high frequencies. However, that model did not include certain features of the auditory periphery including onset/offset neural responses and neural adaptation, which may affect the mid-level hump as a function of pedestal duration. That is, there may be an additional influence of AN firing variance on the mid-level hump (Oxenham and Moore, 1995) that the present study and Heinz et al. (2001) did not explicitly examine or test. In Experiment 2, the NN conditions leading to decreases in WFs at the mid-level hump, while variable across subjects, were all consistent with peripheral mechanisms. Taken together, these results suggest that the mid-level hump may reflect a limitation of basilar-membrane compression which is overcome by peripheral mechanisms (e.g., suppression and the MOCR) that can reduce the influence of compression.
ACKNOWLEDGMENTS
This research was funded by a grant to E.A.S.: NIH (NIDCD) Grant No. R01-DC00837, and by a Purdue Research Foundation fellowship granted to E.R.
Portions of this research were presented at the 37th meeting of the Association for Research in Otolaryngology, San Diego, California, February 2014, and at the 167th meeting of the Acoustical Society of America, Providence, Rhode Island, May 2014.
References
- 1.Backus, B. C. , and Guinan, J. J. (2006). “ Time-course of the human medial olivocochlear reflex,” J. Acoust. Soc. Am. 119(5), 2889–2904 10.1121/1.2169918 [DOI] [PubMed] [Google Scholar]
- 2.Bacon, S. P. , and Takahashi, G. A. (1992). “ Overshoot in normal-hearing and hearing-impaired subjects,” J. Acoust. Soc. Am. 91(5), 2865–2871 10.1121/1.402967 [DOI] [PubMed] [Google Scholar]
- 4.Braida, L. D. , Lim, J. S. , Berliner, J. E. , Durlach, N. I. , Rabinowitz, W. M. , and Purks, S. R. (1984). “ Intensity perception. XIII. Perceptual anchor model of context-coding,” J. Acoust. Soc. Am. 76(3), 722–731 10.1121/1.391258 [DOI] [PubMed] [Google Scholar]
- 5.Carlyon, R. P. , and Moore, B. C. J. (1984). “ Intensity discrimination: A severe departure from Weber's law,” J. Acoust. Soc. Am. 76, 1369–1376 10.1121/1.391453 [DOI] [PubMed] [Google Scholar]
- 6.Champlin, C. A. , and McFadden, D. (1989). “ Reductions in overshoot following intense sound exposures,” J. Acoust. Soc. Am. 85(5), 2005–2011 10.1121/1.397853 [DOI] [PubMed] [Google Scholar]
- 7.Cooper, N. P. , and Guinan, J. J., Jr. (2006). “ Efferent-mediated control of basilar membrane motion,” J. Physiol. 576, 49–54 10.1113/jphysiol.2006.114991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Costalupes, J. A. , Young, E. D. , and Gibson, D. J. (1984). “ Effects of continuous noise backgrounds on rate response of auditory-nerve fibers in cat,” J. Neurophysiol. 51, 1326–1344. [DOI] [PubMed] [Google Scholar]
- 9.Dubno, J. R. , and Ahlstrom, J. B. (2001). “ Psychophysical suppression measured with bandlimited noise extended below and/or above the signal: Effects of age and hearing loss,” J. Acoust. Soc. Am. 110(2), 1058–1066 10.1121/1.1381024 [DOI] [PubMed] [Google Scholar]
- 11.Florentine, M. , and Buus, S. (1981). “ An excitation-pattern model for intensity discrimination,” J. Acoust. Soc. Am. 70(6), 1646–1654 10.1121/1.387219 [DOI] [Google Scholar]
- 12.Florentine, M. , Buus, S. , and Poulsen, T. (1996). “ Temporal integration of loudness as function of level,” J. Acoust. Soc. Am. 99(3), 1633–1644 10.1121/1.415236 [DOI] [PubMed] [Google Scholar]
- 13.Geisler, C. D. , and Sinex, D. G. (1980). “ Response of primary auditory fibers to combined noise and tonal stimuli,” Hear. Res. 3, 317–334 10.1016/0378-5955(80)90026-X [DOI] [PubMed] [Google Scholar]
- 14.Glasberg, B. R. , and Moore, B. C. J. (1990). “ Derivation of auditory filter shapes from notched-noise data,” Hear. Res. 47, 103–138 10.1016/0378-5955(90)90170-T [DOI] [PubMed] [Google Scholar]
- 15.Green, D. M. , Kidd, G. , and Picardi, M. C. (1983). “ Successive versus simultaneous comparison in auditory intensity discrimination,” J. Acoust. Soc. Am. 73, 639–643 10.1121/1.389009 [DOI] [PubMed] [Google Scholar]
- 16.Guinan, J. J., Jr. (2006). “ Olivocochlear efferents: Anatomy, physiology, function, and the measurement of efferent effects in humans,” Ear. Hear. 27, 589–607 10.1097/01.aud.0000240507.83072.e7 [DOI] [PubMed] [Google Scholar]
- 17.Guinan, J. J., Jr. , Backus, B. C. , Lilaonitkul, W. , and Aharonson, V. (2003). “ Medial olivocochlear efferent reflex in humans: Otoacoustic emission (OAE) measurement issues and the advantages of stimulus frequency OAEs,” J. Assoc. Res. Otolaryngol. 4, 521–540 10.1007/s10162-002-3037-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Heinz, M. G. , Colburn, H. S. , and Carney, L. H. (2001). “ Rate and timing cues associated with the cochlear amplifier: Level discrimination based on monaural cross-frequency coincidence detection,” J. Acoust. Soc. Am. 110(4), 2065–2084 10.1121/1.1404977 [DOI] [PubMed] [Google Scholar]
- 19.Hill, J. C. , Prasher, D. K. , and Luxon, L. M. (1997). “ Latency of contralateral sound-evoked auditory efferent suppression of otoacoustic emissions,” Acta Otolaryngol. 117, 343–351 10.3109/00016489709113405 [DOI] [PubMed] [Google Scholar]
- 21.Humes, L. E. , and Jesteadt, W. (1989). “ Models of the additivity of masking,” J. Acoust. Soc. Am. 85(3), 1285–1294 10.1121/1.397459 [DOI] [PubMed] [Google Scholar]
- 22.James, A. L. , Harrison, R. V. , Pienkowski, M. , Dajani, H. R. , and Mount, R. J. (2005). “ Dynamics of real time DPOAE contralateral suppression in chinchillas and humans,” Int. J. Audiol. 44, 118–129 10.1080/14992020400029996 [DOI] [PubMed] [Google Scholar]
- 24.Jennings, S. G. , and Strickland, E. A. (2012). “ Auditory filter tuning inferred with short sinusoidal and notched-noise maskers,” J. Acoust. Soc. Am. 132(4), 2497–2513 10.1121/1.4746029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jennings, S. G. , Strickland, E. A. , and Heinz, M. G. (2009). “ Precursor effects on behavioral estimates of frequency selectivity and gain in forward masking,” J. Acoust. Soc. Am. 125, 2172–2181 10.1121/1.3081383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kawase, T. , and Liberman, M. C. (1993). “ Antimasking effects of the olivocochlear reflex. I. Enhancement of compound action potential to masked tones,” J. Neurophysiol. 70(6), 2519–2532. [DOI] [PubMed] [Google Scholar]
- 27.Kim, D. , Dorn, P. , Neely, S. , and Gorga, M. (2001). “ Adaptation of distortion product otoacoustic emission in humans,” J. Assoc. Res. Otolaryngol. 2, 31–40 10.1007/s101620010066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kohlrausch, A. , Fassel, R. , van der Heijden, M. , Kortekaas, R. , van de Par, S. , Oxenham, A. J. , and Puschel, D. (1997). “ Detection of tones in low-noise noise: Further evidence for the role of envelope fluctuations,” Acust. Acta Acust. 83, 659–669. [Google Scholar]
- 29.Levitt, H. (1971). “ Transformed up−down methods in psychoacoustics,” J. Acoust. Soc. Am. 49, 467–477 10.1121/1.1912375 [DOI] [PubMed] [Google Scholar]
- 30.Liberman, M. C. (1978). “ Auditory-nerve response from cats raised in a low-noise chamber,” J. Acoust. Soc. Am. 63(2), 442–455 10.1121/1.381736 [DOI] [PubMed] [Google Scholar]
- 31.Lilaonitkul, W. , and Guinan, J. J. (2009). “ Human medial olivocochlear reflex: Effects as functions of contralateral, ipsilateral, and bilateral elicitor bandwidths,” J. Assoc. Res. Otolaryngol. 10, 459–470 10.1007/s10162-009-0163-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.McFadden, D. , and Champlin, C. A. (1990). “ Reductions in overshoot during aspirin use,” J. Acoust. Soc. Am. 87(6), 2634–2642 10.1121/1.399056 [DOI] [PubMed] [Google Scholar]
- 65.Moore, B. C. J. , Glasberg, B. R. , Plack, C. J. , and Biswas, A. K. (1988). “ The shape of the ear's temporal window,” J. Acoust. Soc. Am. 83(3), 1102–1116 10.1121/1.396055 [DOI] [PubMed] [Google Scholar]
- 33.Neff, D. L. (1985). “ Stimulus parameters governing confusion effects in forward masking,” J. Acoust. Soc. Am. 78(6), 1966–1976 10.1121/1.392653 [DOI] [PubMed] [Google Scholar]
- 34.Neff, D. L. (1986). “ Confusion effects with sinusoidal and narrow-band noise forward maskers,” J. Acoust. Soc. Am. 79(5), 1519–1529 10.1121/1.393678 [DOI] [PubMed] [Google Scholar]
- 35.Nelson, D. A. , Schroder, A. C. , and Wojtczak, M. (2001). “ A new procedure for measuring peripheral compression in normal-hearing and hearing-impaired listeners,” J. Acoust. Soc. Am. 110(4), 2045–2064 10.1121/1.1404439 [DOI] [PubMed] [Google Scholar]
- 36.Nizami, L. (2006). “ The intensity-difference limen for 6.5 kHz: An even more severe departure from Weber's law,” Attention, Percept. Psychophys. 68(7), 1107–1112 10.3758/BF03193713 [DOI] [PubMed] [Google Scholar]
- 37.Nizami, L. , Reimer, J. F. , and Jesteadt, W. (2001). “ The intensity-difference limen for Gaussian-enveloped stimuli as a function of level: Tones and broadband noise,” J. Acoust. Soc. Am. 110(5), 2505–2515 10.1121/1.1409371 [DOI] [PubMed] [Google Scholar]
- 38.Oberfeld, D. , Stahn, P. , and Kuta, M. (2012). “ Binaural release from masking in forward-masked intensity discrimination: Evidence for effects of selective attention,” Hear. Res. 294, 1–9 10.1016/j.heares.2012.09.004 [DOI] [PubMed] [Google Scholar]
- 39.Oberfeld, D. , Stahn, P. , and Kuta, M. (2014). “ Why do forward maskers affect auditory intensity discrimination evidence from ‘Molecular psychophysics,’ ” PLoS One 9(6), e99745. 10.1371/journal.pone.0099745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Oxenham, A. J. (2001). “ Forward masking: Adaptation or integration?,” J. Acoust. Soc. Am. 109(2), 732–741 10.1121/1.1336501 [DOI] [PubMed] [Google Scholar]
- 41.Oxenham, A. J. , and Moore, B. C. J. (1995). “ Overshoot and the ‘severe departure’ from Weber's law,” J. Acoust. Soc. Am. 97(4), 2442–2453 10.1121/1.411965 [DOI] [Google Scholar]
- 42.Oxenham, A. J. , and Plack, C. J. (1997). “ A behavioral measure of basilar-membrane nonlinearity in listeners with normal and impaired hearing,” J. Acoust. Soc. Am. 101(6), 3666–3675 10.1121/1.418327 [DOI] [PubMed] [Google Scholar]
- 43.Plack, C. J. (1998). “ Beneficial effects of notched noise on intensity discrimination in the region of the ‘severe departure,’ ” J. Acoust. Soc. Am. 103(5), 2530–2538 10.1121/1.422774 [DOI] [PubMed] [Google Scholar]
- 44.Plack, C. J. , and Arifianto, D. (2010). “ On- and off-frequency compression estimated using a new version of the additivity of forward masking technique,” J. Acoust. Soc. Am. 128(2), 771–786 10.1121/1.3455844 [DOI] [PubMed] [Google Scholar]
- 45.Plack, C. J. , Carlyon, R. P. , and Viemeister, N. F. (1995). “ Intensity discrimination under forward and backward masking: Role of referential coding,” J. Acoust. Soc. Am. 97(2), 1141–1149 10.1121/1.412227 [DOI] [PubMed] [Google Scholar]
- 46.Plack, C. J. , Drga, V. , and Lopez-Poveda, E. A. (2004). “ Inferred basilar-membrane response functions for listeners with mild to moderate sensorineural hearing loss,” J. Acoust. Soc. Am. 115(4), 1684–1695 10.1121/1.1675812 [DOI] [PubMed] [Google Scholar]
- 47.Plack, C. J. , and Viemeister, N. F. (1992). “ The effects of notched noise on intensity discrimination under forward masking,” J. Acoust. Soc. Am. 92(6), 1902–1910 10.1121/1.405237 [DOI] [PubMed] [Google Scholar]
- 48.Rhode, W. S. , and Smith, P. H. (1985). “ Characteristics of tone-pip response patterns in relationship to spontaneous rate in cat auditory nerve fibers,” Hear. Res. 18, 159–168 10.1016/0378-5955(85)90008-5 [DOI] [PubMed] [Google Scholar]
- 49.Roverud, E. , and Strickland, E. A. (2010). “ The time course of cochlear gain reduction measured using a more efficient psychophysical technique,” J. Acoust. Soc. Am. 128(3), 1203–1214 10.1121/1.3473695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ruggero, M. A. , Rich, N. C. , Recio, A. , Narayan, S. S. , and Robles, L. (1997). “ Basilar membrane responses to tones at the base of the chinchilla cochlea,” J. Acoust. Soc. Am. 101, 2151–2163 10.1121/1.418265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ruggero, M. A. , Robles, L. , and Rich, N. C. (1992). “ Two-tone suppression in the basilar membrane of the cochlea: Mechanical basis of auditory-nerve rate suppression,” J. Neurophysiol. 68, 1087–1099. [DOI] [PubMed] [Google Scholar]
- 64.Russell, I. J. , and Murugasu, E. (1997). “ Medial efferent inhibition suppresses basilar membrane responses to near characteristic frequency tones of moderate to high intensities,” J. Acoust. Soc. Am. 102(3), 1734–1738 10.1121/1.420083 [DOI] [PubMed] [Google Scholar]
- 52.Smith, R. L. (1977). “ Short-term adaptation in single auditory nerve fibers: Some poststimulatory effects,” J. Neurophysiol. 40(5), 1098–1112. [DOI] [PubMed] [Google Scholar]
- 53.Smith, R. L. , and Zwislocki, J. J. (1975). “ Short-term adaptation and incremental responses of single auditory-nerve fibers,” Biol. Cybern. 17, 169–182 10.1007/BF00364166 [DOI] [PubMed] [Google Scholar]
- 54.Strickland, E. A. (2001). “ Relationship between frequency selectivity and overshoot,” J. Acoust. Soc. Am. 109(5), 2062–2073 10.1121/1.1357811 [DOI] [PubMed] [Google Scholar]
- 55.Strickland, E. A. (2004). “ The temporal effect with notched-noise maskers: Analysis in terms of input–output functions,” J. Acoust. Soc. Am. 115(5), 2234–2245 10.1121/1.1691036 [DOI] [PubMed] [Google Scholar]
- 56.Strickland, E. A. , and Krishnan, L. A. (2005). “ The temporal effect in listeners with mild to moderate cochlear hearing impairment,” J. Acoust. Soc. Am. 118(5), 3211–3217 10.1121/1.2074787 [DOI] [PubMed] [Google Scholar]
- 57.Viemeister, N. F. (1988). “ Intensity coding and the dynamic range problem,” Hear. Res. 34(3), 267–274 10.1016/0378-5955(88)90007-X [DOI] [PubMed] [Google Scholar]
- 58.von Klitzing, R. , and Kohlrausch, A. (1994). “ Effect of masker level on overshoot in running- and frozen-noise maskers,” J. Acoust. Soc. Am. 95(4), 2192–2201 10.1121/1.408679 [DOI] [PubMed] [Google Scholar]
- 59.Wright, B. A. (1996). “ Correlated individual differences in conditions used to measure psychophysical suppression and signal enhancement,” J. Acoust. Soc. Am. 100(5), 3295–3303 10.1121/1.417213 [DOI] [PubMed] [Google Scholar]
- 60.Yasin, I. , Drga, V. , and Plack, C. J. (2013). “ Estimating peripheral gain and compression using fixed-duration masking curves,” J. Acoust. Soc. Am. 133(6), 4145–4155 10.1121/1.4802827 [DOI] [PubMed] [Google Scholar]
- 61.Young, E. D. , and Barta, P. E. (1986). “ Rate responses of auditory nerve fibers to tones in noise near masked threshold,” J. Acoust. Soc. Am. 79(2), 426–442 10.1121/1.393530 [DOI] [PubMed] [Google Scholar]
- 62.Zeng, F. , Turner, C. , and Relkin, E. (1991). “ Recovery from prior stimulation II: Effects upon intensity discrimination,” Hear. Res. 55, 223–230 10.1016/0378-5955(91)90107-K [DOI] [PubMed] [Google Scholar]
- 63.Zwicker, E. (1965). “ Temporal effects in simultaneous masking by white-noise bursts,” J. Acoust. Soc. Am. 37(4), 653–663 10.1121/1.1909389 [DOI] [PubMed] [Google Scholar]