An acoustic filter based on layered structure

Abstract

Acoustic filters (AFs) are key components to control wave propagation in multi-frequency systems. We present a design which selectively achieves acoustic filtering with a stop band and passive amplification at the high- and low-frequencies, respectively. Measurement results from the prototypes closely match the design predictions. The AF suppresses the high frequency aliasing echo by 14.5 dB and amplifies the low frequency transmission by 8.0 dB, increasing an axial resolution from 416 to 86 μm in imaging. The AF design approach is proved to be effective in multi-frequency systems.

Filters are fundamental devices that underpin the functionality of a broad range of multiple frequency systems including microwave,¹ optical,² digital,³ and mechanical^4,5 systems. Specifically in multi-frequency vibration systems, delicate wave propagation control is needed to make sure of the soundness and efficiency of the system. One approach towards the wave propagation control is using acoustic filters (AFs) made of polarization-patterned piezoelectric solids⁶ or periodic structures, namely, phononic crystals.^7–9 Alternative methods include acoustic diodes/switches,^10–12 which combine periodic structures and nonlinear medium.^13–16

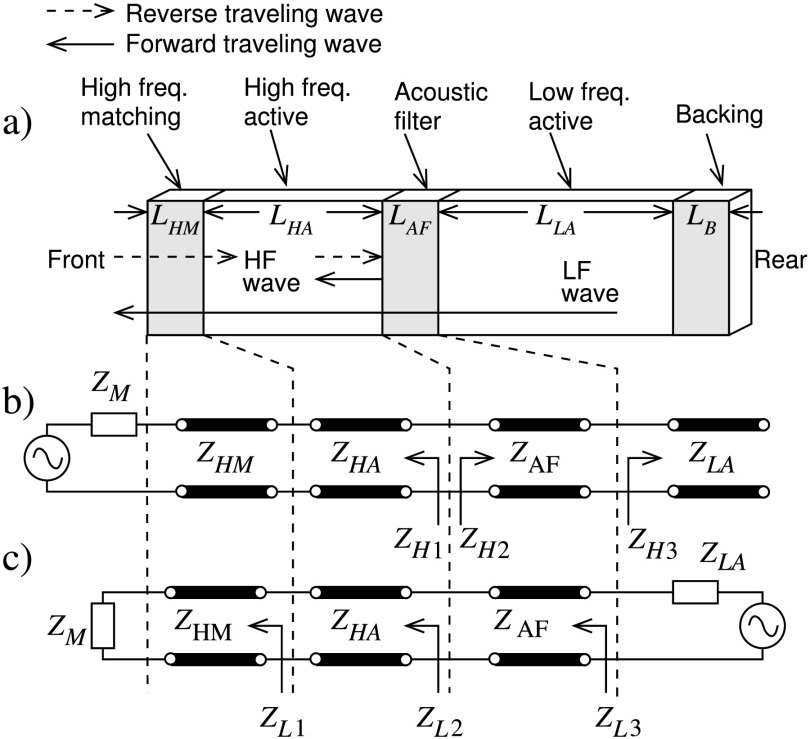
In multi-frequency acoustic systems, the wave sources and propagation are typically spatial-asymmetric. For instance, in dual frequency ultrasound transducers^4,17,18 that showed promising results for super-harmonic microscopy,¹⁹ fundamental, and harmonic frequency ultrasound waves propagate in opposite directions. It is necessary that the low frequency (LF) wave propagates forward efficiently, while the harmonic high frequency (HF) wave does not propagate backward after reaching the high frequency active layer (Fig. 1(a)).²⁰

FIG. 1.

Schematic view of (a) the dual frequency acoustic or laser structure and its equivalent circuits for (b) high frequency reception; (c) low frequency transmission. Parameters L and Z denote the length and impedance of the particular material or port with subscripts M, HM, HA, AF, LA, and B indicating materials of the Medium, High frequency Matching, High frequency Active element, Acoustic Filter, Low frequency Active element, and Backing, respectively. Subscripts H1, H2, H3, L1, L2, and L3 denote the input/output impedance at the ports shown in the figures with H/L denoting the High/Low frequency waves, respectively.

However, few of the present wave control methods have been adapted to multi-frequency ultrasound transducers, due to their bulky size (multiple wavelengths in dimension) or their high cost resulting from very fine microstructures. Based on the space–frequency correlation, an AF can act as a unidirectional switch that allows acoustic penetration in one direction while blocking it in the reverse direction. In this approach, all elements in the system are highly coupled and the design must be undertaken at the system level.

In this letter, we elucidate an AF design with an anti-matching effect for a bandstop of HF ultrasound and a passive amplifier effect for transmission enhancement of LF ultrasound. Inspired by earlier work,^21–24 we applied microwave transmission line theory²⁵ to guide the AF design. The goal of the AF design is to prevent the HF wave from backward propagation while passing the forward LF wave efficiently (Fig. 1(a)). The transmission line equivalent circuit of the system is schematically shown in Figs. 1(b) and 1(c). In a dual frequency system, acoustic structural design for HF acoustic waves is usually more sensitive than that for LF waves due to the wavelength difference. Therefore, our strategy is to first design the HF bandstop filter and subsequently design the LF passive amplifier.

The HF bandstop filter could be designed based on wave reflection (type I) or wave absorption (type II) mechanisms. For the type I filter design, the AF functions as an anti-matching section, shifting the matched impedance (if Z_HA = Z_LA) into a mismatch of Z_H1 and Z_H2. The incident HF wave through the matching layer of the HF element is equivalent to a voltage (stress) source with Z_HA Thevenin's impedance (Fig. 1(b)). Consequently, the output impedance of the HF element is Z_H1 = Z_HA. In order to fulfill the mechanism, the pulse length of the HF wave is required to be spatially shorter than twice that of the LF element thickness. If the short pulse entered the LF element, the pulse would terminate before the reflected wave (from back side of LF element) arrived at the input interface between the AF and LF element again. Then the reflected wave from back side of the LF element could not interfere with the incident wave at the front side of the LF element. Meanwhile, the existence of the backing layer L_B does not affect Z_H2. In this case, Z_H3 = Z_LA and the input impedance Z_H2 at the front surface of the AF layer is

$$Z_{H2}=Z_{\mathit{A}\mathit{F}}\frac{Z_{\mathit{L}\mathit{A}}\text{cosh}({\gamma }_{\mathit{H}\mathit{F}}\ell )+Z_{\mathit{A}\mathit{F}}\text{sinh}({\gamma }_{\mathit{H}\mathit{F}}\ell )}{Z_{\mathit{A}\mathit{F}}\text{cosh}({\gamma }_{\mathit{H}\mathit{F}}\ell )+Z_{\mathit{L}\mathit{A}}\text{sinh}({\gamma }_{\mathit{H}\mathit{F}}\ell )},$$ (1)

where γ_HF is the propagation constant and ℓ is the thickness of the AF layer. The propagation constant is defined as ${\gamma }_{\mathit{H}\mathit{F}}={\alpha }_{\mathit{H}\mathit{F}}+\iota {\beta }_{\mathit{H}\mathit{F}}$, where α_HF is the attenuation coefficient and β_HF is the phase constant. The AF layer is thin compared to the HF wavelength and low attenuation materials can be chosen; as a result, the loss is negligible α_HFℓ ≈ 0 and γ_HFℓ reduces to $\iota {\beta }_{\mathit{H}\mathit{F}}\ell$. Then the intensity transmission coefficient T_I from the HF element to the LF element through the AF layer is (derived in the supplementary material, S1)²⁶

$$\begin{array}{c}{T}_I=4Z_{\mathit{H}\mathit{A}}{Z}_{\mathit{L}\mathit{A}}/[{(Z_{\mathit{H}\mathit{A}}+Z_{\mathit{L}\mathit{A}})}^2\hspace{0.17em}{\text{cos}}^2({\beta }_{\mathit{H}\mathit{F}}\ell )\\ +{(Z_{\mathit{A}\mathit{F}}+\frac{Z_{\mathit{H}\mathit{A}}{Z}_{\mathit{L}\mathit{A}}}{Z_{\mathit{A}\mathit{F}}})}^2\hspace{0.17em}{\text{sin}}^2({\beta }_{\mathit{H}\mathit{F}}\ell )].\end{array}$$ (2)

If β_HFℓ = (2n + 1)λ_HF/4, n = 0, 1, 2,…(n = 0 corresponds to a wide bandwidth and low loss), then Eq. (1) reduces to $Z_{H2}=Z_{\mathit{A}\mathit{F}}^2/Z_{\mathit{L}\mathit{A}}$, which functions as a quarter wavelength impedance transformer. This scheme is similar to the matching layer design, adopting a low Z_LA and a medium Z_AF to generate a high Z_H2 so as to match the high Z_HA. Intriguingly, we utilized the reverse effect with a high Z_LA and a medium Z_AF, resulting in a very low Z_H2 to make a significant mismatching between Z_HA and Z_H2, and hence, the wave propagation toward the LF element is effectively blocked. The HF matching layer is designed using the traditional method as $Z_{\mathit{H}\mathit{M}}=\sqrt{Z_M{Z}_{\mathit{H}\mathit{A}}}$ and L_HM = λ_HF/4.

For the LF acoustic wave, this AF is a bandpass filter, possibly with passive amplification. The equivalent circuit of the system is shown in Fig. 1(c). In the analysis, the active LF element is considered to be a voltage (stress) source with Thevenin's impedance of Z_LA. The medium is large in space with no phase delay between strain and stress, and hence, it is considered as a pure resistive load Z_M. All the front layers of the transducer are thin and, in principle, comparable to the LF wavelength, so each of them performs as a section of the transmission line in a cascade connection. The input impedance Z_L3 was calculated using the cascade ABCD parameters

$$\left[\begin{array}{c}{P}_{L3}\\ V_{L3}\end{array}\right]={\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]}_{\mathit{A}\mathit{F}}{\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]}_{\mathit{H}\mathit{A}}{\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]}_{\mathit{H}\mathit{M}}\left[\begin{array}{c}{P}_M\\ V_M\end{array}\right],$$ (3)

where P_L3 and P_M are the pressure, and V_L3 and V_M are the volume velocity in the respective material, and satisfy P_L3/V_L3 = Z_L3 and P_M/V_M = Z_M. The subscripts AF, HA, and HM in each ABCD matrix indicate the transmission line sections of the AF layer, HF layer, and the HF matching layer, respectively. The ABCD parameter of each section of the transmission line is defined as

$$\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]=\left[\begin{array}{cc}\text{cosh}({\gamma }_{\mathit{L}\mathit{F}}\ell )& Z_0\text{sinh}({\gamma }_{\mathit{L}\mathit{F}}\ell )\\ \text{sinh}({\gamma }_{\mathit{L}\mathit{F}}\ell )/Z_0& \text{cosh}({\gamma }_{\mathit{L}\mathit{F}}\ell )\end{array}\right],$$ (4)

where Z₀ denotes the characteristic impedance of the specific transmission line. The propagation constant γ_LF and the thickness ℓ are also referred to the specific transmission line section. If the attenuation is neglected, then the pressure transmission coefficient is $T_P=2Z_{L3}/(Z_{L3}+Z_{\mathit{L}\mathit{A}}^{*})$. Nevertheless, when the attenuation must be considered, no analytic calculation exists and the performance was estimated as the scattering parameter S₂₁ of a 2–port transmission line network²⁵ simulated using AWR Microwave Office (AWR corp., El Segundo, CA) with simulation circuit shown in the supplementary material, S2.²⁶ Due to the existence of the HF element in front of the LF element, the traditional quarter wavelength matching layer is always disturbed by the HF element. According to the wave theory, the insertion of the AF layer enhances the transmission efficiency and results in a negative insertion loss, suggesting that the passive layer functions as an amplifier, and consequently denominated as a passive amplifier for the LF wave.

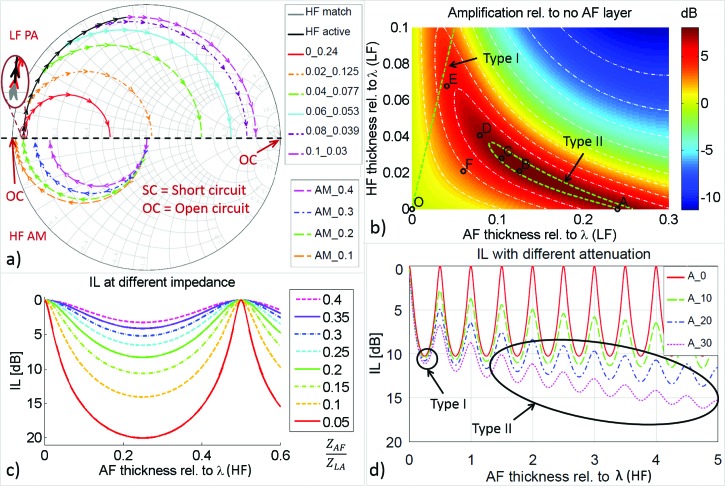
Insertion loss was used to evaluate the performance of the bandstop filter at HF. The insertion loss mainly depends on Z_AF and γ_HFℓ. Starting with Z_HA = Z_LA, the lossless AF layer, acting as a transmission line connected between Z_HA and Z_LA (Fig. 1(b)), shifts from the matched condition Z_H3 (center) to the free–moving boundary condition Z_H2 (close to SC in Fig. 2(a)). The lower Z_AF is accompanied by a lower Z_H2 (lower half of the Smith chart in Fig. 2(a)). The Smith chart is a polar plot with the line from the center to the loci indicating the reflection coefficient.²⁷ At ℓ = λ_HF/4, the reflection coefficient is maximum in amplitude and 0 in phase, so that the insertion loss becomes maximum (Fig. 2(c)). An insertion loss of 10 dB and 20 dB are achievable using a lossless anti-matching layer with a relative impedance $Z_{\mathit{r}\mathit{e}\mathit{l}}=Z_{\mathit{A}\mathit{F}}/\sqrt{Z_{\mathit{H}\mathit{A}}{Z}_{\mathit{L}\mathit{A}}}$ of 0.15 and 0.05, respectively. The AWR software simulation result showed that the propagation loss is low (<1 dB) at λ_HF/4 if the attenuation is less than 30 dB/cm/MHz (type I in Fig. 2(d)). On the contrary, as the thickness of the AF layer increases to more than 1.2λ_HF with 30 dB/cm/MHz attenuation, the insertion loss is dominated by propagation loss and converges to a backing layer (type II in Fig. 2(d)).

FIG. 2.

AF design calculations and simulations. (a) Loci of the AF for HF (lower half) and LF (upper half) shown on a Smith chart normalized to the impedance of piezoelectric material (36.8 MRayl). For HF anti-matching, the numbers in the legend followed AM indicate the Z_rel. Length of all AF is λ/4. For LF passive amplifier, the numbers at both sides of the underscores are L_HA and L_AF relative to λ_LF, respectively. (b) Passive amplifier gain of the AF layer with different L_HA and L_AF. (c) Insertion loss of the HF bandstop filter dependent on the impedance Z_rel = Z_AF/Z_LA (labeled in legend) and thickness L_AF (x–axis). (d) Insertion loss of the HF bandstop filter with attenuation (in dB/cm/MHz) labelled in legend numbers. For (b) and (d), Z_rel = 0.151 according to an actual case. (IL = insertion loss.)

The gain of the passive amplifier for LF ultrasound was determined by the thickness combinations of the HF active layer and the AF layer (Figs. 2(a) and 2(b)). The transmission efficiency with these multi-layers is referred to that with L_AF = 0 because this is the case without the AF layer and the transmission efficiency is almost constant (<0.005 dB variance) at the HF active layer for L_HA ≤ 0.1λ_LF (see point O and the leftmost edge of Fig. 2(b)). The traditional matching layer is at point A in Fig. 2(b) with L_HA = 0 and L_AF = 0.25λ_LF. If L_HA > 0, the transmission efficiency has not been determined because impedances of the layers are far from the ideal multiple matching layer design.²⁸ Positive gains with L_HA > 0 indicate the feasibility of designing a dual frequency transducers with a HF element in front of the LF element with transmission efficiency enhancement of the LF element. For type I reflection-based HF bandstop filters, L_HA ≈ 0.5λ_HF and L_AF = 0.25λ_HF, so that L_AF ≈ 0.5L_HA. Up to 4.95 dB gain is achievable with type I transducers. For type II absorption-based HF bandstop filters, the frequency difference between HF and LF are sufficiently large (L_HA < 0.04λ_LF and f_HF > 12.5f_LF) that the HF attenuation is 12.5 dB, while LF wave attenuation is less than 1 dB. Up to 8.03 dB gain is achievable with a type II transducer, which is higher than the conventional matching (7.73 dB). For both types of filters, positive gains were achievable because the combination of HF active and AF layers caused matching effects for the LF wave (additional rational explained in the supplementary material, S3).²⁶

The AF design approach was validated by comparing the experimental characteristics of piezoelectric transducer prototypes with the theoretical calculation. The HF performance of the type II AF is straightforward and widely accepted.^29,30 The HF performance of the predicted anti-matching effect with type I, and the LF performance of the passive amplifier effect with both types were verified by the transducer prototypes. In the verification, f_HF = 30 MHz and f_LF = 3.5 MHz. The active materials (Z_HA = Z_LA = 36.8 MRayl) are PMN-0.33PT single crystal (HC Materials Corp., Bolingbrook, IL), and the AF material (Z_AF = 5.53 MRayl) is alumina powder (0.3 μm grain size, Lapmaster Int., Mount Prospect, IL) mixed with Epo-tek 301 (Epoxy Technology, Inc., Billerica, MA) and centrifuged. The HF matching layer is parylene C (Z_HM = 3.16 MRayl) coated with a thickness of 15 μm. The thicknesses for the HF anti-matching verification are L_AF = 0.25λ_HF and L_HA = 0.5λ_HF. The thicknesses of the LF passive amplifier designs are marked as A ⇒ F and O in Fig. 2(b). As long as there is reflection at L_B (Z_B ≠ Z_LA), the backing layer L_B has no effect on the transducer performance verification. The verification transducers were bonded to an arbitrarily chosen plastic plate as the backing layer with an acoustic impedance of 3.0 MRrayl.

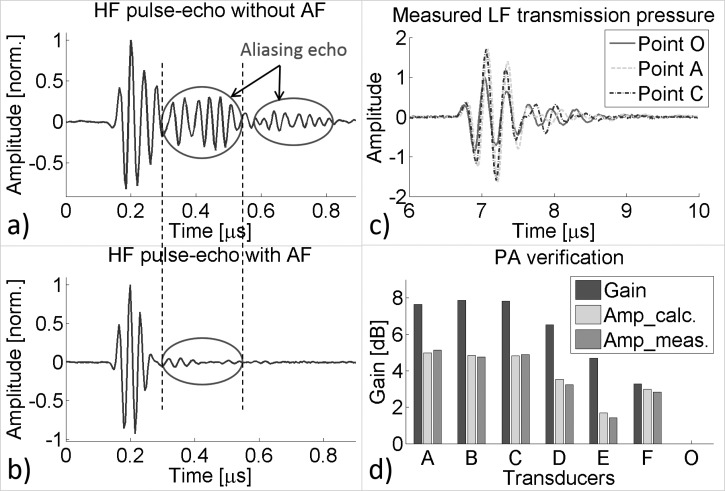
The anti-matching effect of the HF bandstop filter is indicated by the low amplitude of the aliasing echo reflected from the rear side of the LF element. Without the AF layer, the received ultrasound wave would continue propagating from the HF element to the LF element and the reflected wave from the boundary of the LF element and LF backing layer would excite the HF element again, appearing as an aliasing echo. The aliasing echo was verified by the pulse-echo method in a water bath. Such an echo may be reflected back and forth resulting in a series of wave packages following the reflection of the main pulse from the target (−9.2 dB relative to the main pulse, see Fig. 3(a). On the contrary, such aliasing echoes were suppressed by 14.5 dB (−23.7 dB, see Fig. 3(b) with the AF layer sandwiched between the HF and LF elements. The −20 dB pulse length was significantly reduced from 555 ns to 115 ns, leading to an equivalent axial imaging resolution enhancement from 416 μm to 86 μm in water.

FIG. 3.

Verification of the AF in fabricated transducers. (a) HF pulse–echo response without the AF layer, showing a series of aliasing echoes. (b) With the AF layer included, the aliasing echoes are eliminated. (c) Pressure amplitude measured from transducer A (traditional matched) and transducer C (AF enhanced) normalized to transducer O (without matching layers). (d) Actual gain of the AF on transmission and the output amplitude gain considering the reflection from the rear surface (calculated and measured).

As stated earlier, the goal of the AF for the LF ultrasound portion of the transducer is to achieve a proficient transmission efficiency with low or even negative insertion loss. Verification transducers were fabricated with design parameters shown in Fig. 2(b) for (O) reference without matching, (A) ideal traditional matching, and (B ⇒ F) with the HF active element and the AF layer. The output pressure amplitude calculation considered the superposition of the reflected wave from the back surfaces of the LF element. The transmitting pressure verification was measured by a hydrophone (HGL–0085, Onda Corp., Sunnyvale, CA) at 1 cm away from the transducers (aperture: 4 × 4 mm, natural focus at about 9.3 mm) in a water bath. The acoustic waves of transducers A and C are shown in Fig. 3(c) and compared with transducer O. Pressures from both A and C are approximately 1.7 times of that from the non-matching transducer. The measured results of all the prototypes (A ⇒ F and O) were in good agreement with the calculations (see Fig. 3(d).

In conclusion, we demonstrated an acoustic filter-based wave propagation control mechanism that works simultaneously as both a high frequency bandstop filter and a low frequency passive amplifier. This acoustic filter is readily implemented in multi-frequency acoustic systems, such as dual frequency ultrasonic transducers, which could be used in super-harmonic imaging⁴ and therapy–imaging⁵ applications. This acoustic filter design is guided by the microwave circuit design theory, and does not involve any microstructures or non-linearity, making its fabrication cost–effective. The demonstrated acoustic filter is very compact (sub-wavelength along the wave propagation direction), a promising feature in space–limited applications such as biomedical intravascular ultrasound imaging or minimal invasive therapy. This theory and systematic design approach reported in this letter provides a foundation for the design of multi-frequency acoustic or laser systems with desired wave propagation control.