Enhanced correlation between quantitative ultrasound and structural and mechanical properties of bone using combined transmission-reflection measurement

Abstract

Quantitative ultrasound (QUS) is capable of predicting the principal structural orientation of trabecular bone; this orientation is highly correlated with the mechanical strength of trabecular bone. Irregular shape of bone, however, would increase variation in such a prediction, especially under human in vivo measurement. This study was designed to combine transmission and reflection modes of QUS measurement to improve the prediction for the structural and mechanical properties of trabecular bone. QUS, mechanical testing, and micro computed tomography (μCT) scanning were performed on 24 trabecular bone cubes harvested from a bovine distal femur to obtain the mechanical and structural parameters. Transmission and reflection modes of QUS measurement in the transverse and frontal planes were performed in a confined 60° angle range with 5° increment. The QUS parameters, attenuation (ATT) and velocity (UV), obtained from transmission mode, were normalized to the specimen thickness acquired from reflection mode. Analysis of covariance showed that the combined transmission-reflection modes improved prediction for the structural and Young's modulus of bone in comparison to the traditional QUS measurement performed only in the medial-lateral orientation. In the transverse plane, significant improvement between QUS and μCT was found in ATT vs bone surface density (BS/BV) (p < 0.05), ATT vs trabecular thickness (Tb.Th) (p < 0.01), ATT vs degree of anisotropy (DA) (p < 0.05), UV vs trabecular bone number (Tb.N) (p < 0.05), and UV vs Tb.Th (p < 0.001). In the frontal plane, significant improvement was found in ATT vs structural model index (SMI) (p < 0.01), ATT vs bone volume fraction (BV/TV) (p < 0.01), ATT vs BS/BV (p < 0.001), ATT vs Tb.Th (p < 0.001), ATT vs DA (p < 0.001), and ATT vs modulus (p < 0.001), UV vs SMI (p < 0.01), UV vs BV/TV (p < 0.05), UV vs BS/BV (p < 0.05), UV vs Tb.Th (p < 0.01), UV vs trabecular spacing (p < 0.05), and UV vs modulus (p < 0.01). These data suggested that the combined transmission-reflection QUS method is capable of providing information more relevant to the structural and mechanical properties of trabecular bone.

I. INTRODUCTION

It is widely accepted that quantitative ultrasound (QUS) can quantify fracture risk (Glüer et al., 1996; Hans et al., 1996; Bauer et al., 1997; Hadji et al., 2000; Huopio et al., 2004), as well as predict fracture type (Drozdzowska and Pluskiewicz, 2002). When ultrasound waves travel through trabecular bone, a porous media, information regarding material properties, such as density, elastic modulus, and anisotropy, can be calculated by evaluating two main ultrasound parameters, velocity and attenuation (Njeh et al., 1999; Laugier, 2006). These two parameters are heavily influenced by not only the quantity of bone mass, but also the microarchitecture and alignment of trabeculae (Mizuno et al., 2010). The anisotropic structure of trabecular bone is the result of adaptation to its mechanical environment according to “Wolff's Law” (Wolff, 1896). Recent studies described the interaction between trabecular bone structural alignment and ultrasound wave (Gluer et al., 1993; Njeh et al., 1997a; Han and Rho, 1998; Hosokawa and Otani, 1998; Nicholson et al., 1998; Hans et al., 1999; Wear, 2000; Lee et al., 2007; Mizuno et al., 2008; Hosokawa, 2009; Mizuno et al., 2009; Hosokawa, 2010; Mizuno et al., 2010; Cardoso and Cowin, 2011; Cowin and Cardoso, 2011; Hosokawa, 2011; Cardoso and Cowin, 2012; Liu et al., 2014). These researchers all came to the same conclusion: that QUS is sensitive enough to pick up the difference of structural and mechanical properties of trabecular bone in different orientations and, generally, provide more comprehensive information of bone “quality” than simply bone “quantity.”

Our group and others reported a novel QUS method using a three-dimensional rotational ultrasound scan to measure the principal structural orientation (PSO) of spherical trabecular bone specimens (Mizuno et al., 2010; Lin et al., 2012). This work demonstrated that ultrasound has the ability to predict the trabecular structural orientation just as accurately as the current gold standard—the longest vector of mean intercept length (MIL) tensor measured using micro computed tomography (μCT). Further study utilized a finite element modeling of spherical trabecular bone and validated the QUS prediction of PSO (Lin et al., 2014). The mechanical properties in the PSO predicted by QUS are significantly higher than the anatomical orientations and comparatively close to the longest vector of the MIL tensor.

While traditional QUS measurement, especially of the human calcaneus, is performed in medial-lateral orientation, the results of our previous work indicate that QUS measurement can determine the structural alignment of trabecular bone and correlate strongly with mechanical properties of the trabecular bone (Lin et al., 2012; Lin et al., 2014). By performing ultrasound scan in the PSO, the prediction of mechanical properties can be improved from simply performing QUS measurement conventionally in the medial-lateral orientation. This present study aims to improve the correlations between QUS parameters and structural and mechanical properties of trabecular bone by performing QUS measurement in the PSO determined by QUS. To progress from an ideal spherical bone model used in the previous work, trabecular bone specimens with more practical cubic geometry are tested. To eliminate the samples thickness difference in different QUS scanning angles, reflection mode QUS as described by Xia et al. (2007) is performed to measure the sample thickness in different scanning orientations. The sample thickness measured by reflection mode is combined with the transmission mode QUS scan to evaluate the structural and mechanical properties.

II. MATERIALS AND METHODS

A. Trabecular bone cubes preparation

Twenty-four trabecular bone cubes were harvested from the distal end of bovine femurs. The samples were cut into 15–20 mm cubes using a slow speed diamond saw (Microslice, Metals Research Limited, Cambridge, England) with constant water irrigation. The principal anatomical orientations were marked on the surfaces of the bone samples as anterior-posterior, medial-lateral, and proximal-distal. The fat marrow among the trabeculae was flushed out using a dental water pick. For preservation, the bone specimens were soaked in saline and 70% ethanol “half-and-half” solution and stored in a 4 °C refrigerator. Before QUS measurement, the bone cubes were put into a vacuum chamber while in solution for 3 h to remove the air bubbles trapped among the trabeculae.

B. Quantitative ultrasound measurement

Quantitative ultrasound measurements were performed by using a scanning confocal acoustic navigation system (Xia et al., 2007), which consisted of a computer-controlled two-dimensional scanner unit and a pair of focused transducers (V302-SU-F2.00IN, Olympus NDT Inc., Waltham, MA) with a center frequency of 1 MHz. The diameter of the transducers is 25.4 mm and the focal length of the transducers is 50.8 mm. The transducers were coaxially installed 101.6 mm away from each other on a rotational stage, aligning with the center of the bone cube, which was wrapped in acoustic-wave-proof foam at the midpoint of the two transducers. The acoustic-wave-proof foam was made of polyurethane and rich in air cells, which can block the acoustic wave propagated outside detected region. A through void was cut in the foam according to the shape of the bone cube sample, allowing the ultrasound pulse to pass through the sample without the interference of the foam, while blocking the peripheral ultrasound wave passing around the sample. The purpose of this acoustic-wave-proof foam was to make sure that only the ultrasound wave passing through the sample, not around the sample, was picked up by the receiver. QUS measurements were performed in two orthogonal anatomical planes, frontal plane and transverse plane, in a defined range of angle utilizing the rotational stage. As shown in Fig. 1, for QUS measurement on a transverse plane, an angle range of 60° was defined with the medial-lateral axis as the neutral axis. The QUS scans were performed in this 60° range with an interval of 5°, namely, a total of 13 scans on the frontal plane for each sample. As for the QUS scan on the frontal plane, a similar angle range of 60° was also defined for the measurement with the medial-lateral axis as the neutral axis. For each scanning angle on each anatomical plane, the QUS measurement was performed in two different modes: transmission and reflection.

FIG. 1.

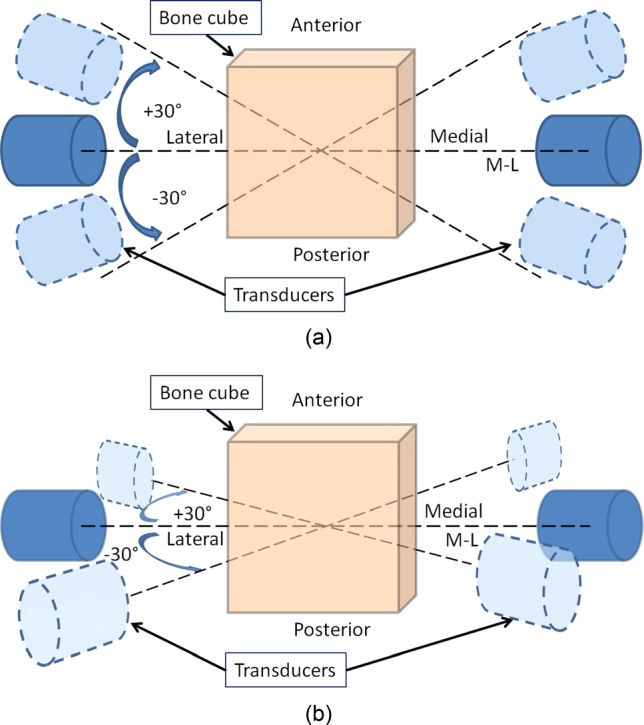
(Color online) Schematic representations of the QUS measurement configuration on (a) transverse plane and (b) frontal plane. For both planes, medial-lateral axis is used as the neutral axis, and the QUS measurement is performed in a 60° angle range, ±30° from the medial-lateral axis. Within the 60° angle scanning range, the interval between every 2 scans is 5°, resulting in 13 scanning angles on each plane of each sample.

1. Transmission mode QUS measurement

The transmission mode QUS measures the interaction between the ultrasound wave and trabecular bone and, therefore, material properties of trabecular bone can be derived from the received ultrasound wave after propagating through the bone sample. As shown in Fig. 3(a), in transmission mode, an ultrasound wave was emitted by one transducer and received by another after traveling through the trabecular bone cube sample. Two QUS parameters, ultrasound attenuation (ATT) and ultrasound velocity (UV), were calculated using the classic substitution method (Langton et al., 1984). ATT is calculated using the following equation:

$$\text{ATT}=\frac{10\hspace{0.17em}\hspace{0.17em}\text{log}\left(I_1/I_2\right)}{d},$$ (1)

where I₁ and I₂ are the intensity of reference and sample wave, respectively, calculated by integrating the square amplitude of the received pulse over time, and d is the thickness of the bone sample. UV is calculated using the following equation:

$$\text{UV}=\frac{C_{r}d}{d-C_r\Delta t},$$ (2)

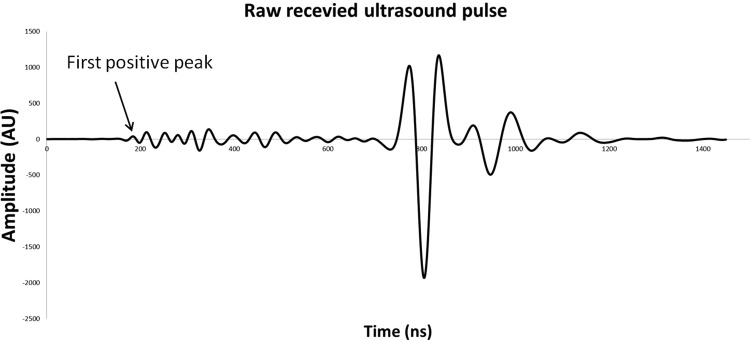
where C_r is the velocity of ultrasound in water, Δt is the arrival time difference between reference and sample wave, and d is the thickness of the bone sample. In this study, the first positive peak of the fast wave is used as the landmark to calculate the time difference, Δt (Fig. 2).

FIG. 3.

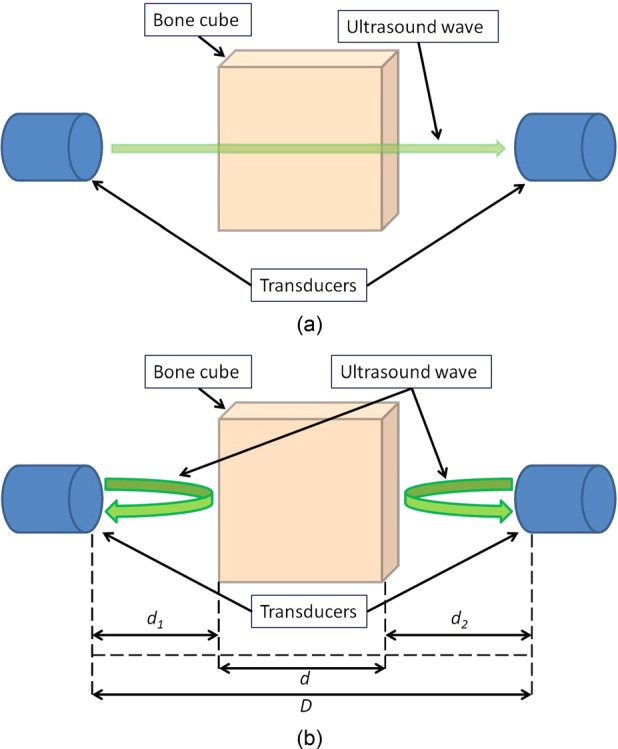
(Color online) Schematic representation of (a) transmission mode QUS measurement and (b) reflection mode measurement. For transmission mode, ultrasound wave is emitted by one transducer and received by the other transducer on the side of the sample after propagating through the sample. For reflection mode, each transducer emits its own ultrasound wave signal and picks up the echo bounced back off the surface of the sample. Based on the time-of-flight of the echo, the distances between the sample surface and the transducer, d1 and d2, can be determined. The sample thickness can also be calculated, given the distance between two transducers, D.

FIG. 2.

Typical received raw ultrasound pulse. The first positive peak of fast wave is used as a landmark to calculate ultrasound velocity.

2. Reflection mode QUS measurement

The reflection mode ultrasound scan was utilized to measure the thickness of trabecular bone for each scanning angle. In this mode, the echo of the ultrasound wave off of the surface of the bone cube sample is picked up by the same transducer which emitted the ultrasound wave. The same measurement was repeated using both transducers to calculate the distance between the transducers and bone cube, d₁ and d₂,

$$\begin{array}{c}{d}_1=C_r{t}_1,\\ d_2=C_r{t}_2,\end{array}$$ (3)

where C_r is the velocity of ultrasound in water, t₁ and t₂ are the times taken for the ultrasound pulses from both transducers to bounce back off the surface of the bone cube and return to the transducers, respectively, and they are calculated by tracking the first positive peak of the ultrasound pulse. With d₁ and d₂, the thickness of the bone cube, d, was calculated

$$d=D-d_1-d_2,$$ (4)

where D is the distance between the two transducers, 101.6 mm. Figure 3(b) illustrates the relation of the measuring of the distances. Then, the calculated bone cube thickness, d, was used in Eq. (2) to calculate the ultrasound velocity and normalize the ultrasound ATT calculated using Eq. (1).

3. Combination of transmission and reflection modes of QUS measurement

For attenuation, the angle with the highest normalized attenuation value was considered to be along the structural orientation of the trabecular architecture. The normalized attenuation value was denoted as ATT_T-R, while the attenuation value in the medial-lateral orientation was denoted as ATT_M-L. The same calculation was also applied to the ultrasound velocity data. The highest normalized velocity value among all scanning angles was denoted as UV_T-R, and the velocity value in the medial-lateral orientation was denoted as UV_M-L.

C. μCT imaging

μCT imaging with a resolution of 30 μm was performed on each trabecular bone cube using a μCT 40 system (SCANCO Medical AG, Brüttisellen, Switzerland) to analyze the structural properties, such as structural model index (SMI), bone volume fraction (BV/TV), bone surface density (BS/BV), trabecular bone number (Tb.N), trabecular thickness (Tb.Th), trabecular spacing (Tb.Sp), and degree of anisotropy (DA).

D. Compressive mechanical loading

Compressive mechanical loading was performed on a MTS MiniBionix 858 (MTS Corporation, Minneapolis, MN) axial load frame with TestStar II control software and an SMT2–2000N load cell (Interface Inc., Scottsdale, AZ). A smooth curved nailhead was placed on the top surface of the bone cube to guide the loading force from the loading piston along the normal orientation of the bone cube surface. This method overcame the slight deviation from the parallelism between the top and bottom surfaces of the bone cube (Mittra et al., 2008). The loading protocol began with a 50N preload to ensure a full contact between the loader and the samples, and to eliminate the error induced by uneven surface condition of the samples. The loading then proceeded for 2000 μstrain at the rate of 0.005 mm/s to minimize the effect caused by the viscosity of bone material. The loading piston retreated back after the compressive loading, and the same loading cycle was repeated five times. The force and displacement data recorded by the system was then used to calculate the Young's modulus (E) of the bone cube using the following equation:

$$E=\frac{\mathit{F}\mathit{d}}{\mathit{l}\mathit{A}},$$ (5)

where F is the loading force of the piston, l is the displacement of the loading piston, d is the thickness of the sample, and A is the cross section area perpendicular to the loading orientation.

E. Data analysis

Linear correlation analysis was performed between the ultrasound parameters and the structural parameters, and between the ultrasound parameters and the mechanical property. Further analysis of covariance (ANCOVA) was made between the correlations of conventional QUS scan in medial-lateral orientation and the combined transmission-reflection method to evaluate the improvement of adapting the new QUS method. ANCOVA was performed using SPSS (IBM SPSS Statistics Release 18.0.0, IBM Corp., Armonk, NY), in which p-value < 0.05 was considered significant.

III. RESULTS

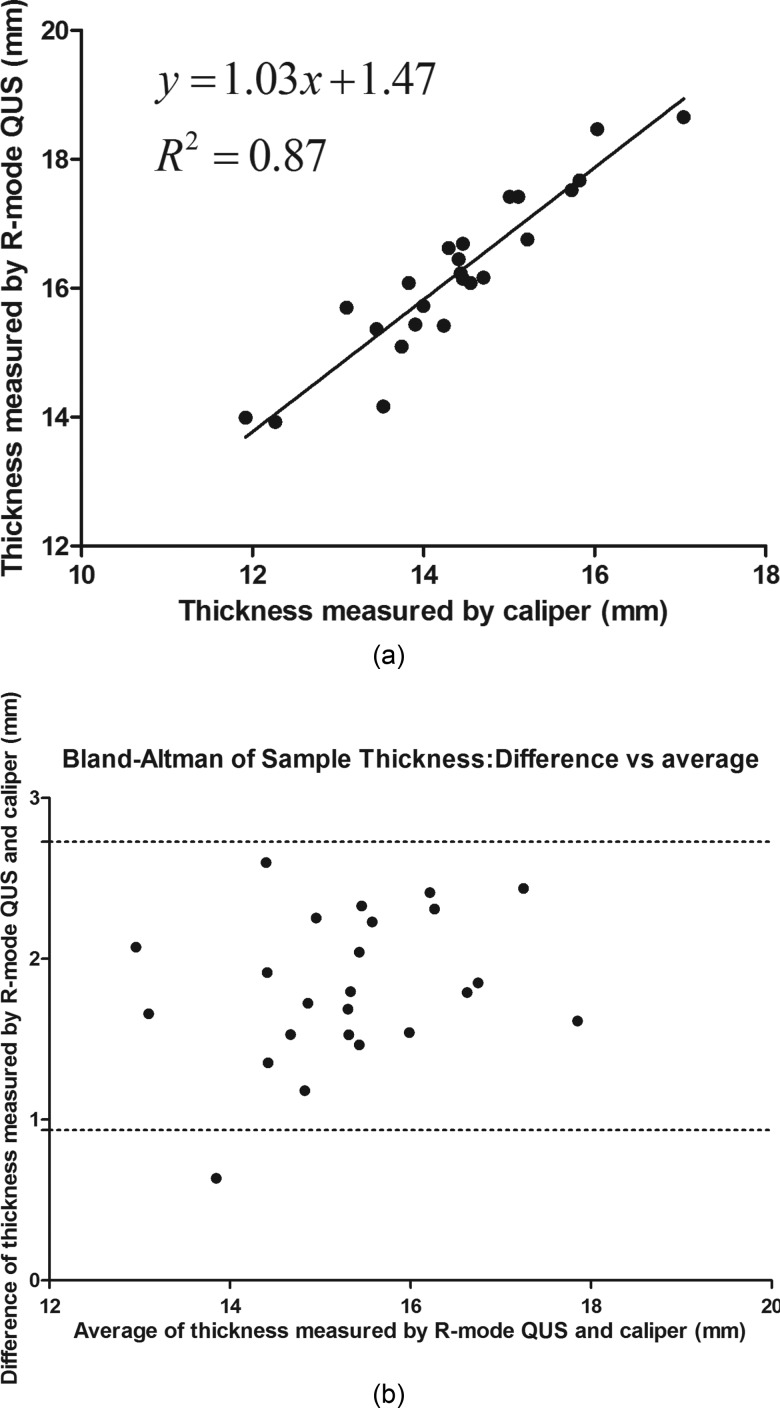
The thickness of the bone cubes in medial-lateral orientation was measured using a caliper to validate the accuracy of the reflection mode ultrasound scan. The reflection mode QUS demonstrated significant agreement with the thickness determined by caliper with correlation coefficient, R²= 0.87 [Fig. 3(a)]. Bland–Altman analysis of the difference and average of the thicknesses measured by caliper and R-mode QUS was performed. The bias between two measurements is 1.83 mm and the standard deviation of bias is 0.46. The upper limit of the 95% agreement is 2.73, and the lower limit is 0.93 [Fig. 4(b)]. The mean, standard deviation, range, and the 95% confidence interval of the structural, mechanical, and QUS parameters are listed in Table I.

FIG. 4.

(a) Linear regression analysis of the sample thickness measured by caliper and reflection mode QUS shows high linear correlation (R²= 0.87). (b) Bland–Altman analysis of the difference and average of the thicknesses measured by caliper and R-mode QUS. The bias between two measurements is 1.83 mm and the standard deviation of bias is 0.46. The upper limit of the 95% agreement is 2.73, and the lower limit is 0.93.

TABLE I.

Mean, standard deviation, maximum, minimum, and the 95% confidence interval of the measured structural, mechanical, and QUS parameters.

	Mean	Standard deviation	Maximum	Minimum	95% Confidence interval
Structural
SMI	−0.43	1.06	1.51	−2.12	−0.85–0.00
BV/TV	0.39	0.10	0.54	0.18	0.35–0.43
BS/BV (1/mm)	10.01	2.27	14.77	6.71	9.11–10.92
Tb.N (1/mm)	1.85	0.20	2.24	1.33	1.77–1.93
Tb.Th (mm)	0.21	0.05	0.30	0.14	0.19–0.23
Tb.Sp (mm)	0.34	0.09	0.62	0.23	0.30–0.38
DA	1.69	0.29	2.39	1.32	1.57–1.81
Mechanical
Modulus (MPa)	304	73	445	120	275–333
QUS (transverse)
ATTM-L (dB/mm)	0.83	0.16	1.15	0.60	0.77–0.90
ATTT-R (dB/mm)	0.95	0.19	1.30	0.60	0.87–1.02
UVM-L (mm/s)	1567	67	1729	1454	1540–1594
UVT-R (mm/s)	1600	77	1777	1485	1570–1631
QUS (frontal)
ATTM-L (dB/mm)	0.86	0.18	1.25	0.58	0.79–0.93
ATTT-R (dB/mm)	0.96	0.19	1.33	0.61	0.89–1.04
UVM-L (mm/s)	1577	75	1731	1446	1547–1608
UVT-R (mm/s)	1626	86	1780	1488	1592–1661

A. QUS measurement on transverse plane

On transverse plane, the average of ATT_M-L was 0.83 ± 0.16 dB/mm, significantly 12% lower than the average of ATT_T-R, 0.95 ± 0.19 dB/mm (p < 0.05). The linear correlation between ATT_M-L and ATT_T-R was significant (R²= 0.79, p < 0.001). For ultrasound velocity, the average of UV_M-L 1567 ± 67 m/s was only 2% lower than the average of UV_T-R, 1600 ± 77 m/s, and the linear correlation between them was also significant (R²= 0.86, p < 0.001).

The correlation between ultrasound parameters and both structural and mechanical parameters were listed in Table II. No significant correlation was found between QUS parameters and DA. All other structural or mechanical parameters had significant correlation with at least one QUS parameter, either ATT or UV.

TABLE II.

Linear correlation coefficient (R) between QUS parameters on transverse plane and structural and mechanical parameters. All structural of mechanical parameters have significant correlations with at least one QUS parameters, except for DA.

	ATTM-L (dB/mm)	ATTT-R (dB/mm)	UVM-L (mm/s)	UVT-R (mm/s)
SMI	−0.66***	−0.70***	−0.47*	−0.46*
BV/TV	0.68***	0.73***	0.44*	0.45*
BS/BV (1/mm)	−0.62**	−0.73***	−0.35	−0.40
Tb.N (1/mm)	0.56**	0.48*	0.58**	0.46*
Tb.Th (mm)	0.59**	0.72***	0.29	0.36
Tb.Sp (mm)	−0.69***	−0.71***	−0.54**	−0.49*
DA	0.12	0.24	0.02	0.13
Modulus (MPa)	0.61**	0.69***	0.46*	0.46*

^*p < 0.05, **p < 0.01, ***p < 0.001.

ANCOVA test showed that ATT_T-R had significantly higher correlations with BS/BV (p < 0.05), Tb.Th (p < 0.01), and DA (p < 0.05) when compared to ATT_M-L (Table III). As for ultrasound velocity measurement, UV_T-R only showed significantly improved prediction for Tb.Th (p < 0.001) when compared to UV_M-L. Tb.N even showed a decreased correlation (p < 0.05) with UV_T-R when compared to UV_M-L (Table IV).

TABLE III.

Comparison of the correlation coefficients (R) between ultrasound attenuation on transverse plane and structural and mechanical parameters shows that ATT_T-R has significantly better prediction for BS/BV, Tb.Th, and DA than ATT_M-L. N.S. = Non-significant.

	ATTM-L	ATTT-R	p
SMI	−0.66	−0.70	N.S.
BV/TV	0.68	0.73	N.S.
BS/BV (1/mm)	−0.62	−0.73	<0.05
Tb.N (1/mm)	0.56	0.48	N.S.
Tb.Th (mm)	0.59	0.72	<0.01
Tb.Sp (mm)	−0.69	−0.71	N.S.
DA	0.12	0.24	<0.05
Modulus (MPa)	0.61	0.69	N.S.

TABLE IV.

Comparison of the correlation coefficients (R) between ultrasound velocity on transverse plane and structural and mechanical parameters shows that UV_T-R has significantly better prediction for Tb.Th than UV_M-L. The correlation between UV_T-R and Tb.N is significantly lower than the correlation between UV_M-L and Tb.N. N.S. = Non-significant.

	UVM-L	UVT-R	p
SMI	−0.47	−0.46	N.S.
BV/TV	0.44	0.45	N.S.
BS/BV (1/mm)	−0.35	−0.40	N.S.
Tb.N (1/mm)	0.58	0.46	<0.05
Tb.Th (mm)	0.29	0.36	<0.001
Tb.Sp (mm)	−0.54	−0.49	N.S.
DA	0.02	0.13	N.S.
Modulus (MPa)	0.46	0.46	N.S.

B. QUS measurement on frontal plane

For QUS measurement in the frontal plane, the average of ATT_M-L was 0.86 ± 0.18 dB/mm, 10.37% lower than the average of ATT_T-R, 0.96 ± 0.19 dB/mm. The linear correlation between ATT_M-L and ATT_T-R was significant (R²= 0.87, p < 0.001). For ultrasound velocity, the average of UV_M-L, 1577 ± 75 m/s, was 3.0% lower than the average of UV_T-R, 1626 ± 86 m/s, and the linear correlation between them was also significant (R²= 0.91, p < 0.001).

The correlation between ultrasound parameters and both structural and mechanical parameters were listed in Table V. No significant correlation was found between QUS parameters and DA. All other structural or mechanical parameters had significant correlation with both ATT and UV. Furthermore, almost all correlation coefficient values from the measurement in frontal plane were higher than those from the measurement on transverse plane, except the correlation between ATT_M-L and Tb.N.

TABLE V.

Linear correlation coefficient (R) between QUS parameters on frontal plane and structural and mechanical parameters. All structural of mechanical parameters have significant correlations with QUS parameters, except for DA.

	ATTM-L (dB/mm)	ATTT-R (dB/mm)	UVM-L (mm/s)	UVT-R (mm/s)
SMI	−0.73***	−0.81***	−0.67***	−0.75***
BV/TV	0.75***	0.83***	0.73***	0.79***
BS/BV (1/mm)	−0.69***	−0.81***	0.56**	−0.64***
Tb.N (1/mm)	0.56**	0.58**	0.59**	0.62**
Tb.Th (mm)	0.67***	0.80***	0.52**	0.62**
Tb.Sp (mm)	−0.74***	−0.79***	−0.66***	−0.73***
DA	0.19	0.35	0.28	0.24
Modulus (MPa)	0.61**	0.73***	0.50*	0.59**

^*p < 0.05, **p < 0.01, ***p < 0.001.

Combined transmission-reflection QUS measurement showed significantly improved correlation with mechanical and structural parameters in the frontal plane compared to transverse plane measurement. ATT_T-R had significantly higher correlations with SMI (p < 0.01), BV/TV (p < 0.01), BS/BV (p < 0.001), Tb.Th (p < 0.001), DA (p < 0.05) and Young's modulus (p < 0.001) when compared to ATT_M-L (Table VI). As for the ultrasound velocity measurement, UV_T-R showed significantly improved prediction for SMI (p < 0.01), BV/TV (p < 0.05), BS/BV (p < 0.05), Tb.Th (p < 0.01), Tb.Sp (p < 0.05), and Young's modulus (p < 0.01) when compared to UV_M-L (Table VII).

TABLE VI.

Comparison of the correlation coefficients (R) between ultrasound attenuation on frontal plane and structural and mechanical parameters shows that ATT_T-R has significantly better prediction for SMI, BV/TV, BS/BV, Tb.Th, DA, and Modulus than ATT_M-L. N.S. = Non-significant.

	ATTM-L	ATTT-R	p
SMI	−0.73	−0.81	<0.01
BV/TV	0.75	0.83	<0.01
BS/BV (1/mm)	−0.69	−0.81	<0.001
Tb.N (1/mm)	0.56	0.58	N.S.
Tb.Th (mm)	0.67	0.80	<0.001
Tb.Sp (mm)	−0.74	−0.79	N.S.
DA	0.19	0.35	<0.001
Modulus (MPa)	0.61	0.73	<0.001

TABLE VII.

Comparison of the correlation coefficients (R) between ultrasound velocity on frontal plane and structural and mechanical parameters shows that UV_T-R has significantly better prediction for SMI, BV/TV, BS/BV, Tb.Th, Tb.Sp, and Modulus than UV_M-L. N.S. = Non-significant.

	UVM-L	UVT-R	p
SMI	−0.67	−0.75	<0.01
BV/TV	0.73	0.79	<0.05
BS/BV (1/mm)	−0.56	−0.64	<0.05
Tb.N (1/mm)	0.59	0.62	N.S.
Tb.Th (mm)	0.52	0.62	<0.01
Tb.Sp (mm)	−0.66	−0.73	<0.05
DA	0.28	0.24	N.S.
Modulus (MPa)	0.50	0.59	<0.01

IV. DISCUSSION

This study was designed to combine transmission and reflection modes of QUS measurement to improve the prediction for the structural and mechanical properties of trabecular bone. Our previous work has shown that the correlation between QUS measurement and mechanical strength of trabecular bone is highly orientation dependent, in the manner that the orientation in which ultrasound attenuation and velocity peak has the highest mechanical strength (Lin et al., 2012; Lin et al., 2014), and these results agreed with the founding of other researchers (Njeh et al., 1997b; Han and Rho, 1998; Nicholson et al., 1998; Hans et al., 1999). These previous results were obtained from ideal spherical trabecular bone specimens or models of which sample thickness remained the same for all measuring orientations. To progress from ideal model to realistic bone geometry, this present study employed cubic trabecular bone sample as an interim model to explore the feasibility of applying the QUS technique on real human bones. The cubic model gave rise to the need of taking the varying sample thickness in different scanning orientations into consideration. Reflection mode QUS is a well-established method of measuring the distance between an object and the ultrasound transducer, based on the time-of-flight of the reflected echo. The high linear correlation shown in Fig. 4 between the medial-lateral thickness measured by caliper and reflection mode QUS validated the accuracy of such distance measurement.

The intended application of this technique is to scan clinically critical sites very rich in trabecular bone that have high fracture risk, such as the human calcaneus. As mentioned before, the current QUS protocol of the calcaneus only includes scanning in the medial-lateral orientation, in which the results may not be the best predictor for the mechanical strength. Considering the location of calcaneus and its surrounding structure, QUS in the frontal and transverse planes was performed to evaluate the efficacy of this combined QUS measurement and to develop the proper protocol to apply it. As shown in Tables III, IV, VI, and VII, linear correlations between QUS and structural and mechanical properties in the frontal plane are generally higher than those in the transverse plane. This trend is expected because the frontal plane is more aligned to the weight bearing orientation, provided that the samples used in this study are from bovine distal femur, and the future intended measuring site is human calcaneus. It is also observed that significant improvement in prediction of elastic modulus was only found in measurement in the frontal plane, not in the transverse plane. This finding supports that measurement in the frontal plane is a better configuration and can provide information more relevant to the mechanical properties than the transverse plane. As shown in Table IV, the correlation between UV_T-R and Tb.N is significantly lower than the correlation between UV_M-L and Tb.N. Because of the technical difficulty of the measurement, we do not have the data to explain this reversed correlation trend for Tb.N on transverse plane. Also, because of the limitation of bone cube tests that cannot cover all the directions, interconnection between trabecular bones may influence the UV results in M-L and T-R directions. Overall, correlation comparison results on the frontal plane are more consistent than one transverse plane.

Most structural and mechanical parameters have significant correlations with both QUS parameters and in both anatomical planes, except for DA, which is defined as the ratio of the longest vector of the MIL tensor over the shortest vector, and is based on the calculation of MIL tensor (Whitehouse, 1974). Therefore, to obtain a reliable prediction of DA using QUS, a complete three-dimensional measurement over the specimen is required. In this study, QUS measurement was only performed on two anatomical planes and within a 60° angle range, and was not able to ensure that the longest and shortest vector of MIL tensor were included in the scanning orientations. While this confined scanning range is a limitation of this QUS technique, it is also realistic, given the fact that full 360° QUS is not possible on any of the three anatomical planes for human calcaneus because of the existence of other bones, like tibia and tarsal bones. Therefore, a confined 60° scanning angle range in the frontal and transverse plane is a practical approach to collect orientation-dependent QUS information in a physiologically feasible configuration.

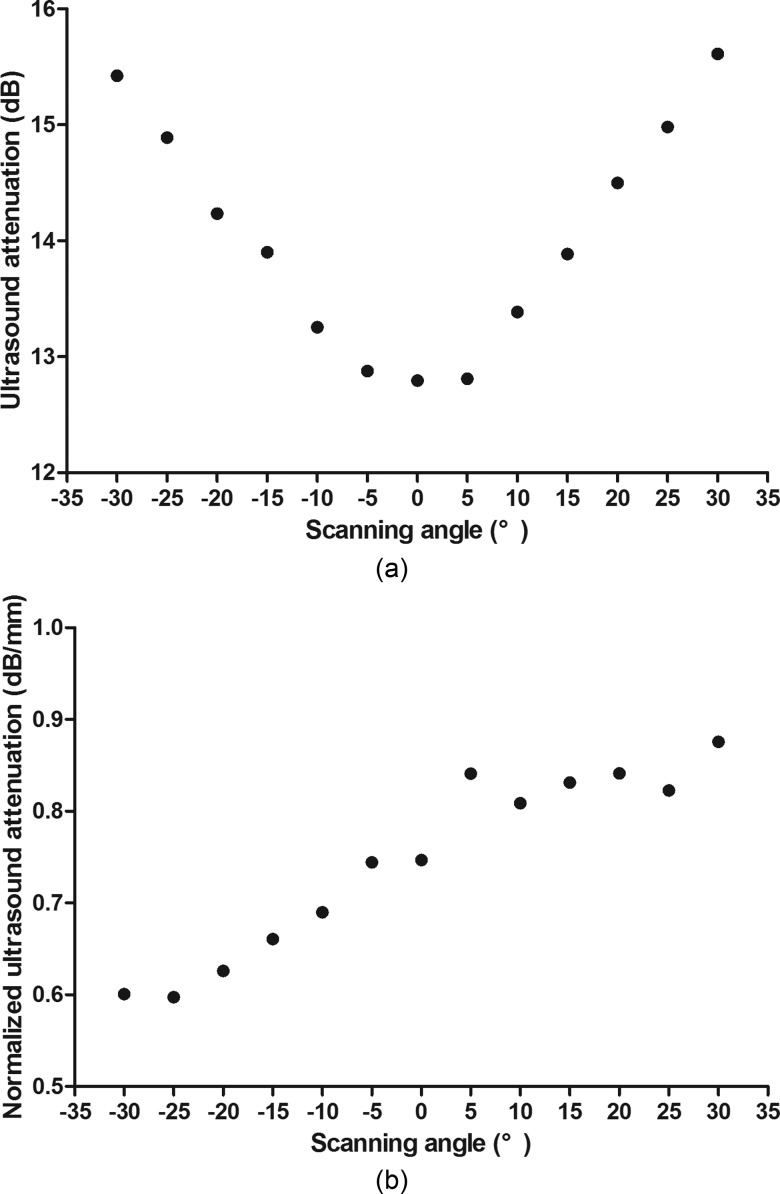
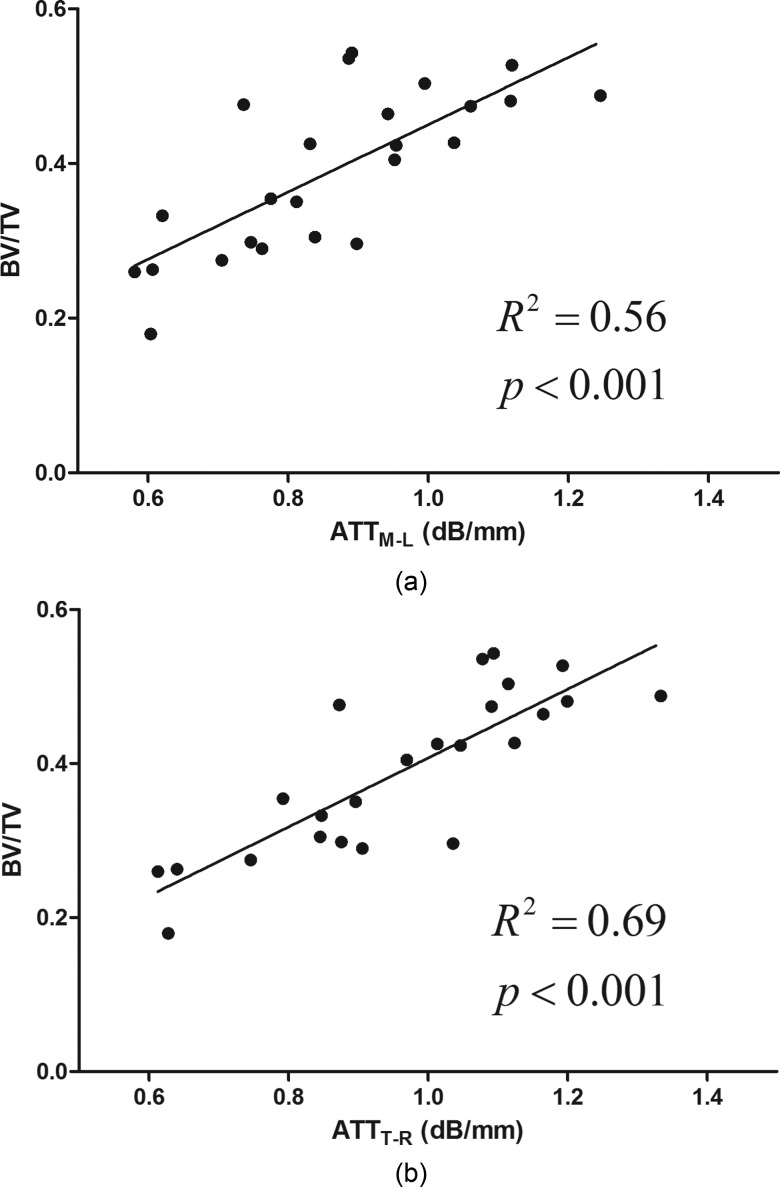
The results showed that combined transmission-reflection QUS significantly improved the ability to determine the structural and mechanical properties when compared to the conventional QUS measurement in medial-lateral orientation. This improvement was achieved by taking additional consideration of the different sample thickness in different scanning orientations and the fact that QUS information more aligned to the weight bearing orientation is more correlated with the mechanical strength. Figure 5(a) detailed the attenuation data in the frontal plane of a bone cube sample before being normalized to the samples thickness. From all the scanning orientations, medial-lateral (0°) had the lowest attenuation value (12.79 dB), whereas measurements in +30° and −30° orientations had relatively higher values (15.42 dB and 15.61 dB). The longer sample thickness in these orientations contributed to the higher ultrasound attenuation values. By normalizing the attenuation values to the corresponding sample thicknesses, the data in Fig. 5(b) showed that QUS measurements at +30° had the highest normalized attenuation value (0.86 dB/mm) and were chosen to represent this sample in the correlation analysis with structural and mechanical properties. As shown in Fig. 6, this method significantly improved the correlation between ultrasound attenuation and BV/TV. The same mechanism applied to the ultrasound velocity analysis in which sample thickness played an intrinsically important role in the calculation process, as indicated in Eq. (2). It has been reported by Xia et al. (2007) that a subtle change in sample thickness can cause significant difference in ultrasound velocity calculation, which implied that simply assuming a uniform sample thickness for ultrasound measurement can cause an error that led to inaccurate prediction for bone strength and fracture risk.

FIG. 5.

Attenuation values of a bone cube sample in all scanning angles on frontal plane (a) before and (b) after normalization of the sample thickness in each scanning angle. Before normalization, medial-lateral orientation (0°) has the lowest attenuation value (12.79 dB), whereas measurements in +30° and −30° orientations have relatively higher values (15.42 dB and 15.61 dB). After normalization, QUS measurement in +30° has the highest normalized attenuation value (0.86 dB/mm) and is chosen to represent this sample in the correlation analysis with structural and mechanical properties.

FIG. 6.

Linear correlation between ultrasound ATT and bone volume fraction (BV/TV) using (a) traditional QUS (ATT_M-L) in medial-lateral orientation and (b) combined transmission-reflection QUS (ATT_T-R) in the frontal plane. Correlation of ATT_T-R vs BV/TV (R²= 0.69) is significantly higher than ATT_M-L vs BV/TV (R²= 0.56), p < 0.01.

V. CONCLUSION

Reflection mode QUS scanning can accurately measure the sample thickness in different scanning orientations; such sample thickness can be used to normalize the transmission mode QUS data, thus, to determine the peak normalized QUS parameters. The normalized QUS values demonstrated significantly improved correlations with structural and mechanical properties of trabecular bone when compared to the QUS values obtained from current QUS measurement protocol. This improvement indicated that better prediction for Young's modulus and structural properties of trabecular bone could be achieved by applying this combined transmission-reflection QUS measurement in proper clinical environment.