Systematic calibration of an integrated x-ray and optical tomography system for preclinical radiation research

Abstract

Purpose:

The cone beam computed tomography (CBCT) guided small animal radiation research platform (SARRP) has been developed for focal tumor irradiation, allowing laboratory researchers to test basic biological hypotheses that can modify radiotherapy outcomes in ways that were not feasible previously. CBCT provides excellent bone to soft tissue contrast, but is incapable of differentiating tumors from surrounding soft tissue. Bioluminescence tomography (BLT), in contrast, allows direct visualization of even subpalpable tumors and quantitative evaluation of tumor response. Integration of BLT with CBCT offers complementary image information, with CBCT delineating anatomic structures and BLT differentiating luminescent tumors. This study is to develop a systematic method to calibrate an integrated CBCT and BLT imaging system which can be adopted onboard the SARRP to guide focal tumor irradiation.

Methods:

The integrated imaging system consists of CBCT, diffuse optical tomography (DOT), and BLT. The anatomy acquired from CBCT and optical properties acquired from DOT serve as a priori information for the subsequent BLT reconstruction. Phantoms were designed and procedures were developed to calibrate the CBCT, DOT/BLT, and the entire integrated system. Geometrical calibration was performed to calibrate the CBCT system. Flat field correction was performed to correct the nonuniform response of the optical imaging system. Absolute emittance calibration was performed to convert the camera readout to the emittance at the phantom or animal surface, which enabled the direct reconstruction of the bioluminescence source strength. Phantom and mouse imaging were performed to validate the calibration.

Results:

All calibration procedures were successfully performed. Both CBCT of a thin wire and a euthanized mouse revealed no spatial artifact, validating the accuracy of the CBCT calibration. The absolute emittance calibration was validated with a 650 nm laser source, resulting in a 3.0% difference between simulated and measured signal. The calibration of the entire system was confirmed through the CBCT and BLT reconstruction of a bioluminescence source placed inside a tissue-simulating optical phantom. Using a spatial region constraint, the source position was reconstructed with less than 1 mm error and the source strength reconstructed with less than 24% error.

Conclusions:

A practical and systematic method has been developed to calibrate an integrated x-ray and optical tomography imaging system, including the respective CBCT and optical tomography system calibration and the geometrical calibration of the entire system. The method can be modified and adopted to calibrate CBCT and optical tomography systems that are operated independently or hybrid x-ray and optical tomography imaging systems.

1. INTRODUCTION

Over the past decade, advances in technology have resulted in highly conformal radiation treatment through the implementation of intensity modulation and image guidance. However, many important biological mechanisms that have great potential of impacting radiotherapy outcome are not yet well understood. Motivated by such rationale, preclinical radiation systems with the capability of cone beam computed tomography (CBCT) guided focal irradiation have been constructed to develop, evaluate, and validate novel treatment strategies by mimicking human treatments in small animal tumor models.¹ The small animal radiation research platform (SARRP)^2,3 developed at the Johns Hopkins University has allowed laboratory researchers to test biological hypotheses that can modify radiotherapy outcomes in ways that were not feasible previously.

The onboard CBCT is indispensable to guide focal tumor irradiation on the SARRP.^4–7 However, it cannot clearly delineate the tumor from the low contrast soft tissue environment. In addition, CBCT does not provide functional information which is essential to study disease progress and therapeutic treatment response. At present, micro-magnetic resonance imaging (μMRI), micro-positron emission tomography (μPET), and micro-single photon emission computed tomography (μSPECT) are among the most common imaging modalities with functional imaging capability at the molecular level,⁸ and have been adapted for preclinical oncology research.⁹ Molecular optical imaging, including both bioluminescence and fluorescence imaging enables the direct visualization of tumor when cancer cells are engineered with luciferase or fluorescence probes and has several unique advantages compared with other functional imaging modalities. First, optical imaging is relatively inexpensive. Second, optimal image acquisition is faster and thus enables higher throughput. Moreover, since many bioluminescent (e.g., firefly luciferase) or fluorescent probes [e.g., green fluorescent protein (GFP)] have been widely applied in molecular or cellular biology research, molecular optical imaging provides a natural bridge connecting in vitro molecular or cellular biology to in vivo small animal models. Consideration of these factors suggests that molecular optical imaging is a highly complementary imaging modality to the x-ray CBCT for image guidance in preclinical radiation research.

Optical imaging provides a wealth of contrast mechanisms through exploitation of a wide range of photophysical and photochemical processes at the molecular level.^10–13 It has transformed preclinical research to a level that even a subpalpable volume of cells can be imaged rapidly and noninvasively,¹³ making it particularly suited for studying early stage tumors¹⁴ as well as metastases.¹⁵ Recently, optical imaging has advanced from two-dimensional planar imaging to three-dimensional tomography to provide improved spatial and quantitative accuracy.^16–19 By integrating the molecular optical imaging with the onboard CBCT, complementary image information can be acquired to guide focal tumor irradiation, with CBCT delineating anatomic structures and optical imaging differentiating and even quantifying luminescent tumor cells. The integrated imaging system can better localize the tumor to guide focal irradiation in the soft tissue environment. It can also provide functional imaging information for monitoring and evaluating the tumor growth and treatment response.

In order to better understand the technical issues associated with the implementation of molecular optical imaging on board the SARRP, we first designed and developed a standalone imaging system that integrates CBCT and diffuse optical tomography (DOT) and bioluminescence tomography (BLT).²⁰ The work in this paper focuses on the calibration of the integrated standalone system. Compared to commercially available optical tomography systems,²¹ our system includes the following novel features: (1) The spatial information obtained from CBCT is used to constrain the optical reconstruction solutions within defined regions. (2) DOT is used to extract three-dimensional tissue optical properties for the imaged subject to improve reconstruction accuracy. However, the DOT function has not been fully implemented yet in current work. (3) The readout pixel values in units of counts per second of the scientific grade charge-coupled device (CCD) camera are calibrated against the emittance at the surface of the imaged subject, eliminating the need for a separate calibration phantom with luminescent sources to quantify absolute power. (4) A rotatable three-mirror system is used to reflect the light emitted from the subject surface to a stationary CCD camera, thus eliminating the need to correct for system flex associated with camera rotation. (5) The geometries of the optical and x-ray systems are cocalibrated to avoid the need for manual or marker-based registration of the optical and CBCT images.

In this work, we present the systematic calibration method for the integrated x-ray/optical tomography imaging system, along with the imaging validation acquired on the system.

2. MATERIALS AND METHODS

2.A. System design

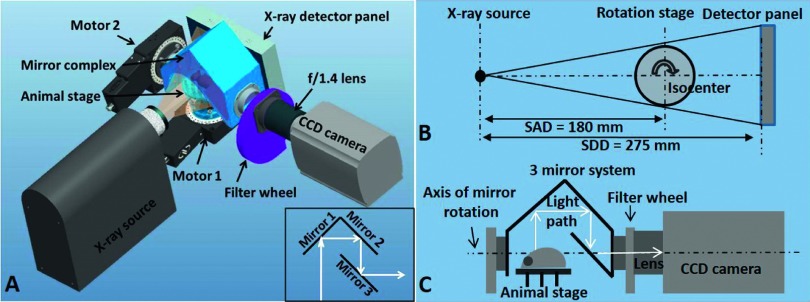
The system configuration and layout is shown in Fig. 1. For CBCT, the rotatable animal stage lies between the stationary and parallel opposed x-ray source and the detector panel. For optical imaging, the rotatable three-mirror system, the filter wheel, and the CCD camera with f/1.4 lens are aligned on the axis perpendicular to the x-ray imaging axis. Imaging is typically performed in the order of CBCT, DOT, and BLT. The order is not rigid provided appropriate information is available for the desired reconstruction. The white light source connected to a nine channel optical switch serves as the light input for DOT. The CBCT provides anatomical information, which can be used as prior information for the subsequent DOT and BLT reconstruction. The surface contour of the imaged object acquired from CBCT is used to generate the mesh for the DOT and BLT. The DOT reconstructs the optical properties of the imaged object for the subsequent light propagation computation in the BLT reconstruction. With prior information of anatomy and optical properties, the BLT algorithm can more accurately reconstruct the position and power of the bioluminescence sources.²²

FIG. 1.

Configuration of the integrated x-ray and optical tomography system. (A): Configuration of the integrated imaging system. The inset demonstrates the arrangement of three mirrors. (B): Top view of the CBCT geometry. SAD: source-to-axis distance; SDD: source-to-detector distance. (C): Side view of the optical imaging geometry. Light emitted from the animal surface is reflected through the three-mirror system to the CCD camera. The mirror system can be rotated to capture light at different angles.

2.B. Cone beam computed tomography

The CBCT system employs an x-ray tube, rotation animal stage, and 15 cm × 12 cm CMOS detector panel (PerkinElmer, Waltham, MA). The CMOS panel operates at a pixel pitch of 74.8 μm laid underneath a 600 μm thick cesium iodide (CsI) scintillator plate on an aluminum substrate. The physical distances from x-ray source to detector panel and from source to stage rotation axis are 275 and 180 mm, respectively. The x-ray beam is provided by a high performance microfocus x-ray source (ThermoFisher Scientific, Waltham, MA) rated at a maximum power of 65 W, maximum voltage limitation of 130 kVp, and maximum current limitation of 0.5 mA. The x-ray source has a spot size automatically tunable from 10 to 100 μm depending on the applied current and voltage. The standard CBCT settings employed in our system are 65 kVp and 0.45 mA, with a 1 mm aluminum filter placed at the x-ray exit. The animal is positioned either supine or prone on the rotation stage. CBCT is achieved by rotating the animal in the horizontal plane between the stationary x-ray source and the detector panel. A top view of the CBCT geometry is presented in Fig. 1(B). The highest achievable image resolution is 50 μm projected at isocenter. The detector panel can sustain a frame rate of 26 Hz at 1 × 1 binning and 70 Hz at 2 × 2 binning. This ultrafast image acquisition allows 4-dimensional CBCT for small animal respiratory motion study. The animal stage (Newport Corp., CA) is backlash-free with a rotation resolution of 0.0005° per turn, at a speed up to 80°/s.

For dark current correction, a series of dark images acquired in the absence of x-rays were averaged and subtracted from raw images. For gain correction, flood images were acquired with the x-ray beam on and without the presence of any imaging object, and then averaged and converted to gain correction map which was calculated as the ratio of the mean value over the entire flood image to the signal intensity of each pixel. The fully corrected image was obtained after subtraction of dark current and multiplication of gain correction map.

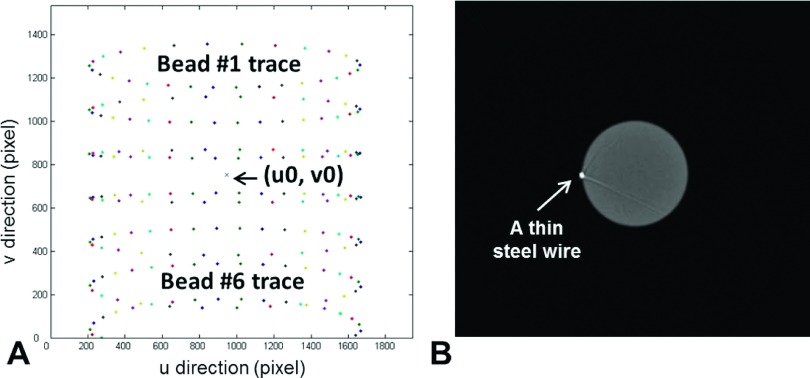
The geometrical calibration of CBCT is performed using an in-house phantom consisting of seven vertically aligned embedded steel beads. The phantom is shown in Fig. 2(A). Planar images of bead projections were acquired every 12° during a 360° rotation. An in-house program written in matlab (The MathWorks, Inc., Natick, MA) was used to calculate the five geometrical parameters used in the calibration method suggested by Noo et al.²³ The five parameters are: distance from source to detector panel, distance from source to the animal stage rotation axis, in-plane imaging panel rotation angle, and the radiation center on the image panel (u0 and v0, the position along horizontal and vertical directions, respectively).

FIG. 2.

Phantoms used in calibration. (A): The seven-bead phantom for CBCT geometrical calibration. (B): The acrylic phantom with holes for the geometrical calibration of the entire imaging system. (C): The half cylinder tissue-simulating phantom for validation of the absolute emittance and BLT reconstruction. The left piece is the cover and the right is the bottom containing 12 holes for placing luminescent sources.

CBCT of an anesthetized mouse bearing lung cancer was performed to verify the in vivo imaging capability. The mouse was anesthetized with subcutaneous injection of a ketamine:xylazine cocktail (100:10 mg/kg body weight) and placed in supine position on the rotation stage. All animal experiments were performed with the approval of the Johns Hopkins Animal Care and Use Committee. The standard CBCT imaging parameters were employed at 65 kVp and 0.45 mA and with a 1 mm aluminum filter. The CBCT was reconstructed at a dimension of 486 × 384 × 256 voxels with 200 μm voxel size.

2.C. Diffuse optical tomography and bioluminescence tomography

DOT is to reconstruct the tissue optical properties by measuring the light transmission at the animal surface, when the animal is irradiated with an external light of known power. Nine optical fibers with 200 μm core diameter are arranged in a 3 × 3 matrix in the animal stage. Each fiber is terminated with a SMA connector tightly placed against the posterior surface of the imaged object. A halogen lamp (Ocean Optics, Dunedin, FL) providing white light illumination is connected to an optical fiber switch (Piezosystem Jena GmbH, Jena, Germany), delivering the light to the nine fibers sequentially. Multiple filters with desired bandwidths and central wavelengths are installed on a filter wheel placed in front of the f/1.4 lens (Rokinon 35 mm f/1.4 wide angle lens, B&H, NY) connected to an ultra-low noise CCD camera (iKon-L 936 BV, Andor Technology, Belfast, UK). The multiple filters combined with the CCD camera allow for multispectral acquisition used in the reconstruction process. The three-mirror system, filters, and CCD camera are used for both multispectral DOT and BLT imaging. External light sources are not needed for BLT. A side view of the optical imaging geometry is presented in Fig. 1(C). The light provided by halogen lamp, transmitted through the imaged object, and filtered at certain wavelengths is collected for DOT, while the light emitted by internal light sources is collected for BLT.

The purpose of the three-mirror system is to reflect the emitted optical signal from the phantom or animal surface to the camera at multiple imaging angles by simply rotating the mirror system while keeping the camera static. The arrangement consists of three mirrors as configured in Fig. 1. As the arrangement rotates, the 1st mirror is set to be at 45° to any view of the imaged object. The 2nd mirror is set perpendicular to the 1st mirror and the 3rd mirror is parallel to the 2nd mirror. The reflected central light ray from the object is thus perpendicularly projected to the image acquisition plane of the CCD camera. At present, computer controlled rotation of three-mirror system allows optical image acquisition at any angle from 0° (top or vertical view) to 90° (lateral or horizontal view). Combined with the 360° animal stage rotation, multiple optical images can be acquired over a 2π solid angle imaging space.

2.D. Optical system calibration

2.D.1. Lens distortion correction

Lens distortion can induce deviation from rectilinear projection of the imaged object. The Computer Vision System Toolbox 5.3.1 from matlab was employed to examine lens distortion in our system. Eight images were taken each with a checkerboard pattern placed close to the field edge covering at least 20% of the field of view. The combination of the eight checkerboard images covered the entire field of view. The same setting for the phantom experiments was applied for imaging the checkerboard. For validation, a 30 × 30 cm paper with a rectilinear grid was imaged to examine the lens distortion correction. Distortion occurred only close to the edge of the camera’s field of view. The central area corresponding to the 10 × 10 cm field of view for animal imaging was not affected. Therefore, distortion correction was not included in our imaging data processing procedure.

2.D.2. Flat field correction

The system employs a large aperture f/1.4 lens, which allows fast image acquisition at the expense of nonuniform intensity response due to lens vignetting effect across the field of view. A flat field correction is necessary to correct for such intensity nonuniformity as well as the nonuniform pixel response of the CCD chip. The experimental setup is shown in Fig. 3(A). A 30 cm diameter integrating sphere with a 10 cm diameter output port (Labsphere, North Sutton, NH) was used to generate a uniform planar light source. The light from an incandescent bulb was filtered through selected wavelength filters at 590, 610, 630, 650 nm (10 nm FWHM, 50 mm diameter, Andover Corporation, Salem, NH), and 830 nm (37 nm FWHM, 25 mm diameter, Semrock, Rochester, NY), and fed into a 4 cm diameter entrance port of the integrating sphere to serve as the input light source. The voltage and current of the light bulb is tunable to provide illumination of variable intensity. The uniform light output port of 10 cm diameter is large enough to illuminate the entire 54 mm diameter lens surface. All measurements were performed inside a dark enclosure to minimize background light contribution. The light intensity is adjusted by tuning the voltage supply to generate a pixel intensity of about 80% of the maximum signal that would saturate the camera at 65 535 counts. An exposure time of 5 s was used for each wavelength. The background acquired with the same exposure time was subtracted from the raw data. The flat field correction factor for each pixel was calculated as the ratio of the mean signal intensity across the entire image to the intensity of the given pixel.

FIG. 3.

Flat field correction for the camera and lens. (A): The setup for the flat field correction procedure. CCD camera with f/1.4 lens was positioned against the light output port of the integrating sphere. The filtered light source provided the input illumination. (B): The flat field correction map. The green box outlines the interested imaging area for in vivo or phantom experiment. (C): Profiles along the dotted line indicated in panel (B). The profiles for 590–650 nm are essentially overlapped. (D)–(F) show the verification of the flat field correction. (D): An image of the integrating sphere output port prior to flat field correction. (E): The same image after the correction. (F): The profiles plotted along the line in panels (D) (raw data) and (E) (corrected).

2.D.3. Absolute emittance calibration

The purpose of the absolute emittance calibration is to convert the light intensity reading (in units of counts per second) from the CCD image to the emittance (in units of power per unit area) at the animal or phantom surface. A power meter (PMKIT-SL-2W, Newport, Irvine, CA) was positioned at the center of the integrating sphere light output port to measure the emittance in units of nW/cm². The sphere output port acts as a Lambertian source with equivalent emittance. The CCD camera was positioned at the same optical distance used for animal or phantom imaging, where the uniform light would be reflected by the three-mirror system and captured by the CCD camera. Briefly, our camera setting is listed as following: f/1.4 lens aperture, 42.5 cm optical distance, pixel size of 0.61 mm at the image plane after 4 × 4 binning, and a 512 × 512 image matrix. Images with 16 bit pixel intensity were acquired and read out at 3 MHz. The intensity of the light source was adjusted to different levels. The white light was transmitted through a band-pass filter at the desired wavelength. The image was flat field corrected before being used to calculate the emittance response curves. The wavelength dependent response curves were obtained as a linear regression of the light intensity measured by the CCD with the emittance readings from the power meter. After converting the CCD reading into the emittance E at the tissue/phantom surface, the emittance was then used to calculate the fluence rate just inside the surface Φ_in by considering the refractive index mismatch between air and tissue/phantom. With Robin type III boundary condition,¹⁷ we can derive

$${\displaystyle E=\frac{1}{2A}{\mathit{\Phi }}_{\text{in}},}$$ (1)

where A can be derived from Fresnel’s law,

$${\displaystyle A=\frac{\left(\frac{2}{1-R_0}-1+{\left|cos\hspace{0.17em}{\theta }_c\right|}^3\right)}{1-{\left|cos\hspace{0.17em}{\theta }_c\right|}^2},}$$ (2)

where θ_c = sin⁻¹(1/η) is the critical angle, R₀ = (η − 1)²/(η + 1)², and η is the tissue/phantom refractive index at the boundary, while the refractive index of the air is assumed to be 1. The validation phantom used in this study had η = 1.56 resulting in A = 3.78.

2.E. Geometrical calibration of the integrated imaging system

Since the CBCT and BLT are physically integrated into one imaging system, it is desirable to establish the geometrical relationship between them, thereby eliminating the need for image registration from the two modalities. A specially designed phantom [Fig. 2(B)], consisting of two acrylic plates perpendicularly aligned in an inverted “T” shape, was fabricated for the geometrical calibration. The acrylic plates have uniformly distributed holes which can be observed in both CBCT and optical images. The phantom was fixed to the animal stage with the long axis of the vertical piece parallel to the mirror rotation axis. CBCT was acquired with a full 360° rotation of the phantom. Following CBCT, two optical images of the phantom were taken at the mirror rotation angles of 0° and 90°, respectively. The geometrical parameters transforming the 2D planar optical image to the 3D CBCT coordinate system were obtained by registering the hole positions in the optical image to their counterparts in the CBCT image. The geometric calibration results are applied to both DOT and BLT reconstructions.

2.F. Optical data processing workflow

The optical data processing flow chart is shown in Fig. 4. First, the 2D optical projection undergoes the background and flat field correction. Because the field of view of the optical imaging system is much larger than the dimension of a typical mouse, the optical image is cropped and only the central region containing the useful information is extracted and processed. The extracted data include location of pixels that have significant bioluminescence signals emitted from the phantom or animal surface. The signal intensity is converted to absolute emittance at the phantom/animal surface by multiplication of the wavelength dependent absolute calibration coefficient obtained from the absolute calibration procedure, and taking into account the air-tissue refractive index mismatch and filter attenuation. The data are then translated and rotated based on geometrical parameters from the geometrical calibration procedure and transformed from the 2D optical imaging coordinates to the 3D CBCT coordinates. The optical data are then projected to the phantom or animal surface. Therefore, the final data are the absolute optical fluence rate mapped to the phantom or animal surface in the CBCT coordinate and serves as input data for the BLT reconstruction. The in-house developed multiwavelength reconstruction algorithm is incorporated into the open source software NIRFAST.^24,25 The multispectral reconstruction provides spectral constraints to reduce the number of potential, and ambiguous, solutions produced by single wavelength reconstruction. It is especially useful for BLT reconstruction due to the wide spread of the bioluminescence spectrum.

FIG. 4.

Data processing flow chart for BLT reconstruction.

2.G. Phantom experiment validation

CBCT and BLT imaging was performed for a homogeneous tissue-simulating phantom shown in Fig. 2(C) to verify the system’s capability. The epoxy phantom is made of a half cylinder, with a diameter of 30 mm and a length of 41 mm and contains titanium dioxide particles to provide scattering and a dye to provide absorption.²⁶ There are 12 cylindrical holes (2 mm diameter and 3 mm length) inside the phantom as receptors for luminescent sources. In this experiment, one Trigalight luminescent source (0.9 mm × 2 mm cylinder, mb-microtec ag, Niederwangen, Switzerland) was placed in the hole at the intersection of the 2nd row and 2nd column. The imaging acquisition was done in the order of CBCT and then BLT. Scattering and absorption coefficients of the phantom were known from a previous study²⁶ and used as prior knowledge in the BLT reconstruction. No DOT was performed in the current study. Image reconstruction was performed with the modified NIRFAST algorithm incorporating multiple wavelength reconstruction.

3. RESULTS

3.A. CBCT geometrical calibration

The geometrical calibration results are shown in Fig. 5, showing the traces of the seven beads in the phantom during a 360° rotation [Fig. 5(A)]. The geometrical parameters can be calculated by curve fitting the traces of each bead to an ellipse and comparing the centers of any two ellipses. Figure 5(A) illustrates the elliptical traces of seven beads and the central x-ray axis located at point (u0, v0). To ensure an adequate separation of two beads and reduce calculation uncertainty, usually one bead above and one below the image center were used. We used two pairs of beads (beads # 1 and # 6 and # 2 and # 5, bead 7 was not used because some of its traces were out of field) to calculate the geometrical parameters shown in Table I and then averaged them to obtain the final results. To verify the accuracy of the geometrical parameters, we acquired a CBCT of a cylindrical phantom with a thin steel wire attached to its side. The reconstructed wire shown in the image should be clear and resemble a single bright point in the image plane perpendicular to the wire direction. If there is any blur or ring artifact to the reconstructed wire, the geometrical parameters would be adjusted until an optimal parameter set is identified. With the optimal geometrical parameters, appearance of the wire in CBCT had a 1.34 mm FWHM compared with its physical diameter of 1.20 mm. A CBCT axial slice of the wire is shown in Fig. 5(B).

FIG. 5.

CBCT geometrical calibration. (A): Traces of the seven beads during a 360° rotation. Projections were acquired every 12° and there were 30 data points for each elliptical track. (u0,v0) indicates the location of the central x-ray. (B): Verification of the calibration parameters by imaging a cylinder phantom with a thin steel wire attached.

TABLE I.

CBCT geometrical calibration parameters.

Bead used	u0 (pixel)	v0 (pixel)	SDD (mm)	SAD (mm)	SDD/SAD	Rotation (deg)
Bead #1 and #6	999.40	754.02	274.12	179.53	1.53	−0.12
Bead #2 and #5	999.30	754.13	274.18	179.64	1.53	−0.12

Note: u0 and v0 are the positions in number of pixels along the horizontal and vertical side of the image panel, respectively. There are 1936 pixels along u0 direction and 1544 pixels along v0 direction. SDD: distance form source to detector panel; SAD: distance from source to animal stage rotation axis; and Rotation: in-plane rotation of imaging panel. SDD/SAD is the ratio for image magnification.

CBCT of an anesthetized mouse was shown in Fig. 6 which displays three orthogonal cross-sections. The reconstructed CBCT images allowed differentiation of bone, lungs, major organs, muscle tissue, and fat. A solid lung tumor was visualized clearly, indicated by the white arrows in the sagittal and coronal cross-sections in Fig. 6. The space below the animal body refers to the animal stage whose visualization is affected by the window/level settings of the image display. The bright enhancement inside the dashed-line box in the sagittal plane indicates the metal optical fiber connector which was attached to the animal stage to provide light illumination for DOT imaging.

FIG. 6.

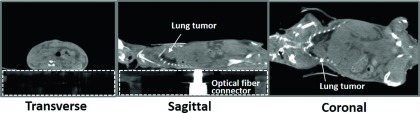
Orthogonal images from a mouse CBCT, in the order of transverse, sagittal, and coronal cross-sections. The white arrows point to a solid lung tumor. The space inside the dashed-line box refers to the plastic animal stage. The bright enhancement in the sagittal cross-section is the metal optical fiber connector attached to the animal stage for DOT imaging purpose.

3.B. Flat field correction for the CCD camera

The flat field correction map is shown in Fig. 3(B). The signal intensity variation over the entire field of view (31 × 31cm²) is up to 80%, defined as the ratio of the maximal signal intensity difference to the mean signal intensity value. For imaging of a single mouse, the region of interest is the 10 × 10 cm² area at the center of the field of view, which has a signal intensity variation of ∼13% [Fig. 3(B)]. There is no obvious difference in image uniformity among the images acquired at wavelengths between 590 and 650 nm. The four profiles, at 590, 610, 630, and 650 nm, across the center of the correction map are essentially identical [Fig. 3(C)]. There is a slight difference between profiles at the 830 nm and the other wavelengths, showing an average difference of 1.3% and a maximal difference of 3.4% [Fig. 3(C)]. Therefore, a common flat field correction map is applied to images acquired at wavelengths from 590 to 650 nm, and a separate map should be used for wavelengths outside this range, such as 830 nm.

To verify the flat field correction, we intentionally shifted the integrating sphere output port so that the port image was displaced to one side. Figures 3(D) and 3(E) show the image before and after the flat field correction. Figure 3(F) shows the horizontal profile plotted across the center of the integrating sphere light source was uniform after the application of the flat field correction.

3.C. Absolute emittance calibration

The absolute emittance calibration was performed for each wavelength to convert the photon count rate detected by the camera to the emittance at the phantom or animal surface. The calibrated conversion coefficients are shown in Table II. The response of the entire light detecting system, including the three-mirror system, lens, and CCD decreases by roughly a factor of seven from the 590–650 nm region to 830 nm, mainly due to the wavelength dependent quantum efficiency of the CCD chip and the spectral sensitivity of the lens.

TABLE II.

Absolute calibration coefficients for the optical imaging system.

Wavelength (nm)	(nW/mm2)/(count/s)	r2
590	1.01 × 10−05	0.96
610	1.34 × 10−05	0.93
630	9.17 × 10−06	0.97
650	1.14 × 10−05	0.96
830	6.94 × 10−05	0.99

The absolute calibration result was confirmed for the case of 650 nm using a 650 nm laser. The emittance at the phantom surface was measured eight times by the CCD camera, with laser power in a range of 174.6–526.5 nW. The CCD readings were converted to the emittance at the phantom boundary via multiplication of the absolute calibration coefficient at 650 nm, and then normalized by the input laser power. The measured emittance, after calibration, at the center of the phantom surface was (8.08 ± 0.05) × 10⁴ (nW/mm²)/W, with a −3.0% difference from the calculated value [8.33 × 10⁴ (nW/mm²)/W] using the NIRFAST program²⁴ with the independently measured optical properties.

3.D. System geometrical calibration

The optical image of the acrylic phantom taken with the mirror at the top of the phantom is shown in Fig. 7(A) and the corresponding CBCT coronal view is displayed in Fig. 7(B). The coordinates of 16 holes marked with crosshairs in the optical and CBCT image space, respectively, were recorded. In the CBCT space, only two coordinates (the x and y position) were recorded, since the coordinates in the z direction were constant. The translation and rotation applied to map the corresponding holes from the optical space to the CBCT space were iteratively calculated until a satisfactory matching of less than 0.1 mm on average was achieved as shown in Fig. 7(C). In the case shown here, the translations were −6.34 and −23.84 mm along the x and y direction, respectively, and the rotation is 1.8° clockwise. Similarly, the translation and rotation required to map the optical data acquired with the mirror at the lateral position (90°) were also calculated, as shown in Figs. 7(D)–7(F). In this case, the sagittal CBCT image of the acrylic phantom including all the holes in the upright piece is used. The translations were 20.08 and 6.44 mm along the y and z direction, respectively, and the rotation is 0.8° clockwise.

FIG. 7.

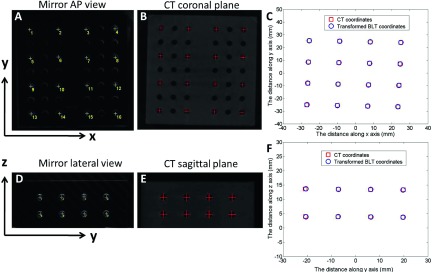
Geometrical registration of the optical and CBCT coordinates. (A): Optical image of the phantom when the mirror system is above the stage (vertical position, 0° angle). Sixteen holes were marked and used in the calibration. (B): The coronal slice of the phantom CBCT corresponding to mirror vertical view in A. AP: anterior–posterior. (C): Registration of the optical and CBCT coordinates at mirror 0° position. (D): Optical image of the phantom when the mirror system is at the lateral position (horizontal position, 90°). (E): The sagittal slice of the phantom CBCT corresponding to mirror lateral view in (D). (F): Registration of the two coordinates at mirror 90° position.

3.E. Phantom experiment validation

The position of the Trigalight source was identified in the CBCT orthogonal images [shown as an orange rectangle and circle in Fig. 8(A)]. The BLT reconstruction was performed using the top view optical projection only, with known phantom optical properties obtained from previous study.²⁶ The transverse profiles of the reconstructed source were plotted along the horizontal axis. The source was positioned at (0,7.50,0) mm in the CBCT coordinates extracted from the CBCT image. The mesh used for the BLT reconstruction was generated from the CBCT volume, and data points in the 2D image measured by the CCD camera were projected to the CBCT phantom surface by applying the procedures presented in Fig. 4. A sphere with 8 mm diameter was used as the spatial region constraint to confine the source position during reconstruction. To eliminate the bias of using the region constraint, which may tend to localize the source at the center of the permissible volume, one reconstruction with the permissible volume shifted 2 mm up was also performed. With no region constraint, the bioluminescence source was reconstructed with center of mass (CoM) at (−0.09,8.16,−1.18) mm, a radial displacement of 1.36 mm from the true (CBCT) source location. The major deviation occurred in the depth direction as the source was reconstructed 1.18 mm shallower than the true position [Fig. 8(B)]. If the center of the permissible volume was placed at the true source location, the CoM of the reconstructed light source was at (−0.05,7.50,−0.06) mm, with a total localization error of 0.08 mm [Fig. 8(C)]. In the case of shifted permissible volume, the reconstructed source location was at (−0.14,7.98,−0.23) mm, a radial displacement of 0.55 mm from the true source location [Fig. 8(D)]. The reconstructed total source power was 31.67 and 31.55 nW, with 23.4% and 23.7% difference, for the spatial constraint region without shift and with 2 mm shift, respectively, from the simulated source power of 41.3 nW obtained based on a forward calculation which fitted the experimental data with the known location of the source.

FIG. 8.

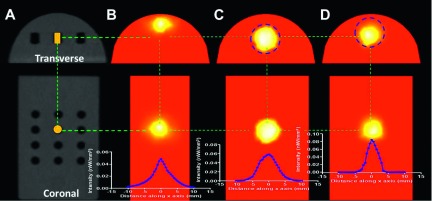
BLT reconstruction result. The transverse and coronal CBCT slices are shown in (A), with the Trigalight bioluminescence source marked with an orange rectangle and circle. The BLT reconstruction was performed with no region of interest (ROI) constraint (B), with an 8 mm diameter spherical ROI centered at the source position (C), and with the constraint ROI shifted up by 2 mm (D), respectively. The vertical axis is the source intensity in units of nW/mm³.

4. DISCUSSION

This paper presents a systematic method to calibrate an integrated optical and x-ray tomography system to ensure optimal image quality and geometric congruency of the dual-modality images.

To the best of our knowledge, we presented a new method of calibrating the absolute emittance at the phantom or animal surface. Since the CCD camera readout is converted to the true emittance at the animal surface, the reconstructed power would represent the true source strength. Once the wavelength-dependent calibration coefficients are obtained, they can be used to reconstruct the strength of any bioluminescence source. Our method can also be applied to fluorescence imaging, in which the calibration is performed on a fluorophore-containing phantom. The reconstructed fluorophore concentration would provide an estimation of the true physical concentration. With this method, one does not need to perform calibration on a fluorophore-containing phantom for each individual fluorophore, assuming the CCD detection quantum efficiency of the fluorophore is known.

The methods for CBCT calibration have been published by several groups.^23,27–30 Here, we adapted the method from Noo et al.²³ and used only five parameters to calibrate our system (Table I). Although application of these five parameters was found adequate for the geometrical calibration purpose, the position of the center x-ray projection on the detector panel was occasionally found to be inaccurate (a few pixels off from the true values). This may be caused by the geometrical uncertainty in the calculation of the center of the ellipse formed by the bead traces [Fig. 5(A)]. Therefore, fine tuning the parameters u0 and v0 by trial and error is necessary to optimize the CBCT geometrical accuracy. The optimal calibration parameters were confirmed with the correct delineation of the position and dimension of the thin steel wire attached to a cylindrical phantom in the CBCT image [Fig. 5(B)].

For the system geometrical calibration, a calibration phantom was used to transform the coordinates in the optical imaging space to those in the CBCT space. Although the geometric calibration with the mirror system at 0° and 90° position is illustrated in this study and found sufficient for our current phantom study, calibration using additional views between 0° and 90° can enhance the reconstruction for more complicated scenarios, such as when multiple bioluminescence tumor nodules are close to the peripheral region of the animal. Incorporating multiple angle projections into BLT reconstruction is an ongoing effort in our group. The need for correction of mirror rotation induced flex and CCD misalignment at any rotation angle will be investigated and implemented.

Tissue optical properties are taken as known input in BLT reconstruction, which can be done in different ways. The simplest but least accurate way is assuming a homogeneous reconstruction volume which can be assigned as a tissue type with known optical properties, e.g., adipose tissue. Another way is taking advantage of volumes reconstructed from other imaging modalities such as CT (Refs. 31 and 32) or MRI.^33,34 The CT or MRI images can be segmented into different organs which are then assigned corresponding optical property values. Consequently, the anatomical and optical information obtained from CT or MRI serves as a prior knowledge for the BLT reconstruction. This strategy provides better estimate of tissue optical properties but still does not reflect the true values for each individual animal. Wang et al. improved BLT reconstruction using the prior knowledge obtained from a micro-CT and concluded that accurate optical properties are of paramount importance for BLT reconstruction and are preferably obtained through DOT.³¹ In our system design, we use CT to acquire anatomical information and DOT to acquire optical information both of which are specific to each individual animal. We use 3 × 3 fibers attached to the animal stage to provide light illumination and a CCD camera to capture the light transmission or emission from the animal top surface. Simulation study on the same imaging geometry using a digital laboratory mouse model suggested this imaging geometry to be sufficient for accurate DOT and BLT reconstruction,³⁵ resulting in maximum relative errors of 2% for scattering, 3% for absorption, and 1% for effective attenuation in the range of 580–630 nm in DOT reconstruction and excellent recovery of the location and power of luminescent sources in BLT reconstruction.

There are a few limitations to this work. First, it focuses on the development of a practical calibration method for the integrated CBCT and optical tomographic imaging systems. Currently, the DOT function has not been completely implemented and the optical reconstruction algorithm has not been optimized. The relatively large error in absolute source power reconstructed for the Trigalight source may have resulted from the nonoptimized reconstruction algorithm which cannot accurately recover the exact shape of the light source. In the reconstruction, we assume that the angular dependence of the emission from the animal or phantom is the same as that from the integrating sphere, i.e., Lambertian, which may not be true. Improvement of the reconstruction algorithms for DOT and BLT are ongoing. Moreover, the absolute calibration was validated with a laser only at 650 nm due to the availability of the laser source. Validation will be performed once laser sources with other wavelengths are available.

The standalone integrated x-ray CBCT/BLT system presented in this paper was constructed to provide a model to study its functionality and to develop refinements to improve its reconstruction accuracy and operational efficiency. For the next generation, we are developing a dual function system, which can act as an optical system on-board SARRP as well as a standalone imaging apparatus, with the primary focus of determination of the trade-off between on-board and off-line optical guidance for accurate focal irradiation.

5. CONCLUSION

A practical and effective method has been developed to calibrate an integrated x-ray and optical tomography imaging system to ensure optimal image quality and geometric congruency of the dual-modality images and to provide quantitative optical imaging information. The absolute emittance calibration method enables the conversion of light intensity in units of counts per second detected by the CCD camera to the absolute emittance at the animal surface, which then allows the direct reconstruction of the real bioluminescence source strength inside the animal. This method can be readily adapted to calibrate other optical imaging systems with the goal of directly quantifying bioluminescence activity. The systematic geometrical calibration method applied to our system can be potentially modified to calibrate other integrated imaging systems that combine x-ray and optical tomography.