Novel spirometry based on optical surface imaging

Abstract

Purpose:

To evaluate the feasibility of using optical surface imaging (OSI) to measure the dynamic tidal volume (TV) of the human torso during free breathing.

Methods:

We performed experiments to measure volume or volume change in geometric and deformable phantoms as well as human subjects using OSI. To assess the accuracy of OSI in volume determination, we performed experiments using five geometric phantoms and two deformable body phantoms and compared the values with those derived from geometric calculations and computed tomography (CT) measurements, respectively. To apply this technique to human subjects, an institutional review board protocol was established and three healthy volunteers were studied. In the human experiment, a high-speed image capture mode of OSI was applied to acquire torso images at 4–5 frames per second, which was synchronized with conventional spirometric measurements at 5 Hz. An in-house matlab program was developed to interactively define the volume of interest (VOI), separate the thorax and abdomen, and automatically calculate the thoracic and abdominal volumes within the VOIs. The torso volume change (TV C = ΔV_torso = ΔV_thorax + ΔV_abdomen) was automatically calculated using full-exhalation phase as the reference. The volumetric breathing pattern (BP_v = ΔV_thorax/ΔV_torso) quantifying thoracic and abdominal volume variations was also calculated. Under quiet breathing, TVC should equal the tidal volume measured concurrently by a spirometer with a conversion factor (1.08) accounting for internal and external differences of temperature and moisture. Another matlab program was implemented to control the conventional spirometer that was used as the standard.

Results:

The volumes measured from the OSI imaging of geometric phantoms agreed with the calculated volumes with a discrepancy of 0.0% ± 1.6% (range −1.9% to 2.5%). In measurements from the deformable torso/thorax phantoms, the volume differences measured using OSI imaging and CT imaging were 1.2% ± 2.1% (range −0.5% to 3.6%), with a linear regression fitting (slope = 1.02 and R² = 0.999). In volunteers, the relative error in OSI tidal volume measurement was −2.2% ± 4.9% (range −9.2% to 4.8%) and a correlation of r = 0.98 was found with spirometric measurement. The breathing pattern values of the three volunteers were substantially different from each other (BP_v = 0.15, 0.45, and 0.32).

Conclusions:

This study demonstrates the feasibility of using OSI to measure breathing tidal volumes and breathing patterns with adequate accuracy. This is the first time that dynamic breathing tidal volume as well as breathing patterns is measured using optical surface imaging. The OSI-observed movement of the entire torso could serve as a new respiratory surrogate in the treatment room during radiation therapy.

1. INTRODUCTION

In the radiotherapy clinic, spirometry has been applied to improve tumor localization and organ sparing in thoracic and abdominal treatments by respiratory monitoring for breath-hold or free-breathing gating^1–3 and respiratory binning in four-dimensional computed tomography (4DCT).^4–6 Among existing, external tumor surrogates, the volumetric surrogate is reportedly more reliable, because it is a location-independent, global parameter, whereas external fiducials and bellows are local parameters that depend on location and placement.^4,5,7,8 Spirometry is a common method used to measure breathing tidal volume (TV), but has the known liability of baseline drift, and therefore requires frequent calibration.^5,9,10 To improve the data quality for minimal baseline drift, spirometry was applied together with a respiratory bellows to serve as a hybrid surrogate for reconstruction of amplitude-binned 4DCT.⁶ Spirometric measurement is also inconvenient for patients, who have to breathe through a tube with the nose clamped. Furthermore, dynamic tidal volume is a one-dimensional signal that does not provide spatial information about the volumetric breathing pattern (BP_v)^11,12 or the involvement of the diaphragm and intercostal muscles,¹³ which are primarily responsible for superior–inferior (SI) and anterior–posterior (AP) motions, respectively. For these reasons, spirometry has not been widely used in the radiotherapy clinic.

Optical surface imaging (OSI) has been applied to monitor respiratory motion without fiducial markers. Hughes et al.¹⁴ applied OSI for monitoring both surface-tracked points and surface-derived volume and demonstrated that they were useful surrogates to lung tumor motion based on external–internal correlation. Specifically, they compared OSI with fiducial points and found that the measured volume from a single OSI camera-pod system showed surface-derived volume correlated with spirometric data better at r > 0.8 in 9 of 11 patients. Glide-Hurst et al.¹⁵ studied the feasibility of correlating surface and fluoroscopic imaging to establish an external–internal relationship. By analyzing various sizes and locations of the regions of interest (ROI) in patients, they found that a small central abdominal region correlated best with fluoroscopic data. Schaerer et al.¹⁶ investigated multidimensional motion tracking using the “markerless surface approach” based on deformable image registration with 1 mm tracking error and suggested that the OSI approach could be potentially useful to establish an internal–external correlation model.

In this paper, we report on a novel OSI-based spirometry with the field of view covering the entire torso. This approach is based on a validated physical relationship of volume conservation among nonexchangeable tissues within the torso and thus the exchanged air volume equals torso volume change (TVC).^11,12 To assess the accuracy of volume measurement using OSI, we will compare the OSI-measured volume results with different ground truths for rigid and deformable phantoms, as well as for human subjects under an institutional review board (IRB) approval. Using a 3-camera-pod OSI system and a upward tilted body position, almost all the moveable torso surfaces were imaged and used to calculate the TVC, which is the internal tidal volume. Simultaneously, dynamic tidal volumes are measured externally using a conventional spirometer. These results are directly compared and contrasted after applying a correction factor for the internal–external volume conversion.

2. METHODS AND MATERIALS

An OSI system (AlignRT HD, Vision RT, London, UK) with 3-ceiling-mounted camera pods was used to acquire high-resolution surface images of objects of interest around the isocenter of a medical linear accelerator. Static image capture was applied for phantom experiments, while the high-speed image capture (HSIC) mode was applied in volunteer experiments at about 5 frames per second (fps). An on-site reference surface image was captured for alignment of the subsequently captured images. Online or offline reconstructions of 3D surface images were performed for volume calculation.

2.A. Experiments using geometric and deformable phantoms

Geometric phantoms include four cups (truncated cones) and three cans (cylinders), with the diameters ranging from 5 to 15 cm. They were imaged individually at the isocenter with the same orientation as shown in Fig. 1(A). The half volume of these objects was first calculated from the >50% captured surface and the total volume was obtaining by multiplying a factor of 2, based on their symmetry. Five replicate images were captured and the results were averaged. The volume accuracy was evaluated by comparing with the ground truth, a parameter that was established from dimensional measurements and geometric calculations. The PlanRT (VisionRT, London, UK) software was applied to convert a 3D surface image to a set of contours with slice thickness of 1.0 mm in DICOM RT (digital imaging and communication in medicine, radiation therapy) structure format. An in-house planning system (Metropolis, research version) was used to process the contours and calculate the contoured volume.

FIG. 1.

The geometric and deformable phantoms used in the study. (A) Seven geometric phantoms in the imaging orientation. (B) and (C) Deformable phantoms with a rigid phantom (thoracic and Rando phantoms, respectively) and a layer of the DPD materials, mimicking body anterior rise during inhalation. (D) A DPD layer on a flat surface.

Deformable phantoms were constructed using rigid body phantoms (thorax and Rando) and deformable Play-Doh™ (DPD; Hasbro, Pawtucket, RI), which can be reshaped as a thin layer on the phantoms, mimicking thoracic and abdominal rises during inhalation, as shown in Figs. 1(B)–1(D). The phantoms with and without the DPD layers were imaged with both OSI and CT imaging and the phantom-only images were used as the reference. Two rigid body phantoms and one flat surface were used and three DPD volumes (typical tidal volumes) of 200, 300, and 500 cm³ were imaged either with the phantoms or alone (deformed) using OSI and CT.

2.B. Volunteer study with simultaneous spirometric and OSI measurements

The human subject study was conducted under an IRB protocol and the data from three volunteers were reported here. The volunteers lay on a breast board with 7.5° tilt, both arms up and the center of the torso around the machine isocenter, and breathed through a preVent™ Pneumotach of a spirometer (CPX, MedGraphics, St Paul, MN). The torso surfaces of the skin (male) or the skin covered by form-fitting leotard (female) were imaged using OSI. Simultaneous measurements using AlignRT and CPX were acquired for 5–10 min under free breathing. Prior to each experiment, both console computer clocks were calibrated in millisecond (ms) precision using a standard time protocol (NISTimer, National Institute of Standard Technology, Gaithersburg, MD) for synchronization.

In AlignRT imaging, the HSIC mode was employed with an image capture rate at 4–5 fps. The raw data were retrospectively reconstructed to a series of 3D surface images. A matlab program was developed as one toolbox of our “in-house” 4D clinical multimodal image processing (4DCMIP) system,^17,18 to process the real-time 4D surface image data (30GB for 10-min acquisition) in batch mode. Using cut planes, the volume of interest (VOI) of the torso was first defined and the thorax and abdomen were separated at the inferior end of the sternum. The posterior cut plane was roughly parallel to the anterior body surface slightly below the midline level in sagittal view and had a polygonal shape to confirm to the body curve in the coronal view. Two more cut planes were used to separate the thorax from the abdomen along the inferior rib edges.¹⁴ It should be noted that it is critical to include the entire torso in the VOI, since this is a required precondition to apply volume conservation to calculate the respiratory tidal volume.^11,12 The superior boundary plane was placed near the clavicle and the inferior boundary plane was near the pubis. After the VOI was interactively defined and automatically applied to an OSI image, a partial-deferential-equation (PDE)-based in-painting interpolation¹⁹ was performed to generate a surface grid array in the unit of 1 × 1 mm² with the surface “holes” filled. The volume was calculated by integrating the volume elements of all grid rods within the VOI, which was applied subsequently to all surface images. The volume variations in the thorax and abdomen were calculated separately (TV C = ΔV_thorax + ΔV_abdomen), by subtracting the reference volumes at full exhalation. The breathing pattern (BP_v = ΔV_thorax/ΔV_torso) was also calculated in like manner.

The spirometric measurement was performed using a CPX, which was a Bernoulli-type spirometer with a preVent™ pressure sensor. The Bernoulli equation was applied to convert the measured pressure to flow rate and volume. Another in-house matlab program was implemented similar to a previously published method¹⁰ to control the CPX acquisition at 5-Hz, down-sampled from the 100 Hz sampling rate. The spirometer was calibrated immediately before an experiment using a 3-L syringe at five different flow rates. An online baseline correction was implemented using linear regression fitting of five consecutive full-exhalation points as the new baseline, assuming reproducible full exhalations. The offline correction for residual baseline drift was also performed. The CPX-measured tidal volumes served as the ground truth.

A volumetric correction from the CPX-measured external tidal volume to the OSI-measured internal tidal volume was performed based on the difference in temperatures and partial water pressure inside and outside the human body using the ideal gas law. The conversion factor of 1.08 was applied, which was detailed in previous publications.^6,11

3. RESULTS

The primary goal of this study is to determine the feasibility and accuracy of using OSI to measure dynamic breathing tidal volumes. Therefore, standard volume measurement methods were applied to serve as the ground truth for evaluation of the OSI-based spirometry.

3.A. Volume determination from geometric phantoms

Table I shows the absolute volumes measured from the OSI surface and calculated based on the phantom geometry. Seven phantoms were employed for the comparison study and the average discrepancy in volume measurement is 0.0% ± 1.6%, ranging from −1.9% to 2.5%.

TABLE I.

Comparison of volumes of seven geometric phantoms calculated mathematically and measured by OSI (AlignRT).

		Volumes measured by OSI (cm3)
Geometric	Calculated			Relative
Phantoms	Volumes (cm3)	Average	Standard deviation	Difference (%)
Cup_1	502.7	494.4	1.2	−1.7
Cup_2	445.2	442.1	1.8	−0.7
Cup_3	557.3	564.9	1.7	1.4
Cup_4	437.8	448.9	2.3	2.5
Cylinder_1	511.7	515.2	2.4	0.7
Cylinder_2	349.1	347.8	2.6	−0.4
Cylinder_3	1442.1	1414.8	14.1	−1.9
Average				0.0
St. dev				1.6

3.B. Volume measurement from deformable phantoms

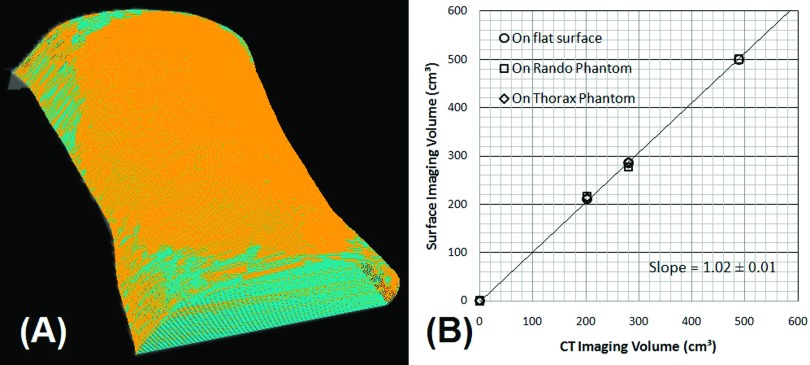
Table II shows the comparison of DPD volumes on the rigid phantoms and on flat surfaces measured by OSI and CT imaging. The average accuracy is 1.2% ± 2.1%, ranging from −0.5% to 3.6%. Figure 2 shows the two overlaid contours from OSI imaging and the highly consistent, linear relationship with a slope of 1.02 (R² = 0.999). These results indicate an excellent agreement between the OSI and CT measurements.

TABLE II.

Volume comparison of three DPD layers measured by OSI and CT volumetric imaging.

	Volume by OSI (cm3)			Volume by CT (cm3)
DPD	On flat surface	On rando phantom	On thorax phantom	On thorax phantom	On foam box (rod)a	Relative difference (%)b
Layer_1	211 ± 1	216 ± 1	213 ± 1	207	205	3.6
Layer_2	285 ± 2	277 ± 2	287 ± 2	⋯	285	−0.5
Layer_3	500 ± 2	501 ± 1	⋯	⋯	497	0.7
Average						1.2
St. dev						2.1

^aThe DPD layers were deformed into rod-shaped objects and scanned on a foam substrate.

^bThe relative error between the average volumes from OSI and CT measurements are presented.

FIG. 2.

(A) The overlay of two converted contours from OSI of the Rando phantom (light blue) and the phantom with DPD layer (orange). (B) The linear plot of OSI-measured volume and CT-segmented volume with a slope of 1.02 (R² = 0.999).

3.C. Volume measurement from three human subjects

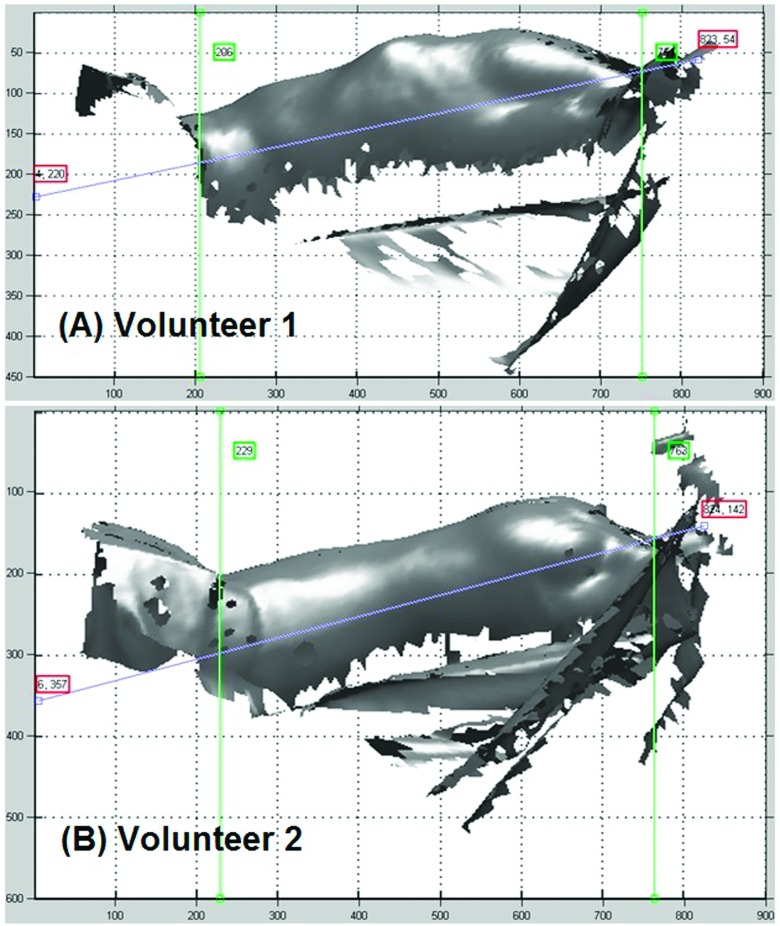
In studying human subjects, conventional spirometric measurements were used as the clinical standard in measuring breathing tidal volume. When calculating the TVC from OSI images, an appropriate VOI is defined to include the moving surface of the entire torso. Figure 3 shows the sagittal views of the torso.

FIG. 3.

Defining VOI of the torso in two of the volunteers (A) and (B) using three cut planes (appears as lines) in sagittal view with our in-house matlab toolbox. The three lines represent three cut planes enclosing the VOI.

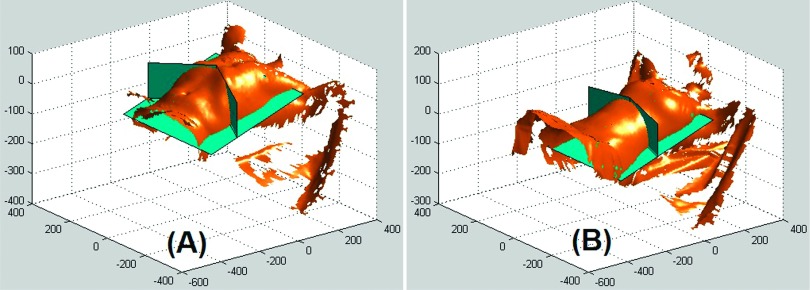
To evaluate the volumetric contribution from the thorax and abdomen, separated by two cut planes as shown in Fig. 4, the two regions were processed separately. The three volunteers produced different breathing patterns: BP_v = 0.15, 0.45, and 0.32.

FIG. 4.

Demonstration of the separation of thoracic and abdominal regions using two vertical cut planes as rendered by our matlab toolbox. The two cut planes join at the inferior end of the sternum and follow the edges of the rib cage. The VOI of two of the volunteers (A) and (B) is shown.

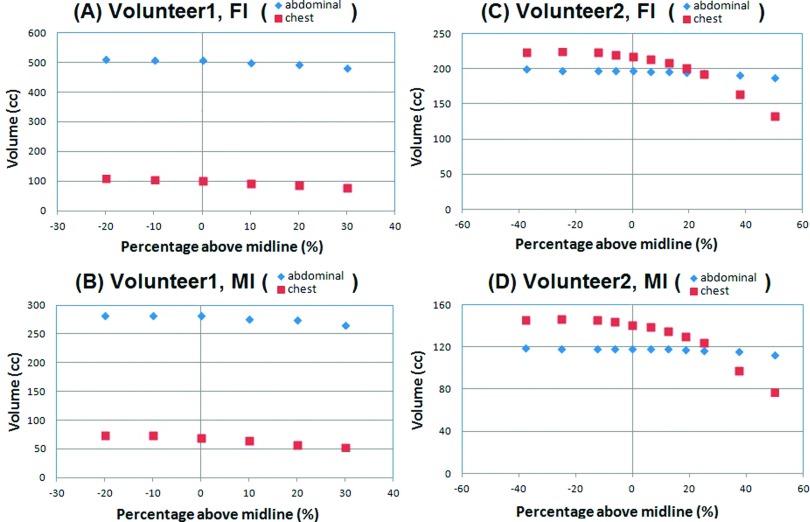
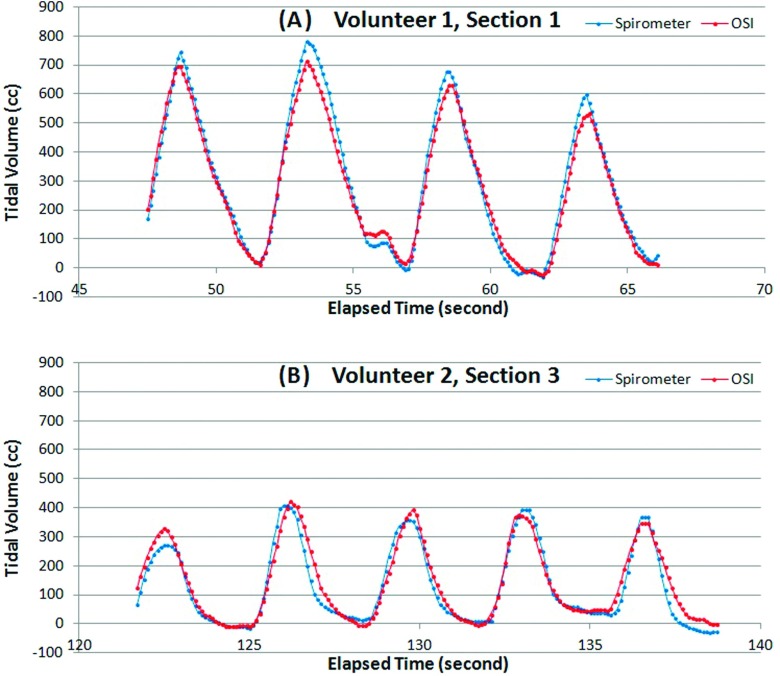
Figure 5 illustrates the calculated TVC (TV C = ΔT_torso = ΔV_abdomen + ΔV_thorax) as a function of posterior cut-plane positions. A series of calculations was performed by moving the posterior cut plane and deviating from the mid plane of the torso in the sagittal view. The fact that the TVC volumes reach a plateau suggests that further lowering the cut plane does not result in additional gains to the volume. Table III shows the comparison between the spirometric and OSI volume measurements, with the discrepancy of −2.2% ± 4.9%, ranging from −9.2% to 4.8%. Figure 6 depicts the comparison of dynamically measured tidal volumes using both spirometer and OSI. The correlation between the two dynamic measurements is greater than 0.98.

FIG. 5.

Determination of the posterior cut plane position to preserve the torso volume change, indicated by reaching a plateau. (A) and (B) volunteer 1 and (C) and (D) volunteer 2. Full exhalation is used as the reference for the plots of full inhalation (FI) and mid inhalation (MI). The sagittal midline is at 0%, while the anterior and posterior surfaces are at +100% and −100%, respectively.

TABLE III.

Comparison of TVs measured from optical surface imaging and conventional spirometry in three volunteers.

		Peak-to-peak volume difference (cm3)b
		Spirometer		OSI			Relative error (%)
Subject	FB sectiona	Average	St. dev	Average	St. dev	BPvc	Average	St. dev
1	1	697	74	633	71	0.15	−9.2	1.9
	2	402	32	414	29		3.0	1.5
2	1	251	15	247	8	0.45	−1.2	5.9
	2	317	49	300	27		−4.3	8.1
	3	360	42	376	47		4.8	10.1
3	1	418	34	403	23	0.32	−3.4	3.4
	2	484	34	458	23		−5.3	3.0
Average							−2.2	4.8
St. dev							4.9

^aWhere no apparent residual baseline draft of the spirometer was found after correction.

^bThe tidal volume is the average of five breathing cycles (full exhalation to full inhalation). The standard deviation represents both measurement uncertainty and breathing irregularities.

^cThe breathing pattern is defined as: BP_v = ΔV_thorax/ΔV_torso.

FIG. 6.

Comparison of the dynamic tidal volume measured by spirometer and OSI. (A) and (B) are two breathing tidal volumes for two of the volunteers (1 and 2). The spirometry curves (blue) were baseline corrected within a consecutive five breaths (the double dips before the last cycle in volunteer 1 was picked by the online correction program as two cycles, which did not affect the baseline correction).

4. DISCUSSION

4.A. A novel OSI-based spirometry

This is the first time that the dynamic breathing tidal volume has been measured by OSI with the accuracy of −2.2% ± 4.9% compared with spirometric measurements. It is worthwhile to note that the paper by Hughes et al.¹⁴ was the first to calculate the volume under the OSI surface images, to correlate it with spirometric measurements, and to use it as a respiratory surrogate. However, the study did not suggest that it was a means to measure the respiratory tidal volume. In fact, to measure the tidal volume from OSI images requires the following two pieces of additional information as previously indicated:^11,12 (1) the complete torso with no tissue moving in and out of the VOI and (2) the volume conservation of the torso except for the exchanging air volume. It is also necessary to examine that the torso surface images with missing posterior surface can still be used to calculate the volume change of the entire torso. In this study, the two physical conditions (closed system and volume conservation) were followed and the feasibility of measuring tidal volume was tested.

As the tidal volume is quantitatively calculated, it is not a surprise to have a correlation between the two time-dependent curves greater than 0.98 for the three human subjects. This is higher than a previously reported correlation (∼0.8),¹⁴ where 1-camera-pod system was applied and the incomplete torso was used as the VOI. In contrast, a 3-camera system provides a complete coverage of the moving surface of the entire torso during quiet respiration (Figs. 3–5). In addition, the VOI used in this study covers the entire torso, assuring that no tissue is moving in and out of the VOI, so that the volume (except for breathing air exchange volume) is conserved.¹¹ Therefore, this method can measure the TVC to represent the tidal volume.

Similar to the OSI-based spirometry, plethysmography^13,20 is well established spirometry based on the ideal gas law with the assumption of volume conservation of body tissue. The tidal volume of a human subject is obtained by measuring the pressure variation in an airtight booth, in which the subject breathes through a tube connecting to outside. The lung volume increase during inhalation is equal to the air volume decrease in the booth, and it can be calculated using the measured pressure inside the booth based on Boyle’s law. The OSI-based spirometry applied the same physical principles but in the format that suits to the radiation therapy clinic.

The average discrepancy of peak-to-peak tidal volume from the measurements of OSI and spirometry is within 10%. The higher uncertainty in human subjects (1σ = 4.9%) than in the deformable phantoms (1σ = 2.1%) is likely a combined result of 1%–2% air volume compression, possible body shift or rotation during experiments, the PDE interpolation to fill the holes on the body surface, as well as the prevailing uncertainty in conventional spirometric measurements, including baseline drift correction. For the female subject (volunteers 2 and 3), a leotard is required to be worn for the torso imaging study. From the volume comparison, it does not seem to affect the accuracy of volume measurement, since the leotard itself does not change the body volume, even though it may be stretched during respiration. The accurate volume measurement depends on the high spatial accuracy of ±0.1 mm of AlignRT system.²¹ Overall, the accuracy in tidal volume detection is acceptable to develop a respiratory or tumor motion surrogate.

In addition, the OSI-based spirometry provides more information about patient respiration, including BP_v (Refs. 11 and 12) or breathing mode,¹⁴ which describes how a patient breathes using the diaphragm and intercostal muscles. By viewing the entire torso, we are able to quantify the breathing pattern to distinguish the components of belly breathing and chest breathing, which primarily affects the SI and AP motions, respectively.^11,12 This is primarily because the diaphragm motion pushes the tissue volume into abdominal region, while the intercostal muscle contraction elevates the chest wall. As shown in Fig. 5, the first two volunteers have very different BP_v (=ΔV_thorax/ΔV_torso) values: 0.15 for volunteer 1 (85% diaphragm contribution) and 0.45 for volunteer 2 (55% diaphragm contribution). The third volunteer has BP_v = 0.32. It is rare to observe a subject with BP_v > 0.5 during free breathing.¹¹ This quantity is useful to estimate the volume allocation for the SI and AP motions.¹²

4.B. Determination of tidal volume from partial surface

The determination of the torso volume change does not require the entire torso surface, but the entire moving surface only. Because the OSI is ceiling-mounted, it only provides the anterior and lateral, but not the posterior surface. Coincidentally, the respiration-induced torso motion appears mostly in the anterior half of the body, when a subject is lying in the supine position.^11,12 This is also shown in 4DCT scans, where the spine and posterior ribs do not move.²² Negligible motion of the posterior skin surface is often observed based on 4DCT. Therefore, missing some of the posterior surface may not affect the calculation of the torso volume change. At a position that is slightly posterior to the mid plane, the change in torso volume reaches a plateau, suggesting negligible motion at the posterior side. Therefore, a complete VOI is used and the calculated TVC reflects the internal tidal volume variation during quiet respiration.

It is worthwhile to mention that there is a volume difference between the tidal volumes when measured from the outside as compared to measurements taken from the inside. The differences in temperature and moisture affect the measured volumes, for which a conversion factor of 1.08 has been previously calculated and verified.⁶ Here, we applied the correction factor to the spirometry data to enable a valid comparison between the external and internal tidal volumes.

4.C. Limitation and future directions

This study demonstrates the proof-of-principle of the OSI-based spirometry; however, there is a limitation that requires further investigation. Given the present conditions, dynamic tidal volume cannot be measured and calculated in real time. The HSIC mode captured the real-time images at 5 Hz; however, the 3D surface images had to be reconstructed retrospectively because of the high demand for computing power. In addition, the volume calculation requires additional time to process. We are currently characterizing and improving this new technology with more human data under the IRB-approved protocol. The entire moving torso surface offers all external motion information, which could be utilized fully to develop a physical model to predict internal organ motion, including tumor motion.^12,23

5. CONCLUSION

Volume determination using OSI provides sufficient accuracy of 0.0% ± 1.6% (range −1.9% to 2.5%) for geometric phantoms and 1.2% ± 2.1% (range −0.5% to 3.6%) for deformable phantom. The breathing study on human subjects shows the accuracy in tidal volume determination at −2.2% ± 4.9% (range −9.2% to 4.8%), in comparison with a conventional spirometer. This OSI-based, spirometric measurement is a promising tool that could be useful in clinical radiotherapy.