The effect of in-plane arterial curvature on blood flow and oxygen transport in arterio-venous fistulae

Abstract

Arterio-Venous Fistulae (AVF) are the preferred method of vascular access for patients with end stage renal disease who need hemodialysis. In this study, simulations of blood flow and oxygen transport were undertaken in various idealized AVF configurations. The objective of the study was to understand how arterial curvature affects blood flow and oxygen transport patterns within AVF, with a focus on how curvature alters metrics known to correlate with vascular pathology such as Intimal Hyperplasia (IH). If one subscribes to the hypothesis that unsteady flow causes IH within AVF, then the results suggest that in order to avoid IH, AVF should be formed via a vein graft onto the outer-curvature of a curved artery. However, if one subscribes to the hypothesis that low wall shear stress and/or low lumen-to-wall oxygen flux (leading to wall hypoxia) cause IH within AVF, then the results suggest that in order to avoid IH, AVF should be formed via a vein graft onto a straight artery, or the inner-curvature of a curved artery. We note that the recommendations are incompatible—highlighting the importance of ascertaining the exact mechanisms underlying development of IH in AVF. Nonetheless, the results clearly illustrate the important role played by arterial curvature in determining AVF hemodynamics, which to our knowledge has been overlooked in all previous studies.

I. INTRODUCTION

Patients with End-Stage Renal Disease (ESRD) suffer from an irreversible reduction in kidney function. Before the introduction of renal replacement therapies, such as hemodialysis, ESRD was a terminal illness. During hemodialysis, blood is drawn from the patient through a vascular access, and circulated through a dialysis filter to remove metabolic waste, before being returned to the body. The “gold-standard” method for creating a vascular access is formation of an Arterio-Venous Fistula (AVF). AVF are arterio-venous connections commonly formed surgically in the wrist or upper arm by connecting or “anastomosing” a vein onto an artery. AVF can take various forms, including end-to-end (where the vein and artery are connected end-to-end), side-to-side (where the vein and artery are connected side-to-side), and end-to-side (where the end of the vein is connected onto the side of the artery). In all cases, the large pressure difference between the artery and vein leads to increased blood flow through the vein, which in turn will (ideally) cause the vein walls to strengthen and the vein itself to enlarge. The result—an enlarged “arterialized” vein, with strengthened walls, and a high blood flow rate—can accommodate a large gauge needle, and provide excellent access for hemodialysis over a period of several years.

Unfortunately, however, ∼50% of AVF fail shortly after they are created,^1–4 causing unfavourable clinical outcomes and significant additional costs for healthcare systems worldwide. The most common reason for failure is an adverse inflammatory process called Intimal Hyperplasia (IH), which causes the intimal layer of the artery and/or vein to grow inwards, reducing the size of the lumen and dramatically reducing blood flow through the AVF. Whilst the exact mechanisms underlying development of IH are unknown, there is considerable evidence to suggest that the inherently unphysiological flow patterns within AVF play an important role. In particular regions of low Wall Shear Stress (WSS), highly oscillatory flow, and low Lumen-to-Wall Oxygen Flux (LWOF), leading to wall hypoxia, are all implicated in the initiation of IH.^5–17 There have been various computational studies of blood flow within AVF and Arterio-Venous Grafts (AVG). In 2003, Loth et al.¹⁸ simulated blood flow within idealized AVG and compared results with those obtained in vivo. The authors observed transitional flow within the AVG and associated this with measured wall vibration in vivo. Moreover, the authors observed that regions of venous intimal thickening collocated with the most unsteady regions of venous flow. In 2008, Krishnamoorthy et al.¹⁹ simulated blood flow within two porcine AVF and compared results with those obtained in vivo. The AVF were formed with curved and straight veins, respectively. In both cases, the authors found regions of low WSS were associated with development of IH. In 2010, Niemann et al.²⁰ simulated blood flow in side-to-side AVF configurations and compared the results with flow fields obtained from ultrasound scans, demonstrating good qualitative agreement. In 2012 and 2013, Remuzzi and Ene-Iordache^21,22 simulated pulsatile blood flow in end-to-end and end-to-side AVF configurations with various anastomotic angles. The authors results suggested that regions of low and oscillatory WSS were collocated with sites of IH. Moreover, the authors found that the anastomotic angle effects the nature of the unsteady flow, and suggested that a smaller angle may inhibit development of IH. In 2013, Sigovan et al.²³ used computational simulations and MRI scan data to investigate how three AVF evolved over a period of ten months, with the objective of identifying hemodynamic factors that contribute to AVF failure. The authors found that regions of the vein subjected to flow instability or recirculation were more prone to remodelling. Finally, in 2013, McGah et al.²⁴ simulated blood flow in four mature AVF. Their results suggested a relationship between regions of high WSS and IH.

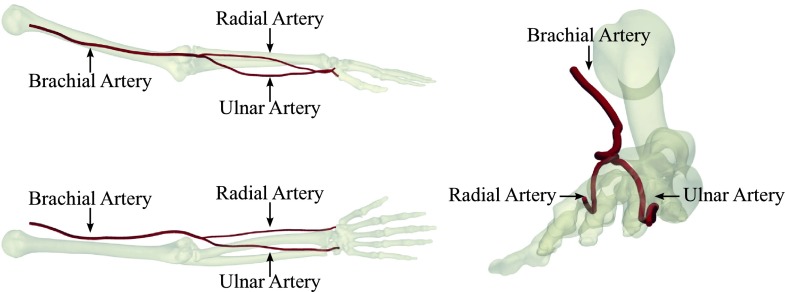
In this study, we investigate the effect of in-plane arterial curvature on flow and oxygen transport in end-to-side AVF, with the objective of understanding whether the natural curvature of the brachial, radial, and ulnar arteries (see Fig. 1) can be leveraged to manipulate flow and oxygen transport patterns within AVF. Whilst flow in curved pipes has been studied extensively before,^25–28 we believe the concept of leveraging arterial curvature to manipulate flow in AVF to be novel.

FIG. 1.

Three views of the principal arteries in the forearm of an adult male human reconstructed from computed tomography data. The brachial, radial, and ulnar arteries all exhibit pronounced curvature.

II. METHODS

A. Idealized geometries

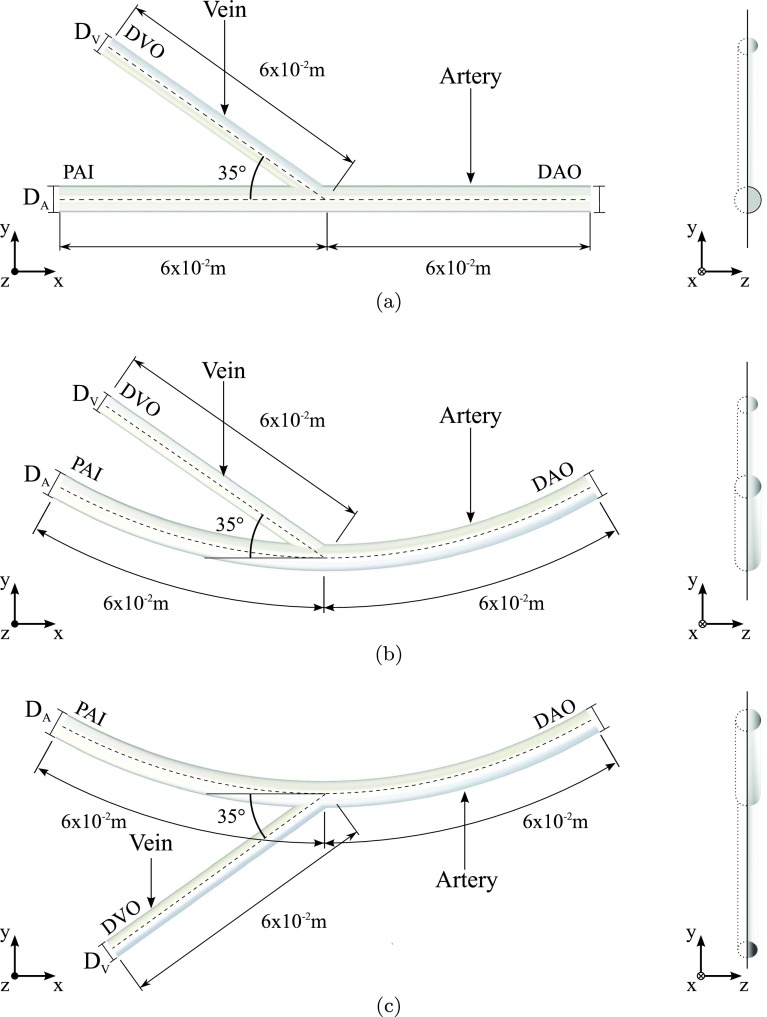
Three-dimensional time-dependent simulations of blood flow and oxygen transport were undertaken in various idealized end-to-side AVF geometries. In total, nine geometries were considered. Specifically, each of the three configurations (straight, inner, and outer) shown in Fig. 2 was studied with a fixed arterial diameter D_A of 6.0 × 10⁻³ m (based on post-operative measurements of Lomonte et al.²⁹ in patients with AVF), and venous diameters D_V of 3.0 × 10⁻³ m, 4.5 × 10⁻³ m, and 6.0 × 10⁻³ m. For the inner and outer configurations, the arterial radius of curvature was fixed at R = 20D_A (based on measurements made in the curved section of brachial artery near the elbow joint in Fig. 1). All geometries were planar; specifically they were symmetric about a plane orthogonal to the z-axis. To reduce computational cost simulations were only undertaken in a semi-domain on one side of this plane.

FIG. 2.

Orthogonal side-on (left) and end-on (right) views of straight (a), inner (b), and outer (c) configurations with D_V = 4.5 × 10⁻³ m.

B. Governing equations

1. Blood flow

In this study, blood was treated as an incompressible Newtonian fluid. Specifically, blood flow was modelled using the time-dependent incompressible Navier-Stokes equations for a fluid with constant viscosity, which can be written as

$${\displaystyle \nabla \cdot \mathbf{u}=0,}$$ (1)

$${\displaystyle \rho \frac{\partial \mathbf{u}}{\partial t}+\rho (\mathbf{u}\cdot \nabla )\mathbf{u}=-\nabla p+\mu {\nabla }^2\mathbf{u},}$$ (2)

where μ is the viscosity of human blood, ρ is the density of human blood, u is the three-dimensional blood velocity (vector) field within the idealized AVF geometry, and p is the pressure field within the idealized AVF geometry. Values of μ = 3.5 × 10⁻³ Pa s and ρ = 1060 kg m⁻³ (Refs. 30 and 23) were used in this study.

The assumption of Newtonian rheology ignores the well known “shear-thinning” property of blood.³¹ However, according to Brooks et al.³² shear thinning is only significant at shear rates below 100 s⁻¹, and in this study, shear rates (specifically volume-averaged square roots of the second invariant of the shear-rate tensor) were ∼300 s⁻¹ and above across all configurations.

2. Oxygen transport

In this study, oxygen was treated as a passive scalar dissolved in blood plasma. Specifically, oxygen transport was modelled using the advection-diffusion equation for a passive scalar, which can be written as

$${\displaystyle \frac{\partial c}{\partial t}=\kappa {\nabla }^{2}c-\mathbf{u}\cdot \nabla c,}$$ (3)

where κ is the diffusivity of oxygen in human plasma, u is the three-dimensional blood velocity (vector) field within the idealized AVF geometry, and c is the oxygen concentration within the idealized AVF geometry. A value of κ = 1.2 × 10⁻⁹ m² s⁻¹ (Ref. 33) was used in this study.

The assumption that oxygen is a passive scalar dissolved in blood plasma ignores the effect of haemoglobin, to which oxygen can bind. However, previous studies suggest that haemoglobin simply acts to augment oxygen transport patterns by a spatially constant factor of approximately two,³⁴ which can be accounted for a posteriori when the results are analysed (see Sec. III B 1).

C. Boundary conditions

1. Blood flow

Steady-state parabolic boundary-normal flow profiles were applied at the Proximal Arterial Inlet (PAI) and the Distal Arterial Outlet (DAO). At the PAI, the profile had a spatially averaged velocity of V_PAI = 0.44 m s⁻¹ (equivalent to 746 ml min⁻¹) into the domain. At the DAO, the profile had a spatially averaged velocity of V_DAO = 0.088 m s⁻¹ (equivalent to 149 ml min⁻¹) out from the domain. A constant (and arbitrary) pressure was applied at the Distal Venous Outlet (DVO). A zero-velocity no-slip condition was applied at the arterial and venous walls, which were assumed to be rigid. A symmetry condition was applied at the symmetry plane orthogonal to the z-axis.

Imposition of steady-state flow profiles at the PAI and DAO is clearly an approximation, since in reality blood flow is pulsatile. The aforementioned conditions enforce an 80:20 flow split between the DVO and the DAO (with antegrade flow in the distal artery). Such a flow split is in line with clinical observations.³⁵

2. Oxygen transport

A steady-state spatially constant oxygen concentration of 1.305 × 10⁻³ mol m⁻³ was applied at the PAI (based on an oxygen partial pressure of 75 mmHg³⁶ and a Henry’s law constant of 1.74 × 10⁻³ mol m⁻³ mmHg^{−1 37}). Zero boundary-normal oxygen concentration gradients were applied at the DAO and DVO. A steady-state spatially constant oxygen concentration of 1.044 × 10⁻³ mol m⁻³ was applied at the arterial and venous walls (based on an oxygen partial pressure of 60 mmHg³⁶ and a Henry’s law constant of 1.74 × 10⁻³ mol m⁻³ mmHg^{−1 37}). A symmetry condition was applied at the symmetry plane orthogonal to the z-axis.

The imposition of a spatially constant oxygen concentration at the PAI is based on the assumption that oxygen is “well mixed” upstream of the AVF. The imposition of zero boundary-normal oxygen concentration gradients at the DAO and DVO is a standard practice^38–41 and minimizes impact on the evolution of the oxygen boundary layer as it exits the domain. The imposition of a spatially constant oxygen concentration at the arterial wall assumes that the arterial wall acts as an oxygen sink, readily consuming excess oxygen, in line with the arguments of Tarbell.¹⁴ The imposition of a spatially constant oxygen concentration at the venous wall is based on a similar argument. However, we note that the structure/biology of the venous wall is different to that of the arterial wall, and moreover when a vein is mobilized during AVF surgery, the adventitial layer undergoes surgical trauma, leading to disruption of the vasa vasorum network. A more comprehensive model of how oxygen interacts with the venous wall may be required to fully capture the aforementioned.

D. Non-dimensional quantities

The simulations have been described above in dimensional form, and will subsequently be analysed in dimensional form. However, it is useful to identify various salient non-dimensional quantities associated with the simulations. These include a Reynolds number Re defined as

$${\displaystyle \mathit{Re}=\frac{\rho D_A{V}_{\mathit{PAI}}}{\mu },}$$ (4)

a Schmidt number Sc defined as

$${\displaystyle \mathit{Sc}=\frac{\mu }{\rho \kappa },}$$ (5)

a Peclet number Pe defined as

$${\displaystyle \mathit{Pe}=\mathit{ReSc},}$$ (6)

and a Dean number De defined as

$${\displaystyle \mathit{De}=\mathit{Re}\sqrt{\frac{D_A}{2R}}.}$$ (7)

In all cases, Re = 800, Sc = 2 700, Pe = 2.16 × 10⁶, and for the inner and outer configurations, De = 126. Re = 800 indicates that inertial forces dominate the fluid dynamics; however, the flow is unlikely to become fully turbulent. Sc = 2 700 indicates that the oxygen boundary layer will be significantly thinner than the momentum boundary layer. Pe = 2.16 × 10⁶ indicates that oxygen transfer is convection dominated. Finally, De = 126 indicates that arterial flow upstream of the anastomosis will be stable (Dennis and Ng⁴² observed stability up to De ∼ 956).

E. Computational method

Suitable unstructured polyhedral meshes with prismatic boundary layers were produced for each of the nine idealized geometries using Star-CCM+ v7.0.6 (CD-Adapco, Melville, NY, USA). The unstructured polyhedral meshes were refined near the anastomosis. Specifically, cells near the anastomosis had an average size of 3.6 × 10⁻⁵ m, expanding progressively to 3.6 × 10⁻⁴ m beyond a distance of ∼4 × 10⁻² m from the anastomosis. The prismatic boundary layers were 17 cells thick, with the first cell having a thickness of 5 × 10⁻⁶ m (in line with the mesh resolution employed by Coppola and Caro⁴¹ in a similar Reynolds/Schmidt number regime). Each mesh had ∼5 × 10⁶ cells in total, and was found a posteriori to satisfy the resolution criteria set out by Valen-Sendstad⁴³ who performed direct numerical simulations of transitional flow in an aneurysm.

Solutions for the blood velocity field and the oxygen distribution were obtained using Star-CCM+ v7.0.6 (CD-Adapco, Melville, NY, USA) via the following procedure:

• •Each simulation was initialized with zero velocity, pressure, and oxygen concentration, and run for 1000 iterations with the segregated steady-state solver.
• •Each steady-state solution was then used as the initial condition for the segregated implicit unsteady solver, which advanced each simulation 0.41 s, until transient “start-up” phenomena left the domain and only periodic “physical” fluctuations remained. For all simulations, a timestep of 1.4 × 10⁻⁴ s was used.
• •The segregated implicit unsteady solver was then used to advance each simulation a further 0.14 s, during which time data were exported for analysis. This period, from 0.41 to 0.55 s, will subsequently be referred to as Δt_E. For all simulations, a timestep of 1.4 × 10⁻⁴ s was used.

Each simulation was carried out on 20 cores of a Dell AMD Opteron 64-core server with 512 GB RAM, and required approximately 7 days to complete.

III. RESULTS

A. Unsteady analysis

1. Velocity and vorticity

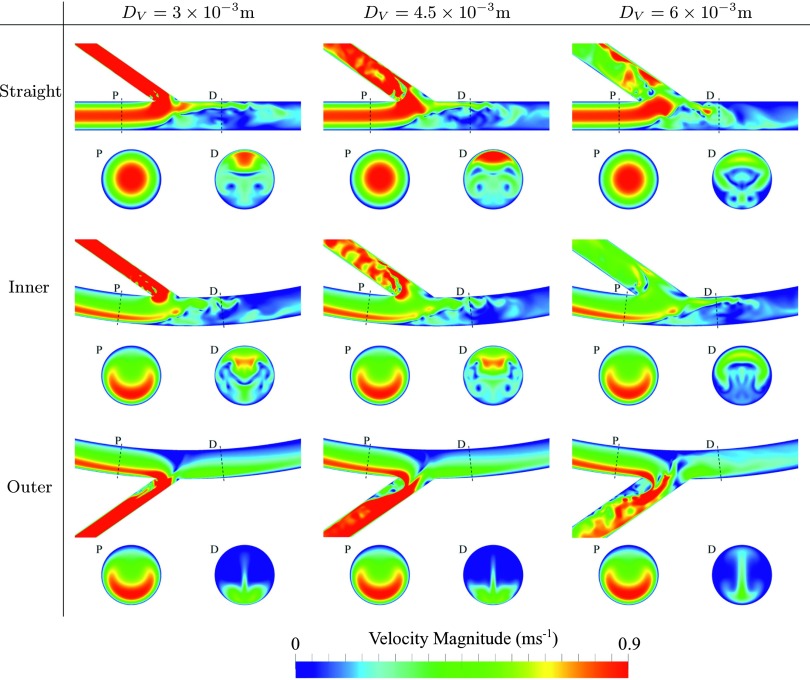
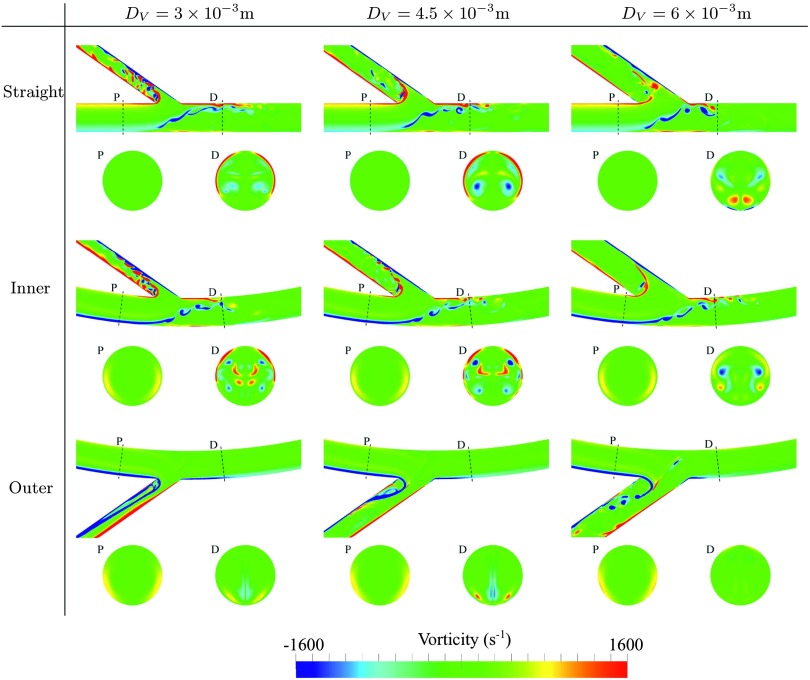
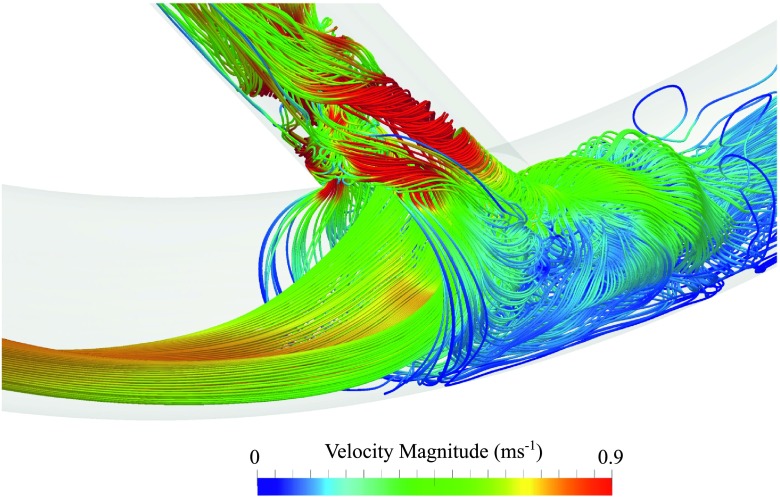
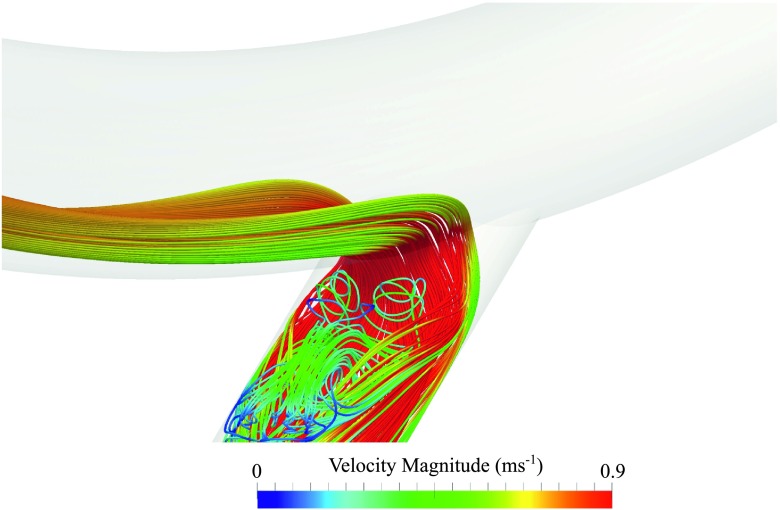
Temporal snapshots of velocity magnitude on various planes within each geometry are shown in Fig. 3, and temporal snapshots of in-plane vorticity on various planes within each geometry are shown in Fig. 4. Finally, temporal snapshots of streamlines coloured by velocity magnitude for inner and outer configurations with D_V = 4.5 × 10⁻³ m are shown in Figs. 5 and 6, respectively. The following observations can be made:

• •For straight and inner configurations, the arterial flow is unsteady, despite the steady inflow conditions. However, for outer configurations, the arterial flow is largely steady. The observed unsteadiness can be explained by studying Figs. 3–6. For straight and inner configurations, the bulk of the axial arterial blood flow (the high speed region of the flow) is either within the center of the artery or on the opposite side of the artery to the venous anastomosis. Consequently, for these cases, the bulk of the flow must traverse the artery laterally in order to enter the vein. This process causes the shear layer on the wall opposite the anastomosis to detach, leading to a free-shear layer in the artery that induces unsteadiness.
• •For straight and inner configurations, the venous flow is unsteady, despite the steady inflow conditions. For outer configurations, the venous flow is also largely unstable, the only exception being when the venous diameter D_V = 3 × 10⁻³ m, in which case the venous flow is stable. Unsteadiness in the vein, when present, appears to be induced by flow separation around the acute (35°) bend at the anastomosis. The mechanism by which unsteadiness is suppressed for outer configurations with D_V = 3 × 10⁻³ m is less clear. However, it appears to be, in part at least, as a result of stabilized arterial flow in these configurations due to the mechanism outlined above.

FIG. 3.

Temporal snapshots of velocity magnitude on the symmetry plane orthogonal to the z-axis, and on two planes orthogonal to the arterial centreline, positioned 12 × 10⁻³ mm proximal (P) and 6 × 10⁻³ mm distal (D) of the intersection between the arterial and venous centrelines.

FIG. 4.

Temporal snapshots of in-plane vorticity on the symmetry plane orthogonal to the z-axis, and on two planes orthogonal to the arterial centreline, positioned 12 × 10⁻³ mm proximal (P) and 6 × 10⁻³ mm distal (D) of the intersection between the arterial and venous centrelines.

FIG. 5.

Temporal snapshot of streamlines coloured by velocity magnitude for an inner configuration with D_V = 4.5 × 10⁻³ m. Streamlines were seeded uniformly within a circle of diameter 0.3D_A positioned at the centre of the PAI.

FIG. 6.

Temporal snapshot of streamlines coloured by velocity magnitude for an outer configuration with D_V = 4.5 × 10⁻³ m. Streamlines were seeded uniformly within a circle of diameter 0.3D_A positioned at the centre of the PAI.

2. Proper orthogonal decomposition (POD) of wall shear stress

POD can be used to decompose a space-time field into a summation of orthonormal spatial POD modes, each modulated by an associated temporal POD mode. POD was originally used in the context of fluid dynamics by Lumley et al. in 1967⁴⁴ for identification of coherent structures in turbulent flow. Classical POD is computationally expensive, and hence POD was seldom applied to large computational fluid dynamics datasets until Sirovich⁴⁵ proposed the “snapshot” POD method in 1987. Grinberg et al. have applied this technique to analyze pulsatile transient flows in a stenosed carotid artery.⁴⁶

In this study, snapshot POD was employed to analyse the WSS vector field, defined here as n ⋅ σ, where n is the outward facing wall normal and

$${\displaystyle \mathit{\sigma }=\mu \left(\left(\mathbf{\nabla }\mathbf{u}\right)+{\left(\mathbf{\nabla }\mathbf{u}\right)}^T\right)}$$ (8)

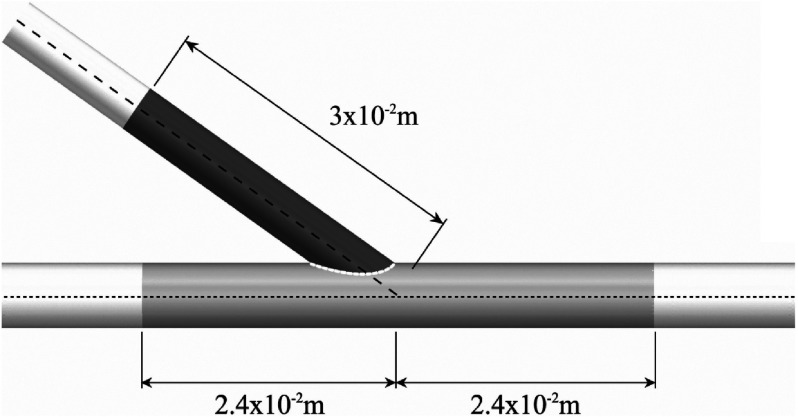
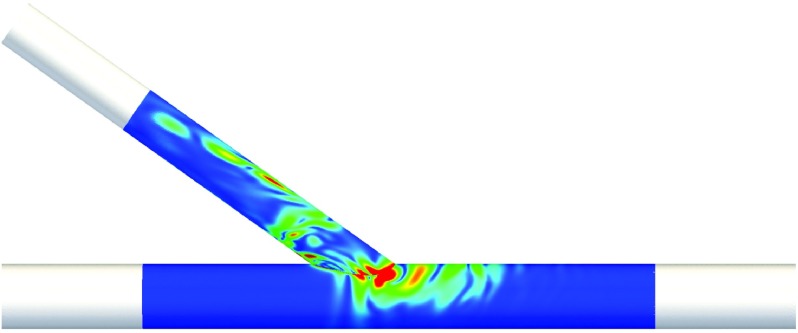
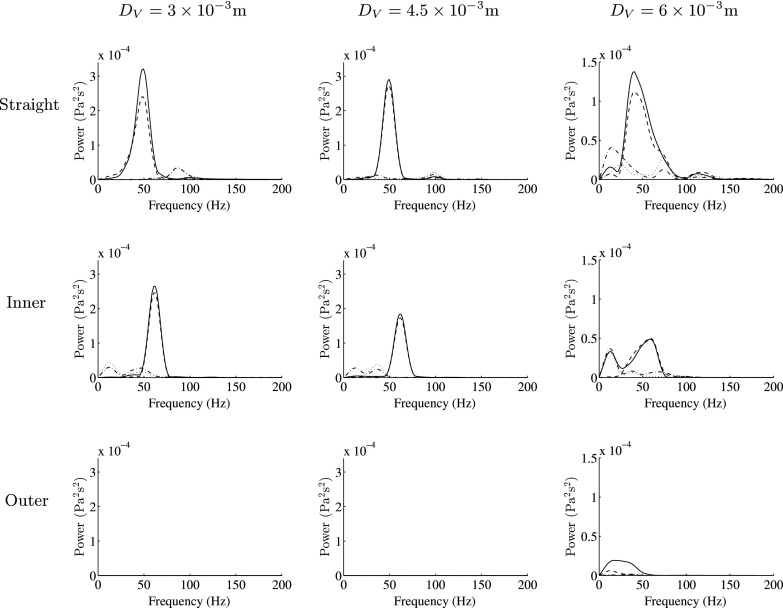
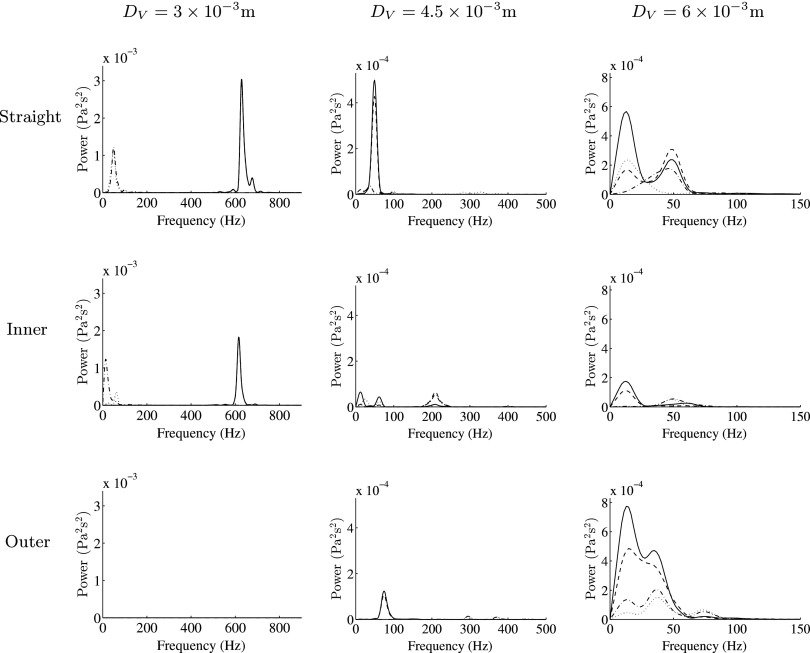
is the viscous stress tensor. Specifically, 300 equispaced temporal snapshots of the WSS vector field in Region of Interest (ROI) 1 (a section of the artery defined in Fig. 7) and ROI 2 (a section of the vein defined in Fig. 7) over the period Δt_E were used to obtain the first four spatial and temporal POD modes in ROI 1 and ROI 2, respectively. Color maps of the first spatial POD modes in ROI 1 and ROI 2 for the straight configuration with D_V = 4.5 × 10⁻³ m are shown in Fig. 8. The power spectra of the first through fourth temporal POD modes in ROI 1 and ROI 2, obtained via fast Fourier transform, are shown in Figs. 9 and 10, respectively, for each geometry considered. The following observations can be made:

• •For straight and inner configurations, the arterial WSS patterns oscillate, with a dominant frequency of ∼50 Hz for the straight cases and ∼60 Hz for the inner cases (independent of the venous diameter D_A). However, for the outer configurations, the WSS patterns are largely stable.
• •For straight and inner configurations, the venous WSS patterns oscillate, with dominant frequencies of up to ∼650 Hz (dependent on the venous diameter D_A). For outer configurations, the venous WSS patterns also oscillate, with dominant frequencies of up to ∼80 Hz, the exception being when the venous diameter D_V = 3 × 10⁻³ m, in which case the venous WSS patterns are stable.

FIG. 7.

ROI 1 (a section of the artery) shaded light grey and ROI 2 (a section of the vein) shaded dark grey for the straight configuration with D_V = 4.5 × 10⁻³ m. ROI 1 and ROI 2 were defined similarly in all other geometries, with ROI 1 extending a distance 2.4 × 10⁻³ m proximal/distal along the arterial centerline from the intersection between the arterial and venous centerlines, and ROI 2 extending a distance 3 × 10⁻³ m along the venous centerline from the intersection between the arterial and venous centerlines.

FIG. 8.

Color maps of the first spatial POD modes in ROI 1 and ROI 2 for the straight configuration with D_V = 4.5 × 10⁻³ m.

FIG. 9.

Power spectra of the first (solid line), second (dashed line), third (dashed-dotted line), and fourth (dotted line) temporal POD modes in ROI 1 for each AVF geometry.

FIG. 10.

Power spectra of the first (solid line), second (dashed line), third (dashed-dotted line), and fourth (dotted line) temporal POD modes in ROI 2 for each AVF geometry.

3. Summary and biological implications

There is evidence to suggest that unsteady blood flow patterns, and in particular, unsteady WSS patterns can disturb the vascular wall leading to pathology.^10–14 The results presented above suggest that forming an AVF via a vein graft onto a straight artery, or onto the inner-curvature of a curved artery, will result in unsteady blood flow patterns and WSS distributions within both the artery (50-60 Hz) and potentially (depending on the venous diameter) within the vein (up to 650 Hz). However, forming an AVF via a vein graft onto the outer-curvature of a curved artery can suppress such unsteadiness. Consequently—if one subscribes to the hypothesis that vascular disturbance due to high-frequency flow unsteadiness leads to IH in AVF—the results suggest that in order to avoid IH, AVF should be formed via a vein graft onto the outer-curvature of a curved artery.

B. Time-averaged analysis

1. Wall shear stress and wall normal oxygen flux

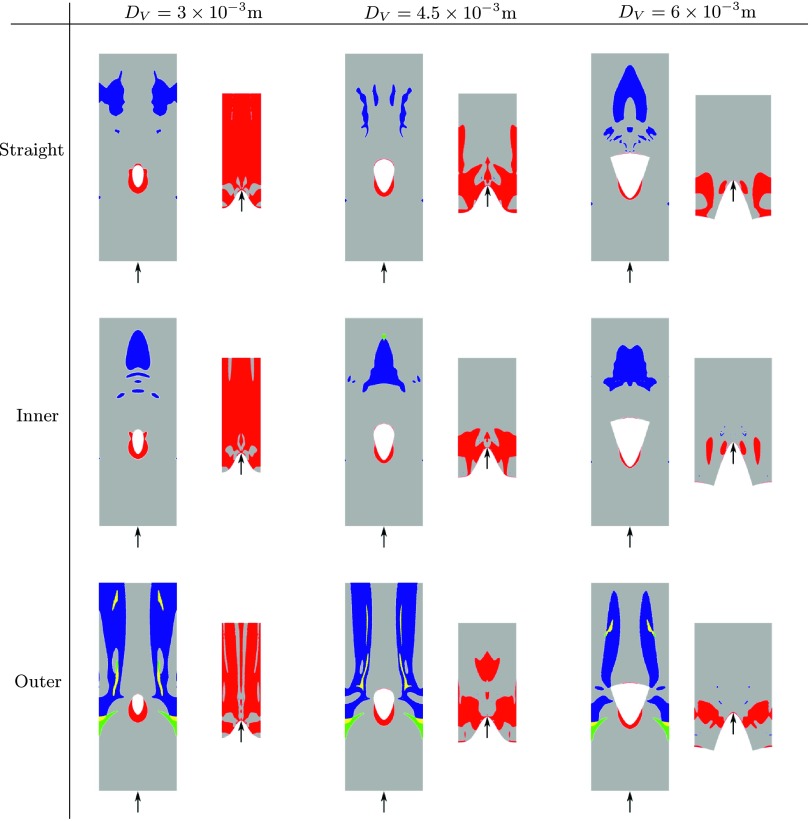
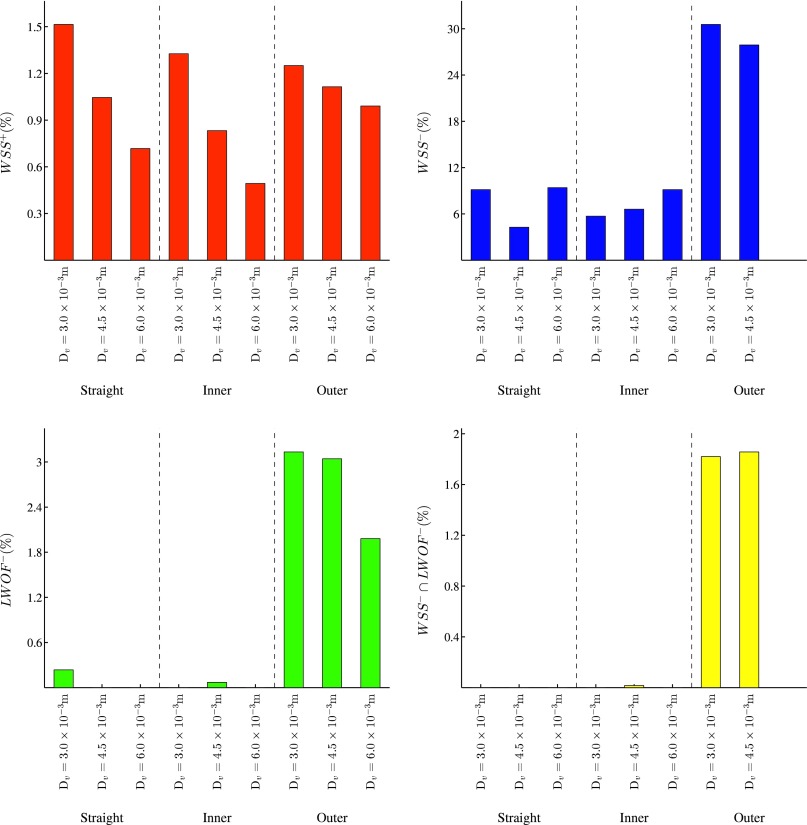
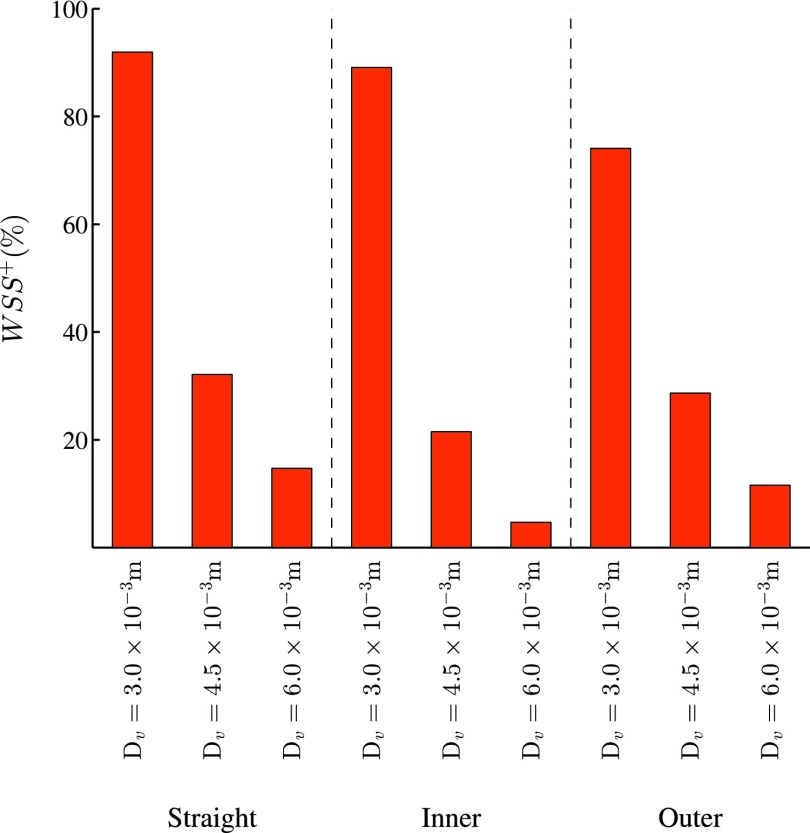
Quad-color maps of WSS⁻ (“pathologically low” time-averaged WSS < 0.5 Pa), WSS⁺ (“pathologically high” time-averaged WSS > 30 Pa), LWOF⁻(“pathologically low” time-averaged LWOF < 4.275 × 10⁻⁷ mol m⁻² s⁻¹), and the intersection between regions of WSS⁻ and LWOF⁻ are shown in excised and flattened views of ROI 1 and ROI 2 for each AVF geometry in Fig. 11. In addition, bar charts showing the percentage area of WSS⁻, WSS⁺, LWOF⁻, and the intersection between regions of WSS⁻ and LWOF⁻ in ROI 1 are shown in Fig. 12, and a bar chart showing the percentage area of WSS⁺ in ROI 2 is shown in Fig. 13. Note that LWOF is defined here as −2κn ⋅ ∇c, where n is the outward facing wall normal and the factor of two accounts for the role of hemoglobin.³⁴

FIG. 11.

Quad-color maps of WSS⁻ (blue), WSS⁺ (red), LWOF⁻ (green), and the intersection between regions of WSS⁻ and LWOF⁻ (yellow) in excised and flattened views of ROI 1 and ROI 2 for each AVF geometry. Arrows indicate the direction of bulk blood flow.

FIG. 12.

Bar charts showing the percentage area of WSS⁺, WSS⁻, LWOF⁻, and the intersection between regions of WSS⁻ and LWOF⁻ in ROI 1 for each AVF geometry.

FIG. 13.

Bar chart showing the percentage area of WSS⁺ in ROI 2 for each AVF geometry.

The pathologically low WSS threshold of 0.5 Pa was chosen to be at the lower-bound of estimates made by various authors, including Masuda et al.⁴⁷ and Sho et al.^48,49 who suggest 0.5 Pa (in rabbits), Dolan et al.⁷ who suggest 1 Pa, and Irace et al.⁵⁰ who suggest 1.8 Pa. The pathologically high WSS threshold of 30 Pa was chosen to be at the upper-bound of estimates made by various authors, including Dolan et al.⁷ who suggest 10 Pa, and Dolan et al.⁵¹ who suggest up to 30 Pa. The pathologically low LWOF threshold was obtained by assuming that the innermost region of the vascular wall (i.e., the intima and media) receives oxygen solely from luminal blood^52,36 and not from the adventitial vasa vasorum. With the further assumptions that this innermost region requires oxygen at a rate of at least 8.55 × 10⁻³ mol m⁻³ s⁻¹ in order to avoid hypoxia (based on measurements of oxygen consumption in smooth muscle cells of dog femoral arteries⁵³), and that it has a thickness of 5 × 10⁻⁵ m (based on measurements in dog femoral arteries⁵⁴), one obtains the threshold of 4.275 × 10⁻⁷ mol m⁻² s⁻¹. The following observations can be made:

• •For outer configurations, the artery is exposed to significantly more WSS⁻ than inner or straight configurations. Also, for outer configurations, a triangular shaped region of LWOF⁻ is present in the artery, opposite the anastomosis. This feature is not present for straight or inner configurations. Finally, for outer configurations, a region of overlap between WSS⁻ and LWOF⁻ is present in the artery opposite the anastomosis. This feature is not present for straight or inner configurations.
• •For all configurations, the vein is exposed to a significant amount of WSS⁺. The percentage area of WSS⁺ in the vein increases as the venous diameter decreases.

2. Summary and biological implications

There is evidence to suggest that low WSS^5–9 and low LWOF (leading to wall hypoxia)^14–17 can disturb the vascular wall leading to pathology. The results presented above suggest that forming an AVF via a vein graft onto the outer-curvature of a curved artery will induce areas of pathologically low WSS and pathologically low LWOF (leading to wall hypoxia) in the artery. However, forming an AVF via a vein graft onto a straight artery, or the inner-curvature of a curved artery, will reduce arterial exposure to areas of pathologically low WSS, and eliminate exposure to areas of pathologically low LWOF. Consequently—if one subscribes to the hypothesis that low WSS and/or low LWOF (leading to wall hypoxia) cause IH within AVF—then the results suggest that in order to avoid IH, AVF should be formed via a vein graft onto a straight artery, or the inner-curvature of a curved artery.

IV. CONCLUSIONS

Simulations of blood flow and oxygen transport were undertaken in various idealized AVF configurations using the software StarCCM+ v7.0.6 (CD-Adapco, Melville, NY, USA). The objective of the study was to understand how arterial curvature affects blood flow and oxygen transport patterns within AVF, with a focus on how curvature alters metrics know to correlate with vascular pathology such as IH. If one subscribes to the hypothesis that unsteady flow causes IH within AVF, then the results suggest that in order to avoid IH, AVF should be formed via a vein graft onto the outer-curvature of a curved artery. However, if one subscribes to the hypothesis that low wall shear stress and/or low lumen-to-wall oxygen flux (leading to wall hypoxia) cause IH within AVF, then the results suggest that in order to avoid IH, AVF should be formed via a vein graft onto a straight artery, or the inner-curvature of a curved artery. We note that the recommendations are incompatible—highlighting the importance of ascertaining the exact mechanisms underlying development of IH in AVF. Nonetheless, the results clearly illustrate the important role played by arterial curvature in determining AVF hemodynamics, which to our knowledge has been overlooked in all previous studies. Future studies should investigate the impact of non-planar arterial/venous curvature (e.g., helicity^55,56) on blood flow and oxygen transport within AVF, as well as the impact of vessel remodelling via IH (or otherwise) on the flow field.