Spectral and Temporal Analysis of Simulated Dead Regions in Cochlear Implants

Abstract

A cochlear implant (CI) electrode in a “cochlear dead region” will excite neighboring neural populations. In previous research that simulated such dead regions, stimulus information in the simulated dead region was either added to the immediately adjacent frequency regions or dropped entirely. There was little difference in speech perception ability between the two conditions. This may imply that there may be little benefit of ensuring that stimulus information on an electrode in a suspected cochlear dead region is transmitted. Alternatively, performance may be enhanced by a broader frequency redistribution, rather than adding stimuli from the dead region to the edges. In the current experiments, cochlear dead regions were introduced by excluding selected CI electrodes or vocoder noise-bands. Participants were assessed for speech understanding as well as spectral and temporal sensitivities as a function of the size of simulated dead regions. In one set of tests, the normal input frequency range of the sound processor was distributed among the active electrodes in bands with approximately logarithmic spacing (“redistributed” maps); in the remaining tests, information in simulated dead regions was dropped (“dropped” maps). Word recognition and Schroeder-phase discrimination performance, which require both spectral and temporal sensitivities, decreased as the size of simulated dead regions increased, but the redistributed and dropped remappings showed similar performance in these two tasks. Psychoacoustic experiments showed that the near match in word scores may reflect a tradeoff between spectral and temporal sensitivity: spectral-ripple discrimination was substantially degraded in the redistributed condition relative to the dropped condition while performance in a temporal modulation detection task degraded in the dropped condition but remained constant in the redistributed condition.

Introduction

The concept of “cochlear dead regions” is related to the fact that the survival of either inner hair cells or auditory neurons is generally not uniform along the entire cochlear length (e.g., Schucknecht 1964; Shannon et al. 2002; Moore 2004; Makary et al. 2011). If threshold and maximum comfort levels are measured without information about the existence and locations of dead regions for cochlear implant (CI) recipients with severe to profound hearing loss, the acoustic information delivered to a CI electrode located in the dead region will stimulate neural regions adjacent to the dead region; therefore, the spectral information will still be delivered but in a distorted manner. Both threshold and maximum comfortable levels are typically elevated for channels with poor electrode-neuron interfaces (Bierer et al. 2011), so the stimulus can excite more distant neurons neighboring the dead region. Such a mapping can have negative consequences because the stimulus from an electrode in the dead region is added to stimulation delivered by electrodes neighboring the dead region.

If the existence and locations of the dead region can be identified, several questions could be raised with regard to CI mapping and signal processing. For example, is it beneficial to add the acoustic information that would have normally been assigned to electrodes in the dead regions to electric stimulation delivered by electrodes neighboring the dead regions (hereafter referred to as “redistributed frequency remapping”)? Or is it beneficial to simply discard the acoustic information from the dead regions entirely (hereafter referred to as “dropped frequency remapping”)?

Several studies have compared dropped frequency remapping to redistributed frequency remapping schemes. For instance, Shannon et al. (2002) examined simulated dead regions in CI users and in subjects with normal-hearing (NH) listening to CI vocoder simulations. They examined dead regions with different sizes and their locations along the cochlea and compared speech perception in a condition in which the information from the dead region was added to the edges of the dead region to a condition in which the information from the dead region was simply dropped. They reported no significant difference between the two frequency remapping conditions. In a follow-up study, Başkent and Shannon (2006) conducted vocoder simulations in NH listeners. They found that consonant and vowel identification in the redistributed conditions was often no better than performance in the dropped conditions. Using vocoder simulations with normal-hearing listeners, Kasturi et al. (2002) measured the effects of the presence of multiple simulated dead regions on vowel and consonant identification and showed that vowel identification is more sensitive to the location of the dead regions, whereas consonant identification remained constant.

It should be also noted that in electric hearing with CIs, frequency-to-place mismatch occurs as a result of shallow insertion of the electrode array, unequal distances between the stimulating electrode and auditory-nerve fibers, and compression of frequency maps between the acoustic spectrum and the corresponding sound processor channel (e.g., Dorman et al. 1997; Shannon et al. 1998, 2002; Fu and Shannon 1999; Başkent and Shannon 2003, 2004, 2005, 2006). Furthermore, the auditory-nerve fibers do not maintain the same relationship of frequency map to distance along the electrode array as inner hair cells (Kawano et al. 1996; Sridhar et al. 2006). It is fortunate, however, that CI users are partially able to adapt to distorted frequency-to-place maps (e.g., Fu and Galvin 2003; Faulkner 2006; Smith and Faulkner 2006). For example, Smith and Faulkner (2006) used vocoder simulations for NH subjects to examine the effects of training as it relates to speech understanding with dead regions. They found that speech identification improved considerably in the redistributed conditions after several hours of training. Performance in the dropped conditions also improved following training, but with smaller effects than the redistributed condition.

None of these previous studies, however, evaluated the tradeoffs between spectral and temporal modulation cues when CI users are fitted with the redistributed or dropped maps. The absence of effects of two different frequency remapping schemes (redistributed vs. dropped) on speech perception could indicate that considerable changes to CI sound processor settings can have little effect on measures of speech perception. Drennan et al. (2010) explored this question by evaluating two different sound processing strategies (HiResolution^™ vs. Fidelity120^™) using speech and psychoacoustic measures. When ten CI subjects were tested on consonant-nucleus vowel-consonant (CNC) word recognition in quiet and spondee word recognition in noise, no difference in speech perception ability was observed between HiResolution^™ and Fidelity120^™. Interestingly, CI subjects’ spectral-ripple discrimination was better with Fidelity120^™, but their spectro-temporal modulation sensitivity measured with Schroeder-phase discrimination was worse with Fidelity120^™ than with HiResolution^™, supporting the view that psychoacoustic measures are more sensitive to changes in CI signal processing than speech perception measures are. Drennan et al. (2010) argued that the null benefit of Fidelity120^™ for speech perception ability may be a result of the tradeoff between the improvement in spectral sensitivity and the degradation in temporal sensitivity.

Therefore, it is plausible to expect that changes in sound processor settings would give rise to changes in spectral or temporal sensitivities, or both. Furthermore, such changes in listeners’ psychoacoustic sensitivities as a result of the sound processor manipulations would interact with different physiologic conditions in the implanted cochlea. The primary goal of the present study was to evaluate the effects of dead regions on spectral and temporal envelope processing and understand how they relate to speech perception in CI users when different sizes and patterns of dead regions are present. It was hypothesized that when CI subjects are fitted with the redistributed and dropped frequency maps, the presence of cochlear dead regions would affect spectral and temporal envelope sensitivities differently for each frequency remapping scheme. To test this hypothesis, multiple patterns of simulated cochlear dead regions were created across the cochlea in CI subjects. As a speech perception measure, CNC word recognition was used. Three different non-speech psychoacoustic experiments were also performed. Spectral-ripple discrimination was evaluated to assess listeners’ sensitivity to spectral envelope cues (Won et al. 2007, 2014; Jones et al. 2013). Temporal modulation detection was used to evaluate listeners’ sensitivity to temporal envelope cues. Schroeder-phase discrimination was used to evaluate listeners’ sensitivity to both spectral and temporal modulations. Two types of frequency remappings were tested for each of these listening tasks: redistributed and dropped conditions. Finally, NH subjects were also tested with “current spread vocoder” simulations that model the spread of excitation occurring in the implanted ears in a far more direct way than traditional vocoding approaches.

Materials and Methods Common to All Experiments

Subjects

Five subjects implanted with the HiRes90K^™ device participated in all four experiments. They were 34–71 years old (mean = 56.6 years, three females, two males). One of the five CI subjects was a bilateral CI user (C5) and she was tested with each CI; thus, data for six implanted ears are reported in this paper. Individual CI subject’s demographic information is listed in Table 1. Five NH subjects also participated in all four experiments, ranged in age 24 to 38 years. All NH subjects had audiometric thresholds of 20 dB HL or less at octave frequencies between 250 and 8000 Hz in both ears. All subjects were native speakers of American English. The use of human subjects in this study was reviewed and approved by the University of Washington Institutional Review Board.

Table 1.

Cochlear implant (CI) subject demographics

Subject ID	Age (years)	Durationa of hearing loss (years)	Duration of CI use (years)	Etiology	Implant type	Default channel stimulation rate (pps)
C1	71	25	6	Unknown	HiRes90K	5156b
C2	81	35	5	Unknown	HiRes90K	1657c
C3	34	0	6	Atypical Meniere’s	HiRes90K	5156d
C4	49	0	30	Genetic	HiRes90K	5156
C5 (L)	48	7	8	Hereditary	HiRes90K	5156d
C5 (R)	48	7	17	Hereditary	HiRes90K	5156d

^aDuration of severe to profound hearing loss is based on subjects’ self-report of the number of years they were unable to understand people on the telephone prior to implantation

^bFor the dropped map with the dead region size of 14 electrodes, a channel stimulation rate of 2900 pulses per second (pps) was used

^cFor the dropped map with the dead region size of 14 electrodes, a channel stimulation rate of 4972 pps was used. For the map with full 16 channels (i.e., no-dead region), a channel stimulation rate of 4094 pps was used

^dFor the dropped map with the dead region size of 14 electrodes, a channel stimulation rate of 2900 pps was used

All testing sessions were conducted in a double-walled sound-attenuating (IAC) booth. For CI subjects, the stimuli were presented in free field at 65 dBA through a loudspeaker (B&W DM303) positioned at 0 ° azimuth and 0 ° elevation. CI subjects sat at 1 m from the loudspeaker and were asked to face it during the course of the experiment. For NH subjects, the stimuli were presented monaurally to the right ear through an ER-3 insert earphone at 65 dBA. Both the loudspeaker and insert earphone exceeded ANSI standards for speech audiometry, varying ±2 dB from 100 to 20,000 Hz. The phase responses of the speaker and earphone were smooth across frequencies, varying ±30 ° from 150 to 20,000 Hz and ±45 ° below 150 Hz. Stimuli were presented with a sampling frequency of 44,100 Hz using custom MATLAB programs. Before actual testing with a specific vocoder processing, NH subjects received training sessions (for about 10 min) where they were presented with spondee words that were processed with the vocoder that was used for the actual testing. Four experiments were administered for each individual subject. The order of four different experiments and testing conditions (i.e., different maps for the sound processors or vocoders) was random within and across subjects.

Signal Processing: CI Subjects

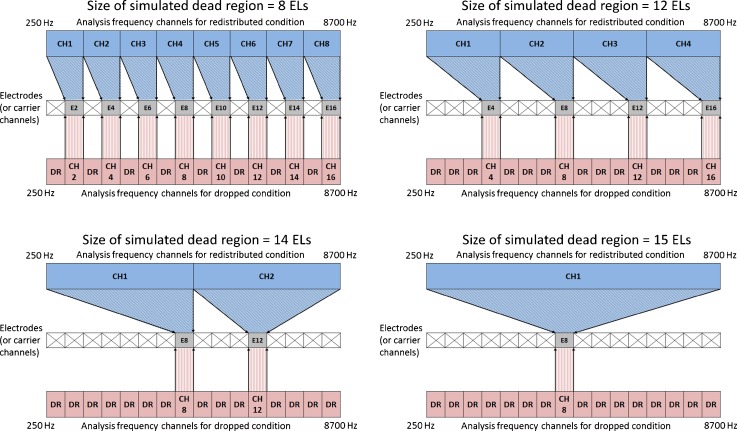
All CI subjects were mapped and tested with a HiResolution^™ strategy. All CI subjects were tested with a laboratory Platinum Speech Processor. All experiments were performed acutely. The HiResolution^™ strategy divides incoming sound into 16 contiguous frequency bands and assigns the output of each frequency analysis band to one stimulating electrode. Cochlear dead regions were simulated by eliminating stimulation to 15, 14, 12, 8, and 0 (i.e., “no-dead region”) electrodes along the array. These conditions correspond to the use of 1, 2, 4, 8, and all 16 active stimulating electrodes, respectively. Note that the current study created multiple relatively narrow simulated dead regions, similar to the approach of Kasturi et al. (2002) but different to the approach of Başkent and Shannon (2003, 2004, 2005) and Smith and Faulkner (2006) where the effects of a single relatively large dead region was tested. When varying the size of simulated dead regions by disabling or enabling stimulating electrodes in the current study, two types of frequency remappings were tested: (1) redistributed maps and (2) dropped maps. Figure 1 shows an example of simulated dead regions with a size of 8, 12, 14, and 15 electrodes and with two different frequency remappings applied. In this paper, “dead region size” refers to the summed size of simulated dead regions along the length of the cochlea. For the redistributed condition, the spectral information that would normally have been presented to the regions of simulated dead regions was evenly redistributed across the remaining electrodes that were not located in the dead regions. This was achieved by changing the frequency range associated with each electrode accordingly as the number of stimulating electrodes varied, while the total bandwidth of 250–8700 Hz for the CI sound processor remained the same. Thus, the bandwidths of the analysis filters associated with stimulating electrodes became wider as the size of simulated dead regions increased from 0 to 15 electrodes. This means that the spectral resolution of hearing determined by the bandwidth of the analysis filters in the sound processor decreased as the size of simulated dead regions increased from 0 to 15 electrodes. Note that the redistributed remapping schemes in the current study are similar to the sound processor manipulations that were often used to examine the effects of number of electrodes on speech understanding in previous studies (e.g., Fishman et al. 1997; Friesen et al. 2001).

Fig. 1.

Two different frequency remapping conditions with simulated dead regions. In the redistributed condition shown in blue, incoming sound was analyzed through 8, 4, 2, or 1 channels of bandpass filters spanning between 250 and 8700 Hz, depending on the testing conditions. Thus, for the redistributed conditions, the number of analysis channels decreased as the size of dead regions increased. Spectral information for each channel was then assigned to stimulating electrodes. In the dropped condition shown in red, incoming sound was always analyzed through 16 channels of bandpass filters. Spectral information for each channel was assigned to each electrode. However, spectral information for the electrodes corresponding to the locations of simulated dead regions was dropped (indicated as “DR” in the figure) by setting those electrodes inaudible. The gray squares represent enabled or audible electrodes for the redistributed and dropped conditions, respectively. The symbol “×” represent the locations of simulated dead regions. Note that the same analysis frequency channels and all 16 stimulating electrodes were enabled and audible for the “no-dead region” condition both for the redistributed and dropped conditions. Also note that “dead region size” refers to the aggregated size of dead regions along the length of the cochlea for each experimental condition.

For the dropped conditions, all 16 electrodes were enabled with the default frequency-to-place map of 16-channel HiResolution^™ strategy. The spectral information in the simulated dead regions was simply dropped by setting the threshold and comfortable listening levels to the device minimum, making those electrodes inaudible to CI subjects. By doing this, the spectral resolution provided to the cochlear locations away from the simulated dead regions remained the same because the dropped conditions did not change the bandwidth of the analysis filters. Tables 2 and 3 show the cutoff frequencies for the analysis filters for the redistributed and dropped conditions, respectively. When the size of dead regions was set to 0 (i.e., all 16 electrodes were active), the frequency allocation for the redistributed and dropped condition was the same by definition. Thus, nine different sound processor settings were tested in total.

Table 2.

Cutoff frequencies of the analysis filters for the redistributed frequency remapping condition as a function of the aggregated size of simulated dead regions (DRs) in electrode numbers or vocoder bands

Size of DRs = 15 ELs			Size of DRs = 14 ELs			Size of DRs = 12 ELs			Size of DRs = 8 ELs			Size of DRs = 0 EL
Disb. ELs	Enb. ELs	Cutoff (Hz)	Disb. ELs	Enb. ELs	Cutoff (Hz)	Disb. ELs	Enb. ELs	Cutoff (Hz)	Disb. ELs	Enb. ELs	Cutoff (Hz)	Disb. ELs	Enb. ELs	Cutoff (Hz)
														250
1			1			1			1			None	1
											250			416
2			2			2				2			2
											494			494
3			3			3			3				3
								250			494			587
4			4				4			4			4
								697			697			697
5			5			5			5				5
											697			828
6			6			6				6			6
											983			983
7			7			7			7				7
		250			250			697			983			1168
	8			8			8			8			8
		8700			1387			1387			1387			1387
9			9			9			9				9
											1387			1648
10			10			10				10			10
											1958			1958
11			11			11			11				11
					1387			1387			1958			2326
12				12			12			12			12
					8700			2762			2762			2762
13			13			13			13				13
											2762			3281
14			14			14				14			14
											3898			3898
15			15			15			15				15
								2762			3898			4630
16			16				16			16			16
								8700			8700			8700

For each condition of dead region size, electrodes that are disabled (Disb.) or enabled (Enb.) are indicated in the first and second columns, respectively. Cutoff frequencies for enabled electrodes are shown in the third column for each condition of dead region size. The same analysis filter cutoff frequencies were used for the “redistributed” vocoder signal processing.

Table 3.

Cutoff frequencies of the analysis filters for the dropped frequency remapping condition as a function of the aggregated size of simulated dead regions (DRs) in electrode numbers or vocoder bands

Size of DRs = 15 ELs			Size of DRs = 14 ELs			Size of DRs = 12 ELs			Size of DRs = 8 ELs			Size of DRs = 0 EL
Inadb. ELs	Adb. ELs	Cutoff (Hz)	Inadb. ELs	Adb. ELs	Cutoff (Hz)	Inadb. ELs	Adb. ELs	Cutoff (Hz)	Inadb. ELs	Adb. ELs	Cutoff (Hz)	Inadb. ELs	Adb. ELs	Cutoff (Hz)
														250
1			1			1			1			None	1
											416			416
2			2			2				2			2
											494			494
3			3			3			3				3
								587			587			587
4			4				4			4			4
								697			697			697
5			5			5			5				5
											828			828
6			6			6				6			6
											983			983
7			7			7			7				7
		1168			1168			1168			1168			1168
	8			8			8			8			8
		1387			1387			1387			1387			1387
9			9			9			9				9
											1648			1648
10			10			10				10			10
											1958			1958
11			11			11			11				11
					2326			2326			2326			2326
12				12			12			12			12
					2762			2762			2762			2762
13			13			13			13				13
											3281			3281
14			14			14				14			14
											3898			3898
15			15			15			15				15
								4630			4630			4630
16			16				16			16			16
								8700			8700			8700

All electrodes were enabled, but dead regions were simulated by setting certain electrodes inaudible. See text for details. For each condition of dead region size, electrodes that are audible (Adb.) or inaudible (Inadb.) are indicated in the first and second columns, respectively. Cutoff frequencies for audible electrodes are shown in the third column for each condition of dead region size. The same analysis filter cutoff frequencies were used for the “dropped” vocoder signal processing.

Overall, the stimulation rate per electrode was maintained the same when changing the sound processor settings. In Table 1, the default channel stimulation rates for each individual CI subjects are shown. However, the stimulation rate had to be adjusted for some testing conditions (particularly for the testing conditions using low numbers of electrodes) to make the sound comfortably loud. Adjusted channel stimulation rates for each CI subject are listed in the footnotes of Table 1. As indicated by Shannon et al. (2002), it is difficult to evaluate any possible effects of variable stimulation rates for each experimental condition. However, it should be noted that several studies have found minimal effects of stimulation rates on perceptual outcomes across a narrow range of rates as done in the current study (e.g., Fu and Shannon 2000; Nie et al. 2006; Weber et al. 2007; Shannon et al. 2011).

Signal Processing: NH Subjects

For NH subjects, “current spread vocoder” processing, which models channel interactions caused by the spread of excitation in implanted ears, was used (Bingabr et al. 2008). Unlike typical vocoder simulations, in which the number of channels has been used as a proxy for spread of excitation, in the “current spread vocoder” approach, the shapes of the synthesis filters are based on a model of the spread of excitation. The vocoder simulations also had two types of frequency remapping conditions: “redistributed” and “dropped” maps. In order to vocode the stimuli, the original stimuli were passed through a bank of 16 “analysis” bandpass filters (sixth order Butterworth) with cutoff frequencies matched to those in the 16-channel HiResolution^™ strategy. The envelopes were extracted from each channel using half-wave rectification and low-pass filtering at 400 Hz (second order Butterworth). These sub-channel envelopes were then used to modulate white noise carriers. The modulated signals were filtered again using 16 “synthesis” bandpass filters to reflect the spread of excitation with a CI. Specifically, each synthesis filter had a narrow peak, and the filter skirts were specified so as to model a broad spread of excitation from a single site of stimulation on the cochlea. The synthesis filters were designed based on the same center frequencies as the analysis filters using the fir2 function in MATLAB (i.e., 4096-order, finite impulse response filters). We simulated a current decay rate of 1 dB/mm, which is comparable to the slopes of the forward-masked psychophysical spatial tuning curves for monopolar stimulation (Nelson et al. 2008) and to the highest level of channel interactions reported for users of the HiRes90K^™ implant devices (Jones et al. 2013). The synthesis filters in the “redistributed” conditions were the same as in the “dropped” conditions, thus the difference between the two frequency remapping conditions was in the analysis filters only. For the redistributed conditions, the number of analysis and synthesis filters and the frequency range associated with each vocoder channel changed as a function of the size of simulated dead regions in the same way as the CI signal processing (see Table 2). For the dropped conditions, the default 16-channel frequency allocation was used and the output modulated signals in simulated dead regions were simply omitted from the processed signal (see Table 3). Based on the Greenwood frequency-to-place function (Greenwood 1990), the sizes of dead regions were 10.4, 14.7, 20.2, and 21.4 mm when 4, 12, 14, and 15 vocoder bands were used to simulate the dead regions. As with the CI signal processing, nine different vocoder processor settings were tested for each listening task.

Data Analysis

For all four listening tasks, we report results for individual subjects as well as mean data averaged across subjects. In each data plot, performance in each listening task is shown as a function of the aggregated size of simulated dead regions (measured in the number of electrodes for CI subjects; measured in the number of vocoder bands for NH subjects). Results for two different frequency remappings, redistributed and dropped maps, are represented by black circles and red triangles, respectively. For each listening task, three different data analyses were planned. We conducted a mixed between-within subjects repeated measures analysis of variance (ANOVA) to compare performance with subject group (CI or NH) as the between-subject factor and the frequency remapping conditions (redistributed vs. dropped) and the size of simulated dead regions as the within-subject factors. Following the mixed ANOVA analysis, a post hoc paired samples t test was performed to systematically compare performance for the redistributed and dropped conditions in pairs for each size of the simulated dead region. These multiple comparisons for the main factor of frequency remapping can identify the specific size of dead region where performance for the redistributed and dropped conditions differed significantly. In Figures 2, 3, 4, 5, 7, 8, 10, and 11, testing conditions for which there was statistically significant difference in performance between the redistributed and dropped conditions are indicated by asterisks above or below the data points. Three asterisks show a significance level of p <0.001, two asterisks show a significance level of p <0.01, and one asterisk shows a significance level of p <0.05. Lastly, post hoc Scheffe tests were performed to evaluate the differences in performance between different sizes of dead regions. These analyses were done separately for each frequency mapping and for each subject group.

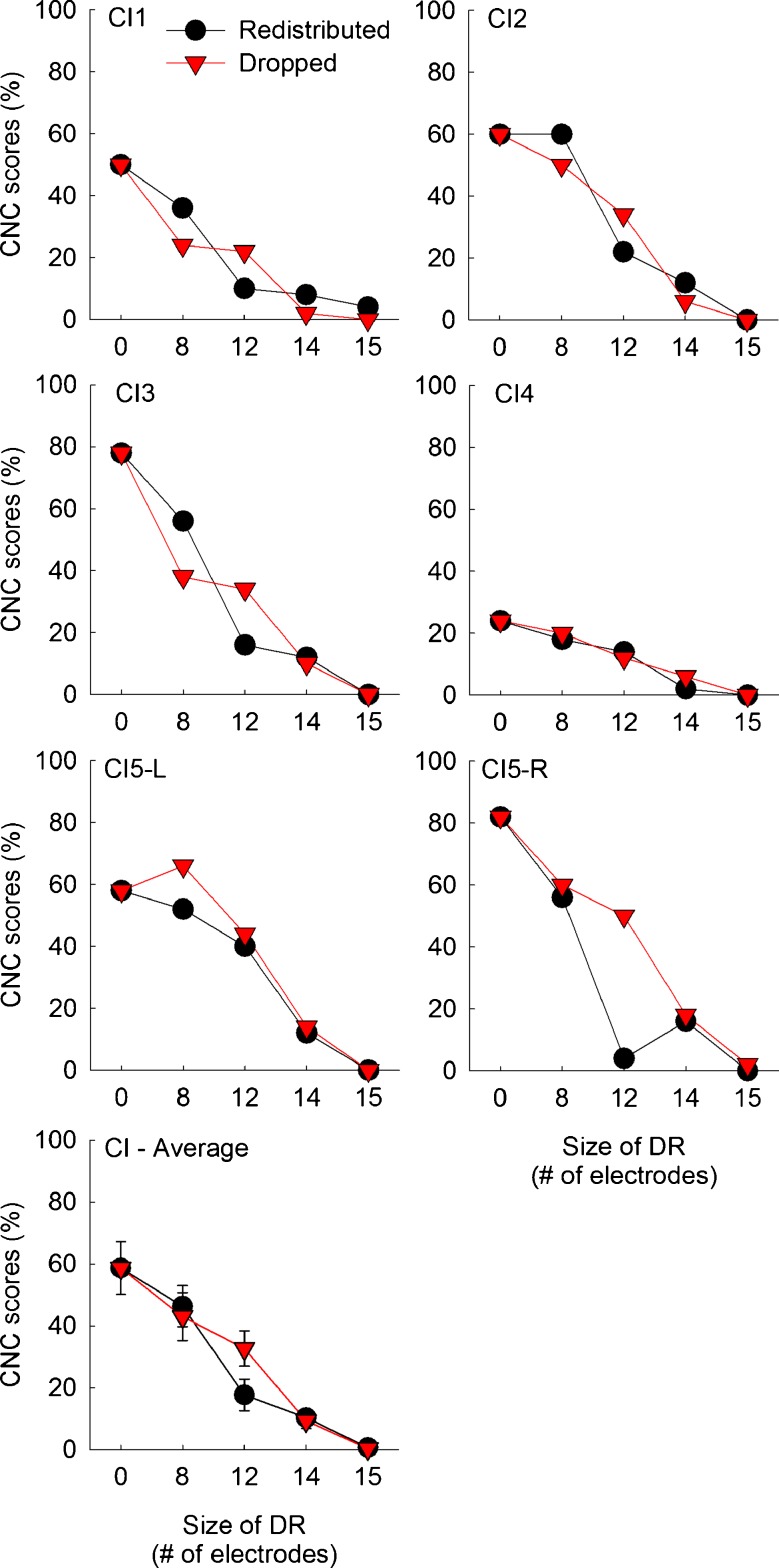
Fig. 2.

Consonant-nucleus-consonant (CNC) word recognition scores for six implanted ears. CI5 was a bilateral CI user and tested with her left and right ear separately. In the bottom panel, mean scores averaged across six implanted ears are shown. Error bars show one standard error. Higher scores indicate better CNC word recognition performance. The black circles represent scores with the redistributed frequency remapping. The red triangles represent scores with the dropped frequency remapping.

Fig. 3.

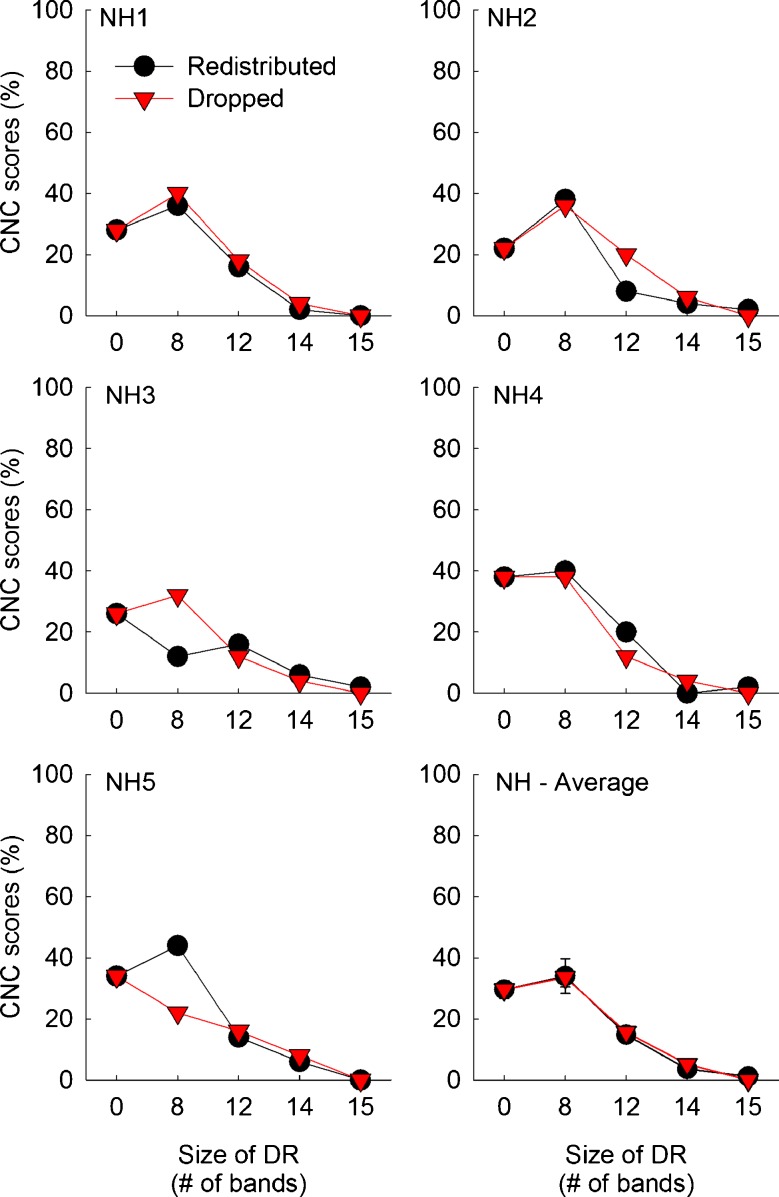
Same as Fig. 2, but for CNC word recognition performance in five normal-hearing subjects.

Fig. 4.

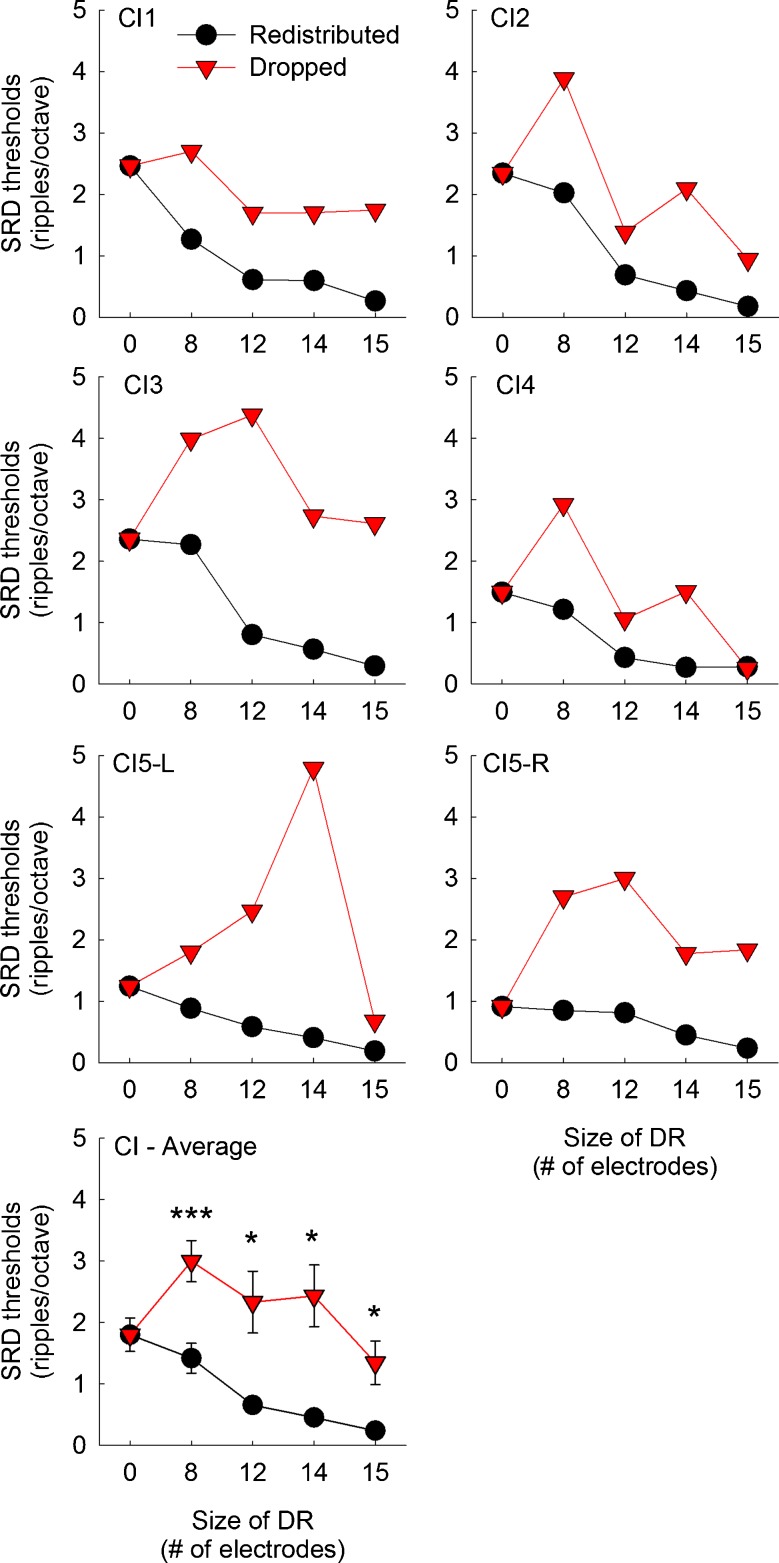
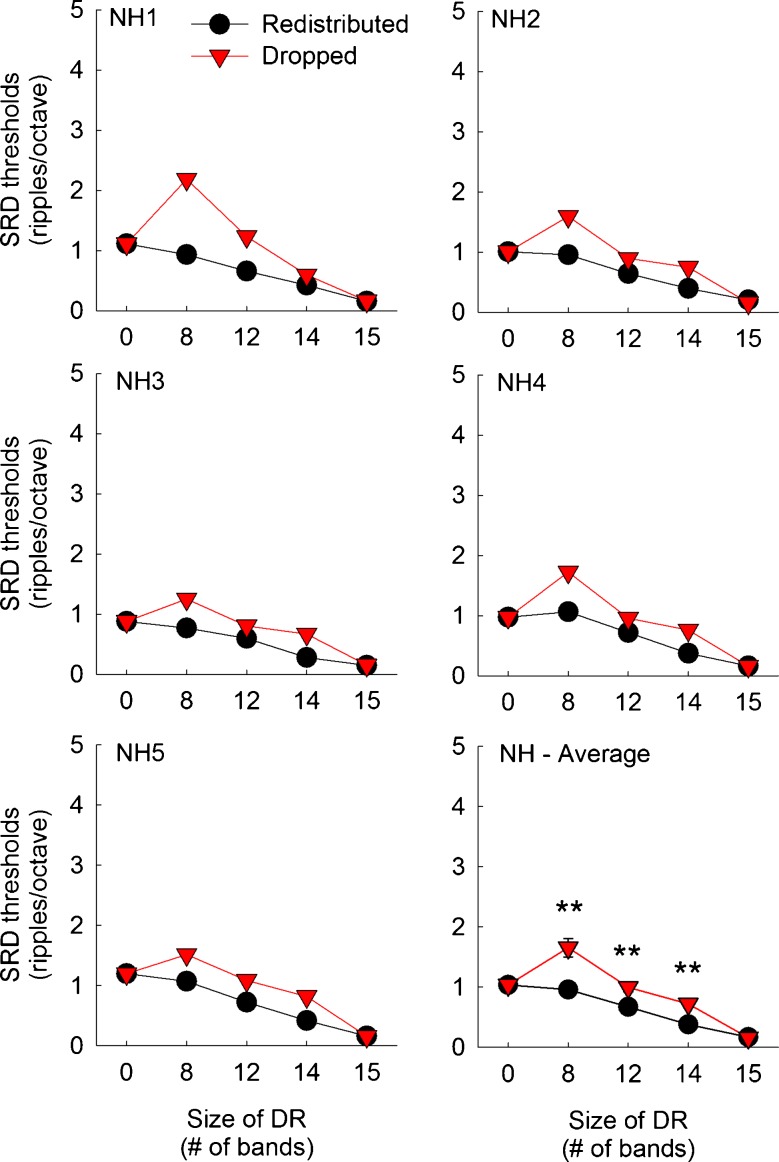
Spectral-ripple discrimination (SRD) thresholds as a function of the frequency remapping and the aggregated size of dead regions for individual CI subjects. CI5 was a bilateral CI user and tested with her left and right ear separately. In the bottom panel, mean scores averaged across six implanted ears are shown. Error bars show one standard error. The black circles represent scores with the redistributed frequency remapping. The red triangles represent scores with the dropped frequency remapping. Higher SRD thresholds indicate better discrimination performance. The asterisks above or below the data points show the dead region size where a significant difference in spectral-ripple discrimination thresholds was observed between the redistributed and dropped conditions, determined by post hoc multiple paired samples t tests. Three asterisks show a significance level of p <0.001, two asterisks show a significance level of p <0.01, and one asterisk shows a significance level of p <0.05.

Fig. 5.

Same as Fig. 4, but for five normal-hearing subjects.

Fig. 7.

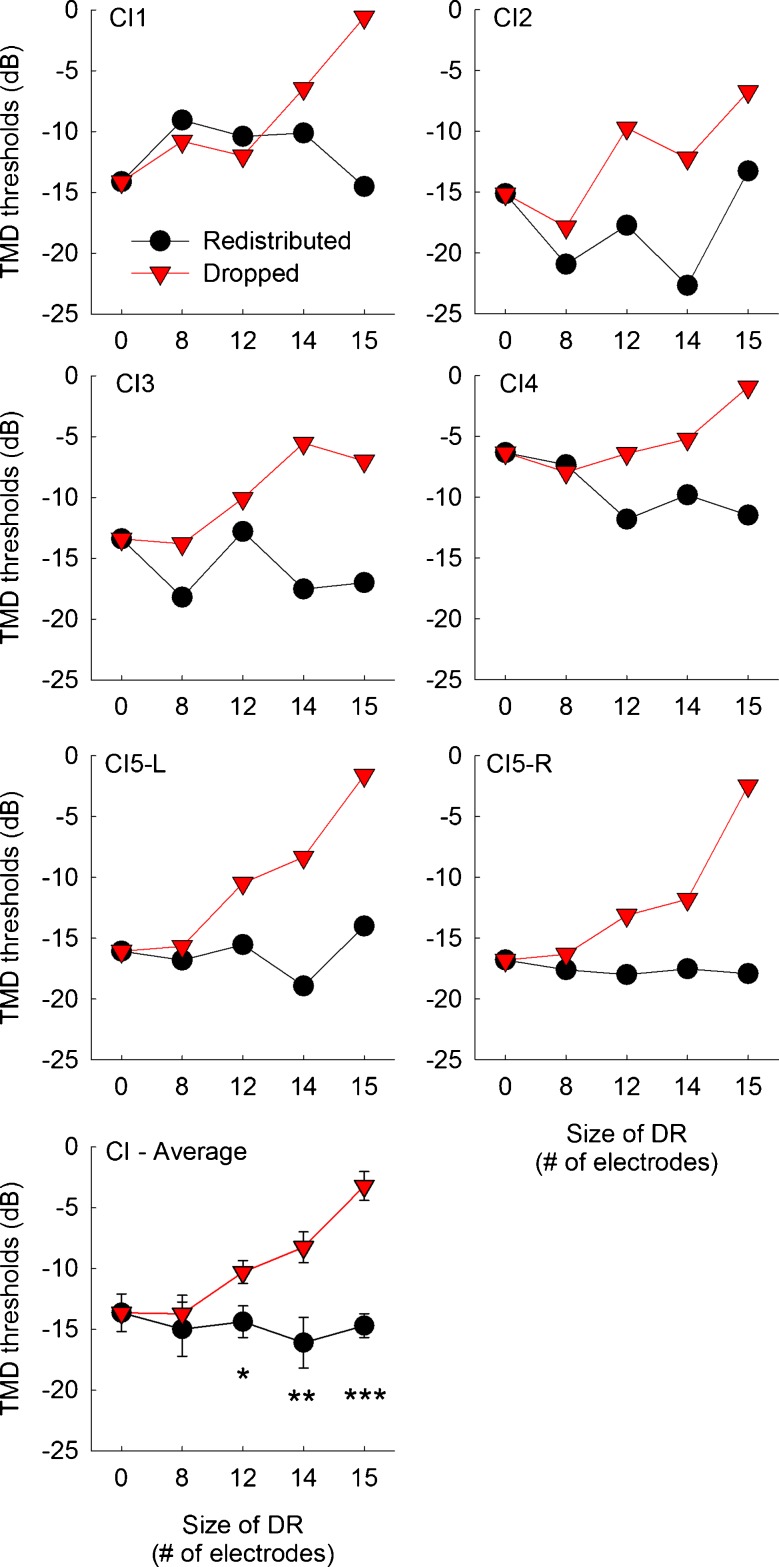
Temporal modulation detection (TMD) thresholds as a function of the frequency remapping and the aggregated size of dead regions for individual CI subjects. CI5 was a bilateral CI user and tested with her left and right ear separately. In the bottom panel, mean detection thresholds averaged across six implanted ears are shown. Error bars show one standard error. The black circles represent scores with the redistributed frequency remapping. The red triangles represent scores with the dropped frequency remapping. More negative thresholds indicate better detection performance. The asterisks above or below the data points show the dead region size where a significant difference in temporal modulation detection thresholds was observed between the redistributed and dropped conditions, determined by post hoc multiple paired samples t tests. Three asterisks show a significance level of p <0.001, two asterisks show a significance level of p <0.01, and one asterisk shows a significance level of p <0.05.

Fig. 8.

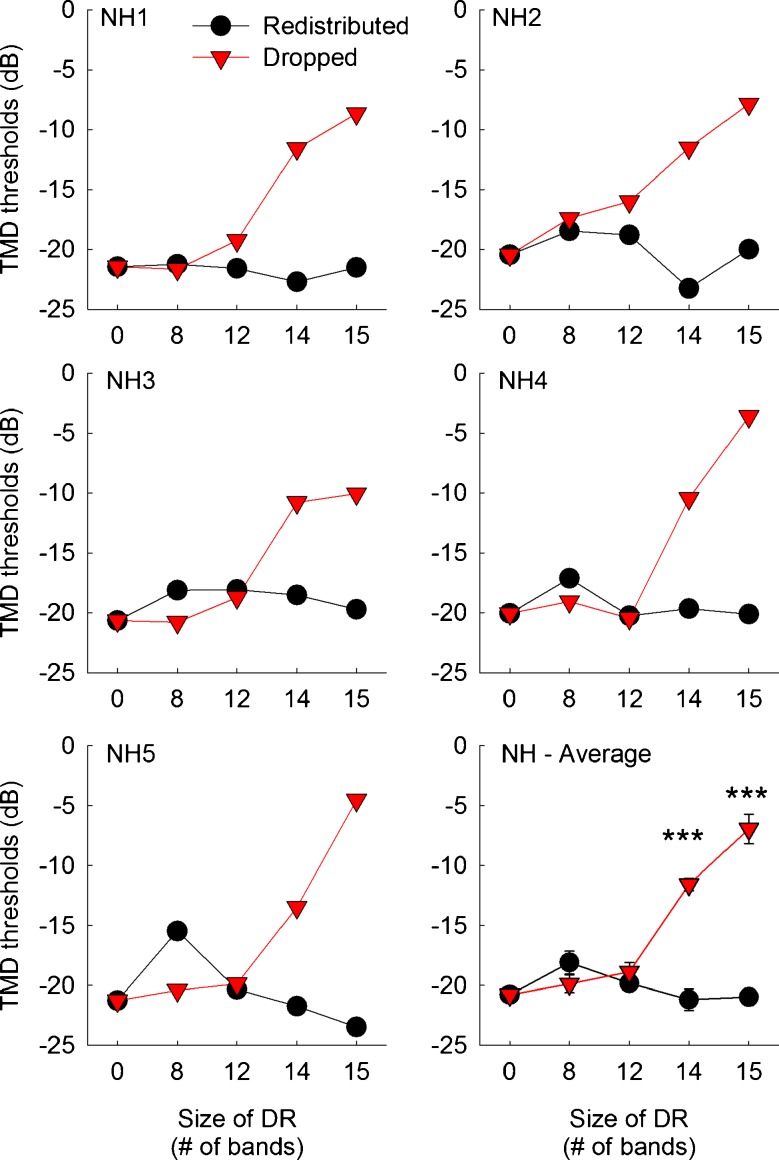
Same as Fig. 7, but for five normal-hearing subjects.

Fig. 10.

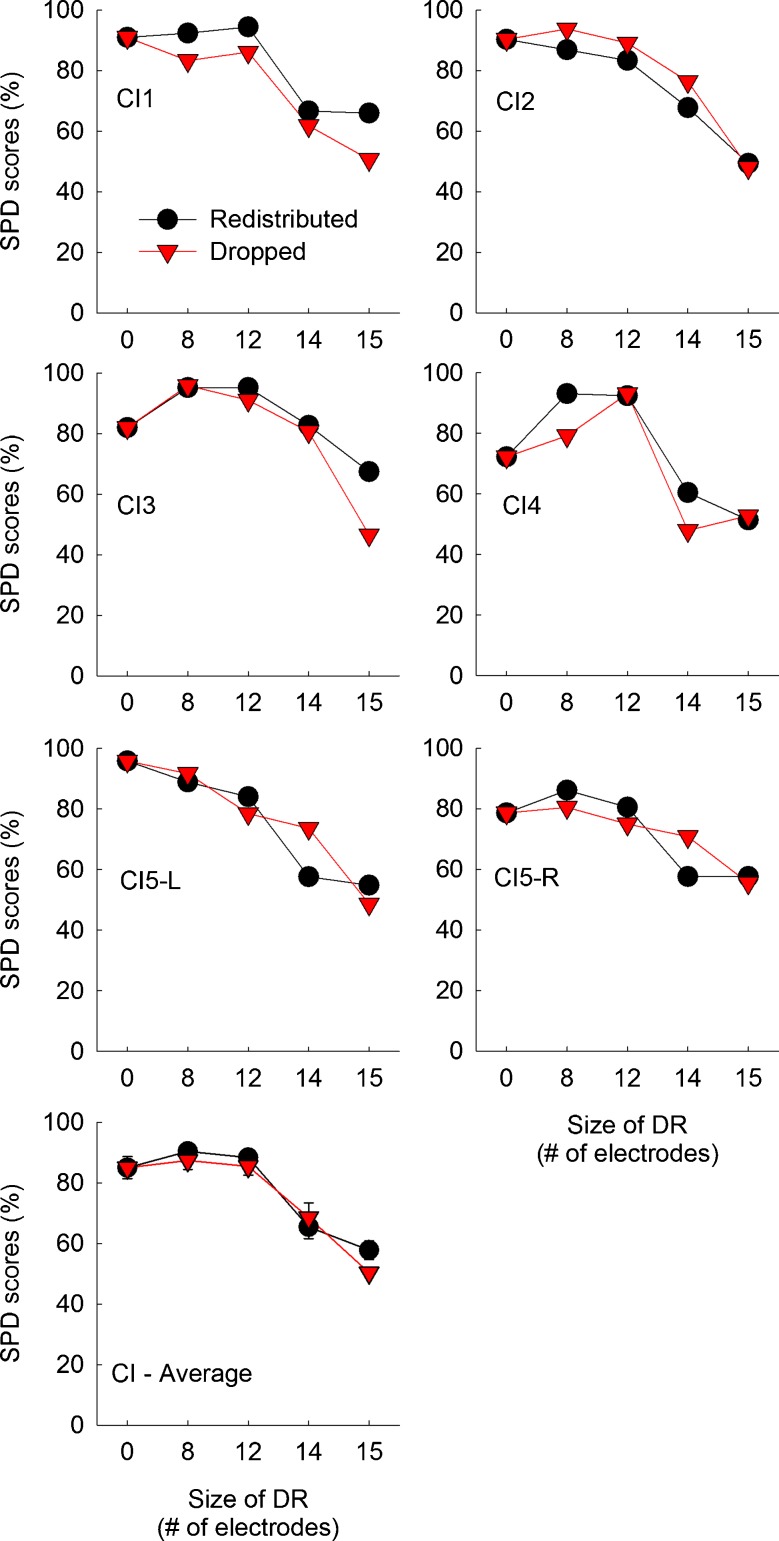
Schroeder-phase discrimination (SPD) scores as a function of the frequency remapping and the aggregated size of dead regions for individual CI subjects. CI5 was a bilateral CI user and tested with her left and right ear separately. In the bottom panel, mean scores averaged across six implanted ears are shown. Error bars show one standard error. The black circles represent scores with the redistributed frequency remapping. The red triangles represent scores with the dropped frequency remapping. Higher scores indicate better performance.

Fig. 11.

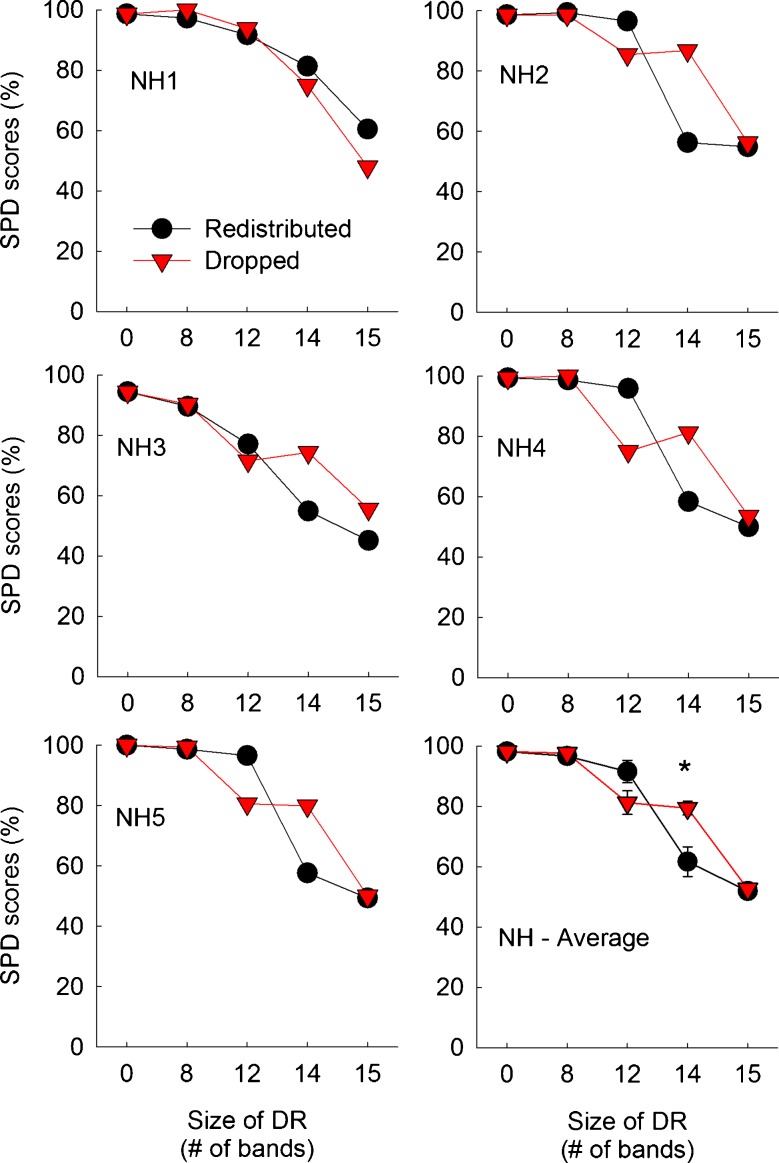
Same as Fig. 10, but for five normal-hearing subjects.

Pulse-Train Output Analysis

Pulse-train outputs of CI processors were analyzed for the three psychoacoustic experiments. Stimuli for the three psychoacoustic experiments present distinct spectro-temporal modulation patterns, offering a unique opportunity to examine the effects of the sound processor settings on the pulse-train outputs that speech signals do not offer. The analysis was done using a custom MATLAB program implementing the HiResolution^™ sound processing strategy that is employed by the actual Advanced Bionics CI sound processor. A generic HiResolution^™ map was used in this electrodogram simulation, where the processing parameters were specified in such a way that the resulting electric signals were representative of the five CI subjects in this study. As with the subject testing, the level of the input stimuli was set to 65 dBA for the pulse-train output analysis. That is, the level of the input signal to the MATLAB code was set to the level that produced the same output in the simulated processor as the acoustic signal produces in the real processor when presented at 65 dBA. Nine different sound processor conditions were created in total: the size of dead regions of 0, 8, 12, 14, and 15 electrodes with the redistributed and dropped frequency remapping, respectively. For the redistributed conditions, certain electrodes were enabled or disabled and the frequency-to-electrode map was changed according to the experimental conditions (see Table 2). For the dropped conditions, the default frequency-to-electrode map for the 16-channel processing was used and inaudible electrodes were simulated by setting the threshold and comfortable listening levels to the device minimum. The pulse-train outputs for each psychoacoustic experiment is presented and discussed in relation to the behavioral data.

Experiment 1: CNC Word Recognition

Testing Procedure

For each experimental condition, a CNC word list with 50 monosyllabic words (Peterson and Lehiste 1962) was randomly chosen out of ten lists for each subject. No CNC list was repeated for any experimental conditions. The selection of CNC word list was random across subjects and experimental conditions. The subjects were instructed to repeat or type the word that they heard in a quiet listening condition. A total percent correct score was calculated after 50 presentations as the percent of words correctly recognized.

Results

Figures 2 and 3 show CNC word identification scores for CI and NH subjects, respectively. In each figure, CNC word scores for individual subjects are shown along with mean scores averaged across subjects. Overall, CNC word identification scores decreased as the size of simulated dead regions increased. When there was no dead region, CI subjects showed an average CNC word recognition score of 58.7 % with a range between 24 and 82 %. Using a larger sample size, Won et al. (2010) reported an average CNC word recognition score of 69.5 % for 42 CI subjects with a range between 18 and 100 %.

More importantly, very similar results were shown for the redistributed and dropped conditions. A mixed between-within subjects ANOVA showed that the main effect of frequency remapping conditions [F(1,9) = 0.93, p = 0.36] did not reach significance, indicating that subjects performed similarly for the two remapping conditions. Almost identical functions were shown for NH subjects (see the average data in the lower right corner in Fig. 3). However, the effect of dead region size was significant [F(4,36) = 29.62, p < 0.001], suggesting that CNC word recognition decreased as the simulated dead region size increased. The interaction between the effects of frequency remapping conditions and dead region size did not reach significance [F(4,36) = 3.18, p = 0.079]. A two-way interaction between the subject group and the frequency remapping did not reach significance [F(1,9) = 0.93, p = 0.36], but the interaction between the subject group and the dead region size reached significance [F(4,36) = 28.93, p < 0.001].

The multiple comparison using a post hoc paired samples t test was performed to compare CNC word scores for the redistributed and dropped conditions. This analysis revealed that CNC word recognition scores did not differ between the redistributed and dropped conditions across all sizes of the dead regions for both CI and NH subjects.

To evaluate the pattern of the change in CNC word scores as a function of the size of the simulated dead region, a separate post hoc Scheffe test was done for each frequency mapping condition and for each subject group. In Table 4, the results for these analyses are summarized. There were no significant differences in CNC word scores between the dead region size of 0 and 8 electrodes (or bands). When the dead region size of 0 and 12 electrodes was compared, CI subjects with the redistributed condition showed a significant difference, but when CI subjects were fitted with the dropped maps, there was no difference. This means that, from the perspective of the number of channels, CNC word recognition scores reached its asymptotic levels with around 4 to 8 active stimulating electrodes. This finding is consistent with earlier reports (e.g., Fishman et al. 1997; Friesen et al. 2001; Xu et al. 2005) where the effects of number of electrodes and the corresponding degree of channel interactions on speech perception were evaluated. These previous studies manipulated the sound processors in a similar way to the redistributed frequency remappings in the current study and showed that speech perception ability by CI users was generally saturated with 4 to 8 active stimulating electrodes, with no further gains as more electrodes were made available for them. In Figure 2, the differences in CNC scores between the dead region sizes of 8 electrodes and beyond (12, 14, and 15 electrodes) were generally significant. However, the differences in CNC scores between the dead region sizes of 12 electrodes and beyond (14 and 15 electrodes) were not significant except for the comparison between the dead region sizes of 12 and 15 electrodes with the dropped condition in CI subjects.

Table 4.

Post hoc Scheffe test results for CNC word recognition

Comparison	CI with RDS	CI with DRP	NH with RDS	NH with DRP
0 vs. 8	–	–	–	–
0 vs. 12	0.001	–	0.043	0.003
0 vs. 14	<0.001	<0.001	<0.001	<0.001
0 vs. 15	<0.001	<0.001	<0.001	<0.001
8 vs. 12	–	–	0.006	<0.001
8 vs. 14	0.003	0.01	<0.001	<0.001
8 vs. 15	<0.001	0.001	<0.001	<0.001
12 vs. 14	–	–	–	0.037
12 vs. 15	–	0.015	–	0.001
14 vs. 15	–	–	–	–

Each column represents the results for cochlear implant (CI) or normal-hearing (NH) subjects tested with the redistributed (RDS) or dropped (DRP) frequency remapping conditions. The numbers in the first column indicate the dead region sizes (in electrodes or bands) that are used for multiple comparisons. In each cell, p values for the Scheffe tests are shown. P values greater than 0.05 are not shown in the table. Bold italic values have p <0.001

Discussion

For the redistributed conditions, spectral resolution for CI subjects was largely determined by the number of analysis filters in the sound processor. For example, for the no-dead region condition, 16 channels of analysis filters were used, but for a simulated dead region size of 15 electrodes, the entire acoustic spectrum has to be processed through a single bandpass filter. This means that, for the redistributed conditions, spectral resolution changed primarily as a function of the dead region size. For the dropped conditions, however, the default 16-channel processing was used for all testing conditions. Therefore, the primary effect would be the loss of acoustic information as the size of the simulated dead region increased from 0 to 15 electrodes without reducing narrowband spectral resolution at the still active electrode.

As dead region size increased, CNC word recognition scores decreased for both the redistributed and dropped conditions. The same pattern was observed for CI and NH subjects. The dropped conditions in the present study were similar to the dropped maps presented in Shannon et al. (2002), Kasturi et al. (2002), and Başkent and Shannon (2006) except that the simulated dead regions were evenly spaced along the length of the cochlea in the present study, whereas those three studies simulated the dead regions in the basal, middle, and apical regions of the cochlea. In the present study, a gradual decrease in CNC word recognition was found for the dropped conditions. Using consonant and vowel identification, Kasturi et al. (2002) and Başkent and Shannon (2006) showed a strong effect of the dead region size on vowel identification (particularly when dead regions were simulated in the apical regions of the cochlea) as a consequence of the loss of spectral modulation cues (which provides information about formants). In contrast, there was a relatively small effect of dead regions on consonant identification, particularly when dead regions were located in the basal or middle regions of the cochlea. It is plausible that consonant identification could be driven with temporal modulation information over a few stimulating electrodes.

In terms of the effect size, the multiple comparison using a post hoc paired samples t test showed that CNC word recognition scores were statistically the same at any pairs corresponding to each size of simulated dead region. This suggests that the effects of the degradation in spectral resolution (in the case of redistributed conditions) and the loss of acoustic speech information (in the case of dropped conditions) may be similar on CNC word recognition. However, speech signals such as CNC words present complex patterns of spectral and temporal modulations. Therefore, it is not possible to disentangle the effects of the degradation in spectral resolution and the loss of acoustic cues on spectral and temporal speech cues, as discussed in the “Introduction” section.

There are at least two more potential factors that could have affected results in the present study, that is, spectral shifts in the frequency-to-place map and channel interactions. First, consider the spectral shifts in the frequency-to-place map using an example of the HiResolution^™ processing strategy in this study. The entire acoustic frequency range of 250–8700 Hz employed in the sound processor is typically mapped onto electrodes that are located in more basal locations than the cochlear locations that would normally process 250–8700 Hz. Physiologically, the frequency range of 250–8700 Hz corresponds to the length of 22.5 mm in the cochlea based on the Greenwood function (Greenwood 1990), but the active length of the HiRes90K implant electrode array is shorter than this (e.g., 17 mm for HiRes90K^™ HiFocus^™ electrode array, reported by the Technical Specifications for HiRes90K^™ implants, Advanced Bionics). Therefore, frequency-to-place mapping employed in the sound processors is designed in a way that acoustic frequency information has to be compressed. Such alteration in the frequency-to-place map varies across CI users as the insertion depth of electrode array varies across individual CI users. Nevertheless, we do not expect that the spectral shift in the frequency-to-place map affected performance for the dropped conditions because the frequency allocation to electrodes remained the same across different dead region sizes. When the redistributed conditions were tested, different frequency allocation was used for each dead region size. Thus, it is possible that the spectral shift in the frequency-to-place map could have affected results for the redistributed conditions, as the testing was done acutely. Hence, it is difficult to evaluate the extent to which the change in performance for the redistributed conditions was attributed to the spectral shift (if any) or to the effects of the size of simulated dead region.

When changing the size of simulated dead regions, one more uncontrolled factor potentially occurs: that is channel interactions. As the size of dead region increased for the redistributed conditions, fewer numbers of stimulating electrodes were used; therefore, the possible negative effects of channel interactions may have been reduced. A similar phenomenon might have occurred for the dropped conditions, where all 16 electrodes were enabled. When certain electrodes were “dropped”, i.e., their output levels were set to the device minimum, those electrodes were still functioning but the net effect of channel interactions due to the minimum current values might be far less than the amount of channel interactions from audible electrodes. Nevertheless, the direction of the effect of channel interactions for the dropped conditions is consistent with the redistributed conditions. As the aggregated size of simulated dead regions increased, the amount of channel interactions decreased, although it is not straightforward to estimate how much channel interactions affected CNC word recognition as a function of experimental conditions.

Experiment 2: Spectral-Ripple Discrimination

Testing Procedure

Spectral-ripple discrimination thresholds were collected using established techniques (Won et al. 2007). Briefly, three rippled noise tokens with a 30-dB peak-to-trough ratio, two with standard ripple phase and one with inverted ripple phase, were selected for each trial. For standard ripples, the phase of the full-wave rectified sinusoidal spectral envelope was set to zero radians, and for inverted ripples, it was set to π/2. A bandwidth of the rippled spectrum was 100 to 5000 Hz. The order of presentation of the three tokens was random, and the subject’s task was to select the “oddball.” A level attenuation of 1–8 dB (in 1-dB increments) was randomly selected for each interval in the three-interval task. Ripple density was varied within the range 0.125–11.314 ripples per octave in equal-ratio steps of 1.414 in an adaptive 2-up and 1-down procedure with 13 reversals that converges to the 70.7 % correct point (Levitt 1971). Thus, the ripple density was increased by a factor of 1.414 after two consecutive correct responses and decreased by a factor of 1.414 after a single incorrect response while the ripple depth was always fixed at 30 dB. The threshold for each adaptive run was calculated as the mean of the last eight reversals. The spectral-ripple discrimination threshold for each subject is the mean of three adaptive runs.

Results

Figures 4 and 5 show spectral-ripple discrimination thresholds for CI and NH subjects, respectively. When there was no dead region, CI subjects showed an average threshold of 1.80 ripples/octave, which is similar to an earlier report using the same spectral-ripple test. Using 31 CI subjects, Won et al. (2007) reported an average threshold of 1.73 ripples/octave. When NH subjects were tested with a 16-channel vocoder with no-dead region, they showed worse performance than CI subjects.

Unlike the CNC scores, more heterogeneous patterns of effects of frequency remapping methods and simulated dead region size were observed for spectral-ripple discrimination thresholds, particularly among CI subjects. For the redistributed conditions, spectral-ripple discrimination performance decreased in a linear fashion as simulated dead region size increased. However, a fluctuating pattern was observed for the dropped conditions. Briefly, spectral-ripple discrimination performance in CI subjects increased when the size of simulated dead regions increased from 0 to 8 electrodes, and then spectral-ripple discrimination performance decreased as it increased further from 8 to 15 electrodes, but these differences in performance for the dropped conditions were in fact not significant (see the next paragraph about post hoc Scheffe test results). A mixed ANOVA analysis indicated that the effect of frequency remapping was significant [F(1,9) = 56.53, p < 0.001], and the effect of dead region size was also significant [F(4,36) = 14.41, p < 0.001]. The interaction between these two factors reached significance [F(4,36) = 7.06, p < 0.001], indicating that the pattern of change in spectral-ripple discrimination thresholds was different for the redistributed and dropped conditions as simulated dead region size increased. The two-way interaction between subject group and simulated dead region size did not reach significance [F(4,36) = 0.26, p = 0.91], but the two-way interaction between subject group and frequency remapping reached significance [F(1,9) = 23.76, p = 0.001]. To explore this interaction between subject group and frequency remapping, two separate mixed ANOVA analyses were performed, one for the redistributed and another for dropped conditions, with subject group (CI or NH) as the between-subject factor and simulated dead region size as the within-subject factor. For the redistributed conditions, there was a significant effect of the size of dead regions [F(4,36) = 40.99, p < 0.001] as well as a significant interaction between the subject group and dead region size [F(4,36) = 4.30, p = 0.006]. Estimated margin means indicated that CI subjects performed slightly better than NH subjects across the dead region sizes, but the difference between the two groups did not reach significance [F(1,9) = 5.06, p > 0.05]. For the dropped conditions, there was a significant effect of the main effect of dead region size [F(4,36) = 7.43, p < 0.001], but the interaction between the subject group and dead region size did not reach significance [F(4,36) = 0.68, p = 0.61]. In the dropped conditions, CI subjects performed significantly better than NH subjects across the dead region sizes [F(1,9) = 138.82, p < 0.001]. Thus, CI and NH subjects differed with regard to the dropped conditions, but not with regard to the redistributed conditions.

The multiple comparison using a post hoc paired samples t test indicated that CI subjects showed significantly better spectral-ripple discrimination performance with the dropped conditions than with the redistributed conditions when the size of simulated dead regions was 8, 12, 14, and 15 electrodes (denoted by asterisks in Fig. 4). For NH subjects, significantly better spectral-ripple discrimination performance with the dropped conditions was shown when the size of simulated dead regions was 8, 12, and 14 bands (denoted by asterisks in Fig. 5).

To evaluate the pattern of the change in spectral-ripple discrimination thresholds as a function of the size of dead regions, a post hoc Scheffe test was done separately for each frequency mapping condition and for each subject group (Table 5). For the redistributed conditions, the largest decrease in performance occurred between the dead region size of 0 and 12 electrodes in CI subjects. Beyond a dead region size of 12 electrodes, the change in spectral-ripple discrimination thresholds was not significant anymore. In the context of the effects of the number of active electrodes, the gradual change in spectral-ripple discrimination performance with the redistributed conditions is consistent with previous reports (Henry and Turner 2003; Won et al. 2011b). For instance, Henry and Turner (2003) evaluated the effects of the number of channels on spectral-ripple discrimination in CI subjects and NH subjects listening to 12-channel vocoder simulations. In their study, CI subjects showed performance saturation at 4 to 6 channels, which is also similar to the saturation pattern observed in the CNC word recognition results in the current study (Fig. 2). However, NH subjects in the study by Henry and Turner (2003) showed a consistent increase in spectral-ripple discrimination performance as the number of channels increased from 1 to 16, which is in contrast to the saturation pattern observed in NH subjects in the current study, highlighting the importance of implementing the effects of “current spread” in vocoder simulations.

Table 5.

Same as Table 4, but for spectral-ripple discrimination

Comparison	CI with RDS	CI with DRP	NH with RDS	NH with DRP
0 vs. 8	–	–	–	0.001
0 vs. 12	0.002	–	<0.001	–
0 vs. 14	<0.001	–	<0.001	–
0 vs. 15	<0.001	–	<0.001	<0.001
8 vs. 12	–	–	0.001	<0.001
8 vs. 14	0.01	–	<0.001	<0.001
8 vs. 15	0.001	–	<0.001	<0.001
12 vs. 14	–	–	0.001	–
12 vs. 15	–	–	<0.001	<0.001
14 vs. 15	–	–	0.02	0.003

When CI subjects were fitted with the dropped frequency remapping, it appears that spectral-ripple discrimination performance initially increased as simulated dead region size increased from 0 to 8 electrodes; however, the post hoc multiple paired samples t tests indicated that the differences in spectral-ripple discrimination thresholds between any pairs of different dead region sizes did not reach significance. When NH subjects were tested with the redistributed conditions, there were significant differences for most comparisons. Likewise, when NH subjects were tested with the dropped conditions, there were significant differences for most comparisons in spectral-ripple discrimination thresholds except for the comparisons between 0 vs. 12 bands, 0 vs. 14 bands, and 12 vs. 14 bands.

Discussion

When CI subjects were fitted with the redistributed remapping, spectral-ripple discrimination performance decreased as the size of simulated dead regions increased. For the dropped conditions, there was a trend that spectral-ripple discrimination performance initially increased between simulated dead region sizes of 0 and 8 electrodes, and performance decreased beyond the dead region size of 8 electrodes; however, changes in spectral-ripple discrimination for the dropped conditions were not significant (Table 5). Thus, when CI subjects were fitted with the dropped frequency remapping, it appears that they do not show any difference in performance regardless of the size of dead region.

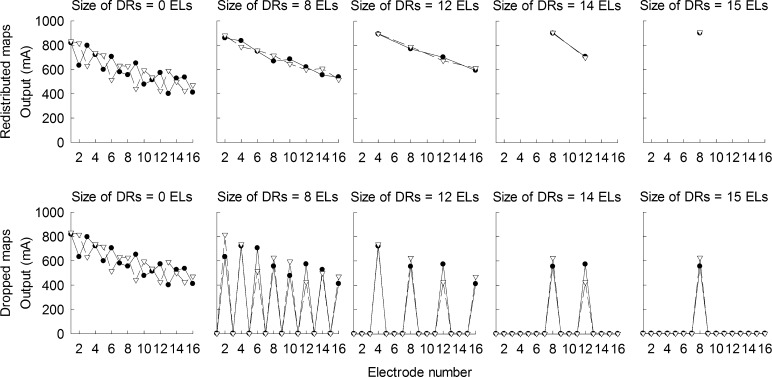
To better understand the spectral-ripple discrimination data observed for CI subjects, electrode outputs for spectral-ripple stimuli are analyzed. Figure 6 shows average pulse outputs over the duration of spectral-ripple stimuli (i.e., 0.5 s) for each electrode. Stimuli with a ripple density of 1.414 ripples/octave and a ripple depth of 30 dB were used for this analysis. This ripple density was chosen because it was similar to the average spectral-ripple discrimination thresholds for the no-dead region condition in the current study as well as to the average performance reported for 31 CI subjects by an earlier report (Won et al. 2007). The top panels show the electrode outputs for the redistributed conditions, whereas the bottom panels show the electrode outputs for the dropped conditions. From the left to the right columns, the electrode outputs for the dead region size of 0, 8, 12, 14, and 15 electrodes are shown, respectively. Note that the redistributed and dropped maps are identical for the no-dead region condition by definition. In these maps, multiple peaks and valleys are faithfully present across the electrode outputs, representing the spectral modulation patterns for standard and inverted ripples. As the size of simulated dead regions increased from 8 to 15 electrodes, the number of enabled electrodes decreased the analysis filter bandwidth associated with each electrode increased. As a result, there was very little contrast between the peaks and valleys as simulated dead region size increased from 12 to 15 electrodes for the redistributed conditions. These patterns suggest an explanation for the finding that, for the redistributed conditions, spectral-ripple discrimination performance decreases as the dead region size increases.

Fig. 6.

CI sound processor output for standard (filled circles with solid lines) and inverted (unfilled triangles with dotted lines) spectral-ripple stimuli. Stimuli with a ripple density of 1.414 ripples/octave and a ripple depth of 30 dB are used. Outputs for the redistributed conditions are shown in the top panels. Outputs for the dropped conditions are shown in the bottom panels. Different dead region sizes are shown in each column. Redist. redistributed, DR simulated dead region, ELs electrodes.

However, when the dropped conditions were used, the analysis filters in the sound processor remained the same across different dead region size conditions. Thus, the spectral resolution determined by the bandwidth of the analysis filters in the sound processor did not change as the simulated dead region size increased from 0 to 15 electrodes. Instead, acoustic information about the spectral modulation patterns of spectral-ripple stimuli was simply missing. The greater loss of acoustic information happened as simulated dead region size increased, but because the bandwidth of the analysis filters did not change as dead region size increased, the relative spectral contrast between standard and inverted ripples remained the same for the audible electrodes. When the dropped frequency remapping was used for the dead region size of 15 electrodes, a single electrode presents the electric pulse train with the amplitude corresponding to the output of the analysis filter for standard and inverted ripples. That is, for this extreme condition, spectral envelope was only sampled in a single CI band, creating a level difference cue between standard and inverted ripples. In contrast, when the redistributed frequency remapping was used for the dead region size of 15 electrodes, the output of a single bandpass filter spanning between 250 and 8700 Hz does not present any difference between standard and inverted ripples, resulting in the lowest discrimination performance.

Won et al. (2011c) has previously demonstrated the effects of electrode separation on spectral-ripple discrimination for CI users. In their study, the total number of stimulating electrodes was fixed at 5 covering the normal input bandwidth of the sound processor, whereas separations between stimulating electrodes were varied parametrically between 1 and 3 electrodes. For these three separation conditions, they used the same filter cutoffs and bandwidths to provide the exact same acoustic information across five stimulating electrodes. They demonstrated that larger electrode separation significantly improved spectral-ripple discrimination, suggesting that less channel interaction would provide better spectral-ripple discrimination performance for CI users. This hypothesis was further supported by significant correlations with channel-interaction index (Jones et al. 2013) and electrically evoked compound action potentials (Won et al. 2014).

The current study further advances understanding on spectral-ripple discrimination performance for CI users. Taken together with the electrode output analysis and spectral-ripple discrimination performance for CI subjects, spectral envelope sensitivity changed in a different manner for the redistributed and dropped conditions as a function of the size of simulated cochlear dead regions. When aggregated dead region size is large (such as the simulated dead region sizes of 12, 14, or 15 electrodes in the present study), the dropped conditions would provide an opportunity for CI subjects to use level cues that are converted from spectral modulation. It is possible that if the spectral-ripple discrimination test used a greater magnitude of level rove for each stimulus presentation, the potential level cues converted from spectral modulations would have been reduced. With an 8 dB level rove in the present study, the difference in performance between the redistributed and dropped conditions for a simulated dead region size of 15 electrodes was not significant. Overall, NH subjects showed less difference in spectral-ripple discrimination performance between the redistributed and dropped conditions than CI subjects. Note that these potential level cues at high hole sizes would only affect the CI results, where the overall level of the signal delivered to the auditory system could not be fully controlled by the experimenter. Thus, results in the dropped condition at the largest hole sizes must be interpreted with extra caution with CI subjects, but not with the NH listeners.

Experiment 3: Temporal Modulation Detection

Testing Procedure

The temporal modulation detection test was administered as previously described by Won et al. (2011a). For the modulated stimuli, sinusoidal amplitude modulation was applied to the wideband noise carrier. The stimulus duration for both modulated and unmodulated signals were 1 s. Modulated and unmodulated signals were gated on and off with 10-ms linear ramps, and they were concatenated with no gap between the two signals. The temporal modulation detection threshold was measured using a two-interval, two-alternative adaptive forced-choice paradigm. One of the intervals consisted of modulated noise, and the other interval consisted of steady noise. Subject’s task was to identify the interval which contained the modulated noise. A modulation frequency of 50 Hz was used. A two-down, one-up adaptive procedure was used to measure the modulation depth threshold, starting with a modulation depth of 100 % and decreasing in steps of 4 dB from the first to the fourth reversal, and 2 dB for the next ten reversals. For each testing run, the final ten reversals were averaged to obtain the MDT. MDTs in dB relative to 100 % modulation (i.e., 20log₁₀(m_i)) were obtained, where m_i indicates the modulation index. The threshold for each subject was calculated as the mean of three testing runs.

Results

Figures 7 and 8 show temporal modulation detection performance for CI and NH subjects, respectively. When there was no-dead region simulated, CI subjects showed an average detection threshold of −13.6 dB. This is slightly worse performance than the previous report using 24 CI subjects (Won et al. 2011a), where an average detection threshold of −16 dB was shown at 50 Hz modulation frequency. For the no-dead region condition, NH subjects showed an average detection threshold of −20.8 dB, which is better than CI subjects.

Most importantly, temporal modulation detection showed very different patterns of results compared to CNC word recognition or spectral-ripple discrimination results. When the redistributed mapping was used, temporal modulation detection thresholds did not change as the size of simulated dead region varied in both CI and NH subjects. However, when the dropped mapping was used, temporal modulation detection performance gradually decreased as the size of simulated dead regions increased from 0 to 15 electrodes or bands for both CI and NH subjects. A mixed between-within subjects ANOVA confirmed this pattern. That is, the effects of frequency remapping [F(1,9) = 183.87, p < 0.001], dead region size [F(4,36) = 22.65, p < 0.001], and the interaction between these two factors [F(4,36) = 56.68, p < 0.001] reached significance. The two-way interactions of the subject type with the frequency remapping [F(1,9) = 0.28, p = 0.61] and with simulated dead region size [F(4,36) = 2.02, p = 0.11] did not reach significance, reflecting the fact that temporal modulation detection performance was similar between CI and NH subjects with regard to the frequency remapping or dead region size.

For both CI and NH subjects, the differences in temporal modulation detection thresholds between the redistributed and dropped conditions increased as the size of simulated dead regions increased. To confirm this pattern, multiple paired samples t tests were performed. For a simulated dead region size of 8 electrodes, the two different frequency remapping conditions showed similar temporal modulation detection thresholds in CI subjects. Likewise, for dead region sizes of 8 and 12 bands, temporal modulation detection thresholds did not differ between the two frequency remapping conditions in NH subjects. However, when the size of simulated dead regions increased further, both CI and NH subjects showed significantly worse temporal modulation detection performance (i.e., higher temporal modulation detection thresholds) with the dropped conditions than with the redistributed conditions. These results are mainly attributed to the fact that, as indicated above, temporal modulation detection performance for the redistributed conditions was consistent regardless of the size of dead regions, but temporal modulation detection performance for the dropped conditions dropped markedly as the size of simulated dead regions increased.

For the redistributed conditions, post hoc Scheffe tests showed no significant differences between any pairs of dead region size conditions for both CI and NH subjects (Table 6). When the dropped frequency remapping was used, temporal modulation detection performance began to degrade significantly when the size of simulated dead regions was greater than 14 electrodes (or bands). That is, when the size of simulated dead regions was smaller or equal to 12 electrodes (or bands), temporal modulation detection performance was statistically the same although there was a pattern of decrease in temporal modulation detection performance. Between simulated dead region sizes of 12 and 15 electrodes (or bands), there was a markedly large drop in temporal modulation detection performance both for CI and NH subjects when they were fitted with dropped maps.

Table 6.

Same as Table 4, but for temporal modulation detection

Comparison	CI with RDS	CI with DRP	NH with RDS	NH with DRP
0 vs. 8	–	–	–	–
0 vs. 12	–	–	–	–
0 vs. 14	–	–	–	<0.001
0 vs. 15	–	<0.001	–	<0.001
8 vs. 12	–	–	–	–
8 vs. 14	–	–	–	<0.001
8 vs. 15	–	<0.001	–	<0.001
12 vs. 14	–	–	–	<0.001
12 vs. 15	–	0.018	–	<0.001
14 vs. 15	–	–	–	0.01

Discussion

Compared to spectral-ripple discrimination, the opposite pattern of results was observed for temporal modulation detection. When the redistributed remapping was used, temporal modulation detection performance did not change as the size of simulated dead regions increased from 0 to 15 electrodes. However, when the dropped remapping was used, temporal modulation detection performance decreased as the size of simulated dead regions increased.

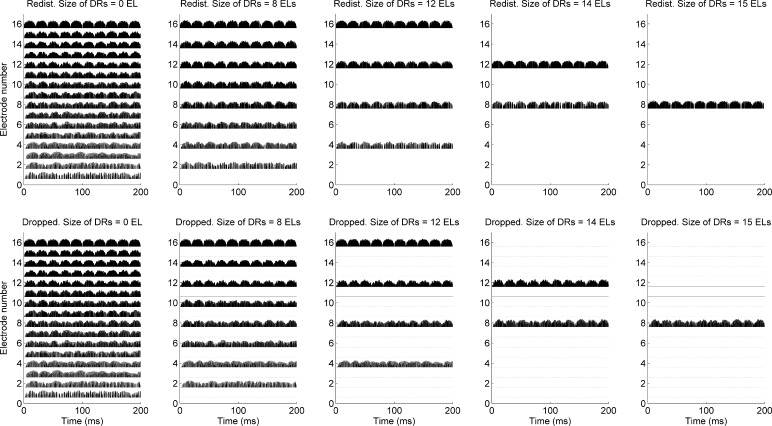
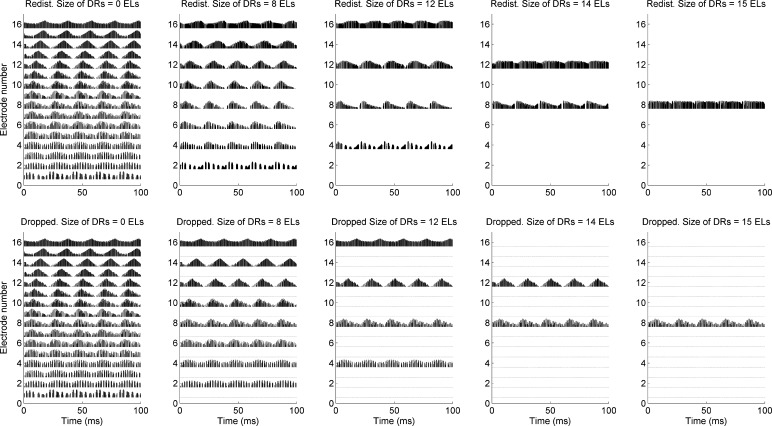
The absence of change in temporal modulation detection for the redistributed conditions is consistent with Won et al. (2011a), where temporal modulation detection thresholds were collected with 1, 2, 4, 8, 12, and 16 active channels. In Won et al. (2011a), when changing the number of channels, the frequency allocation was redistributed to corresponding electrodes. Thus, the present study replicated the findings from Won et al. (2011a) using different CI subjects. When the redistributed conditions were used, a narrower portion of auditory-nerve fibers was excited as the size of simulated dead regions increased. However, the filter bandwidth increased substantially as the size of simulated dead regions increased. Therefore, even for the dead region size of 15 electrodes, a salient modulation cue from a single electrode can provide a salient modulation cue to a narrower region of auditory-nerve fiber, hence enabling CI subjects to detect temporal modulation. The top panel of Fig. 9 shows the electrode outputs as a function of time for the redistributed conditions. For this illustration, sinusoidally amplitude modulated wideband noise with a modulation frequency of 50 Hz and a modulation depth of 0 dB (i.e., 100 % modulation) was used. Ten cycles of modulation over 200 ms are shown. For clarity, only the positive peaks of pulses are plotted. Overall, 50-Hz modulation patterns are clearly presented in the outputs for the redistributed conditions. Based on the electrode outputs presented in Fig. 9, quantitative analyses were done to estimate the amount of modulation in the electrode outputs. Table 7 shows the average peak-to-valley ratios between the mean current values for 10 peaks and 10 valleys over 200 ms. There were variations in the peak-to-valley ratios as a function of experimental conditions. For example, in the no-dead region map, higher peak-to-valley ratios were observed in the high frequency channels than in the low frequency channels because the high frequency channels were associated with the larger bandwidth of bandpass filters in the sound processor.

Fig. 9.

Electrodograms for sinusoidally amplitude modulated noise at 50 Hz processed with different experimental sound processors. In the lower panels, solid lines are shown for the inaudible electrodes for the dropped maps, indicating that minimum current values were set for those electrodes. Quantitative analyses based on these electrodograms are shown in Table 7. Redist. redistributed, DR simulated dead region, ELs electrodes.

Table 7.

Analyses of electrode outputs in response to the sinusoidal amplitude modulated noise at 50 Hz modulation frequency

Testing conditions	Stimulating electrodes
	#1	#2	#3	#4	#5	#6	#7	#8	#9	#10	#11	#12	#13	#14	#15	#16
No-DR	1.24	1.19	1.21	1.25	1.21	1.09	1.34	1.32	1.35	1.38	1.44	1.48	1.52	1.61	1.68	2.01
Redist. DRs = 8 ELs		1.20		1.39		1.39		1.40		1.52		1.56		1.71		2.17
Redist. DRs = 12 ELs				1.42				1.42				1.69				2.11
Redist. DRs = 14 ELs								1.49				1.73
Redist. DRs = 15 ELs								1.71

Related electrode output plots are shown in Fig. 9. Average peak-to-valley ratios between the mean current values (mA) for ten peaks and ten valleys over 200 ms are shown. A greater peak-to-valley ratio means a greater amount of modulation is represented in the outputs. For the testing condition of no-dead region (DR), the acoustic input stimulus was processed with 16 bandpass filters of the HiResolution sound processing strategy. Note that the dropped frequency remapping used the same bandpass filters; thus, peak-to-valley ratios for the dropped maps with dead region sizes of 8, 12, 14, and 15 electrodes can be found in the corresponding electrodes for the no-DR testing condition. The remaining four rows represent average peak-to-valley ratios for the redistributed (Redist.) maps with dead region sizes of 8, 12, 14, and 15 electrodes.

However, the dropped conditions are designed to simply drop the electrode outputs without changing the analysis filter bandwidth. Therefore, the filter bandwidths for the dropped maps remained the same with the filter bandwidths for the map with no-dead region. For example, when comparing the maps with the redistributed and dropped frequency remapping for a simulated dead region size of 15 electrodes, the bandwidth of the eighth channel in the dropped map was much smaller than the filter bandwidth of the eighth channel in the redistributed map. Subsequently, the peak-to-valley ratio for the eighth channel of the redistributed map was 1.71, but it was 1.32 for the eighth channel of the dropped map, thereby significantly worse performance was observed in the dropped condition than the redistributed condition when the size of simulated dead regions was 14 electrodes (see average data for CI subjects in Fig. 7). Similarly, as the size of simulated dead regions increased, the bandwidth for each channel does not change for the dropped maps, thus the amount of modulation information only decreased and CI subjects showed substantially degraded temporal modulation detection performance in the dropped conditions.

The pattern of temporal modulation detection for the dropped conditions would have been different if dead regions were simulated in different locations. For example, if electrode 16 was chosen to be an audible electrode and the rest of the basal region in the cochlea is assumed to represent dead regions, electrode 16 would be able to present more modulation information than electrode 8 does because electrode 16 is associated with a larger filter bandwidth. Likewise, if electrode 1 was chosen to be an audible electrode and the rest of the apical region in the cochlea is assumed to represent dead regions, electrode 1 would show far less modulation information than electrode 8, leading to further degradation in temporal modulation detection performance. This may be partly related to the potential effects of different filtering conditions and the associated channel bandwidth on temporal modulation detection for CI subjects. Note that such bandwidth effects on transmission of temporal modulation information have been previously noted for NH listeners (Strickland and Viemeister 1997). Nevertheless, we used a modulation frequency of 50 Hz in the current study, which was well below the bandwidth of the narrowest analysis filter band, to minimize any potential effect of channel bandwidths on temporal modulation detection for the dropped and redistributed conditions. If a higher modulation frequency was tested, such bandwidth effects would have been greater on temporal modulation detection performance and CI subjects would have potentially shown a greater difference in performance between the redistributed and dropped conditions. In sum, the present study demonstrated that the dropped frequency remapping presents great deficits in encoding temporal modulation. Therefore, for the purpose of presenting a salient temporal modulation cue, the redistributed frequency remapping may be preferable.

Experiment 4: Schroeder-Phase Discrimination

Testing Procedure

The Schroeder-phase discrimination test was implemented using the same method as that previously described by Drennan et al. (2008). Positive and negative Schroeder-phase stimulus pairs were created for two different fundamental frequencies (F0s) of 50 and 200 Hz. The former represents a fairly slow rate of frequency sweep over time, while the other is a relatively fast rate. For each F0, equal-amplitude harmonics from the F0 up to 5 kHz were summed. Phase values for each harmonic were determined by the following equation:

$${\theta }_n=\pm \pi n\left(n+1\right)/N\text{,}$$ 1

where θ_n is the phase of the nth harmonic, n is the nth harmonic, and N is the total number of harmonics in the complex. The positive or negative sign was used for the positive or negative Schroeder-phase stimuli, respectively. A four-interval, two-alternative forced choice procedure was used. One stimulus (i.e., positive Schroeder-phase, test stimulus) occurred in either the second or third interval and was different from three others (i.e., negative Schroeder-phase, reference stimulus). The subject’s task was to discriminate the test stimulus from the reference stimuli. To determine a total percent correct for each F0, the method of constant stimuli was used. In a single test run, each F0 was presented 24 times in random order and a total percent correct for each F0 was calculated as the percent of stimuli correctly identified. For each F0, the Schroeder-phase discrimination score for each subject is the mean of three testing runs. Mean scores averaged across 50 and 200 Hz were used for data analysis.

Results

Figures 10 and 11 show averaged Schroeder-phase discrimination scores for CI and NH subjects, respectively. When there was no dead region present, CI subjects showed a mean score of 85.0 % across six implanted ears. Using a larger sample size, Won et al. (2010) showed a mean score of 66.9 % averaged across 50 and 200 Hz in 42 CI subjects. For the no-dead region condition, NH subjects performed better than CI subjects. However, the overall pattern of performance as a function of the size of simulated dead regions was similar between CI and NH subjects.

More importantly, Schroeder-phase discrimination scores were very similar between the redistributed and dropped conditions. There was a gradual decrease in Schroeder-phase discrimination scores as the size of simulated dead regions increased from 0 to 15 electrodes (or bands). The pattern of Schroeder-phase discrimination scores across different experimental conditions exhibited some interesting similarities to the pattern of CNC word recognition shown in Figures 2 and 3, with no difference between the dropped and redistributed conditions. A mixed ANOVA analysis showed that the effect of the frequency remapping did not reach significance [F(1,9) = 0.008, p = 0.93], but the effect of dead region size did reach significance [F(4,36) = 125.43, p < 0.001]. The interaction between these two factors was significant [F(4,36) = 7.44, p < 0.001], probably due to the different Schroeder-phase discrimination scores between the redistributed and dropped conditions when the size of simulated dead regions was 14 bands in NH subjects. With regard to the subject group, there was a significant interaction with the effect of dead region size [F(4,36) = 4.10, p = 0.008], but with the effect of frequency mapping, the interaction did not reach significance [F(1,9) = 2.69, p = 0.14].

Multiple paired samples t tests showed that a significant difference in Schroeder-phase discrimination scores was observed only in one case: when NH subjects were tested with a simulated dead region size of 14 bands. Otherwise, both CI and NH subjects showed similar Schroeder-phase discrimination scores with the two different frequency remapping across different sizes of dead regions.

Post hoc Scheffe tests showed that CI subjects showed consistent Schroeder-phase discrimination performance until the simulated dead region size increased up to 12 electrodes (Table 8). Beyond a dead region size of 12 electrodes, there was a substantial drop in Schroeder-phase discrimination scores for both the redistributed and dropped conditions. A similar pattern was observed for NH subjects except that a drop in Schroeder-phase discrimination performance began at the dead region size of 12 bands for the dropped conditions.

Table 8.

Same as Table 4, but for Schroeder-phase discrimination

Comparison	CI with RDS	CI with DRP	NH with RDS	NH with DRP
0 vs. 8	–	–	–	–
0 vs. 12	–	–	–	0.002
0 vs. 14	0.004	0.036	< 0.001	0.001
0 vs. 15	< 0.001	< 0.001	< 0.001	< 0.001
8 vs. 12	–	–	–	0.002
8 vs. 14	< 0.001	0.013	< 0.001	0.001
8 vs. 15	< 0.001	< 0.001	< 0.001	< 0.001
12 vs. 14	0.001	0.03	< 0.001	–
12 vs. 15	< 0.001	< 0.001	< 0.001	< 0.001
14 vs. 15	–	0.017	–	< 0.001

Note that mean Schroeder-phase discrimination scores averaged across 50 and 200 Hz were used for this analysis

Discussion

Unlike spectral-ripple discrimination or temporal modulation detection, the effect of frequency remapping was not observed for Schroeder-phase discrimination. The absence of an effect of frequency remapping is similar to the results for CNC word recognition. As indicated in the “Introduction” section, Schroeder-phase discrimination involves both spectral and temporal modulations. Drennan et al. (2008) demonstrated that Schroeder-phase discrimination evaluates the ability of CI subjects to differentiate a rising frequency modulation from a falling frequency modulation. Figure 12 shows the electrode outputs in response to the 50-Hz negative Schroeder-phase discrimination stimuli for different experimental sound processors. Consider the outputs for the redistributed map with a simulated dead region size of 8 electrodes. Each electrode represents within-channel temporal modulation cues, but the pattern of within-channel modulations does not provide a strong perceptual cue to perform Schroeder-phase discrimination. For the negative Schroeder stimuli, the peak of envelope modulation occurs first in the low frequency channel. Subsequently, the peaks of envelope modulations for higher frequency channels occur later, and this pattern repeats for every period of Schroeder-phase stimuli (e.g., 20 ms for the 50-Hz F0). Thus, for the positive Schroeder-phase stimuli, this “sweep” moves from high to low frequency electrodes because the acoustic waveform represents the high frequency component first.

Fig. 12.

Electrodograms for the negative 50-Hz Schroeder-phase stimulus processed with different experimental sound processors. In the lower panels, solid lines are shown for the inaudible electrodes for the dropped maps, indicating that minimum current values were set for those electrodes. Redist. redistributed, DR simulated dead region, ELs electrodes.

Results for Schroeder-phase discrimination in CI subjects (Fig. 10) indicate that the cues necessary to discriminate Schroeder-phase stimuli are preserved in the electrode outputs for simulated dead region sizes of 0, 8, and 12 electrodes. When the dead region sizes of 14 or 15 electrodes were simulated, a substantial drop in discrimination performance was observed. With two active (or audible) electrodes only, the direction of frequency sweep becomes ambiguous, and with only one active electrode, the frequency sweeping cues are essentially gone. Nevertheless, almost identical performance was observed for both the redistributed and dropped conditions across different dead region sizes, suggesting that both frequency remapping schemes presented an equal amount of the frequency sweeping cues for each simulated dead region size.

General Discussion and Conclusions

Previous studies (e.g., Shannon et al. 2002; Kasturi et al. 2002; Başkent and Shannon 2006) demonstrated that speech perception performance was similar between the redistributed and dropped frequency remappings when CI or NH subjects were tested for different patterns of the presence of cochlear dead regions. The present study was designed to understand a possible mechanism for the absence of effects of frequency remapping. Spectral and temporal envelope processing was evaluated using three different psychoacoustic experiments. CNC word recognition was performed to evaluate listeners’ speech identification performance. Four different patterns of cochlear dead regions were simulated in CI and NH subjects. Whereas tests of word identification did not reveal differences between dropped and redistributed conditions, tests of sensitivity to spectral and temporal modulations uncovered potential advantages and drawbacks of differing ways of handling spectral holes. Overall, results supported the hypothesis that the presence of cochlear dead regions would affect spectral and temporal envelope sensitivities differently for each frequency remapping scheme. Specifically, the results showed:

1. CNC word recognition did not reveal any difference between the two different frequency remappings, consistent with previous findings in the literature (e.g., Shannon et al. 2002; Kasturi et al. 2002; Başkent and Shannon 2006).

2. Spectral and temporal envelope sensitivity changed in a very different way for the redistributed and dropped conditions as a function of the pattern of dead regions, supporting the hypothesis of the present study.

3. When CI subjects were tested with the redistributed conditions, their spectral-ripple discrimination performance gradually decreased as simulated dead region size increased from 0 to 15 electrodes; however, their temporal modulation detection performance did not change at all as simulated dead region size increased from 0 to 15 electrodes.

4. In contrast, different patterns of results were observed for the dropped conditions. There was a marked change in temporal modulation detection performance as dead region size increased from 0 to 15 electrodes, but a relatively small change was observed for spectral-ripple discrimination performance as dead region size increased from 0 to 15 electrodes.

5. Schroeder-phase discrimination showed a similar pattern of results between the redistributed and dropped maps.

6. Results with NH listeners were generally quite consistent with CI listeners, indicating that the use of the current spread vocoder approach of Bingabr et al. (2008) modeled CI hearing well for these tasks across a broad range of cochlear dead region sizes.

As discussed in the “Introduction” section, one study that used a (traditional) vocoder simulation noted some learning differences between a set of redistributed and dropped conditions following relatively brief training (Smith and Faulkner 2006). The impact of long-term experience with such remappings, however, is unknown. Altogether, the current results suggest that the tradeoff between spectral and temporal envelope sensitivities for the redistributed and dropped frequency remappings might result in a similar performance for CNC word recognition. Speech signals present complex patterns of both spectral and temporal modulations that may change dynamically across frequency channels in informative ways. This could be a possible reason for the null effect of frequency remapping schemes on CNC word recognition in the current study.

An important area of need in cochlear implant research is simulations of electrical hearing. Cochlear implant users are a very heterogeneous test population, with substantial differences both in the underlying pathology and in patterns of neural survival from one individual to the next. That is, there are unknown, and uncontrolled, sources of variance that create challenges in the interpretation of the results of CI research. Vocoder simulations can play a crucial supporting role in advancing our knowledge of electrical hearing by limiting such unknown sources of variance. However, results with traditional vocoder-based approaches are known to deviate in some key respects from results in CI users (Friesen et al. 2001). The “current spread” vocoding approach might offer a way forward (e.g., Laneau et al. 2006; Bingabr et al. 2008; Crew et al. 2012). Whereas the traditional vocoding approach does not attempt to introduce broad overlap among channels, the “current spread” vocoding approach extracts the stimulus envelope from each input channel and then presents that envelope to the intended output channel and (in a gradually attenuated form) to numerous channels on either side of the intended output channel. This feature of the “current spread” vocoder might help overcome some of the limitations of traditional vocoding-based approaches. However, many questions remain about the “current spread” vocoding approach. To name one example, the method used in the work of Bingabr et al. (2008) and in the current paper depends on crucial assumptions about how to compensate for the large difference in dynamic range between normal-hearing listeners and CI users, and these assumptions are an important topic for further discussion and debate. Thus, it is simply too early to say whether this new approach to vocoding allows one to simulate electrical hearing more accurately than traditional vocoding approaches.

Recently, novel techniques have been developed to identify electrodes with a poor electro-neural interface. For example, Garadat et al. (2012) evaluated the across-site patterns of temporal modulation detection performance in CI subjects and demonstrated that better speech recognition was obtained when the electrodes showing poorer temporal modulation detection were removed. Examination of thresholds for focused electric stimulation (e.g., tri-polar stimulation mode) also provides information about electrode-neural interface (for reviews, see Bierer 2010). Although imaging techniques using high-resolution computed tomography (CT) scans do not directly provide information about electrode-neural interface, the information about electrode-to-modiolus distance positions may help to understand the variability in threshold levels (Noble et al. 2013; Long et al. 2014). If cochlear dead regions or electrodes with poor neural interface or unusually large distance to modiolus are identified, the findings from the current study could provide important implications of the sound processor manipulations to guide deactivation of certain implant channels. A precise understanding of the advantages or disadvantages of deactivating certain channels with different frequency remapping schemes for spectral and temporal perception could lead to improvements in multiple clinical outcomes.