On the High Frequency Transfer of Mechanical Stimuli from the Surface of the Head to the Macular Neuroepithelium of the Mouse

Abstract

Vestibular macular sensors are activated by a shearing motion between the otoconial membrane and underlying receptor epithelium. Shearing motion and sensory activation in response to an externally induced head motion do not occur instantaneously. The mechanically reactive elastic and inertial properties of the intervening tissue introduce temporal constraints on the transfer of the stimulus to sensors. Treating the otoconial sensory apparatus as an overdamped second-order mechanical system, we measured the governing long time constant (Τ_L) for stimulus transfer from the head surface to epithelium. This provided the basis to estimate the corresponding upper cutoff for the frequency response curve for mouse otoconial organs. A velocity step excitation was used as the forcing function. Hypothetically, the onset of the mechanical response to a step excitation follows an exponential rise having the form Vel_shear = U(1-e^−t/TL), where U is the applied shearing velocity step amplitude. The response time of the otoconial apparatus was estimated based on the activation threshold of macular neural responses to step stimuli having durations between 0.1 and 2.0 ms. Twenty adult C57BL/6 J mice were evaluated. Animals were anesthetized. The head was secured to a shaker platform using a non-invasive head clip or implanted skull screws. The shaker was driven to produce a theoretical forcing step velocity excitation at the otoconial organ. Vestibular sensory evoked potentials (VsEPs) were recorded to measure the threshold for macular neural activation. The duration of the applied step motion was reduced systematically from 2 to 0.1 ms and response threshold determined for each duration (nine durations). Hypothetically, the threshold of activation will increase according to the decrease in velocity transfer occurring at shorter step durations. The relationship between neural threshold and stimulus step duration was characterized. Activation threshold increased exponentially as velocity step duration decreased below 1.0 ms. The time constants associated with the exponential curve were Τ_L = 0.50 ms for the head clip coupling and T_L = 0.79 ms for skull screw preparation. These corresponded to upper −3 dB frequency cutoff points of approximately 318 and 201 Hz, respectively. T_L ranged from 224 to 379 across individual animals using the head clip coupling. The findings were consistent with a second-order mass-spring mechanical system. Threshold data were also fitted to underdamped models post hoc. The underdamped fits suggested natural resonance frequencies on the order of 278 to 448 Hz as well as the idea that macular systems in mammals are less damped than generally acknowledged. Although estimated indirectly, it is argued that these time constants reflect largely if not entirely the mechanics of transfer to the sensory apparatus. The estimated governing time constant of 0.50 ms for composite data predicts high frequency cutoffs of at least 318 Hz for the intact otoconial apparatus of the mouse.

Introduction

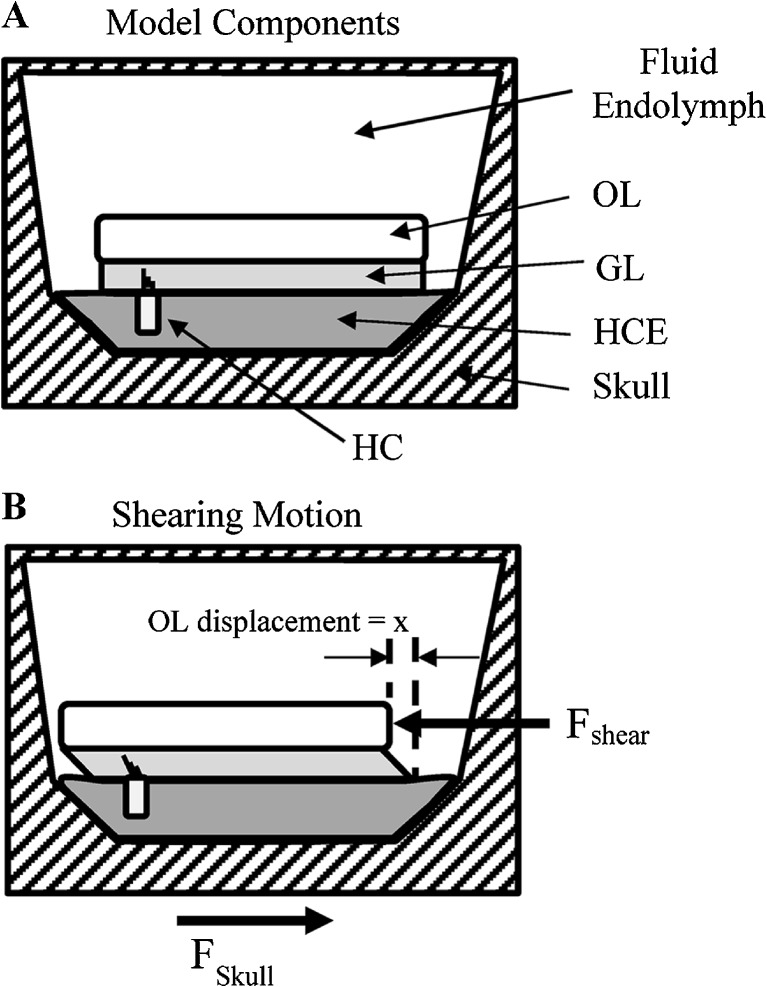
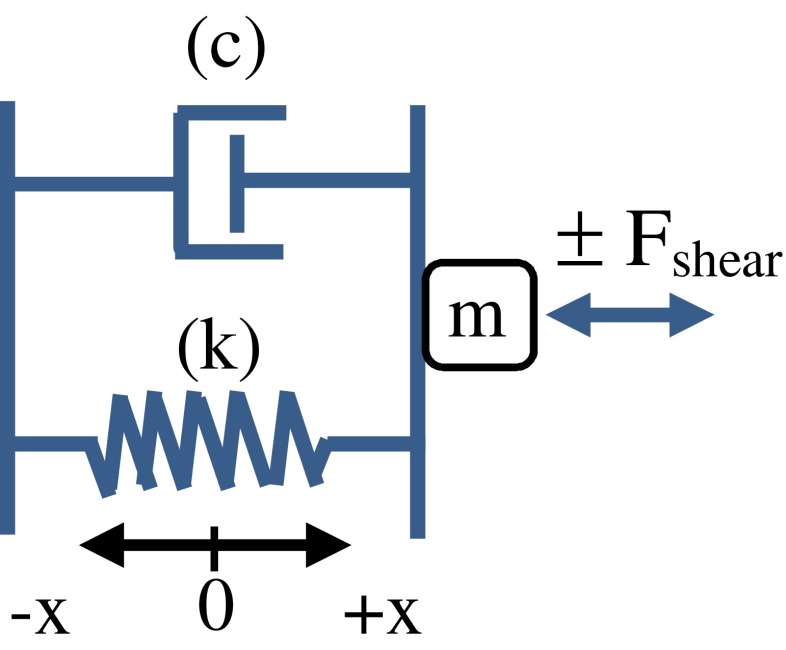
The adequate stimulus for sensory transduction in receptors of the macular neuroepithelium (i.e., sensory component of otoconial organs) is a shearing motion between the apical surface of the neuroepithelium (Fig. 1, HCE) and overlying otoconial membrane (Fig. 1, OL). This action bends the protruding stereociliary bundles of hair cell receptors underlying the OL, the cell bodies of which are fixed in place in the epithelium. The mechanical bending of the hair cell bundle activates transduction channels permeable to cations, which leads to hair cell depolarization, increased release of neurotransmitter, and activation of primary afferent neurons. Owing to the difference in density between the otoconial membrane and surrounding endolymphatic fluid and tissue, the otoconial membrane is displaced relative to the epithelium when subjected to accelerating forces such as gravity or linear head translation (Fig. 1B, F_shear). Indeed, early work has shown (DeVries 1950) and more recent mechanical modeling of otoconial systems predicts that the magnitude of otoconial displacement is proportional to head acceleration over a wide range of frequencies (e.g., Grant et al. 1994; Rabbitt et al. 2004). Such a relationship can also be inferred from the activity patterns of many vestibular primary afferent neurons, which reliably and tonically encode stationary head tilt (e.g., Fernandez et al. 1972; Fernandez and Goldberg 1976a, b). There are other primary afferent neurons innervating otoconial organs that are more sensitive to changes in otoconial displacement and demonstrate activity patterns that are more phasic thus reflecting more dynamic aspects of head movement (e.g., irregular fibers, Fernandez and Goldberg 1976c). Note that since otoconial membrane displacement is proportional to acceleration of the head, it follows that the change in displacement over time (i.e., otoconial membrane shearing velocity) reflects changes in acceleration of the head over time. The rate of change in acceleration with time is kinematic jerk [(m/s²)/s]. Therefore, kinematic jerk applied to the head provides a velocity excitation at the otoconial sensory apparatus (see Appendix).

FIG. 1.

A schematic illustration of the apparatus of the intact vestibular macula including the endolymphatic fluid compartment, the otoconial layer (OL, which incorporates and is often referred to as the otoconial membrane), a gell layer (GL), the neuroepithelium (hair cell epithelium, HCE), and skull boundary. A sensory hair cell (HC) is shown with stereociliary bundle extending into the GL. The inertial properties [mass (m) and density (ρ)] are associated with otoconia of the OL, damping characteristics largely associated with viscous drag of the gel layer and endolymph, whereas the stiffness (k) characteristics are thought to be largely associated with stereociliary bundles and gel layer. See schematic illustration of mechanical model in Appendix-Figure 9. B Illustration of shearing action between the OL and apical surface of the HCE during acceleration of the head. Shearing displacement bends stereociliary bundles, depolarizing hair cells and activating primary afferent neurons. Shearing displacement is proportional to the shearing force (F_shear). The magnitude of shearing displacement between the neuroepithelium and otoconial layer is shown as “x” and is proportional to head acceleration. Shearing velocity is equal to the time derivative of shearing displacement (dx/dt), which is proportional to the time derivative of head acceleration (a_h), which is known as kinematic jerk (j_h) (da_h/dt = j_h(t), head jerk in units of (m/s²)/s = m/s³).

Linear kinematic head jerk has been shown to be the adequate stimulus for linear vestibular sensory evoked potentials (VsEPs) in mammals and birds (Jones et al. 1998; Jones et al. 2011). The linear VsEP is a compound action potential produced by neurons innervating gravity receptors and their central neural relays in the brainstem (Jones et al. 1999, 2004; Nazareth and Jones 1998). Macular neurons giving rise to the VsEP are thought to be irregularly discharging calyx-bearing primary afferent neurons including both dimorphs and calyx-only afferents (Jones et al. 1998, 2011; Lysakowski and Goldberg 2004). The VsEP response is triggered at the onset of the applied stimulus (see Methods), and response threshold is strictly determined by the peak magnitude of the head jerk (Jones et al. 1998, 2011). The stimulus we use to elicit the VsEP is a constant-amplitude kinematic jerk motion applied to the head. The stimulus is stepped on and remains constant for a brief fixed period of time (usually milliseconds) and is then switched off. This jerk stimulus transfers from the skull to the epithelial layer and endolymphatic compartment (Fig. 1, skull to HCE and endolymph) to present a step shearing velocity excitation to the otoconial apparatus. The mechanical response of the otoconial apparatus to this step excitation is a rapid rise in otoconial membrane shearing velocity relative to the underlying epithelium (Fig. 2A, DASHED LINE). The rate of rise in shearing velocity depends on the mechanical transfer characteristics of the structural elements in the pathway from the skull to the otoconial apparatus. The resulting stimulus shearing velocity of the otoconial layer is capable of activating large numbers of gravity receptor primary afferent neurons synchronously during the onset of each stimulus such that their collective activity can be recorded noninvasively at the surface of the skull as the VsEP. Examples of such vestibular compound action potentials are shown in Figure 3.

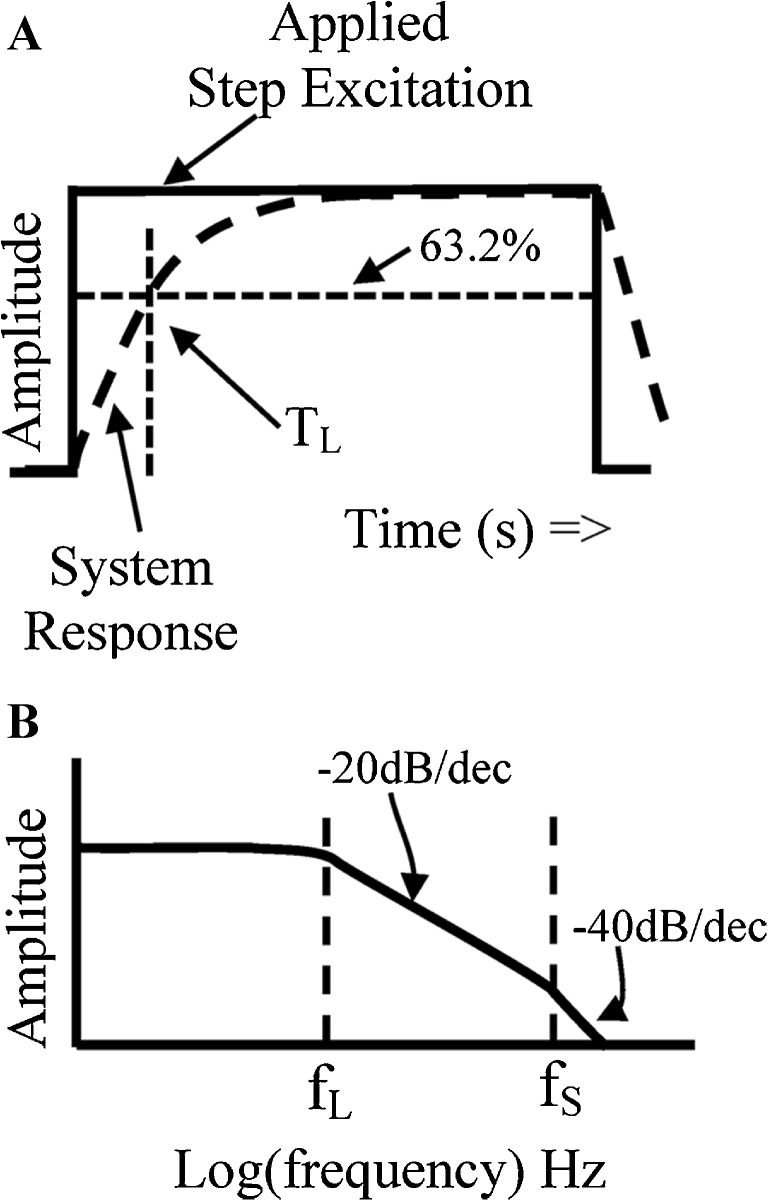
FIG. 2.

Dynamic behavior, bandwidth, and time constants associated with an overdamped second-order mass-spring mechanical system. A Hypothetical otoconial layer (OL) mechanical response (DASHED LINE) to an applied step excitation (SOLID LINE). The shape of the overdamped OL system response is governed primarily by the long time constant T_L. B Low pass frequency response of otoconial mass-spring mechanical system (see also Appendix-Figures 8 and 9). Hypothetical relationships between long and short time constants (T _L, T _S) and associated frequency corners and rolloff slopes are shown. Upper frequency corner ($f_{\mathrm{S}}=\frac{{\omega }_S}{2\pi }=\frac{1}{2\pi T_{\mathrm{S}}}$ in Hz) and lower frequency corner ($f_{\mathrm{L}}=\frac{{\omega }_{\mathrm{L}}}{2\pi }=\frac{1}{2\pi T_{\mathrm{L}}}$ in Hz). f_L is the −3 dB point where at frequencies immediately above this break point the amplitude falls off at −20 dB/frequency decade (−6 dB/octave). Above the second break point, f_S, amplitudes fall off at −40 dB/decade (−12 dB/octave). Note that fs is above frequency regions of practical importance and has little if any effect on the roll off immediately above f_L. The current estimate for the ratio of the two break points is fs/f_L = ω_S/ω_L = 10 (see Appendix-Figure 8).

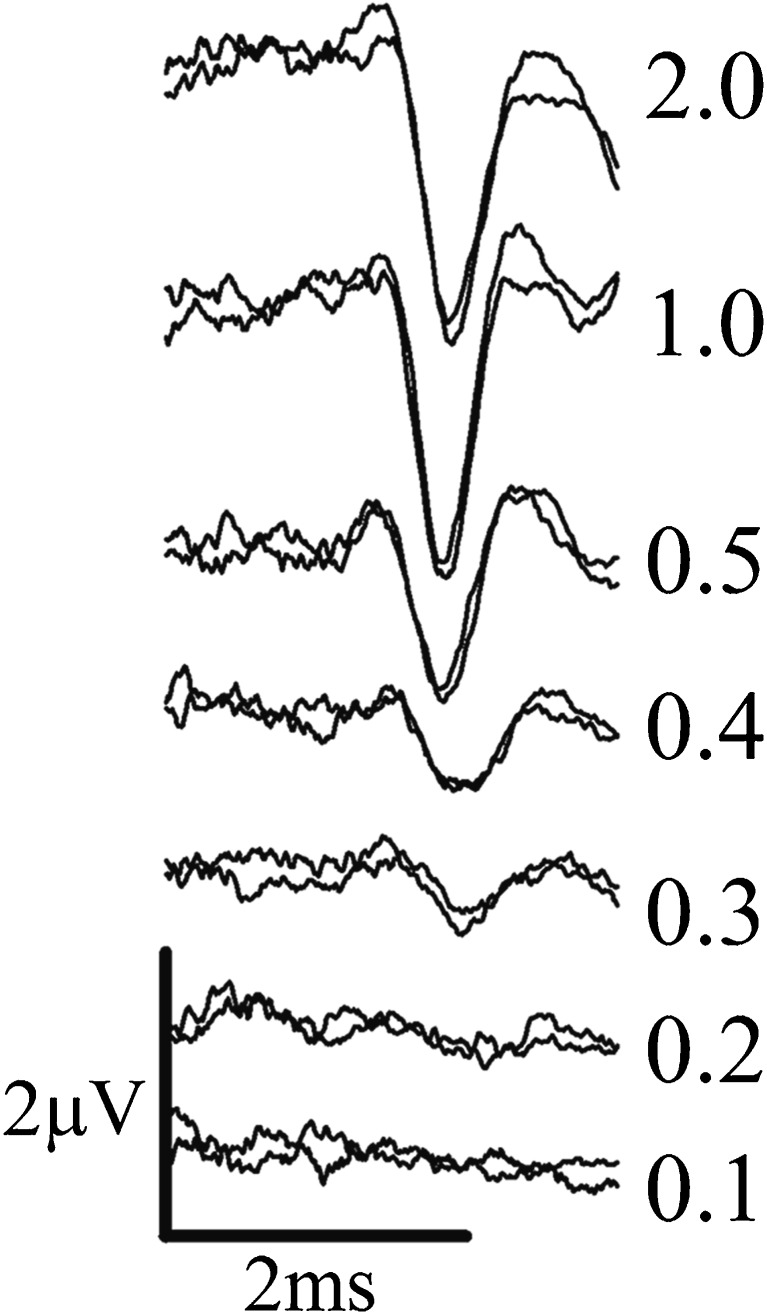
FIG. 3.

Vestibular sensory evoked potential (VsEP) responses to step jerk stimuli. Seven response pairs are shown. The applied stimulus amplitude step was the same for each pair; however, the duration of the step jerk (in ms, shown to right of each pair) was reduced from 2 ms (TOP) to 0.1 ms (BOTTOM). Response amplitude decreases systematically with progressively shorter stimulus duration. The reduction in amplitude is a result of a systematic increase in response threshold with shorter durations. The increase in threshold was due to reduced shearing velocity achieved by the responding otoconial apparatus at shorter stimulus durations. The increase in threshold was measured for each stimulus duration and the resulting curve used to estimate the time constant for the apparent exponential rise in shearing velocity following the application of the step jerk. Calibration bars indicate time (ms) and amplitude scales.

In the present study, we use these stimulus–response features to estimate the governing time constant for the otoconial system response to a step velocity forcing function. To do this, a step velocity excitation at the macular epithelium is produced by applying a rectangular (step) jerk stimulus to the skull surface. We hypothesize that the mechanical response of the macular otoconial layer to this stimulus is manifest as an exponential rise in shearing velocity, the amplitude of which asymptotically approaches the amplitude of the applied velocity step excitation produced by the skull jerk (Fig. 2A). This expectation is based on a second-order mass-spring model of otoconial mechanics (overdamped model elaborated in the Methods section and Appendix). Given such a stimulus profile at the epithelium, one can predict that reduced stimulus levels will be achieved if the duration of the jerk stimulus is shortened and the jerk step ended before the otoconial shearing velocity response reaches the level of applied excitation. At these shorter durations, an increase in head jerk stimulus level will be required to activate neurons at threshold. In fact, response thresholds will increase in direct proportion to the decrease in otoconial shearing velocity achieved by short stimuli. Because of this, stimulus levels required to reach threshold at short durations will trace-out the onset rise in otoconial shearing velocity within the sensory apparatus. Hypothetically, this curve will reflect the effective mechanical characteristics of the structures mediating stimulus transfer from the skull or head surface to the otoconial apparatus.

The aim of the present work was to characterize the relationship between VsEP response threshold and the duration of jerk stimuli at step durations well below 2 ms. Our hypothesis is that threshold will increase exponentially as the applied stimulus step duration is reduced below 1.0 ms. We use the resulting threshold function to estimate the long time constant and corresponding upper frequency cutoff for the overdamped mechanical response of the otoconial organs of the mouse. Prompted by our results and recent observations by others (Dunlap and Grant 2014), we also make a post hoc comparison of upper frequency breakpoints predicted by overdamped and underdamped model fits to our data.

Methods

Models, Assumptions, and Formal Basis of Approach

The mechanics of otoconial sensory organs have been modeled as overdamped second-order mass-spring dynamic systems (DeVries 1950; Rabbitt et al. 2004; Grant and Best 1986; Grant and Cotton 1991; Grant et al. 1984, 1994). In terms of frequency response, macular systems can be represented as second-order lag or low-pass frequency filters of mechanical excitation (see Appendix-Figures 8 and 9). The mechanical response of such a system to a step excitation (e.g., constant stepped velocity) is not instantaneous but rather develops over time. The initial rapid rise in response amplitude approaches the amplitude of the applied step excitation asymptotically (Fig. 2A). Because it is a second-order system, the rate of rise is governed by two time constants, generally one long (T_L) and one short (Ts). In the current model, both time constants can potentially shape the high-frequency response curve of the low-pass transfer function (Fig. 2B). Indeed, the time constants determine two upper frequency break points which combine to produce the high frequency roll-off slopes of the transfer function (−20 and −40 dB/decade, Fig. 2B). The frequency corner associated with each time constant is defined by system characteristics of stiffness (k), mass (m), and frictional drag (expressed here as coefficient of damping (c)) (e.g., Rabbitt et al. 2004). The two corner frequency break points are defined by Eqs. 1 and 2 below:

FIG. 8.

Transfer magnitude as a function of R = ω_S/ω_L.

FIG. 9.

Schematic model representing the configuration of mechanical elements including mass (m), stiffness (k) and viscous drag/damping (C) that govern the response of the otoconial system. Components symbolize elements in the differential Eq. A-1 as follows: Stiffness is represented as a spring with stiffness k, where restoring forces develop with displacement (kx), inertial forces are associated with a lumped otoconial mass (m) and acceleration ($m\ddot{x}$) and the dashpot represents forces associated with viscous drag (C), which develop in association with kinematic velocity ($c\dot{x}$).

The highest frequency cutoff, which is determined by mass and damping elements, corresponds to the short time constant given by Eq. 1

$${\mathrm{\omega }}_{\mathrm{S}}=1/{\mathrm{T}}_{\mathrm{S}}=2\mathrm{\pi }\mathrm{f}\mathrm{s}=\mathrm{c}/\mathrm{m}$$ 1

where fs is the natural frequency in Hz, ω_S the natural frequency in radians/s, and T_S is the short time constant associated with the highest frequency transfer break point (f_S, Fig. 2B). The lower cutoff frequency is governed by the long time constant, which is determined by stiffness and damping elements as follows:

$${\mathrm{\omega }}_{\mathrm{L}}=1/{\mathrm{T}}_{\mathrm{L}}=2{\mathrm{\pi }\mathrm{f}}_{\mathrm{L}}=\mathrm{k}/\mathrm{c}$$ 2

where f_L is the natural frequency in Hz, ω_L the natural frequency in radians/s, and T_L is the long time constant associated with the lowest and the most important upper frequency transfer break point (f_L, Fig. 2B). A reasonable assumption used in the present study was that the corner frequency defined by mass (c/m) is considerably higher than that due to stiffness (k/c) thus ω_S > > ω_L and the ratio ω_S/ω_L is thought to be on the order of 10. As illustrated in Figure 2B, this represents a circumstance where the long time constant (T_L) plays a dominant role in shaping the response inasmuch as it has the most restrictive influence on high frequency transfer at frequencies of interest here (e.g., less than 1000 Hz; see also Appendix-Figure 8).

Because the temporal characteristics of the mechanical response depend strictly on the mechanical properties of the system, one can evaluate the effects of an applied excitation such as a forced displacement or velocity on a systems’ displacement or velocity response and estimate these mechanical properties. Whether one chooses to impose a step displacement, velocity, or acceleration, the dynamic system response will be governed in some fashion by the same time constants T_L and T_S. This is demonstrated in the Appendix.

The purpose of the present study was to test the following hypothesis: VsEP thresholds will increase exponentially as the duration of the step head jerk stimulus decreases. The hypothesis is based on the premise outlined in the introduction (and elaborated below) that VsEP thresholds will increase directly as the stimulus level at the sensor decreases and on an anticipated exponential rise in shear velocity predicted by the overdamped model of otoconial membrane mechanics (see lumped parameter model given in the Appendix). As noted, the shearing velocity response of the otoconial layer in response to an applied velocity step (applied step head jerk) will rise along an exponential course according to Eq. 3 (Appendix Eq. A-15):

$$v\left(t\right)=U\left(1-e^{-\frac{t}{\left(\frac{c}{k}\right)}}\right)$$ 3

where v(t) is the shear velocity of the otoconial layer as a function of time (t), c/k is the long time constant T_L = c/k, and U is the amplitude of the applied excitation velocity step and is given by Eq. 4:

$$U=-J_{\mathrm{x}}\left(1-\frac{{\rho }_e}{{\rho }_{OL}}\right)\left(\frac{m}{k}\right)$$ 4

where J_x is the applied jerk amplitude in the plane of the otoconial layer (the negative sign for Jx indicates that the direction of the velocity step is opposite the applied jerk stimulus), ρ_e is the density of the endolymph (∼1.0 g/cm³), ρ_OL is the density of the otoconial layer (∼1.35 g/cm³), and m/k is the ratio of mass/stiffness for the otoconial mechanical system.

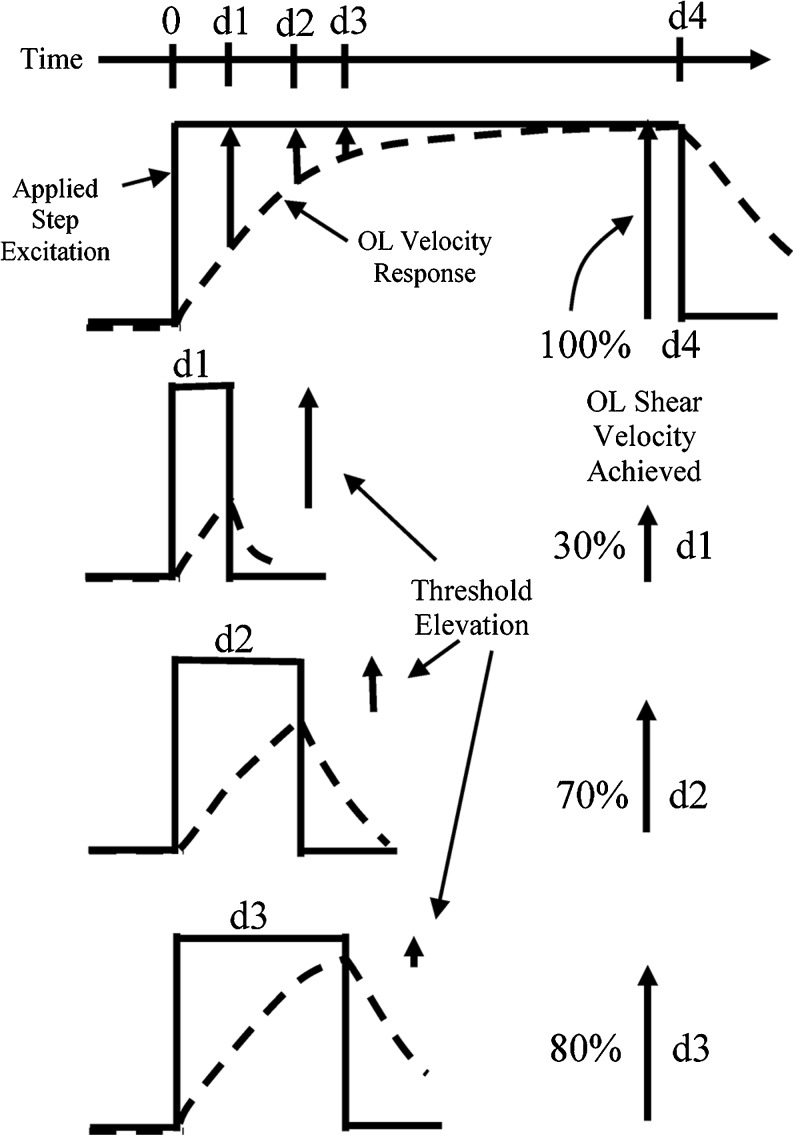
It has been shown that at stimulus durations of 2 ms and longer, VsEP thresholds are essentially constant using methods described here and elsewhere (Jones et al. 1998; Jones et al. 2011). In these cases, the applied stimulus is sufficiently long to permit the otoconial shearing velocity response to rise and attain or equal the full magnitude of the applied excitation step. This is illustrated in Figure 4 for a step stimulus having a schematic duration of “d4”. However, if one shortens the step duration sufficiently, the stimulus excitation will end before the otoconial apparatus has reached the full applied step excitation. This is illustrated for three hypothetical short duration stimuli (Fig. 4, step stimuli; d1, d2, and d3). Since the otoconial shearing stimulus is reduced for these durations, larger stimuli would be required to activate neurons at threshold. Indeed, neural activation threshold will increase in direct proportion to the decreased otoconial shearing velocity. Hence, given the anticipated mechanical response of the otoconial apparatus described above, thresholds should increase exponentially as stimulus duration is reduced towards and below the long time constant of the otoconial apparatus. In that case, the long time constant (T_L) will be equal to the stimulus duration producing a reduction in excitation of 1-1/e = 63.2 % (−3.98 dB). In terms of VsEP threshold, therefore, T_L will be the stimulus duration producing an increase in threshold of 3.98 dB. Figure 3 illustrates VsEP responses recorded using stimuli that apply the same level of jerk to the skull in all cases but for different durations from 2 to 0.1 ms. Notice the reduction in amplitude with shorter and shorter durations. The decrease in amplitude is due to increases in thresholds, where stimuli achieved lower and lower peak values at the otoconial layer. The shortest stimulus in this case produces no response at all. We measured the threshold increase for each stimulus duration.

FIG. 4.

Hypothetically, the response of the otoconial layer (OL) to the step excitation stimulus follows Eq. 3 which is represented here as DASHED LINES. The step velocity excitation (U in Eq. 3) is supplied by the surface jerk stimulation (Jx in Eq. 4). The VsEP response is elicited when the OL layer shear velocity reaches the response threshold level. At sufficiently long stimulus durations (e.g., d4), the OL shear velocity reaches the full level of the applied stimulus (100 %). However, at shorter durations (e.g., d1, d2, and d3) there is insufficient time for the OL velocity to reach the applied velocity. Thus, at short durations, the OL shear stimulus is only a fraction of the applied stimulus (e.g., 30, 70, and 80 % for d1, d2, and d3, respectively, in this example). Thresholds measured at these short durations will be increased in direct proportion to the reduced OL shear stimulus magnitude. 0 = onset of applied stimulus step. d1, d2, d3 and d4 = four arbitrary step durations for illustration.

Post hoc evaluation of threshold data: Results obtained in the present study prompted post hoc evaluation of underdamped models and comparison of damping levels. The underdamped solution for the second-order differential equation is derived in the Appendix. The solution to the underdamped model is given in Eqs. A-22 and A-28 of the Appendix. Estimates of underdamped natural frequencies (f_n) and damping ratios were made by fitting the underdamped solution to threshold data as described below in Analysis and Statistics.

Using neural activation to evaluate the mechanical dynamics of the otoconial apparatus: One tacit premise employed in the present study is that neurons generating the linear VsEP would reliably represent the mechanical behavior of the otoconial apparatus and thus would produce time constant values attributable largely, if not entirely, to the mechanics of stimulus transfer. The basis for this premise lies in the response characteristics of the VsEP. The linear VsEP, although it has been under study for many years (e.g., Jones and Pedersen 1989), has only recently come into more general use. It is the vestibular analog to the widely appreciated auditory brainstem response (ABR) and as such reflects entirely different kinds of neural behavior than that represented in traditional study of vestibular primary afferents.

Traditional vestibular measurements using sine wave stimuli evaluate how well a primary afferent neuron follows sinusoidal head motion over prolonged periods of time (seconds) noting the amplitude (discharge rate and spikes/s) or gain (e.g., spikes/s/g) and phase of the afferent response in relation to the stimulus. Thus, the discharge rate of a single primary afferent is characterized as the stimulus sine wave or complex signal plays out over time. The neurons are evaluated at several frequencies generally below 20 Hz and response amplitude/gain and phase determined as a function of frequency. At these low frequencies, the transfer of mechanical stimuli to the low-pass otoconial apparatus is maximal and constant across frequencies (Fig. 2B and Appendix Figure 8). However, the response of macular neurons is not generally constant across these frequencies. Instead, in many cases, neural responses exhibit substantial changes in gain and phase as a function of frequencies below 20 Hz and bear little resemblance to the actual mechanical response of the otoconial membrane. Instead, neural response behaviors arise largely from the dynamic response characteristics of the particular neuron recorded (e.g., tonic vs. phasic, etc.) rather than the transfer characteristics of the otoconial apparatus. However, this circumstance does not apply to the linear VsEP. Using the VsEP in our studies, we essentially evaluate a single initial action potential discharge (spike) of a population of vestibular afferents that occurs in the first instants after the onset of a stimulus. Despite of the fact that both methods record primary afferents, the measurements could not be more fundamentally different.

Lewis and colleagues (Lewis and Parnas 1994) explored the theoretical basis of short latency spike volleys in vestibular primary afferents. In their theoretical development, they incorporated potential transfer modifications associated with the stimulus transfer from the otoconial membrane to the hair cell and from the hair cell to primary afferent. They showed that vestibular primary afferents possessing dynamic response characteristics (e.g., calyx and dimorph units) and an upper frequency roll off no greater that −6 dB per octave will produce a highly synchronous onset discharge in response to a stimulus transient. Moreover, vestibular afferents responding to jerk (shearing velocity at epithelium) would be the most effective in phase locking and synchronizing to the stimulus onset. The VsEP is precisely the example of a compound action potential produced by a population of such vestibular primary afferents.

The widely varying dynamic characteristics of individual primary afferent responses to low frequency sine wave stimuli are well known and appreciated as noted above. The linear VsEP method of measurement minimizes, if not eliminates, the influence of these characteristics on our results for many reasons outlined below:

1. The VsEP is an onset response and the measurement relies on phase locking properties of individual vestibular primary afferents. Thus, it detects the presence of a stimulus not how well it follows the waveform of the stimulus.

2. Vestibular primary afferents have been shown to have excellent phase locking properties at frequencies as high as 400 Hz (Dickman and Correia 1989). This is a key attribute serving to synchronize onset discharge of vestibular neurons in response to stimulus transients. Moreover, recent work by Curthoys and colleagues reportedly shows that mammalian macular primary afferent neurons readily respond to bone conducted vibration at frequencies on the order of 500 Hz (reviewed by Curthoys et al. 2013).

3. The theoretical work of Ted Lewis and colleagues (e.g., Lewis and Parnas 1994 noted above) has also shown that, for a given neuron, only the first action potential (AP) of a discharge volley in response to a stimulus transient likely contributes significantly to compound responses such as the VsEP, thus the description “an onset response” is truly applicable. Subsequent APs following the first in a discharge volley are insufficiently synchronized across cohort neurons to contribute significantly to the compound VsEP response. This was confirmed by Nazareth and Jones 1998 who showed that primary afferent neurons produced only the first component of the VsEP (P1-N1). No later components arose from primary afferent discharge thus precluding contributions by later secondary peripheral AP discharges. These neurons detect precisely the onset of stimuli.

4. The use of kinematic jerk as a stimulus selects a subpopulation of macular neurons, which collectively have similar dynamics under these circumstances.

5. We are measuring response threshold, thus we characterize whether there is a response to the stimulus or not. For the VsEP, this is strictly determined by the level of shearing velocity achieved by the stimulus at the epithelium. Thus, we are essentially inferring the magnitude of shearing velocity; asking: is shearing velocity of sufficient level to activate the neurons? This is a bioassay of shearing velocity level.

6. Delays introduced by transduction, synaptic transmission, and neural activation must preserve collective phase locking and discharge synchrony across neuron cohorts or there would be no effective collective response. Thus, the temporal course of transfer of the stimulus from the skull to activation of the neuron must be consistent across the cohort of neurons participating in the response. Wide variation in such would preclude recording VsEPs.

7. The overall latency of the collective synchronous discharge is not measured in the present study and thus collective delays introduced by transduction and neural activation have little or no bearing on results.

8. At response threshold, stimulus level actually achieved is low and virtually constant for any stimulus duration. To achieve that threshold level, however, we must increase the level of the applied stimulus at short durations less than 1 ms (owing to mechanical transfer properties). The applied level of stimulation required to reach threshold level thus increases systematically at shorter durations.

9. Low and constant level stimuli (i.e., at threshold) minimize nonlinearities introduced by hair cell transfer characteristics and promote stable sensory sensitivity.

These features of the VsEP allow it to be used to detect the magnitude of shearing velocity present at the level of the epithelium and to report reliably these magnitudes when they are just sufficient to activate macular neurons (i.e., just above threshold). We argue, therefore, that threshold changes obtained from measurements of the present study reflect primarily the properties of mechanical stimulus transfer from the head surface to otoconial apparatus rather than variation in neural dynamics.

Animals

Twenty normal C57BL/6 J mice (females, 2.65 ± 0.7 months old) were evaluated. Animals were anesthetized with a ketamine/xylazine mixture (5 to 7 μl/g body weight) injected intraperitoneally. The mixture consists of 18 mg/ml ketamine and 2 mg/ml xylazine. Maintenance doses of anesthetic (0.05 ml) were administered as necessary. Core temperature was monitored and maintained at 37.0 ± 0.2 using a homeothermic heating pad.

Stimuli

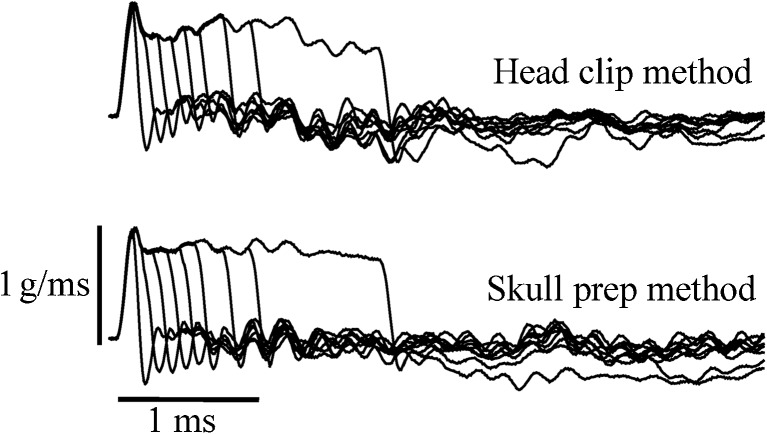
The methods used for stimulation in this study have been detailed previously and will be briefly related here (Jones et al. 2002; Jones and Jones 2007). Rectangular jerk step stimuli were produced by applying a linear voltage ramp to an electromechanical shaker (Labworks, Inc. Model ET2-203). The duration of the control voltage ramp determined the duration of the corresponding shaker acceleration ramp and jerk step. A calibrated accelerometer (100 mv/g, g = 9.81 m/s²) was mounted on the shaker platform. The output of the accelerometer was electronically differentiated to monitor jerk magnitude. Head motion stimuli were presented in the naso-occipital axis (±G_X axis, Fig. 5). Stimuli initiated in an upward direction (+G_X) were designated positive polarity and those initiated in a downward direction (−G_X) termed negative polarity. With the attenuator set to 0 dB, the output of the shaker was adjusted to produce a 1.0 g/ms jerk magnitude. The attenuator was then used to control stimulus level in dB re = 1.0 g/ms. Nine stimulus durations were evaluated including 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8, 1.0, and 2.0 ms. Figure 6 illustrates actual stimuli used in the present study. Note that the real stimuli only approximate an ideal step stimulus in that the electromechanical system evidences a long time constant which can be seen as a sloping step function at long durations. This long time constant originating from the shaker has virtually no effect on VsEP thresholds since the VsEP response is initiated at short latencies during the onset of the step (see Jones et al. 2011). The onset of each of the nine stimuli was virtually identical whereas the duration of each stimulus was systematically varied. The short time constant for the shaker itself was less than 0.1 ms. VsEP threshold (defined below) was determined for each stimulus duration and the testing order for the different durations was randomized.

FIG. 5.

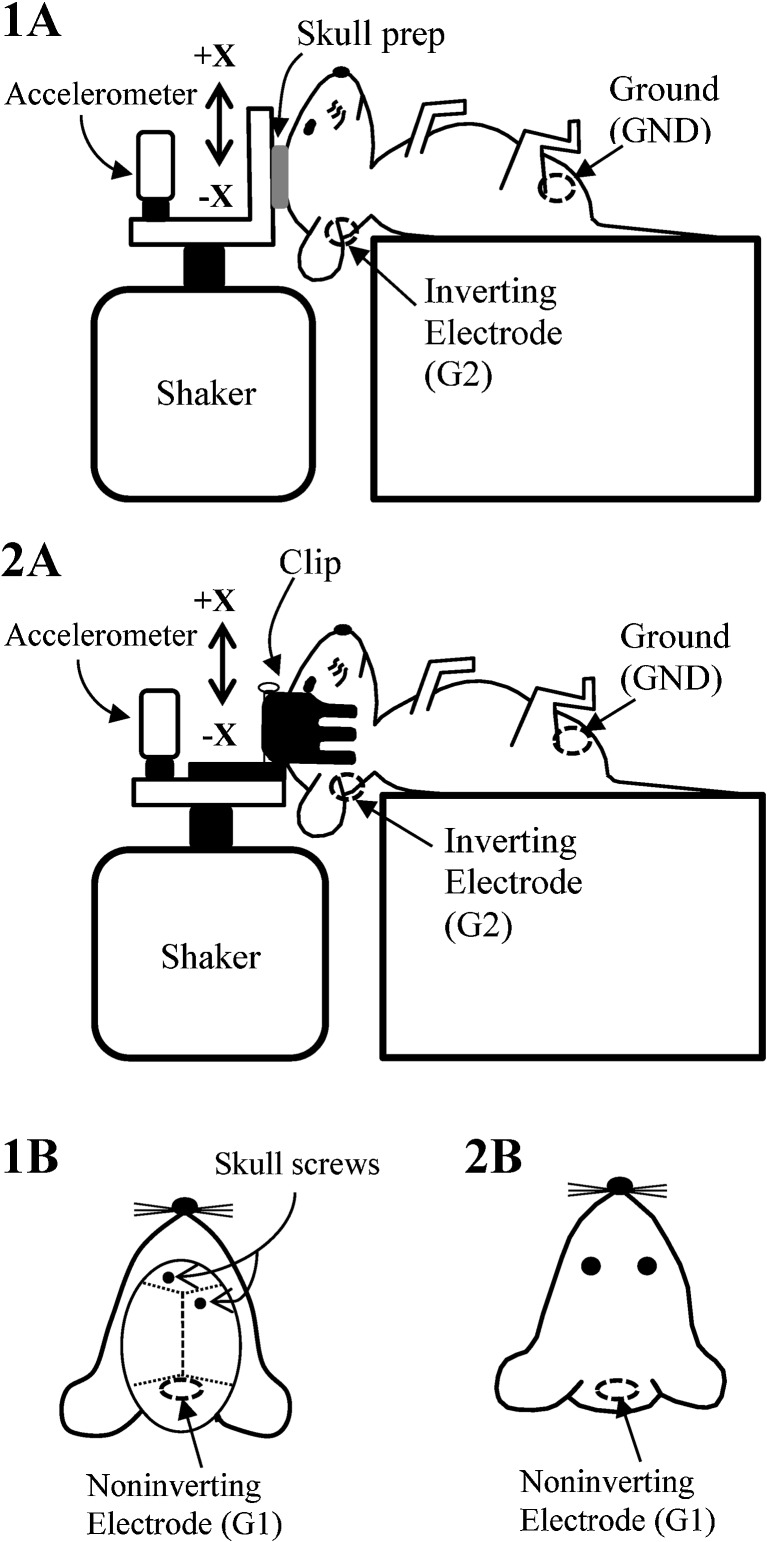
Coupling methods for delivering stimulus. The animal’s head was surgically coupled to the aluminum platform using skull screws (1a and 1b) or coupled non-surgically using a non-invasive head clip (2a and 2b). The electrodes for the skull prep method were placed caudal to the lambdoid suture (1b, non-inverting, G1), below and behind one ear (1a, inverting, G2), and on animal’s hip (1a, ground, GND). The electrodes for the head clip method are placed on the nuchal crest (2b, non-inverting, G1), below and behind the ear (2a, inverting, G2), and on the hip (2a, ground, GND).

FIG. 6.

Jerk stimuli of different step durations (2, 1, 0.8, 0.6, 0.5, 0.4, 0.3, 0.2, and 0.1 ms) delivered at a constant peak jerk level (0 dB re = 1.0 g/ms) Stimuli used for head clip (TOP) and skull preparation (BOTTOM) are shown.

Stimulus Coupling

While anesthetized lying supine, the animal’s head was secured to the shaker platform using skull screws or a non-invasive head clip (Fig. 5). Both coupling methods presented the linear translation stimulus in the naso-occipital (±Gx) axis and have been described in detail elsewhere (Jones and Jones 1999; Jones 2008; Jones et al. 2011). Coupling by skull screws (Fig. 5(1a, 1b)) involved installing two anchoring screws at the bregma (intersection of rostral coronal and sagittal cranial sutures) and inserting and sealing a stainless steel electrode epidurally over the cerebellum at the lamda (Fig. 5(1b)). A stainless steel thumbnut was positioned centrally on the skull surface, and fast setting plaster was poured to embed thumbnut and screws. The head was then bolted to the shaker platform using the thumbnut. For the non-invasive method (Fig. 5(2a, 2b)), a spring-loaded head clip was anchored to the shaker platform. The animal’s head was held snuggly in the clip as shown in Figure 5(2a). We evaluated nine animals using the non-invasive head clip method, eight animals using the skull preparation (hereafter referred to as skull prep), and three animals using both methods.

Recording Responses

Electrophysiological activity was recorded using three stainless steel electrodes (Fig. 5(1b, 2b)). The non-inverting electrode (G1) was placed either epidurally over the cerebellum near the lambda (Fig. 5(1b)) or subcutaneously at the nuchal crest at the midline (Fig. 5(2b)). The inverting electrode was placed subcutaneously behind and below the pinna (G2) and the ground subcutaneously at the hip. Electrical activity was amplified (200,000 times) and filtered at the preferred band-width for recording VsEPs (300–3000 Hz, −6 dB points, Jones et al. 2002). VsEPs were recorded using traditional signal averaging. Stimuli were presented at a rate of 17/s. Analog to digital sampling (10 μs/point, 1024 points, 16 bit conversion) was triggered at the onset of the stimulus. To minimize wire artifact, averaged responses to 128 normal and 128 inverted polarity stimuli were measured and these in turn were averaged together to produce a single response trace composed of the average of 256 sweeps. Two such response traces were recorded for each condition. Examples of VsEP response pairs are shown in Figure 3.

Response threshold was determined by systematically varying stimulus level between +6 and −18 dB re = 1 g/ms using 3 dB intervals. Threshold was defined as the stimulus level half way between the highest level failing to elicit a response and the lowest level producing a response. Thresholds were scored and assigned a consensus value by three investigators. As a standard laboratory procedure (Jones and Jones 2007), a 92 dB SPL wide band forward masker (50 to 50,000 Hz) was presented during recordings to prevent any potential auditory contamination.

We characterized threshold changes resulting from the different stimulus durations in dB SL, where dB SL is the stimulus level in dB above (+) or below (−) the animal’s measured absolute threshold (dB re = 1 g/ms) for the standard 2-ms-duration stimulus. This is traditionally referred to as sensation level (SL). The stimulus level in dB SL was determined for each animal at each stimulus duration. Zero dB SL is therefore threshold for the 2 ms stimulus for each animal.

Analysis and Statistics

VsEP thresholds were determined for each stimulus duration. Descriptive data were reported as mean ±SD (n) where SD = standard deviation, n = sample size unless stated otherwise. Repeated measures analysis of variance (rmANOVA) was used to evaluate the overall effect of stimulus duration on threshold, and the non-parametric Man-Whitney U was used to evaluate the method of head coupling (IBM SPSS Statistics v22). For the traditional overdamped model solution (Eq. 3, Appendix Eqs. A-15 and A-27), least squares exponential curve fitting to threshold data was done using SigmaPlot 12.5 (two-parameter, single exponential). For the underdamped model solution (Appendix Eqs. A-22 and A-28), MatLab curve fitting was used. The underdamped solution was an exact solution where no approximations were utilized. The mean threshold data points for both the head clip and skull prep coupling methods were fitted to the underdamped solution. The technique used was a Nelder–Mead simplex direct search unconstrained nonlinear optimization method using the MatLab function fminsearch. The sum of the errors squared (Σe²) between the underdamped solution and data was minimized in this process. The parameters of natural frequency (f_n), amplitude, and damping ratio (ζ) were allowed to vary in this process (see underdamped solution in Appendix, Eqs. A-22 and A-28).

Results

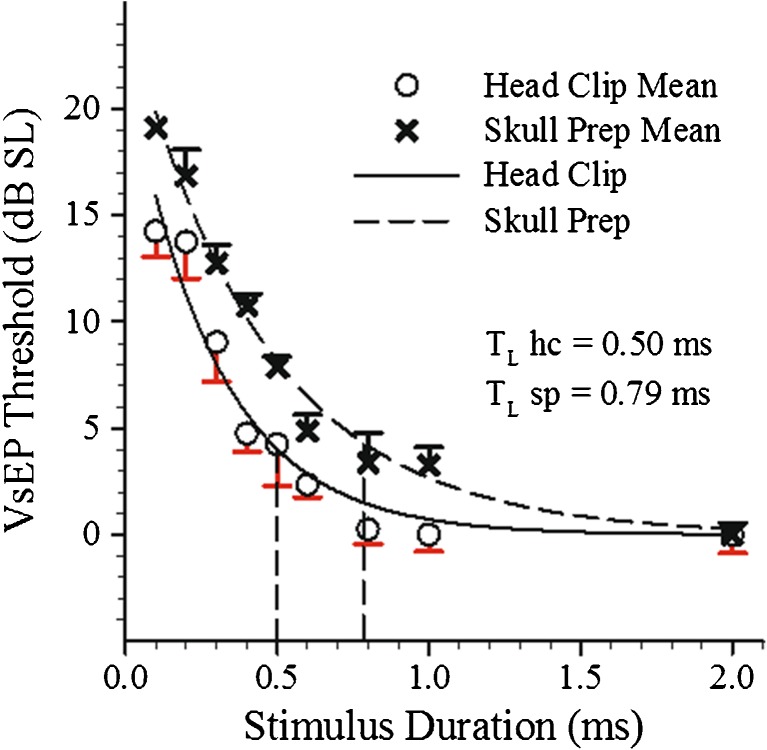
An initial group of animals (n = 13) was measured to evaluate the overall effects of seven stimulus step durations between 2 and 0.1 ms. VsEP threshold increased systematically as stimulus duration was decreased for both head coupling methods (rmANOVA: F_6,6 = 293.3, p = 3.90 × 10⁻⁷). To improve the resolution of our estimate of the threshold versus duration curves, we added seven additional animals and determined thresholds at two additional step durations (0.6 and 0.8 ms). Threshold increased with decreasing stimulus duration also in this group (rmANOVA: F_5,2 = 406.6, p = 0.002). The average thresholds across all animals for each stimulus step duration tested are summarized in Figure 7 for both methods of coupling. Figure 7 summarizes the mean threshold data as well as the variance (standard error represented) across animals for each stimulus step duration. Also shown, are the least-squares exponential fitted curves for the two methods. Table 1 summarizes findings for fitted curves. Time constants were determined from the fitted equations as follows. The upper time constant (T_L) was defined as the time point (duration), t, where threshold was elevated 3.98 dB above the threshold value at 2.0 ms. The estimated time constants for the composite data are shown in Figure 7 and were 0.50 and 0.79 ms for head clip and skull prep methods, respectively. The corresponding upper cutoff frequency estimates are 318 and 201 Hz, respectively.

FIG. 7.

Composite plots for thresholds (mean and standard error) at nine stimulus durations for head clip (OPEN CIRCLES) and skull prep (Xs) coupling methods. LINES through data are exponential fitted curves: Y = Ae^−ωt, where ω is the angular frequency associated with the fitted curves. DASHED CURVE represents skull prep and SOLID CURVE head clip coupling. TWO DASHED VERTICAL LINES mark the stimulus durations where threshold was increased by 3.98 dB above best threshold thus defining T_L for each coupling method. Long time constants for head clip preparation (T_L hc = 0.50 ms) and skull preparation (T_L sp = 0.79 ms) corresponding to 318 and 201 Hz, respectively.

TABLE 1.

Summary information for fitted exponential curves given by y = Ae ^− ωt, where ω is the angular frequency in radians/s and t is time in seconds. Based on composite data across animals. R is the correlation coefficient and R ² is the coefficient of determination.

	A	ω	R	R 2	F	p value
Head clip	22.454	3439.35	0.84	0.70	F 1,67 = 162.1	p < 0.0001
Skull prep	24.820	2226.97	0.95	0.90	F 1,63 = 548.3	p < 0.0001

In addition to the curves generated by composite data, least square fits to individual animals (head clip n = 9, skull prep n = 11) were also completed and time constants estimated using the same method as described above. These provided a basis to compare time constant estimates for the two coupling methods. Mean value for the head clip was 0.55 ± 0.11 (n = 9) ms and skull prep 0.82 ± 0.13 (n = 11) and these values were significantly different (Mann–Whitney U = 2.803, p = 0.003). Table 2 summarizes numerical findings for time constants and frequencies based on composite data as well as those estimated for individual animals.

TABLE 2.

Summary data for upper frequency cutoff and long time constant.

Composite Data			Individual Animals
			TL			fL
Preparation	TL (ms)	fL (Hz)	Mean (Hz)	SD	n	Mean (Hz)	Max	Min
Head clip	0.50	318	0.55	0.11	9	289	379	224
Skull prep	0.79	201	0.82	0.13	11	193	261	158

Discussion

Our two estimates of the long time constant (T_L, overdamped model) for stimulus transfer to the otoconial organs in the mouse correspond to upper corner frequencies of 201 and 318 Hz for composite data, and frequencies ranging from 224 to 379 Hz across individual animals. These values agree favorably with natural frequencies ranging from 328 to 396 determined directly for the isolated utricle in the red-eared turtle (Dunlap et al. 2012; Dunlap and Grant 2014). It is notable that comparable upper frequency characteristics are observed in both the intact otoconial apparatus here and in the isolated case by Dunlap and colleagues.

The present results show that threshold increases systematically as stimulus duration falls below 1 ms. The elevation in threshold is well fitted to single exponentials of the overdamped model for both coupling methods employed (Table 1). These findings support our hypothesis and provide two estimates of upper frequency cutoff points of 201 and 318 Hz. The fact that threshold increases followed closely single exponential fits also supports the assumption that the ratio of ω_S/ω_L is considerably larger than 1. The results show little evidence of corner roll off slopes steeper than −20 dB/decade (i.e., at −40 dB/decade) which would require double exponential fits for best results.

Estimates of upper frequency cutoffs made here for the mammal are considerably higher (an order of magnitude for some) than those estimated in most earlier work (50 Hz, DeVries 1950; 0.25 Hz, Young et al. 1966; 0.03 Hz, Young and Meiry 1968; 23 Hz (highest) 10 Hz (median), Fernandez and Goldberg 1976c). DeVries (1950) made estimates in fish based on direct measurements of the otoconial apparatus itself, whereas other estimates cited relied on human perception or on neural discharge patterns in other mammals to make inferences about motion of the otoconial apparatus. The present findings are consistent with recent direct measurements (Dunlap et al. 2012; Dunlap and Grant 2014).

Our measurements were indirect, but they clearly show the effective transfer of energy at high frequencies. It remains possible that the upper cutoff obtained here (318 Hz) is also an underestimate of the corner frequency. In addition to mechanical transfer to the otoconial membrane, our measurements depended on the kinetics of hair cell transduction, synaptic transmission, and activation of primary afferent neurons. The nature of the VsEP requires that these processes maintain a strict temporal consistency ensuring synchronized activation of neurons contributing to the response. If it were not so, the response would be absent or otherwise useless for the current task. The neurons generating the VsEP also collectively have similar dynamic response characteristics and are particularly suited to high-frequency activation. These features contribute to the reliability and accuracy of the method. Nonetheless, we cannot rule out the possibility that the neural activation process imposes a high-frequency limit and thus that the estimate represents a minimum value for the high-frequency corner of mechanical transfer.

The fitted curve for the head clip preparation, although accounting for about 70 % of variation in threshold, it did so less well than the skull preparation curve (90 %). The difference appears to be due to persistent low thresholds at 0.8 and 1 ms for the head clip group. It is tempting to attribute the low thresholds in this region to reduced damping in which case the exponential fit would be slightly degraded. Prompted by this question and the reduced damping reported by Dunlap and colleagues (Dunlap et al. 2012; Dunlap and Grant 2014), we completed a post hoc analysis fitting the underdamped model (damping ratio < 1.0, Appendix Eq. A-28) to our data. Damping ratio is defined as the ratio of system viscous drag [c] to the ideal critical viscous damping (c_cr), where c_cr is that damping value that provides the fastest rise time possible without oscillatory overshoot in the response to step excitation (damping ratio = ζ = c/c_cr = 1.0). Remarkably, the estimated underdamped natural frequency (f_n) and the upper frequency corner (f_L, overdamped model of 318 Hz) for data reported here were quite similar. The underdamped model produced the following estimates. For the skull prep coupling, f_n = 278 Hz (ζ = 0.9; Σe² = 4.4), whereas for the head clip coupling, f_n = 448 Hz (ζ = 0.5; Σe² = 6.4). Thus, using an underdamped model resulted in a range of frequencies that bracketed the overdamped value of 318 Hz. Significantly, both models appear to successfully fit the current data. The results for the underdamped model suggest slightly higher corner frequencies indicating that our initial overdamped method of estimation likely provided a conservative value. Additionally, the underdamped model provided an estimate of the best-fit damping ratio for the two coupling methods indicating a much higher damping ratio for the skull prep than the head clip coupling as suspected. Both the present studies and those of Dunlap and coworkers thus provide evidence for the idea that damping levels in otoconial systems may be less than traditionally assumed. Based on the present findings, this apparently applies to at least two animal classes. As argued by Dunlap and colleagues, reduced damping may provide a selective advantage in that, when adjusted effectively, it could provide for the most rapid response with minimal overshoot and distortion. The data of the present study show no evidence of substantial overshoot in the mouse otoconial apparatus.

Clearly the method of coupling to the head influenced the threshold curves obtained in the present study. Presumably, the effect of the surgical skull preparation was to reduce slightly high-frequency stimulus transfer from the shaker to the skull rather than reflecting some difference in the mechanics of the otoconial apparatus. As evidenced above, the effect likely arose from increased damping associated with the skull prep coupling. From a practical stand point, it is important to identify the difference in transfer properties for the two coupling methods since both are employed routinely for studies of vestibular function.

Clearly, the present results indicate that the macular sensor is a wideband high-frequency detector in the mouse. One can ask what purpose may be served by a vestibular sensor with these dynamic characteristics? There are likely many advantages of such a system, including the potential advantage of providing improved stability and accuracy for compensation under conditions of highly dynamic behavioral activity or externally imposed mechanical disturbances. Collective neural discharge like that generating the VsEP, for example, clearly would lead to short latency reflex activation of vestibulo-ocular and vestibulo-spinal circuits in a conscious animal. Such discharge presumably would modulate motor tone and modify compensatory motor action. That this is also possible in the human is evidenced by vestibular evoked myogenic potentials (VEMPs) which reflect vestibular-mediated reflex muscle responses to high-frequency stimuli. The present study shows that in the mouse the transfer of skull motion to the inner ear preserves high frequencies with an upper roll off point of at least 300 Hz. Whether or not this holds for the human and remains to be shown. A common complaint from human patients with profound bilateral peripheral vestibular dysfunction is a difficulty reading signage materials while walking (or running) due to oscillopsia (e.g., Bronstein 2004; Straube et al. 2012). Hypothetically, high-frequency transfer could assist in or enhance the compensation for transient disturbances of head position accompanying the impact of a footstep (heel strike) or to support rapid compensation for a brief blow (jolt) to the head.

The theoretical value of our estimate for modeling the motion of the otoconial apparatus is that it sets a lower limit for the upper frequency cutoff specifically for the in situ macular organs of the mouse and it provides general insight regarding transfer characteristics for the mammal. In a practical sense, it apprises us of the frequency response for the collective activation of macular vestibular primary afferents. In that sense, it demonstrates the upper frequency restrictions in place for macular systems, which can be contrasted with those operating for the collective activation of auditory neurons.

In summary, the current estimates of the governing upper frequency cutoff for the transfer of cranial linear translation stimuli to the macular neuroepithelium of the mouse is well above 100 Hz and more than an order of magnitude higher than those reported previously for mammals. The data support the notion that macular systems in mammals are less damped than generally appreciated. Although the transfer characteristics for the human are unknown, it is suggested that high-frequency transfer may be more important for vestibular reflexes operating to stabilize gaze during dynamic motor behavior than is acknowledged in consensus contemporary literature.

Appendix

Macular Otolith—Lumped Parameter Model

Equation of Motion

The governing equation of motion in terms of the relative displacement x (see Fig. 1) between the otoconial layer (OL) and the hair cell epithelium layer (HCE) of the sensory macula is

$$m\ddot{x}+c\dot{x}+kx=-m\left(1-\frac{{\rho }_e}{{\rho }_{OL}}\right)\left(a_{\mathrm{x}}-g_{\mathrm{x}}\right)=-mBA$$ A-1

where the over dot notation on x represents differentiation with respect to time t, x is the shear displacement, $\dot{x}$ is the shear velocity, $\ddot{x}$ is the shear acceleration, m is the mass of the OL and $m\ddot{x}$ is the inertial term, c is the damping coefficient associated with viscous drag and cẋ is the viscous damping term, k is the elastic coefficient, and kx is the elastic term, $B\equiv \left(1-\frac{{\rho }_{\mathrm{e}}}{{\rho }_{\mathrm{O}\mathrm{L}}}\right)$ is the the buoyancy term of the OL, where ρ_e is the endolymph and tissue density and ρ_OL is the OL density, a_x is the head acceleration, and g_x is the acceleration of gravity, both in the x-direction of the plane of the OL, and combining the two accelerations into a single gravitoinertial acceleration term A ≡ (a_x − g_x). The negative sign on the acceleration term indicates that a positive x-displacement of the OL is produced by a negative a_x and positive g_x acceleration components. The x-direction is defined as the direction of the acceleration component in the plane of the macula (Fig. 1). A schematic representation of the lumped parameter mechanical model associated with Eq. A-1 is presented below in the “Lumped Parameter Mechanical Model” section as illustrated in Appendix-Figure 9.

Overdamped System Transfer Function

Dividing by mass m, taking the Laplace transform of Eq. A-1 with zero initial conditions [x(t = 0) = 0; ẋ(t = 0) = 0], where s is the Laplace transform variable, defining X(s) = L[x(t)] and A(s) = L[(A(t))], and solving for the transfer function results in

$$\frac{X}{A}\left(s\right)=-B\frac{1}{\left(s^2+\frac{c}{m}s+\frac{k}{m}\right)}$$ A-2

The ratio of the damping coefficient to mass (c/m) and elastic coefficient to mass (k/m) forms two undetermined coefficients that define the motion of the OL. For an overdamped solution, the denominator of the transfer function can be factored into two first-order terms to approximate the quadratic denominator

$$\left(s^2+\frac{c}{m}s+\frac{k}{m}\right)\cong \left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right)$$ A-3

where the approximation

$$\frac{c}{m}\gg \frac{k}{c}\mathrm{and}/\mathrm{or}\left(\frac{\mathit{km}}{c^2}\right)\ll 1$$ A-4

was used. The transfer function Eq. A-2 then becomes

$$\frac{X}{A}\left(s\right)=-B\frac{1}{\left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right)}$$ A-5

Overdamped Solution for a Step Change in Acceleration

Subjecting the system to a step in acceleration of magnitude A_x and initiating the step at time t = 0 using the unit step function u(t,) the acceleration becomes

$$A\left(s\right)=\mathrm{ℒ}\left[a_{\mathrm{x}}\left(t\right)\right]=\mathrm{ℒ}\left[A_{\mathrm{x}}u\left(t\right)\right]=A_{\mathrm{x}}\frac{1}{s}$$ A-6

and the transfer function Eq. A-5 becomes

$$\frac{X}{A_{\mathrm{x}}}\left(s\right)=-B\frac{1}{s\left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right)}$$ A-7

The inverse Eq. A-7, solving for the displacement as a function of time is

$$x\left(t\right)=-A_{\mathrm{x}}B\left(\frac{m}{k}\right)\left[1+\left(\frac{mk}{c^2}\right)e^{-\left(\frac{t}{\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)}-e^{-\left(\frac{t}{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$k$}\right.}\right)}\right]$$ A-8

Two time constants arise from the overdamped solution; with T_S = short time constant, and T_L = long time constant, and they are defined as

$$T_{\mathrm{S}}\equiv \frac{m}{c}{T}_{\mathrm{L}}\equiv \frac{c}{k}$$ A-9

Using the relationship in Eq. A-4, $\left(\frac{mk}{c^2}\right)\ll 1$, it is seen that the second term in square brackets in Eq. A-8 is negligible compared to the other two terms. Eliminating the negligible middle term and using the time constant designation (T_L), Eq. A-8 becomes

$$x\left(t\right)=-A_{\mathrm{x}}B\left(\frac{m}{k}\right)\left[1-e^{-\left(\frac{t}{T_L}\right)}\right]$$ A-10

where it is seen that the short time constant T_S plays no role in the solution for an overdamped system response to a step in acceleration. This is an approximate solution. The only approximation utilized in this solution was that shown in Eq. A-4, and effects of the approximation are negligible in this solution. This is illustrated in the section below entitled “Overdamped Frequency Response” and in Appendix-Figure 8.

Note: Time constants used here are designated long and short (T_L and T_S). In almost all earlier literature, these are defined as T₁ and T₂, with T₁ being the long or larger value time constant. This is true for both the otoliths and semicircular canals. This long-short designation is used here instead of the one-two version in order to avoid confusion.

Velocity of the OL in Response to a Step in Jerk

Jerk J(s) is defined as the time rate of change of acceleration and in terms of the Laplace transform variable it is defined as

$$J\left(s\right)=sA\left(s\right)$$ A-11

The relative velocity V(s) of the OL in terms of its displacement X(s) in Laplace transform variables is the relative velocity between the OL and HCE, and is defined as

$$V\left(s\right)=sX\left(s\right)$$ A-12

Combining the above two relationships (Eqs. A-11 and A-12), it is seen that the relationship $\frac{X}{A}\left(s\right)=\frac{V}{J}\left(s\right)$ and the two transfer factions are identical.

A unit step in J(s) of constant magnitude J_x results in a constant increase in acceleration, starting from zero. The unit step in jerk is defined as

$$J\left(s\right)=J_{\mathrm{s}}u\left(t\right)=\frac{1}{s}{J}_{\mathrm{s}}\left(s\right)$$ A-13

When the above are substituted into Eq. A-7, it becomes

$$\frac{X}{A_{\mathrm{x}}}\left(s\right)=\frac{V}{J_{\mathrm{x}}}\left(s\right)=-B\frac{1}{s\left(s+\frac{c}{m}\right)\left(s+\frac{k}{c}\right)}$$ A-14

and it is seen that this expression (Eq. A-14) is identical to Eq. A-7, the right hand side of the transfer functions are identical. Likewise, the time solution for the velocity of the OL in response to a step in jerk of magnitude J_x will be identical to Eq. A-8 and is

$$v\left(t\right)=-J_{\mathrm{x}}B\left(\frac{m}{k}\right)\left(1-e^{-\left(\frac{t}{T_L}\right)}\right)$$ A-15

This relationship was used in the measurements of this work.

Overdamped Frequncy Response

Factoring the two coefficient ratios $\left(\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.\right)$ and $\left(\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.\right)$ out of the denominator of Eq. A-5 results in

$$\frac{X}{A}\left(s\right)=-B\frac{1}{\left(\frac{c}{m}\frac{k}{c}\right)}\frac{1}{\left(1+\frac{s}{\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)\left(1+\frac{s}{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\right)}$$ A-16

and recognizing that the two factored terms are frequencies, that $\left(\frac{c}{m}\frac{k}{c}\right)=\frac{k}{m}={\omega }_n^2$, changing s = jω where $j=\sqrt{-1}$, and converting to magnitude notation in terms of the stimulus frequency ω, Eq. A-16 becomes

$$\left|\frac{X}{A}\right|\left(\omega \right)=-B\frac{1}{{\omega }_n^2}\frac{1}{\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)}^2}\right)\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\right)}^2}\right)}$$ A-17

The magnitude term $\left|\frac{X}{A}\right|$ of Eq. A-17 has units of reciprocal seconds squared and this term can be converted to a non-dimensional form by dividing the equation by the reciprocal of ω²_n. Also dividing by the buoyancy term B results in a non-dimensional magnitude form of Eq. A-17

$$M_{\mathrm{N}\mathrm{D}}=\left|\frac{X}{A}\right|\left(\frac{{\omega }_n^2}{B}\right)=-\frac{1}{\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)}^2}\right)\left(\sqrt{1+{\left(\frac{\omega }{\raisebox{1ex}{$c$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\right)}^2}\right)}$$ A-18

where M_ND is defined as the non-dimensional magnitude.

Equation A-18 can be plotted with the horizontal axis as frequency f in Hz or as non-dimensional frequency defined as ω/ω_n and the vertical axis is in decibels. Using the frequency ratio of the two factors, R, which is defined as

$$R=\frac{c/m}{k/c}=\frac{{\omega }_{\mathrm{S}}}{{\omega }_{\mathrm{L}}}$$ A-19

plots for several examples of R values are shown below in Appendix-Figure 8

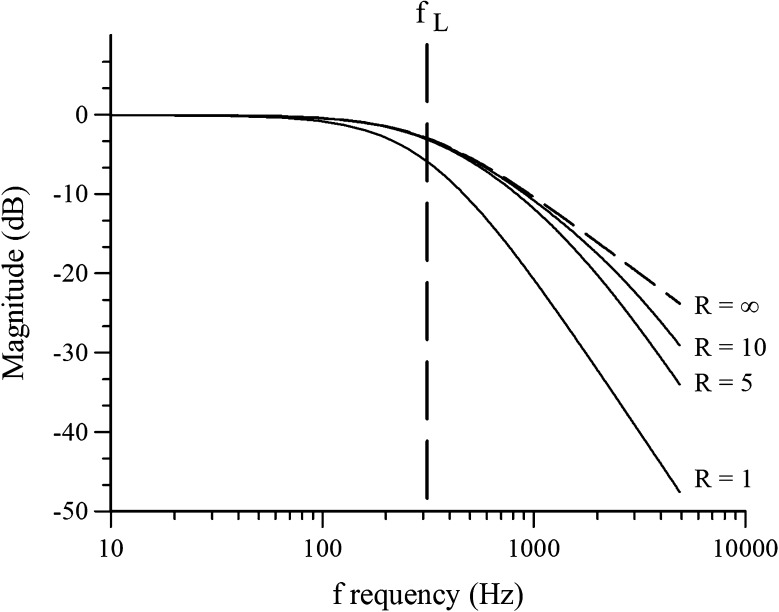
Appendix-Figure

In Appendix-Figure 8 below, the non-dimensional magnitude, Mnd, is plotted in dB and frequency is represented in Hz, where f_L = ω_L/2π, and f_S = ω_S/2π. As can be seen, when R = 1, the two corner frequencies combine to produce a steep roll off slope of −40 dB per frequency decade. At f_L (dashed vertical line), the amplitude of the R = 1 curve is well below the other curves (−6 dB vs. −3 dB) indicating an important influence of f_S on the frequency corner when f_s approaches f_L. However, at higher values of R, f_S has little influence on the magnitude at f_L since curves R = 5, R = 10 and R = ∞ all superpose at f_L. f_S has negligible influence on the magnitudes at f_L in these cases. Dashed curve represents the resulting magnitudes when fs is infinite and this illustrates the slope of −20 dB/decade imposed by f_L alone. In the present study, frequencies well below 1000 Hz are of interest. As can be seen the influence of f_S is negligible below about 700 Hz even for R = 5. f_L = 318 Hz as determined in the present study. It is estimated that R ∼ 10 in the macular system.

Underdamped Transfer Function and Response

Recent work (Dunlap and Grant 2014) has shown that the utricle system dynamics is underdamped in the turtle. It is hypothesized that this may be the case for many animals, especially mammals that have dynamic body and head motion in excess of those of a turtle. Turtles have long flexible necks that are used for feeding strikes that necessitate high-frequency responses from their utricle. The mouse used in these experiments may have an underdamped utricle accelerometer system. Presented here is an underdamped transfer function and it is compared to the overdamped case for the stimulus used in the present study.

An underdamped transfer function is identical to Eq. A-2 and is repeated here with the velocity-jerk relationship included

$$\frac{X}{A}\left(s\right)=\frac{V}{J}\left(s\right)=-B\frac{1}{\left(s^2+\frac{c}{m}s+\frac{k}{m}\right)}$$ A-20

The transfer function for a step in acceleration or a step in jerk is

$$\frac{X}{A_{\mathrm{x}}}\left(s\right)=\frac{V}{J_{\mathrm{x}}}\left(s\right)=-B\frac{1}{s\left(s^2+\frac{c}{m}s+\frac{k}{m}\right)}$$ A-21

where the magnitudes of the steps have x-subscripts. The Laplace inversion of Eq. A-21 gives the time solution for the step excitation and that is

$$\frac{x}{A_{\mathrm{x}}}\left(t\right)=\frac{v}{J_{\mathrm{x}}}\left(t\right)=-B\frac{1}{{\omega }_n^2}\left[1-\frac{1}{\sqrt{1-{\mathrm{\zeta }}^2}}{e}^{-\left(\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$2T_s$}\right.\right)}sin\left({\omega }_{\mathrm{d}}t+\varnothing \right)\right]$$ A-22

where:

$${\omega }_{\mathrm{n}}^2=\frac{k}{m}2\zeta {\omega }_{\mathrm{n}}=\frac{c}{m}$$ A-23

and ω_n is the natural resonant frequency and ζ is the damping ratio. The damping ratio is ζ < 1 in the case for an underdamped solution (ζ = 1 for critical damping);

$${\omega }_{\mathrm{d}}\equiv {\omega }_{\mathrm{n}}\sqrt{1-{\zeta }^2}$$ A-24

where ω_d is the damped natural frequency; and

$$\varnothing ={tan}^{-1}\left(\frac{\sqrt{1-{\zeta }^2}}{\zeta }\right),0<\varnothing <\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$$ A-25

where ∅ is the phase angle. The additional terms introduced here are standards used for underdamped solutions. Unlike the overdamped solution, there are no approximations utilized in this solution.

Comparison of Underdamped and Overdamped Models

A comparison of the above underdamped solution (Eq. A-22) with the overdamped solution (Eqs. A-10 and A-15) is made here. The overall transfer function is rewritten in two terms: with amplitude term Amp and a time response term t_resp

$$\frac{x}{A_{\mathrm{x}}}\left(t\right)=\frac{v}{J_{\mathrm{x}}}\left(t\right)=\left[\mathit{Amp}\right]\left[t_{\mathit{resp}}\right]$$ A-26

where the amplitude $\mathit{Amp}=B\frac{1}{{\omega }_{\mathrm{n}}^2}$, and thus the amplitudes of the overdamped and underdamped responses are identical and this magnitude is set as one for this comparison. The two time response terms, t_RESP, are represented as

$${\left(t_{\mathit{resp}}\right)}_{\mathit{OvrDmp}}=\left(1-e^{-\left(\frac{t}{T_L}\right)}\right)$$ A-27

$${\left(t_{\mathit{resp}}\right)}_{\mathit{UndrDmp}}=\left(1-\frac{1}{\sqrt{1-{\mathrm{\zeta }}^2}}{e}^{-\left(\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$2T_s$}\right.\right)}sin\left({\omega }_{d}t+\varnothing \right)\right)$$ A-28

The underdamped solution (Eq. A-28) was fitted to the data reported in the present study to obtain values for the natural frequency (ω_n), damping ratio (ζ), and sum of the errors squared (Σe²) for the best fit.

Lumped Parameter Mechanical Model

Appendix Figure