A simple routine for quantitative analysis of light and dark kinetics of photochemical and non-photochemical quenching of chlorophyll fluorescence in intact leaves

Abstract

Paper describes principles and application of a novel routine that enables the quantitative analysis of the photochemical O–J phase of the variable fluorescence F _v associated with the reversible photo-reduction of the secondary electron acceptor Q_A of photosystem II (PSII) in algae and intact leaves. The kinetic parameters that determine the variable fluorescence F ^PP(t) associated with the release of photochemical quenching are estimated from 10 µs time-resolved light-on and light-off responses of F _v induced by two subsequent light pulses of 0.25 (default) and 1000 ms duration, respectively. Application of these pulses allows estimations of (i) the actual value of the rate constants k _L and k _AB of the light excitation (photoreduction of Q_A) and of the dark re-oxidation of photoreduced Q_A (${\text{Q}}_{\text{A}}^{-}$), respectively, (ii) the actual maximal normalized variable fluorescence [nF _v] associated with 100 % photoreduction of Q_A of open RCs, and (iii) the actual size β of RCs in which the re-oxidation of ${\text{Q}}_{\text{A}}^{-}$ is largely suppressed (Q_B-nonreducing RC with k _AB ~ 0). The rate constants of the dark reversion of Fv associated with the release of photo-electrochemical quenching F ^PE and photo-electric stimulation F ^CET in the successive J–I and I–P parts of the thermal phase are in the range of (100 ms)⁻¹ and (1 s)⁻¹, respectively. The kinetics of fluorescence changes during and after the I–P phase are given special attention in relation to the hypothesis on the involvement of a Δµ _H+-dependent effect during this phase and thereafter. Paper closes with author’s personal view on the demands that should be fulfilled for chlorophyll fluorescence methods being a correct and unchallenged signature of photosynthesis in algae and plants.

Introduction

The time pattern of variable chlorophyll a (chla) fluorescence of alga and plant leaves (chla fluorescence induction) in an actinic light pulse provides valuable information on properties and characteristics of the photosynthetic processes that are initiated by the light. Amongst those are (i) generation and decay of trans- and inner membrane electric fields associated with primary charge separation in the photochemical systems PSI and PSII, (ii) photochemical reduction of the primary electron acceptor pair [PheQ_A] with pheophytin (Phe) and Q_A acting as primary and secondary electron acceptors and fluorescence quenchers, respectively, (iii) secondary processes that are coupled to electron transport in the photosynthetic transport chains, that among others lead to generation and dissipation of a trans-thylakoid electrochemical proton gradient (Δµ _H) which powers ATP synthesis and transmembrane ion fluxes.

The fluorescence induction pattern F(t) in a dark-adapted leaf or algal suspension shows at high actinic intensities a poly-phasic so-called OJIP increase in variable fluorescence F _v(t) from an initial F _o level at O toward a maximal F _m level at P. The F _o to F _m rise in the light usually covers a time span of five decades from 10 μs to 1 s and is followed in prolonged illumination by a so-called PSMT decay in a time range extending to several minutes (Govindjee 2004; Papageorgiou et al. 2007). The labels in the OJIPSMT (or Kautsky) fluorescence induction curve mark the intercept of subsequent response phases in which the apparent rate of fluorescence increase or decrease is different.

The OJIP part of the Kautsky fluorescence induction curve has received ample attention from distinctly different viewpoints. The first group is primarily focussed upon a mathematical analysis and presentation of the characteristic shape of the constituting O–J, J–I, and I–P components (Pospìsil and Dau 2000; Boisvert et al. 2006; Antal and Rubin 2008; Joly and Carpentier 2009). I will denote it here with the math-fit-test (MFT). MFT leads to the fitting of an OJIP curve with the sum of three exponential functions, including those with a coefficient accommodating the sigmoidal character of the distinguishable phases (Joly and Carpentier 2009). MFT is hampered by the fact that none of its parameters bears a simple relation to those of the photochemical and non-photochemical reactions that are at the basis of and responsible for the bioenergetic performance of the photosynthetic system under study. The second class uses the so called JIP test introduced by Reto Strasser and his coworkers (Strasser et al. 1995, 2004; Stirbet and Govindjee 2012). The JIP test is a systematic method and practical tool to obtain quick information, particularly on PSII, from the OJIP induction curve on various (possibilities of) effects on photosynthesis. The information is gathered and estimated in this test from the fluorescence emission data at a limited number, usually 6, of (time) locations within the monitoring period of the fluorescence emission induced by a fixed actinic light intensity, usually ~3000 µmol photons.m⁻² s⁻¹. The JIP test is, among others, based on the assumption that (i) the maximum fluorescence F _m is exclusively associated with 100 % reduction of the primary quinone acceptor Q_A and (ii) F _m can be reached, for instance in the presence of a herbicide like DCMU, in one single-saturating light flash (STF). The JIP test has found many applications in eco-physiological research dealing with the effect of several environmental stress forms on plant performance (see for a recent review Guo and Tan 2015). The third category uses system approaches in which the variable fluorescence is analyzed in terms of kinetic parameters of primary and associated photosynthetic reactions linked to F _v. One of these is aimed at availability and use of a fluorescence induction algorithm (FIA) with manageable expressions for the photochemical and non photochemical (thermal) components of the variable fluorescence during the OJIP traject. Its application is called FIA methodology. The constituting mathematical expressions are based on analysis and solutions of the kinetic equations of the underlying reactions in terms of identifiable reaction parameters, amongst which the actinic intensity in the range between 30 and 3000 µmol photons.m⁻² s⁻¹. The FIA methodology is conceptually different from the alternate approaches in a sense that it is based on the concept (Vredenberg 2000) of the three-state trapping model (TSTM) and as such not limited by the disputable constraint (Stirbet and Govindjee 2012) that 100 % reduction of the primary quinone acceptor Q_A is required and sufficient for reaching the maximum fluorescence F _m.

The time scale patterns of the OJIP rise in algae and leaves at light intensities of about 1000 μmol quanta m⁻² s⁻¹ commonly shows an initial exponential O–J increase toward a quasi-stationary level J within a few ms and followed by two sequential S-shaped J–I and I–P rises that are completed within 30 and 500 ms, respectively. The patterns show intercept levels at J, I, and P with 2.5 < F _J/F _o < 3.5, 4.5 < F _P/F _o) < 5.5, and F _I ~ 10 % below F _P. The different sensitivities of the OJ and JIP responses to alterations in among others light intensity, temperature or PSII-inhibiting herbicides has led to their distinction as the photochemical (OJ) and a non-photochemical thermal phase (JIP) (for literature survey and reviews see Samson et al. 1999; Stirbet and Govindjee 2012; Schansker et al. 2011).

The interpretation of the OJIP induction profile in terms of reactions and processes that are involved, is under continuing debate (Stirbet and Govindjee 2012; Vredenberg et al. 2012; Schansker et al. 2013). A large variety of simulation models for the OJIP induction curve has been presented that describe the variable fluorescence at a given light intensity (excitation rate) in relation to reaction center closure (Stirbet et al. 1998; Vredenberg 2000; Strasser et al. 2004; Kramer et al. 2004; Zhu et al. 2005; Lazár and Schansker 2009; Belyaeva et al. 2008). RC closure in most of these concepts is assumed to be exclusively due to single-photon trapping in the RC of PSII and the stabilization of an electron at its acceptor side as reflected by the light-driven reduction of the Q_A. Photoreduction of Q_A is thought, following the interpretation of Duysens and Sweers (1963), to release the quenching properties of the oxidized form of Q_A. Fluorescence changes elicited with (sub-)ns excitations have indicated that the oxidized primary donor of PSII (P680⁺) quenches the fluorescence as well (Butler 1972; Mauzerall 1972). A conceptually different so called double-hit three state trapping model (TSTM) has been proposed (Vredenberg 2000, 2004; Vredenberg and Prasil 2009). This takes into account, as outlined in detail in the literature (Vredenberg et al. 2009; Vredenberg et al. 2012) that RC-closure, i.e., the increase in variable fluorescence, is not exclusively and necessarily caused by the photochemical reduction of Q_A, but is also promoted by photo-electrochemical and electrical events in the vicinity of the membrane bound RC. The following characteristic differences between the concept of the ‘classic’ single-hit trapping models and that of TSTM are (i) operation of a double-hit trapping mechanism in TSTM in which the primary PSII electron acceptor pair [PheQ_A] of open RCs acts as a competent two electron trap, (ii) two successive single-turnover excitations are required for semi-closure [PheQ_A]⁻¹ and subsequent closure [PheQ_A]²⁻ of the RC (Vredenberg 2000, 2011), and (iii) semi-closure of all open RCs [inducible in chloroplasts by a saturating single-turnover flash (STF)] is accompanied by a normalized variable fluorescence $n{F}_{\text{v}}^{\text{STF}}=(F_{\text{m}}^{\text{S}}\text{TF}-F_{\text{o}})/(F_{\text{o}})\sim 2;$ full closure [inducible by repetitive STFs or by 250 ms fluorescence saturating pulses (SP)] results in an approximate doubling of the normalized variable fluorescence $n{F}_{\text{v}}^{\text{SP}}=F_{\text{m}}^{\text{SP}}-F_{\text{o}}/F_{\text{o}}\sim 4$, which suggests a normalized variable fluorescence per trapped electron nF _v ~ 2 (Vredenberg et al. 2012), (iv) chlorophyll fluorescence yield is sensitive to electrochemical changes, in particular to that of the transmembrane electrochemical gradient of protons (Δµ _H+) which are (is) coupled to linear and cyclic electron transport between the photosystems and around PSI, respectively, and (v) the concept of so called ‘inactive’ RCs is in TSTM substituted by a dynamic heterogeneity of Q_B-reducing and Q_B-nonreducing RCs (Chylla and Whitmarsh 1989; Lavergne and Leci 1993; Tomek et al. 2003; Vredenberg et al. 2006). The conclusion that the STF-induced saturation of photochemical quenching is associated with approx. 50 % of the SP-induced maximal variable fluorescence F _m has been confirmed in a recent study with the alga Chlorella (Klughammer and Schreiber 2015). An alternate interpretation of the non photochemical thermal JIP phase has been proposed in which the fluorescence de-quenching reaction is presumed to be due to a light-driven conformational change in PSII (Schansker et al. 2011).

This paper gives illustrations and kinetic analyses of the light-on and light-off responses of the variable fluorescence $F_{\text{v}}\left(t\right)/F_{\text{o}}\left[=F\left(t\right)/F_{\text{o}}-1\right]$ in intact leaves and algae upon light pulses variable in duration and intensity. Analysis of the time responses is based on the solution of the equation for a light–dark reversible transfer of an RC with Q_A toward one with ${\text{Q}}_{\text{A}}^{-}$. Application of pulses in the time range between 0.25 and 1 ms enables estimations of (i) the actual value of the rate constants k _L and k _AB of the light excitation (photoreduction of Q_A) and of the dark re-oxidation of photoreduced Q_A (${\text{Q}}_{\text{A}}^{-}$), respectively, (ii) the actual maximal normalized variable fluorescence nF _v associated with 100 % photoreduction of Q_A of open RCs, (iii) the actual size β of RCs in which the re-oxidation of ${\text{Q}}_{\text{A}}^{-}$ is largely suppressed (Q_B-nonreducing RC with k _AB ~ 0), and (iv) a distinct decrease with pulse duration of the initial rate of the fluorescence recovery (re-quenching) at light off, presumably indicating the pH dependence of k _AB. The results give strong support for the hypothesis that the photochemical O–J phase in the 0.01–2 ms time range of the OJIP induction curve is, for the major part, caused by the variable fluorescence F ^PP(t) associated exclusively with the primary photoreduction of Q_A. A simple routine program for estimating the actual kinetic parameters of the photochemical fluorescence induction phase in intact leaves and algae is outlined and is available upon request. Pulses in the time range covering the J–I phase show responses with, for the major components, rate constants in the range of (10 ms)⁻¹ and (100 ms)⁻¹ in the light and dark, respectively. The characteristics of those in the range of the I–P phase add to the evidence that the variable fluorescence F ^CET(t) in this phase originates from the build-up of the proton motive force by the light-driven proton pump coupled to cyclic electron transport around PSI.

The paper is concluded with a personal view on the present status of chlorophyll fluorescence in relation to its potency for being ‘a signature of photosynthesis’. It expresses my feeling on the urgent need for coming to an agreement on the controversial views on the as yet unsolved problem whether or not the closure of the photosynthetic reaction center and its associated maximal increase in variable fluorescence toward F _m can be accomplished only by the photochemical conversion of Q_A. The answer to this question has far reaching consequences for the validity of some of the conclusions on the photosynthetic performance and characteristics of intact leaves and algae obtained with current fluorescence techniques.

Materials and methods

Nannochloropsis sp. (CCAP 211/78) cells were grown in June in an outdoor tubular fence-type photo bioreactor at a dedicated facility of the Wageningen University, (<http://www.algaeparc.com>). Tube diameter was 4.6 cm and the cells were grown in seawater enriched with nutrients at pH 7.5 and at a temperature between 25 and 30 °C. Cell concentration in the photobioreactor was maintained constant at 1.5 g dry weight per liter by continuous reactor dilution. This concentration corresponds to approximately 10 µg chl ml⁻¹; 4 ml samples were directly transferred to 1 × 1 cm cuvettes in the sample holder of the measuring device. Young leaves of Arum italiensis, Rosea gislaine, and Kalanchoë were collected from plants in the home garden; spinach leaves from a fresh batch were from a local supermarket. Leaves were positioned in the leaf holder of the measuring device.

Fluorescence experiments were done using the modulated chlorophyll fluorometer OS1p (Opti-Science Ltd, Hudson, USA) in its so-called FIA-OJIP routine (Vredenberg et al. 2013). Light-on and light-off kinetics of the variable fluorescence in light pulses variable in length from 0.25 ms to tens of seconds, and of intensity in the range between 50 and 5000 µmol photons.m⁻² s⁻¹ can be monitored. The time resolution during a light and dark period is variably programmable at values from 10 µs to 1 s. Special attention is given to application of short saturating pulses (sSPs) in the time range between 250 and 1000 µs. The experimental traces in general represent the averages of five samples. Curve fitting of the experimental quenching responses was done with application of proper routines provided by Excel software.

Theoretical aspects

Light-on and light-off kinetics of variable fluorescence in cells and leaves; photochemical phase

The photochemical-driven dark-reversible change in the fluorescence yield of the PSII antenna’s is variable between F _o and F _m for centers in which the PSII electron acceptor side denoted with [PheQ_A] is oxidized (open centers) and single reduced ([PheQ_A]¹⁻, semi-closed), respectively. The monitoring of light-on and light-off kinetics has been shown to enable a quantitative analysis of alterations in photochemical quenching of PSII fluorescence under variable conditions (Vredenberg and Prasil 2013). The increase in the variable chlorophyll fluorescence $F_{\text{v}}\left(=\frac{F\left(t\right)-F_{\text{o}}}{F_{\text{o}}}\right)$ at the onset of light is attributed, as first demonstrated by Duysens and Sweers (1963), to the de-quenching of PS II antenna fluorescence associated with energy trapping and stabilization in a PSII reaction center leading at the acceptor side to photoreduction of Q_A.

Under conditions at which effects of intersystem energy transfer (connectivity) between photosynthetic units [see for a review (Stirbet 2013)] and of donor side quenching in PS II by the secondary electron donor of PS II ($Y_{\text{z}}^{+}$) are negligible, the photochemical-driven initial F _v increase is theoretically predicted to be exponential (Vredenberg 2008a). The reaction rate at the onset of illumination is determined by the light excitation rate k _L, and has been shown to vary linearly with light intensity. For a great variety of plant species incident PAR intensity at the leaf surface of ~2000 µmol quanta.m⁻² s⁻¹ is found to correspond globally with a value k _L ~ 1 ms⁻¹.

The reversal of the photochemically generated signal at light off (dark decay of variable fluorescence) is the consequence of (re-) quenching associated with re-oxidation of the reduced electron acceptor ${\text{Q}}_{\text{A}}^{-}$ by secondary electron acceptors. This light-independent oxidation proceeds in dark-adapted samples with a rate constant k _AB that has been reported to be in the range between 2 and 5 ms⁻¹ (Robinson and Crofts 1983).

The time pattern of the photochemical de- and re-quenching of the fluorescence by Q_A during and after actinic illumination is predicted by the analytical solution of the ordinary differential equations (ODE’s) for the reversible photoreduction of Q_A (Vredenberg 2011). Briefly, the kinetic analysis of the reaction that describes the photochemical reduction of Q_A gives a quantitative expression for the fraction q ^dsq of centers that has become photochemically closed in the light at time t, with

$$q_0^{\text{dsq}}\left(t\right)=\frac{k_{\text{L}}}{k_{\text{L}}+k_{\text{AB}}}\times [1-e^{-\left(k_{\text{L}}+k_{\text{AB}}\right)t}],$$ 1

where the superscript ^dsq refers to the condition that donor-side quenching (by $Y_{\text{z}}^{+}$) is considered to be negligible (Vredenberg 2011) and the subscript ₀ to that of a homogeneous system in which the fraction of the so-called Q_B-nonreducing RCs, in which k _AB ~ 0, is zero. Accordingly,

$$q_{\mathit{\beta }}^{\text{dsq}}\left(t\right)=[1-e^{-k_{\text{L}}·t}]$$ 1a

For a heterogeneous system with a β-fraction of Q_B-nonreducing RCs

$$q^{\text{dsq}}\left(t\right)=\left(1-\mathit{\beta }\right)·q_0^{\text{dsq}}\left(t\right)+\mathit{\beta }\times q_{\mathit{\beta }}^{\text{dsq}}\left(t\right)$$ 2

The ‘re-opening’ recovery of the fractions in the dark, after light off at t = t ₀, follows the exponential function

$$q_{\text{d}}^{\text{dsq}}\left(t\right)=q^{\text{dsq}}(t_0)\times e^{-\left(k_{\text{AB}}\right)t},$$ 3

where the subscript _d refers to darkness. The variable fluorescence F ^PP1(t) associated with the photochemical-dependent de- and re-quenching during and after illumination is given by

$$F^{\text{PP1}}\left(t\right)=n{F}_{\text{v}}\times q^{\text{dsq}}(t),$$ 4

where nF _v is the maximal fluorescence $F_{\text{m}}^{\text{PP}}$ when Q_A is 100 % (photo-) reduced, i.e., when all RCs are photochemically closed and q ^dsq = 1.

Equations 1–4 demonstrate the inadequacy of the earlier mentioned MTF to fit the O–J phase of the OJIP curve with a single exponential of the form $F=F_{\text{o}}+A_{\text{O - J}}\left[1-exp\left(-k_{\text{O - J}}·t\right)\right]$ (Joly and Carpentier 2009). MFT will not provide handsome information on the processes that are responsible for the O–J rise during fluorescence induction.

It has been shown (Vredenberg et al. 2006) that the β-fraction of Q_B-nonreducing RCs, has a non-zero efficiency Φ for transiently trapping a second electron causing the transient double reduction of the PSII acceptor side in these RCs. This is associated with a variable fluorescence

$$F^{\text{PP2}}\left(t\right)=\mathit{\beta }·n{F}_{\text{v}}·q_{\mathit{\beta }}^{\text{dsq}}\left(t\right)·(1-e^{-\mathrm{\varnothing }·k_{\text{L}}·t})·e^{-k_{2\text{AB}}·t}.$$ 5

In which Φ is the electron trapping efficiency in the fraction with reduced Q_B-nonreducing RCs and k _2AB the re-oxidation rate constant of the double-reduced acceptor pair (Vredenberg and Prasil 2009; Vredenberg 2011). It is noteworthy that, according to Eq. 5, dF ^PP2(t)/dt = 0 at t = 0, which causes an S-shaped F ^PP2(t)-response. The analytical solution for the variables fluorescence associated with the primary photochemical events is obtained after summation of Eqs. 4 and 5

$$F^{\text{PP}}\left(t\right)=F^{\text{PP1}}\left(t\right)+F^{\text{PP2}}\left(t\right).$$ 6

It easily follows from Eqs. 1–4, that F ^PP1(t) reaches for t ≫ (k _L + k _AB)⁻¹ a time-independent equilibrium steady state $F_{\text{ss}}^{\text{PP1}}$ in the light equal to

$$F_{\text{ss}}^{\text{PP1}}=n{F}_{\text{v}}·\frac{k_{\text{L}}}{k_{\text{L}}+k_{\text{AB}}}.$$ 6(a

Similarly one obtains, for t ≫ (k _2AB)⁻¹, $F_{\text{ss}}^{\text{PP}}$ = 0. This makes that

$$F_{\text{ss}}^{\text{pp}}=F_{\text{ss}}^{\text{pp1}}=n{F}_{\text{v}}\frac{k_{\text{L}}}{(k_{\text{L}}+k_{\text{AB}})}$$ 6b

Thus the steady state value in the light $F_{\text{ss}}^{\text{PP}}$ of the variable fluorescence associated with primary photochemical quenching is attenuated with respect to the maximal variable fluorescence nF _v associated with 100 % photochemical reduction of Q_A. The attenuation factor is determined by the light excitation rate k _L and the rate of fluorescence (re-) quenching k _AB in the dark.

Glossary and description of graphic F PP(t) parameters (see Fig. 1)
Fo	experimental value of F exp in sSP (or SP) at t = 0.01 ms; normalization relative to Fo = 1 has been done
nF v	approximated by nF v = (F m – 1)/2 in which F m is the maximum of F exp at the P-level (see inset)
k L	slope (ms−1) of the initial F exp—rise in the 0.01–0.1 time range divided by nF v
β	fraction of Q B-non reducing RCs in dark-adapted sample; equal to amplitude of extrapolated slow decay component at t 0 (sSPoff) divided by (1 − exp(−k L × 0.25)) to account for the incomplete photoreduction of the fraction β at the cessation time (default t 0 = 0.25 ms) of sSP0.25
k AB	decay rate (ms−1) of fast decay component; its reciprocal value equals the length of the (green) vertical line (in ms) between the time t 0 (=0.25 ms) of sSP-off and the time at which the SSP-off slope (interrupted black line) intercepts with the decay curve of (red dots)
Approximation and tuning of ‘guess’ parameters to accommodate the matching of F PP at the junction of O–J and J–I phases
Ø	electron trapping efficiency, which is determined by limitation of rate of P+ oxidation at PSII donor site by that of radical pair recombination in fraction of Qb-nonreducing RCs with single reduced acceptor pair (Vredenberg 2004); actual value, usually in range between 0.1 and 0.5, obtained after varying a tuning factor for matching F PP with F exp at the junction of O–J and J–I phases (see under results)
k 2AB	oxidation rate of double reduced QB-nonreduccing [S0-] RCs in the range between 0.05 and 0.5 ms−1 obtained after varying the tuning factor for matching F PP with F exp at the junction of O–J and J–I phases (see under results).

A graphical representation of F ^PP(t) (Eq. 6) demands substitution of the values of its constituting parameters (Eqs. 1–5). Relevant data for the estimation of most of these parameters can be derived from (i) the maximum fluorescence level F _m at the P-level of an SP-induced OJIP induction curve, (ii) the slopes of the initial rise and of the decay components an sSP-induced response, and (iii) the relative amplitudes of the decay components of an sSP-response. The sSP-off decay (Fig. 1) is resolved in three exponential components (not shown) and attributed to the fast and slow plus moderate decay of Q_B-reducing (open circles) and Q_B-nonreducing RCs (red dots), respectively. An example is illustrated in Fig. 1. A glossary of the parameters that determine the kinetic profile of the variable fluorescence F ^PP(t) associated with primary photochemical quenching is given in the text box (see above).

Fig. 1.

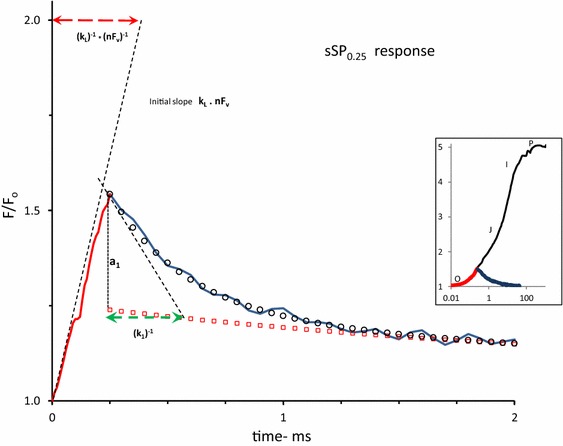
A 2 ms linear time plot of the variable fluorescence F(t)/F _o in a Kalanchoë leaf during (red-colored line) and after (blue-colored line) a short saturating pulse of 250 µs duration (sSP_0.25) and 3000 µmol photons m⁻² s⁻¹ intensity. The pulse is given at t = 0. The insert illustrates the response upon excitation with a 1 s saturating pulse (SP) of the same intensity of 3000 µmol photons m⁻² s⁻¹ on a log time scale and, in red, that upon excitation with sSP_0.25. Upward moving dashed line at t = 0 is the initial slope of the response at the onset of sSP_0.25. The downward-directed dashed line at the start of the decay at t = 0.25 ms is the initial slope of the decay at sSP_off. Open black circles are of the calculated exponential decay $a_1.e^{-k_1.t}$ which, when supplemented with the residual decay (open red squared), simulates the initial F(t)/F _o decay in the 0.25–1.5 ms time range. Further details are given in Fig. 2 and its legend. The length of the red-colored dashed horizontal line that connects the point F/F _o = 2 on the vertical axis with that of its intercept with the black-colored upward moving line of the initial slope of the response at t = 0, gives the value of the reciprocal of the initial slope. Here the sSP_0.25-response at t = 0 apparently occurs with a reciprocal rate of ~ 350 µs. Similarly, the length of the green colored horizontal line from t = 0.25 to the intercept of the slope line with the (calculated) residual curve (red squares) gives a graphical approximation of the reciprocal of the rate constant ((k ₁)⁻¹) of the fast component

The analytical solutions (Eqs. 2–4), representing the fluorescence simulation during and after sSP illumination (Fig. 1), illustrate some particular and important aspects of the reaction kinetics of the light–dark reversible de- and re-quenching by Q_A in the (photochemical) OJ phase of PSII chlorophyll fluorescence under conditions at which connectivity, donor side-, photoelectrochemical-, and non-photochemical quenching are assumed to be negligible. Firstly, the amplitude of the time-independent equilibrium steady state of the variable fluorescence in the light $F_{\text{ss}}^{\text{PP}}$ is, according to Eq. 6b, dependent on and determined by the light excitation rate k _L and the rate of fluorescence (re-)quenching k _AB in the dark. Measurements from which these rates can be determined, like those initiated by short light pulses (Fig. 1) are essential for quantifying the steady state level of the variable fluorescence associated with photochemical quenching. They are for example required for the interpretation of relative changes in the (quasi-)steady state levels of variable fluorescence observed in OJIP induction curves. Secondly, it easily follows from Eqs. 4–6 and recalling that dF ^PP2(t)/dt = 0 at t = 0, that the initial rate (slope) of the variable fluorescence dF ^PP(t)/dt (=dF ^PP1(t)/dt = nF _v·k _L) associated with photochemical reduction of Q _A reduction (de-quenching) is independent of the actual rate k _AB of its dark re-oxidation (quenching). This means for instance that the initial slope of the photochemical-associated variable fluorescence is unaltered under conditions at which k _AB = 0. This condition is clearly not fulfilled for the variable fluorescence kinetics in the presence (k _AB = 0) and absence of the PSII electron transfer inhibitor DCMU. Reasons for the apparent discrepancies and consequences for the validation of quite a number of commonly used trapping models of PSII have been given in Vredenberg and Prasil (2013), but see also Stirbet and Govindjee 2012 for a surveying exposure of pros and cons).

Thermal JIP phase

The JIP phase has been shown to be composed of two protonophore-sensitive fluorescence components with different kinetic profile (Vredenberg 2011). Systematic analyses of each of these components in low frequency single-turnover flashes (STFs) (Vredenberg et al. 2006, 2007) and in low intensity multi-turnover pulses (SPs) (Vredenberg et al. 2012) have led to a descriptive algorithm, in which the major part of the variable fluorescence during I–J phase in the 0–50 ms time range is given by

$$F^{\text{PE}}(t)=1+nF\text{v}·[1-e^{-(k_{\text{qbf}}+k_{\text{-qbf}})·t}]·\frac{k_{\text{qbf}}}{k_{\text{qbf}}+k_{\text{-qbf}}}\left\{1+[1-q^{\text{dsq}}(t)]·[1-e^{-(k_{\text{qbf}}+k_{\text{-qbf}})·t}]·\frac{k_{\text{qbf}}}{k_{\text{qbf}}+k_{\text{-qbf}}}\right\}$$ 7

and that of the IP phase in the 50 to 500 ms by

$$F^{\text{PE}}(t)=1+nF\text{v}·[1-e^{-(k_{\text{qbf}}+k_{\text{-qbf}})·t}]·\frac{k_{\text{qbf}}}{k_{\text{qbf}}+k_{\text{-qbf}}}\left\{1+[1-q^{\text{dsq}}(t)]·[1-e^{-(k_{\text{qbf}}+k_{\text{-qbf}})·t}]·\frac{k_{\text{qbf}}}{k_{\text{qbf}}+k_{\text{-qbf}}}\right\}$$ 8

A glossary of the additional parameters with which the kinetic profiles of the variable fluorescence F ^PE(t) and F ^CET(t) can be simulated is given in the text box.

Glossary and description of graphic F PE(t)- and F CET(t) parameters additional to those of F PP(t)
k qbf	rate constant of increase in variable fluorescence during the thermal phase at which the photochemical trapping has reached an equilibrium steady state; it is attributed to the overall rate constant (ms−1) of lumenal proton transfer reactions that result in local pH change at the QA–QB redox side of PSII
k -qbf	rate constant of dark reversion of variable fluorescence induced during the thermal phase; it is attributed to the re-oxidation rate (constant) of RCs with a double-reduced acceptor pair ([PheQA]2−)
IP	amplitude of IP phase set equal to F SP m– [$F_{\text{m}}^{\text{PP}}$ + F PEm]
k IP	rate constant that determines the increase in F v during the I–P phase
k -IP	rate constant determining the major decay component of F v in the dark
N IP	integer (0 < N IP < 10) to accommodate delay and steepness of F v during I–P phase (F CET(t))

Results and interpretation

Figure 1 shows the responses of the variable fluorescence F(t)/F _o during and after a short saturating pulse (sSP), in this case of 250 µs duration (sSP_0.25), and upon excitation with a 1 s saturating pulse (SP) of the same intensity of 3000 µmol photons m⁻² s⁻¹ (insert). The sSP_0.25-response, plotted on a linear time scale shows at its onset at t = 0 (sSP_on) an initial rise with a reciprocal rate of ~350 µs. This slope, as argued before, is equal to the product of excitation rate k _L and the (maximum) variable fluorescence nF _v associated with 100 % reduction of Q_A of open RCs. It follows, after application of simple math, that the reciprocal of the slope of the initial rise (in ms) can also be read from the length of the horizontal line that connects the point F/F _o = 2 on the vertical axis with that of its intercept with the (dashed) line of the initial slope. The approximate value of nF _v can be estimated, as argued before, from F _m at the P-level of the SP-induced OJIP induction (insert). It gives nF _v ~ 2. Thus, the excitation rate k _L for the Kalanchoë leaf illuminated with an (s)SP of 3000 µmol photons m⁻² s⁻¹ intensity is estimated to be k _L ~ 1.5 ms⁻¹. The decay after sSP_off is poly-phasic with an initial fast phase and a slow tail extending in the 20 ms time range. Similarly as for the on—rate, the length of the green colored horizontal line from t = 0.25 to the intercept of the slope line with the (calculated) residual curve of the tail (red squares) gives a graphical approximation of the reciprocal of the rate constant ((k ₁)⁻¹) of the fast decay component (open circles). The graph shows, for a pulse duration of 250 µs, that the reciprocal of the initial decay rate (k ₁)⁻¹ ~ 280 µs.

Figure 2 shows the 3-exponential deconvolution of the decay on an extended time scale with amplitudes (a _i, i = 1–3) and rate constants (k _i, in ms⁻¹) of the three components. It illustrates, amongst others, the amply documented heterogeneity of PSII RCs with respect to the re-oxidation rate of their reduced primary quinone electron acceptor ${\text{Q}}_{\text{A}}^{-}$ by Q_B, or ${\text{Q}}_{\text{B}}^{-}$. We presume that the components with k ₁ and k ₂ are those of RCs in which ${\text{Q}}_{\text{A}}^{-}$ is re-oxidized by Q_B and ${\text{Q}}_{\text{B}}^{-}$, respectively. This means that under the experimental conditions, owing to this definition and analysis, the rate constant of ${\text{Q}}_{\text{A}}^{-}$ -re-oxidation k _AB equals k _AB = k ₁. The slow phase (k ₃) of the decay is likely to represent the retarded dark recovery of Q_B-nonreducing PSII RCs which occurs with rate constant k ₃. The amplitude a ₃ (Fig. 2) of the extrapolated slow phase of the sSP_off decay at t ₀ = 0.25 ms (sSP_off), enables the estimation of the fractional size β of Q_B-nonreducing RCs. The relative size of this fraction with ${\text{Q}}_{\text{A}}^{-}$ is, according to Eq. 3 and with substitution k _L ~ 1.25 ms⁻¹, equal to 1 – exp(–k _L × 0.25) = 0.27. This means, with a ₃ = 0.08 and nF _v = 2 (Figs. 1, 2, respectively), that β ~ 0.15. Thus the four parameters that define F ^PP1(t) (Eqs. 1–4), can be estimated from the kinetic analyses of experimental sSP- and SP-induced responses (Figs. 1, 2).

Fig. 2.

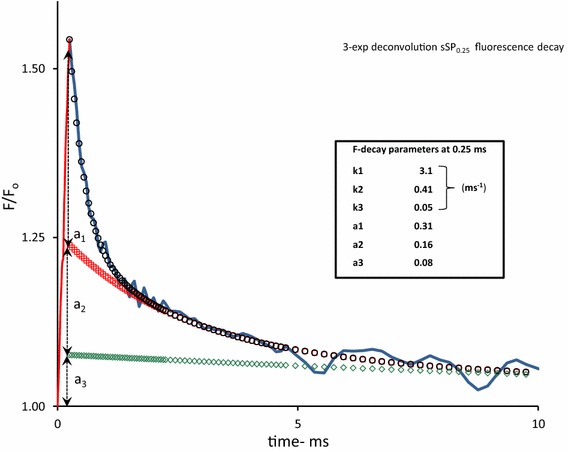
Same experimental sSP_0.25 response as in Fig. 1 but now plotted on a 10 ms linear time scale. The F(t) decay after sSP_off at t = 0.25 is poly-phasic. The symbols in the curve are those of a 3-exponential deconvolution of this decay, with $\frac{F(t)}{F_0}={\sum }_1^3{a}_j·e^{-kj·t}$ The fast, moderate, and slow components, j = 1, 2, and 3, are represented by black open circles, red open squares, and green open diamonds, respectively. The values of amplitudes (a _j) and rate constants (k _j) of each of the components are given in the insert box

Figure 3 shows a reproduction and decay analysis of three subsequent excitations with short saturating pulses of 0.25, 0.5, and 1 ms duration, plotted on top of each other in one figure. The increase in length of the horizontal line connecting the vertical line at sSP_off and the intercept of the slope at light off with the extrapolated curve of the moderate plus slow phase, indicates an increase in the rate constant k _AB with the length of the light (pulse) period in the 0.01–1 ms time range. This is presumed to be due to the light-driven pH shift of the ${\text{Q}}_{\text{A}}^{-}$Q_B ↔ Q_A ${\text{Q}}_{\text{B}}^{-}$ redox equilibrium accompanying progressing H⁺ uptake at the Q_r -site of the cytb₆f complex (Vredenberg and Prasil 2009, 2013). Figure 4 shows, on a linear 3 ms time scale the graphic plot of F ^PP1(t) resulting from application of Eq. 4. The supplementary contribution of fluorescence de-quenching associated with double-hit electron trapping in Q_B-nonreducing RCs [Eq. 5, F ^PP2(t)], is seen by comparing the graphs of F ^PP (Eq. 6) and F ^PP1 (Eq. 4) in Fig. 4. The electron trapping efficiency Φ in the second excitation (hit) has been set at Φ = 0.15. This gives a closest fit of F ^PP + F ^PE with F ^exp in the 1–5 ms time range, as will be discussed below. The steady state $F_{\text{ss}}^{\text{PP}}$ ~ 0.9 of F ^PP(t) (with reference to F _o = 1) is reached after about 10 ms (not shown). This equilibrium state is determined by the fraction q ^dsq of centers that has become photochemically closed in the light. It follows (Eq. 2) that, at the intensity used, this fraction amounts 0.85 × 1.5/4.3 + 0.15 = 0.45.

Fig. 3.

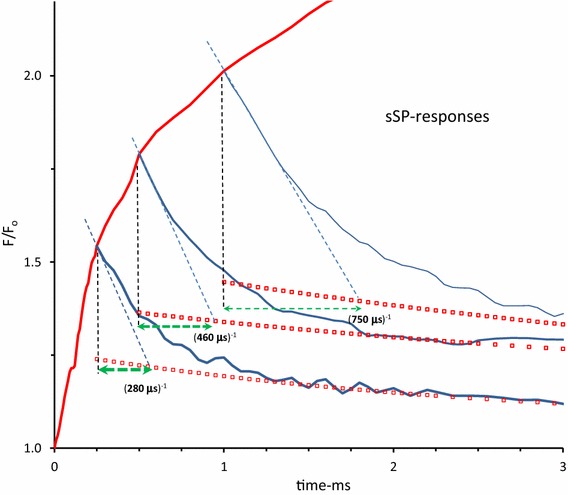
Superposition of the responses of the variable F(t)/F ₀ in a Kalanchoë leaf during (red-colored line) and after (blue-colored) short saturating pulses of 0.25, 0.5, and 1 ms duration and 3000 µmol photons·m⁻² s⁻¹ intensity in the linear 3 ms time range. Pulses are given at t = 0. The ongoing red response after t = 1 ms is of an 1 s SP curve (see insert Fig. 2). The red-colored squares mark the decay of summed moderate and slow phase and the green colored dashed lines the approximate reciprocal of the rate constant of the fast decay component of the respective sSP-responses (see further Fig. 2). Mark, in particular, the increase length of these horizontal lines with increase in duration of the pulses

Fig. 4.

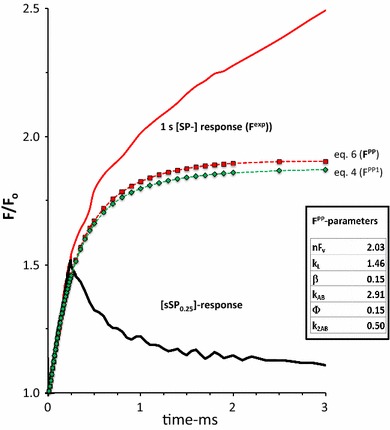
The 3 ms linear time plot of the variable fluorescence response in a Kalanchoë leaf upon a 0.25 ms sSP_0.25 (black-colored) and a 1 s SP (red-colored) both of 3000 µmol photons·m⁻² s⁻¹ intensity. The two pulses are given sequentially at an intermediate dark period of a few seconds. The curves with green diamonds and red squares are the graphic plots of the calculated variable fluorescence associated with the release of primary photochemical quenching without (F ^PP1) and with (F ^PP) supplemental quenching release associated with double reduction of Q_B-nonreducing RCs, respectively. F ^PP1 and F ^PP are calculated using Eqs. 4 and 6 with substitution of the parameter values estimated from the kinetic- and steady state analyses illustrated in Figs. 1 and 2, except φ and k _2AB, and are given in the table in the insert

Figure 5 shows, for the same leaf as in Figs. 1, 2, 3, 4, the variable fluorescence F(t)/F _o in the (linear) time range of 20 ms during the 1 s saturating pulse of 3000 µmol photons m⁻² s⁻¹ and in the 40 ms dark period after a short 10 ms saturating pulse (sSP₁₀). The decay after sSP₁₀ is resolved, after exponential deconvolution, into three components with amplitudes (a _i, i = 1–3) and rate constants (k _i, in ms⁻¹). The values of these F-decay parameters are given in the inset table. Comparison of the decay patterns after sSPs of 1 and 10 ms duration shows that that the fluorescence dark kinetics after short pulse excitation substantially changes with the length of the pulse. Most pronounced is the increase in the slow (a ₃) decay component that apparently has accumulated during the extension of the pulse period from 1 to 10 ms. This would suggest, in terms of TSTM, a stimulated accumulation and photochemical reduction of reduced Q_B-nonreducing RCs in the light period and dark re-oxidation with rate constant k ₃ (~0.02 ms⁻¹). It is further noticeable that the rate constants of the decay components have continued to decrease during the extended sSP duration.

Fig. 5.

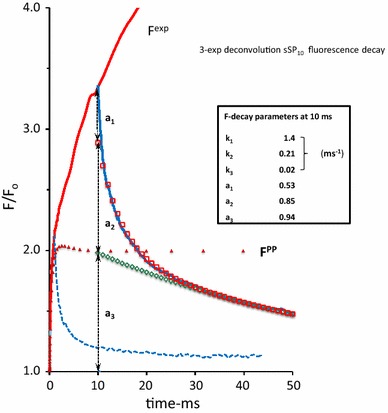
The 50 ms linear time plot of the variable fluorescence response (F ^exp(t)) in a Kalanchoë leaf upon a 10 ms short saturating pulse sSP₁₀ (blue-colored) and a 1 s SP (red-colored), both of 3000 µmol photons m⁻² s⁻¹ intensity. The two pulses are given sequentially at an intermediate dark period of a few seconds; the 10 ms rising part of the sSP₁₀ response coincides with that of the SP response. The green open diamonds and red open squares are of the slow (k ₃) and moderate(k ₂) component, respectively of the 3-exponential deconvolution of the sSP₁₀ decay curve. Values of amplitudes (a _j) and rate constants (k _j) of each of the components are given in the insert. The blue dashed line is, for comparison and reproduced from Fig. 1, the decay of the sSP_0.25 response. The red colored triangles are of the variable fluorescence curve F ^PP (t), reproduced from Fig. 4. Note the substantial increase of, in particular the amplitude of the slow (a ₃) and moderate (a ₂) components of the F(t) dark decay associated with the F(t) rise in the 10 s time domain

Figure 6 (red colored line) shows, on a linear 75 ms time scale, the plot of F ^exp(t) after subtracting F ^PP(t). It shows a bi-phasic increase in fluorescence with an inflection point (at level I) at a time around 30 ms at which a second rise becomes apparent. It is obvious from the slope of the response (dotted line), as compared to that of the initial rise (Fig. 2), that the rate constant of the transfer or process that is responsible for the light-driven increase in variable fluorescence is substantially lower than that of the photochemical conversion at t = 0 (Fig. 1). The red colored diamonds and dotted line in Fig. 6 are those calculated with Eq. 7 for the variable fluorescence F ^PE(t) attributed to photo-electrochemical transfer of RCs into the Q_B-nonreducing form and the sequential trapping, with attenuated efficiency Ø, of a second electron in subsequent hits (excitations). A close matching between experimental (F ^exp − F ^PP) and simulation (F ^PE) curves is obtained with rate constants for the forward light (k _qbf) and reversal back reactions (k _−qbf) of about 0.1 and 0.01 ms⁻¹, respectively. The steady state of the light-driven photo-electrochemical thermal (J–I) phase is F ^PE_ss(t) ~ 2.5.

Fig. 6.

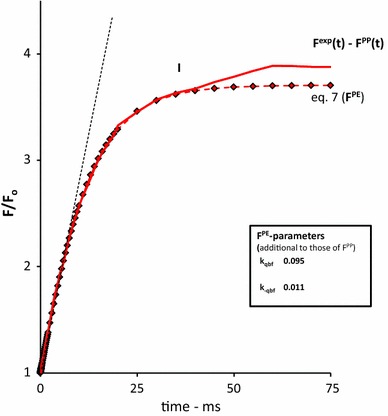
The 75 ms linear time plot of the variable fluorescence response (F ^exp(t) − F ^PP(t)), complementary to the rise exclusively caused by the release of primary photochemical quenching, upon a 1 s saturating pulse SP (red line) of 3000 µmol photons m⁻² s⁻¹ intensity in a Kalanchoë leaf. The curve is obtained after subtraction F ^PP(t) (see Fig. 4, 5) from F ^exp(t) (see insert Fig. 2). The curve with red diamonds is the graphic plot of Eq. 7, attributed to F ^PE(t), with substitution of the parameter values estimated for F ^PP(t) (see insert Fig. 4) and supplemented with those estimated for k _qbf and k _−qbf, given in the insert table, to obtain the best fit with the experimental curve in the 0 to 30 ms time domain, after ‘correction’ for F ^PP(t)

Figure 7 shows, on a 500 ms linear time scale, the variable fluorescence of the same leaf upon a 1 s SP and during and after a 50 ms saturating pulse (sSP₅₀). The closed red diamonds are those obtained after summation of the calculated F ^PP(t) and F ^PE(t) curves of Figs. 4 and 6. They show the closes fit with F ^exp in the 0–50 ms time range and steady state equilibrium above that range. The results of the 3-exponential deconvolution of the decay after sSP₅₀ are summarized in the table in the insert and illustrated with symbols in the decay curve. The major (75 %) contribution of the decay is of a component that recovers with a rate constant k ₃ (~0.02 ms⁻¹). A component with about the same rate constant was apparent in the decay after sSP₁₀, as illustrated in Fig. 5. The similarity between the increase in size of this component [from ~0.9 at 10 ms (Fig. 5) to ~2.8 at 50 ms (Fig. 7)] with that of the fluorescence response suggests that the variable fluorescence in the light in the time domain of 1–50 ms is under control of this component. The reasonable correspondence between the value of the rate constant of the decay after sSP₅₀ (Fig. 7) and that of the reversal reaction (k _−qbf) introduced for simulation (Eq. 7) of the variable fluorescence associated with photo-electrochemical quenching F ^PE(t) is in agreement with this hypothesis.

Fig. 7.

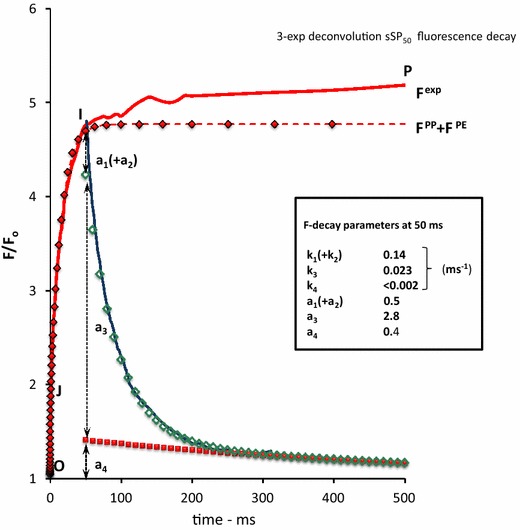
The 500 ms linear time plot of the variable fluorescence response (F ^exp(t)) in a Kalanchoë leaf upon a 50 ms sSP₅₀ (blue-colored) and a 1 s SP (red-colored), both of 3000 µmol photons m⁻² s⁻¹ intensity. The two pulses are given sequentially at an intermediate dark period of a few seconds; the 50 ms rising part of the sSP₅₀ response coincides with that of the SP response. The green open open diamonds and closed red squares are of the intermediate (k ₂) and slow (k ₃) component, respectively of the 3-exponential deconvolution of the sSP50 decay curve. Values of amplitudes (a _j) and rate constants (k _j) of each of the components are given in the insert. The red colored diamonds are of the variable fluorescence curve F ^PP(t) + F ^PE(t), after summation of the respective curves from Fig. 4 (F ^PP) and Fig. 6 (F ^PE), respectively. Note the appearance of the ultra-slow decay component ((k ₃)⁻¹ ~ 0.5 s) in the decay at 50 ms and (ii) approx. equal size of the rate constant k2 in the sSP₅₀ decay and k3 in the sSP₁₀ decay (see Fig. 5)

The red solid curve in Fig. 8 is the linear time plot of F ^exp(t) after subtracting the variable fluorescence associated with release of photochemical [F ^PP(t)] and photo-electrochemical quenching [F ^PE(t)]. It shows an approx. 0.45 increase ($\mathrm{\Delta }{F}_{\text{v}}^{\text{IP}}$) in variable fluorescence in the light toward the final P level at the maximum fluorescence F _m. The response shows a delay of approx. 30 ms and reaches its equilibrium state after about 300 ms. The red diamonds are the fluorescence values of the simulation curve F ^CET(t) using Eq. 8 and substituting parameter values listed in the insert of the figure.

Fig. 8.

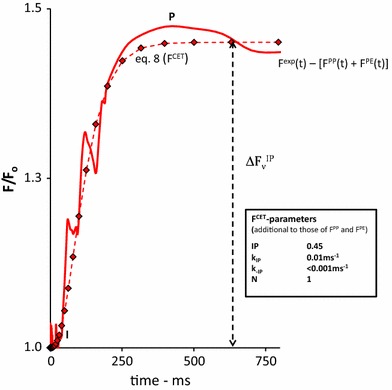
The 750 ms linear time plot of the variable fluorescence response $\left(F^{exp}(t)-\left[F^{\text{pp}}\left(t\right)+F^{\text{pp}}\left(t\right)\right]\right)$, complementary to the fluorescence rise caused by F ^PP(t) and F ^PE(t), upon a 1 s saturating pulse SP (red line) of 3000 µmol photons m⁻² s⁻¹ intensity in a Kalanchoë leaf. The curve is obtained after subtraction the sum of F ^PP(t) and F ^PE(t) from F ^exp(t) (see Fig. 7). The curve with red diamonds is the graphic plot of Eq. 8 attributed to F ^PE(t), with substitution of the parameter values estimated for F ^PP(t) (see insert Fig. 4) and supplemented with those estimated for k _qbf and k _−qbf, given in the insert table, to obtain the best fit with the experimental curve in the 0 to 30 ms time domain, after ‘correction’ for F ^PP(t)

The variable fluorescence response upon a 1.3 s saturating pulse of 3000 µmol photons m⁻² s⁻¹ and of the fluorescence dark decay after a similar pulse of 500 ms duration (sSP₅₀₀) is illustrated in Fig. 9. The characteristic parameters of the three exponential decay components are given in the insert. The decay after a 50 ms short pulse (sSP₅₀), reproduced from Fig. 7, is drawn for comparative reasons. A prominent growth, concurrent with the increase in variable fluorescence in the light, is seen in the size of the slow decay component (a ₃) with a reciprocal rate of approx. (10 s)⁻¹ which has occurred during the final part (IP) of the thermal phase in the 50–500 ms time range. The summed values F ^PP(t) + F ^PE(t) + F^CET(t) which constitute the simulation F ^FIA(t) of the experimental variable fluorescence induction curve F ^exp(t) are also shown as red colored diamonds. The FIA parameters are listed in the left hand table. The same results for F ^exp and F ^FIA, but plotted on a commonly used log-time scale and complemented with the constituting components of F ^FIA are illustrated in the bottom-right hand insert.

Fig. 9.

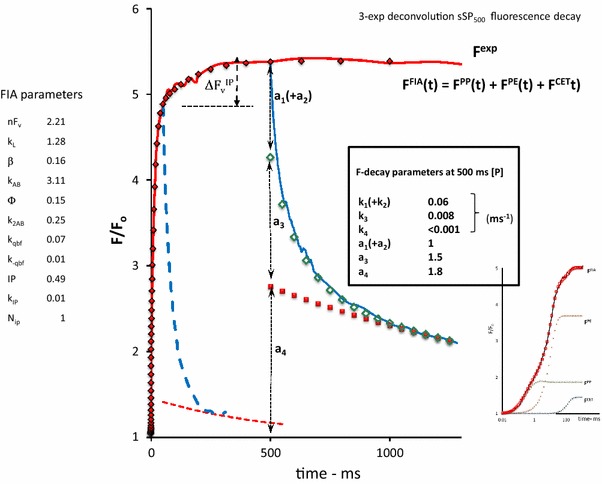
The 1300 ms linear time plot of the variable fluorescence response (F ^exp(t)) in a Kalanchoë leaf upon a 500 ms (s)SP₅₀₀ (blue-colored) and a 1 s SP (red-colored), both of 3000 µmol photons m⁻² s⁻¹ intensity. The two pulses are given sequentially at an intermediate dark interval of a few seconds; the rising part of the (s) SP₅₀₀ response coincides with that of the SP response. The green diamonds and red squares are of the intermediate (k ₃) and slow (k ₄) components, respectively of the 3-exponential deconvolution of the sSP₅₀₀ decay curve. Amplitudes (a _j) and rate constants (k _j) are given in the insert. The blue dashed line is the decay of the sSP₅₀ response and the red dashed curve is of its slow decay component (both reproduced from Fig. 7). The red diamonds are of the FIA-simulation curve F ^FIA(t) = F ^PP(t) + F ^PE(t) + F ^CET(t) resulting after summation of the respective curves from Fig. 4 (F ^PP), Fig. 6 (F ^PE) and Fig. 8 (F ^CET), respectively. The parameters of the constituting components of F ^FIA(t) (Eqs. 6–9) are given in the left hand panel. The bottom-right insert gives the results plotted on a log time scale. Note (i) the nice similarity between F ^exp(t) and F ^FIA(t) and (ii) the substantial increase in the contribution of the ultra-slow decay component ((k ₃)⁻¹ ~ 1 s) that has occurred during the 50–500 ms light period (IP phase) in which F ^exp has increased with a comparably smaller amount $\mathrm{\Delta }{F}_{\text{v}}^{\text{IP}}$

Figure 10 shows the same experiment as Fig. 9 but done at a tenfold lower intensity of the actinic light pulse and in a leaf of a different plant species. The results on the light response at low(er) intensities are in agreement with those of similar experiments in many other plant species (Strasser et al. 1995; Lazár 2006; Schansker et al. 2006; Vredenberg 2011) and demonstrate (i) an apparent increase $\mathrm{\Delta }{F}_{\text{v}}^{\text{IP}}$ of F ^CET, a much lower OI phase (F ^PP + F ^PE) and, (iii) nearly the same F _m as compared to values at a tenfold higher intensity shown in Fig. 9. However, the slow (k ₄) component of the decay is as large as observed at the higher intensity in Fig. 9. This observation, as will be discussed later, hints to the conclusion that the de-quenching process responsible for the IP phase is mechanistically different from those of the O–J–I phase.

Fig. 10.

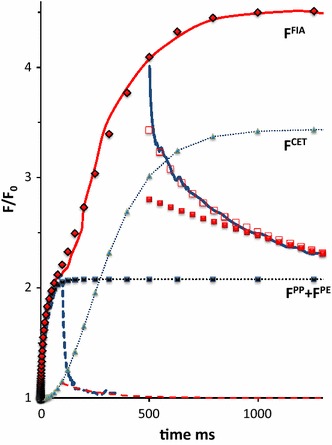
Linear time plot, similar as in Fig. 9, except for ten-fold attenuation of pulse intensity and plant (leaf) species, of F ^exp(t) in a Arum italliensis leaf upon a 500 ms (s) SP₅₀₀ and a 1 s SP, both of 300 µmol photons m⁻² s⁻¹ intensity. Here the blue dashed line is the decay of the sSP₁₀₀ response. Meaning of symbols and labeled curves is the same as in Fig. 9

Figure 11 gives a reaction scheme for the light-induced variable fluorescence associated with F ^PP and F ^PE, in which the estimated rate constants which are characteristic for forward and backward reactions are indicated. The upper line represents the reaction scheme of the photochemical O–J phase which is described by F ^PP. The vertical reaction scheme in the middle represents the photo-electrochemical transfer reaction of ‘normal’ RCs with ${\text{Q}}_{\text{A}}^{-}$ and k _AB > 0 into Q_B-nonreducing RC with k _AB = 0 (indicated by the subscript _nqb). The bottom scheme is of the reversible photochemical reduction of Q_B-nonreducing RCs in which a 2nd electron is trapped. These latter two sequential reactions are representative for F ^PE involved in the I–J phase.

Fig. 11.

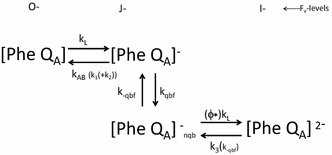
Schematic scheme representing the reactions that cause light-induced variable fluorescence associated with F ^PP and F ^PE in the OJI phase. Rate constants characteristic for forward and backward reactions are indicated. The upper reaction scheme of the photochemical O–J phase and associated with F ^PP. The vertical and bottom scheme is of the J–I phase. Further explanations are in the text

The left hand part of Fig. 12 shows the amply documented effect of DCMU addition on the induction pattern of the variable chlorophyll fluorescence, measured here in an aqueous suspension of Nannochloropsis and plotted on a logarithmic time scale. The initial response in the (linear) 0.5 ms time domain is reproduced for the same experiment in the right hand part. The results in the presence of DCMU illustrate (i) the initial rate of variable fluorescence is not affected, and (ii) an increasing rate of the F _v rise after a delay of ~100 µs. The latter observation makes the rise sigmoidal.

Fig. 12.

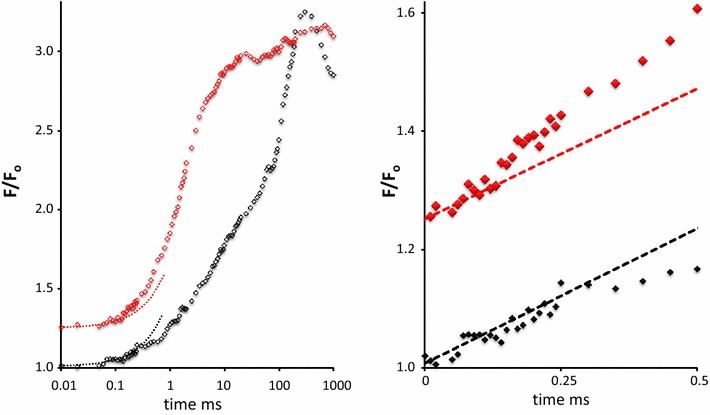
Left hand panel. Variable fluorescence in aqueous suspension of Nannochloropsis upon 1 s SP (500 μmol photons m⁻²s⁻¹) in absence (blacks) and presence (reds) of 1 μM DCMU). The herbicide was added in strict darkness. Data are average of 12 experiments with three samples. Right hand panel: Same data in the 0 to 0.5 ms time range as in left hand panel, but plotted on a linear time scale. It shows the following properties: Fo in the presence of DCMU has increased to 1.25 with unaltered F _m ~ 3F _o. Initial rate of fluorescence increase at onset of SP is insensitive to DCMU (dashed lines in right hand panel). Initial fluorescence increase in the presence of DCMU is sigmoidal

Discussion

The poly-phasic so-called OJIPSMT time pattern of variable chlorophyll fluorescence in algae and intact leaves is generally considered as a valuable source of information on the primary and secondary photosynthetic processes that are involved in bioenergy conversion and biomass production (Kautsky and Hirsch 1931; van Kooten and Snel 1990; Papageorgiou and Govindjee 2004; Suggett et al. 2010; Kalaji et al. 2012). The large amount of experimental fluorescence data, collected from experiments with algae, leaves, chloroplasts, and fragments thereof, has not led so far to a covering interpretation model that has received general acceptance (Stirbet and Govindjee 2012). A likely and probably major reason is a fundamental disagreement on the interpretation of the maximal fluorescence F _m. F _m is measured at the P-level of the OJIP rise, starting at O from F _o, after a light period variable between 200 and 700 ms, depending on light intensity (Figs. 8, 9, 10). F _m is reached at much shorter times in the presence of DCMU (see for instance Fig. 12). F _m is considered) to be exclusively associated with the complete release of photochemical quenching. Reference is then made to the classic paper of Duysens and Sweers (1963) in which convincing evidence has been presented that photochemical reduction of Q_A, which acts as an antenna fluorescence quencher, leads to RC closure and consequently, like in photosynthetic bacteria for the photochemical oxidation of the reaction center (bacterio-)chlorophyll (Vredenberg and Duysens 1963), to an increase in chlorophyll fluorescence yield. However, application of one of the rules of logics does not allow the reverse conclusion that an increase in fluorescence yield is only associated with the photoreduction of a quencher. Thus the assumption that in algae and leaves the maximal variable fluorescence F _m due to closure the RCs of PSII is exclusively associated with full release of photochemical quenching by Q_A is not necessarily correct and requires substantiation and validation. The results of experiments on the light-on and light-off responses of F _v with sSPs in the range between 250 and 1000 ms and the kinetic analyses thereof (Figs. 1, 2, 3, 4) illustrate unequivocally that the maximal variable fluorescence nF_v (~2 for Kalanchoë) associated with complete reduction of Q_A (Fig. 4) is less than the maximal variable fluorescence (~4 for Kalanchoë) associated with F _m ~ 5 (insert Fig. 2). This conclusion is in firm agreement with that obtained with other approaches and species, amongst which estimates that the maximal variable fluorescence F ^STF_m in (µs-) saturating single-turnover flashes is by 25–50 % less than the maximal variable fluorescence F _m in (>300 ms-) multi turnover light pulses, documented for a large variety of algae and plant chloroplasts (Samson and Bruce 1996; Koblizek et al. 2001; Vredenberg et al. 2007; Vredenberg and Prasil 2009; Klughammer and Schreiber 2015).

I will now turn to the analyses of light and dark kinetics of variable fluorescence in the subsequent photochemical (O–J) and thermal phases (J–I and I–P) of the pulse-induced variable fluorescence in intact leaves. Till now, simulated curves of variable chlorophyll fluorescence F ^FIA(t) were obtained by substituting proper values of the constituting parameters in the equations of its photochemical [Eqs. 1–6, F ^PP(t)] and photo-electrochemical components (Eqs. 7–8 for F ^PE(t) and F ^CET(t),respectively). The estimates of the parameters (i) guaranteed the closest fit of F ^FIA(t) (=F ^PP(t) + F ^PE(t) + F ^CET(t)) with the experimental curve F ^exp(t) and (ii) were, for each, within the range of values estimated or concluded in experiments with (sub-) cellular or organellar preparations under comparable conditions. This methodology of our system analysis approach however has been judged as a weakness and deprivation (Stirbet and Govindjee 2012). If it were, this imperfection is overcome for a great deal with the application of sub-saturating pulses (sSPs).

Photochemical O–J phase; F^PP(t)

There are instrumental limitations for applying STFs in fluorescence studies with intact leaves because of the inability of existing LED assemblies to reach fluorescence saturation within the 10 µs time range. This excludes the possibility of estimating the actual value of nF _v with µs-STFs. The application of sSPs in an extended time range and the monitoring of the light-on and light-off variable fluorescence kinetics at an adjustable time resolution above 10 µs has dissolved this limitation. But there are more advantages of using these short duration pulses. So far the simulation and fitting of experimental OJIP (SMT) curves were done starting from the set of equations that describe the reaction kinetics of photochemical quenching of fluorescence (i.e., Eqs. 1–6) supplemented with those for fitting the JIP phase (i.e., Eqs. 7–8) of the OJIP induction curve. These form, except for some slight modifications, the framework of the fluorescence induction algorithm FIA that has been introduced in earlier reports.

The data of Figs. 1, 2, 3, 4 illustrate that implementation of tools enabling high time resolution of fluorescence (F _v) responses and mathematical handling of underlying reaction kinetics serves the approximation and/or estimation of the actual values of the determinant parameters of F ^PP1(t) in a leaf under the measuring conditions: (1) the slope of the initial F _v rise at light on (Fig. 2) equals the product of light excitation rate (k _L) and maximal variable fluorescence (nF _v) associated with release in photochemical quenching and (2) the slope of F _v at light off (Figs. 2, 3) and the decay pattern in the dark (Fig. 1) give estimates of the actual values of the rate of oxidation of ${\text{Q}}_{\text{A}}^{-}$ by Q_B (k _AB = k ₁ in Fig. 1) and presumably by ${\text{Q}}_{\text{B}}^{-}$ (k ₂ in Fig. 2) and of the fraction β of Q_B-nonreducing RCs. With actual data read from F _m (insert Fig. 2), the on- and off-slopes of sSP-induced F _v responses (Fig. 2) and from the 3-exponential decay analysis (Fig. 1), F ^PP1(t) can be estimated using Eq. 4. A first matching of F ^PP(t) with the initial phase of F ^exp(t) usually is done by manually varying the magnitude of k _AB with a small percentage. For example, an increase in k _AB will cause (Eq. 1) a downward movement of the F ^PP(t) without affecting the initial slope, as outlined in an earlier section. The choice of using k _AB as a fine tuner for the matching is not surprising in view of the fact that, as illustrated in Fig. 3, this rate constant of dark oxidation of ${\text{Q}}_{\text{A}}^{-}$ decreases during the approx. 1 ms rise period of F ^PP (t). This means that the actual average value of k _AB is less than the one that is estimated as a rule from the dark decay at 250 µs (Fig. 2). Moreover, and in order to simplify the calculations, the fluorescence decay attributed to oxidation of ${\text{Q}}_{\text{A}}^{-}$ has been approximated by a single exponential. This means that the F _v decay, after correction for the slow decay with rate constant below ~0.05 ms⁻¹, i.e., with amplitude(a ₁ + a ₂) (Fig. 1) is simulated with one reciprocal rate constant that equals the time t at which F _v has decreased toward a value ~0.37 × (a ₁ + a ₂). In the experiment of Fig. 1 this would have given (not shown) a value k _AB ~ 1.8 ms⁻¹. A next refined matching of F ^PP(t) with F ^exp(t) (Fig. 4) is done by varying the magnitude of electron trapping efficiency Ø in fraction β of Q_b-nonreducing RCs with single-reduced acceptor pair. It allows a fine tuning of the rise of F ^PP2(t) and serves a matching of F ^PP with F ^exp at the junction of O–J and J–I phases in the 0.5–1.5 ms time range.

Thus the variable fluorescence F ^PP(t) associated with release of photochemical quenching can be estimated with reasonable precision and accuracy. The example displayed for a Kalanchoë leaf (Fig. 4) but qualitatively representative for leaves of other plant species, illustrates that, at the intensity used, the release associated with photochemical quenching reaches an equilibrium state at $F_{\text{ss}}^{\text{PP}}$ (=F/F _o − 1) ~0.9 after about 1.5 ms, at which (e.g., Eq. 6b) ~45 % of Q_A has become reduced. The figure and Eq. 6b predict a strong dependence of $F_{\text{ss}}^{\text{PP}}$ on k _L (actinic light intensity) and on k _AB. A tenfold attenuation in light intensity will lower $F_{\text{ss}}^{\text{PP}}$ from 0.9 to ~0.3, and a treatment causing k _AB = 0 (for instance addition of DCMU) is predicted to result in its rise toward nF _v (~2). The latter is in conflict with experimental data (see for instance Fig. 12), which show that in the presence of DCMU F ^exp(t) reaches a value $F_{\text{DCMU}}^{exp}\sim F_{\text{m}}$ (~5). This seeming discrepancy has received ample attention in earlier reports (for survey, see Vredenberg and Prasil 2013). The variable fluorescence not associated with primary photochemical quenching and referred to as being associated with the thermal phase is obtained by subtracting F ^PP(t) from F ^exp(t).

Thermal J–I–P phase, J–I component, F^PE(t)

The first part of the thermal phase covering the time domain between ~2 and 50 ms, denoted as the J–I phase, has been interpreted in most models to be caused by processes associated with PQ reduction. The identity of these processes is still under debate (for a survey see Stirbet and Govindjee 2012). An interesting observation has been reported which showed, at an unaltered F _m, a largely suppressed J–I and a stimulated I–P phase in the OJIP induction of etiolated wheat leaves after a greening period of 24 h (Dinc et al. 2012). This effect may hint to a relation of the occurrence of the involved reaction with the assemblage of the photosynthetic machinery. The application of sSPs with a duration that covers the J–I component of the thermal phase in the time domain of tens of ms (Figs. 5, 7), has shown (i) a substantially lower rate for F _v in the light, (ii) an approx. twofold decrease of k ₁ and k ₂ in the dark, attributed to (re-) quenching by Q_A and contributing ~60 % (=100 × (a ₁ + a ₂)/(a ₁ + a ₂ + a ₃)) of the total F _v at t = 10 ms (Fig. 5), and (iii) a growth in the contribution of the slow k ₃-component in the dark decay from ~14 % at 0.25 ms (Fig. 1) to ~40 and 75 % at 10 and 50 ms, respectively (Figs. 5, 7). The fact that the F _v increase during the J–I phase in the light is accompanied by an increase in the slow k ₃-decay phase of comparable size leads to the conclusion that the responsible light-driven process of the J–I phase reverses in the dark with a rate constant of the order of 0.02 ms⁻¹. The process apparently is active under conditions at which Q_A is photochemically reduced in more than 50 % of the fraction of the RCs. An increase in this fraction during the J–I phase is obvious from the decrease in the amplitude (a ₁ + a ₂) attributed to photochemical reduction of Q_A. The simultaneous appearance of an F _v component (a ₃) which relaxes (k ₃) in the dark with an approx. 20-fold slower rate, and the observation that the amplitude a ₃ of this component at the end of the J–I phase (i.e., at ~50 ms (Fig. 7)) exceeds $F_{\text{m}}^{\text{PP}}$ (=nF _v) give support for the hypothesis (Vredenberg et al. 2006; Vredenberg and Prasil 2009) that the component results from variable fluorescence F ^PE(t)associated with RC closure caused by electron trapping in (semi-closed) RCs with ${\text{Q}}_{\text{A}}^{-}$, after their photo-electrochemical conversion into the Q_B-nonreducing form. The simulation of F ^exp(t), after subtraction of F ^PP(t), with F ^PE(t) using the equation (Eq. 7) that represents the reaction kinetics of this double-hit trapping mechanism gives additional support for the hypothesis (Fig. 6). The simulation was done using the parameters estimated for F ^PP(t) (see Fig. 4) complemented with an excitation k _qbf ~ 0.1 (~0.07 k _L) and relaxation rate k _−qbf ~ 0.01 (both in ms⁻¹). The latter compares reasonably with the estimated relaxation rate k ₃ of the major component of the F _v decay during the J–I phase. The attenuated excitation rate k _qbf of F ^PE(t) as compared to that of F ^PP(t) has been ascribed to the rate of the pH change at the Q_A − Q_B reducing site which results from a proton flux, competitive with the larger flux from non-specific H⁺ sources, toward the light-driven H⁺ uptake at the Q_B site that occurs at the excitation rate k _L (Vredenberg 2011). The pH change at the Q_A − Q_B reducing site is reflected by the decrease in the rate of the initial dark decay k ₁ and k ₂, ascribed to the ${\text{Q}}_{\text{A}}^{-}$ re-oxidation rate k _AB with increasing duration of light pulses (Figs. 2, 5, 7, 9).

Thermal J–I–P phase, I–P part, F^CET(t)

There is as yet no consensus on the origin of the IP phase, except for the conclusion that its appearance in the OJIP induction curve requires the activity of PSI (Bulychev and Vredenberg 2001; Schansker et al. 2005; Joly and Carpentier 2009; Ceppi et al. 2011; Vredenberg 2011). Short saturating pulses (sSPs), with a duration that covers the I–P component in the time domain of hundreds of ms, give interesting information on the process that is driving F _v during the I–P phase (Figs. 7, 8, 9). At the intensity used (3000 µmol photons.m⁻² s⁻¹), F _v has increased during the I–P phase from a value ~4.8 at I toward ~5.4 at P in the time span between 50 and 500 ms. The light processes at level I showed, upon termination at t = 50 ms, a poly phasic dark decay of F _v (Fig. 7). The major component (a ₃) reverses with a reciprocal rate constant of ~50 ms and is followed by a component with amplitude a ₄ ~ 0.4 and a reciprocal rate exceeding 500 ms. This pattern is distinctly different from that at the P-level (F _m) at 500 ms at which the major component has decreased and the slow one has raised its amplitude toward a ₄ = 1.8 (Fig. 9). The increment of this dark decay component with reciprocal rate of about 1 s is disproportional with the relatively small increase in variable fluorescence ($\mathrm{\Delta }{F}_{\text{v}}^{\text{IP}}$) during the I–P phase (Fig. 9). This phenomenon sets a constraint to the properties of the process that is responsible for the F _v increase during the I–P phase, in particular in relation to those that associated with F ^PP and F ^PE. The F _v increase during the I–P phase has been termed F ^CET, and has been attributed to a photo-electrical stimulation of the fluorescence yield by cyclic electron transport CET powered by PS1 Vredenberg (2008b, 2011). F ^CET(t) has been derived (Fig. 8) by estimating the best fit for the residual curve obtained after subtracting the sum of F ^PP(t) and F ^PE(t) from F ^exp(t) using Eq. 8. This equation has been discussed to account for the (variability in) sigmoidicity and steepness of the I–P curve under variable conditions. This variability is also obvious from OJIP curves sampled in different species (Ceppi 2010). It is not particularly representative for a photo-(electro)chemical reaction type. It has received ample application in quantitative descriptions of processes involved in bioreactor technology (Walas 1991). It is quite c different from the so-called Chapman-Richards sigmoid function f(t) = A[1 − exp(−kt)]^s in which k is a rate constant and s the variable sigmoidal factor that alters the steepness of the exponential rise at s = 1 (Joly and Carpentier 2009). This function has been applied in comparative MTF in WT and PSI mutants of Arabidopsis (Joly et al. 2010) with special emphasis on the I–P phase. The application in its present form however is hampered by the fact that the estimated values of the simulation parameters s and k cannot easily be related to measurable kinetic parameters or entities of the bioenergetic processes that are involved and operational during the IP phase of the fluorescence induction.

The disproportionally increased magnitude of the F _v− decay component (a ₄ ~ 1.8, and rate k ₄ ~ (1 s)⁻¹) (Fig. 9) as compared to $\mathrm{\Delta }{F}_{\text{v}}^{\text{IP}}$ during the I–P phase in the light period between 50 and 500 ms (Figs. 8, 9), gives strong support for the earlier proposed hypothesis that the variable fluorescence (F ^CET) in this phase is caused by a photo-electric stimulatory effect on the fluorescence yield. An effect of this kind comes into expression in the Boltzmann term $e^{\left({\mathit{\psi }}_0-\mathit{\psi }\right)}$ which equals the ratio k _t/k ₋₁ of the energy transfer parameters for charge separation (k _t) and –recombination (k ₋₁) in the RC. An increase in the strength of an electric field and its associated potential Ψ at the charge-separated state of the RC at a constant value the redox potential Ψ ₀ of this state (with Ψ ₀, like Ψ, in units of the electrochemical entity RT/F ~ 25 mV at room temperature) will down-regulate the occupancy of the charge-separated state and consequently causes an increase in the fluorescence yield Φ _f of the antenna chlorophylls. This phenomenon shows the characteristics of what has been called non photochemical RC quenching (Ivanov et al. 2008). The expression for the fluorescence quantum yield Φ _f accounting for the three types of quenching has been derived (Bulychev and Vredenberg 2001; Vredenberg 2011)

$${\mathit{\varphi }}_{\text{f}}({\mathit{\theta }}_1,{\mathit{\theta }}_2,\mathit{\psi })=\frac{1}{1+\frac{k_{\text{w}}}{k_{\text{f}}}+\frac{[{\mathit{\theta }}_1(k_{\text{e}}+k_{\text{y}})+{\mathit{\theta }}_2{k}_{\text{y}}+k_{\text{d}}]}{k_{\text{f}}N}{e}^{{}^{({\mathit{\psi }}_o-\mathit{\psi })}}}$$ 9

in which probabilities of energy–dissipation in the antennas (N per RC) via fluorescence (k _f,) and heat (k _w), and probabilities of photochemical-(k _e), photoelectrochemical trapping (k _y) and non-radiative dissipation (k _d) in RCs including (photo-)electric control and regulation via the Boltzmann term have come into expression. θ ₁ and θ ₂ are RC-fractions θ (0 ≤ θ ≤ 1) with unaffected (θ ₁) and acceptor side inhibited (θ ₂) charge stabilization, respectively. The difference in fluorescence yield of a closed (θ ₁,θ ₂) = (0,0) and open RC [(θ ₁,θ ₂) = (1,1)], according to Eq. 9, is dependent on the potential Ψ. It follows easily (see for a graphical illustration for instance Fig. 1 in (Vredenberg and Bulychev 2002) that for an open center [(θ ₁,θ ₂) = (1,1)], the increase in φ _f(Θ ₁,Θ ₂,ΔΨ) upon a distinct increase in Ψ (ΔΨ > 0) is larger than for a closed RC [(θ ₁,θ ₂) = (0,0)]. A second conclusion is that the difference in fluorescence yield of an RC in the presence (ΔΨ > 0) and absence of a potential change (ΔΨ = 0) is higher in an open RC as compared to that in a closed one. Both conclusions have their counterparts in what is shown in Fig. 9 for the two major components of the F _v decay at 50 and 500 ms, i.e., at the I and P level, respectively. At the J-level where the RCs are nearly all closed Θ ₁ ~ Θ ₂ ~ 0 the (major) decay component, associated with the re-opening of RCs, is with rate constant k ₃ = k _−qbf = ~(50 ms)⁻¹. The contribution of this component to the re-opening processes at the P-level is smaller, whereas that of the component with k ₄ = k _−IP ~ (1 s)⁻¹ is considerably increased. Thus these results are in harmony with the hypothesis that the I–P part of the thermal JIP phase is caused by a (photo-) potential dependent stimulation of the fluorescence yield. The reversal of this potential in the dark, which might be considered as the release of the RC quenching is substantially slower than that of the photo-(electro) chemical quenching.

A personal view

I started research in bioenergetics of photosynthesis in the young Biophysics Group of Lou Duysens at the University of Leiden, the Netherlands. In my PhD period during 1960–1965. I had the privilege to work in an inspiring scientific environment where novel ideas about the existence and properties of two interacting photochemical systems in algae, plants and isolated chloroplasts, and energy trapping in and closure of photosynthetic reaction centers were given a solid biophysical framework. Part of this work has been published in milestone papers (Duysens et al. 1961; Vredenberg and Duysens 1963; Duysens and Sweers 1963; van Grondelle and van Gorkom 2014). One of the starting points was focused on the relation between the RC closure and the increase in fluorescence yield. It was argued that photochemical conversion of either the primary donor P or primary acceptor, now known as Phe will lead to RC closure and subsequently to an increase in the fluorescence yield of the antenna chlorophyll. The role of the photochemical oxidation of the reaction center chlorophyll P (P890) in RC closure was demonstrated in bacteria from the associated increase in (bacterio-)chlorophyll fluorescence (Vredenberg and Duysens 1963; Vredenberg 1965). In algae and chloroplasts the fluorescence increase by PSII and its reversal by PSI was attributed to the photochemical conversion of a quencher Q and later argued to be identical to the primary quinone acceptor Q_A (Duysens and Sweers 1963). It is of interest to note, certainly in the 60 s, (i) a quencher was qualified by its unique property of causing RC closure upon its photochemical conversion and (ii) closure of RCs could exclusively be accomplished by photochemical conversion. Because of the relation between RC closure and increase in antenna chlorophyll fluorescence, the common opinion then has started to settle that a maximal fluorescence F _m is caused by 100 % photochemical reduction of Q_A, or, cited from a recent review (Stirbet and Govindjee 2012) ‘full reduction of Q_A is required and sufficient for reaching F _m .’ This means, in terms of the original concept that full photochemical conversion of the quencher is required and sufficient for the closure of the reaction center. As a principal investigator at the Wageningen Center of Agro-Biological Research in the 70 s and late 60 s, I focused and performed experimental activities on active transport in plants and in particular on light-driven changes in transmembrane electrical potentials of green characean cells using micro-capillary glass electrodes. This gave me a view among others on the electrogenic properties of proton pumps in biological membranes (Vredenberg 1997). Owing to increased technical possibilities and application of patch-clamp techniques, these properties and light-induced effects were successfully studied in and across the thylakoid membrane of giant chloroplasts in Peperomia metallica. This research has been highly stimulated by frequent cooperation and joint research with Alexander Bulychev from Moscow State University, starting in 1975 and continued in the 80 s in the Photosynthesis group of the Department of Plant Physiology at the Wageningen University (WUR) with a number of PhD students (see http://www.rozenbergps.com/vredenberg/ under tab PhD Theses). For the understanding and able interpretation of electrical signals across the thylakoid membrane induced by one or more (repetitive) saturating single-turnover flashes (STF), I resumed in the mid-90 s the research on chlorophyll fluorescence (changes) under comparable experimental conditions. Since the mid-70 s I had followed the progress in this chlorophyll fluorescence area only at some distance. I was rather surprised to learn that the maximal fluorescence F _m was more or less dogmatically interpreted as the solid indicator of a 100 % reduction of Q_A. This meant the exclusion of any effect in vivo of electrogenic events, for instance RC quenching associated with enhanced radical pair recombination, on RC closure and F _m. The frequent research cooperation since my retirement in 2002 with Ondrej Prasil and coworkers from Trebon has greatly stimulated the final part of my research activities. These dealt with experiments on the fluorescence kinetics in algae, chloroplasts, and intact leaves during and after saturating µs-STFs and short pulses (sSPs) of variable duration and intensity. This paper is an example thereof. All these have given support for and strengthen the conviction that quantitative models for describing the variable chlorophyll fluorescence in relation to photosynthetic energy conversion should incorporate contributions of a second excitation of PSII and of RC quenching to the closure of the RC of this photosystem.

I consider this paper as the closure of a fascinating period in which I had the opportunity to give scientific contributions in the exciting field of photosynthesis research in particular in the area that is focused on the biophysical aspects of the primary and associated reactions in intact photosynthetic organisms ranging from bacteria to intact leaves. The monitoring of light-driven changes in the chlorophyll fluorescence yield has proven to be a sensitive and non-invasive experimental method to get a closer insight in the inner-sanctum of the complex machinery of the ongoing processes and reactions. Chlorophyll fluorescence indeed is, as the sub-title of a frequently cited book says, a signature of photosynthesis. However, for being a signature it demands that applications of the nowadays available fluorescence tools lead to the correct answers. Unfortunately, these demands are not always fulfilled and certainly not in the case of the interpretation of the maximal fluorescence yield F_m in a high intensity light pulse in relation to the properties of the closed state of the reaction center. As long as the debate whether or not the closing of a photosynthetic reaction center is exclusively dependent on the redox state of one or more fluorescence quenchers continues and has not led to a communis opinio, a large number of interpretations and conclusions on photosynthetic parameters are suspicious. I feel it of utmost and urgent importance that the debate is intensified and where needed is fed by new experiments that give added value for a rapid solution of the opposing and sometimes dogmatic views. I believe that the present results on the rate constants of processes that occur after reaction center closure in distinguishable phases of its re-opening in the dark will contribute to the enhancement and decisive phase of the debate. Not surprising my proclaim on the conclusion in the final debate is, in line with what has been expressed in earlier papers, that closing of an RC is not exclusively dependent on the photochemical reduction of Q_A, or paraphrasing the statement in (Stirbet and Govindjee 2012), that ‘..full reduction of Q_A is neither sufficient nor required for reaching Fm…’ Finally, I foresee that future research on the long-term kinetics of fluorescence induction in relation to that of photosynthetic processes will include a focus on (i) validation of the assumption that photochemical conversion of antenna fluorescence quenchers other than those bound to the RC leads to RC closure, (ii) the occurrence, strength, and effect of reaction center quenching in vivo, and (iii) the role of ATPases in acting as a proton leak for the proton motive force generated by the proton pumps generated in particular by cyclic electron transport (F ^CET) around PSI. It is presumed that in particular the latter focus will lead to a better understanding of the kinetic profile of the Kautsky curve and its relation to the initial events of energy storage in the Calvin cycle.

Abbreviations

ß

Fraction of Q_b-nonreducing RCs

Δµ_H

Transmembrane proton motive force

DCMU

3(3,4-Dichlorophenyl)-1,1-dimethylurea

dsq

Donor side quenching

F^PE(t)

Fluorescence emission at time t, relative to Fo, exclusively associated with release of photoelectrochemical quenching

F^PP(t)

Fluorescence emission at time t, relative to Fo, exclusively associated with release of photochemical quenching

F^CET(t)

Fluorescence emission at time t, relative to Fo, exclusively associated with photo-electric stimulation

F₀

Fluorescence level of dark-adapted system with 100 % open RCs

F_m

Fluorescence level of dark-adapted system with 100 % closed RCs after fluorescence saturating pulse excitation

$F_{\text{m}}^{\text{STF(SP)}}$

Fluorescence level after excitation with STF or SP, respectively of system in dark-adapted state

$F_{\text{m}}^{\text{PP}}$

Fluorescence level with 100 % semi-closed RCs after release of photochemical quenching

$F_{\text{ss}}^{\text{PP}}$

Steady state value in the light of the variable fluorescence associated exclusively with primary photochemical quenching

FIA

Fluorescence induction algorithm

k_AB

Rate constant of ${\text{Q}}_{\text{A}}^{-}$ oxidation

k_2AB

Rate constant of oxidation of the double-reduced acceptor pair [PheQ_A]²⁻ in reduced Q_B-nonreducing RCs

k_L

Excitation rate of photosystem in light pulse

k_qbf

Rate constant of increase in variable fluorescence induced by F ^PE in 2–50 ms time domain

k_−qbf

Rate constant of dark reversion of variable fluorescence in 2–50 ms time domain induced by F ^PE

k_IP

Rate constant of F _v fluorescence in 50–500 ms time domain induced by F ^CET

k_-IP

Rate constant determining the major decay component of F _v induced by F ^CET

nF_v

Maximal normalized variable fluorescence associated with 100 % photoreduction of Q_A of open RCs (nF _v = $F_{\text{m}}^{\text{PP}}$ = $F_{\text{m}}^{\text{STF}}$)

OEC

Oxygen evolving complex

Ph(e)

Pheophytin, primary electron acceptor of PSII

PSII

Photosystem II

Q_A

Primary quinone electron acceptor of PSII

Q_B

Secondary quinone electron acceptor of PSII

q^dsq

Fraction of PSII RCs in which photochemical quenching at acceptor and donor side is released

RC

Reaction center of photosystem

SP

Fluorescence saturating pulse with duration exceeding 250 ms

sSP

Short fluorescence excitation light pulse with duration between 0.25 and 500 ms

STF

Single-turnover flash (excitation)

TSTM

Three-state trapping model

Y_Z

Secondary electron donor of PSII