Simultaneous Fat Saturation and Magnetization Transfer Contrast Imaging with Steady-State Incoherent Sequences

Abstract

Purpose

This work combines an n-dimensional (nD) fat sat(uration) RF pulse with steady-state incoherent (SSI) pulse sequences, e.g., spoiled Gradient echo sequence, to simultaneously produce B₀ insensitive fat suppression and magnetization transfer (MT) contrast. This pulse is then referred to as ”fat sat and MT contrast pulse” (FSMT-pulse).

Theory

We discuss the features of the FSMT-pulse and the MT sensitivities of the SSI sequences when combining with fat sat. Moreover, we also introduce an adapted RF spoiling scheme for SSI sequences with fat sat.

Methods

Simulations and phantom experiments were conducted to demonstrate the adapted RF spoiling. Fat suppression and MT effects are shown in 3T phantom experiments and in-vivo experiments, including brain imaging, cartilage imaging and angiography.

Results

To ensure that the sequence reaches steady state, the adapted RF spoiling is required for fat-sat SSI sequences. FSMT-pulse works robustly with field inhomogeneity and also produces MT contrasts.

Conclusion

SSI sequences with FSMT-pulse and adapted RF spoiling can robustly produce fat suppressed and MT contrast images in the presence of field inhomogeneity.

INTRODUCTION

Effective fat suppression or separation is critical for diagnostic quality in body MRI and is commonly used to eliminate undesired adipose tissue signals or prevent chemical shift artifacts. Fat sat(uration) is one popular fat suppression technique that uses a spectrally selective pulse to selectively saturate and dephase fat spins preceding the actual imaging pulse sequence (1). Fat sat typically works well and is compatible with most imaging sequences, but it is sensitive to B₀ and B₁ inhomogeneity. Moreover, the fat sat pulse is long in low field scanners, limiting the minimum T_R for some fast MRI sequences. These problems have been mitigated by using a 4D tailored spectral-spatial fat sat pulse proposed in (2). That fat sat pulse is robust to B₀/B₁ inhomogeneity and more time-efficient than the standard fat sat pulse.

Magnetization transfer (MT) is often used to increase vessel contrast in MR angiography (MRA) (3) and to indirectly image semisolid components of tissue, such as collagen (4) or myelin (5). Protons in these semisolids have a very broad spectrum and can be selectively saturated by off-resonance RF pulses. MT effect is then generated by magnetic exchange between the immobilized components in tissue (proteins, polysaccharides, or lipid bilayers) and the detected water protons. Using this tissue-dependent feature, MT contrast (MTC) sequences can produce MTC images with useful diagnostic information. MTC imaging applies the MT pulse either only once prior to the steady-state imaging sequence (6) (turbo MT preparation) or in every repetition (7); in this paper, we focus on the latter approach because it shows higher MT sensitivity and thus less specific absorption rate (SAR) penalty when T_R is short.

Combining fat sat and MTC is beneficial in many clinical applications, such as cartilage imaging (7)(8), cardiac imaging (6), intracranial angiography (3), breast imaging (9) and lung imaging (10). In angiography applications, spoiled gradient-echo sequence (SPGR) has been widely used to produce T₁-weighted or flow-enhanced images with very short imaging times, e.g., time-of-flight (TOF) angiography(6). SPGR belongs to the class of ”steady-state incoherent (SSI) sequences” that eliminate residual transverse magnetization prior to each RF pulse (11). SSI sequences are usually compatible with using fat sat and MT pulses applied in each repetition. In applications that need more T₂ weighting, e.g., MTC cartilage imaging, the balanced steady-state free precession sequence (bSSFP) is a preferred fast imaging sequence that produces high signal-to-noise ratio (SNR) T₂/T₁ contrast images. However, a drawback of bSSFP is the banding artifacts caused by B₀ field inhomogeneity, and it belongs to ”steady-state coherent (SSC) sequences” (11) that have limited compatibility with fat sat and MT pulses in each repetition. Nielsen et al. (12, 13) proposed an SSI sequence called ”small-tip fast recovery (STFR)” that produces bSSFP-like high SNR T₂/T₁ contrast images that are free of banding artifacts.

Although SSI sequences like SPGR or STFR allow using fat sat and MT pulses in each repetition, some limitations may hamper their practical use. Combining both fat sat and MT pulse into one sequence may increase minimal T_R too much for practical use in applications like breath-hold imaging, especially at low fields. In addition, such combinations may generate SAR problems at high fields.

In this work, we propose to apply the n-dimensional tailored spectral-spatial fat sat (FSMT-pulse) pulse proposed in (2) to SSI sequences, including SPGR and STFR, to produce fat suppressed MTC images. In the context of this paper, such FSMT-pulse is referred to as ”fat sat and MT contrast pulse” (FSMT-pulse). The major contribution of this work is the combination of FSMT-pulse and SSI sequences. FSMT-pulse has short pulse length and very high power efficiency (2). Its pulse length mitigates the issue of limited T_R in steady-state imaging, and the high power efficiency contributes to MT contrasts. The other contributor to MT contrasts is the fat sat SSI sequence itself, which has high sensitivity to MT. The issue of limited T_R is further mitigated by the fact that no special MT pulse is needed. In addition, the FSMT-pulse pulse is also robust to B₀/B₁ inhomogeneity, mitigating a general problem in fat sat imaging. Furthermore, we found that the conventional RF spoiling scheme that is typically used for SPGR and STFR does not always work when pulses with crushers like fat sat are applied, so we introduce an adapted RF spoiling scheme for the proposed sequences.

In this paper, we demonstrate the proposed methods with simulation studies, phantom experiments and in-vivo experiments like human brain imaging, cartilage imaging and TOF-based MR angiography at 3T. Because we had very similar conclusions for the two SSI sequences, i.e., SPGR and STFR, we focus on the proposed SPGR sequence in the rest of the paper. The studies of the proposed STFR sequence are shown in the supplementary material.

THEORY

SPGR with FSMT-pulse

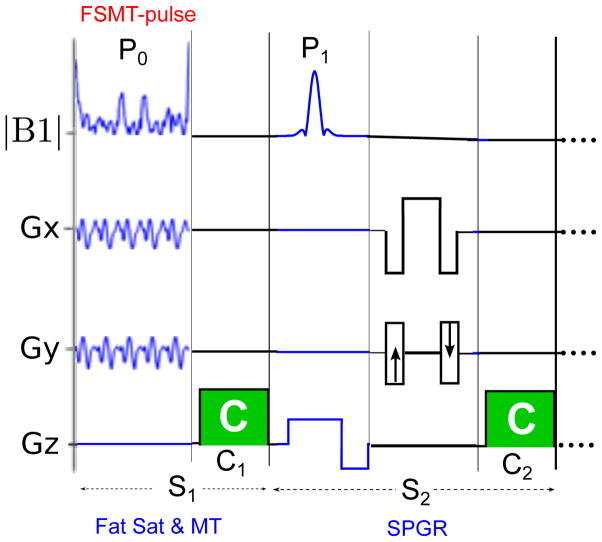
Fig. 1 illustrates the 2D version of the proposed fat sat and MTC SPGR (FSMT-SPGR) sequence. The fat sat and MT part (S₁) with the FSMT-pulse (P₀) is added prior to the regular excitation pulse (P₁) of SPGR (S₂) in each repetition, and both S₁ and S₂ have a gradient crusher, i.e., C₁ & C₂. This 2D version of FSMT-SPGR uses a 3D FSMT-pulse (14) (15) that is tailored to the B₀/B₁ field using the same method proposed in (2), and it uses repeated 2D spiral-out trajectories to cover the 3D spectral-spatial (SPSP) k-space (14) (15). The 3D version of the FSMT-SPGR uses the same FSMT-pulse used in (2). The key features of the FSMT-pulse mentioned in (2) include robustness to field inhomogeneity and shorter pulse lengths. By traversing multi-dimensional spectral and spatial excitatoin k-space very efficiently, FSMT-pulse has much higher power efficiency, e.g., up to 60 – 100 times, than the regular spectral-select fat sat pulse at 3T (2). This feature contributes to the MT contrast discussed in the next section. In addition, these concise pulse sequences mitigate the issue of limited T_R in steady-state imaging.

Figure 1.

Illustration of the 2D version of the proposed FSMT-SPGR sequence.

Simultaneous Fat Sat and MTC Imaging

For a given MT pulse, SPGR with the MT pulse applied in each repetition produces higher MT effects than the one with the turbo type MT prep. Defining MT ratio (MTR) as the ratio between the amount of magnetization reduced by MT and the original magnetization, the Appendix shows that the steady-state longitudinal magnetization of MTC SPGR prior to each P₁ with respect to MTR is:

$$M_z(\text{MTR})=M_0\frac{(1-\text{MTR})E_{1s}(1-E_{1d})+(1-E_{1s})}{1-(1-\text{MTR})E_{1,s}{E}_{1,d}cos\alpha }$$ [1]

where M₀ is equilibrium magnetization, $E_{1s}\triangleq e^{-\frac{T_s}{T_1}},E_1\triangleq e^{-\frac{T_d}{T_1}}$, T_s is the duration of each gradient crusher, T_d is the duration of each repetition excluding the MT part, α is the flip angle, relaxation during the MT pulse is ignored.

To show that MTC SPGR is more efficient in producing MT effects than the turbo MT-prep sequences, Fig. 2 shows curves of 1-M_z(MTR)/M_z(0) for ranges of T₁ and T₂ values, where 1-M_z(MTR)/M_z(0) is the ”effective MTR” of SPGR. Note that MTR defined above is not necessarily equal to effective MTR, as MTR reflects only the magnetization change caused by the MT pulse, while the effective MTR represents the steady-state magnetization change, which is a combined effect of the MT pulse and the steady-state sequence. The simulation was run with T_d = 10 ms and T_s = 1 ms. Note that MTR is equal to the effective MTR of the turbo MT prep sequences, so the plots show that with reasonable T₁ and T₂ values, MTC SPGR with MT pulses applied in each repetition are much more efficient in producing MT effects than the corresponding turbo MT prep sequence. Such MT sensitivity increases with shorter T_R or longer T₁ and does not change much with different T₂ values.

Figure 2.

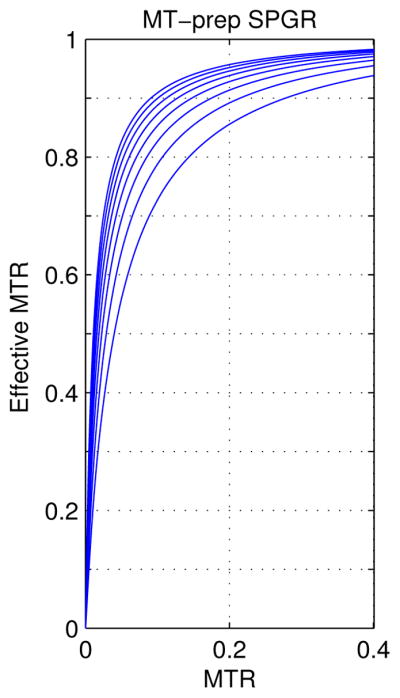
Plots of the effective MTR in terms of MTR for MTC SPGR; The plots are from all the combinations of the following relaxation parameters: T₁ = [0.5, 0.7, …, 1.7, 1.9] s, and T₂ = [50, 70, …, 170, 190] ms. SPGR is sensitive to small magnetization attenuation caused by MT effect.

With this property, we propose to use SPGR with FSMT-pulse to generate MT effect and suppress fat simultaneously. Although SPGR is MT sensitive, SPGR with the conventional spectrally selective fat sat pulse produces too little MT effect for clinical use, because the conventional fat sat pulses are low energy pulses compared to typical MT pulses (6) and MT effects increase with RF energy (16). However, the proposed FSMT-pulse produces much higher RF energy than the conventional fat sat pulse, because this short efficient tailored spectral-spatial pulse needs to handle both spectral and spatial variations by traversing the excitation k-space very rapidly, leading to higher RF amplitude and thus higher RF energy (2). In addition, the FSMT-pulse is about 3.5 ppm off the center frequency, which is much lower than the off-resonance frequency of the conventional MT pulses. This can further increase the MT effects induced by the FSMT-pulse, as MT effects decrease with off-resonance frequency (16). Thus, the proposed FSMT-pulse can potentially produce useful MT effects while suppressing fat signal.

On the other hand, in practice, it is hard to separte MT effects and direct water spectrum excitation caused by fat sat pulse. Direct excitation to water causes the same effects as if there were MT effects. Thus, the property shown in Fig. 2 also indicates that these sequences are very sensitive to direct excitation of water by imperfect FSMT-pulse or SLR fat sat pulses in the presence of field inhomogeneity. Such direct water excitation should be minimized to avoid confusion with MT effects. We observed significant signal drop in MT-free materials when using a SLR pulse that has ripples in the water band smaller than 5% of the fat band amplitude, which is consistent to Fig. 2. Thus, the SLR fat sat pulse used in our experiments was designed with very strict restriction on the amplitude of ripples around the water spectrum. Similarly, the FSMT-pulse design also needs to fit the target pattern of the water bands very strictly. In contrast, these sequences are not so sensitive to inaccurate fat suppression, so the FSMT-pulse design allows less accurate fat band fitting to accommodate the high demands in water bands. Specifically, we set the bandwidths of water much wider than the corresponding fat bandwidths in the pulse design.

Adapted RF Spoiling Scheme

Conventional SPGR without fat sat needs gradient crushers to spoil the residual transverse magnetization before the next imaging cycle, and RF spoiling is also required when T_R < T₂ (12, 17). RF spoiling removes the residual transverse signal by quadratically varying the global RF phase, producing incoherent intra-voxel spin behaviors. In SPGR without fat sat, the global phase of P₁ varies as the following quadratic function (17):

$${\mathrm{\Phi }}_{P_1}(n)=\frac{a}{2}{n}^2+bn+c$$ [2]

where a, b, c are constants, and n is the number of repetitions. The quadratically changing phase guarantees that the signal of each voxel reaches a homogeneous steady-state, and the residual transverse magnetization at the end of each repetition can be kept to almost zero by choosing a particular value of a, e.g., 117⁰.

However, sequences with additional crushers in each repetition, e.g., fat sat sequences, may not work robustly with the conventional RF spoiling scheme, i.e., P₀ keeps the same global phase as P₁. For SPGR with fat sat, conventional RF spoiling scheme needs perfect fat sat to guarantees that the signals reach steady state. In this ideal situation, water or fat experiences only one RF pulse, i.e., P₁ or P₀, in each repetition. However, fat sat is imperfect in practice. When using conventional fat sat, even if the B₀ inhomogeneity is not severe enough to have water excited by the fat sat pulse, fat signals can never be perfectly eliminated in the presence of B₀/B₁ inhomogeneity; then fat spins can be excited both by P₀ and P₁, and the additional crusher C₁ will alter the signal’s progression to steady state. Although the FSMT-pulse can greatly improve fat sat in the presence of B₀/B₁ inhomogeneity, it still can not work perfectly.

To improve robustness of SPGR with fat sat, we propose to adapt the conventional RF spoiling scheme to better approach steady state with imperfect fat sat. The new RF spoiling scheme applies the quadratic RF phase variation to each ”sub-unit that contains a crusher” instead of to each repetition. We use the following global phase of each pulse in SPGR with fat sat:

$$\begin{array}{l}{\mathrm{\Phi }}_{P_0}(n)=\frac{a}{2}{(2n-1)}^2+b(2n-1)+c\\ {\mathrm{\Phi }}_{P_1}(n)=\frac{a}{2}{(2n)}^2+b(2n)+c\end{array}$$ [3]

If the two crushers C₁ and C₂ have the same area, this adapted RF spoiling ensures that the sequence reaches steady state (17).

Furthermore, one must properly choose the parameter a in [3] to completely remove the remnant transverse magnetization at the end of each repetition. We empirically chose a = 117⁰ for all our experiments based on simulations and some phantom experiments. There are also other good values for the fat-sat SPGR with the adapted RF spoiling, such as 74⁰. When B₀ map is close to uniform, the transverse magnetization of most spins experience only one crusher in each repetition, and then the sequence would almost work as the conventional RF spoiling but with 4 times linear phase increments. In this case, a = 117⁰/4 may be a good choice.

METHODS

Simulation and Phantom Experiment I: RF Spoiling Schemes

We first compared the conventional RF spoiling scheme and the adapted RF spoiling scheme by Bloch equation simulations. We simulated the signal evolutions of the integrated magnetization of a 0.5 cm voxel with 5000 equally-spaced isochromats for fat or water with fat-sat SPGR. We chose some typical values for the fat spin and the water spin: T_1,fat/T_2,fat = 200 ms/70 ms, T_1,water/T_2,water = 1 s/100 ms; the sequence parameters were: T_R = 10 ms, the tip angle of P₁ was 20⁰ for both water and fat, the tip angle of P₀ was 80⁰ for fat and 20⁰ for water to simulate imperfect fat sat, and the parameter a in [2] and [3] was 117⁰. We simulated evolutions of the transverse magnetization of fat and water right after P₁ for the first 200 and 500 repetitions (2 s and 5 s) respectively, which were sufficient to test whether the signals reach steady state.

In addition, we also applied fat-sat SPGR in a phantom scan on a 3T GE scanner (GE Healthcare, Milwaukee, WI, USA). The phantom was a cylindrical phantom filled with distilled water and vegetable oil. The fat sat part used a conventional spectrally selective fat sat pulse designed by the Shinnar-Le Roux (SLR) algorithm (18). The SLR fat sat pulse is 5 ms long and has a 400 Hz minimal phase passband for fat (center frequency is −435 Hz), which is a standard setting for 3T fat sat. With this fat sat pulse, a 3D SPGR with spin-warp readout was applied using the conventional and the adapted RF spoiling schemes respectively, and the imaging parameters were: T_R = 13 ms, FOV = 14 cm ×14 cm ×14 cm, data size = 64 × 64 × 14, a = 117⁰. A set of images without fat sat also were acquired for reference.

Phantom Experiment II: Fat Sat Pulses

The FSMT-pulse used for 3D or multi-slice imaging has been demonstrated in (2). In our experiments with FSMT-SPGR sequences, we also performed 2D scans that need only a 3D version of the FSMT-pulse. Phantom experiments were performed at 3T to test 2D SPGR sequences with 3D FSMT-pulse. The phantom was the same cylindrical water/oil phantom used in the previous experiment. Similar to (2), we designed each 3D FSMT-pulse using only a 2D B₀ field map, assuming that B₁ homogeneity is acceptable in our single channel excitation experiments. These FSMT-pulses were compared with the 5 ms SLR fat sat pulse used in the previous experiment. The goal of this study was to demonstrate that SPGR with 3D FSMT-pulse is more robust to B₀ inhomogeneity than using the SLR fat sat pulse.

The sequence was applied to different slices of the phantom to acquire multiple 2D axial slice images, where each FSMT-pulse was designed using the corresponding 2D B₀ map. We acquired B₀ maps from two gradient echo images with different echo times, and the echo time difference had water and fat spins in-phase, e.g., ΔT_E = 2.272 ms at 3T, to eliminate the phase difference caused by chemical shift. All the FSMT-pulses, which were only 2.1 ms long, used 5 repetitions of 2D spiral-out excitation k-space trajectories, and the adapted RF spoiling scheme [3] was applied to those sequences. All the data were acquired with 2D spin-warp k-space trajectories, and the imaging parameters of the SPGR sequences were: FOV = 14 cm ×14 cm, slice thickness = 6 mm, data size = 64 × 64, a = 117⁰, and T_R = 11.6 ms and 14.5 ms for the sequence with the 2.1 ms FSMT-pulse and the 5 ms SLR fat sat pulse respectively. For each fat suppressed image, we also acquired its corresponding non-fat-suppressed image with the fat sat pulse turned off.

Phantom Experiment III: Simultaneous Fat Sat and MTC Imaging

To test MT effects, we made a special cylindrical MT phantom filled with mixture of Prolipid 161 (Ashland Specialty Ingredients) and NiCl₂ solution. The material has similar T₁, T₂ and MT values to white matter at 3T. In addition, we made a spherical phantom filled with mineral oil and distilled water doped with MnCl₂, and the MnCl₂ solution was carefully tuned to match the T₁ and T₂ values of the MT phantom material at 3T. To test the effect of simultaneous fat sat and MTC, we put both phantoms in one field of view and applied the proposed FSMT-SPGR on the 3T scanner. Similar to the previous phantom experiment, we first acquired a 2D B₀ map, and then designed the FSMT-pulse based on the field map. FOV of the field map used in the design was 18 cm ×18 cm, and the pulse length was increased to 2.7 ms with 7 repetitions of spiral-out trajectories to accommodate the B₀ field that has big variations between the two phantoms (Fig. 6). 2D spin-warp readouts were applied to the same part of the object with the FSMT part on or off, and the imaging parameters were: FOV = 18 cm ×18 cm, slice thickness = 6 mm, data size = 64 × 64, a = 117⁰, and T_R = 16 ms.

Figure 6.

The B₀ map and the resulting images of Phantom experiment III. Left: B₀ map in Hz; middle: the original SPGR image with FSMT disabled where oil, water and the MT phantom are labeled; right: the ratio image taken between the one with FSMT contrast and the one without.

In-Vivo Experiments I: Simultaneous Fat Sat and MTC Imaging in Brain

We tested the proposed FSMT-SPGR in an in-vivo experiment on the 3T GE scanner, where we scanned axial brain slices of a healthy subject. Similar to the phantom experiments, 2D B₀ maps were first acquired for the FSMT-pulse design. The FSMT-pulse was 2.3 ms long with 7 repetitions of 2D spiral-out trajectories. 2D spin-warp readout was used to acquire an axial slice around the level of eyes, where the designed FSMT part was on or off respectively. The imaging parameters were: FOV= 24 cm ×24 cm, slice thickness = 6 mm, data size = 256 × 256, a = 117⁰, and T_R = 15.3 ms.

In-Vivo Experiments II: MR Angiography in Brain

Lastly, we applied the proposed FSMT-SPGR to MR angiography (MRA) in human cerebral arteries where fat suppression and MT can help suppress surrounding fat and other background tissue respectively. We acquired 3D time-of-flight (TOF) images over a 4 cm thick axial slab around the circle of Willis with a 3D SPGR sequence. In addition, FSMT-pulse was designed based on the 3D B₀ map of an extended 3D axial slab that covered the imaging slab and its adjacent inferior axial slab (4 cm thick). By designing for this extended volume, direct excitation of the arterial blood in the upstream region by the FSMT-pulse can be largely reduced, because the FSMT-pulse has unpredictable effects to out-of-ROI regions. The FSMT-pulse was 2.5 ms long using a repeated 3D spiral trajectory (2)(19). The image data were acquired with 3D spin-warp readout, and two sets of images were taken with the proposed FSMT part on or off respectively. The imaging parameters were: T_E = 3.28 ms, T_R = 11.4 ms, flip angle = 20⁰, a = 117⁰, 0.94 mm×0.94 mm×2 mm resolution, FOV = 24 cm ×24 cm ×4 cm.

RESULTS

Simulation and Phantom Experiment I: RF Spoiling Schemes

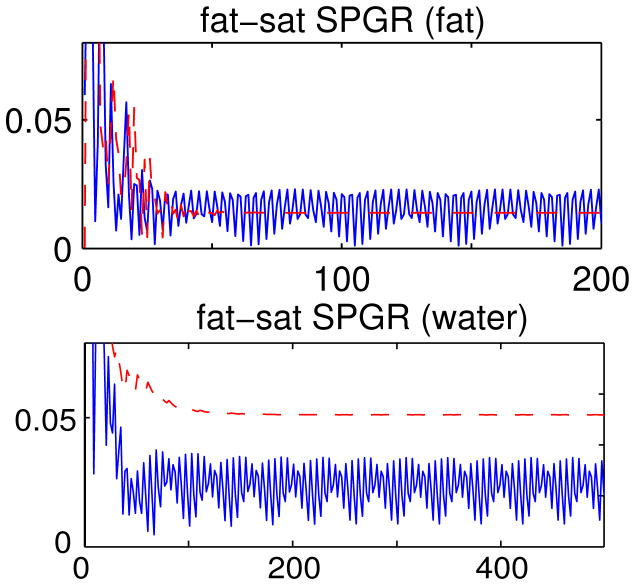
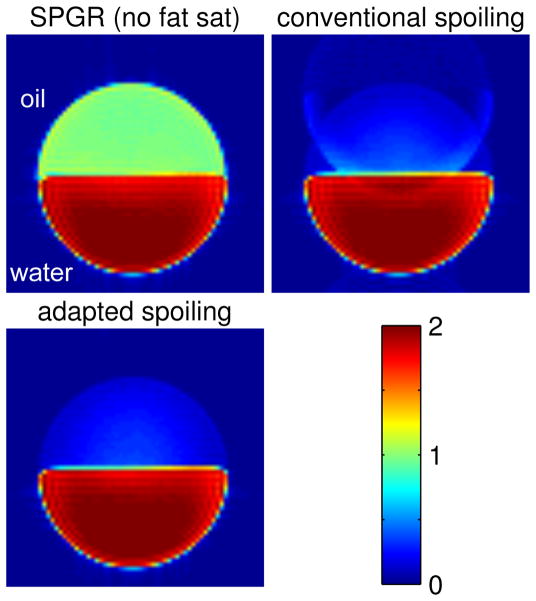
Fig. 3 shows the signal evolutions of fat or water when fat-sat SPGR is applied with the conventional RF spoiling scheme or the adapted RF spoiling scheme. In all the plots, the sequence with the conventional RF spoiling scheme did not reach steady state (blue solid lines), but the one with the adapted RF spoiling scheme reached steady state after 100 repetitions at most (red dashed lines). With the signal oscillating over repetitions, the data of the conventional RF spoiling scheme are inconsistent in the k-space, causing ghosting artifacts. This is shown in Fig. 4 where the image acquired with the conventional RF spoiling scheme has ghosting artifacts along the phase-encoding direction of the spin-warp trajectory, while the one with the adapted RF spoiling scheme shows a fat-suppressed image free of ghosting artifacts.

Figure 3.

Signal evolutions of fat spin (upper row) and water spin (lower row) using fat-sat SPGR with different RF spoiling schemes. Both vertical axes denote the ratio between the transverse magnetization right after P₁ and the magnetization at equilibrium, M_xy/M₀; the horizontal axes denote the number of repetitions. The signal reaches steady state with the adapted RF spoiling scheme (dashed lines), but not with the conventional RF spoiling scheme (solid lines).

Figure 4.

An axial slice of the 3D SPGR images of the cylindrical phantom (oil on top of water) where all three images are at the same color scale: upper-left: fat sat off; upper-right: fat sat on with conventional RF spoiling; lower-left: fat sat on with adapted RF spoiling. The image with the conventional RF spoiling has ghosting artifacts due to data inconsistency, whereas the one with the adapted spoiling scheme is free of these artifacts.

Phantom Experiment II: Fat Sat Pulses

Fig. 5 shows the resulting images produced by the SPGR sequences and the corresponding B₀ maps. The original images without fat sat are in the first column, the B₀ maps are in the second column, and the ratio images by the FSMT-pulse and the SLR fat sat are shown in the third and fourth columns respectively. The ratio image is calculated by taking the ratio between the image with fat sat and the corresponding image without fat sat, so it should range from 0 to 1 in theory.

Figure 5.

The results of the phantom experiments for testing fat-sat SPGR where we picked two representative slices for each sequence. From left to right, 1st column: the original images with no fat sat (oil on top of water), 2nd column: B₀ maps, 3rd column: the ratio images with the 3D fat sat pulse, 4th column: the ratio images with the SLR fat sat pulse. The ratio image is calculated by taking the ratio between the image with fat sat and the corresponding image without fat sat.

As seen in the B₀ maps, we picked two slices of the phantom that have relatively extreme off-resonance frequencies to demonstrate the principle. As seen in the last column in Fig. 5, SLR fat sat did not suppress fat signal completely in regions with large off-resonance frequencies. SLR fat sat worked generally well for water parts, except for the edges where off-resonance frequencies are negative (last row), which is because the frequency response of the SLR pulse is asymmetric around the center frequency of water. In contrast, the FSMT-pulse worked more robustly for both water and fat in the presence of B₀ inhomogeneities. In addition, the FSMT-pulse is 58% shorter than the SLR fat sat pulse.

Phantom Experiment III: Simultaneous Fat Sat and MTC Imaging

Fig. 6 shows the B₀ map and the corresponding ratio images produced by FSMT-SPGR, where the ratio image is taken between the image with FSMT contrasts and the one without FSMT contrasts. The proposed sequence simultaneously suppressed fat and attenuated the MT phantom signal while the water signal maintains a similar level. By manually segmenting each image into the three parts, we calculated the average signal ratios of oil, water and MT phantom, i.e., 0.076, 0.97 and 0.62, respectively. There may be some direct excitation of the FSMT-pulse to the MT phantom that can contribute to the attenuation in the MT phantom regions, and it is hard to separate this effect and MT effects. However, according to the simulation of the pulse (not shown), direct excitation in the MT phantom regions was very similar to direct excitation in the water regions. Since we observed very little direct excitation in the water regions, we believe the attenuation in the MT phantom regions were caused primarily by the MT effects from the FSMT-pulse.

In-Vivo Experiments I: Simultaneous Fat Sat and MTC Imaging in Brain

Fig. 7 shows brain imaging results, where the proposed sequence effectively suppressed the fat tissue around the skull and optical nerves. In addition, white matter is significantly attenuated due to MT effects. As shown in the right image of Fig. 7, the effective MTR in white matter is around 30% to 50%.

Figure 7.

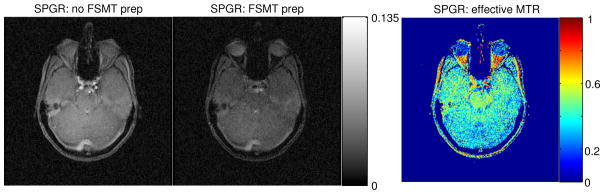
SPGR images acquired in the in-vivo experiments on human head. Left: without FSMT contrast; middle: with FSMT contrast; right: effective MTR maps. The left two images have the same gray scale.

In-Vivo Experiments II: MR Angiography in Brain

Fig. 8 shows the results of the MRA experiment with the maximum intensity projections (MIP) of the image with no FSMT-pulse (left) and with FSMT-pulse (right). Despite the presence of B₀ inhomogeneity, the FSMT-pulse greatly suppressed the fat tissue around the skull in the MIP with FSMT contrasts, except that part of the fat around the left optical nerve was suppressed poorly due to large off-resonance effect (about 300 Hz). Furthermore, MT effects produced by the FSMT-pulse significantly reduced the background signals, and the arteries are better delineated in the MIP compared to the one without FSMT contrasts, as pointed out by the red arrows. Those two images are each normalized to their own maximal intensity, because the blood signal was also attenuated due to its own MT effect and some direct excitation from the imperfect fat sat pulse, which is why the unsuppressed fat and optical nerve posterior to the left eye appears brighter in the FSMT contrast image. In addition, some veins, especially the ones anterior to the circle of Willis, are darker in the FSMT contrast image, because the FSMT-pulse, which was designed only for the imaging slab and the upstream region of the arteries, may suppress the upstream regions of the veins. This feature may help reduce the need for vein suppression pulses. In general, the proposed FSMT-SPGR sequence improved the TOF MRA in the brain by simultaneously suppressing fat and background tissue.

Figure 8.

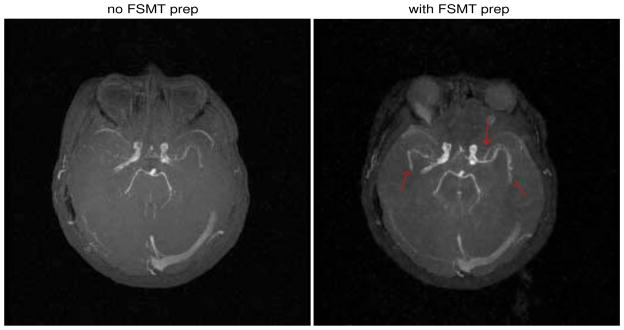
The results of the MRA experiment where the MIP with no FSMT contrast is on the left and the one with FSMT contrast on the right. Red arrows point to the arteries that are better delineated.

DISCUSSION AND CONCLUSIONS

In addition to the proposed FSMT SPGR sequence, we also show studies of the proposed FSMT STFR sequence in the supplementary material. We proposed to apply the FSMT-pulse to SSI sequences, e.g., SPGR and STFR, to simultaneously do fat suppression and MTC. We demonstrated that an adapted RF spoiling scheme is required for fat-sat SSI sequences to reach steady state. Compared to the conventional SLR fat sat, the FSMT-pulse is more robust to field inhomogeneity, and it can additionally produce MTC with SSI sequences having high sensitivity to magnetization attenuation. Examples of cartilage imaging (in supplementary material) and brain MRA show that the proposed FSMT-SSI sequences can produce images that appear to be better for clinical use.

B₁ inhomogeneity could be ignored in our 3T experiments, but there are cases where B₁ inhomogeneity can be a potential issue, e.g., breast imaging (20). Then the FSMT-pulse can help to compensate for B₁ inhomogeneity or even use parallel excitation (2), requiring B₁ mapping (21, 22, 23). This is another advantage over the conventional SLR fat sat. Although global SAR was kept below the limit in our experiments, local SAR penalty may be problematic when parallel excitation is used. Moreover, MT effects by the parallel excitation version of the FSMT-pulse may need further investigation.

We used 2D SSI sequences with 3D FSMT-pulse in most of the experiments. If a volumetric scan is needed, one may either do 3D imaging with 4D FSMT-pulse as used in the MRA experiment, or do 2D imaging slice by slice in a non-interleaved way. For the latter approach, the FSMT-pulses need to be designed for each slice individually based on multi-slice or 3D B₀ map. Comparing the MT effects of these two approaches, 4D FSMT-pulse is slightly longer than 3D FSMT-pulse, which is 2.5 ms versus 2.3 or 2.1 ms, but the 4D FSMT-pulse usually has similar or even higher energy, because it typically traverses the origin of the excitation k-space more densely than the 3D FSMT-pulse.

One advantage of SSI sequences over bSSFP for MTC imaging is that MTC SSI sequences can adjust the amplitude of MT effects more easily. The proposed sequences can adjust MT effects by changing the RF power constraints in the pulse design, e.g., by adjusting the corresponding regularization parameter. In our experiments, the RF energy of the FSMT-pulse could be reduced by up to 5–10 times with acceptable degradation in fat suppression performance, which may have very minimal MT effects. Thus, the proposed sequences with RF power penalization can potentially be used for applications that need only fat suppression.

Furthermore, tt would be interesting to investigate the proposed sequences in more clinical applications that can benefit from fat suppression and MTC, e.g., cardiac imaging and breast imaging. Furthermore, as (2) has pointed out other potential benefits and issues of the FSMT-pulse at other field strengths than 3T, future work may include studies of the proposed sequences at those non-3T field strengths.

APPENDIX

This appendix derives [1]. Referring to Fig. 1a, we calculate the magnetizations at certain time points and each repetition of the sequence is segmented at those time points:

$${\overrightarrow{M}}_1\to P_1\to {\overrightarrow{M}}_2\to \text{free}\text{precession}\text{and}{C}_2\to {\overrightarrow{M}}_3\to S_1\to {\overrightarrow{M}}_4$$

where

$${\overrightarrow{M}}_1=\left[\begin{array}{c}0\\ 0\\ M_z\end{array}\right],{\overrightarrow{M}}_2=\left[\begin{array}{c}0\\ M_{z}sin\alpha \\ M_{z}cos\alpha \end{array}\right]$$

After the free precession and C₁, we have

$${\overrightarrow{M}}_3=\left[\begin{array}{c}0\\ 0\\ {\overrightarrow{M}}_2(3)E_{1d}+(1-E_{1d})M_0\end{array}\right]$$

In the MT part, i.e., S₁, the overall effect is a change in longitudinal magnetization followed by T₁ relaxation during C₂. Therefore, we have

$${\overrightarrow{M}}_4=\left[\begin{array}{c}0\\ 0\\ (1-\text{MTR}){\overrightarrow{M}}_3(3)E_{1s}+(1-E_{1s})M_0\end{array}\right]$$

When the sequence reach a steady state, we have M⃗₄ = M⃗₁ or M⃗₄(3) = M_z. Then the steady-state longitudinal magnetization of MTC SPGR prior to each P₁ can be expressed as a function of MTR, which is equation [1].