Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Mar 23;5:9361. doi: 10.1038/srep09361

Enhanced Magnetic Anisotropies of Single Transition-Metal Adatoms on a Defective MoS2 Monolayer

W T Cong 1, Z Tang 1,a, X G Zhao 1, J H Chu 1
PMCID: PMC4369737  PMID: 25797135

Abstract

Single magnetic atoms absorbed on an atomically thin layer represent the ultimate limit of bit miniaturization for data storage. To approach the limit, a critical step is to find an appropriate material system with high chemical stability and large magnetic anisotropic energy. Here, on the basis of first-principles calculations and the spin-orbit coupling theory, it is elucidated that the transition-metal Mn and Fe atoms absorbed on disulfur vacancies of MoS2 monolayers are very promising candidates. It is analysed that these absorption systems are of not only high chemical stabilities but also much enhanced magnetic anisotropies and particularly the easy magnetization axis is changed from the in-plane one for Mn to the out-of-plane one for Fe by a symmetry-lowering Jahn-Teller distortion. The results point out a promising direction to achieve the ultimate goal of single adatomic magnets with utilizing the defective atomically thin layers.

Single magnetic atoms absorbed on a surface represent the ultimate limit of bit miniaturization for the magnetic data storage1,2. To achieve this ideal goal, a critical step is to find an appropriate material system in which there are not only strong enough binding between the absorption atoms and the substrate surface to guarantee the system's chemical stability but also large enough magnetic anisotropic energy (MAE) to ensure the magnetic stability of the atomic magnets over thermal fluctuations and spin decoherence. After intensive studies in the last decade3,4,5, impressive progresses have been achieved towards the goal. It has been elucidated both experimentally and theoretically that, because of symmetry breaking and hybridization, the MAE of the transition metal adatoms, such as Co on a Pt surface3, Fe or Mn on a CuN surface4, etc., can be greatly enhanced.

Recently, discovery of graphene6 has raised exciting prospects to approaching the ultimate goal by utilizing the atomically thin layers as the substrate7. It has been predicted that single magnetic atoms absorbed on graphene as well as hexagonal boron nitride (h-BN) are of huge uniaxial magnetic anisotropies8,9,10,11,12 and experimentally, a large magnetic anisotropy of 8.1 meV or about 3.0 meV has been observed for Co adatoms on graphene13 or on Cu2N surface14. However, as a consequence of the single atom thickness of both graphene and h-BN and their strong covalent binding in plane, the implanted transition metal atoms significantly stick out of the plane of the host material, which leads to a chemical instability if the system is exposed to the air.

Monolayer molybdenum disulfide (MoS2) is another atomic-scale thin layer material. It is a prototypical quasi-two-dimensional crystal consisting of two close-packed S layers separated by a Mo atomic layer. Different from graphene, the MoS2 monolayer is a direct band-gap semiconductor15. Recently, high quality MoS2 monolayers with large areas have been achieved by using the chemical vapor deposition technology16,17,18, which paves the way to a number of promising applications of the MoS2 monolayer in semiconductor optoelectronic and spintronic devices. For instance, a transistor with a high mobility at room temperature19 and nonvolatile memory cells20 based on monolayer MoS2 have been successfully fabricated. Moreover, experiments have shown that various structural defects occur in the MoS2 monolayers21,22, which provide further exciting opportunities to tailor the local properties of the substrate to create new functionalities.

For this reason, we investigated the stabilities and the MAE's of the single transition-metal atoms (Mn and Fe) absorbed on the pristine and defective MoS2 monolayers by first-principles calculations. By combining the spin-orbit coupling theory, it is elucidated that the TM atoms absorbed on the disulfur vacancies of the MoS2 monolayer are of high chemical stabilities as well as much enhanced magnetic anisotropic energies. Particularly, it is analysed that, as a consequence of a symmetry-lowering Jahn-Teller distortion, the easy axis of magnetization can be changed from the one on the MoS2 plane to the one out of the plane by changing the absorption adatom from Mn to Fe. These results indicate that the single TM adatoms absorbed on the defects of the MoS2 monolayers are very promising candidates for fabricating the atomic-scale magnetic bit for data storage.

Results

At first, we calculated the stability and the MAE of a single Fe or Mn absorbed on a pristine MoS2 monolayer. There are several possible absorption positions for the TM adatom on the MoS2 monolayer. We found that, similar to a TM atom absorbed on graphene23, the most stable absorption site is also the octahedron site as shown in Figure 1a. At this site, the binding energy of a single Fe (Mn) adatom is 1.34 (1.18) eV and the calculated total magnetic moment of the absorption system is 4.0 (5.0) μB. As demonstrated by the spin density distributions shown in Figure 2a, the magnetic moments are mainly contributed from the TM adatoms. The obtained high spin configurations agree with the Hund's rule.

Figure 1. Top and side views of the optimized geometries of the Fe adatom absorbed on the pristine MoS2 monolayer (a) and on its disulfur vacancies (b).

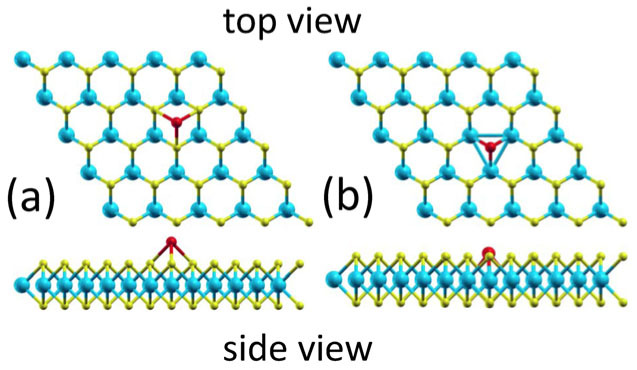
Figure 1

Open in a new tab

The cyan, yellow, and red balls denote Mo, S, and Fe atoms, respectively.

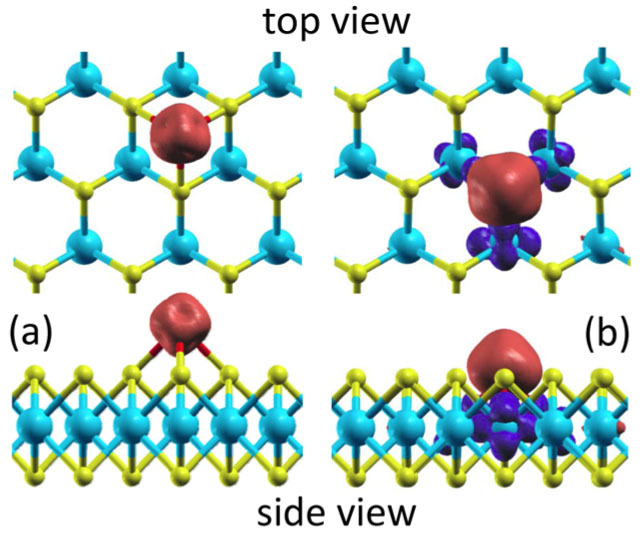
Figure 2. Enlarged isosurfaces of the calculated spin density distributions for the Fe adatom absorbed on the pristine MoS2 monolayer (a) and on its disulfur vacancies (b) (upper panel: top view, lower panel: side view).

Figure 2

Open in a new tab

However, as presented in Table 1, the MAE's of the TM adatoms on the pristine MoS2 monolayer are rather lower, only −0.2 and −0.3 meV for the Mn and Fe, respectively (the negative sign indicating an out-of-plane magnetic anisotropic axis). Particularly, the optimized structure shown in Figure 1 indicates that, although the binding energy of an absorbed Fe atom on the MoS2 monolayer is 1.34 eV, the adatom is still lying far above the layer (about 1.75 Å from the top S layer), indicating that the system may be unstable when exposed to air. Similar situations are obtained for the Mn adatom as well (Table 1). These results imply that the TM adatoms absorbed on the pristine MoS2 monolayers are not the ideal material systems.

Table 1. Calculated binding energies (EB), distances to the top sulfur layer (Δh), total magnetic moments (m.m.), and magnetic anisotropic energies (MAE) of the Mn and Fe adatoms absorbed on the pristine MoS2 monolayer and its disulfur vacancies (VS2). The values in the parentheses are the magnetic moments of the adatoms.

Absorption systems EB (eV) Δh (Å) m.m. (μB) MAE (meV)
Fe on pristine MoS2 1.34 1.75 4.0 (4.0) −0.3
Mn on pristine MoS2 1.18 1.77 5.0 (5.0) −0.2
Fe on VS2 of MoS2 3.51 0.28 2.0 (3.0) −3.6
Mn on VS2 of MoS2 3.50 0.34 3.0 (4.0) 1.3
Open in a new tab

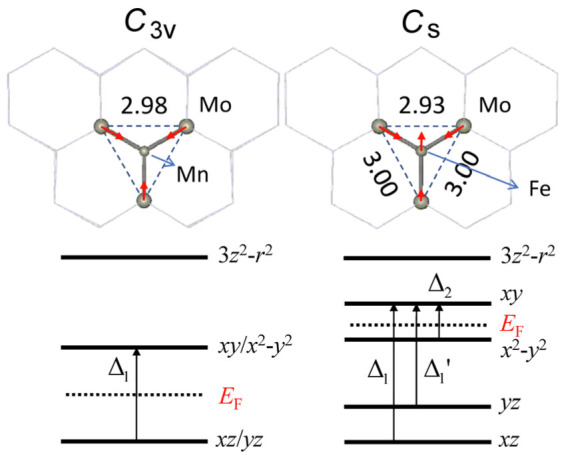
We then studied the stabilities and the MAE's of the TM adatoms absorbed on the defective MoS2 monolayers. Zhou et al.22 have shown that the as-grown monolayer MoS2 is very defective and by using an aberration-corrected scanning transmission electron microscope a number of intrinsic defects are identified, such as a disulfur vacancy (VS2) with a pair of S atoms (i.e., a S2 column) missing and an antisite Mo to the VS2 (MoS2), etc. It is thereby natural to consider replacing the antisite Mo atom in the MoS2 by a different TM atom, which is effectively equivalent to the case that the TM atom is absorbed on the VS2 site. Figure 1b presents the optimized structure of a Fe atom absorbed on the VS2 site and details about the local atomic structures around the Mn and Fe adatoms are presented in the enlarged geometries shown in Figure 3. It is found that the absorption of the TM atoms on the VS2 causes significant rearrangements of the atoms around the defects. For the case of the Mn adatom on the VS2, three Mo atoms in the first-nearest neighboring sites to the defect symmetrically relax inward to the defect center by 0.10 Å and the absorption system still possesses a C3v symmetry [Figure 3a]. In the case of the Fe absorbed on the VS2, a symmetry-lowering distortion is observed with two Mo relaxed inward by 0.13 Å and another one relaxed inward by 0.07 Å so that the system's symmetry reduces to Cs.

Figure 3. Enlarged optimized geometries around the Mn (left panel) and Fe (right panel) adatoms absorbed on the disulfur vacancies of the defective MoS2 monolayer, together with sketches of the localized impurity levels around EF and their dominant 3d atomic orbital characteristics.

Figure 3

Open in a new tab

The calculated binding energies of the Mn and Fe adatoms are 3.50 and 3.51 eV, respectively, while the calculated total magnetic moments of the Mn and Fe absorption systems are, respectively, 3.0 and 2.0 μB (Table 1). Similarly, the magnetic moments are mainly contributed from the TM adatoms as well (Figure 2). For instance, the net magnetic moment of the Fe adatom is 3.0 μB (Table 1). The decomposed Mulliken charges indicate that the Fe adatom is of 4.8 (1.8) 3d electrons with the majority (minority) spin. Because the total number of 3d electrons (6.6) in the Fe adatom exceeds that of an isolated Fe atom (6.0), there must be orbital-hybridization-induced 3d electron transform from the surrounding Mo atoms, which results in a net magnetic moment of −1.0 μB in the surrounding Mo atoms (Figure 2). Moreover, as a consequence of the stronger 3d orbital hybridization (Figure 2), the binding energy of a Fe (Mn) adatom on the VS2 increases to 3.51 (3.50) eV, more than doubled compared to that of a Fe adatom (1.34 eV) or Mn adatom (1.18 eV) on the pristine MoS2 monolayer. The optimized structure presented in Figure 1b shows that the TM atoms absorbed on the VS2 defects only slightly stick out of the top sulfur layer by 0.28 Å (Mn) or 0.34 Å (Fe), implying that the TM adatoms are stable in various application environments, such as exposed to air.

The most interesting property revealed by the present calculations is the enhanced MAE's of the TM adatoms on the VS2 defects. For the Mn adatom, a large MAE of 1.3 meV with the easy axis of magnetization on the MoS2 plane is obtained, while for the Fe adatom an even larger MAE of −3.6 meV with the out-of-plane easy axis is observed. So far, the highest MAE record of the TM adatoms is −9.3 meV and such a giant perpendicular MAE was observed on the single Co atoms absorbed on Pt (111) surface by Gambardella et al.3. Similarly, the large values of MAE were observed for the Co adatoms on Cu2N surface by Oberg et al.14. We also calculated the MAE of a Co adatom absorbed on the pristine MoS2 monolayer and on its VS2 defect and the perpendicular MAE of 0.7 and 4.2 meV were obtained, respectively. Although the enhanced MAE of −3.6 meV (Fe) or −4.2 meV (Co) obtained in the present work is still less than half of the current record, it points out a promising direction with utilizing the defective atomically thin layers. Particularly, from the experimental point of view, a large out-of-plane MAE is more helpful to achieve the single atom bit on surfaces. The present calculations indicate that both Fe and Co adatoms absorbed on the defective MoS2 monolayer are of the out-of-plane MAE and thus they are the promising candidates for single-atom data storage.

Discussion

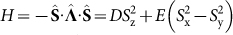Next, we analysed the calculated MAE's and discuss their physical origin based on the molecular orbital (MO) theory and the spin-orbit coupling (SOC) interaction. According to the theory of Bruno24, the MAE is determined by the anisotropic orbital moments restored by the spin-orbit coupling interaction, Inline graphic (here λ is the SOC constant). For the TM adatoms, as the electrostatic interaction of the surrounding ions is larger than the SOC interaction, the latter is treated as a perturbation. Thereby, the energy gain induced by the SOC to the first order reads25,26, Inline graphic. Here, the spin-flip terms are neglected27, 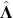Inline graphic is the tensor of the SOC, D = Λzz − (Λxx + Λyy)/2 and E = (Λxx − Λyy)/2. Λxx, Λyy and Λzz are the diagonal elements of the SOC tensor given by

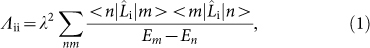graphic file with name srep09361-m1.jpg

where 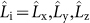Inline graphic stands for three anisotropic components of the orbital moment operator 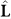Inline graphic, |n> and En (|m> and Em) are the wavefunctions and the corresponding eigen-energies of the occupied (unoccupied) electron states, respectively, and if omitting the prefactor λ2, the diagonal elements Λii are actually the expected values of the anisotropic orbital moment operator 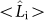Inline graphic to the first order of perturbation, i.e., the unquenched orbital moment24,28.

The above Eq. (1) indicates that the localized electronic states around the Fermi energy level are of dominant effects to the calculated unquenched orbital moments. These localized impurity/adatom states are formed by the hybridizations of the 3d orbitals of the TM adatoms with those of the surrounding Mo atoms. Because the net magnetic moments of the absorption systems are mainly contributed from the TM adatoms, we here consider only the SOC of the TM adatoms and thereby their unquenched orbital moments can be rewritten as

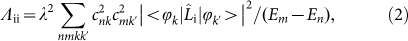graphic file with name srep09361-m2.jpg

where cnk (cmk′) is the LCPAO coefficient of the primary 3d pseudo atomic orbital (PAO) ϕk (ϕk′) of the TM adatom in the state |n> (|m>) obtained from the first-principles calculations.

Figure 4 presents the calculated partial density of states (PDOS) projected to the Mn and Fe adatoms on the VS2 site. As shown in Figure 4, for the case of the Mn adatom, two localized energy levels with the minority spin around the EF have to be taken into account in the calculations of Λii [as the majority-spin states are almost fully occupied (Figure 4), their contribution to Λii is negligible]. Because the Mn adatom on the VS2 possesses the C3v symmetry, the localized states are doubly degenerate and the one below (above) EF is dominated by the Mn adatom's dxz (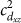Inline graphic ~ 0.45) and dyz (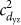Inline graphic ~ 0.45) orbitals [dxy (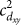Inline graphic ~ 0.41) and 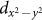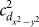Inline graphic (Inline graphic ~ 0.41) orbitals]. 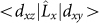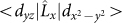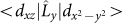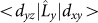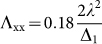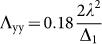Therefore, only the following items have nonzero contributions to Λii, i.e., Inline graphic, Inline graphic, Inline graphic, and Inline graphic, so that Λzz = 0, Inline graphic, and Inline graphic. Based on the calculated Λii, we get that 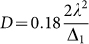Inline graphic, E = 0, and the MAE of the Mn adatom on the VS2 as 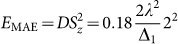Inline graphic. The SOC constants λ for the TM elements are usually around 10–50 meV26 and here by taking λ = 30 meV as a parameter, Δ1 = 0.96 eV (Figure 4), the MAE is estimated to be 1.35 meV with the easy axis on the MoS2 monolayer. This result is consistent with 1.3 meV of the first-principles calculation (Table 1).

Figure 4. Partial density of states (PDOS) projected to the Mn (upper panel) and Fe (lower panel) adatoms absorbed on the disulfur vacancies of the defective MoS2 monolayer.

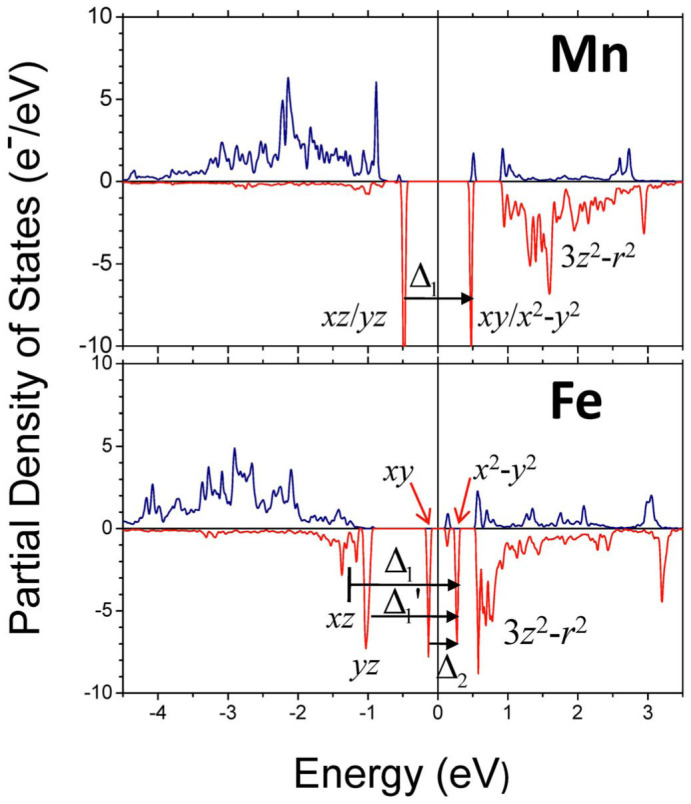
Figure 4

Open in a new tab

Positive (negative) PDOS denotes the majority (minority) spin state.

It has to be aware of that, as shown by the theoretical analyses for the magnetic properties of single holmium atoms on Pt(111) surface29, the in-plane SOC terms in the case of the C3v symmetry have only vanishing contributions to the MAE. Our perturbation calculation shows that the in-plane SOC term 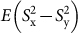Inline graphic is effectively zero due to the exact cancelling effect between the diagonal elements Λxx and Λyy of the SOC tensor under the C3v symmetry. To verify these symmetric analyses for the MAE, we also calculated the MAE's of the Mn adatom on the VS2 defect with two different in-plane magnetization directions, i.e., along the x axis and the y axis, respectively. In both the cases the same MAE of 1.3 meV are obtained, which are consistent with the symmetric analyses.

When the TM adatom is changed from Mn (3d5) to Fe (3d6), the number of the d electrons increases by one and the upper empty energy level above the EF is now half occupied. As a result, the symmetry-lowering Jahn-Teller distortion is expected. As shown in Figure 3, the symmetry of the TM adatom is reduced from C3v for the Mn adatom to Cs for the Fe adatom and the degeneracy of both the upper and lower levels is lifted as well (Figures 3 and 4). 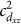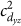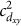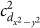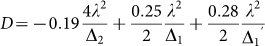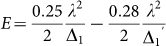With use of the four localized energy levels split from the upper and lower levels as shown in Figures 3 and 4 and their 3d PAO's LCPAO coefficients (Inline graphic ~ 0.60, Inline graphic ~ 0.68, Inline graphic ~ 0.46, and Inline graphic ~ 0.41), we get Inline graphic and Inline graphic with the transition energies of Δ1 = 1.51 eV, Δ1′ = 1.27 eV, and Δ2 = 0.39 eV, respectively. Thereby, the MAE of the Fe adatom on the VS2 is estimated as 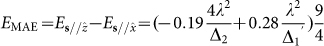Inline graphic, i.e., EMAE = −3.5 meV (here λ = 30 meV is also employed, implying that we omit the difference in the SOC constants for these two TM adatoms). The result indicates that the easy axis of magnetization is perpendicular to the MoS2 plane and the obtained MAE value agrees well with the first-principles calculation. It is noteworthy that, as 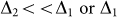Inline graphic, both the sign and the value of the MAE is dominated by the transition from dxy to 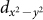Inline graphic with the energy of Δ2 (Figure 3). As a matter of fact, the first item associated with Δ2 in EMAE contributes −4.0 meV to the estimated MAE (−3.5 meV), elucidating that the energy level splitting induced by the Jahn-Teller distortion plays a very essential role in enhancing the magnetic anisotropy and in tuning its easy axis.

In conclusion, the stabilities and the magnetic anisotropic energies of the single transition-metal (TM) atoms (Mn and Fe) absorbed on the pristine and defective MoS2 monolayers are studied on the basis of the first-principles calculations and the spin-orbit coupling theory. It is elucidated that the TM atoms absorbed on the disulfur vacancies of the MoS2 monolayer are of high chemical stabilities as well as much enhanced magnetic anisotropic energies. Particularly, it is analysed that the easy magnetization axis of the atomic magnets is changed by the symmetry-lowering Jahn-Teller distortion. These results indicate that the single TM adatoms absorbed on the defects of the MoS2 monolayers are very promising candidates for fabricating the atomic-scale magnetic bit for data storage.

Methods

To simulate the transition metal adatoms on the pristine and defective MoS2 monolayers, an 75-site slab supercell of MoS2 with two vacuum layers of 20 Å on both the top and down sides of the MoS2 layer were constructed. The first-principles calculations were performed based on the spin-polarized density functional theory within the generalized gradient approximation (GGA). The electron-ion interactions are presented by the Troullier-Martins-type norm-conserving pseudopotentials30 with a partial core correction and the GGA exchange-correlation potential in the form of Perdew-Burke-Ernzerhof (PBE) functional is adopted. The electron wavefunctions are expanded as linear combinations of pseudo atomic orbitals (LCPAOs)31, which are generated by using a confinement potential scheme32,33 with the cutoff radius of 7.0, 7.0, 6.0, and 6.0 a.u. for Mo, S, Fe, and Mn, respectively. In the self-consistent calculations of charge density a 9 × 9 × 1 Monkhorst-Pack k grid is employed and in the structure relaxations the atomic geometries are fully optimized until the Hellmann-Feynman forces are less than 0.01 eV/Å.

The stability of the adatoms on the MoS2 monolayers is characterized by their binding energy given by EB = E[MoS2] + μTM − E[TM + MoS2]. For the TM adatom on the pristine MoS2, E[TM + MoS2] and E[MoS2] are, respectively, the calculated system total energies of the pristine MoS2 absorbed with the TM adatom and of the pristine MoS2 only. While for the TM adatom on the defective MoS2, E[TM + MoS2] and E[MoS2] are the calculated system total energies of the defective MoS2 absorbed with the TM adatom and of the defective MoS2, respectively. μTM is the chemical potential of the transition metal adatom, which is obtained as the calculated total energy of the single isolated TM atom in the same supercell (in the absence of MoS2). The MAE is calculated as EMAE = E[θ = 0°] − E[θ = 90°]25, where θ denotes the angle of the spin polarization with respect to the c axis (namely the perpendicular direction of the MoS2 monolayer) and the total energies are obtained by means of the self-consistent full-relativistic calculations34 with a converging standard of 1.0 × 10−6 eV. To verify the plausible anisotropy of different in-plane directions, the in-plane total energies are further calculated with the magnetization direction fixed to the x-axis (θ = 90°, φ = 0°) and the y-axis (θ = φ = 90°), respectively.

Author Contributions

Z.T. conceived the idea, designed the research, and prepared the manuscript. W.T.C. performed the calculations. W.T.C., X.G.Z. and J.H.C. contributed to the analysis/interpretation of the results and the preparation/revision of the manuscript.

Acknowledgments

This work is supported by the National Science Foundation of China (Grant Nos. 61425004, 61227902, and 11175066), by the State Key Basic Research Program of China (Grant No. 2013CB922301), and by the Ministry of Education of China.

References

  1. Gambardella P., Rusponi S., Cren T., Weiss N. & Brune H. Magnetic Anisotropy from Single Atoms to Large Monodomain Islands of Co/Pt(111). C. R. Physique 6, 75–87 (2005). [Google Scholar]
  2. Carbone C. et al. Self-Assembled Nanometer-Scale Magnetic Networks on Surfaces: Fundamental Interactions and Functional Properties. Adv. Funct. Mater. 21, 1212–1228 (2011). [Google Scholar]
  3. Gambardella P. et al. Giant Magnetic Anisotropy of Single Cobalt Atoms and Nanoparticles. Science 300, 1130 (2003). [DOI] [PubMed] [Google Scholar]
  4. Hirjibehedin C. F. et al. Large Magnetic Anisotropy of a Single Atomic Spin Embedded in a Surface Molecular Network. Science 317, 1199 (2003). [DOI] [PubMed] [Google Scholar]
  5. Bryant B., Spinelli A., Wagenaar J. J. T., Gerrits M. & Otte A. F. Local Control of Single Atom Magnetocrystalline Anisotropy. Phys. Rev. Lett. 111, 127203 (2013). [DOI] [PubMed] [Google Scholar]
  6. Novoselov K. S. et al. Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666 (2004). [DOI] [PubMed] [Google Scholar]
  7. Xie L. M., Ling X., Fang Y., Zhang J. & Liu Z. F. Graphene as a Substrate to Suppress Fluorescence in Resonance Raman Spectroscopy. J. Am. Chem. Soc. 131, 9890–9891 (2009). [DOI] [PubMed] [Google Scholar]
  8. Xiao R. J. et al. Co Dimers on Hexagonal Carbon Rings Proposed as Subnanometer Magnetic Storage Bits. Phys. Rev. Lett. 103, 187201 (2009). [DOI] [PubMed] [Google Scholar]
  9. Zhou Y. G., Zu X. T., Gao F., Lv H. F. & Xiao H. Y. Adsorption-Induced Magnetic Properties and Metallic Behavior of Graphene. Appl. Phys. Lett. 95, 123119 (2009). [Google Scholar]
  10. Xiao R. J., Kuz'min M. D., Koepernik K. & Richter M. CoIr-Carbon Complexes with Magnetic Anisotropies Larger than 0.2 eV: A Density-Functional-Theory Prediction. Appl. Phys. Lett. 97, 232501 (2010). [Google Scholar]
  11. Kandpal H. C., Koepernik K. & Richter M. Strong Magnetic Anisotropy of Chemically Bound Co Dimers in a Graphene Sheet. Phys. Rev. B 86, 235430 (2012). [Google Scholar]
  12. Lu Y., Zuo X., Feng M. & Zhou T. Magnetic Anisotropy in the Boron Nitride Monolayer Doped by 3d Transitional Metal Substitutes at Boron-Site. J. Appl. Phys. 113, 17C304 (2013). [Google Scholar]
  13. Donati F. et al. Magnetic Moment and Anisotropy of Individual Co Atoms on Graphene. Phys. Rev. Lett. 111, 236801 (2013). [DOI] [PubMed] [Google Scholar]
  14. Oberg J. C. et al. Control of single-spin magnetic anisotropy by exchange coupling. Nature Nanotechnol. 9, 64–68 (2014). [DOI] [PubMed] [Google Scholar]
  15. Mak K. F., Lee C., Hone J., Shan J. & Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 105, 136805 (2010). [DOI] [PubMed] [Google Scholar]
  16. Lee Y. H. et al. Synthesis of Large-Area MoS2 Atomic Layers with Chemical Vapor Deposition. Adv. Mater. 24, 2320–2325 (2012). [DOI] [PubMed] [Google Scholar]
  17. Zhan Y., Liu Z., Najmaei S., Ajayan P. M. & Lou J. Large Area Vapor Phase Growth and Characterization of MoS2 Atomic Layers on SiO2 Substrate. Small 8, 966–971 (2012). [DOI] [PubMed] [Google Scholar]
  18. Liu K. K. et al. Growth of Large-Area and Highly Crystalline MoS2 Thin Layers on Insulating Substrates. Nano Lett. 12, 1538–1544 (2012). [DOI] [PubMed] [Google Scholar]
  19. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-Layer MoS2 Transistors. Nat. Nanotechnol. 6, 147–150 (2011). [DOI] [PubMed] [Google Scholar]
  20. Bertolazzi S., Krasnozhon D. & Kis A. Nonvolatile Memory Cells Based on MoS2/Graphene Heterostructures. ACS Nano 7, 3246–3252 (2013). [DOI] [PubMed] [Google Scholar]
  21. Komsa H. P. et al. Two-Dimensional Transition Metal Dichalcogenides under Electron Irradiation: Defect Production and Doping. Phys. Rev. Lett. 109, 035503 (2012). [DOI] [PubMed] [Google Scholar]
  22. Zhou W. et al. Intrinsic Structural Defects in Monolayer Molybdenum Disulfide. Nano Lett. 13, 2615–2622 (2013). [DOI] [PubMed] [Google Scholar]
  23. Cha K. T., Neaton J. B. & Cohen M. L. First-Principles Study of Metal Adatom Adsorption on Graphene. Phys. Rev. B 77, 235430 (2008). [Google Scholar]
  24. Bruno P. Tight-Binding Approach to the Orbital Magnetic Moment and Magnetocrystalline Anisotropy of Transition-Metal Monolayers. Phys. Rev. B. 39, 865 (1989). [DOI] [PubMed] [Google Scholar]
  25. Stöhr J. & Siegmann H. C. in Magnetism: From Fundamentals to Nanoscale Dynamics, (Springer-Verlag, Berlin, 2006). [Google Scholar]
  26. Loubser J. H. N. & van Wyk J. A. Electron Spin Resonance in the Study of Diamond. Rep. Prog. Phys. 41, 1201 (1978). [Google Scholar]
  27. van der Laan G. Microscopic origin of magnetocrystalline anisotropy in transition metal thin films. J. Phys.: Condens. Matter 10, 3239–3253 (1998). [Google Scholar]
  28. Stöhr J. Exploring the Microscopic Origin of Magnetic Anisotropies with X-ray Magnetic Circular Dichroism (XMCD) Spectroscopy. J. Magn. Magn. Mater. 200, 470 (1999). [Google Scholar]
  29. Miyamachi T. et al. Stabilizing the magnetic moment of single holmium atoms by symmetry. Nature 503, 242–246 (2013). [DOI] [PubMed] [Google Scholar]
  30. Troullier N. & Martins J. L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 43, 1993–2006 (1991). [DOI] [PubMed] [Google Scholar]
  31. Ozaki T. Variationally Optimized Atomic Orbitals for Large-Scale Electronic Structures. Phys. Rev. B 67, 155108 (2003). [Google Scholar]
  32. Ozaki T. & Kino H. Variationally Optimized Basis Orbitals for Biological Molecules. J. Chem. Phys. 121, 10879 (2004). [DOI] [PubMed] [Google Scholar]
  33. Ozaki T. & Kino H. Numerical Atomic Basis Orbitals from H to Kr. Phys. Rev. B 69, 195113 (2004). [Google Scholar]
  34. Theurich G. & Hill N. A. Self-Consistent Treatment of Spin-Orbit Coupling in Solids using Relativistic Fully Separable ab initio Pseudopotentials. Phys. Rev. B 64, 073106 (2001). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES