Lean Mass Asymmetry Influences Force and Power Asymmetry During Jumping in Collegiate Athletes

Abstract

The purpose of this investigation was to: (1) examine how asymmetry in lower extremity lean mass influenced force and power asymmetry during jumping, (2) determine how power and force asymmetry affected jump height, and (3) report normative values in collegiate athletes. Force and power were assessed from each limb using bilateral force plates during a countermovement jump in 167 Division 1 athletes (mass=85.7±20.3kg, age=20.0±1.2years, 103M/64F). Lean mass of the pelvis, thigh, and shank was assessed via dual-energy X-ray absorptiometry. Percent asymmetry was calculated for lean mass at each region (pelvis, thigh, and shank) as well as force and power. Forward stepwise regressions were performed to determine the influence of lean mass asymmetry on force and power asymmetry. Thigh and shank lean mass asymmetry explained 20% of the variance in force asymmetry (R²=0.20, P<0.001), while lean mass asymmetry of the pelvis, thigh and shank explained 25% of the variance in power asymmetry (R²=0.25, P<0.001). Jump height was compared across level of force and power asymmetry (P>0.05) and greater than 10% asymmetry in power tended to decrease performance (effect size>1.0). Ninety-five percent of this population (2.5^th to 97.5^th percentile) displayed force asymmetry between −11.8 to 16.8% and a power asymmetry between −9.9 to 11.5%. A small percentage (<4%) of these athletes displayed more than 15% asymmetry between limbs. These results demonstrate that lean mass asymmetry in the lower extremity is at least partially responsible for asymmetries in force and power. However, a large percentage remains unexplained by lean mass asymmetry.

INTRODUCTION

Coaches, strength/conditioning staff, and sports medicine professionals frequently assess vertical jumping because of its sport specific relevance. Vertical jumping provides an estimate of muscle function (14, 16) that is useful in evaluation of readiness during pre-participation physical exams. This baseline is useful to evaluate injury risk prior to injury and also assists with return to sport decision-making. During a vertical jump, it is typically expected that both limbs will contribute equal force and power, otherwise performance could be compromised (28) and the potential for injury is increased (12). However, this may be an incorrect assumption. For example, Impellizzeri et al (14) measured ground reaction forces bilaterally during a countermovement jump (CMJ) in 313 male soccer players and observed an average asymmetry of 6%. While higher levels of asymmetry (10%) were observed in a physically active, but not highly trained, population (2). Further, the asymmetry in force during jumping was correlated with strength asymmetry, as measured by isometric leg press (r = .83) and isokinetic concentric knee extension torque (r = .48) (14).

Knowledge of lower extremity asymmetry may provide insights into injury risk, rehabilitation, and performance (7, 15, 21). For example, individuals with ACL reconstruction land with approximately 15% more force on their uninvolved limb during a jump landing task (23, 24). Similarly, strength asymmetries greater than 15% have been associated with increased risk of lower extremity injury (14, 15). However, other investigations observed no relationship between strength asymmetries and injury (3, 11). Indeed, a certain amount of strength asymmetry is expected, especially when confounding factors such as dominance and injury history are considered (14, 23, 24). Additionally, to our knowledge no research has investigated the relationship of between limb asymmetries and how this affects performance such as jump height. Given such conflicting information, additional performance factors should be explored to help elucidate the relationship between muscle function, performance, injury, and asymmetry.

One such factor, lean mass, is directly related to joint torque (10) and significantly contributes to energy absorption during landing (20). Lean mass explains a significant portion of the variance in power output during a CMJ in boys, girls and older adults (4). Thus, deficiencies in lower extremity lean mass, particularly of the pelvis, thigh, and shank, may reduce the ability to produce force and power during jumping. While force production is important in the sagittal plane, lower extremity lean mass has injury implications in the frontal and rotational planes as well. Lower levels of lean mass are associated with greater laxity and less stiffness in the frontal and rotational planes at the knee (27). Greater levels of joint laxity are risk factors for noncontact ACL injuries (29) and are associated with excessive frontal and rotational plane motion. These motions increase ACL loading (18) and are associated with high risk movements such as dynamic knee valgus (26). Following injury, loss of lean mass may be limited to the involved limb thereby creating an asymmetry in force production capacity and subsequent performance during a vertical jump (9, 28). Additionally, dominance may exacerbate lean muscle mass asymmetry by repetitively performing sport specific skills such as planting and cutting on one foot.

Lean mass measurement may provide important insight into force and power asymmetry during jumping, and elucidate the contributions of morphological versus neuromuscular mechanisms to asymmetry. Therefore, the primary purpose of this project was to determine how lower extremity lean mass asymmetry as measured by dual-energy x-ray absorptiometry (DXA) influenced force and power asymmetry during a CMJ. A secondary purpose was to determine if between limb asymmetry in power and force affected jump height. Our final purpose was to provide normative data for these variables in a highly active and trained collegiate athletic population since there is a lack of information relative to this population in the literature. We hypothesized that asymmetries in lean mass would predict a significant amount of variance in force and power asymmetries and that asymmetries in force and power would negatively affect jumping performance.

METHODS

Experimental Approach to the Problem

This study utilized a cross sectional analysis of a pre-existing database designed to examine athletic performance in NCAA Division 1 athletes. Participants were tested after their competitive season in the spring of 2012. The maximal force and power were collected using force plate technology during the propulsion phase of a CMJ. Lower extremity lean mass was collected using DXA. Force and power asymmetry were used as criterion variables while lean mass asymmetry of the pelvis, thigh, and shank were used as predictor variables. Forward stepwise regression models were used to determine if the asymmetries in force and power could be predicted by the asymmetries in lean mass.

Subjects

Data were collected on 167 student-athletes (85.7 ± 20.3 kg, 20.0 ± 1.2 yrs, 103 males (M)). In order to be included in the study the participant must have been an athlete enrolled at the University, be at least 18 years of age, and able to complete the CMJ without any medical restriction. The dataset included athletes from the following sports: hockey (23 M / 18 Female (F)), golf (8 M / 9 F), soccer (17 M / 11 F), volleyball (10 F), softball (16 F), and football (55 M). The University of XXXX Health Sciences Institutional Review Board approved this study. Written informed consent was obtained from all subjects prior to participating.

Procedures

A GE Lunar iDXA densitometer with EnCORE software version 11.0 (GE Healthcare, Madison, WI) was used to obtain all total body scans. These scans were acquired and analyzed following manufacturer recommendations following standard operating procedures in place at the DXA facility (1). The total body analysis included standard regions of interest (ROI), i.e., left and right limbs and pelvis and custom ROIs (thigh and shank). The shank included the lower leg and the foot. Lean and fat mass were calculated from each ROI and used in the subsequent analyses (Figure 1). The proximal boarder of the pelvic ROI included a horizontal line at the level of the iliac crest, the medial boarder was a vertical line bisecting the pubic symphysis, and the lateral boarder was a diagonal line bisecting the femoral neck. The proximal boarder of the shank was a horizontal line bisecting the knee joint line, the medial border extended distally to include the great toe, and lateral to include entire mass of the shank and foot. The proximal and distal boarders of the thigh ROI were shared with the pelvis and shank. The medial and lateral borders were extended to include the entire mass of the thigh. The ability to identify custom ROI using these anatomical landmarks was highly reliable [ICC_2,1 = .99–1.0].

Figure 1.

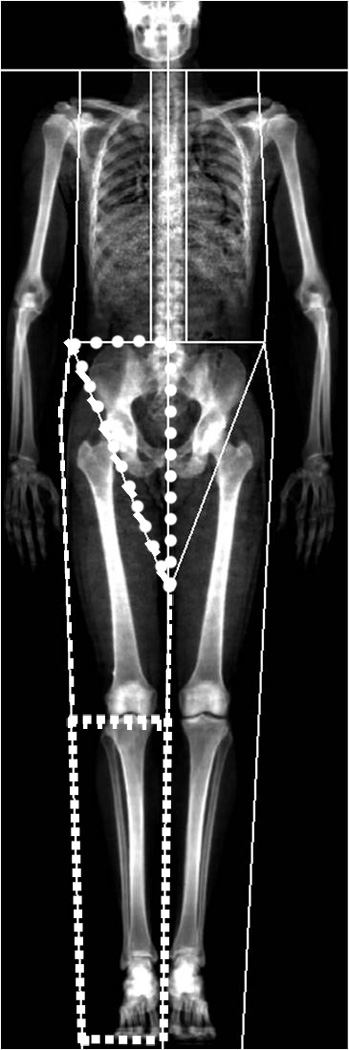
Regions of interest for iDXA scanning of the pelvis (circle dotted line), thigh (dashed line), and shank (square dotted line).

A CMJ was performed on the same day as DXA scanning. The CMJ was performed on a portable platform with individual force plates for each limb (Leonardo Mechanograph; Novotec Medical, Pforzheim, Germany). Each participant started from a standardized position with their feet shoulder width apart, toes straight ahead, and hands on hips (14). Keeping the hands on the hips reduces the influence of arm motion to better reflect lower limb function (14). All participants were instructed to jump as high as possible and land back on the force plates for the trial to be considered successful. Forces during each of three trials were recorded (800 Hz), with ample rest between trials to eliminate the impact of fatigue. The manufacturer’s software was used to calculate the peak force (kN) and peak power (kW) prior to take off during each CMJ (Figure 2). Jump height (cm) was also calculated using previously a model previously established by Davies and Rennie (8). Data were extracted during each trial, averaged, and then used for analysis.

Figure 2.

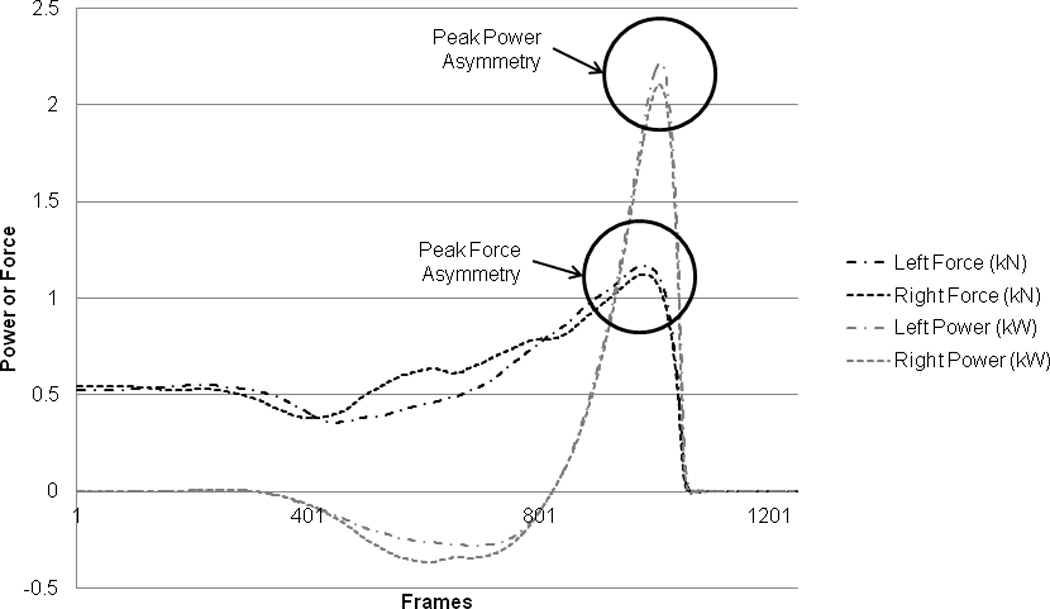
Example of force and power profiles during the initiation and take-off phases of the countermovement jump (sampling rate = 800 Hz).

Asymmetry was established for each variable (except jump height) using a Limb Symmetry Index (LSI) calculated using the following standard equation:

$$\text{Asymmetry}=[(\text{Right Limb}-\text{Left Limb})/½(\text{Right Limb}+\text{Left Limb})]\times 100\%$$

where zero indicates symmetry between limbs; a positive (+) value indicates that the right limb was greater; and a negative (−) value indicates the left limb was greater.

Statistical Analyses

Data were screened to verify normal distribution and that no assumptions of statistical tests were violated. Forward stepwise regressions were performed to determine the influence of lean and fat mass asymmetry on force and power asymmetry. Gender and age were entered into the models as covariates. Normative data was determined by reporting the 2.5^th and 97.5^th percentiles for each variable of interest and the number of subjects that fell within each range of asymmetry. One-way ANOVAs with LSI at 4-levels (0–5%, 5–10%, 10–15%, and >15%) were used to compare jump height across force and power LSI. Statistical significance was set a priori at P < 0.05 and all statistical analyses were performed in R Statistical Software (Vienna, Austria). Effect sizes (d) were calculated to and interpreted as small (0.2), medium (.5), or large (.8) (6).

RESULTS

Descriptive values for each variable can be found in table 1, while regression results can be found in tables 2 and 3. Lean mass LSI of the thigh and shank entered into the model and explained 20% of the variance in force LSI (R² = .20, P < .001). For peak power LSI, lean mass LSI of the pelvis, thigh and shank all contributed to the model, explaining 25% (R² = .25, P < .001) of the variance. Gender and age did not significantly influence either model.

Table 1.

Descriptive values for each variable of interest.

	Mean (sd)	Minimum	Maximum
Lean Mass (kg)
Left Pelvis	5.33 (1.07)	3.35	7.82
Right Pelvis	5.34 (1.09)	3.04	8.15
Left Thigh	8.06 (2.36)	3.92	15.12
Right Thigh	8.26 (2.33)	4.53	15.11
Left Shank	3.17 (7.80)	1.91	5.57
Right Shank	3.25 (8.01)	1.99	5.61
Fat Mass (kg)
Left Limb	4.51 (2.01)	1.71	12.68
Right Limb	4.44 (2.02)	1.60	12.95
Peak Force (kN)
Left	0.99 (.29)	0.51	1.73
Right	1.00 (.30)	0.52	1.83
Peak Power (kW)
Left	2.15 (.72)	0.98	4.06
Right	2.15 (.71)	1.02	4.08
Asymmetry (%)
Peak Force	1.17 (7.42)	−15.46	24.53
Peak Power	0.44 (5.76)	−16.94	22.94
Pelvic Lean Mass	0.15 (5.85)	−20.41	24.93
Thigh Lean Mass	2.72 (6.68)	−12.33	21.18
Shank Lean Mass	2.62 (3.34)	−8.42	11.56
Fat Mass	−1.97 (4.39)	−15.90	10.62

Table 2.

Linear regression models of peak force and power asymmetries with lower extremity lean mass asymmetries.

		Unadjusted Analysis			Adjusted Analysis*
Dependent Variable	Independent Variable	Coefficient (95%CI)	R2	P-value	Coefficient (95%CI)	P-value
Peak Force Asymmetry	Pelvis	−0.05 (−0.25, 0.14h)	0.002	0.59	−0.04 (−0.24, 0.15)	0.66
	Thigh	0.38 (0.22, 0.54)	0.12	<0.001	0.38 (0.22, 0.54)	<0.001
	Shank	0.72 (0.40, 1.05)	0.11	<0.001	0.73 (0.41, 1.06)	<0.001
	Fat	0.06 (−0.20, 0.32)	0.001	0.67	0.08 (−0.18, 0.34)	0.54
Peak Power Asymmetry	Pelvis	0.08 (−0.46, 1.30)	0.006	0.30	0.08 (−0.07, 0.23)	0.29
	Thigh	0.26 (0.13, 0.38)	0.09	<0.001	0.26 (0.13, 0.38)	<0.001
	Shank	0.66 (0.42, 0.91)	0.15	<0.001	0.66 (0.42, 0.91)	<0.001
	Fat	0.10 (−0.10, 0.30)	0.007	0.33	0.11 (−0.09, 0.32)	0.28

^*Adjusted for age and gender.

Table 3.

Final forward regression models while controlling for gender and age.

Dependent Variable	Independent Variable	Coefficient (95%CI)	R2	P-value
Peak Force Asymmetry	Thigh	0.32 (0.17, 0.48)	0.20	<0.001
	Shank	0.62 (0.30, 0.93)		<0.001
	Gender – Females	−1.57 (−3.69, 0.54)		0.14
	Age	−0.09 (−0.99, 0.81)		0.84
Peak Power Asymmetry	Pelvis	0.52 (0.28, 0.76)	0.25	<0.001
	Thigh	0.32 (0.18, 0.45)		<0.001
	Shank	0.24 (0.08, 0.40)		0.003
	Gender – Females	−0.89 (−2.49, 0.71)		0.28
	Age	−0.17 (−0.85, 0.51)		0.63

Jump height was not statistically significant across different levels of force (F_(3,162)=1.05, P=0.37) or power (F_(3,162)=2.24, P=0.08) asymmetry (table 4). However, greater than 10% power asymmetry resulted in decreased jump height of nine centimeters (approximately 3.5 inches) and was associated with large effect size (d > .80) when compared to the other groups. Ninety-five percent of the population (2.5^th to 97.5^th percentile) ranged between −11.79% to 16.79% for force LSI and −9.89% to 11.45% for power LSI. For lean mass, 95% of the population ranged between −10.63 to 11.86 for pelvic LSI, −9.83 to 16.46 for thigh LSI, and −3.7 to 9.1 for Shank LSI. Table 5 depicts the number and percentage of athletes that fell within certain ranges of asymmetry for each variable of interest.

Table 4.

Jump height by level of asymmetry of asymmetry for power and force.

	Power				Force
Level of Asymmetry	n	Jump Height Mean (sd)	d	95%CI	n	Jump Height Mean (sd)	95%CI
0 to 5	110	35.5 (8.6)	0.97	33.9–37.0	88	36.1 (8.5)	34.2–37.9
5 to 10	48	36.3 (7.8)	1.08	34.1–38.7	45	34.8 (7.5)	32.6–37.1
10 to 15	6	27.2 (8.5)	--	18.2–36.2	27	33.6 (8.6)	30.2–37.0
>15	3	36.8 (12.2)	0.78	6.4–67.2	7	38.8 (7.9)	31.5–46.1

Effect size (d) compares the lowest jump height (10–15% LSI) to each level and were calculated as mean 1-mean 2 / larger sd.

Table 5.

Number (%) of individuals falling within defined intervals of asymmetry for each dependent variable.

	Percent Asymmetry
Dependent Variable	0 to 5	5 to 10	10 to 15	>15
Peak Force	88 (52%)	45 (27%)	27 (16%)	7 (4%)
Football	27 (49%)	11 (20%)	13 (24%)	4 (7%)
Volleyball	5 (50%)	4 (40%)	1 (10%)	--
Softball	11 (69%)	4 (25%)	1 (6%)	--
Golf	8 (47%)	5 (29%)	4 (24%)	--
Hockey	22 (54%)	13 (31%)	4 (10%)	2 (5%)
Soccer	15 (54%)	8 (28%)	4 (14%)	1 (4%)
Peak Power	110 (66%)	48 (29%)	6 (4%)	3 (2%)
Football	33(60%)	19 (34%)	1 (%)	2 (%)
Volleyball	8 (80%)	2 (20%)	--	--
Softball	11 (69%)	5 (31%)	--	--
Golf	11 (65%)	4 (23%)	2 (12%)	--
Hockey	31 (76%)	9 (22%)	1 (2%)	--
Soccer	16 (57%)	9 (32%)	2 (7%)	1 (4%)
Lean Mass
Pelvis	107 (64%)	50 (30%)	7 (4%)	3 (2%)
Thigh	84 (50%)	56 (34%)	22 (13%)	5 (3%)
Shank	127 (76%)	37 (22%)	3 (2%)	--
Fat Mass
Pelvis	69 (41%)	45 (27%)	32 (19%)	21 (13%)
Thigh	93 (56%)	51 (31%)	14 (8%)	9 (5%)
Shank	71 (43%)	52 (31%)	21 (12%)	23 (14%)

DISCUSSION

The most important finding of this study is that lean mass asymmetry is a factor in explaining force and power asymmetry during jumping which supports our hypothesis. However, the amount of variance explained in force and power asymmetry is similar and lower than expected at 20% and 25%, respectively. While not statistically significant, our data support the notion that asymmetry in power negatively influences jumping performance. In fact, our results show that, greater than 10% asymmetry in power results in performance deficits of 3.5 inches (d > .80) which is directly translatable to and correctable by the strength and conditioning professional. The normative data in this study also reveals that a small number of division one athletes are considered “high risk of injury” using an arbitrary cut off level of 15% asymmetry. This suggests that 15% cutoff might be too high given the nature of this data and should be identified for each unique variable.

Lean mass appears to be a contributing factor to force and power LSI, but a large percentage of the variance remains unexplained by lean mass LSI. These findings allow us to conclude that the morphological factor of lean mass asymmetry is a contributor to force and power asymmetry. Other factors not assessed in this study most likely account for the remaining variance and include neuromuscular control (30), muscular strength (20), muscle cross sectional area (10), and joint coordination (17). However, we cannot speculate on the relative contribution of each of these factors since we were unable to collect these variables. Limb lengths, tendon properties, tendon lengths are important factors for total force and power output. However, these factors most likely have relatively minimal impact on between limb asymmetry since these are morphological factors that cannot be altered. In contrast, lean mass, may be altered through appropriate strength training interventions (27). Other researchers have investigated the influence of lean mass on energy absorption during landing with similar correlations (e.g., R² values ranging from 0.001 to 0.216) (20, 27). To our knowledge, this study, and the works of Montgomery et al (20) and Shultz et al (27) are the only reports investigating the role of lean mass and lower extremity function. Thus, while lean mass asymmetry does entirely explain functional asymmetry, improved understanding of this relationship is a logical and potentially important avenue to pursue to advance understanding of how asymmetry in the lower extremity contributes to injury and injury prevention.

During a maximal CMJ, the work performed at the ankle, knee, and hip all influence performance (17). However, during maximal jumping the hip has the greatest influence on performance by generating the most power, work, and torques compared to the ankle and knee. Knee extensor strength explains 23% of the variance in jump height whereas more functional assessments of strength, such as an isometric squat leg press have better associations with jump height and explain a greater percentage of the variance (69%) (13, 14). To our knowledge, this is the first study to investigate contributions of lean mass asymmetry on force and power asymmetry during the propulsion phase of the CMJ.

Jumping performance is usually evaluated in single leg jumping tasks and asymmetry is traditionally calculated as a percentage of jump height or jump distance between limbs. However, bilateral tasks are becoming increasingly common in an attempt to evaluate injury risk (12) and the relative contribution of each limb is best evaluated using instrumented testing devices such as force platforms. In fact, previous research has concluded that the best predictor of vertical jump height is power normalized to body weight (19) or vertical impulse (2). Recent research has also observed poor association between asymmetries between double- and single-leg CMJs which suggests that both tasks are important for identification of asymmetry (2). Our data support the notion that between limb asymmetry greater than 10% negatively effects jump performance (d > 0.80). Sample sizes at the extremes of asymmetry were small with six athletes having power asymmetry between 10–15% and three athletes having asymmetry >15%. When cases were examined at the >15% level, one individual had extraordinary jumping ability even with severe asymmetry in power production (jump height = 51cm). Other athletes in the >15% asymmetry level had comparable jump heights (28 cm and 31 cm) to the average athlete in the 10–15% level. While these values are not statistically significant the effect sizes are large which indicate that these findings are clinically relevant as performance was impaired by approximately 3.5 inches. Restoring between limb power asymmetry would have a positive impact on athletic performance which is important to the strength and conditioning professional.

In the current study, the average levels of asymmetry are relatively low and range within one to three percentage points. However, the range of asymmetry (Table 1) is important and demonstrates the individual variability not captured with group mean analysis. For example, the range of values for force asymmetry is almost 25% (0 to 24.53%). For force asymmetry, 95% of the population sampled fell between −11.79% (2.5^th percentile) and 16.79% (97.5^th percentile). Percentiles were calculated for 15% asymmetry since this is an important theoretical benchmark that may indicate “high risk” for injury (15, 22). Fifteen percent force asymmetry fell at the 1.25 and 96.75 percentiles with seven individuals (4%) having asymmetry greater than 15% and 34 (20%) having asymmetry greater than 10%. Force asymmetry values in this study are similar to those reported by Impellizzeri et al (14) who reported male average force asymmetry of 0.8% with the 15% normative ranges falling at the 2.5 and 97.5 percentiles. These results were comparable even though Impellizzeri et al focused on male soccer players and we analyzed males and females with a variety of sporting backgrounds.

Normative values for power asymmetry were similar with 95% of the population falling between −9.89% (2.5^th percentile) and 11.45% (96.5^th percentile). The 15% cutoff represents the 0.85^th percentile and the 98.25^th percentile for this population. Only 3 of 167 individuals (2%) would be identified as “high risk” using the 15% cutoff in power asymmetry while 9 individuals (5%) would be identified as “high risk” using a 10% cut off. Future research should determine the clinical usefulness of these cut points to determine if asymmetry in force and power production is related to lower extremity injury. Approximately 20% of individuals will suffer a lower extremity injury that require missing at least one day of activity during a sport season (25). However, these numbers don’t seem to align well with the 15% high risk cutoff. A different level of asymmetry may be more sensitive and specific and more research is needed to properly identify these values.

Limitations of this study include the fact that gender was not a factor in this analysis, even though it is well accepted that force, power, and strength differ between genders (20). These results agree with previous research that observed no relationship between asymmetry and gender in health teenagers (5). However, excessive asymmetry (>15%) was observed in 20–30% of individuals (5). These contradictory findings may indicate that age and training level influence asymmetry and thus future research should account for these factors. Our data was reduced into units of asymmetry as the primary variable of interest which may explain why gender is not a factor in our study. This study supports the notion that both males and females have similar levels of asymmetry in lean mass, force, and power.

Additionally, age is not a factor in this analysis. The study participants ranged from 18–23 years of age which is typical of collegiate athletes. Age may factor in more strongly as age increases across the lifespan. Unfortunately, we did not have the statistical power to analyze participants by sport. Future research should consider this analysis as asymmetry could vary by sport especially in sports such as soccer where dominance may play a significant role. The hands on the hips during a CMJ is not a natural motion for athletes but was necessary to standardize the task. We acknowledge that injury history of the participants was not controlled for and may have contributed to the range of asymmetry, however, all participants were cleared to complete the test by the team’s medical staff.

PRACTICAL APPLICATIONS.

The results of this study demonstrate that lean mass is an important factor to force and power production. Power asymmetry greater than 10% impairs jumping performance at clinically relevant levels as jump height decreases by approximately 3.5 inches. Restoring between limb power asymmetry would have a positive impact on athletic performance which is important to the strength and conditioning professional. The primary mechanism of addressing lean mass asymmetry is through resistance training. But other factors influence CMJ performance, such as neuromuscular control, which is modifiable through feedback or other intervention strategies. Future research should investigate between limb asymmetry and the influence on injury rates and determine the best method to correct these deficiencies.