Magnetoencephalography in the study of brain dynamics

Summary

To progress toward understanding of the mechanisms underlying the functional organization of the human brain, either a bottom-up or a top-down approach may be adopted. The former starts from the study of the detailed functioning of a small number of neuronal assemblies, while the latter tries to decode brain functioning by considering the brain as a whole. This review discusses the top-down approach and the use of magnetoencephalography (MEG) to describe global brain properties. The main idea behind this approach is that the concurrence of several areas is required for the brain to instantiate a specific behavior/functioning. A central issue is therefore the study of brain functional connectivity and the concept of brain networks as ensembles of distant brain areas that preferentially exchange information. Importantly, the human brain is a dynamic device, and MEG is ideally suited to investigate phenomena on behaviorally relevant timescales, also offering the possibility of capturing behaviorally-related brain connectivity dynamics.

Introduction

Achieving understanding of the mechanisms underlying the functional organization of the human brain, a highly complex system featuring 10¹² deeply interconnected neurons (plus 10¹³ glia cells), is undoubtedly one of the major challenges of this century. Although this goal is still far from being reached, neuroscientists have several techniques at their disposal allowing effective advances in this direction. Overall, two possible approaches may be used: an analytical one and a holistic one.

The analytical approach seeks to characterize brain functioning by understanding the details of neuronal activity, i.e. starting from the study of the organization of a small number of cells and scaling up to the organization of larger assemblies and eventually up to the whole brain (bottom-up approach). On the other hand, the holistic approach aims to decode brain functioning by considering the brain as a whole, starting from an analysis of its general features (top-down approach). This latter approach stems from the idea that the brain is not a mere (linear) superimposition of small low-power units, and that many of its features would not emerge if small brain units were to be analyzed independently.

Although the analytical approach provides an insight into the innermost workings of the brain, it requires the use of invasive electrophysiology, which is practically impossible to utilize in healthy humans and poses difficulties even in the absence of ethical concerns (e.g. in low IQ animals), since the detector itself may perturb the brain system. Moreover, it is difficult to collect data from several distinct brain areas simultaneously. Conversely, the holistic approach, although unable to investigate brain activity on a sub-millimeter scale, may exploit noninvasive methods, making it an approach that is easily applied in humans. Moreover, it allows simultaneous recording of data from the whole brain.

In this paper, the holistic approach to the study of human brain functioning will be discussed. In particular, magnetoencephalography (MEG) and its use to investigate global brain properties, including brain dynamics, will be described. MEG is a non-invasive technique that records the magnetic fields generated by neuronal activity. Details of this technique can be found in Hämäläinen et al. (1993). Here, we just remark that from the measured magnetic fields it is possible to infer the current density flowing inside the brain, and consequently the neuronal activity (Baillet et al., 2001). The neuromagnetic field is extremely small, and its detection requires high-end instrumentation (Pizzella et al., 2001), yet it allows the generation of a temporally accurate map of the neural processes implicated in various aspects of brain functioning during rest or task execution. MEG is often performed in addition to (or jointly with) electroencephalography (EEG), since both techniques are sensitive to the same underlying neurophysiological phenomena, i.e. the current flow associated with neuronal activity. However, MEG features a higher spatial resolution than EEG and is therefore more often used in brain mapping where the highest achievable resolution is needed (10–15 mm). Although, in the present paper, only MEG data will be presented, most of the considerations put forward herein are also applicable to EEG alone or to combined EEG/MEG measurements.

In the early years of MEG (1975–1990), the instrumentation and the available data analysis methods allowed the mapping of only a few segregated brain areas according to their specific function in task execution/stimulus processing, and did not take into account their relationship with the rest of the brain. This latter aspect, which is often shared with other neuroimaging techniques such as functional magnetic resonance imaging (fMRI) (Huettel et al., 2009), may be questionable since the approach, as a result, resembles a sort of modern phrenology. Indeed, it has now been challenged by the idea that the concurrence of several areas is required by the brain in order to instantiate a specific functioning/behavior, and that these areas must cooperate in a synergistic manner. This idea has led to the concept of the brain network, i.e. an ensemble of spatially distinct areas that must cooperate to accomplish a specific task. Accordingly, new approaches have been developed to map brain connectivity, i.e. to build a map of how the different brain areas are interconnected, and from that to identify brain networks.

To date, brain networks have been recognized and characterized using several neuroimaging techniques. Structural connections may be identified using diffusion tensor imaging, a magnetic resonance imaging (MRI) method that exploits diffusion to identify axonal fibers (Le Bihan, 2003), while functional connections may be investigated using fMRI. To these techniques, MEG, thanks to its unmatched temporal resolution, adds the unique capability to study the dynamics of brain connectivity.

In the following sections, the MEG technique is described in relation to the different stages necessary for achieving an understanding of brain functions. First, MEG is introduced as a tool for imaging brain activity; second, brain networks as revealed by MEG are discussed; finally, the authors discuss brain dynamics as characterized by MEG. A series of boxes is provided to help the reader (see Appendix).

Magnetoencephalography as a tool for imaging brain activity

Neuronal electric currents generate magnetic fields, as all electric currents do (see Box 1). Given the low strength and the high temporal specificity of neuronal electric signals, hundreds of thousands of neurons must be synchronously active to generate a field detectable outside the head. Even when this condition is met, ultra-sensitive devices are required to detect the magnetic field in a practical and usable way (see Box 2 for a quick glance at MEG instrumentation).

BOX 1.

MEG signal generation

MEG (and EEG) signals are generated by the ionic currents flowing inside and outside neurons. These currents are driven mainly by excitatory postsynaptic activity, and can be modeled as current dipoles, i.e. short segments along which the current flows from a source to a sink. It is worth noting that action potentials do not usually produce an observable field, mainly because the currents associated with action potentials flow in opposite directions and the magnetic fields are canceled out. However, action fields have been measured from peripheral nerves. The current dipole thus models only the intracellular (or primary) current and is the basic element for building up the observed signals.

The magnetic field generated by a current dipole may be easily computed using Maxwell’s equations in the quasistatic approximation. The current flowing along one dendrite is far too weak to produce a measurable signal. The magnetic field strength at 4 cm from the neuron (a realistic distance, given the typical skull+scalp thickness and a typical MEG cryostat geometry) is about 2·10⁻¹⁸ T, thus hundreds of thousands dendrites need to be active synchronously in order to produce an observable signal. Among all neurons, cortical pyramidal cells have similar orientations and thus generate magnetic fields that reinforce each other. The spatial and temporal summation of all individual current dipoles is called equivalent current dipole (ECD), and can be interpreted as an active portion of cortex. Because this activity directly reflects processing involving specific neurons, EEG and MEG are the most direct correlates of on-line brain processing that can be detected non-invasively.

The neurons are embedded in a conductive medium, i.e. the brain tissue and CSF. Therefore, the primary current generated by neuronal functioning induces a current which flows through these media, as well as through the skull and scalp. This current is referred to as secondary or volume current. EEG would not be possible without volume currents, which reach the scalp surface and cause voltage differences at the scalp that can be picked up by EEG electrodes.

Both primary and volume currents produce magnetic fields, which sum up and can be measured, by means of detection coils placed over the head, using MEG devices. However, if the conductive medium has homogeneous conductivity and has a spherical shape, it can be shown that only primary currents contribute to the external magnetic field. Although the head is not spherical, the effect of volume currents may be negligible for some brain areas (where the head shape can reasonably be approximated by a spherical surface such as in the occipital part), thus it is conceivable that MEG may constitute a technique able to sense mainly true neuronal activity.

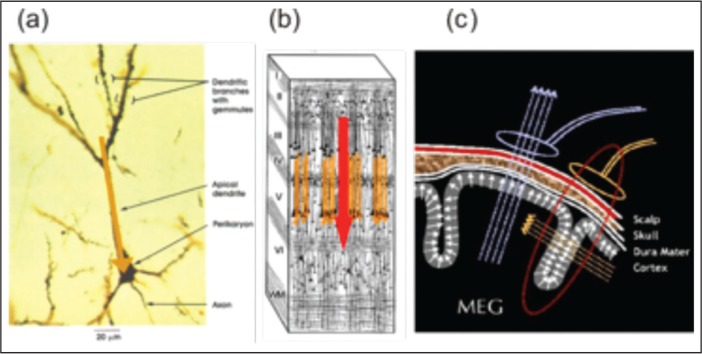
(a) Post-synaptic activity of a single neuron can be effectively modeled by a single current dipole (orange arrow); (b) when many pyramidal neurons are synchronously active and spatially well aligned, an equivalent current dipole may be used to model cortical activity (red arrow); (c) if a spherical model for the head is used, only dipoles located in the fissures generate a magnetic field outside the head.

Finally, it is important to note that dipole orientation is crucial for the generation of the MEG signal. Indeed, radial dipoles produce a negligible magnetic field outside the head (an exactly zero field if a spherical head model is used), thus only tangential dipoles, i.e. only sources located in the cortical sulci, produce magnetic fields that are detected through MEG measurements (Hämäläinen et al., 1993).

BOX 2.

Instrumentation for MEG

Detection of the tiny magnetic field generated by cerebral activity demands ultra-sensitive magnetic detectors in the DC to 1 kHz band. The only practical magnetic sensors meeting this requirement are the superconducting quantum interference devices (SQUIDs). An extensive description of the theory, design and applications of SQUIDs can be found in Clarke and Braginski (2006). Briefly, the SQUID is a superconducting magnetic flux-to-voltage transducer featuring extremely low noise, with a field sensitivity of about 1fT/√Hz. At present, all commercial MEG systems use low-Tc SQUIDs, i.e. SQUIDs operating at a temperature of 4.2 K. The SQUIDs building up a MEG system must therefore be enclosed in a non-magnetic (fiberglass) cryostat. As a result the sensor array has to be rigid and is therefore not adjustable to the patient’s head (as it is for EEG measurements, for example). The neuromagnetic field is sensed by the SQUID through a pick-up loop with a diameter ∼ 1 cm coupled to the SQUID loop through a flux transformer. Different pick-up loops may be used to maximize noise reduction (gradiometric configuration) or field sensitivity (magnetometric configuration). The geometry of the pick-up loops is one of the distinguishing characteristics of the different MEG systems currently in operation.

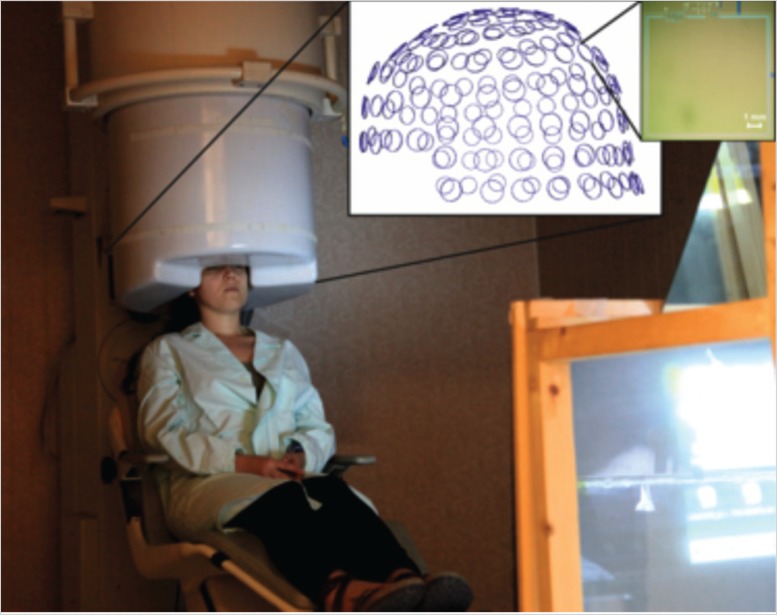
The 153-channel MEG system installed at ITAB -University of Chieti. It consists of 153 channels arranged on a helmet surface, so as to simultaneously record the brain magnetic field at multiple sampling points. Each channel is based on superconducting devices acting as magnetic field sensors. The sensor array is contained in a non-magnetic cryostat. The whole system is installed in a high quality magnetically shielded room.

A typical MEG system comprises several hundred channels arranged on a helmet surface, making it possible simultaneously sample the brain magnetic field at multiple points over the scalp. Each sampling point consists of one (magnetometer or axial gradiometer) or multiple (magnetometer and two orthogonal planar gradiometers) detection channels. A review of the existing MEG systems can be found in Della Penna et al. (2014).

To reduce the contribution of the environmental magnetic field (noise) to the measured field, MEG systems are usually operated inside a magnetically shielded room. The shielding consists of an aluminum layer designed to attenuate external electromagnetic field noise at frequencies ranging from 50 Hz to the radiofrequency band, and by two or more layers of high permeability material to reduce low-frequency external noise (e.g. the earth magnetic field).

The easiest way to elicit detectable neuromagnetic activity is to stimulate the sensory systems, e.g. with a tone burst, a flash or a somatosensory (low-intensity) electric shock. The stimulation synchronizes the neurons of the corresponding primary sensory cortices in the first 100–150 ms after the stimulus. To enhance the signal-to-noise ratio, the stimulation must be repeated several (∼100) times and the corresponding signals must be averaged. The resulting magnetic field distribution (event-related field) may thus be used to identify the active brain area(s). To this end, i.e. to estimate the currents generating the recorded magnetic field, an inverse problem must be solved (see Box 3). Finally, active neuronal pools can be described in terms of current dipole(s) latency and strength (see Boxes 1 and 3). Given the characteristics of neuronal pools and the physics of electromagnetism, the spatial resolution of the MEG technique is limited to about 5 mm. However, thanks to the exquisite temporal resolution (∼1 ms) of MEG it is possible to study the dynamics of brain sources by investigating multiple aspects of the event-related (as well as the spontaneous) activity of the brain. Event-related signals have been analyzed in the different sensory domains, and a few examples will be provided herein. In the visual domain, mechanisms of visual perception have been analyzed through study of the sequence of activation of brain areas, with the findings suggesting early top-down priming of the primary visual cortex (V1) (Vanni et al., 2001). In the sensori-motor domain, evidence from MEG studies has suggested that the secondary somatosensory cortex plays an integrative role during the processing of different classes of stimuli, ranging from simple painful/non-painful stimuli (Torquati et al., 2003) up to complex bimanual object manipulation (Jung et al., 2012). In the auditory domain, selective response modulations have been found in the primary auditory cortices at middle latencies, namely during dichotic listening when compared to non-dichotic stimulation based on vowels (Della Penna et al., 2007). Another study in which deaf native signers were compared with normal-hearing signers during processing of concrete nouns delivered through videos and speech, analysis of early and late responses showed that similar frontotemporal networks are involved in semantic processing, irrespective of the modality or the subject population (Leonard et al., 2012). At a higher level, analysis of conscious perception of an auditory illusion and the sequence of activation elicited by the perception has shown that neural correlates of consciousness are stimulus dependent (Brancucci et al., 2011).

BOX 3.

MEG inverse problem

The inverse problem framework is a well-known concept in a variety of scientific fields (Tarantola, 2004). Predicting observations from a model by assuming a given set of parameters is called solving the forward problem. The reverse situation, i.e. the use of observations to estimate the model parameters, is the inverse problem. In MEG, the estimation of the neural sources that generate the electromagnetic signals observed outside the head is an inverse problem in which the unknown parameters are the source locations and their amplitude as a function of time/frequency. Forward modeling in this context consists of predicting the electromagnetic field generated by an arbitrary source configuration given some other a priori fixed parameters, e.g. head geometry, sensor locations, etc. The MEG forward problem has a unique solution that can be derived by using the laws of classical physics. Unfortunately, the same does not apply to the inverse problem for which a set of observations can be associated with multiple (infinite) solutions, thus making the MEG inverse problem inherently ill-posed. Although this could, at a first glance, seem to be a major limitation for the impact of MEG/EEG on brain imaging, the situation is in practice less dramatic thanks to the use of other information about source configuration. In this framework, the use of suitable constraints (e.g. suitable regularization techniques) makes it possible to recover solution uniqueness. MEG source imaging has thus reached a technical maturity that allows neural activity to be reliably estimated.

More specifically, the MEG forward problem solution requires the definition of a model of neural sources and of the surrounding conducting medium. The former is based on the concept of the equivalent current dipole (ECD) as a building block for cortical current distributions. The ECD is the reference source model of the primary intracellular current within a neuronal ensemble. The latter includes the modeling of the head geometry and of the electromagnetic properties of head tissues. As a general principle, given a model of neural currents (e.g. ECD), the physics of MEG is ruled by Maxwell’s equations under quasistatic assumptions (i.e., the propagation delay of the electromagnetic signal from sources to sensors is negligible) (Hämäläinen et al., 1993). Indeed, such assumptions determine the existence of an analytical, closed-form solution to MEG forward modeling for a spherical homogeneous head geometry, which thus constitutes the simplest model of head geometry (Sarvas, 1987). Although mathematically and computationally convenient, spherical head models represent a poor approximation of the head shape. More realistic geometries have been developed that require the magnetostatic problem to be solved using numerical methods, such as the boundary element (Fuchs et al., 1998) or finite element methods (Wolters et al., 2006; Stenroos et al., 2014). Approximate analytical solutions for the magnetic field in a realistic volume conductor can also be derived using spherical harmonic expansions (Nolte et al., 2001). To model a realistic head, a geometric tessellation of the head tissues is derived from high quality individual MRI data by accurate segmentation algorithms (Dale et al., 1999).

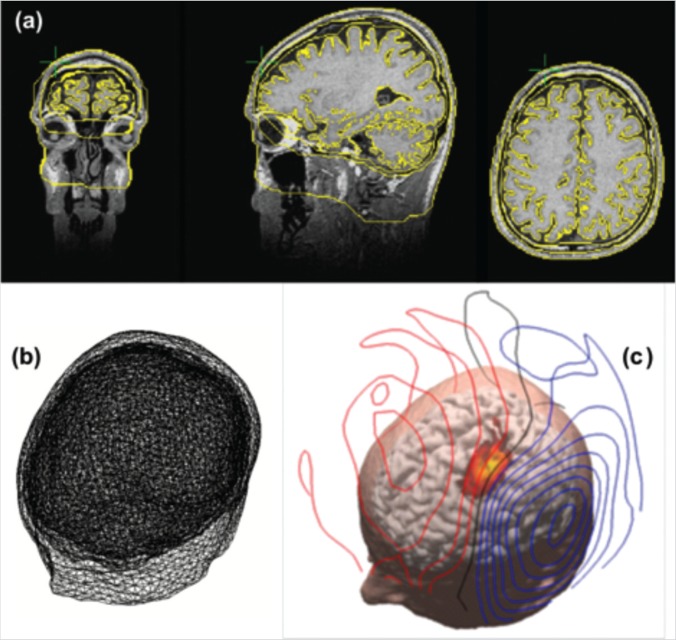
(a) Individual MRI data and superimposed results of tissue boundary segmentation (yellow contours).

(b) Realistic volume conductor head model reconstructed from the geometric tessellation of the head tissue.

(c) Source and volume conductor model are used to identify brain sources from MEG data. Images derived from the Curry 6.0 (Neuroscan) analysis software.

The MEG inverse problem is usually solved by using one of the two following strategies: the localization approach or the imaging approach. The former assumes brain activity at any time point to be generated by a small number of brain regions (usually less than 10), each represented by an ECD, the location, orientation and amplitude of which need to be estimated. The latter aims at estimating the overall distribution of neural currents by discretizing the brain into a finite set of locations. This is typically achieved by using a grid of ECDs, fixed in location and, possibly, in orientation, in the brain volume or limited to the cortical gray matter surface. The inverse problem solution for the imaging approach results in the estimation of the amplitudes of all these elementary currents.

In the first case, only a restricted number of parameters needs to be estimated, thus solving the ill-posedness of the inverse problem since the number of unknowns is smaller than that of the instantaneous observations of the magnetic field. Numerical approaches are used to estimate the unknown source parameters generally on the basis of the least-squares technique, i.e. finding the set of parameter values that minimizes the square of the difference between observations and predictions from the model.

In the second case, a larger set of linear parameters needs to be estimated, the size of which depends on the source space discretization. Among imaging approaches, several strategies have been developed, such as distributed source imaging methods, scanning methods and spatial filter methods. For a review on the different imaging approaches see Baillet et al. (2001).

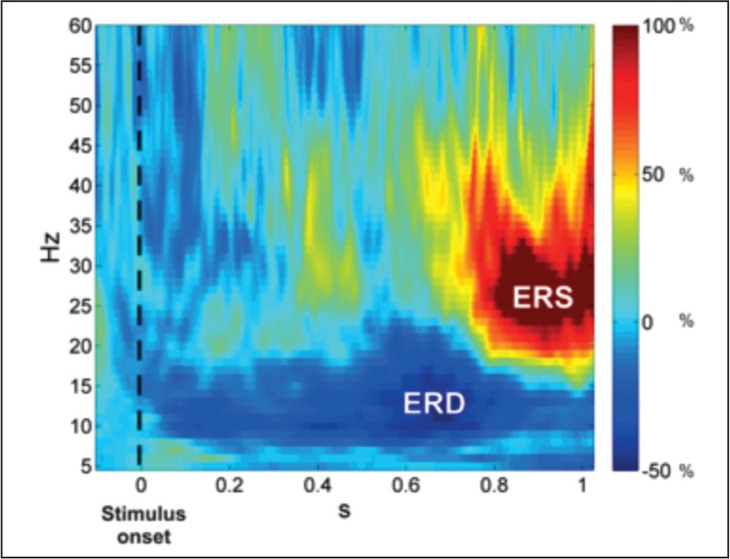
Massive neuronal pool synchronization is less likely to take place when higher-level brain functions, i.e. language processing, are under investigation or when considering long-latency responses. In this context, it is instead useful to analyze the oscillatory activity of the brain (see Box 4). Oscillatory brain activity is modulated during task execution according to two different phenomena: decreased synchronization of brain oscillatory activity, or event-related desynchronization (ERD), and increased synchronization of brain oscillatory activity, or event-related synchronization (ERS) (Pfurtscheller and Lopes da Silva, 1999) (Fig. 1).

BOX 4.

Brain rhythms

Brain rhythms are the product of synchronized activity between and within neuronal assemblies, and rhythmic modulation of signal power is assumed to reflect the underlying changes in neuronal synchrony. Indeed, in the central nervous system, oscillations have been observed at various spatial levels, from spike train activity in single cells to local field potentials and to oscillations involving the activity of a more spatial diffuse neural network (see Buzsáki, 2006 for a comprehensive review). These oscillations are fully described by their amplitude, frequency and phase. In particular, time-frequency analysis of MEG signals provides information on the dynamic modulation of rhythmic brain activity at various frequencies.

Traditionally, brain rhythms have been classified on the basis of their frequency content. Even though there is no hypothesis of a single physiological origin and a unique functional relevance of rhythms, the different frequency bands of brain oscillations are believed to have functional significance and probably represent the brain strategy for processing parallel information and handling the co-occurrence of multiple processes at different spatial and temporal scales.

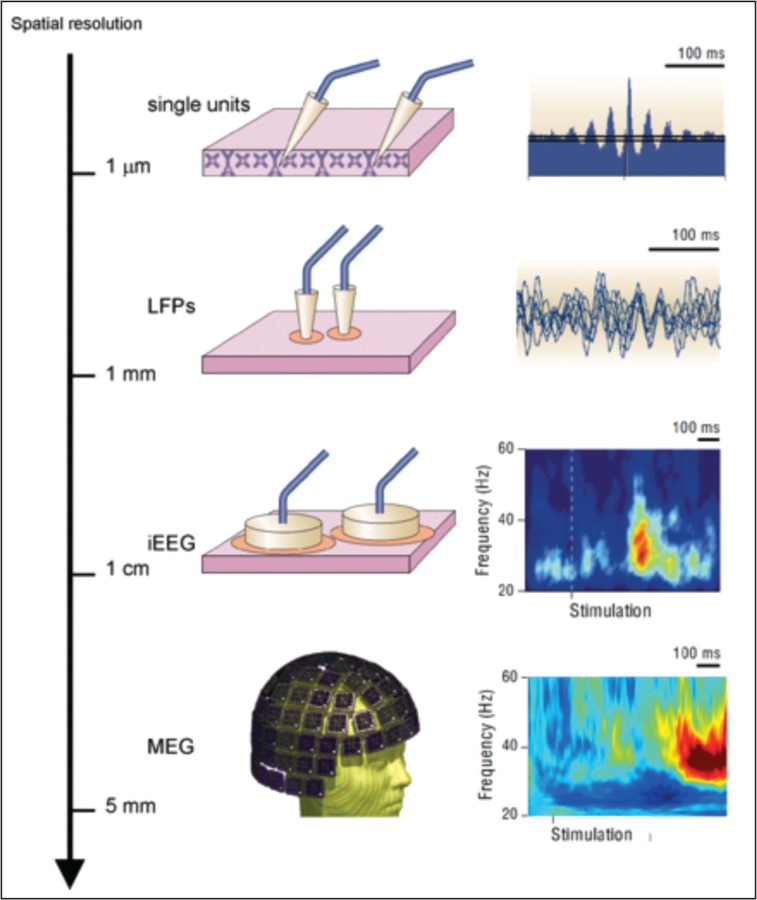
Neuronal oscillations can be observed at different spatial scales: from single units, to local field potential, intracranial EEG, and MEG (modified from Varela et al., 2001). Oscillations generated by a large amount of cells, like those recorded by scalp EEG or MEG, have a spectral content that can be divided into different bands. Modified from Varela et al. (2001).

Oscillations in the alpha band (8–12 Hz), the first discovered and best-known frequency band, constitute the functional correlate of drowsiness. They are the sign of a disengagement of task-irrelevant brain areas. For example, alpha suppression during the execution of a task is correlated with the activation of the recruited cortical areas (Pfurtscheller and Lopes da Silva, 1999). Recently, evidence also points toward the functional relevance of alpha power modulation in the sensory gating mechanism deployed by attention and related to mechanisms reflecting the advancing of task-related neurocognitive strategies (van Dijk et al., 2010) as well as for conscious perception (Palva and Palva, 2007). The beta band (15–25 Hz) has traditionally been related to motor processing, sensorimotor control, sensory-motor integration, corticospinal coupling and proprioception. A recent theory suggests that a beta-band power increase could be the functional correlate of a sort of inertia of cortical areas that maintain the status quo during information processing (Engel and Fries, 2010).

Theta-band power (4–7.5 Hz) has been described to increase in emotional arousal and working memory tasks. A significant delta band activity (1–4 Hz) has been observed during sleep in the healthy population, while the presence of high slow activity in rest EEG/MEG of waking adults is often interpreted as a sign of neurological disorders. Finally, a high-frequency band, namely the gamma band (above 30 Hz), has been related to activity of limited cortical areas for stimulus selection, feature integration, pattern recognition, attention, multisensory integration, sensorimotor integration, pain processing, empathy and memory.

Figure 1.

Event-related synchronization and desynchronization in the right secondary somatosensory area after galvanic stimulation.

Power changes in the right secondary somatosensory area as a function of time (seconds) and frequency (Hz) relative to the baseline period (−0.1s–0s), zero being the onset of a galvanic stimulation delivered to the index of the left hand in a single right-handed subject). Blue indicates a power decrease, i.e. ERD, and red indicates a power increase (ERS). ERD/ERS phenomena show different latencies and spectral contents, with ERD in the alpha-frequency range (8–12 Hz) and ERS in the beta range (15–25 Hz).

These modulations have been extensively used to analyze specific aspects of brain activity and have proven to be frequency specific and related to the particular processing occurring in the brain. For example, cognitive processes involving the motor system have been extensively studied, e.g. to infer and decode movements (Waldert et al., 2008). Similarly, motor planning in decision making is encoded by increased gamma oscillations and decreases of alpha and beta power in the motor cortex before the execution of the motor response (Donner et al., 2009). Oscillatory brain activity and its modulation have also been linked to visual attention. In particular, site-specific gamma oscillations have been linked to the individual’s attention capacity, whereas suppression of theta to beta amplitudes has been correlated with attentional load (Rouhinen et al., 2013). In addition to the visual modality, auditory attention has been shown to modulate alpha power in auditory regions, and specifically in relation to the information content of the auditory cue (Weisz et al., 2014). Modulations of the power of oscillatory brain activity have also been linked to mentalizing processes such as those related to non-verbal communication (Brunetti et al., 2014).

Brain functional information gathered by MEG by means of the above-mentioned analysis strategies can be integrated with the information obtained using other functional imaging techniques such as fMRI. Indeed, fMRI features a very high spatial resolution (∼1 mm), since it relies on the same principles as MRI. However, functional information is obtained from the blood oxygenation level-dependent (BOLD) effect, i.e. a signal linked to the hemodynamic response that is much slower than the neuronal response, and is indirectly linked to the neuronal electric activity. Integration of the two techniques is possible at the data processing level, when either the fMRI maps are used to constrain MEG sources (Ahlfors et al., 1999) or both functional maps are projected into a common space and interpreted simultaneously (Del Gratta et al., 2002). MEG-fMRI integration allows the disentangling of sources that are closer than the spatial resolution of MEG. For example, the latency and amplitude of the different activities of two populations in the secondary somatosensory cortex, responding either to nociceptive or to non-nociceptive stimuli and lying close to one another, have been revealed through spatial priors obtained from fMRI (Torquati et al., 2005), as MEG alone was not able to discriminate between them. Other multimodal studies were able to disclose the temporal signature of higher-order functional areas, and thus to estimate the sequence of brain activation in more complex networks. As an example, the activation sequence in the circuit devoted to spatial re-orienting of attention was obtained from MEG-fMRI during passive listening to stimuli coming from random directions (Brunetti et al., 2008). More sophisticated approaches for multimodal imaging, such as representational similarity analysis, allowed analysis of transient and persistent activities in the V1 during object processing (Cichy et al., 2014). Additionally, the spatial consistency of MEG power modulations and BOLD activity made it possible to investigate the near-miss effect, which is a marker of pathological gambling in pathological and non-pathological gamblers (Dymond et al., 2014).

Finally, MEG has also proven to be useful in clinical studies, see Stufflebeam et al. (2009) for a review. The most important clinical results obtained using MEG derive from the detection and localization of pathological activity in patients with epilepsy, as well as from surgical planning in patients with brain tumors. Indeed, in surgical planning, knowledge of the position of critical brain regions (e.g. primary sensory areas, and areas involved in speech production and comprehension) is a prerequisite for avoiding potential neurological deficits induced by the surgery.

Magnetoencephalographic connectivity and brain networks

One of the central issues in neuroscience is the organization of communication in the brain, both in healthy, physiological conditions and in neurological diseases. Indeed, in the last decade it has become clear that depicting brain functioning as the overlapping of the activities of segregated areas is no longer sufficient to properly describe system behavior. A more factual theory describes the brain as a complex structurally and functionally integrated system. Although this concept is well defined, the idea of brain connectivity in neuroscience refers to several different and interrelated aspects of brain organization (Horwitz, 2003; Friston, 2011). In particular, the term anatomical connectivity refers to the study of patterns of anatomical links between brain areas; the statistical dependence between functional data (measured by a variety of approaches) is referred to as functional connectivity; and causal (or directed) interactions are studied by effective connectivity approaches. See Lang et al. (2012), Stam and van Straaten (2012), and Sakkalis et al. (2011) for an overview. We will here concentrate on the exquisite contribution of MEG to functional connectivity.

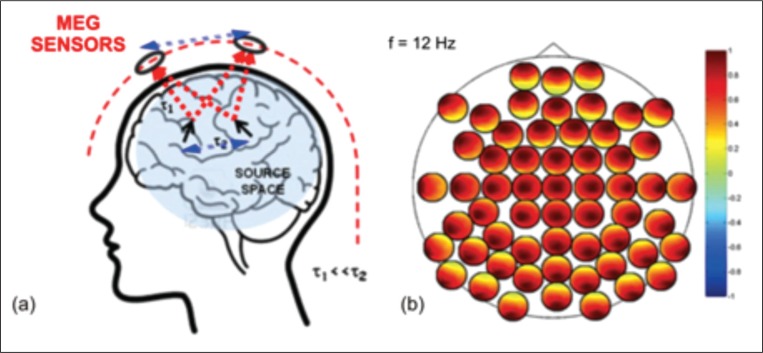
From a historical perspective, the first attempts to investigate pairwise interactions between MEG and EEG data were performed at the sensor level. Although these first results constituted a conceptual breakthrough in the systemic approach to brain functioning, MEG and EEG sensor-level connectivity might not be a sensitive index of brain functioning due to the severe bias induced by volume conduction effects (Nolte et al., 2004, Marzetti et al., 2007, Nolte and Marzetti, 2014). Volume conduction effects are smearing distortion effects on the MEG/EEG signals generated by the low-pass spatial properties of the mapping of source to sensor activities (Fig. 2a). Therefore, when studying the interaction between signals, the spread of the source activity to the sensors artificially enhances the degree of coupling between channels independently of the actual interactions between brain sources (Fig. 2b).

Figure 2.

Schematic representation of signal propagation from brain sources to MEG sensors (a) and of channel-level interactions for a subset of MEG channels (b).

a) signal propagation to the sensors is assumed to be instantaneous in comparison to the timescales of signal propagation within the brain (τ1<<τ2); at a given time instant, the different MEG sensors capture a weighted sum of the activities of all brain sources. b) Schematic representation of channel-level interactions for a subset of MEG channels. The larger black circle indicates the system layout and each smaller circle indicates the coupling of one sensor (black dot) with all the others. The spread of the source activity to the sensors artificially enhances the degree of coupling between channels independently of the actual brain source interaction. Indeed, in this toy example all channels appear to be highly coupled with all the others although only two interacting sources were simulated (a).

An important step forward toward understanding of true brain connectivity is constituted by the evaluation of interaction at the level of brain sources, either by first estimating brain activity from the electromagnetic field through an inverse approach (Schoffelen and Gross, 2009; de Pasquale et al., 2010; Marzetti et al., 2013) (see Box 3), or by projecting coupling matrices (e.g. cross-spectral density, covariance) into the brain source space (Marzetti et al., 2008; Nolte et al., 2009; Chella et al., 2014). Although this approach greatly reduces the self-coupling effects, it does not solve the issue of spurious connectivity per se. Indeed, neighboring sources share a common activity that results in spurious auto-interaction patterns. Great care should thus be taken in designing connectivity metrics robust to this effect in source space (Sekihara et al., 2011; Brookes et al., 2012; Marzetti et al., 2013) and in interpreting the results in relation to the specific connectivity metric properties and to the spatial filtering properties of the inverse operator used to estimate source activities (Hauk and Stenroos, 2014).

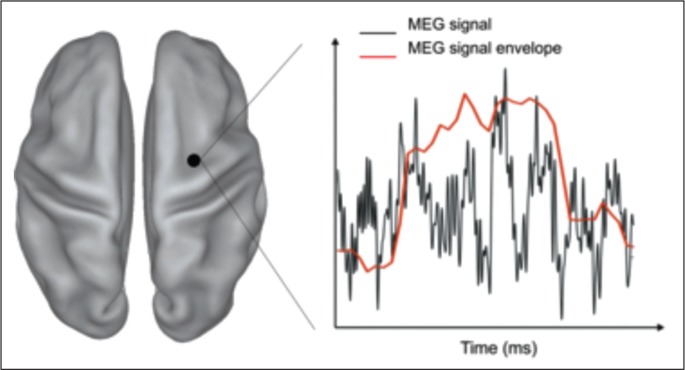
Among the large spectrum of metrics used for estimating pairwise MEG functional connectivity, we will here describe two major strategies that aim to capture connectivity information from MEG at different timescales: coupled aperiodic fluctuations of signal envelopes and phase coupling of band-limited oscillatory signals (Fig. 3). These two coupling modes differ in their dynamics, their origins and their putative functions. Envelope couplings are observed on slow timescales, ranging from several seconds to minutes, and share several common features with structural connectivity as well as with fMRI connectivity. Phase couplings, on the other hand, have been observed in multiple defined frequency bands, i.e. from ∼1 Hz to 150 Hz, are less constrained by structural coupling, and show strong condition-specific modulations. At present, the relationship between these two types of coupling is not yet understood. An intriguing hypothesis by Engel et al. (2013) is that envelope couplings represent coherent excitability fluctuations that lead to coordinated changes in the activation of brain areas, thus possibly regulating the availability of neuronal populations for participation in an upcoming task. By contrast, the putative role of phase coupling is to facilitate communication between separate neuronal populations during stimulus or cognitive processing, which may serve to regulate the integration and flow of cognitive contents on fast timescales relevant to behavior.

Figure 3.

Dynamic information of the MEG signal.

MEG signal estimated at one brain location (black dot) shows a rich temporal structure at the millisecond timescale (black curve). Fluctuations of signal envelope capture slowly varying MEG power dynamics (red curve) with a timescale similar to fMRI signal fluctuations.

These two connectivity strategies make it possible to highlight ensembles of brain regions that in a synergistic manner participate in the execution of a given task or show coherent activations during ongoing spontaneous activity. Such ensembles are characterized by spatially organized topographies referred to as brain networks. Importantly, although the brain network concept provides a unifying framework for understanding brain functioning, it is not univocally determined. Indeed, the available evidence suggests that a number of factors such as structural connectivity, conduction delays, level of neuromodulators, as well as previous task-related activation or coupling, contribute to a network-like behavior. Thus, brain networks are not invariant patterns, but rather patterns that change in a use-dependent as well as in a context-dependent manner. In this framework, it is not surprising that different neuroimaging modalities, by capturing different aspects of information integration in the brain, may lead to different operative definitions of brain network.

To begin with, we should mention that the first demonstration of spatially organized networks in ongoing activity in the brain was achieved by using fMRI (Biswal et al., 1995) and it raised the idea of resting-state networks (RSNs). Using fMRI, different RSNs – including the default-mode network (DMN), the dorsal attention network (DAN), as well as executive control, visual, auditory and sensorimotor networks – were identified as networks of brain areas that show correlated fluctuations in the infra-slow frequency range (<0.1 Hz) in the absence of a stimulus or task (Raichle, 2010; Deco and Corbetta, 2011).

Only recently, novel EEG/MEG methods have become available that allow the characterization of frequency-specific coupling, possibly leading to network-like behavior, in spontaneous activity at the brain source level (de Pasquale et al., 2012; Hipp et al., 2012; Hillebrand et al., 2012; Marzetti et al., 2013). In this framework, the study of coupled aperiodic fluctuations of MEG signal envelopes highlighted correlated patterns that resemble fMRI RSN topographies, whereas phase coupling of band-limited oscillatory MEG signals revealed a more sophisticated picture in which different frequency-specific communication channels allow the binding of different networks. In the near future, efforts will need to be made to achieve full characterization of these phenomena through MEG.

Magnetoencephalography in the study of brain dynamics

The human brain is a self-evolving system whose structure and function are able to adapt and reorganize over time. Long-term modifications are induced by learning throughout one’s lifespan, but changes can also occur on much shorter timescales. Temporal fluctuations of brain activity show properties that are informative about the functional characteristics of the brain itself. These temporal variations are the result of the integration at multiple scales of the local temporal fluctuations of individual neuronal populations. Although it is not yet fully understood how the local activity of an ensemble of neurons is bound to the “macroscopic” electrophysiological patterns generated by huge groups of neuronal pools (see Box 4), evidence has emerged that neuronal temporal dynamics show similar characteristics at various spatial and temporal scales. In fact, signal temporal fluctuations show statistical similarities across a wide range of timescales, from seconds to hundreds of seconds, namely a scale-free behavior (He, 2014). This behavior has also been observed with MEG for amplitude fluctuations of brain oscillations, and long-range temporal correlations (Palva et al., 2013).

Moreover, at a shorter (millisecond) timescale and at a local level, neuronal populations self-organize in such a way that their activity comprises cascade-like neuronal avalanches. The distribution of the size of these avalanches exhibits a power-law behavior, i.e. the number of avalanches observed in the data scales inversely with the size of the avalanche (Beggs and Plenz, 2003). These dynamics characterize spontaneous neuronal activity in organotypic cultures, brain slices in vitro, and monkey and human cortex in vivo (Petermann et al., 2009; Tetzlaff et al., 2010). Additionally, the brain’s dynamic properties proved to be behaviorally relevant. Indeed, the long-range temporal correlation recovered from source-reconstructed MEG oscillatory activity correlates with both behavioral performance fluctuations and neuronal avalanche occurrences in anatomically well-identified brain regions (Palva et al., 2013).

The existence of scale-free dynamics at different spatial and temporal scales and at different levels of organization has been interpreted as a sign of brain complexity reflecting the ability of the system to efficiently adapt to upcoming demands (Deco and Jirsa, 2012). The term complexity reflects a rich, temporally ordered structure found in the brain signal at different levels. Brain complexity ranges between a situation of pure randomness, associated with dysfunction, and of pure absence of variability, associated with the inability to facilitate state changes (Zappasodi et al., 2014). In this framework, metrics able to capture non-linear dynamics of EEG/MEG signals are an invaluable tool for addressing the system-level complexity of the brain. Importantly, the characterization of brain complexity can improve the ability to distinguish between a healthy, physiological state and a pathological one, opening up new perspectives for the comprehension of normal and altered brain functions (e.g. epilepsy, schizophrenia, Alzheimer’s disease; for a review see Stam, 2010).

Not only brain activity per se, but also brain activity coupling as measured by functional connectivity has been shown to exhibit dynamic properties. Indeed, brain structural organization shows a highly sophisticated wiring architecture, but only a small fraction of all the possible connections is employed at any time. This allows dynamic changes of functional and effective connectivity, giving rise to short-lived oscillations which are built and destroyed by the brain’s internal dynamics. Interestingly, neuronal ensembles switch between interference-prone states to oscillatory synchrony. This behavior seems to represent an efficient way for the brain to detect changes in the body and in the surrounding physical world while maintaining its internal organization (Buzsáki and Draguhn, 2004). In this scenario, MEG is a very promising tool for capturing the dynamics of network coupling since its high temporal resolution allows the study of within- and across-network interactions and their modulation across frequencies and over time on behaviorally relevant timescales (Varela et al., 2001).

In this framework, frequency-specific functional connectivity patterns have been observed using phase coupling of band-limited oscillatory signals by the multivariate interaction measure (Ewald et al., 2012) in the resting human brain. Specifically, coupling of regions in the DAN was revealed by the delta and alpha rhythms and coupling of the DAN with the visual and the sensorimotor networks was observed in the alpha and beta bands respectively. This indicates that the interaction between the attention control system and sensory systems is served by the same frequency bands in which the sensory system’s task-related response is known to occur (Marzetti et al., 2013). Additionally, with the same approach, coupling of the posterior cingulate cortex to nodes of the executive control brain network and of the default brain network in the alpha-frequency band was shown to be related to different attentional and cognitive control processes in meditating Buddhist monks, thus suggesting the importance of the alpha rhythm for attention and consciousness (Marzetti et al., 2014).

The slow fluctuations of band power envelopes of resting-state MEG have shown close similarities to the topography of the reported resting-state BOLD fMRI (de Pasquale et al., 2010). Indeed, MEG revealed fluctuations in the temporal dynamics of coupling of RSN nodes, i.e. periods of high coupling alternated with periods of low coupling.

In this scenario, different measures of interactions between RSN nodes exhibited a peak at ∼0.1 Hz (Brookes et al., 2011a,b; de Pasquale et al., 2010, 2012; Hipp et al., 2012; Liu et al., 2010), supporting the theory that the low-frequency spontaneous BOLD fluctuations are of neural origin (Palva and Palva, 2012). Subsequent studies have begun to uncover rules governing the variability of functional connectivity within and across networks. For example, the DMN (especially its posterior cingulate node) was identified to be the network most strongly interacting with all the other examined networks, specifically when its internal coupling was high (de Pasquale et al., 2012). This cross-network interaction requires a partial decoupling of some nodes in other networks that become functionally coupled with the DMN. However, this functional relationship breaks down when the DMN internal correlation is relatively low. Similarly, viewing natural scenes modulated functional connectivity in a dynamic fashion according to the scenes perceived as “event boundaries” by the participants, who were asked to segment the movie into temporal chunks that they found natural and meaningful (Betti et al., 2013). Such data suggest that the DMN serves to transiently integrate systems, likely via beta-band synchronization, which might be linked to the transient periods of strong within-network synchronization, reported using fMRI (Hutchison et al., 2013).

Future trends

Magnetoencephalography is an invaluable tool for understanding brain dynamics and addressing the issue of functional connectivity as a mechanism for instantiating specific behavior/functioning. MEG indeed captures several aspects of functional integration in the brain through a large spectrum of metrics for estimating pairwise functional connectivity. The richness of MEG makes it possible to bridge slow power fluctuations related to large neuronal assemblies as seen, e.g. by fMRI, with small-scale, fast-occurring signals like those generated by local neuronal pools. For this reason, in the near future MEG is expected to play a more central role in characterizing brain networks and to significantly contribute to the construction of the human connectome, i.e. a comprehensive map of the human brain circuitry. Several large cooperative projects are endeavoring to provide a detailed description of the human connectome, e.g. the NIH Human Connectome Project (R01 MH091657), an ambitious effort to map the neural pathways that underlie human brain function. To reach this goal, there must be cooperation, anatomical and functional, between different imaging techniques. In this framework, MEG, thanks to its excellent time resolution and its non-invasiveness, is ideally suited to investigate phenomena on behaviorally relevant timescales, including the possibility of capturing behaviorally-related brain connectivity dynamics (Larson-Prior et al., 2013). The understanding of global and local network properties can also be further increased by the use of graph theory metrics (Stam, 2010; Di Lanzo et al., 2012). Finally, the integration of human connectome maps with other important information, like genetics, may lead to a comprehensive characterization of functional brain connectivity even at the individual level. This would represent a first step toward understanding the basis of network alterations in patients, e.g. in Alzheimer’s disease, multiple sclerosis, Parkinson’s disease or stroke. In fact, in several disorders, clear and testable hypotheses on causal relations between functional network changes and clinical phenotype have been formulated, which cannot be straightforwardly predicted from structural alterations (Stam, 2010).

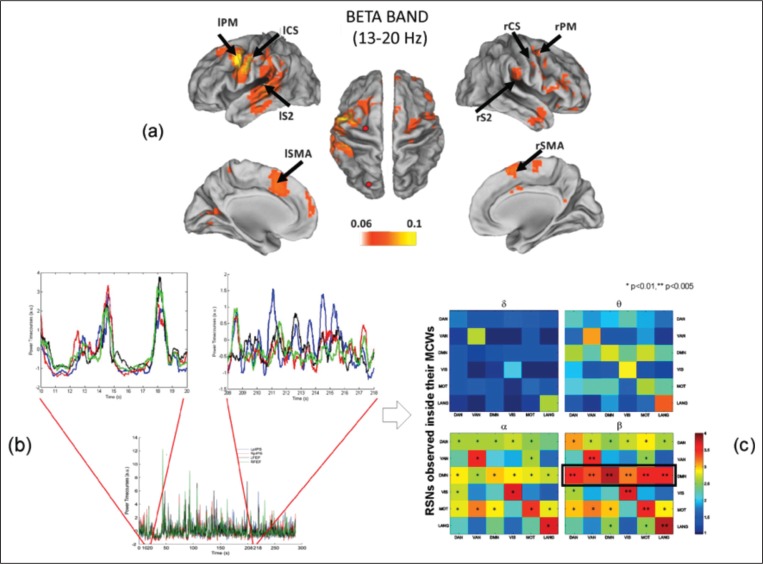
Figure 4.

Brain networks as observed by magnetoencephalography.

(a) Phase coupling of band-limited oscillatory signals as identified by multivariate interaction measure between the dorsal attention network (DAN) and the motor network in the beta band. (b) Correlated fluctuations of band power envelopes of resting-state MEG show time-variant profiles, e.g., when the within-DAN connectivity is computed in two different temporal epochs. Time windows of stronger connectivity alternate with periods of lower connectivity. (c) Correlated fluctuations of band power envelope for various RSNs show different behaviors for different frequencies. Notably, the default mode network plays a central role in brain functional connectivity in the beta band. Modified from de Pasquale et al. (2012) and Marzetti et al. (2013).