Abstract
We investigated the view angle dependence of domain mean Moderate Resolution Imaging Spectroradiometer (MODIS) liquid water path (LWP) and that of corresponding cloud optical thickness, effective radius, and liquid cloud fraction as proxy for plane-parallel retrieval biases. Independent Advanced Microwave Scanning Radiometer–EOS LWP was used to corroborate that the observed variations with sun-view geometry were not severely affected by seasonal/latitudinal changes in cloud properties. Microwave retrievals showed generally small (<10%) cross-swath variations. The view angle (cross-swath) dependence of MODIS optical thickness was weaker in backscatter than forward scatter directions and transitioned from mild ∩ shape to stronger ∪ shape as heterogeneity, sun angle, or latitude increased. The 2.2 µm effective radius variations always had a ∪ shape, which became pronounced and asymmetric toward forward scatter in the most heterogeneous clouds and/or at the lowest sun. Cloud fraction had the strongest and always ∪-shaped view angle dependence. As a result, in-cloud MODIS cloud liquid water path (CLWP) showed surprisingly good view angle (cross-swath) consistency, usually comparable to that of microwave retrievals, due to cancelation between optical thickness and effective radius biases. Larger (20–40%) nadir-relative increases were observed in the most extreme heterogeneity and sun angle bins, that is, typically in the polar regions, which, however, constituted only 3–8% of retrievals. The good consistency of MODIS in-cloud CLWP was lost for gridbox mean LWP, which was dominated by the strong cloud fraction increase with view angle. More worryingly, MODIS LWP exhibited significant and systematic absolute increases with heterogeneity and sun angle that is not present in microwave LWP.
Key Points
Microwave LWP shows small overall and cross-swath variations
MODIS in-cloud LWP also shows good view angle consistency in most cases
MODIS retrievals show strong overall increase with heterogeneity and sun angle
Keywords: liquid water path, plane-parallel bias, three-dimensional effects, view angle dependence, cloud remote sensing
1. Introduction
Liquid water path (LWP) forms a link between hydrological and radiative properties of the climate system through controlling the radiative effects of ubiquitous marine boundary layer clouds. Establishing the error characteristics of existing LWP data sets is, thus, crucial for climate monitoring and model evaluation. Passive satellite sensors routinely estimate LWP from two independent methods. Microwave instruments, such as Advanced Microwave Scanning Radiometer–Earth Observing System (AMSR-E), derive LWP directly from brightness temperatures [Wentz, 1997; Wentz and Spencer, 1998; Wentz and Meissner, 2000; Hilburn and Wentz, 2008]. Multispectral imagers, such as Moderate Resolution Imaging Spectroradiometer (MODIS), on the other hand, use the visible/near-infrared (VNIR) solar reflectance method to retrieve cloud optical thickness and droplet effective radius, the product of which is proportional to LWP [Nakajima and King, 1990; Platnick et al., 2003].
Several studies compared coincident microwave and VNIR LWPs from AMSR-E and MODIS over ocean, establishing robust results [Bennartz, 2007; Borg and Bennartz, 2007; Horváth and Gentemann, 2007; Greenwald et al., 2007; Greenwald, 2009; Seethala and Horváth, 2010]. The state-of-the-art Wentz microwave algorithm has a wet bias in broken cloud fields that increases with decreasing cloud fraction and surface wind speed, and LWPs are correlated with water vapor amount. These findings suggest uncertainties in surface emissivity and gaseous absorption included in the microwave forward model. For overcast marine Sc, the two techniques agree well and for global means are even unbiased relative to each other if vertically stratified water content is assumed in the VNIR parameterization. As shown by Seethala and Horváth [2010], however, large regional differences remain, the most striking of which is a severe (up to 90%) overestimation in VNIR LWPs at high latitudes, that is, at low sun. Seethala and Horváth [2010] also proposed potential causes for microwave-VNIR differences in overcast scenes: cloud temperature and cloud versus rain water partitioning errors affecting the Wentz retrievals and inaccurate cloud vertical stratification and 3-D errors affecting MODIS retrievals.
Our follow-on study investigates the view zenith angle (VZA) dependence of MODIS LWPs, unexplored by Seethala and Horváth [2010], using AMSR-E retrievals as an independent check. Significant differences among LWPs obtained at different sun-view geometries are indicative of retrieval model shortcomings, especially of 3-D/heterogeneity effects. Both techniques rely on 1-D radiative transfer through homogeneous plane-parallel clouds, which can lead to retrieval biases when interpreting the radiative signature of heterogeneous 3-D clouds. Although microwave retrievals are not immune to 3-D effects, corresponding biases in warm (ice-free) nonprecipitating clouds are relatively small and to first order can be corrected for by scaling LWPs with cloud fraction [Greenwald et al., 1997; Lafont and Guillemet, 2004]. Therefore, contrasting the cross-swath dependence of AMSR-E and MODIS LWPs can yield important clues about the sign and magnitude of much larger biases in 1-D VNIR retrievals resulting from 3-D radiative effects—cross-swath variations are equivalent to VZA variations in the case of MODIS.
Numerous observational and modeling studies investigated variations in 1-D VNIR retrievals with view geometry, most focusing on optical thickness and a handful on effective radius. The majority of satellite studies used data from single-view sensors, which observe any given cloud in only one view direction, preventing scene-by-scene analysis. These studies analyzed changes in retrieval frequency distributions instead, and in so doing implicitly assumed seasonal and latitudinal invariance in cloud properties because robust statistics for a particular sun-view combination could only be accumulated over a range of seasons and geographic areas. Although such an approach precludes precise decoupling of view-dependent retrieval biases from true regional changes in cloud properties, important insights were gained into 3-D effects.
Based on Earth Radiation Budget Satellite (ERBS) nadir observations, Loeb and Davies [1996, 1997] found a systematic increase in 1-D cloud optical thickness with increasing solar zenith angle (SZA), especially for SZA > 60°. Monte Carlo simulations were used to attribute this SZA bias to cloud side illumination and sloped cloud tops, which enhance incident solar radiation and, thus, nadir reflectance compared to the 1-D model [Loeb et al., 1997]. Loeb and Coakley [1998] investigated Advanced Very High Resolution Radiometer retrievals in extensive marine Sc and confirmed the positive SZA bias in nadir optical thickness found in ERBS data. Extending their analysis to oblique view angles, they also found insignificant VZA dependence in optical thickness in the backscatter direction but noted a strong decrease, up to 40% at low sun, in the forward scatter direction. Monte Carlo simulations explained the different VZA dependence in backscatter and forward scatter directions by cloud top height variations leading to low-order scattering and shadowing in the forward direction [Loeb et al., 1998; Kato and Marshak, 2009].
In contrast, Várnai and Marshak [2007] found MODIS optical thickness increasing up to 40% with VZA in both backscatter and forward scatter directions for heterogeneous clouds and low sun. Retrievals were, however, remarkably consistent in all view directions for homogeneous clouds and high/moderate sun. They concluded that the increase in 1-D optical thickness was likely due to 3-D effects associated with enhanced viewing of cloud sides from oblique but predominantly side scattering directions (filling of cloud gaps and photon leakage through cloud sides).
Maddux et al. [2010] observed a global decrease in MODIS optical thickness between near nadir and edge of scan retrievals, yet again implying a decrease with VZA. Finally, Grosvenor and Wood [2014] found small VZA dependence but a rapid increase for SZA > 65° in MODIS optical thickness over Artic stratocumulus. Note, however, that both of these studies use Level 3 data and average together backward and forward scatter directions. Although the Grosvenor and Wood [2014] analysis was limited in sun-view geometry sampling (SZA > 50° and mostly side scatter views), it better isolated SZA retrieval effects than previous work by considering a short time period and narrow latitude range with one of the weakest diurnal cycles in LWP.
The handful of studies investigating 1-D retrieval biases in effective radius mostly interpreted results as shadowing and illumination effects [Cornet et al., 2004, 2005; Marshak et al., 2006; Vant-Hull et al., 2007]. When well-illuminated cloud surfaces are seen near the backscatter direction, 1-D effective radius is underestimated, while the reverse is true away from the backscatter position when shadowed portions of clouds dominate the field of view. Shadowing tends to produce larger biases than illumination, leading to an overall positive bias in effective radius. Consistent with this reasoning, Kato et al. [2006] found an overestimation in domain-averaged retrieved effective radius, with errors increasing from the orthogonal toward the solar principal plane and being largest in oblique forward scatter directions. Zhang et al. [2012] additionally introduced the concept of the “plane-parallel effective radius bias” in analogy to the “plane-parallel albedo bias” [Cahalan et al., 1994], demonstrating that the nonorthogonality of retrieval look-up tables can lead to a simultaneous underestimate of optical thickness and overestimate of effective radius. Zhang et al. [2012] argued that although shadowing and illumination have an influence on MODIS-resolution retrievals, these opposing 3-D effects partially cancel out, leaving the plane-parallel effective radius bias as the dominant factor. Generally speaking, the description and understanding of effective radius biases lag behind those of optical thickness biases, because most of our relevant knowledge was gleaned from retrieval simulations for a limited set of modeled cloud fields and sun-view geometries.
Nevertheless, the overestimation of effective radius often seems to go in pair with underestimation of optical thickness, which could yield partial cancelation of errors in 1-D VNIR LWP. Consistent with this observation, Maddux et al. [2010] found a global increase in MODIS Level 3 effective radius with increasing VZA, a trend opposite to that seen in optical thickness. Grosvenor and Wood [2014] also noted hint of a weak VZA increase in MODIS effective radius over Arctic stratocumulus, but the dominant variation in their results was a decrease with sun angle for SZA > 65°.
A few investigators employed near-simultaneous multiview observations from Multiangle Imaging Spectroradiometer (MISR) and Polarization and Directionality of the Earth's Reflectances (POLDER) to test the consistency of 1-D retrievals. Unlike single-view statistical studies, multiview studies allow scene-by-scene analysis. In a limited MISR data set, Horváth and Davies [2004] found the observed angular reflectance pattern being within 5% of plane-parallel values for only ∼20% of clouds. Di Girolamo et al. [2010] extended this approach to a multiyear data set, revising the 1-D angular consistency rate for reflectance upward to 24% and showing its strong correlation with spatial homogeneity. They also obtained, however, a much higher 79% angular consistency rate for 1-D optical thickness, likely due to the nonlinear relationship between reflectance and optical thickness. In a study combining MISR optical thickness with MODIS effective radius, Horváth and Davies [2007] analyzed the VZA dependence of resulting LWPs relative to coincident estimates from Tropical Rainfall Measurement Mission Microwave Imager. They found a weak (≤15%) but systematic increase in 1-D VNIR LWP with VZA driven by cloud optical thickness, also noting a slightly larger increase in the backscatter than forward scatter direction.
Analysis of POLDER retrievals by Buriez et al. [2001] and Zeng et al. [2012] showed a general increase in optical thickness with SZA and a decrease with VZA, especially for forward scatter and heterogeneous clouds. They also reported underestimated optical thicknesses in the rainbow direction. The larger negative biases in forward scatter direction were attributed mainly to shadowing effects, while the smaller ones in backscatter and rainbow directions to the use of a too large constant effective radius (11 µm over ocean and 9 µm over land).
What emerges from the above studies is that 1-D retrieval biases are a complicated function of sun-view geometry, cloud heterogeneity and the specific metric used to characterize it (horizontal variability in reflectance, or optical thickness, or cloud top height), averaging scale, and instrument/orbit properties. From a recent MISR-MODIS data fusion analysis, Liang and Di Girolamo [2013] concluded that the observed VZA dependence of optical thickness is the weighted sum of three potentially competing factors: One, the “gap factor” identified by Várnai and Marshak [2007], which fills dark gaps between clouds when partly cloudy scenes are viewed obliquely and, thereby, increases optical thickness with VZA in both backscatter and forward scatter directions; two, the “concavity factor,” which decreases retrieved optical thickness of heterogeneous pixels in both backscatter and forward scatter directions due to increasing concavity with VZA of the optical thickness-reflectance relationship; and three, the varying fraction of illuminated and shadowed sides of bumpy clouds, which strongly depends on relative azimuth angle (RAZ). This “bump RAZ factor” decreases optical thickness with VZA in the forward scatter direction as shadowed/illuminated fraction increases/decreases and increases optical thickness in the backscatter direction where the reverse is true. The at times opposing results of previous studies could then be explained by instrument- and orbit-specific sampling favoring one factor over another.
The goal of our paper is to investigate the VZA-dependence specifically of 1-D VNIR LWP, a quantity that has largely been neglected save for the limited study of Horváth and Davies [2007]. This necessitates analyzing dependencies in cloud optical thickness, droplet effective radius, and cloud fraction, from which VNIR LWP is parameterized. The focus is on 0.25° domain means, dictated by the relatively coarse resolution of the microwave retrievals used as reference. Due to the single-view nature and sun-synchronous orbit of MODIS, our data set suffers from previously described aliasing between sun-view geometry and seasonal/latitudinal variations, which complicates isolating view-dependent 1-D retrieval biases. This complication, however, is mitigated by contrasting MODIS LWPs with coincident and fully independent AMSR-E LWPs, which are less prone to 3-D effects and exhibit the same seasonal/latitudinal sampling as MODIS.
The remainder of the paper is organized as follows. Section 2 describes the AMSR-E and MODIS data sets and caveats of their comparison. Section 3 gives an overview of the primary absolute differences between microwave and VNIR LWPs and then presents the relative VZA dependence of global annual means as well as that of data subsets stratified by cloud heterogeneity, SZA, or geographic region, relating our results to previous findings. Finally, we offer a summary and concluding remarks in section 4.
2. Data and Methodology
2.1. AMSR-E and MODIS LWPs
We used the Seethala and Horváth [2010] data set comprising collocated AMSR-E and MODIS LWPs from Aqua, covering the 1 year period December 2006 to November 2007. The AMSR-E LWPs were derived from 37 GHz observations by the absorption-emission based algorithm of Remote Sensing Systems (RSS) [Wentz and Meissner, 2000]. Specifically, we used the RSS Version 5 quarter-degree gridded daytime product. Since Seethala and Horváth [2010], the latest Version 7 RSS product became available. Algorithm improvements from V5 to V7 mostly affected calibration methodology and rain rate retrievals but had only a minor impact on LWP [Hilburn et al., 2010; Wentz, 2013]. The clear-sky LWP bias noted in Horváth and Gentemann [2007] was reduced by 8 g m−2 in V7 at the calibration stage. In addition, V7 now provides the negative LWP values arising from random brightness temperature errors, which were previously set to zero and, thus, produced a slight bias in V5. Negative LWP values accounted for ∼9% of the data and had a 2% effect on the mean rain-free LWP. Overall, these changes had an insignificant impact on our results.
The MODIS LWPs were parameterized from optical thickness (τ) and effective radius (re)—themselves inferred from 0.86 and 2.2 µm solar reflectances—using the well-known formula
| (1) |
Here ρw = 1 g cm−3 is water density and cv is a constant depending on the assumed vertical stratification. From equation (1) it follows that the relative error in LWP is the sum of relative errors in τ and re, which can lead to partial cancelation of errors. The operational Collection 5 MYD06 product was given at 1 km resolution and assumed vertical homogeneity, for which cv = 2/3. For a vertically stratified cloud where liquid water content linearly increases from cloud base to top and droplet number concentration is constant with height, cv = 5/9 [Szczodrak et al., 2001], amounting to a 17% reduction in LWP. This simple stratified cloud model was shown to yield better absolute agreement between microwave and VNIR LWP global means [Borg and Bennartz, 2007; Seethala and Horváth, 2010].
A more sophisticated approach would be to derive linear re profiles on a case-by-case basis from the three water-absorbing MODIS channels, as in the retrieval method of Chang and Li [2002, 2003]. Although this technique yielded a small (∼10%) improvement for MODIS LWPs in limited case studies [Chen et al., 2007, 2008], more recent investigations expressed reservations about such profiling algorithms. The MODIS re differences strongly depend on sun/view geometry and scene heterogeneity [Zhang et al., 2012], are generally too small compared to measurement and plane-parallel modeling uncertainties [King and Vaughan, 2012], and, thus, mainly represent cloud inhomogeneity rather than vertical droplet size structure [Painemal et al., 2013]. In any event, correcting for vertical stratification primarily affects the absolute value as opposed to the VZA variation of VNIR LWP; therefore, we only show results for the operational MODIS product.
2.2. Comparison Methodology
The higher-resolution MODIS retrievals were linearly averaged down to the 0.25° scale of the AMSR-E retrievals, considering only completely ice- and precipitation-free domains. Note that the RSS microwave LWPs are provided on a regular grid and usually interpreted as averages over clear sky and cloud, mostly because such a gridded product facilitates simple averaging of comparison VNIR data (although it is also true that the relationship between 37 GHz measurements and subfield-of-view cloud amount is nearly linear over the elliptical microwave footprint [Greenwald et al., 1997; Lafont and Guillemet, 2004]). Collocating microwave measurements at their native resolution with a VNIR sensor offers several advantages, such as reducing noise and weighting the higher-resolution VNIR retrievals by the microwave sensor's effective antenna pattern, as aptly demonstrated by Greenwald et al. [2007]. This, however, comes at the cost of greatly increased computational burden. Here, as in Seethala and Horváth [2010], we were willing to trade off a reduction in information content for the ability to analyze an entire year of data. Our choice was further motivated by climate model diagnostics strongly favoring the gridded RSS product.
MODIS data, on the other hand, are in-cloud LWPs, henceforth referred to as cloud liquid water paths (CLWPs), representing only those cloudy pixels for which both τ and re retrievals were successful. To facilitate comparison of the gridded microwave and the VNIR cloudy retrieval values, MODIS CLWPs need to be multiplied by the gridbox mean retrieval fraction. Due to occasional failures for thin clouds or cloud edges, retrieval fraction is usually smaller than the fraction of cloudy pixels [Pincus et al., 2012]; nevertheless, the former is still referred to as “cloud fraction” here. Cloud fraction, however, strongly increases with VZA and, thus, dominates the VZA dependence of scaled MODIS LWP, masking that of other variables. Therefore, we plot results for unscaled MODIS CLWP along with variations in corresponding τ, re, and cloud fraction. This is in line with our desire to investigate the VZA dependence of retrievals relative to the nadir view as opposed to analyze absolute differences between microwave and VNIR estimates, already covered in Seethala and Horváth [2010].
As an example, Figure 1 shows variation of SZA and Aqua-MODIS VZA, RAZ, and scattering angle (SCA) across the AMSR-E swath for a daytime orbit on 21 March 2007. (The 1445 km AMSR-E swath is centered within the 2330 km MODIS swath.) The SZA tends to increase toward the poles, highlighting its season-dependent covariation with latitude. The MODIS VZA increases from near-nadir values at swath center up to 60° at swath edges. In contrast, the view zenith angle of the conically scanning AMSR-E is practically constant and only varies by a few tenths of a degree about 55°, depending on the satellite altitude. The MODIS RAZ is <90° in the western half and >90° in the eastern half of the swath. We refer to RAZ < 90° as “forward scatter” and RAZ > 90° as “backscatter,” although as shown in Figure 1d “forward scatter” azimuths may correspond to scattering angles that, strictly speaking, indicate side scatter or slightly backscatter directions. All results are presented for 10° wide MODIS VZA bins ([−55°,−45°],..,[−5°,+5°],..,[+45°,+55°]), with VZAs corresponding to forward scatter and backscatter azimuths labeled positive and negative, respectively. Note that AMSR-E LWP is also binned according to MODIS VZA. Thus, in describing microwave retrievals the term “VZA variations” is simply shorthand for “east-west cross-swath variations.”
Figure 1.
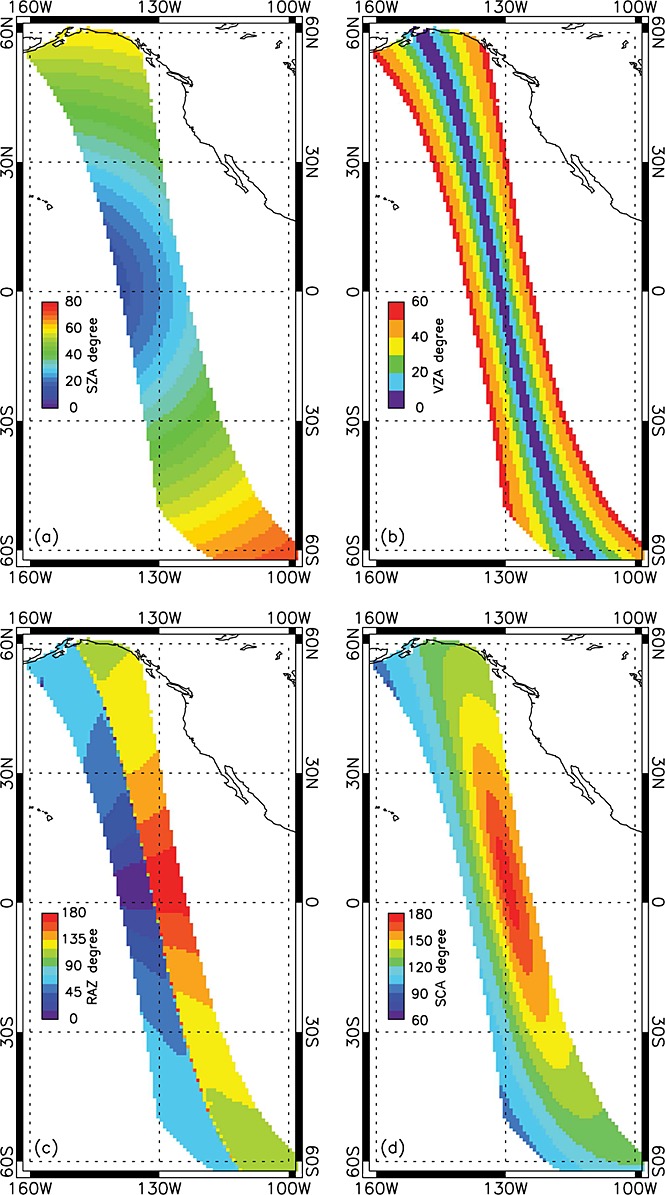
Variation of (a) solar zenith angle and Aqua-MODIS (b) view zenith angle, (c) relative azimuth angle, and (d) scattering angle across the AMSR-E swath for a daytime orbit on 21 March 2007.
The two basic shapes describing variations in a retrieved parameter are the ∪ or “bowl” shape, which implies an increase with VZA in both backscatter and forward scatter directions, and the opposite ∩ or “bell” shape. Both of these shapes may show backscatter-forward scatter asymmetry. A third typical case corresponds to approximate invariability or slight increase in the backscatter direction but considerable decrease in the forward scatter direction. Following Várnai and Marshak [2007], the VZA (θ) behavior of a given parameter (LWP, CLWP, τ, re, or cloud fraction) is approximated by a quadratic function
| (2) |
with fitting coefficients a, b, and c. The sign and magnitude of coefficient c indicate the shape (positive ∪ and negative ∩) and strength of VZA dependence. The VZA behavior depends on SZA and in-cloud heterogeneity, the latter being characterized for each 0.25° grid cell by the ratio of the logarithmic and linear average of 1 km cloud optical thicknesses, or Cahalan et al.'s [1994] χ parameter, as in Seethala and Horváth [2010]. The χ parameter varies from 0 to 1, with smaller values indicating more heterogeneity.
2.3. Sampled Relative Azimuth and Scattering Angles
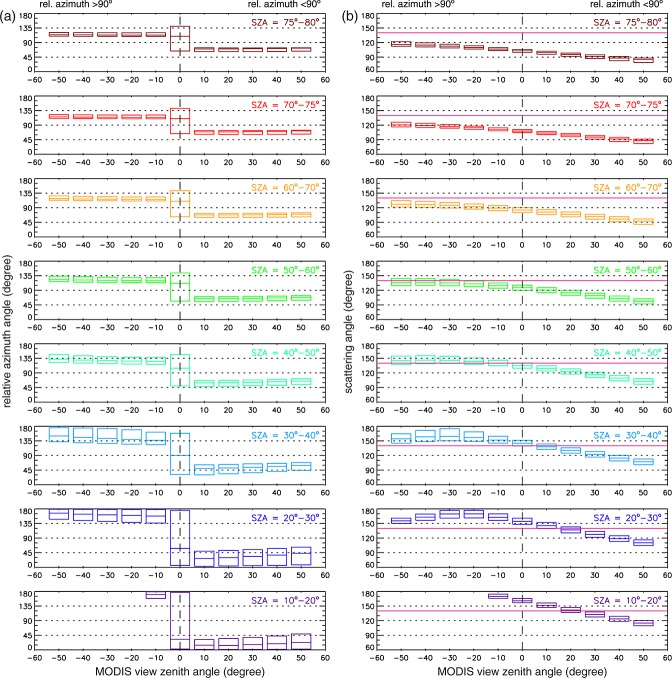
Box plots in Figure 2 summarize the statistics of conditionally sampled Aqua-MODIS relative azimuth and scattering angles as a function of VZA and SZA. Observations were close to the solar principal plane (RAZ = 0°/180°) at high sun but gradually moved closer to the orthogonal side scattering plane (RAZ = 90°) at moderate and low sun. (Note that the RAZ-SZA relationship in our data set was opposite to that in Liang and Di Girolamo's [2013] MISR data, where RAZ was close to side scattering at small SZA and moved closer to the solar plane at large SZA. The contrasting RAZ-SZA relationships can be explained by MISR “scanning” along track as opposed to the cross track scanning of MODIS, and the different equator-crossing times of Terra and Aqua: 10:30 A.M. versus 01:30 P.M.)
Figure 2.
Distribution of sampled Aqua-MODIS (a) relative azimuth angles and (b) scattering angles as a function of VZA and SZA. The top and bottom of a box represent the 5th and 95th percentiles, while the horizontal line within a box is the median. The rainbow scattering angle of 139° is also marked.
The corresponding scattering angles generally decreased east-to-west across the swath. Although SCA was smaller for RAZ < 90° than for RAZ > 90°, forward scatter (SCA < 90°), strictly speaking, only occurred at the most oblique VZAs for SZA > 60°, even for RAZ < 90°. At low sun, SCA mostly indicated observations near side scattering directions. In Figure 2b, we also marked rainbow scattering at SCA ∼139°. As discussed in section 3.4, MODIS optical thickness retrievals showed reduced values in this direction. Rainbow scattering was encountered over a narrow range of view angles at forward scatter RAZs for high/moderate sun (VZA near 20° for SZA < 30° and VZA near 10° for 30° < SZA < 40°) but over a wider range of VZAs, mostly at backscattering RAZs, for 40° < SZA < 60°. No rainbow scattering was observed at low sun with SZA > 60°.
3. Results
3.1. Primary Dependencies of AMSR-E LWP and MODIS LWP Absolute Deviations
Although the focus of this paper is on relative VZA variations, here we briefly illustrate the main dependencies of AMSR-E LWP and MODIS LWP absolute deviations on scene brokenness, heterogeneity, and sun angle. The plots below correspond to averages over all VZAs.
Figure 3 shows variations of AMSR-E LWP and MODIS LWP correlation and mean difference versus liquid cloud fraction for various heterogeneity and SZA bins. In general, correlation steadily decreased with decreasing cloud fraction and was also a strong function of χ and to a lesser degree of SZA. Microwave and VNIR LWPs were significantly better correlated for homogeneous clouds and/or high sun than for heterogeneous clouds and/or low sun. The curves converged to low correlation values between 0.10 and 0.35 at cloud fractions <10%, indicating largely decoupled retrievals in the most broken scenes.
Figure 3.
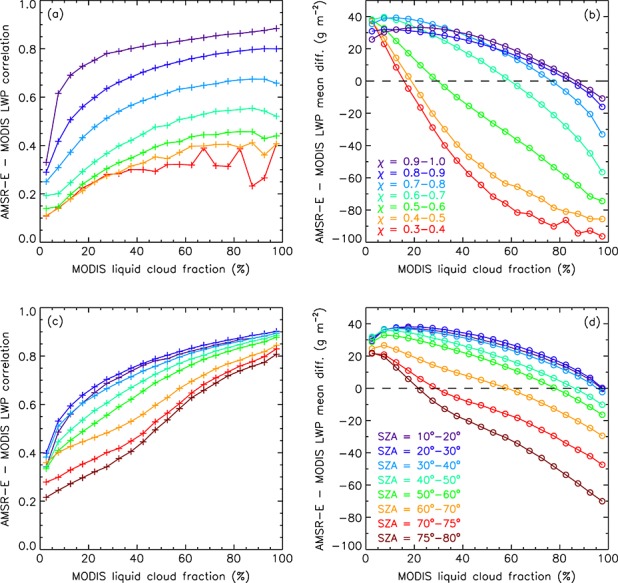
Liquid cloud fraction dependence of AMSR-E LWP and MODIS LWP (a and c) correlation and (b and d) absolute mean difference for various heterogeneity (Figures 3a and 3b) and SZA (Figures 3c and 3d) bins.
Simultaneously, MODIS overestimated AMSR-E LWPs at higher cloud fractions, with small biases for homogeneous clouds and/or high sun but very large biases for heterogeneous clouds and/or low sun. The MODIS overestimation decreased and eventually switched to AMSR-E overestimation as cloud fraction decreased. The sign change (i.e., the minimum) in mean difference occurred at increasingly lower cloud fractions as heterogeneity and SZA increased. The mean difference curves also converged to 20–40 g m−2 AMSR-E overestimations at cloud fractions <10%, where MODIS LWPs approached zero. The AMSR-E overestimation and decorrelation between the retrieval techniques at the smallest cloud fractions were partly caused by the reduced sensitivity of 37 GHz microwave measurements to low LWPs and a wet bias in Wentz retrievals due to uncertainties in surface emissivity and gaseous absorption [Seethala and Horváth, 2010]. (As discussed in section 3.4, the clear-sky microwave wet bias was slightly reduced by 8 g m−2 in V7 AMSR-E LWPs, but otherwise, results did not change compared to the V5 retrievals used here.) MODIS retrievals, especially cloud fraction, were also likely to be biased low in broken clouds due to clear-sky restoral in the Collection 5 product, which could contribute to the positive microwave-VNIR LWP differences.
To summarize, the best overall agreement between microwave and VNIR LWPs was found in the most homogeneous overcast scenes at high sun with SZA < 30°, where the techniques were practically unbiased relative to each other and showed a high correlation of ∼0.90. The strong and systematic decrease in correlation and increase in MODIS overestimation with increasing heterogeneity and SZA (especially in higher cloud fraction scenes at SZA > 40°) were likely indicative of 3-D biases in 1-D VNIR LWPs. The decorrelation between the techniques and systematically higher AMSR-E LWPs in broken clouds, on the other hand, were probably the combination of a wet bias in microwave retrievals and a dry bias in MODIS retrievals due to clear-sky contamination. Repeating the analysis for individual VZA bins not only yielded generally similar results to the above cross-swath means but also indicated that sensitivity to χ and SZA, that is, the spread of curves, was more pronounced at oblique views than at nadir/moderate views.
A caveat worth noting is that the χ parameter, being calculated from 1-D VNIR optical thicknesses, is itself subject to 3-D radiative effects and measures apparent rather than true heterogeneity. Consequently, χ is not completely independent of, but broadly correlated with, SZA. Analyzing synthetic 1-D VNIR retrievals based on large eddy simulation (LES) input fields, Seethala [2012] found satellite-retrieved χ underestimating heterogeneity at high to moderate sun but overestimating it at low sun. Such biases notwithstanding, retrieved heterogeneity was well correlated with the LES truth. Therefore, χ derived from MODIS retrievals is still considered here a useful relative measure of scene heterogeneity.
3.2. VZA Dependence of Global Annual Means
The VZA dependence of global annual mean retrievals, averaged over all χ and SZA, is plotted in Figure 4. When all cloud fractions were considered (Figure 4a), the mean AMSR-E LWP showed minor view angle variations within ±5% of the nadir value (black diamonds). Retrievals tended to be slightly larger in the backscatter than forward scatter direction, but otherwise, VZA dependence was small and should not be overinterpreted. VZA variations were larger and more systematic in unscaled MODIS CLWP (red crosses). Retrievals increased/decreased with view angle for backward/forward scatters up to 8% relative to nadir in both directions. As a result, when backward and forward scatter values were averaged together, as in Maddux et al. [2010], MODIS CLWP showed practically no VZA dependence (dotted red line).
Figure 4.
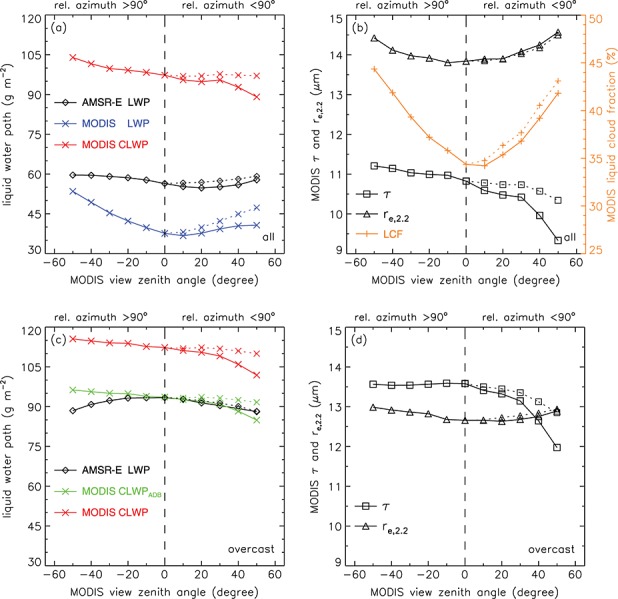
View zenith angle dependence of global annual mean (a and c) AMSR-E LWP and MODIS LWP and CLWP and (b and d) MODIS optical thickness, 2.2 µm effective radius, and liquid cloud fraction (LCF), for (Figures 4a and 4b) all domains and (Figures 4c and 4d) overcast domains with LCF = 95–100%. The green curve corresponds to assuming linearly stratified (“adiabatic,” ADB) water content in MODIS CLWP, while the dotted curves are VZA bin means over both forward and backward scattering relative azimuths.
View angle variations in corresponding MODIS optical thickness and effective radius are given in Figure 4b. Optical thickness showed a slight, less than 4% increase with VZA in the backscatter direction but decreased up to 14% in the forward scatter direction, especially for VZA > 30° (black squares). Effective radius, on the other hand, mildly increased with VZA in both directions, exhibiting a characteristic ∪ shape (black triangles). For global mean re, the ∪ was quite symmetric about the nadir value, with a maximum increase of 5–6% for both backward and forward scatter. When calculating CLWP, the increase of re with VZA reinforced the similar increase of τ in the backscatter direction but partially canceled out the strong decrease of τ in the forward scatter direction.
The observed VZA dependence of mean optical thickness could be qualitatively explained as the combination of the three factors identified in Liang and Di Girolamo [2013], although quantifying the individual contribution of the various effects would be difficult. In the forward scatter direction, the decrease in τ due to both the concavity and bump RAZ factors dominated the increase due to the gap factor. In the backscatter direction, however, the τ decrease due to the concavity factor was canceled out and even overcompensated by the increase due to the bump RAZ factor, with perhaps a slight positive contribution from the gap factor as well. As we later show, the minor impact of the gap factor on global mean optical thickness was not surprising, because this factor was only prominent for the most heterogeneous scenes (χ < 0.5) and largest sun angles (SZA > 70°), which constituted a mere 3–8% of our data.
In Figure 4b we also plotted the fraction of successful liquid cloud retrievals, hereafter referred to as liquid cloud fraction (LCF, orange pluses). Cloud fraction is well known to increase with VZA mainly due to increased viewing of cloud sides, longer slant paths, and larger pixel sizes at oblique angles, yielding a markedly ∪-shaped LCF curve in our data set. Compared to near-nadir values, LCF showed a 22%/29% relative increase at the most oblique forward/backward scatter view angles, which represented considerably larger VZA variations in cloud fraction than in τ or re. The global mean LCF was a minimum at VZA ≈ 10° rather than at nadir. Also note that the backward-forward scatter asymmetry in our LCF data was opposite to that found in MISR and MODIS total (liquid + ice) cloud fraction by Zhao and Di Girolamo [2004] and Zeng et al. [2011], respectively, where the increase was larger in the forward scatter than backscatter direction. A detailed analysis of MODIS cloud detection is beyond the scope of this paper, but we suppose that this discrepancy was likely caused by the exclusion of ice clouds from our data, the potential VZA dependence of cloud phase identification, the different “scan” pattern and sun/view geometry sampling of MISR and MODIS, and the use of successful retrieval fraction rather than strict cloud fraction here.
The pronounced VZA dependence of LCF dominated that of scaled MODIS LWP (blue crosses in Figure 4a). The strong increase of LCF with VZA added to smaller increases in τ and re in the backscatter direction, and overcompensated the decreasing τ in the forward scatter direction. This led to a ∪-shaped MODIS LWP curve with a sharp asymmetry about nadir: the value at the most oblique view angle increased by 42% in the backscatter and 8% in the forward scatter direction. In contrast to MODIS CLWP, LCF-scaled MODIS LWP was smaller than but somewhat more comparable to AMSR-E LWP, at least in an absolute sense. As discussed earlier, a significant portion of the remaining mean discrepancy could be attributed to a positive bias in microwave LWPs over the most broken cloud scenes, caused by uncertainties in surface emissivity (wind speed dependence) and gaseous absorption of the forward model [Greenwald et al., 2007; Greenwald, 2009; Seethala and Horváth, 2010], as well as to the clear-sky restoral in Collection 5 MODIS data that excludes retrievals over partly cloudy pixels at cloud edges and in thin clouds.
The results for overcast domains with LCF = 95–100% are given in Figures 4c and 4d. (Here LWP ≈ CLWP.) For this data subset, the VZA dependence of AMSR-E LWP became bell shaped (∩), but the magnitude of variation was within ±5% of the nadir value as before. The VZA variations of MODIS retrievals were slightly reduced but remained generally similar to the “all” case. The operational MODIS CLWP showed a maximum 2% increase in the backscatter and a 10% decrease in the forward scatter direction relative to nadir and had an overall positive bias compared with microwave retrievals. This MODIS overestimation, however, could be almost completely eliminated by replacing the operational homogeneous vertical stratification with linearly increasing water content in the VNIR parameterization (green crosses in Figure 4c). Using the linear stratification assumption MODIS CLWP agreed well with AMSR-E LWP not only for cross-swath means—90 g m−2 for both as already found by Seethala and Horváth [2010]—but also for individual VZA bins. Agreement was particularly good in the forward scatter direction, but even at the most oblique backscatter VZA, the difference was no more than 8%.
MODIS optical thickness exhibited a pronounced (12%) decrease in the forward scatter direction similar to the all case. In the backscatter direction, however, the weak increase observed for the all case disappeared and retrievals became very consistent with VZA. Effective radius kept its mild ∪ shape but with a reduced, maximum 3% increase with view angle. The main change in MODIS overcast retrievals was not of shape but of overall magnitude. Optical thickness increased by ∼2.5 and effective radius decreased by 1–1.5 µm compared to all clouds. Some of these changes no doubt reflected genuine differences between cloud types and geographic regions; however, as later sections demonstrate, τ and re had strong and systematic variations with heterogeneity and SZA, indicating significant 3-D effects as well.
3.3. Stratification of VZA Dependence by Scene Heterogeneity
The VZA dependence of the various retrievals stratified by scene heterogeneity but averaged over all SZAs is given in Figure 5. (A three-dimensional surface representation of results for finer χ bins of 0.02 is shown in Figure S1 in the supporting information.) In order to help compare the shapes of microwave and VNIR VZA variations, we also plotted the nadir-relative AMSR-E LWP and MODIS CLWP and LWP in Figure 6; that is, AMSR-E and MODIS oblique retrievals were here normalized by their corresponding nadir value.
Figure 5.
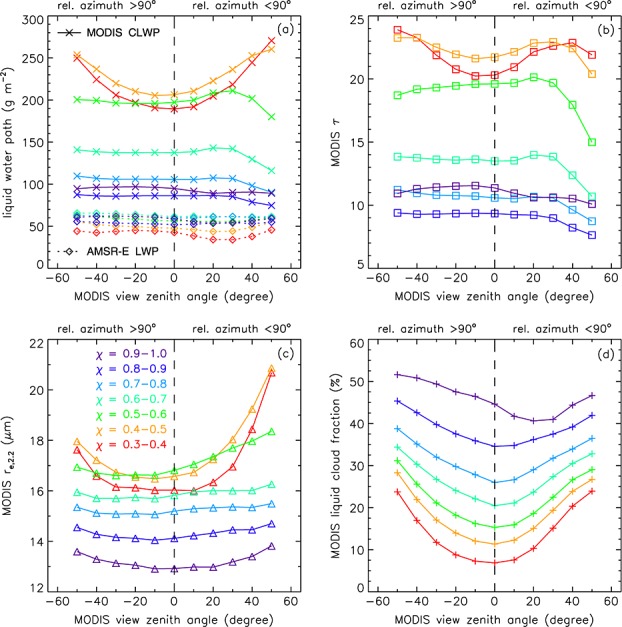
View zenith angle dependence of (a) AMSR-E LWP and MODIS CLWP and MODIS (b) optical thickness, (c) 2.2 µm effective radius, and (d) liquid cloud fraction for various heterogeneity bins.
Figure 6.
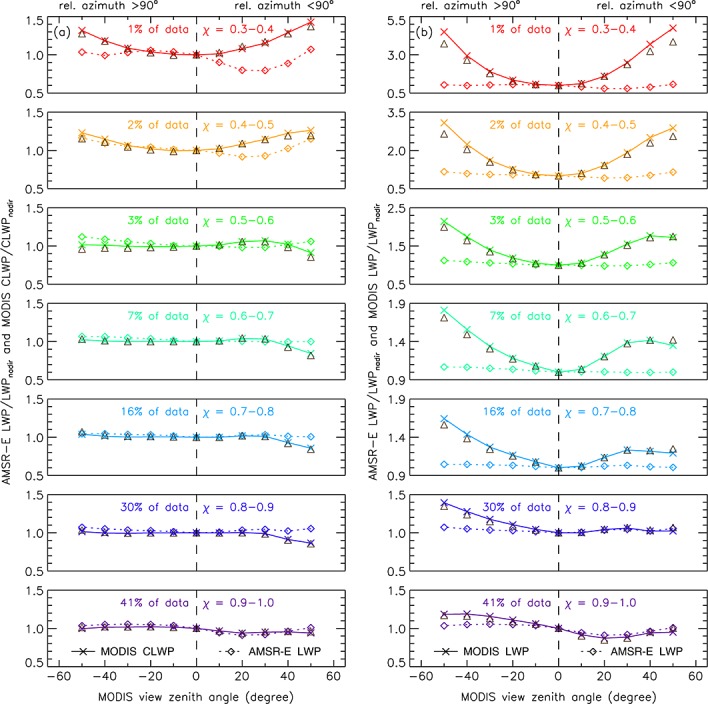
Nadir-normalized view zenith angle dependence of (a) MODIS CLWP and AMSR-E LWP and (b) MODIS LWP and AMSR-E LWP for various heterogeneity bins. Triangles mark the sum of nadir-normalized variations in MODIS (a) τ and re, (b) τ, re, and LCF. The percentage of data within a χ bin is also indicated. Note the varying ordinate scale in Figure 6b.
The AMSR-E LWPs were within 40–70 g m−2 and tended to decrease somewhat with increasing heterogeneity (Figure 5a). Retrievals were fairly consistent across VZAs, variations being within ±10% of the nadir value for most χ bins (Figure 6a). The magnitude of VZA variations reached 20% only in the most heterogeneous scenes (χ < 0.5). The two smallest χ bins, however, comprised a mere 3% of data between them; therefore, the stronger VZA dependence of AMSR-E LWPs was likely indicative of sampling uncertainties rather than genuine cross-swath variations.
The MODIS CLWPs showed a strong increase with heterogeneity (Figure 5a), which, however, was compensated by an equally strong decrease in cloud fraction (Figure 5d). As a result, the LCF-scaled MODIS LWPs (not shown) were generally smaller than AMSR-E LWPs and exhibited a similar decreasing tendency with heterogeneity. (This simply indicated that broken clouds were usually less homogeneous and contained less liquid water than more uniform scenes.) More importantly, MODIS CLWPs were also quite consistent, particularly so in the backscatter direction, and showed nadir-relative variations similar to AMSR-E LWPs for most χ bins and VZAs (Figure 6a). For the most homogeneous clouds with χ = 0.9–1.0 constituting 41% of our data, relative variations in MODIS CLWP and AMSR-E LWP were in excellent agreement at all view angles. For χ > 0.6, in general, VZA variations in MODIS CLWP were even smaller, typically ±5%, than in AMSR-E LWP, except at the two most oblique forward scatter VZAs where MODIS values decreased by 10–15%. Note that the distinct MODIS CLWP decrease at oblique forward scatter views was already present in the second most homogeneous cloud bin with χ = 0.8–0.9. The VZA variations in MODIS CLWP became substantial only in the two most heterogeneous bins (χ < 0.5), indicating a marked and slightly asymmetric ∪ shape with a maximum increase of 23–32% in the backward and 26–43% in the forward scatter direction. The discrepancy between the relative shapes of MODIS CLWP and AMSR-E LWP VZA dependence was also largest for these two smallest χ bins, especially in the forward scatter direction.
The VZA dependence of MODIS CLWP was caused by the interplay between that of optical thickness and effective radius, with the former being the primary driver. MODIS optical thickness rapidly increased with heterogeneity (Figure 5b) and had VZA variations generally similar to CLWP. For χ > 0.5, τ was either constant or showed only small, less than 5% increases or decreases with VZA in the backscatter direction. This indicated that the decrease due to the concavity factor was of comparable magnitude to the increase due to the combined effects of the RAZ-bump and gap factors. In the forward scatter direction, τ showed a pronounced decrease at the most oblique VZAs, whose magnitude increased from 10% to 25% between the most homogeneous bin and χ = 0.5–0.6. The characteristic τ decrease in oblique forward scatter directions indicated the dominance of the RAZ-bump and concavity factors, which the weak gap factor could not counteract in most χ bins. As heterogeneity increased, so did the influence of the gap factor, resulting in mostly ∪-shaped τ curves for χ < 0.5. However, for the most oblique forward scatter VZA, the RAZ-bump and concavity factors remained stronger than the gap factor, leading to a τ decrease even in the most heterogeneous clouds. The opposite effects of the RAZ-bump factor in the forward scatter direction, where it diminishes the gap factor, and in the backscatter direction, where it adds to the gap factor, thus explains the slight backward-forward scatter τ asymmetry observed for the smallest χ values.
MODIS effective radius also systematically increased with heterogeneity, similar to optical thickness (Figure 5c). Its VZA dependence always showed a ∪ shape, which was weak in most χ bins but became pronounced and strongly asymmetric, favoring the forward scatter direction, in the most heterogeneous clouds. For example, in the smallest χ bin, re increased by a maximum of 10% in the backscatter and 30% in the forward scatter direction. These results were in qualitative agreement with the modeling study of Kato et al. [2006], which showed domain-averaged retrieved effective radius increasingly overestimating the truth as horizontal inhomogeneity increased, with the largest errors occurring in oblique forward scatter directions. Although Kato et al. [2006] considered the 3.7 µm rather than the operational 2.2 µm effective radius and analyzed only three cloud scenes at two SZAs (30° and 50°), the VZA variation of their simulated retrievals was also roughly ∪ shaped for stratus/stratocumulus, as found here (differences between the three MODIS re values are further discussed in section 3.5).
Effective radius biases due to the three factors influencing optical thickness retrievals are as yet uncharacterized, and thus, 3-D effects on re are usually interpreted within the simpler framework of shadowing versus illumination primarily caused by cloud top variations (which, however, is analogous to the RAZ-bump factor). As pointed out by Marshak et al. [2006], shadowing tends to increase re more than illumination decreases it, leading to an overall positive bias in domain mean effective radius, consistent with our results. Effects similar to shadowing/illumination can also result from horizontal τ variations. Considering 1-D re retrievals for an idealized flat-topped cloud field with a step function like increase in optical thickness, Zhang and Platnick [2011] found underestimation where reflectivity was enhanced and a larger overestimation where it was reduced by horizontal photon transport. Interestingly, they also noted elevated re values over the sunward transition zone near the “bright” (enhanced reflectivity) cloud region, which further increased the net positive bias in domain mean re.
The forward-backward scatter re asymmetry observed in the most heterogeneous clouds could perhaps be explained by a similar asymmetry in the fraction of “shadowed” cloud sides. Smaller χ values (larger apparent heterogeneities) tended to be more often retrieved at larger SZAs, when MODIS observations were closer to the side scattering plane (see Figure 2). Therefore, a considerable number of shadowed cloud sides were present in oblique views for both backscatter and forward scatter azimuths, but with a higher shadowed fraction for the latter. Combined with the dominance of shadowing over illumination, this could explain the asymmetric ∪ shape of effective radius VZA variations.
When calculating CLWP, the weak VZA dependence of effective radius had a small effect for χ > 0.6, but the overall increase of re with heterogeneity added to that of optical thickness. The small re increases with VZA could cancel out comparably small τ decreases in the backscatter direction, leading to consistent CLWPs with view angle, while in the forward scatter direction they somewhat reduced the stronger τ decreases. In the most heterogeneous clouds (χ < 0.5), however, the effective radius increase with VZA had a significant positive contribution to the ∪ shape of CLWP, even counterbalancing the optical thickness decrease at the most oblique forward scatter VZAs.
As mentioned previously, liquid cloud fraction showed a strong general decrease with increasing heterogeneity (Figure 5d). A similar correlation between MODIS-retrieved χ and LCF was also observed by Oreopoulos and Cahalan [2005]. The VZA dependence of LCF always had a ∪ shape with a slight asymmetry favoring the backscatter direction and depth increasing with heterogeneity. Note that nadir-relative view angle variations in LCF considerably exceeded those in τ or re. As a result, LCF had the largest effect on the shape of the MODIS LWP curve, especially for more heterogeneous clouds (Figure 6b). For χ > 0.8, the LCF increase with VZA in the forward scatter direction canceled out the corresponding CLWP decrease and led to a better agreement between the shapes of MODIS LWP and AMSR-E LWP in the forward scatter than backscatter direction, while the opposite was true regarding MODIS CLWP and AMSR-E LWP. As heterogeneity increased, LCF-scaled MODIS LWP exhibited progressively larger and symmetric ∪-shaped VZA variations. In the two most heterogeneous bins, MODIS LWP increased from nadir to the most oblique view angles by a factor of 3–5, although its absolute value was generally small.
As indicated by the triangles in Figure 6, nadir-relative variations in MODIS domain mean CLWP and LWP could be well approximated by the sum of the corresponding nadir-relative variations in τ, re, and LCF. The small discrepancies were due to the covariance between retrieved cloud parameters.
Results for overcast domains with LCF = 95–100% are plotted in Figures S2a–S2c and S3a in the supporting information (here LWP ≈ CLWP). These domains constituted 18% of all data and spanned a narrower χ range at higher values of 0.6–1.0. As before, MODIS τ and CLWP increased with heterogeneity but for a given χ bin they were larger than the corresponding all values. AMSR-E CLWP also generally increased with heterogeneity and was larger than in the all case. (In the all case, however, AMSR-E LWP and LCF-scaled MODIS LWP decreased with heterogeneity due to broken clouds, which tended to be considerably more heterogeneous and contain less water than overcast clouds.) MODIS τ and CLWP showed the characteristic decrease in oblique forward scatter directions and, for the more heterogeneous scenes, an increase with VZA in the backscatter direction, suggesting the dominance of the RAZ-bump factor. The most significant difference to the all results was the much-reduced variation of re with χ. Overcast effective radius retrievals were very consistent not only with VZA but also with heterogeneity, typically being within 13 ± 0.5 µm, while over the same χ range re increased from 13 to 16 µm when broken scenes were also considered.
The relative shapes of the MODIS CLWP and AMSR-E CLWP curves generally agreed better for overcast scenes than for all scenes. AMSR-E CLWP showed weak ∩-shaped cross-swath variations. For the most homogeneous clouds (75% of all overcast domains), nadir-relative variations in MODIS CLWP and AMSR-E CLWP were in excellent agreement at all view angles. For more heterogeneous clouds, the agreement was better in the forward scatter direction and the largest discrepancies occurred at oblique backscatter angles due to an increase in the MODIS retrievals. Note that for overcast scenes, the absolute values of the operational (vertically homogeneous) MODIS CLWP were also more comparable to those of AMSR-E CLWP, and with the assumption of linearly stratified water content (amounting to a 17% reduction in MODIS CLWP), the two techniques were unbiased relative to each other in a global mean sense (cf. Figure 4c).
3.4. Stratification of VZA Dependence by SZA
The VZA dependence of the various retrievals stratified by solar zenith angle but averaged over all heterogeneity values is given in Figure 7, while the corresponding nadir-relative AMSR-E LWP, and MODIS CLWP and LWP are plotted in Figure 8. (A three-dimensional surface representation of results for finer SZA bins of 2° is shown in Figure S4 in the supporting information).
Figure 7.
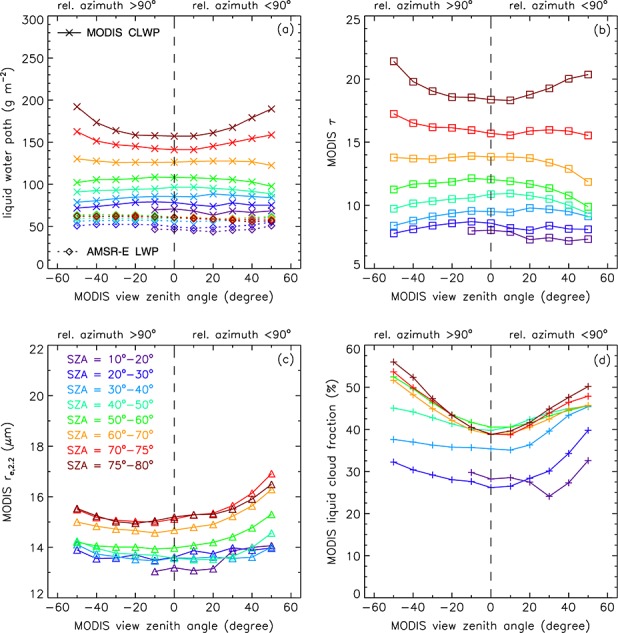
Same as Figure 5 but for various SZA bins.
Figure 8.
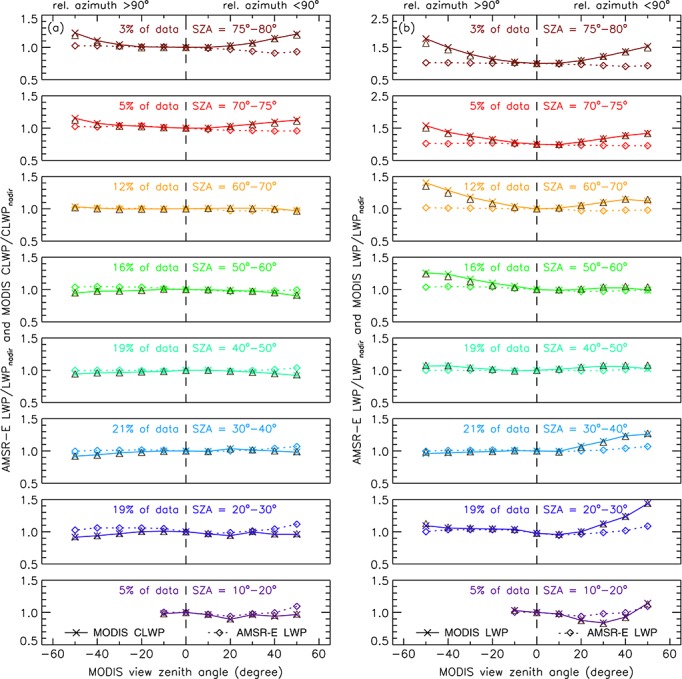
Same as Figure 6 but for various SZA bins.
The AMSR-E LWPs varied between 40 and 70 g m−2 and tended to increase somewhat with increasing solar zenith angle, especially between SZA = 10°–50°, probably indicating slight latitudinal variations (Figure 7a). The microwave retrievals were fairly consistent with VZA as variations were always within ±10% of the nadir value (Figure 8a).
The MODIS CLWPs steadily increased with SZA, but with a sensitivity smaller than that found for χ (Figure 7a). Because cloud fraction was also generally larger at oblique sun (Figure 7d), the LCF-scaled MODIS LWPs (not shown) exhibited a similar increasing tendency with solar zenith angle. With the exception of the most extreme SZAs, MODIS CLWPs were fairly consistent with VZA not only in the backscatter but also in the forward scatter direction. The marked decrease of CLWP at the largest forward scatter VZAs found in χ-binned results was absent in SZA-binned retrievals. MODIS CLWP usually had a weak ∩ shape with a decrease no more than 10% of the nadir value. Larger VZA variations, a maximum increase of 15–22% in the backward and 12–21% in the forward scatter direction, were only observed in the two largest SZA bins, which showed a distinct ∪ shape but represented only 8% of our data (Figure 8a). (Note that the ∪ shape was less pronounced in the most oblique SZA bins than in the most heterogeneous χ bins.) The overall agreement between the nadir-relative variations in AMSR-E LWP and MODIS CLWP was best for 30° ≤ SZA ≤ 70° and particularly for SZA = 60°–70°.
The good VZA consistency of MODIS CLWP—including in the forward scatter direction—for all but the most extreme SZAs was the result of cancelation between the VZA dependence of optical thickness and that of effective radius. Optical thickness steadily increased with SZA but not as strongly as it did with χ (Figure 7b). Compared to χ-binned results, SZA-binned τ showed larger variations (decreases) in the backscatter direction but smaller decreases in the forward scatter direction. The VZA-τ curve, thus, had a ∩ shape with a maximum decrease of 7–12% in the backscatter and 5–18% in the forward scatter direction, depending on SZA. This indicated the dominance of the concavity factor for SZA ≤ 60°. The RAZ-bump factor added to the concavity factor in the forward scatter direction but diminished it in the backscatter direction, explaining the slight forward-backward scatter asymmetry in the τ decrease with VZA for moderate SZAs. As SZA increased, so did the strength of the gap factor, resulting in compensation of the concavity factor and, hence, consistent τ retrievals in the backscatter direction for SZA = 60°–70°, and a generally ∪-shaped VZA-τ curve for the two most oblique SZA bins. The ∪ shape had a small backward-forward scatter asymmetry, because the RAZ-bump factor added to the gap factor in the backscatter direction but diminished it in the forward scatter direction. We also note a hint of slightly reduced optical thicknesses in the rainbow direction, which was encountered at forward scatter VZA near +20° for SZA ≤ 30° and VZA near +10° for 30° ≤ SZA ≤ 40°. Plotting retrievals as a function of scattering angle clearly confirmed a drop in MODIS τ and CLWP at the rainbow angle of ∼139°, likely caused by an overestimated re as suggested in previous studies [Buriez et al., 2001; Zeng et al., 2012; Liang and Di Girolamo, 2013].
The mean MODIS effective radius also generally increased with SZA and always had a ∪ shape, which became more asymmetric toward the forward scatter direction at more oblique sun (Figure 7c). As discussed earlier, such VZA dependence emerged due to the dominance of shadowing over illumination combined with a forward scatter-backscatter asymmetry in shadowed cloud fraction in oblique but close to side scattering directions at low sun. The overall increase in re and the depth of its ∪ shape, however, were considerably smaller in SZA-binned retrievals than in χ-binned retrievals. The maximum re increase with VZA was 2–5% in the backscatter and 3–11% in the forward scatter direction, depending on sun angle. For SZA ≤ 70° the ∪ shape of effective radius largely compensated for the ∩ shape of optical thickness, resulting in CLWPs which were approximately constant with view angle (but which increased with SZA due to a general increase in re and τ). At the lowest sun, however, both re and τ increased with VZA and, acting in concert, produced the ∪-shaped VZA variations in CLWP.
The MODIS liquid cloud fraction also systematically varied with SZA, but the range of variation was significantly narrower than in χ-binned data due to larger values at the lower end (Figure 7d). LCF rapidly increased with SZA at all view angles for SZA ≤ 50°, above which, however, LCF showed much-reduced sensitivity to sun angle especially at nadir/near-nadir VZAs. This was probably indicative of geographic variations in cloud type and spatial structure. Smaller SZAs corresponded to lower latitudes characterized by more frequent broken clouds such as trade wind Cu, while larger SZAs corresponded to higher latitudes dominated by more extensive and uniform Sc fields with less overall and view angle variation in cloud fraction. As before, LCF systematically increased with VZA but with a backward-forward scatter asymmetry that depended on SZA, while in χ-binned data, LCF values were always slightly larger in the backscatter direction as discussed previously. Here for SZA < 40° LCF increased faster in the forward scatter than backscatter direction, for SZA = 40°–50° the VZA-LCF curve was symmetric, and for SZA > 50° LCF was larger in the backscatter direction. These results suggest that the exact nature of the backward-forward scatter asymmetry in LCF is a complicated function of sun-view geometry and cloud heterogeneity and also depends on the choice of binning. We finally note that for the highest sun, LCF was minimum at forward scatter VZA = 20° rather than at nadir. Similarly, for the largest χ values, which tend to occur at the highest sun, the LCF minimum was also at forward scatter VZA = 20°–30° (Figure 5d).
As before, nadir-relative variations in LCF were larger than those in τ or re and, thus, played the major role in determining the shape of VZA variations in LCF-scaled MODIS LWP (Figure 8b). For SZA < 40° VZA variations in MODIS LWP and AMSR-E LWP agreed well in the backscatter direction, but in the forward scatter direction, MODIS LWP showed a significant increase unlike AMSR-E LWP. For SZA = 40°–50° the VNIR and microwave LWPs both had small VZA variations and were consistent at all view angles. For SZA > 50° differences between the VZA variation of MODIS LWP and AMSR-E LWP were larger in the backscatter direction, reflecting the switch in the backward-forward scatter asymmetry of LCF, and the MODIS LWP curve became increasingly ∪ shaped. Note, however, that the maximum MODIS LWP increase from nadir to the most oblique view angles was significantly smaller in SZA-binned data (a factor of 2) than in χ-binned data (a factor of 3–5).
Complementing the above results averaged over all χ, Figure S5 in the supporting information gives the VZA dependence of the various retrieved parameters as a function of SZA separately for the most homogeneous (0.92 < χ ≤ 1.00), medium heterogeneous (0.82 < χ ≤ 0.92), and most heterogeneous (χ ≤ 0.82) tercile of domains. These plots demonstrate that SZA variations, in the overall magnitude and/or the VZA dependence of MODIS retrievals, tended to become more pronounced as heterogeneity increased. As before, the VZA dependence of effective radius was always ∪ shaped, while that of optical thickness and CLWP was slightly ∩ shaped in most cases. Distinctly ∪ shaped VZA variations in optical thickness and CLWP were only observed at the largest SZAs in the most heterogeneous clouds.
Results for overcast domains are plotted in Figures S2d–S2f and S3b in the supporting information. As before, MODIS τ and re both increased with SZA, but the former was larger while the latter was smaller for overcast cases. Due to this compensation, overcast MODIS CLWP values were comparable to the all values and also increased with SZA. Up to SZA = 30°–40° MODIS CLWP was in good absolute agreement with AMSR-E CLWP, especially when assuming linearly stratified water content. For larger SZAs, however, MODIS CLWP rapidly increased while AMSR-E CLWP leveled off around 90 g m−2, as previously noted by Seethala and Horváth [2010]. The VZA dependence of MODIS τ and CLWP was similar to the all case, the main difference being the absence of the pronounced ∪ shape at the most oblique sun, which was the consequence of a weaker gap factor in overcast than broken scenes. The VZA variations in re were significantly weaker, even at low sun, than in all retrievals, although they still had a mild ∪ shape slightly asymmetric toward the forward scatter direction. The relative shapes of the MODIS CLWP and AMSR-E CLWP curves were in better agreement than for all domains, including the largest SZA bins.
In general, stratification of our comparison indicated that the absolute value of MODIS retrievals as well as the relative magnitude of their VZA variations had a stronger correlation with χ than SZA. This is not surprising considering that the χ parameter is computed from 1-D plane-parallel optical thickness, which is subject to 3-D effects that tend to increase with SZA. Therefore, the SZA dependence is implicitly included in χ, which makes χ a better predictor of the significance of 3-D effects.
3.5. VZA Dependence of MODIS 3.7 µm and 1.6 µm Effective Radius
Our focus is the operational MODIS product based on the 2.2 µm channel; however, given the renewed interest in the information content of the various water-absorbing MODIS bands here, we investigate effective radius derived from the 3.7 µm and 1.6 µm channels as well. Lebsock et al. [2011] found that re,3.7 was less sensitive to the presence of large precipitation/drizzle drops and, combined with an assumed adiabatic stratification, minimized the bias between MODIS CLWP and CloudSat attenuation even in nonprecipitating clouds. Zhang and Platnick [2011] and Zhang et al. [2012] showed that 3-D effects and the “plane-parallel re bias” (attributable to horizontal subpixel τ variability) both tended to be smaller for re,3.7 than re,2.2 or re,1.6. In addition, Painemal et al. [2013] observed that re,3.7 was insensitive to cloud fraction variations, while re,2.2 increased up to 5 µm with decreasing cloud fraction in southeast Pacific marine stratocumulus. Therefore, re,3.7 might be expected to exhibit smaller variations with sun/view geometry and cloud inhomogeneity.
The comparison between the VZA dependencies of the three different effective radii is given in Figure 9. On average, re,3.7 < re,2.2 < re,1.6, as previously noted by Seethala and Horváth [2010] and Zhang and Platnick [2011]. In contrast, Grosvenor and Wood [2014] found the opposite mean relationship, re,3.7 > re,2.2 > re,1.6, for homogeneous near-overcast (LCF > 90%) Arctic stratocumulus observed at SZA > 50°. The latter work used the standard deviation of cloud top temperature to characterize heterogeneity, which suggests that our results might have been caused by cloud top bumpiness. In our data set all three re retrievals increased with heterogeneity and SZA (even in overcast scenes, as shown for re,2.2 in Figure S2 in the supporting information). This again is the opposite of Grosvenor and Wood's [2014] findings, where re values decreased with both SZA and cloud top temperature variability. Using yet another heterogeneity index, the normalized standard deviation of 0.86 µm reflectances or Hσ [Liang et al., 2009], Zhang and Platnick [2011] found a sharp increase with heterogeneity in re,1.6 and re,2.2 for Hσ > 0.3, but no obvious correlation between re,3.7 and heterogeneity. Painemal et al. [2013], on the other hand, found both re,2.2 and re,3.7 increasing with Hσ for overcast stratocumulus scenes, although re,2.2 increased more than re,3.7. Reconciling these divergent results will require further work that considers the effect of the different sampling strategies and cloud heterogeneity metrics used in the above studies.
Figure 9.
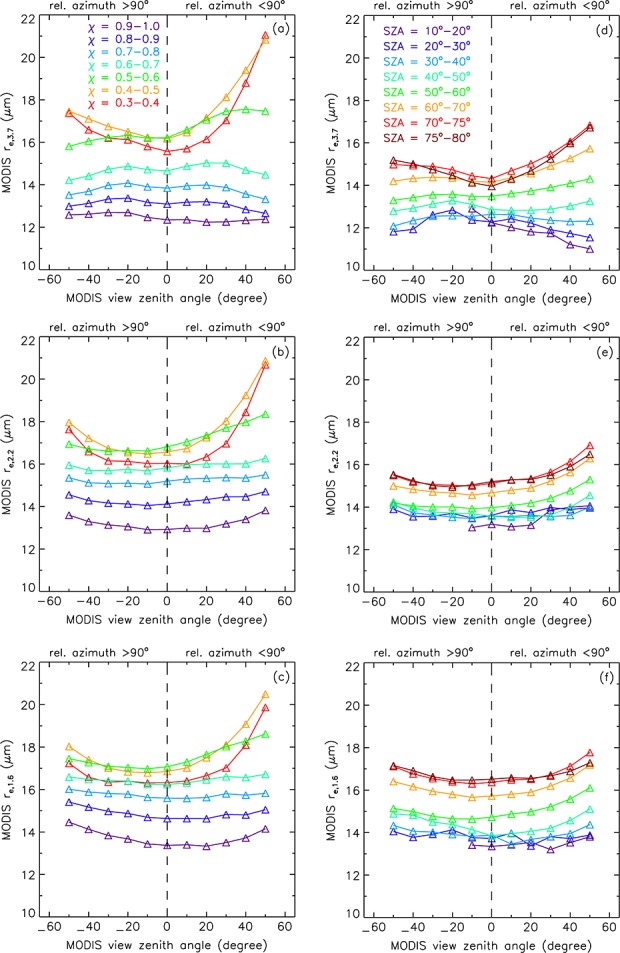
View zenith angle dependence of MODIS (a and d) 3.7 µm, (b and e) 2.2 µm, and (c and f) 1.6 µm effective radius for (Figures 9a–9c) various heterogeneity bins and (Figures 9d–9f) various SZA bins.
VZA variations in re,1.6 were fundamentally similar to those in re,2.2. VZA variations in re,3.7 were of comparable magnitude; however, they were ∩ shaped for χ > 0.6 and SZA < 40° as opposed to ∪ shaped variations in the other two channels. For the most heterogeneous clouds and largest SZAs, re,3.7 showed the same pronounced and asymmetric ∪ shape present in re,2.2 and re,1.6. Based on these results, the 3.7 µm channel does not offer any advantage over the other two bands, at least for 0.25° domain means. To the contrary, whereas the ∪ shaped VZA variations of re,2.2 and re,1.6 partly canceled out the ∩-shaped variations of τ and, thus, yielded fairly consistent cross-swath CLWPs over a wide range of SZA and χ, re,3.7 reinforced the ∩-shaped variations of τ and increased the VZA dependency of MODIS CLWP. Consistent with re,3.7 decreasing with VZA and being generally smaller than re,2.2 as found here, Painemal et al. [2013] observed systematic underestimations in MODIS CLWP3.7 but negligible biases in MODIS CLWP2.2 relative to AMSR-E CLWP for moderately heterogeneous stratocumulus domains. Regarding the potential benefit of the 3.7 µm band, we are also in agreement with Grosvenor and Wood [2014], who found that re,3.7 is more prone to retrieval biases at large SZAs than the other two re values.
Resolving the ∩-shaped behavior of re,3.7 for weakly/moderately heterogeneous clouds and high sun is beyond the scope of this paper, but perhaps, a concavity factor, analogous to the one for optical thickness, also exists for effective radius and dominates the 3.7 µm channel under certain conditions. We note that VZA variations in re,3.7 retrievals simulated by Kato et al. [2006] using three LES (large eddy simulation) scenes were ∩ shaped for broken trade wind cumulus but ∪ shaped for stratus/stratocumulus, although no interpretation of the different results was given. This indicates that domain mean retrieval biases also depend on cloud type. A satisfactory explanation will require more comprehensive simulation studies that consider a wide range of cloud scenes and sun-view geometries.
3.6. Geographic Variation of Annual Mean VZA Dependence
Regional variations in the general shape of annual mean VZA dependence are shown in Figures 10 and 1. Here we plotted the quadratic coefficient c of the second-order polynomial (equation (2)) fitted to the view angle variations of the various retrievals. Results represent the VZA dependence averaged over the range of SZAs and cloud heterogeneities encountered within 5° × 5° gridboxes in the course of a year. Positive and negative c values correspond, respectively, to ∪ shape and ∩ shape, while the magnitude of c indicates the strength of VZA variations. (A second-order polynomial is a poor approximation of VZA variations when the RAZ-bump factor dominates; however, this case was uncommon for the annual gridbox means presented here and the parabolic fit was formally significant at the 95% level if VZA bin standard deviations were used as retrieval uncertainties.)
Figure 10.
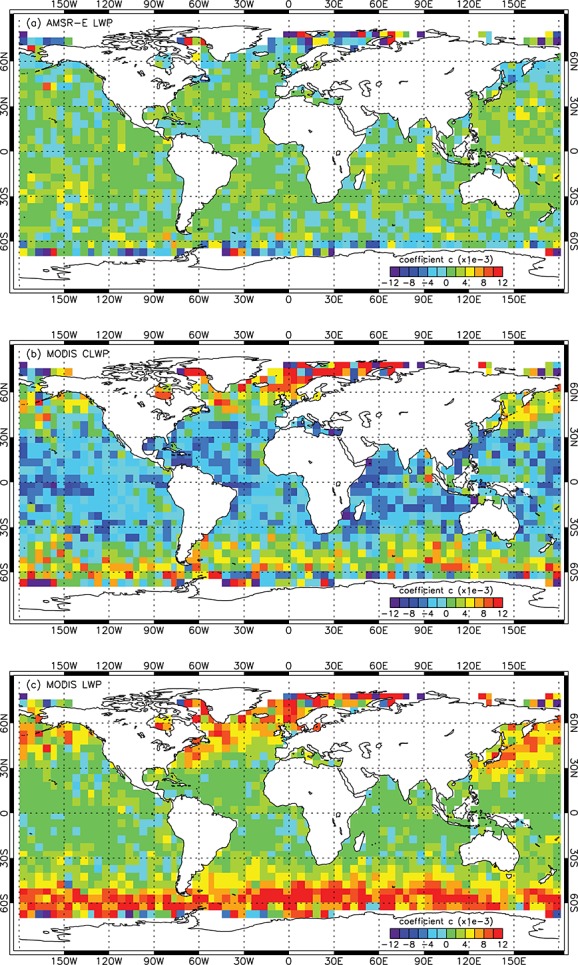
Geographic distribution of the quadratic coefficient c of the second-order polynomial fit to the annual mean VZA dependence of (a) AMSR-E LWP, (b) MODIS CLWP, and (c) MODIS LWP. The sign and magnitude of c indicate the general shape (positive ∪ and negative ∩) and strength of view angle variations, respectively.
The AMSR-E LWP showed generally weak cross-swath dependence with little regional variations, but the ∪ shape was slightly more frequent than the ∩ shape (Figure 10a). Larger cross-swath variations only occurred at the highest latitudes (>60° N/S), perhaps indicating the occasional failure of the sea ice mask in microwave retrievals [Wentz and Meissner, 2000]. The VZA dependence of MODIS CLWP, on the other hand, showed a sharp regional contrast (Figure 10b). In the tropics/subtropics (30°S–30°N) the ∩ shape dominated, while at middle and polar latitudes the ∪ shape was prevalent. The VZA dependence of LCF-scaled MODIS LWP was ∪ shaped basically everywhere but showed a similar regional contrast in strength with middle to high latitudes experiencing significantly more pronounced ∪ shapes than the tropics/subtropics (Figure 10c).
The regional VZA variations of MODIS CLWP and LWP can be explained by those of their components: τ, re, and LCF. In accordance with our results shown in Figure 7b, the VZA dependence of optical thickness was predominantly ∩-shaped for high/moderate sun within 45°S–45°N (Figure 11a). Pronounced ∪ shape was only observed for the most oblique sun in the polar regions. The VZA dependence of effective radius, on the other hand, was ∪ shaped in the vast majority of areas, in general agreement with our earlier results (Figure 11b). The VZA dependence of LCF also showed a ∪ shape in most regions and was usually stronger than that of either τ or re (Figure 11c). The most pronounced ∪ shapes occurred over the southern oceans around 60°S. Significant ∩-shaped variation in LCF was only observed in the Arctic ocean, which, perhaps, indicated seasonal cloud detection artifacts due to changes in sea ice cover.
Figure 11.
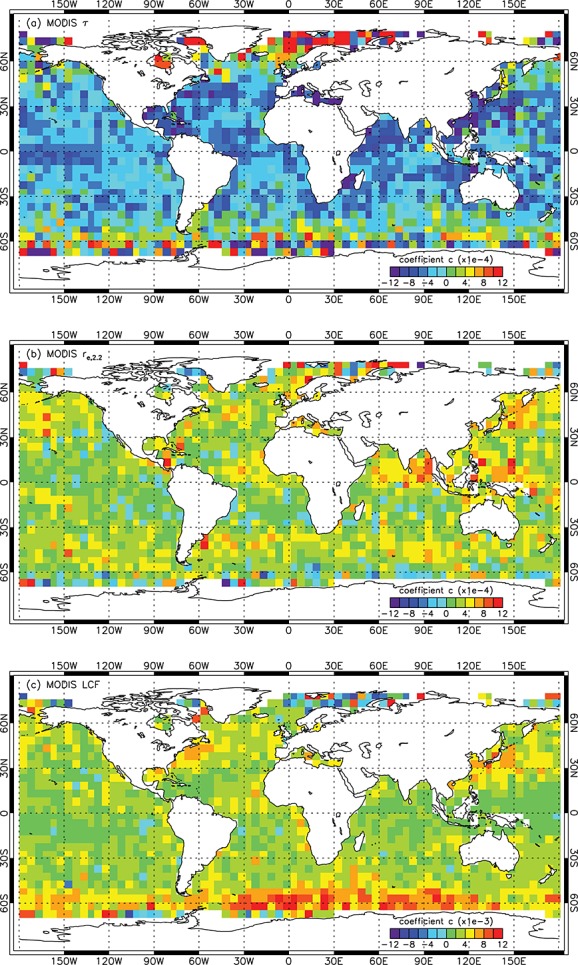
Same as Figure 10 but for MODIS (a) optical thickness, (b) 2.2 µm effective radius, and (c) liquid cloud fraction. Note the different scale for LCF.
As a result, in the tropics/subtropics the ∩ shape of τ VZA variations was partially canceled out by the ∪ shape of re VZA variations when calculating MODIS CLWP and was even overcompensated when the strong ∪ shape of LCF VZA variations was additionally factored into the calculation of MODIS LWP. In the polar/near-polar regions, that is, at large SZAs, all three components had ∪-shaped VZA variations, producing the pronounced ∪-shaped VZA variations in MODIS CLWP and LWP, not seen in AMSR-E LWP. However, in the tropics/subtropics the VZA dependence of AMSR-E LWP and that of MODIS LWP were similar: view angle variations were generally small and more frequently ∪ shaped than ∩ shaped.
Maps of coefficient c corresponding to overcast domains are given in Figure S6 in the supporting information. In contrast to the all results, VZA variations in both AMSR-E CLWP and MODIS CLWP were dominated by ∩ shapes with only a faint hint of ∪ shapes in the polar regions—the ∪ shape at large SZAs is more pronounced in broken clouds due to a stronger gap factor. MODIS CLWP variations were mostly driven by those in optical thickness. The VZA dependence of effective radius remained predominantly ∪ shaped but was considerably weaker than in the all case. Overall, VZA variations in AMSR-E CLWP and MODIS CLWP were fairly consistent for overcast scenes, even at higher latitudes.
4. Summary and Concluding Remarks
This study investigated the view angle dependence of Aqua-MODIS plane-parallel liquid water path retrievals and that of cloud optical thickness, 2.2 µm droplet effective radius, and liquid cloud fraction, from which the operational VNIR LWP was parameterized. The single-view sun-synchronous MODIS measurements suffer from aliasing between sun-view geometry and seasonal/latitudinal changes in cloud properties, which complicates isolating view-dependent 3-D retrieval biases. This complication, however, was mitigated here by contrasting MODIS LWPs with coincident and fully independent AMSR-E microwave LWPs, which were less prone to 3-D effects and had the same seasonal/latitudinal sampling as MODIS. The view angle of the conically scanning AMSR-E is practically constant; therefore, MODIS VZA-binned microwave LWPs only exhibited cross-swath variations. The focus was on 0.25°, ice- and precipitation-free oceanic domain means in order to facilitate comparison with the coarser resolution microwave observations. The current study used the same 1 year data set as Seethala and Horváth [2010], complementing this earlier work on absolute differences between AMSR-E and MODIS LWPs. In addition to obtaining global annual mean results, we stratified the view angle dependence by cloud heterogeneity, solar zenith angle, and geographic location.
Microwave retrievals showed generally small variations, both in absolute value and cross-swath dependence. AMSR-E LWPs varied between 40 and 70 g m−2 slightly decreasing with heterogeneity and increasing with SZA, which likely indicated genuine latitudinal/regional variations. Nadir-relative LWP variations were within ±5% for global annual means and typically within ±10% when stratified by χ or SZA. The mild cross-swath dependence exhibited both ∪ (bowl) shape and ∩ (bell) shape, with the former being somewhat more frequent than the latter.
The unscaled in-cloud MODIS CLWP strongly increased with increasing heterogeneity. Surprisingly, however, the VZA dependence of MODIS CLWP was weak and comparable in magnitude to that of AMSR-E LWP in most cases. Nadir-relative variations, an increase in the backscatter and a decrease in the forward scatter direction, were within ±8% for global annual means, which practically canceled out when averaging backscatter and forward scatter views. VZA variations were generally small, ±10% or less, in most χ and SZA bins as well. MODIS CLWP showed very good VZA consistency in both backward and forward scatter directions up to an SZA of 70°. When stratified by χ, consistency was equally good in the backscatter direction and at most forward scatter VZAs, but CLWP had a distinct 10–15% drop in the most oblique forward scatter views. Overall, the VZA dependence of MODIS CLWP had a mild ∩ shape in most χ and SZA bins. Larger, 20–40%, and ∪-shaped VZA variations were only observed in the most heterogeneous clouds (χ < 0.5) and/or at the most oblique sun (SZA > 70°), which, however, constituted only 3–8% of our data. The ∪ shape was more pronounced for χ binning than for SZA binning, supporting the effectiveness of χ as a heterogeneity index. Geographically, the weak ∩ shape was prevalent in the tropics/subtropics, while the stronger ∪ shape corresponded to the midlatitudes and especially the polar regions.
The LCF-scaled MODIS LWP was on average more comparable to AMSR-E LWP than its unscaled counterpart but still showed larger variations with χ and SZA than the microwave estimates. The VZA dependence of MODIS LWP was strongly ∪ shaped for all χ and SZA values and geographic regions. The maximum nadir-relative increase in VNIR LWP was particularly large, a factor of 2–5, for the most heterogeneous clouds and/or the most oblique sun, that is, generally in the polar regions.
The variations in MODIS CLWP and LWP with χ, SZA, and VZA arose due to the interplay between corresponding variations in optical thickness, effective radius, and LCF. In-cloud CLWP was largely driven by optical thickness. As such, τ showed a strong increase with χ and SZA and transitioned from a weak ∩ shape to a stronger ∪ shape as heterogeneity, sun angle, and latitude increased. The ∩-shaped variations were somewhat larger while the ∪-shaped variations were smaller in τ than in CLWP due to the added effect of re VZA variations on CLWP. VZA consistency was better for backscatter than forward scatter as before, but the drop in τ with view angle, especially in the forward scatter direction, was larger than in CLWP, reaching 20–25% for the most oblique VZAs. Similar backscatter-forward scatter VZA dependencies in plane-parallel τ were also noted by Loeb and Coakley [1998] and Loeb et al. [1998]. In contrast, the τ increase with VZA in the most heterogeneous clouds and/or at the lowest sun was smaller than the corresponding increase in CLWP, reaching only 17% at most. We also note that the τ increase in these most extreme χ and SZA bins was smaller than the 40% value found in the pixel-level analysis of Várnai and Marshak [2007], likely because of averaging over shadowed and illuminated sides and other small-scale heterogeneity fluctuations within our 0.25° domains.
The observed VZA dependence of optical thickness could be qualitatively explained as the weighted sum of the three factors proposed by Liang and Di Girolamo [2013]: the concavity factor decreasing τ for both forward and backward scatters (∩ shape), the RAZ-bump factor decreasing τ for forward scatter but increasing it for backscatter, and the gap factor increasing τ in both directions (∪ shape). The combination of the concavity and RAZ-bump factors seemed to dominate in most χ and SZA bins. The gap factor was dominant only in the most heterogeneous clouds and/or at the lowest sun, although for the most oblique forward scatter VZA the concavity and RAZ-bump factors remained stronger, leading to a reduced τ.
Effective radius also showed a systematic overall increase with χ and a smaller one with SZA. Unlike optical thickness, re always increased with VZA. The ∪ shape was weak (<10% increases) for most χ and SZA; however, it became well pronounced and asymmetric favoring forward scatter in the most heterogeneous clouds and (to a lesser degree) at the lowest sun (10–30% increases). This asymmetry in re VZA dependence can perhaps be explained as the combination of shadowing (positive biases) dominating over illumination (negative biases) [Marshak et al., 2006] and a forward scatter-backscatter asymmetry in shadowed cloud fraction at oblique but near side scattering directions.
The VZA, SZA, and χ variations in 1.6 µm and 3.7 µm effective radius were similar and comparable in magnitude to those in the operational 2.2 µm retrievals, with the exception of the ∩ shaped VZA dependence of re,3.7 for moderately heterogeneous clouds and high sun, which requires further investigation. Although previous studies indicated that the 3.7 µm band is less affected by rain/drizzle and heterogeneity/3-D effects, it did not offer any apparent advantage over the other two bands in our comparison.
Liquid cloud fraction showed a strong general decrease with increasing heterogeneity. In contrast, LCF tended to increase with SZA, especially for SZA ≤ 50°, probably indicating geographic variations in cloud type and spatial structure. More importantly, VZA variations in LCF were always ∪ shaped and significantly larger than those in either τ or re.
As a result, when calculating MODIS CLWP the ∩-shaped VZA variations in τ were partially canceled out by the ∪-shaped VZA variations in re, for most χ, SZA, and geographic regions. In MODIS LWP estimates, LCF was an additional and dominant factor, explaining the strong ∪-shaped VZA variations. For the largest SZAs and most heterogeneous clouds, all three MODIS-retrieved parameters were ∪ shaped, leading to strongly ∪ shaped VZA variations in CLWP and LWP at higher latitudes, particularly the polar regions.
For overcast domains the nadir-relative variations in AMSR-E CLWP and MODIS CLWP were consistent even at higher latitudes, but otherwise, the VZA, SZA, and χ dependence of optical thickness and effective radius were quite similar to the all results. The most significant differences were the reduced variation of re with χ and the absence of the pronounced ∪ shape in τ at the most oblique sun.
The upcoming MODIS Collection 6 product will do away with clear-sky restoral, which mostly eliminates thin partly cloudy edge pixels in broken clouds and thus significantly reduces retrieval cloud fraction. Including these pixels in the comparison might result in a better absolute agreement between AMSR-E LWP and LCF-scaled MODIS LWP at the lowest cloud fractions but might also exacerbate relative view angle variations due to increased 1-D model errors. Some even argue that such partly cloudy retrievals should be aggregated separately [Pincus et al., 2012]. The similarity between the overcast and all results indicate a level of confidence in the robustness of our findings.
Overall, VZA variations in MODIS domain means were relatively small compared to the much more significant general increases with χ and SZA (these strong dependencies on heterogeneity and sun angle were not present in microwave retrievals and, thus, require further study). The VZA consistency was particularly good for in-cloud CLWP in the vast majority of cases due to (partial) cancelation of errors between optical thickness and effective radius. This good consistency, however, was lost for scaled LWP, which included the strong and dominant ∪-shaped VZA artifacts in LCF. Therefore, it might be worthwhile to explore scaling CLWP with a fixed LCF—one corresponding to nadir or the view angle of the microwave instrument or an appropriately chosen effective cloud fraction—that would preserve the VZA consistency of in-cloud retrievals but would yield VNIR LWPs more comparable in magnitude to microwave estimates. Future research could also try to quantify the biases in effective radius due to the three specific factors that were introduced for optical thickness by Liang and Di Girolamo [2013] in order to put the analysis of VZA variations in cloud microphysical retrievals in a unified framework.
Acknowledgments
This work was partially supported by the European Commission's Marie Curie Actions under grant agreement MIRG-CT-2007-208245 and the Hans Ertel Centre for Weather Research (HErZ) initiative of the German Weather Service (DWD). AMSR-E data are produced by Remote Sensing Systems (RSS) and sponsored by the NASA Earth Science MEaSUREs DISCOVER Project and the AMSR-E Science Team. Data are available at www.remss.com. We thank Kyle Hilburn of RSS for his always prompt and enthusiastic help with AMSR-E data. The suggestions of three anonymous reviewers greatly improved the paper.
Erratum
The copyright line for this article was changed on 22 August 2014.
Supporting Information
• Readme
• Figure S1
• Figure S2
• Figure S3
• Figure S4
• Figure S5
• Figure S6
References
- Bennartz R. Global assessment of marine boundary layer cloud droplet number concentration from satellite. J. Geophys. Res. 2007;112 D02201, doi: 10.1029/2006JD007547. [Google Scholar]
- Borg LA. Bennartz R. Vertical structure of stratiform marine boundary layer clouds and its impact on cloud albedo. Geophys. Res. Lett. 2007;34 L05807, doi: 10.1029/2006GL028713. [Google Scholar]
- Buriez J-C, Doutriaux-Boucher M, Parol F. Loeb N. Angular variability of the liquid water cloud optical thickness retrieved from ADEOS-POLDER. J. Atmos. Sci. 2001;58:3007–3018. doi: 10.1175/1520-0469(2001)058<3007:AVOTLW>2.0.CO;2. [Google Scholar]
- Cahalan RF, Ridgway W, Wiscombe WJ, Bell TL. Snider JB. The albedo of fractal stratocumulus clouds. J. Atmos. Sci. 1994;51:2434–2455. doi: 10.1175/1520-0469(1994)051<2434:TAOFSC>2.0.CO;2. [Google Scholar]
- Chang F-L. Li Z. Estimating the vertical variation of cloud droplet effective radius using multispectral near-infrared satellite measurements. J. Geophys. Res. 2002;107(D15) 4257, doi: 10.1029/2001JD000766. [Google Scholar]
- Chang F-L. Li Z. Retrieving vertical profiles of water-cloud droplet effective radius: Algorithm modification and preliminary application. J. Geophys. Res. 2003;108(D24) 4763, doi: 10.1029/2003JD003906. [Google Scholar]
- Chen R, Chang F-L, Li Z, Ferraro R. Weng F. Impact of the vertical variation of cloud droplet size on the estimation of cloud liquid water path and rain detection. J. Atmos. Sci. 2007;64:3843–3853. doi: 10.1175/2007JAS2126.1. [Google Scholar]
- Chen R, Wood R, Li Z, Ferraro R. Chang F-L. Studying the vertical variation of cloud droplet effective radius using ship and spaceborne remote sensing data. J. Geophys. Res. 2008;113 D00A02, doi: 10.1029/2007JD009596. [Google Scholar]
- Cornet C, Isaka H, Guillemet B. Szczap F. Neural network retrieval of cloud parameters of inhomogeneous clouds from multispectral and multiscale radiance data: Feasibility study. J. Geophys. Res. 2004;109 D12203, doi: 10.1029/2003JD004186. [Google Scholar]
- Cornet C, Buriez J-C, Riédi J, Isaka H. Guillemet B. Case study of inhomogeneous cloud parameter retrieval from MODIS data. Geophys. Res. Lett. 2005;32 L13807, doi: 10.1029/2005GL022791. [Google Scholar]
- Di Girolamo L, Liang L. Platnick S. A global view of one-dimensional solar radiative transfer through oceanic water clouds. Geophys. Res. Lett. 2010;37 L18809, doi: 10.1029/2010GL044094. [Google Scholar]
- Greenwald TJ. A 2 year comparison of AMSR-E and MODIS cloud liquid water path observations. Geophys. Res. Lett. 2009;36 L20805, doi: 10.1029/2009GL040394. [Google Scholar]
- Greenwald TJ, Christopher SA. Chou J. Cloud liquid water path comparisons from passive microwave and solar reflectance satellite measurements: Assessment of sub-field-of-view clouds effects in microwave retrievals. J. Geophys. Res. 1997;102:19,585–19,596. doi: 10.1029/97JD01257. [Google Scholar]
- Greenwald TJ, L'Ecuyer TS. Christopher SA. Evaluating specific error characteristics of microwave-derived cloud liquid water products. Geophys. Res. Lett. 2007;34 L22807, doi: 10.1029/2007GL031180. [Google Scholar]
- Grosvenor DP. Wood R. The effect of solar zenith angle on MODIS cloud optical and microphysical retrievals. Atmos. Chem. Phys. Discuss. 2014;14:303–375. doi: 10.5194/acpd-14-303-2014. [Google Scholar]
- Hilburn KA. Wentz FJ. Intercalibrated passive microwave rain products from the Unified Microwave Ocean Retrieval Algorithm (UMORA) J. Appl. Meteorol. Climatol. 2008;47:778–794. doi: 10.1175/2007JAMC1635.1. [Google Scholar]
- Hilburn K, Wentz FJ, Mears C, Meissner T. Smith D. Description of Remote Sensing Systems version-7 geophysical retrievals. 2010. paper presented at Seventeenth Conference on Satellite Meteorology and Oceanography, Annapolis, Md.
- Horváth Á. Davies R. Anisotropy of water cloud reflectance: A comparison of measurements and 1D theory. Geophys. Res. Lett. 2004;31 L01102, doi: 10.1029/2003GL018386. [Google Scholar]
- Horváth Á. Davies R. Comparison of microwave and optical cloud water path estimates from TMI, MODIS, and MISR. J. Geophys. Res. 2007;112 D01202, doi: 10.1029/2006JD007101. [Google Scholar]
- Horváth Á. Gentemann C. Cloud-fraction-dependent bias in satellite liquid water path retrievals of shallow, non-precipitating marine clouds. Geophys. Res. Lett. 2007;34 L22806, doi: 10.1029/2007GL030625. [Google Scholar]
- Kato S. Marshak A. Solar zenith and viewing geometry-dependent errors in satellite retrieved cloud optical thickness: Marine stratocumulus case. J. Geophys. Res. 2009;114 D01202, doi: 10.1029/2008JD010579. [Google Scholar]
- Kato S, Hinkelman LM. Cheng A. Estimate of satellite-derived cloud optical thickness and effective radius errors and their effect on computed domain-averaged irradiances. J. Geophys. Res. 2006;111 D17201, doi: 10.1029/2005JD006668. [Google Scholar]
- King NJ. Vaughan G. Using passive remote sensing to retrieve the vertical variation of cloud droplet size in marine stratocumulus: An assessment of information content and the potential for improved retrievals from hyperspectral measurements. J. Geophys. Res. 2012;117 D15206, doi: 10.1029/2012JD017896. [Google Scholar]
- Lafont D. Guillemet B. Subpixel fractional cloud cover and inhomogeneity effects on microwave beam-filling error. Atmos. Res. 2004;72:149–168. doi: 10.1016/j.atmosres.2004.03.013. [Google Scholar]
- Lebsock MD, L'Ecuyer TS. Stephens GL. Detecting the ratio of rain and cloud water in low-latitude shallow marine clouds. J. Appl. Meteorol. Climatol. 2011;50:419–432. doi: 10.1175/2010JAMC2494.1. [Google Scholar]
- Liang L. Di Girolamo L. A global analysis on the view-angle dependence of plane-parallel oceanic liquid water cloud optical thickness using data synergy from MISR and MODIS. J. Geophys. Res. Atmos. 2013;118:2389–2403. doi: 10.1029/2012JD018201. [Google Scholar]
- Liang L, Di Girolamo L. Platnick S. View-angle consistency in reflectance, optical thickness and spherical albedo of marine water-clouds over the northeastern Pacific through MISR-MODIS fusion. Geophys. Res. Lett. 2009;36 L09811, doi: 10.1029/2008GL037124. [Google Scholar]
- Loeb NG. Coakley JA., Jr Inference of marine stratus cloud optical depths from satellite measurements: Does 1D theory apply? J. Clim. 1998;11:215–233. doi: 10.1175/1520-0442(1998)011<0215:IOMSCO2.0.CO;2. [Google Scholar]
- Loeb NG. Davies R. Observational evidence of plane parallel model biases: The apparent dependence of cloud optical depth on solar zenith angle. J. Geophys. Res. 1996;101:1621–1634. doi: 10.1029/95JD03298. [Google Scholar]
- Loeb NG. Davies R. Angular dependence of observed reflectances: A comparison with plane parallel theory. J. Geophys. Res. 1997;102:6865–6881. doi: 10.1029/96JD03586. [Google Scholar]
- Loeb NG, Várnai T. Davies R. Effect of cloud inhomogeneities on the solar zenith angle dependence of nadir reflectance. J. Geophys. Res. 1997;102(DD8):9387–9395. doi: 10.1029/96JD03719. [Google Scholar]
- Loeb NG, Várnai T. Winker DM. Influence of subpixel-scale cloud-top structure on reflectances from overcast stratiform cloud layers. J. Atmos. Sci. 1998;55:2960–2973. doi: 10.1175/1520-0469(1998)055<2960:IOSSCT>2.0.CO;2. [Google Scholar]
- Maddux BC, Ackerman SA. Platnick S. Viewing geometry dependencies in MODIS cloud products. J. Atmos. Oceanic Technol. 2010;27:1519–1528. doi: 10.1175/2010JTECHA1432.1. [Google Scholar]
- Marshak A, Platnick S, Várnai T, Wen G. Cahalan RF. Impact of three-dimensional radiative effects on satellite retrievals of cloud droplet sizes. J. Geophys. Res. 2006;111 D09207, doi: 10.1029/2005JD006686. [Google Scholar]
- Nakajima T. King MD. Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part I: Theory. J. Atmos. Sci. 1990;47:1878–1893. doi: 10.1175/1520-0469(1990)047<1878:DOTOTA>2.0.CO;2. [Google Scholar]
- Oreopoulos L. Cahalan RF. Cloud inhomogeneity from MODIS. J. Clim. 2005;18:5110–5124. doi: 10.1175/JCLI3591.1. [Google Scholar]
- Painemal D, Minnis P. Sun-Mack S. The impact of horizontal heterogeneities, cloud fraction, and liquid water path on warm cloud effective radii from CERES-like Aqua MODIS retrievals. Atmos. Chem. Phys. 2013;13:9997–10,003. doi: 10.5194/acp-13-9997-2013. [Google Scholar]
- Pincus R, Platnick S, Ackerman SA, Hemler RS. Hofmann RJP. Reconciling simulated and observed views of clouds: MODIS, ISCCP, and the limits of instrument simulators. J. Clim. 2012;25:4699–4720. doi: 10.1175/JCLI-D-11-00267.1. [Google Scholar]
- Platnick S, King MD, Ackerman SA, Menzel WP, Baum BA, Riedi JC. Frey RA. The MODIS cloud products: Algorithms and examples from Terra. IEEE Trans. Geosci. Remote Sens. 2003;41:459–473. doi: 10.1109/TGRS.2002.808301. [Google Scholar]
- Seethala C. Hamburg, Germany: Max Planck Inst. for Meteorol; 2012. Evaluating the state-of-the-art of and errors in 1D satellite cloud liquid water path retrievals with large eddy simulations and realistic radiative transfer models; p. 160. PhD dissertation. [Google Scholar]
- Seethala C. Horváth Á. Global assessment of AMSR-E and MODIS cloud liquid water path retrievals in warm oceanic clouds. J. Geophys. Res. 2010;115 doi: 10.1002/jgrd.51506. D13202, doi: 10.1029/2009JD012662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczodrak M, Austin PH. Krummel PB. Variability of optical depth and effective radius in marine stratocumulus clouds. J. Atmos. Sci. 2001;58:2912–2926. [Google Scholar]
- Vant-Hull B, Marshak A, Remer LA. Li Z. The effects of scattering angle and cumulus cloud geometry on satellite retrievals of cloud droplet effective radius. IEEE Trans. Geosci. Remote Sens. 2007;45(4):1039–1045. doi: 10.1109/TGRS.2006.890416. [Google Scholar]
- Várnai T. Marshak A. View angle dependence of cloud optical thicknesses retrieved by Moderate Resolution Imaging Spectroradiometer (MODIS) J. Geophys. Res. 2007;112 D06203, doi: 10.1029/2005JD06912. [Google Scholar]
- Wentz FJ. A well-calibrated ocean algorithm for special sensor microwave/imager. J. Geophys. Res. 1997;102:8703–8718. doi: 10.1029/96JC01751. [Google Scholar]
- Wentz FJ. RSS Tech. Rep. 011012. Remote Sens. Syst., Santa Rosa, Calif; 2013. SSM/I version-7 calibration report; p. 46. [Google Scholar]
- Wentz FJ. Meissner T. RSS Tech. Rep. 121599A-1. Remote Sens. Syst., Santa Rosa, Calif; 2000. AMSR ocean algorithm, version 2; p. 66. [Google Scholar]
- Wentz FJ. Spencer R. SSM/I rain retrievals within a unified all-weather ocean algorithm. J. Atmos. Sci. 1998;55:1613–1627. doi: 10.1175/1520-0469(1998)055<1613:SIRRWA>2.0.CO;2. [Google Scholar]
- Zeng S, Parol F, Riedi J, Cornet C. Thieuleux F. Examination of POLDER/PARASOL and MODIS/Aqua Cloud fractions and properties representativeness. J. Clim. 2011;24:4435–4450. doi: 10.1175/2011JCLI3857.1. [Google Scholar]
- Zeng S, Cornet C, Parol F, Riedi J. Thieuleux F. A better understanding of cloud optical thickness derived from the passive sensors MODIS/AQUA and POLDER/PARASOL in the A-Train constellation. Atmos. Chem. Phys. 2012;12:11,245–11,259. doi: 10.5194/acp-12-11245-2012. [Google Scholar]
- Zhang Z. Platnick S. An assessment of differences between cloud effective particle radius retrievals for marine water clouds from three MODIS spectral bands. J. Geophys. Res. 2011;116 D20215, doi: 10.1029/2011JD016216. [Google Scholar]
- Zhang Z, Ackerman AS, Feingold G, Platnick S, Pincus R. Xue H. Effects of cloud horizontal inhomogeneity and drizzle on remote sensing of cloud droplet effective radius: Case studies based on large-eddy simulations. J. Geophys. Res. 2012;117 D19208, doi: 10.1029/2012JD017655. [Google Scholar]
- Zhao G. Di Girolamo L. A cloud fraction versus view angle technique for automatic in-scene evaluation of the MISR cloud mask. J. Appl. Meteorol. 2004;43:860–869. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
• Readme
• Figure S1
• Figure S2
• Figure S3
• Figure S4
• Figure S5
• Figure S6