Semi-Markov models for interval censored transient cognitive states with back transitions and a competing risk

Abstract

Continuous-time multi-state stochastic processes are useful for modeling the flow of subjects from intact cognition to dementia with mild cognitive impairment and global impairment as intervening transient, cognitive states and death as a competing risk (Figure 1). Each subject's cognition is assessed periodically resulting in interval censoring for the cognitive states while death without dementia is not interval censored. Since back transitions among the transient states are possible, Markov chains are often applied to this type of panel data. In this manuscript we apply a Semi-Markov process in which we assume that the waiting times are Weibull distributed except for transitions from the baseline state, which are exponentially distributed and in which we assume no additional changes in cognition occur between two assessments. We implement a quasi-Monte Carlo (QMC) method to calculate the higher order integration needed for likelihood estimation. We apply our model to a real dataset, the Nun Study, a cohort of 461 participants.

1. INTRODUCTION

In longitudinal analysis, the continuous-time multi-state stochastic process has a wide application in modeling the complex evolution of chronic diseases. Analysis of panel data is greatly simplified by the time homogeneous Markov assumption, especially when observations are made at some pre-specified evenly spaced time spots. Kalbfleisch and Lawless¹ proposed a quasi-Newton algorithm for maximum likelihood estimation that could effectively handle the case of unevenly spaced observation times.

Often it is the case that the transition intensities of the process depend on the time elapsed at the current state, which makes the process semi-Markov. There has been much literature on the application of semi-Markov models in very general statistical problems. When the exact transition times are fully observed, the likelihood function has a relatively elegant form, which also simplifies the subsequent maximization procedure.² The R package SemiMarkov recently developed by Listwon and Saint-Pierre³ offers a convenient tool to implement general homogenous semi-Markov models that could flexibly incorporate diagnostic covariates through parametric proportional hazards models. However, in many instances, the subjects are only periodically assessed resulting in interval censoring, with no information about the types of events between the observations and the associated transition instants. When the process only has right shift paths, namely, a subject can only visit a state at most once, and has only a small number of states, e.g., three or four, the length of all possible paths will be limited. In the parametric setting, the likelihood function will only involve integrations of low orders and therefore standard numerical methods such as Gaussian Quadrature or Monte-Carlo methods can be applied to approximate the likelihood.^4,5,6,7 Nonparametric estimation is also possible via self-consistent estimators in the case of a unidirectional model without covariates.⁸ Commenges⁹ discusses the need to develop more stable and efficient algorithms when employing nonparametric inference for multistate models subject to interval censoring. A semi-parametric based on a penalized likelihood function for a three state progressive semi-Markov model with interval censored data is presented by Joly et al.^10,11 Recently, Kapetanakis et al.¹² studied a three-state illness-death model with piecewise-constant hazards in the presence of left, right and interval censoring.

Little work has been done to handle reverse transitions (namely, a subject can visit one state multiple times) in the presence of interval censoring, apparently due to the fact that reverse transitions will potentially lead to lengthy paths and hence prohibitively complicated high order integrations in the likelihood function. An important contribution is credited to Kang and Lagakos¹³ who introduced a multi-state semi-Markov process with at least one state that has time homogenous transition intensity, namely, the holding time at that state is exponentially distributed. In that case, they were able to divide a long trajectory into smaller fragments according to the time homogenous transition intensity state. Although their method could be extended with minimal modification to incorporate time-independent covariates, dealing with time-dependent covariates may be problematic. An alternative approach based on the use of phase type sojourn distributions and hidden Markov models is presented by Titman and Sharples¹⁴. In the Nun study, one of our primary research interests is the effect of age (calendar time, with 15 years follow up period) on the holding time, which makes the approach of Kang and Lagakos inapplicable. We implement the quasi-Monte Carlo (QMC) method¹⁵ which will provide considerably better accuracy, with the expected integration error of the order of N⁻¹ (N being the number of Halton sequence points from the high-dimensional integration space), to approximate the higher order integrations of the likelihood function.

A second issue in using a semi-Markov model is identifying the time origin, the exact time of entrance into the initial state (first observed state). For the semi-Markov model, the transition intensity of each state depends on the length of time at which each subject stayed at the current state. For the initial state, we do not have the exact time of entrance, which results in the left censoring for the holding time of the initial state. We identified some common strategies in the literature to deal with this problem. Kryscio and Abner¹⁶ assume a unique time (age 60) as the time origin for all subjects. This works well if each subject is in the same initial state and all paths are right shift. Kapetanakis et al.¹² apply the EM inspired algorithm to find the unique age as the time origin. Satten and Sternberg⁸ assume that the time elapsed before the first observation follows a given distribution and is independent of the time to the next transition from the first observation. Satten and Longini¹⁷ develop a procedure to estimate Markov model parameters that conditions on the initiation time in order to remove dependence on this time. Kalbfleisch and Lawless¹ simply assume that the holding time of the initial state is exponentially distributed, rendering the time origin unnecessary due to the memory less property of the exponential distribution. In this manuscript, we use this strategy to simplify our model.

In this manuscript, a general approach to fitting the semi-Markov model to panel data is derived. The method, which allows for backward transition is used to model the unevenly spaced periodically observed transition data assuming no unobserved transitions. Different distributions for the holding time according to baseline state are assumed. There are two absorbing states, dementia (interval censored) and death (competing risk to dementia and with exactly observed transition time). We expect that the incorporation of the time-dependent covariate (age, the calendar time) will lead to better parameter estimates. The advantage of this method is that it allows us to check which variables are related to the backwards transaction and the holding time of each state.

The remainder of the manuscript is structured as follows. Notation and likelihood of the semi-Markov is defined in Section 2. In Section 3, a simulation study is conducted to check the model robustness against certain violations of the distributional assumptions. Section 4 applies this new method to a real dataset, the Nun data. Conclusion and discussion are provided in Section 5.

2. METHODOLOGY

We first introduce the notation and establish the likelihood function of the semi-Markov process where sample paths are only periodically observed.

2.1 The Semi-Markov Process

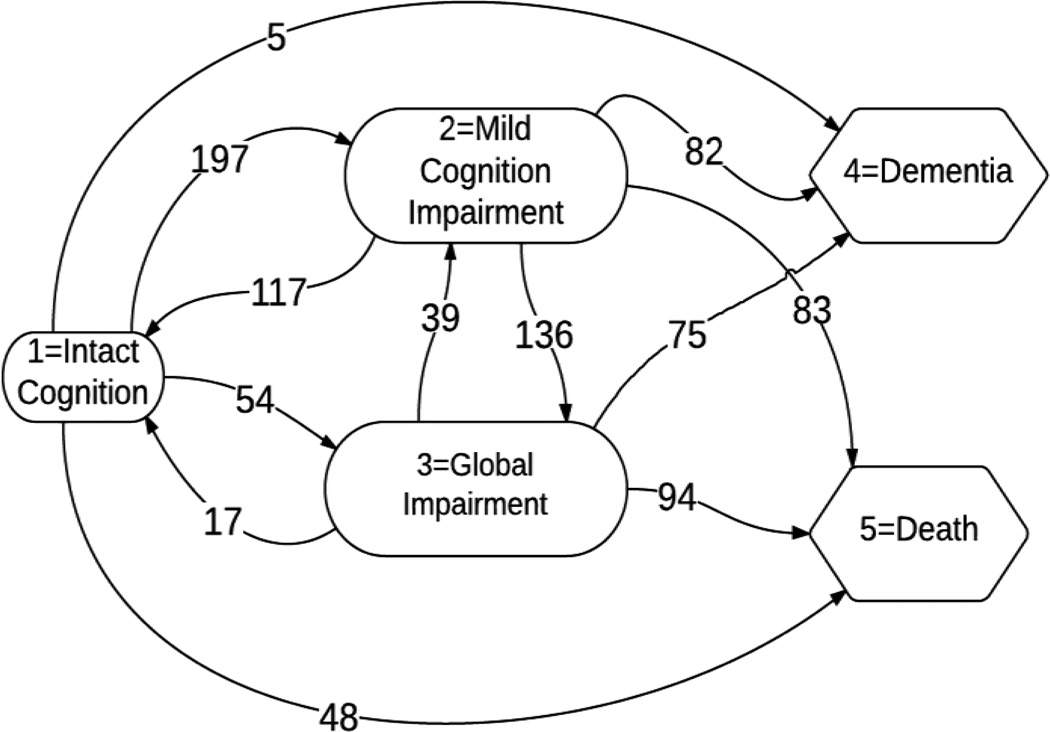
Suppose there are m subjects in the study, denoted by i = 1, 2, 3, ⋯, m. Let SP = {1, 2, 3, ⋯, S} be the finite state space representing the possible states of the evolution of a subject. For ease of exposition, the subsequent notations will be based on the Nun study data and extensions to more general semi-Markov process should be straightforward. In the Nun study, the status of a participant at each visit was recorded as being in one of the following states: 1 = intact cognition, 2 = mild cognitive impairments (M.C.I.), 3 = global impairments (G.I.), 4 = dementia,¹⁸ and 5 = death, i.e. S = 5 in this case. States 1–3 are transient while 4 and 5 are absorbing with 5 considered to be a competing risk to state 4. Transition times between the states 1, 2, 3 and 4 are not exactly known and a patient may begin his/her evolution in any of these three transient states (Figure 1). The exact occurrence time of state 5 is known. The list of follow up states of a subject is denoted by v_k, where k = 0, 1, 2, 3, ⋯, n, v₀ is the baseline state, n is the number of jumps for the subject and each v_k is in SP. We assume the Markov property holds for the sequence V = (v₀, v₁, …, v_n). In all subsequent exposition, we assume that j runs through 1 to 3, j′ runs through 1 to 5 and j ≠ j′.

Figure 1.

Frequency of the One-step Transitions

Let d_k be the holding time in the state v_k, defined by d_k = t_k+1 − t_k, where t_k is the calendar time of entrance into state v_k. If v_k is an absorbing state, we define d_k = 0. Let Z = (z₁, z₂, ⋯, z_p)^T be a vector of p fixed (e.g. baseline) covariates. Let w_k be age at time t_k (w₀ denotes baseline age).

The probability of one step transition from state j to j' at k + 1th jump can be expressed as

$$P_{kjj\prime }=P(v_{k+1}=j\prime |v_k=j,\mathit{Z},w_k)$$

with the constraints ∑_j′≠jP_kjj′ = 1 and P_kjj′ ≥ 0.

Following Salazar et al.,¹⁹ a multinomial logit parameterization could be applied to link these transition probabilities in the following way:

$$\text{log}\left(\frac{P_{ksv}}{P_{ks5}}\right)={\alpha }_{sv}+\mathit{Z}\mathbf{\prime }{\mathit{\beta }}_{\mathbf{1}\mathit{s}\mathit{v}}+w_k{\beta }_{2sv},v=1,2,3,4\mathit{\text{and}}s=1,2,3.$$ (1)

Here α_sv is the intercept, β_1sv and β_2sv are the unknown regression coefficients. It follows that the transition probabilities are given by:

$$P_{ksv}=\{\begin{array}{cc}\frac{1}{1+{\sum }_{h=1}^4\text{exp}({\alpha }_{sh}+\mathit{Z}\mathbf{\prime }{\mathit{\beta }}_{\mathbf{1}\mathit{s}\mathit{h}}+w_k{\beta }_{2sh})},\hfill & v=5\hfill \\ \frac{\text{exp}({\alpha }_{sv}+\mathit{Z}\prime {\mathit{\beta }}_{\mathbf{1}\mathit{s}\mathit{v}}+w_k{\beta }_{2sv}}{1+{\sum }_{h=1}^4\text{exp}({\alpha }_{sh}+\mathit{Z}\mathbf{\prime }{\mathit{\beta }}_{\mathbf{1}\mathit{s}\mathit{h}}+w_k{\beta }_{2sh})},\hfill & v<5\hfill \end{array}.$$ (2)

We assume two types of distributions for the holding time according to the initial state, due to the left censoring of exact transition times to the initial state. Specifically,

• The distribution of the holding time for moving out of the initial state is exponential, with the hazard function

  $${\mathrm{\lambda }}_{0\mathrm{j}\mathrm{j}\prime }(\mathrm{t})=\text{exp}(-\mathbf{Z}\mathbf{\prime }{\mathbf{\gamma }}_{\mathbf{1}\mathbf{j}\mathbf{j}\mathbf{\prime }}-w_0{\mathrm{\gamma }}_{2\mathrm{j}\mathrm{j}\prime }).$$ (3)
• The distribution of the holding time for all other transitions is Weibull. The corresponding hazard function is given by

  $${\mathrm{\lambda }}_{\mathrm{k}\mathrm{j}\mathrm{j}\prime }(\mathrm{t})={\mathrm{\alpha }}_{0\mathrm{j}\mathrm{j}\prime }(\mathrm{t})\text{exp}(-\mathbf{Z}\mathbf{\prime }{\mathbf{\gamma }}_{\mathbf{3}\mathbf{j}\mathbf{j}\mathbf{\prime }}-w_k{\mathrm{\gamma }}_{4\mathrm{j}\mathrm{j}\prime }),$$ (4)

  where α_0jj′(t) = k_jj′ t^k_jj′⁻¹ and k_jj′ is an unknown fixed constant.

The corresponding survival function and density function are

$$S_{kjj\prime }(t)=P(D_k\ge t|V_{k+1}=j\prime ,V_k=j,\mathit{Z},w_k)=\mathit{\text{exp}}(-{\int }_t^{\infty }{\lambda }_{kjj\prime }(s)ds),f_{kjj\prime }(t)={\lambda }_{kjj\prime }(t)\times \mathit{\text{exp}}(-{\int }_t^{\infty }{\lambda }_{kjj\prime }(s)ds).$$

If the last observed state is a transient state, the holding time of that state will be right censored. Moreover, we do not even know what will be the next state, so for the last state we have:

$$S_{kj.}(t)=P(D_k\ge t|V_k=j,\mathit{Z},w_k)={\sum }_{j\prime \ne j}P(V_{k+1}=j\prime |V_k=j,\mathit{Z},w_k)P(D_k\ge t|V_{k+1}=j\prime ,V_k=j,\mathit{Z},w_k)={\sum }_{j\prime \ne j}{P}_{kjj\prime }{S}_{kjj\prime }(t).$$

2.2 The Likelihood Function

Let T = (t₀, t₁, ⋯, t_n) be the vector of transition instants and D = (d₀, d₁, ⋯, d_n) be the vector of holding times. Let u be the time of the last assessment. Note that if v_n ∈ {1, 2, 3}, d_n is right censored in the sense that it's only known up to d_n ≥ u − t_n; if v_n ∈ {4, 5}, d_n will not enter our likelihood function since we are not interested in the holding time of dementia or death. Then, conditional on the initial state, the contribution to the likelihood from the subject is

$$\mathcal{l}(\mathit{\Theta }|\mathit{Z},\mathit{W},\mathit{T},\mathit{V})={\prod }_{k=1}^n{P}_{k-1,v_{k-1}{v}_k}{\prod }_{k=1}^n\{f_{k-1,v_{k-1},v_k}(t_k-t_{k-1})\}\times {\left\{S_{n{v}_n.}\right(u-t_n\left)\right\}}^{I[v_n\le 3]}.$$ (5)

Here Θ represents the set of all the unknown parameters, W = (w₀, w₁, ⋯, w_n) and I[.] denotes the indicator function.

Due to the fact that a subject is only periodically assessed, we do not fully observe T or D and therefore the specification of ℓ in (5) needs some modifications. What we observe instead, except for the state at each assessment, is a sequence of lower bounds L = (0, l₁, …, l_n) and upper bounds U = (u₀, u₁, ⋯, u_n) for T such that l_k ≤ t_k ≤ u_k, k = 0,1,⋯, n. As mentioned in subsection 2.1, we assume that the holding time of the initial state is exponentially distributed. Due to the memoryless property, we could simply treat the time of transition to the initial state as the time of the first assessment, namely the baseline age, or mathematically, t₀ = l₀ = u₀. To obtain the correct likelihood contribution, basically we could integrate out T in (5), where T falls in the domain implied by U and L. Specifically, we propose to modify the likelihood as follows:

$$\mathcal{l}(\mathit{\Theta }|\mathit{Z},\mathit{W},\mathit{U},\mathit{L},\mathit{V})=\underset{\mathit{A}}{\int }{\prod }_{k=1}^n{P}_{k-1,v_{k-1}{v}_k}{\prod }_{k=1}^n\{f_{k,v_{k-1},v_k}(t_k-t_{k-1})\}\times {\left\{S_{n,v_n.}\right(u-t_n\left)\right\}}^{I[v_n\le 3]}d({\mathit{T}}^{*}).$$ (6)

Here T^* = (t₁, t₂, ⋯, t_n). The integration domain A will incorporate the lower and upper bounds of T to reflect the fact that we only have partial information on T. We have

$$\mathit{A}=\{{\mathit{T}}^{*}|l_k\le t_k\le u_k,k=1,2,\cdots ,n\}.$$

When the last observation is a death, t_n is exactly observed, and therefore the integration in (6) along the axis t_n is with respect to the probability measure that puts unit mass on t = t_n. The integration in (6) can be lengthy but the idea is straightforward.

One implication of the modeling assumption (1) is that the transition probability P_ksv is conditioned on the value of the time-dependent covariate w_k at the time of t_k. Therefore the associated interpretation of the regression coefficient β_2sv is conditioned on the unobserved random variable t_k. In order for the regression coefficient to have an interpretation that only depends on what we can actually observe, we replace w_k in (1) by its value at the upper bound u_k. This results in our ability to predict the next state of a subject given his/her information at the current assessment. Moreover, under this modification, P_ksv does not depend on t_k, and therefore it allows us to pull P_ksv outside of the integration in (6) and thus significantly reduces the computational burden.

2.3 Parameter Estimation

The multi-dimensional integration in (6) could be approximated by numerical methods, including importance sampling, quasi-Monte Carlo (QMC) approximation¹⁵ and so on. In this manuscript, we use the QMC method due to the fact that the highest order of integration is eight, which is relatively high. Estimation and inference on the parameters Θ can be achieved by maximizing the likelihood function in Equation (6), where the optimization procedure could be implemented for example by PROC NLMIXED in SAS. The likelihood function takes a complicated form and is not convex in the parameters, therefore convergence of the optimization algorithm is not guaranteed for an arbitrary set of initial values. It is advisable to start with multiple sets of initial values and select the maximizers accordingly.

3. SIMULATION STUDY

In this section for simplicity we only consider the effects of baseline age and age as motivated by the Nun Study example. The purpose of the simulations is to determine how well the averaged odds ratios and hazard ratios for age in Tables 6–8 will be estimated when the model assumed in Section 2.1 is correct and then when the assumption made on the distribution of the holding time for the initial state is violated. With respect to the latter a Generalized Weibull distribution WG(γ,µ,θ), with the hazard function $\mathrm{\lambda }\left(\mathrm{t}\right)=\frac{\mathrm{\gamma }\mathrm{\mu }}{\mathrm{\theta }}{(1+\mathrm{\mu }{\mathrm{t}}^{\mathrm{\gamma }})}^{\frac{1}{\mathrm{\theta }}-1}{\mathrm{t}}^{\mathrm{\gamma }-1}$, where t>0, γ > 0, µ > 0 and θ > 0, is used to check the robustness of the maximum likelihood estimate (MLE) to the violation of the holding time assumption. If we fix θ at 1, we obtain the Weibull formulation. We set θ and γ to be constants and log(µ) to be a linear function of age. Different options of θ and γ with 1000 simulations was tested but the following tables only show the result for θ = 2 and γ = 2. Simulations were carried out using Intel i5-650 professor (4M Cache, 3.20 GHz). The computational time for 1000 simulations of sample size 300 and 1000 with 500 Halton numbers are 20.43 hours and 50.61 hours respectively.

Table 6.

The odds ratio and confidence interval for significant effects on each transition probability (base state: 5=Death)

Transition	Covariate	Odds Ratio	95% Low	95% Upper	P-value
2→1	Apoe4	0.363	0.1842	0.7137	0.0034
2→3	Apoe4	1.726	1.0313	2.889	0.0379
3→4	Apoe4	2.623	1.4232	4.8337	0.0021
2→1	No College	0.249	0.1051	0.5895	0.0016
1→2	College	1.661	1.0174	2.7118	0.0425
2→3	College	1.734	1.2459	2.4112	0.0011
2→1	Age	0.927	0.892	0.9616	<.0001
3→1	Age	0.804	0.7653	0.8446	<.0001
3→2	Age	0.900	0.8763	0.9231	<.0001
3→4	Age	0.975	0.9573	0.9918	0.004

States: 1=Intact Cognition, 2=Mild Cognitive Impairment, 3=Global Impairment, 4=Dementia;

Table 8.

The hazard ratio and confidence interval estimate for significant effects in the Weibull distribution

Transition	Covariate	Hazard Ratio	95% Low	95% Upper	P-value
1→2	Apoe4	2.569	1.168	5.65	0.019
1→3	Apoe4	16.856	2.072	137.14	0.008
3→4	Apoe4	0.286	0.13	0.634	0.002
2→4	No College	9.575	1.315	69.735	0.026
3→4	No College	0.290	0.090	0.934	0.038
1→2	Age	1.06	1.012	1.110	0.014
1→3	Age	1.243	1.114	1.386	<.001
1→5	Age	1.349	1.187	1.534	<.001
2→1	Age	1.064	1.007	1.125	0.028
2→3	Age	1.09	1.027	1.158	0.005
2→5	Age	1.092	1.028	1.160	0.005
3→5	Age	1.055	1.013	1.097	0.01

Hazard ratio in age is the hazard ratio for one year increase in age.

Similar results are obtained when the assumption of Weibull distribution (versus a Generalized Weibull) is violated for the holding time in the non-initial states (results not shown).

Specific steps in the simulation process follow. For each subject:

1. Generate initial age w₀ using a truncated normal distribution that has the same range, mean, and standard deviation as age in the real dataset and generate the initial state v₀ using the probabilities 140/511, 272/511, and 99/511 for initial states 1, 2, and 3, respectively.

2. Then in the order i = 0, 1, … generate the next state v_i+1 given v_i and w_i according to the transition probabilities in Equation (2).

3. Generate holding time d_i at state v_i according to exponential (i = 0) or Weibull distribution (i > 0). This determines w_i = w_i-1 + d_i.

   Repeat Steps 2 and 3 until either death, or dementia, or any age exceeds the largest planned observation time. Finally, record the observed states at the predetermined assessment times to define the interval censored observations (if any) for that subject.

Choice of the model parameters were made to come as close to those estimated from the real dataset of the next section without producing simulations that lead to non-estimable parameters (i.e. the likelihood function fails to converge). In the real dataset, the corresponding probabilities for the initial state are 140/461, 272/461, and 49/461 for states 1, 2, and 3. These were changed slightly in Step 1 to avoid convergence problems on too many simulations when using a smaller sample size (i.e. the simulated path of the process yields a likelihood that does not converge due to few transitions into some of the states). The selection of the regression coefficients required less trial and error. For Table 1 a hazard ratio of 0.905 was selected which is close to the average of the hazard ratios in Table 6 after log transformation (average −0.11 versus −0.10). For Tables 2 and 3 an odds ratio of 1.051 was selected which is to the average odds ratios in Tables 7 and 8 (after log transformation and after including the nonsignificant coefficients).

Table 1.

Bias and mean square error (MSE) of the estimate of the age odds ratio, exp(β_age), in Equation (2) for sample sizes 300 and 1000

		Sample Size 300						Sample Size 1000
		Model		Weibull		G Weibull		Model		Weibull		G Weibull
	Odds Ratio (OR)	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103
1→2	0.905	0.0298	1.31	0.0272	1.15	0.0285	1.15	0.0276	0.92	0.0266	0.90	0.0258	0.88
1→3	0.905	0.0295	1.24	0.0296	1.29	0.0298	1.27	0.0276	0.95	0.0275	0.95	0.0268	0.93
2→1	0.905	0.0290	1.18	0.0285	1.19	0.0294	1.12	0.0303	1.05	0.0306	1.11	0.0291	0.99
2→3	0.905	0.0267	1.06	0.0268	1.11	0.0269	1.11	0.0253	0.81	0.0253	0.82	0.0250	0.81
2→4	0.905	0.0439	3.03	0.0403	2.72	0.0409	2.65	0.0356	2.00	0.0310	1.88	0.0340	1.98
3→1	0.905	0.0242	0.92	0.0242	0.94	0.0260	0.95	0.0252	0.76	0.0244	0.74	0.0240	0.71
3→2	0.905	0.0239	0.96	0.0226	0.87	0.0247	0.95	0.0220	0.63	0.0213	0.64	0.0211	0.65
3→4	0.905	0.0339	2.09	0.0338	2.25	0.0357	2.17	0.0272	1.41	0.0225	1.37	0.0268	1.44

Model: the holding time satisfied our model assumption;

Weibull: the holding time for the baseline state follows Weibull distribution;

G Weibull: the holding time for the baseline state follows Generalized Weibull Distribution;

Table 2.

Bias and MSE of the estimate of the exponential hazard ratio, exp(γ_age), in Equation(3) for sample sizes 300 and 1000

		Sample Size 300						Sample Size 1000
		Model		Weibull		G Weibull		Model		Weibull		G Weibull
	Hazard Ratio (HR)	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103
1→2	1.051	−0.0133	0.50	−0.0127	0.54	−0.0124	0.59	−0.0105	0.23	−0.009	0.21	−0.0106	0.25
1→3	1.051	−0.0135	0.58	−0.0123	0.49	−0.0135	0.46	−0.0116	0.25	−0.0104	0.23	−0.0103	0.22
1→5	1.051	−0.0166	0.47	−0.0145	0.46	−0.0153	0.45	−0.0145	0.27	−0.0138	0.28	−0.0142	0.28
2→1	1.051	−0.0216	0.98	−0.0225	0.94	−0.0217	0.93	−0.0201	0.52	−0.018	0.47	−0.0191	0.50
2→3	1.051	−0.0217	0.86	−0.0215	0.81	−0.0228	0.87	−0.0206	0.55	−0.0204	0.56	−0.0221	0.61
2→4	1.051	−0.0201	0.75	−0.0203	0.79	−0.0212	0.72	−0.0202	0.52	−0.0189	0.47	−0.0195	0.50
2→5	1.051	−0.0193	0.67	−0.0181	0.64	−0.0196	0.60	−0.0186	0.44	−0.0173	0.4	−0.018	0.41
3→1	1.051	0.0029	0.17	0.0025	0.16	0.0034	0.15	0.0007	0.07	−0.0005	0.12	−0.0004	0.10
3→2	1.051	−0.0211	0.86	−0.0188	0.84	−0.0197	0.75	−0.0177	0.43	−0.0180	0.47	−0.0175	0.40
3→4	1.051	−0.0194	0.63	−0.0183	0.72	−0.0168	0.63	−0.0175	0.40	−0.0162	0.37	−0.0160	0.37
3→5	1.051	−0.0205	0.62	−0.0193	0.63	−0.0191	0.60	−0.0196	0.47	−0.0194	0.48	−0.0193	0.46

Table 3.

Bias and MSE of the estimate of the Weibull hazard ratio, exp(γ_age), in Equation (4) for sample size 300, 1000

		Sample Size 300						Sample Size 1000
		Model		Weibull		G Weibull		Model		Weibull		G Weibull
	Hazard Ratio (HR)	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103	bias	mse*103	Bias	mse*103
1→2	1.051	−0.0436	2.66	−0.0533	3.67	−0.0504	2.95	−0.0434	2.15	−0.0500	2.95	−0.0486	2.58
1→3	1.051	−0.0475	2.78	−0.0519	3.66	−0.0488	2.78	−0.0445	2.20	−0.0491	3.06	−0.0469	2.41
1→5	1.051	−0.0401	2.9	−0.0598	5.51	−0.0446	2.66	−0.0415	2.05	−0.0577	4.01	−0.0444	2.21
2→1	1.051	−0.0323	1.33	−0.0393	2.14	−0.040	1.83	−0.0302	1.11	−0.0336	1.42	−0.0359	1.47
2→3	1.051	−0.0329	1.48	−0.0369	1.97	−0.0394	1.78	−0.0302	1.11	−0.0326	1.48	−0.0358	1.45
2→4	1.051	−0.0325	1.36	−0.0373	2.12	−0.0378	1.69	−0.0292	1.05	−0.0344	1.69	−0.0333	1.35
2→5	1.051	−0.0269	1.04	−0.0319	1.65	−0.0329	1.42	−0.0261	0.80	−0.0296	1.09	−0.0319	1.13
3→1	1.051	−0.0283	1.08	−0.0336	1.35	−0.0361	1.47	−0.0286	0.90	−0.0316	1.12	−0.0340	1.25
3→2	1.051	−0.0272	1.03	−0.0322	1.34	−0.0358	1.46	−0.0285	0.89	−0.0299	1.07	−0.0345	1.27
3→4	1.051	−0.0262	0.89	−0.0302	1.14	−0.0345	1.36	−0.0267	0.78	−0.0290	0.96	−0.0329	1.17
3→5	1.051	−0.0234	0.77	−0.0232	0.83	−0.0304	1.11	−0.0230	0.61	−0.0254	0.73	−0.0301	0.96

Table 7.

The hazard ratio and confidence interval for significant covariates in the exponential distribution

Transition	Covariate	Hazard Ratio	95% Low	95% Upper	P-value
2→3	Apoe4	2.386	1.369	4.159	0.0022
2→3	No College	3.191	1.496	6.809	0.0028
2→1	Baseline Age	1.091	1.017	1.17	0.0158
2→3	Baseline Age	1.101	1.049	1.154	0.0001
2→4	Baseline Age	1.063	1.010	1.119	0.0213

Hazard ratio for baseline age is the hazard ratio for a one year increase in age.

The bias and mean square error (MSE) of age odds ratios in Equation (2) for sample sizes 300 and 1000 are shown in Table 1. From this table, we can see the effect of age on all forward transitions and the backward transitions can be well estimated, with the maximum bias 0.0439 (4.9%). Biases and MSEs stay the same when the initial holding time assumption is violated. MSE decreases as the sample size increases but biases stay almost the same, with the maximum difference 0.0113.

Table 2 lists the bias and MSE of estimated exponential hazard ratios in Equation (3) under different sample sizes. In this table, most of the biases are negative and small. The changes in MSEs and biases are very small when the exponential assumption on the holding time for the initial state is violated.

Table 3 presents the bias and MSE of the estimated Weibull hazard ratios in Equation (4) under different sample sizes. Most of the biases are negative in this table, indicating that our proposed estimation method will slightly underestimate the effect of age. It is also clear that violations to the distributional assumptions on the holding time for the initial state lead to moderately worse biases and MSEs. Additionally, increasing sample size decreases the bias and MSEs. For examples, the bias and MSE are -0.0234 and 0.77 for model assumption with sample size 300 and 0.0230 and 0.61 with sample size 1000.

A clear pattern that is perceivable from these three tables, especially Table 1 and 2, is that the bias does not shrink to zero as the sample size increases from 300 to 1000, which suggests that our estimation method may yield slightly biased estimates. The systematic bias may have two sources. The first one is due to our data generating mechanism. Specifically, we use exponential, Weibull or generalized Weibull distribution, to generate the holding time and naturally we will occasionally encounter a transition with very short holding times, which will result in missing transitions under intermittent observation scheme. The second one relates to our treatment of P_ksv in (6) where we approximate the value of P_ksv at w_k by its value at the upper bound u_k. While this approximation greatly facilitates our computation it affects our ability to precisely estimate the parameters.

These simulation studies indicate that estimation for the effect of an important covariate in Equations (2) and (3) is robust against a violation of the exponential assumption on the holding time for the initial state provided the sample size is large enough to assure adequate observations on all transitions. This is not true for estimation in Equation (4) where the lack of robustness is likely due to the effect of interval censoring on both ends of the estimation interval for the hazard function.

1. APPLICATION TO THE NUN DATA

The Nun Study began enrolment in 1991. The cohort consists of 672 members of the School Sisters of Notre Dame born before 1917 and living in retirement communities in the midwestern, eastern, and southern United States. The participants were recruited in phases and received annual cognitive assessments with brain donation at death. Analyses were based on data from up to ten unevenly spaced examinations, with time spans between two assessment ranging from 0.421 to 3.911 and mean 1.441, made in fifteen-year period. The status of a participant at each visit was recorded as being one of the states: intact cognition, mild cognitive impairments (M.C.I.), global impairments (G.I.), or dementia.¹⁸ A total of 211 subjects were excluded from the study due to: missing examinations, presence of dementia at baseline visit or missing APOE4 data. The final analytic sample consisted of 461 participants, of which 74 survived without dementia, 162 developed dementia and 225 died before converting to dementia. Among those final participants, 158 of them missed one examination and 7 of them had more than one missing examinations. The variables of interest include presence or absence of the APOE-4 allele (APOE4), education (no college, college and graduate education (reference)), and age. The transitions among the cognitive states are summarized in Figure 1.

4.1 Examples of Nun's Cognitive Paths

To better understand the data, we classified the trajectory of each Nun using three criteria. (i) Initial state: 1, 2, or 3. (ii) Final state: 1, 2, 3, 4, or 5 and (iii) Path type: non-terminal, right shift, or reversal. Non-terminal means final observed state is transient (i.e. 1, 2 or 3). Right shift means the final state is 4 or 5 and no back transition occurred. Reversal means the final state is 4 or 5 and at least one back transition occurred. The frequency of non-terminal, reversal and right shift paths, are 74 (16.1%), 131 (28.4%), and 256 (55.5%), respectively implying back transitions in these data frequently occurred. Table 4 shows some examples of these cognitive paths. The two most frequently observed paths are 2 → 4 and 2 → 5 with 100 out of 461 (21.7%) nuns having those trajectories. The total number of distinct paths observed in the Nun dataset is 84 but 32 of those have a frequency one (not shown in the table).

Table 4.

Examples of Nun's Cognitive Path

Visit Pattern	Freq	Initial State	Final State	Path Type
1	11	1	1	Non-terminal
2→4	61	2	4	Right Shift
2→5	39	2	5	Right Shift
3→4	23	3	4	Right Shift
2→3→5	32	2	5	Right Shift
2→3→4	30	2	4	Right Shift
2→1→2→5	14	2	5	Reversal
3→2→3→5	3	3	5	Reversal
1→2→1→3→5	4	1	5	Reversal
1→3→1→3→5	2	1	5	Reversal
2→1→2→1→2	3	2	2	Non-terminal
2→3→2→3→4	5	2	4	Reversal

4.2 Risk factors

The main purpose of this subsection is to identify the risk factors associated with the probability and the holding time of each transition.

Table 5 shows the frequency table for the integration orders of the likelihood (6). From the table, we can see the highest order of integration is 8 and the percentage of integration order higher than 3 is 14.31%, which makes the use of the traditional GAUSS method difficult. Therefore, we implemented a quasi-random Monte Carlo (QMC) method¹⁵ which will provide considerably better accuracy with much fewer draws and less computational time to estimate the likelihood function. In this manuscript, we choose 1000 draws with the average computational time about 30 minutes.

Table 5.

Frequency table of order of integration of the likelihood

Order of integration	Count	Relative frequency	Cumulative Relative frequency
0	63	13.67	13.67
1	177	38.39	52.06
2	108	23.43	75.49
3	47	10.20	85.69
4	36	7.83	93.50
5	13	2.82	96.32
6	8	1.74	98.06
7	7	1.52	99.58
8	2	0.43	100

The parameters associated with transition 1→4 are eliminated from our model since there are only 5 such transitions (Figure 1). Therefore, we have 942 transitions in the final analytic data which is a moderate number compared to the 145 potential parameters without interactions in our full model. Backward elimination with significance level to stay 0.05 was used to identify the covariates in the final reported model and only 57 remained after backward selection.

The odds ratios and 95% confidence intervals for the significant covariates affecting each transition probability are provided in Table 6 (base state: 5=death). The reversal path is more likely in younger Nuns. For example, the odds ratios for the three possible backward transitions (2 → 1, 3 → 1 and 3 → 2) with one year increases in age are 0.927, 0.804 and 0.900 respectively, as opposed to death. The effect of age for all the forward transitions is not significant as opposed to death except 3 → 4. Concerning the effect of APOE4 or education, the results show that the presence of APOE4 and no college education decreases the odds of the backward transition from mild impairments to intact cognition with the corresponding odds ratios being much less than 1, but the presence of APOE4 and college education increases the odds of a forward transition. The result is consistent with the historical result that the presence of APOE4 and college education promotes the probability of a right shift compared to reversal. Presence of APOE4 will promote the Nuns to dementia if the prior state is global impairment with OR=2.623 (p-value=0.0021).

The effects of covariates on the duration time for the initial state that follows an exponential distribution are also tested (see Table 7). Baseline age, APOE4 and education all have no significant influence on the holding time of transitions out of intact cognition or the global impairment. Baseline age increases the hazard ratio of transitions moving out of mild impairments to states 1, 3, and 4 with a hazard ratio 1.091, 1.101, and 1.063 respectively. Presence of APOE4 and no college education significantly promote the transition 2 → 3, by shorter the holding time with hazard ratio 2.386 and 3.191 respectively.

Table 8 lists the hazard ratio and 95% confidence interval estimate for significant effects in the non-initial transitions assuming Weibull distribution. Increasing in age increases the hazard ratio for almost all the transitions to the three transient states and death, except dementia. In other words, as the Nun gets older, the holding time at each state will be shorter on average, which makes the homogeneous semi-Markov model inappropriate. There are no differences on the holding time for transitions 2 to 3 and 2 to 5 when the Nun’s gets one year older. The holding time will be shorter for transition from 1 to 5 than to 3 with the corresponding hazard ratio 1.349 versus 1.243. APOE promotes forward transitions by shorter the holding time from 1 to 2 and 1 to 3 with the corresponding hazard ratios 2.569 and 16.856 respectively. Also if nun is in state 3, APOE keeps a nun from being demented by longer the holding time. No college education has an influence on the transitions to dementia with hazard ratio 9.575 and 0.290 for prior state 2 and 3, respectively. Some of the hazard ratios are much larger than the majority of the hazard ratios partially due to the rare observations we have. For example, we only have 3 observations in the Nun’s data for transition from 1 to 3 with the presence of APOE4.

The estimates, standard deviation, and p-values of the shape parameters (k_jj′) of the Weibull distributions are summarized in Table 9. The highly significance of these parameters justifies the use of Weibull distributions over exponential distributions.

Table 9.

The p-values of the significant shape parameters in the Weibull distribution

Transition	kjj′
	Coeff.	Std. Dev.	p-value
1→2	1.729	0.147	<.0001
1→3	2.145	0.360	<.0001
1→6	1.757	0.255	0.0001
2→1	1.863	0.173	<.0001
2→3	1.752	0.211	<.0001
2→4	2.384	0.454	<.0001
2→6	1.595	0.194	0.0001
3→2	1.852	0.348	0.0011
3→4	2.24	0.32	<.0001
3→6	1.352	0.122	0.0009

2. DISCUSSION AND CONCLUSION

In this manuscript we implemented a quasi-Monte Carlo (QMC) method to evaluate the likelihood function in a semi-Markov process with interval censored observations and backward transitions. To the best of our knowledge few researchers consider the case of semi-Markov processes with backward transitions in the presence of interval censored data. We showed that use of the QMC makes the computation of the likelihood function possible provided we assume that the time interval from the initial state to the first transition is exponentially distributed and that no additional transitions occur between successive observations of the process.

Application of our method to the Nun Study data showed that older age diminishes the chances that any back transition occurs while less than a college education and presence of an APOE 4 allele diminishes the chance of a back transition to the normal cognitive state from the mild cognitive impairments state. Further, if the latter transition does occur the time interval associated with this transition is significantly abbreviated by older age. The reason additional factors are not significant for back transitions likely have to do with the small frequency of some of these transitions as shown in Figure 1. The use of a semi-Markov process in this application is motivated by up to ten serial assessments (approximately every 15 months apart) over a fifteen-year period of the cognitive status of each participant in the study. It is possible but unlikely that the cognitive status of each nun fluctuated much in the interval between cognitive assessments meeting the assumptions of our model.

Simulation studies determined how the parameters will be estimated when the assumption made on the holding time is violated. The simulation result shows that the maximum likelihood estimates in Equations (2) and (3) are not sensitive to the violation of the assumption on the holding time for the initial state. But it is sensitive to the sample size due to the chance of observing few transitions. However, the change of observing few transitions will be very rare when the sample is larger than 500. Simulation results also show there is a persistent bias in Table 1–3. This is likely due to the replacement of w_k with u_k in Equation (6) for P_ksv. We recalculated the MLEs for the Nun study by making w_k a function of t^* in Equation (6); the resulting MLEs were no different than reported here.

Semi-Markov model has a wide application to be more accurately describing the process of interest. However, a general problem of panel data is lack of sufficient information for the progress, such as interval censoring data or some of the important transitions between two assessments are missing. Hence, despite the advantage of the semi-Markov process, the applications to the semi-Markov are limited as compared to Markov process.

Here, we only consider the situation where there is no misclassification. However, misclassification is a problem, especially for subjects with very frequently jump between two states. Therefore a possible extension of semi-Markov model is to incorporate the information of misclassification. Another possible extension of semi-Markov model is to incorporate the information between two assessments¹³, especially when the time span between two assessments is long.