Enhancement of optical coherence microscopy in turbid media by an optical parametric amplifier

Abstract

We report the enhancement in imaging performance of a spectral-domain optical coherence microscope (OCM) in turbid media by incorporating an optical parametric amplifier (OPA). The OPA provides a high level of optical gain to the sample arm, thereby improving the signal-to-noise ratio of the OCM by a factor of up to 15 dB. A unique nonlinear confocal gate is automatically formed in the OPA, which enables selective amplification of singly scattered (ballistic) photons against the multiply-scattered light background. Simultaneous enhancement in both imaging depth and spatial resolution in imaging microstructures in highly light-scattering media are demonstrated with the combined OPA-OCM setup. Typical OCM inteferograms (left) and images (right) without and with OPA.

1. Introduction

Optical coherence tomography (OCT) has emerged as an important in vivo imaging tool in modern biology and medicine [1–3]. In comparison to other existing ballistic photon imaging techniques, OCT shows two prominent advantages. First, it has excellent detection sensitivity, which is achieved based on the interferometric heterodyne process and can potentially approach the shot noise limit (the single photon limit in optical measurement) [4–6]. This high sensitivity allows OCT to efficiently detect the weak scattered light signals coming from structures deep inside light scattering tissues, thus yielding large imaging depth. Second, OCT possesses a strong coherence gate (an effective time gate) which is determined by the low temporal coherence of the broadband light source. Such an optical gate not only enables high axial resolution and optical sectioning capability, but also helps OCT to effectively reject multiply scattered background light which would otherwise degrade both the resolution and contrast [7, 8]. Owing to these advantages, OCT is able to perform high-speed and three-dimensional (3-D) imaging of bulk biological samples, which has been well appreciated in the investigation of the biological activities in living tissue and the diagnoses of different pathological states in vivo.

Optical coherence microscopy (OCM) is a high-resolution variant of OCT that normally uses objectives of large numerical aperture (NA) to achieve high lateral resolution [7, 8]. As another benefit given by the high NA objective, a strong confocal gate is formed in OCM as well, which is in part attributed to the mode confinement effect in the single-mode fibres that are commonly used in modern OCT systems. Consequently, combining the coherence and confocal gates, OCM shows advantages over confocal microscopy in imaging of microstructures deep inside biological tissues. Significantly improved imaging depth in scattering media has been demonstrated with OCM, thanks to its high efficiency in the rejection of the multiply-scattered background enabled by the optical gates and the high sensitivity given by heterodyne detection [7, 9]. However, a number of studies have shown that both the confocal and coherence gates have limited efficiency in the rejection of the multiply-scattered light [8, 10–12]. In particular, when imaging deep microstructures in tissue where the multiply-scattered photons overwhelm the ballistic signal, a large amount of unremoved background could exist. While this effect has been recognized as beneficial to increase the imaging depth in OCT, the multiply-scattered light can substantially degrade the spatial resolution and image contrast, and introduce greater speckle noise as well [13, 14]. One may resort to the use of stronger gates (such as a smaller pinhole in the confocal gate or a shorter coherence time in the coherence gate) to remove more background, but these stronger gates inevitably result in reduced signal collection efficiency, a lower signal-to-noise ratio (SNR), and eventually, limit the attainable imaging depth [10, 12]. This compromise between signal strength and background rejection is a common issue that generally affects all the existing gating approaches, including the confocal gating [11, 12], temporal gating [15, 16], and polarization gating [17, 18]. It is also recognized as a fundamental reason for the trade-off between imaging depth and spatial resolution in optical imaging of bulk scattering tissues [19, 20].

Given this intrinsic compromise in the gating approaches, a high sensitivity in the detection of weak ballistic signals under strong gating conditions is crucial in high-resolution imaging in turbid media. In this sense, the high detection sensitivity of OCM/OCT is highly desirable. While OCM/OCT, in principle, have the potential for shot-noise limited sensitivity, a number of practical issues often restrict the real sensitivity of OCT to the level of at least several decibels away from the shot-noise limit [6, 21]. In particular, in the charge-coupled detector (CCD)-based spectral domain (SD) OCM/OCT systems, where balanced detection cannot be easily implemented to suppress the excess photon (or referred to as relative intensity (RIN) [22]) noise from the light source, more than 10 dB away from the shot-noise limit is commonly expected [21, 23]. Limited dynamic range (bit depth) of the CCD and sensitivity roll-off associated with the finite spectral resolution also make considerable contributions to the degradation of sensitivity in practical SD-OCM/OCT imaging. This has raised much attention from the OCT community and many efforts have been devoted to improving the sensitivity in practical OCT imaging [24, 25].

Here we introduce an optical parametric amplifier (OPA) [26, 27] to address these challenges in OCM imaging in scattering media. First, the OPA offers a high level of signal gain with minimal extra noise, which helps suppress multiple types of noise contributions so that a significant improvement in the sensitivity of OCM is achieved. Second, a unique confocal gate is formed in the OPA, which enhances the selective detection of the ballistic photon signals against the multiply-scattered background. More prominently, the high-order nonlinear optics based confocal gate enables the OPA detection to simultaneously achieve a stronger signal and higher efficiency in the removal of multiply-scattered background, based on the generation of both a smaller pinhole and a higher signal gain at the same time. Incorporating the OPA into a SD-OCM, we demonstrate the improvement in sensitivity, imaging depth, and resolution in imaging microstructures through highly scattering media.

2. Principle

Optical parametric amplification is a nonlinear optical process in which energy is transferred among the interacting light waves. This energy and momentum conservative process has been widely utilized for the generation of laser sources of different wavelengths [26, 27]. The OPA implemented in our experiments is based on a second order optical nonlinear process in an optical crystal. During the parametric interaction, an input pump photon on the crystal is divided into two daughter photons, called the signal and idler by convention, with the sum of their energy equal to that of the pump. Any photons incident on the crystal with the same wavelength as the OPA signal will be amplified under phase-matching (determined by the conservation of momentum), along with the generation of an idler beam. Under perfect phase matching and in the large gain approximation, the amplified signal by the OPA is approximated by

$$I_s\cong \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.I_{s0}\text{exp}(2L\gamma \sqrt{I_p})$$ (1)

where γ is a crystal related constant, I_s0 and I_p are the intensities of input signal and pump, and L is the phase-matched interaction length [26, 27].

For the amplification of weak light signals, OPAs are advantageous because of their high gain (up to 80 dB) and excellent noise figure down to the quantum limit (as low as 0 dB in a phase-sensitive mode and 3 dB in a phase-insensitive mode) [28, 29]. The coherent nature of parametric process enables the optical properties of signal photons to be preserved during the amplification, making OPAs particularly suitable for amplifying weak signals for optical imaging and sensing, where the information of interest is embedded into the parameters of the coherent signal photons. OPAs has been implemented previously to improve the performance of optical imaging, but the spatial resolution was limited to a level in the order of tens of microns [30–32]. In the current work we demonstrate the benefits given by an OPA to OCM imaging in scattering media, including the improvement in SNR and the enhancement of both spatial resolution and imaging depth.

To investigate the enhancement to the SNR of OCT/OCM by the OPA, we follow the well-developed SNR analysis in the OCT literature [3–5]. Specifically, the SNR of a standard SD-OCT setup is given by

$${\mathit{\text{SNR}}}_{\mathit{\text{SD-OCT}}}=\frac{\langle S_{\mathit{\text{SD-OCT}}}^2\rangle }{{\sigma }_{\mathit{\text{receiver}}}^2+{\sigma }_{\mathit{\text{shot}}}^2+{\sigma }_{\mathit{\text{RIN}}}^2}$$ (2)

where S_SD–OCT is the interference signal, and ${\sigma }_{\mathit{\text{receiver}}}^2,{\sigma }_{\mathit{\text{shot}}}^2$, and ${\sigma }_{\mathit{\text{RIN}}}^2$ represent the receiver noise, shot noise, and relative intensity noise, respectively. In our OPA-enhanced OCT/OCM setup, the back-reflected light in the sample arm is first amplified by the OPA, then mixed with the light from the reference arm for interferometric measurement. Theoretical signals and noise contributions for a typical SD-OCT setup with and without the OPA gain are listed in Table 1. In these equations, P_r and P_s are the reference and sample arm powers incident on the CCD sensor in the spectrometer; η and τ are the quantum efficiency and pixel integration time of the CCD; ${\sigma }_{\mathit{\text{read}}}^2$ and ${\sigma }_{\mathit{\text{dark}}}^2$ are the read-out and dark-photon noises of the CCD Γ and Δv are the polarization degree and frequency bandwidth of the light source; and G and P_sf are the gain factor and superfluorescence introduced by the OPA, respectively [33]. Note that G² is adopted in the formula for the shot noise in the amplified case to account for the quantum noise introduced by the OPA [28, 29]. The relative intensity noise, ${\sigma }_{\mathit{\text{RIN}}}^2$, originates from the beating of various spectral components having random phases, including self-beating and cross-beating between the reference and sample arm beams [22, 24]. When no OPA gain is present, and the reference arm power is much higher than that of the sample arm, only self-beating of the reference beam is considered to account for the RIN source. When OPA gain is involved, the RIN consists of the self-beating of the reference beam and the amplified sample beam, and the cross-beating between these two beams.

Table 1.

Signal and noise sources for a typical SD-OCT system.

	Without OPA	Without OPA
SSD–OCT	η2τ2PrPs	η2τ2PrPsG
${\sigma }_{\mathit{\text{receiver}}}^2$	${\sigma }_{\mathit{\text{read}}}^2+{\sigma }_{\mathit{\text{dark}}}^2$	${\sigma }_{\mathit{\text{read}}}^2+{\sigma }_{\mathit{\text{dark}}}^2$
${\sigma }_{\mathit{\text{shot}}}^2$	ητ(Pr + Ps)	ητ(Pr + PsG2 + Psf)
${\sigma }_{\mathit{\text{RIN}}}^2$	$\frac{(1+{\mathrm{\Gamma }}^2){\eta }^2{\tau }^2[{(P_r+P_s)}^2+P_r{P}_s]}{2\mathrm{\Delta }v}$	$\frac{(1+{\mathrm{\Gamma }}^2){\eta }^2{\tau }^2[{(P_r+P_{s}G+P_{\mathit{\text{sf}}})}^2+P_r(P_{s}G+P_{\mathit{\text{sf}}})]}{2\mathrm{\Delta }\mathit{\text{vN}}}$

The predicted noise sources and SNRs are plotted in Fig. 1, which were calculated based on Eq. 2 and the formulas in Table 1. As shown in Fig. 1(a), the SNR in the OPA enhanced OCM increases with OPA gain in the low gain regime and saturates when the gain ratio is close to ~28 dB. In the large gain regime, the OPA enhanced SNR turns down and enters the region where the SNR is limited by the increased relative intensity noise and shot noise associated with the amplified signal beam of high power. Maximum SNR enhancement of 16 dB is observed when the OPA gain is about 28 dB.

Figure 1.

Theoretical results of the OCM SNR and different noise powers at various OPA gain ratios (a) and reference powers (b). The data were calculated based on the equations in Table 1.

In CCD-based SD-OCT systems, where balanced detection cannot be easily implemented, the reference power needs to be carefully chosen to obtain the optimal SNR. While we need to use sufficient reference power to suppress the contributions from the receiver noise sources, too high of reference power will introduce strong RIN noise that drives the SNR away from the shot-noise limit [25]. The effect of the reference power on our OCM (both with and without the OPA gain) is calculated and depicted in Fig. 1(b). By comparing the two curves, it is shown that higher SNR is obtainable when using higher reference power in OPA-enhanced OCM. This may seem counter-intuitive because one would expect more RIN noise when using higher reference power. In fact, because the OPA amplified sample arm has a better match with the reference power, the RIN noise can be effectively suppressed, thereby leading to a higher SNR, as shown in the blue cure in the Fig. 1(b).

Another benefit offered by the OPA is a unique confocal gate that is intrinsically formed due to the nonlinear nature of the parametric amplification process. In our unique OPA setup (as detailed in the Experiments and Results section), the pump and signal beam are both focused and superimposed in the optical crystal. Under this geometry, because of the high order nonlinear dependence of the amplified signal on the pump and signal light intensities, the interaction volume of the OPA process is confined within the focal region in the crystal, forming a virtual pinhole, which has an analogous principle to other nonlinear optical imaging techniques [34–36]. The OPA confocal gate not only enables high axial resolution and optical sectioning capability, as in a conventional confocal gate, but also has a distinctive feature that can enhance high-resolution OCM imaging in scattering media (such as bulk or in vivo biological tissues).

Because of the exponential relationship (Eq. 1), higher order nonlinearity is expected with a higher pump intensity. For example, in the low-gain regime (e.g. less than two for single-pass amplification), the exponential relationship is approximated as a linear function. The equation can then be simplified as $I_s~I_{s0}\sqrt{I_p}$. Under our typical experimental conditions, the single-pass gain is in the approximate range of 71~84 (5000~7000 for double-pass amplification), and the relationship is approximated by I_s ~ I_s0I_p^4.3. According to principles in nonlinear imaging [35, 37] and assuming the two foci have the same focal size (taking no account of the difference in wavelength and beam diameter before the focusing lens), the full-width-at-half-maximum (FWHM) of the intensity point-spread-functions (PSFs), i.e., the diameter of the virtual pinhole in the OPA, are reduced by a factor of $1/\sqrt{1.5}$ and $1/\sqrt{5.3}$ in the low and high gain regimes, respectively. Apparently, a smaller virtual pinhole is expected with a higher pump power. The smaller pinhole results in a higher rate of rejection of multiply-scattered background light, which is of substantial significance in imaging structures in scattering media. Although this decreased pinhole size will also reduce the strength of the ballistic imaging signal, the low signal can be compensated for by the high optical gain associated with the high pump intensity. As a result, the enhancement in both the rejection of the multiply-scattered background light and the strength of the ballistic signal are achieved simultaneously, which is in sharp contrast to the well-known trade-off between these two in conventional optical gating approaches, including confocal and coherence gates.

Confocal gating plays an important role in high-resolution imaging in scattering media, which helps filter out the ballistic photons from the multiply-scattered light background [11, 12]. However, the fundamental compromise between gating efficiency and signal strength in the conventional confocal gate limits its effect in deep tissue imaging. For example, for a conventional confocal gate based on a physical pinhole, a smaller pinhole is required to provide efficient rejection of multiply-scattered background, but in the meanwhile, the reduced pinhole size leads to decreased efficiency in the collection of the imaging-bearing ballistic photon signals. This subsequently imposes a fundamental limit on the penetration depth in optical imaging of scattering tissue, which essentially affects all other linear gating technologies, including time and polarization gates. Therefore, by alleviating the trade-off and providing both a higher signal and a smaller pinhole, the OPA confocal gate is expected to make a substantial contribution to high-resolution OCM imaging in scattering media.

3. Experiments and results

The schematic setup of the OPA-OCM imaging system is shown in Fig. 2(a). The laser source was a 250 kHz Ti:sapphire regenerative amplifier system (RegA 9000, Coherent), which provides 100 fs, 800 nm laser pulses with maximum energies of approximately 4 µJ. The laser pulses were split into two parts by a 75:25 beam splitter (BS1). The first part, with pulse energy of ~3 µJ, was frequency doubled in a 0.5 mm type I beta barium borate (BBO) to generate 400 nm pulses as the pump of the OPA. A white light supercontinuum (SC) was generated by focusing the weak part (with pulse energy of ~0.7 µJ) into a 1 mm thick sapphire plate, which served as the broadband low coherence source for OCM. The white light was passed through a 50:50 beam splitter (BS2) and a band-pass filter (620 ± 40 nm), then focused onto the sample by an objective (20×, 0.5 NA). The signal light (i.e., the sample arm of the OCM), which is back-scattered from the sample, propagated in the backward direction along the same path and passed through the 50:50 beam splitter towards the OPA setup.

Figure 2.

OPA-OCM imaging setup and OPA gain. (a) Schematic of the OPA-OCM imaging setup. BBO: beta-barium borate crystal; BS: beam splitter; DC: dichroic mirror; DL: delay line. (b) Supercontinuum spectra measured without (pink curve) and with (blue curve) the OPA gain.

For the OPA setup, both the re-collimated signal and pump beams, after passing through separately controlled delay paths, were combined collinearly by a dichroic mirror. The collinearly aligned signal and pump were then focused and mixed in another 0.5 mm type I BBO crystal to generate the optical parametric process. Afterwards, the two beams were separated and recombined for the second round amplification to obtain large OPA gain. The other portion of the SC beam, which passed through the 50:50 beam splitter (BS2) served as the reference arm for OCM. This OCM reference arm and the amplified (or unamplified when the OPA pump beam was blocked) signal (sample) beam were combined at another 50:50 beam splitter (BS3), forming a Mach-Zehnder interferometer. The interference signal was measured by a single-mode fiber-coupled spectrometer composed of a grating (1200 lines/mm), a collimating lens (f=150 mm) and a line-scan CCD (P2-22-02k40, Dalsa). The interferogram output from the CCD was recorded by a camera-link card (PCI-1428, National Instruments) and post-processed by a custom-written Labview (NI) interface program. A spectral region spanning from 600 nm to 660 nm was selected for the OCM image formation. Scanning of samples was achieved by translating the samples with a motorized translation stage. This experimental setup allowed for the direct comparison of the performance of the OCM imaging with and without the OPA, by simply blocking and unblocking the OPA pump beam.

The optical gain of the OPA was first investigated by comparing the amplified (blue circles) and unamplified (pink crosses) sample arm spectra (Fig. 2(b)). The spectra were back-reflected SC from a silver mirror placed at the focus of the objective (0.5 NA), measured with (OPA amplified) and without (unamplified) the presence of the OPA pump beam. It is observed from Fig. 2(b) that a signal gain of ~ 5500 (37 dB) at a peak wavelength of 636 nm was provided by the OPA. The gain bandwidth was ~ 16 nm, which was determined by the pump bandwidth and the phase matching in the crystal. We should note that a much broader gain bandwidth of up to a few hundreds of nanometers is attainable based on non-collinear OPA geometry or in quasi-phase matched crystals [36].

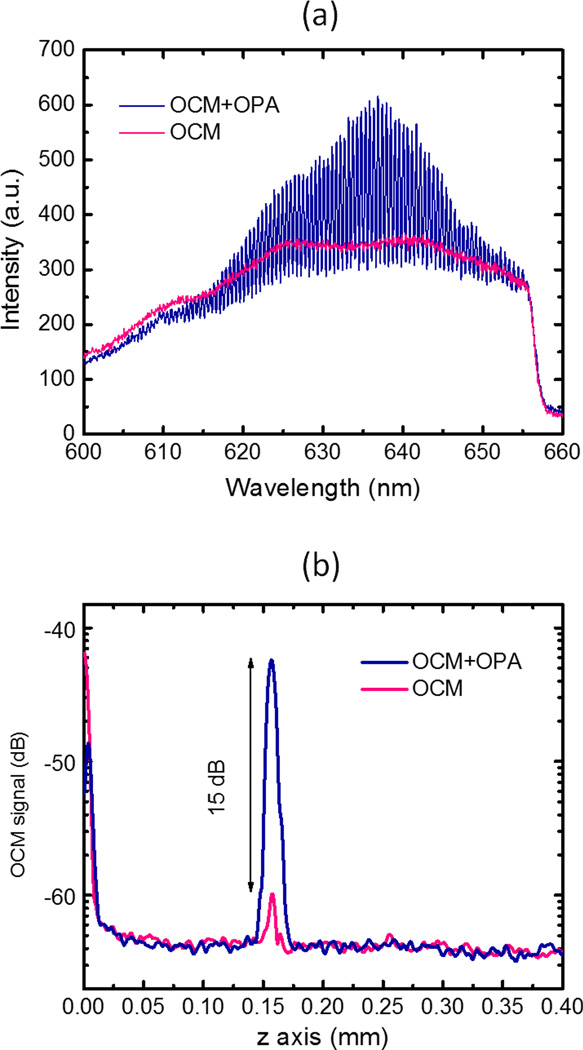
Figure 3(a) shows two measured interferograms between the reference and the sample arms with and without the OPA gain. Because of the weakness of the unamplified sample arm in comparison to the reference arm, an interference pattern is barely visible in the spectra measured without the OPA. In contrast, because of the matched power of the amplified sample arm and reference arm, significantly enhanced fringes are observed from the spectra measured with the OPA. The improved fringe visibility results in substantial enhancement of the OCM signal and SNR. This is manifested by the two OCT/OCM A-scans shown in Fig. 3(b), which were derived based on the Fourier transform of the two interferograms in Fig. 3(a). The measured ~15 dB SNR improvment is in good agreement well with the calculated 16 dB (Fig. 1(a)). The slight broadening of the point spread function (PSF) is due to the narrowed bandwidth of the sample arm with the OPA gain (16 nm), compared to that of the unamplified SC sample arm (50 nm).

Figure 3.

OCT/OCM interferograms (a) and A-scan signals (b) measured with (blue curve) and without (pink curve) the OPA gain. The signals were measured by placing a silver mirror at the focus of the objective in the sample arm.

The improved SNR of OCM imaging by the OPA gain is demonstrated by the images of a United States Air Force (USAF) resolution target (Fig. 4). At low incident power (0.2 µW), a highly noisy OCM image was obtained without the OPA gain (Fig. 4(a)). The horizontal striping seen in this OCM image is attributed primarily to the effect of low frequency laser amplitude fluctuations. In contrast, a clear image was recovered from the noisy background in OPA-enhanced OCM (Fig. 4(b)). In comparison to the reference image (Fig. 4(c)), which was obtained by OCM (without OPA) with intentionally increased incident power (18 µW), no resolution degradation is observed from the OPA enhanced OCM image. It should be noted that despite the similarity in the two images, the substantially lower incident power is of important significance for reducing or eliminating photo damage when biological samples are investigated.

Figure 4.

OCM images of a USAF resolution chart (group 7) obtained without (a,c) and with (b) the OPA gain. The incident powers used are 0.2 µW and 1.8 µW for (a, b) and (c), respectively. The scale bar represents 50 µm.

The confocal gate, as a more prominent benefit of the OPA, was first investigated by measuring the axial resolution of the OPA based imaging system. Figure 5 shows the axial point spread functions (PSF) of the OPA and a conventional confocal setup with and without the presence of scattering media, which was measured by blocking the reference arm to rule out the effect of the coherence gate. In OPA detection, the amplified signal is coupled into a multimode fiber with a core size of 62.5 µm, which is much larger than the beam waist (~3 µm in diameter) focused by the coupling objective (10× 0.25 NA). This implies that there is no significant effect imposed on the axial response by the fiber coupling. For comparison, in a conventional confocal setup, the unamplified signal (by blocking the OPA pump) was coupled into a single mode fiber with a core size of 3.7 µm. As shown by Fig. 5(a), the OPA PSF is approximately the same as that of the conventional confocal setup. However, when scattering media (two sheets of lens paper) are present, the PSF of the conventional confocal gate is substantially degraded, whereas the OPA PSF is well conserved. This suggests that the OPA confocal gate has a higher efficiency for removing the multiply scattered light, which is attributed to the smaller pinhole generated in the OPA versus that in the conventional confocal gate.

Figure 5.

Axial point spread functions from an OPA (blue curves) and conventional confocal (pink curves) microscope setups, which were measured when no scattering media (a) and two sheets of lens cleaning paper (b) were placed on top of the sample. The curves were measured by translating a silver mirror along the axial direction through the focus.

The benefit of the OPA confocal gate to OCM for high-resolution imaging through scattering media is manifested in the images of the USAF target in the presence of scattering media of different thicknesses (Fig. 6). Enhancement of imaging depth by the OPA in (thicker) scattering media is observed by the comparison of the OCM images obtained with and without the OPA. Moreover, under the same conditions, stronger blurring effect is seen in the OCM image (Fig. 6(b)), which suggests more multiply-scattered light remains present in the conventional OCM. Excluding the contributions from multiply-scattered light, the imaging depth of the OCM-OPA setup is improved by about 1.7 mean free paths (corresponding to approximately 150–200 µm in a typical biological sample). In these experiments, different layers of lens cleaning paper were used as the scattering media. It was measured that one sheet/layer of lens cleaning paper attenuated ballistic photons at 638 nm by 8.9 dB, corresponding to 1.95 mean free paths [39]. In biological samples, the scattering mean free path for near infrared light is typically of the order of 100 µm [2]. This enhancement of the imaging depth indicates that the OPA forms a smaller virtual pinhole (with a high pump intensity) that enables an improved rejection of multiply-scattered light as well as a higher gain of the image-bearing ballistic photons.

Figure 6.

OPA-OCM imaging through scattering media. (a) OCM images of the USAF resolution chart (group 7) obtained without (left column) and with (right column) the OPA gain. Zero, two, three, and four sheets of lens paper were introduced when obtaining the images from the top row to the bottom row, respectively. (b) Enlarged images of the top third row in (a). The scale bars represent 50 µm.

4. Discussion

Given its advantages in amplifying weak signals (such as high gain, low excess noise, and its coherent nature), OPAs have been used for amplification of signals from a variety of optical imaging methods, including optical projection tomography [30] and image amplification [31, 32, 39]. However, to our knowledge, no previous investigations have studied the combination of OPA and OCT/OCM imaging. In this work, we investigated the benefits that OPA can provide to OCM imaging in scattering media, which includes the enhancement in SNR, imaging depth, and spatial resolution.

In the last few decades, there has been vigorous debates in the OCT community about the SNR benefits from optical amplifiers. Theoretically by itself, OCT can reach the shot-noise limit, which is referred to as the single photon limit in light detection set by the laws of quantum physics. Because the optical amplifiers have no effect on the quantum state of the photons (such as state squeezing [40]), the use of these amplifiers in OCT is not expected to overcome the shot-noise limit. In contradiction, however, several groups have demonstrated improved SNR of OCT by using different optical amplifiers, such as semiconductor amplifiers and fiber amplifiers based on stimulated emission and stimulated Raman scattering, respectively. SNR improvements on the order of 10 to 20 dB [24, 41–43], extended depth, and improved contrast in OCT imaging, have been reported when optical amplifiers are used.

To understand this contradiction, we should first note that the shot-noise limit regime in OCT refers to the condition where the shot noise dominates other noise sources, which does not require that the other noise components make no contribution to the SNR of OCT. Considering the multiple practical factors in different OCT systems, the optimal sensitivity is in fact often away from the true shot-noise limit by at least several decibels [6]. For example, as aforementioned and extensively discussed in the literature, in SD-OCT systems where balanced detection is often not implemented, the sensitivity can be restricted by the RIN by more than 10 dB away from the shot-noise limit [21, 23, 25]. Also, due to the signal roll-off as a result of the finite spectral resolution, SNR degradation is expected with increasing imaging depth. In these cases, the optical amplifiers that boost the signal to match the reference power will certainly suppress the noise contributions from the light sources (RIN) and the receiver noise sources, as shown by our data and the discussions in Section 2 of this paper. Although some excess noise sources will be introduced by the amplifiers, particularly in the high gain region, these noise contributions are still considered to be subordinate to the shot-noise as shown by our theory. In comparison to semiconductor amplifiers that are based on stimulated emission, the OPA is advantageous because of the lower additive noise associated with the spontaneous emission in gain media [24, 41], despite the favourable simplicity, low-cost, and vesartile operation wavelengths of the semicondutor amplifiers.

In addition to the SNR benefit, more importantly, we showed that the OPA confocal gate helps to alleviate the conventional trade-off between signal strength and background removal in high-resolution OCM imaging in scattering media. This unique OPA confocal gate makes remarkable contributions to enhance both resolution and imaging depth in high-resolution imaging of highly scattering samples. It is also important to note that this nonlinear optics based confocal gate is formed within the crystal placed in the signal detection arm, instead of taking place in the focal region within sample, as in most of the existing nonlinear optical imaging techniques [34–36]. In fact, this configuration in this study made it possible to use high laser intensity to take advantage of the higher order nonlinearity of the optical parametric process. This would otherwise be impossible if the interaction were to occur inside the sample, where the incident laser intensity would be limited by the risk of photo-damage to the sample.

Another important property of the OPA is its coherent nature, which enables the physical parameters of the signal photons to be preserved and measured following the amplification. This is particularly important in high-resolution optical imaging, because conservation of the spatial frequency bandwidth is crucial to obtain optimal (diffraction limited) spatial resolution [31, 32, 39]. Theoretically, this is expected when considering the coherence nature of the optical parametric process. However, constrained by the phase-matching, narrowed bandwidths of amplified spatial frequencies have been reported in many previous OPA imaging studies, where the obtainable spatial resolutions were limited to no better than several tens of microns [30–32]. In the past, this limitation has put into question the feasibility and advantage of using OPA for high resolution imaging. The results in Fig. 2 and 3, which show that the amplified signal is coherent with the reference, are considered as important experimental evidence confirming the coherent nature of the optical parametric process. No resolution degradation is observed in the OPA-enhanced imaging, which demonstrates that it is possible to overcome the resolution limitations presented in previous studies when applying OPA for high resolution imaging and microscopy. Although some spectral narrowing is seen, this can be overcome by using different OPA geometries or crystals, and OPA gain bandwidths of a few hundreds of nanometers have been reported based on non-collinear OPAs [38]. This high bandwidth enables sufficiently high axial resolution when using the OPA for cross-sectional OCT imaging.

5. Conclusion

In conclusion, we have demonstrated that a specially designed OPA enhances the performance of SD-OCM when imaging microfeatures through scattering media. The benefits given by the OPA include high gain and low excess noise, which improves the SNR of OCM, and a unique confocal gate that contributes to the improvement of both imaging depth and spatial resolution. The demonstrated success of combining the OPA with OCM imaging is important evidence that confirms the coherent nature of the OPA process, suggesting that OPA detection can preserve the optical information carried by the signal photons. This makes the OPA potentially useful as a general purpose optical amplifier in other optical biomedical imaging modalities where the detection of weak signals is a pervasive challenge. The unique feature of the OPA confocal gate is considered as another benefit given by the high-order nonlinearity of the process in the nonlinear crystal. Because of the high laser intensity requirement, this is only made possible by shifting the nonlinear process to the crystal placed in the detection arm of the system. This differentiates the technology from other existing nonlinear imaging methods in which the incident laser is restricted by the photo-damage to the sample. Although this work only demonstrated the enhancement in OCM, this technology should similarly be useful for OCT, provided a larger amplification bandwidth is available to support a higher axial resolution. In particular, since the four-wave mixing based parametric amplification has been demonstrated in optical fibres [44, 45], this technology should be easily implemented in fibre-based OCT systems as well.

Biographies

Youbo Zhao received his B.S. degree in applied physics from Beijing Institute of Technology, Beijing, China, in 1997, and his Ph.D. degree in optical engineering from Nankai University, Tianjin, China, in 2007. He is currently a postdoctoral research associate in the Biophotonics Imaging Laboratory at the University of Illinois at Urbana-Champaign, Urbana, IL. His research interests include developing and using novel optical imaging technologies for biomedical studies.

Haohua Tu was born in Wuhan, China, in 1969. He received the B.S. degree in chemical engineering from TsingHua University, Beijing, China, and the Ph.D. degree in chemical engineering and material science from the University of Kentucky, Lexington. From 2001 to 2005, he was a Postdoctoral Scientist at University of North Carolina, and at University of California-Merced. Since 2005, he has been a Research Scientist at the Biophotonics Imaging Laboratory, Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana.

Yuan Liu received his B.S. and M.S. degrees in physics from National Taiwan University, Taipei, Taiwan, in 2004 and 2006. He is currently working toward the Ph.D. degree in Bioengineering at University of Illinois at Urbana-Champaign, Urbana, Illinois. His research interests include developing novel fiber supercontinuum sources and pulse shaping techniques for biophotonic imaging and spectroscopy.

Andrew J. Bower received the B.S. degree in optical engineering and physics from Rose-Hulman Institute of Technology in 2012. He is currently a Ph.D. candidate in electrical and computer engineering at the University of Illinois at Urbana-Champaign. He is a research assistant in the Biophotonics Imaging Laboratory at the Beckman Institute for Advanced Science and Technology. His research interests include the development of quantitative analysis tools for multimodal optical microscopy.

Stephen A. Boppart is currently a Bliss Professor of Engineering in the Departments of Electrical and Computer Engineering, Bioengineering, and Medicine, University of Illinois at Urbana-Champaign. He received the B.S. degree in electrical and bioengineering and the M.S. degree in electrical engineering from the University of Illinois at Urbana-Champaign, Urbana, IL, in 1990 and 1991, respectively, the Ph.D. degree in electrical and medical engineering from the Massachusetts Institute of Technology, Cambridge, in 1998, and the M.D. degree from Harvard Medical School, Boston, MA, in 2000. His research interests include the development of novel optical imaging technologies for biological and medical applications, with particular emphasis on translating these to clinical applications.