The ATLAS Collaboration1,
G Aad
G Aad
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
T Abajyan
T Abajyan
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
B Abbott
B Abbott
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
J Abdallah
J Abdallah
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
S Abdel Khalek
S Abdel Khalek
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
A A Abdelalim
A A Abdelalim
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
O Abdinov
O Abdinov
15Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
15,
R Aben
R Aben
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
B Abi
B Abi
141Department of Physics, Oklahoma State University, Stillwater, OK United States of America
141,
M Abolins
M Abolins
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
O S AbouZeid
O S AbouZeid
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
H Abramowicz
H Abramowicz
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
H Abreu
H Abreu
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
Y Abulaiti
Y Abulaiti
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
B S Acharya
B S Acharya
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
209ICTP, Trieste, Italy
208,209,
L Adamczyk
L Adamczyk
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
D L Adams
D L Adams
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
T N Addy
T N Addy
79Department of Physics, Hampton University, Hampton, VA United States of America
79,
J Adelman
J Adelman
222Department of Physics, Yale University, New Haven, CT United States of America
222,
S Adomeit
S Adomeit
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
T Adye
T Adye
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
S Aefsky
S Aefsky
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
T Agatonovic-Jovin
T Agatonovic-Jovin
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
J A Aguilar-Saavedra
J A Aguilar-Saavedra
156Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
156,
M Agustoni
M Agustoni
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
S P Ahlen
S P Ahlen
30Department of Physics, Boston University, Boston, MA United States of America
30,
F Ahles
F Ahles
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
A Ahmad
A Ahmad
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
M Ahsan
M Ahsan
62Physics Department, University of Texas at Dallas, Richardson, TX United States of America
62,
G Aielli
G Aielli
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
T P A Åkesson
T P A Åkesson
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
G Akimoto
G Akimoto
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
A V Akimov
A V Akimov
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
M A Alam
M A Alam
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
J Albert
J Albert
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
S Albrand
S Albrand
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
M J Alconada Verzini
M J Alconada Verzini
95Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
95,
M Aleksa
M Aleksa
44CERN, Geneva, Switzerland
44,
I N Aleksandrov
I N Aleksandrov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
F Alessandria
F Alessandria
116INFN Sezione di Milano, Milano, Italy
116,
C Alexa
C Alexa
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
G Alexander
G Alexander
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
G Alexandre
G Alexandre
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
T Alexopoulos
T Alexopoulos
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
M Alhroob
M Alhroob
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
M Aliev
M Aliev
21Department of Physics, Humboldt University, Berlin, Germany
21,
G Alimonti
G Alimonti
116INFN Sezione di Milano, Milano, Italy
116,
J Alison
J Alison
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
B M M Allbrooke
B M M Allbrooke
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
L J Allison
L J Allison
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
P P Allport
P P Allport
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
S E Allwood-Spiers
S E Allwood-Spiers
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J Almond
J Almond
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
A Aloisio
A Aloisio
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
R Alon
R Alon
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
A Alonso
A Alonso
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
F Alonso
F Alonso
95Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
95,
A Altheimer
A Altheimer
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
B Alvarez Gonzalez
B Alvarez Gonzalez
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
M G Alviggi
M G Alviggi
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
K Amako
K Amako
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
Y Amaral Coutinho
Y Amaral Coutinho
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
C Amelung
C Amelung
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
V V Ammosov
V V Ammosov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
S P Amor Dos Santos
S P Amor Dos Santos
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
A Amorim
A Amorim
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
S Amoroso
S Amoroso
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
N Amram
N Amram
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
C Anastopoulos
C Anastopoulos
44CERN, Geneva, Switzerland
44,
L S Ancu
L S Ancu
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
N Andari
N Andari
44CERN, Geneva, Switzerland
44,
T Andeen
T Andeen
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
C F Anders
C F Anders
82Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
82,
G Anders
G Anders
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
K J Anderson
K J Anderson
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A Andreazza
A Andreazza
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
V Andrei
V Andrei
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
X S Anduaga
X S Anduaga
95Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
95,
S Angelidakis
S Angelidakis
13Physics Department, University of Athens, Athens, Greece
13,
P Anger
P Anger
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
A Angerami
A Angerami
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
F Anghinolfi
F Anghinolfi
44CERN, Geneva, Switzerland
44,
A V Anisenkov
A V Anisenkov
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
N Anjos
N Anjos
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
A Annovi
A Annovi
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
A Antonaki
A Antonaki
13Physics Department, University of Athens, Athens, Greece
13,
M Antonelli
M Antonelli
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
A Antonov
A Antonov
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
J Antos
J Antos
184Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
184,
F Anulli
F Anulli
164INFN Sezione di Roma I, Roma, Italy
164,
M Aoki
M Aoki
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
L Aperio Bella
L Aperio Bella
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
R Apolle
R Apolle
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
G Arabidze
G Arabidze
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
I Aracena
I Aracena
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
Y Arai
Y Arai
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
A T H Arce
A T H Arce
66Department of Physics, Duke University, Durham, NC United States of America
66,
S Arfaoui
S Arfaoui
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
J-F Arguin
J-F Arguin
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
S Argyropoulos
S Argyropoulos
63DESY, Hamburg and Zeuthen, Germany
63,
E Arik
E Arik
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
M Arik
M Arik
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
A J Armbruster
A J Armbruster
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
O Arnaez
O Arnaez
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
V Arnal
V Arnal
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
A Artamonov
A Artamonov
123Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
123,
G Artoni
G Artoni
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
D Arutinov
D Arutinov
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Asai
S Asai
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
N Asbah
N Asbah
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
S Ask
S Ask
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
B Åsman
B Åsman
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
L Asquith
L Asquith
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
K Assamagan
K Assamagan
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
R Astalos
R Astalos
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
A Astbury
A Astbury
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
M Atkinson
M Atkinson
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
B Auerbach
B Auerbach
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
E Auge
E Auge
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
K Augsten
K Augsten
158Czech Technical University in Prague, Praha, Czech Republic
158,
M Aurousseau
M Aurousseau
186Department of Physics, University of Johannesburg, Johannesburg, South Africa
186,
G Avolio
G Avolio
44CERN, Geneva, Switzerland
44,
D Axen
D Axen
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
G Azuelos
G Azuelos
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
Y Azuma
Y Azuma
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
M A Baak
M A Baak
44CERN, Geneva, Switzerland
44,
G Baccaglioni
G Baccaglioni
116INFN Sezione di Milano, Milano, Italy
116,
C Bacci
C Bacci
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
A M Bach
A M Bach
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
H Bachacou
H Bachacou
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
K Bachas
K Bachas
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
M Backes
M Backes
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
M Backhaus
M Backhaus
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J Backus Mayes
J Backus Mayes
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
E Badescu
E Badescu
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
P Bagiacchi
P Bagiacchi
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
P Bagnaia
P Bagnaia
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
Y Bai
Y Bai
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
D C Bailey
D C Bailey
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
T Bain
T Bain
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
J T Baines
J T Baines
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
O K Baker
O K Baker
222Department of Physics, Yale University, New Haven, CT United States of America
222,
S Baker
S Baker
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
P Balek
P Balek
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
F Balli
F Balli
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
E Banas
E Banas
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
P Banerjee
P Banerjee
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
Sw Banerjee
Sw Banerjee
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
D Banfi
D Banfi
44CERN, Geneva, Switzerland
44,
A Bangert
A Bangert
193School of Physics, University of Sydney, Sydney, Australia
193,
V Bansal
V Bansal
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
H S Bansil
H S Bansil
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
L Barak
L Barak
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
S P Baranov
S P Baranov
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
T Barber
T Barber
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
E L Barberio
E L Barberio
113School of Physics, University of Melbourne, Victoria, Australia
113,
D Barberis
D Barberis
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
M Barbero
M Barbero
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
D Y Bardin
D Y Bardin
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
T Barillari
T Barillari
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
M Barisonzi
M Barisonzi
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
T Barklow
T Barklow
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
N Barlow
N Barlow
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
B M Barnett
B M Barnett
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
R M Barnett
R M Barnett
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
A Baroncelli
A Baroncelli
168INFN Sezione di Roma Tre, Roma, Italy
168,
G Barone
G Barone
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
A J Barr
A J Barr
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
F Barreiro
F Barreiro
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
J Barreiro Guimarães da Costa
J Barreiro Guimarães da Costa
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
R Bartoldus
R Bartoldus
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
A E Barton
A E Barton
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
V Bartsch
V Bartsch
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
A Basye
A Basye
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
R L Bates
R L Bates
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
L Batkova
L Batkova
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
J R Batley
J R Batley
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
A Battaglia
A Battaglia
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
M Battistin
M Battistin
44CERN, Geneva, Switzerland
44,
F Bauer
F Bauer
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
H S Bawa
H S Bawa
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
S Beale
S Beale
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
T Beau
T Beau
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
P H Beauchemin
P H Beauchemin
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
R Beccherle
R Beccherle
71INFN Sezione di Genova, Genova, Italy
71,
P Bechtle
P Bechtle
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
H P Beck
H P Beck
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
K Becker
K Becker
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
S Becker
S Becker
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
M Beckingham
M Beckingham
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
K H Becks
K H Becks
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
A J Beddall
A J Beddall
26Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
26,
A Beddall
A Beddall
26Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
26,
S Bedikian
S Bedikian
222Department of Physics, Yale University, New Haven, CT United States of America
222,
V A Bednyakov
V A Bednyakov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
C P Bee
C P Bee
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
L J Beemster
L J Beemster
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
T A Beermann
T A Beermann
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
M Begel
M Begel
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
C Belanger-Champagne
C Belanger-Champagne
112Department of Physics, McGill University, Montreal, QC Canada
112,
P J Bell
P J Bell
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
W H Bell
W H Bell
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
G Bella
G Bella
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
L Bellagamba
L Bellagamba
27INFN Sezione di Bologna, Bologna, Italy
27,
A Bellerive
A Bellerive
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
M Bellomo
M Bellomo
44CERN, Geneva, Switzerland
44,
A Belloni
A Belloni
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
O L Beloborodova
O L Beloborodova
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
K Belotskiy
K Belotskiy
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
O Beltramello
O Beltramello
44CERN, Geneva, Switzerland
44,
O Benary
O Benary
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
D Benchekroun
D Benchekroun
170Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
170,
K Bendtz
K Bendtz
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
N Benekos
N Benekos
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
Y Benhammou
Y Benhammou
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
E Benhar Noccioli
E Benhar Noccioli
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
J A Benitez Garcia
J A Benitez Garcia
203Department of Physics and Astronomy, York University, Toronto, ON Canada
203,
D P Benjamin
D P Benjamin
66Department of Physics, Duke University, Durham, NC United States of America
66,
J R Bensinger
J R Bensinger
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
K Benslama
K Benslama
162Physics Department, University of Regina, Regina, SK Canada
162,
S Bentvelsen
S Bentvelsen
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
D Berge
D Berge
44CERN, Geneva, Switzerland
44,
E Bergeaas Kuutmann
E Bergeaas Kuutmann
21Department of Physics, Humboldt University, Berlin, Germany
21,
N Berger
N Berger
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
F Berghaus
F Berghaus
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
E Berglund
E Berglund
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
J Beringer
J Beringer
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
P Bernat
P Bernat
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
R Bernhard
R Bernhard
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
C Bernius
C Bernius
104Louisiana Tech University, Ruston, LA United States of America
104,
F U Bernlochner
F U Bernlochner
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
T Berry
T Berry
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
C Bertella
C Bertella
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
F Bertolucci
F Bertolucci
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
M I Besana
M I Besana
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
G J Besjes
G J Besjes
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
N Besson
N Besson
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
S Bethke
S Bethke
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
W Bhimji
W Bhimji
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
R M Bianchi
R M Bianchi
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
L Bianchini
L Bianchini
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
M Bianco
M Bianco
97INFN Sezione di Lecce, Lecce, Italy
98Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
97,98,
O Biebel
O Biebel
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
S P Bieniek
S P Bieniek
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
K Bierwagen
K Bierwagen
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
J Biesiada
J Biesiada
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Biglietti
M Biglietti
168INFN Sezione di Roma Tre, Roma, Italy
168,
H Bilokon
H Bilokon
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
M Bindi
M Bindi
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S Binet
S Binet
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
A Bingul
A Bingul
26Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
26,
C Bini
C Bini
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
B Bittner
B Bittner
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
C W Black
C W Black
193School of Physics, University of Sydney, Sydney, Australia
193,
J E Black
J E Black
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
K M Black
K M Black
30Department of Physics, Boston University, Boston, MA United States of America
30,
D Blackburn
D Blackburn
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
R E Blair
R E Blair
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
J-B Blanchard
J-B Blanchard
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
T Blazek
T Blazek
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
I Bloch
I Bloch
63DESY, Hamburg and Zeuthen, Germany
63,
C Blocker
C Blocker
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
J Blocki
J Blocki
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
W Blum
W Blum
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
U Blumenschein
U Blumenschein
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
G J Bobbink
G J Bobbink
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
V S Bobrovnikov
V S Bobrovnikov
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
S S Bocchetta
S S Bocchetta
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
A Bocci
A Bocci
66Department of Physics, Duke University, Durham, NC United States of America
66,
C R Boddy
C R Boddy
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
M Boehler
M Boehler
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
J Boek
J Boek
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
T T Boek
T T Boek
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
N Boelaert
N Boelaert
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
J A Bogaerts
J A Bogaerts
44CERN, Geneva, Switzerland
44,
A G Bogdanchikov
A G Bogdanchikov
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
A Bogouch
A Bogouch
118B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
118,
C Bohm
C Bohm
188Department of Physics, Stockholm University, Stockholm, Sweden
188,
J Bohm
J Bohm
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
V Boisvert
V Boisvert
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
T Bold
T Bold
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
V Boldea
V Boldea
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
N M Bolnet
N M Bolnet
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
M Bomben
M Bomben
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
M Bona
M Bona
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
M Boonekamp
M Boonekamp
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
S Bordoni
S Bordoni
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
C Borer
C Borer
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
A Borisov
A Borisov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
G Borissov
G Borissov
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
M Borri
M Borri
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
S Borroni
S Borroni
63DESY, Hamburg and Zeuthen, Germany
63,
J Bortfeldt
J Bortfeldt
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
V Bortolotto
V Bortolotto
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
K Bos
K Bos
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
D Boscherini
D Boscherini
27INFN Sezione di Bologna, Bologna, Italy
27,
M Bosman
M Bosman
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
H Boterenbrood
H Boterenbrood
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
J Bouchami
J Bouchami
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
J Boudreau
J Boudreau
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
E V Bouhova-Thacker
E V Bouhova-Thacker
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
D Boumediene
D Boumediene
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
C Bourdarios
C Bourdarios
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
N Bousson
N Bousson
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
S Boutouil
S Boutouil
173Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
173,
A Boveia
A Boveia
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
J Boyd
J Boyd
44CERN, Geneva, Switzerland
44,
I R Boyko
I R Boyko
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
I Bozovic-Jelisavcic
I Bozovic-Jelisavcic
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
J Bracinik
J Bracinik
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
P Branchini
P Branchini
168INFN Sezione di Roma Tre, Roma, Italy
168,
A Brandt
A Brandt
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
G Brandt
G Brandt
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
O Brandt
O Brandt
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
U Bratzler
U Bratzler
199Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
199,
B Brau
B Brau
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
J E Brau
J E Brau
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
H M Braun
H M Braun
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
S F Brazzale
S F Brazzale
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
B Brelier
B Brelier
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
J Bremer
J Bremer
44CERN, Geneva, Switzerland
44,
K Brendlinger
K Brendlinger
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
R Brenner
R Brenner
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
S Bressler
S Bressler
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
T M Bristow
T M Bristow
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
D Britton
D Britton
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
F M Brochu
F M Brochu
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
I Brock
I Brock
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
R Brock
R Brock
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
F Broggi
F Broggi
116INFN Sezione di Milano, Milano, Italy
116,
C Bromberg
C Bromberg
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
J Bronner
J Bronner
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
G Brooijmans
G Brooijmans
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
T Brooks
T Brooks
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
W K Brooks
W K Brooks
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
G Brown
G Brown
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
P A Bruckman de Renstrom
P A Bruckman de Renstrom
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
D Bruncko
D Bruncko
184Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
184,
R Bruneliere
R Bruneliere
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
S Brunet
S Brunet
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
A Bruni
A Bruni
27INFN Sezione di Bologna, Bologna, Italy
27,
G Bruni
G Bruni
27INFN Sezione di Bologna, Bologna, Italy
27,
M Bruschi
M Bruschi
27INFN Sezione di Bologna, Bologna, Italy
27,
L Bryngemark
L Bryngemark
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
T Buanes
T Buanes
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
Q Buat
Q Buat
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
F Bucci
F Bucci
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
J Buchanan
J Buchanan
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
P Buchholz
P Buchholz
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
R M Buckingham
R M Buckingham
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
A G Buckley
A G Buckley
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
S I Buda
S I Buda
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
I A Budagov
I A Budagov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
B Budick
B Budick
137Department of Physics, New York University, New York, NY United States of America
137,
L Bugge
L Bugge
146Department of Physics, University of Oslo, Oslo, Norway
146,
O Bulekov
O Bulekov
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
A C Bundock
A C Bundock
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
M Bunse
M Bunse
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
T Buran
T Buran
146Department of Physics, University of Oslo, Oslo, Norway
146,
H Burckhart
H Burckhart
44CERN, Geneva, Switzerland
44,
S Burdin
S Burdin
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
T Burgess
T Burgess
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
S Burke
S Burke
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
E Busato
E Busato
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
V Büscher
V Büscher
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
P Bussey
P Bussey
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
C P Buszello
C P Buszello
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
B Butler
B Butler
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
J M Butler
J M Butler
30Department of Physics, Boston University, Boston, MA United States of America
30,
C M Buttar
C M Buttar
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J M Butterworth
J M Butterworth
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
W Buttinger
W Buttinger
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
M Byszewski
M Byszewski
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
S Cabrera Urbán
S Cabrera Urbán
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
D Caforio
D Caforio
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
O Cakir
O Cakir
5Department of Physics, Ankara University, Ankara, Turkey
5,
P Calafiura
P Calafiura
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
G Calderini
G Calderini
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
P Calfayan
P Calfayan
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
R Calkins
R Calkins
135Department of Physics, Northern Illinois University, DeKalb, IL United States of America
135,
L P Caloba
L P Caloba
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
R Caloi
R Caloi
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
D Calvet
D Calvet
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
S Calvet
S Calvet
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
R Camacho Toro
R Camacho Toro
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
P Camarri
P Camarri
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
D Cameron
D Cameron
146Department of Physics, University of Oslo, Oslo, Norway
146,
L M Caminada
L M Caminada
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
R Caminal Armadans
R Caminal Armadans
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
S Campana
S Campana
44CERN, Geneva, Switzerland
44,
M Campanelli
M Campanelli
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
V Canale
V Canale
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
F Canelli
F Canelli
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A Canepa
A Canepa
202TRIUMF, Vancouver, BC Canada
202,
J Cantero
J Cantero
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
R Cantrill
R Cantrill
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
T Cao
T Cao
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
M D M Capeans Garrido
M D M Capeans Garrido
44CERN, Geneva, Switzerland
44,
I Caprini
I Caprini
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
M Caprini
M Caprini
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
D Capriotti
D Capriotti
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
M Capua
M Capua
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
R Caputo
R Caputo
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
R Cardarelli
R Cardarelli
166INFN Sezione di Roma Tor Vergata, Roma, Italy
166,
T Carli
T Carli
44CERN, Geneva, Switzerland
44,
G Carlino
G Carlino
130INFN Sezione di Napoli, Napoli, Italy
130,
L Carminati
L Carminati
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
S Caron
S Caron
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
E Carquin
E Carquin
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
G D Carrillo-Montoya
G D Carrillo-Montoya
187School of Physics, University of the Witwatersrand, Johannesburg, South Africa
187,
A A Carter
A A Carter
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
J R Carter
J R Carter
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
J Carvalho
J Carvalho
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
D Casadei
D Casadei
137Department of Physics, New York University, New York, NY United States of America
137,
M P Casado
M P Casado
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
M Cascella
M Cascella
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
C Caso
C Caso
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
E Castaneda-Miranda
E Castaneda-Miranda
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
A Castelli
A Castelli
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
V Castillo Gimenez
V Castillo Gimenez
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
N F Castro
N F Castro
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
G Cataldi
G Cataldi
97INFN Sezione di Lecce, Lecce, Italy
97,
P Catastini
P Catastini
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
A Catinaccio
A Catinaccio
44CERN, Geneva, Switzerland
44,
J R Catmore
J R Catmore
44CERN, Geneva, Switzerland
44,
A Cattai
A Cattai
44CERN, Geneva, Switzerland
44,
G Cattani
G Cattani
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
S Caughron
S Caughron
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
V Cavaliere
V Cavaliere
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
D Cavalli
D Cavalli
116INFN Sezione di Milano, Milano, Italy
116,
M Cavalli-Sforza
M Cavalli-Sforza
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
V Cavasinni
V Cavasinni
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
F Ceradini
F Ceradini
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
B Cerio
B Cerio
66Department of Physics, Duke University, Durham, NC United States of America
66,
A S Cerqueira
A S Cerqueira
33Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
33,
A Cerri
A Cerri
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
L Cerrito
L Cerrito
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
F Cerutti
F Cerutti
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
A Cervelli
A Cervelli
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
S A Cetin
S A Cetin
25Department of Physics, Dogus University, Istanbul, Turkey
25,
A Chafaq
A Chafaq
170Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
170,
D Chakraborty
D Chakraborty
135Department of Physics, Northern Illinois University, DeKalb, IL United States of America
135,
I Chalupkova
I Chalupkova
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
K Chan
K Chan
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
P Chang
P Chang
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
B Chapleau
B Chapleau
112Department of Physics, McGill University, Montreal, QC Canada
112,
J D Chapman
J D Chapman
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
J W Chapman
J W Chapman
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
D G Charlton
D G Charlton
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
V Chavda
V Chavda
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
C A Chavez Barajas
C A Chavez Barajas
44CERN, Geneva, Switzerland
44,
S Cheatham
S Cheatham
112Department of Physics, McGill University, Montreal, QC Canada
112,
S Chekanov
S Chekanov
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
S V Chekulaev
S V Chekulaev
202TRIUMF, Vancouver, BC Canada
202,
G A Chelkov
G A Chelkov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
M A Chelstowska
M A Chelstowska
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
C Chen
C Chen
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
H Chen
H Chen
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
S Chen
S Chen
50Department of Physics, Nanjing University, Jiangsu, China
50,
X Chen
X Chen
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
Y Chen
Y Chen
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
Y Cheng
Y Cheng
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A Cheplakov
A Cheplakov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
R Cherkaoui El Moursli
R Cherkaoui El Moursli
174Faculté des sciences, Université Mohammed V-Agdal, Rabat, Morocco
174,
V Chernyatin
V Chernyatin
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
E Cheu
E Cheu
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
S L Cheung
S L Cheung
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
L Chevalier
L Chevalier
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
V Chiarella
V Chiarella
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
G Chiefari
G Chiefari
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
J T Childers
J T Childers
44CERN, Geneva, Switzerland
44,
A Chilingarov
A Chilingarov
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
G Chiodini
G Chiodini
97INFN Sezione di Lecce, Lecce, Italy
97,
A S Chisholm
A S Chisholm
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
R T Chislett
R T Chislett
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
A Chitan
A Chitan
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
M V Chizhov
M V Chizhov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
G Choudalakis
G Choudalakis
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
S Chouridou
S Chouridou
13Physics Department, University of Athens, Athens, Greece
13,
B K B Chow
B K B Chow
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
I A Christidi
I A Christidi
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
A Christov
A Christov
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
D Chromek-Burckhart
D Chromek-Burckhart
44CERN, Geneva, Switzerland
44,
M L Chu
M L Chu
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
J Chudoba
J Chudoba
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
G Ciapetti
G Ciapetti
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
A K Ciftci
A K Ciftci
5Department of Physics, Ankara University, Ankara, Turkey
5,
R Ciftci
R Ciftci
5Department of Physics, Ankara University, Ankara, Turkey
5,
D Cinca
D Cinca
87University of Iowa, Iowa City, IA United States of America
87,
V Cindro
V Cindro
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
A Ciocio
A Ciocio
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Cirilli
M Cirilli
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
P Cirkovic
P Cirkovic
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
Z H Citron
Z H Citron
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
M Citterio
M Citterio
116INFN Sezione di Milano, Milano, Italy
116,
M Ciubancan
M Ciubancan
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
A Clark
A Clark
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
P J Clark
P J Clark
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
R N Clarke
R N Clarke
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
J C Clemens
J C Clemens
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
B Clement
B Clement
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
C Clement
C Clement
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
Y Coadou
Y Coadou
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
M Cobal
M Cobal
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
A Coccaro
A Coccaro
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
J Cochran
J Cochran
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
S Coelli
S Coelli
116INFN Sezione di Milano, Milano, Italy
116,
L Coffey
L Coffey
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
J G Cogan
J G Cogan
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
J Coggeshall
J Coggeshall
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
J Colas
J Colas
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Cole
S Cole
135Department of Physics, Northern Illinois University, DeKalb, IL United States of America
135,
A P Colijn
A P Colijn
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
N J Collins
N J Collins
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
C Collins-Tooth
C Collins-Tooth
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J Collot
J Collot
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
T Colombo
T Colombo
148INFN Sezione di Pavia, Pavia, Italy
149Dipartimento di Fisica, Università di Pavia, Pavia, Italy
148,149,
G Colon
G Colon
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
G Compostella
G Compostella
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
P Conde Muiño
P Conde Muiño
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
E Coniavitis
E Coniavitis
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
M C Conidi
M C Conidi
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
S M Consonni
S M Consonni
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
V Consorti
V Consorti
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
S Constantinescu
S Constantinescu
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
C Conta
C Conta
148INFN Sezione di Pavia, Pavia, Italy
149Dipartimento di Fisica, Università di Pavia, Pavia, Italy
148,149,
G Conti
G Conti
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
F Conventi
F Conventi
130INFN Sezione di Napoli, Napoli, Italy
130,
M Cooke
M Cooke
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
B D Cooper
B D Cooper
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
A M Cooper-Sarkar
A M Cooper-Sarkar
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
N J Cooper-Smith
N J Cooper-Smith
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
K Copic
K Copic
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
T Cornelissen
T Cornelissen
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
M Corradi
M Corradi
27INFN Sezione di Bologna, Bologna, Italy
27,
F Corriveau
F Corriveau
112Department of Physics, McGill University, Montreal, QC Canada
112,
A Corso-Radu
A Corso-Radu
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
A Cortes-Gonzalez
A Cortes-Gonzalez
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
G Cortiana
G Cortiana
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
G Costa
G Costa
116INFN Sezione di Milano, Milano, Italy
116,
M J Costa
M J Costa
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
D Costanzo
D Costanzo
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
D Côté
D Côté
44CERN, Geneva, Switzerland
44,
G Cottin
G Cottin
46Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
46,
L Courneyea
L Courneyea
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
G Cowan
G Cowan
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
B E Cox
B E Cox
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
K Cranmer
K Cranmer
137Department of Physics, New York University, New York, NY United States of America
137,
S Crépé-Renaudin
S Crépé-Renaudin
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
F Crescioli
F Crescioli
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
M Cristinziani
M Cristinziani
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
G Crosetti
G Crosetti
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
C-M Cuciuc
C-M Cuciuc
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
C Cuenca Almenar
C Cuenca Almenar
222Department of Physics, Yale University, New Haven, CT United States of America
222,
T Cuhadar Donszelmann
T Cuhadar Donszelmann
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
J Cummings
J Cummings
222Department of Physics, Yale University, New Haven, CT United States of America
222,
M Curatolo
M Curatolo
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
C J Curtis
C J Curtis
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
C Cuthbert
C Cuthbert
193School of Physics, University of Sydney, Sydney, Australia
193,
H Czirr
H Czirr
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
P Czodrowski
P Czodrowski
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
Z Czyczula
Z Czyczula
222Department of Physics, Yale University, New Haven, CT United States of America
222,
S D’Auria
S D’Auria
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
M D’Onofrio
M D’Onofrio
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
A D’Orazio
A D’Orazio
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
M J Da Cunha Sargedas De Sousa
M J Da Cunha Sargedas De Sousa
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
C Da Via
C Da Via
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
W Dabrowski
W Dabrowski
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
A Dafinca
A Dafinca
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
T Dai
T Dai
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
F Dallaire
F Dallaire
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
C Dallapiccola
C Dallapiccola
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
M Dam
M Dam
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
D S Damiani
D S Damiani
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
A C Daniells
A C Daniells
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
H O Danielsson
H O Danielsson
44CERN, Geneva, Switzerland
44,
V Dao
V Dao
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
G Darbo
G Darbo
71INFN Sezione di Genova, Genova, Italy
71,
G L Darlea
G L Darlea
39University Politehnica Bucharest, Bucharest, Romania
39,
S Darmora
S Darmora
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
J A Dassoulas
J A Dassoulas
63DESY, Hamburg and Zeuthen, Germany
63,
W Davey
W Davey
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Davidek
T Davidek
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
N Davidson
N Davidson
113School of Physics, University of Melbourne, Victoria, Australia
113,
E Davies
E Davies
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
M Davies
M Davies
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
O Davignon
O Davignon
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
A R Davison
A R Davison
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
Y Davygora
Y Davygora
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
E Dawe
E Dawe
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
I Dawson
I Dawson
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
R K Daya-Ishmukhametova
R K Daya-Ishmukhametova
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
K De
K De
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
R de Asmundis
R de Asmundis
130INFN Sezione di Napoli, Napoli, Italy
130,
S De Castro
S De Castro
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S De Cecco
S De Cecco
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
J de Graat
J de Graat
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
N De Groot
N De Groot
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
P de Jong
P de Jong
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
C De La Taille
C De La Taille
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
H De la Torre
H De la Torre
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
F De Lorenzi
F De Lorenzi
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
L De Nooij
L De Nooij
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
D De Pedis
D De Pedis
164INFN Sezione di Roma I, Roma, Italy
164,
A De Salvo
A De Salvo
164INFN Sezione di Roma I, Roma, Italy
164,
U De Sanctis
U De Sanctis
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
A De Santo
A De Santo
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
J B De Vivie De Regie
J B De Vivie De Regie
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
G De Zorzi
G De Zorzi
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
W J Dearnaley
W J Dearnaley
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
R Debbe
R Debbe
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
C Debenedetti
C Debenedetti
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
B Dechenaux
B Dechenaux
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
D V Dedovich
D V Dedovich
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
J Degenhardt
J Degenhardt
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
J Del Peso
J Del Peso
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
T Del Prete
T Del Prete
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
T Delemontex
T Delemontex
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
M Deliyergiyev
M Deliyergiyev
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
A Dell’Acqua
A Dell’Acqua
44CERN, Geneva, Switzerland
44,
L Dell’Asta
L Dell’Asta
30Department of Physics, Boston University, Boston, MA United States of America
30,
M Della Pietra
M Della Pietra
130INFN Sezione di Napoli, Napoli, Italy
130,
D della Volpe
D della Volpe
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
M Delmastro
M Delmastro
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
P A Delsart
P A Delsart
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
C Deluca
C Deluca
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
S Demers
S Demers
222Department of Physics, Yale University, New Haven, CT United States of America
222,
M Demichev
M Demichev
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A Demilly
A Demilly
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
B Demirkoz
B Demirkoz
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
S P Denisov
S P Denisov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
D Derendarz
D Derendarz
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
J E Derkaoui
J E Derkaoui
173Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
173,
F Derue
F Derue
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
P Dervan
P Dervan
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
K Desch
K Desch
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
P O Deviveiros
P O Deviveiros
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
A Dewhurst
A Dewhurst
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
B DeWilde
B DeWilde
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
S Dhaliwal
S Dhaliwal
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
R Dhullipudi
R Dhullipudi
104Louisiana Tech University, Ruston, LA United States of America
104,
A Di Ciaccio
A Di Ciaccio
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
L Di Ciaccio
L Di Ciaccio
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
C Di Donato
C Di Donato
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
A Di Girolamo
A Di Girolamo
44CERN, Geneva, Switzerland
44,
B Di Girolamo
B Di Girolamo
44CERN, Geneva, Switzerland
44,
S Di Luise
S Di Luise
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
A Di Mattia
A Di Mattia
195Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
195,
B Di Micco
B Di Micco
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
R Di Nardo
R Di Nardo
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
A Di Simone
A Di Simone
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
R Di Sipio
R Di Sipio
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
M A Diaz
M A Diaz
46Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
46,
E B Diehl
E B Diehl
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
J Dietrich
J Dietrich
63DESY, Hamburg and Zeuthen, Germany
63,
T A Dietzsch
T A Dietzsch
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
S Diglio
S Diglio
113School of Physics, University of Melbourne, Victoria, Australia
113,
K Dindar Yagci
K Dindar Yagci
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
J Dingfelder
J Dingfelder
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
F Dinut
F Dinut
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
C Dionisi
C Dionisi
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
P Dita
P Dita
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
S Dita
S Dita
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
F Dittus
F Dittus
44CERN, Geneva, Switzerland
44,
F Djama
F Djama
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
T Djobava
T Djobava
74High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
74,
M A B do Vale
M A B do Vale
34Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
34,
A Do Valle Wemans
A Do Valle Wemans
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
T K O Doan
T K O Doan
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
D Dobos
D Dobos
44CERN, Geneva, Switzerland
44,
E Dobson
E Dobson
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
J Dodd
J Dodd
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
C Doglioni
C Doglioni
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
T Doherty
T Doherty
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
T Dohmae
T Dohmae
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
Y Doi
Y Doi
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
J Dolejsi
J Dolejsi
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
Z Dolezal
Z Dolezal
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
B A Dolgoshein
B A Dolgoshein
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
M Donadelli
M Donadelli
35Instituto de Fisica, Universidade de Sao Paulo, Sao Paulo, Brazil
35,
J Donini
J Donini
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
J Dopke
J Dopke
44CERN, Geneva, Switzerland
44,
A Doria
A Doria
130INFN Sezione di Napoli, Napoli, Italy
130,
A Dos Anjos
A Dos Anjos
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
A Dotti
A Dotti
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
M T Dova
M T Dova
95Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
95,
A T Doyle
A T Doyle
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
M Dris
M Dris
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
J Dubbert
J Dubbert
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
S Dube
S Dube
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Dubreuil
E Dubreuil
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
E Duchovni
E Duchovni
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
G Duckeck
G Duckeck
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
D Duda
D Duda
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
A Dudarev
A Dudarev
44CERN, Geneva, Switzerland
44,
F Dudziak
F Dudziak
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
L Duflot
L Duflot
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
M-A Dufour
M-A Dufour
112Department of Physics, McGill University, Montreal, QC Canada
112,
L Duguid
L Duguid
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
M Dührssen
M Dührssen
44CERN, Geneva, Switzerland
44,
M Dunford
M Dunford
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
H Duran Yildiz
H Duran Yildiz
5Department of Physics, Ankara University, Ankara, Turkey
5,
M Düren
M Düren
75II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
75,
M Dwuznik
M Dwuznik
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
J Ebke
J Ebke
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
S Eckweiler
S Eckweiler
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
W Edson
W Edson
3Physics Department, SUNY Albany, Albany, NY United States of America
3,
C A Edwards
C A Edwards
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
N C Edwards
N C Edwards
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
W Ehrenfeld
W Ehrenfeld
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Eifert
T Eifert
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
G Eigen
G Eigen
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
K Einsweiler
K Einsweiler
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Eisenhandler
E Eisenhandler
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
T Ekelof
T Ekelof
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
M El Kacimi
M El Kacimi
172Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Morocco
172,
M Ellert
M Ellert
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
S Elles
S Elles
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
F Ellinghaus
F Ellinghaus
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
K Ellis
K Ellis
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
N Ellis
N Ellis
44CERN, Geneva, Switzerland
44,
J Elmsheuser
J Elmsheuser
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
M Elsing
M Elsing
44CERN, Geneva, Switzerland
44,
D Emeliyanov
D Emeliyanov
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
Y Enari
Y Enari
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
O C Endner
O C Endner
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
R Engelmann
R Engelmann
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
A Engl
A Engl
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
J Erdmann
J Erdmann
222Department of Physics, Yale University, New Haven, CT United States of America
222,
A Ereditato
A Ereditato
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
D Eriksson
D Eriksson
188Department of Physics, Stockholm University, Stockholm, Sweden
188,
J Ernst
J Ernst
3Physics Department, SUNY Albany, Albany, NY United States of America
3,
M Ernst
M Ernst
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
J Ernwein
J Ernwein
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
D Errede
D Errede
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
S Errede
S Errede
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
E Ertel
E Ertel
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
M Escalier
M Escalier
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
H Esch
H Esch
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
C Escobar
C Escobar
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
X Espinal Curull
X Espinal Curull
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
B Esposito
B Esposito
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
F Etienne
F Etienne
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
A I Etienvre
A I Etienvre
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
E Etzion
E Etzion
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
D Evangelakou
D Evangelakou
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
H Evans
H Evans
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
L Fabbri
L Fabbri
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
C Fabre
C Fabre
44CERN, Geneva, Switzerland
44,
G Facini
G Facini
44CERN, Geneva, Switzerland
44,
R M Fakhrutdinov
R M Fakhrutdinov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
S Falciano
S Falciano
164INFN Sezione di Roma I, Roma, Italy
164,
Y Fang
Y Fang
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
M Fanti
M Fanti
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
A Farbin
A Farbin
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
A Farilla
A Farilla
168INFN Sezione di Roma Tre, Roma, Italy
168,
T Farooque
T Farooque
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
S Farrell
S Farrell
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
S M Farrington
S M Farrington
216Department of Physics, University of Warwick, Coventry, United Kingdom
216,
P Farthouat
P Farthouat
44CERN, Geneva, Switzerland
44,
F Fassi
F Fassi
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
P Fassnacht
P Fassnacht
44CERN, Geneva, Switzerland
44,
D Fassouliotis
D Fassouliotis
13Physics Department, University of Athens, Athens, Greece
13,
B Fatholahzadeh
B Fatholahzadeh
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
A Favareto
A Favareto
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
L Fayard
L Fayard
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
P Federic
P Federic
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
O L Fedin
O L Fedin
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
W Fedorko
W Fedorko
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
M Fehling-Kaschek
M Fehling-Kaschek
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
L Feligioni
L Feligioni
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
C Feng
C Feng
51School of Physics, Shandong University, Shandong, China
51,
E J Feng
E J Feng
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
H Feng
H Feng
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
A B Fenyuk
A B Fenyuk
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
J Ferencei
J Ferencei
184Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
184,
W Fernando
W Fernando
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
S Ferrag
S Ferrag
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J Ferrando
J Ferrando
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
V Ferrara
V Ferrara
63DESY, Hamburg and Zeuthen, Germany
63,
A Ferrari
A Ferrari
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
P Ferrari
P Ferrari
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
R Ferrari
R Ferrari
148INFN Sezione di Pavia, Pavia, Italy
148,
D E Ferreira de Lima
D E Ferreira de Lima
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
A Ferrer
A Ferrer
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
D Ferrere
D Ferrere
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
C Ferretti
C Ferretti
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
A Ferretto Parodi
A Ferretto Parodi
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
M Fiascaris
M Fiascaris
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
F Fiedler
F Fiedler
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
A Filipčič
A Filipčič
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
F Filthaut
F Filthaut
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
M Fincke-Keeler
M Fincke-Keeler
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
K D Finelli
K D Finelli
66Department of Physics, Duke University, Durham, NC United States of America
66,
M C N Fiolhais
M C N Fiolhais
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
L Fiorini
L Fiorini
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
A Firan
A Firan
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
J Fischer
J Fischer
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
M J Fisher
M J Fisher
138Ohio State University, Columbus, OH United States of America
138,
E A Fitzgerald
E A Fitzgerald
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
M Flechl
M Flechl
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
I Fleck
I Fleck
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
P Fleischmann
P Fleischmann
220Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
220,
S Fleischmann
S Fleischmann
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
G T Fletcher
G T Fletcher
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
G Fletcher
G Fletcher
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
T Flick
T Flick
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
A Floderus
A Floderus
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
L R Flores Castillo
L R Flores Castillo
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
A C Florez Bustos
A C Florez Bustos
203Department of Physics and Astronomy, York University, Toronto, ON Canada
203,
M J Flowerdew
M J Flowerdew
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
T Fonseca Martin
T Fonseca Martin
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
A Formica
A Formica
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
A Forti
A Forti
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
D Fortin
D Fortin
202TRIUMF, Vancouver, BC Canada
202,
D Fournier
D Fournier
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
H Fox
H Fox
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
P Francavilla
P Francavilla
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
M Franchini
M Franchini
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S Franchino
S Franchino
44CERN, Geneva, Switzerland
44,
D Francis
D Francis
44CERN, Geneva, Switzerland
44,
M Franklin
M Franklin
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
S Franz
S Franz
44CERN, Geneva, Switzerland
44,
M Fraternali
M Fraternali
148INFN Sezione di Pavia, Pavia, Italy
149Dipartimento di Fisica, Università di Pavia, Pavia, Italy
148,149,
S Fratina
S Fratina
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
S T French
S T French
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
C Friedrich
C Friedrich
63DESY, Hamburg and Zeuthen, Germany
63,
F Friedrich
F Friedrich
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
D Froidevaux
D Froidevaux
44CERN, Geneva, Switzerland
44,
J A Frost
J A Frost
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
C Fukunaga
C Fukunaga
199Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
199,
E Fullana Torregrosa
E Fullana Torregrosa
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
B G Fulsom
B G Fulsom
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
J Fuster
J Fuster
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
C Gabaldon
C Gabaldon
44CERN, Geneva, Switzerland
44,
O Gabizon
O Gabizon
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
A Gabrielli
A Gabrielli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
A Gabrielli
A Gabrielli
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
S Gadatsch
S Gadatsch
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
T Gadfort
T Gadfort
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
S Gadomski
S Gadomski
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
G Gagliardi
G Gagliardi
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
P Gagnon
P Gagnon
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
C Galea
C Galea
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
B Galhardo
B Galhardo
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
E J Gallas
E J Gallas
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
V Gallo
V Gallo
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
B J Gallop
B J Gallop
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
P Gallus
P Gallus
158Czech Technical University in Prague, Praha, Czech Republic
158,
K K Gan
K K Gan
138Ohio State University, Columbus, OH United States of America
138,
R P Gandrajula
R P Gandrajula
87University of Iowa, Iowa City, IA United States of America
87,
Y S Gao
Y S Gao
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
A Gaponenko
A Gaponenko
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
F M Garay Walls
F M Garay Walls
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
F Garberson
F Garberson
222Department of Physics, Yale University, New Haven, CT United States of America
222,
C García
C García
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
J E García Navarro
J E García Navarro
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
M Garcia-Sciveres
M Garcia-Sciveres
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
R W Gardner
R W Gardner
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
N Garelli
N Garelli
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
V Garonne
V Garonne
44CERN, Geneva, Switzerland
44,
C Gatti
C Gatti
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
G Gaudio
G Gaudio
148INFN Sezione di Pavia, Pavia, Italy
148,
B Gaur
B Gaur
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
L Gauthier
L Gauthier
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
P Gauzzi
P Gauzzi
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
I L Gavrilenko
I L Gavrilenko
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
C Gay
C Gay
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
G Gaycken
G Gaycken
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
E N Gazis
E N Gazis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
P Ge
P Ge
51School of Physics, Shandong University, Shandong, China
51,
Z Gecse
Z Gecse
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
C N P Gee
C N P Gee
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
D A A Geerts
D A A Geerts
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
Ch Geich-Gimbel
Ch Geich-Gimbel
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
K Gellerstedt
K Gellerstedt
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
C Gemme
C Gemme
71INFN Sezione di Genova, Genova, Italy
71,
A Gemmell
A Gemmell
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
M H Genest
M H Genest
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
S Gentile
S Gentile
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
M George
M George
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
S George
S George
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
D Gerbaudo
D Gerbaudo
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
A Gershon
A Gershon
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
H Ghazlane
H Ghazlane
171Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
171,
N Ghodbane
N Ghodbane
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
B Giacobbe
B Giacobbe
27INFN Sezione di Bologna, Bologna, Italy
27,
S Giagu
S Giagu
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
V Giangiobbe
V Giangiobbe
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
P Giannetti
P Giannetti
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
F Gianotti
F Gianotti
44CERN, Geneva, Switzerland
44,
B Gibbard
B Gibbard
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
A Gibson
A Gibson
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
S M Gibson
S M Gibson
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
M Gilchriese
M Gilchriese
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
T P S Gillam
T P S Gillam
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
D Gillberg
D Gillberg
44CERN, Geneva, Switzerland
44,
A R Gillman
A R Gillman
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
D M Gingrich
D M Gingrich
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
N Giokaris
N Giokaris
13Physics Department, University of Athens, Athens, Greece
13,
M P Giordani
M P Giordani
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
R Giordano
R Giordano
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
F M Giorgi
F M Giorgi
21Department of Physics, Humboldt University, Berlin, Germany
21,
P Giovannini
P Giovannini
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
P F Giraud
P F Giraud
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
D Giugni
D Giugni
116INFN Sezione di Milano, Milano, Italy
116,
C Giuliani
C Giuliani
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
M Giunta
M Giunta
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
B K Gjelsten
B K Gjelsten
146Department of Physics, University of Oslo, Oslo, Norway
146,
I Gkialas
I Gkialas
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
L K Gladilin
L K Gladilin
125D.V. Skobeltsyn Institute of Nuclear Physics, M.V.Lomonosov Moscow State University, Moscow, Russia
125,
C Glasman
C Glasman
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
J Glatzer
J Glatzer
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Glazov
A Glazov
63DESY, Hamburg and Zeuthen, Germany
63,
G L Glonti
G L Glonti
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
M Goblirsch-Kolb
M Goblirsch-Kolb
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
J R Goddard
J R Goddard
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
J Godfrey
J Godfrey
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
J Godlewski
J Godlewski
44CERN, Geneva, Switzerland
44,
M Goebel
M Goebel
63DESY, Hamburg and Zeuthen, Germany
63,
C Goeringer
C Goeringer
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
S Goldfarb
S Goldfarb
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
T Golling
T Golling
222Department of Physics, Yale University, New Haven, CT United States of America
222,
D Golubkov
D Golubkov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
A Gomes
A Gomes
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
L S Gomez Fajardo
L S Gomez Fajardo
63DESY, Hamburg and Zeuthen, Germany
63,
R Gonçalo
R Gonçalo
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
J Goncalves Pinto Firmino Da Costa
J Goncalves Pinto Firmino Da Costa
63DESY, Hamburg and Zeuthen, Germany
63,
L Gonella
L Gonella
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S González de la Hoz
S González de la Hoz
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
G Gonzalez Parra
G Gonzalez Parra
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
M L Gonzalez Silva
M L Gonzalez Silva
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
S Gonzalez-Sevilla
S Gonzalez-Sevilla
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
J J Goodson
J J Goodson
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
L Goossens
L Goossens
44CERN, Geneva, Switzerland
44,
P A Gorbounov
P A Gorbounov
123Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
123,
H A Gordon
H A Gordon
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
I Gorelov
I Gorelov
132Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
132,
G Gorfine
G Gorfine
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
B Gorini
B Gorini
44CERN, Geneva, Switzerland
44,
E Gorini
E Gorini
97INFN Sezione di Lecce, Lecce, Italy
98Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
97,98,
A Gorišek
A Gorišek
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
E Gornicki
E Gornicki
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
A T Goshaw
A T Goshaw
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
C Gössling
C Gössling
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
M I Gostkin
M I Gostkin
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
I Gough Eschrich
I Gough Eschrich
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
M Gouighri
M Gouighri
170Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
170,
D Goujdami
D Goujdami
172Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Morocco
172,
M P Goulette
M P Goulette
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
A G Goussiou
A G Goussiou
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
C Goy
C Goy
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Gozpinar
S Gozpinar
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
L Graber
L Graber
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
I Grabowska-Bold
I Grabowska-Bold
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
P Grafström
P Grafström
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
K-J Grahn
K-J Grahn
63DESY, Hamburg and Zeuthen, Germany
63,
E Gramstad
E Gramstad
146Department of Physics, University of Oslo, Oslo, Norway
146,
F Grancagnolo
F Grancagnolo
97INFN Sezione di Lecce, Lecce, Italy
97,
S Grancagnolo
S Grancagnolo
21Department of Physics, Humboldt University, Berlin, Germany
21,
V Grassi
V Grassi
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
V Gratchev
V Gratchev
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
H M Gray
H M Gray
44CERN, Geneva, Switzerland
44,
J A Gray
J A Gray
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
E Graziani
E Graziani
168INFN Sezione di Roma Tre, Roma, Italy
168,
O G Grebenyuk
O G Grebenyuk
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
T Greenshaw
T Greenshaw
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
Z D Greenwood
Z D Greenwood
104Louisiana Tech University, Ruston, LA United States of America
104,
K Gregersen
K Gregersen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
I M Gregor
I M Gregor
63DESY, Hamburg and Zeuthen, Germany
63,
P Grenier
P Grenier
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
J Griffiths
J Griffiths
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
N Grigalashvili
N Grigalashvili
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A A Grillo
A A Grillo
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
K Grimm
K Grimm
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
S Grinstein
S Grinstein
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
Ph Gris
Ph Gris
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
Y V Grishkevich
Y V Grishkevich
125D.V. Skobeltsyn Institute of Nuclear Physics, M.V.Lomonosov Moscow State University, Moscow, Russia
125,
J-F Grivaz
J-F Grivaz
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
J P Grohs
J P Grohs
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
A Grohsjean
A Grohsjean
63DESY, Hamburg and Zeuthen, Germany
63,
E Gross
E Gross
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
J Grosse-Knetter
J Grosse-Knetter
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
J Groth-Jensen
J Groth-Jensen
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
K Grybel
K Grybel
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
F Guescini
F Guescini
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
D Guest
D Guest
222Department of Physics, Yale University, New Haven, CT United States of America
222,
O Gueta
O Gueta
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
C Guicheney
C Guicheney
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
E Guido
E Guido
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
T Guillemin
T Guillemin
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
S Guindon
S Guindon
3Physics Department, SUNY Albany, Albany, NY United States of America
3,
U Gul
U Gul
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J Gunther
J Gunther
158Czech Technical University in Prague, Praha, Czech Republic
158,
J Guo
J Guo
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
P Gutierrez
P Gutierrez
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
N Guttman
N Guttman
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
O Gutzwiller
O Gutzwiller
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
C Guyot
C Guyot
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
C Gwenlan
C Gwenlan
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
C B Gwilliam
C B Gwilliam
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
A Haas
A Haas
137Department of Physics, New York University, New York, NY United States of America
137,
S Haas
S Haas
44CERN, Geneva, Switzerland
44,
C Haber
C Haber
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
H K Hadavand
H K Hadavand
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
P Haefner
P Haefner
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
Z Hajduk
Z Hajduk
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
H Hakobyan
H Hakobyan
223Yerevan Physics Institute, Yerevan, Armenia
223,
D Hall
D Hall
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
G Halladjian
G Halladjian
87University of Iowa, Iowa City, IA United States of America
87,
K Hamacher
K Hamacher
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
P Hamal
P Hamal
142RCPTM, Palacký University, Olomouc, Czech Republic
142,
K Hamano
K Hamano
113School of Physics, University of Melbourne, Victoria, Australia
113,
M Hamer
M Hamer
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
A Hamilton
A Hamilton
185Department of Physics, University of Cape Town, Cape Town, South Africa
185,
S Hamilton
S Hamilton
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
L Han
L Han
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
K Hanagaki
K Hanagaki
145Graduate School of Science, Osaka University, Osaka, Japan
145,
K Hanawa
K Hanawa
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
M Hance
M Hance
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
C Handel
C Handel
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
P Hanke
P Hanke
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
J R Hansen
J R Hansen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
J B Hansen
J B Hansen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
J D Hansen
J D Hansen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
P H Hansen
P H Hansen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
P Hansson
P Hansson
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
K Hara
K Hara
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
A S Hard
A S Hard
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
T Harenberg
T Harenberg
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
S Harkusha
S Harkusha
118B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
118,
D Harper
D Harper
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
R D Harrington
R D Harrington
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
O M Harris
O M Harris
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
J Hartert
J Hartert
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
F Hartjes
F Hartjes
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
T Haruyama
T Haruyama
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
A Harvey
A Harvey
79Department of Physics, Hampton University, Hampton, VA United States of America
79,
S Hasegawa
S Hasegawa
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
Y Hasegawa
Y Hasegawa
179Department of Physics, Shinshu University, Nagano, Japan
179,
S Hassani
S Hassani
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
S Haug
S Haug
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
M Hauschild
M Hauschild
44CERN, Geneva, Switzerland
44,
R Hauser
R Hauser
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
M Havranek
M Havranek
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
C M Hawkes
C M Hawkes
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
R J Hawkings
R J Hawkings
44CERN, Geneva, Switzerland
44,
A D Hawkins
A D Hawkins
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
T Hayakawa
T Hayakawa
91Graduate School of Science, Kobe University, Kobe, Japan
91,
T Hayashi
T Hayashi
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
D Hayden
D Hayden
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
C P Hays
C P Hays
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
H S Hayward
H S Hayward
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
S J Haywood
S J Haywood
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
S J Head
S J Head
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
T Heck
T Heck
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
V Hedberg
V Hedberg
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
L Heelan
L Heelan
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
S Heim
S Heim
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
B Heinemann
B Heinemann
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
S Heisterkamp
S Heisterkamp
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
J Hejbal
J Hejbal
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
L Helary
L Helary
30Department of Physics, Boston University, Boston, MA United States of America
30,
C Heller
C Heller
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
M Heller
M Heller
44CERN, Geneva, Switzerland
44,
S Hellman
S Hellman
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
D Hellmich
D Hellmich
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
C Helsens
C Helsens
44CERN, Geneva, Switzerland
44,
J Henderson
J Henderson
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
R C W Henderson
R C W Henderson
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
M Henke
M Henke
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
A Henrichs
A Henrichs
222Department of Physics, Yale University, New Haven, CT United States of America
222,
A M Henriques Correia
A M Henriques Correia
44CERN, Geneva, Switzerland
44,
S Henrot-Versille
S Henrot-Versille
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
C Hensel
C Hensel
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
G H Herbert
G H Herbert
21Department of Physics, Humboldt University, Berlin, Germany
21,
C M Hernandez
C M Hernandez
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
Y Hernández Jiménez
Y Hernández Jiménez
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
R Herrberg-Schubert
R Herrberg-Schubert
21Department of Physics, Humboldt University, Berlin, Germany
21,
G Herten
G Herten
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
R Hertenberger
R Hertenberger
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
L Hervas
L Hervas
44CERN, Geneva, Switzerland
44,
G G Hesketh
G G Hesketh
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
N P Hessey
N P Hessey
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
R Hickling
R Hickling
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
E Higón-Rodriguez
E Higón-Rodriguez
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
J C Hill
J C Hill
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
K H Hiller
K H Hiller
63DESY, Hamburg and Zeuthen, Germany
63,
S Hillert
S Hillert
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S J Hillier
S J Hillier
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
I Hinchliffe
I Hinchliffe
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Hines
E Hines
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
M Hirose
M Hirose
145Graduate School of Science, Osaka University, Osaka, Japan
145,
D Hirschbuehl
D Hirschbuehl
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
J Hobbs
J Hobbs
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
N Hod
N Hod
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
M C Hodgkinson
M C Hodgkinson
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
P Hodgson
P Hodgson
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
A Hoecker
A Hoecker
44CERN, Geneva, Switzerland
44,
M R Hoeferkamp
M R Hoeferkamp
132Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
132,
J Hoffman
J Hoffman
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
D Hoffmann
D Hoffmann
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
J I Hofmann
J I Hofmann
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
M Hohlfeld
M Hohlfeld
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
S O Holmgren
S O Holmgren
188Department of Physics, Stockholm University, Stockholm, Sweden
188,
J L Holzbauer
J L Holzbauer
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
T M Hong
T M Hong
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
L Hooft van Huysduynen
L Hooft van Huysduynen
137Department of Physics, New York University, New York, NY United States of America
137,
J-Y Hostachy
J-Y Hostachy
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
S Hou
S Hou
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
A Hoummada
A Hoummada
170Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
170,
J Howard
J Howard
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
J Howarth
J Howarth
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
M Hrabovsky
M Hrabovsky
142RCPTM, Palacký University, Olomouc, Czech Republic
142,
I Hristova
I Hristova
21Department of Physics, Humboldt University, Berlin, Germany
21,
J Hrivnac
J Hrivnac
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
T Hryn’ova
T Hryn’ova
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
P J Hsu
P J Hsu
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
S-C Hsu
S-C Hsu
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
D Hu
D Hu
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
X Hu
X Hu
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
Z Hubacek
Z Hubacek
44CERN, Geneva, Switzerland
44,
F Hubaut
F Hubaut
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
F Huegging
F Huegging
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Huettmann
A Huettmann
63DESY, Hamburg and Zeuthen, Germany
63,
T B Huffman
T B Huffman
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
E W Hughes
E W Hughes
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
G Hughes
G Hughes
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
M Huhtinen
M Huhtinen
44CERN, Geneva, Switzerland
44,
T A Hülsing
T A Hülsing
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
M Hurwitz
M Hurwitz
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
N Huseynov
N Huseynov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
J Huston
J Huston
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
J Huth
J Huth
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
G Iacobucci
G Iacobucci
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
G Iakovidis
G Iakovidis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
I Ibragimov
I Ibragimov
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
L Iconomidou-Fayard
L Iconomidou-Fayard
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
J Idarraga
J Idarraga
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
P Iengo
P Iengo
130INFN Sezione di Napoli, Napoli, Italy
130,
O Igonkina
O Igonkina
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
Y Ikegami
Y Ikegami
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
K Ikematsu
K Ikematsu
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
M Ikeno
M Ikeno
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
D Iliadis
D Iliadis
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
N Ilic
N Ilic
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
T Ince
T Ince
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
P Ioannou
P Ioannou
13Physics Department, University of Athens, Athens, Greece
13,
M Iodice
M Iodice
168INFN Sezione di Roma Tre, Roma, Italy
168,
K Iordanidou
K Iordanidou
13Physics Department, University of Athens, Athens, Greece
13,
V Ippolito
V Ippolito
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
A Irles Quiles
A Irles Quiles
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
C Isaksson
C Isaksson
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
M Ishino
M Ishino
92Faculty of Science, Kyoto University, Kyoto, Japan
92,
M Ishitsuka
M Ishitsuka
200Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
200,
R Ishmukhametov
R Ishmukhametov
138Ohio State University, Columbus, OH United States of America
138,
C Issever
C Issever
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
S Istin
S Istin
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
A V Ivashin
A V Ivashin
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
W Iwanski
W Iwanski
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
H Iwasaki
H Iwasaki
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
J M Izen
J M Izen
62Physics Department, University of Texas at Dallas, Richardson, TX United States of America
62,
V Izzo
V Izzo
130INFN Sezione di Napoli, Napoli, Italy
130,
B Jackson
B Jackson
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
J N Jackson
J N Jackson
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
P Jackson
P Jackson
2School of Chemistry and Physics, University of Adelaide, Adelaide, Australia
2,
M R Jaekel
M R Jaekel
44CERN, Geneva, Switzerland
44,
V Jain
V Jain
3Physics Department, SUNY Albany, Albany, NY United States of America
3,
K Jakobs
K Jakobs
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
S Jakobsen
S Jakobsen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
T Jakoubek
T Jakoubek
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
J Jakubek
J Jakubek
158Czech Technical University in Prague, Praha, Czech Republic
158,
D O Jamin
D O Jamin
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
D K Jana
D K Jana
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
E Jansen
E Jansen
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
H Jansen
H Jansen
44CERN, Geneva, Switzerland
44,
J Janssen
J Janssen
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Jantsch
A Jantsch
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
M Janus
M Janus
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
R C Jared
R C Jared
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
G Jarlskog
G Jarlskog
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
L Jeanty
L Jeanty
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
G-Y Jeng
G-Y Jeng
193School of Physics, University of Sydney, Sydney, Australia
193,
I Jen-La Plante
I Jen-La Plante
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
D Jennens
D Jennens
113School of Physics, University of Melbourne, Victoria, Australia
113,
P Jenni
P Jenni
44CERN, Geneva, Switzerland
44,
J Jentzsch
J Jentzsch
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
C Jeske
C Jeske
216Department of Physics, University of Warwick, Coventry, United Kingdom
216,
P Jež
P Jež
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
S Jézéquel
S Jézéquel
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
M K Jha
M K Jha
27INFN Sezione di Bologna, Bologna, Italy
27,
H Ji
H Ji
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
W Ji
W Ji
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
J Jia
J Jia
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
Y Jiang
Y Jiang
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
M Jimenez Belenguer
M Jimenez Belenguer
63DESY, Hamburg and Zeuthen, Germany
63,
S Jin
S Jin
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
O Jinnouchi
O Jinnouchi
200Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
200,
M D Joergensen
M D Joergensen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
D Joffe
D Joffe
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
M Johansen
M Johansen
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
K E Johansson
K E Johansson
188Department of Physics, Stockholm University, Stockholm, Sweden
188,
P Johansson
P Johansson
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
S Johnert
S Johnert
63DESY, Hamburg and Zeuthen, Germany
63,
K A Johns
K A Johns
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
K Jon-And
K Jon-And
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
G Jones
G Jones
216Department of Physics, University of Warwick, Coventry, United Kingdom
216,
R W L Jones
R W L Jones
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
T J Jones
T J Jones
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
P M Jorge
P M Jorge
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
K D Joshi
K D Joshi
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
J Jovicevic
J Jovicevic
190Physics Department, Royal Institute of Technology, Stockholm, Sweden
190,
X Ju
X Ju
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
C A Jung
C A Jung
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
R M Jungst
R M Jungst
44CERN, Geneva, Switzerland
44,
P Jussel
P Jussel
86Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
86,
A Juste Rozas
A Juste Rozas
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
S Kabana
S Kabana
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
M Kaci
M Kaci
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
A Kaczmarska
A Kaczmarska
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
P Kadlecik
P Kadlecik
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
M Kado
M Kado
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
H Kagan
H Kagan
138Ohio State University, Columbus, OH United States of America
138,
M Kagan
M Kagan
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
E Kajomovitz
E Kajomovitz
195Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
195,
S Kalinin
S Kalinin
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
S Kama
S Kama
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
N Kanaya
N Kanaya
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
M Kaneda
M Kaneda
44CERN, Geneva, Switzerland
44,
S Kaneti
S Kaneti
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
T Kanno
T Kanno
200Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
200,
V A Kantserov
V A Kantserov
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
J Kanzaki
J Kanzaki
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
B Kaplan
B Kaplan
137Department of Physics, New York University, New York, NY United States of America
137,
A Kapliy
A Kapliy
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
D Kar
D Kar
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
K Karakostas
K Karakostas
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
M Karnevskiy
M Karnevskiy
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
V Kartvelishvili
V Kartvelishvili
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
A N Karyukhin
A N Karyukhin
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
L Kashif
L Kashif
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
G Kasieczka
G Kasieczka
82Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
82,
R D Kass
R D Kass
138Ohio State University, Columbus, OH United States of America
138,
A Kastanas
A Kastanas
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
Y Kataoka
Y Kataoka
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
J Katzy
J Katzy
63DESY, Hamburg and Zeuthen, Germany
63,
V Kaushik
V Kaushik
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
K Kawagoe
K Kawagoe
94Department of Physics, Kyushu University, Fukuoka, Japan
94,
T Kawamoto
T Kawamoto
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
G Kawamura
G Kawamura
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
S Kazama
S Kazama
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
V F Kazanin
V F Kazanin
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
M Y Kazarinov
M Y Kazarinov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
R Keeler
R Keeler
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
P T Keener
P T Keener
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
R Kehoe
R Kehoe
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
M Keil
M Keil
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
J S Keller
J S Keller
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
H Keoshkerian
H Keoshkerian
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
O Kepka
O Kepka
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
B P Kerševan
B P Kerševan
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
S Kersten
S Kersten
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
K Kessoku
K Kessoku
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
J Keung
J Keung
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
F Khalil-zada
F Khalil-zada
15Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
15,
H Khandanyan
H Khandanyan
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
A Khanov
A Khanov
141Department of Physics, Oklahoma State University, Stillwater, OK United States of America
141,
D Kharchenko
D Kharchenko
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A Khodinov
A Khodinov
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
A Khomich
A Khomich
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
T J Khoo
T J Khoo
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
G Khoriauli
G Khoriauli
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Khoroshilov
A Khoroshilov
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
V Khovanskiy
V Khovanskiy
123Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
123,
E Khramov
E Khramov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
J Khubua
J Khubua
74High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
74,
H Kim
H Kim
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
S H Kim
S H Kim
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
N Kimura
N Kimura
217Waseda University, Tokyo, Japan
217,
O Kind
O Kind
21Department of Physics, Humboldt University, Berlin, Germany
21,
B T King
B T King
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
M King
M King
91Graduate School of Science, Kobe University, Kobe, Japan
91,
R S B King
R S B King
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
S B King
S B King
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
J Kirk
J Kirk
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
A E Kiryunin
A E Kiryunin
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
T Kishimoto
T Kishimoto
91Graduate School of Science, Kobe University, Kobe, Japan
91,
D Kisielewska
D Kisielewska
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
T Kitamura
T Kitamura
91Graduate School of Science, Kobe University, Kobe, Japan
91,
T Kittelmann
T Kittelmann
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
K Kiuchi
K Kiuchi
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
E Kladiva
E Kladiva
184Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
184,
M Klein
M Klein
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
U Klein
U Klein
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
K Kleinknecht
K Kleinknecht
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
M Klemetti
M Klemetti
112Department of Physics, McGill University, Montreal, QC Canada
112,
A Klier
A Klier
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
P Klimek
P Klimek
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
A Klimentov
A Klimentov
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
R Klingenberg
R Klingenberg
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
J A Klinger
J A Klinger
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
E B Klinkby
E B Klinkby
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
T Klioutchnikova
T Klioutchnikova
44CERN, Geneva, Switzerland
44,
P F Klok
P F Klok
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
E-E Kluge
E-E Kluge
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
P Kluit
P Kluit
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
S Kluth
S Kluth
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
E Kneringer
E Kneringer
86Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
86,
E B F G Knoops
E B F G Knoops
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
A Knue
A Knue
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
B R Ko
B R Ko
66Department of Physics, Duke University, Durham, NC United States of America
66,
T Kobayashi
T Kobayashi
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
M Kobel
M Kobel
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
M Kocian
M Kocian
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
P Kodys
P Kodys
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
S Koenig
S Koenig
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
F Koetsveld
F Koetsveld
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
P Koevesarki
P Koevesarki
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Koffas
T Koffas
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
E Koffeman
E Koffeman
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
L A Kogan
L A Kogan
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
S Kohlmann
S Kohlmann
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
F Kohn
F Kohn
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
Z Kohout
Z Kohout
158Czech Technical University in Prague, Praha, Czech Republic
158,
T Kohriki
T Kohriki
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
T Koi
T Koi
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
H Kolanoski
H Kolanoski
21Department of Physics, Humboldt University, Berlin, Germany
21,
I Koletsou
I Koletsou
116INFN Sezione di Milano, Milano, Italy
116,
J Koll
J Koll
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
A A Komar
A A Komar
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
Y Komori
Y Komori
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
T Kondo
T Kondo
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
K Köneke
K Köneke
44CERN, Geneva, Switzerland
44,
A C König
A C König
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
T Kono
T Kono
63DESY, Hamburg and Zeuthen, Germany
63,
A I Kononov
A I Kononov
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
R Konoplich
R Konoplich
137Department of Physics, New York University, New York, NY United States of America
137,
N Konstantinidis
N Konstantinidis
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
R Kopeliansky
R Kopeliansky
195Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
195,
S Koperny
S Koperny
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
L Köpke
L Köpke
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
A K Kopp
A K Kopp
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
K Korcyl
K Korcyl
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
K Kordas
K Kordas
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
A Korn
A Korn
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
A A Korol
A A Korol
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
I Korolkov
I Korolkov
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
E V Korolkova
E V Korolkova
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
V A Korotkov
V A Korotkov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
O Kortner
O Kortner
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
S Kortner
S Kortner
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
V V Kostyukhin
V V Kostyukhin
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Kotov
S Kotov
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
V M Kotov
V M Kotov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A Kotwal
A Kotwal
66Department of Physics, Duke University, Durham, NC United States of America
66,
C Kourkoumelis
C Kourkoumelis
13Physics Department, University of Athens, Athens, Greece
13,
V Kouskoura
V Kouskoura
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
A Koutsman
A Koutsman
202TRIUMF, Vancouver, BC Canada
202,
R Kowalewski
R Kowalewski
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
T Z Kowalski
T Z Kowalski
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
W Kozanecki
W Kozanecki
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
A S Kozhin
A S Kozhin
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
V Kral
V Kral
158Czech Technical University in Prague, Praha, Czech Republic
158,
V A Kramarenko
V A Kramarenko
125D.V. Skobeltsyn Institute of Nuclear Physics, M.V.Lomonosov Moscow State University, Moscow, Russia
125,
G Kramberger
G Kramberger
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
M W Krasny
M W Krasny
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
A Krasznahorkay
A Krasznahorkay
137Department of Physics, New York University, New York, NY United States of America
137,
J K Kraus
J K Kraus
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Kravchenko
A Kravchenko
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
S Kreiss
S Kreiss
137Department of Physics, New York University, New York, NY United States of America
137,
J Kretzschmar
J Kretzschmar
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
K Kreutzfeldt
K Kreutzfeldt
75II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
75,
N Krieger
N Krieger
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
P Krieger
P Krieger
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
K Kroeninger
K Kroeninger
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
H Kroha
H Kroha
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
J Kroll
J Kroll
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
J Kroseberg
J Kroseberg
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J Krstic
J Krstic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
U Kruchonak
U Kruchonak
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
H Krüger
H Krüger
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Kruker
T Kruker
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
N Krumnack
N Krumnack
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
Z V Krumshteyn
Z V Krumshteyn
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A Kruse
A Kruse
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
M K Kruse
M K Kruse
66Department of Physics, Duke University, Durham, NC United States of America
66,
T Kubota
T Kubota
113School of Physics, University of Melbourne, Victoria, Australia
113,
S Kuday
S Kuday
5Department of Physics, Ankara University, Ankara, Turkey
5,
S Kuehn
S Kuehn
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
A Kugel
A Kugel
83ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
83,
T Kuhl
T Kuhl
63DESY, Hamburg and Zeuthen, Germany
63,
V Kukhtin
V Kukhtin
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
Y Kulchitsky
Y Kulchitsky
118B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
118,
S Kuleshov
S Kuleshov
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
M Kuna
M Kuna
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
J Kunkle
J Kunkle
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
A Kupco
A Kupco
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
H Kurashige
H Kurashige
91Graduate School of Science, Kobe University, Kobe, Japan
91,
M Kurata
M Kurata
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
Y A Kurochkin
Y A Kurochkin
118B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
118,
V Kus
V Kus
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
E S Kuwertz
E S Kuwertz
190Physics Department, Royal Institute of Technology, Stockholm, Sweden
190,
M Kuze
M Kuze
200Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
200,
J Kvita
J Kvita
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
R Kwee
R Kwee
21Department of Physics, Humboldt University, Berlin, Germany
21,
A La Rosa
A La Rosa
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
L La Rotonda
L La Rotonda
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
L Labarga
L Labarga
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
S Lablak
S Lablak
170Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
170,
C Lacasta
C Lacasta
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
F Lacava
F Lacava
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
J Lacey
J Lacey
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
H Lacker
H Lacker
21Department of Physics, Humboldt University, Berlin, Germany
21,
D Lacour
D Lacour
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
V R Lacuesta
V R Lacuesta
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
E Ladygin
E Ladygin
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
R Lafaye
R Lafaye
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
B Laforge
B Laforge
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
T Lagouri
T Lagouri
222Department of Physics, Yale University, New Haven, CT United States of America
222,
S Lai
S Lai
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
H Laier
H Laier
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
E Laisne
E Laisne
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
L Lambourne
L Lambourne
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
C L Lampen
C L Lampen
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
W Lampl
W Lampl
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
E Lançon
E Lançon
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
U Landgraf
U Landgraf
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
M P J Landon
M P J Landon
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
V S Lang
V S Lang
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
C Lange
C Lange
63DESY, Hamburg and Zeuthen, Germany
63,
A J Lankford
A J Lankford
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
F Lanni
F Lanni
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
K Lantzsch
K Lantzsch
44CERN, Geneva, Switzerland
44,
A Lanza
A Lanza
148INFN Sezione di Pavia, Pavia, Italy
148,
S Laplace
S Laplace
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
C Lapoire
C Lapoire
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J F Laporte
J F Laporte
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
T Lari
T Lari
116INFN Sezione di Milano, Milano, Italy
116,
A Larner
A Larner
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
M Lassnig
M Lassnig
44CERN, Geneva, Switzerland
44,
P Laurelli
P Laurelli
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
V Lavorini
V Lavorini
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
W Lavrijsen
W Lavrijsen
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
P Laycock
P Laycock
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
O Le Dortz
O Le Dortz
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
E Le Guirriec
E Le Guirriec
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
E Le Menedeu
E Le Menedeu
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
T LeCompte
T LeCompte
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
F Ledroit-Guillon
F Ledroit-Guillon
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
H Lee
H Lee
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
J S H Lee
J S H Lee
145Graduate School of Science, Osaka University, Osaka, Japan
145,
S C Lee
S C Lee
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
L Lee
L Lee
222Department of Physics, Yale University, New Haven, CT United States of America
222,
G Lefebvre
G Lefebvre
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
M Lefebvre
M Lefebvre
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
M Legendre
M Legendre
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
F Legger
F Legger
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
C Leggett
C Leggett
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Lehmacher
M Lehmacher
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
G Lehmann Miotto
G Lehmann Miotto
44CERN, Geneva, Switzerland
44,
A G Leister
A G Leister
222Department of Physics, Yale University, New Haven, CT United States of America
222,
M A L Leite
M A L Leite
35Instituto de Fisica, Universidade de Sao Paulo, Sao Paulo, Brazil
35,
R Leitner
R Leitner
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
D Lellouch
D Lellouch
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
B Lemmer
B Lemmer
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
V Lendermann
V Lendermann
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
K J C Leney
K J C Leney
187School of Physics, University of the Witwatersrand, Johannesburg, South Africa
187,
T Lenz
T Lenz
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
G Lenzen
G Lenzen
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
B Lenzi
B Lenzi
44CERN, Geneva, Switzerland
44,
K Leonhardt
K Leonhardt
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
S Leontsinis
S Leontsinis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
F Lepold
F Lepold
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
C Leroy
C Leroy
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
J-R Lessard
J-R Lessard
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
C G Lester
C G Lester
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
C M Lester
C M Lester
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
J Levêque
J Levêque
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
D Levin
D Levin
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
L J Levinson
L J Levinson
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
A Lewis
A Lewis
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
G H Lewis
G H Lewis
137Department of Physics, New York University, New York, NY United States of America
137,
A M Leyko
A M Leyko
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Leyton
M Leyton
21Department of Physics, Humboldt University, Berlin, Germany
21,
B Li
B Li
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
B Li
B Li
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
H Li
H Li
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
H L Li
H L Li
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
S Li
S Li
66Department of Physics, Duke University, Durham, NC United States of America
66,
X Li
X Li
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
Z Liang
Z Liang
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
H Liao
H Liao
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
B Liberti
B Liberti
166INFN Sezione di Roma Tor Vergata, Roma, Italy
166,
P Lichard
P Lichard
44CERN, Geneva, Switzerland
44,
K Lie
K Lie
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
J Liebal
J Liebal
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
W Liebig
W Liebig
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
C Limbach
C Limbach
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Limosani
A Limosani
113School of Physics, University of Melbourne, Victoria, Australia
113,
M Limper
M Limper
87University of Iowa, Iowa City, IA United States of America
87,
S C Lin
S C Lin
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
F Linde
F Linde
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
B E Lindquist
B E Lindquist
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
J T Linnemann
J T Linnemann
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
E Lipeles
E Lipeles
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
A Lipniacka
A Lipniacka
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
M Lisovyi
M Lisovyi
63DESY, Hamburg and Zeuthen, Germany
63,
T M Liss
T M Liss
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
D Lissauer
D Lissauer
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
A Lister
A Lister
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
A M Litke
A M Litke
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
D Liu
D Liu
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
J B Liu
J B Liu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
K Liu
K Liu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
L Liu
L Liu
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
M Liu
M Liu
66Department of Physics, Duke University, Durham, NC United States of America
66,
M Liu
M Liu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
Y Liu
Y Liu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
M Livan
M Livan
148INFN Sezione di Pavia, Pavia, Italy
149Dipartimento di Fisica, Università di Pavia, Pavia, Italy
148,149,
S S A Livermore
S S A Livermore
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
A Lleres
A Lleres
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
J Llorente Merino
J Llorente Merino
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
S L Lloyd
S L Lloyd
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
F Lo Sterzo
F Lo Sterzo
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
E Lobodzinska
E Lobodzinska
63DESY, Hamburg and Zeuthen, Germany
63,
P Loch
P Loch
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
W S Lockman
W S Lockman
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
T Loddenkoetter
T Loddenkoetter
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
F K Loebinger
F K Loebinger
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
A E Loevschall-Jensen
A E Loevschall-Jensen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
A Loginov
A Loginov
222Department of Physics, Yale University, New Haven, CT United States of America
222,
C W Loh
C W Loh
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
T Lohse
T Lohse
21Department of Physics, Humboldt University, Berlin, Germany
21,
K Lohwasser
K Lohwasser
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
M Lokajicek
M Lokajicek
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
V P Lombardo
V P Lombardo
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
R E Long
R E Long
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
L Lopes
L Lopes
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
D Lopez Mateos
D Lopez Mateos
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
J Lorenz
J Lorenz
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
N Lorenzo Martinez
N Lorenzo Martinez
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
M Losada
M Losada
206Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
206,
P Loscutoff
P Loscutoff
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M J Losty
M J Losty
202TRIUMF, Vancouver, BC Canada
202,
X Lou
X Lou
62Physics Department, University of Texas at Dallas, Richardson, TX United States of America
62,
A Lounis
A Lounis
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
K F Loureiro
K F Loureiro
206Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
206,
J Love
J Love
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
P A Love
P A Love
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
A J Lowe
A J Lowe
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
F Lu
F Lu
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
H J Lubatti
H J Lubatti
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
C Luci
C Luci
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
A Lucotte
A Lucotte
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
D Ludwig
D Ludwig
63DESY, Hamburg and Zeuthen, Germany
63,
I Ludwig
I Ludwig
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
J Ludwig
J Ludwig
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
F Luehring
F Luehring
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
W Lukas
W Lukas
86Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
86,
L Luminari
L Luminari
164INFN Sezione di Roma I, Roma, Italy
164,
E Lund
E Lund
146Department of Physics, University of Oslo, Oslo, Norway
146,
J Lundberg
J Lundberg
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
O Lundberg
O Lundberg
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
B Lund-Jensen
B Lund-Jensen
190Physics Department, Royal Institute of Technology, Stockholm, Sweden
190,
J Lundquist
J Lundquist
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
M Lungwitz
M Lungwitz
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
D Lynn
D Lynn
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
R Lysak
R Lysak
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
E Lytken
E Lytken
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
H Ma
H Ma
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
L L Ma
L L Ma
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
G Maccarrone
G Maccarrone
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
A Macchiolo
A Macchiolo
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
B Maček
B Maček
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
J Machado Miguens
J Machado Miguens
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
D Macina
D Macina
44CERN, Geneva, Switzerland
44,
R Mackeprang
R Mackeprang
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
R Madar
R Madar
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
R J Madaras
R J Madaras
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
H J Maddocks
H J Maddocks
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
W F Mader
W F Mader
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
A Madsen
A Madsen
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
M Maeno
M Maeno
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
T Maeno
T Maeno
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
L Magnoni
L Magnoni
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
E Magradze
E Magradze
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
K Mahboubi
K Mahboubi
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
J Mahlstedt
J Mahlstedt
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
S Mahmoud
S Mahmoud
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
G Mahout
G Mahout
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
C Maiani
C Maiani
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
C Maidantchik
C Maidantchik
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
A Maio
A Maio
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
S Majewski
S Majewski
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
Y Makida
Y Makida
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
N Makovec
N Makovec
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
P Mal
P Mal
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
B Malaescu
B Malaescu
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
Pa Malecki
Pa Malecki
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
P Malecki
P Malecki
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
V P Maleev
V P Maleev
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
F Malek
F Malek
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
U Mallik
U Mallik
87University of Iowa, Iowa City, IA United States of America
87,
D Malon
D Malon
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
C Malone
C Malone
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
S Maltezos
S Maltezos
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
V M Malyshev
V M Malyshev
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
S Malyukov
S Malyukov
44CERN, Geneva, Switzerland
44,
J Mamuzic
J Mamuzic
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
L Mandelli
L Mandelli
116INFN Sezione di Milano, Milano, Italy
116,
I Mandić
I Mandić
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
R Mandrysch
R Mandrysch
87University of Iowa, Iowa City, IA United States of America
87,
J Maneira
J Maneira
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
A Manfredini
A Manfredini
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
L Manhaes de Andrade Filho
L Manhaes de Andrade Filho
33Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
33,
J A Manjarres Ramos
J A Manjarres Ramos
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
A Mann
A Mann
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
P M Manning
P M Manning
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
A Manousakis-Katsikakis
A Manousakis-Katsikakis
13Physics Department, University of Athens, Athens, Greece
13,
B Mansoulie
B Mansoulie
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
R Mantifel
R Mantifel
112Department of Physics, McGill University, Montreal, QC Canada
112,
L Mapelli
L Mapelli
44CERN, Geneva, Switzerland
44,
L March
L March
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
J F Marchand
J F Marchand
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
F Marchese
F Marchese
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
G Marchiori
G Marchiori
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
M Marcisovsky
M Marcisovsky
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
C P Marino
C P Marino
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
C N Marques
C N Marques
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
F Marroquim
F Marroquim
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
Z Marshall
Z Marshall
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
L F Marti
L F Marti
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
S Marti-Garcia
S Marti-Garcia
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
B Martin
B Martin
44CERN, Geneva, Switzerland
44,
B Martin
B Martin
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
J P Martin
J P Martin
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
T A Martin
T A Martin
216Department of Physics, University of Warwick, Coventry, United Kingdom
216,
V J Martin
V J Martin
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
B Martin dit Latour
B Martin dit Latour
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
H Martinez
H Martinez
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
M Martinez
M Martinez
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
S Martin-Haugh
S Martin-Haugh
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
A C Martyniuk
A C Martyniuk
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
M Marx
M Marx
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
F Marzano
F Marzano
164INFN Sezione di Roma I, Roma, Italy
164,
A Marzin
A Marzin
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
L Masetti
L Masetti
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
T Mashimo
T Mashimo
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
R Mashinistov
R Mashinistov
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
J Masik
J Masik
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
A L Maslennikov
A L Maslennikov
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
I Massa
I Massa
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
N Massol
N Massol
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
P Mastrandrea
P Mastrandrea
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
A Mastroberardino
A Mastroberardino
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
T Masubuchi
T Masubuchi
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
H Matsunaga
H Matsunaga
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
T Matsushita
T Matsushita
91Graduate School of Science, Kobe University, Kobe, Japan
91,
P Mättig
P Mättig
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
S Mättig
S Mättig
63DESY, Hamburg and Zeuthen, Germany
63,
C Mattravers
C Mattravers
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
J Maurer
J Maurer
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
S J Maxfield
S J Maxfield
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
D A Maximov
D A Maximov
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
R Mazini
R Mazini
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
M Mazur
M Mazur
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
L Mazzaferro
L Mazzaferro
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
M Mazzanti
M Mazzanti
116INFN Sezione di Milano, Milano, Italy
116,
S P Mc Kee
S P Mc Kee
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
A McCarn
A McCarn
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
R L McCarthy
R L McCarthy
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
T G McCarthy
T G McCarthy
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
N A McCubbin
N A McCubbin
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
K W McFarlane
K W McFarlane
79Department of Physics, Hampton University, Hampton, VA United States of America
79,
J A Mcfayden
J A Mcfayden
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
G Mchedlidze
G Mchedlidze
74High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
74,
T Mclaughlan
T Mclaughlan
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
S J McMahon
S J McMahon
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
R A McPherson
R A McPherson
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
A Meade
A Meade
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
J Mechnich
J Mechnich
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
M Mechtel
M Mechtel
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
M Medinnis
M Medinnis
63DESY, Hamburg and Zeuthen, Germany
63,
S Meehan
S Meehan
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
R Meera-Lebbai
R Meera-Lebbai
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
T Meguro
T Meguro
145Graduate School of Science, Osaka University, Osaka, Japan
145,
S Mehlhase
S Mehlhase
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
A Mehta
A Mehta
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
K Meier
K Meier
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
C Meineck
C Meineck
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
B Meirose
B Meirose
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
C Melachrinos
C Melachrinos
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
B R Mellado Garcia
B R Mellado Garcia
187School of Physics, University of the Witwatersrand, Johannesburg, South Africa
187,
F Meloni
F Meloni
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
L Mendoza Navas
L Mendoza Navas
206Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
206,
A Mengarelli
A Mengarelli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S Menke
S Menke
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
E Meoni
E Meoni
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
K M Mercurio
K M Mercurio
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
N Meric
N Meric
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
P Mermod
P Mermod
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
L Merola
L Merola
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
C Meroni
C Meroni
116INFN Sezione di Milano, Milano, Italy
116,
F S Merritt
F S Merritt
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
H Merritt
H Merritt
138Ohio State University, Columbus, OH United States of America
138,
A Messina
A Messina
44CERN, Geneva, Switzerland
44,
J Metcalfe
J Metcalfe
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
A S Mete
A S Mete
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
C Meyer
C Meyer
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
C Meyer
C Meyer
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
J-P Meyer
J-P Meyer
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
J Meyer
J Meyer
44CERN, Geneva, Switzerland
44,
J Meyer
J Meyer
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
S Michal
S Michal
44CERN, Geneva, Switzerland
44,
R P Middleton
R P Middleton
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
S Migas
S Migas
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
L Mijović
L Mijović
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
G Mikenberg
G Mikenberg
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
M Mikestikova
M Mikestikova
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
M Mikuž
M Mikuž
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
D W Miller
D W Miller
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
W J Mills
W J Mills
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
C Mills
C Mills
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
A Milov
A Milov
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
D A Milstead
D A Milstead
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
D Milstein
D Milstein
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
A A Minaenko
A A Minaenko
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
M Miñano Moya
M Miñano Moya
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
I A Minashvili
I A Minashvili
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A I Mincer
A I Mincer
137Department of Physics, New York University, New York, NY United States of America
137,
B Mindur
B Mindur
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
M Mineev
M Mineev
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
Y Ming
Y Ming
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
L M Mir
L M Mir
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
G Mirabelli
G Mirabelli
164INFN Sezione di Roma I, Roma, Italy
164,
J Mitrevski
J Mitrevski
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
V A Mitsou
V A Mitsou
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
S Mitsui
S Mitsui
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
P S Miyagawa
P S Miyagawa
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
J U Mjörnmark
J U Mjörnmark
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
T Moa
T Moa
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
V Moeller
V Moeller
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
S Mohapatra
S Mohapatra
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
W Mohr
W Mohr
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
R Moles-Valls
R Moles-Valls
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
A Molfetas
A Molfetas
44CERN, Geneva, Switzerland
44,
K Mönig
K Mönig
63DESY, Hamburg and Zeuthen, Germany
63,
C Monini
C Monini
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
J Monk
J Monk
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
E Monnier
E Monnier
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
J Montejo Berlingen
J Montejo Berlingen
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
F Monticelli
F Monticelli
95Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
95,
S Monzani
S Monzani
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
R W Moore
R W Moore
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
C Mora Herrera
C Mora Herrera
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
A Moraes
A Moraes
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
N Morange
N Morange
87University of Iowa, Iowa City, IA United States of America
87,
J Morel
J Morel
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
D Moreno
D Moreno
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
M Moreno Llácer
M Moreno Llácer
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
P Morettini
P Morettini
71INFN Sezione di Genova, Genova, Italy
71,
M Morgenstern
M Morgenstern
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
M Morii
M Morii
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
S Moritz
S Moritz
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
A K Morley
A K Morley
44CERN, Geneva, Switzerland
44,
G Mornacchi
G Mornacchi
44CERN, Geneva, Switzerland
44,
J D Morris
J D Morris
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
L Morvaj
L Morvaj
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
N Möser
N Möser
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
H G Moser
H G Moser
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
M Mosidze
M Mosidze
74High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
74,
J Moss
J Moss
138Ohio State University, Columbus, OH United States of America
138,
R Mount
R Mount
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
E Mountricha
E Mountricha
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
S V Mouraviev
S V Mouraviev
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
E J W Moyse
E J W Moyse
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
R D Mudd
R D Mudd
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
F Mueller
F Mueller
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
J Mueller
J Mueller
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
K Mueller
K Mueller
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Mueller
T Mueller
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
T Mueller
T Mueller
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
D Muenstermann
D Muenstermann
44CERN, Geneva, Switzerland
44,
Y Munwes
Y Munwes
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
J A Murillo Quijada
J A Murillo Quijada
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
W J Murray
W J Murray
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
I Mussche
I Mussche
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
E Musto
E Musto
195Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
195,
A G Myagkov
A G Myagkov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
M Myska
M Myska
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
O Nackenhorst
O Nackenhorst
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
J Nadal
J Nadal
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
K Nagai
K Nagai
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
R Nagai
R Nagai
200Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
200,
Y Nagai
Y Nagai
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
K Nagano
K Nagano
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
A Nagarkar
A Nagarkar
138Ohio State University, Columbus, OH United States of America
138,
Y Nagasaka
Y Nagasaka
84Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
84,
M Nagel
M Nagel
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
A M Nairz
A M Nairz
44CERN, Geneva, Switzerland
44,
Y Nakahama
Y Nakahama
44CERN, Geneva, Switzerland
44,
K Nakamura
K Nakamura
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
T Nakamura
T Nakamura
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
I Nakano
I Nakano
139Faculty of Science, Okayama University, Okayama, Japan
139,
H Namasivayam
H Namasivayam
62Physics Department, University of Texas at Dallas, Richardson, TX United States of America
62,
G Nanava
G Nanava
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
A Napier
A Napier
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
R Narayan
R Narayan
82Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
82,
M Nash
M Nash
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
T Nattermann
T Nattermann
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Naumann
T Naumann
63DESY, Hamburg and Zeuthen, Germany
63,
G Navarro
G Navarro
206Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
206,
H A Neal
H A Neal
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
P Yu Nechaeva
P Yu Nechaeva
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
T J Neep
T J Neep
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
A Negri
A Negri
148INFN Sezione di Pavia, Pavia, Italy
149Dipartimento di Fisica, Università di Pavia, Pavia, Italy
148,149,
G Negri
G Negri
44CERN, Geneva, Switzerland
44,
M Negrini
M Negrini
27INFN Sezione di Bologna, Bologna, Italy
27,
S Nektarijevic
S Nektarijevic
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
A Nelson
A Nelson
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
T K Nelson
T K Nelson
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
S Nemecek
S Nemecek
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
P Nemethy
P Nemethy
137Department of Physics, New York University, New York, NY United States of America
137,
A A Nepomuceno
A A Nepomuceno
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
M Nessi
M Nessi
44CERN, Geneva, Switzerland
44,
M S Neubauer
M S Neubauer
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
M Neumann
M Neumann
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
A Neusiedl
A Neusiedl
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
R M Neves
R M Neves
137Department of Physics, New York University, New York, NY United States of America
137,
P Nevski
P Nevski
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
F M Newcomer
F M Newcomer
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
P R Newman
P R Newman
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
D H Nguyen
D H Nguyen
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
V Nguyen Thi Hong
V Nguyen Thi Hong
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
R B Nickerson
R B Nickerson
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
R Nicolaidou
R Nicolaidou
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
B Nicquevert
B Nicquevert
44CERN, Geneva, Switzerland
44,
F Niedercorn
F Niedercorn
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
J Nielsen
J Nielsen
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
N Nikiforou
N Nikiforou
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
A Nikiforov
A Nikiforov
21Department of Physics, Humboldt University, Berlin, Germany
21,
V Nikolaenko
V Nikolaenko
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
I Nikolic-Audit
I Nikolic-Audit
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
K Nikolics
K Nikolics
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
K Nikolopoulos
K Nikolopoulos
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
P Nilsson
P Nilsson
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
Y Ninomiya
Y Ninomiya
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
A Nisati
A Nisati
164INFN Sezione di Roma I, Roma, Italy
164,
R Nisius
R Nisius
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
T Nobe
T Nobe
200Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
200,
L Nodulman
L Nodulman
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
M Nomachi
M Nomachi
145Graduate School of Science, Osaka University, Osaka, Japan
145,
I Nomidis
I Nomidis
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
S Norberg
S Norberg
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
M Nordberg
M Nordberg
44CERN, Geneva, Switzerland
44,
J Novakova
J Novakova
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
M Nozaki
M Nozaki
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
L Nozka
L Nozka
142RCPTM, Palacký University, Olomouc, Czech Republic
142,
A-E Nuncio-Quiroz
A-E Nuncio-Quiroz
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
G Nunes Hanninger
G Nunes Hanninger
113School of Physics, University of Melbourne, Victoria, Australia
113,
T Nunnemann
T Nunnemann
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
E Nurse
E Nurse
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
B J O’Brien
B J O’Brien
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
D C O’Neil
D C O’Neil
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
V O’Shea
V O’Shea
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
L B Oakes
L B Oakes
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
F G Oakham
F G Oakham
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
H Oberlack
H Oberlack
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
J Ocariz
J Ocariz
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
A Ochi
A Ochi
91Graduate School of Science, Kobe University, Kobe, Japan
91,
M I Ochoa
M I Ochoa
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
S Oda
S Oda
94Department of Physics, Kyushu University, Fukuoka, Japan
94,
S Odaka
S Odaka
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
J Odier
J Odier
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
H Ogren
H Ogren
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
A Oh
A Oh
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
S H Oh
S H Oh
66Department of Physics, Duke University, Durham, NC United States of America
66,
C C Ohm
C C Ohm
44CERN, Geneva, Switzerland
44,
T Ohshima
T Ohshima
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
W Okamura
W Okamura
145Graduate School of Science, Osaka University, Osaka, Japan
145,
H Okawa
H Okawa
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
Y Okumura
Y Okumura
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
T Okuyama
T Okuyama
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
A Olariu
A Olariu
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
A G Olchevski
A G Olchevski
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
S A Olivares Pino
S A Olivares Pino
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
M Oliveira
M Oliveira
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
D Oliveira Damazio
D Oliveira Damazio
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
E Oliver Garcia
E Oliver Garcia
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
D Olivito
D Olivito
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
A Olszewski
A Olszewski
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
J Olszowska
J Olszowska
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
A Onofre
A Onofre
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
P U E Onyisi
P U E Onyisi
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
C J Oram
C J Oram
202TRIUMF, Vancouver, BC Canada
202,
M J Oreglia
M J Oreglia
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
Y Oren
Y Oren
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
D Orestano
D Orestano
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
N Orlando
N Orlando
97INFN Sezione di Lecce, Lecce, Italy
98Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
97,98,
C Oropeza Barrera
C Oropeza Barrera
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
R S Orr
R S Orr
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
B Osculati
B Osculati
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
R Ospanov
R Ospanov
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
G Otero y Garzon
G Otero y Garzon
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
J P Ottersbach
J P Ottersbach
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
M Ouchrif
M Ouchrif
173Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
173,
E A Ouellette
E A Ouellette
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
F Ould-Saada
F Ould-Saada
146Department of Physics, University of Oslo, Oslo, Norway
146,
A Ouraou
A Ouraou
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
Q Ouyang
Q Ouyang
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
A Ovcharova
A Ovcharova
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Owen
M Owen
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
S Owen
S Owen
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
V E Ozcan
V E Ozcan
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
N Ozturk
N Ozturk
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
A Pacheco Pages
A Pacheco Pages
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
C Padilla Aranda
C Padilla Aranda
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
S Pagan Griso
S Pagan Griso
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Paganis
E Paganis
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
C Pahl
C Pahl
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
F Paige
F Paige
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
P Pais
P Pais
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
K Pajchel
K Pajchel
146Department of Physics, University of Oslo, Oslo, Norway
146,
G Palacino
G Palacino
203Department of Physics and Astronomy, York University, Toronto, ON Canada
203,
C P Paleari
C P Paleari
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
S Palestini
S Palestini
44CERN, Geneva, Switzerland
44,
D Pallin
D Pallin
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
A Palma
A Palma
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
J D Palmer
J D Palmer
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
Y B Pan
Y B Pan
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
E Panagiotopoulou
E Panagiotopoulou
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
J G Panduro Vazquez
J G Panduro Vazquez
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
P Pani
P Pani
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
N Panikashvili
N Panikashvili
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
S Panitkin
S Panitkin
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
D Pantea
D Pantea
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
A Papadelis
A Papadelis
188Department of Physics, Stockholm University, Stockholm, Sweden
188,
Th D Papadopoulou
Th D Papadopoulou
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
K Papageorgiou
K Papageorgiou
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
A Paramonov
A Paramonov
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
D Paredes Hernandez
D Paredes Hernandez
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
W Park
W Park
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
M A Parker
M A Parker
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
F Parodi
F Parodi
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
J A Parsons
J A Parsons
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
U Parzefall
U Parzefall
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
S Pashapour
S Pashapour
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
E Pasqualucci
E Pasqualucci
164INFN Sezione di Roma I, Roma, Italy
164,
S Passaggio
S Passaggio
71INFN Sezione di Genova, Genova, Italy
71,
A Passeri
A Passeri
168INFN Sezione di Roma Tre, Roma, Italy
168,
F Pastore
F Pastore
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
Fr Pastore
Fr Pastore
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
G Pásztor
G Pásztor
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
S Pataraia
S Pataraia
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
N D Patel
N D Patel
193School of Physics, University of Sydney, Sydney, Australia
193,
J R Pater
J R Pater
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
S Patricelli
S Patricelli
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
T Pauly
T Pauly
44CERN, Geneva, Switzerland
44,
J Pearce
J Pearce
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
M Pedersen
M Pedersen
146Department of Physics, University of Oslo, Oslo, Norway
146,
S Pedraza Lopez
S Pedraza Lopez
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
M I Pedraza Morales
M I Pedraza Morales
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
S V Peleganchuk
S V Peleganchuk
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
D Pelikan
D Pelikan
212Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
212,
H Peng
H Peng
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
B Penning
B Penning
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A Penson
A Penson
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
J Penwell
J Penwell
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
T Perez Cavalcanti
T Perez Cavalcanti
63DESY, Hamburg and Zeuthen, Germany
63,
E Perez Codina
E Perez Codina
202TRIUMF, Vancouver, BC Canada
202,
M T Pérez García-Estañ
M T Pérez García-Estañ
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
V Perez Reale
V Perez Reale
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
L Perini
L Perini
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
H Pernegger
H Pernegger
44CERN, Geneva, Switzerland
44,
R Perrino
R Perrino
97INFN Sezione di Lecce, Lecce, Italy
97,
P Perrodo
P Perrodo
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
V D Peshekhonov
V D Peshekhonov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
K Peters
K Peters
44CERN, Geneva, Switzerland
44,
R F Y Peters
R F Y Peters
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
B A Petersen
B A Petersen
44CERN, Geneva, Switzerland
44,
J Petersen
J Petersen
44CERN, Geneva, Switzerland
44,
T C Petersen
T C Petersen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
E Petit
E Petit
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
A Petridis
A Petridis
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
C Petridou
C Petridou
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
E Petrolo
E Petrolo
164INFN Sezione di Roma I, Roma, Italy
164,
F Petrucci
F Petrucci
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
D Petschull
D Petschull
63DESY, Hamburg and Zeuthen, Germany
63,
M Petteni
M Petteni
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
R Pezoa
R Pezoa
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
A Phan
A Phan
113School of Physics, University of Melbourne, Victoria, Australia
113,
P W Phillips
P W Phillips
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
G Piacquadio
G Piacquadio
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
E Pianori
E Pianori
216Department of Physics, University of Warwick, Coventry, United Kingdom
216,
A Picazio
A Picazio
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
E Piccaro
E Piccaro
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
M Piccinini
M Piccinini
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
S M Piec
S M Piec
63DESY, Hamburg and Zeuthen, Germany
63,
R Piegaia
R Piegaia
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
D T Pignotti
D T Pignotti
138Ohio State University, Columbus, OH United States of America
138,
J E Pilcher
J E Pilcher
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A D Pilkington
A D Pilkington
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
J Pina
J Pina
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
M Pinamonti
M Pinamonti
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
A Pinder
A Pinder
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
J L Pinfold
J L Pinfold
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
A Pingel
A Pingel
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
B Pinto
B Pinto
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
C Pizio
C Pizio
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
M-A Pleier
M-A Pleier
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
V Pleskot
V Pleskot
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
E Plotnikova
E Plotnikova
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
P Plucinski
P Plucinski
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
S Poddar
S Poddar
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
F Podlyski
F Podlyski
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
R Poettgen
R Poettgen
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
L Poggioli
L Poggioli
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
D Pohl
D Pohl
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Pohl
M Pohl
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
G Polesello
G Polesello
148INFN Sezione di Pavia, Pavia, Italy
148,
A Policicchio
A Policicchio
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
R Polifka
R Polifka
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
A Polini
A Polini
27INFN Sezione di Bologna, Bologna, Italy
27,
V Polychronakos
V Polychronakos
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
D Pomeroy
D Pomeroy
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
K Pommès
K Pommès
44CERN, Geneva, Switzerland
44,
L Pontecorvo
L Pontecorvo
164INFN Sezione di Roma I, Roma, Italy
164,
B G Pope
B G Pope
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
G A Popeneciu
G A Popeneciu
38Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj Napoca, Romania
38,
D S Popovic
D S Popovic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
A Poppleton
A Poppleton
44CERN, Geneva, Switzerland
44,
X Portell Bueso
X Portell Bueso
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
G E Pospelov
G E Pospelov
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
S Pospisil
S Pospisil
158Czech Technical University in Prague, Praha, Czech Republic
158,
I N Potrap
I N Potrap
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
C J Potter
C J Potter
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
C T Potter
C T Potter
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
G Poulard
G Poulard
44CERN, Geneva, Switzerland
44,
J Poveda
J Poveda
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
V Pozdnyakov
V Pozdnyakov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
R Prabhu
R Prabhu
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
P Pralavorio
P Pralavorio
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
A Pranko
A Pranko
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
S Prasad
S Prasad
44CERN, Geneva, Switzerland
44,
R Pravahan
R Pravahan
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
S Prell
S Prell
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
K Pretzl
K Pretzl
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
D Price
D Price
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
J Price
J Price
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
L E Price
L E Price
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
D Prieur
D Prieur
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
M Primavera
M Primavera
97INFN Sezione di Lecce, Lecce, Italy
97,
M Proissl
M Proissl
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
K Prokofiev
K Prokofiev
137Department of Physics, New York University, New York, NY United States of America
137,
F Prokoshin
F Prokoshin
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
E Protopapadaki
E Protopapadaki
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
S Protopopescu
S Protopopescu
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
J Proudfoot
J Proudfoot
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
X Prudent
X Prudent
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
M Przybycien
M Przybycien
58Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Krakow, Poland
58,
H Przysiezniak
H Przysiezniak
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Psoroulas
S Psoroulas
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
E Ptacek
E Ptacek
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
E Pueschel
E Pueschel
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
D Puldon
D Puldon
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
M Purohit
M Purohit
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
P Puzo
P Puzo
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
Y Pylypchenko
Y Pylypchenko
87University of Iowa, Iowa City, IA United States of America
87,
J Qian
J Qian
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
A Quadt
A Quadt
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
D R Quarrie
D R Quarrie
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
W B Quayle
W B Quayle
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
D Quilty
D Quilty
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
M Raas
M Raas
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
V Radeka
V Radeka
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
V Radescu
V Radescu
63DESY, Hamburg and Zeuthen, Germany
63,
P Radloff
P Radloff
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
F Ragusa
F Ragusa
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
G Rahal
G Rahal
224Centre de Calcul de l’Institut National de Physique Nucléaire et de Physique des Particules (IN2P3), Villeurbanne, France
224,
S Rajagopalan
S Rajagopalan
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
M Rammensee
M Rammensee
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
M Rammes
M Rammes
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
A S Randle-Conde
A S Randle-Conde
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
K Randrianarivony
K Randrianarivony
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
C Rangel-Smith
C Rangel-Smith
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
K Rao
K Rao
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
F Rauscher
F Rauscher
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
T C Rave
T C Rave
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
T Ravenscroft
T Ravenscroft
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
M Raymond
M Raymond
44CERN, Geneva, Switzerland
44,
A L Read
A L Read
146Department of Physics, University of Oslo, Oslo, Norway
146,
D M Rebuzzi
D M Rebuzzi
148INFN Sezione di Pavia, Pavia, Italy
149Dipartimento di Fisica, Università di Pavia, Pavia, Italy
148,149,
A Redelbach
A Redelbach
220Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
220,
G Redlinger
G Redlinger
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
R Reece
R Reece
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
K Reeves
K Reeves
62Physics Department, University of Texas at Dallas, Richardson, TX United States of America
62,
A Reinsch
A Reinsch
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
I Reisinger
I Reisinger
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
M Relich
M Relich
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
C Rembser
C Rembser
44CERN, Geneva, Switzerland
44,
Z L Ren
Z L Ren
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
A Renaud
A Renaud
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
M Rescigno
M Rescigno
164INFN Sezione di Roma I, Roma, Italy
164,
S Resconi
S Resconi
116INFN Sezione di Milano, Milano, Italy
116,
B Resende
B Resende
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
P Reznicek
P Reznicek
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
R Rezvani
R Rezvani
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
R Richter
R Richter
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
E Richter-Was
E Richter-Was
59Marian Smoluchowski Institute of Physics, Jagiellonian University, Krakow, Poland
59,
M Ridel
M Ridel
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
P Rieck
P Rieck
21Department of Physics, Humboldt University, Berlin, Germany
21,
M Rijssenbeek
M Rijssenbeek
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
A Rimoldi
A Rimoldi
148INFN Sezione di Pavia, Pavia, Italy
149Dipartimento di Fisica, Università di Pavia, Pavia, Italy
148,149,
L Rinaldi
L Rinaldi
27INFN Sezione di Bologna, Bologna, Italy
27,
R R Rios
R R Rios
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
E Ritsch
E Ritsch
86Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
86,
I Riu
I Riu
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
G Rivoltella
G Rivoltella
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
F Rizatdinova
F Rizatdinova
141Department of Physics, Oklahoma State University, Stillwater, OK United States of America
141,
E Rizvi
E Rizvi
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
S H Robertson
S H Robertson
112Department of Physics, McGill University, Montreal, QC Canada
112,
A Robichaud-Veronneau
A Robichaud-Veronneau
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
D Robinson
D Robinson
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
J E M Robinson
J E M Robinson
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
A Robson
A Robson
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J G Rocha de Lima
J G Rocha de Lima
135Department of Physics, Northern Illinois University, DeKalb, IL United States of America
135,
C Roda
C Roda
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
D Roda Dos Santos
D Roda Dos Santos
44CERN, Geneva, Switzerland
44,
A Roe
A Roe
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
S Roe
S Roe
44CERN, Geneva, Switzerland
44,
O Røhne
O Røhne
146Department of Physics, University of Oslo, Oslo, Norway
146,
S Rolli
S Rolli
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
A Romaniouk
A Romaniouk
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
M Romano
M Romano
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
G Romeo
G Romeo
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
E Romero Adam
E Romero Adam
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
N Rompotis
N Rompotis
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
L Roos
L Roos
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
E Ros
E Ros
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
S Rosati
S Rosati
164INFN Sezione di Roma I, Roma, Italy
164,
K Rosbach
K Rosbach
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
A Rose
A Rose
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
M Rose
M Rose
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
G A Rosenbaum
G A Rosenbaum
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
P L Rosendahl
P L Rosendahl
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
O Rosenthal
O Rosenthal
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
V Rossetti
V Rossetti
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
E Rossi
E Rossi
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
L P Rossi
L P Rossi
71INFN Sezione di Genova, Genova, Italy
71,
M Rotaru
M Rotaru
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
I Roth
I Roth
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
J Rothberg
J Rothberg
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
D Rousseau
D Rousseau
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
C R Royon
C R Royon
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
A Rozanov
A Rozanov
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
Y Rozen
Y Rozen
195Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
195,
X Ruan
X Ruan
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
F Rubbo
F Rubbo
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
I Rubinskiy
I Rubinskiy
63DESY, Hamburg and Zeuthen, Germany
63,
N Ruckstuhl
N Ruckstuhl
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
V I Rud
V I Rud
125D.V. Skobeltsyn Institute of Nuclear Physics, M.V.Lomonosov Moscow State University, Moscow, Russia
125,
C Rudolph
C Rudolph
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
M S Rudolph
M S Rudolph
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
F Rühr
F Rühr
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
A Ruiz-Martinez
A Ruiz-Martinez
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
L Rumyantsev
L Rumyantsev
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
Z Rurikova
Z Rurikova
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
N A Rusakovich
N A Rusakovich
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A Ruschke
A Ruschke
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
J P Rutherfoord
J P Rutherfoord
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
N Ruthmann
N Ruthmann
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
P Ruzicka
P Ruzicka
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
Y F Ryabov
Y F Ryabov
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
M Rybar
M Rybar
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
G Rybkin
G Rybkin
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
N C Ryder
N C Ryder
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
A F Saavedra
A F Saavedra
193School of Physics, University of Sydney, Sydney, Australia
193,
A Saddique
A Saddique
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
I Sadeh
I Sadeh
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
H F-W Sadrozinski
H F-W Sadrozinski
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
R Sadykov
R Sadykov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
F Safai Tehrani
F Safai Tehrani
164INFN Sezione di Roma I, Roma, Italy
164,
H Sakamoto
H Sakamoto
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
G Salamanna
G Salamanna
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
A Salamon
A Salamon
166INFN Sezione di Roma Tor Vergata, Roma, Italy
166,
M Saleem
M Saleem
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
D Salek
D Salek
44CERN, Geneva, Switzerland
44,
D Salihagic
D Salihagic
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
A Salnikov
A Salnikov
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
J Salt
J Salt
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
B M Salvachua Ferrando
B M Salvachua Ferrando
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
D Salvatore
D Salvatore
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
F Salvatore
F Salvatore
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
A Salvucci
A Salvucci
133Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
133,
A Salzburger
A Salzburger
44CERN, Geneva, Switzerland
44,
D Sampsonidis
D Sampsonidis
197Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
197,
A Sanchez
A Sanchez
130INFN Sezione di Napoli, Napoli, Italy
131Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
130,131,
J Sánchez
J Sánchez
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
V Sanchez Martinez
V Sanchez Martinez
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
H Sandaker
H Sandaker
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
H G Sander
H G Sander
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
M P Sanders
M P Sanders
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
M Sandhoff
M Sandhoff
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
T Sandoval
T Sandoval
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
C Sandoval
C Sandoval
206Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
206,
R Sandstroem
R Sandstroem
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
D P C Sankey
D P C Sankey
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
A Sansoni
A Sansoni
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
C Santoni
C Santoni
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
R Santonico
R Santonico
166INFN Sezione di Roma Tor Vergata, Roma, Italy
167Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
166,167,
H Santos
H Santos
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
I Santoyo Castillo
I Santoyo Castillo
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
K Sapp
K Sapp
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
J G Saraiva
J G Saraiva
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
T Sarangi
T Sarangi
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
E Sarkisyan-Grinbaum
E Sarkisyan-Grinbaum
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
B Sarrazin
B Sarrazin
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
F Sarri
F Sarri
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
G Sartisohn
G Sartisohn
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
O Sasaki
O Sasaki
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
Y Sasaki
Y Sasaki
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
N Sasao
N Sasao
92Faculty of Science, Kyoto University, Kyoto, Japan
92,
I Satsounkevitch
I Satsounkevitch
118B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
118,
G Sauvage
G Sauvage
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
E Sauvan
E Sauvan
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
J B Sauvan
J B Sauvan
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
P Savard
P Savard
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
V Savinov
V Savinov
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
D O Savu
D O Savu
44CERN, Geneva, Switzerland
44,
C Sawyer
C Sawyer
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
L Sawyer
L Sawyer
104Louisiana Tech University, Ruston, LA United States of America
104,
D H Saxon
D H Saxon
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J Saxon
J Saxon
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
C Sbarra
C Sbarra
27INFN Sezione di Bologna, Bologna, Italy
27,
A Sbrizzi
A Sbrizzi
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
D A Scannicchio
D A Scannicchio
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
M Scarcella
M Scarcella
193School of Physics, University of Sydney, Sydney, Australia
193,
J Schaarschmidt
J Schaarschmidt
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
P Schacht
P Schacht
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
D Schaefer
D Schaefer
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
A Schaelicke
A Schaelicke
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
S Schaepe
S Schaepe
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Schaetzel
S Schaetzel
82Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
82,
U Schäfer
U Schäfer
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
A C Schaffer
A C Schaffer
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
D Schaile
D Schaile
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
R D Schamberger
R D Schamberger
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
V Scharf
V Scharf
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
V A Schegelsky
V A Schegelsky
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
D Scheirich
D Scheirich
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
M Schernau
M Schernau
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
M I Scherzer
M I Scherzer
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
C Schiavi
C Schiavi
71INFN Sezione di Genova, Genova, Italy
72Dipartimento di Fisica, Università di Genova, Genova, Italy
71,72,
J Schieck
J Schieck
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
C Schillo
C Schillo
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
M Schioppa
M Schioppa
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
S Schlenker
S Schlenker
44CERN, Geneva, Switzerland
44,
E Schmidt
E Schmidt
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
K Schmieden
K Schmieden
44CERN, Geneva, Switzerland
44,
C Schmitt
C Schmitt
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
C Schmitt
C Schmitt
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
S Schmitt
S Schmitt
82Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
82,
B Schneider
B Schneider
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
Y J Schnellbach
Y J Schnellbach
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
U Schnoor
U Schnoor
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
L Schoeffel
L Schoeffel
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
A Schoening
A Schoening
82Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
82,
A L S Schorlemmer
A L S Schorlemmer
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
M Schott
M Schott
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
D Schouten
D Schouten
202TRIUMF, Vancouver, BC Canada
202,
J Schovancova
J Schovancova
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
M Schram
M Schram
112Department of Physics, McGill University, Montreal, QC Canada
112,
C Schroeder
C Schroeder
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
N Schroer
N Schroer
83ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
83,
M J Schultens
M J Schultens
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
H-C Schultz-Coulon
H-C Schultz-Coulon
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
H Schulz
H Schulz
21Department of Physics, Humboldt University, Berlin, Germany
21,
M Schumacher
M Schumacher
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
B A Schumm
B A Schumm
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
Ph Schune
Ph Schune
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
A Schwartzman
A Schwartzman
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
Ph Schwegler
Ph Schwegler
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
Ph Schwemling
Ph Schwemling
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
R Schwienhorst
R Schwienhorst
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
J Schwindling
J Schwindling
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
T Schwindt
T Schwindt
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Schwoerer
M Schwoerer
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
F G Sciacca
F G Sciacca
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
E Scifo
E Scifo
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
G Sciolla
G Sciolla
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
W G Scott
W G Scott
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
F Scutti
F Scutti
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J Searcy
J Searcy
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
G Sedov
G Sedov
63DESY, Hamburg and Zeuthen, Germany
63,
E Sedykh
E Sedykh
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
S C Seidel
S C Seidel
132Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
132,
A Seiden
A Seiden
176Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
176,
F Seifert
F Seifert
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
J M Seixas
J M Seixas
32Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
32,
G Sekhniaidze
G Sekhniaidze
130INFN Sezione di Napoli, Napoli, Italy
130,
S J Sekula
S J Sekula
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
K E Selbach
K E Selbach
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
D M Seliverstov
D M Seliverstov
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
G Sellers
G Sellers
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
M Seman
M Seman
184Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
184,
N Semprini-Cesari
N Semprini-Cesari
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
C Serfon
C Serfon
44CERN, Geneva, Switzerland
44,
L Serin
L Serin
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
L Serkin
L Serkin
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
T Serre
T Serre
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
R Seuster
R Seuster
202TRIUMF, Vancouver, BC Canada
202,
H Severini
H Severini
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
A Sfyrla
A Sfyrla
44CERN, Geneva, Switzerland
44,
E Shabalina
E Shabalina
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
M Shamim
M Shamim
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
L Y Shan
L Y Shan
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
J T Shank
J T Shank
30Department of Physics, Boston University, Boston, MA United States of America
30,
Q T Shao
Q T Shao
113School of Physics, University of Melbourne, Victoria, Australia
113,
M Shapiro
M Shapiro
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
P B Shatalov
P B Shatalov
123Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
123,
K Shaw
K Shaw
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
P Sherwood
P Sherwood
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
S Shimizu
S Shimizu
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
M Shimojima
M Shimojima
128Nagasaki Institute of Applied Science, Nagasaki, Japan
128,
T Shin
T Shin
79Department of Physics, Hampton University, Hampton, VA United States of America
79,
M Shiyakova
M Shiyakova
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
A Shmeleva
A Shmeleva
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
M J Shochet
M J Shochet
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
D Short
D Short
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
S Shrestha
S Shrestha
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
E Shulga
E Shulga
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
M A Shupe
M A Shupe
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
P Sicho
P Sicho
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
A Sidoti
A Sidoti
164INFN Sezione di Roma I, Roma, Italy
164,
F Siegert
F Siegert
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
Dj Sijacki
Dj Sijacki
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
O Silbert
O Silbert
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
J Silva
J Silva
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
Y Silver
Y Silver
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
D Silverstein
D Silverstein
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
S B Silverstein
S B Silverstein
188Department of Physics, Stockholm University, Stockholm, Sweden
188,
V Simak
V Simak
158Czech Technical University in Prague, Praha, Czech Republic
158,
O Simard
O Simard
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
Lj Simic
Lj Simic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
S Simion
S Simion
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
E Simioni
E Simioni
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
B Simmons
B Simmons
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
R Simoniello
R Simoniello
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
M Simonyan
M Simonyan
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
P Sinervo
P Sinervo
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
N B Sinev
N B Sinev
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
V Sipica
V Sipica
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
G Siragusa
G Siragusa
220Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
220,
A Sircar
A Sircar
104Louisiana Tech University, Ruston, LA United States of America
104,
A N Sisakyan
A N Sisakyan
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
S Yu Sivoklokov
S Yu Sivoklokov
125D.V. Skobeltsyn Institute of Nuclear Physics, M.V.Lomonosov Moscow State University, Moscow, Russia
125,
J Sjölin
J Sjölin
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
T B Sjursen
T B Sjursen
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
L A Skinnari
L A Skinnari
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
H P Skottowe
H P Skottowe
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
K Yu Skovpen
K Yu Skovpen
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
P Skubic
P Skubic
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
M Slater
M Slater
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
T Slavicek
T Slavicek
158Czech Technical University in Prague, Praha, Czech Republic
158,
K Sliwa
K Sliwa
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
V Smakhtin
V Smakhtin
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
B H Smart
B H Smart
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
L Smestad
L Smestad
146Department of Physics, University of Oslo, Oslo, Norway
146,
S Yu Smirnov
S Yu Smirnov
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
Y Smirnov
Y Smirnov
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
L N Smirnova
L N Smirnova
125D.V. Skobeltsyn Institute of Nuclear Physics, M.V.Lomonosov Moscow State University, Moscow, Russia
125,
O Smirnova
O Smirnova
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
K M Smith
K M Smith
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
M Smizanska
M Smizanska
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
K Smolek
K Smolek
158Czech Technical University in Prague, Praha, Czech Republic
158,
A A Snesarev
A A Snesarev
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
G Snidero
G Snidero
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
J Snow
J Snow
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
S Snyder
S Snyder
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
R Sobie
R Sobie
215Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
215,
J Sodomka
J Sodomka
158Czech Technical University in Prague, Praha, Czech Republic
158,
A Soffer
A Soffer
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
D A Soh
D A Soh
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
C A Solans
C A Solans
44CERN, Geneva, Switzerland
44,
M Solar
M Solar
158Czech Technical University in Prague, Praha, Czech Republic
158,
J Solc
J Solc
158Czech Technical University in Prague, Praha, Czech Republic
158,
E Yu Soldatov
E Yu Soldatov
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
U Soldevila
U Soldevila
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
E Solfaroli Camillocci
E Solfaroli Camillocci
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
A A Solodkov
A A Solodkov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
O V Solovyanov
O V Solovyanov
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
V Solovyev
V Solovyev
151Petersburg Nuclear Physics Institute, Gatchina, Russia
151,
N Soni
N Soni
2School of Chemistry and Physics, University of Adelaide, Adelaide, Australia
2,
A Sood
A Sood
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
V Sopko
V Sopko
158Czech Technical University in Prague, Praha, Czech Republic
158,
B Sopko
B Sopko
158Czech Technical University in Prague, Praha, Czech Republic
158,
M Sosebee
M Sosebee
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
R Soualah
R Soualah
208INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
210Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
208,210,
P Soueid
P Soueid
121Group of Particle Physics, University of Montreal, Montreal, QC Canada
121,
A M Soukharev
A M Soukharev
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
D South
D South
63DESY, Hamburg and Zeuthen, Germany
63,
S Spagnolo
S Spagnolo
97INFN Sezione di Lecce, Lecce, Italy
98Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
97,98,
F Spanò
F Spanò
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
R Spighi
R Spighi
27INFN Sezione di Bologna, Bologna, Italy
27,
G Spigo
G Spigo
44CERN, Geneva, Switzerland
44,
R Spiwoks
R Spiwoks
44CERN, Geneva, Switzerland
44,
M Spousta
M Spousta
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
T Spreitzer
T Spreitzer
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
B Spurlock
B Spurlock
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
R D St Denis
R D St Denis
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
J Stahlman
J Stahlman
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
R Stamen
R Stamen
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
E Stanecka
E Stanecka
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
R W Stanek
R W Stanek
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
C Stanescu
C Stanescu
168INFN Sezione di Roma Tre, Roma, Italy
168,
M Stanescu-Bellu
M Stanescu-Bellu
63DESY, Hamburg and Zeuthen, Germany
63,
M M Stanitzki
M M Stanitzki
63DESY, Hamburg and Zeuthen, Germany
63,
S Stapnes
S Stapnes
146Department of Physics, University of Oslo, Oslo, Norway
146,
E A Starchenko
E A Starchenko
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
J Stark
J Stark
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
P Staroba
P Staroba
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
P Starovoitov
P Starovoitov
63DESY, Hamburg and Zeuthen, Germany
63,
R Staszewski
R Staszewski
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
A Staude
A Staude
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
P Stavina
P Stavina
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
G Steele
G Steele
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
P Steinbach
P Steinbach
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
P Steinberg
P Steinberg
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
I Stekl
I Stekl
158Czech Technical University in Prague, Praha, Czech Republic
158,
B Stelzer
B Stelzer
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
H J Stelzer
H J Stelzer
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
O Stelzer-Chilton
O Stelzer-Chilton
202TRIUMF, Vancouver, BC Canada
202,
H Stenzel
H Stenzel
75II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
75,
S Stern
S Stern
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
G A Stewart
G A Stewart
44CERN, Geneva, Switzerland
44,
J A Stillings
J A Stillings
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M C Stockton
M C Stockton
112Department of Physics, McGill University, Montreal, QC Canada
112,
M Stoebe
M Stoebe
112Department of Physics, McGill University, Montreal, QC Canada
112,
K Stoerig
K Stoerig
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
G Stoicea
G Stoicea
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
S Stonjek
S Stonjek
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
A R Stradling
A R Stradling
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
A Straessner
A Straessner
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
J Strandberg
J Strandberg
190Physics Department, Royal Institute of Technology, Stockholm, Sweden
190,
S Strandberg
S Strandberg
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
A Strandlie
A Strandlie
146Department of Physics, University of Oslo, Oslo, Norway
146,
M Strang
M Strang
138Ohio State University, Columbus, OH United States of America
138,
E Strauss
E Strauss
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
M Strauss
M Strauss
140Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
140,
P Strizenec
P Strizenec
184Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
184,
R Ströhmer
R Ströhmer
220Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
220,
D M Strom
D M Strom
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
J A Strong
J A Strong
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
R Stroynowski
R Stroynowski
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
B Stugu
B Stugu
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
I Stumer
I Stumer
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
J Stupak
J Stupak
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
P Sturm
P Sturm
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
N A Styles
N A Styles
63DESY, Hamburg and Zeuthen, Germany
63,
D Su
D Su
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
HS Subramania
HS Subramania
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
R Subramaniam
R Subramaniam
104Louisiana Tech University, Ruston, LA United States of America
104,
A Succurro
A Succurro
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
Y Sugaya
Y Sugaya
145Graduate School of Science, Osaka University, Osaka, Japan
145,
C Suhr
C Suhr
135Department of Physics, Northern Illinois University, DeKalb, IL United States of America
135,
M Suk
M Suk
158Czech Technical University in Prague, Praha, Czech Republic
158,
V V Sulin
V V Sulin
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
S Sultansoy
S Sultansoy
7Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
7,
T Sumida
T Sumida
92Faculty of Science, Kyoto University, Kyoto, Japan
92,
X Sun
X Sun
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
J E Sundermann
J E Sundermann
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
K Suruliz
K Suruliz
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
G Susinno
G Susinno
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
M R Sutton
M R Sutton
192Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
192,
Y Suzuki
Y Suzuki
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
Y Suzuki
Y Suzuki
91Graduate School of Science, Kobe University, Kobe, Japan
91,
M Svatos
M Svatos
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
S Swedish
S Swedish
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
M Swiatlowski
M Swiatlowski
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
I Sykora
I Sykora
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
T Sykora
T Sykora
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
D Ta
D Ta
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
K Tackmann
K Tackmann
63DESY, Hamburg and Zeuthen, Germany
63,
A Taffard
A Taffard
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
R Tafirout
R Tafirout
202TRIUMF, Vancouver, BC Canada
202,
N Taiblum
N Taiblum
196Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
196,
Y Takahashi
Y Takahashi
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
H Takai
H Takai
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
R Takashima
R Takashima
93Kyoto University of Education, Kyoto, Japan
93,
H Takeda
H Takeda
91Graduate School of Science, Kobe University, Kobe, Japan
91,
T Takeshita
T Takeshita
179Department of Physics, Shinshu University, Nagano, Japan
179,
Y Takubo
Y Takubo
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
M Talby
M Talby
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
A A Talyshev
A A Talyshev
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
J Y C Tam
J Y C Tam
220Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
220,
M C Tamsett
M C Tamsett
104Louisiana Tech University, Ruston, LA United States of America
104,
K G Tan
K G Tan
113School of Physics, University of Melbourne, Victoria, Australia
113,
J Tanaka
J Tanaka
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
R Tanaka
R Tanaka
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
S Tanaka
S Tanaka
163Ritsumeikan University, Kusatsu, Shiga Japan
163,
S Tanaka
S Tanaka
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
A J Tanasijczuk
A J Tanasijczuk
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
K Tani
K Tani
91Graduate School of Science, Kobe University, Kobe, Japan
91,
N Tannoury
N Tannoury
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
S Tapprogge
S Tapprogge
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
S Tarem
S Tarem
195Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
195,
F Tarrade
F Tarrade
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
G F Tartarelli
G F Tartarelli
116INFN Sezione di Milano, Milano, Italy
116,
P Tas
P Tas
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
M Tasevsky
M Tasevsky
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
T Tashiro
T Tashiro
92Faculty of Science, Kyoto University, Kyoto, Japan
92,
E Tassi
E Tassi
56INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Rende, Italy
57Dipartimento di Fisica, Università della Calabria, Rende, Italy
56,57,
Y Tayalati
Y Tayalati
173Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
173,
C Taylor
C Taylor
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
F E Taylor
F E Taylor
120Department of Physics, Massachusetts Institute of Technology, Cambridge, MA United States of America
120,
G N Taylor
G N Taylor
113School of Physics, University of Melbourne, Victoria, Australia
113,
W Taylor
W Taylor
203Department of Physics and Astronomy, York University, Toronto, ON Canada
203,
M Teinturier
M Teinturier
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
F A Teischinger
F A Teischinger
44CERN, Geneva, Switzerland
44,
M Teixeira Dias Castanheira
M Teixeira Dias Castanheira
101School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
101,
P Teixeira-Dias
P Teixeira-Dias
102Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
102,
K K Temming
K K Temming
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
H Ten Kate
H Ten Kate
44CERN, Geneva, Switzerland
44,
P K Teng
P K Teng
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
S Terada
S Terada
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
K Terashi
K Terashi
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
J Terron
J Terron
107Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
107,
M Testa
M Testa
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
R J Teuscher
R J Teuscher
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
J Therhaag
J Therhaag
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
T Theveneaux-Pelzer
T Theveneaux-Pelzer
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
S Thoma
S Thoma
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
J P Thomas
J P Thomas
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
E N Thompson
E N Thompson
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
P D Thompson
P D Thompson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
P D Thompson
P D Thompson
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
A S Thompson
A S Thompson
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
L A Thomsen
L A Thomsen
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
E Thomson
E Thomson
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
M Thomson
M Thomson
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
W M Thong
W M Thong
113School of Physics, University of Melbourne, Victoria, Australia
113,
R P Thun
R P Thun
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
F Tian
F Tian
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
M J Tibbetts
M J Tibbetts
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
T Tic
T Tic
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
V O Tikhomirov
V O Tikhomirov
122P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
122,
Yu A Tikhonov
Yu A Tikhonov
136Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
136,
S Timoshenko
S Timoshenko
124Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
124,
E Tiouchichine
E Tiouchichine
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
P Tipton
P Tipton
222Department of Physics, Yale University, New Haven, CT United States of America
222,
S Tisserant
S Tisserant
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
T Todorov
T Todorov
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Todorova-Nova
S Todorova-Nova
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
B Toggerson
B Toggerson
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
J Tojo
J Tojo
94Department of Physics, Kyushu University, Fukuoka, Japan
94,
S Tokár
S Tokár
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
K Tokushuku
K Tokushuku
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
K Tollefson
K Tollefson
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
L Tomlinson
L Tomlinson
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
M Tomoto
M Tomoto
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
L Tompkins
L Tompkins
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
K Toms
K Toms
132Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
132,
A Tonoyan
A Tonoyan
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
C Topfel
C Topfel
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
N D Topilin
N D Topilin
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
E Torrence
E Torrence
143Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
143,
H Torres
H Torres
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
E Torró Pastor
E Torró Pastor
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
J Toth
J Toth
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
F Touchard
F Touchard
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
D R Tovey
D R Tovey
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
H L Tran
H L Tran
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
T Trefzger
T Trefzger
220Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
220,
L Tremblet
L Tremblet
44CERN, Geneva, Switzerland
44,
A Tricoli
A Tricoli
44CERN, Geneva, Switzerland
44,
I M Trigger
I M Trigger
202TRIUMF, Vancouver, BC Canada
202,
S Trincaz-Duvoid
S Trincaz-Duvoid
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
M F Tripiana
M F Tripiana
95Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
95,
N Triplett
N Triplett
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
W Trischuk
W Trischuk
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
B Trocmé
B Trocmé
78Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
78,
C Troncon
C Troncon
116INFN Sezione di Milano, Milano, Italy
116,
M Trottier-McDonald
M Trottier-McDonald
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
M Trovatelli
M Trovatelli
168INFN Sezione di Roma Tre, Roma, Italy
169Dipartimento di Matematica e Fisica, Università Roma Tre, Roma, Italy
168,169,
P True
P True
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
M Trzebinski
M Trzebinski
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
A Trzupek
A Trzupek
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
C Tsarouchas
C Tsarouchas
44CERN, Geneva, Switzerland
44,
J C-L Tseng
J C-L Tseng
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
M Tsiakiris
M Tsiakiris
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
P V Tsiareshka
P V Tsiareshka
118B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
118,
D Tsionou
D Tsionou
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
G Tsipolitis
G Tsipolitis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
S Tsiskaridze
S Tsiskaridze
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona, Barcelona, Spain
16,
V Tsiskaridze
V Tsiskaridze
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
E G Tskhadadze
E G Tskhadadze
73E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
73,
I I Tsukerman
I I Tsukerman
123Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
123,
V Tsulaia
V Tsulaia
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
J-W Tsung
J-W Tsung
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Tsuno
S Tsuno
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
D Tsybychev
D Tsybychev
191Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
191,
A Tua
A Tua
178Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
178,
A Tudorache
A Tudorache
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
V Tudorache
V Tudorache
37National Institute of Physics and Nuclear Engineering, Bucharest, Romania
37,
J M Tuggle
J M Tuggle
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A N Tuna
A N Tuna
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
M Turala
M Turala
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
D Turecek
D Turecek
158Czech Technical University in Prague, Praha, Czech Republic
158,
I Turk Cakir
I Turk Cakir
8Turkish Atomic Energy Authority, Ankara, Turkey
8,
R Turra
R Turra
116INFN Sezione di Milano, Milano, Italy
117Dipartimento di Fisica, Università di Milano, Milano, Italy
116,117,
P M Tuts
P M Tuts
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
A Tykhonov
A Tykhonov
100Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
100,
M Tylmad
M Tylmad
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
M Tyndel
M Tyndel
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
K Uchida
K Uchida
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
I Ueda
I Ueda
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
R Ueno
R Ueno
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
M Ughetto
M Ughetto
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
M Ugland
M Ugland
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
M Uhlenbrock
M Uhlenbrock
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
F Ukegawa
F Ukegawa
204Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
204,
G Unal
G Unal
44CERN, Geneva, Switzerland
44,
A Undrus
A Undrus
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
G Unel
G Unel
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
F C Ungaro
F C Ungaro
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
Y Unno
Y Unno
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
D Urbaniec
D Urbaniec
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
P Urquijo
P Urquijo
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
G Usai
G Usai
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
L Vacavant
L Vacavant
110CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
110,
V Vacek
V Vacek
158Czech Technical University in Prague, Praha, Czech Republic
158,
B Vachon
B Vachon
112Department of Physics, McGill University, Montreal, QC Canada
112,
S Vahsen
S Vahsen
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
N Valencic
N Valencic
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
S Valentinetti
S Valentinetti
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
A Valero
A Valero
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
L Valery
L Valery
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
S Valkar
S Valkar
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
E Valladolid Gallego
E Valladolid Gallego
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
S Vallecorsa
S Vallecorsa
195Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
195,
J A Valls Ferrer
J A Valls Ferrer
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
R Van Berg
R Van Berg
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
P C Van Der Deijl
P C Van Der Deijl
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
R van der Geer
R van der Geer
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
H van der Graaf
H van der Graaf
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
R Van Der Leeuw
R Van Der Leeuw
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
D van der Ster
D van der Ster
44CERN, Geneva, Switzerland
44,
N van Eldik
N van Eldik
44CERN, Geneva, Switzerland
44,
P van Gemmeren
P van Gemmeren
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
J Van Nieuwkoop
J Van Nieuwkoop
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
I van Vulpen
I van Vulpen
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
M Vanadia
M Vanadia
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
W Vandelli
W Vandelli
44CERN, Geneva, Switzerland
44,
A Vaniachine
A Vaniachine
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
P Vankov
P Vankov
63DESY, Hamburg and Zeuthen, Germany
63,
F Vannucci
F Vannucci
105Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
105,
R Vari
R Vari
164INFN Sezione di Roma I, Roma, Italy
164,
E W Varnes
E W Varnes
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
T Varol
T Varol
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
D Varouchas
D Varouchas
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
A Vartapetian
A Vartapetian
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
K E Varvell
K E Varvell
193School of Physics, University of Sydney, Sydney, Australia
193,
V I Vassilakopoulos
V I Vassilakopoulos
79Department of Physics, Hampton University, Hampton, VA United States of America
79,
F Vazeille
F Vazeille
53Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Clermont-Ferrand, France
53,
T Vazquez Schroeder
T Vazquez Schroeder
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
F Veloso
F Veloso
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
S Veneziano
S Veneziano
164INFN Sezione di Roma I, Roma, Italy
164,
A Ventura
A Ventura
97INFN Sezione di Lecce, Lecce, Italy
98Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
97,98,
D Ventura
D Ventura
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
M Venturi
M Venturi
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
N Venturi
N Venturi
201Department of Physics, University of Toronto, Toronto, ON Canada
201,
V Vercesi
V Vercesi
148INFN Sezione di Pavia, Pavia, Italy
148,
M Verducci
M Verducci
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
W Verkerke
W Verkerke
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
J C Vermeulen
J C Vermeulen
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
A Vest
A Vest
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
M C Vetterli
M C Vetterli
181Department of Physics, Simon Fraser University, Burnaby, BC Canada
181,
I Vichou
I Vichou
211Department of Physics, University of Illinois, Urbana, IL United States of America
211,
T Vickey
T Vickey
187School of Physics, University of the Witwatersrand, Johannesburg, South Africa
187,
O E Vickey Boeriu
O E Vickey Boeriu
187School of Physics, University of the Witwatersrand, Johannesburg, South Africa
187,
G H A Viehhauser
G H A Viehhauser
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
S Viel
S Viel
214Department of Physics, University of British Columbia, Vancouver, BC Canada
214,
M Villa
M Villa
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
M Villaplana Perez
M Villaplana Perez
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
E Vilucchi
E Vilucchi
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
M G Vincter
M G Vincter
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
V B Vinogradov
V B Vinogradov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
J Virzi
J Virzi
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
O Vitells
O Vitells
218Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
218,
M Viti
M Viti
63DESY, Hamburg and Zeuthen, Germany
63,
I Vivarelli
I Vivarelli
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
F Vives Vaque
F Vives Vaque
4Department of Physics, University of Alberta, Edmonton, AB Canada
4,
S Vlachos
S Vlachos
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
D Vladoiu
D Vladoiu
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
M Vlasak
M Vlasak
158Czech Technical University in Prague, Praha, Czech Republic
158,
A Vogel
A Vogel
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
P Vokac
P Vokac
158Czech Technical University in Prague, Praha, Czech Republic
158,
G Volpi
G Volpi
68Laboratori Nazionali di Frascati, INFN, Frascati, Italy
68,
M Volpi
M Volpi
113School of Physics, University of Melbourne, Victoria, Australia
113,
G Volpini
G Volpini
116INFN Sezione di Milano, Milano, Italy
116,
H von der Schmitt
H von der Schmitt
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
H von Radziewski
H von Radziewski
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
E von Toerne
E von Toerne
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
V Vorobel
V Vorobel
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
M Vos
M Vos
213Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
213,
R Voss
R Voss
44CERN, Geneva, Switzerland
44,
J H Vossebeld
J H Vossebeld
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
N Vranjes
N Vranjes
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
M Vranjes Milosavljevic
M Vranjes Milosavljevic
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
V Vrba
V Vrba
157Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
157,
M Vreeswijk
M Vreeswijk
134Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
134,
T Vu Anh
T Vu Anh
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
R Vuillermet
R Vuillermet
44CERN, Geneva, Switzerland
44,
I Vukotic
I Vukotic
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
Z Vykydal
Z Vykydal
158Czech Technical University in Prague, Praha, Czech Republic
158,
W Wagner
W Wagner
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
P Wagner
P Wagner
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Wahrmund
S Wahrmund
65Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
65,
J Wakabayashi
J Wakabayashi
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
S Walch
S Walch
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
J Walder
J Walder
96Physics Department, Lancaster University, Lancaster, United Kingdom
96,
R Walker
R Walker
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
W Walkowiak
W Walkowiak
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
R Wall
R Wall
222Department of Physics, Yale University, New Haven, CT United States of America
222,
P Waller
P Waller
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
B Walsh
B Walsh
222Department of Physics, Yale University, New Haven, CT United States of America
222,
C Wang
C Wang
66Department of Physics, Duke University, Durham, NC United States of America
66,
H Wang
H Wang
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
H Wang
H Wang
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
J Wang
J Wang
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
J Wang
J Wang
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
K Wang
K Wang
112Department of Physics, McGill University, Montreal, QC Canada
112,
R Wang
R Wang
132Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
132,
S M Wang
S M Wang
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
T Wang
T Wang
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
X Wang
X Wang
222Department of Physics, Yale University, New Haven, CT United States of America
222,
A Warburton
A Warburton
112Department of Physics, McGill University, Montreal, QC Canada
112,
C P Ward
C P Ward
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
D R Wardrope
D R Wardrope
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
M Warsinsky
M Warsinsky
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
A Washbrook
A Washbrook
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
C Wasicki
C Wasicki
63DESY, Hamburg and Zeuthen, Germany
63,
I Watanabe
I Watanabe
91Graduate School of Science, Kobe University, Kobe, Japan
91,
P M Watkins
P M Watkins
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
A T Watson
A T Watson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
I J Watson
I J Watson
193School of Physics, University of Sydney, Sydney, Australia
193,
M F Watson
M F Watson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
G Watts
G Watts
177Department of Physics, University of Washington, Seattle, WA United States of America
177,
S Watts
S Watts
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
A T Waugh
A T Waugh
193School of Physics, University of Sydney, Sydney, Australia
193,
B M Waugh
B M Waugh
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
M S Weber
M S Weber
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
J S Webster
J S Webster
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A R Weidberg
A R Weidberg
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
P Weigell
P Weigell
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
J Weingarten
J Weingarten
77II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
77,
C Weiser
C Weiser
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
P S Wells
P S Wells
44CERN, Geneva, Switzerland
44,
T Wenaus
T Wenaus
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
D Wendland
D Wendland
21Department of Physics, Humboldt University, Berlin, Germany
21,
Z Weng
Z Weng
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
T Wengler
T Wengler
44CERN, Geneva, Switzerland
44,
S Wenig
S Wenig
44CERN, Geneva, Switzerland
44,
N Wermes
N Wermes
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
M Werner
M Werner
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
P Werner
P Werner
44CERN, Geneva, Switzerland
44,
M Werth
M Werth
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
M Wessels
M Wessels
81Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
J Wetter
J Wetter
205Department of Physics and Astronomy, Tufts University, Medford, MA United States of America
205,
K Whalen
K Whalen
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
A White
A White
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
M J White
M J White
113School of Physics, University of Melbourne, Victoria, Australia
113,
R White
R White
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
S White
S White
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
S R Whitehead
S R Whitehead
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
D Whiteson
D Whiteson
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
D Whittington
D Whittington
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
D Wicke
D Wicke
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
F J Wickens
F J Wickens
161Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
161,
W Wiedenmann
W Wiedenmann
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
M Wielers
M Wielers
106Fysiska institutionen, Lunds universitet, Lund, Sweden
106,
P Wienemann
P Wienemann
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
C Wiglesworth
C Wiglesworth
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
L A M Wiik-Fuchs
L A M Wiik-Fuchs
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
P A Wijeratne
P A Wijeratne
103Department of Physics and Astronomy, University College London, London, United Kingdom
103,
A Wildauer
A Wildauer
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
M A Wildt
M A Wildt
63DESY, Hamburg and Zeuthen, Germany
63,
I Wilhelm
I Wilhelm
159Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
159,
H G Wilkens
H G Wilkens
44CERN, Geneva, Switzerland
44,
J Z Will
J Z Will
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
E Williams
E Williams
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
H H Williams
H H Williams
150Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
150,
S Williams
S Williams
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
W Willis
W Willis
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
S Willocq
S Willocq
111Department of Physics, University of Massachusetts, Amherst, MA United States of America
111,
J A Wilson
J A Wilson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
A Wilson
A Wilson
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
I Wingerter-Seez
I Wingerter-Seez
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Winkelmann
S Winkelmann
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
F Winklmeier
F Winklmeier
44CERN, Geneva, Switzerland
44,
M Wittgen
M Wittgen
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
T Wittig
T Wittig
64Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
64,
J Wittkowski
J Wittkowski
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
S J Wollstadt
S J Wollstadt
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
M W Wolter
M W Wolter
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
H Wolters
H Wolters
155Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
155,
W C Wong
W C Wong
62Physics Department, University of Texas at Dallas, Richardson, TX United States of America
62,
G Wooden
G Wooden
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
B K Wosiek
B K Wosiek
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
J Wotschack
J Wotschack
44CERN, Geneva, Switzerland
44,
M J Woudstra
M J Woudstra
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
K W Wozniak
K W Wozniak
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
K Wraight
K Wraight
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
M Wright
M Wright
76SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
76,
B Wrona
B Wrona
99Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
99,
S L Wu
S L Wu
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
X Wu
X Wu
70Section de Physique, Université de Genève, Geneva, Switzerland
70,
Y Wu
Y Wu
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
E Wulf
E Wulf
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
B M Wynne
B M Wynne
67SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
67,
S Xella
S Xella
55Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
55,
M Xiao
M Xiao
175DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
175,
S Xie
S Xie
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
C Xu
C Xu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
D Xu
D Xu
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
L Xu
L Xu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
B Yabsley
B Yabsley
193School of Physics, University of Sydney, Sydney, Australia
193,
S Yacoob
S Yacoob
186Department of Physics, University of Johannesburg, Johannesburg, South Africa
186,
M Yamada
M Yamada
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
H Yamaguchi
H Yamaguchi
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
Y Yamaguchi
Y Yamaguchi
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
A Yamamoto
A Yamamoto
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
K Yamamoto
K Yamamoto
88Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
88,
S Yamamoto
S Yamamoto
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
T Yamamura
T Yamamura
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
T Yamanaka
T Yamanaka
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
K Yamauchi
K Yamauchi
129Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
129,
T Yamazaki
T Yamazaki
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
Y Yamazaki
Y Yamazaki
91Graduate School of Science, Kobe University, Kobe, Japan
91,
Z Yan
Z Yan
30Department of Physics, Boston University, Boston, MA United States of America
30,
H Yang
H Yang
52Physics Department, Shanghai Jiao Tong University, Shanghai, China
52,
H Yang
H Yang
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
U K Yang
U K Yang
109School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
109,
Y Yang
Y Yang
138Ohio State University, Columbus, OH United States of America
138,
Z Yang
Z Yang
188Department of Physics, Stockholm University, Stockholm, Sweden
189The Oskar Klein Centre, Stockholm, Sweden
188,189,
S Yanush
S Yanush
119National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
119,
L Yao
L Yao
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
Y Yasu
Y Yasu
90KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
90,
E Yatsenko
E Yatsenko
63DESY, Hamburg and Zeuthen, Germany
63,
K H Yau Wong
K H Yau Wong
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
J Ye
J Ye
61Physics Department, Southern Methodist University, Dallas, TX United States of America
61,
S Ye
S Ye
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
A L Yen
A L Yen
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
E Yildirim
E Yildirim
63DESY, Hamburg and Zeuthen, Germany
63,
M Yilmaz
M Yilmaz
6Department of Physics, Gazi University, Ankara, Turkey
6,
R Yoosoofmiya
R Yoosoofmiya
154Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
154,
K Yorita
K Yorita
217Waseda University, Tokyo, Japan
217,
R Yoshida
R Yoshida
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
K Yoshihara
K Yoshihara
198International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
198,
C Young
C Young
182SLAC National Accelerator Laboratory, Stanford, CA United States of America
182,
C J S Young
C J S Young
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
S Youssef
S Youssef
30Department of Physics, Boston University, Boston, MA United States of America
30,
D Yu
D Yu
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
D R Yu
D R Yu
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
J Yu
J Yu
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
J Yu
J Yu
141Department of Physics, Oklahoma State University, Stillwater, OK United States of America
141,
L Yuan
L Yuan
91Graduate School of Science, Kobe University, Kobe, Japan
91,
A Yurkewicz
A Yurkewicz
135Department of Physics, Northern Illinois University, DeKalb, IL United States of America
135,
B Zabinski
B Zabinski
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
R Zaidan
R Zaidan
87University of Iowa, Iowa City, IA United States of America
87,
A M Zaitsev
A M Zaitsev
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
S Zambito
S Zambito
31Department of Physics, Brandeis University, Waltham, MA United States of America
31,
L Zanello
L Zanello
164INFN Sezione di Roma I, Roma, Italy
165Dipartimento di Fisica, Università La Sapienza, Roma, Italy
164,165,
D Zanzi
D Zanzi
127Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
127,
A Zaytsev
A Zaytsev
36Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
36,
C Zeitnitz
C Zeitnitz
221Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
221,
M Zeman
M Zeman
158Czech Technical University in Prague, Praha, Czech Republic
158,
A Zemla
A Zemla
60The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
60,
O Zenin
O Zenin
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
T Ženiš
T Ženiš
183Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
183,
D Zerwas
D Zerwas
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
G Zevi della Porta
G Zevi della Porta
80Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
80,
D Zhang
D Zhang
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
H Zhang
H Zhang
115Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
115,
J Zhang
J Zhang
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
L Zhang
L Zhang
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
X Zhang
X Zhang
51School of Physics, Shandong University, Shandong, China
51,
Z Zhang
Z Zhang
144LAL, Université Paris-Sud and CNRS/IN2P3, Orsay, France
144,
Z Zhao
Z Zhao
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
A Zhemchugov
A Zhemchugov
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
J Zhong
J Zhong
147Department of Physics, Oxford University, Oxford, United Kingdom
147,
B Zhou
B Zhou
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
N Zhou
N Zhou
207Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
207,
Y Zhou
Y Zhou
194Institute of Physics, Academia Sinica, Taipei, Taiwan
194,
C G Zhu
C G Zhu
51School of Physics, Shandong University, Shandong, China
51,
H Zhu
H Zhu
63DESY, Hamburg and Zeuthen, Germany
63,
J Zhu
J Zhu
114Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
114,
Y Zhu
Y Zhu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
X Zhuang
X Zhuang
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
A Zibell
A Zibell
126Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
126,
D Zieminska
D Zieminska
85Department of Physics, Indiana University, Bloomington, IN United States of America
85,
N I Zimin
N I Zimin
89Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
89,
C Zimmermann
C Zimmermann
108Institut für Physik, Universität Mainz, Mainz, Germany
108,
R Zimmermann
R Zimmermann
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Zimmermann
S Zimmermann
29Physikalisches Institut, University of Bonn, Bonn, Germany
29,
S Zimmermann
S Zimmermann
69Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
69,
Z Zinonos
Z Zinonos
152INFN Sezione di Pisa, Pisa, Italy
153Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
152,153,
M Ziolkowski
M Ziolkowski
180Fachbereich Physik, Universität Siegen, Siegen, Germany
180,
R Zitoun
R Zitoun
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
L Živković
L Živković
54Nevis Laboratory, Columbia University, Irvington, NY United States of America
54,
V V Zmouchko
V V Zmouchko
160State Research Center Institute for High Energy Physics, Protvino, Russia
160,
G Zobernig
G Zobernig
219Department of Physics, University of Wisconsin, Madison, WI United States of America
219,
A Zoccoli
A Zoccoli
27INFN Sezione di Bologna, Bologna, Italy
28Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
27,28,
M zur Nedden
M zur Nedden
21Department of Physics, Humboldt University, Berlin, Germany
21,
V Zutshi
V Zutshi
135Department of Physics, Northern Illinois University, DeKalb, IL United States of America
135,
L Zwalinski
L Zwalinski
44CERN, Geneva, Switzerland
44
 pp collision data recorded by the ATLAS detector at the LHC is presented. Samples of top-quark pair events are selected in both the single-lepton and dilepton final states. The differential and integrated shapes of the jets initiated by bottom-quarks from the top-quark decays are compared with those of the jets originated by light-quarks from the hadronic W-boson decays
pp collision data recorded by the ATLAS detector at the LHC is presented. Samples of top-quark pair events are selected in both the single-lepton and dilepton final states. The differential and integrated shapes of the jets initiated by bottom-quarks from the top-quark decays are compared with those of the jets originated by light-quarks from the hadronic W-boson decays  in the single-lepton channel. The light-quark jets are found to have a narrower distribution of the momentum flow inside the jet area than b-quark jets.
in the single-lepton channel. The light-quark jets are found to have a narrower distribution of the momentum flow inside the jet area than b-quark jets. and pp collisions and this is interpreted as a result of the different admixtures of quark and gluon jets present in these different types of interactions [12]. Furthermore, at high momentum transfer, where fragmentation effects are less relevant, jet shapes have been found to be in qualitative agreement with next-to-leading-order (NLO) QCD predictions and in quantitative agreement with those including leading logarithm corrections [13]. Jet shapes have also been proposed as a tool for studies of substructure or in searches for new phenomena in final states with highly boosted particles [14–17].
and pp collisions and this is interpreted as a result of the different admixtures of quark and gluon jets present in these different types of interactions [12]. Furthermore, at high momentum transfer, where fragmentation effects are less relevant, jet shapes have been found to be in qualitative agreement with next-to-leading-order (NLO) QCD predictions and in quantitative agreement with those including leading logarithm corrections [13]. Jet shapes have also been proposed as a tool for studies of substructure or in searches for new phenomena in final states with highly boosted particles [14–17]. final states are a source of b-jets, as the top quark decays almost exclusively via t→Wb. While the dilepton channel, where both W bosons decay to leptons, is a very pure source of b-jets, the single-lepton channel contains b-jets and light jets, the latter originating from the dominant
final states are a source of b-jets, as the top quark decays almost exclusively via t→Wb. While the dilepton channel, where both W bosons decay to leptons, is a very pure source of b-jets, the single-lepton channel contains b-jets and light jets, the latter originating from the dominant 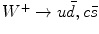 decays and their charge conjugates. A comparison of the light- and b-jet shapes measured in the
decays and their charge conjugates. A comparison of the light- and b-jet shapes measured in the 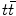 decays improves the CDF measurement discussed above, as the jet purity achieved using
decays improves the CDF measurement discussed above, as the jet purity achieved using  events is much higher. In addition, these measurements could be used to improve the modelling of jets in
events is much higher. In addition, these measurements could be used to improve the modelling of jets in  production Monte Carlo (MC) models in a new kinematic regime.
production Monte Carlo (MC) models in a new kinematic regime. samples is presented. Section 6 is devoted to the description of both the b-jet and light-jet samples obtained in the single-lepton final state. The differential and the integrated shape distributions of these jets are derived in Sect. 7. In Sect. 8 the results on the average values of the jet shape variables at the detector level are presented, including those for the b-jets in the dilepton channel. Results corrected for detector effects are presented in Sect. 9. In Sect. 10 the systematic uncertainties are discussed, and Sect. 11 contains a discussion of the results. Finally, Sect. 12 includes the summary and conclusions.
samples is presented. Section 6 is devoted to the description of both the b-jet and light-jet samples obtained in the single-lepton final state. The differential and the integrated shape distributions of these jets are derived in Sect. 7. In Sect. 8 the results on the average values of the jet shape variables at the detector level are presented, including those for the b-jets in the dilepton channel. Results corrected for detector effects are presented in Sect. 9. In Sect. 10 the systematic uncertainties are discussed, and Sect. 11 contains a discussion of the results. Finally, Sect. 12 includes the summary and conclusions. production is implemented with matrix elements calculated up to NLO accuracy. The generated events are then passed through a detailed Geant4 simulation [21, 22] of the ATLAS detector. The baseline MC samples used here are produced with the MC@NLO [23] or Powheg [24] generators for the matrix element calculation; the parton shower and hadronisation processes are implemented with Herwig [25] using the cluster hadronisation model [26] and CTEQ6.6 [27] parton distribution functions (PDFs). Multi-parton interactions are simulated using Jimmy [28] with the AUET1 tune [29]. This MC generator package has been used for the description of the
production is implemented with matrix elements calculated up to NLO accuracy. The generated events are then passed through a detailed Geant4 simulation [21, 22] of the ATLAS detector. The baseline MC samples used here are produced with the MC@NLO [23] or Powheg [24] generators for the matrix element calculation; the parton shower and hadronisation processes are implemented with Herwig [25] using the cluster hadronisation model [26] and CTEQ6.6 [27] parton distribution functions (PDFs). Multi-parton interactions are simulated using Jimmy [28] with the AUET1 tune [29]. This MC generator package has been used for the description of the 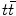 final states for ATLAS measurements of the cross section [30, 31] and studies of the kinematics [32].
final states for ATLAS measurements of the cross section [30, 31] and studies of the kinematics [32]. signal is normalised to the cross section calculated at approximate next-to-next-to-leading order (NNLO) using the Hathor package [41], while for the single-top production cross section, the calculations in Refs. [42–44] are used. The W+jets and Z+jets cross sections are taken from Alpgen [39] with additional NNLO K-factors as given in Ref. [45].
signal is normalised to the cross section calculated at approximate next-to-next-to-leading order (NNLO) using the Hathor package [41], while for the single-top production cross section, the calculations in Refs. [42–44] are used. The W+jets and Z+jets cross sections are taken from Alpgen [39] with additional NNLO K-factors as given in Ref. [45]. ) is summed in a cone in η–ϕ space of radius2
ΔR=0.2 around the electron. The
) is summed in a cone in η–ϕ space of radius2
ΔR=0.2 around the electron. The  value is required to be less than 3.5 GeV. For muon candidates, both the corresponding calorimeter isolation
value is required to be less than 3.5 GeV. For muon candidates, both the corresponding calorimeter isolation  and the analogous track isolation transverse momentum (
and the analogous track isolation transverse momentum ( ) must be less than 4 GeV in a cone of ΔR=0.3. The track isolation is calculated from the scalar sum of the transverse momenta of tracks with p
T>1 GeV, excluding the muon.
) must be less than 4 GeV in a cone of ΔR=0.3. The track isolation is calculated from the scalar sum of the transverse momenta of tracks with p
T>1 GeV, excluding the muon. , where the sum runs over the tracks with p
T>150 MeV associated with the vertex.
, where the sum runs over the tracks with p
T>150 MeV associated with the vertex. ) of the missing transverse momentum is described in Ref. [56] and begins with the vector sum of the transverse momenta of all jets with p
T>20 GeV and |η|<4.5. The transverse momenta of electron candidates are added. The contributions from all muon candidates and from all calorimeter clusters not belonging to a reconstructed object are also included.
) of the missing transverse momentum is described in Ref. [56] and begins with the vector sum of the transverse momenta of all jets with p
T>20 GeV and |η|<4.5. The transverse momenta of electron candidates are added. The contributions from all muon candidates and from all calorimeter clusters not belonging to a reconstructed object are also included. pair, giving rise to two more jets (see Fig. 1). The selection criteria follow those in Ref. [30] for the single-lepton sample and Ref. [31] for the dilepton sample. Events are triggered by inclusive high-p
T electron or muon EF triggers. The trigger thresholds are 18 GeV for muons and 20 GeV for electrons. The dataset used for the analysis corresponds to the first half of the data collected in 2011, with a centre-of-mass energy
pair, giving rise to two more jets (see Fig. 1). The selection criteria follow those in Ref. [30] for the single-lepton sample and Ref. [31] for the dilepton sample. Events are triggered by inclusive high-p
T electron or muon EF triggers. The trigger thresholds are 18 GeV for muons and 20 GeV for electrons. The dataset used for the analysis corresponds to the first half of the data collected in 2011, with a centre-of-mass energy  and an integrated luminosity of 1.8 fb−1. This data-taking period is characterised by an instantaneous luminosity smaller than 1.5×1033 cm−2 s−1, for which the mean number of interactions per bunch crossing is less than six. To reject the non-collision background, the primary vertex is required to have at least four tracks, each with p
T>150 MeV, associated with it. Pile-up effects are therefore small and have been taken into account as a systematic uncertainty.
and an integrated luminosity of 1.8 fb−1. This data-taking period is characterised by an instantaneous luminosity smaller than 1.5×1033 cm−2 s−1, for which the mean number of interactions per bunch crossing is less than six. To reject the non-collision background, the primary vertex is required to have at least four tracks, each with p
T>150 MeV, associated with it. Pile-up effects are therefore small and have been taken into account as a systematic uncertainty.
 in the dilepton (left) and single-lepton (right) decay modes
in the dilepton (left) and single-lepton (right) decay modes from the leptonic W-boson decays to a neutrino and an electron or muon. The offline lepton selection requires two isolated leptons (e or μ) with opposite charge and with transverse momenta p
T(e)>25 GeV, where p
T(e)=E
clustersin(θ
track), E
cluster being the cluster energy and θ
track the track polar angle, and p
T(μ)>20 GeV. At least one of the selected leptons has to match the corresponding trigger object.
from the leptonic W-boson decays to a neutrino and an electron or muon. The offline lepton selection requires two isolated leptons (e or μ) with opposite charge and with transverse momenta p
T(e)>25 GeV, where p
T(e)=E
clustersin(θ
track), E
cluster being the cluster energy and θ
track the track polar angle, and p
T(μ)>20 GeV. At least one of the selected leptons has to match the corresponding trigger object. for the ee and μμ channels. For the eμ channel, H
T is required to be greater than 130 GeV, where H
T is the scalar sum of the p
T of all muons, electrons and jets. To reject the Drell–Yan lepton pair background in the ee and μμ channels, the lepton pair is required to have an invariant mass m
ℓℓ greater than 15 GeV and to lie outside of a Z-boson mass window, rejecting all events where the two-lepton invariant mass satisfies |m
ℓℓ−m
Z|<10 GeV.
for the ee and μμ channels. For the eμ channel, H
T is required to be greater than 130 GeV, where H
T is the scalar sum of the p
T of all muons, electrons and jets. To reject the Drell–Yan lepton pair background in the ee and μμ channels, the lepton pair is required to have an invariant mass m
ℓℓ greater than 15 GeV and to lie outside of a Z-boson mass window, rejecting all events where the two-lepton invariant mass satisfies |m
ℓℓ−m
Z|<10 GeV. events, but also backgrounds from the final states W+jets and Z+jets, where the gauge bosons decay to leptons. All backgrounds, with the exception of multi-jet production, have been estimated using MC samples. The multi-jet background has been estimated using the jet–electron method [60]. This method relies on the identification of jets which, due to their high electromagnetic energy fraction, can fake electron candidates. The jet–electron method is applied with some modifications to the muon channel as well. The normalisation is estimated using a binned likelihood fit to the
events, but also backgrounds from the final states W+jets and Z+jets, where the gauge bosons decay to leptons. All backgrounds, with the exception of multi-jet production, have been estimated using MC samples. The multi-jet background has been estimated using the jet–electron method [60]. This method relies on the identification of jets which, due to their high electromagnetic energy fraction, can fake electron candidates. The jet–electron method is applied with some modifications to the muon channel as well. The normalisation is estimated using a binned likelihood fit to the  distribution. The results are summarised in Table 1.
distribution. The results are summarised in Table 1.


 is required to be greater than 35 GeV in the electron channel and greater than 20 GeV in the muon channel. The
is required to be greater than 35 GeV in the electron channel and greater than 20 GeV in the muon channel. The  resolution is below 10 GeV [56]. Furthermore, the transverse mass3 (m
T) is required to be greater than 25 GeV in the e-channel and to satisfy the condition
resolution is below 10 GeV [56]. Furthermore, the transverse mass3 (m
T) is required to be greater than 25 GeV in the e-channel and to satisfy the condition  in the μ-channel.
in the μ-channel. events in the sample is 77 %; the main background contributions for the single-lepton channel have been studied as in the previous case, and are summarised in Table 2. As in the dileptonic case, the multi-jet background has been estimated using the jet–electron method.
events in the sample is 77 %; the main background contributions for the single-lepton channel have been studied as in the previous case, and are summarised in Table 2. As in the dileptonic case, the multi-jet background has been estimated using the jet–electron method.
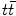
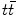 events, and a u,d,s-quark jet rejection factor of about 400, as well as a c-jet rejection factor of about 10 [62, 63]. The resulting number of b-jets selected in the dilepton (single-lepton) sample is 2279 (16735). A second working point with a b-tagging efficiency of 70 % is also used in order to evaluate the dependence of the measured jet shapes on b-tagging.
events, and a u,d,s-quark jet rejection factor of about 400, as well as a c-jet rejection factor of about 10 [62, 63]. The resulting number of b-jets selected in the dilepton (single-lepton) sample is 2279 (16735). A second working point with a b-tagging efficiency of 70 % is also used in order to evaluate the dependence of the measured jet shapes on b-tagging.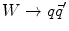 are a clean source of light-quark jets, as gluons and b-jets are highly suppressed; the former because gluons would originate in radiative corrections of order
are a clean source of light-quark jets, as gluons and b-jets are highly suppressed; the former because gluons would originate in radiative corrections of order  , and the latter because of the smallness of the CKM matrix elements |V
ub| and |V
cb|. To select the light-jet sample, the jet pair in the event which has the invariant mass closest to the W-boson mass is selected. Both jets are also required to be non-tagged by the b-tagging algorithm. The number of jets satisfying these criteria is 7158. Figure 3 shows the transverse momentum distribution of these jets together with the invariant mass of the dijet system. As expected, the p
T distribution of the light jets from W-boson decays exhibits a stronger fall-off than that for the b-jets. This dependence is again well described by the MC simulations in the jet p
T region used in this analysis. Agreement between the invariant mass distributions for observed and simulated events is good, in particular in the region close to the W-boson mass.
, and the latter because of the smallness of the CKM matrix elements |V
ub| and |V
cb|. To select the light-jet sample, the jet pair in the event which has the invariant mass closest to the W-boson mass is selected. Both jets are also required to be non-tagged by the b-tagging algorithm. The number of jets satisfying these criteria is 7158. Figure 3 shows the transverse momentum distribution of these jets together with the invariant mass of the dijet system. As expected, the p
T distribution of the light jets from W-boson decays exhibits a stronger fall-off than that for the b-jets. This dependence is again well described by the MC simulations in the jet p
T region used in this analysis. Agreement between the invariant mass distributions for observed and simulated events is good, in particular in the region close to the W-boson mass.

 ,
,  are the number of fakes (jets not assigned to the correct flavour, e.g. charm jets in the b-jet sample), and the total number of jets in a given sample, respectively. The purity in the multi-jet background is determined using Pythia MC samples.
are the number of fakes (jets not assigned to the correct flavour, e.g. charm jets in the b-jet sample), and the total number of jets in a given sample, respectively. The purity in the multi-jet background is determined using Pythia MC samples.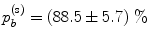 , while the purity of the light-jet sample is found to be
, while the purity of the light-jet sample is found to be  , as shown in Table 3. The uncertainty on the purity arises from the uncertainties on the signal and background fractions in each sample. The charm content in the light-jet sample is found to be 16 %, with the remaining 50 % ascribed to u,d and s.
, as shown in Table 3. The uncertainty on the purity arises from the uncertainties on the signal and background fractions in each sample. The charm content in the light-jet sample is found to be 16 %, with the remaining 50 % ascribed to u,d and s.

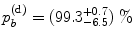 as shown in Table 4. Thus, the b-jet sample purity achieved using
as shown in Table 4. Thus, the b-jet sample purity achieved using  final states is much higher than that obtained in inclusive b-jet measurements at the Tevatron [18] or the LHC [55].
final states is much higher than that obtained in inclusive b-jet measurements at the Tevatron [18] or the LHC [55].


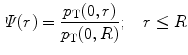



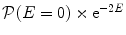 , where
, where  is the measured probability (28 %) of a charged particle track to be associated with a zero energy deposit in the calorimeter and E is the cluster energy in GeV. As a result, approximately 6 % of the total number of clusters are discarded. The impact of this cluster-removing algorithm on the measured jet shapes is smaller than 2 %.
is the measured probability (28 %) of a charged particle track to be associated with a zero energy deposit in the calorimeter and E is the cluster energy in GeV. As a result, approximately 6 % of the total number of clusters are discarded. The impact of this cluster-removing algorithm on the measured jet shapes is smaller than 2 %.
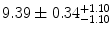









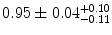












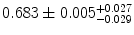





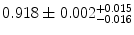


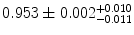



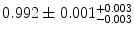






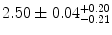
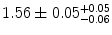
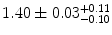



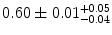



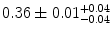

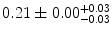












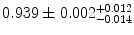













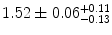



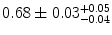


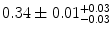
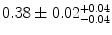

























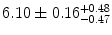
























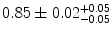
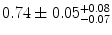



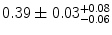

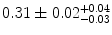




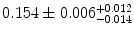

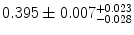












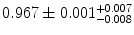









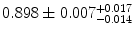
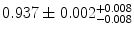





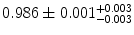


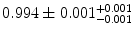
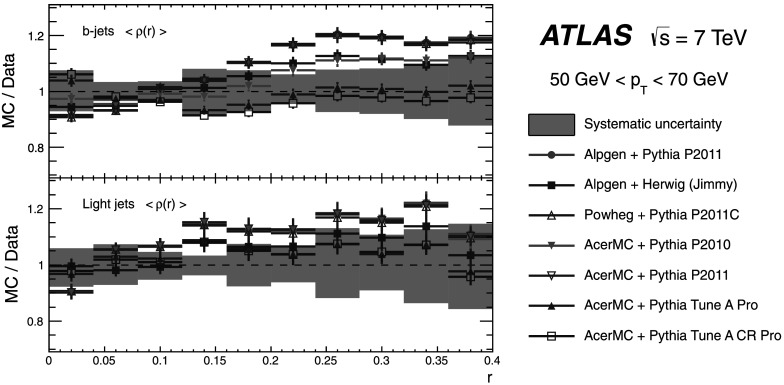
 differential jet shape data for 50 GeV<p
T<70 GeV with several MC event generators. As stated in the text, AcerMC [35] coupled to Pythia [33] with the A Pro and A CR Pro tunes [69, 70] give the best description of the data, while the Perugia 2011 [36] tunes are found to be slightly disfavoured. Alpgen+Jimmy [28, 39] provides an intermediate description.
differential jet shape data for 50 GeV<p
T<70 GeV with several MC event generators. As stated in the text, AcerMC [35] coupled to Pythia [33] with the A Pro and A CR Pro tunes [69, 70] give the best description of the data, while the Perugia 2011 [36] tunes are found to be slightly disfavoured. Alpgen+Jimmy [28, 39] provides an intermediate description. final states.
final states. and gb→gb with gluon splitting
and gb→gb with gluon splitting  included in the subsequent parton shower, are wider than those obtained in the
included in the subsequent parton shower, are wider than those obtained in the  final states. The differences are interpreted as due to the different colour flows in the two different final states i.e.
final states. The differences are interpreted as due to the different colour flows in the two different final states i.e.  and inclusive multi-jet production. Similar differences are also found for light-jet shapes, with jets generated in inclusive multi-jet samples being wider than those from W-boson decays in top-quark pair-production.
and inclusive multi-jet production. Similar differences are also found for light-jet shapes, with jets generated in inclusive multi-jet samples being wider than those from W-boson decays in top-quark pair-production. final states has been studied in both the dilepton and single-lepton modes using the ATLAS detector at the LHC. The first sample proves to be a very clean and copious source of b-jets, as the top-quark decays predominantly via t→Wb. The second is also a clean source of light jets produced in the hadronic decays of one of the W bosons in the final state. The differences between the b-quark and light-quark jets obtained in this environment have been studied in terms of the differential jet shapes ρ(r) and integrated jet shapes Ψ(r). These variables exhibit a marked (mild) dependence on the jet transverse momentum (pseudorapidity).
final states has been studied in both the dilepton and single-lepton modes using the ATLAS detector at the LHC. The first sample proves to be a very clean and copious source of b-jets, as the top-quark decays predominantly via t→Wb. The second is also a clean source of light jets produced in the hadronic decays of one of the W bosons in the final state. The differences between the b-quark and light-quark jets obtained in this environment have been studied in terms of the differential jet shapes ρ(r) and integrated jet shapes Ψ(r). These variables exhibit a marked (mild) dependence on the jet transverse momentum (pseudorapidity). .
. , where Δϕ
ℓν is the angle in the transverse plane between the selected lepton and the
, where Δϕ
ℓν is the angle in the transverse plane between the selected lepton and the  direction.
direction.