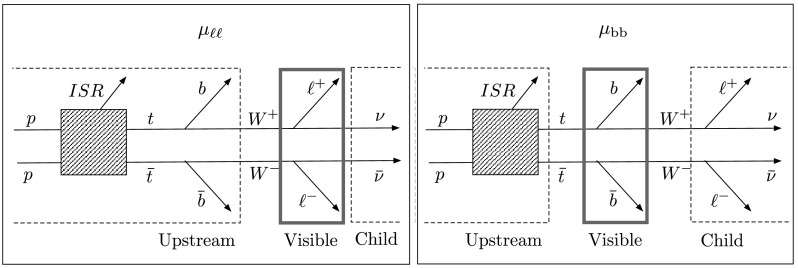
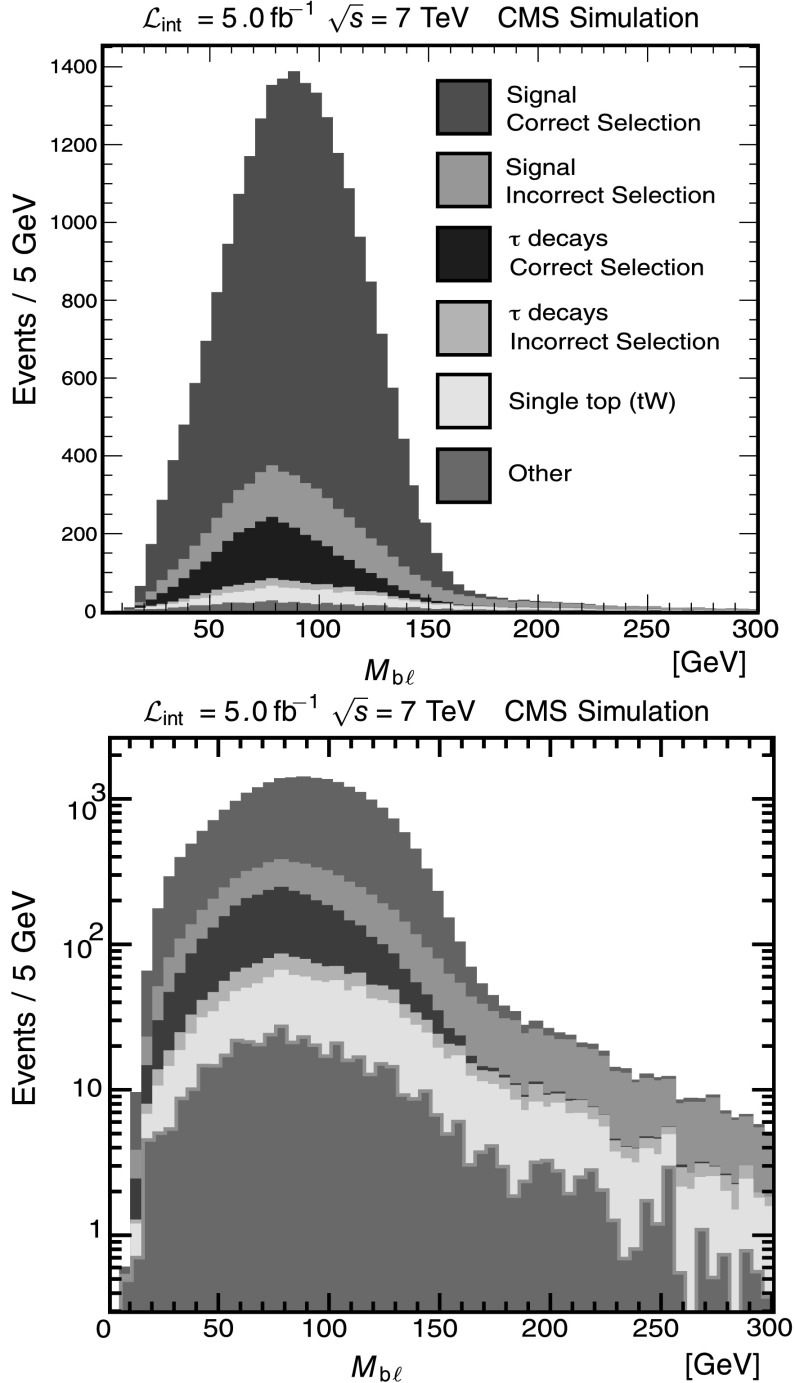
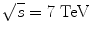The CMS Collaboration1,
S Chatrchyan
S Chatrchyan
2Yerevan Physics Institute, Yerevan, Armenia
2,
V Khachatryan
V Khachatryan
2Yerevan Physics Institute, Yerevan, Armenia
2,
A M Sirunyan
A M Sirunyan
2Yerevan Physics Institute, Yerevan, Armenia
2,
A Tumasyan
A Tumasyan
2Yerevan Physics Institute, Yerevan, Armenia
2,
W Adam
W Adam
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
T Bergauer
T Bergauer
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
M Dragicevic
M Dragicevic
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
J Erö
J Erö
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
C Fabjan
C Fabjan
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
M Friedl
M Friedl
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
R Frühwirth
R Frühwirth
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
V M Ghete
V M Ghete
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
N Hörmann
N Hörmann
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
J Hrubec
J Hrubec
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
M Jeitler
M Jeitler
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
W Kiesenhofer
W Kiesenhofer
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
V Knünz
V Knünz
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
M Krammer
M Krammer
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
I Krätschmer
I Krätschmer
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
D Liko
D Liko
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
I Mikulec
I Mikulec
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
D Rabady
D Rabady
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
B Rahbaran
B Rahbaran
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
C Rohringer
C Rohringer
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
H Rohringer
H Rohringer
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
R Schöfbeck
R Schöfbeck
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
J Strauss
J Strauss
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
A Taurok
A Taurok
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
W Treberer-Treberspurg
W Treberer-Treberspurg
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
W Waltenberger
W Waltenberger
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
C-E Wulz
C-E Wulz
3Institut für Hochenergiephysik der OeAW, Wien, Austria
3,
V Mossolov
V Mossolov
4National Centre for Particle and High Energy Physics, Minsk, Belarus
4,
N Shumeiko
N Shumeiko
4National Centre for Particle and High Energy Physics, Minsk, Belarus
4,
J Suarez Gonzalez
J Suarez Gonzalez
4National Centre for Particle and High Energy Physics, Minsk, Belarus
4,
S Alderweireldt
S Alderweireldt
5Universiteit Antwerpen, Antwerpen, Belgium
5,
M Bansal
M Bansal
5Universiteit Antwerpen, Antwerpen, Belgium
5,
S Bansal
S Bansal
5Universiteit Antwerpen, Antwerpen, Belgium
5,
T Cornelis
T Cornelis
5Universiteit Antwerpen, Antwerpen, Belgium
5,
E A De Wolf
E A De Wolf
5Universiteit Antwerpen, Antwerpen, Belgium
5,
X Janssen
X Janssen
5Universiteit Antwerpen, Antwerpen, Belgium
5,
A Knutsson
A Knutsson
5Universiteit Antwerpen, Antwerpen, Belgium
5,
S Luyckx
S Luyckx
5Universiteit Antwerpen, Antwerpen, Belgium
5,
L Mucibello
L Mucibello
5Universiteit Antwerpen, Antwerpen, Belgium
5,
S Ochesanu
S Ochesanu
5Universiteit Antwerpen, Antwerpen, Belgium
5,
B Roland
B Roland
5Universiteit Antwerpen, Antwerpen, Belgium
5,
R Rougny
R Rougny
5Universiteit Antwerpen, Antwerpen, Belgium
5,
H Van Haevermaet
H Van Haevermaet
5Universiteit Antwerpen, Antwerpen, Belgium
5,
P Van Mechelen
P Van Mechelen
5Universiteit Antwerpen, Antwerpen, Belgium
5,
N Van Remortel
N Van Remortel
5Universiteit Antwerpen, Antwerpen, Belgium
5,
A Van Spilbeeck
A Van Spilbeeck
5Universiteit Antwerpen, Antwerpen, Belgium
5,
F Blekman
F Blekman
6Vrije Universiteit Brussel, Brussel, Belgium
6,
S Blyweert
S Blyweert
6Vrije Universiteit Brussel, Brussel, Belgium
6,
J D’Hondt
J D’Hondt
6Vrije Universiteit Brussel, Brussel, Belgium
6,
A Kalogeropoulos
A Kalogeropoulos
6Vrije Universiteit Brussel, Brussel, Belgium
6,
J Keaveney
J Keaveney
6Vrije Universiteit Brussel, Brussel, Belgium
6,
M Maes
M Maes
6Vrije Universiteit Brussel, Brussel, Belgium
6,
A Olbrechts
A Olbrechts
6Vrije Universiteit Brussel, Brussel, Belgium
6,
S Tavernier
S Tavernier
6Vrije Universiteit Brussel, Brussel, Belgium
6,
W Van Doninck
W Van Doninck
6Vrije Universiteit Brussel, Brussel, Belgium
6,
P Van Mulders
P Van Mulders
6Vrije Universiteit Brussel, Brussel, Belgium
6,
G P Van Onsem
G P Van Onsem
6Vrije Universiteit Brussel, Brussel, Belgium
6,
I Villella
I Villella
6Vrije Universiteit Brussel, Brussel, Belgium
6,
B Clerbaux
B Clerbaux
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
G De Lentdecker
G De Lentdecker
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
A P R Gay
A P R Gay
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
T Hreus
T Hreus
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
A Léonard
A Léonard
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
P E Marage
P E Marage
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
A Mohammadi
A Mohammadi
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
T Reis
T Reis
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
L Thomas
L Thomas
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
C Vander Velde
C Vander Velde
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
P Vanlaer
P Vanlaer
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
J Wang
J Wang
7Université Libre de Bruxelles, Bruxelles, Belgium
7,
V Adler
V Adler
8Ghent University, Ghent, Belgium
8,
K Beernaert
K Beernaert
8Ghent University, Ghent, Belgium
8,
L Benucci
L Benucci
8Ghent University, Ghent, Belgium
8,
A Cimmino
A Cimmino
8Ghent University, Ghent, Belgium
8,
S Costantini
S Costantini
8Ghent University, Ghent, Belgium
8,
S Dildick
S Dildick
8Ghent University, Ghent, Belgium
8,
G Garcia
G Garcia
8Ghent University, Ghent, Belgium
8,
B Klein
B Klein
8Ghent University, Ghent, Belgium
8,
J Lellouch
J Lellouch
8Ghent University, Ghent, Belgium
8,
A Marinov
A Marinov
8Ghent University, Ghent, Belgium
8,
J Mccartin
J Mccartin
8Ghent University, Ghent, Belgium
8,
A A Ocampo Rios
A A Ocampo Rios
8Ghent University, Ghent, Belgium
8,
D Ryckbosch
D Ryckbosch
8Ghent University, Ghent, Belgium
8,
M Sigamani
M Sigamani
8Ghent University, Ghent, Belgium
8,
N Strobbe
N Strobbe
8Ghent University, Ghent, Belgium
8,
F Thyssen
F Thyssen
8Ghent University, Ghent, Belgium
8,
M Tytgat
M Tytgat
8Ghent University, Ghent, Belgium
8,
S Walsh
S Walsh
8Ghent University, Ghent, Belgium
8,
E Yazgan
E Yazgan
8Ghent University, Ghent, Belgium
8,
N Zaganidis
N Zaganidis
8Ghent University, Ghent, Belgium
8,
S Basegmez
S Basegmez
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
G Bruno
G Bruno
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
R Castello
R Castello
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
A Caudron
A Caudron
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
L Ceard
L Ceard
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
C Delaere
C Delaere
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
T du Pree
T du Pree
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
D Favart
D Favart
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
L Forthomme
L Forthomme
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
A Giammanco
A Giammanco
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
J Hollar
J Hollar
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
V Lemaitre
V Lemaitre
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
J Liao
J Liao
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
O Militaru
O Militaru
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
C Nuttens
C Nuttens
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
D Pagano
D Pagano
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
A Pin
A Pin
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
K Piotrzkowski
K Piotrzkowski
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
A Popov
A Popov
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
M Selvaggi
M Selvaggi
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
J M Vizan Garcia
J M Vizan Garcia
9Université Catholique de Louvain, Louvain-la-Neuve, Belgium
9,
N Beliy
N Beliy
10Université de Mons, Mons, Belgium
10,
T Caebergs
T Caebergs
10Université de Mons, Mons, Belgium
10,
E Daubie
E Daubie
10Université de Mons, Mons, Belgium
10,
G H Hammad
G H Hammad
10Université de Mons, Mons, Belgium
10,
G A Alves
G A Alves
11Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
11,
M Correa Martins Junior
M Correa Martins Junior
11Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
11,
T Martins
T Martins
11Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
11,
M E Pol
M E Pol
11Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
11,
M H G Souza
M H G Souza
11Centro Brasileiro de Pesquisas Fisicas, Rio de Janeiro, Brazil
11,
W L Aldá Júnior
W L Aldá Júnior
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
W Carvalho
W Carvalho
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
J Chinellato
J Chinellato
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
A Custódio
A Custódio
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
E M Da Costa
E M Da Costa
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
D De Jesus Damiao
D De Jesus Damiao
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
C De Oliveira Martins
C De Oliveira Martins
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
S Fonseca De Souza
S Fonseca De Souza
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
H Malbouisson
H Malbouisson
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
M Malek
M Malek
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
D Matos Figueiredo
D Matos Figueiredo
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
L Mundim
L Mundim
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
H Nogima
H Nogima
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
W L Prado Da Silva
W L Prado Da Silva
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
A Santoro
A Santoro
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
L Soares Jorge
L Soares Jorge
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
A Sznajder
A Sznajder
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
E J Tonelli Manganote
E J Tonelli Manganote
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
A Vilela Pereira
A Vilela Pereira
12Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
12,
T S Anjos
T S Anjos
14Universidade Federal do ABC, São Paulo, Brazil
14,
C A Bernardes
C A Bernardes
14Universidade Federal do ABC, São Paulo, Brazil
14,
F A Dias
F A Dias
13Universidade Estadual Paulista, São Paulo, Brazil
13,
T R Fernandez Perez Tomei
T R Fernandez Perez Tomei
13Universidade Estadual Paulista, São Paulo, Brazil
13,
E M Gregores
E M Gregores
14Universidade Federal do ABC, São Paulo, Brazil
14,
C Lagana
C Lagana
13Universidade Estadual Paulista, São Paulo, Brazil
13,
F Marinho
F Marinho
13Universidade Estadual Paulista, São Paulo, Brazil
13,
P G Mercadante
P G Mercadante
14Universidade Federal do ABC, São Paulo, Brazil
14,
S F Novaes
S F Novaes
13Universidade Estadual Paulista, São Paulo, Brazil
13,
Sandra S Padula
Sandra S Padula
13Universidade Estadual Paulista, São Paulo, Brazil
13,
V Genchev
V Genchev
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
P Iaydjiev
P Iaydjiev
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
S Piperov
S Piperov
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
M Rodozov
M Rodozov
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
S Stoykova
S Stoykova
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
G Sultanov
G Sultanov
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
V Tcholakov
V Tcholakov
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
R Trayanov
R Trayanov
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
M Vutova
M Vutova
15Institute for Nuclear Research and Nuclear Energy, Sofia, Bulgaria
15,
A Dimitrov
A Dimitrov
16University of Sofia, Sofia, Bulgaria
16,
R Hadjiiska
R Hadjiiska
16University of Sofia, Sofia, Bulgaria
16,
V Kozhuharov
V Kozhuharov
16University of Sofia, Sofia, Bulgaria
16,
L Litov
L Litov
16University of Sofia, Sofia, Bulgaria
16,
B Pavlov
B Pavlov
16University of Sofia, Sofia, Bulgaria
16,
P Petkov
P Petkov
16University of Sofia, Sofia, Bulgaria
16,
J G Bian
J G Bian
17Institute of High Energy Physics, Beijing, China
17,
G M Chen
G M Chen
17Institute of High Energy Physics, Beijing, China
17,
H S Chen
H S Chen
17Institute of High Energy Physics, Beijing, China
17,
C H Jiang
C H Jiang
17Institute of High Energy Physics, Beijing, China
17,
D Liang
D Liang
17Institute of High Energy Physics, Beijing, China
17,
S Liang
S Liang
17Institute of High Energy Physics, Beijing, China
17,
X Meng
X Meng
17Institute of High Energy Physics, Beijing, China
17,
J Tao
J Tao
17Institute of High Energy Physics, Beijing, China
17,
J Wang
J Wang
17Institute of High Energy Physics, Beijing, China
17,
X Wang
X Wang
17Institute of High Energy Physics, Beijing, China
17,
Z Wang
Z Wang
17Institute of High Energy Physics, Beijing, China
17,
H Xiao
H Xiao
17Institute of High Energy Physics, Beijing, China
17,
M Xu
M Xu
17Institute of High Energy Physics, Beijing, China
17,
C Asawatangtrakuldee
C Asawatangtrakuldee
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
Y Ban
Y Ban
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
Y Guo
Y Guo
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
Q Li
Q Li
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
W Li
W Li
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
S Liu
S Liu
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
Y Mao
Y Mao
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
S J Qian
S J Qian
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
D Wang
D Wang
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
L Zhang
L Zhang
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
W Zou
W Zou
18State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing, China
18,
C Avila
C Avila
19Universidad de Los Andes, Bogota, Colombia
19,
C A Carrillo Montoya
C A Carrillo Montoya
19Universidad de Los Andes, Bogota, Colombia
19,
J P Gomez
J P Gomez
19Universidad de Los Andes, Bogota, Colombia
19,
B Gomez Moreno
B Gomez Moreno
19Universidad de Los Andes, Bogota, Colombia
19,
J C Sanabria
J C Sanabria
19Universidad de Los Andes, Bogota, Colombia
19,
N Godinovic
N Godinovic
20Technical University of Split, Split, Croatia
20,
D Lelas
D Lelas
20Technical University of Split, Split, Croatia
20,
R Plestina
R Plestina
20Technical University of Split, Split, Croatia
20,
D Polic
D Polic
20Technical University of Split, Split, Croatia
20,
I Puljak
I Puljak
20Technical University of Split, Split, Croatia
20,
Z Antunovic
Z Antunovic
21University of Split, Split, Croatia
21,
M Kovac
M Kovac
21University of Split, Split, Croatia
21,
V Brigljevic
V Brigljevic
22Institute Rudjer Boskovic, Zagreb, Croatia
22,
S Duric
S Duric
22Institute Rudjer Boskovic, Zagreb, Croatia
22,
K Kadija
K Kadija
22Institute Rudjer Boskovic, Zagreb, Croatia
22,
J Luetic
J Luetic
22Institute Rudjer Boskovic, Zagreb, Croatia
22,
D Mekterovic
D Mekterovic
22Institute Rudjer Boskovic, Zagreb, Croatia
22,
S Morovic
S Morovic
22Institute Rudjer Boskovic, Zagreb, Croatia
22,
L Tikvica
L Tikvica
22Institute Rudjer Boskovic, Zagreb, Croatia
22,
A Attikis
A Attikis
23University of Cyprus, Nicosia, Cyprus
23,
G Mavromanolakis
G Mavromanolakis
23University of Cyprus, Nicosia, Cyprus
23,
J Mousa
J Mousa
23University of Cyprus, Nicosia, Cyprus
23,
C Nicolaou
C Nicolaou
23University of Cyprus, Nicosia, Cyprus
23,
F Ptochos
F Ptochos
23University of Cyprus, Nicosia, Cyprus
23,
P A Razis
P A Razis
23University of Cyprus, Nicosia, Cyprus
23,
M Finger
M Finger
24Charles University, Prague, Czech Republic
24,
M Finger Jr
M Finger Jr
24Charles University, Prague, Czech Republic
24,
Y Assran
Y Assran
25Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
25,
A Ellithi Kamel
A Ellithi Kamel
25Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
25,
M A Mahmoud
M A Mahmoud
25Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
25,
A Mahrous
A Mahrous
25Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
25,
A Radi
A Radi
25Academy of Scientific Research and Technology of the Arab Republic of Egypt, Egyptian Network of High Energy Physics, Cairo, Egypt
25,
M Kadastik
M Kadastik
26National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
26,
M Müntel
M Müntel
26National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
26,
M Murumaa
M Murumaa
26National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
26,
M Raidal
M Raidal
26National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
26,
L Rebane
L Rebane
26National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
26,
A Tiko
A Tiko
26National Institute of Chemical Physics and Biophysics, Tallinn, Estonia
26,
P Eerola
P Eerola
27Department of Physics, University of Helsinki, Helsinki, Finland
27,
G Fedi
G Fedi
27Department of Physics, University of Helsinki, Helsinki, Finland
27,
M Voutilainen
M Voutilainen
27Department of Physics, University of Helsinki, Helsinki, Finland
27,
J Härkönen
J Härkönen
28Helsinki Institute of Physics, Helsinki, Finland
28,
V Karimäki
V Karimäki
28Helsinki Institute of Physics, Helsinki, Finland
28,
R Kinnunen
R Kinnunen
28Helsinki Institute of Physics, Helsinki, Finland
28,
M J Kortelainen
M J Kortelainen
28Helsinki Institute of Physics, Helsinki, Finland
28,
T Lampén
T Lampén
28Helsinki Institute of Physics, Helsinki, Finland
28,
K Lassila-Perini
K Lassila-Perini
28Helsinki Institute of Physics, Helsinki, Finland
28,
S Lehti
S Lehti
28Helsinki Institute of Physics, Helsinki, Finland
28,
T Lindén
T Lindén
28Helsinki Institute of Physics, Helsinki, Finland
28,
P Luukka
P Luukka
28Helsinki Institute of Physics, Helsinki, Finland
28,
T Mäenpää
T Mäenpää
28Helsinki Institute of Physics, Helsinki, Finland
28,
T Peltola
T Peltola
28Helsinki Institute of Physics, Helsinki, Finland
28,
E Tuominen
E Tuominen
28Helsinki Institute of Physics, Helsinki, Finland
28,
J Tuominiemi
J Tuominiemi
28Helsinki Institute of Physics, Helsinki, Finland
28,
E Tuovinen
E Tuovinen
28Helsinki Institute of Physics, Helsinki, Finland
28,
L Wendland
L Wendland
28Helsinki Institute of Physics, Helsinki, Finland
28,
A Korpela
A Korpela
29Lappeenranta University of Technology, Lappeenranta, Finland
29,
T Tuuva
T Tuuva
29Lappeenranta University of Technology, Lappeenranta, Finland
29,
M Besancon
M Besancon
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
S Choudhury
S Choudhury
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
F Couderc
F Couderc
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
M Dejardin
M Dejardin
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
D Denegri
D Denegri
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
B Fabbro
B Fabbro
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
J L Faure
J L Faure
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
F Ferri
F Ferri
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
S Ganjour
S Ganjour
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
A Givernaud
A Givernaud
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
P Gras
P Gras
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
G Hamel de Monchenault
G Hamel de Monchenault
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
P Jarry
P Jarry
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
E Locci
E Locci
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
J Malcles
J Malcles
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
L Millischer
L Millischer
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
A Nayak
A Nayak
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
J Rander
J Rander
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
A Rosowsky
A Rosowsky
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
M Titov
M Titov
30DSM/IRFU, CEA/Saclay, Gif-sur-Yvette, France
30,
S Baffioni
S Baffioni
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
F Beaudette
F Beaudette
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
L Benhabib
L Benhabib
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
L Bianchini
L Bianchini
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
M Bluj
M Bluj
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
P Busson
P Busson
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
C Charlot
C Charlot
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
N Daci
N Daci
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
T Dahms
T Dahms
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
M Dalchenko
M Dalchenko
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
L Dobrzynski
L Dobrzynski
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
A Florent
A Florent
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
R Granier de Cassagnac
R Granier de Cassagnac
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
M Haguenauer
M Haguenauer
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
P Miné
P Miné
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
C Mironov
C Mironov
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
I N Naranjo
I N Naranjo
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
M Nguyen
M Nguyen
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
C Ochando
C Ochando
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
P Paganini
P Paganini
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
D Sabes
D Sabes
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
R Salerno
R Salerno
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
Y Sirois
Y Sirois
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
C Veelken
C Veelken
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
A Zabi
A Zabi
31Laboratoire Leprince-Ringuet, Ecole Polytechnique, IN2P3-CNRS, Palaiseau, France
31,
J-L Agram
J-L Agram
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
J Andrea
J Andrea
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
D Bloch
D Bloch
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
D Bodin
D Bodin
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
J-M Brom
J-M Brom
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
E C Chabert
E C Chabert
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
C Collard
C Collard
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
E Conte
E Conte
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
F Drouhin
F Drouhin
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
J-C Fontaine
J-C Fontaine
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
D Gelé
D Gelé
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
U Goerlach
U Goerlach
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
C Goetzmann
C Goetzmann
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
P Juillot
P Juillot
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
A-C Le Bihan
A-C Le Bihan
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
P Van Hove
P Van Hove
32Institut Pluridisciplinaire Hubert Curien, Université de Strasbourg, Université de Haute Alsace Mulhouse, CNRS/IN2P3, Strasbourg, France
32,
S Beauceron
S Beauceron
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
N Beaupere
N Beaupere
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
G Boudoul
G Boudoul
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
S Brochet
S Brochet
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
J Chasserat
J Chasserat
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
R Chierici
R Chierici
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
D Contardo
D Contardo
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
P Depasse
P Depasse
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
H El Mamouni
H El Mamouni
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
J Fay
J Fay
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
S Gascon
S Gascon
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
M Gouzevitch
M Gouzevitch
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
B Ille
B Ille
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
T Kurca
T Kurca
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
M Lethuillier
M Lethuillier
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
L Mirabito
L Mirabito
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
S Perries
S Perries
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
L Sgandurra
L Sgandurra
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
V Sordini
V Sordini
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
Y Tschudi
Y Tschudi
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
M Vander Donckt
M Vander Donckt
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
P Verdier
P Verdier
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
S Viret
S Viret
33Université de Lyon, Université Claude Bernard Lyon 1, Institut de Physique Nucléaire de Lyon, CNRS-IN2P3, Villeurbanne, France
33,
Z Tsamalaidze
Z Tsamalaidze
34Institute of High Energy Physics and Informatization, Tbilisi State University, Tbilisi, Georgia
34,
C Autermann
C Autermann
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
S Beranek
S Beranek
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
B Calpas
B Calpas
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
M Edelhoff
M Edelhoff
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
L Feld
L Feld
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
N Heracleous
N Heracleous
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
O Hindrichs
O Hindrichs
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
K Klein
K Klein
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
J Merz
J Merz
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
A Ostapchuk
A Ostapchuk
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
A Perieanu
A Perieanu
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
F Raupach
F Raupach
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
J Sammet
J Sammet
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
S Schael
S Schael
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
D Sprenger
D Sprenger
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
H Weber
H Weber
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
B Wittmer
B Wittmer
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
V Zhukov
V Zhukov
35I. Physikalisches Institut, RWTH Aachen University, Aachen, Germany
35,
M Ata
M Ata
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
J Caudron
J Caudron
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
E Dietz-Laursonn
E Dietz-Laursonn
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
D Duchardt
D Duchardt
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
M Erdmann
M Erdmann
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
R Fischer
R Fischer
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
A Güth
A Güth
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
T Hebbeker
T Hebbeker
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
C Heidemann
C Heidemann
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
K Hoepfner
K Hoepfner
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
D Klingebiel
D Klingebiel
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
P Kreuzer
P Kreuzer
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
M Merschmeyer
M Merschmeyer
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
A Meyer
A Meyer
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
M Olschewski
M Olschewski
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
K Padeken
K Padeken
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
P Papacz
P Papacz
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
H Pieta
H Pieta
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
H Reithler
H Reithler
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
S A Schmitz
S A Schmitz
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
L Sonnenschein
L Sonnenschein
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
J Steggemann
J Steggemann
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
D Teyssier
D Teyssier
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
S Thüer
S Thüer
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
M Weber
M Weber
36III. Physikalisches Institut A, RWTH Aachen University, Aachen, Germany
36,
V Cherepanov
V Cherepanov
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
Y Erdogan
Y Erdogan
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
G Flügge
G Flügge
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
H Geenen
H Geenen
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
M Geisler
M Geisler
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
W Haj Ahmad
W Haj Ahmad
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
F Hoehle
F Hoehle
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
B Kargoll
B Kargoll
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
T Kress
T Kress
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
Y Kuessel
Y Kuessel
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
J Lingemann
J Lingemann
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
A Nowack
A Nowack
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
I M Nugent
I M Nugent
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
L Perchalla
L Perchalla
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
O Pooth
O Pooth
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
A Stahl
A Stahl
37III. Physikalisches Institut B, RWTH Aachen University, Aachen, Germany
37,
M Aldaya Martin
M Aldaya Martin
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
I Asin
I Asin
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
N Bartosik
N Bartosik
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
J Behr
J Behr
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
W Behrenhoff
W Behrenhoff
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
U Behrens
U Behrens
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
M Bergholz
M Bergholz
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Bethani
A Bethani
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
K Borras
K Borras
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Burgmeier
A Burgmeier
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Cakir
A Cakir
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
L Calligaris
L Calligaris
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Campbell
A Campbell
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
F Costanza
F Costanza
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
D Dammann
D Dammann
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
C Diez Pardos
C Diez Pardos
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
T Dorland
T Dorland
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
G Eckerlin
G Eckerlin
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
D Eckstein
D Eckstein
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
G Flucke
G Flucke
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Geiser
A Geiser
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
I Glushkov
I Glushkov
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
P Gunnellini
P Gunnellini
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
S Habib
S Habib
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
J Hauk
J Hauk
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
G Hellwig
G Hellwig
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
H Jung
H Jung
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
M Kasemann
M Kasemann
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
P Katsas
P Katsas
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
C Kleinwort
C Kleinwort
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
H Kluge
H Kluge
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
M Krämer
M Krämer
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
D Krücker
D Krücker
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
E Kuznetsova
E Kuznetsova
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
W Lange
W Lange
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
J Leonard
J Leonard
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
K Lipka
K Lipka
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
W Lohmann
W Lohmann
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
B Lutz
B Lutz
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
R Mankel
R Mankel
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
I Marfin
I Marfin
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
M Marienfeld
M Marienfeld
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
I-A Melzer-Pellmann
I-A Melzer-Pellmann
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A B Meyer
A B Meyer
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
J Mnich
J Mnich
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Mussgiller
A Mussgiller
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
S Naumann-Emme
S Naumann-Emme
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
O Novgorodova
O Novgorodova
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
F Nowak
F Nowak
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
J Olzem
J Olzem
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
H Perrey
H Perrey
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Petrukhin
A Petrukhin
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
D Pitzl
D Pitzl
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
A Raspereza
A Raspereza
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
P M Ribeiro Cipriano
P M Ribeiro Cipriano
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
C Riedl
C Riedl
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
E Ron
E Ron
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
M Rosin
M Rosin
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
J Salfeld-Nebgen
J Salfeld-Nebgen
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
R Schmidt
R Schmidt
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
T Schoerner-Sadenius
T Schoerner-Sadenius
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
N Sen
N Sen
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
M Stein
M Stein
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
R Walsh
R Walsh
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
C Wissing
C Wissing
38Deutsches Elektronen-Synchrotron, Hamburg, Germany
38,
V Blobel
V Blobel
39University of Hamburg, Hamburg, Germany
39,
H Enderle
H Enderle
39University of Hamburg, Hamburg, Germany
39,
J Erfle
J Erfle
39University of Hamburg, Hamburg, Germany
39,
U Gebbert
U Gebbert
39University of Hamburg, Hamburg, Germany
39,
M Görner
M Görner
39University of Hamburg, Hamburg, Germany
39,
M Gosselink
M Gosselink
39University of Hamburg, Hamburg, Germany
39,
J Haller
J Haller
39University of Hamburg, Hamburg, Germany
39,
K Heine
K Heine
39University of Hamburg, Hamburg, Germany
39,
R S Höing
R S Höing
39University of Hamburg, Hamburg, Germany
39,
G Kaussen
G Kaussen
39University of Hamburg, Hamburg, Germany
39,
H Kirschenmann
H Kirschenmann
39University of Hamburg, Hamburg, Germany
39,
R Klanner
R Klanner
39University of Hamburg, Hamburg, Germany
39,
J Lange
J Lange
39University of Hamburg, Hamburg, Germany
39,
T Peiffer
T Peiffer
39University of Hamburg, Hamburg, Germany
39,
N Pietsch
N Pietsch
39University of Hamburg, Hamburg, Germany
39,
D Rathjens
D Rathjens
39University of Hamburg, Hamburg, Germany
39,
C Sander
C Sander
39University of Hamburg, Hamburg, Germany
39,
H Schettler
H Schettler
39University of Hamburg, Hamburg, Germany
39,
P Schleper
P Schleper
39University of Hamburg, Hamburg, Germany
39,
E Schlieckau
E Schlieckau
39University of Hamburg, Hamburg, Germany
39,
A Schmidt
A Schmidt
39University of Hamburg, Hamburg, Germany
39,
M Schröder
M Schröder
39University of Hamburg, Hamburg, Germany
39,
T Schum
T Schum
39University of Hamburg, Hamburg, Germany
39,
M Seidel
M Seidel
39University of Hamburg, Hamburg, Germany
39,
J Sibille
J Sibille
39University of Hamburg, Hamburg, Germany
39,
V Sola
V Sola
39University of Hamburg, Hamburg, Germany
39,
H Stadie
H Stadie
39University of Hamburg, Hamburg, Germany
39,
G Steinbrück
G Steinbrück
39University of Hamburg, Hamburg, Germany
39,
J Thomsen
J Thomsen
39University of Hamburg, Hamburg, Germany
39,
L Vanelderen
L Vanelderen
39University of Hamburg, Hamburg, Germany
39,
C Barth
C Barth
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
C Baus
C Baus
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
J Berger
J Berger
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
C Böser
C Böser
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
T Chwalek
T Chwalek
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
W De Boer
W De Boer
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
A Descroix
A Descroix
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
A Dierlamm
A Dierlamm
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
M Feindt
M Feindt
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
M Guthoff
M Guthoff
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
C Hackstein
C Hackstein
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
F Hartmann
F Hartmann
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
T Hauth
T Hauth
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
M Heinrich
M Heinrich
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
H Held
H Held
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
K H Hoffmann
K H Hoffmann
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
U Husemann
U Husemann
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
I Katkov
I Katkov
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
J R Komaragiri
J R Komaragiri
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
A Kornmayer
A Kornmayer
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
P Lobelle Pardo
P Lobelle Pardo
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
D Martschei
D Martschei
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
S Mueller
S Mueller
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
Th Müller
Th Müller
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
M Niegel
M Niegel
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
A Nürnberg
A Nürnberg
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
O Oberst
O Oberst
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
J Ott
J Ott
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
G Quast
G Quast
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
K Rabbertz
K Rabbertz
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
F Ratnikov
F Ratnikov
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
N Ratnikova
N Ratnikova
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
S Röcker
S Röcker
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
F-P Schilling
F-P Schilling
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
G Schott
G Schott
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
H J Simonis
H J Simonis
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
F M Stober
F M Stober
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
D Troendle
D Troendle
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
R Ulrich
R Ulrich
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
J Wagner-Kuhr
J Wagner-Kuhr
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
S Wayand
S Wayand
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
T Weiler
T Weiler
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
M Zeise
M Zeise
40Institut für Experimentelle Kernphysik, Karlsruhe, Germany
40,
G Anagnostou
G Anagnostou
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
G Daskalakis
G Daskalakis
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
T Geralis
T Geralis
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
S Kesisoglou
S Kesisoglou
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
A Kyriakis
A Kyriakis
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
D Loukas
D Loukas
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
A Markou
A Markou
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
C Markou
C Markou
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
E Ntomari
E Ntomari
41Institute of Nuclear and Particle Physics (INPP), NCSR Demokritos, Aghia Paraskevi, Greece
41,
L Gouskos
L Gouskos
42University of Athens, Athens, Greece
42,
T J Mertzimekis
T J Mertzimekis
42University of Athens, Athens, Greece
42,
A Panagiotou
A Panagiotou
42University of Athens, Athens, Greece
42,
N Saoulidou
N Saoulidou
42University of Athens, Athens, Greece
42,
E Stiliaris
E Stiliaris
42University of Athens, Athens, Greece
42,
X Aslanoglou
X Aslanoglou
43University of Ioánnina, Ioánnina, Greece
43,
I Evangelou
I Evangelou
43University of Ioánnina, Ioánnina, Greece
43,
G Flouris
G Flouris
43University of Ioánnina, Ioánnina, Greece
43,
C Foudas
C Foudas
43University of Ioánnina, Ioánnina, Greece
43,
P Kokkas
P Kokkas
43University of Ioánnina, Ioánnina, Greece
43,
N Manthos
N Manthos
43University of Ioánnina, Ioánnina, Greece
43,
I Papadopoulos
I Papadopoulos
43University of Ioánnina, Ioánnina, Greece
43,
E Paradas
E Paradas
43University of Ioánnina, Ioánnina, Greece
43,
G Bencze
G Bencze
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
C Hajdu
C Hajdu
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
P Hidas
P Hidas
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
D Horvath
D Horvath
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
B Radics
B Radics
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
F Sikler
F Sikler
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
V Veszpremi
V Veszpremi
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
G Vesztergombi
G Vesztergombi
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
A J Zsigmond
A J Zsigmond
44KFKI Research Institute for Particle and Nuclear Physics, Budapest, Hungary
44,
N Beni
N Beni
45Institute of Nuclear Research ATOMKI, Debrecen, Hungary
45,
S Czellar
S Czellar
45Institute of Nuclear Research ATOMKI, Debrecen, Hungary
45,
J Molnar
J Molnar
45Institute of Nuclear Research ATOMKI, Debrecen, Hungary
45,
J Palinkas
J Palinkas
45Institute of Nuclear Research ATOMKI, Debrecen, Hungary
45,
Z Szillasi
Z Szillasi
45Institute of Nuclear Research ATOMKI, Debrecen, Hungary
45,
J Karancsi
J Karancsi
46University of Debrecen, Debrecen, Hungary
46,
P Raics
P Raics
46University of Debrecen, Debrecen, Hungary
46,
Z L Trocsanyi
Z L Trocsanyi
46University of Debrecen, Debrecen, Hungary
46,
B Ujvari
B Ujvari
46University of Debrecen, Debrecen, Hungary
46,
S B Beri
S B Beri
47Panjab University, Chandigarh, India
47,
V Bhatnagar
V Bhatnagar
47Panjab University, Chandigarh, India
47,
N Dhingra
N Dhingra
47Panjab University, Chandigarh, India
47,
R Gupta
R Gupta
47Panjab University, Chandigarh, India
47,
M Kaur
M Kaur
47Panjab University, Chandigarh, India
47,
M Z Mehta
M Z Mehta
47Panjab University, Chandigarh, India
47,
M Mittal
M Mittal
47Panjab University, Chandigarh, India
47,
N Nishu
N Nishu
47Panjab University, Chandigarh, India
47,
L K Saini
L K Saini
47Panjab University, Chandigarh, India
47,
A Sharma
A Sharma
47Panjab University, Chandigarh, India
47,
J B Singh
J B Singh
47Panjab University, Chandigarh, India
47,
Ashok Kumar
Ashok Kumar
48University of Delhi, Delhi, India
48,
Arun Kumar
Arun Kumar
48University of Delhi, Delhi, India
48,
S Ahuja
S Ahuja
48University of Delhi, Delhi, India
48,
A Bhardwaj
A Bhardwaj
48University of Delhi, Delhi, India
48,
B C Choudhary
B C Choudhary
48University of Delhi, Delhi, India
48,
S Malhotra
S Malhotra
48University of Delhi, Delhi, India
48,
M Naimuddin
M Naimuddin
48University of Delhi, Delhi, India
48,
K Ranjan
K Ranjan
48University of Delhi, Delhi, India
48,
P Saxena
P Saxena
48University of Delhi, Delhi, India
48,
V Sharma
V Sharma
48University of Delhi, Delhi, India
48,
R K Shivpuri
R K Shivpuri
48University of Delhi, Delhi, India
48,
S Banerjee
S Banerjee
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Bhattacharya
S Bhattacharya
49Saha Institute of Nuclear Physics, Kolkata, India
49,
K Chatterjee
K Chatterjee
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Dutta
S Dutta
49Saha Institute of Nuclear Physics, Kolkata, India
49,
B Gomber
B Gomber
49Saha Institute of Nuclear Physics, Kolkata, India
49,
Sa Jain
Sa Jain
49Saha Institute of Nuclear Physics, Kolkata, India
49,
Sh Jain
Sh Jain
49Saha Institute of Nuclear Physics, Kolkata, India
49,
R Khurana
R Khurana
49Saha Institute of Nuclear Physics, Kolkata, India
49,
A Modak
A Modak
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Mukherjee
S Mukherjee
49Saha Institute of Nuclear Physics, Kolkata, India
49,
D Roy
D Roy
49Saha Institute of Nuclear Physics, Kolkata, India
49,
S Sarkar
S Sarkar
49Saha Institute of Nuclear Physics, Kolkata, India
49,
M Sharan
M Sharan
49Saha Institute of Nuclear Physics, Kolkata, India
49,
A Abdulsalam
A Abdulsalam
50Bhabha Atomic Research Centre, Mumbai, India
50,
D Dutta
D Dutta
50Bhabha Atomic Research Centre, Mumbai, India
50,
S Kailas
S Kailas
50Bhabha Atomic Research Centre, Mumbai, India
50,
V Kumar
V Kumar
50Bhabha Atomic Research Centre, Mumbai, India
50,
A K Mohanty
A K Mohanty
50Bhabha Atomic Research Centre, Mumbai, India
50,
L M Pant
L M Pant
50Bhabha Atomic Research Centre, Mumbai, India
50,
P Shukla
P Shukla
50Bhabha Atomic Research Centre, Mumbai, India
50,
A Topkar
A Topkar
50Bhabha Atomic Research Centre, Mumbai, India
50,
T Aziz
T Aziz
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
R M Chatterjee
R M Chatterjee
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
S Ganguly
S Ganguly
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
M Guchait
M Guchait
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
A Gurtu
A Gurtu
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
M Maity
M Maity
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
G Majumder
G Majumder
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
K Mazumdar
K Mazumdar
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
G B Mohanty
G B Mohanty
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
B Parida
B Parida
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
K Sudhakar
K Sudhakar
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
N Wickramage
N Wickramage
51Tata Institute of Fundamental Research - EHEP, Mumbai, India
51,
S Banerjee
S Banerjee
52Tata Institute of Fundamental Research - HECR, Mumbai, India
52,
S Dugad
S Dugad
52Tata Institute of Fundamental Research - HECR, Mumbai, India
52,
H Arfaei
H Arfaei
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
H Bakhshiansohi
H Bakhshiansohi
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
S M Etesami
S M Etesami
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
A Fahim
A Fahim
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
H Hesari
H Hesari
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
A Jafari
A Jafari
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
M Khakzad
M Khakzad
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
M Mohammadi Najafabadi
M Mohammadi Najafabadi
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
S Paktinat Mehdiabadi
S Paktinat Mehdiabadi
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
B Safarzadeh
B Safarzadeh
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
M Zeinali
M Zeinali
53Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
53,
M Grunewald
M Grunewald
54University College Dublin, Dublin, Ireland
54,
M Abbrescia
M Abbrescia
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
L Barbone
L Barbone
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
C Calabria
C Calabria
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
S S Chhibra
S S Chhibra
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
A Colaleo
A Colaleo
55INFN Sezione di Bari, Bari, Italy
55,
D Creanza
D Creanza
55INFN Sezione di Bari, Bari, Italy
57Politecnico di Bari, Bari, Italy
55,57,
N De Filippis
N De Filippis
55INFN Sezione di Bari, Bari, Italy
57Politecnico di Bari, Bari, Italy
55,57,
M De Palma
M De Palma
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
L Fiore
L Fiore
55INFN Sezione di Bari, Bari, Italy
55,
G Iaselli
G Iaselli
55INFN Sezione di Bari, Bari, Italy
57Politecnico di Bari, Bari, Italy
55,57,
G Maggi
G Maggi
55INFN Sezione di Bari, Bari, Italy
57Politecnico di Bari, Bari, Italy
55,57,
M Maggi
M Maggi
55INFN Sezione di Bari, Bari, Italy
55,
B Marangelli
B Marangelli
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
S My
S My
55INFN Sezione di Bari, Bari, Italy
57Politecnico di Bari, Bari, Italy
55,57,
S Nuzzo
S Nuzzo
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
N Pacifico
N Pacifico
55INFN Sezione di Bari, Bari, Italy
55,
A Pompili
A Pompili
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
G Pugliese
G Pugliese
55INFN Sezione di Bari, Bari, Italy
57Politecnico di Bari, Bari, Italy
55,57,
G Selvaggi
G Selvaggi
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
L Silvestris
L Silvestris
55INFN Sezione di Bari, Bari, Italy
55,
G Singh
G Singh
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
R Venditti
R Venditti
55INFN Sezione di Bari, Bari, Italy
56Università di Bari, Bari, Italy
55,56,
P Verwilligen
P Verwilligen
55INFN Sezione di Bari, Bari, Italy
55,
G Zito
G Zito
55INFN Sezione di Bari, Bari, Italy
55,
G Abbiendi
G Abbiendi
58INFN Sezione di Bologna, Bologna, Italy
58,
A C Benvenuti
A C Benvenuti
58INFN Sezione di Bologna, Bologna, Italy
58,
D Bonacorsi
D Bonacorsi
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
S Braibant-Giacomelli
S Braibant-Giacomelli
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
L Brigliadori
L Brigliadori
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
R Campanini
R Campanini
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
P Capiluppi
P Capiluppi
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
A Castro
A Castro
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
F R Cavallo
F R Cavallo
58INFN Sezione di Bologna, Bologna, Italy
58,
M Cuffiani
M Cuffiani
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
G M Dallavalle
G M Dallavalle
58INFN Sezione di Bologna, Bologna, Italy
58,
F Fabbri
F Fabbri
58INFN Sezione di Bologna, Bologna, Italy
58,
A Fanfani
A Fanfani
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
D Fasanella
D Fasanella
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
P Giacomelli
P Giacomelli
58INFN Sezione di Bologna, Bologna, Italy
58,
C Grandi
C Grandi
58INFN Sezione di Bologna, Bologna, Italy
58,
L Guiducci
L Guiducci
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
S Marcellini
S Marcellini
58INFN Sezione di Bologna, Bologna, Italy
58,
G Masetti
G Masetti
58INFN Sezione di Bologna, Bologna, Italy
58,
M Meneghelli
M Meneghelli
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
A Montanari
A Montanari
58INFN Sezione di Bologna, Bologna, Italy
58,
F L Navarria
F L Navarria
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
F Odorici
F Odorici
58INFN Sezione di Bologna, Bologna, Italy
58,
A Perrotta
A Perrotta
58INFN Sezione di Bologna, Bologna, Italy
58,
F Primavera
F Primavera
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
A M Rossi
A M Rossi
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
T Rovelli
T Rovelli
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
G P Siroli
G P Siroli
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
N Tosi
N Tosi
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
R Travaglini
R Travaglini
58INFN Sezione di Bologna, Bologna, Italy
59Università di Bologna, Bologna, Italy
58,59,
S Albergo
S Albergo
60INFN Sezione di Catania, Catania, Italy
61Università di Catania, Catania, Italy
60,61,
M Chiorboli
M Chiorboli
60INFN Sezione di Catania, Catania, Italy
61Università di Catania, Catania, Italy
60,61,
S Costa
S Costa
60INFN Sezione di Catania, Catania, Italy
61Università di Catania, Catania, Italy
60,61,
R Potenza
R Potenza
60INFN Sezione di Catania, Catania, Italy
61Università di Catania, Catania, Italy
60,61,
A Tricomi
A Tricomi
60INFN Sezione di Catania, Catania, Italy
61Università di Catania, Catania, Italy
60,61,
C Tuve
C Tuve
60INFN Sezione di Catania, Catania, Italy
61Università di Catania, Catania, Italy
60,61,
G Barbagli
G Barbagli
62INFN Sezione di Firenze, Firenze, Italy
62,
V Ciulli
V Ciulli
62INFN Sezione di Firenze, Firenze, Italy
63Università di Firenze, Firenze, Italy
62,63,
C Civinini
C Civinini
62INFN Sezione di Firenze, Firenze, Italy
62,
R D’Alessandro
R D’Alessandro
62INFN Sezione di Firenze, Firenze, Italy
63Università di Firenze, Firenze, Italy
62,63,
E Focardi
E Focardi
62INFN Sezione di Firenze, Firenze, Italy
63Università di Firenze, Firenze, Italy
62,63,
S Frosali
S Frosali
62INFN Sezione di Firenze, Firenze, Italy
63Università di Firenze, Firenze, Italy
62,63,
E Gallo
E Gallo
62INFN Sezione di Firenze, Firenze, Italy
62,
S Gonzi
S Gonzi
62INFN Sezione di Firenze, Firenze, Italy
63Università di Firenze, Firenze, Italy
62,63,
P Lenzi
P Lenzi
62INFN Sezione di Firenze, Firenze, Italy
63Università di Firenze, Firenze, Italy
62,63,
M Meschini
M Meschini
62INFN Sezione di Firenze, Firenze, Italy
62,
S Paoletti
S Paoletti
62INFN Sezione di Firenze, Firenze, Italy
62,
G Sguazzoni
G Sguazzoni
62INFN Sezione di Firenze, Firenze, Italy
62,
A Tropiano
A Tropiano
62INFN Sezione di Firenze, Firenze, Italy
63Università di Firenze, Firenze, Italy
62,63,
L Benussi
L Benussi
64INFN Laboratori Nazionali di Frascati, Frascati, Italy
64,
S Bianco
S Bianco
64INFN Laboratori Nazionali di Frascati, Frascati, Italy
64,
F Fabbri
F Fabbri
64INFN Laboratori Nazionali di Frascati, Frascati, Italy
64,
D Piccolo
D Piccolo
64INFN Laboratori Nazionali di Frascati, Frascati, Italy
64,
P Fabbricatore
P Fabbricatore
65INFN Sezione di Genova, Genova, Italy
65,
R Musenich
R Musenich
65INFN Sezione di Genova, Genova, Italy
65,
S Tosi
S Tosi
65INFN Sezione di Genova, Genova, Italy
66Università di Genova, Genova, Italy
65,66,
A Benaglia
A Benaglia
67INFN Sezione di Milano-Bicocca, Milano, Italy
67,
F De Guio
F De Guio
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
L Di Matteo
L Di Matteo
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
S Fiorendi
S Fiorendi
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
S Gennai
S Gennai
67INFN Sezione di Milano-Bicocca, Milano, Italy
67,
A Ghezzi
A Ghezzi
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
P Govoni
P Govoni
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
M T Lucchini
M T Lucchini
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
S Malvezzi
S Malvezzi
67INFN Sezione di Milano-Bicocca, Milano, Italy
67,
R A Manzoni
R A Manzoni
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
A Martelli
A Martelli
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
A Massironi
A Massironi
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
D Menasce
D Menasce
67INFN Sezione di Milano-Bicocca, Milano, Italy
67,
L Moroni
L Moroni
67INFN Sezione di Milano-Bicocca, Milano, Italy
67,
M Paganoni
M Paganoni
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
D Pedrini
D Pedrini
67INFN Sezione di Milano-Bicocca, Milano, Italy
67,
S Ragazzi
S Ragazzi
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
N Redaelli
N Redaelli
67INFN Sezione di Milano-Bicocca, Milano, Italy
67,
T Tabarelli de Fatis
T Tabarelli de Fatis
67INFN Sezione di Milano-Bicocca, Milano, Italy
68Università di Milano-Bicocca, Milano, Italy
67,68,
S Buontempo
S Buontempo
69INFN Sezione di Napoli, Napoli, Italy
69,
N Cavallo
N Cavallo
69INFN Sezione di Napoli, Napoli, Italy
71Università della Basilicata (Potenza), Napoli, Italy
69,71,
A De Cosa
A De Cosa
69INFN Sezione di Napoli, Napoli, Italy
70Università di Napoli ’Federico II’, Napoli, Italy
69,70,
F Fabozzi
F Fabozzi
69INFN Sezione di Napoli, Napoli, Italy
71Università della Basilicata (Potenza), Napoli, Italy
69,71,
A O M Iorio
A O M Iorio
69INFN Sezione di Napoli, Napoli, Italy
70Università di Napoli ’Federico II’, Napoli, Italy
69,70,
L Lista
L Lista
69INFN Sezione di Napoli, Napoli, Italy
69,
S Meola
S Meola
69INFN Sezione di Napoli, Napoli, Italy
72Università G. Marconi (Roma), Napoli, Italy
69,72,
M Merola
M Merola
69INFN Sezione di Napoli, Napoli, Italy
69,
P Paolucci
P Paolucci
69INFN Sezione di Napoli, Napoli, Italy
69,
P Azzi
P Azzi
73INFN Sezione di Padova, Padova, Italy
73,
N Bacchetta
N Bacchetta
73INFN Sezione di Padova, Padova, Italy
73,
P Bellan
P Bellan
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
D Bisello
D Bisello
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
A Branca
A Branca
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
R Carlin
R Carlin
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
P Checchia
P Checchia
73INFN Sezione di Padova, Padova, Italy
73,
T Dorigo
T Dorigo
73INFN Sezione di Padova, Padova, Italy
73,
M Galanti
M Galanti
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
F Gasparini
F Gasparini
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
U Gasparini
U Gasparini
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
P Giubilato
P Giubilato
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
A Gozzelino
A Gozzelino
73INFN Sezione di Padova, Padova, Italy
73,
K Kanishchev
K Kanishchev
73INFN Sezione di Padova, Padova, Italy
75Università di Trento (Trento), Padova, Italy
73,75,
S Lacaprara
S Lacaprara
73INFN Sezione di Padova, Padova, Italy
73,
I Lazzizzera
I Lazzizzera
73INFN Sezione di Padova, Padova, Italy
75Università di Trento (Trento), Padova, Italy
73,75,
M Margoni
M Margoni
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
A T Meneguzzo
A T Meneguzzo
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
M Michelotto
M Michelotto
73INFN Sezione di Padova, Padova, Italy
73,
F Montecassiano
F Montecassiano
73INFN Sezione di Padova, Padova, Italy
73,
M Nespolo
M Nespolo
73INFN Sezione di Padova, Padova, Italy
73,
J Pazzini
J Pazzini
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
M Pegoraro
M Pegoraro
73INFN Sezione di Padova, Padova, Italy
73,
N Pozzobon
N Pozzobon
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
P Ronchese
P Ronchese
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
F Simonetto
F Simonetto
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
E Torassa
E Torassa
73INFN Sezione di Padova, Padova, Italy
73,
M Tosi
M Tosi
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
P Zotto
P Zotto
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
G Zumerle
G Zumerle
73INFN Sezione di Padova, Padova, Italy
74Università di Padova, Padova, Italy
73,74,
M Gabusi
M Gabusi
76INFN Sezione di Pavia, Pavia, Italy
77Università di Pavia, Pavia, Italy
76,77,
S P Ratti
S P Ratti
76INFN Sezione di Pavia, Pavia, Italy
77Università di Pavia, Pavia, Italy
76,77,
C Riccardi
C Riccardi
76INFN Sezione di Pavia, Pavia, Italy
77Università di Pavia, Pavia, Italy
76,77,
P Vitulo
P Vitulo
76INFN Sezione di Pavia, Pavia, Italy
77Università di Pavia, Pavia, Italy
76,77,
M Biasini
M Biasini
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
G M Bilei
G M Bilei
78INFN Sezione di Perugia, Perugia, Italy
78,
L Fanò
L Fanò
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
P Lariccia
P Lariccia
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
G Mantovani
G Mantovani
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
M Menichelli
M Menichelli
78INFN Sezione di Perugia, Perugia, Italy
78,
A Nappi
A Nappi
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
F Romeo
F Romeo
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
A Saha
A Saha
78INFN Sezione di Perugia, Perugia, Italy
78,
A Santocchia
A Santocchia
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
A Spiezia
A Spiezia
78INFN Sezione di Perugia, Perugia, Italy
79Università di Perugia, Perugia, Italy
78,79,
K Androsov
K Androsov
80INFN Sezione di Pisa, Pisa, Italy
80,
P Azzurri
P Azzurri
80INFN Sezione di Pisa, Pisa, Italy
80,
G Bagliesi
G Bagliesi
80INFN Sezione di Pisa, Pisa, Italy
80,
T Boccali
T Boccali
80INFN Sezione di Pisa, Pisa, Italy
80,
G Broccolo
G Broccolo
80INFN Sezione di Pisa, Pisa, Italy
82Scuola Normale Superiore di Pisa, Pisa, Italy
80,82,
R Castaldi
R Castaldi
80INFN Sezione di Pisa, Pisa, Italy
80,
R T D’Agnolo
R T D’Agnolo
80INFN Sezione di Pisa, Pisa, Italy
82Scuola Normale Superiore di Pisa, Pisa, Italy
80,82,
R Dell’Orso
R Dell’Orso
80INFN Sezione di Pisa, Pisa, Italy
80,
F Fiori
F Fiori
80INFN Sezione di Pisa, Pisa, Italy
82Scuola Normale Superiore di Pisa, Pisa, Italy
80,82,
L Foà
L Foà
80INFN Sezione di Pisa, Pisa, Italy
82Scuola Normale Superiore di Pisa, Pisa, Italy
80,82,
A Giassi
A Giassi
80INFN Sezione di Pisa, Pisa, Italy
80,
A Kraan
A Kraan
80INFN Sezione di Pisa, Pisa, Italy
80,
F Ligabue
F Ligabue
80INFN Sezione di Pisa, Pisa, Italy
82Scuola Normale Superiore di Pisa, Pisa, Italy
80,82,
T Lomtadze
T Lomtadze
80INFN Sezione di Pisa, Pisa, Italy
80,
L Martini
L Martini
80INFN Sezione di Pisa, Pisa, Italy
80,
A Messineo
A Messineo
80INFN Sezione di Pisa, Pisa, Italy
81Università di Pisa, Pisa, Italy
80,81,
F Palla
F Palla
80INFN Sezione di Pisa, Pisa, Italy
80,
A Rizzi
A Rizzi
80INFN Sezione di Pisa, Pisa, Italy
81Università di Pisa, Pisa, Italy
80,81,
A T Serban
A T Serban
80INFN Sezione di Pisa, Pisa, Italy
80,
P Spagnolo
P Spagnolo
80INFN Sezione di Pisa, Pisa, Italy
80,
P Squillacioti
P Squillacioti
80INFN Sezione di Pisa, Pisa, Italy
80,
R Tenchini
R Tenchini
80INFN Sezione di Pisa, Pisa, Italy
80,
G Tonelli
G Tonelli
80INFN Sezione di Pisa, Pisa, Italy
81Università di Pisa, Pisa, Italy
80,81,
A Venturi
A Venturi
80INFN Sezione di Pisa, Pisa, Italy
80,
P G Verdini
P G Verdini
80INFN Sezione di Pisa, Pisa, Italy
80,
C Vernieri
C Vernieri
80INFN Sezione di Pisa, Pisa, Italy
82Scuola Normale Superiore di Pisa, Pisa, Italy
80,82,
L Barone
L Barone
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
F Cavallari
F Cavallari
83INFN Sezione di Roma, Roma, Italy
83,
D Del Re
D Del Re
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
M Diemoz
M Diemoz
83INFN Sezione di Roma, Roma, Italy
83,
C Fanelli
C Fanelli
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
M Grassi
M Grassi
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
E Longo
E Longo
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
F Margaroli
F Margaroli
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
P Meridiani
P Meridiani
83INFN Sezione di Roma, Roma, Italy
83,
F Micheli
F Micheli
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
S Nourbakhsh
S Nourbakhsh
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
G Organtini
G Organtini
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
R Paramatti
R Paramatti
83INFN Sezione di Roma, Roma, Italy
83,
S Rahatlou
S Rahatlou
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
L Soffi
L Soffi
83INFN Sezione di Roma, Roma, Italy
84Università di Roma, Roma, Italy
83,84,
N Amapane
N Amapane
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
R Arcidiacono
R Arcidiacono
85INFN Sezione di Torino, Torino, Italy
87Università del Piemonte Orientale (Novara), Torino, Italy
85,87,
S Argiro
S Argiro
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
M Arneodo
M Arneodo
85INFN Sezione di Torino, Torino, Italy
87Università del Piemonte Orientale (Novara), Torino, Italy
85,87,
C Biino
C Biino
85INFN Sezione di Torino, Torino, Italy
85,
N Cartiglia
N Cartiglia
85INFN Sezione di Torino, Torino, Italy
85,
S Casasso
S Casasso
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
M Costa
M Costa
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
P De Remigis
P De Remigis
85INFN Sezione di Torino, Torino, Italy
85,
N Demaria
N Demaria
85INFN Sezione di Torino, Torino, Italy
85,
C Mariotti
C Mariotti
85INFN Sezione di Torino, Torino, Italy
85,
S Maselli
S Maselli
85INFN Sezione di Torino, Torino, Italy
85,
E Migliore
E Migliore
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
V Monaco
V Monaco
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
M Musich
M Musich
85INFN Sezione di Torino, Torino, Italy
85,
M M Obertino
M M Obertino
85INFN Sezione di Torino, Torino, Italy
87Università del Piemonte Orientale (Novara), Torino, Italy
85,87,
N Pastrone
N Pastrone
85INFN Sezione di Torino, Torino, Italy
85,
M Pelliccioni
M Pelliccioni
85INFN Sezione di Torino, Torino, Italy
85,
A Potenza
A Potenza
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
A Romero
A Romero
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
M Ruspa
M Ruspa
85INFN Sezione di Torino, Torino, Italy
87Università del Piemonte Orientale (Novara), Torino, Italy
85,87,
R Sacchi
R Sacchi
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
A Solano
A Solano
85INFN Sezione di Torino, Torino, Italy
86Università di Torino, Torino, Italy
85,86,
A Staiano
A Staiano
85INFN Sezione di Torino, Torino, Italy
85,
U Tamponi
U Tamponi
85INFN Sezione di Torino, Torino, Italy
85,
S Belforte
S Belforte
88INFN Sezione di Trieste, Trieste, Italy
88,
V Candelise
V Candelise
88INFN Sezione di Trieste, Trieste, Italy
89Università di Trieste, Trieste, Italy
88,89,
M Casarsa
M Casarsa
88INFN Sezione di Trieste, Trieste, Italy
88,
F Cossutti
F Cossutti
88INFN Sezione di Trieste, Trieste, Italy
88,
G Della Ricca
G Della Ricca
88INFN Sezione di Trieste, Trieste, Italy
89Università di Trieste, Trieste, Italy
88,89,
B Gobbo
B Gobbo
88INFN Sezione di Trieste, Trieste, Italy
88,
C La Licata
C La Licata
88INFN Sezione di Trieste, Trieste, Italy
89Università di Trieste, Trieste, Italy
88,89,
M Marone
M Marone
88INFN Sezione di Trieste, Trieste, Italy
89Università di Trieste, Trieste, Italy
88,89,
D Montanino
D Montanino
88INFN Sezione di Trieste, Trieste, Italy
89Università di Trieste, Trieste, Italy
88,89,
A Penzo
A Penzo
88INFN Sezione di Trieste, Trieste, Italy
88,
A Schizzi
A Schizzi
88INFN Sezione di Trieste, Trieste, Italy
89Università di Trieste, Trieste, Italy
88,89,
A Zanetti
A Zanetti
88INFN Sezione di Trieste, Trieste, Italy
88,
T Y Kim
T Y Kim
90Kangwon National University, Chunchon, Korea
90,
S K Nam
S K Nam
90Kangwon National University, Chunchon, Korea
90,
S Chang
S Chang
91Kyungpook National University, Daegu, Korea
91,
D H Kim
D H Kim
91Kyungpook National University, Daegu, Korea
91,
G N Kim
G N Kim
91Kyungpook National University, Daegu, Korea
91,
J E Kim
J E Kim
91Kyungpook National University, Daegu, Korea
91,
D J Kong
D J Kong
91Kyungpook National University, Daegu, Korea
91,
Y D Oh
Y D Oh
91Kyungpook National University, Daegu, Korea
91,
H Park
H Park
91Kyungpook National University, Daegu, Korea
91,
D C Son
D C Son
91Kyungpook National University, Daegu, Korea
91,
J Y Kim
J Y Kim
92Institute for Universe and Elementary Particles, Chonnam National University, Kwangju, Korea
92,
Zero J Kim
Zero J Kim
92Institute for Universe and Elementary Particles, Chonnam National University, Kwangju, Korea
92,
S Song
S Song
92Institute for Universe and Elementary Particles, Chonnam National University, Kwangju, Korea
92,
S Choi
S Choi
93Korea University, Seoul, Korea
93,
D Gyun
D Gyun
93Korea University, Seoul, Korea
93,
B Hong
B Hong
93Korea University, Seoul, Korea
93,
M Jo
M Jo
93Korea University, Seoul, Korea
93,
H Kim
H Kim
93Korea University, Seoul, Korea
93,
T J Kim
T J Kim
93Korea University, Seoul, Korea
93,
K S Lee
K S Lee
93Korea University, Seoul, Korea
93,
D H Moon
D H Moon
93Korea University, Seoul, Korea
93,
S K Park
S K Park
93Korea University, Seoul, Korea
93,
Y Roh
Y Roh
93Korea University, Seoul, Korea
93,
M Choi
M Choi
94University of Seoul, Seoul, Korea
94,
J H Kim
J H Kim
94University of Seoul, Seoul, Korea
94,
C Park
C Park
94University of Seoul, Seoul, Korea
94,
I C Park
I C Park
94University of Seoul, Seoul, Korea
94,
S Park
S Park
94University of Seoul, Seoul, Korea
94,
G Ryu
G Ryu
94University of Seoul, Seoul, Korea
94,
Y Choi
Y Choi
95Sungkyunkwan University, Suwon, Korea
95,
Y K Choi
Y K Choi
95Sungkyunkwan University, Suwon, Korea
95,
J Goh
J Goh
95Sungkyunkwan University, Suwon, Korea
95,
M S Kim
M S Kim
95Sungkyunkwan University, Suwon, Korea
95,
E Kwon
E Kwon
95Sungkyunkwan University, Suwon, Korea
95,
B Lee
B Lee
95Sungkyunkwan University, Suwon, Korea
95,
J Lee
J Lee
95Sungkyunkwan University, Suwon, Korea
95,
S Lee
S Lee
95Sungkyunkwan University, Suwon, Korea
95,
H Seo
H Seo
95Sungkyunkwan University, Suwon, Korea
95,
I Yu
I Yu
95Sungkyunkwan University, Suwon, Korea
95,
I Grigelionis
I Grigelionis
96Vilnius University, Vilnius, Lithuania
96,
A Juodagalvis
A Juodagalvis
96Vilnius University, Vilnius, Lithuania
96,
H Castilla-Valdez
H Castilla-Valdez
97Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
97,
E De La Cruz-Burelo
E De La Cruz-Burelo
97Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
97,
I Heredia-de La Cruz
I Heredia-de La Cruz
97Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
97,
R Lopez-Fernandez
R Lopez-Fernandez
97Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
97,
J Martínez-Ortega
J Martínez-Ortega
97Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
97,
A Sanchez-Hernandez
A Sanchez-Hernandez
97Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
97,
L M Villasenor-Cendejas
L M Villasenor-Cendejas
97Centro de Investigacion y de Estudios Avanzados del IPN, Mexico City, Mexico
97,
S Carrillo Moreno
S Carrillo Moreno
98Universidad Iberoamericana, Mexico City, Mexico
98,
F Vazquez Valencia
F Vazquez Valencia
98Universidad Iberoamericana, Mexico City, Mexico
98,
H A Salazar Ibarguen
H A Salazar Ibarguen
99Benemerita Universidad Autonoma de Puebla, Puebla, Mexico
99,
E Casimiro Linares
E Casimiro Linares
100Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico
100,
A Morelos Pineda
A Morelos Pineda
100Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico
100,
M A Reyes-Santos
M A Reyes-Santos
100Universidad Autónoma de San Luis Potosí, San Luis Potosí, Mexico
100,
D Krofcheck
D Krofcheck
101University of Auckland, Auckland, New Zealand
101,
A J Bell
A J Bell
102University of Canterbury, Christchurch, New Zealand
102,
P H Butler
P H Butler
102University of Canterbury, Christchurch, New Zealand
102,
R Doesburg
R Doesburg
102University of Canterbury, Christchurch, New Zealand
102,
S Reucroft
S Reucroft
102University of Canterbury, Christchurch, New Zealand
102,
H Silverwood
H Silverwood
102University of Canterbury, Christchurch, New Zealand
102,
M Ahmad
M Ahmad
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
M I Asghar
M I Asghar
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
J Butt
J Butt
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
H R Hoorani
H R Hoorani
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
S Khalid
S Khalid
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
W A Khan
W A Khan
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
T Khurshid
T Khurshid
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
S Qazi
S Qazi
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
M A Shah
M A Shah
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
M Shoaib
M Shoaib
103National Centre for Physics, Quaid-I-Azam University, Islamabad, Pakistan
103,
H Bialkowska
H Bialkowska
104National Centre for Nuclear Research, Swierk, Poland
104,
B Boimska
B Boimska
104National Centre for Nuclear Research, Swierk, Poland
104,
T Frueboes
T Frueboes
104National Centre for Nuclear Research, Swierk, Poland
104,
M Górski
M Górski
104National Centre for Nuclear Research, Swierk, Poland
104,
M Kazana
M Kazana
104National Centre for Nuclear Research, Swierk, Poland
104,
K Nawrocki
K Nawrocki
104National Centre for Nuclear Research, Swierk, Poland
104,
K Romanowska-Rybinska
K Romanowska-Rybinska
104National Centre for Nuclear Research, Swierk, Poland
104,
M Szleper
M Szleper
104National Centre for Nuclear Research, Swierk, Poland
104,
G Wrochna
G Wrochna
104National Centre for Nuclear Research, Swierk, Poland
104,
P Zalewski
P Zalewski
104National Centre for Nuclear Research, Swierk, Poland
104,
G Brona
G Brona
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
K Bunkowski
K Bunkowski
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
M Cwiok
M Cwiok
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
W Dominik
W Dominik
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
K Doroba
K Doroba
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
A Kalinowski
A Kalinowski
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
M Konecki
M Konecki
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
J Krolikowski
J Krolikowski
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
M Misiura
M Misiura
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
W Wolszczak
W Wolszczak
105Institute of Experimental Physics, Faculty of Physics, University of Warsaw, Warsaw, Poland
105,
N Almeida
N Almeida
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
P Bargassa
P Bargassa
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
A David
A David
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
P Faccioli
P Faccioli
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
P G Ferreira Parracho
P G Ferreira Parracho
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
M Gallinaro
M Gallinaro
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
J Seixas
J Seixas
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
J Varela
J Varela
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
P Vischia
P Vischia
106Laboratório de Instrumentação e Física Experimental de Partículas, Lisboa, Portugal
106,
P Bunin
P Bunin
107Joint Institute for Nuclear Research, Dubna, Russia
107,
M Gavrilenko
M Gavrilenko
107Joint Institute for Nuclear Research, Dubna, Russia
107,
I Golutvin
I Golutvin
107Joint Institute for Nuclear Research, Dubna, Russia
107,
I Gorbunov
I Gorbunov
107Joint Institute for Nuclear Research, Dubna, Russia
107,
A Kamenev
A Kamenev
107Joint Institute for Nuclear Research, Dubna, Russia
107,
V Karjavin
V Karjavin
107Joint Institute for Nuclear Research, Dubna, Russia
107,
V Konoplyanikov
V Konoplyanikov
107Joint Institute for Nuclear Research, Dubna, Russia
107,
G Kozlov
G Kozlov
107Joint Institute for Nuclear Research, Dubna, Russia
107,
A Lanev
A Lanev
107Joint Institute for Nuclear Research, Dubna, Russia
107,
A Malakhov
A Malakhov
107Joint Institute for Nuclear Research, Dubna, Russia
107,
P Moisenz
P Moisenz
107Joint Institute for Nuclear Research, Dubna, Russia
107,
V Palichik
V Palichik
107Joint Institute for Nuclear Research, Dubna, Russia
107,
V Perelygin
V Perelygin
107Joint Institute for Nuclear Research, Dubna, Russia
107,
S Shmatov
S Shmatov
107Joint Institute for Nuclear Research, Dubna, Russia
107,
V Smirnov
V Smirnov
107Joint Institute for Nuclear Research, Dubna, Russia
107,
A Volodko
A Volodko
107Joint Institute for Nuclear Research, Dubna, Russia
107,
A Zarubin
A Zarubin
107Joint Institute for Nuclear Research, Dubna, Russia
107,
S Evstyukhin
S Evstyukhin
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
V Golovtsov
V Golovtsov
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
Y Ivanov
Y Ivanov
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
V Kim
V Kim
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
P Levchenko
P Levchenko
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
V Murzin
V Murzin
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
V Oreshkin
V Oreshkin
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
I Smirnov
I Smirnov
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
V Sulimov
V Sulimov
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
L Uvarov
L Uvarov
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
S Vavilov
S Vavilov
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
A Vorobyev
A Vorobyev
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
An Vorobyev
An Vorobyev
108Petersburg Nuclear Physics Institute, Gatchina (St. Petersburg), Russia
108,
Yu Andreev
Yu Andreev
109Institute for Nuclear Research, Moscow, Russia
109,
A Dermenev
A Dermenev
109Institute for Nuclear Research, Moscow, Russia
109,
S Gninenko
S Gninenko
109Institute for Nuclear Research, Moscow, Russia
109,
N Golubev
N Golubev
109Institute for Nuclear Research, Moscow, Russia
109,
M Kirsanov
M Kirsanov
109Institute for Nuclear Research, Moscow, Russia
109,
N Krasnikov
N Krasnikov
109Institute for Nuclear Research, Moscow, Russia
109,
V Matveev
V Matveev
109Institute for Nuclear Research, Moscow, Russia
109,
A Pashenkov
A Pashenkov
109Institute for Nuclear Research, Moscow, Russia
109,
D Tlisov
D Tlisov
109Institute for Nuclear Research, Moscow, Russia
109,
A Toropin
A Toropin
109Institute for Nuclear Research, Moscow, Russia
109,
V Epshteyn
V Epshteyn
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
M Erofeeva
M Erofeeva
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
V Gavrilov
V Gavrilov
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
N Lychkovskaya
N Lychkovskaya
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
V Popov
V Popov
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
G Safronov
G Safronov
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
S Semenov
S Semenov
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
A Spiridonov
A Spiridonov
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
V Stolin
V Stolin
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
E Vlasov
E Vlasov
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
A Zhokin
A Zhokin
110Institute for Theoretical and Experimental Physics, Moscow, Russia
110,
V Andreev
V Andreev
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
M Azarkin
M Azarkin
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
I Dremin
I Dremin
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
M Kirakosyan
M Kirakosyan
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
A Leonidov
A Leonidov
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
G Mesyats
G Mesyats
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
S V Rusakov
S V Rusakov
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
A Vinogradov
A Vinogradov
111P.N. Lebedev Physical Institute, Moscow, Russia
111,
A Belyaev
A Belyaev
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
E Boos
E Boos
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
V Bunichev
V Bunichev
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
M Dubinin
M Dubinin
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
L Dudko
L Dudko
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
A Ershov
A Ershov
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
A Gribushin
A Gribushin
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
V Klyukhin
V Klyukhin
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
I Lokhtin
I Lokhtin
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
A Markina
A Markina
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
S Obraztsov
S Obraztsov
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
M Perfilov
M Perfilov
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
V Savrin
V Savrin
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
N Tsirova
N Tsirova
112Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
112,
I Azhgirey
I Azhgirey
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
I Bayshev
I Bayshev
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
S Bitioukov
S Bitioukov
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
V Kachanov
V Kachanov
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
A Kalinin
A Kalinin
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
D Konstantinov
D Konstantinov
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
V Krychkine
V Krychkine
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
V Petrov
V Petrov
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
R Ryutin
R Ryutin
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
A Sobol
A Sobol
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
L Tourtchanovitch
L Tourtchanovitch
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
S Troshin
S Troshin
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
N Tyurin
N Tyurin
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
A Uzunian
A Uzunian
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
A Volkov
A Volkov
113State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, Russia
113,
P Adzic
P Adzic
114Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
114,
M Ekmedzic
M Ekmedzic
114Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
114,
D Krpic
D Krpic
114Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
114,
J Milosevic
J Milosevic
114Faculty of Physics and Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
114,
M Aguilar-Benitez
M Aguilar-Benitez
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
J Alcaraz Maestre
J Alcaraz Maestre
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
C Battilana
C Battilana
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
E Calvo
E Calvo
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
M Cerrada
M Cerrada
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
M Chamizo Llatas
M Chamizo Llatas
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
N Colino
N Colino
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
B De La Cruz
B De La Cruz
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
A Delgado Peris
A Delgado Peris
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
D Domínguez Vázquez
D Domínguez Vázquez
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
C Fernandez Bedoya
C Fernandez Bedoya
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
J P Fernández Ramos
J P Fernández Ramos
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
A Ferrando
A Ferrando
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
J Flix
J Flix
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
M C Fouz
M C Fouz
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
P Garcia-Abia
P Garcia-Abia
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
O Gonzalez Lopez
O Gonzalez Lopez
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
S Goy Lopez
S Goy Lopez
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
J M Hernandez
J M Hernandez
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
M I Josa
M I Josa
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
G Merino
G Merino
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
E Navarro De Martino
E Navarro De Martino
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
J Puerta Pelayo
J Puerta Pelayo
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
A Quintario Olmeda
A Quintario Olmeda
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
I Redondo
I Redondo
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
L Romero
L Romero
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
J Santaolalla
J Santaolalla
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
M S Soares
M S Soares
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
C Willmott
C Willmott
115Centro de Investigaciones Energéticas Medioambientales y Tecnológicas (CIEMAT), Madrid, Spain
115,
C Albajar
C Albajar
116Universidad Autónoma de Madrid, Madrid, Spain
116,
J F de Trocóniz
J F de Trocóniz
116Universidad Autónoma de Madrid, Madrid, Spain
116,
H Brun
H Brun
117Universidad de Oviedo, Oviedo, Spain
117,
J Cuevas
J Cuevas
117Universidad de Oviedo, Oviedo, Spain
117,
J Fernandez Menendez
J Fernandez Menendez
117Universidad de Oviedo, Oviedo, Spain
117,
S Folgueras
S Folgueras
117Universidad de Oviedo, Oviedo, Spain
117,
I Gonzalez Caballero
I Gonzalez Caballero
117Universidad de Oviedo, Oviedo, Spain
117,
L Lloret Iglesias
L Lloret Iglesias
117Universidad de Oviedo, Oviedo, Spain
117,
J Piedra Gomez
J Piedra Gomez
117Universidad de Oviedo, Oviedo, Spain
117,
J A Brochero Cifuentes
J A Brochero Cifuentes
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
I J Cabrillo
I J Cabrillo
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
A Calderon
A Calderon
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
S H Chuang
S H Chuang
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
J Duarte Campderros
J Duarte Campderros
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
M Fernandez
M Fernandez
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
G Gomez
G Gomez
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
J Gonzalez Sanchez
J Gonzalez Sanchez
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
A Graziano
A Graziano
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
C Jorda
C Jorda
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
A Lopez Virto
A Lopez Virto
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
J Marco
J Marco
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
R Marco
R Marco
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
C Martinez Rivero
C Martinez Rivero
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
F Matorras
F Matorras
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
F J Munoz Sanchez
F J Munoz Sanchez
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
T Rodrigo
T Rodrigo
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
A Y Rodríguez-Marrero
A Y Rodríguez-Marrero
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
A Ruiz-Jimeno
A Ruiz-Jimeno
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
L Scodellaro
L Scodellaro
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
I Vila
I Vila
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
R Vilar Cortabitarte
R Vilar Cortabitarte
118Instituto de Física de Cantabria (IFCA), CSIC-Universidad de Cantabria, Santander, Spain
118,
D Abbaneo
D Abbaneo
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
E Auffray
E Auffray
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
G Auzinger
G Auzinger
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Bachtis
M Bachtis
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Baillon
P Baillon
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A H Ball
A H Ball
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
D Barney
D Barney
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
J Bendavid
J Bendavid
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
J F Benitez
J F Benitez
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
C Bernet
C Bernet
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
G Bianchi
G Bianchi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Bloch
P Bloch
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Bocci
A Bocci
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Bonato
A Bonato
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
O Bondu
O Bondu
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
C Botta
C Botta
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
H Breuker
H Breuker
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
T Camporesi
T Camporesi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
G Cerminara
G Cerminara
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
T Christiansen
T Christiansen
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
J A Coarasa Perez
J A Coarasa Perez
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
S Colafranceschi
S Colafranceschi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
D d’Enterria
D d’Enterria
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Dabrowski
A Dabrowski
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A De Roeck
A De Roeck
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
S De Visscher
S De Visscher
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
S Di Guida
S Di Guida
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Dobson
M Dobson
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
N Dupont-Sagorin
N Dupont-Sagorin
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Elliott-Peisert
A Elliott-Peisert
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
J Eugster
J Eugster
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
W Funk
W Funk
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
G Georgiou
G Georgiou
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Giffels
M Giffels
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
D Gigi
D Gigi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
K Gill
K Gill
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
D Giordano
D Giordano
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Girone
M Girone
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Giunta
M Giunta
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
F Glege
F Glege
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
R Gomez-Reino Garrido
R Gomez-Reino Garrido
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
S Gowdy
S Gowdy
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
R Guida
R Guida
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
J Hammer
J Hammer
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Hansen
M Hansen
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Harris
P Harris
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
C Hartl
C Hartl
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
B Hegner
B Hegner
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Hinzmann
A Hinzmann
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
V Innocente
V Innocente
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Janot
P Janot
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
K Kaadze
K Kaadze
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
E Karavakis
E Karavakis
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
K Kousouris
K Kousouris
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
K Krajczar
K Krajczar
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Lecoq
P Lecoq
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
Y-J Lee
Y-J Lee
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
C Lourenço
C Lourenço
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
N Magini
N Magini
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Malberti
M Malberti
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
L Malgeri
L Malgeri
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Mannelli
M Mannelli
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
L Masetti
L Masetti
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
F Meijers
F Meijers
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
S Mersi
S Mersi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
E Meschi
E Meschi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
R Moser
R Moser
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Mulders
M Mulders
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Musella
P Musella
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
E Nesvold
E Nesvold
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
L Orsini
L Orsini
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
E Palencia Cortezon
E Palencia Cortezon
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
E Perez
E Perez
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
L Perrozzi
L Perrozzi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Petrilli
A Petrilli
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Pfeiffer
A Pfeiffer
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Pierini
M Pierini
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Pimiä
M Pimiä
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
D Piparo
D Piparo
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
G Polese
G Polese
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
L Quertenmont
L Quertenmont
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Racz
A Racz
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
W Reece
W Reece
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
J Rodrigues Antunes
J Rodrigues Antunes
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
G Rolandi
G Rolandi
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
C Rovelli
C Rovelli
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Rovere
M Rovere
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
H Sakulin
H Sakulin
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
F Santanastasio
F Santanastasio
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
C Schäfer
C Schäfer
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
C Schwick
C Schwick
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
I Segoni
I Segoni
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
S Sekmen
S Sekmen
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Sharma
A Sharma
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Siegrist
P Siegrist
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Silva
P Silva
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Simon
M Simon
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
P Sphicas
P Sphicas
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
D Spiga
D Spiga
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
M Stoye
M Stoye
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
A Tsirou
A Tsirou
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
G I Veres
G I Veres
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
J R Vlimant
J R Vlimant
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
H K Wöhri
H K Wöhri
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
S D Worm
S D Worm
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
W D Zeuner
W D Zeuner
119European Organization for Nuclear Research, CERN, Geneva, Switzerland
119,
W Bertl
W Bertl
120Paul Scherrer Institut, Villigen, Switzerland
120,
K Deiters
K Deiters
120Paul Scherrer Institut, Villigen, Switzerland
120,
W Erdmann
W Erdmann
120Paul Scherrer Institut, Villigen, Switzerland
120,
K Gabathuler
K Gabathuler
120Paul Scherrer Institut, Villigen, Switzerland
120,
R Horisberger
R Horisberger
120Paul Scherrer Institut, Villigen, Switzerland
120,
Q Ingram
Q Ingram
120Paul Scherrer Institut, Villigen, Switzerland
120,
H C Kaestli
H C Kaestli
120Paul Scherrer Institut, Villigen, Switzerland
120,
S König
S König
120Paul Scherrer Institut, Villigen, Switzerland
120,
D Kotlinski
D Kotlinski
120Paul Scherrer Institut, Villigen, Switzerland
120,
U Langenegger
U Langenegger
120Paul Scherrer Institut, Villigen, Switzerland
120,
F Meier
F Meier
120Paul Scherrer Institut, Villigen, Switzerland
120,
D Renker
D Renker
120Paul Scherrer Institut, Villigen, Switzerland
120,
T Rohe
T Rohe
120Paul Scherrer Institut, Villigen, Switzerland
120,
F Bachmair
F Bachmair
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
L Bäni
L Bäni
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
P Bortignon
P Bortignon
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
M A Buchmann
M A Buchmann
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
B Casal
B Casal
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
N Chanon
N Chanon
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
A Deisher
A Deisher
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
G Dissertori
G Dissertori
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
M Dittmar
M Dittmar
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
M Donegà
M Donegà
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
M Dünser
M Dünser
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
P Eller
P Eller
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
C Grab
C Grab
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
D Hits
D Hits
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
P Lecomte
P Lecomte
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
W Lustermann
W Lustermann
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
A C Marini
A C Marini
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
P Martinez Ruiz del Arbol
P Martinez Ruiz del Arbol
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
N Mohr
N Mohr
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
F Moortgat
F Moortgat
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
C Nägeli
C Nägeli
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
P Nef
P Nef
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
F Nessi-Tedaldi
F Nessi-Tedaldi
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
F Pandolfi
F Pandolfi
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
L Pape
L Pape
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
F Pauss
F Pauss
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
M Peruzzi
M Peruzzi
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
F J Ronga
F J Ronga
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
M Rossini
M Rossini
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
L Sala
L Sala
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
A K Sanchez
A K Sanchez
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
A Starodumov
A Starodumov
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
B Stieger
B Stieger
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
M Takahashi
M Takahashi
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
L Tauscher
L Tauscher
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
A Thea
A Thea
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
K Theofilatos
K Theofilatos
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
D Treille
D Treille
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
C Urscheler
C Urscheler
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
R Wallny
R Wallny
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
H A Weber
H A Weber
121Institute for Particle Physics, ETH Zurich, Zurich, Switzerland
121,
C Amsler
C Amsler
122Universität Zürich, Zurich, Switzerland
122,
V Chiochia
V Chiochia
122Universität Zürich, Zurich, Switzerland
122,
C Favaro
C Favaro
122Universität Zürich, Zurich, Switzerland
122,
M Ivova Rikova
M Ivova Rikova
122Universität Zürich, Zurich, Switzerland
122,
B Kilminster
B Kilminster
122Universität Zürich, Zurich, Switzerland
122,
B Millan Mejias
B Millan Mejias
122Universität Zürich, Zurich, Switzerland
122,
P Otiougova
P Otiougova
122Universität Zürich, Zurich, Switzerland
122,
P Robmann
P Robmann
122Universität Zürich, Zurich, Switzerland
122,
H Snoek
H Snoek
122Universität Zürich, Zurich, Switzerland
122,
S Taroni
S Taroni
122Universität Zürich, Zurich, Switzerland
122,
S Tupputi
S Tupputi
122Universität Zürich, Zurich, Switzerland
122,
M Verzetti
M Verzetti
122Universität Zürich, Zurich, Switzerland
122,
M Cardaci
M Cardaci
123National Central University, Chung-Li, Taiwan
123,
K H Chen
K H Chen
123National Central University, Chung-Li, Taiwan
123,
C Ferro
C Ferro
123National Central University, Chung-Li, Taiwan
123,
C M Kuo
C M Kuo
123National Central University, Chung-Li, Taiwan
123,
S W Li
S W Li
123National Central University, Chung-Li, Taiwan
123,
W Lin
W Lin
123National Central University, Chung-Li, Taiwan
123,
Y J Lu
Y J Lu
123National Central University, Chung-Li, Taiwan
123,
R Volpe
R Volpe
123National Central University, Chung-Li, Taiwan
123,
S S Yu
S S Yu
123National Central University, Chung-Li, Taiwan
123,
P Bartalini
P Bartalini
124National Taiwan University (NTU), Taipei, Taiwan
124,
P Chang
P Chang
124National Taiwan University (NTU), Taipei, Taiwan
124,
Y H Chang
Y H Chang
124National Taiwan University (NTU), Taipei, Taiwan
124,
Y W Chang
Y W Chang
124National Taiwan University (NTU), Taipei, Taiwan
124,
Y Chao
Y Chao
124National Taiwan University (NTU), Taipei, Taiwan
124,
K F Chen
K F Chen
124National Taiwan University (NTU), Taipei, Taiwan
124,
C Dietz
C Dietz
124National Taiwan University (NTU), Taipei, Taiwan
124,
U Grundler
U Grundler
124National Taiwan University (NTU), Taipei, Taiwan
124,
W-S Hou
W-S Hou
124National Taiwan University (NTU), Taipei, Taiwan
124,
Y Hsiung
Y Hsiung
124National Taiwan University (NTU), Taipei, Taiwan
124,
K Y Kao
K Y Kao
124National Taiwan University (NTU), Taipei, Taiwan
124,
Y J Lei
Y J Lei
124National Taiwan University (NTU), Taipei, Taiwan
124,
R-S Lu
R-S Lu
124National Taiwan University (NTU), Taipei, Taiwan
124,
D Majumder
D Majumder
124National Taiwan University (NTU), Taipei, Taiwan
124,
E Petrakou
E Petrakou
124National Taiwan University (NTU), Taipei, Taiwan
124,
X Shi
X Shi
124National Taiwan University (NTU), Taipei, Taiwan
124,
J G Shiu
J G Shiu
124National Taiwan University (NTU), Taipei, Taiwan
124,
Y M Tzeng
Y M Tzeng
124National Taiwan University (NTU), Taipei, Taiwan
124,
M Wang
M Wang
124National Taiwan University (NTU), Taipei, Taiwan
124,
B Asavapibhop
B Asavapibhop
125Chulalongkorn University, Bangkok, Thailand
125,
N Suwonjandee
N Suwonjandee
125Chulalongkorn University, Bangkok, Thailand
125,
A Adiguzel
A Adiguzel
126Cukurova University, Adana, Turkey
126,
M N Bakirci
M N Bakirci
126Cukurova University, Adana, Turkey
126,
S Cerci
S Cerci
126Cukurova University, Adana, Turkey
126,
C Dozen
C Dozen
126Cukurova University, Adana, Turkey
126,
I Dumanoglu
I Dumanoglu
126Cukurova University, Adana, Turkey
126,
E Eskut
E Eskut
126Cukurova University, Adana, Turkey
126,
S Girgis
S Girgis
126Cukurova University, Adana, Turkey
126,
G Gokbulut
G Gokbulut
126Cukurova University, Adana, Turkey
126,
E Gurpinar
E Gurpinar
126Cukurova University, Adana, Turkey
126,
I Hos
I Hos
126Cukurova University, Adana, Turkey
126,
E E Kangal
E E Kangal
126Cukurova University, Adana, Turkey
126,
A Kayis Topaksu
A Kayis Topaksu
126Cukurova University, Adana, Turkey
126,
G Onengut
G Onengut
126Cukurova University, Adana, Turkey
126,
K Ozdemir
K Ozdemir
126Cukurova University, Adana, Turkey
126,
S Ozturk
S Ozturk
126Cukurova University, Adana, Turkey
126,
A Polatoz
A Polatoz
126Cukurova University, Adana, Turkey
126,
K Sogut
K Sogut
126Cukurova University, Adana, Turkey
126,
D Sunar Cerci
D Sunar Cerci
126Cukurova University, Adana, Turkey
126,
B Tali
B Tali
126Cukurova University, Adana, Turkey
126,
H Topakli
H Topakli
126Cukurova University, Adana, Turkey
126,
M Vergili
M Vergili
126Cukurova University, Adana, Turkey
126,
I V Akin
I V Akin
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
T Aliev
T Aliev
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
B Bilin
B Bilin
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
S Bilmis
S Bilmis
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
M Deniz
M Deniz
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
H Gamsizkan
H Gamsizkan
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
A M Guler
A M Guler
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
G Karapinar
G Karapinar
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
K Ocalan
K Ocalan
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
A Ozpineci
A Ozpineci
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
M Serin
M Serin
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
R Sever
R Sever
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
U E Surat
U E Surat
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
M Yalvac
M Yalvac
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
M Zeyrek
M Zeyrek
127Physics Department, Middle East Technical University, Ankara, Turkey
127,
E Gülmez
E Gülmez
128Bogazici University, Istanbul, Turkey
128,
B Isildak
B Isildak
128Bogazici University, Istanbul, Turkey
128,
M Kaya
M Kaya
128Bogazici University, Istanbul, Turkey
128,
O Kaya
O Kaya
128Bogazici University, Istanbul, Turkey
128,
S Ozkorucuklu
S Ozkorucuklu
128Bogazici University, Istanbul, Turkey
128,
N Sonmez
N Sonmez
128Bogazici University, Istanbul, Turkey
128,
H Bahtiyar
H Bahtiyar
129Istanbul Technical University, Istanbul, Turkey
129,
E Barlas
E Barlas
129Istanbul Technical University, Istanbul, Turkey
129,
K Cankocak
K Cankocak
129Istanbul Technical University, Istanbul, Turkey
129,
Y O Günaydin
Y O Günaydin
129Istanbul Technical University, Istanbul, Turkey
129,
F I Vardarlı
F I Vardarlı
129Istanbul Technical University, Istanbul, Turkey
129,
M Yücel
M Yücel
129Istanbul Technical University, Istanbul, Turkey
129,
L Levchuk
L Levchuk
130National Scientific Center, Kharkov Institute of Physics and Technology, Kharkov, Ukraine
130,
P Sorokin
P Sorokin
130National Scientific Center, Kharkov Institute of Physics and Technology, Kharkov, Ukraine
130,
J J Brooke
J J Brooke
131University of Bristol, Bristol, United Kingdom
131,
E Clement
E Clement
131University of Bristol, Bristol, United Kingdom
131,
D Cussans
D Cussans
131University of Bristol, Bristol, United Kingdom
131,
H Flacher
H Flacher
131University of Bristol, Bristol, United Kingdom
131,
R Frazier
R Frazier
131University of Bristol, Bristol, United Kingdom
131,
J Goldstein
J Goldstein
131University of Bristol, Bristol, United Kingdom
131,
M Grimes
M Grimes
131University of Bristol, Bristol, United Kingdom
131,
G P Heath
G P Heath
131University of Bristol, Bristol, United Kingdom
131,
H F Heath
H F Heath
131University of Bristol, Bristol, United Kingdom
131,
L Kreczko
L Kreczko
131University of Bristol, Bristol, United Kingdom
131,
S Metson
S Metson
131University of Bristol, Bristol, United Kingdom
131,
D M Newbold
D M Newbold
131University of Bristol, Bristol, United Kingdom
131,
K Nirunpong
K Nirunpong
131University of Bristol, Bristol, United Kingdom
131,
A Poll
A Poll
131University of Bristol, Bristol, United Kingdom
131,
S Senkin
S Senkin
131University of Bristol, Bristol, United Kingdom
131,
V J Smith
V J Smith
131University of Bristol, Bristol, United Kingdom
131,
T Williams
T Williams
131University of Bristol, Bristol, United Kingdom
131,
L Basso
L Basso
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
K W Bell
K W Bell
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
A Belyaev
A Belyaev
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
C Brew
C Brew
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
R M Brown
R M Brown
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
D J A Cockerill
D J A Cockerill
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
J A Coughlan
J A Coughlan
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
K Harder
K Harder
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
S Harper
S Harper
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
J Jackson
J Jackson
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
E Olaiya
E Olaiya
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
D Petyt
D Petyt
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
B C Radburn-Smith
B C Radburn-Smith
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
C H Shepherd-Themistocleous
C H Shepherd-Themistocleous
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
I R Tomalin
I R Tomalin
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
W J Womersley
W J Womersley
132Rutherford Appleton Laboratory, Didcot, United Kingdom
132,
R Bainbridge
R Bainbridge
133Imperial College, London, United Kingdom
133,
O Buchmuller
O Buchmuller
133Imperial College, London, United Kingdom
133,
D Burton
D Burton
133Imperial College, London, United Kingdom
133,
D Colling
D Colling
133Imperial College, London, United Kingdom
133,
N Cripps
N Cripps
133Imperial College, London, United Kingdom
133,
M Cutajar
M Cutajar
133Imperial College, London, United Kingdom
133,
P Dauncey
P Dauncey
133Imperial College, London, United Kingdom
133,
G Davies
G Davies
133Imperial College, London, United Kingdom
133,
M Della Negra
M Della Negra
133Imperial College, London, United Kingdom
133,
W Ferguson
W Ferguson
133Imperial College, London, United Kingdom
133,
J Fulcher
J Fulcher
133Imperial College, London, United Kingdom
133,
D Futyan
D Futyan
133Imperial College, London, United Kingdom
133,
A Gilbert
A Gilbert
133Imperial College, London, United Kingdom
133,
A Guneratne Bryer
A Guneratne Bryer
133Imperial College, London, United Kingdom
133,
G Hall
G Hall
133Imperial College, London, United Kingdom
133,
Z Hatherell
Z Hatherell
133Imperial College, London, United Kingdom
133,
J Hays
J Hays
133Imperial College, London, United Kingdom
133,
G Iles
G Iles
133Imperial College, London, United Kingdom
133,
M Jarvis
M Jarvis
133Imperial College, London, United Kingdom
133,
G Karapostoli
G Karapostoli
133Imperial College, London, United Kingdom
133,
M Kenzie
M Kenzie
133Imperial College, London, United Kingdom
133,
R Lane
R Lane
133Imperial College, London, United Kingdom
133,
R Lucas
R Lucas
133Imperial College, London, United Kingdom
133,
L Lyons
L Lyons
133Imperial College, London, United Kingdom
133,
A-M Magnan
A-M Magnan
133Imperial College, London, United Kingdom
133,
J Marrouche
J Marrouche
133Imperial College, London, United Kingdom
133,
B Mathias
B Mathias
133Imperial College, London, United Kingdom
133,
R Nandi
R Nandi
133Imperial College, London, United Kingdom
133,
J Nash
J Nash
133Imperial College, London, United Kingdom
133,
A Nikitenko
A Nikitenko
133Imperial College, London, United Kingdom
133,
J Pela
J Pela
133Imperial College, London, United Kingdom
133,
M Pesaresi
M Pesaresi
133Imperial College, London, United Kingdom
133,
K Petridis
K Petridis
133Imperial College, London, United Kingdom
133,
M Pioppi
M Pioppi
133Imperial College, London, United Kingdom
133,
D M Raymond
D M Raymond
133Imperial College, London, United Kingdom
133,
S Rogerson
S Rogerson
133Imperial College, London, United Kingdom
133,
A Rose
A Rose
133Imperial College, London, United Kingdom
133,
C Seez
C Seez
133Imperial College, London, United Kingdom
133,
P Sharp
P Sharp
133Imperial College, London, United Kingdom
133,
A Sparrow
A Sparrow
133Imperial College, London, United Kingdom
133,
A Tapper
A Tapper
133Imperial College, London, United Kingdom
133,
M Vazquez Acosta
M Vazquez Acosta
133Imperial College, London, United Kingdom
133,
T Virdee
T Virdee
133Imperial College, London, United Kingdom
133,
S Wakefield
S Wakefield
133Imperial College, London, United Kingdom
133,
N Wardle
N Wardle
133Imperial College, London, United Kingdom
133,
T Whyntie
T Whyntie
133Imperial College, London, United Kingdom
133,
M Chadwick
M Chadwick
134Brunel University, Uxbridge, United Kingdom
134,
J E Cole
J E Cole
134Brunel University, Uxbridge, United Kingdom
134,
P R Hobson
P R Hobson
134Brunel University, Uxbridge, United Kingdom
134,
A Khan
A Khan
134Brunel University, Uxbridge, United Kingdom
134,
P Kyberd
P Kyberd
134Brunel University, Uxbridge, United Kingdom
134,
D Leggat
D Leggat
134Brunel University, Uxbridge, United Kingdom
134,
D Leslie
D Leslie
134Brunel University, Uxbridge, United Kingdom
134,
W Martin
W Martin
134Brunel University, Uxbridge, United Kingdom
134,
I D Reid
I D Reid
134Brunel University, Uxbridge, United Kingdom
134,
P Symonds
P Symonds
134Brunel University, Uxbridge, United Kingdom
134,
L Teodorescu
L Teodorescu
134Brunel University, Uxbridge, United Kingdom
134,
M Turner
M Turner
134Brunel University, Uxbridge, United Kingdom
134,
J Dittmann
J Dittmann
135Baylor University, Waco, USA
135,
K Hatakeyama
K Hatakeyama
135Baylor University, Waco, USA
135,
A Kasmi
A Kasmi
135Baylor University, Waco, USA
135,
H Liu
H Liu
135Baylor University, Waco, USA
135,
T Scarborough
T Scarborough
135Baylor University, Waco, USA
135,
O Charaf
O Charaf
136The University of Alabama, Tuscaloosa, USA
136,
S I Cooper
S I Cooper
136The University of Alabama, Tuscaloosa, USA
136,
C Henderson
C Henderson
136The University of Alabama, Tuscaloosa, USA
136,
P Rumerio
P Rumerio
136The University of Alabama, Tuscaloosa, USA
136,
A Avetisyan
A Avetisyan
137Boston University, Boston, USA
137,
T Bose
T Bose
137Boston University, Boston, USA
137,
C Fantasia
C Fantasia
137Boston University, Boston, USA
137,
A Heister
A Heister
137Boston University, Boston, USA
137,
P Lawson
P Lawson
137Boston University, Boston, USA
137,
D Lazic
D Lazic
137Boston University, Boston, USA
137,
J Rohlf
J Rohlf
137Boston University, Boston, USA
137,
D Sperka
D Sperka
137Boston University, Boston, USA
137,
J St John
J St John
137Boston University, Boston, USA
137,
L Sulak
L Sulak
137Boston University, Boston, USA
137,
J Alimena
J Alimena
138Brown University, Providence, USA
138,
S Bhattacharya
S Bhattacharya
138Brown University, Providence, USA
138,
G Christopher
G Christopher
138Brown University, Providence, USA
138,
D Cutts
D Cutts
138Brown University, Providence, USA
138,
Z Demiragli
Z Demiragli
138Brown University, Providence, USA
138,
A Ferapontov
A Ferapontov
138Brown University, Providence, USA
138,
A Garabedian
A Garabedian
138Brown University, Providence, USA
138,
U Heintz
U Heintz
138Brown University, Providence, USA
138,
G Kukartsev
G Kukartsev
138Brown University, Providence, USA
138,
E Laird
E Laird
138Brown University, Providence, USA
138,
G Landsberg
G Landsberg
138Brown University, Providence, USA
138,
M Luk
M Luk
138Brown University, Providence, USA
138,
M Narain
M Narain
138Brown University, Providence, USA
138,
M Segala
M Segala
138Brown University, Providence, USA
138,
T Sinthuprasith
T Sinthuprasith
138Brown University, Providence, USA
138,
T Speer
T Speer
138Brown University, Providence, USA
138,
R Breedon
R Breedon
139University of California, Davis, Davis, USA
139,
G Breto
G Breto
139University of California, Davis, Davis, USA
139,
M Calderon De La Barca Sanchez
M Calderon De La Barca Sanchez
139University of California, Davis, Davis, USA
139,
S Chauhan
S Chauhan
139University of California, Davis, Davis, USA
139,
M Chertok
M Chertok
139University of California, Davis, Davis, USA
139,
J Conway
J Conway
139University of California, Davis, Davis, USA
139,
R Conway
R Conway
139University of California, Davis, Davis, USA
139,
P T Cox
P T Cox
139University of California, Davis, Davis, USA
139,
R Erbacher
R Erbacher
139University of California, Davis, Davis, USA
139,
M Gardner
M Gardner
139University of California, Davis, Davis, USA
139,
R Houtz
R Houtz
139University of California, Davis, Davis, USA
139,
W Ko
W Ko
139University of California, Davis, Davis, USA
139,
A Kopecky
A Kopecky
139University of California, Davis, Davis, USA
139,
R Lander
R Lander
139University of California, Davis, Davis, USA
139,
O Mall
O Mall
139University of California, Davis, Davis, USA
139,
T Miceli
T Miceli
139University of California, Davis, Davis, USA
139,
R Nelson
R Nelson
139University of California, Davis, Davis, USA
139,
D Pellett
D Pellett
139University of California, Davis, Davis, USA
139,
F Ricci-Tam
F Ricci-Tam
139University of California, Davis, Davis, USA
139,
B Rutherford
B Rutherford
139University of California, Davis, Davis, USA
139,
M Searle
M Searle
139University of California, Davis, Davis, USA
139,
J Smith
J Smith
139University of California, Davis, Davis, USA
139,
M Squires
M Squires
139University of California, Davis, Davis, USA
139,
M Tripathi
M Tripathi
139University of California, Davis, Davis, USA
139,
R Yohay
R Yohay
139University of California, Davis, Davis, USA
139,
V Andreev
V Andreev
140University of California, Los Angeles, USA
140,
D Cline
D Cline
140University of California, Los Angeles, USA
140,
R Cousins
R Cousins
140University of California, Los Angeles, USA
140,
S Erhan
S Erhan
140University of California, Los Angeles, USA
140,
P Everaerts
P Everaerts
140University of California, Los Angeles, USA
140,
C Farrell
C Farrell
140University of California, Los Angeles, USA
140,
M Felcini
M Felcini
140University of California, Los Angeles, USA
140,
J Hauser
J Hauser
140University of California, Los Angeles, USA
140,
M Ignatenko
M Ignatenko
140University of California, Los Angeles, USA
140,
C Jarvis
C Jarvis
140University of California, Los Angeles, USA
140,
G Rakness
G Rakness
140University of California, Los Angeles, USA
140,
P Schlein
P Schlein
140University of California, Los Angeles, USA
140,
P Traczyk
P Traczyk
140University of California, Los Angeles, USA
140,
V Valuev
V Valuev
140University of California, Los Angeles, USA
140,
M Weber
M Weber
140University of California, Los Angeles, USA
140,
J Babb
J Babb
141University of California, Riverside, Riverside, USA
141,
R Clare
R Clare
141University of California, Riverside, Riverside, USA
141,
M E Dinardo
M E Dinardo
141University of California, Riverside, Riverside, USA
141,
J Ellison
J Ellison
141University of California, Riverside, Riverside, USA
141,
J W Gary
J W Gary
141University of California, Riverside, Riverside, USA
141,
F Giordano
F Giordano
141University of California, Riverside, Riverside, USA
141,
G Hanson
G Hanson
141University of California, Riverside, Riverside, USA
141,
H Liu
H Liu
141University of California, Riverside, Riverside, USA
141,
O R Long
O R Long
141University of California, Riverside, Riverside, USA
141,
A Luthra
A Luthra
141University of California, Riverside, Riverside, USA
141,
H Nguyen
H Nguyen
141University of California, Riverside, Riverside, USA
141,
S Paramesvaran
S Paramesvaran
141University of California, Riverside, Riverside, USA
141,
J Sturdy
J Sturdy
141University of California, Riverside, Riverside, USA
141,
S Sumowidagdo
S Sumowidagdo
141University of California, Riverside, Riverside, USA
141,
R Wilken
R Wilken
141University of California, Riverside, Riverside, USA
141,
S Wimpenny
S Wimpenny
141University of California, Riverside, Riverside, USA
141,
W Andrews
W Andrews
142University of California, San Diego, La Jolla, USA
142,
J G Branson
J G Branson
142University of California, San Diego, La Jolla, USA
142,
G B Cerati
G B Cerati
142University of California, San Diego, La Jolla, USA
142,
S Cittolin
S Cittolin
142University of California, San Diego, La Jolla, USA
142,
D Evans
D Evans
142University of California, San Diego, La Jolla, USA
142,
A Holzner
A Holzner
142University of California, San Diego, La Jolla, USA
142,
R Kelley
R Kelley
142University of California, San Diego, La Jolla, USA
142,
M Lebourgeois
M Lebourgeois
142University of California, San Diego, La Jolla, USA
142,
J Letts
J Letts
142University of California, San Diego, La Jolla, USA
142,
I Macneill
I Macneill
142University of California, San Diego, La Jolla, USA
142,
B Mangano
B Mangano
142University of California, San Diego, La Jolla, USA
142,
S Padhi
S Padhi
142University of California, San Diego, La Jolla, USA
142,
C Palmer
C Palmer
142University of California, San Diego, La Jolla, USA
142,
G Petrucciani
G Petrucciani
142University of California, San Diego, La Jolla, USA
142,
M Pieri
M Pieri
142University of California, San Diego, La Jolla, USA
142,
M Sani
M Sani
142University of California, San Diego, La Jolla, USA
142,
V Sharma
V Sharma
142University of California, San Diego, La Jolla, USA
142,
S Simon
S Simon
142University of California, San Diego, La Jolla, USA
142,
E Sudano
E Sudano
142University of California, San Diego, La Jolla, USA
142,
M Tadel
M Tadel
142University of California, San Diego, La Jolla, USA
142,
Y Tu
Y Tu
142University of California, San Diego, La Jolla, USA
142,
A Vartak
A Vartak
142University of California, San Diego, La Jolla, USA
142,
S Wasserbaech
S Wasserbaech
142University of California, San Diego, La Jolla, USA
142,
F Würthwein
F Würthwein
142University of California, San Diego, La Jolla, USA
142,
A Yagil
A Yagil
142University of California, San Diego, La Jolla, USA
142,
J Yoo
J Yoo
142University of California, San Diego, La Jolla, USA
142,
D Barge
D Barge
143University of California, Santa Barbara, Santa Barbara, USA
143,
R Bellan
R Bellan
143University of California, Santa Barbara, Santa Barbara, USA
143,
C Campagnari
C Campagnari
143University of California, Santa Barbara, Santa Barbara, USA
143,
M D’Alfonso
M D’Alfonso
143University of California, Santa Barbara, Santa Barbara, USA
143,
T Danielson
T Danielson
143University of California, Santa Barbara, Santa Barbara, USA
143,
A Dishaw
A Dishaw
143University of California, Santa Barbara, Santa Barbara, USA
143,
K Flowers
K Flowers
143University of California, Santa Barbara, Santa Barbara, USA
143,
P Geffert
P Geffert
143University of California, Santa Barbara, Santa Barbara, USA
143,
C George
C George
143University of California, Santa Barbara, Santa Barbara, USA
143,
F Golf
F Golf
143University of California, Santa Barbara, Santa Barbara, USA
143,
J Incandela
J Incandela
143University of California, Santa Barbara, Santa Barbara, USA
143,
C Justus
C Justus
143University of California, Santa Barbara, Santa Barbara, USA
143,
P Kalavase
P Kalavase
143University of California, Santa Barbara, Santa Barbara, USA
143,
D Kovalskyi
D Kovalskyi
143University of California, Santa Barbara, Santa Barbara, USA
143,
V Krutelyov
V Krutelyov
143University of California, Santa Barbara, Santa Barbara, USA
143,
S Lowette
S Lowette
143University of California, Santa Barbara, Santa Barbara, USA
143,
R Magaña Villalba
R Magaña Villalba
143University of California, Santa Barbara, Santa Barbara, USA
143,
N Mccoll
N Mccoll
143University of California, Santa Barbara, Santa Barbara, USA
143,
V Pavlunin
V Pavlunin
143University of California, Santa Barbara, Santa Barbara, USA
143,
J Ribnik
J Ribnik
143University of California, Santa Barbara, Santa Barbara, USA
143,
J Richman
J Richman
143University of California, Santa Barbara, Santa Barbara, USA
143,
R Rossin
R Rossin
143University of California, Santa Barbara, Santa Barbara, USA
143,
D Stuart
D Stuart
143University of California, Santa Barbara, Santa Barbara, USA
143,
W To
W To
143University of California, Santa Barbara, Santa Barbara, USA
143,
C West
C West
143University of California, Santa Barbara, Santa Barbara, USA
143,
A Apresyan
A Apresyan
144California Institute of Technology, Pasadena, USA
144,
A Bornheim
A Bornheim
144California Institute of Technology, Pasadena, USA
144,
J Bunn
J Bunn
144California Institute of Technology, Pasadena, USA
144,
Y Chen
Y Chen
144California Institute of Technology, Pasadena, USA
144,
E Di Marco
E Di Marco
144California Institute of Technology, Pasadena, USA
144,
J Duarte
J Duarte
144California Institute of Technology, Pasadena, USA
144,
D Kcira
D Kcira
144California Institute of Technology, Pasadena, USA
144,
Y Ma
Y Ma
144California Institute of Technology, Pasadena, USA
144,
A Mott
A Mott
144California Institute of Technology, Pasadena, USA
144,
H B Newman
H B Newman
144California Institute of Technology, Pasadena, USA
144,
C Rogan
C Rogan
144California Institute of Technology, Pasadena, USA
144,
M Spiropulu
M Spiropulu
144California Institute of Technology, Pasadena, USA
144,
V Timciuc
V Timciuc
144California Institute of Technology, Pasadena, USA
144,
J Veverka
J Veverka
144California Institute of Technology, Pasadena, USA
144,
R Wilkinson
R Wilkinson
144California Institute of Technology, Pasadena, USA
144,
S Xie
S Xie
144California Institute of Technology, Pasadena, USA
144,
Y Yang
Y Yang
144California Institute of Technology, Pasadena, USA
144,
R Y Zhu
R Y Zhu
144California Institute of Technology, Pasadena, USA
144,
V Azzolini
V Azzolini
145Carnegie Mellon University, Pittsburgh, USA
145,
A Calamba
A Calamba
145Carnegie Mellon University, Pittsburgh, USA
145,
R Carroll
R Carroll
145Carnegie Mellon University, Pittsburgh, USA
145,
T Ferguson
T Ferguson
145Carnegie Mellon University, Pittsburgh, USA
145,
Y Iiyama
Y Iiyama
145Carnegie Mellon University, Pittsburgh, USA
145,
D W Jang
D W Jang
145Carnegie Mellon University, Pittsburgh, USA
145,
Y F Liu
Y F Liu
145Carnegie Mellon University, Pittsburgh, USA
145,
M Paulini
M Paulini
145Carnegie Mellon University, Pittsburgh, USA
145,
J Russ
J Russ
145Carnegie Mellon University, Pittsburgh, USA
145,
H Vogel
H Vogel
145Carnegie Mellon University, Pittsburgh, USA
145,
I Vorobiev
I Vorobiev
145Carnegie Mellon University, Pittsburgh, USA
145,
J P Cumalat
J P Cumalat
146University of Colorado at Boulder, Boulder, USA
146,
B R Drell
B R Drell
146University of Colorado at Boulder, Boulder, USA
146,
W T Ford
W T Ford
146University of Colorado at Boulder, Boulder, USA
146,
A Gaz
A Gaz
146University of Colorado at Boulder, Boulder, USA
146,
E Luiggi Lopez
E Luiggi Lopez
146University of Colorado at Boulder, Boulder, USA
146,
U Nauenberg
U Nauenberg
146University of Colorado at Boulder, Boulder, USA
146,
J G Smith
J G Smith
146University of Colorado at Boulder, Boulder, USA
146,
K Stenson
K Stenson
146University of Colorado at Boulder, Boulder, USA
146,
K A Ulmer
K A Ulmer
146University of Colorado at Boulder, Boulder, USA
146,
S R Wagner
S R Wagner
146University of Colorado at Boulder, Boulder, USA
146,
J Alexander
J Alexander
147Cornell University, Ithaca, USA
147,
A Chatterjee
A Chatterjee
147Cornell University, Ithaca, USA
147,
N Eggert
N Eggert
147Cornell University, Ithaca, USA
147,
L K Gibbons
L K Gibbons
147Cornell University, Ithaca, USA
147,
W Hopkins
W Hopkins
147Cornell University, Ithaca, USA
147,
A Khukhunaishvili
A Khukhunaishvili
147Cornell University, Ithaca, USA
147,
B Kreis
B Kreis
147Cornell University, Ithaca, USA
147,
N Mirman
N Mirman
147Cornell University, Ithaca, USA
147,
B Nachman
B Nachman
147Cornell University, Ithaca, USA
147,
G Nicolas Kaufman
G Nicolas Kaufman
147Cornell University, Ithaca, USA
147,
J R Patterson
J R Patterson
147Cornell University, Ithaca, USA
147,
A Ryd
A Ryd
147Cornell University, Ithaca, USA
147,
E Salvati
E Salvati
147Cornell University, Ithaca, USA
147,
W Sun
W Sun
147Cornell University, Ithaca, USA
147,
W D Teo
W D Teo
147Cornell University, Ithaca, USA
147,
J Thom
J Thom
147Cornell University, Ithaca, USA
147,
J Thompson
J Thompson
147Cornell University, Ithaca, USA
147,
J Tucker
J Tucker
147Cornell University, Ithaca, USA
147,
Y Weng
Y Weng
147Cornell University, Ithaca, USA
147,
L Winstrom
L Winstrom
147Cornell University, Ithaca, USA
147,
P Wittich
P Wittich
147Cornell University, Ithaca, USA
147,
D Winn
D Winn
148Fairfield University, Fairfield, USA
148,
S Abdullin
S Abdullin
149Fermi National Accelerator Laboratory, Batavia, USA
149,
M Albrow
M Albrow
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J Anderson
J Anderson
149Fermi National Accelerator Laboratory, Batavia, USA
149,
G Apollinari
G Apollinari
149Fermi National Accelerator Laboratory, Batavia, USA
149,
L A T Bauerdick
L A T Bauerdick
149Fermi National Accelerator Laboratory, Batavia, USA
149,
A Beretvas
A Beretvas
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J Berryhill
J Berryhill
149Fermi National Accelerator Laboratory, Batavia, USA
149,
P C Bhat
P C Bhat
149Fermi National Accelerator Laboratory, Batavia, USA
149,
K Burkett
K Burkett
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J N Butler
J N Butler
149Fermi National Accelerator Laboratory, Batavia, USA
149,
V Chetluru
V Chetluru
149Fermi National Accelerator Laboratory, Batavia, USA
149,
H W K Cheung
H W K Cheung
149Fermi National Accelerator Laboratory, Batavia, USA
149,
F Chlebana
F Chlebana
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Cihangir
S Cihangir
149Fermi National Accelerator Laboratory, Batavia, USA
149,
V D Elvira
V D Elvira
149Fermi National Accelerator Laboratory, Batavia, USA
149,
I Fisk
I Fisk
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J Freeman
J Freeman
149Fermi National Accelerator Laboratory, Batavia, USA
149,
Y Gao
Y Gao
149Fermi National Accelerator Laboratory, Batavia, USA
149,
E Gottschalk
E Gottschalk
149Fermi National Accelerator Laboratory, Batavia, USA
149,
L Gray
L Gray
149Fermi National Accelerator Laboratory, Batavia, USA
149,
D Green
D Green
149Fermi National Accelerator Laboratory, Batavia, USA
149,
O Gutsche
O Gutsche
149Fermi National Accelerator Laboratory, Batavia, USA
149,
R M Harris
R M Harris
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J Hirschauer
J Hirschauer
149Fermi National Accelerator Laboratory, Batavia, USA
149,
B Hooberman
B Hooberman
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Jindariani
S Jindariani
149Fermi National Accelerator Laboratory, Batavia, USA
149,
M Johnson
M Johnson
149Fermi National Accelerator Laboratory, Batavia, USA
149,
U Joshi
U Joshi
149Fermi National Accelerator Laboratory, Batavia, USA
149,
B Klima
B Klima
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Kunori
S Kunori
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Kwan
S Kwan
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J Linacre
J Linacre
149Fermi National Accelerator Laboratory, Batavia, USA
149,
D Lincoln
D Lincoln
149Fermi National Accelerator Laboratory, Batavia, USA
149,
R Lipton
R Lipton
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J Lykken
J Lykken
149Fermi National Accelerator Laboratory, Batavia, USA
149,
K Maeshima
K Maeshima
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J M Marraffino
J M Marraffino
149Fermi National Accelerator Laboratory, Batavia, USA
149,
V I Martinez Outschoorn
V I Martinez Outschoorn
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Maruyama
S Maruyama
149Fermi National Accelerator Laboratory, Batavia, USA
149,
D Mason
D Mason
149Fermi National Accelerator Laboratory, Batavia, USA
149,
P McBride
P McBride
149Fermi National Accelerator Laboratory, Batavia, USA
149,
K Mishra
K Mishra
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Mrenna
S Mrenna
149Fermi National Accelerator Laboratory, Batavia, USA
149,
Y Musienko
Y Musienko
149Fermi National Accelerator Laboratory, Batavia, USA
149,
C Newman-Holmes
C Newman-Holmes
149Fermi National Accelerator Laboratory, Batavia, USA
149,
V O’Dell
V O’Dell
149Fermi National Accelerator Laboratory, Batavia, USA
149,
O Prokofyev
O Prokofyev
149Fermi National Accelerator Laboratory, Batavia, USA
149,
E Sexton-Kennedy
E Sexton-Kennedy
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Sharma
S Sharma
149Fermi National Accelerator Laboratory, Batavia, USA
149,
W J Spalding
W J Spalding
149Fermi National Accelerator Laboratory, Batavia, USA
149,
L Spiegel
L Spiegel
149Fermi National Accelerator Laboratory, Batavia, USA
149,
L Taylor
L Taylor
149Fermi National Accelerator Laboratory, Batavia, USA
149,
S Tkaczyk
S Tkaczyk
149Fermi National Accelerator Laboratory, Batavia, USA
149,
N V Tran
N V Tran
149Fermi National Accelerator Laboratory, Batavia, USA
149,
L Uplegger
L Uplegger
149Fermi National Accelerator Laboratory, Batavia, USA
149,
E W Vaandering
E W Vaandering
149Fermi National Accelerator Laboratory, Batavia, USA
149,
R Vidal
R Vidal
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J Whitmore
J Whitmore
149Fermi National Accelerator Laboratory, Batavia, USA
149,
W Wu
W Wu
149Fermi National Accelerator Laboratory, Batavia, USA
149,
F Yang
F Yang
149Fermi National Accelerator Laboratory, Batavia, USA
149,
J C Yun
J C Yun
149Fermi National Accelerator Laboratory, Batavia, USA
149,
D Acosta
D Acosta
150University of Florida, Gainesville, USA
150,
P Avery
P Avery
150University of Florida, Gainesville, USA
150,
D Bourilkov
D Bourilkov
150University of Florida, Gainesville, USA
150,
M Chen
M Chen
150University of Florida, Gainesville, USA
150,
T Cheng
T Cheng
150University of Florida, Gainesville, USA
150,
S Das
S Das
150University of Florida, Gainesville, USA
150,
M De Gruttola
M De Gruttola
150University of Florida, Gainesville, USA
150,
G P Di Giovanni
G P Di Giovanni
150University of Florida, Gainesville, USA
150,
D Dobur
D Dobur
150University of Florida, Gainesville, USA
150,
A Drozdetskiy
A Drozdetskiy
150University of Florida, Gainesville, USA
150,
R D Field
R D Field
150University of Florida, Gainesville, USA
150,
M Fisher
M Fisher
150University of Florida, Gainesville, USA
150,
Y Fu
Y Fu
150University of Florida, Gainesville, USA
150,
I K Furic
I K Furic
150University of Florida, Gainesville, USA
150,
J Hugon
J Hugon
150University of Florida, Gainesville, USA
150,
B Kim
B Kim
150University of Florida, Gainesville, USA
150,
J Konigsberg
J Konigsberg
150University of Florida, Gainesville, USA
150,
A Korytov
A Korytov
150University of Florida, Gainesville, USA
150,
A Kropivnitskaya
A Kropivnitskaya
150University of Florida, Gainesville, USA
150,
T Kypreos
T Kypreos
150University of Florida, Gainesville, USA
150,
J F Low
J F Low
150University of Florida, Gainesville, USA
150,
K Matchev
K Matchev
150University of Florida, Gainesville, USA
150,
P Milenovic
P Milenovic
150University of Florida, Gainesville, USA
150,
G Mitselmakher
G Mitselmakher
150University of Florida, Gainesville, USA
150,
L Muniz
L Muniz
150University of Florida, Gainesville, USA
150,
R Remington
R Remington
150University of Florida, Gainesville, USA
150,
A Rinkevicius
A Rinkevicius
150University of Florida, Gainesville, USA
150,
N Skhirtladze
N Skhirtladze
150University of Florida, Gainesville, USA
150,
M Snowball
M Snowball
150University of Florida, Gainesville, USA
150,
J Yelton
J Yelton
150University of Florida, Gainesville, USA
150,
M Zakaria
M Zakaria
150University of Florida, Gainesville, USA
150,
V Gaultney
V Gaultney
151Florida International University, Miami, USA
151,
S Hewamanage
S Hewamanage
151Florida International University, Miami, USA
151,
L M Lebolo
L M Lebolo
151Florida International University, Miami, USA
151,
S Linn
S Linn
151Florida International University, Miami, USA
151,
P Markowitz
P Markowitz
151Florida International University, Miami, USA
151,
G Martinez
G Martinez
151Florida International University, Miami, USA
151,
J L Rodriguez
J L Rodriguez
151Florida International University, Miami, USA
151,
T Adams
T Adams
152Florida State University, Tallahassee, USA
152,
A Askew
A Askew
152Florida State University, Tallahassee, USA
152,
J Bochenek
J Bochenek
152Florida State University, Tallahassee, USA
152,
J Chen
J Chen
152Florida State University, Tallahassee, USA
152,
B Diamond
B Diamond
152Florida State University, Tallahassee, USA
152,
S V Gleyzer
S V Gleyzer
152Florida State University, Tallahassee, USA
152,
J Haas
J Haas
152Florida State University, Tallahassee, USA
152,
S Hagopian
S Hagopian
152Florida State University, Tallahassee, USA
152,
V Hagopian
V Hagopian
152Florida State University, Tallahassee, USA
152,
K F Johnson
K F Johnson
152Florida State University, Tallahassee, USA
152,
H Prosper
H Prosper
152Florida State University, Tallahassee, USA
152,
V Veeraraghavan
V Veeraraghavan
152Florida State University, Tallahassee, USA
152,
M Weinberg
M Weinberg
152Florida State University, Tallahassee, USA
152,
M M Baarmand
M M Baarmand
153Florida Institute of Technology, Melbourne, USA
153,
B Dorney
B Dorney
153Florida Institute of Technology, Melbourne, USA
153,
M Hohlmann
M Hohlmann
153Florida Institute of Technology, Melbourne, USA
153,
H Kalakhety
H Kalakhety
153Florida Institute of Technology, Melbourne, USA
153,
F Yumiceva
F Yumiceva
153Florida Institute of Technology, Melbourne, USA
153,
M R Adams
M R Adams
154University of Illinois at Chicago (UIC), Chicago, USA
154,
L Apanasevich
L Apanasevich
154University of Illinois at Chicago (UIC), Chicago, USA
154,
V E Bazterra
V E Bazterra
154University of Illinois at Chicago (UIC), Chicago, USA
154,
R R Betts
R R Betts
154University of Illinois at Chicago (UIC), Chicago, USA
154,
I Bucinskaite
I Bucinskaite
154University of Illinois at Chicago (UIC), Chicago, USA
154,
J Callner
J Callner
154University of Illinois at Chicago (UIC), Chicago, USA
154,
R Cavanaugh
R Cavanaugh
154University of Illinois at Chicago (UIC), Chicago, USA
154,
O Evdokimov
O Evdokimov
154University of Illinois at Chicago (UIC), Chicago, USA
154,
L Gauthier
L Gauthier
154University of Illinois at Chicago (UIC), Chicago, USA
154,
C E Gerber
C E Gerber
154University of Illinois at Chicago (UIC), Chicago, USA
154,
D J Hofman
D J Hofman
154University of Illinois at Chicago (UIC), Chicago, USA
154,
S Khalatyan
S Khalatyan
154University of Illinois at Chicago (UIC), Chicago, USA
154,
P Kurt
P Kurt
154University of Illinois at Chicago (UIC), Chicago, USA
154,
F Lacroix
F Lacroix
154University of Illinois at Chicago (UIC), Chicago, USA
154,
C O’Brien
C O’Brien
154University of Illinois at Chicago (UIC), Chicago, USA
154,
C Silkworth
C Silkworth
154University of Illinois at Chicago (UIC), Chicago, USA
154,
D Strom
D Strom
154University of Illinois at Chicago (UIC), Chicago, USA
154,
P Turner
P Turner
154University of Illinois at Chicago (UIC), Chicago, USA
154,
N Varelas
N Varelas
154University of Illinois at Chicago (UIC), Chicago, USA
154,
U Akgun
U Akgun
155The University of Iowa, Iowa City, USA
155,
E A Albayrak
E A Albayrak
155The University of Iowa, Iowa City, USA
155,
B Bilki
B Bilki
155The University of Iowa, Iowa City, USA
155,
W Clarida
W Clarida
155The University of Iowa, Iowa City, USA
155,
K Dilsiz
K Dilsiz
155The University of Iowa, Iowa City, USA
155,
F Duru
F Duru
155The University of Iowa, Iowa City, USA
155,
S Griffiths
S Griffiths
155The University of Iowa, Iowa City, USA
155,
J-P Merlo
J-P Merlo
155The University of Iowa, Iowa City, USA
155,
H Mermerkaya
H Mermerkaya
155The University of Iowa, Iowa City, USA
155,
A Mestvirishvili
A Mestvirishvili
155The University of Iowa, Iowa City, USA
155,
A Moeller
A Moeller
155The University of Iowa, Iowa City, USA
155,
J Nachtman
J Nachtman
155The University of Iowa, Iowa City, USA
155,
C R Newsom
C R Newsom
155The University of Iowa, Iowa City, USA
155,
H Ogul
H Ogul
155The University of Iowa, Iowa City, USA
155,
Y Onel
Y Onel
155The University of Iowa, Iowa City, USA
155,
F Ozok
F Ozok
155The University of Iowa, Iowa City, USA
155,
S Sen
S Sen
155The University of Iowa, Iowa City, USA
155,
P Tan
P Tan
155The University of Iowa, Iowa City, USA
155,
E Tiras
E Tiras
155The University of Iowa, Iowa City, USA
155,
J Wetzel
J Wetzel
155The University of Iowa, Iowa City, USA
155,
T Yetkin
T Yetkin
155The University of Iowa, Iowa City, USA
155,
K Yi
K Yi
155The University of Iowa, Iowa City, USA
155,
B A Barnett
B A Barnett
156Johns Hopkins University, Baltimore, USA
156,
B Blumenfeld
B Blumenfeld
156Johns Hopkins University, Baltimore, USA
156,
S Bolognesi
S Bolognesi
156Johns Hopkins University, Baltimore, USA
156,
D Fehling
D Fehling
156Johns Hopkins University, Baltimore, USA
156,
G Giurgiu
G Giurgiu
156Johns Hopkins University, Baltimore, USA
156,
A V Gritsan
A V Gritsan
156Johns Hopkins University, Baltimore, USA
156,
G Hu
G Hu
156Johns Hopkins University, Baltimore, USA
156,
P Maksimovic
P Maksimovic
156Johns Hopkins University, Baltimore, USA
156,
M Swartz
M Swartz
156Johns Hopkins University, Baltimore, USA
156,
A Whitbeck
A Whitbeck
156Johns Hopkins University, Baltimore, USA
156,
P Baringer
P Baringer
157The University of Kansas, Lawrence, USA
157,
A Bean
A Bean
157The University of Kansas, Lawrence, USA
157,
G Benelli
G Benelli
157The University of Kansas, Lawrence, USA
157,
R P Kenny III
R P Kenny III
157The University of Kansas, Lawrence, USA
157,
M Murray
M Murray
157The University of Kansas, Lawrence, USA
157,
D Noonan
D Noonan
157The University of Kansas, Lawrence, USA
157,
S Sanders
S Sanders
157The University of Kansas, Lawrence, USA
157,
R Stringer
R Stringer
157The University of Kansas, Lawrence, USA
157,
J S Wood
J S Wood
157The University of Kansas, Lawrence, USA
157,
A F Barfuss
A F Barfuss
158Kansas State University, Manhattan, USA
158,
I Chakaberia
I Chakaberia
158Kansas State University, Manhattan, USA
158,
A Ivanov
A Ivanov
158Kansas State University, Manhattan, USA
158,
S Khalil
S Khalil
158Kansas State University, Manhattan, USA
158,
M Makouski
M Makouski
158Kansas State University, Manhattan, USA
158,
Y Maravin
Y Maravin
158Kansas State University, Manhattan, USA
158,
S Shrestha
S Shrestha
158Kansas State University, Manhattan, USA
158,
I Svintradze
I Svintradze
158Kansas State University, Manhattan, USA
158,
J Gronberg
J Gronberg
159Lawrence Livermore National Laboratory, Livermore, USA
159,
D Lange
D Lange
159Lawrence Livermore National Laboratory, Livermore, USA
159,
F Rebassoo
F Rebassoo
159Lawrence Livermore National Laboratory, Livermore, USA
159,
D Wright
D Wright
159Lawrence Livermore National Laboratory, Livermore, USA
159,
A Baden
A Baden
160University of Maryland, College Park, USA
160,
B Calvert
B Calvert
160University of Maryland, College Park, USA
160,
S C Eno
S C Eno
160University of Maryland, College Park, USA
160,
J A Gomez
J A Gomez
160University of Maryland, College Park, USA
160,
N J Hadley
N J Hadley
160University of Maryland, College Park, USA
160,
R G Kellogg
R G Kellogg
160University of Maryland, College Park, USA
160,
T Kolberg
T Kolberg
160University of Maryland, College Park, USA
160,
Y Lu
Y Lu
160University of Maryland, College Park, USA
160,
M Marionneau
M Marionneau
160University of Maryland, College Park, USA
160,
A C Mignerey
A C Mignerey
160University of Maryland, College Park, USA
160,
K Pedro
K Pedro
160University of Maryland, College Park, USA
160,
A Peterman
A Peterman
160University of Maryland, College Park, USA
160,
A Skuja
A Skuja
160University of Maryland, College Park, USA
160,
J Temple
J Temple
160University of Maryland, College Park, USA
160,
M B Tonjes
M B Tonjes
160University of Maryland, College Park, USA
160,
S C Tonwar
S C Tonwar
160University of Maryland, College Park, USA
160,
A Apyan
A Apyan
161Massachusetts Institute of Technology, Cambridge, USA
161,
G Bauer
G Bauer
161Massachusetts Institute of Technology, Cambridge, USA
161,
W Busza
W Busza
161Massachusetts Institute of Technology, Cambridge, USA
161,
E Butz
E Butz
161Massachusetts Institute of Technology, Cambridge, USA
161,
I A Cali
I A Cali
161Massachusetts Institute of Technology, Cambridge, USA
161,
M Chan
M Chan
161Massachusetts Institute of Technology, Cambridge, USA
161,
V Dutta
V Dutta
161Massachusetts Institute of Technology, Cambridge, USA
161,
G Gomez Ceballos
G Gomez Ceballos
161Massachusetts Institute of Technology, Cambridge, USA
161,
M Goncharov
M Goncharov
161Massachusetts Institute of Technology, Cambridge, USA
161,
Y Kim
Y Kim
161Massachusetts Institute of Technology, Cambridge, USA
161,
M Klute
M Klute
161Massachusetts Institute of Technology, Cambridge, USA
161,
Y S Lai
Y S Lai
161Massachusetts Institute of Technology, Cambridge, USA
161,
A Levin
A Levin
161Massachusetts Institute of Technology, Cambridge, USA
161,
P D Luckey
P D Luckey
161Massachusetts Institute of Technology, Cambridge, USA
161,
T Ma
T Ma
161Massachusetts Institute of Technology, Cambridge, USA
161,
S Nahn
S Nahn
161Massachusetts Institute of Technology, Cambridge, USA
161,
C Paus
C Paus
161Massachusetts Institute of Technology, Cambridge, USA
161,
D Ralph
D Ralph
161Massachusetts Institute of Technology, Cambridge, USA
161,
C Roland
C Roland
161Massachusetts Institute of Technology, Cambridge, USA
161,
G Roland
G Roland
161Massachusetts Institute of Technology, Cambridge, USA
161,
G S F Stephans
G S F Stephans
161Massachusetts Institute of Technology, Cambridge, USA
161,
F Stöckli
F Stöckli
161Massachusetts Institute of Technology, Cambridge, USA
161,
K Sumorok
K Sumorok
161Massachusetts Institute of Technology, Cambridge, USA
161,
K Sung
K Sung
161Massachusetts Institute of Technology, Cambridge, USA
161,
D Velicanu
D Velicanu
161Massachusetts Institute of Technology, Cambridge, USA
161,
R Wolf
R Wolf
161Massachusetts Institute of Technology, Cambridge, USA
161,
B Wyslouch
B Wyslouch
161Massachusetts Institute of Technology, Cambridge, USA
161,
M Yang
M Yang
161Massachusetts Institute of Technology, Cambridge, USA
161,
Y Yilmaz
Y Yilmaz
161Massachusetts Institute of Technology, Cambridge, USA
161,
A S Yoon
A S Yoon
161Massachusetts Institute of Technology, Cambridge, USA
161,
M Zanetti
M Zanetti
161Massachusetts Institute of Technology, Cambridge, USA
161,
V Zhukova
V Zhukova
161Massachusetts Institute of Technology, Cambridge, USA
161,
B Dahmes
B Dahmes
162University of Minnesota, Minneapolis, USA
162,
A De Benedetti
A De Benedetti
162University of Minnesota, Minneapolis, USA
162,
G Franzoni
G Franzoni
162University of Minnesota, Minneapolis, USA
162,
A Gude
A Gude
162University of Minnesota, Minneapolis, USA
162,
J Haupt
J Haupt
162University of Minnesota, Minneapolis, USA
162,
S C Kao
S C Kao
162University of Minnesota, Minneapolis, USA
162,
K Klapoetke
K Klapoetke
162University of Minnesota, Minneapolis, USA
162,
Y Kubota
Y Kubota
162University of Minnesota, Minneapolis, USA
162,
J Mans
J Mans
162University of Minnesota, Minneapolis, USA
162,
N Pastika
N Pastika
162University of Minnesota, Minneapolis, USA
162,
R Rusack
R Rusack
162University of Minnesota, Minneapolis, USA
162,
M Sasseville
M Sasseville
162University of Minnesota, Minneapolis, USA
162,
A Singovsky
A Singovsky
162University of Minnesota, Minneapolis, USA
162,
N Tambe
N Tambe
162University of Minnesota, Minneapolis, USA
162,
J Turkewitz
J Turkewitz
162University of Minnesota, Minneapolis, USA
162,
L M Cremaldi
L M Cremaldi
163University of Mississippi, Oxford, USA
163,
R Kroeger
R Kroeger
163University of Mississippi, Oxford, USA
163,
L Perera
L Perera
163University of Mississippi, Oxford, USA
163,
R Rahmat
R Rahmat
163University of Mississippi, Oxford, USA
163,
D A Sanders
D A Sanders
163University of Mississippi, Oxford, USA
163,
D Summers
D Summers
163University of Mississippi, Oxford, USA
163,
E Avdeeva
E Avdeeva
164University of Nebraska-Lincoln, Lincoln, USA
164,
K Bloom
K Bloom
164University of Nebraska-Lincoln, Lincoln, USA
164,
S Bose
S Bose
164University of Nebraska-Lincoln, Lincoln, USA
164,
D R Claes
D R Claes
164University of Nebraska-Lincoln, Lincoln, USA
164,
A Dominguez
A Dominguez
164University of Nebraska-Lincoln, Lincoln, USA
164,
M Eads
M Eads
164University of Nebraska-Lincoln, Lincoln, USA
164,
R Gonzalez Suarez
R Gonzalez Suarez
164University of Nebraska-Lincoln, Lincoln, USA
164,
J Keller
J Keller
164University of Nebraska-Lincoln, Lincoln, USA
164,
I Kravchenko
I Kravchenko
164University of Nebraska-Lincoln, Lincoln, USA
164,
J Lazo-Flores
J Lazo-Flores
164University of Nebraska-Lincoln, Lincoln, USA
164,
S Malik
S Malik
164University of Nebraska-Lincoln, Lincoln, USA
164,
G R Snow
G R Snow
164University of Nebraska-Lincoln, Lincoln, USA
164,
J Dolen
J Dolen
165State University of New York at Buffalo, Buffalo, USA
165,
A Godshalk
A Godshalk
165State University of New York at Buffalo, Buffalo, USA
165,
I Iashvili
I Iashvili
165State University of New York at Buffalo, Buffalo, USA
165,
S Jain
S Jain
165State University of New York at Buffalo, Buffalo, USA
165,
A Kharchilava
A Kharchilava
165State University of New York at Buffalo, Buffalo, USA
165,
A Kumar
A Kumar
165State University of New York at Buffalo, Buffalo, USA
165,
S Rappoccio
S Rappoccio
165State University of New York at Buffalo, Buffalo, USA
165,
Z Wan
Z Wan
165State University of New York at Buffalo, Buffalo, USA
165,
G Alverson
G Alverson
166Northeastern University, Boston, USA
166,
E Barberis
E Barberis
166Northeastern University, Boston, USA
166,
D Baumgartel
D Baumgartel
166Northeastern University, Boston, USA
166,
M Chasco
M Chasco
166Northeastern University, Boston, USA
166,
J Haley
J Haley
166Northeastern University, Boston, USA
166,
D Nash
D Nash
166Northeastern University, Boston, USA
166,
T Orimoto
T Orimoto
166Northeastern University, Boston, USA
166,
D Trocino
D Trocino
166Northeastern University, Boston, USA
166,
D Wood
D Wood
166Northeastern University, Boston, USA
166,
J Zhang
J Zhang
166Northeastern University, Boston, USA
166,
A Anastassov
A Anastassov
167Northwestern University, Evanston, USA
167,
K A Hahn
K A Hahn
167Northwestern University, Evanston, USA
167,
A Kubik
A Kubik
167Northwestern University, Evanston, USA
167,
L Lusito
L Lusito
167Northwestern University, Evanston, USA
167,
N Mucia
N Mucia
167Northwestern University, Evanston, USA
167,
N Odell
N Odell
167Northwestern University, Evanston, USA
167,
B Pollack
B Pollack
167Northwestern University, Evanston, USA
167,
A Pozdnyakov
A Pozdnyakov
167Northwestern University, Evanston, USA
167,
M Schmitt
M Schmitt
167Northwestern University, Evanston, USA
167,
S Stoynev
S Stoynev
167Northwestern University, Evanston, USA
167,
M Velasco
M Velasco
167Northwestern University, Evanston, USA
167,
S Won
S Won
167Northwestern University, Evanston, USA
167,
D Berry
D Berry
168University of Notre Dame, Notre Dame, USA
168,
A Brinkerhoff
A Brinkerhoff
168University of Notre Dame, Notre Dame, USA
168,
K M Chan
K M Chan
168University of Notre Dame, Notre Dame, USA
168,
M Hildreth
M Hildreth
168University of Notre Dame, Notre Dame, USA
168,
C Jessop
C Jessop
168University of Notre Dame, Notre Dame, USA
168,
D J Karmgard
D J Karmgard
168University of Notre Dame, Notre Dame, USA
168,
J Kolb
J Kolb
168University of Notre Dame, Notre Dame, USA
168,
K Lannon
K Lannon
168University of Notre Dame, Notre Dame, USA
168,
W Luo
W Luo
168University of Notre Dame, Notre Dame, USA
168,
S Lynch
S Lynch
168University of Notre Dame, Notre Dame, USA
168,
N Marinelli
N Marinelli
168University of Notre Dame, Notre Dame, USA
168,
D M Morse
D M Morse
168University of Notre Dame, Notre Dame, USA
168,
T Pearson
T Pearson
168University of Notre Dame, Notre Dame, USA
168,
M Planer
M Planer
168University of Notre Dame, Notre Dame, USA
168,
R Ruchti
R Ruchti
168University of Notre Dame, Notre Dame, USA
168,
J Slaunwhite
J Slaunwhite
168University of Notre Dame, Notre Dame, USA
168,
N Valls
N Valls
168University of Notre Dame, Notre Dame, USA
168,
M Wayne
M Wayne
168University of Notre Dame, Notre Dame, USA
168,
M Wolf
M Wolf
168University of Notre Dame, Notre Dame, USA
168,
L Antonelli
L Antonelli
169The Ohio State University, Columbus, USA
169,
B Bylsma
B Bylsma
169The Ohio State University, Columbus, USA
169,
L S Durkin
L S Durkin
169The Ohio State University, Columbus, USA
169,
C Hill
C Hill
169The Ohio State University, Columbus, USA
169,
R Hughes
R Hughes
169The Ohio State University, Columbus, USA
169,
K Kotov
K Kotov
169The Ohio State University, Columbus, USA
169,
T Y Ling
T Y Ling
169The Ohio State University, Columbus, USA
169,
D Puigh
D Puigh
169The Ohio State University, Columbus, USA
169,
M Rodenburg
M Rodenburg
169The Ohio State University, Columbus, USA
169,
G Smith
G Smith
169The Ohio State University, Columbus, USA
169,
C Vuosalo
C Vuosalo
169The Ohio State University, Columbus, USA
169,
G Williams
G Williams
169The Ohio State University, Columbus, USA
169,
B L Winer
B L Winer
169The Ohio State University, Columbus, USA
169,
H Wolfe
H Wolfe
169The Ohio State University, Columbus, USA
169,
E Berry
E Berry
170Princeton University, Princeton, USA
170,
P Elmer
P Elmer
170Princeton University, Princeton, USA
170,
V Halyo
V Halyo
170Princeton University, Princeton, USA
170,
P Hebda
P Hebda
170Princeton University, Princeton, USA
170,
J Hegeman
J Hegeman
170Princeton University, Princeton, USA
170,
A Hunt
A Hunt
170Princeton University, Princeton, USA
170,
P Jindal
P Jindal
170Princeton University, Princeton, USA
170,
S A Koay
S A Koay
170Princeton University, Princeton, USA
170,
D Lopes Pegna
D Lopes Pegna
170Princeton University, Princeton, USA
170,
P Lujan
P Lujan
170Princeton University, Princeton, USA
170,
D Marlow
D Marlow
170Princeton University, Princeton, USA
170,
T Medvedeva
T Medvedeva
170Princeton University, Princeton, USA
170,
M Mooney
M Mooney
170Princeton University, Princeton, USA
170,
J Olsen
J Olsen
170Princeton University, Princeton, USA
170,
P Piroué
P Piroué
170Princeton University, Princeton, USA
170,
X Quan
X Quan
170Princeton University, Princeton, USA
170,
A Raval
A Raval
170Princeton University, Princeton, USA
170,
H Saka
H Saka
170Princeton University, Princeton, USA
170,
D Stickland
D Stickland
170Princeton University, Princeton, USA
170,
C Tully
C Tully
170Princeton University, Princeton, USA
170,
J S Werner
J S Werner
170Princeton University, Princeton, USA
170,
S C Zenz
S C Zenz
170Princeton University, Princeton, USA
170,
A Zuranski
A Zuranski
170Princeton University, Princeton, USA
170,
E Brownson
E Brownson
171University of Puerto Rico, Mayaguez, USA
171,
A Lopez
A Lopez
171University of Puerto Rico, Mayaguez, USA
171,
H Mendez
H Mendez
171University of Puerto Rico, Mayaguez, USA
171,
J E Ramirez Vargas
J E Ramirez Vargas
171University of Puerto Rico, Mayaguez, USA
171,
E Alagoz
E Alagoz
172Purdue University, West Lafayette, USA
172,
D Benedetti
D Benedetti
172Purdue University, West Lafayette, USA
172,
G Bolla
G Bolla
172Purdue University, West Lafayette, USA
172,
D Bortoletto
D Bortoletto
172Purdue University, West Lafayette, USA
172,
M De Mattia
M De Mattia
172Purdue University, West Lafayette, USA
172,
A Everett
A Everett
172Purdue University, West Lafayette, USA
172,
Z Hu
Z Hu
172Purdue University, West Lafayette, USA
172,
M Jones
M Jones
172Purdue University, West Lafayette, USA
172,
O Koybasi
O Koybasi
172Purdue University, West Lafayette, USA
172,
M Kress
M Kress
172Purdue University, West Lafayette, USA
172,
N Leonardo
N Leonardo
172Purdue University, West Lafayette, USA
172,
V Maroussov
V Maroussov
172Purdue University, West Lafayette, USA
172,
P Merkel
P Merkel
172Purdue University, West Lafayette, USA
172,
D H Miller
D H Miller
172Purdue University, West Lafayette, USA
172,
N Neumeister
N Neumeister
172Purdue University, West Lafayette, USA
172,
I Shipsey
I Shipsey
172Purdue University, West Lafayette, USA
172,
D Silvers
D Silvers
172Purdue University, West Lafayette, USA
172,
A Svyatkovskiy
A Svyatkovskiy
172Purdue University, West Lafayette, USA
172,
M Vidal Marono
M Vidal Marono
172Purdue University, West Lafayette, USA
172,
H D Yoo
H D Yoo
172Purdue University, West Lafayette, USA
172,
J Zablocki
J Zablocki
172Purdue University, West Lafayette, USA
172,
Y Zheng
Y Zheng
172Purdue University, West Lafayette, USA
172,
S Guragain
S Guragain
173Purdue University Calumet, Hammond, USA
173,
N Parashar
N Parashar
173Purdue University Calumet, Hammond, USA
173,
A Adair
A Adair
174Rice University, Houston, USA
174,
B Akgun
B Akgun
174Rice University, Houston, USA
174,
K M Ecklund
K M Ecklund
174Rice University, Houston, USA
174,
F J M Geurts
F J M Geurts
174Rice University, Houston, USA
174,
W Li
W Li
174Rice University, Houston, USA
174,
B P Padley
B P Padley
174Rice University, Houston, USA
174,
R Redjimi
R Redjimi
174Rice University, Houston, USA
174,
J Roberts
J Roberts
174Rice University, Houston, USA
174,
J Zabel
J Zabel
174Rice University, Houston, USA
174,
B Betchart
B Betchart
175University of Rochester, Rochester, USA
175,
A Bodek
A Bodek
175University of Rochester, Rochester, USA
175,
R Covarelli
R Covarelli
175University of Rochester, Rochester, USA
175,
P de Barbaro
P de Barbaro
175University of Rochester, Rochester, USA
175,
R Demina
R Demina
175University of Rochester, Rochester, USA
175,
Y Eshaq
Y Eshaq
175University of Rochester, Rochester, USA
175,
T Ferbel
T Ferbel
175University of Rochester, Rochester, USA
175,
A Garcia-Bellido
A Garcia-Bellido
175University of Rochester, Rochester, USA
175,
P Goldenzweig
P Goldenzweig
175University of Rochester, Rochester, USA
175,
J Han
J Han
175University of Rochester, Rochester, USA
175,
A Harel
A Harel
175University of Rochester, Rochester, USA
175,
D C Miner
D C Miner
175University of Rochester, Rochester, USA
175,
G Petrillo
G Petrillo
175University of Rochester, Rochester, USA
175,
D Vishnevskiy
D Vishnevskiy
175University of Rochester, Rochester, USA
175,
M Zielinski
M Zielinski
175University of Rochester, Rochester, USA
175,
A Bhatti
A Bhatti
176The Rockefeller University, New York, USA
176,
R Ciesielski
R Ciesielski
176The Rockefeller University, New York, USA
176,
L Demortier
L Demortier
176The Rockefeller University, New York, USA
176,
K Goulianos
K Goulianos
176The Rockefeller University, New York, USA
176,
G Lungu
G Lungu
176The Rockefeller University, New York, USA
176,
S Malik
S Malik
176The Rockefeller University, New York, USA
176,
C Mesropian
C Mesropian
176The Rockefeller University, New York, USA
176,
S Arora
S Arora
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
A Barker
A Barker
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
J P Chou
J P Chou
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
C Contreras-Campana
C Contreras-Campana
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
E Contreras-Campana
E Contreras-Campana
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
D Duggan
D Duggan
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
D Ferencek
D Ferencek
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
Y Gershtein
Y Gershtein
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
R Gray
R Gray
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
E Halkiadakis
E Halkiadakis
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
D Hidas
D Hidas
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
A Lath
A Lath
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
S Panwalkar
S Panwalkar
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
M Park
M Park
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
R Patel
R Patel
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
V Rekovic
V Rekovic
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
J Robles
J Robles
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
K Rose
K Rose
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
S Salur
S Salur
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
S Schnetzer
S Schnetzer
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
C Seitz
C Seitz
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
S Somalwar
S Somalwar
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
R Stone
R Stone
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
M Walker
M Walker
177Rutgers, The State University of New Jersey, Piscataway, USA
177,
G Cerizza
G Cerizza
178University of Tennessee, Knoxville, USA
178,
M Hollingsworth
M Hollingsworth
178University of Tennessee, Knoxville, USA
178,
S Spanier
S Spanier
178University of Tennessee, Knoxville, USA
178,
Z C Yang
Z C Yang
178University of Tennessee, Knoxville, USA
178,
A York
A York
178University of Tennessee, Knoxville, USA
178,
R Eusebi
R Eusebi
179Texas A&M University, College Station, USA
179,
W Flanagan
W Flanagan
179Texas A&M University, College Station, USA
179,
J Gilmore
J Gilmore
179Texas A&M University, College Station, USA
179,
T Kamon
T Kamon
179Texas A&M University, College Station, USA
179,
V Khotilovich
V Khotilovich
179Texas A&M University, College Station, USA
179,
R Montalvo
R Montalvo
179Texas A&M University, College Station, USA
179,
I Osipenkov
I Osipenkov
179Texas A&M University, College Station, USA
179,
Y Pakhotin
Y Pakhotin
179Texas A&M University, College Station, USA
179,
A Perloff
A Perloff
179Texas A&M University, College Station, USA
179,
J Roe
J Roe
179Texas A&M University, College Station, USA
179,
A Safonov
A Safonov
179Texas A&M University, College Station, USA
179,
T Sakuma
T Sakuma
179Texas A&M University, College Station, USA
179,
I Suarez
I Suarez
179Texas A&M University, College Station, USA
179,
A Tatarinov
A Tatarinov
179Texas A&M University, College Station, USA
179,
D Toback
D Toback
179Texas A&M University, College Station, USA
179,
N Akchurin
N Akchurin
180Texas Tech University, Lubbock, USA
180,
J Damgov
J Damgov
180Texas Tech University, Lubbock, USA
180,
C Dragoiu
C Dragoiu
180Texas Tech University, Lubbock, USA
180,
P R Dudero
P R Dudero
180Texas Tech University, Lubbock, USA
180,
C Jeong
C Jeong
180Texas Tech University, Lubbock, USA
180,
K Kovitanggoon
K Kovitanggoon
180Texas Tech University, Lubbock, USA
180,
S W Lee
S W Lee
180Texas Tech University, Lubbock, USA
180,
T Libeiro
T Libeiro
180Texas Tech University, Lubbock, USA
180,
I Volobouev
I Volobouev
180Texas Tech University, Lubbock, USA
180,
E Appelt
E Appelt
181Vanderbilt University, Nashville, USA
181,
A G Delannoy
A G Delannoy
181Vanderbilt University, Nashville, USA
181,
S Greene
S Greene
181Vanderbilt University, Nashville, USA
181,
A Gurrola
A Gurrola
181Vanderbilt University, Nashville, USA
181,
W Johns
W Johns
181Vanderbilt University, Nashville, USA
181,
C Maguire
C Maguire
181Vanderbilt University, Nashville, USA
181,
Y Mao
Y Mao
181Vanderbilt University, Nashville, USA
181,
A Melo
A Melo
181Vanderbilt University, Nashville, USA
181,
M Sharma
M Sharma
181Vanderbilt University, Nashville, USA
181,
P Sheldon
P Sheldon
181Vanderbilt University, Nashville, USA
181,
B Snook
B Snook
181Vanderbilt University, Nashville, USA
181,
S Tuo
S Tuo
181Vanderbilt University, Nashville, USA
181,
J Velkovska
J Velkovska
181Vanderbilt University, Nashville, USA
181,
M W Arenton
M W Arenton
182University of Virginia, Charlottesville, USA
182,
M Balazs
M Balazs
182University of Virginia, Charlottesville, USA
182,
S Boutle
S Boutle
182University of Virginia, Charlottesville, USA
182,
B Cox
B Cox
182University of Virginia, Charlottesville, USA
182,
B Francis
B Francis
182University of Virginia, Charlottesville, USA
182,
J Goodell
J Goodell
182University of Virginia, Charlottesville, USA
182,
R Hirosky
R Hirosky
182University of Virginia, Charlottesville, USA
182,
A Ledovskoy
A Ledovskoy
182University of Virginia, Charlottesville, USA
182,
C Lin
C Lin
182University of Virginia, Charlottesville, USA
182,
C Neu
C Neu
182University of Virginia, Charlottesville, USA
182,
J Wood
J Wood
182University of Virginia, Charlottesville, USA
182,
S Gollapinni
S Gollapinni
183Wayne State University, Detroit, USA
183,
R Harr
R Harr
183Wayne State University, Detroit, USA
183,
P E Karchin
P E Karchin
183Wayne State University, Detroit, USA
183,
C Kottachchi Kankanamge Don
C Kottachchi Kankanamge Don
183Wayne State University, Detroit, USA
183,
P Lamichhane
P Lamichhane
183Wayne State University, Detroit, USA
183,
A Sakharov
A Sakharov
183Wayne State University, Detroit, USA
183,
M Anderson
M Anderson
184University of Wisconsin, Madison, USA
184,
D A Belknap
D A Belknap
184University of Wisconsin, Madison, USA
184,
L Borrello
L Borrello
184University of Wisconsin, Madison, USA
184,
D Carlsmith
D Carlsmith
184University of Wisconsin, Madison, USA
184,
M Cepeda
M Cepeda
184University of Wisconsin, Madison, USA
184,
S Dasu
S Dasu
184University of Wisconsin, Madison, USA
184,
E Friis
E Friis
184University of Wisconsin, Madison, USA
184,
K S Grogg
K S Grogg
184University of Wisconsin, Madison, USA
184,
M Grothe
M Grothe
184University of Wisconsin, Madison, USA
184,
R Hall-Wilton
R Hall-Wilton
184University of Wisconsin, Madison, USA
184,
M Herndon
M Herndon
184University of Wisconsin, Madison, USA
184,
A Hervé
A Hervé
184University of Wisconsin, Madison, USA
184,
P Klabbers
P Klabbers
184University of Wisconsin, Madison, USA
184,
J Klukas
J Klukas
184University of Wisconsin, Madison, USA
184,
A Lanaro
A Lanaro
184University of Wisconsin, Madison, USA
184,
C Lazaridis
C Lazaridis
184University of Wisconsin, Madison, USA
184,
R Loveless
R Loveless
184University of Wisconsin, Madison, USA
184,
A Mohapatra
A Mohapatra
184University of Wisconsin, Madison, USA
184,
M U Mozer
M U Mozer
184University of Wisconsin, Madison, USA
184,
I Ojalvo
I Ojalvo
184University of Wisconsin, Madison, USA
184,
G A Pierro
G A Pierro
184University of Wisconsin, Madison, USA
184,
I Ross
I Ross
184University of Wisconsin, Madison, USA
184,
A Savin
A Savin
184University of Wisconsin, Madison, USA
184,
W H Smith
W H Smith
184University of Wisconsin, Madison, USA
184,
J Swanson
J Swanson
184University of Wisconsin, Madison, USA
184
 events selected in the dilepton final state from a data sample corresponding to an integrated luminosity of 5.0 fb−1 collected by the CMS experiment in pp collisions at
events selected in the dilepton final state from a data sample corresponding to an integrated luminosity of 5.0 fb−1 collected by the CMS experiment in pp collisions at 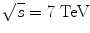 . The analysis is based on endpoint determinations in kinematic distributions. When the neutrino and W-boson masses are constrained to their world-average values, a top-quark mass value of
. The analysis is based on endpoint determinations in kinematic distributions. When the neutrino and W-boson masses are constrained to their world-average values, a top-quark mass value of  is obtained. When such constraints are not used, the three particle masses are obtained in a simultaneous fit. In this unconstrained mode the study serves as a test of mass determination methods that may be used in beyond standard model physics scenarios where several masses in a decay chain may be unknown and undetected particles lead to underconstrained kinematics.
is obtained. When such constraints are not used, the three particle masses are obtained in a simultaneous fit. In this unconstrained mode the study serves as a test of mass determination methods that may be used in beyond standard model physics scenarios where several masses in a decay chain may be unknown and undetected particles lead to underconstrained kinematics. events include those reported by ATLAS [6], M
t=174.5±0.6 (stat.)±2.3 (syst.) GeV, and by the Compact Muon Solenoid (CMS) [7], M
t=173.49±0.43 (stat.)±0.98 (syst.) GeV, using the semileptonic decay channel of the
events include those reported by ATLAS [6], M
t=174.5±0.6 (stat.)±2.3 (syst.) GeV, and by the Compact Muon Solenoid (CMS) [7], M
t=173.49±0.43 (stat.)±0.98 (syst.) GeV, using the semileptonic decay channel of the  pair. The CMS Collaboration has also reported a measurement [8] in the dilepton channel, M
t=172.5±0.4 (stat.)±1.5 (syst.) GeV. A recent summary of top-quark mass measurements conducted by the CDF and D0 Collaborations [9] reports a combined result M
t=173.18±0.56 (stat.)±0.75 (syst.) GeV.
pair. The CMS Collaboration has also reported a measurement [8] in the dilepton channel, M
t=172.5±0.4 (stat.)±1.5 (syst.) GeV. A recent summary of top-quark mass measurements conducted by the CDF and D0 Collaborations [9] reports a combined result M
t=173.18±0.56 (stat.)±0.75 (syst.) GeV.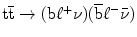 ) provide challenges in mass measurement very similar to the ones that these methods were designed to solve. A key feature of many current theories of physics beyond the standard model is the existence of a candidate for dark matter, such as a weakly interacting massive particle (WIMP). These particles are usually stabilized in a theory by a conserved parity, often introduced ad hoc, under which SM particles are even and new-physics particles are odd. Examples include R-parity in supersymmetry (SUSY) and T-parity in little-Higgs models. One consequence of this parity is that new physics particles must be produced in pairs. Each of the pair-produced particles will then decay to a cascade of SM particles, terminating with the lightest odd-parity particle of the new theory. In such cases, there will be two particles which do not interact with the detector, yielding events where the observable kinematics are underconstrained. Mass measurements in these events are further complicated by the presence of multiple new particles with unknown masses.
) provide challenges in mass measurement very similar to the ones that these methods were designed to solve. A key feature of many current theories of physics beyond the standard model is the existence of a candidate for dark matter, such as a weakly interacting massive particle (WIMP). These particles are usually stabilized in a theory by a conserved parity, often introduced ad hoc, under which SM particles are even and new-physics particles are odd. Examples include R-parity in supersymmetry (SUSY) and T-parity in little-Higgs models. One consequence of this parity is that new physics particles must be produced in pairs. Each of the pair-produced particles will then decay to a cascade of SM particles, terminating with the lightest odd-parity particle of the new theory. In such cases, there will be two particles which do not interact with the detector, yielding events where the observable kinematics are underconstrained. Mass measurements in these events are further complicated by the presence of multiple new particles with unknown masses. events at the LHC offer a rich source of symmetric decay chains terminating in two neutrinos. With their combination of jets, leptons, and undetected particles, these
events at the LHC offer a rich source of symmetric decay chains terminating in two neutrinos. With their combination of jets, leptons, and undetected particles, these  events bear close kinematic and topological resemblance to new-physics scenarios such as the supersymmetric decay chain illustrated in Fig. 1. This correspondence has motivated [10] the idea to use the abundant
events bear close kinematic and topological resemblance to new-physics scenarios such as the supersymmetric decay chain illustrated in Fig. 1. This correspondence has motivated [10] the idea to use the abundant  samples of the LHC as a testbed for the new methods and novel observables that have been proposed to handle mass measurement in new-physics events [11]. A simultaneous measurement of the top-quark, W-boson, and neutrino masses in dilepton
samples of the LHC as a testbed for the new methods and novel observables that have been proposed to handle mass measurement in new-physics events [11]. A simultaneous measurement of the top-quark, W-boson, and neutrino masses in dilepton  decays closely mimics the strategies needed for studies of new physics.
decays closely mimics the strategies needed for studies of new physics.
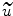 ,
,  ,
,  , and
, and  denote the u-squark, chargino, sneutrino, and neutralino respectively; an asterisk indicates the antiparticle of the corresponding SUSY particle
denote the u-squark, chargino, sneutrino, and neutralino respectively; an asterisk indicates the antiparticle of the corresponding SUSY particle system assuming no knowledge of the W-boson or neutrino masses. This allows us to measure the masses of all three undetected particles involved in the dilepton decay: the top quark, W boson, and neutrino. This “unconstrained” fit provides a test of the method under conditions similar to what one might expect to find when attempting to measure the masses of new particles. In order to make a precise measurement of the top-quark mass, on the other hand, we assume the world-average values for the W boson and neutrino masses. This “doubly-constrained” fit achieves a precision in the top-quark mass determination similar to that obtained by traditional methods. The M
T2 observable has been previously suggested [13] or used [14] in top-quark mass measurements.
system assuming no knowledge of the W-boson or neutrino masses. This allows us to measure the masses of all three undetected particles involved in the dilepton decay: the top quark, W boson, and neutrino. This “unconstrained” fit provides a test of the method under conditions similar to what one might expect to find when attempting to measure the masses of new particles. In order to make a precise measurement of the top-quark mass, on the other hand, we assume the world-average values for the W boson and neutrino masses. This “doubly-constrained” fit achieves a precision in the top-quark mass determination similar to that obtained by traditional methods. The M
T2 observable has been previously suggested [13] or used [14] in top-quark mass measurements.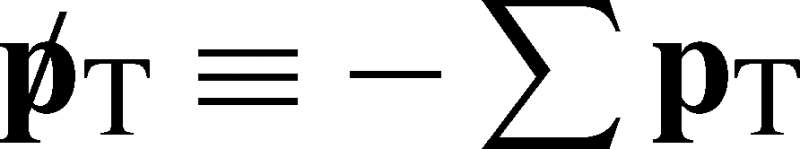 where the sum is taken over all particle-flow objects in the event; and missing transverse “energy” is given by
where the sum is taken over all particle-flow objects in the event; and missing transverse “energy” is given by  .
.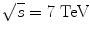 recorded by the CMS detector in 2011. We apply an event selection to isolate a dilepton sample that is largely free of backgrounds. We require two well-identified and isolated opposite-sign leptons (electrons or muons) passing dilepton trigger requirements; the minimum p
T requirements for the triggers are 17 GeV and 8 GeV for the leading and sub-leading leptons. In addition we require at least two b-tagged jets, subsequently used in the top-quark reconstruction, and missing transverse energy. Here and throughout this paper, we use ℓ (and “lepton”) to denote an electron or muon; the signal decays of interest are t→bℓν. Leptons must satisfy p
T>20 GeV and the event is vetoed if the leptons have the same flavor and their dilepton invariant mass is within 15 GeV of the Z boson mass. If three leptons are found, the two highest-p
T leptons forming an opposite-sign pair are selected. Jets must satisfy p
T>30 GeV after correcting for additive effects of pileup (multiple proton collisions in a single crossing) and multiplicative effects of jet energy scale calibration. Jets are further required to lie within |η|<2.5, where η is the pseudorapidity variable, η≡−ln[tan(θ/2)]. The b-tagging algorithm is the Combined Secondary Vertex (CSV) tagger of Ref. [23], deployed here with an operating point that yields a tagging efficiency of 85 % and mistag rate of 10 %. The mistag rate measures the probability for a light quark or gluon jet to be misidentified as a b jet. In the subsample of events passing all selection requirements of this analysis the b-jet purity is 91 %. Jet masses are required to satisfy a very loose requirement m
jet<40 GeV to assure the existence of kinematic solutions and reject poorly reconstructed jets. The missing transverse energy must satisfy
recorded by the CMS detector in 2011. We apply an event selection to isolate a dilepton sample that is largely free of backgrounds. We require two well-identified and isolated opposite-sign leptons (electrons or muons) passing dilepton trigger requirements; the minimum p
T requirements for the triggers are 17 GeV and 8 GeV for the leading and sub-leading leptons. In addition we require at least two b-tagged jets, subsequently used in the top-quark reconstruction, and missing transverse energy. Here and throughout this paper, we use ℓ (and “lepton”) to denote an electron or muon; the signal decays of interest are t→bℓν. Leptons must satisfy p
T>20 GeV and the event is vetoed if the leptons have the same flavor and their dilepton invariant mass is within 15 GeV of the Z boson mass. If three leptons are found, the two highest-p
T leptons forming an opposite-sign pair are selected. Jets must satisfy p
T>30 GeV after correcting for additive effects of pileup (multiple proton collisions in a single crossing) and multiplicative effects of jet energy scale calibration. Jets are further required to lie within |η|<2.5, where η is the pseudorapidity variable, η≡−ln[tan(θ/2)]. The b-tagging algorithm is the Combined Secondary Vertex (CSV) tagger of Ref. [23], deployed here with an operating point that yields a tagging efficiency of 85 % and mistag rate of 10 %. The mistag rate measures the probability for a light quark or gluon jet to be misidentified as a b jet. In the subsample of events passing all selection requirements of this analysis the b-jet purity is 91 %. Jet masses are required to satisfy a very loose requirement m
jet<40 GeV to assure the existence of kinematic solutions and reject poorly reconstructed jets. The missing transverse energy must satisfy  for e+e− and
for e+e− and  events and
events and  for
for 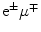 events, where Drell–Yan backgrounds are smaller. With the exception of the b-tagging criteria and the b-jet mass requirement, all selection requirements summarized here are discussed in more detail in [24, 25]. The sample of events in data meeting all of the signal selection criteria contains 8700 events.
events, where Drell–Yan backgrounds are smaller. With the exception of the b-tagging criteria and the b-jet mass requirement, all selection requirements summarized here are discussed in more detail in [24, 25]. The sample of events in data meeting all of the signal selection criteria contains 8700 events. system is produced with unknown center-of-mass energy and has an event-dependent p
T-boost due to recoil from the initial-state radiation (ISR). Furthermore, in pp collisions we can apply constraints of momentum conservation only in the two dimensions transverse to the beam direction. Since top quarks are normally produced in pairs, the individual neutrino momenta are indeterminate, adding further complication. These obstacles seem daunting but can be overcome by the use of “designer” kinematic variables M
T2 [12] and M
CT [26], which, by construction, address precisely these issues. In this paper we use M
T2. Because the transverse momentum of the
system is produced with unknown center-of-mass energy and has an event-dependent p
T-boost due to recoil from the initial-state radiation (ISR). Furthermore, in pp collisions we can apply constraints of momentum conservation only in the two dimensions transverse to the beam direction. Since top quarks are normally produced in pairs, the individual neutrino momenta are indeterminate, adding further complication. These obstacles seem daunting but can be overcome by the use of “designer” kinematic variables M
T2 [12] and M
CT [26], which, by construction, address precisely these issues. In this paper we use M
T2. Because the transverse momentum of the  system varies from event to event, the p
T-insensitive version [27, 28], M
T2⊥, is particularly useful. To measure the masses of the top-quark, W-boson, and neutrino, we measure the endpoints of three kinematic distributions, μ
ℓℓ, μ
bb, and M
bℓ, as discussed in the following subsections.
system varies from event to event, the p
T-insensitive version [27, 28], M
T2⊥, is particularly useful. To measure the masses of the top-quark, W-boson, and neutrino, we measure the endpoints of three kinematic distributions, μ
ℓℓ, μ
bb, and M
bℓ, as discussed in the following subsections. and
and  . The utility of M
T lies in the fact that M
T≤M
W is guaranteed for W bosons with low transverse momentum. For a single W→ℓν decay such a lower limit is only marginally informative, but in an ensemble of events, the maximum value achieved, i.e. the endpoint of the M
T distribution, directly reveals the W boson mass. This observation suggests a “min-max” strategy which is generalized by the invention of M
T2.
. The utility of M
T lies in the fact that M
T≤M
W is guaranteed for W bosons with low transverse momentum. For a single W→ℓν decay such a lower limit is only marginally informative, but in an ensemble of events, the maximum value achieved, i.e. the endpoint of the M
T distribution, directly reveals the W boson mass. This observation suggests a “min-max” strategy which is generalized by the invention of M
T2. . In practice the two missing momenta cannot be known separately, and are observable only in the combination
. In practice the two missing momenta cannot be known separately, and are observable only in the combination 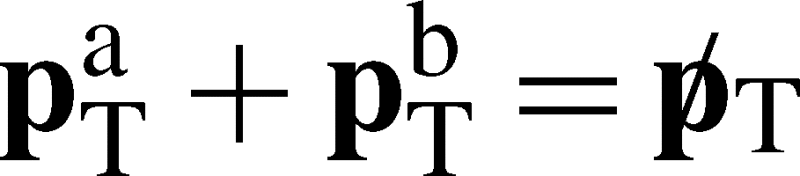 . This compels one to consider all possible partitions of
. This compels one to consider all possible partitions of  into two hypothetical constituents
into two hypothetical constituents  and
and  , evaluating within this ensemble of partitions the minimum parent mass M consistent with the observed event kinematics. With this extension of the M
T concept, the variable is now called M
T2:
, evaluating within this ensemble of partitions the minimum parent mass M consistent with the observed event kinematics. With this extension of the M
T concept, the variable is now called M
T2: 
 in Eq. (4.1) implies that one must either know (as in the case of W→ℓν) or assume (as in the case of unknown new physics) a value of the mass m of the undetected particle(s). In this paper we will refer to an assumed mass as the “test mass” and distinguish it with a tilde (i.e.
in Eq. (4.1) implies that one must either know (as in the case of W→ℓν) or assume (as in the case of unknown new physics) a value of the mass m of the undetected particle(s). In this paper we will refer to an assumed mass as the “test mass” and distinguish it with a tilde (i.e.  ); the actual mass of the missing particle, whether known or not, will be referred to as the “true mass”, and written without the tilde. Both the value of M
T2 in any event and the value of the endpoint of the M
T2 distribution in an ensemble of events are in the end functions of the test mass.
); the actual mass of the missing particle, whether known or not, will be referred to as the “true mass”, and written without the tilde. Both the value of M
T2 in any event and the value of the endpoint of the M
T2 distribution in an ensemble of events are in the end functions of the test mass. is the unit vector parallel to the transverse momentum of the two-parent system.
is the unit vector parallel to the transverse momentum of the two-parent system. daughters for M
T2 calculations. The μ
ℓℓ variable, known as
daughters for M
T2 calculations. The μ
ℓℓ variable, known as  in Ref. [10], uses the two leptons of the
in Ref. [10], uses the two leptons of the  dilepton decays, treating the neutrinos as lost child particles (which they are), and combining the b jets with all other “upstream” momentum in the event. The μ
bb variable, known as
dilepton decays, treating the neutrinos as lost child particles (which they are), and combining the b jets with all other “upstream” momentum in the event. The μ
bb variable, known as  in Ref. [10], uses the b jets, and treats the W bosons as lost child particles (ignoring the fact that their charged daughter leptons are in fact observable). It considers only ISR jets as generators of upstream momentum.
in Ref. [10], uses the b jets, and treats the W bosons as lost child particles (ignoring the fact that their charged daughter leptons are in fact observable). It considers only ISR jets as generators of upstream momentum.
 dilepton decay with the two subsystems for computing μ
ℓℓ and μ
bb indicated. The “upstream” and “child” objects are enclosed in dashed rectangles, while the visible objects, which enter into the computation, are enclosed in solid rectangles. The μ
ℓℓ and μ
bb variables used here are identical to
dilepton decay with the two subsystems for computing μ
ℓℓ and μ
bb indicated. The “upstream” and “child” objects are enclosed in dashed rectangles, while the visible objects, which enter into the computation, are enclosed in solid rectangles. The μ
ℓℓ and μ
bb variables used here are identical to  and
and  of Ref. [10]
of Ref. [10] in the nomenclature of Ref. [10], exhibits significant correlation with M
bℓ, the invariant mass of the b jet and lepton. A third observable is needed to solve the underlying system of equations, and for this we choose M
bℓ.
in the nomenclature of Ref. [10], exhibits significant correlation with M
bℓ, the invariant mass of the b jet and lepton. A third observable is needed to solve the underlying system of equations, and for this we choose M
bℓ. otherwise.
otherwise. , the endpoint is related to the masses via [10, 27]:
, the endpoint is related to the masses via [10, 27]: 
 case, we set the test mass to
case, we set the test mass to  . We then expect the endpoint at
. We then expect the endpoint at 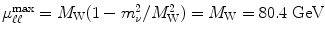 . Note that m
ν is the true mass of the child and M
W is the true parent mass; these should be viewed as variables in a function for which
. Note that m
ν is the true mass of the child and M
W is the true parent mass; these should be viewed as variables in a function for which  is a parameter. In a new-physics application, the analogs of M
W and m
ν are not known; but given Eq. (4.5), the measurement of the endpoint, and an arbitrary choice of child mass
is a parameter. In a new-physics application, the analogs of M
W and m
ν are not known; but given Eq. (4.5), the measurement of the endpoint, and an arbitrary choice of child mass  , one can fix a relationship between the two unknown masses. We emphasize that the equality expressed by Eq. (4.5) holds regardless of the value of the test mass, because the test mass enters into both sides of the equation (see discussion in Sect. 4.1.1). This applies below to Eq. (4.6) also.
, one can fix a relationship between the two unknown masses. We emphasize that the equality expressed by Eq. (4.5) holds regardless of the value of the test mass, because the test mass enters into both sides of the equation (see discussion in Sect. 4.1.1). This applies below to Eq. (4.6) also. . For an assumed child mass
. For an assumed child mass  , the endpoint is given by [10, 27]:
, the endpoint is given by [10, 27]:  case, we set the test mass to
case, we set the test mass to  . We then expect the endpoint at
. We then expect the endpoint at  . As in the previous case, in a new-physics application where the analogs of M
t and M
W are not known, the measurement of the endpoint together with an arbitrary choice of the child mass
. As in the previous case, in a new-physics application where the analogs of M
t and M
W are not known, the measurement of the endpoint together with an arbitrary choice of the child mass  yields a relationship between the two unknown masses.
yields a relationship between the two unknown masses. event, one for each top decay. In practice four are calculated because one does not know a priori how to associate the b jets and leptons; we discuss later an algorithm for mitigating the combinatorial effects on the endpoint. The shape of the distribution is known for correct combinations but is not used here since correct combinations cannot be guaranteed (see Sect. 5.3). The endpoint is given by:
event, one for each top decay. In practice four are calculated because one does not know a priori how to associate the b jets and leptons; we discuss later an algorithm for mitigating the combinatorial effects on the endpoint. The shape of the distribution is known for correct combinations but is not used here since correct combinations cannot be guaranteed (see Sect. 5.3). The endpoint is given by:  ,
,  , and p
∗ are energies and momenta of the daughters of t→bW in the top-quark rest frame. In these formulae the charged-lepton mass is neglected but the observed b-jet mass m
b is finite and varies event-to-event.
, and p
∗ are energies and momenta of the daughters of t→bW in the top-quark rest frame. In these formulae the charged-lepton mass is neglected but the observed b-jet mass m
b is finite and varies event-to-event.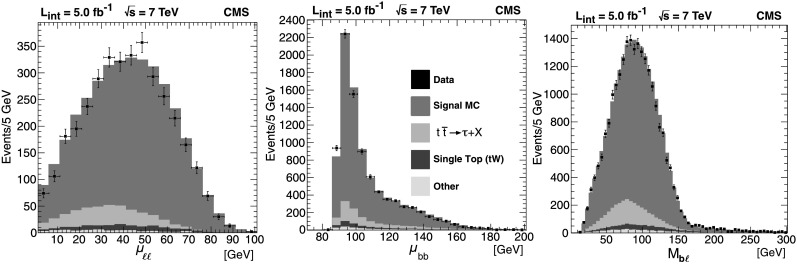
 ) are shown with error bars. MC simulation is overlaid in solid color to illustrate the approximate
) are shown with error bars. MC simulation is overlaid in solid color to illustrate the approximate  signal and background content of the distributions. The backgrounds contained in “Other” are listed in Table 1. The zero-bin of the μ
ℓℓ plot is suppressed for clarity. The M
bℓ plot contains multiple entries per event (see Sect. 5.3 for details). In all cases, the simulation is normalized to an integrated luminosity of 5.0 fb−1 with next-to-leading-order (NLO) cross sections as described in the text
signal and background content of the distributions. The backgrounds contained in “Other” are listed in Table 1. The zero-bin of the μ
ℓℓ plot is suppressed for clarity. The M
bℓ plot contains multiple entries per event (see Sect. 5.3 for details). In all cases, the simulation is normalized to an integrated luminosity of 5.0 fb−1 with next-to-leading-order (NLO) cross sections as described in the text decays that do not conform to the dilepton topology of interest, as well as non-
decays that do not conform to the dilepton topology of interest, as well as non- decays. Table 1 shows the estimation of signal and background events in MC simulation. The MC generators used throughout this study are mc@nlo 3.41 [29] for all
decays. Table 1 shows the estimation of signal and background events in MC simulation. The MC generators used throughout this study are mc@nlo 3.41 [29] for all  samples, pythia 6.4 [30] for the diboson samples, and MadGraph 5.1.1.0 [31] for all others. The simulated data samples are normalized to 7 TeV NLO cross sections and an integrated luminosity of 5.0 fb−1.
samples, pythia 6.4 [30] for the diboson samples, and MadGraph 5.1.1.0 [31] for all others. The simulated data samples are normalized to 7 TeV NLO cross sections and an integrated luminosity of 5.0 fb−1.
 signal (no τ)
signal (no τ) signal (τ→ℓν)
signal (τ→ℓν) )
) with misreconstructed lepton(s)
with misreconstructed lepton(s) ), constitute about 13 % of the events surviving all selection requirements. From the point of view of event selection, these events are background. The unobserved momentum carried by the extra neutrinos, however, ensures that these events reconstruct to M
T2 and M
bℓ values below their true values and hence fall below the endpoint of signal events with direct decays to e or
), constitute about 13 % of the events surviving all selection requirements. From the point of view of event selection, these events are background. The unobserved momentum carried by the extra neutrinos, however, ensures that these events reconstruct to M
T2 and M
bℓ values below their true values and hence fall below the endpoint of signal events with direct decays to e or  final states. We therefore include these events among the signal sample. This leaves in principle a small distortion to the kinematic shapes, but the distortion is far from the endpoint and its impact on the mass extraction is negligible.
final states. We therefore include these events among the signal sample. This leaves in principle a small distortion to the kinematic shapes, but the distortion is far from the endpoint and its impact on the mass extraction is negligible. events where one of the jets not originating from a top-quark decay is mistagged as a b jet. An event in which a light-quark or gluon jet is treated as coming from a top quark can result in events beyond the endpoint in the μ
bb and M
bℓ distributions, as can be seen in Fig. 4. The measurement of μ
ℓℓ, on the other hand, depends primarily on the two leptons and is unaffected by mistags.
events where one of the jets not originating from a top-quark decay is mistagged as a b jet. An event in which a light-quark or gluon jet is treated as coming from a top quark can result in events beyond the endpoint in the μ
bb and M
bℓ distributions, as can be seen in Fig. 4. The measurement of μ
ℓℓ, on the other hand, depends primarily on the two leptons and is unaffected by mistags.
 dilepton events. In the case of the M
bℓ distribution the matching problem arises in pairing the b jet to the lepton: for b jets j
1 and j
2, and leptons ℓ
+ and ℓ
−, two pairings are possible: j
1
ℓ
+,j
2
ℓ
− and j
1
ℓ
−,j
2
ℓ
+. Four values of M
bℓ will thus be available in every event, but only two of them are correct. The two incorrect pairings can (but do not have to) generate values of M
bℓ beyond the kinematic endpoint of M
bℓ in top-quark decay. To minimize the unwanted background of incorrect pairings while maximizing the chance of retaining the highest values of M
bℓ in correct bℓ pairings, which do respect the endpoint, we employ the following algorithm.
dilepton events. In the case of the M
bℓ distribution the matching problem arises in pairing the b jet to the lepton: for b jets j
1 and j
2, and leptons ℓ
+ and ℓ
−, two pairings are possible: j
1
ℓ
+,j
2
ℓ
− and j
1
ℓ
−,j
2
ℓ
+. Four values of M
bℓ will thus be available in every event, but only two of them are correct. The two incorrect pairings can (but do not have to) generate values of M
bℓ beyond the kinematic endpoint of M
bℓ in top-quark decay. To minimize the unwanted background of incorrect pairings while maximizing the chance of retaining the highest values of M
bℓ in correct bℓ pairings, which do respect the endpoint, we employ the following algorithm. contains the mass parameters to be determined by the fit, and each u
i comprises the set of transverse momentum vectors, reconstructed object masses, and missing-particle test masses from which the kinematic observables μ
ℓℓ, μ
bb, and M
bℓ of the event i are computed. We fit for
contains the mass parameters to be determined by the fit, and each u
i comprises the set of transverse momentum vectors, reconstructed object masses, and missing-particle test masses from which the kinematic observables μ
ℓℓ, μ
bb, and M
bℓ of the event i are computed. We fit for  rather than m
ν because only
rather than m
ν because only  appears in the endpoint formulae (Eqs. (4.5) and (4.7)); we do not constrain
appears in the endpoint formulae (Eqs. (4.5) and (4.7)); we do not constrain  to be positive. As will be described more fully below, only the endpoint region of each variable is used in the fit. If an event i does not fall within the endpoint region of a given variable, the corresponding likelihood component (
to be positive. As will be described more fully below, only the endpoint region of each variable is used in the fit. If an event i does not fall within the endpoint region of a given variable, the corresponding likelihood component ( ,
,  , or
, or  ) defaults to unity.
) defaults to unity. in Eq. (6.1) can be expressed in terms of the value of the observable itself, x
i=x(u
i), and its kinematic endpoint, x
max=x
max(M). Explicit formulae for x
max(M) are given in Eqs. (4.5), (4.6), and (4.7); in the first two cases there is additional dependence on the missing-particle test mass. Letting the label a∈{ℓℓ,bb,bℓ} index the three flavors of observables, we can write the signal, background, and resolution shapes as
in Eq. (6.1) can be expressed in terms of the value of the observable itself, x
i=x(u
i), and its kinematic endpoint, x
max=x
max(M). Explicit formulae for x
max(M) are given in Eqs. (4.5), (4.6), and (4.7); in the first two cases there is additional dependence on the missing-particle test mass. Letting the label a∈{ℓℓ,bb,bℓ} index the three flavors of observables, we can write the signal, background, and resolution shapes as  , B
a(x), and
, B
a(x), and 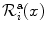 . While the form of the signal shape S(x) is common to all three fits, the background shape B
a(x) is specific to each observable and the resolution function
. While the form of the signal shape S(x) is common to all three fits, the background shape B
a(x) is specific to each observable and the resolution function  is specific to both the observable and the individual event. Then each function
is specific to both the observable and the individual event. Then each function  appearing on the right-hand side of Eq. (6.1) is given by the general form:
appearing on the right-hand side of Eq. (6.1) is given by the general form:  we use an approximation consisting of a kinked-line shape, constructed piecewise from a descending straight line in the region just below the endpoint and a constant zero value above the endpoint. The kinked-line function is defined over a range from x
lo to x
hi. The generic form is:
we use an approximation consisting of a kinked-line shape, constructed piecewise from a descending straight line in the region just below the endpoint and a constant zero value above the endpoint. The kinked-line function is defined over a range from x
lo to x
hi. The generic form is:  is fixed by normalization. The fidelity of this first-order approximation to the underlying shape depends on both the shape and the value of x
lo. The range of the fit, (x
lo,x
hi), is chosen to minimize the dependence of the fit results on the range, and then the values of x
lo and x
hi are subsequently varied to estimate the corresponding systematic uncertainties.
is fixed by normalization. The fidelity of this first-order approximation to the underlying shape depends on both the shape and the value of x
lo. The range of the fit, (x
lo,x
hi), is chosen to minimize the dependence of the fit results on the range, and then the values of x
lo and x
hi are subsequently varied to estimate the corresponding systematic uncertainties. for each of the three kinematic distributions.
for each of the three kinematic distributions.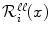 . In this procedure a sharp Jacobian peak appears wherever the P
T smearing can cause μ
ℓℓ to pass through a local maximum or minimum value. These peaks depend only on azimuthal angles and occur at any value of μ
ℓℓ. The detailed shape of the highly non-Gaussian μ
ℓℓ resolution and its convolution with the underlying signal shape, as specified in Eq. (6.2), are handled by exact formulae derived analytically (see the Appendix). The background in the μ
ℓℓ distribution is vanishingly small, so we set B
ℓℓ(x)=0.
. In this procedure a sharp Jacobian peak appears wherever the P
T smearing can cause μ
ℓℓ to pass through a local maximum or minimum value. These peaks depend only on azimuthal angles and occur at any value of μ
ℓℓ. The detailed shape of the highly non-Gaussian μ
ℓℓ resolution and its convolution with the underlying signal shape, as specified in Eq. (6.2), are handled by exact formulae derived analytically (see the Appendix). The background in the μ
ℓℓ distribution is vanishingly small, so we set B
ℓℓ(x)=0.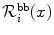 , numerically in each event, using the known p
T and ϕ resolution functions for the jets. As with the μ
ℓℓ resolutions, Jacobian peaks appear in the μ
bb resolutions. The mistag background is included by scaling the shape B
bb(x) obtained from the AKDE procedure as discussed in Sect. 5.2.
, numerically in each event, using the known p
T and ϕ resolution functions for the jets. As with the μ
ℓℓ resolutions, Jacobian peaks appear in the μ
bb resolutions. The mistag background is included by scaling the shape B
bb(x) obtained from the AKDE procedure as discussed in Sect. 5.2. of M
bℓ, as one expects in this case. The background shape B
bℓ(x) is given by the AKDE procedure as discussed in Sect. 5.2.
of M
bℓ, as one expects in this case. The background shape B
bℓ(x) is given by the AKDE procedure as discussed in Sect. 5.2. , and mistag background B(x). Although a simultaneous fit for all three masses is an important goal of this study, it is useful in the context of the
, and mistag background B(x). Although a simultaneous fit for all three masses is an important goal of this study, it is useful in the context of the  data sample to explore subclasses of the fit in which some masses are constrained to their known values. For this purpose we define: (a) the unconstrained fit, in which all three masses are fit simultaneously; (b) the singly-constrained fit, in which m
ν=0 is imposed; and (c) the doubly-constrained fit, in which both m
ν=0 and M
W=80.4 GeV are imposed [33]. The unconstrained fit is well-suited to testing mass measurement techniques for new physics, while the doubly-constrained fit is optimal for a SM determination of the top-quark mass.
data sample to explore subclasses of the fit in which some masses are constrained to their known values. For this purpose we define: (a) the unconstrained fit, in which all three masses are fit simultaneously; (b) the singly-constrained fit, in which m
ν=0 is imposed; and (c) the doubly-constrained fit, in which both m
ν=0 and M
W=80.4 GeV are imposed [33]. The unconstrained fit is well-suited to testing mass measurement techniques for new physics, while the doubly-constrained fit is optimal for a SM determination of the top-quark mass. . In this expression m
gen is the top-quark mass used in generating events while m
meas and σ
meas are the fitted mass and its uncertainty, determined for each pseudo-experiment. For an unbiased fit, the pull distribution will be a Gaussian of unit width and zero mean. A non-zero mean indicates the method is biased, while a non-unit width indicates that the uncertainty is over- or under-estimated. We increase the precision with which we determine the pull distribution width by bootstrapping the simulation to generate multiple pseudo-experiments. The results of Ref. [36] are then used to calculate the mean and standard deviation of the pull distribution, along with uncertainties on each, taking into account the correlations between pseudo-experiments introduced by over-sampling.
. In this expression m
gen is the top-quark mass used in generating events while m
meas and σ
meas are the fitted mass and its uncertainty, determined for each pseudo-experiment. For an unbiased fit, the pull distribution will be a Gaussian of unit width and zero mean. A non-zero mean indicates the method is biased, while a non-unit width indicates that the uncertainty is over- or under-estimated. We increase the precision with which we determine the pull distribution width by bootstrapping the simulation to generate multiple pseudo-experiments. The results of Ref. [36] are then used to calculate the mean and standard deviation of the pull distribution, along with uncertainties on each, taking into account the correlations between pseudo-experiments introduced by over-sampling. for the top-quark mass (other masses are fixed) across 150 MC pseudo-experiments. (Bottom) Fit results obtained in MC
for the top-quark mass (other masses are fixed) across 150 MC pseudo-experiments. (Bottom) Fit results obtained in MC  -only samples generated with MadGraph for various top-quark masses. The best-fit calibration is shown by the solid line and the line of unit slope is shown in the dashed line. Data points are from doubly-constrained fits. The line of unit slope agrees with the fit results with χ
2/degree of freedom=10.7/9
-only samples generated with MadGraph for various top-quark masses. The best-fit calibration is shown by the solid line and the line of unit slope is shown in the dashed line. Data points are from doubly-constrained fits. The line of unit slope agrees with the fit results with χ
2/degree of freedom=10.7/9 and ±0.5 GeV on the measured top-quark mass, respectively. For the electrons, the absolute energy scale is known to 0.5 % in the barrel region and 1.5 % in the endcap region, while for the muons the uncertainty is 0.2 % throughout the sensitive volume. Varying the lepton energy scale accordingly leads to a systematic uncertainty in M
t of
and ±0.5 GeV on the measured top-quark mass, respectively. For the electrons, the absolute energy scale is known to 0.5 % in the barrel region and 1.5 % in the endcap region, while for the muons the uncertainty is 0.2 % throughout the sensitive volume. Varying the lepton energy scale accordingly leads to a systematic uncertainty in M
t of  .
. uncertainty to the measured top-quark mass.
uncertainty to the measured top-quark mass.


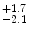
 , M
W, and M
t. A complete summary of central values and statistical and systematic uncertainties for all three mass constraints can be found in Table 5. Figure 8 shows the corresponding fits.
, M
W, and M
t. A complete summary of central values and statistical and systematic uncertainties for all three mass constraints can be found in Table 5. Figure 8 shows the corresponding fits.
 (GeV2)
(GeV2)
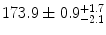

 , M
W, and M
t. The upper red line is in all cases the full fit, while the green (middle) and blue (lowest) curves are for the signal and background shapes, respectively. While the fit is performed event-by-event for all measured kinematic values, the line shown is an approximate extrapolation of the total fit likelihood function over the entire fit range. Top row: unconstrained fit; Middle row: singly-constrained fit; Bottom row: doubly-constrained fit. The inset shows a zoom of the tail region in M
bℓ for the doubly-constrained case to illustrate the level of agreement between the background shape and the data points
, M
W, and M
t. The upper red line is in all cases the full fit, while the green (middle) and blue (lowest) curves are for the signal and background shapes, respectively. While the fit is performed event-by-event for all measured kinematic values, the line shown is an approximate extrapolation of the total fit likelihood function over the entire fit range. Top row: unconstrained fit; Middle row: singly-constrained fit; Bottom row: doubly-constrained fit. The inset shows a zoom of the tail region in M
bℓ for the doubly-constrained case to illustrate the level of agreement between the background shape and the data points dilepton system suggests the technique will be a viable option for mass measurements in a variety of new-physics scenarios. The precision on M
t given by the doubly-constrained fit, for example, is indicative of the precision with which we might determine the masses of new colored particles (like squarks), as a function of the input test mass
dilepton system suggests the technique will be a viable option for mass measurements in a variety of new-physics scenarios. The precision on M
t given by the doubly-constrained fit, for example, is indicative of the precision with which we might determine the masses of new colored particles (like squarks), as a function of the input test mass  . Of course, as shown in the second column of Table 5, the input mass m
ν itself will be determined less precisely. Another plausible scenario is one in which new physics mimics the leptonic decay of the W boson. This can arise in SUSY with R-parity violation and a lepton-number violating term in the superpotential. In this case, the lightest superpartner could be the charged slepton, which decays to a lepton and neutrino, just like the SM W boson. Current bounds from LEP indicate that the slepton must be heavier than 100 GeV. Given the ∼1 GeV precision provided by the singly-constrained fit on the W boson mass, the W boson can easily be discriminated from such an object based on its mass.
. Of course, as shown in the second column of Table 5, the input mass m
ν itself will be determined less precisely. Another plausible scenario is one in which new physics mimics the leptonic decay of the W boson. This can arise in SUSY with R-parity violation and a lepton-number violating term in the superpotential. In this case, the lightest superpartner could be the charged slepton, which decays to a lepton and neutrino, just like the SM W boson. Current bounds from LEP indicate that the slepton must be heavier than 100 GeV. Given the ∼1 GeV precision provided by the singly-constrained fit on the W boson mass, the W boson can easily be discriminated from such an object based on its mass. signal is due to SM neutrinos, rather than heavy WIMPs with masses of order 100 GeV, this level of precision is sufficient to distinguish the two cases. If, on the other hand, the
signal is due to SM neutrinos, rather than heavy WIMPs with masses of order 100 GeV, this level of precision is sufficient to distinguish the two cases. If, on the other hand, the  signal is indeed due to heavy WIMPs, one might expect that the precision on the WIMP mass determination will be no worse than what is shown here for the neutrino, assuming comparable levels of signal and background.
signal is indeed due to heavy WIMPs, one might expect that the precision on the WIMP mass determination will be no worse than what is shown here for the neutrino, assuming comparable levels of signal and background. dilepton events. Motivated primarily by future application to new-physics scenarios, the technique is based on endpoint measurements of new kinematic variables. The three mass parameters
dilepton events. Motivated primarily by future application to new-physics scenarios, the technique is based on endpoint measurements of new kinematic variables. The three mass parameters 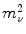 , M
W, and M
t are obtained in a simultaneous fit to three endpoints. In an unconstrained fit to the three masses, the measurement confirms the utility of the techniques proposed for new-physics mass measurements. When
, M
W, and M
t are obtained in a simultaneous fit to three endpoints. In an unconstrained fit to the three masses, the measurement confirms the utility of the techniques proposed for new-physics mass measurements. When  and M
W are constrained to 0 and 80.4 GeV respectively, we find
and M
W are constrained to 0 and 80.4 GeV respectively, we find  , comparable to other dilepton measurements. This is the first measurement of the top-quark mass with an endpoint method. In addition to providing a novel approach to a traditional problem, it achieves a precision similar to that found in standard methods, and its use lays a foundation for application of similar methods to future studies of new physics.
, comparable to other dilepton measurements. This is the first measurement of the top-quark mass with an endpoint method. In addition to providing a novel approach to a traditional problem, it achieves a precision similar to that found in standard methods, and its use lays a foundation for application of similar methods to future studies of new physics.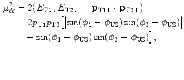
 is the azimuthal angle of the upstream momentum in the CMS reference frame.
is the azimuthal angle of the upstream momentum in the CMS reference frame. and
and  (or vice-versa) then the value of μ
ℓℓ is identically zero. This is the origin of the delta function in Eq. (4.4). It is convenient to measure
(or vice-versa) then the value of μ
ℓℓ is identically zero. This is the origin of the delta function in Eq. (4.4). It is convenient to measure  from the midline between the lepton p
T vectors rather than from the CMS-defined x axis, and hence we define
from the midline between the lepton p
T vectors rather than from the CMS-defined x axis, and hence we define  . We also define the separation between the two lepton vectors: Δϕ≡ϕ
1−ϕ
2.
. We also define the separation between the two lepton vectors: Δϕ≡ϕ
1−ϕ
2.
 , and is exactly zero in the neighboring regions
, and is exactly zero in the neighboring regions  and
and 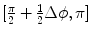 . The function is periodic in Φ with period π, but because of the condition σ
Φ≪π we restrict our attention to the interval 0≤Φ≤π. For the non-zero portion of μ(Φ) there is also an inverse function:
. The function is periodic in Φ with period π, but because of the condition σ
Φ≪π we restrict our attention to the interval 0≤Φ≤π. For the non-zero portion of μ(Φ) there is also an inverse function:  . Thus the total resolution function is given by
. Thus the total resolution function is given by  and π/2 and the σ
Φ is relatively narrow; in the bottom panel, Φ is closer to π/2 and has a large value of σ
Φ that allows smearing into the
and π/2 and the σ
Φ is relatively narrow; in the bottom panel, Φ is closer to π/2 and has a large value of σ
Φ that allows smearing into the  region. The high bin at −45 GeV in the histogram component of the bottom panel contains events in which the resolution smearing of the upstream momentum vector pushed the μ
ℓℓ value into the delta function at μ
ℓℓ=0. In the analytic form, the corresponding feature would be the delta function R
0
δ(μ); but, as noted above, this has not been explicitly drawn.
region. The high bin at −45 GeV in the histogram component of the bottom panel contains events in which the resolution smearing of the upstream momentum vector pushed the μ
ℓℓ value into the delta function at μ
ℓℓ=0. In the analytic form, the corresponding feature would be the delta function R
0
δ(μ); but, as noted above, this has not been explicitly drawn.
 channel using ATLAS data. Eur. Phys. J. C. 2012;72:2046. doi: 10.1140/epjc/s10052-012-2046-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
channel using ATLAS data. Eur. Phys. J. C. 2012;72:2046. doi: 10.1140/epjc/s10052-012-2046-6. [DOI] [PMC free article] [PubMed] [Google Scholar] events with lepton+jets final states in pp collisions at
events with lepton+jets final states in pp collisions at 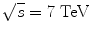 J. High Energy Phys. 2012;12:105. [Google Scholar]
J. High Energy Phys. 2012;12:105. [Google Scholar] events with dilepton final states in pp collisions at
events with dilepton final states in pp collisions at 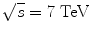 Eur. Phys. J. C. 2012;72:2202. doi: 10.1140/epjc/s10052-012-2202-z. [DOI] [Google Scholar]
Eur. Phys. J. C. 2012;72:2202. doi: 10.1140/epjc/s10052-012-2202-z. [DOI] [Google Scholar] . CMS physics analysis summary CMS-PAS-PFT-09-001 (2009). http://cdsweb.cern.ch/record/1194487
. CMS physics analysis summary CMS-PAS-PFT-09-001 (2009). http://cdsweb.cern.ch/record/1194487
 production cross section in the dilepton channel in pp collisions at
production cross section in the dilepton channel in pp collisions at 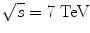 J. High Energy Phys. 2012;1211:067. [Google Scholar]
J. High Energy Phys. 2012;1211:067. [Google Scholar] events with dilepton final states in pp collisions at
events with dilepton final states in pp collisions at 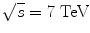 Eur. Phys. J. C. 2012;72:2202. doi: 10.1140/epjc/s10052-012-2202-z. [DOI] [Google Scholar]
Eur. Phys. J. C. 2012;72:2202. doi: 10.1140/epjc/s10052-012-2202-z. [DOI] [Google Scholar]