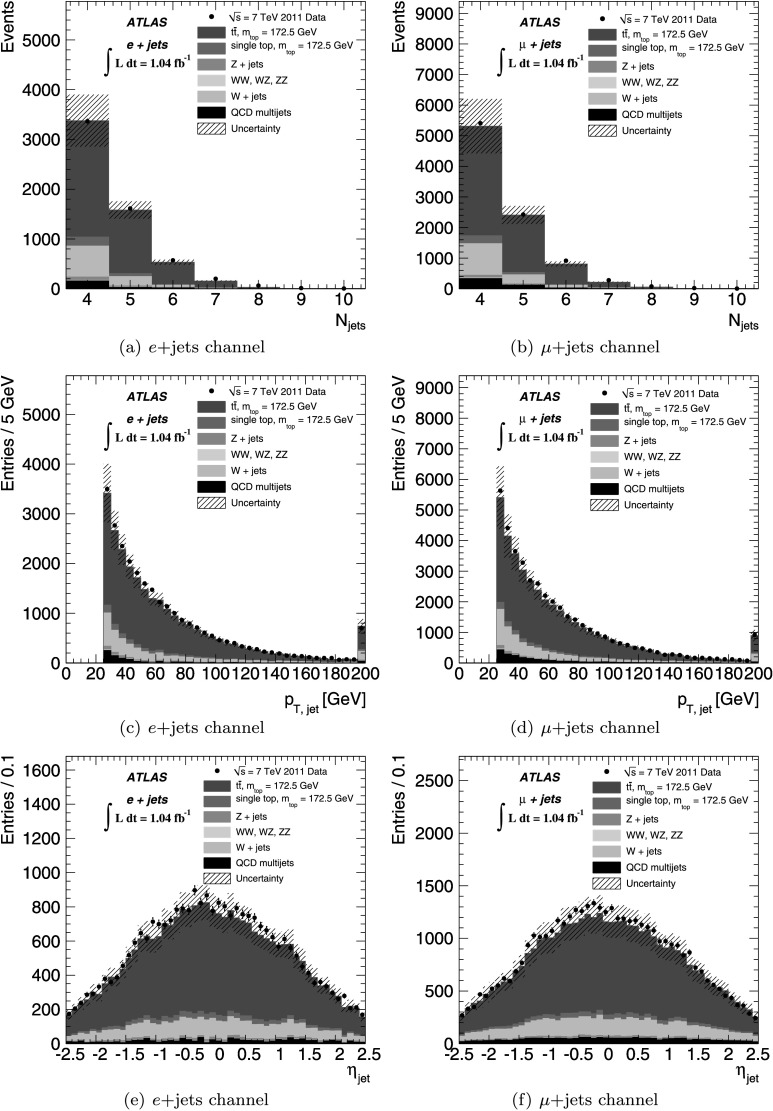
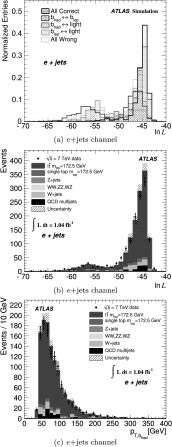
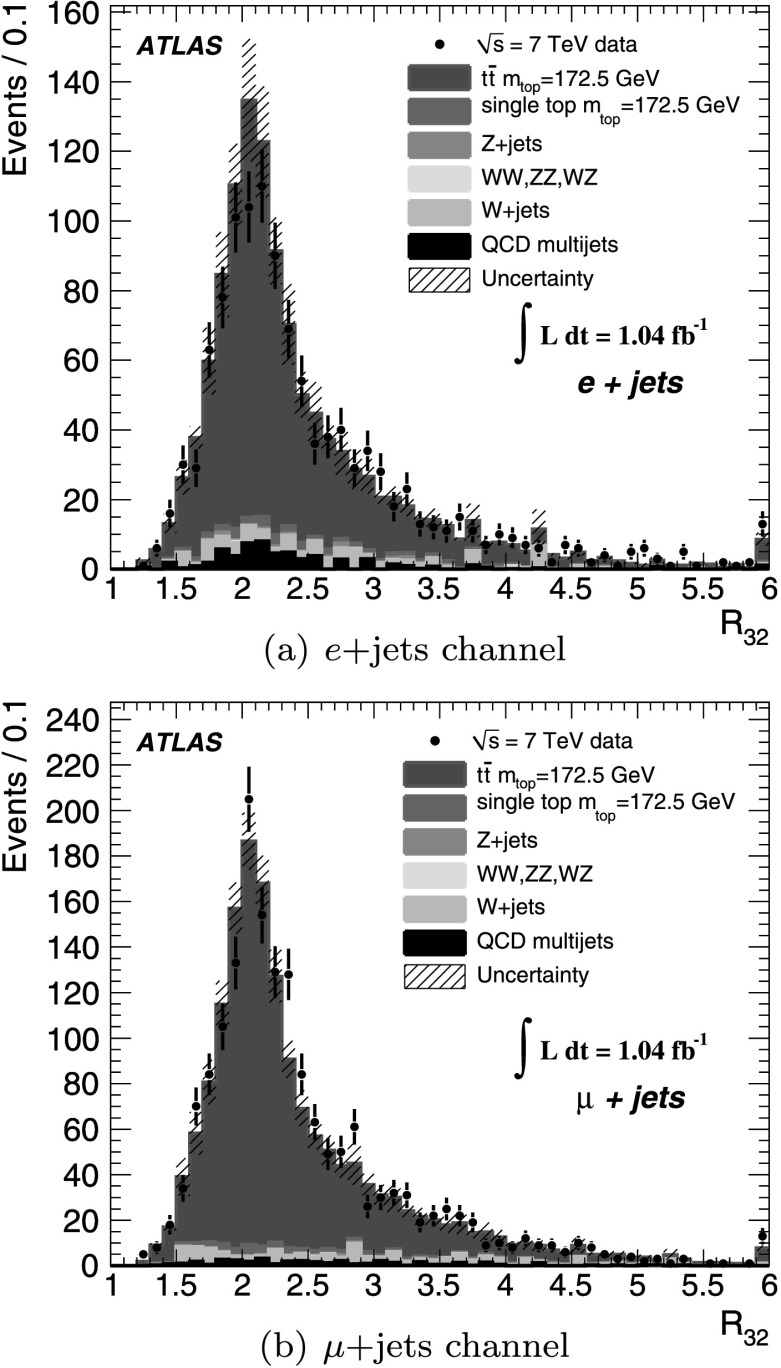
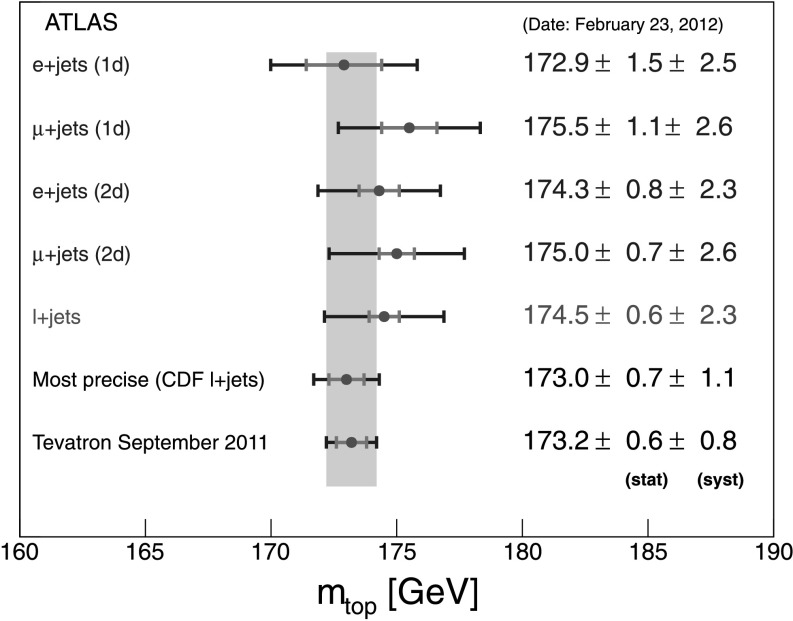
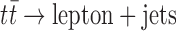The ATLAS Collaboration1,
G Aad
G Aad
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
B Abbott
B Abbott
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
J Abdallah
J Abdallah
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
A A Abdelalim
A A Abdelalim
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
A Abdesselam
A Abdesselam
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
O Abdinov
O Abdinov
15Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
15,
B Abi
B Abi
138Department of Physics, Oklahoma State University, Stillwater, OK United States of America
138,
M Abolins
M Abolins
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
O S AbouZeid
O S AbouZeid
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
H Abramowicz
H Abramowicz
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
H Abreu
H Abreu
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
E Acerbi
E Acerbi
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
B S Acharya
B S Acharya
204INFN Gruppo Collegato di Udine, Udine, Italy
205ICTP, Trieste, Italy
204,205,
L Adamczyk
L Adamczyk
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
D L Adams
D L Adams
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
T N Addy
T N Addy
78Department of Physics, Hampton University, Hampton, VA United States of America
78,
J Adelman
J Adelman
217Department of Physics, Yale University, New Haven, CT United States of America
217,
M Aderholz
M Aderholz
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
S Adomeit
S Adomeit
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
P Adragna
P Adragna
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
T Adye
T Adye
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
S Aefsky
S Aefsky
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
J A Aguilar-Saavedra
J A Aguilar-Saavedra
153Departamento de Fisica Teorica y del Cosmos and CAFPE, Universidad de Granada, Granada, Spain
153,
M Aharrouche
M Aharrouche
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
S P Ahlen
S P Ahlen
31Department of Physics, Boston University, Boston, MA United States of America
31,
F Ahles
F Ahles
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
A Ahmad
A Ahmad
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
M Ahsan
M Ahsan
60Physics Department, University of Texas at Dallas, Richardson, TX United States of America
60,
G Aielli
G Aielli
163INFN Sezione di Roma Tor Vergata, Roma, Italy
164Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
163,164,
T Akdogan
T Akdogan
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
T P A Åkesson
T P A Åkesson
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
G Akimoto
G Akimoto
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
A V Akimov
A V Akimov
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
A Akiyama
A Akiyama
90Graduate School of Science, Kobe University, Kobe, Japan
90,
M S Alam
M S Alam
2University at Albany, Albany, NY United States of America
2,
M A Alam
M A Alam
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
J Albert
J Albert
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
S Albrand
S Albrand
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
M Aleksa
M Aleksa
44CERN, Geneva, Switzerland
44,
I N Aleksandrov
I N Aleksandrov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
F Alessandria
F Alessandria
113INFN Sezione di Milano, Milano, Italy
113,
C Alexa
C Alexa
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
G Alexander
G Alexander
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
G Alexandre
G Alexandre
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
T Alexopoulos
T Alexopoulos
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
M Alhroob
M Alhroob
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Aliev
M Aliev
21Department of Physics, Humboldt University, Berlin, Germany
21,
G Alimonti
G Alimonti
113INFN Sezione di Milano, Milano, Italy
113,
J Alison
J Alison
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
M Aliyev
M Aliyev
15Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
15,
B M M Allbrooke
B M M Allbrooke
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
P P Allport
P P Allport
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
S E Allwood-Spiers
S E Allwood-Spiers
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
J Almond
J Almond
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
A Aloisio
A Aloisio
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
R Alon
R Alon
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
A Alonso
A Alonso
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
B Alvarez Gonzalez
B Alvarez Gonzalez
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
M G Alviggi
M G Alviggi
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
K Amako
K Amako
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
P Amaral
P Amaral
44CERN, Geneva, Switzerland
44,
C Amelung
C Amelung
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
V V Ammosov
V V Ammosov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
A Amorim
A Amorim
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
G Amorós
G Amorós
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
N Amram
N Amram
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
C Anastopoulos
C Anastopoulos
44CERN, Geneva, Switzerland
44,
L S Ancu
L S Ancu
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
N Andari
N Andari
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
T Andeen
T Andeen
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
C F Anders
C F Anders
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
G Anders
G Anders
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
K J Anderson
K J Anderson
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A Andreazza
A Andreazza
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
V Andrei
V Andrei
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
M-L Andrieux
M-L Andrieux
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
X S Anduaga
X S Anduaga
93Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
93,
A Angerami
A Angerami
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
F Anghinolfi
F Anghinolfi
44CERN, Geneva, Switzerland
44,
A Anisenkov
A Anisenkov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
N Anjos
N Anjos
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
A Annovi
A Annovi
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
A Antonaki
A Antonaki
13Physics Department, University of Athens, Athens, Greece
13,
M Antonelli
M Antonelli
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
A Antonov
A Antonov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
J Antos
J Antos
181Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
181,
F Anulli
F Anulli
161INFN Sezione di Roma I, Roma, Italy
161,
S Aoun
S Aoun
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
L Aperio Bella
L Aperio Bella
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
R Apolle
R Apolle
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
G Arabidze
G Arabidze
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
I Aracena
I Aracena
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
Y Arai
Y Arai
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
A T H Arce
A T H Arce
64Department of Physics, Duke University, Durham, NC United States of America
64,
S Arfaoui
S Arfaoui
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
J-F Arguin
J-F Arguin
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Arik
E Arik
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
M Arik
M Arik
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
A J Armbruster
A J Armbruster
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
O Arnaez
O Arnaez
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
C Arnault
C Arnault
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
A Artamonov
A Artamonov
120Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
120,
G Artoni
G Artoni
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
D Arutinov
D Arutinov
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
S Asai
S Asai
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
R Asfandiyarov
R Asfandiyarov
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
S Ask
S Ask
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
B Åsman
B Åsman
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
L Asquith
L Asquith
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
K Assamagan
K Assamagan
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
A Astbury
A Astbury
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
A Astvatsatourov
A Astvatsatourov
74II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
74,
B Aubert
B Aubert
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
E Auge
E Auge
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
K Augsten
K Augsten
156Czech Technical University in Prague, Praha, Czech Republic
156,
M Aurousseau
M Aurousseau
182Department of Physics, University of Johannesburg, Johannesburg, South Africa
182,
G Avolio
G Avolio
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
R Avramidou
R Avramidou
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
D Axen
D Axen
210Department of Physics, University of British Columbia, Vancouver, BC Canada
210,
C Ay
C Ay
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
G Azuelos
G Azuelos
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
Y Azuma
Y Azuma
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
M A Baak
M A Baak
44CERN, Geneva, Switzerland
44,
G Baccaglioni
G Baccaglioni
113INFN Sezione di Milano, Milano, Italy
113,
C Bacci
C Bacci
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
A M Bach
A M Bach
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
H Bachacou
H Bachacou
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
K Bachas
K Bachas
44CERN, Geneva, Switzerland
44,
M Backes
M Backes
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
M Backhaus
M Backhaus
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
E Badescu
E Badescu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
P Bagnaia
P Bagnaia
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
S Bahinipati
S Bahinipati
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
Y Bai
Y Bai
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
D C Bailey
D C Bailey
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
T Bain
T Bain
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
J T Baines
J T Baines
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
O K Baker
O K Baker
217Department of Physics, Yale University, New Haven, CT United States of America
217,
M D Baker
M D Baker
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S Baker
S Baker
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
E Banas
E Banas
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
P Banerjee
P Banerjee
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
Sw Banerjee
Sw Banerjee
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
D Banfi
D Banfi
44CERN, Geneva, Switzerland
44,
A Bangert
A Bangert
189School of Physics, University of Sydney, Sydney, Australia
189,
V Bansal
V Bansal
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
H S Bansil
H S Bansil
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
L Barak
L Barak
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
S P Baranov
S P Baranov
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
A Barashkou
A Barashkou
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A Barbaro Galtieri
A Barbaro Galtieri
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
T Barber
T Barber
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
E L Barberio
E L Barberio
110School of Physics, University of Melbourne, Victoria, Australia
110,
D Barberis
D Barberis
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
M Barbero
M Barbero
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
D Y Bardin
D Y Bardin
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
T Barillari
T Barillari
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
M Barisonzi
M Barisonzi
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
T Barklow
T Barklow
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
N Barlow
N Barlow
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
B M Barnett
B M Barnett
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
R M Barnett
R M Barnett
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
A Baroncelli
A Baroncelli
165INFN Sezione di Roma Tre, Roma, Italy
165,
G Barone
G Barone
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
A J Barr
A J Barr
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
F Barreiro
F Barreiro
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
J Barreiro Guimarães da Costa
J Barreiro Guimarães da Costa
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
P Barrillon
P Barrillon
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
R Bartoldus
R Bartoldus
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
A E Barton
A E Barton
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
V Bartsch
V Bartsch
188Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
188,
R L Bates
R L Bates
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
L Batkova
L Batkova
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
J R Batley
J R Batley
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
A Battaglia
A Battaglia
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
M Battistin
M Battistin
44CERN, Geneva, Switzerland
44,
F Bauer
F Bauer
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
H S Bawa
H S Bawa
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S Beale
S Beale
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
B Beare
B Beare
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
T Beau
T Beau
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
P H Beauchemin
P H Beauchemin
201Science and Technology Center, Tufts University, Medford, MA United States of America
201,
R Beccherle
R Beccherle
70INFN Sezione di Genova, Genova, Italy
70,
P Bechtle
P Bechtle
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
H P Beck
H P Beck
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
S Becker
S Becker
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Beckingham
M Beckingham
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
K H Becks
K H Becks
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
A J Beddall
A J Beddall
26Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
26,
A Beddall
A Beddall
26Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
26,
S Bedikian
S Bedikian
217Department of Physics, Yale University, New Haven, CT United States of America
217,
V A Bednyakov
V A Bednyakov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
C P Bee
C P Bee
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
M Begel
M Begel
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S Behar Harpaz
S Behar Harpaz
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
P K Behera
P K Behera
86University of Iowa, Iowa City, IA United States of America
86,
M Beimforde
M Beimforde
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
C Belanger-Champagne
C Belanger-Champagne
109Department of Physics, McGill University, Montreal, QC Canada
109,
P J Bell
P J Bell
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
W H Bell
W H Bell
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
G Bella
G Bella
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
L Bellagamba
L Bellagamba
28INFN Sezione di Bologna, Bologna, Italy
28,
F Bellina
F Bellina
44CERN, Geneva, Switzerland
44,
M Bellomo
M Bellomo
44CERN, Geneva, Switzerland
44,
A Belloni
A Belloni
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
O Beloborodova
O Beloborodova
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
K Belotskiy
K Belotskiy
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
O Beltramello
O Beltramello
44CERN, Geneva, Switzerland
44,
S Ben Ami
S Ben Ami
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
O Benary
O Benary
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
D Benchekroun
D Benchekroun
167Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
167,
C Benchouk
C Benchouk
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
M Bendel
M Bendel
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
N Benekos
N Benekos
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
Y Benhammou
Y Benhammou
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
E Benhar Noccioli
E Benhar Noccioli
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
J A Benitez Garcia
J A Benitez Garcia
199Department of Physics and Astronomy, York University, Toronto, ON Canada
199,
D P Benjamin
D P Benjamin
64Department of Physics, Duke University, Durham, NC United States of America
64,
M Benoit
M Benoit
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
J R Bensinger
J R Bensinger
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
K Benslama
K Benslama
159Physics Department, University of Regina, Regina, SK Canada
159,
S Bentvelsen
S Bentvelsen
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
D Berge
D Berge
44CERN, Geneva, Switzerland
44,
E Bergeaas Kuutmann
E Bergeaas Kuutmann
61DESY, Hamburg and Zeuthen, Germany
61,
N Berger
N Berger
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
F Berghaus
F Berghaus
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
E Berglund
E Berglund
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
J Beringer
J Beringer
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
P Bernat
P Bernat
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
R Bernhard
R Bernhard
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
C Bernius
C Bernius
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
T Berry
T Berry
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
C Bertella
C Bertella
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
A Bertin
A Bertin
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
F Bertinelli
F Bertinelli
44CERN, Geneva, Switzerland
44,
F Bertolucci
F Bertolucci
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
M I Besana
M I Besana
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
N Besson
N Besson
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
S Bethke
S Bethke
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
W Bhimji
W Bhimji
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
R M Bianchi
R M Bianchi
44CERN, Geneva, Switzerland
44,
M Bianco
M Bianco
95INFN Sezione di Lecce, Lecce, Italy
96Dipartimento di Fisica, Università del Salento, Lecce, Italy
95,96,
O Biebel
O Biebel
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
S P Bieniek
S P Bieniek
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
K Bierwagen
K Bierwagen
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
J Biesiada
J Biesiada
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Biglietti
M Biglietti
165INFN Sezione di Roma Tre, Roma, Italy
165,
H Bilokon
H Bilokon
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
M Bindi
M Bindi
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
S Binet
S Binet
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
A Bingul
A Bingul
26Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
26,
C Bini
C Bini
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
C Biscarat
C Biscarat
219Domaine scientifique de la Doua, Centre de Calcul CNRS/IN2P3, Villeurbanne Cedex, France
219,
U Bitenc
U Bitenc
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
K M Black
K M Black
31Department of Physics, Boston University, Boston, MA United States of America
31,
R E Blair
R E Blair
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
J-B Blanchard
J-B Blanchard
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
G Blanchot
G Blanchot
44CERN, Geneva, Switzerland
44,
T Blazek
T Blazek
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
C Blocker
C Blocker
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
J Blocki
J Blocki
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
A Blondel
A Blondel
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
W Blum
W Blum
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
U Blumenschein
U Blumenschein
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
G J Bobbink
G J Bobbink
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
V B Bobrovnikov
V B Bobrovnikov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
S S Bocchetta
S S Bocchetta
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
A Bocci
A Bocci
64Department of Physics, Duke University, Durham, NC United States of America
64,
C R Boddy
C R Boddy
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
M Boehler
M Boehler
61DESY, Hamburg and Zeuthen, Germany
61,
J Boek
J Boek
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
N Boelaert
N Boelaert
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
J A Bogaerts
J A Bogaerts
44CERN, Geneva, Switzerland
44,
A Bogdanchikov
A Bogdanchikov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
A Bogouch
A Bogouch
115B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
115,
C Bohm
C Bohm
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
V Boisvert
V Boisvert
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
T Bold
T Bold
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
V Boldea
V Boldea
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
N M Bolnet
N M Bolnet
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
M Bona
M Bona
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
V G Bondarenko
V G Bondarenko
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
M Bondioli
M Bondioli
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
M Boonekamp
M Boonekamp
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
C N Booth
C N Booth
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
S Bordoni
S Bordoni
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
C Borer
C Borer
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
A Borisov
A Borisov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
G Borissov
G Borissov
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
I Borjanovic
I Borjanovic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
M Borri
M Borri
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
S Borroni
S Borroni
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
V Bortolotto
V Bortolotto
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
K Bos
K Bos
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
D Boscherini
D Boscherini
28INFN Sezione di Bologna, Bologna, Italy
28,
M Bosman
M Bosman
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
H Boterenbrood
H Boterenbrood
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
D Botterill
D Botterill
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
J Bouchami
J Bouchami
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
J Boudreau
J Boudreau
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
E V Bouhova-Thacker
E V Bouhova-Thacker
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
D Boumediene
D Boumediene
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
C Bourdarios
C Bourdarios
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
N Bousson
N Bousson
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
A Boveia
A Boveia
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
J Boyd
J Boyd
44CERN, Geneva, Switzerland
44,
I R Boyko
I R Boyko
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
N I Bozhko
N I Bozhko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
I Bozovic-Jelisavcic
I Bozovic-Jelisavcic
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
J Bracinik
J Bracinik
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
A Braem
A Braem
44CERN, Geneva, Switzerland
44,
P Branchini
P Branchini
165INFN Sezione di Roma Tre, Roma, Italy
165,
G W Brandenburg
G W Brandenburg
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
A Brandt
A Brandt
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
G Brandt
G Brandt
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
O Brandt
O Brandt
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
U Bratzler
U Bratzler
195Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
195,
B Brau
B Brau
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
J E Brau
J E Brau
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
H M Braun
H M Braun
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
B Brelier
B Brelier
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
J Bremer
J Bremer
44CERN, Geneva, Switzerland
44,
R Brenner
R Brenner
208Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
208,
S Bressler
S Bressler
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
D Breton
D Breton
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
D Britton
D Britton
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
F M Brochu
F M Brochu
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
I Brock
I Brock
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
R Brock
R Brock
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
T J Brodbeck
T J Brodbeck
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
E Brodet
E Brodet
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
F Broggi
F Broggi
113INFN Sezione di Milano, Milano, Italy
113,
C Bromberg
C Bromberg
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
J Bronner
J Bronner
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
G Brooijmans
G Brooijmans
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
W K Brooks
W K Brooks
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
G Brown
G Brown
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
H Brown
H Brown
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
P A Bruckman de Renstrom
P A Bruckman de Renstrom
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
D Bruncko
D Bruncko
181Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
181,
R Bruneliere
R Bruneliere
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
S Brunet
S Brunet
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
A Bruni
A Bruni
28INFN Sezione di Bologna, Bologna, Italy
28,
G Bruni
G Bruni
28INFN Sezione di Bologna, Bologna, Italy
28,
M Bruschi
M Bruschi
28INFN Sezione di Bologna, Bologna, Italy
28,
T Buanes
T Buanes
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
Q Buat
Q Buat
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
F Bucci
F Bucci
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
J Buchanan
J Buchanan
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
N J Buchanan
N J Buchanan
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
P Buchholz
P Buchholz
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
R M Buckingham
R M Buckingham
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
A G Buckley
A G Buckley
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
S I Buda
S I Buda
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
I A Budagov
I A Budagov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
B Budick
B Budick
134Department of Physics, New York University, New York, NY United States of America
134,
V Büscher
V Büscher
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
L Bugge
L Bugge
143Department of Physics, University of Oslo, Oslo, Norway
143,
O Bulekov
O Bulekov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
M Bunse
M Bunse
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
T Buran
T Buran
143Department of Physics, University of Oslo, Oslo, Norway
143,
H Burckhart
H Burckhart
44CERN, Geneva, Switzerland
44,
S Burdin
S Burdin
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
T Burgess
T Burgess
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
S Burke
S Burke
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
E Busato
E Busato
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
P Bussey
P Bussey
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
C P Buszello
C P Buszello
208Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
208,
F Butin
F Butin
44CERN, Geneva, Switzerland
44,
B Butler
B Butler
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
J M Butler
J M Butler
31Department of Physics, Boston University, Boston, MA United States of America
31,
C M Buttar
C M Buttar
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
J M Butterworth
J M Butterworth
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
W Buttinger
W Buttinger
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
S Cabrera Urbán
S Cabrera Urbán
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
D Caforio
D Caforio
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
O Cakir
O Cakir
4Department of Physics, Ankara University, Ankara, Turkey
4,
P Calafiura
P Calafiura
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
G Calderini
G Calderini
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
P Calfayan
P Calfayan
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
R Calkins
R Calkins
132Department of Physics, Northern Illinois University, DeKalb, IL United States of America
132,
L P Caloba
L P Caloba
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
R Caloi
R Caloi
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
D Calvet
D Calvet
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
S Calvet
S Calvet
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
R Camacho Toro
R Camacho Toro
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
P Camarri
P Camarri
163INFN Sezione di Roma Tor Vergata, Roma, Italy
164Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
163,164,
M Cambiaghi
M Cambiaghi
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
D Cameron
D Cameron
143Department of Physics, University of Oslo, Oslo, Norway
143,
L M Caminada
L M Caminada
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
S Campana
S Campana
44CERN, Geneva, Switzerland
44,
M Campanelli
M Campanelli
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
V Canale
V Canale
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
F Canelli
F Canelli
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A Canepa
A Canepa
198TRIUMF, Vancouver, BC Canada
198,
J Cantero
J Cantero
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
L Capasso
L Capasso
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
M D M Capeans Garrido
M D M Capeans Garrido
44CERN, Geneva, Switzerland
44,
I Caprini
I Caprini
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
M Caprini
M Caprini
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
D Capriotti
D Capriotti
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
M Capua
M Capua
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
R Caputo
R Caputo
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
C Caramarcu
C Caramarcu
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
R Cardarelli
R Cardarelli
163INFN Sezione di Roma Tor Vergata, Roma, Italy
163,
T Carli
T Carli
44CERN, Geneva, Switzerland
44,
G Carlino
G Carlino
127INFN Sezione di Napoli, Napoli, Italy
127,
L Carminati
L Carminati
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
B Caron
B Caron
109Department of Physics, McGill University, Montreal, QC Canada
109,
S Caron
S Caron
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
G D Carrillo Montoya
G D Carrillo Montoya
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
A A Carter
A A Carter
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
J R Carter
J R Carter
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
J Carvalho
J Carvalho
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
D Casadei
D Casadei
134Department of Physics, New York University, New York, NY United States of America
134,
M P Casado
M P Casado
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
M Cascella
M Cascella
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
C Caso
C Caso
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
A M Castaneda Hernandez
A M Castaneda Hernandez
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
E Castaneda-Miranda
E Castaneda-Miranda
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
V Castillo Gimenez
V Castillo Gimenez
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
N F Castro
N F Castro
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
G Cataldi
G Cataldi
95INFN Sezione di Lecce, Lecce, Italy
95,
F Cataneo
F Cataneo
44CERN, Geneva, Switzerland
44,
A Catinaccio
A Catinaccio
44CERN, Geneva, Switzerland
44,
J R Catmore
J R Catmore
44CERN, Geneva, Switzerland
44,
A Cattai
A Cattai
44CERN, Geneva, Switzerland
44,
G Cattani
G Cattani
163INFN Sezione di Roma Tor Vergata, Roma, Italy
164Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
163,164,
S Caughron
S Caughron
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
D Cauz
D Cauz
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
P Cavalleri
P Cavalleri
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
D Cavalli
D Cavalli
113INFN Sezione di Milano, Milano, Italy
113,
M Cavalli-Sforza
M Cavalli-Sforza
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
V Cavasinni
V Cavasinni
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
F Ceradini
F Ceradini
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
A S Cerqueira
A S Cerqueira
34Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
34,
A Cerri
A Cerri
44CERN, Geneva, Switzerland
44,
L Cerrito
L Cerrito
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
F Cerutti
F Cerutti
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
S A Cetin
S A Cetin
25Division of Physics, Dogus University, Istanbul, Turkey
25,
F Cevenini
F Cevenini
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
A Chafaq
A Chafaq
167Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
167,
D Chakraborty
D Chakraborty
132Department of Physics, Northern Illinois University, DeKalb, IL United States of America
132,
K Chan
K Chan
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
B Chapleau
B Chapleau
109Department of Physics, McGill University, Montreal, QC Canada
109,
J D Chapman
J D Chapman
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
J W Chapman
J W Chapman
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
E Chareyre
E Chareyre
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
D G Charlton
D G Charlton
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
V Chavda
V Chavda
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
C A Chavez Barajas
C A Chavez Barajas
44CERN, Geneva, Switzerland
44,
S Cheatham
S Cheatham
109Department of Physics, McGill University, Montreal, QC Canada
109,
S Chekanov
S Chekanov
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
S V Chekulaev
S V Chekulaev
198TRIUMF, Vancouver, BC Canada
198,
G A Chelkov
G A Chelkov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
M A Chelstowska
M A Chelstowska
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
C Chen
C Chen
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
H Chen
H Chen
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S Chen
S Chen
50Department of Physics, Nanjing University, Jiangsu, China
50,
T Chen
T Chen
50Department of Physics, Nanjing University, Jiangsu, China
50,
X Chen
X Chen
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
S Cheng
S Cheng
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
A Cheplakov
A Cheplakov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
V F Chepurnov
V F Chepurnov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
R Cherkaoui El Moursli
R Cherkaoui El Moursli
171Faculté des Sciences, Université Mohammed V-Agdal, Rabat, Morocco
171,
V Chernyatin
V Chernyatin
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
E Cheu
E Cheu
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
S L Cheung
S L Cheung
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
L Chevalier
L Chevalier
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
G Chiefari
G Chiefari
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
L Chikovani
L Chikovani
72E.Andronikashvili Institute of Physics, Tbilisi State University, Tbilisi, Georgia
72,
J T Childers
J T Childers
44CERN, Geneva, Switzerland
44,
A Chilingarov
A Chilingarov
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
G Chiodini
G Chiodini
95INFN Sezione di Lecce, Lecce, Italy
95,
A S Chisholm
A S Chisholm
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
M V Chizhov
M V Chizhov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
G Choudalakis
G Choudalakis
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
S Chouridou
S Chouridou
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
I A Christidi
I A Christidi
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
A Christov
A Christov
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
D Chromek-Burckhart
D Chromek-Burckhart
44CERN, Geneva, Switzerland
44,
M L Chu
M L Chu
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
J Chudoba
J Chudoba
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
G Ciapetti
G Ciapetti
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
K Ciba
K Ciba
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
A K Ciftci
A K Ciftci
4Department of Physics, Ankara University, Ankara, Turkey
4,
R Ciftci
R Ciftci
4Department of Physics, Ankara University, Ankara, Turkey
4,
D Cinca
D Cinca
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
V Cindro
V Cindro
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
M D Ciobotaru
M D Ciobotaru
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
C Ciocca
C Ciocca
28INFN Sezione di Bologna, Bologna, Italy
28,
A Ciocio
A Ciocio
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Cirilli
M Cirilli
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
M Citterio
M Citterio
113INFN Sezione di Milano, Milano, Italy
113,
M Ciubancan
M Ciubancan
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
A Clark
A Clark
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
P J Clark
P J Clark
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
W Cleland
W Cleland
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
J C Clemens
J C Clemens
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
B Clement
B Clement
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
C Clement
C Clement
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
R W Clifft
R W Clifft
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
Y Coadou
Y Coadou
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
M Cobal
M Cobal
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
A Coccaro
A Coccaro
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
J Cochran
J Cochran
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
P Coe
P Coe
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
J G Cogan
J G Cogan
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
J Coggeshall
J Coggeshall
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
E Cogneras
E Cogneras
219Domaine scientifique de la Doua, Centre de Calcul CNRS/IN2P3, Villeurbanne Cedex, France
219,
J Colas
J Colas
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
A P Colijn
A P Colijn
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
N J Collins
N J Collins
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
C Collins-Tooth
C Collins-Tooth
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
J Collot
J Collot
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
G Colon
G Colon
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
P Conde Muiño
P Conde Muiño
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
E Coniavitis
E Coniavitis
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
M C Conidi
M C Conidi
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
M Consonni
M Consonni
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
V Consorti
V Consorti
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
S Constantinescu
S Constantinescu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
C Conta
C Conta
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
F Conventi
F Conventi
127INFN Sezione di Napoli, Napoli, Italy
127,
J Cook
J Cook
44CERN, Geneva, Switzerland
44,
M Cooke
M Cooke
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
B D Cooper
B D Cooper
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
A M Cooper-Sarkar
A M Cooper-Sarkar
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
K Copic
K Copic
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
T Cornelissen
T Cornelissen
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
M Corradi
M Corradi
28INFN Sezione di Bologna, Bologna, Italy
28,
F Corriveau
F Corriveau
109Department of Physics, McGill University, Montreal, QC Canada
109,
A Cortes-Gonzalez
A Cortes-Gonzalez
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
G Cortiana
G Cortiana
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
G Costa
G Costa
113INFN Sezione di Milano, Milano, Italy
113,
M J Costa
M J Costa
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
D Costanzo
D Costanzo
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
T Costin
T Costin
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
D Côté
D Côté
44CERN, Geneva, Switzerland
44,
R Coura Torres
R Coura Torres
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
L Courneyea
L Courneyea
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
G Cowan
G Cowan
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
C Cowden
C Cowden
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
B E Cox
B E Cox
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
K Cranmer
K Cranmer
134Department of Physics, New York University, New York, NY United States of America
134,
F Crescioli
F Crescioli
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
M Cristinziani
M Cristinziani
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
G Crosetti
G Crosetti
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
R Crupi
R Crupi
95INFN Sezione di Lecce, Lecce, Italy
96Dipartimento di Fisica, Università del Salento, Lecce, Italy
95,96,
S Crépé-Renaudin
S Crépé-Renaudin
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
C-M Cuciuc
C-M Cuciuc
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
C Cuenca Almenar
C Cuenca Almenar
217Department of Physics, Yale University, New Haven, CT United States of America
217,
T Cuhadar Donszelmann
T Cuhadar Donszelmann
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
M Curatolo
M Curatolo
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
C J Curtis
C J Curtis
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
C Cuthbert
C Cuthbert
189School of Physics, University of Sydney, Sydney, Australia
189,
P Cwetanski
P Cwetanski
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
H Czirr
H Czirr
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
P Czodrowski
P Czodrowski
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
Z Czyczula
Z Czyczula
217Department of Physics, Yale University, New Haven, CT United States of America
217,
S D’Auria
S D’Auria
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
M D’Onofrio
M D’Onofrio
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
A D’Orazio
A D’Orazio
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
P V M Da Silva
P V M Da Silva
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
C Da Via
C Da Via
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
W Dabrowski
W Dabrowski
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
T Dai
T Dai
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
C Dallapiccola
C Dallapiccola
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
M Dam
M Dam
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
M Dameri
M Dameri
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
D S Damiani
D S Damiani
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
H O Danielsson
H O Danielsson
44CERN, Geneva, Switzerland
44,
D Dannheim
D Dannheim
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
V Dao
V Dao
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
G Darbo
G Darbo
70INFN Sezione di Genova, Genova, Italy
70,
G L Darlea
G L Darlea
39University Politehnica Bucharest, Bucharest, Romania
39,
W Davey
W Davey
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
T Davidek
T Davidek
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
N Davidson
N Davidson
110School of Physics, University of Melbourne, Victoria, Australia
110,
R Davidson
R Davidson
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
E Davies
E Davies
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
M Davies
M Davies
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
A R Davison
A R Davison
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
Y Davygora
Y Davygora
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
E Dawe
E Dawe
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
I Dawson
I Dawson
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
J W Dawson
J W Dawson
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
R K Daya-Ishmukhametova
R K Daya-Ishmukhametova
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
K De
K De
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
R de Asmundis
R de Asmundis
127INFN Sezione di Napoli, Napoli, Italy
127,
S De Castro
S De Castro
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
P E De Castro Faria Salgado
P E De Castro Faria Salgado
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S De Cecco
S De Cecco
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
J de Graat
J de Graat
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
N De Groot
N De Groot
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
P de Jong
P de Jong
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
C De La Taille
C De La Taille
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
H De la Torre
H De la Torre
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
B De Lotto
B De Lotto
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
L de Mora
L de Mora
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
L De Nooij
L De Nooij
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
D De Pedis
D De Pedis
161INFN Sezione di Roma I, Roma, Italy
161,
A De Salvo
A De Salvo
161INFN Sezione di Roma I, Roma, Italy
161,
U De Sanctis
U De Sanctis
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
A De Santo
A De Santo
188Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
188,
J B De Vivie De Regie
J B De Vivie De Regie
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
S Dean
S Dean
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
W J Dearnaley
W J Dearnaley
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
R Debbe
R Debbe
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
C Debenedetti
C Debenedetti
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
D V Dedovich
D V Dedovich
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
J Degenhardt
J Degenhardt
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
M Dehchar
M Dehchar
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
C Del Papa
C Del Papa
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
J Del Peso
J Del Peso
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
T Del Prete
T Del Prete
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
T Delemontex
T Delemontex
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
M Deliyergiyev
M Deliyergiyev
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
A Dell’Acqua
A Dell’Acqua
44CERN, Geneva, Switzerland
44,
L Dell’Asta
L Dell’Asta
31Department of Physics, Boston University, Boston, MA United States of America
31,
M Della Pietra
M Della Pietra
127INFN Sezione di Napoli, Napoli, Italy
127,
D della Volpe
D della Volpe
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
M Delmastro
M Delmastro
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
N Delruelle
N Delruelle
44CERN, Geneva, Switzerland
44,
P A Delsart
P A Delsart
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
C Deluca
C Deluca
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
S Demers
S Demers
217Department of Physics, Yale University, New Haven, CT United States of America
217,
M Demichev
M Demichev
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
B Demirkoz
B Demirkoz
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
J Deng
J Deng
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
S P Denisov
S P Denisov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
D Derendarz
D Derendarz
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
J E Derkaoui
J E Derkaoui
170Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
170,
F Derue
F Derue
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
P Dervan
P Dervan
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
K Desch
K Desch
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
E Devetak
E Devetak
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
P O Deviveiros
P O Deviveiros
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
A Dewhurst
A Dewhurst
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
B DeWilde
B DeWilde
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
S Dhaliwal
S Dhaliwal
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
R Dhullipudi
R Dhullipudi
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
A Di Ciaccio
A Di Ciaccio
163INFN Sezione di Roma Tor Vergata, Roma, Italy
164Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
163,164,
L Di Ciaccio
L Di Ciaccio
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
A Di Girolamo
A Di Girolamo
44CERN, Geneva, Switzerland
44,
B Di Girolamo
B Di Girolamo
44CERN, Geneva, Switzerland
44,
S Di Luise
S Di Luise
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
A Di Mattia
A Di Mattia
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
B Di Micco
B Di Micco
44CERN, Geneva, Switzerland
44,
R Di Nardo
R Di Nardo
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
A Di Simone
A Di Simone
163INFN Sezione di Roma Tor Vergata, Roma, Italy
164Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
163,164,
R Di Sipio
R Di Sipio
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
M A Diaz
M A Diaz
46Departamento de Fisica, Pontificia Universidad Católica de Chile, Santiago, Chile
46,
F Diblen
F Diblen
26Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
26,
E B Diehl
E B Diehl
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
J Dietrich
J Dietrich
61DESY, Hamburg and Zeuthen, Germany
61,
T A Dietzsch
T A Dietzsch
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
S Diglio
S Diglio
110School of Physics, University of Melbourne, Victoria, Australia
110,
K Dindar Yagci
K Dindar Yagci
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
J Dingfelder
J Dingfelder
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
C Dionisi
C Dionisi
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
P Dita
P Dita
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
S Dita
S Dita
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
F Dittus
F Dittus
44CERN, Geneva, Switzerland
44,
F Djama
F Djama
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
T Djobava
T Djobava
73High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
73,
M A B do Vale
M A B do Vale
35Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
35,
A Do Valle Wemans
A Do Valle Wemans
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
T K O Doan
T K O Doan
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
M Dobbs
M Dobbs
109Department of Physics, McGill University, Montreal, QC Canada
109,
R Dobinson
R Dobinson
44CERN, Geneva, Switzerland
44,
D Dobos
D Dobos
44CERN, Geneva, Switzerland
44,
E Dobson
E Dobson
44CERN, Geneva, Switzerland
44,
J Dodd
J Dodd
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
C Doglioni
C Doglioni
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
T Doherty
T Doherty
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
Y Doi
Y Doi
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
J Dolejsi
J Dolejsi
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
I Dolenc
I Dolenc
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
Z Dolezal
Z Dolezal
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
B A Dolgoshein
B A Dolgoshein
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
T Dohmae
T Dohmae
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
M Donadelli
M Donadelli
36Instituto de Fisica, Universidade de Sao Paulo, Sao Paulo, Brazil
36,
M Donega
M Donega
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
J Donini
J Donini
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
J Dopke
J Dopke
44CERN, Geneva, Switzerland
44,
A Doria
A Doria
127INFN Sezione di Napoli, Napoli, Italy
127,
A Dos Anjos
A Dos Anjos
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
M Dosil
M Dosil
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
A Dotti
A Dotti
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
M T Dova
M T Dova
93Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
93,
J D Dowell
J D Dowell
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
A D Doxiadis
A D Doxiadis
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
A T Doyle
A T Doyle
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
Z Drasal
Z Drasal
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
J Drees
J Drees
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
N Dressnandt
N Dressnandt
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
H Drevermann
H Drevermann
44CERN, Geneva, Switzerland
44,
C Driouichi
C Driouichi
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
M Dris
M Dris
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
J Dubbert
J Dubbert
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
S Dube
S Dube
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Duchovni
E Duchovni
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
G Duckeck
G Duckeck
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
A Dudarev
A Dudarev
44CERN, Geneva, Switzerland
44,
F Dudziak
F Dudziak
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
M Dührssen
M Dührssen
44CERN, Geneva, Switzerland
44,
I P Duerdoth
I P Duerdoth
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
L Duflot
L Duflot
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
M-A Dufour
M-A Dufour
109Department of Physics, McGill University, Montreal, QC Canada
109,
M Dunford
M Dunford
44CERN, Geneva, Switzerland
44,
H Duran Yildiz
H Duran Yildiz
4Department of Physics, Ankara University, Ankara, Turkey
4,
R Duxfield
R Duxfield
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
M Dwuznik
M Dwuznik
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
F Dydak
F Dydak
44CERN, Geneva, Switzerland
44,
M Düren
M Düren
74II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
74,
W L Ebenstein
W L Ebenstein
64Department of Physics, Duke University, Durham, NC United States of America
64,
J Ebke
J Ebke
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
S Eckweiler
S Eckweiler
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
K Edmonds
K Edmonds
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
C A Edwards
C A Edwards
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
N C Edwards
N C Edwards
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
W Ehrenfeld
W Ehrenfeld
61DESY, Hamburg and Zeuthen, Germany
61,
T Ehrich
T Ehrich
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
T Eifert
T Eifert
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
G Eigen
G Eigen
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
K Einsweiler
K Einsweiler
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Eisenhandler
E Eisenhandler
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
T Ekelof
T Ekelof
208Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
208,
M El Kacimi
M El Kacimi
169Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Morocco
169,
M Ellert
M Ellert
208Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
208,
S Elles
S Elles
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
F Ellinghaus
F Ellinghaus
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
K Ellis
K Ellis
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
N Ellis
N Ellis
44CERN, Geneva, Switzerland
44,
J Elmsheuser
J Elmsheuser
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Elsing
M Elsing
44CERN, Geneva, Switzerland
44,
D Emeliyanov
D Emeliyanov
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
R Engelmann
R Engelmann
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
A Engl
A Engl
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
B Epp
B Epp
85Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
85,
A Eppig
A Eppig
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
J Erdmann
J Erdmann
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
A Ereditato
A Ereditato
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
D Eriksson
D Eriksson
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
J Ernst
J Ernst
2University at Albany, Albany, NY United States of America
2,
M Ernst
M Ernst
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
J Ernwein
J Ernwein
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
D Errede
D Errede
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
S Errede
S Errede
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
E Ertel
E Ertel
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
M Escalier
M Escalier
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
C Escobar
C Escobar
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
X Espinal Curull
X Espinal Curull
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
B Esposito
B Esposito
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
F Etienne
F Etienne
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
A I Etienvre
A I Etienvre
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
E Etzion
E Etzion
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
D Evangelakou
D Evangelakou
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
H Evans
H Evans
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
L Fabbri
L Fabbri
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
C Fabre
C Fabre
44CERN, Geneva, Switzerland
44,
R M Fakhrutdinov
R M Fakhrutdinov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
S Falciano
S Falciano
161INFN Sezione di Roma I, Roma, Italy
161,
Y Fang
Y Fang
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
M Fanti
M Fanti
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
A Farbin
A Farbin
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
A Farilla
A Farilla
165INFN Sezione di Roma Tre, Roma, Italy
165,
J Farley
J Farley
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
T Farooque
T Farooque
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
S M Farrington
S M Farrington
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
P Farthouat
P Farthouat
44CERN, Geneva, Switzerland
44,
P Fassnacht
P Fassnacht
44CERN, Geneva, Switzerland
44,
D Fassouliotis
D Fassouliotis
13Physics Department, University of Athens, Athens, Greece
13,
B Fatholahzadeh
B Fatholahzadeh
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
A Favareto
A Favareto
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
L Fayard
L Fayard
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
S Fazio
S Fazio
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
R Febbraro
R Febbraro
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
P Federic
P Federic
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
O L Fedin
O L Fedin
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
W Fedorko
W Fedorko
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
M Fehling-Kaschek
M Fehling-Kaschek
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
L Feligioni
L Feligioni
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
D Fellmann
D Fellmann
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
C Feng
C Feng
51School of Physics, Shandong University, Shandong, China
51,
E J Feng
E J Feng
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A B Fenyuk
A B Fenyuk
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
J Ferencei
J Ferencei
181Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
181,
J Ferland
J Ferland
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
W Fernando
W Fernando
135Ohio State University, Columbus, OH United States of America
135,
S Ferrag
S Ferrag
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
J Ferrando
J Ferrando
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
V Ferrara
V Ferrara
61DESY, Hamburg and Zeuthen, Germany
61,
A Ferrari
A Ferrari
208Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
208,
P Ferrari
P Ferrari
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
R Ferrari
R Ferrari
145INFN Sezione di Pavia, Pavia, Italy
145,
A Ferrer
A Ferrer
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
M L Ferrer
M L Ferrer
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
D Ferrere
D Ferrere
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
C Ferretti
C Ferretti
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
A Ferretto Parodi
A Ferretto Parodi
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
M Fiascaris
M Fiascaris
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
F Fiedler
F Fiedler
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
A Filipčič
A Filipčič
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
A Filippas
A Filippas
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
F Filthaut
F Filthaut
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
M Fincke-Keeler
M Fincke-Keeler
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
M C N Fiolhais
M C N Fiolhais
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
L Fiorini
L Fiorini
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
A Firan
A Firan
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
G Fischer
G Fischer
61DESY, Hamburg and Zeuthen, Germany
61,
P Fischer
P Fischer
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M J Fisher
M J Fisher
135Ohio State University, Columbus, OH United States of America
135,
M Flechl
M Flechl
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
I Fleck
I Fleck
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
J Fleckner
J Fleckner
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
P Fleischmann
P Fleischmann
215Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
215,
S Fleischmann
S Fleischmann
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
T Flick
T Flick
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
L R Flores Castillo
L R Flores Castillo
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
M J Flowerdew
M J Flowerdew
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
M Fokitis
M Fokitis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
T Fonseca Martin
T Fonseca Martin
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
D A Forbush
D A Forbush
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
A Formica
A Formica
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
A Forti
A Forti
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
D Fortin
D Fortin
198TRIUMF, Vancouver, BC Canada
198,
J M Foster
J M Foster
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
D Fournier
D Fournier
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
A Foussat
A Foussat
44CERN, Geneva, Switzerland
44,
A J Fowler
A J Fowler
64Department of Physics, Duke University, Durham, NC United States of America
64,
K Fowler
K Fowler
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
H Fox
H Fox
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
P Francavilla
P Francavilla
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
S Franchino
S Franchino
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
D Francis
D Francis
44CERN, Geneva, Switzerland
44,
T Frank
T Frank
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
M Franklin
M Franklin
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
S Franz
S Franz
44CERN, Geneva, Switzerland
44,
M Fraternali
M Fraternali
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
S Fratina
S Fratina
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
S T French
S T French
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
F Friedrich
F Friedrich
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
R Froeschl
R Froeschl
44CERN, Geneva, Switzerland
44,
D Froidevaux
D Froidevaux
44CERN, Geneva, Switzerland
44,
J A Frost
J A Frost
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
C Fukunaga
C Fukunaga
195Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
195,
E Fullana Torregrosa
E Fullana Torregrosa
44CERN, Geneva, Switzerland
44,
J Fuster
J Fuster
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
C Gabaldon
C Gabaldon
44CERN, Geneva, Switzerland
44,
O Gabizon
O Gabizon
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
T Gadfort
T Gadfort
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S Gadomski
S Gadomski
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
G Gagliardi
G Gagliardi
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
P Gagnon
P Gagnon
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
C Galea
C Galea
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
E J Gallas
E J Gallas
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
V Gallo
V Gallo
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
B J Gallop
B J Gallop
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
P Gallus
P Gallus
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
K K Gan
K K Gan
135Ohio State University, Columbus, OH United States of America
135,
Y S Gao
Y S Gao
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
V A Gapienko
V A Gapienko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
A Gaponenko
A Gaponenko
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
F Garberson
F Garberson
217Department of Physics, Yale University, New Haven, CT United States of America
217,
M Garcia-Sciveres
M Garcia-Sciveres
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
C García
C García
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
J E García Navarro
J E García Navarro
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
R W Gardner
R W Gardner
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
N Garelli
N Garelli
44CERN, Geneva, Switzerland
44,
H Garitaonandia
H Garitaonandia
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
V Garonne
V Garonne
44CERN, Geneva, Switzerland
44,
J Garvey
J Garvey
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
C Gatti
C Gatti
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
G Gaudio
G Gaudio
145INFN Sezione di Pavia, Pavia, Italy
145,
B Gaur
B Gaur
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
L Gauthier
L Gauthier
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
I L Gavrilenko
I L Gavrilenko
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
C Gay
C Gay
210Department of Physics, University of British Columbia, Vancouver, BC Canada
210,
G Gaycken
G Gaycken
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
J-C Gayde
J-C Gayde
44CERN, Geneva, Switzerland
44,
E N Gazis
E N Gazis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
P Ge
P Ge
51School of Physics, Shandong University, Shandong, China
51,
C N P Gee
C N P Gee
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
D A A Geerts
D A A Geerts
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
Ch Geich-Gimbel
Ch Geich-Gimbel
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
K Gellerstedt
K Gellerstedt
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
C Gemme
C Gemme
70INFN Sezione di Genova, Genova, Italy
70,
A Gemmell
A Gemmell
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
M H Genest
M H Genest
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
S Gentile
S Gentile
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
M George
M George
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
S George
S George
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
P Gerlach
P Gerlach
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
A Gershon
A Gershon
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
C Geweniger
C Geweniger
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
H Ghazlane
H Ghazlane
168Centre National de l’Energie des Sciences Techniques Nucleaires, Rabat, Morocco
168,
N Ghodbane
N Ghodbane
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
B Giacobbe
B Giacobbe
28INFN Sezione di Bologna, Bologna, Italy
28,
S Giagu
S Giagu
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
V Giakoumopoulou
V Giakoumopoulou
13Physics Department, University of Athens, Athens, Greece
13,
V Giangiobbe
V Giangiobbe
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
F Gianotti
F Gianotti
44CERN, Geneva, Switzerland
44,
B Gibbard
B Gibbard
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
A Gibson
A Gibson
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
S M Gibson
S M Gibson
44CERN, Geneva, Switzerland
44,
L M Gilbert
L M Gilbert
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
V Gilewsky
V Gilewsky
116National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
116,
D Gillberg
D Gillberg
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
A R Gillman
A R Gillman
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
D M Gingrich
D M Gingrich
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
J Ginzburg
J Ginzburg
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
N Giokaris
N Giokaris
13Physics Department, University of Athens, Athens, Greece
13,
M P Giordani
M P Giordani
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
206,
R Giordano
R Giordano
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
F M Giorgi
F M Giorgi
21Department of Physics, Humboldt University, Berlin, Germany
21,
P Giovannini
P Giovannini
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
P F Giraud
P F Giraud
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
D Giugni
D Giugni
113INFN Sezione di Milano, Milano, Italy
113,
M Giunta
M Giunta
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
P Giusti
P Giusti
28INFN Sezione di Bologna, Bologna, Italy
28,
B K Gjelsten
B K Gjelsten
143Department of Physics, University of Oslo, Oslo, Norway
143,
L K Gladilin
L K Gladilin
122Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
122,
C Glasman
C Glasman
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
J Glatzer
J Glatzer
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
A Glazov
A Glazov
61DESY, Hamburg and Zeuthen, Germany
61,
K W Glitza
K W Glitza
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
G L Glonti
G L Glonti
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
J R Goddard
J R Goddard
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
J Godfrey
J Godfrey
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
J Godlewski
J Godlewski
44CERN, Geneva, Switzerland
44,
M Goebel
M Goebel
61DESY, Hamburg and Zeuthen, Germany
61,
T Göpfert
T Göpfert
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
C Goeringer
C Goeringer
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
C Gössling
C Gössling
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
T Göttfert
T Göttfert
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
S Goldfarb
S Goldfarb
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
T Golling
T Golling
217Department of Physics, Yale University, New Haven, CT United States of America
217,
A Gomes
A Gomes
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
L S Gomez Fajardo
L S Gomez Fajardo
61DESY, Hamburg and Zeuthen, Germany
61,
R Gonçalo
R Gonçalo
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
J Goncalves Pinto Firmino Da Costa
J Goncalves Pinto Firmino Da Costa
61DESY, Hamburg and Zeuthen, Germany
61,
L Gonella
L Gonella
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Gonidec
A Gonidec
44CERN, Geneva, Switzerland
44,
S Gonzalez
S Gonzalez
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
S González de la Hoz
S González de la Hoz
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
G Gonzalez Parra
G Gonzalez Parra
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
M L Gonzalez Silva
M L Gonzalez Silva
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
S Gonzalez-Sevilla
S Gonzalez-Sevilla
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
J J Goodson
J J Goodson
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
L Goossens
L Goossens
44CERN, Geneva, Switzerland
44,
P A Gorbounov
P A Gorbounov
120Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
120,
H A Gordon
H A Gordon
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
I Gorelov
I Gorelov
129Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
129,
G Gorfine
G Gorfine
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
B Gorini
B Gorini
44CERN, Geneva, Switzerland
44,
E Gorini
E Gorini
95INFN Sezione di Lecce, Lecce, Italy
96Dipartimento di Fisica, Università del Salento, Lecce, Italy
95,96,
A Gorišek
A Gorišek
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
E Gornicki
E Gornicki
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
S A Gorokhov
S A Gorokhov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
V N Goryachev
V N Goryachev
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
B Gosdzik
B Gosdzik
61DESY, Hamburg and Zeuthen, Germany
61,
M Gosselink
M Gosselink
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
M I Gostkin
M I Gostkin
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
I Gough Eschrich
I Gough Eschrich
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
M Gouighri
M Gouighri
167Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
167,
D Goujdami
D Goujdami
169Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Morocco
169,
M P Goulette
M P Goulette
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
A G Goussiou
A G Goussiou
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
C Goy
C Goy
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Gozpinar
S Gozpinar
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
I Grabowska-Bold
I Grabowska-Bold
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
P Grafström
P Grafström
44CERN, Geneva, Switzerland
44,
K-J Grahn
K-J Grahn
61DESY, Hamburg and Zeuthen, Germany
61,
F Grancagnolo
F Grancagnolo
95INFN Sezione di Lecce, Lecce, Italy
95,
S Grancagnolo
S Grancagnolo
21Department of Physics, Humboldt University, Berlin, Germany
21,
V Grassi
V Grassi
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
V Gratchev
V Gratchev
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
N Grau
N Grau
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
H M Gray
H M Gray
44CERN, Geneva, Switzerland
44,
J A Gray
J A Gray
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
E Graziani
E Graziani
165INFN Sezione di Roma Tre, Roma, Italy
165,
O G Grebenyuk
O G Grebenyuk
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
T Greenshaw
T Greenshaw
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
Z D Greenwood
Z D Greenwood
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
K Gregersen
K Gregersen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
I M Gregor
I M Gregor
61DESY, Hamburg and Zeuthen, Germany
61,
P Grenier
P Grenier
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
J Griffiths
J Griffiths
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
N Grigalashvili
N Grigalashvili
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A A Grillo
A A Grillo
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
S Grinstein
S Grinstein
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
Y V Grishkevich
Y V Grishkevich
122Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
122,
J-F Grivaz
J-F Grivaz
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
M Groh
M Groh
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
E Gross
E Gross
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
J Grosse-Knetter
J Grosse-Knetter
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
J Groth-Jensen
J Groth-Jensen
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
K Grybel
K Grybel
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
V J Guarino
V J Guarino
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
D Guest
D Guest
217Department of Physics, Yale University, New Haven, CT United States of America
217,
C Guicheney
C Guicheney
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
A Guida
A Guida
95INFN Sezione di Lecce, Lecce, Italy
96Dipartimento di Fisica, Università del Salento, Lecce, Italy
95,96,
S Guindon
S Guindon
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
H Guler
H Guler
109Department of Physics, McGill University, Montreal, QC Canada
109,
J Gunther
J Gunther
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
B Guo
B Guo
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
J Guo
J Guo
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
A Gupta
A Gupta
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
Y Gusakov
Y Gusakov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
V N Gushchin
V N Gushchin
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
P Gutierrez
P Gutierrez
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
N Guttman
N Guttman
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
O Gutzwiller
O Gutzwiller
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
C Guyot
C Guyot
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
C Gwenlan
C Gwenlan
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
C B Gwilliam
C B Gwilliam
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
A Haas
A Haas
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S Haas
S Haas
44CERN, Geneva, Switzerland
44,
C Haber
C Haber
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
H K Hadavand
H K Hadavand
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
D R Hadley
D R Hadley
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
P Haefner
P Haefner
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
F Hahn
F Hahn
44CERN, Geneva, Switzerland
44,
S Haider
S Haider
44CERN, Geneva, Switzerland
44,
Z Hajduk
Z Hajduk
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
H Hakobyan
H Hakobyan
218Yerevan Physics Institute, Yerevan, Armenia
218,
D Hall
D Hall
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
J Haller
J Haller
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
K Hamacher
K Hamacher
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
P Hamal
P Hamal
139Palacký University, RCPTM, Olomouc, Czech Republic
139,
M Hamer
M Hamer
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
A Hamilton
A Hamilton
183School of Physics, University of the Witwatersrand, Johannesburg, South Africa
183,
S Hamilton
S Hamilton
201Science and Technology Center, Tufts University, Medford, MA United States of America
201,
H Han
H Han
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
L Han
L Han
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
K Hanagaki
K Hanagaki
142Graduate School of Science, Osaka University, Osaka, Japan
142,
K Hanawa
K Hanawa
200Institute of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571 Japan
200,
M Hance
M Hance
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
C Handel
C Handel
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
P Hanke
P Hanke
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
J R Hansen
J R Hansen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
J B Hansen
J B Hansen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
J D Hansen
J D Hansen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
P H Hansen
P H Hansen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
P Hansson
P Hansson
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
K Hara
K Hara
200Institute of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571 Japan
200,
G A Hare
G A Hare
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
T Harenberg
T Harenberg
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
S Harkusha
S Harkusha
115B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
115,
D Harper
D Harper
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
R D Harrington
R D Harrington
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
O M Harris
O M Harris
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
K Harrison
K Harrison
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
J Hartert
J Hartert
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
F Hartjes
F Hartjes
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
T Haruyama
T Haruyama
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
A Harvey
A Harvey
78Department of Physics, Hampton University, Hampton, VA United States of America
78,
S Hasegawa
S Hasegawa
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
Y Hasegawa
Y Hasegawa
176Department of Physics, Shinshu University, Nagano, Japan
176,
S Hassani
S Hassani
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
M Hatch
M Hatch
44CERN, Geneva, Switzerland
44,
D Hauff
D Hauff
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
S Haug
S Haug
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
M Hauschild
M Hauschild
44CERN, Geneva, Switzerland
44,
R Hauser
R Hauser
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
M Havranek
M Havranek
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
B M Hawes
B M Hawes
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
C M Hawkes
C M Hawkes
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
R J Hawkings
R J Hawkings
44CERN, Geneva, Switzerland
44,
A D Hawkins
A D Hawkins
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
D Hawkins
D Hawkins
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
T Hayakawa
T Hayakawa
90Graduate School of Science, Kobe University, Kobe, Japan
90,
T Hayashi
T Hayashi
200Institute of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571 Japan
200,
D Hayden
D Hayden
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
H S Hayward
H S Hayward
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
S J Haywood
S J Haywood
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
E Hazen
E Hazen
31Department of Physics, Boston University, Boston, MA United States of America
31,
M He
M He
51School of Physics, Shandong University, Shandong, China
51,
S J Head
S J Head
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
V Hedberg
V Hedberg
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
L Heelan
L Heelan
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
S Heim
S Heim
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
B Heinemann
B Heinemann
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
S Heisterkamp
S Heisterkamp
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
L Helary
L Helary
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
C Heller
C Heller
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Heller
M Heller
44CERN, Geneva, Switzerland
44,
S Hellman
S Hellman
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
D Hellmich
D Hellmich
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
C Helsens
C Helsens
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
R C W Henderson
R C W Henderson
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
M Henke
M Henke
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
A Henrichs
A Henrichs
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
A M Henriques Correia
A M Henriques Correia
44CERN, Geneva, Switzerland
44,
S Henrot-Versille
S Henrot-Versille
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
F Henry-Couannier
F Henry-Couannier
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
C Hensel
C Hensel
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
T Henß
T Henß
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
C M Hernandez
C M Hernandez
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
Y Hernández Jiménez
Y Hernández Jiménez
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
R Herrberg
R Herrberg
21Department of Physics, Humboldt University, Berlin, Germany
21,
A D Hershenhorn
A D Hershenhorn
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
G Herten
G Herten
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
R Hertenberger
R Hertenberger
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
L Hervas
L Hervas
44CERN, Geneva, Switzerland
44,
N P Hessey
N P Hessey
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
E Higón-Rodriguez
E Higón-Rodriguez
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
D Hill
D Hill
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
J C Hill
J C Hill
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
N Hill
N Hill
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
K H Hiller
K H Hiller
61DESY, Hamburg and Zeuthen, Germany
61,
S Hillert
S Hillert
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
S J Hillier
S J Hillier
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
I Hinchliffe
I Hinchliffe
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Hines
E Hines
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
M Hirose
M Hirose
142Graduate School of Science, Osaka University, Osaka, Japan
142,
F Hirsch
F Hirsch
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
D Hirschbuehl
D Hirschbuehl
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
J Hobbs
J Hobbs
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
N Hod
N Hod
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
M C Hodgkinson
M C Hodgkinson
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
P Hodgson
P Hodgson
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
A Hoecker
A Hoecker
44CERN, Geneva, Switzerland
44,
M R Hoeferkamp
M R Hoeferkamp
129Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
129,
J Hoffman
J Hoffman
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
D Hoffmann
D Hoffmann
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
M Hohlfeld
M Hohlfeld
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
M Holder
M Holder
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
S O Holmgren
S O Holmgren
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
T Holy
T Holy
156Czech Technical University in Prague, Praha, Czech Republic
156,
J L Holzbauer
J L Holzbauer
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
Y Homma
Y Homma
90Graduate School of Science, Kobe University, Kobe, Japan
90,
T M Hong
T M Hong
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
L Hooft van Huysduynen
L Hooft van Huysduynen
134Department of Physics, New York University, New York, NY United States of America
134,
T Horazdovsky
T Horazdovsky
156Czech Technical University in Prague, Praha, Czech Republic
156,
C Horn
C Horn
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S Horner
S Horner
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
J-Y Hostachy
J-Y Hostachy
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
S Hou
S Hou
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
M A Houlden
M A Houlden
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
A Hoummada
A Hoummada
167Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
167,
J Howarth
J Howarth
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
D F Howell
D F Howell
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
I Hristova
I Hristova
21Department of Physics, Humboldt University, Berlin, Germany
21,
J Hrivnac
J Hrivnac
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
I Hruska
I Hruska
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
T Hryn’ova
T Hryn’ova
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
P J Hsu
P J Hsu
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
S-C Hsu
S-C Hsu
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
G S Huang
G S Huang
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
Z Hubacek
Z Hubacek
156Czech Technical University in Prague, Praha, Czech Republic
156,
F Hubaut
F Hubaut
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
F Huegging
F Huegging
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Huettmann
A Huettmann
61DESY, Hamburg and Zeuthen, Germany
61,
T B Huffman
T B Huffman
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
E W Hughes
E W Hughes
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
G Hughes
G Hughes
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
R E Hughes-Jones
R E Hughes-Jones
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
M Huhtinen
M Huhtinen
44CERN, Geneva, Switzerland
44,
P Hurst
P Hurst
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
M Hurwitz
M Hurwitz
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
U Husemann
U Husemann
61DESY, Hamburg and Zeuthen, Germany
61,
N Huseynov
N Huseynov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
J Huston
J Huston
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
J Huth
J Huth
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
G Iacobucci
G Iacobucci
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
G Iakovidis
G Iakovidis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
M Ibbotson
M Ibbotson
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
I Ibragimov
I Ibragimov
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
R Ichimiya
R Ichimiya
90Graduate School of Science, Kobe University, Kobe, Japan
90,
L Iconomidou-Fayard
L Iconomidou-Fayard
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
J Idarraga
J Idarraga
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
P Iengo
P Iengo
127INFN Sezione di Napoli, Napoli, Italy
127,
O Igonkina
O Igonkina
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
Y Ikegami
Y Ikegami
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
M Ikeno
M Ikeno
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
Y Ilchenko
Y Ilchenko
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
D Iliadis
D Iliadis
193Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
193,
N Ilic
N Ilic
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
M Imori
M Imori
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
T Ince
T Ince
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
J Inigo-Golfin
J Inigo-Golfin
44CERN, Geneva, Switzerland
44,
P Ioannou
P Ioannou
13Physics Department, University of Athens, Athens, Greece
13,
M Iodice
M Iodice
165INFN Sezione di Roma Tre, Roma, Italy
165,
V Ippolito
V Ippolito
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
A Irles Quiles
A Irles Quiles
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
C Isaksson
C Isaksson
208Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
208,
A Ishikawa
A Ishikawa
90Graduate School of Science, Kobe University, Kobe, Japan
90,
M Ishino
M Ishino
91Faculty of Science, Kyoto University, Kyoto, Japan
91,
R Ishmukhametov
R Ishmukhametov
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
C Issever
C Issever
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
S Istin
S Istin
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
A V Ivashin
A V Ivashin
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
W Iwanski
W Iwanski
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
H Iwasaki
H Iwasaki
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
J M Izen
J M Izen
60Physics Department, University of Texas at Dallas, Richardson, TX United States of America
60,
V Izzo
V Izzo
127INFN Sezione di Napoli, Napoli, Italy
127,
B Jackson
B Jackson
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
J N Jackson
J N Jackson
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
P Jackson
P Jackson
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
M R Jaekel
M R Jaekel
44CERN, Geneva, Switzerland
44,
V Jain
V Jain
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
K Jakobs
K Jakobs
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
S Jakobsen
S Jakobsen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
J Jakubek
J Jakubek
156Czech Technical University in Prague, Praha, Czech Republic
156,
D K Jana
D K Jana
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
E Jankowski
E Jankowski
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
E Jansen
E Jansen
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
H Jansen
H Jansen
44CERN, Geneva, Switzerland
44,
A Jantsch
A Jantsch
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
M Janus
M Janus
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
G Jarlskog
G Jarlskog
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
L Jeanty
L Jeanty
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
K Jelen
K Jelen
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
I Jen-La Plante
I Jen-La Plante
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
P Jenni
P Jenni
44CERN, Geneva, Switzerland
44,
A Jeremie
A Jeremie
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
P Jež
P Jež
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
S Jézéquel
S Jézéquel
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
M K Jha
M K Jha
28INFN Sezione di Bologna, Bologna, Italy
28,
H Ji
H Ji
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
W Ji
W Ji
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
J Jia
J Jia
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
Y Jiang
Y Jiang
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
M Jimenez Belenguer
M Jimenez Belenguer
61DESY, Hamburg and Zeuthen, Germany
61,
G Jin
G Jin
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
S Jin
S Jin
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
O Jinnouchi
O Jinnouchi
196Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
196,
M D Joergensen
M D Joergensen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
D Joffe
D Joffe
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
L G Johansen
L G Johansen
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
M Johansen
M Johansen
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
K E Johansson
K E Johansson
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
P Johansson
P Johansson
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
S Johnert
S Johnert
61DESY, Hamburg and Zeuthen, Germany
61,
K A Johns
K A Johns
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
K Jon-And
K Jon-And
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
G Jones
G Jones
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
R W L Jones
R W L Jones
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
T W Jones
T W Jones
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
T J Jones
T J Jones
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
O Jonsson
O Jonsson
44CERN, Geneva, Switzerland
44,
C Joram
C Joram
44CERN, Geneva, Switzerland
44,
P M Jorge
P M Jorge
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
J Joseph
J Joseph
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
T Jovin
T Jovin
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
X Ju
X Ju
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
C A Jung
C A Jung
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
R M Jungst
R M Jungst
44CERN, Geneva, Switzerland
44,
V Juranek
V Juranek
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
P Jussel
P Jussel
85Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
85,
A Juste Rozas
A Juste Rozas
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
V V Kabachenko
V V Kabachenko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
S Kabana
S Kabana
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
M Kaci
M Kaci
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
A Kaczmarska
A Kaczmarska
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
P Kadlecik
P Kadlecik
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
M Kado
M Kado
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
H Kagan
H Kagan
135Ohio State University, Columbus, OH United States of America
135,
M Kagan
M Kagan
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
S Kaiser
S Kaiser
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
E Kajomovitz
E Kajomovitz
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
S Kalinin
S Kalinin
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
L V Kalinovskaya
L V Kalinovskaya
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
S Kama
S Kama
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
N Kanaya
N Kanaya
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
M Kaneda
M Kaneda
44CERN, Geneva, Switzerland
44,
S Kaneti
S Kaneti
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
T Kanno
T Kanno
196Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
196,
V A Kantserov
V A Kantserov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
J Kanzaki
J Kanzaki
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
B Kaplan
B Kaplan
217Department of Physics, Yale University, New Haven, CT United States of America
217,
A Kapliy
A Kapliy
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
J Kaplon
J Kaplon
44CERN, Geneva, Switzerland
44,
D Kar
D Kar
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
M Karagounis
M Karagounis
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Karagoz
M Karagoz
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
M Karnevskiy
M Karnevskiy
61DESY, Hamburg and Zeuthen, Germany
61,
K Karr
K Karr
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
V Kartvelishvili
V Kartvelishvili
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
A N Karyukhin
A N Karyukhin
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
L Kashif
L Kashif
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
G Kasieczka
G Kasieczka
81Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
R D Kass
R D Kass
135Ohio State University, Columbus, OH United States of America
135,
A Kastanas
A Kastanas
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
M Kataoka
M Kataoka
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
Y Kataoka
Y Kataoka
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
E Katsoufis
E Katsoufis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
J Katzy
J Katzy
61DESY, Hamburg and Zeuthen, Germany
61,
V Kaushik
V Kaushik
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
K Kawagoe
K Kawagoe
90Graduate School of Science, Kobe University, Kobe, Japan
90,
T Kawamoto
T Kawamoto
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
G Kawamura
G Kawamura
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
M S Kayl
M S Kayl
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
V A Kazanin
V A Kazanin
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
M Y Kazarinov
M Y Kazarinov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
R Keeler
R Keeler
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
R Kehoe
R Kehoe
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
M Keil
M Keil
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
G D Kekelidze
G D Kekelidze
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
J Kennedy
J Kennedy
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
C J Kenney
C J Kenney
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
M Kenyon
M Kenyon
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
O Kepka
O Kepka
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
N Kerschen
N Kerschen
44CERN, Geneva, Switzerland
44,
B P Kerševan
B P Kerševan
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
S Kersten
S Kersten
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
K Kessoku
K Kessoku
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
J Keung
J Keung
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
F Khalil-zada
F Khalil-zada
15Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
15,
H Khandanyan
H Khandanyan
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
A Khanov
A Khanov
138Department of Physics, Oklahoma State University, Stillwater, OK United States of America
138,
D Kharchenko
D Kharchenko
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A Khodinov
A Khodinov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
A G Kholodenko
A G Kholodenko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
A Khomich
A Khomich
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
T J Khoo
T J Khoo
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
G Khoriauli
G Khoriauli
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Khoroshilov
A Khoroshilov
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
N Khovanskiy
N Khovanskiy
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
V Khovanskiy
V Khovanskiy
120Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
120,
E Khramov
E Khramov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
J Khubua
J Khubua
73High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
73,
H Kim
H Kim
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
M S Kim
M S Kim
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
P C Kim
P C Kim
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S H Kim
S H Kim
200Institute of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571 Japan
200,
N Kimura
N Kimura
212Waseda University, Tokyo, Japan
212,
O Kind
O Kind
21Department of Physics, Humboldt University, Berlin, Germany
21,
B T King
B T King
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
M King
M King
90Graduate School of Science, Kobe University, Kobe, Japan
90,
R S B King
R S B King
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
J Kirk
J Kirk
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
L E Kirsch
L E Kirsch
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
A E Kiryunin
A E Kiryunin
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
T Kishimoto
T Kishimoto
90Graduate School of Science, Kobe University, Kobe, Japan
90,
D Kisielewska
D Kisielewska
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
T Kittelmann
T Kittelmann
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
A M Kiver
A M Kiver
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
E Kladiva
E Kladiva
181Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
181,
J Klaiber-Lodewigs
J Klaiber-Lodewigs
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
M Klein
M Klein
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
U Klein
U Klein
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
K Kleinknecht
K Kleinknecht
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
M Klemetti
M Klemetti
109Department of Physics, McGill University, Montreal, QC Canada
109,
A Klier
A Klier
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
P Klimek
P Klimek
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
A Klimentov
A Klimentov
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
R Klingenberg
R Klingenberg
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
J A Klinger
J A Klinger
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
E B Klinkby
E B Klinkby
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
T Klioutchnikova
T Klioutchnikova
44CERN, Geneva, Switzerland
44,
P F Klok
P F Klok
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
S Klous
S Klous
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
E-E Kluge
E-E Kluge
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
T Kluge
T Kluge
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
P Kluit
P Kluit
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
S Kluth
S Kluth
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
N S Knecht
N S Knecht
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
E Kneringer
E Kneringer
85Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
85,
J Knobloch
J Knobloch
44CERN, Geneva, Switzerland
44,
E B F G Knoops
E B F G Knoops
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
A Knue
A Knue
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
B R Ko
B R Ko
64Department of Physics, Duke University, Durham, NC United States of America
64,
T Kobayashi
T Kobayashi
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
M Kobel
M Kobel
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
M Kocian
M Kocian
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
P Kodys
P Kodys
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
K Köneke
K Köneke
44CERN, Geneva, Switzerland
44,
A C König
A C König
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
S Koenig
S Koenig
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
L Köpke
L Köpke
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
F Koetsveld
F Koetsveld
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
P Koevesarki
P Koevesarki
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
T Koffas
T Koffas
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
E Koffeman
E Koffeman
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
L A Kogan
L A Kogan
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
F Kohn
F Kohn
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
Z Kohout
Z Kohout
156Czech Technical University in Prague, Praha, Czech Republic
156,
T Kohriki
T Kohriki
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
T Koi
T Koi
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
T Kokott
T Kokott
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
G M Kolachev
G M Kolachev
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
H Kolanoski
H Kolanoski
21Department of Physics, Humboldt University, Berlin, Germany
21,
V Kolesnikov
V Kolesnikov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
I Koletsou
I Koletsou
113INFN Sezione di Milano, Milano, Italy
113,
J Koll
J Koll
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
D Kollar
D Kollar
44CERN, Geneva, Switzerland
44,
M Kollefrath
M Kollefrath
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
S D Kolya
S D Kolya
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
A A Komar
A A Komar
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
Y Komori
Y Komori
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
T Kondo
T Kondo
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
T Kono
T Kono
61DESY, Hamburg and Zeuthen, Germany
61,
A I Kononov
A I Kononov
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
R Konoplich
R Konoplich
134Department of Physics, New York University, New York, NY United States of America
134,
N Konstantinidis
N Konstantinidis
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
A Kootz
A Kootz
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
S Koperny
S Koperny
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
K Korcyl
K Korcyl
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
K Kordas
K Kordas
193Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
193,
V Koreshev
V Koreshev
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
A Korn
A Korn
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
A Korol
A Korol
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
I Korolkov
I Korolkov
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
E V Korolkova
E V Korolkova
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
V A Korotkov
V A Korotkov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
O Kortner
O Kortner
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
S Kortner
S Kortner
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
V V Kostyukhin
V V Kostyukhin
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M J Kotamäki
M J Kotamäki
44CERN, Geneva, Switzerland
44,
S Kotov
S Kotov
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
V M Kotov
V M Kotov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A Kotwal
A Kotwal
64Department of Physics, Duke University, Durham, NC United States of America
64,
C Kourkoumelis
C Kourkoumelis
13Physics Department, University of Athens, Athens, Greece
13,
V Kouskoura
V Kouskoura
193Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
193,
A Koutsman
A Koutsman
198TRIUMF, Vancouver, BC Canada
198,
R Kowalewski
R Kowalewski
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
T Z Kowalski
T Z Kowalski
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
W Kozanecki
W Kozanecki
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
A S Kozhin
A S Kozhin
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
V Kral
V Kral
156Czech Technical University in Prague, Praha, Czech Republic
156,
V A Kramarenko
V A Kramarenko
122Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
122,
G Kramberger
G Kramberger
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
M W Krasny
M W Krasny
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
A Krasznahorkay
A Krasznahorkay
134Department of Physics, New York University, New York, NY United States of America
134,
J Kraus
J Kraus
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
J K Kraus
J K Kraus
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Kreisel
A Kreisel
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
F Krejci
F Krejci
156Czech Technical University in Prague, Praha, Czech Republic
156,
J Kretzschmar
J Kretzschmar
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
N Krieger
N Krieger
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
P Krieger
P Krieger
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
K Kroeninger
K Kroeninger
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
H Kroha
H Kroha
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
J Kroll
J Kroll
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
J Kroseberg
J Kroseberg
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
J Krstic
J Krstic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
U Kruchonak
U Kruchonak
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
H Krüger
H Krüger
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
T Kruker
T Kruker
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
N Krumnack
N Krumnack
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
Z V Krumshteyn
Z V Krumshteyn
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A Kruth
A Kruth
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
T Kubota
T Kubota
110School of Physics, University of Melbourne, Victoria, Australia
110,
S Kuday
S Kuday
4Department of Physics, Ankara University, Ankara, Turkey
4,
S Kuehn
S Kuehn
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
A Kugel
A Kugel
82ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
82,
T Kuhl
T Kuhl
61DESY, Hamburg and Zeuthen, Germany
61,
D Kuhn
D Kuhn
85Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
85,
V Kukhtin
V Kukhtin
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
Y Kulchitsky
Y Kulchitsky
115B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
115,
S Kuleshov
S Kuleshov
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
C Kummer
C Kummer
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Kuna
M Kuna
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
N Kundu
N Kundu
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
J Kunkle
J Kunkle
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
A Kupco
A Kupco
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
H Kurashige
H Kurashige
90Graduate School of Science, Kobe University, Kobe, Japan
90,
M Kurata
M Kurata
200Institute of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571 Japan
200,
Y A Kurochkin
Y A Kurochkin
115B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
115,
V Kus
V Kus
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
E S Kuwertz
E S Kuwertz
186Physics Department, Royal Institute of Technology, Stockholm, Sweden
186,
M Kuze
M Kuze
196Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
196,
J Kvita
J Kvita
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
R Kwee
R Kwee
21Department of Physics, Humboldt University, Berlin, Germany
21,
A La Rosa
A La Rosa
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
L La Rotonda
L La Rotonda
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
L Labarga
L Labarga
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
J Labbe
J Labbe
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Lablak
S Lablak
167Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies - Université Hassan II, Casablanca, Morocco
167,
C Lacasta
C Lacasta
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
F Lacava
F Lacava
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
H Lacker
H Lacker
21Department of Physics, Humboldt University, Berlin, Germany
21,
D Lacour
D Lacour
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
V R Lacuesta
V R Lacuesta
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
E Ladygin
E Ladygin
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
R Lafaye
R Lafaye
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
B Laforge
B Laforge
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
T Lagouri
T Lagouri
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
S Lai
S Lai
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
E Laisne
E Laisne
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
M Lamanna
M Lamanna
44CERN, Geneva, Switzerland
44,
C L Lampen
C L Lampen
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
W Lampl
W Lampl
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
E Lancon
E Lancon
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
U Landgraf
U Landgraf
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
M P J Landon
M P J Landon
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
J L Lane
J L Lane
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
C Lange
C Lange
61DESY, Hamburg and Zeuthen, Germany
61,
A J Lankford
A J Lankford
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
F Lanni
F Lanni
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
K Lantzsch
K Lantzsch
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
S Laplace
S Laplace
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
C Lapoire
C Lapoire
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
J F Laporte
J F Laporte
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
T Lari
T Lari
113INFN Sezione di Milano, Milano, Italy
113,
A V Larionov
A V Larionov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
A Larner
A Larner
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
C Lasseur
C Lasseur
44CERN, Geneva, Switzerland
44,
M Lassnig
M Lassnig
44CERN, Geneva, Switzerland
44,
P Laurelli
P Laurelli
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
W Lavrijsen
W Lavrijsen
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
P Laycock
P Laycock
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
A B Lazarev
A B Lazarev
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
O Le Dortz
O Le Dortz
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
E Le Guirriec
E Le Guirriec
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
C Le Maner
C Le Maner
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
E Le Menedeu
E Le Menedeu
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
C Lebel
C Lebel
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
T LeCompte
T LeCompte
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
F Ledroit-Guillon
F Ledroit-Guillon
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
H Lee
H Lee
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
J S H Lee
J S H Lee
142Graduate School of Science, Osaka University, Osaka, Japan
142,
S C Lee
S C Lee
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
L Lee
L Lee
217Department of Physics, Yale University, New Haven, CT United States of America
217,
M Lefebvre
M Lefebvre
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
M Legendre
M Legendre
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
A Leger
A Leger
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
B C LeGeyt
B C LeGeyt
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
F Legger
F Legger
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
C Leggett
C Leggett
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Lehmacher
M Lehmacher
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
G Lehmann Miotto
G Lehmann Miotto
44CERN, Geneva, Switzerland
44,
X Lei
X Lei
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
M A L Leite
M A L Leite
36Instituto de Fisica, Universidade de Sao Paulo, Sao Paulo, Brazil
36,
R Leitner
R Leitner
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
D Lellouch
D Lellouch
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
M Leltchouk
M Leltchouk
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
B Lemmer
B Lemmer
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
V Lendermann
V Lendermann
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
K J C Leney
K J C Leney
183School of Physics, University of the Witwatersrand, Johannesburg, South Africa
183,
T Lenz
T Lenz
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
G Lenzen
G Lenzen
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
B Lenzi
B Lenzi
44CERN, Geneva, Switzerland
44,
K Leonhardt
K Leonhardt
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
S Leontsinis
S Leontsinis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
C Leroy
C Leroy
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
J-R Lessard
J-R Lessard
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
J Lesser
J Lesser
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
C G Lester
C G Lester
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
A Leung Fook Cheong
A Leung Fook Cheong
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
J Levêque
J Levêque
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
D Levin
D Levin
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
L J Levinson
L J Levinson
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
M S Levitski
M S Levitski
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
A Lewis
A Lewis
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
G H Lewis
G H Lewis
134Department of Physics, New York University, New York, NY United States of America
134,
A M Leyko
A M Leyko
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Leyton
M Leyton
21Department of Physics, Humboldt University, Berlin, Germany
21,
B Li
B Li
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
H Li
H Li
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
S Li
S Li
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
X Li
X Li
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
Z Liang
Z Liang
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
H Liao
H Liao
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
B Liberti
B Liberti
163INFN Sezione di Roma Tor Vergata, Roma, Italy
163,
P Lichard
P Lichard
44CERN, Geneva, Switzerland
44,
M Lichtnecker
M Lichtnecker
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
K Lie
K Lie
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
W Liebig
W Liebig
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
R Lifshitz
R Lifshitz
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
C Limbach
C Limbach
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Limosani
A Limosani
110School of Physics, University of Melbourne, Victoria, Australia
110,
M Limper
M Limper
86University of Iowa, Iowa City, IA United States of America
86,
S C Lin
S C Lin
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
F Linde
F Linde
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
J T Linnemann
J T Linnemann
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
E Lipeles
E Lipeles
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
L Lipinsky
L Lipinsky
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
A Lipniacka
A Lipniacka
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
T M Liss
T M Liss
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
D Lissauer
D Lissauer
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
A Lister
A Lister
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
A M Litke
A M Litke
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
C Liu
C Liu
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
D Liu
D Liu
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
H Liu
H Liu
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
J B Liu
J B Liu
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
M Liu
M Liu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
Y Liu
Y Liu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
M Livan
M Livan
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
S S A Livermore
S S A Livermore
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
A Lleres
A Lleres
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
J Llorente Merino
J Llorente Merino
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
S L Lloyd
S L Lloyd
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
E Lobodzinska
E Lobodzinska
61DESY, Hamburg and Zeuthen, Germany
61,
P Loch
P Loch
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
W S Lockman
W S Lockman
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
T Loddenkoetter
T Loddenkoetter
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
F K Loebinger
F K Loebinger
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
A Loginov
A Loginov
217Department of Physics, Yale University, New Haven, CT United States of America
217,
C W Loh
C W Loh
210Department of Physics, University of British Columbia, Vancouver, BC Canada
210,
T Lohse
T Lohse
21Department of Physics, Humboldt University, Berlin, Germany
21,
K Lohwasser
K Lohwasser
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
M Lokajicek
M Lokajicek
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
J Loken
J Loken
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
V P Lombardo
V P Lombardo
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
R E Long
R E Long
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
L Lopes
L Lopes
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
D Lopez Mateos
D Lopez Mateos
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
J Lorenz
J Lorenz
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
N Lorenzo Martinez
N Lorenzo Martinez
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
M Losada
M Losada
202Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
202,
P Loscutoff
P Loscutoff
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
F Lo Sterzo
F Lo Sterzo
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
M J Losty
M J Losty
198TRIUMF, Vancouver, BC Canada
198,
X Lou
X Lou
60Physics Department, University of Texas at Dallas, Richardson, TX United States of America
60,
A Lounis
A Lounis
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
K F Loureiro
K F Loureiro
202Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
202,
J Love
J Love
31Department of Physics, Boston University, Boston, MA United States of America
31,
P A Love
P A Love
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
A J Lowe
A J Lowe
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
F Lu
F Lu
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
H J Lubatti
H J Lubatti
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
C Luci
C Luci
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
A Lucotte
A Lucotte
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
A Ludwig
A Ludwig
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
D Ludwig
D Ludwig
61DESY, Hamburg and Zeuthen, Germany
61,
I Ludwig
I Ludwig
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
J Ludwig
J Ludwig
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
F Luehring
F Luehring
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
G Luijckx
G Luijckx
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
D Lumb
D Lumb
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
L Luminari
L Luminari
161INFN Sezione di Roma I, Roma, Italy
161,
E Lund
E Lund
143Department of Physics, University of Oslo, Oslo, Norway
143,
B Lund-Jensen
B Lund-Jensen
186Physics Department, Royal Institute of Technology, Stockholm, Sweden
186,
B Lundberg
B Lundberg
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
J Lundberg
J Lundberg
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
J Lundquist
J Lundquist
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
M Lungwitz
M Lungwitz
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
G Lutz
G Lutz
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
D Lynn
D Lynn
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
J Lys
J Lys
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Lytken
E Lytken
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
H Ma
H Ma
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
L L Ma
L L Ma
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
J A Macana Goia
J A Macana Goia
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
G Maccarrone
G Maccarrone
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
A Macchiolo
A Macchiolo
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
B Maček
B Maček
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
J Machado Miguens
J Machado Miguens
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
R Mackeprang
R Mackeprang
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
R J Madaras
R J Madaras
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
W F Mader
W F Mader
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
R Maenner
R Maenner
82ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
82,
T Maeno
T Maeno
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
P Mättig
P Mättig
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
S Mättig
S Mättig
61DESY, Hamburg and Zeuthen, Germany
61,
L Magnoni
L Magnoni
44CERN, Geneva, Switzerland
44,
E Magradze
E Magradze
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
Y Mahalalel
Y Mahalalel
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
K Mahboubi
K Mahboubi
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
G Mahout
G Mahout
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
C Maiani
C Maiani
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
C Maidantchik
C Maidantchik
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
A Maio
A Maio
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
S Majewski
S Majewski
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
Y Makida
Y Makida
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
N Makovec
N Makovec
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
P Mal
P Mal
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
B Malaescu
B Malaescu
44CERN, Geneva, Switzerland
44,
Pa Malecki
Pa Malecki
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
P Malecki
P Malecki
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
V P Maleev
V P Maleev
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
F Malek
F Malek
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
U Mallik
U Mallik
86University of Iowa, Iowa City, IA United States of America
86,
D Malon
D Malon
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
C Malone
C Malone
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S Maltezos
S Maltezos
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
V Malyshev
V Malyshev
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
S Malyukov
S Malyukov
44CERN, Geneva, Switzerland
44,
R Mameghani
R Mameghani
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
J Mamuzic
J Mamuzic
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
A Manabe
A Manabe
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
L Mandelli
L Mandelli
113INFN Sezione di Milano, Milano, Italy
113,
I Mandić
I Mandić
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
R Mandrysch
R Mandrysch
21Department of Physics, Humboldt University, Berlin, Germany
21,
J Maneira
J Maneira
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
P S Mangeard
P S Mangeard
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
L Manhaes de Andrade Filho
L Manhaes de Andrade Filho
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
I D Manjavidze
I D Manjavidze
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A Mann
A Mann
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
P M Manning
P M Manning
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
A Manousakis-Katsikakis
A Manousakis-Katsikakis
13Physics Department, University of Athens, Athens, Greece
13,
B Mansoulie
B Mansoulie
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
A Manz
A Manz
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
A Mapelli
A Mapelli
44CERN, Geneva, Switzerland
44,
L Mapelli
L Mapelli
44CERN, Geneva, Switzerland
44,
L March
L March
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
J F Marchand
J F Marchand
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
F Marchese
F Marchese
163INFN Sezione di Roma Tor Vergata, Roma, Italy
164Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
163,164,
G Marchiori
G Marchiori
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
M Marcisovsky
M Marcisovsky
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
A Marin
A Marin
31Department of Physics, Boston University, Boston, MA United States of America
31,
C P Marino
C P Marino
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
F Marroquim
F Marroquim
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
R Marshall
R Marshall
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
Z Marshall
Z Marshall
44CERN, Geneva, Switzerland
44,
F K Martens
F K Martens
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
S Marti-Garcia
S Marti-Garcia
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
A J Martin
A J Martin
217Department of Physics, Yale University, New Haven, CT United States of America
217,
B Martin
B Martin
44CERN, Geneva, Switzerland
44,
B Martin
B Martin
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
F F Martin
F F Martin
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
J P Martin
J P Martin
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
Ph Martin
Ph Martin
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
T A Martin
T A Martin
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
V J Martin
V J Martin
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
B Martin dit Latour
B Martin dit Latour
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
S Martin-Haugh
S Martin-Haugh
188Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
188,
M Martinez
M Martinez
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
V Martinez Outschoorn
V Martinez Outschoorn
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
A C Martyniuk
A C Martyniuk
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
M Marx
M Marx
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
F Marzano
F Marzano
161INFN Sezione di Roma I, Roma, Italy
161,
A Marzin
A Marzin
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
L Masetti
L Masetti
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
T Mashimo
T Mashimo
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
R Mashinistov
R Mashinistov
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
J Masik
J Masik
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
A L Maslennikov
A L Maslennikov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
I Massa
I Massa
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
G Massaro
G Massaro
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
N Massol
N Massol
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
P Mastrandrea
P Mastrandrea
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
A Mastroberardino
A Mastroberardino
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
T Masubuchi
T Masubuchi
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
M Mathes
M Mathes
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
P Matricon
P Matricon
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
H Matsumoto
H Matsumoto
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
H Matsunaga
H Matsunaga
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
T Matsushita
T Matsushita
90Graduate School of Science, Kobe University, Kobe, Japan
90,
C Mattravers
C Mattravers
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
J M Maugain
J M Maugain
44CERN, Geneva, Switzerland
44,
J Maurer
J Maurer
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
S J Maxfield
S J Maxfield
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
D A Maximov
D A Maximov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
E N May
E N May
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
A Mayne
A Mayne
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
R Mazini
R Mazini
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
M Mazur
M Mazur
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Mazzanti
M Mazzanti
113INFN Sezione di Milano, Milano, Italy
113,
E Mazzoni
E Mazzoni
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
S P Mc Kee
S P Mc Kee
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
A McCarn
A McCarn
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
R L McCarthy
R L McCarthy
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
T G McCarthy
T G McCarthy
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
N A McCubbin
N A McCubbin
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
K W McFarlane
K W McFarlane
78Department of Physics, Hampton University, Hampton, VA United States of America
78,
J A Mcfayden
J A Mcfayden
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
H McGlone
H McGlone
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
G Mchedlidze
G Mchedlidze
73High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
73,
R A McLaren
R A McLaren
44CERN, Geneva, Switzerland
44,
T Mclaughlan
T Mclaughlan
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
S J McMahon
S J McMahon
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
R A McPherson
R A McPherson
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
A Meade
A Meade
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
J Mechnich
J Mechnich
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
M Mechtel
M Mechtel
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
M Medinnis
M Medinnis
61DESY, Hamburg and Zeuthen, Germany
61,
R Meera-Lebbai
R Meera-Lebbai
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
T Meguro
T Meguro
142Graduate School of Science, Osaka University, Osaka, Japan
142,
R Mehdiyev
R Mehdiyev
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
S Mehlhase
S Mehlhase
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
A Mehta
A Mehta
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
K Meier
K Meier
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
B Meirose
B Meirose
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
C Melachrinos
C Melachrinos
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
B R Mellado Garcia
B R Mellado Garcia
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
L Mendoza Navas
L Mendoza Navas
202Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
202,
Z Meng
Z Meng
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
A Mengarelli
A Mengarelli
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
S Menke
S Menke
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
C Menot
C Menot
44CERN, Geneva, Switzerland
44,
E Meoni
E Meoni
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
K M Mercurio
K M Mercurio
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
P Mermod
P Mermod
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
L Merola
L Merola
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
C Meroni
C Meroni
113INFN Sezione di Milano, Milano, Italy
113,
F S Merritt
F S Merritt
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
H Merritt
H Merritt
135Ohio State University, Columbus, OH United States of America
135,
A Messina
A Messina
44CERN, Geneva, Switzerland
44,
J Metcalfe
J Metcalfe
129Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
129,
A S Mete
A S Mete
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
C Meyer
C Meyer
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
C Meyer
C Meyer
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
J-P Meyer
J-P Meyer
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
J Meyer
J Meyer
215Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
215,
J Meyer
J Meyer
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
T C Meyer
T C Meyer
44CERN, Geneva, Switzerland
44,
W T Meyer
W T Meyer
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
J Miao
J Miao
51School of Physics, Shandong University, Shandong, China
51,
S Michal
S Michal
44CERN, Geneva, Switzerland
44,
L Micu
L Micu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
R P Middleton
R P Middleton
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
S Migas
S Migas
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
L Mijović
L Mijović
61DESY, Hamburg and Zeuthen, Germany
61,
G Mikenberg
G Mikenberg
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
M Mikestikova
M Mikestikova
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
M Mikuž
M Mikuž
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
D W Miller
D W Miller
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
R J Miller
R J Miller
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
W J Mills
W J Mills
210Department of Physics, University of British Columbia, Vancouver, BC Canada
210,
C Mills
C Mills
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
A Milov
A Milov
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
D A Milstead
D A Milstead
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
D Milstein
D Milstein
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
A A Minaenko
A A Minaenko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
M Miñano Moya
M Miñano Moya
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
I A Minashvili
I A Minashvili
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A I Mincer
A I Mincer
134Department of Physics, New York University, New York, NY United States of America
134,
B Mindur
B Mindur
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
M Mineev
M Mineev
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
Y Ming
Y Ming
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
L M Mir
L M Mir
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
G Mirabelli
G Mirabelli
161INFN Sezione di Roma I, Roma, Italy
161,
L Miralles Verge
L Miralles Verge
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
A Misiejuk
A Misiejuk
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
J Mitrevski
J Mitrevski
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
G Y Mitrofanov
G Y Mitrofanov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
V A Mitsou
V A Mitsou
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
S Mitsui
S Mitsui
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
P S Miyagawa
P S Miyagawa
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
K Miyazaki
K Miyazaki
90Graduate School of Science, Kobe University, Kobe, Japan
90,
J U Mjörnmark
J U Mjörnmark
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
T Moa
T Moa
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
P Mockett
P Mockett
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
S Moed
S Moed
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
V Moeller
V Moeller
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
K Mönig
K Mönig
61DESY, Hamburg and Zeuthen, Germany
61,
N Möser
N Möser
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
S Mohapatra
S Mohapatra
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
W Mohr
W Mohr
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
S Mohrdieck-Möck
S Mohrdieck-Möck
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
A M Moisseev
A M Moisseev
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
R Moles-Valls
R Moles-Valls
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
J Molina-Perez
J Molina-Perez
44CERN, Geneva, Switzerland
44,
J Monk
J Monk
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
E Monnier
E Monnier
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
S Montesano
S Montesano
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
F Monticelli
F Monticelli
93Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
93,
S Monzani
S Monzani
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
R W Moore
R W Moore
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
G F Moorhead
G F Moorhead
110School of Physics, University of Melbourne, Victoria, Australia
110,
C Mora Herrera
C Mora Herrera
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
A Moraes
A Moraes
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
N Morange
N Morange
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
J Morel
J Morel
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
G Morello
G Morello
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
D Moreno
D Moreno
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
M Moreno Llácer
M Moreno Llácer
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
P Morettini
P Morettini
70INFN Sezione di Genova, Genova, Italy
70,
M Morii
M Morii
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
J Morin
J Morin
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
A K Morley
A K Morley
44CERN, Geneva, Switzerland
44,
G Mornacchi
G Mornacchi
44CERN, Geneva, Switzerland
44,
S V Morozov
S V Morozov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
J D Morris
J D Morris
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
L Morvaj
L Morvaj
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
H G Moser
H G Moser
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
M Mosidze
M Mosidze
73High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
73,
J Moss
J Moss
135Ohio State University, Columbus, OH United States of America
135,
R Mount
R Mount
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
E Mountricha
E Mountricha
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
S V Mouraviev
S V Mouraviev
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
E J W Moyse
E J W Moyse
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
M Mudrinic
M Mudrinic
18Vinca Institute of Nuclear Sciences, University of Belgrade, Belgrade, Serbia
18,
F Mueller
F Mueller
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
J Mueller
J Mueller
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
K Mueller
K Mueller
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
T A Müller
T A Müller
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
T Mueller
T Mueller
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
D Muenstermann
D Muenstermann
44CERN, Geneva, Switzerland
44,
A Muir
A Muir
210Department of Physics, University of British Columbia, Vancouver, BC Canada
210,
Y Munwes
Y Munwes
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
W J Murray
W J Murray
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
I Mussche
I Mussche
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
E Musto
E Musto
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
A G Myagkov
A G Myagkov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
M Myska
M Myska
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
J Nadal
J Nadal
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
K Nagai
K Nagai
200Institute of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571 Japan
200,
K Nagano
K Nagano
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
A Nagarkar
A Nagarkar
135Ohio State University, Columbus, OH United States of America
135,
Y Nagasaka
Y Nagasaka
83Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
83,
M Nagel
M Nagel
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
A M Nairz
A M Nairz
44CERN, Geneva, Switzerland
44,
Y Nakahama
Y Nakahama
44CERN, Geneva, Switzerland
44,
K Nakamura
K Nakamura
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
T Nakamura
T Nakamura
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
I Nakano
I Nakano
136Faculty of Science, Okayama University, Okayama, Japan
136,
G Nanava
G Nanava
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Napier
A Napier
201Science and Technology Center, Tufts University, Medford, MA United States of America
201,
R Narayan
R Narayan
81Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
M Nash
M Nash
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
N R Nation
N R Nation
31Department of Physics, Boston University, Boston, MA United States of America
31,
T Nattermann
T Nattermann
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
T Naumann
T Naumann
61DESY, Hamburg and Zeuthen, Germany
61,
G Navarro
G Navarro
202Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
202,
H A Neal
H A Neal
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
E Nebot
E Nebot
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
P Yu Nechaeva
P Yu Nechaeva
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
T J Neep
T J Neep
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
A Negri
A Negri
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
G Negri
G Negri
44CERN, Geneva, Switzerland
44,
S Nektarijevic
S Nektarijevic
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
A Nelson
A Nelson
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
S Nelson
S Nelson
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
T K Nelson
T K Nelson
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S Nemecek
S Nemecek
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
P Nemethy
P Nemethy
134Department of Physics, New York University, New York, NY United States of America
134,
A A Nepomuceno
A A Nepomuceno
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
M Nessi
M Nessi
44CERN, Geneva, Switzerland
44,
M S Neubauer
M S Neubauer
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
A Neusiedl
A Neusiedl
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
R M Neves
R M Neves
134Department of Physics, New York University, New York, NY United States of America
134,
P Nevski
P Nevski
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
P R Newman
P R Newman
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
V Nguyen Thi Hong
V Nguyen Thi Hong
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
R B Nickerson
R B Nickerson
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
R Nicolaidou
R Nicolaidou
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
L Nicolas
L Nicolas
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
B Nicquevert
B Nicquevert
44CERN, Geneva, Switzerland
44,
F Niedercorn
F Niedercorn
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
J Nielsen
J Nielsen
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
T Niinikoski
T Niinikoski
44CERN, Geneva, Switzerland
44,
N Nikiforou
N Nikiforou
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
A Nikiforov
A Nikiforov
21Department of Physics, Humboldt University, Berlin, Germany
21,
V Nikolaenko
V Nikolaenko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
K Nikolaev
K Nikolaev
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
I Nikolic-Audit
I Nikolic-Audit
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
K Nikolics
K Nikolics
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
K Nikolopoulos
K Nikolopoulos
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
H Nilsen
H Nilsen
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
P Nilsson
P Nilsson
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
Y Ninomiya
Y Ninomiya
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
A Nisati
A Nisati
161INFN Sezione di Roma I, Roma, Italy
161,
T Nishiyama
T Nishiyama
90Graduate School of Science, Kobe University, Kobe, Japan
90,
R Nisius
R Nisius
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
L Nodulman
L Nodulman
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
M Nomachi
M Nomachi
142Graduate School of Science, Osaka University, Osaka, Japan
142,
I Nomidis
I Nomidis
193Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
193,
M Nordberg
M Nordberg
44CERN, Geneva, Switzerland
44,
B Nordkvist
B Nordkvist
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
P R Norton
P R Norton
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
J Novakova
J Novakova
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
M Nozaki
M Nozaki
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
L Nozka
L Nozka
139Palacký University, RCPTM, Olomouc, Czech Republic
139,
I M Nugent
I M Nugent
198TRIUMF, Vancouver, BC Canada
198,
A-E Nuncio-Quiroz
A-E Nuncio-Quiroz
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
G Nunes Hanninger
G Nunes Hanninger
110School of Physics, University of Melbourne, Victoria, Australia
110,
T Nunnemann
T Nunnemann
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
E Nurse
E Nurse
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
B J O’Brien
B J O’Brien
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
S W O’Neale
S W O’Neale
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
D C O’Neil
D C O’Neil
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
V O’Shea
V O’Shea
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
L B Oakes
L B Oakes
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
F G Oakham
F G Oakham
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
H Oberlack
H Oberlack
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
J Ocariz
J Ocariz
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
A Ochi
A Ochi
90Graduate School of Science, Kobe University, Kobe, Japan
90,
S Oda
S Oda
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
S Odaka
S Odaka
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
J Odier
J Odier
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
H Ogren
H Ogren
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
A Oh
A Oh
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
S H Oh
S H Oh
64Department of Physics, Duke University, Durham, NC United States of America
64,
C C Ohm
C C Ohm
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
T Ohshima
T Ohshima
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
H Ohshita
H Ohshita
176Department of Physics, Shinshu University, Nagano, Japan
176,
T Ohsugi
T Ohsugi
220Faculty of Science, Hiroshima University, Hiroshima, Japan
220,
S Okada
S Okada
90Graduate School of Science, Kobe University, Kobe, Japan
90,
H Okawa
H Okawa
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
Y Okumura
Y Okumura
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
T Okuyama
T Okuyama
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
A Olariu
A Olariu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
M Olcese
M Olcese
70INFN Sezione di Genova, Genova, Italy
70,
A G Olchevski
A G Olchevski
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
M Oliveira
M Oliveira
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
D Oliveira Damazio
D Oliveira Damazio
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
E Oliver Garcia
E Oliver Garcia
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
D Olivito
D Olivito
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
A Olszewski
A Olszewski
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
J Olszowska
J Olszowska
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
C Omachi
C Omachi
90Graduate School of Science, Kobe University, Kobe, Japan
90,
A Onofre
A Onofre
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
P U E Onyisi
P U E Onyisi
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
C J Oram
C J Oram
198TRIUMF, Vancouver, BC Canada
198,
M J Oreglia
M J Oreglia
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
Y Oren
Y Oren
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
D Orestano
D Orestano
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
I Orlov
I Orlov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
C Oropeza Barrera
C Oropeza Barrera
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
R S Orr
R S Orr
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
B Osculati
B Osculati
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
R Ospanov
R Ospanov
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
C Osuna
C Osuna
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
G Otero y Garzon
G Otero y Garzon
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
J P Ottersbach
J P Ottersbach
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
M Ouchrif
M Ouchrif
170Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
170,
E A Ouellette
E A Ouellette
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
F Ould-Saada
F Ould-Saada
143Department of Physics, University of Oslo, Oslo, Norway
143,
A Ouraou
A Ouraou
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
Q Ouyang
Q Ouyang
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
A Ovcharova
A Ovcharova
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
M Owen
M Owen
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
S Owen
S Owen
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
V E Ozcan
V E Ozcan
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
N Ozturk
N Ozturk
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
A Pacheco Pages
A Pacheco Pages
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
C Padilla Aranda
C Padilla Aranda
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
S Pagan Griso
S Pagan Griso
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
E Paganis
E Paganis
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
F Paige
F Paige
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
P Pais
P Pais
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
K Pajchel
K Pajchel
143Department of Physics, University of Oslo, Oslo, Norway
143,
G Palacino
G Palacino
199Department of Physics and Astronomy, York University, Toronto, ON Canada
199,
C P Paleari
C P Paleari
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
S Palestini
S Palestini
44CERN, Geneva, Switzerland
44,
D Pallin
D Pallin
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
A Palma
A Palma
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
J D Palmer
J D Palmer
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
Y B Pan
Y B Pan
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
E Panagiotopoulou
E Panagiotopoulou
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
B Panes
B Panes
46Departamento de Fisica, Pontificia Universidad Católica de Chile, Santiago, Chile
46,
N Panikashvili
N Panikashvili
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
S Panitkin
S Panitkin
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
D Pantea
D Pantea
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
M Panuskova
M Panuskova
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
V Paolone
V Paolone
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
A Papadelis
A Papadelis
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
Th D Papadopoulou
Th D Papadopoulou
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
A Paramonov
A Paramonov
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
W Park
W Park
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
M A Parker
M A Parker
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
F Parodi
F Parodi
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
J A Parsons
J A Parsons
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
U Parzefall
U Parzefall
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
E Pasqualucci
E Pasqualucci
161INFN Sezione di Roma I, Roma, Italy
161,
S Passaggio
S Passaggio
70INFN Sezione di Genova, Genova, Italy
70,
A Passeri
A Passeri
165INFN Sezione di Roma Tre, Roma, Italy
165,
F Pastore
F Pastore
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
Fr Pastore
Fr Pastore
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
G Pásztor
G Pásztor
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
S Pataraia
S Pataraia
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
N Patel
N Patel
189School of Physics, University of Sydney, Sydney, Australia
189,
J R Pater
J R Pater
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
S Patricelli
S Patricelli
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
T Pauly
T Pauly
44CERN, Geneva, Switzerland
44,
M Pecsy
M Pecsy
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
M I Pedraza Morales
M I Pedraza Morales
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
S V Peleganchuk
S V Peleganchuk
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
H Peng
H Peng
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
R Pengo
R Pengo
44CERN, Geneva, Switzerland
44,
A Penson
A Penson
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
J Penwell
J Penwell
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
M Perantoni
M Perantoni
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
K Perez
K Perez
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
T Perez Cavalcanti
T Perez Cavalcanti
61DESY, Hamburg and Zeuthen, Germany
61,
E Perez Codina
E Perez Codina
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
M T Pérez García-Estañ
M T Pérez García-Estañ
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
V Perez Reale
V Perez Reale
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
L Perini
L Perini
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
H Pernegger
H Pernegger
44CERN, Geneva, Switzerland
44,
R Perrino
R Perrino
95INFN Sezione di Lecce, Lecce, Italy
95,
P Perrodo
P Perrodo
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Persembe
S Persembe
4Department of Physics, Ankara University, Ankara, Turkey
4,
A Perus
A Perus
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
V D Peshekhonov
V D Peshekhonov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
K Peters
K Peters
44CERN, Geneva, Switzerland
44,
B A Petersen
B A Petersen
44CERN, Geneva, Switzerland
44,
J Petersen
J Petersen
44CERN, Geneva, Switzerland
44,
T C Petersen
T C Petersen
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
E Petit
E Petit
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
A Petridis
A Petridis
193Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
193,
C Petridou
C Petridou
193Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
193,
E Petrolo
E Petrolo
161INFN Sezione di Roma I, Roma, Italy
161,
F Petrucci
F Petrucci
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
D Petschull
D Petschull
61DESY, Hamburg and Zeuthen, Germany
61,
M Petteni
M Petteni
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
R Pezoa
R Pezoa
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
A Phan
A Phan
110School of Physics, University of Melbourne, Victoria, Australia
110,
P W Phillips
P W Phillips
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
G Piacquadio
G Piacquadio
44CERN, Geneva, Switzerland
44,
E Piccaro
E Piccaro
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
M Piccinini
M Piccinini
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
S M Piec
S M Piec
61DESY, Hamburg and Zeuthen, Germany
61,
R Piegaia
R Piegaia
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
D T Pignotti
D T Pignotti
135Ohio State University, Columbus, OH United States of America
135,
J E Pilcher
J E Pilcher
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
A D Pilkington
A D Pilkington
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
J Pina
J Pina
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
M Pinamonti
M Pinamonti
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
A Pinder
A Pinder
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
J L Pinfold
J L Pinfold
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
J Ping
J Ping
50Department of Physics, Nanjing University, Jiangsu, China
50,
B Pinto
B Pinto
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
O Pirotte
O Pirotte
44CERN, Geneva, Switzerland
44,
C Pizio
C Pizio
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
M Plamondon
M Plamondon
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
M-A Pleier
M-A Pleier
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
A V Pleskach
A V Pleskach
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
A Poblaguev
A Poblaguev
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S Poddar
S Poddar
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
F Podlyski
F Podlyski
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
L Poggioli
L Poggioli
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
T Poghosyan
T Poghosyan
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Pohl
M Pohl
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
F Polci
F Polci
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
G Polesello
G Polesello
145INFN Sezione di Pavia, Pavia, Italy
145,
A Policicchio
A Policicchio
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
A Polini
A Polini
28INFN Sezione di Bologna, Bologna, Italy
28,
J Poll
J Poll
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
V Polychronakos
V Polychronakos
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
D M Pomarede
D M Pomarede
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
D Pomeroy
D Pomeroy
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
K Pommès
K Pommès
44CERN, Geneva, Switzerland
44,
L Pontecorvo
L Pontecorvo
161INFN Sezione di Roma I, Roma, Italy
161,
B G Pope
B G Pope
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
G A Popeneciu
G A Popeneciu
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
D S Popovic
D S Popovic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
A Poppleton
A Poppleton
44CERN, Geneva, Switzerland
44,
X Portell Bueso
X Portell Bueso
44CERN, Geneva, Switzerland
44,
C Posch
C Posch
31Department of Physics, Boston University, Boston, MA United States of America
31,
G E Pospelov
G E Pospelov
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
S Pospisil
S Pospisil
156Czech Technical University in Prague, Praha, Czech Republic
156,
I N Potrap
I N Potrap
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
C J Potter
C J Potter
188Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
188,
C T Potter
C T Potter
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
G Poulard
G Poulard
44CERN, Geneva, Switzerland
44,
J Poveda
J Poveda
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
R Prabhu
R Prabhu
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
P Pralavorio
P Pralavorio
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
A Pranko
A Pranko
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
S Prasad
S Prasad
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
R Pravahan
R Pravahan
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
S Prell
S Prell
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
K Pretzl
K Pretzl
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
L Pribyl
L Pribyl
44CERN, Geneva, Switzerland
44,
D Price
D Price
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
J Price
J Price
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
L E Price
L E Price
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
M J Price
M J Price
44CERN, Geneva, Switzerland
44,
D Prieur
D Prieur
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
M Primavera
M Primavera
95INFN Sezione di Lecce, Lecce, Italy
95,
K Prokofiev
K Prokofiev
134Department of Physics, New York University, New York, NY United States of America
134,
F Prokoshin
F Prokoshin
47Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile
47,
S Protopopescu
S Protopopescu
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
J Proudfoot
J Proudfoot
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
X Prudent
X Prudent
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
M Przybycien
M Przybycien
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
H Przysiezniak
H Przysiezniak
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Psoroulas
S Psoroulas
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
E Ptacek
E Ptacek
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
E Pueschel
E Pueschel
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
J Purdham
J Purdham
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
M Purohit
M Purohit
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
P Puzo
P Puzo
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
Y Pylypchenko
Y Pylypchenko
86University of Iowa, Iowa City, IA United States of America
86,
J Qian
J Qian
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
Z Qian
Z Qian
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
Z Qin
Z Qin
61DESY, Hamburg and Zeuthen, Germany
61,
A Quadt
A Quadt
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
D R Quarrie
D R Quarrie
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
W B Quayle
W B Quayle
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
F Quinonez
F Quinonez
46Departamento de Fisica, Pontificia Universidad Católica de Chile, Santiago, Chile
46,
M Raas
M Raas
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
V Radescu
V Radescu
81Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
B Radics
B Radics
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
P Radloff
P Radloff
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
T Rador
T Rador
24Department of Physics, Bogazici University, Istanbul, Turkey
24,
F Ragusa
F Ragusa
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
G Rahal
G Rahal
219Domaine scientifique de la Doua, Centre de Calcul CNRS/IN2P3, Villeurbanne Cedex, France
219,
A M Rahimi
A M Rahimi
135Ohio State University, Columbus, OH United States of America
135,
D Rahm
D Rahm
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S Rajagopalan
S Rajagopalan
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
M Rammensee
M Rammensee
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
M Rammes
M Rammes
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
A S Randle-Conde
A S Randle-Conde
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
K Randrianarivony
K Randrianarivony
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
P N Ratoff
P N Ratoff
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
F Rauscher
F Rauscher
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Raymond
M Raymond
44CERN, Geneva, Switzerland
44,
A L Read
A L Read
143Department of Physics, University of Oslo, Oslo, Norway
143,
D M Rebuzzi
D M Rebuzzi
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
A Redelbach
A Redelbach
215Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
215,
G Redlinger
G Redlinger
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
R Reece
R Reece
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
K Reeves
K Reeves
60Physics Department, University of Texas at Dallas, Richardson, TX United States of America
60,
A Reichold
A Reichold
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
E Reinherz-Aronis
E Reinherz-Aronis
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
A Reinsch
A Reinsch
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
I Reisinger
I Reisinger
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
D Reljic
D Reljic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
C Rembser
C Rembser
44CERN, Geneva, Switzerland
44,
Z L Ren
Z L Ren
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
A Renaud
A Renaud
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
P Renkel
P Renkel
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
M Rescigno
M Rescigno
161INFN Sezione di Roma I, Roma, Italy
161,
S Resconi
S Resconi
113INFN Sezione di Milano, Milano, Italy
113,
B Resende
B Resende
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
P Reznicek
P Reznicek
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
R Rezvani
R Rezvani
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
A Richards
A Richards
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
R Richter
R Richter
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
E Richter-Was
E Richter-Was
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
M Ridel
M Ridel
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
M Rijpstra
M Rijpstra
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
M Rijssenbeek
M Rijssenbeek
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
A Rimoldi
A Rimoldi
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
L Rinaldi
L Rinaldi
28INFN Sezione di Bologna, Bologna, Italy
28,
R R Rios
R R Rios
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
I Riu
I Riu
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
G Rivoltella
G Rivoltella
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
F Rizatdinova
F Rizatdinova
138Department of Physics, Oklahoma State University, Stillwater, OK United States of America
138,
E Rizvi
E Rizvi
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
S H Robertson
S H Robertson
109Department of Physics, McGill University, Montreal, QC Canada
109,
A Robichaud-Veronneau
A Robichaud-Veronneau
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
D Robinson
D Robinson
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
J E M Robinson
J E M Robinson
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
M Robinson
M Robinson
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
A Robson
A Robson
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
J G Rocha de Lima
J G Rocha de Lima
132Department of Physics, Northern Illinois University, DeKalb, IL United States of America
132,
C Roda
C Roda
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
D Roda Dos Santos
D Roda Dos Santos
44CERN, Geneva, Switzerland
44,
D Rodriguez
D Rodriguez
202Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
202,
A Roe
A Roe
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
S Roe
S Roe
44CERN, Geneva, Switzerland
44,
O Røhne
O Røhne
143Department of Physics, University of Oslo, Oslo, Norway
143,
V Rojo
V Rojo
2University at Albany, Albany, NY United States of America
2,
S Rolli
S Rolli
201Science and Technology Center, Tufts University, Medford, MA United States of America
201,
A Romaniouk
A Romaniouk
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
M Romano
M Romano
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
V M Romanov
V M Romanov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
G Romeo
G Romeo
41Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
41,
E Romero Adam
E Romero Adam
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
L Roos
L Roos
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
E Ros
E Ros
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
S Rosati
S Rosati
161INFN Sezione di Roma I, Roma, Italy
161,
K Rosbach
K Rosbach
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
A Rose
A Rose
188Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
188,
M Rose
M Rose
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
G A Rosenbaum
G A Rosenbaum
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
E I Rosenberg
E I Rosenberg
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
P L Rosendahl
P L Rosendahl
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
O Rosenthal
O Rosenthal
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
L Rosselet
L Rosselet
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
V Rossetti
V Rossetti
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
E Rossi
E Rossi
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
L P Rossi
L P Rossi
70INFN Sezione di Genova, Genova, Italy
70,
M Rotaru
M Rotaru
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
I Roth
I Roth
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
J Rothberg
J Rothberg
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
D Rousseau
D Rousseau
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
C R Royon
C R Royon
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
A Rozanov
A Rozanov
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
Y Rozen
Y Rozen
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
X Ruan
X Ruan
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
I Rubinskiy
I Rubinskiy
61DESY, Hamburg and Zeuthen, Germany
61,
B Ruckert
B Ruckert
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
N Ruckstuhl
N Ruckstuhl
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
V I Rud
V I Rud
122Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
122,
C Rudolph
C Rudolph
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
G Rudolph
G Rudolph
85Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
85,
F Rühr
F Rühr
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
F Ruggieri
F Ruggieri
165INFN Sezione di Roma Tre, Roma, Italy
166Dipartimento di Fisica, Università Roma Tre, Roma, Italy
165,166,
A Ruiz-Martinez
A Ruiz-Martinez
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
V Rumiantsev
V Rumiantsev
116National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
116,
L Rumyantsev
L Rumyantsev
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
K Runge
K Runge
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
Z Rurikova
Z Rurikova
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
N A Rusakovich
N A Rusakovich
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
D R Rust
D R Rust
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
J P Rutherfoord
J P Rutherfoord
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
C Ruwiedel
C Ruwiedel
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
P Ruzicka
P Ruzicka
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
Y F Ryabov
Y F Ryabov
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
V Ryadovikov
V Ryadovikov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
P Ryan
P Ryan
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
M Rybar
M Rybar
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
G Rybkin
G Rybkin
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
N C Ryder
N C Ryder
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
S Rzaeva
S Rzaeva
15Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
15,
A F Saavedra
A F Saavedra
189School of Physics, University of Sydney, Sydney, Australia
189,
I Sadeh
I Sadeh
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
H F-W Sadrozinski
H F-W Sadrozinski
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
R Sadykov
R Sadykov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
F Safai Tehrani
F Safai Tehrani
161INFN Sezione di Roma I, Roma, Italy
161,
H Sakamoto
H Sakamoto
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
G Salamanna
G Salamanna
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
A Salamon
A Salamon
163INFN Sezione di Roma Tor Vergata, Roma, Italy
163,
M Saleem
M Saleem
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
D Salihagic
D Salihagic
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
A Salnikov
A Salnikov
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
J Salt
J Salt
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
B M Salvachua Ferrando
B M Salvachua Ferrando
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
D Salvatore
D Salvatore
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
F Salvatore
F Salvatore
188Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
188,
A Salvucci
A Salvucci
130Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, Netherlands
130,
A Salzburger
A Salzburger
44CERN, Geneva, Switzerland
44,
D Sampsonidis
D Sampsonidis
193Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
193,
B H Samset
B H Samset
143Department of Physics, University of Oslo, Oslo, Norway
143,
A Sanchez
A Sanchez
127INFN Sezione di Napoli, Napoli, Italy
128Dipartimento di Scienze Fisiche, Università di Napoli, Napoli, Italy
127,128,
V Sanchez Martinez
V Sanchez Martinez
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
H Sandaker
H Sandaker
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
H G Sander
H G Sander
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
M P Sanders
M P Sanders
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Sandhoff
M Sandhoff
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
T Sandoval
T Sandoval
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
C Sandoval
C Sandoval
202Centro de Investigaciones, Universidad Antonio Narino, Bogota, Colombia
202,
R Sandstroem
R Sandstroem
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
S Sandvoss
S Sandvoss
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
D P C Sankey
D P C Sankey
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
A Sansoni
A Sansoni
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
C Santamarina Rios
C Santamarina Rios
109Department of Physics, McGill University, Montreal, QC Canada
109,
C Santoni
C Santoni
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
R Santonico
R Santonico
163INFN Sezione di Roma Tor Vergata, Roma, Italy
164Dipartimento di Fisica, Università di Roma Tor Vergata, Roma, Italy
163,164,
H Santos
H Santos
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
J G Saraiva
J G Saraiva
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
T Sarangi
T Sarangi
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
E Sarkisyan-Grinbaum
E Sarkisyan-Grinbaum
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
F Sarri
F Sarri
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
G Sartisohn
G Sartisohn
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
O Sasaki
O Sasaki
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
N Sasao
N Sasao
91Faculty of Science, Kyoto University, Kyoto, Japan
91,
I Satsounkevitch
I Satsounkevitch
115B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
115,
G Sauvage
G Sauvage
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
E Sauvan
E Sauvan
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
J B Sauvan
J B Sauvan
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
P Savard
P Savard
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
V Savinov
V Savinov
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
D O Savu
D O Savu
44CERN, Geneva, Switzerland
44,
L Sawyer
L Sawyer
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
D H Saxon
D H Saxon
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
L P Says
L P Says
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
C Sbarra
C Sbarra
28INFN Sezione di Bologna, Bologna, Italy
28,
A Sbrizzi
A Sbrizzi
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
O Scallon
O Scallon
118Group of Particle Physics, University of Montreal, Montreal, QC Canada
118,
D A Scannicchio
D A Scannicchio
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
M Scarcella
M Scarcella
189School of Physics, University of Sydney, Sydney, Australia
189,
J Schaarschmidt
J Schaarschmidt
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
P Schacht
P Schacht
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
U Schäfer
U Schäfer
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
S Schaepe
S Schaepe
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
S Schaetzel
S Schaetzel
81Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
A C Schaffer
A C Schaffer
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
D Schaile
D Schaile
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
R D Schamberger
R D Schamberger
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
A G Schamov
A G Schamov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
V Scharf
V Scharf
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
V A Schegelsky
V A Schegelsky
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
D Scheirich
D Scheirich
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
M Schernau
M Schernau
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
M I Scherzer
M I Scherzer
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
C Schiavi
C Schiavi
70INFN Sezione di Genova, Genova, Italy
71Dipartimento di Fisica, Università di Genova, Genova, Italy
70,71,
J Schieck
J Schieck
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Schioppa
M Schioppa
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
S Schlenker
S Schlenker
44CERN, Geneva, Switzerland
44,
J L Schlereth
J L Schlereth
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
E Schmidt
E Schmidt
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
K Schmieden
K Schmieden
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
C Schmitt
C Schmitt
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
S Schmitt
S Schmitt
81Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
M Schmitz
M Schmitz
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Schöning
A Schöning
81Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
81,
M Schott
M Schott
44CERN, Geneva, Switzerland
44,
D Schouten
D Schouten
198TRIUMF, Vancouver, BC Canada
198,
J Schovancova
J Schovancova
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
M Schram
M Schram
109Department of Physics, McGill University, Montreal, QC Canada
109,
C Schroeder
C Schroeder
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
N Schroer
N Schroer
82ZITI Institut für technische Informatik, Ruprecht-Karls-Universität Heidelberg, Mannheim, Germany
82,
S Schuh
S Schuh
44CERN, Geneva, Switzerland
44,
G Schuler
G Schuler
44CERN, Geneva, Switzerland
44,
M J Schultens
M J Schultens
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
J Schultes
J Schultes
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
H-C Schultz-Coulon
H-C Schultz-Coulon
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
H Schulz
H Schulz
21Department of Physics, Humboldt University, Berlin, Germany
21,
J W Schumacher
J W Schumacher
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Schumacher
M Schumacher
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
B A Schumm
B A Schumm
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
Ph Schune
Ph Schune
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
C Schwanenberger
C Schwanenberger
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
A Schwartzman
A Schwartzman
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
Ph Schwemling
Ph Schwemling
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
R Schwienhorst
R Schwienhorst
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
R Schwierz
R Schwierz
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
J Schwindling
J Schwindling
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
T Schwindt
T Schwindt
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Schwoerer
M Schwoerer
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
W G Scott
W G Scott
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
J Searcy
J Searcy
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
G Sedov
G Sedov
61DESY, Hamburg and Zeuthen, Germany
61,
E Sedykh
E Sedykh
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
E Segura
E Segura
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
S C Seidel
S C Seidel
129Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
129,
A Seiden
A Seiden
173Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA United States of America
173,
F Seifert
F Seifert
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
J M Seixas
J M Seixas
33Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
33,
G Sekhniaidze
G Sekhniaidze
127INFN Sezione di Napoli, Napoli, Italy
127,
K E Selbach
K E Selbach
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
D M Seliverstov
D M Seliverstov
148Petersburg Nuclear Physics Institute, Gatchina, Russia
148,
B Sellden
B Sellden
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
G Sellers
G Sellers
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
M Seman
M Seman
181Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
181,
N Semprini-Cesari
N Semprini-Cesari
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
C Serfon
C Serfon
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
L Serin
L Serin
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
L Serkin
L Serkin
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
R Seuster
R Seuster
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
H Severini
H Severini
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
M E Sevior
M E Sevior
110School of Physics, University of Melbourne, Victoria, Australia
110,
A Sfyrla
A Sfyrla
44CERN, Geneva, Switzerland
44,
E Shabalina
E Shabalina
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
M Shamim
M Shamim
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
L Y Shan
L Y Shan
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
J T Shank
J T Shank
31Department of Physics, Boston University, Boston, MA United States of America
31,
Q T Shao
Q T Shao
110School of Physics, University of Melbourne, Victoria, Australia
110,
M Shapiro
M Shapiro
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
P B Shatalov
P B Shatalov
120Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
120,
L Shaver
L Shaver
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
K Shaw
K Shaw
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
D Sherman
D Sherman
217Department of Physics, Yale University, New Haven, CT United States of America
217,
P Sherwood
P Sherwood
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
A Shibata
A Shibata
134Department of Physics, New York University, New York, NY United States of America
134,
H Shichi
H Shichi
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
S Shimizu
S Shimizu
44CERN, Geneva, Switzerland
44,
M Shimojima
M Shimojima
125Nagasaki Institute of Applied Science, Nagasaki, Japan
125,
T Shin
T Shin
78Department of Physics, Hampton University, Hampton, VA United States of America
78,
M Shiyakova
M Shiyakova
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
A Shmeleva
A Shmeleva
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
M J Shochet
M J Shochet
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
D Short
D Short
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
S Shrestha
S Shrestha
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
E Shulga
E Shulga
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
M A Shupe
M A Shupe
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
P Sicho
P Sicho
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
A Sidoti
A Sidoti
161INFN Sezione di Roma I, Roma, Italy
161,
F Siegert
F Siegert
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
Dj Sijacki
Dj Sijacki
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
O Silbert
O Silbert
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
J Silva
J Silva
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
Y Silver
Y Silver
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
D Silverstein
D Silverstein
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S B Silverstein
S B Silverstein
184Department of Physics, Stockholm University, Stockholm, Sweden
184,
V Simak
V Simak
156Czech Technical University in Prague, Praha, Czech Republic
156,
O Simard
O Simard
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
Lj Simic
Lj Simic
17Institute of Physics, University of Belgrade, Belgrade, Serbia
17,
S Simion
S Simion
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
B Simmons
B Simmons
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
M Simonyan
M Simonyan
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
P Sinervo
P Sinervo
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
N B Sinev
N B Sinev
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
V Sipica
V Sipica
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
G Siragusa
G Siragusa
215Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
215,
A Sircar
A Sircar
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
A N Sisakyan
A N Sisakyan
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
S Yu Sivoklokov
S Yu Sivoklokov
122Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
122,
J Sjölin
J Sjölin
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
T B Sjursen
T B Sjursen
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
L A Skinnari
L A Skinnari
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
H P Skottowe
H P Skottowe
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
K Skovpen
K Skovpen
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
P Skubic
P Skubic
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
N Skvorodnev
N Skvorodnev
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
M Slater
M Slater
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
T Slavicek
T Slavicek
156Czech Technical University in Prague, Praha, Czech Republic
156,
K Sliwa
K Sliwa
201Science and Technology Center, Tufts University, Medford, MA United States of America
201,
J Sloper
J Sloper
44CERN, Geneva, Switzerland
44,
V Smakhtin
V Smakhtin
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
S Yu Smirnov
S Yu Smirnov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
Y Smirnov
Y Smirnov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
L N Smirnova
L N Smirnova
122Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University, Moscow, Russia
122,
O Smirnova
O Smirnova
103Fysiska institutionen, Lunds universitet, Lund, Sweden
103,
B C Smith
B C Smith
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
D Smith
D Smith
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
K M Smith
K M Smith
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
M Smizanska
M Smizanska
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
K Smolek
K Smolek
156Czech Technical University in Prague, Praha, Czech Republic
156,
A A Snesarev
A A Snesarev
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
S W Snow
S W Snow
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
J Snow
J Snow
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
J Snuverink
J Snuverink
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
S Snyder
S Snyder
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
M Soares
M Soares
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
R Sobie
R Sobie
211Department of Physics and Astronomy, University of Victoria, Victoria, BC Canada
211,
J Sodomka
J Sodomka
156Czech Technical University in Prague, Praha, Czech Republic
156,
A Soffer
A Soffer
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
C A Solans
C A Solans
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
M Solar
M Solar
156Czech Technical University in Prague, Praha, Czech Republic
156,
J Solc
J Solc
156Czech Technical University in Prague, Praha, Czech Republic
156,
E Soldatov
E Soldatov
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
U Soldevila
U Soldevila
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
E Solfaroli Camillocci
E Solfaroli Camillocci
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
A A Solodkov
A A Solodkov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
O V Solovyanov
O V Solovyanov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
N Soni
N Soni
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
V Sopko
V Sopko
156Czech Technical University in Prague, Praha, Czech Republic
156,
B Sopko
B Sopko
156Czech Technical University in Prague, Praha, Czech Republic
156,
M Sosebee
M Sosebee
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
R Soualah
R Soualah
204INFN Gruppo Collegato di Udine, Udine, Italy
206Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
204,206,
A Soukharev
A Soukharev
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
S Spagnolo
S Spagnolo
95INFN Sezione di Lecce, Lecce, Italy
96Dipartimento di Fisica, Università del Salento, Lecce, Italy
95,96,
F Spanò
F Spanò
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
R Spighi
R Spighi
28INFN Sezione di Bologna, Bologna, Italy
28,
G Spigo
G Spigo
44CERN, Geneva, Switzerland
44,
F Spila
F Spila
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
R Spiwoks
R Spiwoks
44CERN, Geneva, Switzerland
44,
M Spousta
M Spousta
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
T Spreitzer
T Spreitzer
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
B Spurlock
B Spurlock
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
R D St Denis
R D St Denis
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
J Stahlman
J Stahlman
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
R Stamen
R Stamen
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
E Stanecka
E Stanecka
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
R W Stanek
R W Stanek
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
C Stanescu
C Stanescu
165INFN Sezione di Roma Tre, Roma, Italy
165,
S Stapnes
S Stapnes
143Department of Physics, University of Oslo, Oslo, Norway
143,
E A Starchenko
E A Starchenko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
J Stark
J Stark
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
P Staroba
P Staroba
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
P Starovoitov
P Starovoitov
116National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
116,
A Staude
A Staude
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
P Stavina
P Stavina
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
G Stavropoulos
G Stavropoulos
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
G Steele
G Steele
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
P Steinbach
P Steinbach
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
P Steinberg
P Steinberg
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
I Stekl
I Stekl
156Czech Technical University in Prague, Praha, Czech Republic
156,
B Stelzer
B Stelzer
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
H J Stelzer
H J Stelzer
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
O Stelzer-Chilton
O Stelzer-Chilton
198TRIUMF, Vancouver, BC Canada
198,
H Stenzel
H Stenzel
74II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
74,
S Stern
S Stern
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
K Stevenson
K Stevenson
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
G A Stewart
G A Stewart
44CERN, Geneva, Switzerland
44,
J A Stillings
J A Stillings
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M C Stockton
M C Stockton
109Department of Physics, McGill University, Montreal, QC Canada
109,
K Stoerig
K Stoerig
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
G Stoicea
G Stoicea
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
S Stonjek
S Stonjek
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
P Strachota
P Strachota
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
A R Stradling
A R Stradling
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
A Straessner
A Straessner
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
J Strandberg
J Strandberg
186Physics Department, Royal Institute of Technology, Stockholm, Sweden
186,
S Strandberg
S Strandberg
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
A Strandlie
A Strandlie
143Department of Physics, University of Oslo, Oslo, Norway
143,
M Strang
M Strang
135Ohio State University, Columbus, OH United States of America
135,
E Strauss
E Strauss
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
M Strauss
M Strauss
137Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK United States of America
137,
P Strizenec
P Strizenec
181Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
181,
R Ströhmer
R Ströhmer
215Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
215,
D M Strom
D M Strom
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
J A Strong
J A Strong
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
R Stroynowski
R Stroynowski
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
J Strube
J Strube
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
B Stugu
B Stugu
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
I Stumer
I Stumer
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
J Stupak
J Stupak
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
P Sturm
P Sturm
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
N A Styles
N A Styles
61DESY, Hamburg and Zeuthen, Germany
61,
D A Soh
D A Soh
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
D Su
D Su
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
HS Subramania
HS Subramania
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
A Succurro
A Succurro
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
Y Sugaya
Y Sugaya
142Graduate School of Science, Osaka University, Osaka, Japan
142,
T Sugimoto
T Sugimoto
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
C Suhr
C Suhr
132Department of Physics, Northern Illinois University, DeKalb, IL United States of America
132,
K Suita
K Suita
90Graduate School of Science, Kobe University, Kobe, Japan
90,
M Suk
M Suk
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
V V Sulin
V V Sulin
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
S Sultansoy
S Sultansoy
7Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
7,
T Sumida
T Sumida
91Faculty of Science, Kyoto University, Kyoto, Japan
91,
X Sun
X Sun
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
J E Sundermann
J E Sundermann
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
K Suruliz
K Suruliz
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
S Sushkov
S Sushkov
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
G Susinno
G Susinno
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
M R Sutton
M R Sutton
188Department of Physics and Astronomy, University of Sussex, Brighton, United Kingdom
188,
Y Suzuki
Y Suzuki
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
Y Suzuki
Y Suzuki
90Graduate School of Science, Kobe University, Kobe, Japan
90,
M Svatos
M Svatos
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
Yu M Sviridov
Yu M Sviridov
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
S Swedish
S Swedish
210Department of Physics, University of British Columbia, Vancouver, BC Canada
210,
I Sykora
I Sykora
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
T Sykora
T Sykora
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
B Szeless
B Szeless
44CERN, Geneva, Switzerland
44,
J Sánchez
J Sánchez
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
D Ta
D Ta
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
K Tackmann
K Tackmann
61DESY, Hamburg and Zeuthen, Germany
61,
A Taffard
A Taffard
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
R Tafirout
R Tafirout
198TRIUMF, Vancouver, BC Canada
198,
N Taiblum
N Taiblum
192Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
192,
Y Takahashi
Y Takahashi
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
H Takai
H Takai
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
R Takashima
R Takashima
92Kyoto University of Education, Kyoto, Japan
92,
H Takeda
H Takeda
90Graduate School of Science, Kobe University, Kobe, Japan
90,
T Takeshita
T Takeshita
176Department of Physics, Shinshu University, Nagano, Japan
176,
Y Takubo
Y Takubo
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
M Talby
M Talby
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
A Talyshev
A Talyshev
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
M C Tamsett
M C Tamsett
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
J Tanaka
J Tanaka
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
R Tanaka
R Tanaka
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
S Tanaka
S Tanaka
160Ritsumeikan University, Kusatsu, Shiga, Japan
160,
S Tanaka
S Tanaka
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
Y Tanaka
Y Tanaka
125Nagasaki Institute of Applied Science, Nagasaki, Japan
125,
A J Tanasijczuk
A J Tanasijczuk
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
K Tani
K Tani
90Graduate School of Science, Kobe University, Kobe, Japan
90,
N Tannoury
N Tannoury
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
G P Tappern
G P Tappern
44CERN, Geneva, Switzerland
44,
S Tapprogge
S Tapprogge
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
D Tardif
D Tardif
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
S Tarem
S Tarem
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
F Tarrade
F Tarrade
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
G F Tartarelli
G F Tartarelli
113INFN Sezione di Milano, Milano, Italy
113,
P Tas
P Tas
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
M Tasevsky
M Tasevsky
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
E Tassi
E Tassi
55INFN Gruppo Collegato di Cosenza, Arcavata di Rende, Italy
56Dipartimento di Fisica, Università della Calabria, Arcavata di Rende, Italy
55,56,
M Tatarkhanov
M Tatarkhanov
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
Y Tayalati
Y Tayalati
170Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
170,
C Taylor
C Taylor
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
F E Taylor
F E Taylor
117Department of Physics, Massachusetts Institute of Technology, Cambridge, MA United States of America
117,
G N Taylor
G N Taylor
110School of Physics, University of Melbourne, Victoria, Australia
110,
W Taylor
W Taylor
199Department of Physics and Astronomy, York University, Toronto, ON Canada
199,
M Teinturier
M Teinturier
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
M Teixeira Dias Castanheira
M Teixeira Dias Castanheira
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
P Teixeira-Dias
P Teixeira-Dias
100Department of Physics, Royal Holloway University of London, Surrey, United Kingdom
100,
K K Temming
K K Temming
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
H Ten Kate
H Ten Kate
44CERN, Geneva, Switzerland
44,
P K Teng
P K Teng
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
S Terada
S Terada
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
K Terashi
K Terashi
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
J Terron
J Terron
104Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
104,
M Testa
M Testa
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
R J Teuscher
R J Teuscher
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
J Thadome
J Thadome
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
J Therhaag
J Therhaag
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
T Theveneaux-Pelzer
T Theveneaux-Pelzer
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
M Thioye
M Thioye
217Department of Physics, Yale University, New Haven, CT United States of America
217,
S Thoma
S Thoma
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
J P Thomas
J P Thomas
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
E N Thompson
E N Thompson
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
P D Thompson
P D Thompson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
P D Thompson
P D Thompson
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
A S Thompson
A S Thompson
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
E Thomson
E Thomson
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
M Thomson
M Thomson
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
R P Thun
R P Thun
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
F Tian
F Tian
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
M J Tibbetts
M J Tibbetts
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
T Tic
T Tic
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
V O Tikhomirov
V O Tikhomirov
119P.N. Lebedev Institute of Physics, Academy of Sciences, Moscow, Russia
119,
Y A Tikhonov
Y A Tikhonov
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
S Timoshenko
S Timoshenko
121Moscow Engineering and Physics Institute (MEPhI), Moscow, Russia
121,
P Tipton
P Tipton
217Department of Physics, Yale University, New Haven, CT United States of America
217,
F J Tique Aires Viegas
F J Tique Aires Viegas
44CERN, Geneva, Switzerland
44,
S Tisserant
S Tisserant
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
B Toczek
B Toczek
57AGH University of Science and Technology, Faculty of Physics and Applied Computer Science, Krakow, Poland
57,
T Todorov
T Todorov
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Todorova-Nova
S Todorova-Nova
201Science and Technology Center, Tufts University, Medford, MA United States of America
201,
B Toggerson
B Toggerson
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
J Tojo
J Tojo
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
S Tokár
S Tokár
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
K Tokunaga
K Tokunaga
90Graduate School of Science, Kobe University, Kobe, Japan
90,
K Tokushuku
K Tokushuku
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
K Tollefson
K Tollefson
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
M Tomoto
M Tomoto
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
L Tompkins
L Tompkins
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
K Toms
K Toms
129Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
129,
G Tong
G Tong
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
A Tonoyan
A Tonoyan
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
C Topfel
C Topfel
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
N D Topilin
N D Topilin
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
I Torchiani
I Torchiani
44CERN, Geneva, Switzerland
44,
E Torrence
E Torrence
140Center for High Energy Physics, University of Oregon, Eugene, OR United States of America
140,
H Torres
H Torres
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
E Torró Pastor
E Torró Pastor
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
J Toth
J Toth
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
F Touchard
F Touchard
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
D R Tovey
D R Tovey
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
T Trefzger
T Trefzger
215Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
215,
L Tremblet
L Tremblet
44CERN, Geneva, Switzerland
44,
A Tricoli
A Tricoli
44CERN, Geneva, Switzerland
44,
I M Trigger
I M Trigger
198TRIUMF, Vancouver, BC Canada
198,
S Trincaz-Duvoid
S Trincaz-Duvoid
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
T N Trinh
T N Trinh
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
M F Tripiana
M F Tripiana
93Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
93,
W Trischuk
W Trischuk
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
A Trivedi
A Trivedi
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
B Trocmé
B Trocmé
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
C Troncon
C Troncon
113INFN Sezione di Milano, Milano, Italy
113,
M Trottier-McDonald
M Trottier-McDonald
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
M Trzebinski
M Trzebinski
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
A Trzupek
A Trzupek
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
C Tsarouchas
C Tsarouchas
44CERN, Geneva, Switzerland
44,
J C-L Tseng
J C-L Tseng
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
M Tsiakiris
M Tsiakiris
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
P V Tsiareshka
P V Tsiareshka
115B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
115,
D Tsionou
D Tsionou
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
G Tsipolitis
G Tsipolitis
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
V Tsiskaridze
V Tsiskaridze
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
E G Tskhadadze
E G Tskhadadze
72E.Andronikashvili Institute of Physics, Tbilisi State University, Tbilisi, Georgia
72,
I I Tsukerman
I I Tsukerman
120Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
120,
V Tsulaia
V Tsulaia
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
J-W Tsung
J-W Tsung
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
S Tsuno
S Tsuno
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
D Tsybychev
D Tsybychev
187Departments of Physics & Astronomy and Chemistry, Stony Brook University, Stony Brook, NY United States of America
187,
A Tua
A Tua
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
A Tudorache
A Tudorache
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
V Tudorache
V Tudorache
38National Institute of Physics and Nuclear Engineering, Bucharest, Romania
38,
J M Tuggle
J M Tuggle
45Enrico Fermi Institute, University of Chicago, Chicago, IL United States of America
45,
M Turala
M Turala
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
D Turecek
D Turecek
156Czech Technical University in Prague, Praha, Czech Republic
156,
I Turk Cakir
I Turk Cakir
8Turkish Atomic Energy Authority, Ankara, Turkey
8,
E Turlay
E Turlay
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
R Turra
R Turra
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
P M Tuts
P M Tuts
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
A Tykhonov
A Tykhonov
98Department of Physics, Jožef Stefan Institute and University of Ljubljana, Ljubljana, Slovenia
98,
M Tylmad
M Tylmad
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
M Tyndel
M Tyndel
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
G Tzanakos
G Tzanakos
13Physics Department, University of Athens, Athens, Greece
13,
K Uchida
K Uchida
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
I Ueda
I Ueda
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
R Ueno
R Ueno
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
M Ugland
M Ugland
19Department for Physics and Technology, University of Bergen, Bergen, Norway
19,
M Uhlenbrock
M Uhlenbrock
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Uhrmacher
M Uhrmacher
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
F Ukegawa
F Ukegawa
200Institute of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571 Japan
200,
G Unal
G Unal
44CERN, Geneva, Switzerland
44,
D G Underwood
D G Underwood
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
A Undrus
A Undrus
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
G Unel
G Unel
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
Y Unno
Y Unno
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
D Urbaniec
D Urbaniec
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
G Usai
G Usai
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
M Uslenghi
M Uslenghi
145INFN Sezione di Pavia, Pavia, Italy
146Dipartimento di Fisica, Università di Pavia, Pavia, Italy
145,146,
L Vacavant
L Vacavant
107CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
107,
V Vacek
V Vacek
156Czech Technical University in Prague, Praha, Czech Republic
156,
B Vachon
B Vachon
109Department of Physics, McGill University, Montreal, QC Canada
109,
S Vahsen
S Vahsen
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
J Valenta
J Valenta
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
P Valente
P Valente
161INFN Sezione di Roma I, Roma, Italy
161,
S Valentinetti
S Valentinetti
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
S Valkar
S Valkar
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
E Valladolid Gallego
E Valladolid Gallego
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
S Vallecorsa
S Vallecorsa
191Department of Physics, Technion: Israel Inst. of Technology, Haifa, Israel
191,
J A Valls Ferrer
J A Valls Ferrer
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
H van der Graaf
H van der Graaf
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
E van der Kraaij
E van der Kraaij
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
R Van Der Leeuw
R Van Der Leeuw
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
E van der Poel
E van der Poel
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
D van der Ster
D van der Ster
44CERN, Geneva, Switzerland
44,
N van Eldik
N van Eldik
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
P van Gemmeren
P van Gemmeren
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
Z van Kesteren
Z van Kesteren
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
I van Vulpen
I van Vulpen
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
M Vanadia
M Vanadia
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
W Vandelli
W Vandelli
44CERN, Geneva, Switzerland
44,
G Vandoni
G Vandoni
44CERN, Geneva, Switzerland
44,
A Vaniachine
A Vaniachine
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
P Vankov
P Vankov
61DESY, Hamburg and Zeuthen, Germany
61,
F Vannucci
F Vannucci
102Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
102,
F Varela Rodriguez
F Varela Rodriguez
44CERN, Geneva, Switzerland
44,
R Vari
R Vari
161INFN Sezione di Roma I, Roma, Italy
161,
E W Varnes
E W Varnes
11Department of Physics, University of Arizona, Tucson, AZ United States of America
11,
D Varouchas
D Varouchas
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
A Vartapetian
A Vartapetian
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
K E Varvell
K E Varvell
189School of Physics, University of Sydney, Sydney, Australia
189,
V I Vassilakopoulos
V I Vassilakopoulos
78Department of Physics, Hampton University, Hampton, VA United States of America
78,
F Vazeille
F Vazeille
52Laboratoire de Physique Corpusculaire, Clermont Université and Université Blaise Pascal and CNRS/IN2P3, Aubiere Cedex, France
52,
G Vegni
G Vegni
113INFN Sezione di Milano, Milano, Italy
114Dipartimento di Fisica, Università di Milano, Milano, Italy
113,114,
J J Veillet
J J Veillet
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
C Vellidis
C Vellidis
13Physics Department, University of Athens, Athens, Greece
13,
F Veloso
F Veloso
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
R Veness
R Veness
44CERN, Geneva, Switzerland
44,
S Veneziano
S Veneziano
161INFN Sezione di Roma I, Roma, Italy
161,
A Ventura
A Ventura
95INFN Sezione di Lecce, Lecce, Italy
96Dipartimento di Fisica, Università del Salento, Lecce, Italy
95,96,
D Ventura
D Ventura
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
M Venturi
M Venturi
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
N Venturi
N Venturi
197Department of Physics, University of Toronto, Toronto, ON Canada
197,
V Vercesi
V Vercesi
145INFN Sezione di Pavia, Pavia, Italy
145,
M Verducci
M Verducci
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
W Verkerke
W Verkerke
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
J C Vermeulen
J C Vermeulen
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
A Vest
A Vest
63Institut für Kern- und Teilchenphysik, Technical University Dresden, Dresden, Germany
63,
M C Vetterli
M C Vetterli
178Department of Physics, Simon Fraser University, Burnaby, BC Canada
178,
I Vichou
I Vichou
207Department of Physics, University of Illinois, Urbana, IL United States of America
207,
T Vickey
T Vickey
183School of Physics, University of the Witwatersrand, Johannesburg, South Africa
183,
O E Vickey Boeriu
O E Vickey Boeriu
183School of Physics, University of the Witwatersrand, Johannesburg, South Africa
183,
G H A Viehhauser
G H A Viehhauser
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
S Viel
S Viel
210Department of Physics, University of British Columbia, Vancouver, BC Canada
210,
M Villa
M Villa
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
M Villaplana Perez
M Villaplana Perez
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
E Vilucchi
E Vilucchi
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
M G Vincter
M G Vincter
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
E Vinek
E Vinek
44CERN, Geneva, Switzerland
44,
V B Vinogradov
V B Vinogradov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
M Virchaux
M Virchaux
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
J Virzi
J Virzi
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
O Vitells
O Vitells
213Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
213,
M Viti
M Viti
61DESY, Hamburg and Zeuthen, Germany
61,
I Vivarelli
I Vivarelli
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
F Vives Vaque
F Vives Vaque
3Department of Physics, University of Alberta, Edmonton, AB Canada
3,
S Vlachos
S Vlachos
14Physics Department, National Technical University of Athens, Zografou, Greece
14,
D Vladoiu
D Vladoiu
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
M Vlasak
M Vlasak
156Czech Technical University in Prague, Praha, Czech Republic
156,
N Vlasov
N Vlasov
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
A Vogel
A Vogel
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
P Vokac
P Vokac
156Czech Technical University in Prague, Praha, Czech Republic
156,
G Volpi
G Volpi
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
M Volpi
M Volpi
110School of Physics, University of Melbourne, Victoria, Australia
110,
G Volpini
G Volpini
113INFN Sezione di Milano, Milano, Italy
113,
H von der Schmitt
H von der Schmitt
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
J von Loeben
J von Loeben
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
H von Radziewski
H von Radziewski
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
E von Toerne
E von Toerne
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
V Vorobel
V Vorobel
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
A P Vorobiev
A P Vorobiev
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
V Vorwerk
V Vorwerk
16Institut de Física d’Altes Energies and Departament de Física de la Universitat Autònoma de Barcelona and ICREA, Barcelona, Spain
16,
M Vos
M Vos
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
R Voss
R Voss
44CERN, Geneva, Switzerland
44,
T T Voss
T T Voss
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
J H Vossebeld
J H Vossebeld
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
N Vranjes
N Vranjes
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
M Vranjes Milosavljevic
M Vranjes Milosavljevic
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
V Vrba
V Vrba
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
M Vreeswijk
M Vreeswijk
131Nikhef National Institute for Subatomic Physics and University of Amsterdam, Amsterdam, Netherlands
131,
T Vu Anh
T Vu Anh
105Institut für Physik, Universität Mainz, Mainz, Germany
105,
R Vuillermet
R Vuillermet
44CERN, Geneva, Switzerland
44,
I Vukotic
I Vukotic
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
W Wagner
W Wagner
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
P Wagner
P Wagner
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
H Wahlen
H Wahlen
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
J Wakabayashi
J Wakabayashi
126Graduate School of Science, Nagoya University, Nagoya, Japan
126,
J Walbersloh
J Walbersloh
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
S Walch
S Walch
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
J Walder
J Walder
94Physics Department, Lancaster University, Lancaster, United Kingdom
94,
R Walker
R Walker
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
W Walkowiak
W Walkowiak
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
R Wall
R Wall
217Department of Physics, Yale University, New Haven, CT United States of America
217,
P Waller
P Waller
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
C Wang
C Wang
64Department of Physics, Duke University, Durham, NC United States of America
64,
H Wang
H Wang
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
H Wang
H Wang
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
J Wang
J Wang
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
J Wang
J Wang
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
J C Wang
J C Wang
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
R Wang
R Wang
129Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM United States of America
129,
S M Wang
S M Wang
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
A Warburton
A Warburton
109Department of Physics, McGill University, Montreal, QC Canada
109,
C P Ward
C P Ward
42Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom
42,
M Warsinsky
M Warsinsky
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
P M Watkins
P M Watkins
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
A T Watson
A T Watson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
I J Watson
I J Watson
189School of Physics, University of Sydney, Sydney, Australia
189,
M F Watson
M F Watson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
G Watts
G Watts
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
S Watts
S Watts
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
A T Waugh
A T Waugh
189School of Physics, University of Sydney, Sydney, Australia
189,
B M Waugh
B M Waugh
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
M Weber
M Weber
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
M S Weber
M S Weber
22Albert Einstein Center for Fundamental Physics and Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
22,
P Weber
P Weber
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
A R Weidberg
A R Weidberg
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
P Weigell
P Weigell
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
J Weingarten
J Weingarten
76II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
76,
C Weiser
C Weiser
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
H Wellenstein
H Wellenstein
32Department of Physics, Brandeis University, Waltham, MA United States of America
32,
P S Wells
P S Wells
44CERN, Geneva, Switzerland
44,
M Wen
M Wen
67INFN Laboratori Nazionali di Frascati, Frascati, Italy
67,
T Wenaus
T Wenaus
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
S Wendler
S Wendler
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
Z Weng
Z Weng
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
T Wengler
T Wengler
44CERN, Geneva, Switzerland
44,
S Wenig
S Wenig
44CERN, Geneva, Switzerland
44,
N Wermes
N Wermes
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
M Werner
M Werner
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
P Werner
P Werner
44CERN, Geneva, Switzerland
44,
M Werth
M Werth
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
M Wessels
M Wessels
80Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
80,
C Weydert
C Weydert
77Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier and CNRS/IN2P3 and Institut National Polytechnique de Grenoble, Grenoble, France
77,
K Whalen
K Whalen
43Department of Physics, Carleton University, Ottawa, ON Canada
43,
S J Wheeler-Ellis
S J Wheeler-Ellis
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
S P Whitaker
S P Whitaker
31Department of Physics, Boston University, Boston, MA United States of America
31,
A White
A White
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
M J White
M J White
110School of Physics, University of Melbourne, Victoria, Australia
110,
S R Whitehead
S R Whitehead
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
D Whiteson
D Whiteson
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
D Whittington
D Whittington
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
F Wicek
F Wicek
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
D Wicke
D Wicke
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
F J Wickens
F J Wickens
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
W Wiedenmann
W Wiedenmann
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
M Wielers
M Wielers
158Particle Physics Department, Rutherford Appleton Laboratory, Didcot, United Kingdom
158,
P Wienemann
P Wienemann
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
C Wiglesworth
C Wiglesworth
99School of Physics and Astronomy, Queen Mary University of London, London, United Kingdom
99,
L A M Wiik-Fuchs
L A M Wiik-Fuchs
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
P A Wijeratne
P A Wijeratne
101Department of Physics and Astronomy, University College London, London, United Kingdom
101,
A Wildauer
A Wildauer
209Instituto de Física Corpuscular (IFIC) and Departamento de Física Atómica, Molecular y Nuclear and Departamento de Ingeniería Electrónica and Instituto de Microelectrónica de Barcelona (IMB-CNM), University of Valencia and CSIC, Valencia, Spain
209,
M A Wildt
M A Wildt
61DESY, Hamburg and Zeuthen, Germany
61,
I Wilhelm
I Wilhelm
155Faculty of Mathematics and Physics, Charles University in Prague, Praha, Czech Republic
155,
H G Wilkens
H G Wilkens
44CERN, Geneva, Switzerland
44,
J Z Will
J Z Will
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
E Williams
E Williams
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
H H Williams
H H Williams
147Department of Physics, University of Pennsylvania, Philadelphia, PA United States of America
147,
W Willis
W Willis
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
S Willocq
S Willocq
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
J A Wilson
J A Wilson
23School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom
23,
M G Wilson
M G Wilson
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
A Wilson
A Wilson
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
I Wingerter-Seez
I Wingerter-Seez
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
S Winkelmann
S Winkelmann
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
F Winklmeier
F Winklmeier
44CERN, Geneva, Switzerland
44,
M Wittgen
M Wittgen
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
M W Wolter
M W Wolter
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
H Wolters
H Wolters
152Laboratorio de Instrumentacao e Fisica Experimental de Particulas - LIP, Lisboa, Portugal
152,
W C Wong
W C Wong
60Physics Department, University of Texas at Dallas, Richardson, TX United States of America
60,
G Wooden
G Wooden
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
B K Wosiek
B K Wosiek
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
J Wotschack
J Wotschack
44CERN, Geneva, Switzerland
44,
M J Woudstra
M J Woudstra
108Department of Physics, University of Massachusetts, Amherst, MA United States of America
108,
K W Wozniak
K W Wozniak
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
K Wraight
K Wraight
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
C Wright
C Wright
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
M Wright
M Wright
75SUPA - School of Physics and Astronomy, University of Glasgow, Glasgow, United Kingdom
75,
B Wrona
B Wrona
97Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom
97,
S L Wu
S L Wu
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
X Wu
X Wu
69Section de Physique, Université de Genève, Geneva, Switzerland
69,
Y Wu
Y Wu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
E Wulf
E Wulf
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
R Wunstorf
R Wunstorf
62Institut für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
62,
B M Wynne
B M Wynne
65SUPA - School of Physics and Astronomy, University of Edinburgh, Edinburgh, United Kingdom
65,
S Xella
S Xella
54Niels Bohr Institute, University of Copenhagen, Kobenhavn, Denmark
54,
M Xiao
M Xiao
172DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat a l’Energie Atomique), Gif-sur-Yvette, France
172,
S Xie
S Xie
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
Y Xie
Y Xie
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
C Xu
C Xu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
D Xu
D Xu
175Department of Physics and Astronomy, University of Sheffield, Sheffield, United Kingdom
175,
G Xu
G Xu
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
B Yabsley
B Yabsley
189School of Physics, University of Sydney, Sydney, Australia
189,
S Yacoob
S Yacoob
183School of Physics, University of the Witwatersrand, Johannesburg, South Africa
183,
M Yamada
M Yamada
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
H Yamaguchi
H Yamaguchi
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
A Yamamoto
A Yamamoto
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
K Yamamoto
K Yamamoto
87Department of Physics and Astronomy, Iowa State University, Ames, IA United States of America
87,
S Yamamoto
S Yamamoto
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
T Yamamura
T Yamamura
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
T Yamanaka
T Yamanaka
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
J Yamaoka
J Yamaoka
64Department of Physics, Duke University, Durham, NC United States of America
64,
T Yamazaki
T Yamazaki
194International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
194,
Y Yamazaki
Y Yamazaki
90Graduate School of Science, Kobe University, Kobe, Japan
90,
Z Yan
Z Yan
31Department of Physics, Boston University, Boston, MA United States of America
31,
H Yang
H Yang
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
U K Yang
U K Yang
106School of Physics and Astronomy, University of Manchester, Manchester, United Kingdom
106,
Y Yang
Y Yang
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
Y Yang
Y Yang
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
Z Yang
Z Yang
184Department of Physics, Stockholm University, Stockholm, Sweden
185The Oskar Klein Centre, Stockholm, Sweden
184,185,
S Yanush
S Yanush
116National Scientific and Educational Centre for Particle and High Energy Physics, Minsk, Republic of Belarus
116,
Y Yao
Y Yao
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
Y Yasu
Y Yasu
89KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
89,
G V Ybeles Smit
G V Ybeles Smit
159Physics Department, University of Regina, Regina, SK Canada
159,
J Ye
J Ye
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
S Ye
S Ye
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
M Yilmaz
M Yilmaz
6Department of Physics, Gazi University, Ankara, Turkey
6,
R Yoosoofmiya
R Yoosoofmiya
151Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA United States of America
151,
K Yorita
K Yorita
212Waseda University, Tokyo, Japan
212,
R Yoshida
R Yoshida
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
C Young
C Young
179SLAC National Accelerator Laboratory, Stanford, CA United States of America
179,
S Youssef
S Youssef
31Department of Physics, Boston University, Boston, MA United States of America
31,
D Yu
D Yu
37Physics Department, Brookhaven National Laboratory, Upton, NY United States of America
37,
J Yu
J Yu
12Department of Physics, The University of Texas at Arlington, Arlington, TX United States of America
12,
J Yu
J Yu
138Department of Physics, Oklahoma State University, Stillwater, OK United States of America
138,
L Yuan
L Yuan
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
A Yurkewicz
A Yurkewicz
132Department of Physics, Northern Illinois University, DeKalb, IL United States of America
132,
B Zabinski
B Zabinski
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
V G Zaets
V G Zaets
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
R Zaidan
R Zaidan
86University of Iowa, Iowa City, IA United States of America
86,
A M Zaitsev
A M Zaitsev
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
Z Zajacova
Z Zajacova
44CERN, Geneva, Switzerland
44,
L Zanello
L Zanello
161INFN Sezione di Roma I, Roma, Italy
162Dipartimento di Fisica, Università La Sapienza, Roma, Italy
161,162,
P Zarzhitsky
P Zarzhitsky
59Physics Department, Southern Methodist University, Dallas, TX United States of America
59,
A Zaytsev
A Zaytsev
133Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
133,
C Zeitnitz
C Zeitnitz
216Fachbereich C Physik, Bergische Universität Wuppertal, Wuppertal, Germany
216,
M Zeller
M Zeller
217Department of Physics, Yale University, New Haven, CT United States of America
217,
M Zeman
M Zeman
154Institute of Physics, Academy of Sciences of the Czech Republic, Praha, Czech Republic
154,
A Zemla
A Zemla
58The Henryk Niewodniczanski Institute of Nuclear Physics, Polish Academy of Sciences, Krakow, Poland
58,
C Zendler
C Zendler
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
O Zenin
O Zenin
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
T Ženiš
T Ženiš
180Faculty of Mathematics, Physics & Informatics, Comenius University, Bratislava, Slovak Republic
180,
Z Zinonos
Z Zinonos
149INFN Sezione di Pisa, Pisa, Italy
150Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
149,150,
S Zenz
S Zenz
20Physics Division, Lawrence Berkeley National Laboratory and University of California, Berkeley, CA United States of America
20,
D Zerwas
D Zerwas
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
G Zevi della Porta
G Zevi della Porta
79Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA United States of America
79,
Z Zhan
Z Zhan
51School of Physics, Shandong University, Shandong, China
51,
D Zhang
D Zhang
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
H Zhang
H Zhang
112Department of Physics and Astronomy, Michigan State University, East Lansing, MI United States of America
112,
J Zhang
J Zhang
10High Energy Physics Division, Argonne National Laboratory, Argonne, IL United States of America
10,
X Zhang
X Zhang
51School of Physics, Shandong University, Shandong, China
51,
Z Zhang
Z Zhang
141LAL, Univ. Paris-Sud and CNRS/IN2P3, Orsay, France
141,
L Zhao
L Zhao
134Department of Physics, New York University, New York, NY United States of America
134,
T Zhao
T Zhao
174Department of Physics, University of Washington, Seattle, WA United States of America
174,
Z Zhao
Z Zhao
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
A Zhemchugov
A Zhemchugov
88Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
88,
S Zheng
S Zheng
48Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
48,
J Zhong
J Zhong
144Department of Physics, Oxford University, Oxford, United Kingdom
144,
B Zhou
B Zhou
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
N Zhou
N Zhou
203Department of Physics and Astronomy, University of California Irvine, Irvine, CA United States of America
203,
Y Zhou
Y Zhou
190Institute of Physics, Academia Sinica, Taipei, Taiwan
190,
C G Zhu
C G Zhu
51School of Physics, Shandong University, Shandong, China
51,
H Zhu
H Zhu
61DESY, Hamburg and Zeuthen, Germany
61,
J Zhu
J Zhu
111Department of Physics, The University of Michigan, Ann Arbor, MI United States of America
111,
Y Zhu
Y Zhu
49Department of Modern Physics, University of Science and Technology of China, Anhui, China
49,
X Zhuang
X Zhuang
123Fakultät für Physik, Ludwig-Maximilians-Universität München, München, Germany
123,
V Zhuravlov
V Zhuravlov
124Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), München, Germany
124,
D Zieminska
D Zieminska
84Department of Physics, Indiana University, Bloomington, IN United States of America
84,
R Zimmermann
R Zimmermann
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
S Zimmermann
S Zimmermann
30Physikalisches Institut, University of Bonn, Bonn, Germany
30,
S Zimmermann
S Zimmermann
68Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg i.Br., Germany
68,
M Ziolkowski
M Ziolkowski
177Fachbereich Physik, Universität Siegen, Siegen, Germany
177,
R Zitoun
R Zitoun
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
L Živković
L Živković
53Nevis Laboratory, Columbia University, Irvington, NY United States of America
53,
V V Zmouchko
V V Zmouchko
157State Research Center Institute for High Energy Physics, Protvino, Russia
157,
G Zobernig
G Zobernig
214Department of Physics, University of Wisconsin, Madison, WI United States of America
214,
A Zoccoli
A Zoccoli
28INFN Sezione di Bologna, Bologna, Italy
29Dipartimento di Fisica, Università di Bologna, Bologna, Italy
28,29,
Y Zolnierowski
Y Zolnierowski
9LAPP, CNRS/IN2P3 and Université de Savoie, Annecy-le-Vieux, France
9,
A Zsenei
A Zsenei
44CERN, Geneva, Switzerland
44,
M zur Nedden
M zur Nedden
21Department of Physics, Humboldt University, Berlin, Germany
21,
V Zutshi
V Zutshi
132Department of Physics, Northern Illinois University, DeKalb, IL United States of America
132,
L Zwalinski
L Zwalinski
44CERN, Geneva, Switzerland
44
 channel based on data recorded in 2011 with the ATLAS detector at the LHC. The data were taken at a proton-proton centre-of-mass energy of
channel based on data recorded in 2011 with the ATLAS detector at the LHC. The data were taken at a proton-proton centre-of-mass energy of  and correspond to an integrated luminosity of 1.04 fb−1. The analyses in the e+jets and μ+jets decay channels yield consistent results. The top quark mass is measured to be mtop=174.5±0.6stat±2.3syst GeV.
and correspond to an integrated luminosity of 1.04 fb−1. The analyses in the e+jets and μ+jets decay channels yield consistent results. The top quark mass is measured to be mtop=174.5±0.6stat±2.3syst GeV. events in which both W bosons from the top quark decays themselves decay into a charged lepton and a neutrino [4].
events in which both W bosons from the top quark decays themselves decay into a charged lepton and a neutrino [4].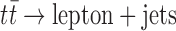 channel, i.e. the decay
channel, i.e. the decay 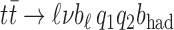 with ℓ=e,μ, where one of the W bosons from the
with ℓ=e,μ, where one of the W bosons from the 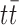 decay decays into a charged lepton and a neutrino and the other into a pair of quarks, and where bℓ(bhad) denotes the b-quark associated to the leptonic (hadronic) W boson decay. In this paper these
decay decays into a charged lepton and a neutrino and the other into a pair of quarks, and where bℓ(bhad) denotes the b-quark associated to the leptonic (hadronic) W boson decay. In this paper these 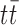 decay channels are referred to as e+jets and μ+jets channels.
decay channels are referred to as e+jets and μ+jets channels.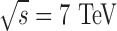 with the ATLAS detector during March–June 2011. An integrated luminosity of 1.04 fb−1 is included.
with the ATLAS detector during March–June 2011. An integrated luminosity of 1.04 fb−1 is included. events and single top quark production are both generated using the Next-to-Leading Order (NLO) Monte Carlo program MC@NLO [8, 9] with the NLO parton density function set CTEQ6.6 [10]. Parton showering and underlying event (i.e. additional interactions of the partons within the protons that underwent the hard interaction) are modelled using the Herwig [11] and Jimmy [12] programs. For the construction of signal templates, the
events and single top quark production are both generated using the Next-to-Leading Order (NLO) Monte Carlo program MC@NLO [8, 9] with the NLO parton density function set CTEQ6.6 [10]. Parton showering and underlying event (i.e. additional interactions of the partons within the protons that underwent the hard interaction) are modelled using the Herwig [11] and Jimmy [12] programs. For the construction of signal templates, the  and single top quark production samples are generated for different assumptions on mtop using six values (in GeV) namely (160,170,172.5,175,180,190), and with the largest samples at mtop=172.5 GeV. All
and single top quark production samples are generated for different assumptions on mtop using six values (in GeV) namely (160,170,172.5,175,180,190), and with the largest samples at mtop=172.5 GeV. All  samples are normalised to the corresponding cross-sections, obtained with the latest theoretical computation approximating the NNLO prediction and implemented in the HATHOR package [13]. The predicted
samples are normalised to the corresponding cross-sections, obtained with the latest theoretical computation approximating the NNLO prediction and implemented in the HATHOR package [13]. The predicted 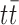 cross-section for a top quark mass of mtop=172.5 GeV is 164.6 pb, with an uncertainty of about 8 %.
cross-section for a top quark mass of mtop=172.5 GeV is 164.6 pb, with an uncertainty of about 8 %.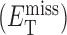 . An electron candidate is defined as an energy deposit in the electromagnetic calorimeter with an associated well-reconstructed track. Electron candidates are required to have transverse energy ET>25 GeV and |ηcluster|<2.47, where ηcluster is the pseudorapidity of the electromagnetic cluster associated with the electron. Candidates in the transition region between the barrel and end-cap calorimeter, i.e. candidates fulfilling 1.37<|ηcluster|<1.52, are excluded. Muon candidates are reconstructed from track segments in different layers of the muon chambers. These segments are combined starting from the outermost layer, with a procedure that takes material effects into account, and matched with tracks found in the inner detector. The final candidates are refitted using the complete track information, and are required to satisfy pT>20 GeV and |η|<2.5. Isolation criteria, which restrict the amount of energy deposits near the candidates, are applied to both electron and muon candidates to reduce the background from hadrons mimicking lepton signatures and backgrounds from heavy flavour decays inside jets. For electrons, the energy not associated to the electron cluster and contained in a cone of
. An electron candidate is defined as an energy deposit in the electromagnetic calorimeter with an associated well-reconstructed track. Electron candidates are required to have transverse energy ET>25 GeV and |ηcluster|<2.47, where ηcluster is the pseudorapidity of the electromagnetic cluster associated with the electron. Candidates in the transition region between the barrel and end-cap calorimeter, i.e. candidates fulfilling 1.37<|ηcluster|<1.52, are excluded. Muon candidates are reconstructed from track segments in different layers of the muon chambers. These segments are combined starting from the outermost layer, with a procedure that takes material effects into account, and matched with tracks found in the inner detector. The final candidates are refitted using the complete track information, and are required to satisfy pT>20 GeV and |η|<2.5. Isolation criteria, which restrict the amount of energy deposits near the candidates, are applied to both electron and muon candidates to reduce the background from hadrons mimicking lepton signatures and backgrounds from heavy flavour decays inside jets. For electrons, the energy not associated to the electron cluster and contained in a cone of 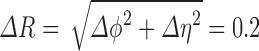 must not exceed 3.5 GeV, after correcting for energy deposits from pileup, which in the order of 0.5 GeV. For muons, the sum of track transverse momenta and the total energy deposited in a cone of ΔR=0.3 around the muon are both required to be less than 4 GeV.
must not exceed 3.5 GeV, after correcting for energy deposits from pileup, which in the order of 0.5 GeV. For muons, the sum of track transverse momenta and the total energy deposited in a cone of ΔR=0.3 around the muon are both required to be less than 4 GeV.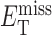 is based upon the vector sum of calorimeter energy deposits projected onto the transverse plane. It is reconstructed from topological clusters, calibrated at the EM scale and corrected according to the energy scale of the associated physics object. Contributions from muons are included by using their momentum measured from the track and muon spectrometer systems in the
is based upon the vector sum of calorimeter energy deposits projected onto the transverse plane. It is reconstructed from topological clusters, calibrated at the EM scale and corrected according to the energy scale of the associated physics object. Contributions from muons are included by using their momentum measured from the track and muon spectrometer systems in the 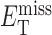 reconstruction.
reconstruction.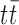 events and a light quark jet rejection factor of about 100. Irrespective of their origin, jets tagged by this algorithm are called b-jets in the following, whereas those not tagged are called light jets.
events and a light quark jet rejection factor of about 100. Irrespective of their origin, jets tagged by this algorithm are called b-jets in the following, whereas those not tagged are called light jets.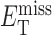 arising from the neutrino from the leptonic W boson decay, two b-quark jets, and two light quark jets from the hadronic W boson decay. The selection of events consists of a series of requirements on general event quality and the reconstructed objects designed to select the event topology described above. The following event selections are applied:
arising from the neutrino from the leptonic W boson decay, two b-quark jets, and two light quark jets from the hadronic W boson decay. The selection of events consists of a series of requirements on general event quality and the reconstructed objects designed to select the event topology described above. The following event selections are applied: 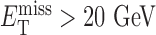 and in addition
and in addition 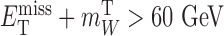 is required;2
is required;2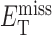 and
and 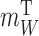 are required because of the higher level of QCD multijet background, these being
are required because of the higher level of QCD multijet background, these being 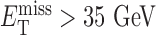 and
and 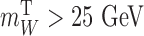 ;
; signal
signal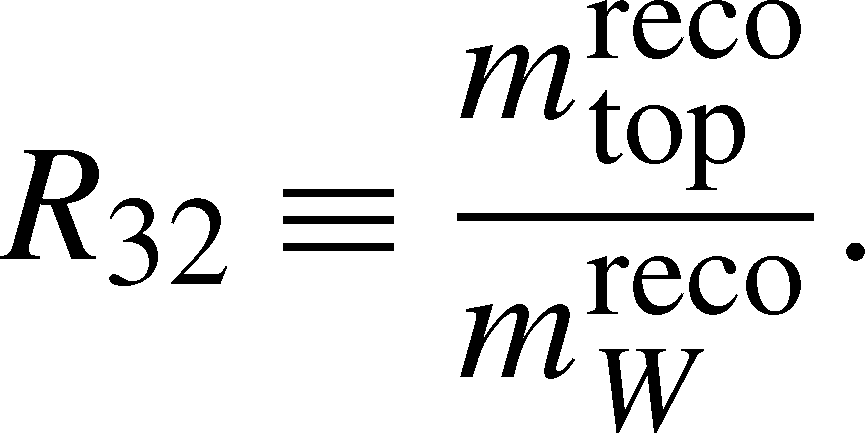
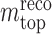 and
and 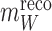 are the per event reconstructed invariant masses of the hadronically decaying top quark and W boson, respectively.
are the per event reconstructed invariant masses of the hadronically decaying top quark and W boson, respectively.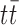 decay products (quarks and leptons) predicted by the NLO signal Monte Carlo, albeit in a Leading Order (LO) kinematic approach, using
decay products (quarks and leptons) predicted by the NLO signal Monte Carlo, albeit in a Leading Order (LO) kinematic approach, using 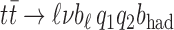 . In this procedure, the measured jets relate to the quark decay products of the W boson, q1 and q2, and to the b-quarks, bℓ and bhad, produced in the top quark decays. The
. In this procedure, the measured jets relate to the quark decay products of the W boson, q1 and q2, and to the b-quarks, bℓ and bhad, produced in the top quark decays. The 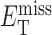 vector is identified with the transverse momentum components of the neutrino,
vector is identified with the transverse momentum components of the neutrino, 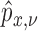 and
and 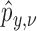 .
.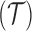 , Breit-Wigner
, Breit-Wigner 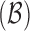 distributions, and a weight Wbtag accounting for the b-tagging information:
distributions, and a weight Wbtag accounting for the b-tagging information:
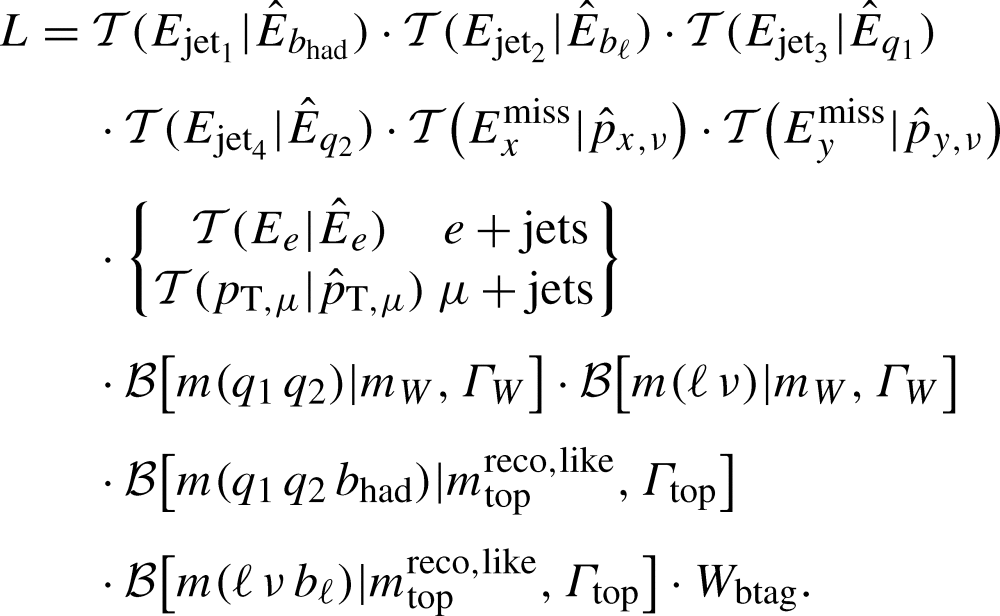
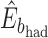 ), i.e. the energy of the b-quark from the hadronic decay of the top quark. The quantities mW and ΓW (which amounts to about one fifth of the Gaussian resolution of the
), i.e. the energy of the b-quark from the hadronic decay of the top quark. The quantities mW and ΓW (which amounts to about one fifth of the Gaussian resolution of the 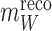 distribution) are taken from Ref. [6], and
distribution) are taken from Ref. [6], and 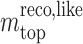 is the likelihood estimator for the top quark mass, i.e. the per event result of maximising this likelihood. Transfer functions are derived from the MC@NLO
is the likelihood estimator for the top quark mass, i.e. the per event result of maximising this likelihood. Transfer functions are derived from the MC@NLO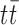 signal Monte Carlo sample at an input mass of mtop=172.5 GeV, based on reconstructed objects that are matched to their generator predicted quarks and leptons. When using a maximum separation of ΔR=0.4 between a quark and the corresponding jet, the fraction of events with four matched jets from all selected events amounts to 30 %–40 %. The transfer functions are obtained in three bins of η for the energies of b-quark jets,
signal Monte Carlo sample at an input mass of mtop=172.5 GeV, based on reconstructed objects that are matched to their generator predicted quarks and leptons. When using a maximum separation of ΔR=0.4 between a quark and the corresponding jet, the fraction of events with four matched jets from all selected events amounts to 30 %–40 %. The transfer functions are obtained in three bins of η for the energies of b-quark jets, 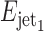 and
and 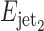 , light quark jets,
, light quark jets, 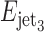 and
and 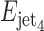 , the energy, Ee, (or transverse momentum,
, the energy, Ee, (or transverse momentum, 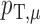 ) of the charged lepton, and the two components of the
) of the charged lepton, and the two components of the 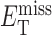 ,
, 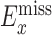 and
and 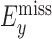 . In addition, the likelihood exploits the values of mW and ΓW to constrain the reconstructed leptonic, m(ℓ
ν), and hadronic, m(q1
q2), W boson masses using Breit–Wigner distributions. Similarly, the reconstructed leptonic, m(ℓ
ν
bℓ), and hadronic, m(q1
q2
bhad), top quark masses are constrained to be identical, where the width of the corresponding Breit Wigner distribution is identified with the predicted Γtop (using its top quark mass dependence) [6]. Including the b-tagging information into the likelihood as a weight Wbtag, derived from the efficiency and mistag rate of the b-tagging algorithm, and assigned per jet permutation according to the role of each jet for a given jet permutation, improves the selection of the correct jet permutation. As an example, for a permutation with two b-jets assigned to the b-quark positions and two light jets to the light quark positions, the weight Wbtag amounts to 0.48, i.e. it corresponds to the square of the b-tagging efficiency times the square of one minus the fake rate, both given in Sect. 4.
. In addition, the likelihood exploits the values of mW and ΓW to constrain the reconstructed leptonic, m(ℓ
ν), and hadronic, m(q1
q2), W boson masses using Breit–Wigner distributions. Similarly, the reconstructed leptonic, m(ℓ
ν
bℓ), and hadronic, m(q1
q2
bhad), top quark masses are constrained to be identical, where the width of the corresponding Breit Wigner distribution is identified with the predicted Γtop (using its top quark mass dependence) [6]. Including the b-tagging information into the likelihood as a weight Wbtag, derived from the efficiency and mistag rate of the b-tagging algorithm, and assigned per jet permutation according to the role of each jet for a given jet permutation, improves the selection of the correct jet permutation. As an example, for a permutation with two b-jets assigned to the b-quark positions and two light jets to the light quark positions, the weight Wbtag amounts to 0.48, i.e. it corresponds to the square of the b-tagging efficiency times the square of one minus the fake rate, both given in Sect. 4.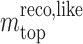 and
and 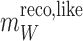 , is taken, a large residual jet energy scale (JES) dependence of R32 remains. This is because in the fit
, is taken, a large residual jet energy scale (JES) dependence of R32 remains. This is because in the fit 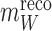 is constrained to mW, while
is constrained to mW, while 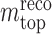 is only constrained to be equal for the leptonic and hadronic decays of the top quarks. This spoils the desired event-by-event reduction of the JES uncertainty in the ratio R32 [25]. To make best use of the high selection efficiency for the correct jet permutation from the likelihood fit, and the stabilisation of R32 against JES variations, the jet permutation derived in the fit is used, but
is only constrained to be equal for the leptonic and hadronic decays of the top quarks. This spoils the desired event-by-event reduction of the JES uncertainty in the ratio R32 [25]. To make best use of the high selection efficiency for the correct jet permutation from the likelihood fit, and the stabilisation of R32 against JES variations, the jet permutation derived in the fit is used, but 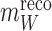 ,
, 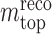 and therefore R32, are constructed from the unconstrained four-vectors of the jet triplet as given by the jet reconstruction.
and therefore R32, are constructed from the unconstrained four-vectors of the jet triplet as given by the jet reconstruction.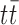 signal Monte Carlo. The figures (b, c) compare two output variables of the likelihood fit as observed in the data with their respective prediction. These are (b) the lnL value, and (c) the p
T of the b-jet associated to the hadronic decay of the top quark
signal Monte Carlo. The figures (b, c) compare two output variables of the likelihood fit as observed in the data with their respective prediction. These are (b) the lnL value, and (c) the p
T of the b-jet associated to the hadronic decay of the top quark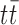 signal events, together with single top quark production events. This procedure is adopted, firstly, because single top quark production, although formally a background process, still carries information about the top quark mass and, secondly, by doing so mtop independent background templates can be used. The templates are constructed for the six mtop choices using the specifically generated Monte Carlo samples, see Sect. 3.
signal events, together with single top quark production events. This procedure is adopted, firstly, because single top quark production, although formally a background process, still carries information about the top quark mass and, secondly, by doing so mtop independent background templates can be used. The templates are constructed for the six mtop choices using the specifically generated Monte Carlo samples, see Sect. 3.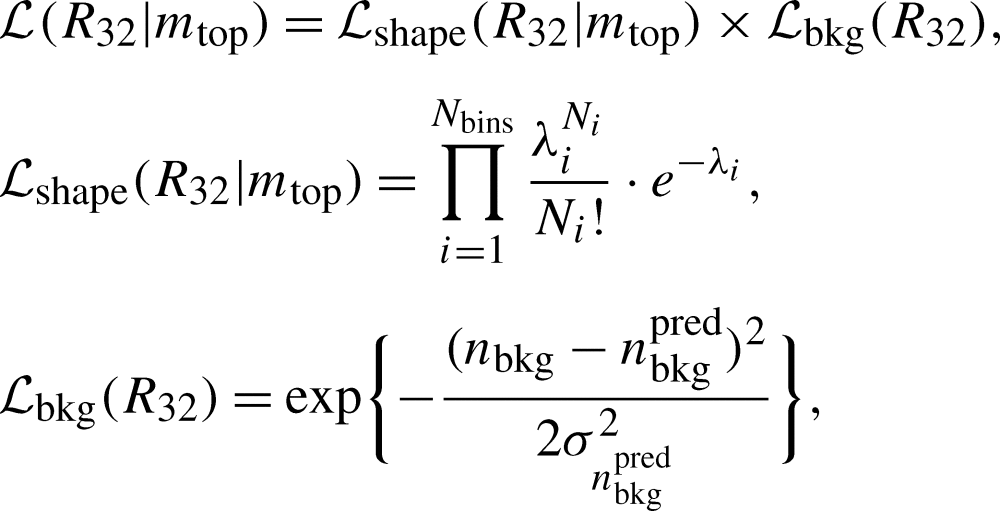
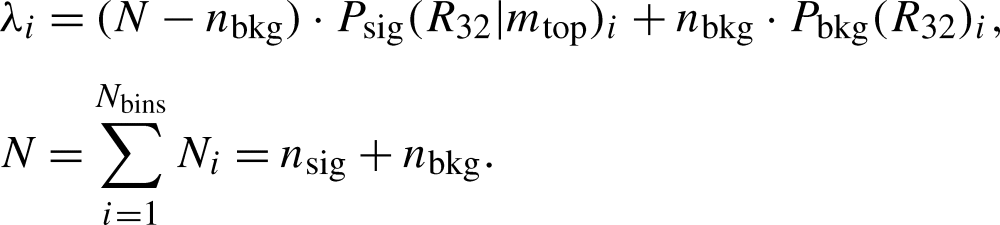
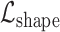 accounts for the shape of the R32 distribution and its dependence on the top quark mass mtop. The term
accounts for the shape of the R32 distribution and its dependence on the top quark mass mtop. The term 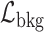 constrains the total number of background events, nbkg, using its prediction,
constrains the total number of background events, nbkg, using its prediction, 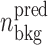 , and the background uncertainty, chosen to be 50 %, see Table 1. In addition, the number of background events is restricted to be positive. The two free parameters of the fit are the total number of background events, nbkg, and mtop. The performance of this algorithm is assessed with the pseudo-experiment technique. For each mtop value, distributions from pseudo-experiments are constructed by random sampling of the simulated signal and background events used to construct the corresponding templates. Using Poisson statistics, the numbers of signal events and total background events in each pseudo-experiment are fluctuated around the expectation values, either calculated assuming SM cross-sections and the integrated luminosity of the data, or taken from the data estimate. A good linearity is found between the input top quark mass used to perform the pseudo-experiments, and the result of the fit. Within their statistical uncertainties, the mean values and width of the pull distributions are consistent with the expectations of zero and one, respectively. The expected statistical uncertainties (mean ± RMS) obtained from pseudo-experiments with an input top quark mass of mtop=172.5 GeV, and for a luminosity of 1 fb−1, are 1.36±0.16 GeV and 1.11±0.06 GeV for the e+jets and μ+jets channels, respectively.
, and the background uncertainty, chosen to be 50 %, see Table 1. In addition, the number of background events is restricted to be positive. The two free parameters of the fit are the total number of background events, nbkg, and mtop. The performance of this algorithm is assessed with the pseudo-experiment technique. For each mtop value, distributions from pseudo-experiments are constructed by random sampling of the simulated signal and background events used to construct the corresponding templates. Using Poisson statistics, the numbers of signal events and total background events in each pseudo-experiment are fluctuated around the expectation values, either calculated assuming SM cross-sections and the integrated luminosity of the data, or taken from the data estimate. A good linearity is found between the input top quark mass used to perform the pseudo-experiments, and the result of the fit. Within their statistical uncertainties, the mean values and width of the pull distributions are consistent with the expectations of zero and one, respectively. The expected statistical uncertainties (mean ± RMS) obtained from pseudo-experiments with an input top quark mass of mtop=172.5 GeV, and for a luminosity of 1 fb−1, are 1.36±0.16 GeV and 1.11±0.06 GeV for the e+jets and μ+jets channels, respectively.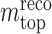 and
and 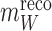 distributions.3 Instead of stabilising the estimator of mtop against JES variations as done for the 1d-analysis, the emphasis here is on an in-situ jet scaling. A global JSF (averaged over η and pT) is obtained, which is mainly based on the observed differences between the predicted
distributions.3 Instead of stabilising the estimator of mtop against JES variations as done for the 1d-analysis, the emphasis here is on an in-situ jet scaling. A global JSF (averaged over η and pT) is obtained, which is mainly based on the observed differences between the predicted 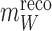 distribution and the one observed for the data. This algorithm predicts which global JSF correction should be applied to all jets to best fit the data. Due to this procedure, the JSF is sensitive not only to the JES, but also to all possible differences in data and predictions from specific assumptions made in the simulation that can lead to differences in the observed jets. These comprise: the fragmentation model, initial state and final state QCD radiation (ISR and FSR), the underlying event, and also pileup. In this method, the systematic uncertainty on mtop stemming from the JES is reduced and partly transformed into an additional statistical uncertainty on mtop due to the two-dimensional fit. The precisely measured values of mW and ΓW [6] are used to improve on the experimental resolution of
distribution and the one observed for the data. This algorithm predicts which global JSF correction should be applied to all jets to best fit the data. Due to this procedure, the JSF is sensitive not only to the JES, but also to all possible differences in data and predictions from specific assumptions made in the simulation that can lead to differences in the observed jets. These comprise: the fragmentation model, initial state and final state QCD radiation (ISR and FSR), the underlying event, and also pileup. In this method, the systematic uncertainty on mtop stemming from the JES is reduced and partly transformed into an additional statistical uncertainty on mtop due to the two-dimensional fit. The precisely measured values of mW and ΓW [6] are used to improve on the experimental resolution of 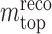 by relating the observed jet energies to the corresponding parton energies as predicted by the signal Monte Carlo (i.e. to the two quarks from the hadronic W boson decay, again using LO kinematics). Thereby, this method offers a complementary determination of mtop to the 1d-analysis method, described in Sect. 6, with different sensitivity to systematic effects and data statistics.
by relating the observed jet energies to the corresponding parton energies as predicted by the signal Monte Carlo (i.e. to the two quarks from the hadronic W boson decay, again using LO kinematics). Thereby, this method offers a complementary determination of mtop to the 1d-analysis method, described in Sect. 6, with different sensitivity to systematic effects and data statistics.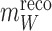 within 50 GeV–110 GeV. Amongst those, the jet triplet with maximum pT is chosen as the top quark candidate. For the light jet pair, i.e. for the hadronic W boson decay candidates, a kinematic fit is then performed by minimising the following χ2:
within 50 GeV–110 GeV. Amongst those, the jet triplet with maximum pT is chosen as the top quark candidate. For the light jet pair, i.e. for the hadronic W boson decay candidates, a kinematic fit is then performed by minimising the following χ2:
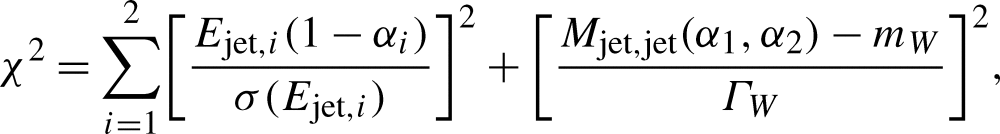
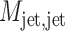 , and mW, divided by the W boson width. From these jets the two observables
, and mW, divided by the W boson width. From these jets the two observables 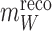 and
and 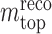 are constructed. The
are constructed. The 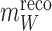 is calculated using the reconstructed light jet four-vectors (i.e. jet energies are not corrected using αi), retaining the full sensitivity of
is calculated using the reconstructed light jet four-vectors (i.e. jet energies are not corrected using αi), retaining the full sensitivity of 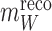 to the JSF. In contrast,
to the JSF. In contrast, 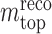 is calculated from these light jet four-vectors scaled to the parton level (i.e. jet energies are corrected using αi) and the above determined b-jet. In this way light jets in
is calculated from these light jet four-vectors scaled to the parton level (i.e. jet energies are corrected using αi) and the above determined b-jet. In this way light jets in 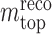 exhibit a much reduced JES sensitivity by construction, and only the b-jet is directly sensitive to the JES. The
exhibit a much reduced JES sensitivity by construction, and only the b-jet is directly sensitive to the JES. The 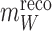 and
and 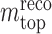 distributions are shown in Fig. 5 for both lepton channels, together with the predictions for signal and background. These, in both cases describe the observed distributions well. The correlation of these two observables is found to be small for data and predictions, and amounts to about −0.06.
distributions are shown in Fig. 5 for both lepton channels, together with the predictions for signal and background. These, in both cases describe the observed distributions well. The correlation of these two observables is found to be small for data and predictions, and amounts to about −0.06. 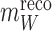 and
and 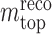 , observed in the data together with the signal and background predictions. Shown are (a, c) the e+jets channel, and (b, d) the μ+jets channel
, observed in the data together with the signal and background predictions. Shown are (a, c) the e+jets channel, and (b, d) the μ+jets channel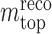 as a function of an input top quark mass in the range 160 GeV–190 GeV, and of an input value for the JSF in the range 0.9–1.1, and, finally, for
as a function of an input top quark mass in the range 160 GeV–190 GeV, and of an input value for the JSF in the range 0.9–1.1, and, finally, for 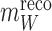 as a function of the assumed JSF for the same range. The signal templates for the
as a function of the assumed JSF for the same range. The signal templates for the 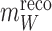 and
and 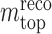 distributions, shown for the μ+jets channel and for JSF=1 in Fig. 6(a) and 6(b), are fitted to a sum of two Gaussian functions for
distributions, shown for the μ+jets channel and for JSF=1 in Fig. 6(a) and 6(b), are fitted to a sum of two Gaussian functions for 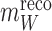 , and to the sum of a Gaussian and a Landau function for
, and to the sum of a Gaussian and a Landau function for 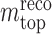 . Since, for this analysis, the background templates are constructed including single top quark production events, the background fit for the
. Since, for this analysis, the background templates are constructed including single top quark production events, the background fit for the 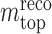 distribution is assumed to be mtop dependent. For the background, the
distribution is assumed to be mtop dependent. For the background, the 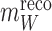 distribution, again shown for the μ+jets channel in Fig. 6(c), is fitted to a Gaussian function and the
distribution, again shown for the μ+jets channel in Fig. 6(c), is fitted to a Gaussian function and the 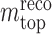 distribution, Fig. 6(d), to a Landau function. For all parameters of the functions that also depend on the JSF, a linear parameterisation is chosen. The quality of all fits is good for the signal and background contributions and for both channels.
distribution, Fig. 6(d), to a Landau function. For all parameters of the functions that also depend on the JSF, a linear parameterisation is chosen. The quality of all fits is good for the signal and background contributions and for both channels. 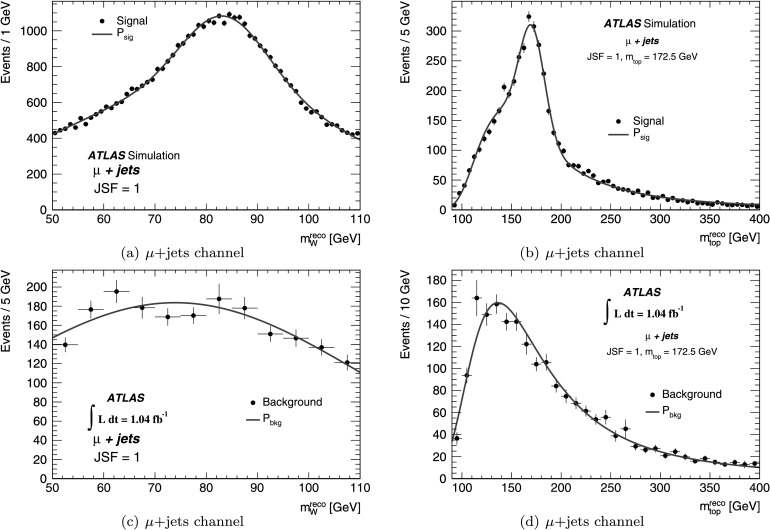
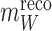 and
and 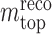 distributions for signal and background events for the μ+jets channel. Shown are (a, b) the
distributions for signal and background events for the μ+jets channel. Shown are (a, b) the 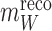 and
and 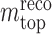 distributions for signal events, and (c, d) the corresponding distributions for background events, see Table 1. All distributions are for JSF=1
distributions for signal events, and (c, d) the corresponding distributions for background events, see Table 1. All distributions are for JSF=1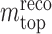 and
and 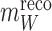 distributions are used in an unbinned likelihood fit to the data for all events, i=1,…,N. The likelihood function maximised is:
distributions are used in an unbinned likelihood fit to the data for all events, i=1,…,N. The likelihood function maximised is:
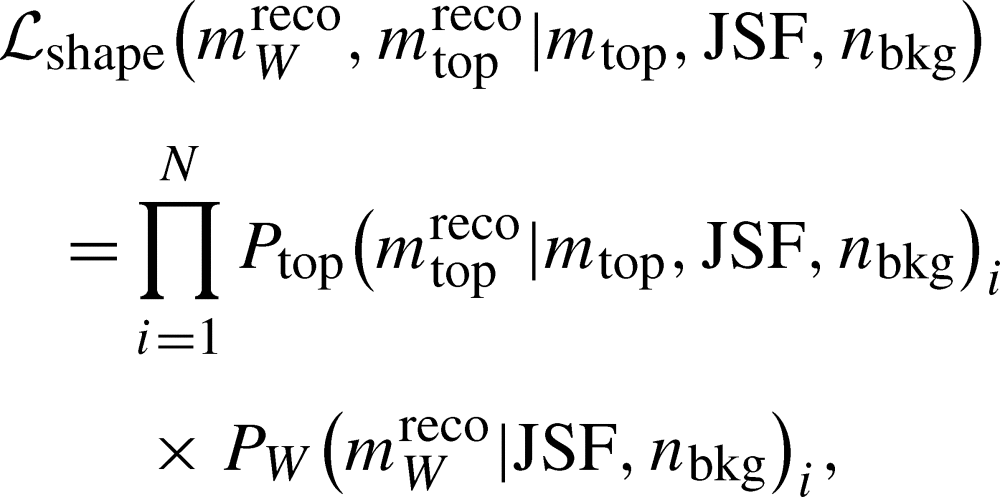
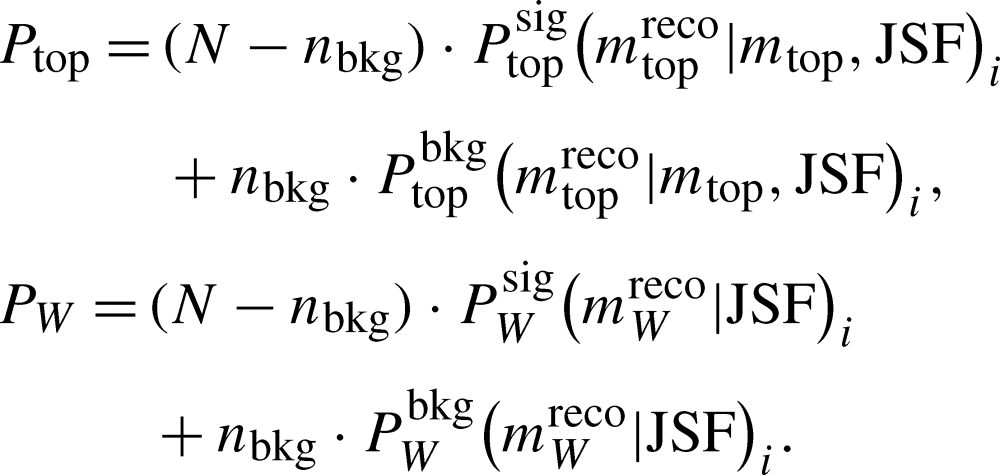
 and
and  distributions. This effect is evaluated by performing pseudo-experiments for which signal templates are derived from seven dedicated AcerMC signal samples in which Pythia parameters that control the showering are varied in ranges that are compatible with those used in the Perugia Hard/Soft tune variations [32]. The systematic uncertainty is taken as half the maximum difference between any two samples.
distributions. This effect is evaluated by performing pseudo-experiments for which signal templates are derived from seven dedicated AcerMC signal samples in which Pythia parameters that control the showering are varied in ranges that are compatible with those used in the Perugia Hard/Soft tune variations [32]. The systematic uncertainty is taken as half the maximum difference between any two samples. is used in the event selection and also in the likelihood for the 1d-analysis, but is not used in the mtop estimator for either analysis. Consequently, the uncertainty due to any mis-calibration is expected to be small. The impact of a possible mis-calibration is assessed by changing the measured
is used in the event selection and also in the likelihood for the 1d-analysis, but is not used in the mtop estimator for either analysis. Consequently, the uncertainty due to any mis-calibration is expected to be small. The impact of a possible mis-calibration is assessed by changing the measured 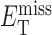 within its uncertainty.
within its uncertainty.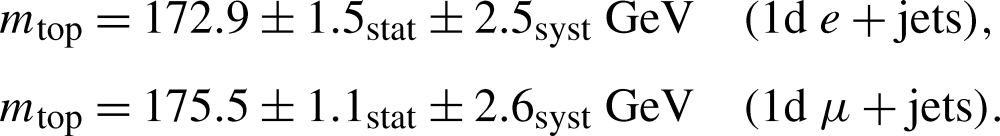
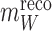 and
and 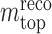 distributions in the e+jets (μ+jets) channels. The two-dimensional uncertainty ellipses for both channels are shown in Fig. 9. The results from both channels are:
distributions in the e+jets (μ+jets) channels. The two-dimensional uncertainty ellipses for both channels are shown in Fig. 9. The results from both channels are:
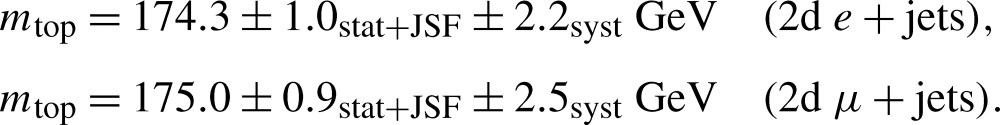
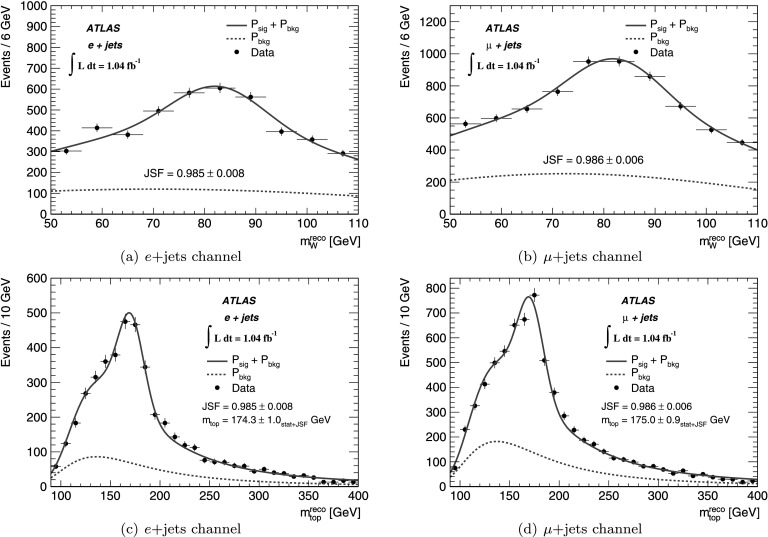
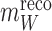 distributions, and in (c, d) the
distributions, and in (c, d) the 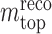 distributions. The data points are shown with their statistical uncertainties. The lines denote the background probability density function (dashed) and the sum of the signal and background probability density functions (full)
distributions. The data points are shown with their statistical uncertainties. The lines denote the background probability density function (dashed) and the sum of the signal and background probability density functions (full)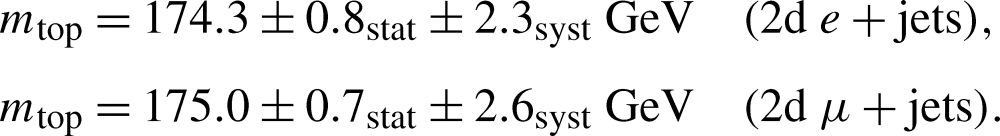
 and single top quark production, whereas for the 2d-analysis the single top quark production process is included in the background, see Table 1. Consequently, the MC@NLO samples generated at mtop=172.5 GeV for both processes are used appropriately for each analysis in determining the statistical correlations. The statistical correlation between the results of the two analyses is 0.15 (0.16) in the e+jets (μ+jets) channels, respectively. Given these correlations, the two measurements for each lepton channel are statistically consistent for both lepton flavours.
and single top quark production, whereas for the 2d-analysis the single top quark production process is included in the background, see Table 1. Consequently, the MC@NLO samples generated at mtop=172.5 GeV for both processes are used appropriately for each analysis in determining the statistical correlations. The statistical correlation between the results of the two analyses is 0.15 (0.16) in the e+jets (μ+jets) channels, respectively. Given these correlations, the two measurements for each lepton channel are statistically consistent for both lepton flavours.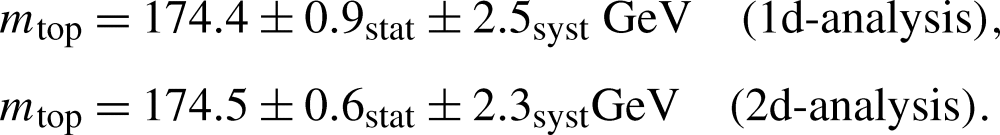
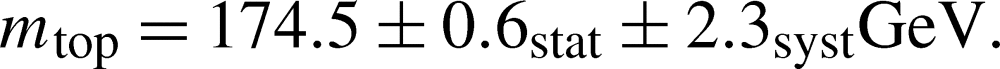
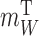 is the W-boson transverse mass, defined as
is the W-boson transverse mass, defined as 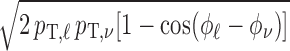 , where the measured
, where the measured 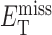 vector provides the neutrino (ν) information.
vector provides the neutrino (ν) information.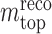 and
and 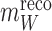 are calculated differently, the same symbols are used to indicate that these are estimates of the same quantities.
are calculated differently, the same symbols are used to indicate that these are estimates of the same quantities.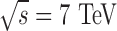 at the LHC, ATLAS-CONF-2011-157 (2011). http://cdsweb.cern.ch/record/1399599
at the LHC, ATLAS-CONF-2011-157 (2011). http://cdsweb.cern.ch/record/1399599
 production cross section and the top quark mass in the dilepton channel in pp collisions at
production cross section and the top quark mass in the dilepton channel in pp collisions at 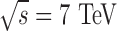 J. High Energy Phys. 2011;07 [Google Scholar]
J. High Energy Phys. 2011;07 [Google Scholar]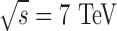 . Eur. Phys. J. C (2011), submitted. arXiv:1112.6426 [DOI] [PMC free article] [PubMed]
. Eur. Phys. J. C (2011), submitted. arXiv:1112.6426 [DOI] [PMC free article] [PubMed]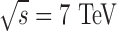 using the ATLAS Detector in 2011. ATLAS-CONF-2011-116 (2011). http://cdsweb.cern.ch/record/1367408
using the ATLAS Detector in 2011. ATLAS-CONF-2011-116 (2011). http://cdsweb.cern.ch/record/1367408
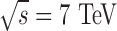 using the ATLAS detector at the LHC. Eur. Phys. J. C. 2011;71:1630. doi: 10.1140/epjc/s10052-011-1630-5. [DOI] [Google Scholar]
using the ATLAS detector at the LHC. Eur. Phys. J. C. 2011;71:1630. doi: 10.1140/epjc/s10052-011-1630-5. [DOI] [Google Scholar]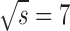 TeV with the ATLAS detector. ATLAS-CONF-2011-033 (2011). http://cdsweb.cern.ch/record/1337783
TeV with the ATLAS detector. ATLAS-CONF-2011-033 (2011). http://cdsweb.cern.ch/record/1337783
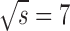 TeV measured with the ATLAS detector at the LHC. ATLAS-CONF-2011-142 (2011). http://cdsweb.cern.ch/record/1385518
TeV measured with the ATLAS detector at the LHC. ATLAS-CONF-2011-142 (2011). http://cdsweb.cern.ch/record/1385518
 production with a veto on additional central jet activity in pp collisions at
production with a veto on additional central jet activity in pp collisions at 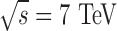 using the ATLAS detector. Eur. Phys. J. C. 2012 doi: 10.1140/epjc/s10052-012-2043-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
using the ATLAS detector. Eur. Phys. J. C. 2012 doi: 10.1140/epjc/s10052-012-2043-9. [DOI] [PMC free article] [PubMed] [Google Scholar]