Slow updating of the achromatic point after a change in illumination

Abstract

For a colour constant observer, the colour appearance of a surface is independent of the spectral composition of the light illuminating it. We ask how rapidly colour appearance judgements are updated following a change in illumination. We obtained repeated binary colour classifications for a set of stimuli defined by their reflectance functions and rendered under either sunlight or skylight. We used these classifications to derive boundaries in colour space that identify the observer’s achromatic point. In steady-state conditions of illumination, the achromatic point lay close to the illuminant chromaticity. In our experiment the illuminant changed abruptly every 21 seconds (at the onset of every 10^th trial), allowing us to track changes in the achromatic point that were caused by the cycle of illuminant changes. In one condition, the test reflectance was embedded in a spatial pattern of reflectance samples under consistent illumination. The achromatic point migrated across colour space between the chromaticities of the steady-state achromatic points. This update took several trials rather than being immediate. To identify the factors that governed perceptual updating of appearance judgements we used two further conditions, one in which the test reflectance was presented in isolation and one in which the surrounding reflectances were rendered under an inconsistent and unchanging illumination. Achromatic settings were not well predicted by the information available from scenes at a single time-point. Instead the achromatic points showed a strong dependence on the history of chromatic samples. The strength of this dependence differed between observers and was modulated by the spatial context.

Introduction

The spectral composition of light that reaches the eye from the surface of an object often changes. Usually, the spectral reflectance functions of surfaces remain stable, but the spectral composition of the light incident on them changes. Our perception of surface colour is generally well predicted by the unchanging surface reflectance, in a process known as colour constancy (see Brainard and Maloney (2011), Foster (2011), Smithson (2005), Maloney (1999) and Hurlbert (1998) for reviews). This study aims to investigate time-course of colour constancy after a change in illumination. In the natural environment, with multiple sources of illumination, these changes can occur for a number of reasons. The position of a light source can change, light can be occluded by clouds and other objects and can be modified by mutual reflections. We probe colour appearance at regular time intervals for tens of seconds after a simulated change in the spectrum of illumination.

Most of the studies on colour constancy do not explicitly consider the amount of time needed to achieve constancy. They use simulated environments that are static, with spatially distributed cues to the illuminant. However, there are several reasons why the time-course of colour constancy may be worthy of study. Colour appearance is heavily influenced by chromatic adaptation, components of which have been identified over a range of time scales (Jameson, Hurvich, & Varner, 1979; Rinner & Gegenfurtner, 2000). In natural viewing, even a static visual environment will generate time-varying retinal signals as eye-movements and self-motion convert spatial variation in the scene to temporal variation in the retinal image. The mean chromaticity of a scene has been identified as a potentially useful cue to the illuminant chromaticity (Buchsbaum, 1980; Helson, 1964; Land, 1983, 1986) and a process of adaptation that integrates over an appropriate time-scale could extract this cue (D’Zmura & Lennie, 1986; Fairchild & Lennie, 1992; Land, 1983). If the process of constancy uses such temporally distributed information, it cannot also be achieved instantaneously following a change in illumination conditions. Estimates of the time-course of constancy may allow us to infer the type of mechanisms involved. For example, we know that the effects of local retinal adaptation can be measured after fractions of a second (Crawford, 1947) but those involving post-receptoral mechanisms may take longer (Pugh & Mollon, 1979).

Previous work

Much of the relevant work on the time-course of perceptual constancy has studied lightness constancy, not specifically colour constancy. A prevalent model of lightness constancy is an anchoring one, where the surface with highest reflectance in a scene is treated as white, and other surfaces in the scene take on brightnesses relative to this (e.g. Gilchrist et al., 1999; Land & McCann, 1971). Is has been demonstrated that the strength of constancy can be affected by the complexity (or articulation) of the scene (Cataliotti & Bonato, 2003; Gilchrist, et al., 1999). A well-known phenomenon is the Gelb effect (Gelb, 1929), in which a surface of low reflectance appears white when it is the only thing illuminated by a bright spotlight. Most research emphasises the role of surfaces that are simultaneously present rather than surfaces viewed previously but Gelb reported that moving a high reflectance surface close to the low reflectance test surface makes it immediately appear dark (Gelb, 1929). The test surface appears white again when the high reflectance surface is removed, though this can take several seconds (Newson, 1958). The time-course of this perceptual change depends on the relative reflectances of the two surfaces, being longer when the differences in reflectance are small. Such influences of prior knowledge also show considerable individual variation.

More recetly, Cataliotti & Gilchrist (1995) introduced light grey and white patches into an artificial Mondrian environment consisting of dark grey patches (the brightest of which initially appeared white). They found that the new patches initially appeared self-luminous and that it took two minutes for the original dark grey patches to appear darker. Annan & Gilchrist (2004) conclude that this is due to anchor persistence – the surfaces that do not change from one view to another provide cues that the illumination has not changed so re-anchoring is not immediate. The size of the effect depends on the number of unchanged patches, and not on retinal adaptation and lightness persistence. Cataliotti & Bonato (2003) make an analogy between spatial anchoring and temporal anchoring in lightness constancy. They show that the lightness of even a spot-in-a-void can be affected by intense elements of a complex stimulus presented several seconds earlier. They demonstrate that the effect is not due to adaptation in peripheral mechanisms, nor to a judgement relative to the spatial mean of the first stimulus.

There is some evidence for colour constancy mechanisms that are extended in time, since appearance is influenced by the history of colour stimuli and not only by the information present in one instant. Smithson and Zaidi (2004) found strong influences of the chromatic statistics of preceding stimuli, such that appearance judgements were better predicted by the illuminant history than by a conflicting illuminant that was used in the spatial surround. A spatially localised but temporally extended process is required to account for these results. Schultz, Doerschner, and Maloney (2006) found that constancy was greater for a series of isolated simulated reflectances when these reflectances were presented in blocks in which the illuminant was constant, compared to blocks in which the illuminant and reflectance were randomised on each presentation. They conclude that judgements must have been dependent on information integrated temporally over preceding samples, and that this process could be explained by a process of slow chromatic adaptation.

Given that the recent history of illumination matters, it becomes interesting to ask how soon after an illuminant change an observer’s colour classifications become consistent with those they would make under prolonged exposure to the new illuminant. A global change in illumination produces structured changes in ratios of signals in each cone photoreceptor class. The ratios of cone excitations for a pair of surfaces under one illuminant is approximately equal to the ratio associated with that pair of surfaces under a second illuminant (Figure 3 in Foster & Nascimento, 1994). Equivalently, the ratios of cone excitations for a single surface under two illuminants is approximately equal to the ratio associated with a second surface under the same two illuminants. In other words, R_1,1 / R_2,1 ≈ R_1,2 / R_2,2 and R_1,1 / R_1,2 ≈ R_2,1 / R_2,2 where R_s,i is the cone signal associated with surface s under illuminant i.

The change in cone excitation imposed by a change in illumination is approximately equal for each surface (Figure 2 in Smithson, 2005). Observers associate these consistent changes in cone-excitation ratios with a change in illumination (Nascimento & Foster, 1997). Moreover, observers readily detect surfaces that elicit inconsistent changes in cone excitation ratios (Craven & Foster, 1992; Foster et al., 2001), even when the illuminant change is accompanied by changes in the positions of the test surfaces (Foster, Amano, & Nascimento, 2006), probably on the basis of cone-ratios between the test surfaces and a spatial average over the whole image (Amano & Foster, 2004). Interestingly, performance is best with fast illuminant changes, suggesting that observers have access to a transient signal that is associated with a global illuminant change (Linnell & Foster, 1996). The ability to identify a global change in illumination might imply that colour constancy (or an adjustment to take account of the illumination) occurs instantaneously, but detection of an illuminant change does not necessarily imply that the perceptual system makes associated adjustments to colour appearance (e.g. Foster, 2003).

Barbur, de Cunha, Williams, & Plant (2004) employed a dynamic colour matching technique, in which observers were asked to adjust the colour of a test patch to make its perceived colour invariant under a change in simulated illumination on surrounding patches. The observers’ settings under abrupt changes in illumination that followed a 1.25 Hz squarewave cycle showed high levels of constancy. Further experiments implied that instantaneous compensation for the illuminant is mediated mostly by early, monocular chromatic mechanisms in V1 with little contribution from later areas (Barbur & Spang, 2008), although greater constancy is achieved with binocular stimuli. For this task, mechanisms comparing spatially local contrasts are more important than those integrating spatially distributed information (Barbur, et al., 2004).The spatial arrangement of patches in Barbur et al.’s experiments was fixed, so one solution that would give a high constancy setting would be to find the colour of the test patch that matches the local change in cone-ratios for the test patch to the changes exhibited by each of the surrounding patches. Goddard, Solomon and Clifford (2010) provide evidence for an adaptable mechanism that produces greater colour opponent aftereffects during adaptation to a constant scene under a 1 Hz cycle of changing illumination than to a changing scene that produced equivalent levels of receptoral stimulation. The results are consistent with adaptation to a neural representation from which correlated changes in local cone-ratios across the scene are (immediately) discounted.

Our experiment

The purpose of our study was to investigate the time-course of appearance-based colour constancy. We used simulated environments that consisted of several reflectance patches rendered under particular illuminants. From trial-to-trial the spatial layout of reflecting surfaces could change and these changes were sometimes accompanied by changes in illumination. The observers’ task was to classify the colour appearance of a series of test patches and from these judgements we estimated the observers’ achromatic points at each of several intervals after a simulated change of illuminant.

To track the time-course of appearance-based constancy following an illuminant change we required a measure of constancy that was localised in time. Standard methods of measuring colour constancy include asymmetric colour-matching and achromatic setting, via Method of Adjustment (MoA). This has two consequences: the stimulus itself is dynamically adjusted by the observer (so exposure to the stimulus is not under direct experimental control) and the observer’s judgement is not made at a precisely specified time. We instead chose to use a Method of Constant Stimuli (MCS), with a single binary decision per presentation (Chichilnisky & Wandell, 1999; Smithson & Zaidi, 2004). By making periodic transitions between two illuminants, we were able to construct our experiment to contain multiple instances of trials with a particular relationship to the time-course of illumination.

In our rendering, we used simulated illuminants with the spectral power distributions of sunlight and skylight. Each test stimulus was defined as a surface with the reflectance function of an environmental material. Materials were chosen so that their rendered colour coordinates sampled a three-dimensional volume in colour space that was transformed by a change in illuminant spectrum. Over the course of the experiment, we obtained colour classifications for the complete set of materials under sunlight and skylight, as a function of time following an illuminant change from sunlight to skylight and from skylight to sunlight. The classifications of test reflectances under different conditions allow us to track differences in appearance-based constancy. The boundaries in colour space that separate regions associated with different binary colour-classifications (red vs green and yellow vs blue) identify the loci of physical stimuli that elicit an unchanging set of percepts, and specifically the intersection of boundaries identifies the observer’s achromatic locus (a curve that is localised in chromaticity but extended in the lightness dimension).

We compared three spatial conditions. In the first condition, the test patches were presented against a variegated background composed of simulated surfaces, drawn from the test set, and rendered under the same illuminant spectrum as the test. In this condition, a change of illuminant on the test was accompanied by the same change on the background. We call this the “global” illuminant condition. The illuminant change in this condition was accompanied by the structured changes in cone-ratios that have been highlighted by Foster and colleagues (e.g. Foster & Nascimento, 1994). If colour constancy were perfect and instantaneous, the classification applied to each sample reflectance would remain unchanged, and the achromatic point would shift immediately from the chromaticity of the illuminant before the change to the chromaticity of the illuminant after the change.

In the second condition, the sequence of test reflectances rendered under alternating illuminants was presented on a black background. We call this the “isolated” condition. In a single trial there was only one chromaticity present and the reflectance spectrum was confounded with the illuminant spectrum under which it is rendered. However a running-mean of test chromaticities would change gradually after an illuminant shift, and could be used as a reference against which to make judgements, as proposed in the classical literature (e.g. Helson, 1948). In this case, any adjustments to the achromatic point must lag the physical change in illuminant.

In the third condition, the sequence of test reflectances rendered under alternating illuminants was presented on a background composed of simulated surfaces rendered under CIE Illuminant C, which has a chromaticity in between sunlight and skylight. We call this the “inconsistent” condition. In this case, if all judgements were made relative to the constant spatial context, the achromatic point would remain steady and close to the coordinates of the background illuminant.

Methods

Observers

Three observers obtained complete datasets in the study. Observers RJL and WS were experienced psychophysical observers; observer KAD was not. Observer WS was naive to the purpose of the study; observers RJL and KAD were not. Observers RJL and WS are male, observer KAD is female. All observers had normal colour vision (based on the Hardy Rand and Rittler (HRR) 4^th Edition pseudoisochromatic plates and Rayleigh anomaloscope matches), and corrected to normal acuity.

Apparatus

Stimuli were presented on a CRT monitor (Mitsubishi DiamondPro 2070SB). The monitor display had size 0.386×0.295m, a spatial resolution of 1024×768 pixels (each pixel measured 0.4mm) and a refresh rate of 100Hz. The display was driven by a ViSaGe system (Cambridge Research Systems Ltd., Rochester, U.K.). A box with a rectangular aperture the same size as the display abutted the monitor, and observers viewed the display binocularly through holes in the opposite side of the box. The interior of the box was painted matt black and baffles were used to prevent multiple reflections that might provide the observer with a physical signal corresponding to the spatial average of stimulus chromaticities. The distance between the observer and the monitor face was 0.56m. The horizontal dimension of the monitor subtended a visual angle of 38°, and the vertical dimension an angle of 29.5°.

Stimuli

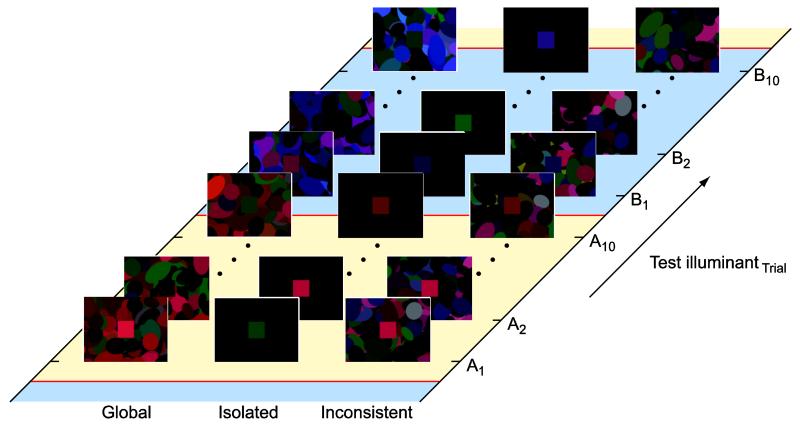
Examples of the stimuli are shown in Figure 1. Each scene comprised a background and a test patch. The background was made from 252 ellipses, each randomly oriented and positioned across the display. The size of each ellipse was also randomised, so that one axis of the ellipse was fixed at 50 pixels (~2°) and the other varied between 25 and 100 pixels (~ 1° to 4°). The ellipses were placed so that many overlapped. Each ellipse was assigned a spectral reflectance function from a predetermined set of 120 measurements of materials (see below), and rendered under the specified illuminant. All the ellipses in the background were illuminated by the same simulated light. The random positions, sizes, orientations and assigned reflectances of the ellipses were generated each trial. The test patch was a square of side length 100 pixels (~ 4°), placed in the centre of the screen. The test patch was not overlapped by any of the background ellipses. The test patch was assigned a spectral reflectance function from a predetermined sequence that will be described later. The illumination of the background and test patch could be different, depending on the experimental condition.

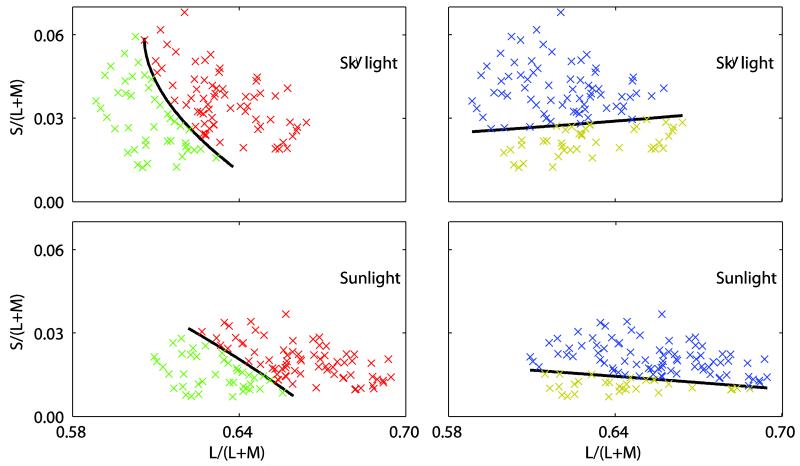
Figure 1.

Examples of stimuli. The left panel shows background and test under sunlight (“global”), the middle panel shows the test under sunlight and the background unilluminated (the simulated illuminant was a zero-energy-spectrum, “isolated”) and the right panel shows the test under skylight and background under Illuminant C (“inconsistent”). Note that variations in display and printing processes make it impossible to exactly reproduce here the colours presented under experimental conditions.

The chromaticity of each material under each illuminant, and therefore the colours to be displayed by the monitor, were calculated using the spectral reflectance and radiance functions of the materials and illuminants, respectively. The procedure is described below. The material reflectances were from spectrophotometric measurements of man-made and natural surfaces, obtained from various sources (Chittka, Shmida, Troje, & Menzel, 1994; Hiltunen, 1996; Marshall, 2000; Vrhel, Gershon, & Iwan, 1994), and chosen to obtain an even coverage of colour space within the gamut afforded by our monitor. The simulated illuminants were measurements of sunlight and skylight (measured by Taylor & Kerr, 1941), as well as the standard spectrum of CIE Illuminant C, which has a chromaticity intermediate between the chromaticities of sunlight and skylight.

Generation of chromaticities

The desired RGB levels of any patch of the stimulus display were calculated as follows. First, the spectral reflectance function of the specified material was multiplied by the spectral power distribution of the desired illuminant, wavelength by wavelength, to give the spectral power distribution of the light after reflection from the material. Multiplying by each of the three cone sensitivity fundamentals and summing over wavelength then results in a triplet of values representing the relative cone excitations produced in the standard observer by this spectral distribution. A matrix constructed by multiplying the cone fundamentals with the measured spectral power distributions of the monitor primaries allowed us to transform between cone excitations (LMS) and monitor primary output ratios (RGB). The spectral output distributions of the monitor primaries were measured with a spectroradiometer (RadOMA, Gamma Scientific, San Diego, CA, U.S.A.). The output of each primary was linearised (gamma corrected) using measurements from an OptiCAL (Cambridge Research Systems Ltd., Rochester, U.K.).

Procedure and task

At the start of each trial, the display changed to the appropriate stimulus, which remained for the whole duration of the trial. The observer’s task was to decide if the test patch appeared red or green in one set of sessions, or blue or yellow in another set of sessions. Responses were given by pressing one of two buttons. An audio-tone signalled the onset of each trial and a second tone signalled the acquisition of a response. The inter-trial interval was 2100ms. The observer could make a response at any time during this period, but the next stimulus was presented whether the observer made a response or not. The same stimuli were repeated in separate sessions (see below) so that both red vs. green and blue vs. yellow classifications could be obtained for all stimuli. This method is the one used by Smithson & Zaidi (2004), who found it more robust than obtaining two separate judgements per trial.

In each of the three experimental conditions, the test-patch illuminant changed from sunlight to skylight or vice-versa after every tenth trial. The conditions differed in the simulated illumination of the background. In the first condition (global), the background illumination was always the same as the test-patch illumination, and changed also every tenth trial. Illuminant changes were coincident with the onset of the following trial. In the second condition (isolated), the background illumination was always a zero-energy-spectrum, so the entire background field appeared black, while the test-patch illumination changed as before. In the third condition (inconsistent), the background illumination was always Illuminant C while the test patch-illumination alternated between sunlight and skylight as before. These three spatial illumination conditions are similar to those used by Nascimento & Foster (1996).

Within each session, the presentation order of stimuli was pseudo-randomised after being arranged to satisfy two requirements: over the course of the experiment each material had to be presented in the test-patch position under both sunlight and skylight, and in each of ten temporal positions (trials) after an illuminant change. Since this would require many trials, the set of 120 materials was split into four subsets. Data for the four subsets were collected in separate sessions, each fulfilling the two requirements above. Each observer ran each session twice, so that data could be averaged later. This leads to a total of sixteen sessions in each of the three conditions: four sets of materials, two decisions and two repeats. The requirement to have each material in each temporal position after a change from sunlight to skylight and after a change from skylight to sunlight means that each session contained 600 trials and lasted for approximately 40 minutes.

The set of material reflectances were divided into the four subsets at random, and we determined that the distributions of chromaticities and luminance of the simulated surfaces (as if rendered under an illuminant with an equal-energy spectral distribution) did not differ significantly between the groups. One-way ANOVAs indicate the means do not differ between subsets (within chromaticity dimensions) and Levene’s tests indicate that the variances do not differ significantly.

Additional “steady-state” conditions were designed to determine the observer’s classification of each material under each illuminant, under steady illumination. The test patch and background illuminants were constant throughout each session and consistent across the test patch and background. In separate sessions, the simulated illuminant was sunlight, skylight, or Illuminant C. Red vs. green and blue vs. yellow responses were obtained in separate sessions, and sessions were repeated to collect more data for averaging. There were a total of 12 steady-state sessions, each of which comprised 120 trials and lasted 10 minutes.

Results

The first stage in our analysis is to determine the boundaries in colour space that divide chromaticities classified as red from those classified as green, and chromaticities classified as blue from those classified as yellow (Smithson & Zaidi, 2004).

Classification boundaries and achromatic points

Each of these boundaries is found by performing a least-squares regression analysis on the classification probabilities. That is, the observed probability of classifying the material as red (for the red/green boundary) or blue (for the blue/yellow boundary). The regressors were the chromaticity and luminance coordinates of each material, and those coordinates squared. We assume that a classification probability of 0.5 (an equal chance of classifying a material as, for example, red or green) defines the boundary we seek. We solve the predictive equation from the regression to find the chromaticity coordinates that are associated with this classification probability. These coordinates describe a surface in MB-DKL space (Derrington, Krauskopf, & Lennie, 1984; MacLeod & Boynton, 1979). For ease of visualisation and subsequent analysis, it is helpful to consider the intersection of these surfaces with an equiluminant plane. The classification boundary intersects the equiluminant plane to define a curve, examples of which are shown in Figure 3.

Figure 3.

Coloured crosses represent the material chromaticities (under skylight in the top panels and sunlight in the bottom panels), projected onto an equiluminant plane of MB-DKL space. These points are coded according to an observer’s classifications (as red or green in the left-hand plots and as yellow or blue in the right-hand plots). Black lines are examples of the intersection of fitted classification boundaries and the mean-luminance equiluminant plane. The chromaticity at which the red-green and blue-yellow classification boundaries intersect locates the chromaticity that is equally likely to be classified as red, green, yellow or blue. We infer this to be an observer’s achromatic point.

Considering any equiluminant plane, the red-green and blue-yellow classification curves intersect to locate a single chromaticity that, under the particular experimental conditions, is equally likely to be classified as red, green, yellow or blue. It is this single point that we refer to as the achromatic point and use to summarise the data when comparing colour appearance under different experimental conditions. The red-green and blue-yellow classification surfaces intersect in a curve that defines the loci of achromatic points at all luminance values. The extent to which this curve is parallel to the luminance axis indicates the stability of the achromatic point as a function of luminance. The value of luminance at which we extract the achromatic point is somewhat arbitrary. For all subsequent analyses we use the mean luminance of all samples. Re-running the main analyses for different luminance levels does not change the conclusions.

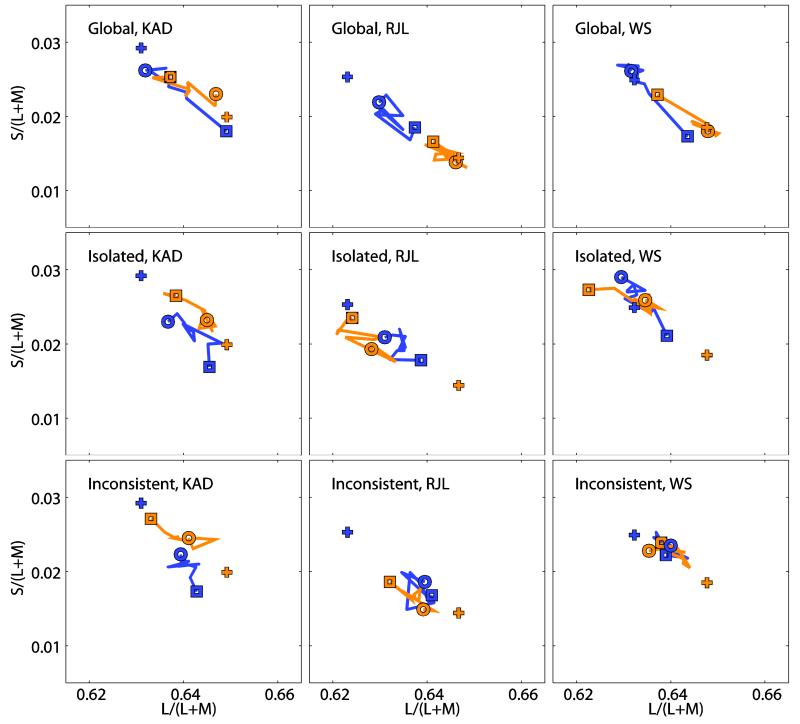
The data we collected allowed us to plot the position of the achromatic point for each of the two illuminant transitions (sunlight to skylight and skylight to sunlight) and at ten time points after the illuminant switch. Figure 4 shows these points for the global, isolated and inconsistent conditions respectively. In each figure, the left hand panel shows data from observer KAD, the middle panel shows data from observer RJL, and the right panel from observer WS. Each panel represents a portion of the Macleod-Boynton chromaticity diagram, and plots the path of the achromatic point as it moves over time after an illuminant change from sunlight to skylight (blue line) or skylight to sunlight (orange line). In all cases, the square symbol represents the position of the achromatic point measured in the trial immediately after the illuminant switch, and the jagged line joins achromatic points at successive temporal intervals until the 10^th trial after the illuminant switch, represented by the circular symbol. The crosses represent the achromatic points measured in the steady-state condition, when all the materials were viewed under an illuminant that did not change and was the same for both test patch and background. We might expect that, after an illuminant change, the position of the achromatic point would migrate over time, from its chromaticity under the illuminant before the shift, to its chromaticity under the illuminant after the shift. This can be seen clearly in the data from the global condition, and less clearly in the isolated and inconsistent conditions.

Figure 4.

Migration of the achromatic point in all experimental conditions. Each panel shows a section of the MacLeod-Boynton Chromaticity Diagram and indicates the path taken by the achromatic point as it moved following a change of illuminant from skylight to sunlight (orange lines) and sunlight to skylight (blue lines). The squares show the position measured in the trial immediately after the switch, and the circles show the position in the tenth trial after the switch. Data are shown in separate plots for each of the three observers (KAD: left column, RJL: middle column, WS: right column), in each of the three experimental conditions (global: top row, isolated: middle row, inconsistent: bottom row). The crosses show the position of the achromatic point measured in the steady-state conditions under one illuminant (orange: sunlight, blue: skylight).

Colour constancy in steady-state conditions

A common way of quantifying colour constancy is to calculate a constancy index, which typically uses the relationship between the difference in chromaticity of the achromatic points under different illuminants, and the difference between the chromaticites of a material of uniform spectral reflectance under those illuminants (equivalent to the chromaticity of the illuminant) (Brainard, 1998). The more closely the magnitude of the shift in the chromaticity of the achromatic point matches the magnitude of the shift in illuminant chromaticity, the higher the level of constancy (Foster, 2011). Since the mapping between chromaticity space and perceptually uniform colour space is not known, no single index provides a complete characterisation of the extent of constancy.

The chromaticities of the illuminants and the measured steady-state achromatic points are shown in Figure 5.

Figure 5.

Chromaticity coordinates of the simulated CIE Illuminant C (grey symbols), sunlight (orange symbols), skylight (blue symbols) illuminants and of the achromatic points measured in our steady-state conditions, under prolonged viewing of constant illumination conditions over the whole stimulus by each of the three observers. The chromaticities of the sunlight and skylight illuminants are joined with a dashed line to indicate the vector along which colour constancy is calculated (described in text).

For the steady-state conditions, comparing two illuminants (1 and 2), we calculate a constancy index C_ss with the following equation:

$$C_{SS}=\frac{({\mathit{a}}_1-{\mathit{a}}_2)\cdot ({\mathit{i}}_2-{\mathit{i}}_1)}{({\mathit{i}}_1-{\mathit{i}}_2)\cdot ({\mathit{i}}_2-{\mathit{i}}_1)}$$ (1)

where a₁ and a₂ are the chromaticity coordinate vectors (L/(L+M), S/(L+M)) of the achromatic points measured under illuminant 1 and 2 respectively, and i₁ and i₂ are the chromaticity coordinate vectors of those illuminants. The symbol · denotes the dot product. The vector a₁ – a₂ provides an estimate of the putative neural constancy transformation; i₁ – i₂ provides a summary of the colour conversion imposed by the illuminant change (Smithson & Zaidi, 2004; Yang & Shevell, 2002). For perfect constancy a₁ – a₂ = i₁ – i₂ and the index is equal to unity. If there is no neural transformation due to the illuminant, a₁ = a₂ and the index is zero. Comparing achromatic points obtained in our steady-state conditions, under prolonged exposure to sunlight and to skylight over the whole scene, the indexes are 0.66, 0.84 and 0.54 for observers KAD, RJL and WS. These values are within the range of values seen in comparable experiments (see Foster, 2011, for a tabulated summary).

Colour constancy following an illuminant switch

Data from the main experiment provide estimates of the achromatic point at specific times after an illuminant switch from sunlight to skylight and from skylight to sunlight. To quantify the time-course of colour constancy, we express the position of these achromatic points relative to the achromatic points in the steady-state conditions. The achromatic point after a switch should approach the steady-state value. At each time-point we express the compensation in appearance relative to the perceptual difference between achromatic points obtained in steady-state conditions for the new and old illuminants. Our constancy index, C(t), represents the migration of the achromatic point in colour space projected on to a vector joining the chromaticities of the steady-state achromatic points.

Our constancy index C(t) is calculated with equation 2:

$$C\left(t\right)=\frac{\left(\mathit{b}\right(t)-{\mathit{a}}_2)\cdot ({\mathit{a}}_2-{\mathit{a}}_1)}{({\mathit{a}}_1-{\mathit{a}}_2)\cdot ({\mathit{a}}_2-{\mathit{a}}_1)}$$ (2)

where b(t) is the chromaticity coordinate vector (L/(L+M), S/(L+M)) of the achromatic point measured under the new illuminant at presentation t, and a₁ and a₂ are the chromaticity coordinate vectors of the achromatic point measured in the steady-state conditions for the current and previous illuminants, respectively.

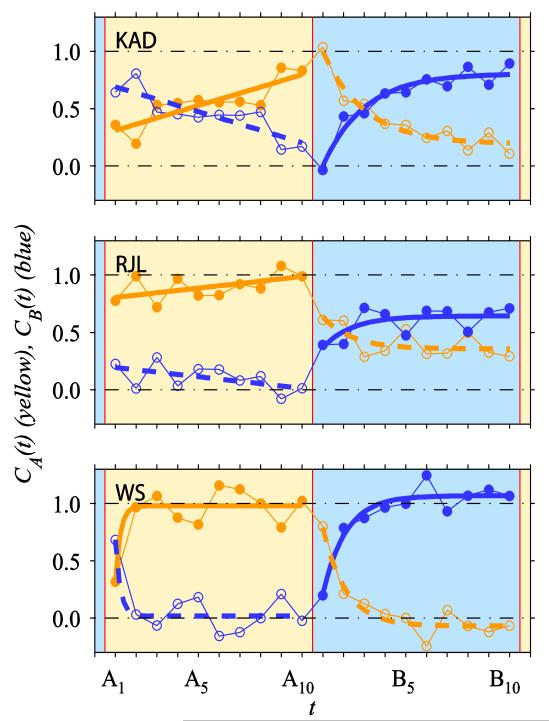
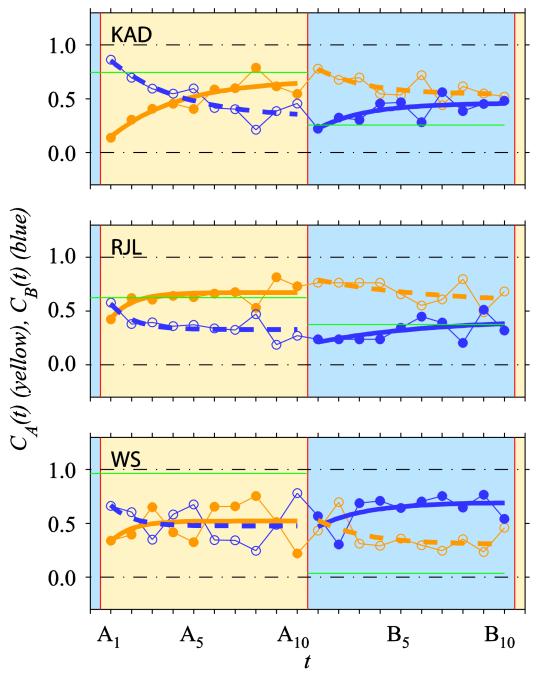
Figure 6 shows how our calculated constancy index C changes with sequential stimulus presentation after changes in illuminant in the global condition. The ordinate represents the constancy index calculated under sunlight (C_A(t), yellow symbols) or skylight (C_B(t), blue symbols). The constancy index relative to skylight is simply one minus the constancy index relative to sunlight, and vice versa (C_B(t) = 1-C_A(t)). Recall that the illuminant switches between sunlight and skylight after every tenth stimulus presentation. This generates 20 unique temporal contexts of illumination: Ten following the switch to sunlight (indicated by the region of the graph with a yellow background) and ten following the switch to skylight (indicated by the region of the graph with a blue background). The plots show one full cycle of illumination change. Data points are derived by collating responses from many transitions from sunlight to skylight and vice versa. Although these plots show the sunlight to skylight transition most clearly, the skylight to sunlight transition is equally important.

Figure 6.

Data from the global condition. Colour constancy index C, calculated along a vector joining the steady-state achromatic points for the two illuminants, plotted against number of trials since an illuminant shift t (2.1s inter-trial interval). The colour of the symbols and lines represents the illuminant chromaticity relative to which the constancy index was calculated: sunlight (yellow) or skylight (blue). Filled symbols indicate the constancy index calculated relative to the illuminant chromaticity used on that trial, and open symbols represent the index calculated relative to the other illuminant, for comparison. The shaded regions of the plot indicate the time-course of the illuminant switch: sunlight (yellow) or skylight (blue). Presentations are labelled such that A_n is the nth trial after a change in simulated illuminant to sunlight, and B_n is the nth trial after a change in simulated illuminant to skylight.

For each stimulus presentation, it is possible to calculate a constancy index relative to the illuminant used in that trial of the experiment, or to the previous illuminant. The two symbols plotted at each presentation, t, show constancy indices relative to the current illuminant (yellow symbols in the yellow region, and blue symbols in the blue region) or relative to the previous illuminant (when symbol and background colour are different). To emphasize these differences filled symbols indicate where the illuminant used to calculate the constancy index corresponds to the illuminant used in that trial of the experiment, and open symbols indicate when the calculation is relative to the previous illuminant. At each time-point, the filled and open symbols are derived from the same set of responses. However, by plotting both C_A(t) and C_B(t) it is possible to see the influence of each illuminant over the full cycle of illumination.

If observers’ achromatic points moved instantaneously between the achromatic points obtained in the steady-state conditions, all filled symbols would plot at 1.0 and all open symbols would plot at 0.0. If observers’ achromatic points were not dependent on the cycle of illumination, the yellow and blue lines would be perfectly horizontal. If one or other illuminant dominated, either the yellow or the blue lines would plot at higher values on the ordinate.

The solid lines fitted to the points with filled symbols show an exponential function:

$$C_{fit}\left(t\right)=-A{e}^{-t∕\tau }+d$$ (3)

with parameters A, τ and d adjusted to obtain a least-squares best-fit to the data. We chose an exponential function because it models a classic leaky integrator mechanism that maintains a running average of chromaticities (Watson, 1986). Helson (1948) has previously suggested that some form of running average is used in setting a perceptual reference against which judgments are made. The migration of the achromatic point in our experiment might be driven by such a perceptual reference accumulated via a leaky integrator. The exponential allows us to fit all the data with a function of the same form. Other mathematical functions did not produce consistently better fits. Further, conveniently, the parameter τ is interpretable as the time constant of integration.

Since the values shown by open symbols are simply one minus the corresponding values shown by filled symbols, we use the function 1-C_fit(t) for the open symbols. Separate functions are fitted to the calculated indices for trials under sunlight and trials under skylight. The best-fitting values of parameters τ and d are given in the Appendix. The design of our experiment does not allow us to separate the effects of time from the effects of number of stimulus presentations, since stimuli are presented at regular time-intervals. The variable t is expressed in multiples of trial-duration. Values of τ quoted in the text and in the Appendix are expressed both in number of trials and in seconds.

These data indicate that after a switch to the new illuminant the constancy index relative to that illuminant increases, at least over the first few presentations. The rate of this increase varies between observers. RJL and WS show constancy indices that appear to reach a plateau before five presentations; KAD’s constancy indices take longer to asymptote. These differences are captured in the best fitting values of τ which are larger for KAD (sunlight: 6×10⁷ trials or 1×10⁸s, skylight: 2 trials or 4s) than for RJL (sunlight: 2×10⁸ trials or 5×10⁸s, skylight: 1 trial or 3s) and WS (sunlight: <1 trial or <1s, skylight: 1 trial or 2s). See Table 2 in Appendix for values for all conditions. The very large fitted values of τ and A seen in the table occur when the fitted function has a very linear, less exponential form.

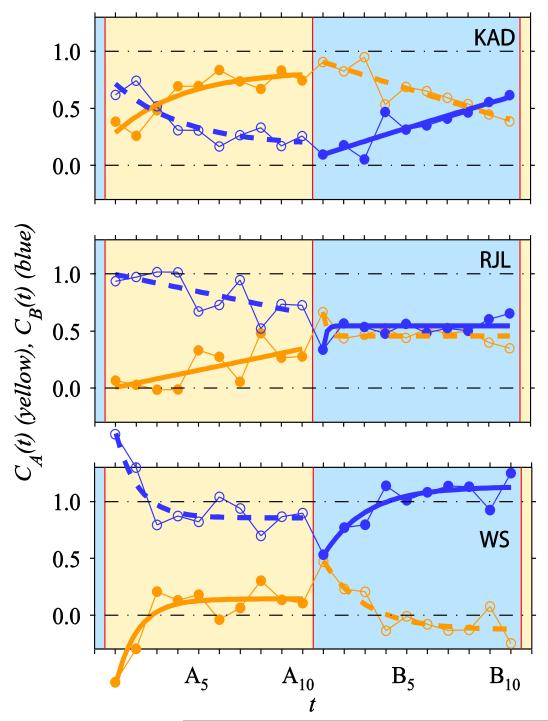
Figure 7 shows constancy indices, calculated in the same way as above, for the isolated condition. The shaded areas now represent the time-course of changes in the simulated illuminant over the test patch, whilst the background was black. Other plotting conventions are the same as before, and a function of the same form is fitted.

Figure 7.

Data from the isolated condition. Colour constancy C index plotted against t, as in Figure 6. The colour of the shaded background now indicates the simulated illuminant over the test patch only.

Again, the constancy index increases over the presentations following an illuminant shift, but this increase appears more gradual and the final constancy index reached at t = A₁₀ and t = B₁₀ is generally lower than in the global condition. For observer KAD, the achromatic point after ten trials in sunlight or ten trials in skylight approaches the corresponding steady-state achromatic points obtained under prolonged exposure to each illuminant. For observers RJL and WS, the constancy indices calculated relative to sunlight (yellow lines) and to skylight (blue lines) each show a dependence on the time-course of the illuminant change (i.e. the yellow line shows a maximum and the blue line shows a minimum over the 20-trial cycle). However, for these observers the achromatic points are displaced relative to the steady-state conditions, with relatively low constancy indices relative to sunlight and relatively high indices relative to skylight.

Figure 8 shows data for the inconsistent condition, plotted as before. The shaded areas again represent the time-course of the changes in the simulated illuminant over the test patch, but in this condition the background was always Illuminant C. These plots indicate a much smaller increase in constancy index following an illuminant switch. Some of the differences between observers that were apparent in the global condition (Figure 6) are repeated in the isolated and inconsistent conditions, specifically the tendency of the curves fitted to observer KAD’s data to show relatively strong dependence on the illuminant and to plateau relatively late, and for RJL’s data to show weaker dependence.

Figure 8.

Data from the inconsistent condition. Colour constancy C index plotted against t, as in Figure 6. The colour of the shaded background indicates the simulated illuminant over the test patch, whilst the illuminant over the background ellipses was Illuminant C. The green horizontal lines show the relative location of the steady-state achromatic point measured under Illuminant C, relative to the steady-state achromatic point measured under either sunlight or skylight as indicated by the shaded background.

In these plots, the level of constancy is expressed relative to the achromatic points obtained in the steady-state conditions with either sunlight or skylight over the whole scene. It is also instructive to consider the data from the inconsistent condition in relation to the achromatic points obtained in the steady-state conditions with Illuminant C over the whole scene (see Figure 5). The green horizontal lines in Figure 8 indicate the expected values of the constancy index C if the observer operated as they did for the steady-state Illuminant C condition. The expected values are calculated by inserting the steady-state achromatic points in place of b_t in Equation 2, relative to the achromatic points obtained either under sunlight (for C_A(t)) or skylight (for C_B(t)). For RJL this value is a good predictor of the asymptotic levels of C(t). For KAD this value predicts the asymptotic levels less well, though it captures the difference in asymptotic levels of C_A(t) and C_B(t) (i.e. C_A(t) > C_B(t)). Data for WS show less dependence of C on the time-course of illumination changes. For this observer, the steady-state achromatic point measured under Illuminant C was very close to that measured under sunlight (see Figure 5), and does not predict his asymptotic performance in the inconsistent condition, which was closer to the setting predicted by the Illuminant C chromaticity.

Statistical analysis

We wished to distinguish between the effects on the colour constancy index that result from the time since an illuminant change, and the effects resulting from other factors, primarily between-observer differences and differences between the three illumination conditions. We used a factorial ANCOVA to determine significant effects on C from the illumination condition (global, isolated or inconsistent), illumination switch direction (skylight to sunlight vs. sunlight to skylight), the observer, the number of presentations t since an illuminant switch (a covariate representing the 10 trials between switches), and interactions of these variables.

As expected, the main effect of t was significant (F_(1,144)=111.1, p<0.001) and we give this as evidence for the colour constancy index being affected by the number of presentations since an illuminant shift. We also see a significant effect of the illumination condition (F_(1,144)=14.5, p<0.001). All illumination conditions share the same time-course of illumination changes on the test region; they differ only in the background illumination properties. The significant difference we find confirms the importance of this spatially extended context. The significant effect of the observer (F_(2,144)=8.6712, p<0.001) confirms the obvious differences between observers seen in the plots. The main effect of the illuminant switch direction is not significant. However, there are some significant interactions of factors. The full results of the ANCOVA are summarised in the Appendix, Table 3. The most relevant is the significant interaction between t and illumination condition (F_(2,144)=4.22, p<0.05) which suggests that the rate at which C changes with t is affected by the illumination condition.

To investigate the effect of t separately for each illumination condition (global, isolated, inconsistent) and illumination transition (skylight to sunlight and sunlight to skylight), we performed six two-way ANCOVAs with t as a covariate and observer as a factor. These statistics are summarised in the Appendix. In all cases, these analyses indicate significant effects of t, and the gradients of linear regression lines fitted to the data, after removal of the between-observer effects (Bland & Altman, 1995), are positive. This is supportive of our prediction of an increase in constancy index with number of presentations. The plots and linear regression gradients indicate more rapid changes in constancy index in the global condition, particularly compared to the inconsistent condition.

The periodic nature of the constancy index

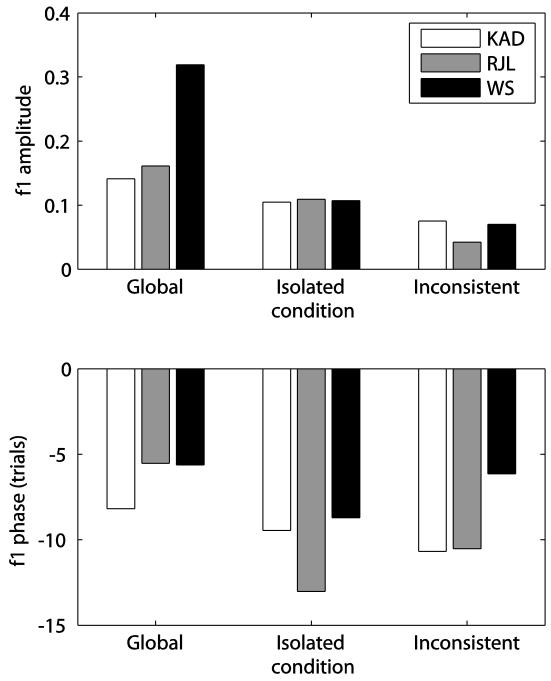
An alternative analysis of the time-dependence of the colour constancy index is to transform the measurements of C(t), over all 20 temporal positions, to the frequency domain using a discrete fast Fourier transform (FFT). We chose to use the values of C relative to sunlight (i.e. C_A(t)) but the values relative to skylight could be used equivalently (although an additional phase-shift of 10 trials would be present, see below). The Fourier coefficients for the separate data from all observers in all conditions indicate that the component with a period of 20 trials – a complete cycle of both test illuminants – has amplitude greater than that of all other frequency components. Hartley’s test was used to compare the variance accounted for by each frequency component with the combined variance of all the others and this ratio was tested against the F-distribution (Thibos, 2003). This procedure confirmed that the first fundamental component was the only one with amplitude significantly different from zero. From this we can conclude that the colour constancy index calculated relative to sunlight, C_A, oscillated periodically with one cycle lasting 20 trials, increasing during 10 trials in which the simulated illuminant over the test patch was sunlight and decreasing during the following trials when the test-patch illuminant was skylight.

The amplitudes of the fundamental components are, in general, largest in the global condition, smaller in the isolated condition and smallest in the inconsistent condition (see Figure 9, top panel). These amplitudes correspond to the change in C over the course of 10 trials. The differences between observers are clear, but nevertheless the data reveal systematic differences between conditions. This reinforces our statement above that the final constancy index achieved in isolated conditions is smaller than in the global condition and smaller still in the inconsistent condition.

Figure 9.

Amplitudes (top panel) and phases (bottom panel) of the first fundamental Fourier components of the measured constancy indices, relative to sunlight, over the course of the 20 possible temporal positions (C_A(t)).

The phases of the fundamental components indicate the lag in the change in C after the illuminant switch. A phase of -10 trials indicates a minimum constancy index in the trial immediately after an illuminant switch and a maximum constancy index on the 11^th trial after a switch. Smaller (less negative) phases are consistent with the value of C reaching its maximum earlier, and a phase of zero locates the peak on the trial immediately after the switch. Because the fundamental component must have a cosinusoidal form and our data indicate that C tends to plateau after reaching its maximum, the values of the phase shifts are indicative of, but do not directly indicate, the number of trials taken for C to reach its maximum. The values are shown in Figure 9 (bottom panel). The measured phases of the first fundamental component are consistent with the constancy index reaching its maximum fastest in the global condition, and slowest in the inconsistent and isolated conditions. Again, individual differences are apparent.

Discussion

The achromatic point is updated only gradually following an abrupt change in illumination

In the global condition, we presented observers with a scene on which the illumination switched between sunlight and skylight. The illuminant transitions were abrupt, and the sequence was described with a square-wave temporal profile. The plots of colour constancy index (C) relative to the time-course of illuminant switching indicate that observers adjusted their achromatic points depending on the illumination. The temporal frequency of adjustments is matched to the illuminant cycle. However, the temporal profile of these adjustments differs from that of changes in illumination, in two respects. Firstly, the adjustment is delayed relative to the illuminant switch, and secondly changes in the achromatic point are gradual rather than abrupt.

For each observer, the calculated colour constancy index increases over the ten trials after a global illuminant change. The evidence for this non-instantaneous adjustment is strongest for observers KAD and WS, while RJL shows weaker effects. The constancy indices are relatively low at t=1, which indicates that constancy was far from perfect during the trials immediately after an illuminant change. Over the subsequent trials, the constancy values tend towards 1.0, which indicates that the achromatic point measured at these successive points moved towards, and almost reached, the point measured in the steady-state condition under prolonged exposure to that illuminant. The time-course of this compensation differs between observers. For RJL and WS, asymptotic constancy is achieved within three to five trials whereas, for KAD, asymptotic constancy is not achieved even within ten trials (a duration of 21 seconds). Since trial duration was fixed in our experiment, we cannot distinguish between processes that depend upon number of samples and those that depend upon exposure time.

The temporal profile of colour constancy indices is not determined solely by the cycle of illumination on the test patch. This cycle was matched across the global, isolated and inconsistent conditions of our experiment. Differences in colour constancy indices between these conditions, and particularly the significant interaction between the effect of condition and number of presentations, indicates that additional spatial cues to the test illuminant produce more rapid adjustments to the achromatic point and higher asymptotic levels of constancy.

Cues to the illuminant change

One possible reason we see a gradual migration of the achromatic point is that the stimulus configuration, even in the global condition, was insufficient to simulate a real illuminant change. Certainly, we used only flat patches, with Lambertian reflectance. Maloney (1999) has described such stimuli as representing a “flat world”, which lacks many cues to the illumination conditions, like the shadows, mutual reflections, and specular highlights that characterise a three-dimensional world of illuminated objects. The rich array of cues to the illuminant contained in real-world stimuli can produce higher constancy (Kraft & Brainard, 1999) and it is possible that such stimuli would produce more immediate compensation to an illuminant switch. However, a survey of published studies has found that similar constancy values are reported for experimental stimuli composed of real objects and those rendered on monitors, as well as for three-dimensional and two-dimensional stimuli (Foster 2011).

Although they are impoverished, the scenes we used in the global condition contained multiple cues to the illuminant transition. Such cues have been thoroughly investigated by Foster and colleagues (e.g. Foster & Nascimento, 1994). Even under transpositions of the spatial location of particular patches, a reliable cue to surface reflectance is available from the ratio of cone excitations between the test surface and a spatial average over the whole scene (Amano & Foster, 2004). In the global condition, this signal was available in each trial, and could in principle be updated immediately following the illuminant change. Our results from the global condition suggest that this information was not used instantaneously to set the observer’s achromatic point.

There has been considerable debate over whether von Kries adaptation (e.g. von Kries, 1902) can account for colour constancy (see Smithson, 2005 for review). Receptor scaling (a diagonal transform) cannot correct perfectly for the changes in cone signals that accompany a change in the spectral content of the light illuminating a set of reflectances (Brill & West, 1986). But, to first approximation, a diagonal transform will correct quite well for the colour conversions encountered with real-world spectra and illuminants (Dannemiller, 1993; Foster & Nascimento, 1994). The coefficients of this transformation could be estimated from a number of scene characteristics (see Smithson, 2005 for discussion). Ives (1912) proposed normalising to the cone-signals elicited by the illuminant but, in scenes like ours where that signal is unavailable, normalising to the mean L-, M- and S-cone signal taken over a number of reflectance samples can provide a good solution, provided the samples are drawn from the same distribution of reflectances under the different illuminants (Golz & MacLeod, 2002). Importantly for the interpretation of the present results, this mean could be taken over successively or simultaneously presented samples.

The three conditions of our experiment differed in the spatially distributed cues to the illuminant that they offered. In the inconsistent condition, the spatial average of the scene was almost constant for the entire experiment, since it was determined primarily by the chromaticity of Illuminant C that was used for the background. If observers’ achromatic settings were determined wholly by the spatial mean in each trial, the inconsistent condition would show no temporal dependence of the colour constancy index. However, for both directions of illuminant change, our results show that the constancy index depends on number of presentations following the switch (see Table 1 in Appendix for significant main effects of t for all tests). The rate of improvement as a function of presentation number was lower for the inconsistent condition than for the isolated and global conditions (see significant interaction between t and condition above, and Table 1 in Appendix for β estimates for each test).

For the inconsistent condition, a spatial average over the whole scene is predicted to be relatively stable from trial-to-trial and to be a good predictor of the illuminant chromaticity. A similarly stable anchor, which also co-varies with illuminant chromaticity, is a spatially-averaged measure of chromatic contrast along the border between the central test patch and the several abutting background ellipses. Hansen et al. (2007) have argued that observers use this cue, but here we see that the availability of this cue is insufficient to promote immediate updating of observers’ judgements following the illuminant change.

In the isolated condition, the spatial average from a single trial confounded sample reflectance and the spectral content of the illumination. The range of chromaticities produced by the population of surfaces under the two illuminants provided some constraint on the likely illumination on a single sample (Finlayson, Hordley, & Hubel, 2001). For example, lights with the highest S-cone signals were much more likely to be produced under skylight than under sunlight. However, this is a relatively unreliable cue because chromatic distributions produced by the set of surfaces rendered under the two illuminants overlap substantially. The data from the isolated condition therefore also point to the importance of the history of preceding test chromaticities.

The three experimental conditions were matched in terms of the statistical properties of the stream of test chromaticities (i.e. samples were chosen at random from the population of reflectances and rendered under a temporal cycle of illumination that switched between sunlight and skylight). In all conditions, a possible cue to the test-illuminant could be derived from a running-average of the test chromaticities (see also Morgan et al. (2000) for discussion of similar temporal averaging to derive a standard against which to make line-separation judgements). Under a single, steady illuminant, the reliability of this cue improves with an increase in the number of samples contributing to the average. A mechanism with too fast a time-course would not integrate information from sufficient samples, and would also render changes in illumination unnoticeable. We used a computer simulation to repeatedly calculate an average of samples drawn at random from the set of stimuli used in this experiment, with an exponentially-weighted integration window and an adjustable time-constant parameter. Based on the variability of these averages, we estimate that the time-constant that produces reference signals that are reliably different under the two illuminants is one that corresponds to five to seven samples.

However, inclusion of samples that are obtained under a different illuminant will contaminate this estimate. In an environment in which the illuminant changes over time, the likelihood of such contamination is higher the longer the time-constant of the mechanism that maintains the running-average. In the present experiment, the best opportunity for an accurate estimate from the test region is available in the tenth trial after an illuminant switch, and the worst opportunity comes immediately following the illuminant switch. The accuracy of the estimate following transition to a new illuminant will asymptote after the number of trials that contribute to the estimate. Again, we used a computer simulation to obtain estimates of the average chromaticity as a function of time following an abrupt illuminant change. To obtain an estimate of the illuminant that changes with a time-course that approximates the one we measure for the migration of the achromatic point in the global condition required an exponentially weighted integration window with a time constant corresponding to three samples (6300ms).

Differences between the time-constants of the fitted exponential functions for different observers may reflect differences in the number of trials over which they compute an average, or differences in other factors that influence temporal adaptation (see discussion of eye-movements below). Using as a perceptual reference a temporal average of the test chromaticities alone cannot explain differences between conditions, since conditions are matched in this regard.

The three conditions of our experiment show the relative influence of spatially and temporally distributed cues to the illuminant. Observers are neither wholly dependent on spatial nor on temporal cues.

Mechanisms that modify colour appearance

Colour appearance can be heavily modified by chromatic adaptation, through both subtractive and multiplicative processes (see Lennie & D’Zmura, 1988; Pokorny & Smith, 2004, for review). Adjustments to the visual response are made at multiple levels in the visual system – within the photoreceptors themselves and in post-receptoral pathways (e.g. Walraven, Enroth-Cugell, Hood, MacLeod, & Schnapf, 1990), and at higher, cortical levels (e.g. Solomon & Lennie, 2005). The spatial and temporal parameters of the signals that drive adaptation are also varied, operating over timescales ranging from milliseconds (e.g. Crawford, 1947) to several minutes (Jameson, et al., 1979), hours and days (e.g. Delahunt, Webster, Ma, & Werner, 2004) and over spatial scales from local (He & MacLeod, 1998; MacLeod & He, 1993) to remote (e.g. Valberg, Lee, Tigwell, & Creutzfeldt, 1985). In the following paragraphs we discuss the relationship between these mechanisms and the spatial and temporal effects we measure.

Temporal and spatial signatures

Rinner and Gegenfurtner (2000) measured changes in colour appearance (achromatic matching) produced by step-changes in the chromaticity of a large background field. Three processes operated over distinct temporal scales: A slow exponential process with a half-life of about 20s (see also Fairchild & Reniff, 1995); a faster process with a half-life of 40 to 70 ms (which Rinner and Gegenfurtner link to photoreceptor adaptation, see also Stockman, Langendorfer, Smithson, & Sharpe, (2006)) and an extremely rapid process with a half-life of less than 10 ms. The slower processes were apparent in both appearance and discrimination measurements, whereas the most rapid process was apparent only from appearance data, where it accounted for approximately 60% of the difference observed in steady-state settings. Rinner and Gegenfurtner argue that the rapid phase depends on spatial interactions, instantaneously available in the stimulus. Since the rapid phase is not apparent in the discrimination data, they suggest that it is determined by mechanisms that operate at a late cortical stage, after V1.

Highlighting the importance of instantaneous spatial contrast in setting colour appearance is consistent with the strong shifts in lightness, brightness and colour appearance that are common in demonstrations of simultaneous contrast. Shapiro (2008) provides striking demonstrations that in temporally modulated displays perception can be dominated by the instantaneous contrast signal at the boundary between a central stimulus and its surround, rather than by the magnitude of the central stimulus.

However, the data we present here show relatively little contribution of the immediate spatial surround: In the global condition, the abrupt change in the chromatic bias of the surround that accompanies the illuminant switch is not accompanied by a rapid updating of appearance; and in the inconsistent condition the stable background statistics do not prevent migration of the achromatic point. With our stimulus parameters, appearance is influenced by the absolute chromaticity of the test patch, and by the history of preceding chromaticities, and not only by the contrast between those patches and the background.

Importantly, the background field used by Rinner and Gegenfurtner was uniform, whereas the background used in the present study was a pattern of simulated reflectance samples. The difference in the relative contributions of simultaneous contrast in these two studies is consistent with Zaidi et al.’s (1997) observation that simultaneous contrast effects are reduced with variegated (compared to uniform) surrounds. The importance of surround complexity, both in terms of chromatic and luminance contrast, is also highlighted by Werner et al. (Werner, Sharpe, & Zrenner, 2000), who find different patterns of results with uniform versus complex surrounds. The spatial filters that determine how local and remote regions contribute to colour appearance are likely to be complex (e.g. Monnier & Shevell, 2003) and differences in stimulus complexity should not be overlooked when comparing studies.

The contribution of eye-movements

Observers in our study were not explicitly instructed to fixate the test patch. However, the demands of the task required attention to be directed towards the test patch for a large proportion of the trial-period. For sinusoidal variations in adapting chromaticity, at frequencies of 0.5 Hz or higher, the response to moderate contrasts is well predicted by the response to the mean, which suggests that the effective integration time for chromatic adaptation is on the order of several seconds (Webster & Wilson, 2000). The trial duration in our experiment was 2.1 seconds, so such a process would maintain a running-average of the test patches presented over the last few trials. Since test patches were selected at random, such averaging provides a reasonable estimate of the mean of the chromaticity distribution, which in turn provides an estimate of the illuminant chromaticity (see previous section).

In addition to considering how successive test samples might set the adaptation state, we should also consider the way in which eye-movements across the scene might introduce successive sampling of other chromaticities. Retinal adaptation mechanisms have been shown to be highly localised (He & MacLeod, 1998; MacLeod & He, 1993) but extended in time. Since eye-movements can convert static spatial variation in a scene to temporal variation at each point on the retina, a retinal adaptation mechanism might, in the presence of eye-movements, become dependent on the statistics of an extended spatial area (D’Zmura & Lennie, 1986).

It is unlikely that observers in our experiments maintained fixation on the test patch for the full duration of an experimental session (~40 minutes). So we might consider the different effects of this in our three experimental conditions. For the global condition, the spatial surround provided samples with the same chromatic statistics as the test patch, so the predicted effect of eye-movements on adaptation state depends primarily on the relative time-course of test presentations and sampling of other chromatic patches via eye-movements. It is possible that multiple fixations across the variegated surround during a trial might have improved the reliability of the illuminant estimate since a greater number of samples would be included. Eye-movements in this case are predicted to reduce the number of trials required before the achromatic point is appropriate for the new illuminant. For the isolated condition, eye-movements across the dark surround could not bias the state of adaptation towards either illuminant and would have shifted relative photoreceptor adaptation levels towards a neutral state, probably between that set by the chromaticity of sunlight and that of skylight. Eye movements in this condition are therefore predicted to slow the migration of the achromatic point and potentially to limit the asymptotic levels of constancy achieved. For the inconsistent condition, eye-movements might have contaminated the temporal average to include samples drawn from a conflicting illuminant distribution. Since the chromaticity of Illuminant C, which was used for the surround in this condition, lies between the chromaticites of sunlight and skylight, such contamination result in similar predictions to those made for the isolated condition.

With the data reported here, it is not possible to separate the effects that arise from spatial interactions in visual processing from those that may have been introduced by any eye-movements our observers made. Investigating the interaction between eye-movements and the spatial and temporal distribution of adapting elements is the focus of a separate study (Lee & Smithson, under review). Golz (2010) has already shown that viewing behaviour influences achromatic settings. The differences between observers in the data from the present experiment may in part be due to different proportions of time spent fixating the test patch and regions of the surround. It is also the case that there are substantial individual differences in the completeness of adaptation to a chromatically biased uniform field (Fairchild, 1991; Webster & Wilson, 2000). Incomplete adaptation would cause the neutral point to shift only partway towards each adapting chromaticity, and such a compression of the chromatic differences between stimuli in the way in which they contribute to the perceptual reference would slow the updating of the achromatic point.

Colour appearance away from the achromatic point

We analyse our data only for adjustments to the achromatic point, which has been taken to indicate the stimulus for which the visual response is normalised (Walraven & Werner, 1991). Adjustments to relative cone sensitivities, and adjustments at post-receptoral (opponent) sites are expected to shift the achromatic point. Our data allow estimation of the full colour boundaries between red and green and between yellow and blue, though the reliability with which we can estimate boundaries deteriorates towards the extremes of our gamut. The boundaries we derive at successive time-points after an illuminant-switch differ only slightly in shape. In fact, the boundaries for any one temporal position can be fitted to the data from other temporal positions by only adjusting scale factors on the contributions from the cone excitations, without large increases in the sum-squared predictive error. This is consistent with the chromatic adjustment after an illuminant change being a result of von Kries-type adaptation. Our data however do not provide a strong test of this model.

Our analysis does not test for changes in chromatic sensitivity – the ability to discriminate neighbouring chromaticities – that might accompany adaptation. Although our classification data effectively provide 3-dimensional psychometric functions from which we extract the point of subjective equivalence, we have insufficient data to reliably extract the slopes of these functions, so we do not test for compressions or expansions of perceptual space.

The preceding discussion has emphasized adaptation to the mean of the stimulus set. Colour appearance is additionally influenced by adaptation to chromatic contrast (Webster & Mollon, 1994). Contrast adaptation reduces perceived contrast. Our stimulus set comprised a constant set of reflectances. However, the transition between illuminants changes the variance of the chromaticity distribution, particularly in the S-opponent direction (see Figure 3). To the extent to which a diagonal transform of cone signals compensates for an illuminant change, von Kries-type normalisation to the mean, implemented at an early stage of processing, would present constant variance signals to later stages. Incomplete adaptation at an early stage would allow differences in chromatic variances to propagate. Differences in contrast adaptation might then additionally distort perceptual space and influence the migration of the achromatic point through it.

Under conditions in which chromatic adaptation adjusts only partially to the colour of the stimulus, leaving a residual bias in the colour appearance of the field, Webster and Wilson (2000) show that contrast adaptation reduces contrast relative to the residual colour (rather than relative to the achromatic point) and that the enhancement of contrast discrimination is similarly centred on the residual colour. This implies a dissociation between two perceptual referents, one identified by the achromatic point and the other identified by the residual perceptual bias in the colour appearance of the field. The concept of multiple adjustments, in different visual pathways, and at different levels of processing, is important in understanding colour appearance. This echoes the dissociation we find between slow updating of the achromatic point following an abrupt illuminant change and the instantaneous detection of aberrant cone-ratios during such a change, which we discuss next.

Comparison with other studies that have used similar simulated illuminant changes

As discussed above, there have not been a great many studies of the time-course of colour constancy. However, Foster et al. (2001) show that, for a Mondrian scene, a change in the simulated reflectance of one test patch is noticeable and causes the test patch to ‘pop-out’ even when the change is coincident with a global change in the illumination. This might suggest that the change in illumination is accounted for instantaneously, providing access to a residual signal that corresponds to the change in reflectance. Barbur and colleagues also find high levels of constancy under instantaneous changes in illumination with a 1.25 Hz squarewave time-course (Barbur, et al., 2004).

The “illuminant change” described by Foster and colleagues and by Barbur and colleagues is very similar to the one we used here: a simulated illuminant falling on a variegated array of patches of simulated Lambertian reflectance. In most of their experiments, the spatial arrangement of the surrounding patches remained unchanged during the illuminant switch. In our experiment, the spatial parameters of the ellipses, and the reflectances assigned to them, were chosen afresh in each trial. Although this disturbed the local changes in cone-ratios associated with the illuminant change, the ratio of cone excitations between the test surface and a spatial average over the whole scene still provideed a reliable cue to test reflectance, as identified by Amano and Foster (2004).

To account for the difference between our results and theirs, we might appeal to differences in the tasks used. In the studies that imply that observers account instantaneously for a change in illumination, observers’ performance could be explained by a process that detects a change in cone-ratios that is inconsistent with the prevailing change in cone-ratios. Sensitivity to such a signal is clearly related to the phenomenon of colour constancy – the ability to disentangle a change in illumination from a change in surface reflectance. But, it does not test colour constancy explicitly – the stability of the colour appearance of an object under a change in illumination conditions. The limitations of tests of “colour constancy” have been discussed by Foster (2003).

In our task, observers were asked to classify the colour appearance of the test patch. They were not asked to identify whether the patch had undergone a reflectance change that accompanied the illuminant change. Nor were they asked directly about the illuminant change. They may have been sensitive to both these features, and have been able to extract them instantaneously, but this was not what we tested.

Response bias in successive judgements

Our requirement that the observers made a series of successive judgements means that we must consider the effects of response bias. The condition with “isolated” test patches is closely related to work by Helson and others (e.g. Helson, 1948). The re-centring on the mean of the set that we observe in this condition is captured by Helson’s level-of-reference theory, which postulates that observers maintain an internal standard against which judgements are made, and that this internal standard is simply a running average (e.g. weighted geometric mean, Helson, 1938, 1947, 1964) of preceding stimuli to which the observer has been exposed. It is likely that this re-centring on the mean plays a role in all conditions. While it is difficult to disentangle perceptual and cognitive (or distal and central) components of this process, it is likely that both components play a part. It is known that observers are unwilling to continually produce one of two responses (e.g. redder) and that they will aim to distribute their responses evenly between the options available to them (e.g. Poulton, 1979). It is also true that low-level mechanisms of chromatic adaptation with long-time constants would normalise to the temporal mean of the set, which is a good predictor of the illuminant chromaticity.

In the isolated condition, observers were presented with ten samples from one set of chromaticities, followed by ten samples from a second set, and followed by another ten samples from the first set, etc. This condition therefore allows us to test for purely temporal processes of normalisation to the chromatic properties of the sets. The data from this condition show significant temporal dependence of the colour constancy index, indicating that observers did adjust their classifications to the change in chromatic distribution. Differences between conditions (see interaction between t and condition, above) indicate that these adjustments are not the only active mechanism.

It is interesting to ask whether a slow-acting response bias that accumulates over several trials could mask instantaneous compensation for the illuminant change. If we assume perfect colour constancy for the stimuli used in this experiment, then the reflectance functions of the simulated materials would be sufficient to describe perceptual differences between them. We are in effect asking our observers to judge a constant set of stimuli, that is, the unchanging set of reflectance functions. Under the assumption of perfect constancy, a change in response bias (i.e. a re-centring on the mean of the set) should have no dependence on time: We should expect to see no change in the achromatic point expressed relative to the reflectance functions (i.e. surfaces should receive the same colour classification whatever the illuminant). However, when the illuminant changes we should see an instantaneous change in the achromatic point expressed relative to the test chromaticities. This is not what we observe in our data, so perfect instantaneous constancy is clearly not an accurate account of observers’ performance, even in the global condition.

The assumption of perfect colour constancy for our stimuli is known to be incorrect from the steady-state conditions. The achromatic point falls at a location determined in part by the set of reflectances and in part by the illuminant chromaticity (see Brainard, Brunt and Speigle (1997) for discussion of this equivalent illuminant model, and Figure 4). Under a more relaxed assumption that constancy is instantaneous but incomplete, we can again make predictions about performance in the global condition of our experiment. The illuminant change should cause an immediate shift in the location of the achromatic point, causing it to switch abruptly between the two illuminant-biased achromatic points measured in the steady-state conditions under prolonged exposure to a single illuminant. If response bias, or another process of normalisation to the central tendency of the set of stimuli, played a part in this process, we would have to assume that it acted to track the difference between a set of reflectances that were contaminated with a residual component from the illuminant preceding a switch, and a set of reflectances that were contaminated with a residual component from the illuminant following a switch. The difference between the sets to be judged could blur the transition from one set to another. However, the difference in perceived chromaticities under prolonged exposure to a single illuminant is generally small (see Figure 5), and represents only a small fraction of the variance of the distribution of chromaticities. So instantaneous but imperfect constancy might produce a rapid change in achromatic point (accounting for most of the difference between illuminants), followed by smaller and more gradual changes due to response bias, or similar normalisation. There is no evidence that the change in achromatic point that accompanies a global illuminant change is greater than the change in achromatic point between any pair of successive trials within a single illuminant.

It is important to distinguish between distal and central adjustments to colour appearance. If we assume that the signal reaching central stages passes through distal mechanisms, the gradual changes we observe in the global condition suggest that there is no instantaneous distal compensation for an illuminant change that feeds colour appearance mechanisms.

Summary.

We measured changes in observers’ achromatic points following an abrupt change in illumination. In simulated Mondrian scenes, a global change of illumination produced changes in our observers’ achromatic points that were gradual and delayed relative to the illuminant change. In conditions in which the background was replaced by a black field, and only a single test patch was visible at once, updating of observers’ achromatic points was further delayed and less complete than in the global condition. This condition revealed the limits of a mechanism that is based solely on temporal collation of the test patches. In conditions in which the background was steadily illuminated, observers’ achromatic points still did not remain stable. The history of chromatic samples exerts a persistent influence on the observers’ achromatic points, even when the background is available as a stable reference. A relatively local adaptation mechanism with a time-constant of around six seconds, in combination with eye-movements across the field, can account for the pattern of results we see. A purely spatial mechanism cannot account for our results, though our experiment does not rule out the possibility of contributions from mechanisms that act instantaneously on spatially distributed information.

Figure 2.

Features of the sequences of trials in the three experimental conditions. The background colour wash and test illuminant letter indicates the simulated illumination on the test patch: sunlight (A) or skylight (B). The number with each illuminant letter indicates the number of trials since the test patch illumination changed, which happened every 10^th trial. The three conditions are matched in the sequence of illumination on the test patch, but differ in the illumination of the background region. This was (i) the same as the test patch in the global condition, (ii) black in the isolated condition, and (iii) Illuminant C in the inconsistent condition. The stimulus examples in this figure have been cropped so that the test patch is clear.

Appendix

Table 1. Relevant ANCOVA statistics for separate analyses carried out on constancy index data for each condition and illuminant switch direction.

Condition	Test patch illuminant switch	ANCOVA F for main effect of t	ANCOVA F for main effect of observer	Linear regression gradient for C(t) independent of observer
Global	Skylight → Sunlight	F(1,26) = 13.0060 p<0.01	F(1,26) = 16.4049 p<0.01	β = 0.0364
	Sunlight → Skylight	F(1,26) = 26.9403 p<0.01	F(1,26) = 12.2622 p<0.01	β = 0.0565
Isolated	Skylight → Sunlight	F(1,26) = 22.5122 p<0.01	F(1,26) = 39.4218 p<0.01	β = 0.0485
	Sunlight → Skylight	F(1,26) = 33.5246 p<0.01	F(1,26) = 75.0807 p<0.01	β = 0.0435
Inconsistent	Skylight → Sunlight	F(1,26) = 9.5211 p<0.01	F(1,26) = 3.5799 p<0.05	β = 0.0274
	Sunlight → Skylight	F(1,26) = 9.2977 p<0.01	F(1,26) = 25.7660 p<0.01	βt = 0.0199

Table 2. Parameters for Equation 3 fitted to constancy index C as a function of t. We report sufficient decimal places to reproduce the curves as shown in Figure 6, Figure 7 and Figure 8.

Obs	Test patch illuminant	Global				Isolated				Inconsistent
		d	τ (trials)	τ (time)	A	d	τ (trials)	τ (time)	A	d	τ (trials)	τ (time)	A
KAD	Sunlight	3.0×106	5.5×107	1.2×108	3.0×106	0.8	3.3	6.9	0.7	0.7	3.3	7.0	0.7
	Skylight	0.8	2.0	4.2	1.3	5.3	88.0	184.9	5.2	0.5	2.4	5.0	0.4
RJL	Sunlight	4.4×106	2.2×108	4.6×108	4.4×106	2.3×104	6.0×105	1.3×106	0.0	0.7	1.1	2.2	0.6
	Skylight	0.6	1.4	3.0	0.6	0.5	0.1	0.3	361.8	0.4	5.6	11.7	0.3
WS	Sunlight	1.0	0.2	0.5	46.3	0.1	1.1	2.2	2.0	0.5	1.0	2.1	0.5
	Skylight	1.1	1.1	2.3	2.1	1.1	2.0	4.2	1.0	0.7	2.3	4.9	0.3

Table 3. Factorial analysis of covariance of complete dataset of calculated constancy indices.

	SS	df	MS	F	p
t	2.225	1	2.225	111.078	1.32×10−19
subject	0.347	2	0.174	8.671	2.78×10−4
switch	0.018	1	0.018	0.890	0.347
condition	0.579	2	0.290	14.456	1.90×10−6
t × subject	0.201	2	0.100	5.008	0.008
t × switch	0.002	1	0.002	0.120	0.730
t × condition	0.169	2	0.085	4.220	0.017
subject × switch	0.303	2	0.151	7.554	7.59×10−4
subject × condition	0.269	4	0.067	3.359	0.0116
switch × condition	0.546	2	0.273	13.639	3.76×10−16
t × subject × switch	0.028	2	0.014	0.690	0.503
t × subject × condition	0.091	4	0.023	1.139	0.341
t × switch × condition	0.058	2	0.029	1.444	0.239
subject × switch × condition	0.704	4	0.176	8.785	2.25×10−6
t × subject × switch × condition	0.032	4	0.008	0.397	0.810
Error	2.884	144	0.020
Total	17.197	179