The Role of Fluid Dynamics and Inflammation in Intracranial Aneurysm Formation

Abstract

The emergence of inflammation as a key mediator of aneurysmogenesis provides new opportunities to understand the processes underlying development of intracranial aneurysms (IA). Inflammation unifies the triptych influences of alterations in local flow, mechanical properties of the wall and biochemical mediators and opens new avenues for building robust predictive tools. This review discusses the impact of the inflammatory cascade during the formation of intracranial aneurysms, and its associated morphological, structural and mechanical changes especially in the setting of flow-induced endothelial dysfunction.

Overview of the disease

Intracranial aneurysms are dynamic but silent and as such their true prevalence is not known and the first manifestation may be catastrophic. Mortality and morbidity are high: aneurysm rupture is sudden, and devastating in its side effects. Subarachnoid hemorrhage (SAH) is a common consequence of IA rupture, which occurs in ~1/10,000¹ in the general population, translates into ~30,000 new cases yearly, in the United States alone. Twelve percent of these patients die before medical attention, 40% of hospitalized patients die within a month and more than one-third of survivors are left with permanent neurological deficits². Yet, aneurysm initiation, propagation and rupture remain poorly defined, hindering optimal treatment.

Three options are available for management of unruptured IA: monitored follow-up, surgical clipping or endovascular occlusion. Observation and monitoring assumes that there is a premonitory sign or critical dimensional threshold for destabilization and that there is adequate time for warning before catastrophic failure – yet, neither may be true. The first clinical evidence of IA destabilization may be complete rupture and it is not clear if size alone or rate of dimensional change are determinant. Correlation of static anatomic images and clinical presentation with past experience is challenging and ambiguous. At the same time surgical and endovascular interventions are not without significant complications. The International Study of Unruptured Intracranial Aneurysms³ (ISUIA) recommends interventions when IA exceed 7 mm in diameter but sequential images are rarely obtained because of the burden imposed on the patient and/or the lax enforcement of periodic follow-ups. There is therefore little mechanistic insight to predict IA fate from first principles such as change in arterial dimensions, flow characteristics etc., and a limited experiential data set for comparison. Clinical decisions are often made in the face of sparse data and comparison to incompletely applicable predicate lesions or clinical conditions, and treatment choices force a tradeoff between procedural risks and the probability of SAH. It is imperative to understand the origin and physiology of IA and in particular the emerging role of inflammation and interaction with mechanical and flow forces.

Mechanical and flow properties of intracranial aneurysms

Current understanding of IA natural history, including growth and rupture, and to a lesser extent initiation, consider vascular wall mechanical properties key. Growth is considered to result from a combination of cell proliferation and wall distension whereas rupture occurs when blood pressure-induced tension exceeds aneurysmal wall strength, a consequence of wall degeneration. In addition, quantitative values of mechanical properties are required for computational fluid dynamics (CFD) simulations.

Aneurysm lifespan can be divided into three separate stages: initiation, growth and rupture. In each of these stages, blood flow plays an important role through the conversion of mechanical stimuli into biological signaling^{4, 5}. The focal nature of lesions, preferentially located at bifurcations or sharp curves⁶ supports the role of hemodynamics in IA biology. Flow is a central process in many of the components of aneurysm formation. Flow determines where inflammatory cells will adhere and how the endothelium and its endothelial cells will respond to local inflammation^7–9. The endothelium is the primary interfacial surface with flowing blood and the endothelial cells are premier sensors of shear from above and strain from below¹⁰. An intact endothelium and “normal” near-parabolic laminar flow insures vascular homeostasis through the controlled secretion of an array of anti-thrombotic and anti-inflammatory factors. Yet, this fragile equilibrium can be thrown off-balance by external stimuli that alter flow and damage the vessel wall. The preponderance of IA at bifurcations and segments with large curvature correlates with disturbed flow patterns characterized by large swings in shear stress. The focal nature of IA manifestation supports the role of flow as the driving force of inflammation. When applied to vascular aneurysms, we surmise that aneurysm-protective flows and wall states maintain vascular homeostasis throughout the cerebral tree despite the large number of circulating inflammatory cells, while aneurysm-prone waveforms are responsible for remodeling and inflammation. The initiation of IA is a complex interaction of mechanics, fluid dynamics and biology. Alterations in shear stress may be required but are not sufficient to explain the pathogenesis of IA. Instead, we regard anatomically-driven flow disturbances in the cerebral vasculature as a trigger that acts on the substrate of genetic heterogeneity and superimposes on other environmental cues to affect the kinetics of the progression of the disease.

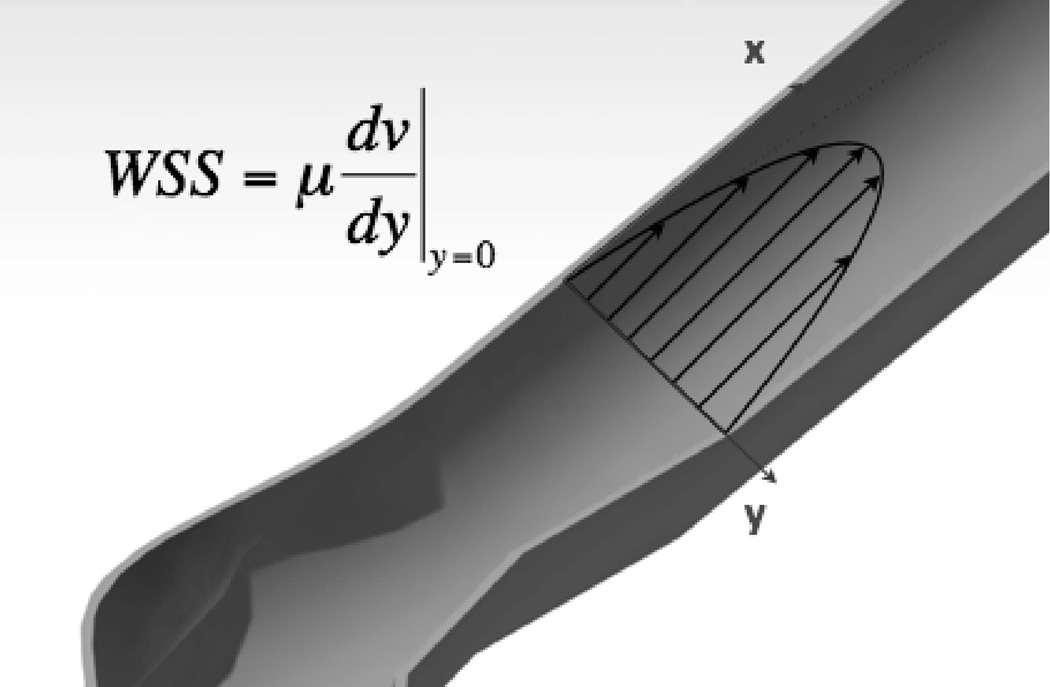
Blood applies pressure and wall shear stress on the lumen (Figure 1), however peak pressure alone is not enough to explain the initiation of intracranial aneurysms. The extra pressure applied to an IA from jet impingement is only ~1 mmHg, 1–2% of the peak pressure¹¹. In this review, we will not discuss the biological implications of pressure changes in IA formation. Other physical properties of the flow, such as wall shear stress (WSS) or the gradient of WSS must play a role, similar to other cardiovascular diseases e.g. intimal hyperplasia¹². Cells of the vascular endothelium respond to flow^{13, 14} converting mechanical stimuli into biological processes. Thus, measuring or estimating the physical properties of the cerebral flow is critical to the study of IA. Yet, the researcher’s toolbox is limited vis-à-vis in vivo measurements of flow. Phase-contrast magnetic resonance imaging (PC-MRI) allows for the measurement of velocity fields, but its spatial and temporal resolution are too low to practically compute WSS¹⁵. Computational fluid dynamics can augment imaging and physiologic data to provide a convenient way to quantify patient-specific flow parameters. The combination of sequential imaging and blood flow simulation can be used to track regions of growth. Over the years, CFD methods have gained in precision and power, enabling the progression from 2D idealized geometries¹⁶ to 3D patient-specific problems with non-rigid walls¹⁷.

Figure 1.

Flow and wall shear stress.

Flowing blood applies two types of stress on the vascular bed: pressure, which acts normal to the lumen and can affect the physiology of the endothelium and the tension of the smooth muscle cells (SMC), and wall shear stress or endothelial shear stress. Wall shear stress corresponds to the force per unit area applied by the blood in a direction tangential to the wall; it is also defined as the product of viscosity, the friction between layers of the flow with different velocities, and shear rate. In general and when parabolic flow dominates blood flow can be considered as a series of parallel flow lines whose velocity is maximal at the centerline and zero at the walls. The change in velocity follows inversely, maximum at the walls and zero at the centerline. Shear rate describes the rate by which the velocity changes as a distance from the wall. Wall shear stress and rate computed from the derivation of velocities throughout the fluid domain are particularly interesting in the study of vascular diseases as ECs respond to variations in WSS, eliciting different phenotypes and biological processes.

Computational fluid dynamics

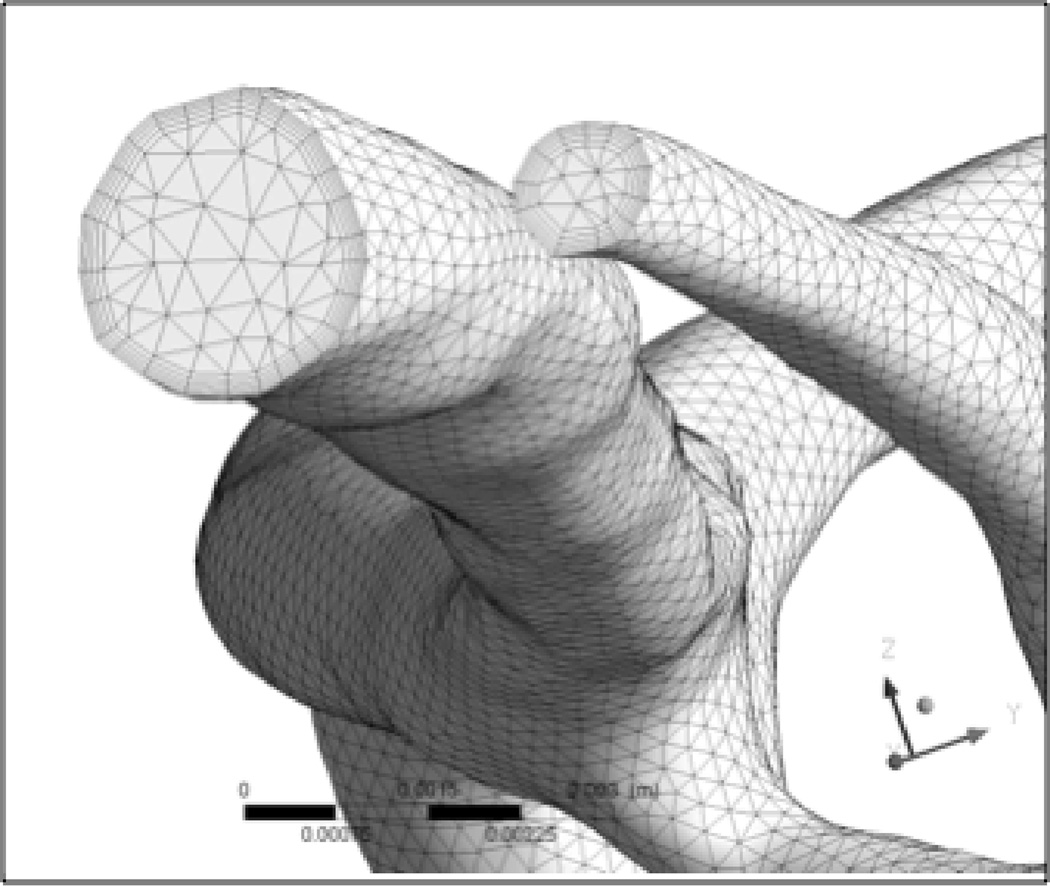
Computational fluid dynamics emerged in the 1930s as a branch of fluid mechanics to solve problems too complex for analytical solutions. CFD is based on the strategic partition of a fluid domain into small elements, usually tetrahedrons or hexahedrons. The equations that define fluid mechanics in each element provide neighboring elements with boundary conditions for their equations of state and when coupled, provide an integrated view of the fluid dynamics of the system. The quality of the results depend on many parameters including the partitioning strategy and number of elements used to divide the fluid domain (the mesh, Figure 2), the original boundary conditions, the algorithm used to solve the equations and the time steps between each calculation, in the case of a time-dependent simulation. As discussed in detail later in this section, the geometry of the vasculature, the fluid boundary conditions, the constitutive laws describing the vessel rigidity and blood, collectively determine the degree of precision of the solution and extra care should be taken to generate a solution that matches the level of understanding of the biological phenomenon studied.

Figure 2.

Example of mesh generated for a computational fluid dynamics analysis in a rigid-boundary IA model. The size of the meshing elements, arrangement and topology condition the precision of the solution and the convergence and speed of the solving algorithm. Here we use tetrahedrons at the center of the lumen and smaller hexahedrons at the periphery to account for smaller variations near the fluid boundary layer.

Modeling of intracranial aneurysm blood flow has helped confirm and explain the role of hemodynamics in the pathogenesis of IA – though much needs to be done. Knowledge of the mechanical properties of IA is needed to circumvent the use of rigid boundaries in classical simulations, yet little of the relevant data are available. To date, no method can reliably measure the mechanical properties of the aneurysmal wall in vivo. Grasping the mechanical properties of cerebrovascular lesions ex vivo is equally challenging because of the imperative to manipulate small, highly anisotropic¹⁸, and fresh human tissue samples of limited availability - preservation with fixation for later analysis is not an option as tissue mechanical properties are modified in the processing. Furthermore, though a map of sample thickness is necessary to translate a force into a stress, there is no valid method to map thickness in vivo, which varies in space – ranging from 16 to 500 microns in the unloaded state^{19, 20} – and time during the progression of the disease.

Few published studies have reported the mechanical properties of IA^{18, 21–23}; those that do have generally reported on uniaxial or biaxial tension tests to measure the critical stress of the tissue. MacDonald et al. did measure the behavior of every sheet of collagen in IA to infer global values. They adapted work relating the birefringence of collagen to the mechanical properties of the fabric²⁴ and reported significant anisotropy. However, the relationship linking critical stress to birefringence was obtained from experiments on scar tissue, which is probably not accurate for aneurysms; moreover the tissue specimens were obtained from autopsy (Table 1). Mixing of tissue source – fresh and post-mortem – and preservation post-resection reduces the accuracy of the study as tissue quickly loses its mechanical integrity²⁵. In comparison, Monson et al.²⁶ investigated the mechanical properties of healthy cerebral arteries under both static and dynamic uniaxial loading and reported a critical stress of 3.68 MPa. Despite variable results, the tear stress of the aneurysmal wall is reportedly lower than healthy arteries, matching intuition. The fundus is weaker than the neck²⁷ possibly because of the preponderance of immature collagen²⁸. Yet, extensive experimental characterization of the mechanical behavior of a large cohort of intracranial aneurysms remains to be done.

Table 1.

Summary of experimental results for the properties of intracranial aneurysms

	Scott et al.	Steiger et al.	Tóth et al.	MacDonald et al.	Monson et al.
Stress to rupture (MPa)	2–324	0.5–1.225	0.14–1.0026	0.73–1.921	3.6823
Comments	Post-mortem tissue	Fresh and post-mortem tissue	Sample used within 24h of resection	Based on correlation made on scar tissue	Fresh healthy cerebral arteries

The reliability of CFD has been assessed by comparing simulation results with various forms of experimental measurements. Ford et al.²⁹ measured the velocity field of fluid mimicking blood flow in phantoms with particle image velocimetry and found good agreement with CFD predictions, although simulation tended to overestimate the velocity. Similarly, Hollnagel et al.³⁰ reported good qualitative agreement of CFD predictions with phase contrast magnetic resonance angiography (PC-MRA) and laser Doppler velocimetry, but quantitative differences with PC-MRA, especially in zones of complex flow. Virtual angiography was proposed as an indirect validation of CFD^{31, 32}. Ford et al.³¹ recorded the error between virtual and true angiograms in healthy patients and despite decoupled flow and diffusion equations, the best-suited model yielded less than 10% of error for 80% of the pixels in the sac.

There is no consensus on whether IA initiation is ascribable to high or low WSS nor is there agreement as to the type of WSS that promotes growth of the lesion and where the process initiates. Most simulations verify that mean WSS is elevated in pre-aneurysmal vascular segments and falls in the IA once the aneurysm is formed^{4, 33, 34}. Simulations on 17 patients with IA found almost three-fold lower WSS in the sac than in the parent artery. Similarly, simulation of the vasculature where the aneurysm was virtually ablated demonstrated a rotating flow pattern with low WSS³⁵ compared to the rest of the artery. This study has been interpreted to suggest that low WSS is responsible for IA lesion initiation. Yet, most aneurysms form at arterial branch points or curved arteries, known to experience significant shear stress, and analysis of empiric data defies the notion of low WSS alone as causal⁶. CFD analysis of surgically created carotid arterial bifurcations in dogs revealed high values of WSS³⁶. The animals were sacrificed after up to two months and histologic analysis showed common features with aneurysmal morphology – destructive remodeling – advocating for a role of high WSS in the genesis. Cebral et al.³⁷ observed that most blebs develop at regions with the highest WSS. Jou et al.³⁸ reported that ruptured aneurysms have the same maximal values as unruptured IA and that the sac is predominantly subjected to low shear stress – 48–59% of the mean arterial shear stress, excluding the aneurysm. Additionally, they observed that the area of the sac under low WSS (<0.4 Pa) is 3-fold greater in ruptured as opposed to unruptured aneurysm (27% vs. 11%). Cebral et al.³³ also analyzed the hemodynamics on a large number of IA lesions and found that unruptured aneurysms tended to have a stable flow pattern, with large impingement region, i.e. the zone where the jet hits the wall, and inflow jet sizes, while ruptured lesions mostly showed unstable patterns with small impingement regions and jets. Thus, we remain with evidence that indict both low and high WSS in IA biology, with high WSS probably driving initiation and low WSS progression.

Parameters and sensitivity of flow simulation in IA

As noted, the overall relevance of CFD depends on the definition of the boundary conditions: the geometry describing the arterial wall, the inflow and outflow conditions and the model used to describe the behavior of the blood. CFD is a tool and one should not expect that the precision of the simulation will be greater than the precision of the input values or constitutive models. The CFD procedure to model IA begins with the reconstruction of the geometry of the lumen obtained from a range of medical imaging modalities. The gold standard is 3D rotational angiography (3DRA), which produces contrast maps of the brain and the vascular lumen. Angiography is often used in concert with iodine-based contrast agents that increase the quality and contrast of the images. Software is used to segment and stack together sequential images, and then clean and smooth the volume. The most delicate steps in setting up a CFD analysis are adequately meshing the fluid domain and prescribing the fluid boundary conditions. See the example of a mesh used to compute physical properties in branches of the ICA of a patient with a sidewall Middle Cerebral Artery aneurysm (Figure 2, IA not shown). An ideal mesh should be fine enough such that increasing the number of elements does not affect the solution of the problem. Detailed procedures and information are available in Finite element procedure by K. J. Bathe³⁹. The precision and relevance of the waveforms/flow rates imposed at inlets and outlets are the subject of debate. Options include PC-MRI, Doppler or intravascular ultrasound (IVUS) velocimetry. MRI gives the most precise information as it yields a map of velocities in a section of the artery, but will extend the diagnostic time, so it is not always available. Alternatively, one can compute the Womersley profiles at the inlet from the waveform of the flow rate, which correspond to the analytic solution of the specific waveform in a pipe. The pipe’s cross-section is scaled to fit the size of the feeding artery.

Four major areas require definition to more completely understand the hemodynamics of IA - in decreasing order of sensitivity to modeling⁴⁰ they include the: arterial geometry, fluid boundary conditions, rigid-wall assumption, and description of the physics of blood.

The reconstruction of the arterial geometry is crucial as real images rarely delineate a clean border between tissue and blood; thus, image segmentation and smoothing is left to the judgment of the operator. This is all the more important as such considerations freeze the geometry, impacting subsequent results. Fluid boundary conditions include evaluation of the flow inlets and outlets. Classically, inlets are set to drive the simulation by specifying the velocity or flow rate in a cross-section, while outlets insure the continuity of the flow through setting the exit pressure. Controversy remains as to whether these data should be measured from the same patient or can be measured in different patients and scaled, and as to the degree of precision required. Ideally, PC-MRI at the inlet and pressure measurements at the outlet, in the same patient, should be used for maximal precision. Differences in spatial average of WSS values derived from an archetypal volumetric flow rate waveform⁴¹ compared to patient-specific data might be as high as 30%^{42, 43}. The sample size of this study was 6 cases, and overall results with archetypal waveforms overestimated mean WSS by ~15%. Yet, PC-MRI is not a panacea, it is highly dependent on the parameters specified for acquisition and the range of velocities that can be tracked is limited. Thus, heterogeneous flows have larger uncertainty and may require extrapolation of the velocity distribution near the wall. Fortunately, the characteristics of the flow change as it develops in the vasculature, decreasing its dependence on the boundary condition away from the inlet; consequently, it is key to keep enough length before the region of interest⁴⁴. Aneurysms often rupture during a spike of heart rate e.g. physical activity⁴⁵. As a result, it was suggested that simulation be carried at higher volumetric flow rates, which was shown to modify the flow patterns and WSS values⁴⁶.

Many neurosurgeons have reported the cyclic expansion of the IA cavity throughout the cardiac cycle and inhomogeneity in thickness of IA wall. If detected by human eye, the change in geometry should be sufficient to affect computed characteristics of flow yet classic assumptions and boundary conditions may have interfered with modeling such deformations. Significant deformation was indeed detected in model systems^{17, 47} configured with elastic boundaries. Rigid boundaries overestimate shear stress in IA and by definition dampen deformation. These results are interesting as proof of concept of fluid structure interaction (FSI) in IA, but require validation as they rely on uncertain wall mechanic data and arbitrary choice of IA thickness. FSI simulations couple CFD (fluids) and solid (wall and perianeurysmal structures) interactions.

Blood parameters are similarly fraught with assumption-dependence. Blood is a viscous fluid, described with classical Newtonian physics, but more appropriately considered with more complex models. Carreau-Yasuda or Casson approximations offer a more general framework, allowing viscosity to vary with the shear rate. Rheological effects can be important depending on the geometry. Newtonian models can degrade the results of the simulation^{48, 49}, while Casson models do not significantly burden computational cost.

The trend in CFD is to bring additional physiological relevance and complexity to the models and boundary conditions, in particular, to circumvent the rigid wall assumption. FSI takes into account a model of deformation of the wall to constantly iterate on the mechanical model of the artery to make the geometry current – pulses of flow induce the dilation of the vasculature. The challenges that remain are to obtain more precise and appropriate experimental data on the mechanics and patient-specific topology of the wall to drive the models proposed.

Thus, assessment of flow is essential to understanding initiation, development and rupture of intracranial aneurysms. CFD is a valuable tool because of the dearth of adequate in vivo imaging that can reliably measure flow parameters such as WSS, but as a sensitive tool, requires careful selection of boundary conditions. The precision of CFD should match the level of understanding required. General mechanistic processes, such as mechanotransduction, need only low precision and averages, as they seek to reach global conclusions. Case-specific problems, such as rupture, are in contrast highly dependent on the level of details (Figure 3). We believe that careful CFD analysis is valuable and will be best used to further characterize the mechanism that lead to IA initiation and enlargement in vitro.

Figure 3.

Summary of the CFD procedure

The biology of intracranial aneurysm remodeling

A simple analysis of the thicknesses shows that aneurysm expansion is dynamic: cells and/or collagen must be produced throughout the growth of the lesion (Figure 4 and Table 2). The observation of the thicknesses of aneurysmal wall of various sizes and morphologies rules out theories suggesting that aneurysms grow only through a rearrangement of mass in the wall, due to tension. In effect, the average thickness reported for IA is inconsistent with values predicted by simple distention of the wall - aneurysmal growth must have associated addition of mass either from cell proliferation and/or collagen production. Consider an idealized model of aneurysm built from a sphere of radius r₁ intersecting a cylinder of radius r₂, such that the size of neck in the direction of the cylinder’s axis is n. If the aneurysm balloons out from a bent disk of diameter n without change in arterial wall density, then conservation of mass should allow us to approximate the aneurysm, t_aneurysm as a function of the average thickness of the arterial wall (t_artery) and the ratio of arterial and aneurysmal surface areas S_artery and S_aneurysm. This ratio can be approximated in the case of pure distention in terms of the radius of the aneurysm: r₂, and diameter of the neck of the aneurysm: n.

$${\mathit{t}}_{\mathit{\text{aneurysm}}}={\mathit{t}}_{\mathit{\text{artery}}}\frac{S_{\mathit{\text{artery}}}}{S_{\mathit{\text{aneurysm}}}}\approx {\mathit{t}}_{\mathit{\text{artery}}}\frac{\prod {\left(\frac{\mathit{n}}{2}\right)}^2}{4\prod {\mathit{r}}_2^2}={\mathit{t}}_{\mathit{\text{artery}}}{\left(\frac{\mathit{n}}{4{\mathit{r}}_2}\right)}^2$$

Figure 4.

Aneurysm propagation must be accompanied by cell proliferation and/or extracellular matrix production. Modeling of the process of ballooning out of an artery during aneurysmogenesis. Part of the artery (left) remodels to form a spherical aneurysm (right).

Table 2.

Estimation of the thicknesses of aneurysmal wall in the hypothesis of pure-distention. The thickness of a healthy artery is taken to be 300 microns.

Aneurysm radius (r2, mm)	Aneurysm neck (n, mm)	taneurysm (µm)
5.0	4.0	12.0
6.0	4.0	8.3
8.0	6.0	10.5

The calculated aneurysm thicknesses computed for pure distention for an artery 300 µm thick with an aneurysm arising from a 4–6 mm neck that balloons to a sphere 5–8 mm in radius (table 2) should then be 8–12 µm. This value however is far lower than the average thickness observed on aneurysmal specimens (16–500 µm) - implying that distention alone cannot likely be responsible and that there must be additional sources of cell gain or extracellular matrix accumulation. Increasingly inflammation is perceived as central to these remodeling events.

Evidence of inflammation

The inflammation cascade is critical to the pathogenesis of cardiovascular diseases. All intracranial aneurysms show evidence of intense inflammatory remodeling^50–53, including the presence of monocytes⁵⁴, macrophages^{54, 55} mast cells⁵⁶ and T-lymphocytes^{54, 55} and complement activation⁵⁷. Gene expression analysis of IA specimens corroborates the prevalence of inflammation through the upregulation of multiple pro-inflammatory genes^{58, 59}, highlighting the critical role of antigen-presenting cells⁵⁸. The genetic dependence of IA will not be discussed in this review but can be found elsewhere⁶⁰.

Potential mechanisms of flow-driven inflammation

The endothelial monolayer is the center of command of vascular health. Its endothelial cells are the first line of exposure to luminal elements. Residing at the privileged vantage point at the frontier between vessel and blood on the one hand and smooth muscle from the opposing side, the endothelium is ideally suited to orchestrate the sensing of complex forces and flows, surveillance of circulating elements, and right of passage and defense of the vessel against these entities. Changes in endothelial connectivity, in endothelial cell shape and cytoskeleton are followed by dynamic alterations to the cell’s secretome and with that regulation of state and environment. For example under laminar flow, endothelial cells become spindoidal and align with the flow but lose a preferential orientation and turn cuboidal under disturbed or turbulent flow due to F-actin reorganization⁶¹, and while the former inhibit thrombosis, leukocyte adhesion, smooth muscle proliferation and vasoconstriction that latter phenotype promotes these processes.

The transmission of force to the cell is carried through intracellular tension created by the contraction of cytoskeletal filaments influenced by flow via the anchorage of the cell membrane to the substrate⁶², the nucleus⁶³ or neighboring cells⁶⁴. Intracellular forces act on the conformation of intracellular proteins⁶⁵ to modify the physiology of the cell and consequently the extracellular milieu, including the mechanical properties of the substrate, indirectly influences through this mechanism, the biology of the cell⁶⁶. During initiation of aneurysms, the luminal surface of the vessel becomes irregular and often damaged⁶⁷, even denuded⁵⁵, a probable consequence of disturbed hemodynamic stress⁶⁸. The changing vessel’s topology, in turn, modifies the local hemodynamic environment that loop around to command intracellular forces and cellular biology. This dynamic actuation of the flow force elicits changing biochemical signaling throughout the pathogenesis of IA. If intense hemodynamic stress seems to be incriminated over the course of initiation, low athero-prone-like shear stress dominates in the cavity during progression, which might explain why over 40% of unruptured IA present intimal hyperplasia⁵⁵.

Several mechanosensors have been identified at the apical and basal surfaces of the endothelium, such as ion channels⁶⁹, integrins⁷⁰, cell adhesion molecules¹⁰, G-protein coupled receptors⁷¹ or others cellular organelles⁷² and can lead to the activation of inflammation mediators such as the master regulator NF-κB, which is active in experimental IA^{8, 73} or potent anti-inflammatory factor like Krüppel-Like Factor-2⁷⁴ depending on the waveform applied to the cells. Further details on endothelial flow-mediated mechanotransduction are summarized in an exhaustive review by Davies⁷⁵.

Flow-mediated endothelial dysfunction and the subsequent modulation of SMC to a synthetic phenotype reinforce the belief that inflammation is at the heart of the IA genesis. The contractile phenotype contributes to the inflammation across many vascular diseases by generating a pro-inflammatory and pro-remodeling milieu⁷⁶, which in turn sustains and amplifies endothelial dysfunction and the recruitment of immune cells. This applies to IA as well beginning with the reduction of the contractile apparatus of the cell such as α-actin⁷⁷, changes in differentiation regulatory mechanisms⁷⁸ and the expression of transcriptions factors mediating inflammation, for example p47phox⁷⁹ and Ets-1⁸⁰. During the development of aneurysmal lesions, SMC of the media progressively transition from a quiescent contractile to a pathophysiologic synthetic phenotype, as observed on histological sections of human samples⁸¹, and express pro-inflammatory cytokines and matrix metalloproteinases (MMP)^{73, 82, 83}. These proteases can degrade the extracellular matrix⁸⁴ and participate in the regulation of inflammation⁸⁵, and are believed to contribute to the remodeling of IA lesions through the breakdown of the cellular substrate and ultimately achieving weakening of the vascular wall.

The media of diseased cerebral arteries gets thinner as the disease progresses and forms the aneurysmal cavity⁶⁸. This process occurs collectively through the degeneration⁸⁶ or apoptosis of SMC, the inhibition of proliferation of SMC and the inhibition of collagen production and processing by SMC, which was observed in rat models of IA⁸⁷. However, the predominant driving force for the remodeling of the media is unknown.

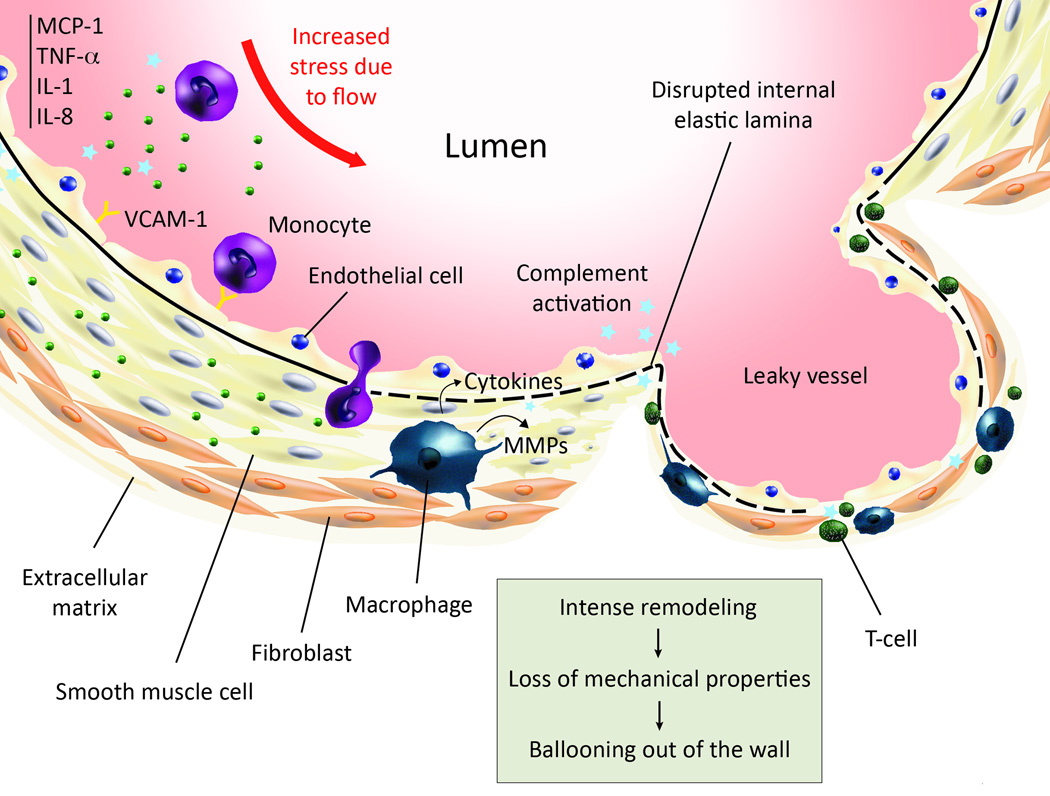
Inflammation builds up through the synergistic combination of leukocyte chemoattraction, activation, adhesion, and transmigration into the arterial wall. Monocyte chemoattractant protein-1 (MCP-1) and interleukin-8 (IL-8) are expressed in human and experimental IA^88–90, and vascular cell adhesion molecule-1 (VCAM-1) in the IA walls of human⁵⁴ and rat⁹¹ wall but not in control arteries. MCP-1 knock-out rats were six times less likely to develop IA or have a ruptured internal elastic lamina than wild type rats at five months and had almost 10 times less macrophages infiltrates. Leukocyte invasion is fostered by the secretion of two potent pro-inflammatory cytokines: tumor necrosis factor-α (TNF-α) and interleukin-1 (IL-1) that are abundantly expressed in human aneurysmal wall^{88, 90} and which activate and increase the permeability of the endothelium. Upon transmigration in the arterial intima, some monocytes mature and acquire the phenotype of macrophages (Figure 5). These latter cells secrete proteins that modify the vascular morphology. In particular, the balance of MMP and their tissue inhibitors, and the cathepsins and cystatin C, tightly regulate the morphology of the extracellular matrix. In aneurysmal lesions, the expression pattern of these proteins diverges from healthy arteries^{73, 92–94}. This imbalance is likely linked to the disruption of the internal elastic lamina (IEL) and the thinning of the wall, which causes the loss of mechanical properties. The quasi-disappearance of the medial layer is still an open question. Several plausible hypotheses, biomechanical or biochemical were proposed, while the reality might be a combination of processes. Matrix degradation for example can lead to anoikis. Tumor Necrosis Factor-α/TRADD/Caspase-3, 6, 7 is a known pathway for apoptosis for ECs and SMCs, relevant in our context⁹⁵. Alternative proposed mechanisms include the inhibition of collagen production or processing⁸⁷. It is noteworthy that remodeling of the wall might begin before the trafficking of immune cells, since aneurysm-prone flows may not allow for firm adhesion of inflammatory cells due to the intensity of the fluid forces.

Figure 5.

This cartoon summarizes the main steps of the establishment of inflammation in intracranial aneurysms. Going anti-clockwise: increased mechanical stress in aneurysm-prone regions is believed to trigger events that culminate in vascular dysfunctional, leaving the endothelium nude from anti-thrombotic protection. The inflammatory cascade then begins, with the expression of chemoattractants, pro-inflammatory cytokines and burgeoning of cell adhesion molecules at the surface of ECs, which attract peripheral blood mononuclear cells, including monocytes and T-cells. The complement is also activated through the classical pathway. Monocytes are able to adhere and transmigrate into the endothelium, which they would not do under normal conditions. They subsequently differentiate into macrophages, as observed in morphological studies of IA wall. The level of proteases in aneurysmal wall is increased and given literature knowledge about macrophages, there is good evidence that macrophages are responsible for the imbalance of proteases. During remodeling, the medial layer is destroyed, so is the internal elastic lamina, leading to lower mechanical properties and finally ballooning of the wall.

Comparison with other vascular aneurysms

All vessels can become aneurysmal, as such deformation is part of the minimization of wall stress. Laplace’s law dictates that wall stress in spherical coordinates is half of the stress in cylindrical systems, and as a result all vessels under stress will naturally seek a new spherical setpoint. The means by which aneurysms form in different vascular beds therefore not unexpectedly shares common features but is also unique. Aortic abdominal aneurysms (AAA) are common lesions of the aorta characterized by a focal increase of the diameter of the vessel exceeding half of its original size. Like IA, they remain silent until catastrophic rupture and have a poor prognosis. Previously thought to originate from the progression of atherosclerosis, novel hypotheses advocate distinct causes and pathogenesis. AAA and IA share many features including the same risks factors and inflammation biology but their origin, which remains under debate, may be separate. Some key histopathological traits are shared, such as the remodeling and degradation of the wall through imbalance of proteases and their inhibitors⁹⁶ or the loss of medial elastin and SMC. Both types of aneurysms may be local manifestations of a systemic condition since patients with AAA present biomechanical alterations in vessels distant from the AAA, while 15%–35% of people bearing aneurysms have multiple ones⁹⁷. The canonical cocktail of inflammatory mediators along with the presence of the same immune cells infiltrates also contributes to the development of both diseases, however these similarities may only underline the universality of the mechanisms of inflammation.

Besides their similarities, important differences are noted, such as the fusiform laminated AAA shape versus the quasi-spheroid IA shape. Critical questions on whether leukocyte trafficking occurs from the same vascular beds in AAA and IA remain unanswered at this time and would shed light on the filiation of these lesions. Does inflammation proceed through the vasa vasorum⁹⁸ or the intima in AAA⁹⁹? No clear answer has emerged for IA, although morphological evidence would support intimal trafficking.

Inflammation guiding modeling

Understanding the kinetics of matrix degradation and remodeling in aneurysmal lesions can help predict IA fate. The need for innovations in simulation stems from the inability of current models to bridge the gap between physics and medicine or help plan current intervention. The failure of current strategies arises often from decoupled analysis, which focuses solely on flow and lesion morphology to address a problem inherently translational. Neither flow patterns, nor specific intensities of the physical parameters can be consistently associated with a state of the disease. As aneurysms evolve over years, in vivo correlations are by definition restricted to be quasi-static – only a handful of lesions are sufficiently documented throughout their life span to serve CFD analyses – whereas stabilization or catastrophic progression are dynamic processes. Thus, predictive tools should take this time-dependency into account. Future directions in modeling aneurysms include integrating constitutive laws of mechanics and mechanotransduction. The introduction of FSI is a first step that opens the possibility to gauge the maturity of the lesion – comparing patient-specific stress states to the ultimate stress of IA and intact cerebrovascular beds. Yet, identifying the advancement of disease within the spectrum healthy:rupture is insufficient to estimate whether lesions will stabilize or fail catastrophically. Early stages of aneurysm expansion are critical and deserve further investigation, for example flow-driven phenotypic modulation of the endothelium in aneurysm-prone regions. Once remodeling of the wall begins, the loss of mechanical strength imposes ballooning out of the involved area, which coincides with a drastic reduction in wall shear stress eliciting a cascade of events, which promote IA further. Future modeling must account for all of these effects and with sufficient precision and time scale to account for the kinetics of flow alteration.

Conclusion

Intracranial aneurysms are silent killers – hidden from view they remain occult before they strike and first symptoms are often fatal. This silence has muted investigative ardor as well as clinical insight and mechanistic insight lags medical significance. General aspects of vascular biology coupled with specific elements of the cerebral circulation can add greater insight into the nature, diagnosis and potential intervention for these lesions. Advances in the understanding of the inflammatory cascade and vascular remodeling, and improvements in mathematical modeling techniques to compute patient-specific flow open the possibility of designing new therapies individualized to specific patients. As we seek to use numerical simulation to guide clinical intervention, we will need to bridge a still significant gap between the precision of definition of the physical parameters and the biological events. Research in the field must explain the role of inflammatory cells in the initiation and propagation of the aneurysmal wall and most importantly, the coupling of these inflammatory processes with hemodynamic stress. As we define inflammation with greater precision, we can also begin to assign specific flow patterns and physical boundary conditions to aneurysms of different shapes, forms, morphology and position. It is time to expand our knowledge of the effects of aneurysm-prone flow patterns on the biochemical remodeling of the wall, by combining experimental techniques of vascular biology, molecular biology and computational data.