Contribution of sublinear and supralinear dendritic integration to neuronal computations

Abstract

Nonlinear dendritic integration is thought to increase the computational ability of neurons. Most studies focus on how supralinear summation of excitatory synaptic responses arising from clustered inputs within single dendrites result in the enhancement of neuronal firing, enabling simple computations such as feature detection. Recent reports have shown that sublinear summation is also a prominent dendritic operation, extending the range of subthreshold input-output (sI/O) transformations conferred by dendrites. Like supralinear operations, sublinear dendritic operations also increase the repertoire of neuronal computations, but feature extraction requires different synaptic connectivity strategies for each of these operations. In this article we will review the experimental and theoretical findings describing the biophysical determinants of the three primary classes of dendritic operations: linear, sublinear, and supralinear. We then review a Boolean algebra-based analysis of simplified neuron models, which provides insight into how dendritic operations influence neuronal computations. We highlight how neuronal computations are critically dependent on the interplay of dendritic properties (morphology and voltage-gated channel expression), spiking threshold and distribution of synaptic inputs carrying particular sensory features. Finally, we describe how global (scattered) and local (clustered) integration strategies permit the implementation of similar classes of computations, one example being the object feature binding problem.

Introduction

In order to control behavior, the brain relies on the ability of its neuronal networks to process information arising from external and internal sources. How single neurons decode combinations of sensory features and transform them into a spiking output is still unknown, and represents a subject of intense study. The complexity of the single neuronal coding problem can be illustrated by the paradoxical finding that neurons exhibiting narrowly tuned receptive fields often appear to be driven by synaptic inputs that themselves are broadly tuned (Chadderton et al., 2014). One hypothesis is that nonlinear dendritic transformations are critical for such neuronal computations. Decades of experimental and modeling studies on dendrites have led to the consensus that active properties of dendrites are primarily responsible for nonlinear integration, in particular supralinear operations (Mel, 1994; Spruston and Kath, 2004; Johnston and Narayanan, 2008). Nonetheless other findings indicate that sublinear integration of synaptic inputs is possible in multiple neuron types, and results from either active (Cash and Yuste, 1998; Hu et al., 2010) or passive dendritic properties (Abrahamsson et al., 2012; Vervaeke et al., 2012).

What is the evidence that nonlinear dendritic properties contribute to neuronal computations? Numerical simulations suggest that supralinear dendritic operations are essential for translation-invariant orientation tuning (Mel et al., 1998) and binocular disparity tuning (Archie and Mel, 2000), while sublinear dendritic operations contribute to coincidence detection of auditory stimuli (Agmon-Snir et al., 1998). Recently, state-of-the-art in vivo recordings have shown that dendritic supralinearities are associated with various other neuronal computations: formation of hippocampal place fields (Lee et al., 2012), detection of multi-modal sensory stimuli (Xu et al., 2012), angular tuning of barrel cortex pyramidal neurons (Lavzin et al., 2012), and enhancement of orientation tuning (Smith et al., 2013). Sublinear operations have also been shown to underlie orientation selectivity of binocular neurons in visual cortex in vivo (Longordo et al., 2013).

Nevertheless, a direct link between the dendritic transformations and the associated neuronal computations is still lacking. Analytical methods implementing mathematical approximations of measured dendritic operations can be used to make estimates of the possible number and type of neuronal computations. For example, binary neuron models were used to quantify what was previously shown with biophysical models (Mel, 1994), namely that nonlinear dendrites support a larger number of neuronal computations (Poirazi and Mel, 2001; Cazé et al., 2013). Such simplifications can provide analytical insight and make testable predictions as to which computations are made possible by dendritic operations. Moreover, analytical methods show under which conditions the expanded computational capacities are generic, i.e., not tied to the specific example parameters of the biophysical model.

Here we review the biophysical determinants of different classes of dendritic operations (linear, sublinear and supralinear), how they are measured experimentally, and finally, using a recently published Boolean-based analysis of equivalent dendritic trees (Cazé et al., 2012, 2013, 2014), we review how these operations combine with other cellular properties to determine neuronal computations.

Dendritic Integration

Neurons integrate synaptic inputs arriving primarily on dendritic trees carrying information from presynaptic neurons, by transforming them into synaptic potentials using a variety of cell-specific synaptic and cellular mechanisms. During synaptic transmission, the activation of neurotransmitter-gated conductances results in either a transient depolarization or hyperpolarization of the postsynaptic membrane potential. When the net depolarization resulting from synaptic integration of multiple synaptic inputs is greater than the spike threshold potential, the neuron generates an action potential (AP), or spike. Synaptic integration is a critical determinant of neuronal computations, the process by which a postsynaptic neuron transforms presynaptic information (coded in input activation patterns) into an output signal (encoded in a firing pattern) (Häusser and Mel, 2003; London and Häusser, 2005; Silver, 2010; Larkum, 2013; Chadderton et al., 2014). This review will focus primarily on the integration of excitatory post-synaptic potentials (EPSPs) mediated by ionotropic glutamate receptors.

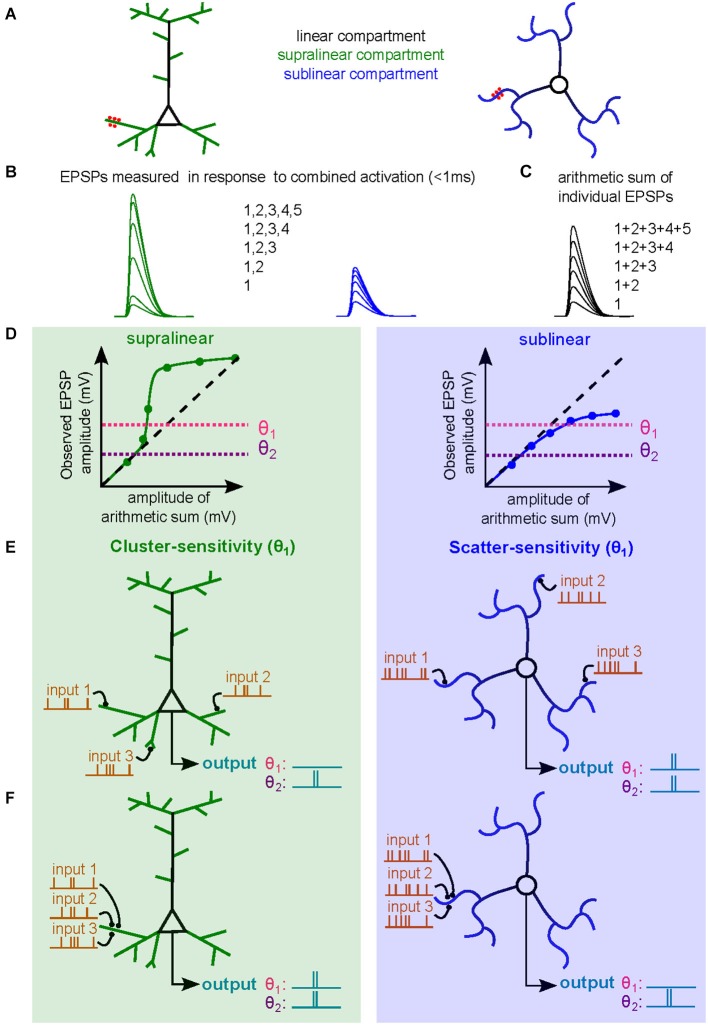
Dendritic integration can be quantified by comparing the observed depolarization resulting from the simultaneous activation of the same synaptic inputs (Figure 1B), also called a compound EPSP, and the arithmetic sum of individual EPSPs (expected membrane depolarization) (Figure 1C). The dendritic subthreshold input-output (sI/O) relationship is easily described by plotting observed vs. expected depolarizations for different numbers of co-activated synapses (Figure 1). Mathematical functions can be used to describe the operation performed. The sI/O relationships fall into three categories of dendritic operations: (1) linear, where the observed depolarization equals the expected depolarization; (2) supralinear, where the observed depolarization exceeds the expected depolarization (above the linear line; Figure 1D, left); and (3) sublinear, where the observed depolarization is less than the expected depolarization (below the linear line; Figure 1D, right). Much of the experimental evidence of nonlinear integration suggests dendrites perform supralinear operations, resulting from the contribution of active dendritic conductances (Mel, 1994; Johnston and Narayanan, 2008; Spruston, 2008). Recent studies suggest that sublinear operations could be mediated solely by passive properties (Abrahamsson et al., 2012; Vervaeke et al., 2012), while other studies have shown that activation of potassium channels can produce sublinear summation (Cash and Yuste, 1999; Hu et al., 2010). The detailed biophysical mechanisms determining specific dendritic operations are discussed in depth below.

Figure 1.

Dendritic operations and their influence on neuronal firing. (A) Schematic diagram of a subthreshold synaptic input-output experiment in a neuron with supralinear dendritic compartments (left, supralinear compartments in green, linear compartments in black) or in a neuron with sublinear dendritic compartments (right, sublinear compartments in blue). The red spots are sites of synaptic activation or sites of glutamate uncaging. (B) Somatic voltage responses evoked by simultaneous synaptic activation or uncaging. Green curves are responses evoked with increasing number of synapses activated within a supralinear dendrites. Blue traces are similarly obtained within a sublinear dendrite. (C) Arithmetic sum of individual responses to synaptic activation or uncaging. (D) Subthreshold input/output relationships (sI/O) used to quantify dendritic operations. The dashed line represents a linear releationship. Two horizontal dotted lines indicate two example somatic spike thresholds (θ₁ and θ₂). (E,F) Example of synaptic integration of three synaptic inputs distributed across the dendritic tree (E) or clustered on a single dendritic branch (F) of a neuron with supralinear dendritic compartments (left) or sublinear compartments (right). The output spike train, and hence neuronal computation, differs depending on the threshold. The more depolarized threshold value (θ₁) allows the neuron with supralinear dendrites to exhibit a cluster-sensitive neuronal computation (fires only when three inputs are activated in the same compartment). The θ₁ threshold also allows a neuron with sublinear dendrites to exhibit scatter-sensitive neuronal computations. The lower threshold (θ₂) imparts a different neuronal computation based on simple linear summation and is not sensitive to activated synapse location.

The type of dendritic operation strongly contributes to the nature of the resultant neuronal computation. For example, co-activation of synapses within a single electrical compartment that exhibits supralinear integration will produce dendritic voltage signals that are larger than expected due to amplification by activation of voltage-sensitive channels. This large depolarization is thereby more likely to drive the neuron to spike threshold. The resulting sI/O will reflect a neuronal computation that is cluster sensitive (Figures 1E,F, left, θ₁). For a neuron with sublinear dendrites, clustered synaptic activity will be less efficient at triggering a spike than if the same inputs were distributed in different compartments, thus promoting computations that are scatter sensitive (Figures 1E,F, right, θ₁; Cazé et al., 2013). Such neuronal computations enable the discrimination of patterns of synaptic activation with different levels of spatial and temporal correlations, which could not be otherwise performed by linear dendrites (Mel, 1992). Nevertheless, it should be noted that the dendritic operation is insufficient to define the computation, synaptic placement and spike threshold also influence the final neuronal computation. In Figures 1D–F we show that lowering the spike threshold (θ₂) would restrict the access to only the linear regime of the subthreshold dendritic operation. Finally, ongoing synaptic activity can occur in the presence of AP firing, and thus constitutes supra-threshold synaptic integration (Silver, 2010), which we will not address in this review.

Biophysical Mechanisms Influencing Synaptic Integration

Effect of Passive Membrane Properties on EPSPs Summation

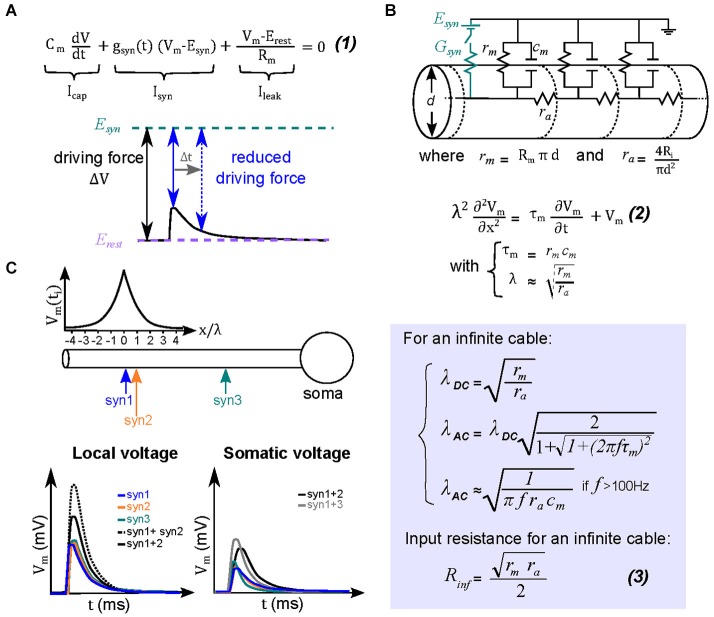
Because neurons communicate with each other using electrical signals, the analysis of their signaling properties is generally performed using principles of electrical circuits. A single compartment equivalent circuit describes well the electrical behavior of a cell without any dendrite or active properties. Four parameters determine the amplitude and time course of the EPSP: a transient synaptic conductance (G_syn), the electromotive force of its ion flux (driving force), the membrane resistance (specific membrane resistance; R_m), and the specific membrane capacitance (C_m). The difference between the membrane potential and the reversal potential for G_syn sets the driving force (V_m − E_rev; Figure 2A), thus as G_syn increases, I_syn increases, and V_m becomes more depolarized. For large conductances, V_m approaches E_rev and the driving force is reduced, resulting in decreased current flow for the same G_syn (Figure 2A). This results in a sublinear relationship between G_syn and EPSP size. Since quantal synaptic conductances are generally small, it is when multiple synapses are activated simultaneously that the driving force decreases sufficiently to produce sublinear integration (Figure 2C). Therefore, for passive single compartment model cells, synaptic summation is already essentially sublinear, which was first demonstrated at the neuromuscular junction (Martin, 1955).

Figure 2.

Theoretical basis for sublinear summation within passive dendrites. (A) Equation (1) describes the different current components underlying an EPSP in a single electrical compartment. Integration of this equation describes the variation of the membrane voltage over time. The transient change in driving force (ΔV = V_m − E_syn) is determined by the amplitude and time course of the local dendritic EPSP (black trace). At the peak of the EPSP (solid blue arrow) the driving force is maximally reduced, and then recovers back to that at resting membrane potentials during the EPSP decay (dotted blue arrow). The reduced driving force decreases the synaptic current, and hence the net depolarization, creating a sublinear relationship between EPSP and its underlying conductance. (B) Equivalent circuit for dendritic cables, where g_m and c_m are the membrane conductance and capacitance, respectively, and r_a is the axial resistance of a unit of cable. A synapse is represented in the circuit (by the synaptic conductance G_syn and the synaptic reversal potential E_syn). For an infinite cable, the spatio-temporal distribution of voltage is described by the relation (2), where τ_m is the membrane time constant, and λ is the length constant. The length constant relationships are derived from solving the cable equation (2) for step changes in membrane voltage (λ_DC) or for a sinusoidal membrane potential change (λ_AC). The latter is helpful to understand the dendritic filtering of transient EPSPs. Equation (3) is the relation for the input resistance R_D for an infinite cable. (C) Top, ball-and-stick model of a neuron with colored arrows indicating the location of three synapses (Syn 1–3). The graph above the diagram represents the peak amplitude of a dendritic EPSP as a function of distance. Bottom, the two graphs describe respectively the dendritic and somatic depolarizations in response to individual (colored lines) or combined synaptic inputs (black lines). Concomitant activation of two neighboring synaptic inputs (within ~λ_AC) will therefore mutually reduce their driving force and sum sublinearly (for example synapses 1 and 2, solid black trace for the EPSP observed in response to their simultaneous activation, dashed black trace for the arithmetic sum of the individual EPSPs). More separated synapses will, however, sum more linearly (synapses 1 and 3, gray trace).

More complex, but also more realistic, equivalent circuit models take into account neuronal morphology, such as dendritic arborizations. Wilfrid Rall pioneered the use of such multi-compartmental equivalent circuit models in order to study synaptic integration in neurons with passive dendrites. His primary advance was to consider dendrites as electrical cables (Rall, 1967) that contained an additional parameter, the axial resistance (r_a), which electrically couples multiple elementary single compartment models (Figure 2B). Because each elementary compartment will allow current to leak across the membrane, the current injected in the next compartment (across r_a) decreases progressively as it travels along the cable or dendrite, which results in an attenuation of the local EPSP amplitude and a slowing of its time course. Such dendritic filtering accounts for why local EPSPs in dendrites tend to be larger and faster than those recorded in the soma. It therefore follows that more distal synaptic inputs (for a given G_syn) would result in a progressively smaller somatic depolarization and thus a smaller influence on the firing output of a neuron (Rinzel and Rall, 1974; Magee and Cook, 2000; Spruston, 2008). Also in dendrites the local input resistance (R_D) or impedance (Z_D; to account for the effect of capacitance on fast time-varying inputs) increases with increasing distance from the soma due to a diminished shunt effect of the soma and the high resistance of the sealed cable (Rinzel and Rall, 1974). We will henceforth refer to Z_D, since it is the more general form that accounts for the capacitive current dependance on synaptic conductance time course. It should be noted that at steady state Z_D = R_D. This distance-dependent increase in Z_D results progressively larger local EPSPs, which in some morphologies, can combine with an efficient passive propagation of EPSPs to the soma (transfer impedance), thereby counteracting the distance-dependance reduction in the somatic EPSP amplitude due to cable filtering (Jaffe and Carnevale, 1999; Nevian et al., 2007; Schmidt-Hieber et al., 2007). This location independence of EPSP amplitude is also referred to as passive normalization (Jaffe and Carnevale, 1999). Distance-dependent increases in Z_D are also thought to be important to increase the probability of evoking a local dendritic spike at distal inputs of basal dendrites of pyramidal neurons, which can then propagate to the soma (Rudolph and Destexhe, 2003).

Rall provided a simple parameter that describes cable filtering: the space constant (λ), derived from the steady state (λ_DC) or frequency-dependent (λ_AC) solution to the cable equations. It represents the distance along a cable where the membrane potential is 63% of the maximal at the site of current injection. Therefore if the dendrite length is longer than λ, significant cable filtering can be expected; similarly, if the dendritic length is much shorter than λ then EPSPs propagating to the soma are filtered very little. A critical morphological parameter determining λ is the dendritic diameter, to which λ is proportional (Figure 2B); meaning a larger diameter produces a longer λ (Figure 3A, left). For fast synaptic conductances (rise and decay <2 ms), the capacitive current acts as a frequency-dependent shunt and can dramatically alter λ. In cerebellar molecular layer interneurons, for example, the frequency-dependent length constant (λ_AC) can be over a factor of 5 shorter than λ_DC. Their thin (~0.4 µm diameter), 100 µm long dendrites are electrically compact for steady-state depolarizations (with total length 3 times shorter than λ_DC, 300 µm). But for rapid synaptic conductances λ_AC is 50 µm (half the dendritic length), resulting in significant dendritic filtering of EPSPs for distances greater than 20 µm (Abrahamsson et al., 2012). Dendritic branching tends to shorten the space constant, since it effectively decreases the membrane resistance (acting like a shunt for current flow (Figure 3A; right; Abrahamsson et al., 2012). It is also worth noting that λ also serves as a rough indicator of the size of effective dendritic compartments. Synapses located within a distance of λ are more likely to interact than non-neighboring synapses (Figure 2C; Abrahamsson et al., 2012).

Figure 3.

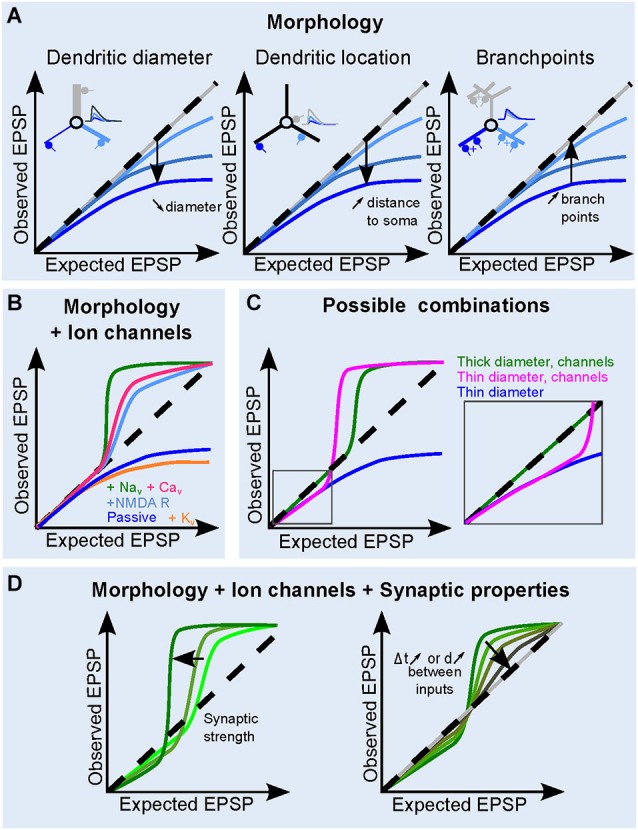
Contribution of dendritic and synaptic properties to EPSP summation. (A) Influence of morphological parameters dendritic: diameter (left), increasing distance to soma (middle) and increasing dendritic branching (right) on the dendritic sI/O. The inserts illustrate the effect of morphology on somatic EPSPs under the different conditions. Synapse location and traces are color coded. Dashed line shows a linear I/O for reference. (B) The role of ion channels on the shape of the sI/O, for a given morphology. Either K⁺ channels, (orange), Na⁺ channels (green), VGCC (pink), or NMDA receptors (sky blue) are added to a passive dendrite (blue). (C) Example of sI/O in three realistic combinations: thick (>2 µm) dendrites with active conductances (blue curve, as in Branco and Häusser, 2011), thinner dendrites with active conductances (brown curve, <1 µm, Losonczy and Magee, 2006), or thin dendrites with only passive properties (blue curve, Abrahamsson et al., 2012). (D) Influence of synaptic properties on the sI/O for a given morphology and ion channel combination. An increase in synaptic strength makes the sI/O diverge from linearity both in the sublinear and the supralinear regime, whereas increasing the interval or the distance between synaptic inputs tends to linearize the curve (right).

The Influence of Passive Dendrites on sI/Os

As described above, sublinear summation of simultaneously occurring EPSPs within an electrical compartment is a natural consequence of the loss of driving force for synaptic currents. Dendritic compartments with narrow diameters are particularly sensitive to this due to a high Z_D. Therefore when multiple dendritic synapses are activated simultaneously within a close proximity (<λ), the local depolarization resulting from the activation of a given synaptic input will be large, thus decreasing the local driving force, resulting in a sublinear sI/O (Figures 1D, 2B). As the diameter of the passive dendrite decreases, Z_D will increase and the local EPSPs will be even larger (Abrahamsson et al., 2012). One can use the equation for input resistance of an infinite cable to appreciate the influence of dendritic diameter (Figure 2B, equation 3). The larger Z_D causes a larger depolarization, thus the sublinear summation of synaptic inputs will be more prominent with fewer active inputs (Figure 3A, left; see also Rinzel and Rall, 1974). If the distance of the synapse from the soma increases, the current sink of the soma, the end effect of the dendrite and/or dendritic tapering will contribute to a distance-dependent increase in Z_D, together resulting in more pronounced sublinear sI/O curves particularly for more distal dendritic compartments (Figure 3A, middle). Finally, the number of dendritic branch points, despite increasing dendritic filtering, tends to decrease the local Z_D by adding a current sink, thus favoring a more linear sI/O (Figure 3A, right). Gap junctions have also been shown to reduce sublinear summation by providing a current sink (Vervaeke et al., 2012).

Although passive membrane properties are sufficient to produce sublinear dendritic operations, experimental evidence of such a mechanism has only recently been described (Abrahamsson et al., 2012; Vervaeke et al., 2012). The authors concluded that the combination of thin dendrites and low levels of expression of voltage-gated channels favors sublinear dendritic operations. In these neurons, sublinear summation is apparent even for as few as two active synapses (Abrahamsson et al., 2012). Synapses activated on separate dendrites summed linearly, supporting a scatter sensitive neuronal computation (Abrahamsson et al., 2012), that was confirmed in a realistic active model (Cazé et al., 2013).

The Influence of Active Dendrites on sI/Os

The large local synaptic depolarizations produced in dendrites can also recruit the activation of voltage-dependent channels (NMDARs, Na⁺, Ca²⁺, K⁺ and HCN channels, see Johnston and Narayanan, 2008; Figure 3B). The number of activated synaptic inputs needed to engage active conductances is determined, in part, by the passive properties of the dendrite, the amplitude and kinetics of the synaptic conductance, the voltage-dependance of channel gating, and the channel density and distribution along the somato-dendritic axis. Active conductances can either enhance (Williams and Stuart, 2000; Migliore and Shepherd, 2002) or dampen (Cash and Yuste, 1999; Hu et al., 2010) local dendritic depolarizations, depending on whether the channels mediate inward (depolarizing) or outward (hyperpolarizing) currents, respectively. Distance-dependent increases in I_h currents have been shown to compensate for the temporal slowing caused by dendritic filtering (Magee and Cook, 2000; Williams and Stuart, 2002). Differential expression of HCN channels across mitral cells has also been shown to increase the membrane noise and lower the rheobase, thus facilitating AP generation (Angelo and Margrie, 2011). Because of the presence of NMDARs at many glutamatergic synapses, most studies find that NMDARs activate other voltage-dependent channels by boosting local synaptic depolarization (Schiller et al., 2000; Losonczy and Magee, 2006; Nevian et al., 2007; Makara et al., 2009; Branco and Häusser, 2011; Katona et al., 2011; Krueppel et al., 2011). The resulting dendritic operation is determined by the concurrence of a passively determined sublinear (Losonczy and Magee, 2006; Krueppel et al., 2011; Chiovini et al., 2014) or linear operation (Branco and Häusser, 2011), and a supralinear operation.

In some cases, the voltage activation of conductances results not only in EPSP boosting, but in a threshold-dependent, all-or-none regenerative response, often called a dendritic spike. This regenerative behavior is characterized by a steep change in the sI/O followed by a plateau (Figures 1D, 3B; Polsky et al., 2004; Losonczy and Magee, 2006; Larkum, 2013). Locally-generated dendritic spikes can be mediated by either Na⁺ channels, Ca²⁺ channels or NMDA receptors (NMDARs). Na⁺-spikes are triggered by high-amplitude local depolarization, are relatively brief, and can be accompanied by entry of Ca²⁺ through VGCC or NMDARs. In pyramidal cells, these dendritic Na⁺ spikes can be generated in most regions of the dendritic tree, propagate throughout the dendritic tree, albeit with some attenuation, but can still trigger somatic spiking (Golding and Spruston, 1998; Rudolph and Destexhe, 2003; Nevian et al., 2007). Recent findings have also shown Na⁺-channel dependent spikes in dendrites of dentate gyrus granule cells (Chiovini et al., 2014). On the other hand, Ca²⁺ and NMDA spikes are longer, plateau-like events, that are thought to be generated in particular regions of the dendritic tree, and require the synchronous activation of many clustered synapses. The biophysical mechanisms of the NMDA spikes and their functional consequences have been described in detail in a recent review (Major et al., 2013). In cortical pyramidal neurons, the Ca²⁺ spike is likely to propagate actively from the primary apical dendrite to the soma, thereby representing a more global dendritic operation, whereas NMDA spikes are locally restricted to dendritic compartments such as tufts or basal dendrites (Larkum, 2013). In contrast, simulations of in vivo spontaneous synaptic activity allow glutamate-bound NMDARs to act as global nonlinearities providing an entirely different computation than those initiated in single dendrites (Farinella et al., 2014). Nevertheless, several recent in vivo studies have reported the involvement of local NMDA spikes during sensory processing, across all layers of the cortex (Lavzin et al., 2012; Xu et al., 2012; Smith et al., 2013; Gambino et al., 2014; Palmer et al., 2014). It should also be noted that Polsky et al. (Polsky et al., 2004) pointed out that a Ca²⁺-spike exhibits saturation of the voltage response and thus can also be considered sublinear for very high stimulation strengths.

In summary, the modus operandi of supralinear dendritic compartments is comprised of a continuum of voltage-dependent operations from simple boosting of synaptic depolarization to regenerative spikes. Considering the biophysical underpinnings of this range of operations, it follows that the interplay of the active and passive properties of dendrites ultimately determines the shape of the sI/O (Figure 3C). For example, sI/Os of thick dendrites, which have a low Z_D, do not suffer from driving force losses, thus sum linearly for low numbers of activated synapses, then transition into supralinear summation (Makara and Magee, 2013). Thin dendrites on the other hand may exhibit sublinear sI/O relationships for only a few inputs, but then easily engage NMDAR and Ca²⁺ channels (Losonczy and Magee, 2006; Chiovini et al., 2014) with fewer synaptic inputs than in larger dendrites (Figure 3C). Due to tapering of dendritic width, which increases the Z_D along the dendrite with increasing distance to the soma, the dendritic operations can be altered as a function of distance from the soma (Branco and Häusser, 2010, 2011).

The Influence of the Size, Time Course and Location of the Synaptic Conductance on sI/Os

The strength of synaptic conductance varies from synapse to synapse across neuron types, but also within neurons. The synaptic strength not only serves to bias the output of a neuron to particular inputs (Ko et al., 2011), but it can also be tuned to compensate for dendritic attenuation by passive dendritic properties (Magee, 2000). Synaptic strength influences dendritic operations by modulating the gain (slope) and shape of the sI/O, which is achieved by engaging sub- and supralinear transformations with different numbers of synaptic inputs (Figure 3D). Larger synaptic conductances will lead to larger dendritic depolarizations, and in turn either a larger reduction in driving force or increased activation of voltage-gated conductances. Depending on the intrinsic membrane properties and synaptic conductance amplitude the “linear regime” may be more or less prominent in the sI/O relationship.

The temporal window for synaptic interactions depends ultimately on the time course of local EPSPs, which is itself shaped by the local passive dendritic properties and the time course of the synaptic conductance (Jonas, 2000). Although the local dendritic EPSPs are larger than those at the soma, it is important to note that their time course is generally much faster, due to charge redistribution down the dendrite (Schmidt-Hieber et al., 2007). The degree to which nonlinear mechanisms are engaged during EPSP summation also depends on the temporal summation of local EPSPs (Losonczy and Magee, 2006; Abrahamsson et al., 2012; Makara and Magee, 2013). Simultaneous synaptic activation enables the largest degree of nonlinear summation, which will progressively decrease as the time difference between synaptic events increases (Figures 2A, 3D). Thus, combined with the synaptic strength, the temporal coincidence between co-activated synapses within a single dendritic compartment will determine gain of the dendritic operations (Gómez González et al., 2011; Abrahamsson et al., 2012; Makara and Magee, 2013).

The location of synapses carrying similar information (e.g., a single sensory feature) determines which dendritic mechanism is recruited. For example, if features of an object are always clustered on a single dendritic compartment, then nonlinear summation will be the prominent operation influencing integration. Below we will use a mathematical formalism to provide insight into how synaptic placement and dendritic operations influence neuronal computations.

Experimental Strategies for Studying Dendritic Integration

How do researchers study the biophysical properties of dendrites and their influence on excitatory synaptic integration? Classical electrophysiology methods such as sharp electrode- or patch-clamp-based recordings of somatic membrane potential provided insight into the intrinsic passive electrical properties of neurons by measuring the input resistance and the membrane time constant (τ = R_m*C_m) (Spruston and Johnston, 1992). When combined with multi-compartmental dendritic models, with either simplified morphologies (equivalent cylinder approximation) or full anatomical reconstructions (Clements and Redman, 1989; Major et al., 1994), the passive electrotonic properties of dendrites can be estimated from model parameters that predict the membrane potential decay from somatic current injections (Rall et al., 1992). These constrained models are then used to examine dendritic transformations of EPSPs as they propagate to the soma.

Unfortunately, single electrode recordings at the soma do not provide sufficient information about dendritic properties to constrain complex morphological models. With the advent of dendritic patch recordings (Stuart et al., 1993), at least for large diameter dendrites (≥1 µm), cable model predictions could be directly verified. This powerful recording method allows estimations of the critical parameters influencing dendritic filtering, such as internal resistivity (R_i; Stuart et al., 1993; Stuart and Spruston, 1998; Roth and Häusser, 2001; Nevian et al., 2007; Schmidt-Hieber et al., 2007; Hu et al., 2010), R_m and voltage-gated channel properties and density along the somato-dendritic axis (Magee and Johnston, 1995; Stuart and Spruston, 1998; Hu et al., 2010). Dendritic recordings also enabled the measurement of local EPSPs and EPSCs, which allowed the authors to conclude that dendritic filtering can be compensated by a distance-dependent increase in synaptic conductance in certain neuron types (Magee and Cook, 2000).

More recently, fluorescence imaging techniques have greatly increased the toolkit for studying dendritic integration, particularly in those dendrites with narrow diameters (<1 µm). Ca²⁺ indicators are one of the most popular class of fluorescence probes, which are used to indirectly study dendritic nonlinearities resulting from activation of voltage-dependent ion channels, provided at least one type of Ca²⁺ conductance was activated (Markram et al., 1995; Schiller et al., 1995, 1997, 2000). Ca²⁺ indicators have also been used to monitor synaptic activity because of the prevalence of NMDAR activation in single spines and Ca²⁺-permeable AMPARs at synapses in interneurons (Soler-Llavina and Sabatini, 2006). In vivo two-photon Ca²⁺ imaging experiments provided the first insights into the spatial and temporal distribution of sensory-evoked synaptic signaling within dendrites (Varga et al., 2011; Lavzin et al., 2012; Smith et al., 2013; Jia et al., 2014; Palmer et al., 2014). The contribution of in vivo Ca²⁺ imaging studies to understanding dendritic function has been recently reviewed by Grienberger et al (Grienberger et al., 2015). However, a limitation of using Ca²⁺ imaging to study synaptic integration is that it does not report the true dendritic voltage, a parameter critically influencing dendritic operations. Also, the slow nature of the whole-cell averaged [Ca²⁺] and the use of high affinity Ca²⁺ indicators limits the temporal resolution of this method (Farinella et al., 2014; Fernández-Alfonso et al., 2014). Voltage-sensitive dyes are, in principle, an ideal alternative for direct measurement of dendritic integration. Whereas voltage-sensitive dye recordings have provided unprecedented optical reports of the spatial and temporal distribution of APs in axons (Foust et al., 2010; Popovic et al., 2011) and dendrites (Acker and Antic, 2009; Casale and McCormick, 2011), their use to monitor EPSPs in dendrites has been less successful due to poor signal-to-noise ratio, typically requiring hundreds of trials of averaging (Palmer and Stuart, 2009). However, inhibitory post-synaptic potentials (IPSPs) have been detected (Canepari et al., 2008) and a recent study reports good signal-to-noise ratios sufficient to detect spine EPSPs (Popovic et al., 2014). The advances in genetically-encoded voltage indicators are also rapidly maturing (Hochbaum et al., 2014; St-Pierre et al., 2014; Zou et al., 2014), and could eventually provide a powerful tool for studying dendritic integration in vivo.

Another widely-used in vitro technique to characterize the integration properties of dendrites is to directly activate postsynaptic receptors using photolysis of caged-neurotransmitter (i.e., caged-glutamate) within the diffraction-limited focal volume of the microscope (Gasparini and Magee, 2006; Losonczy and Magee, 2006). Using galvanometer-driven mirrors, the type regularly used in scanning confocal microscopy, the focal illumination volume can be rapidly moved (within 0.1–1 ms) and positioned at multiple locations. The uncaging light pulse is then rapidly gated at each location to focally release glutamate. This allows for the near simultaneous activation of many postsynaptic sites. The somatic depolarization is then recorded using standard whole-cell patch-clamp methods. The observed response to uncaging at multiple synaptic locations (typically within 1 ms) is compared to the arithmetic sum of the uncaging-evoked responses at individual sites. The resulting plot is identical to the sI/O plots described in Figures 1, 3, provided that the uncaging responses are similar to synaptic activation. Using light, rather than presynaptic vesicular release, to activate neurotransmitter receptors provides a more flexible strategy to systematically vary the number, pattern, and timing of synapse activation. Electrical stimulation does not permit a precise identification of the synapses being activated, nor precise control of the number of synapses activated. Holographic illumination provides an alternative strategy for true simultaneous glutamate uncaging at multiple sites within the dendrites and is more amenable to multibranch activation (Lutz et al., 2008; Yang et al., 2014, 2011). The only potential drawback of uncaging is the difficulty in some preparations to accurately reproduce very fast synaptic conductances due to the large volume of diffraction-limited focal spots relative to the point source nature of neurotransmitter release from synaptic vesicles (DiGregorio et al., 2007), as well as a tendency to partially block GABARs (Fino et al., 2009). Nevertheless, neurotransmitter uncaging is an essential tool for quantifying the biophysical properties underlying dendritic operations.

Linking Dendritic Operations to Neuronal Computations Using Mathematical Models

Because experimental evidence of a direct link between the dendritic operations and the associated neuronal computations is still lacking, a parallel strategy is to use analytical models to make testable predictions (Poirazi and Mel, 2001; Legenstein and Maass, 2011; Cazé et al., 2013). These methods take advantage of mathematical approximations of measured dendritic operations to make estimates of the possible number and type of neuronal computations. Biophysical models, in contrast, although explicit, do not easily provide insight into the classes of possible computations because of the large parameter space. There is no doubt that such models have provided deep insights into neuronal computations that involve nonlinear dendritic operations. They have been used to show that neurons with supralinear dendrites are cluster-sensitive (Mel, 1993) and neurons with sublinear dendrites are scatter-sensitive (Koch et al., 1983; Cazé et al., 2013). Yet it was not clear whether either type of nonlinearity provides similar computational advantages. To examine the difference between supralinear and sublinear operations of binary neuron models Cazé et al. (2013) used a Boolean-based analysis. Here we review how this Boolean framework can be used to argue that either supralinear or sublinear summation is sufficient to endow neurons with a new class of computations.

Within this analytical framework, neurons are modeled as having binary inputs (x_i), which can be weighted and integrated, resulting in binary outputs (y). In this context the input-output relation is described by a unique truth table, corresponding to a Boolean function. In Figure 4A, the truth table describes three simple Boolean functions: OR, AND and XOR. This well-known mathematical framework (Wegener, 1987; Crama and Hammer, 2011), which deals with binary classifications of binary words, allows us to analytically determine what type of classifications are possible with nonlinear dendrites and which are otherwise impossible.

Figure 4.

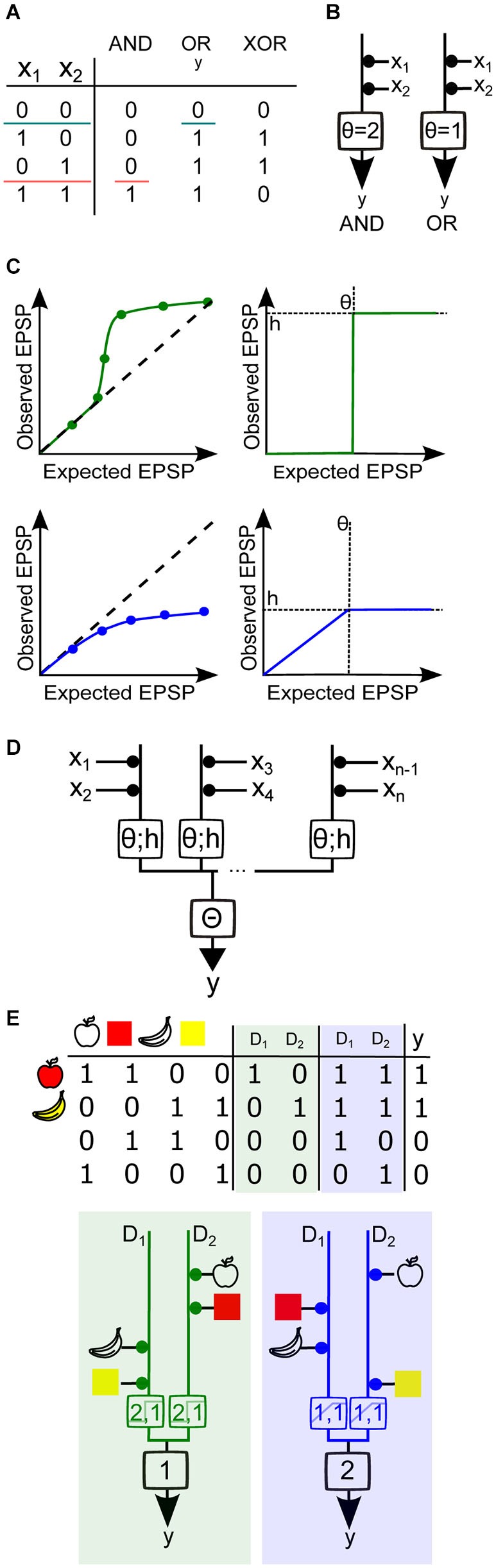
Using Boolean algebra to analyze binary neuron models with dendritic nonlinearities. (A) Truth tables for the Boolean functions AND, OR and XOR for two synaptic inputs (x₁ and x₂). The two colored horizontal lines illustrate how the AND and OR functions are linearly separable, i.e., a single line divides all inputs between two groups, one group having an output of 0 and the other group having an output of 1. Neuron output binary value is denoted as y. (B) Threshold linear unit model neuron with two inputs. The weight of each input is represented by the area of the black disc drawn between the input and the model neuron. Here all weights are equal to 1. A spiking threshold (θ) of 2 allows the model neuron to compute the AND function (left), whereas if θ =1 the neuron computes the OR function (right). (C) Top, Simplified representations of a supralinear sI/O (left) and its mathematical approximation by a Heaviside function (right) with a height h and a threshold θ. Bottom, simplified representation of a sublinear sI/O and its mathematical approximation by a piecewise linear, then saturating function. (D) Generalized diagram representing a two-layer integration model neuron with several compartments and n inputs. Each branch represents a dendritic compartment, and the integration operation performed by this compartment is represented by the box on the branch. The threshold θ and the output value h of the nonlinearity are indicated within the box. The result from the integration from each branch is then linearly summed and compared to the somatic spike threshold Θ. (E) Implementation of the (partial) feature binding problem (pFBP) by binary neurons with two dendritic compartments D₁ and D₂, either supralinear or sublinear. Top, truth table describing various input feature combinations, the response of each dendritic compartment, D (0:inactive/1:active), and the final neuronal output, y. Columns with green shading are the outputs of dendrites exhibiting supralinear operations, while columns shaded in blue contain outputs of dendrites that exhibit sublinear operations. Bottom, Model neuron with equivalent dendrite representation that can implement the pFBP using supralinear (left) or sublinear dendritic compartments (right), with θ and h values indicated in the box. If dendritic integration is supralinear, two groups of inputs are needed to activate a compartment, and a single compartment can trigger a spike. If dendritic integration is sublinear, a single input can activate the dendritic compartment and the two compartments must be active to trigger a spike.

The simplest binary neuron model is called the threshold linear unit, also known as the point neuron model as described first by McCulloch and Pitts (Figure 4B; McCulloch and Pitts, 1943). Synapses are assigned a binary value of 0 or 1, for inactive or active states, which is then multiplied by a positive synaptic weight for excitatory synapses. The sum of the active weighted inputs is then compared to a somatic spike threshold Θ. If this weighted sum is greater than the threshold, the output is assigned a value of 1, and otherwise zero. If one considers a neuron with linearly summing excitatory inputs, adjustment of the threshold allows it to either perform a Boolean AND or OR (Figure 4B). However, it is not possible to find a threshold value and positive synaptic weight that allows the computation of the XOR, the function corresponding to a binary neuron that would fire only when one synapse is active, but not otherwise. This illustrates well the fact that the threshold linear unit can only perform functions that are linearly separable, i.e., there is a set of weights and a spike threshold that categorizes the inputs into two distinct groups, which differ by their output values (Figure 4A). The XOR does not meet this criterion and is therefore a part of the class of functions that are linearly non-separable. To solve this problem we must either invoke a non-monotone function to combine synaptic values (Zador et al., 1992) or consider synaptic inhibition by using negative weights (Mel, 1994; Cazé et al., 2014). Because the former has not been described experimentally, and the latter requires specific wiring within the network, we will focus here on linearly non-separable functions that can be implemented with only excitatory synapses and monotone dendritic operations. These functions are known as positive Boolean functions (Cazé et al., 2013).

Linearly–separable functions represent only a small fraction of all the possible computations (Cazé et al., 2013). However, a neuron with nonlinear dendritic compartments can implement the set of linearly non-separable functions, which encompasses a much larger fraction of all computations (Cazé et al., 2013). Thus both supralinear and sublinear compartments unlock the access to all the possible computations (Mel and Koch, 1990; Mel, 1991). This formal result is true for an infinite number of dendritic compartments (Poirazi and Mel, 2001). This is clearly impossible in practice. So what can a neuron compute with a finite number of dendritic compartments?

To address this question we can construct a two-layer binary model with nonlinear dendritic compartments. We first approximated the dendritic sI/O with functions each having a characteristic dendritic threshold θ, which represents the threshold of the dendritic nonlinearity, and h, which represents the maximal value of the dendritic nonlinearity. To approximate supralinear compartments we used a Heaviside function, and for sublinear functions we used a piecewise linear saturating function (Figure 4C). The output of the dendritic compartments is then linearly summed and compared with spike threshold (Figure 4D). If we vary synaptic weights, the thresholds, and the nonlinear dendritic operations, we can use Boolean analysis to examine the different functions this model can implement. A functionally salient neuronal computation that requires dendritic nonlinearities is the association (or binding) of two features of an object (for example, their shape and color). This is known as the feature binding problem (FBP). If we suppose that that different features of objects are encoded by different groups of pre synaptic neurons impinging on the same post synaptic neuron, then it is obvious that by allowing the features of an object to target the same supralinear dendrite, the coincidence of those features can be easily detected when co-active (i.e., “red” + “apple shape”; Figure 4E). It can also be shown that a sublinear operation can bind features if the inputs that encode object features are distributed onto different dendritic subunits (and the spiking threshold increased). From these simple binary models it is again clear that supralinear operations favor cluster sensitivity and sublinear operations favor scatter sensitivity. However, a keen eye may notice that the sublinear model will also produce a spike if the apple shape and banana shape are both activated. This therefore constitutes a partial FBP. Below we will describe a neuron model with equivalent dendrites that can implement the complete FBP.

Because neurons are known to have both linear and nonlinear compartments, we considered how more realistic dendritic trees could be represented using our simple binary model, by creating a neuron model with equivalent dendrites (Figures 5A,B). All linear regions of the dendritic tree (typically, the perisomatic compartment or the large diameter primary dendrites) were collapsed to a single equivalent “linear” compartment (black regions of schematic neuron and left branch of the model neuron). The nonlinear dendritic compartments receiving more than one synaptic input were represented as a second equivalent dendritic branch. This then generalizes to an equivalent dendritic branch for each nonlinear electrical compartment (Figure 4D). The presence of a linear compartment is important, since inputs contacting two separate nonlinear dendrites will sum linearly (Figure 5A). Also, even inputs contacting the same nonlinear dendrite, provided they are not in the same electrical compartment, will sum linearly.

Figure 5.

Computing a linearly non-separable function (full FBP) with supralinear and sublinear dendrites and using local vs. global synaptic wiring strategies. (A) Left, model neuron with equivalent dendrite representation of two compartments, linear (black) and supralinear (green), and a clustered distribution of object features (object 1 : ×1, ×2 and object 2 : ×3, x4) (local strategy). Right, schematic representations of synaptic placements equivalent to the model on the left. (B) Left, model neuron with equivalent dendrite representation of two compartments, linear (black) and sublinear (blue), and a distributed placement of inputs carrying object features. (C–E) Implementation of the full FBP (y = 1; “apple shape and red” or “banana shape and yellow”). (C), implementation of the full FBP using a model with a supralinear compartment and a local wiring strategy. Inactive inputs are represented in light gray and the corresponding feature in lighter color. (D) Implementation of the full FBP using a model with a supralinear compartment and a global wiring strategy. The area of the disc adjacent to a compartment next to each object feature represents the relative weight of this feature. Here the relative weights used are of 1 and 2. (E) Implementation of the full FBP using a model with sublinear compartment and a global wiring strategy.

Legenstein et al. demonstrated that a model neuron with supralinear dendritic integration is capable of learning and computing the FBP (Legenstein and Maass, 2011). This function detects any correct combination of features for an object, but not incorrect combinations. In the Boolean framework this would be the truth table corresponding to (“red” + “apple shape”) or (“yellow” + “banana shape”). In Figure 4 we showed that two supralinear dendrites are sufficient to solve the FBP for two objects made of two features each. In Figure 5, a neuron displaying at least one supralinear compartment and a linear compartment can also solve the FBP for four inputs. In this case, inputs encoding the features of one object are assigned to the supralinear compartment, and the features corresponding to the other object are assigned to the linear compartment (Figure 5C). Because the features of the object must “cluster” on the same compartment we refer to this model as using a local strategy of computation. Interestingly, it is also possible to implement the same computation using a global strategy, meaning that the features corresponding to one object need to be “scattered” onto both the nonlinear and the linear compartment (Figure 5D), provided that appropriate changes in the synaptic weights and threshold values are also implemented. As shown by Cazé et al. (2013), a model with a linear and sublinear compartment requires the global strategy to perform the FBP (Figure 5E). The synaptic weights and threshold will also be different than in the case of a model neuron with a supralinear compartment. The fact that the FBP can be implemented using a global strategy contrasts with the notion that recognition of an object required the clustering of the inputs carrying its features onto a same dendritic branch (Legenstein and Maass, 2011), and the assumption that two-layer integration models require independent branch-specific operations (Behabadi and Mel, 2014). Using a biophysical model with a model stellate cell morphology, Cazé et al. showed the predictions are robust, since only passive thin dendrites were necessary to convey a scatter sensitivity of output firing, even in the presence of synaptic noise (Cazé et al., 2013).

How might simplified Boolean models be modified for more features and/or more objects? For objects represented by more than two features, clustered strategies would simply require more synaptic inputs, such that the number of the number of inputs per subunit (dendritic compartment) equals the number features. A change in threshold would also be required. The requirements for neuronal computations using sublinear dendrites, however, depend on the type of computation and are less straightforward to determine explicitly. The necessary number of nonlinear subunits also varies given the implementation strategy, the number of objects, the type of nonlinear subunits and the number of features. To solve the FBP with more objects using supralinear operations, each object will require at least one subunit (Cazé et al., 2012). For computations with sublinear operations, Cazé et al. showed that using binary weights, the FBP requires a maximum of 2ⁿ subunits (Cazé et al., 2012). Considering non-binary weights then reduces the number of subunits needed, but this number is still higher than the number of necessary supralinear subunits (n_subunits = n_objects).

In summary, neurons with sublinear dendrites are capable of solving linearly non-separable functions, but require using a distributed strategy of synaptic placement (Figure 5E). These neurons will be scatter sensitive. On the other hand, neurons with supralinear dendrites can also access the same class of computations either by using this strategy (Figure 5C) or by clustering functionally relevant inputs onto the same compartment (Figure 5C). Hence they can be either scatter or cluster sensitive. Thus, the final neuronal computations depend not only on the type of dendritic operation and the dendritic and axosomatic thresholds, but also the global mapping of input features throughout the dendritic tree.

Open Questions

To understand how a neuron integrates its synaptic inputs we need precise knowledge of the morphology, ion channel distribution along the tree, strength and time course of synaptic conductances carrying particular information features, the output spike threshold, and the spatio-temporal pattern of activation of the synapses carrying these features. Although we can determine most of these parameters, as we reviewed above, the most challenging experiments are those designed to estimate the spatio-temporal distribution of all synapses carrying relevant sensory features (i.e., a functional connectivity map). Strategies using injection of viral-based retrograde tracers (Marshel et al., 2010) are powerful for the identification of connected presynaptic cells, but these methods lack information about features conveyed by the inputs. Using in vivo Ca²⁺ imaging, researchers have begun the herculean task of estimating how sensory features are mapped onto dendritic trees by examining how single synapses and dendrites respond to behavioral stimuli. It is not clear whether such feature mapping can be performed on the entire dendritic tree, but initial results provide hints as to whether there may be general mapping rules. Some studies argue that features are clustered in single dendrites within the somato-sensory cortex (Takahashi et al., 2012), consistent with a local computation strategy, while other studies have shown that neighboring synapses onto layer 2/3 pyramidal neurons of the visual and auditory cortex respond maximally for activation of inputs carrying different sensory features (Jia et al., 2010; Chen et al., 2011), consistent with a global strategy. In light of the conclusions described here, both computation strategies are capable of performing linearly non-separable functions.

Why might neurons use different dendritic operations and wiring strategies? It is conceivable that differences in timing of sensory development or optimal local circuit wiring may constrain wiring strategies for particular neurons. Thus to perform the same computation, different wiring and dendritic strategies are needed. Global wiring strategies are more amenable to “random wiring,” in contrast to the specific connectivity required for engaging local strategies. We speculate that different dendritic operations may be implemented by neurons given certain biological constraints, such as limitations in the number and location of synapses carrying a particular feature, or spike threshold. For example when both principal neurons and interneurons receive a common set of input features along relatively fixed axonal projections, but are required to perform different computations, they may engage different dendritic operations. In the cerebellum interneurons have been shown to exhibit sublinear dendritic operations (Abrahamsson et al., 2012; Vervaeke et al., 2012) on their parallel fiber inputs, while Purkinje cells are thought to receive the same or similar features from the same set of input fibers, yet display supralinear dendritic operations (Rancz and Häusser, 2006). One could speculate that the different nonlinearities and synaptic placement strategies of Purkinje neurons and interneurons may enable them to implement complementary computations, which ultimately could result in a microcircuit that is highly selective for specific input patterns.

What are the wiring rules? Three possible wiring strategies are (1) predetermined connectivity (genetically encoded); (2) random connectivity; and (3) activity-dependent pruning and stabilization of connections. Although the exact contribution of each mechanism is yet to be determined, synaptic plasticity has been shown to modify and ultimately determine the functional connectivity. For example computational modeling showed that a local wiring strategy, in which synapses carrying features of objects are clustered, can be learned using simple plasticity rules (Legenstein and Maass, 2011). Experimental evidence supports this theoretical work, suggesting that activity-dependent, branch-specific plasticity strengthens clustered synaptic inputs and their compartmentalization (Makara et al., 2009; Makino and Malinow, 2011; Takahashi et al., 2012). On the other hand, synaptic plasticity could also reinforce global computational strategies. In cerebellar stellate cells, high-frequency firing of clustered inputs has been described to induce profound presynaptic short- and long-term synaptic depression (Beierlein and Regehr, 2006; Soler-Llavina and Sabatini, 2006). Such plasticity mechanisms would reinforce the neuron’s scatter sensitivity, and thus tend to optimize the output firing for specific spatially and temporally sparse synaptic activity patterns (Abrahamsson et al., 2012; Cazé et al., 2013).

Synchronized neuronal activity is known to cause oscillations of the dendritic voltage, which would inevitably reinforce electrical interactions between dendrites and thus alter the effective number of isolated dendritic subunits that contribute to the neuronal computation. For example, Remme et al. (2009) showed theoretically that input-dependent synchronization of intrinsic dendritic voltage oscillations can facilitate global voltage propagation, even throughout highly distributed dendritic trees. It will be important to examine how local and global dendritic integration strategies might be influenced by brain oscillations, thus ultimately altering neuronal and even circuit computations.

Since many types of interneurons are known to contact specific locations within the dendritic tree, inhibition will undoubtedly influence integration properties and information processing by neuronal circuits (as reviewed by Palmer et al., 2012). Nevertheless, the experimental challenge is to determine not only the timing and location of inhibition within the dendrite, in order to determine their alteration of dendritic operations, but also whether particular features are conveyed similarly or differently by excitatory and inhibitory inputs. Although complex, the problem is critical to understanding brain function as the balance of excitation and inhibition is well known to be tightly regulated, with alterations being implicated in disease (Yizhar et al., 2011). Using the Boolean analysis of equivalent dendrites, one can deduce that negative weight associated with inhibition is capable of performing the Boolean NOT function. Such a function would enable a simple implementation of XOR computations, further expanding the number of computable linearly non-separable functions.

Summary

In this review we described categories of biophysical and cellular mechanisms that influence dendritic operations: passive and active membrane properties of the dendritic tree, the time course and amplitude of synaptic activation, the output spike threshold, and finally the location and pattern of the activation of synaptic inputs. We discussed how each of these parameters shapes and tunes the sI/O. We briefly discussed techniques for the characterization of dendritic operations, including electrode-based methods to stimulate and/or record from dendrites, optical techniques to image dendritic activity or uncage neurotransmitter, and biophysical modeling. In order to understand how the major classes of dendritic operations (linear, sublinear and supralinear) link to neuronal computations, we reviewed the use of binary models associated with Boolean analysis. This analysis provides insight into the types of computable neuronal functions, such as the object feature binding problem. We also reviewed how such functions can be implemented with either supralinear or sublinear dendrites depending on the spatial mapping of those features within the dendritic tree. Because the synaptic activity pattern ultimately determines the neuronal computations, we propose that the elemental computational unit is the neuron rather than the dendrite (Cazé et al., 2014). Although there are cases (local strategies) where dendritic operations can dictate the neuronal computation, dendritic operations must be studied and understood in the context of the knowledge of the wiring of specific features onto the dendritic tree.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.