Two-Dimensional Informative Array Testing

Summary

Array-based group testing algorithms for case identification are widely used in infectious disease testing, drug discovery, and genetics. In this paper, we generalize previous statistical work in array testing to account for heterogeneity among individuals being tested. We first derive closed-form expressions for the expected number of tests (efficiency) and misclassification probabilities (sensitivity, specificity, predictive values) for two-dimensional array testing in a heterogeneous population. We then propose two “informative” array construction techniques which exploit population heterogeneity in ways that can substantially improve testing efficiency when compared to classical approaches which regard the population as homogeneous. Furthermore, a useful byproduct of our methodology is that misclassification probabilities can be estimated on a per-individual basis. We illustrate our new procedures using chlamydia and gonorrhea testing data collected in Nebraska as part of the Infertility Prevention Project.

1. Introduction

Group testing, where individual specimens are first pooled together and then tested simultaneously, is recognized as a cost-effective strategy to screen large numbers of individuals for infection or other binary characteristics. Dorfman (1943) first conceptualized the idea of group testing (pooled testing) in screening military inductees for syphilis during World War II. Since this seminal work, group testing has been applied to a variety of areas, including infectious disease testing (Pilcher et al., 2005; Westreich et al., 2008), drug discovery (Xie et al., 2001; Remlinger et al., 2006), and genetics (Berger, Mandell, and Subrahmanya, 2000).

Statistical research in group testing has traditionally followed a bifurcated structure, consisting of work in case identification and prevalence estimation (including regression modeling). This paper deals with the former in the context of infectious disease testing, motivated by our involvement with the Infertility Prevention Project; see Section 5. In the case identification problem, the primary goal is to classify each individual as positive or negative. If a pool tests negative, then all individuals in the pool can be declared negative; this enables one to diagnose multiple individuals at the expense of a single test. If a pool tests positive, further testing is required to determine the diagnosis of each individual in the pool. We refer to the process of retesting individuals in positive pools as decoding.

Decoding positive pools can take on many forms. This has triggered the development of many decoding algorithms which, when compared to individual testing, can greatly reduce the number of tests needed. Each algorithm can be categorized as one of two types: hierarchical or non-hierarchical. A hierarchical algorithm involves retesting non-overlapping subsets of individuals from positive pools, in multiple stages, until each individual is classified as positive or negative. Dorfman’s original strategy is a two-stage hierarchical algorithm. In the first stage, the (master) pool is tested; if positive, each individual is retested in the second stage. Higher-stage algorithms can be effective at increasing efficiency but are also more complex. For example, Pilcher et al. (2005) consider a three-stage algorithm where individuals are first tested in a master pool of size 90. If positive, subpools of size 10 are tested in the second stage, and individual testing is used to decode all positive subpools in the third stage. Litvak, Tu, and Pagano (1994) propose a multiple-stage hierarchical algorithm where positive pools are subsequently “halved” until all positive and negative individuals have been identified.

The most commonly used non-hierarchical procedure is array testing, where individual specimens are assigned to the cells of an array. In two-dimensional array testing, also known as matrix pooling, row pools and column pools are tested in the first stage. The second stage involves individual testing for specimens not classified as negative in the first stage. Phatarfod and Sudbury (1994) introduced the statistical community to array testing for blood screening, although its previous use in genetics applications is well documented; see Berger et al. (2000) and the references therein. Berger et al. (2000) describe two- and higher-dimensional arrays for DNA library screening; however, like Phatarfod and Sudbury (1994), their work assumes that diagnostic tests are error-free. Kim et al. (2007) and Kim and Hudgens (2009) have recently proposed array testing decoding algorithms which account for imperfect testing; their work provides a comprehensive investigation of the operating characteristics of two- and higher-dimensional array testing, including efficiency and classification accuracy. Perhaps because of these advances, array testing is now commonly used for case identification in infectious disease testing and related applications (May et al., 2010, Tilghman et al., 2011).

Until now, statistical research in array testing for case identification has assumed that each individual has the same probability of positivity, say, p. However, in most infectious disease situations where array testing is potentially applicable, available covariates can provide valuable information about the true statuses of the individuals. For example, clinical, demographic, and behavioral information can shed enormous light on which individuals are more likely to be positive for chlamydia, gonorrhea, and other infections (Centers for Disease Control and Prevention, CDC, 2010). If this information is available, then it is more natural to conceptualize the population of individuals as heterogeneous with different probabilities of positivity. Recent research by Bilder, Tebbs, and Chen (2010) and McMahan, Tebbs, and Bilder (2011) has shown that exploiting this information can provide large gains in efficiency when using Sterrett (1957) and Dorfman (1943) retesting algorithms, respectively, both of which are hierarchical in nature. In the light of this work, one might naturally wonder if incorporating covariate information could lead to similar gains when array testing is used.

In this paper, we generalize the two-dimensional array testing work of Kim et al. (2007) to account for population heterogeneity. In Section 2, we derive expressions for the efficiency and for individual-specific probabilities of misclassification in a heterogeneous population. In Section 3, we propose two “informative” array testing procedures which exploit population heterogeneity, and in Section 4, we demonstrate that these are more efficient than traditional array procedures which regard the population as homogeneous. Additionally, we provide a thorough comparison involving our new procedures and the most efficient hierarchical procedures proposed by Bilder et al. (2010) and McMahan et al. (2011). In Section 5, we implement our methods using chlamydia and gonorrhea testing data collected in Nebraska for the Infertility Prevention Project. In Section 6, we conclude with a discussion.

2. Operating Characteristics

2.1 Notation and Assumptions

Consider an array with J > 1 rows and K > 1 columns, and denote by ${\mathcal{I}}_{\mathit{jk}}$ the individual assigned to the (j, k) cell, for j = 1, 2,…, J and k = 1,2,…, K. Let ${\stackrel{\sim }{g}}_{\mathit{jk}}$ denote the true binary status of ${\mathcal{I}}_{\mathit{jk}}$, and let $p_{\mathit{jk}}=\mathrm{pr}({\stackrel{\sim }{g}}_{\mathit{jk}}=1)$ denote the true probability of positivity. We assume that the ${\stackrel{\sim }{g}}_{\mathit{jk}}’\mathrm{s}$ are mutually independent random variables.

Array testing begins by testing the J rows and K columns. Define ${\stackrel{\sim }{R}}_J=I({\sum }_{k=1}^K{\stackrel{\sim }{g}}_{\mathit{jk}}>0)$ and ${\stackrel{\sim }{C}}_k=I({\sum }_{j=1}^J{\stackrel{\sim }{g}}_{\mathit{jk}}>0)$, for j = 1,2,…, J and k = 1,2, …, K, where I(·) is the indicator function. That is, ${\stackrel{\sim }{R}}_j=1({\stackrel{\sim }{C}}_k=1)$ if the jth row (kth column) contains at least one positive individual and ${\stackrel{\sim }{R}}_j=0({\stackrel{\sim }{C}}_k=0)$ otherwise. Let R_j = 1 (C_k = 1) if the jth row (kth column) tests positive and let R_j = 0 (C_k = 0) otherwise. As in Kim et al. (2007), we assume that diagnostic test outcomes are independent, conditional on the true statuses of the pools (individuals) being tested. We also assume that if a pool contains at least one positive individual, it will test positive with probability S_e (test sensitivity) and if a pool consists entirely of negative individuals, it will test negative with probability S_p (test specificity). Finally, we assume that S_e and S_p do not depend on the size of the pool; this assumption is standard in the group testing literature.

Under the assumption that S_e = S_p = 1, Phatarfod and Sudbury (1994) propose that ${\mathcal{I}}_{\mathit{jk}}$ be classified as negative if R_j = 0 or C_k = 0 and that ${\mathcal{I}}_{\mathit{jk}}$ be retested individually if R_j = 1 and C_k = 1. However, when diagnostic tests are not perfect, it is possible that one or more row (column) tests positive while all columns (rows) test negative. Acknowledging this potential ambiguity, we partition all individuals in the array into one of two classes:

$${\mathcal{M}}_{+}=\{{\mathcal{I}}_{\mathit{jk}}:I(R_j=1,C_k=1)+I(R_j=1,{\sum }_{k=1}^K{C}_k=0)+I({\sum }_{j=1}^J{R}_j=0,C_k=1)=1\}$$

and ${\mathcal{M}}_{-}={\overline{\mathcal{M}}}_{+}$. In this paper, we adopt the classification methodology in Kim et al. (2007); that is, individuals in ${\mathcal{M}}_{+}$ are classified by individual testing and individuals in ${\mathcal{M}}_{-}$ are classified as negative without additional testing.

2.2 Efficiency

Let T_jk denote the number of tests required to classify ${\mathcal{I}}_{\mathit{jk}}$ after initial row and column testing has been completed. Similarly, let T denote the number of tests required to decode the full array so that $E(T)=J+K+{\sum }_{j=1}^J{\sum }_{k=1}^{K}E(T_{\mathit{jk}})$, where

$$E(T_{\mathit{jk}})=\mathrm{pr}(R_j=1,C_k=1)+\mathrm{pr}\left(R_j=1,{\displaystyle \sum _{k\prime =1}^K{C}_{k\prime }=0}\right)+\mathrm{pr}\left({\displaystyle \sum _{j\prime =1}^J{R}_{j\prime }=0,C_k=1}\right).$$ (1)

We call E(T) the efficiency and now present closed-form expressions for each probability in (1). Derivations are in Web Appendix A.

The first probability in (1) is the easiest to calculate; it is given by

$$\mathrm{pr}(R_j=1,C_k=1)=S_e^2+{(1-S_e-S_p)}^2\left\{\frac{{\pi }_C(k){\pi }_R(j)}{1-p_{\mathit{jk}}}\right\}+\{S_e(1-S_p)-S_e^2\}\{{\pi }_R(j)+{\pi }_C(k)\},$$

where ${\pi }_R(j)={\prod }_{k=1}^K(1-p_{\mathit{jk}})$ and ${\pi }_C(k)={\prod }_{j=1}^J(1-p_{\mathit{jk}})$ denote the probability that the jth row and kth column, respectively, are truly negative. To find the second probability in (1), one must consider each of the 2^K configurations of the true column statuses; i.e., $\{{\stackrel{\sim }{C}}_1={\stackrel{\sim }{c}}_1,{\stackrel{\sim }{C}}_2={\stackrel{\sim }{c}}_2,\dots ,{\stackrel{\sim }{C}}_K={\stackrel{\sim }{c}}_K\}$, where ${\stackrel{\sim }{c}}_k\in \{0,1\}$, for k = 1,2,…, K. Define ${\mathcal{B}}_c$, for c = 1,2,…, K, to be the set of all c-combinations of ${\mathcal{K}}_0=\{1,2,\dots ,K\}$ and let ${\mathcal{B}}_0=\varnothing$, the empty set. In our notation, the set $\mathcal{B}\in {\mathcal{B}}_c$ corresponds to the event

$$\{{\stackrel{\sim }{C}}_1=I(1\in \mathcal{B}),{\stackrel{\sim }{C}}_2=I(2\in \mathcal{B}),\dots ,{\stackrel{\sim }{C}}_K=I(K\in \mathcal{B})\}.$$

For example, suppose that K = 3 so that ${\mathcal{K}}_0=\{1,2,3\}$, ${\mathcal{B}}_0=\varnothing$, ${\mathcal{B}}_1=\left\{\right\{1\},\{2\},\{3\left\}\right\}$, ${\mathcal{B}}_2=\left\{\right\{1,2\},\{1,3\},\{2,3\left\}\right\}$, and ${\mathcal{B}}_3=\left\{\right\{1,2,3\left\}\right\}$. In this example, the set $\mathcal{B}=\{1,2\}\in {\mathcal{B}}_2$ corresponds to $\{{\stackrel{\sim }{C}}_1=1,{\stackrel{\sim }{C}}_2=1,{\stackrel{\sim }{C}}_3=0\}$, the event that columns 1 and 2 are truly positive and column 3 is truly negative. We show in Web Appendix A that

$$\mathrm{pr}\left(R_j=1,{\displaystyle \sum _{k\prime =1}^K{C}_{k\prime }=0}\right)={\displaystyle \sum _{c=0}^K{\displaystyle \sum _{\mathcal{B}\in {\mathcal{B}}_c}\{{\gamma }_0(c,K){\lambda }_{\mathcal{C}}(\mathcal{B}|{\mathcal{B}}_0,j)+{\gamma }_1(c,K){\pi }_R(j){\lambda }_{\mathcal{C}}(\mathcal{B}|{\mathcal{K}}_0,j)\}}},$$

where ${\gamma }_0(c,K)=S_e{(1-S_e)}^c{S}_p^{K-c},{\gamma }_1(c,K)=(1-S_e-S_p){(1-S_e)}^c{S}_p^{K-c}$, and the set function

$${\lambda }_{\mathcal{C}}(\mathcal{B}|\mathcal{S},j)=\prod _{k\prime \in \mathcal{B}}\left\{1-\frac{{\pi }_C(k\prime )}{{(1-p_{\mathit{jk}\prime })}^{I(k\prime \in \mathcal{S})}}\right\}\prod _{k\prime \in \overline{\mathcal{B}}}\frac{{\pi }_C(k\prime )}{{(1-p_{\mathit{jk}\prime })}^{I(k\prime \in \mathcal{S})}},$$

where $\overline{\mathcal{B}}={\mathcal{K}}_0\backslash \mathcal{B}$. Finding the third probability in (1) proceeds analogously. Define ${\mathcal{A}}_r$, for r = 1, 2, …, J, to be the set of all r-combinations of ${\mathcal{J}}_0=\{1,2,\dots ,J\}$ and let ${\mathcal{A}}_0=\varnothing$. The set $\mathcal{A}\in {\mathcal{A}}_r$ corresponds to

$$\{{\stackrel{\sim }{R}}_1=I(1\in \mathcal{A}),{\stackrel{\sim }{R}}_2=I(2\in \mathcal{A}),\dots ,{\stackrel{\sim }{R}}_J=I(K\in \mathcal{A})\}$$

and

$$\mathrm{pr}\left({\displaystyle \sum _{j\prime =1}^J{R}_{j\prime }=0,C_k=1}\right)={\displaystyle \sum _{r=0}^J{\displaystyle \sum _{\mathcal{A}\in {\mathcal{A}}_r}\{{\gamma }_0(r,J){\lambda }_{\mathcal{R}}(\mathcal{A}|{\mathcal{A}}_0,k)+{\gamma }_1(r,J){\pi }_C(k){\lambda }_{\mathcal{R}}(\mathcal{A}|{\mathcal{J}}_0,k)\},}}$$

where, with $\overline{\mathcal{A}}={\mathcal{J}}_0\backslash \mathcal{A}$ the set function

$${\lambda }_{\mathcal{R}}(\mathcal{A}|\mathcal{S},k)=\underset{j\prime \in \mathcal{A}}{\Pi }\{1-\frac{{\pi }_R(j\prime )}{{(1-p_{j\prime k})}^{I(j\prime \in \mathcal{S})}}\}\prod _{j\prime \in \overline{\mathcal{A}}}\frac{{\pi }_R(j\prime )}{{(1-p_{j\prime k})}^{I(j\prime \in \mathcal{S})}}.$$

2.3 Classification Accuracy

Let ${\mathcal{I}}_{\mathit{jk}}^{+}({\mathcal{I}}_{\mathit{jk}}^{-})$ denote the event that individual ${\mathcal{I}}_{\mathit{jk}}$ is classified as positive (negative) and define the pooling sensitivity to be $P{S}_e^{{\mathcal{I}}_{\mathit{jk}}}=\mathrm{pr}({\mathcal{I}}_{\mathit{jk}}^{+}|{\stackrel{\sim }{g}}_{\mathit{jk}}=1)$ and the pooling specificity to be $P{S}_e^{{\mathcal{I}}_{\mathit{jk}}}=\mathrm{pr}({\mathcal{I}}_{\mathit{jk}}^{-}|{\stackrel{\sim }{g}}_{\mathit{jk}}=0)$. We emphasize that pooling sensitivity and pooling specificity are individual-specific; i.e., $P{S}_e^{{\mathcal{I}}_{\mathit{jk}}}$ and $P{S}_p^{{\mathcal{I}}_{\mathit{jk}}}$ are different for different individuals (a byproduct of heterogeneity). We show in Web Appendix B that, under two-dimensional array testing,

$$P{S}_e^{{\mathcal{I}}_{\mathit{jk}}}=S_e^3+S_e^2(1-S_e)\left\{{\displaystyle \prod _{k\prime \ne k}\mathrm{pr}(C_{k\prime }=0)+{\displaystyle \prod _{j\prime \ne j}\mathrm{pr}(R_{j\prime }=0)}}\right\},$$

where $\mathrm{pr}(C_{k\prime }=0)=1-S_e-(1-S_e-S_p){\pi }_C(k\prime )$ and $\mathrm{pr}(R_{j\prime }=0)=1-S_e-(1-S_e-S_p){\pi }_R(j\prime )$.

We also show in Web Appendix B that ${\mathit{PS}}_p^{{\mathcal{I}}_{\mathit{jk}}}$ satisfies the equation

$$\begin{array}{c}\frac{1-P{S}_p^{{\mathcal{I}}_{\mathit{jk}}}}{1-S_p}=S_e^2+{(1-S_e-S_p)}^2\left\{\frac{{\pi }_C(k){\pi }_R(j)}{{(1-p_{\mathit{jk}})}^2}\right\}+\{S_e(1-S_p)-S_e^2\}\left\{\frac{{\pi }_R(j)+{\pi }_C(k)}{1-p_{\mathit{jk}}}\right\}\\ +{\displaystyle \sum _{c=0}^K{\displaystyle \sum _{\mathcal{B}\in {\mathcal{B}}_c}\left[{\gamma }_0(c,K){\lambda }_{\mathcal{C}}(\mathcal{B}|\{k\},j)+\frac{{\gamma }_1(c,K){\pi }_R(j){\lambda }_{\mathcal{C}}(\mathcal{B}|{\mathcal{K}}_0,j)}{1-p_{\mathit{jk}}}\right]}}\\ +{\displaystyle \sum _{r=0}^J{\displaystyle \sum _{\mathcal{A}\in {\mathcal{A}}_r}\left[{\gamma }_0(r,J){\lambda }_{\mathcal{R}}(\mathcal{A}|\{j\},k)+\frac{{\gamma }_1(r,J){\pi }_C(k){\lambda }_{\mathcal{R}}(\mathcal{A}|{\mathcal{J}}_0,k)}{1-p_{\mathit{jk}}}\right]}},\end{array}$$

where γ₀(·, ·), γ₁(·, ·), ${\lambda }_{\mathcal{C}}(\mathcal{B}|·,j)$ and ${\lambda }_{\mathcal{R}}(\mathcal{A}|·,k)$ were defined in Section 2.2. Define the pooling positive predictive value to be $PP{V}^{{\mathcal{I}}_{\mathit{jk}}}=\mathrm{pr}({\stackrel{\sim }{g}}_{\mathit{jk}}=1|{\mathcal{I}}_{\mathit{jk}}^{+})$ and the pooling negative predictive value to be $NP{V}^{{\mathcal{I}}_{\mathit{jk}}}=\mathrm{pr}({\stackrel{\sim }{g}}_{\mathit{jk}}=0|{\mathcal{I}}_{\mathit{jk}}^{-})$. Direct applications of Bayes’ Rule give

$$\begin{array}{l}PP{V}^{{\mathcal{I}}_{\mathit{jk}}}=\frac{p_{\mathit{jk}}P{S}_e^{{\mathcal{I}}_{\mathit{jk}}}}{p_{\mathit{jk}}P{S}_e^{{\mathcal{I}}_{\mathit{jk}}}+(1-p_{\mathit{jk}})(1-P{S}_p^{{\mathcal{I}}_{\mathit{jk}}})}\\ NP{V}^{{\mathcal{I}}_{\mathit{jk}}}=\frac{(1-p_{\mathit{jk}})P{S}_p^{{\mathcal{I}}_{\mathit{jk}}}}{(1-p_{\mathit{jk}})P{S}_p^{{\mathcal{I}}_{\mathit{jk}}}+p_{\mathit{jk}}(1-P{S}_e^{{\mathcal{I}}_{\mathit{jk}}})}.\end{array}$$

These formulae are also individual-specific, and therefore provide valuable information about which individuals are more likely to be correctly diagnosed. In Section 5, we illustrate the potential use of these probabilities to detect those individuals most likely to be misdiagnosed for chlamydia and gonorrhea. When p_jk = p, for all j and k, ${\mathit{PPV}}^{{\mathcal{I}}_{\mathit{jk}}}$ and ${\mathit{NPV}}^{{\mathcal{I}}_{\mathit{jk}}}$ are constant functions of p, S_e, and S_p (Kim et al., 2007). In other words, treating the population as homogeneous offers no insight on which specific individuals may be misdiagnosed.

3. Informative Array Construction

3.1 Motivation

In this section, we describe two construction techniques which exploit heterogeneity among individuals in an array. The goal of using each construction is to reduce E(T) when compared to traditional (random) assignments which do not acknowledge heterogeneity. We henceforth restrict attention to square arrays with dimensions K × K; i.e., J = K.

Suppose N = K² individuals are to be assigned to an array, and denote the true status of ${\mathcal{I}}_i$, the ith individual, by ${\stackrel{\sim }{g}}_i$, where $\mathrm{pr}({\stackrel{\sim }{g}}_i=1)=p_i$. Note that we have adjusted our double subscript notation from Section 2 to acknowledge that individuals have not yet been assigned to the array. To motivate an informative construction, we take an Oracle’s perspective under the assumption of no testing error. Suppose the true statuses ${\stackrel{\sim }{g}}_1,{\stackrel{\sim }{g}}_2,\dots ,{\stackrel{\sim }{g}}_N$ are known before testing begins and define ${\mathcal{C}}_0=\{{\mathcal{I}}_i:\stackrel{\sim }{g}=0,i=1,2,\dots ,N\}$ and ${\mathcal{C}}_1=\{{\mathcal{I}}_i:{\stackrel{\sim }{g}}_i=1,i=1,2,\dots ,N\}$. In this situation, to minimize the total number of tests, an Oracle would assign individuals to the array in a way that minimizes the number of rows and columns that are positive. Of course, depending on the size of the array and the size of ${\mathcal{C}}_1$, there are multiple arrangements available. The salient point is that many of these arrangements would “cluster” individuals belonging to ${\mathcal{C}}_1$ within the array. By ordering the N individuals ${\mathcal{I}}_{(1)},{\mathcal{I}}_{(2)},\dots ,{\mathcal{I}}_{(N)}$ corresponding to p₍₁₎ ≤ p₍₂₎ ≤ ⋯ ≤ p_(N), we propose two specific arrangements that preserve the underlying flavor of the Oracle’s approach.

3.2 Gradient Design

Our gradient construction clusters higher-risk individuals in the left-most columns of the array. Specifically, we start by placing the highest-risk individual ${\mathcal{I}}_{(N)}$ in the (1,1) cell, the second highest-risk individual ${\mathcal{I}}_{(N-1)}$ in the (2,1) cell, and so on, until the first column is filled. Then, individual ${\mathcal{I}}_{(N-K-1)}$ is placed in the (1, 2) cell, individual ${\mathcal{I}}_{(N-K-2)}$ in the (2, 2) cell, and so on, until the second column is filled. This process continues, moving from left to right across the array, until the lowest-risk individual ${\mathcal{I}}_{(1)}$ is placed in the (K, K) cell. The motivation for this design is that, especially in low prevalence settings, only a small number of the K² individuals are likely positive. Therefore, when compared to an uninformative arrangement, placing the highest-risk individuals on one side of the array can reduce the number of columns which test positive. Figure 1 (left) illustrates the gradient design when K = 3. A gradient arrangement could also target the right-hand side of the array or the rows instead of the columns; we adopt the left-hand/column arrangement, as depicted in Figure 1, without loss of generality.

Figure 1.

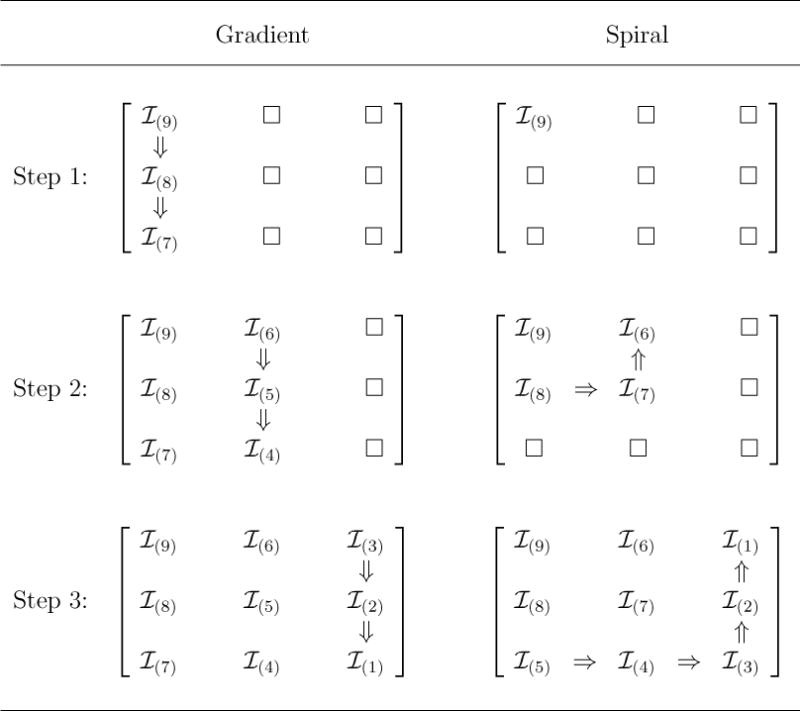
Gradient and spiral array construction. We depict 3×3 constructions using individuals ${\mathcal{I}}_{(1)},{\mathcal{I}}_{(2)},\dots ,{\mathcal{I}}_{(9)}$ corresponding to p₍₁₎ ≤ p₍₂₎ ≤ ⋯ ≤ p₍₉₎. Constructing K × K arrays for other values of K is done similarly.

3.3 Spiral Design

Another method of clustering is to assign the higher-risk individuals to a square sub-array within the master array. Specifically, starting at the upper left-hand corner of the array (again, without loss), our spiral construction technique assigns the highest-risk individual ${\mathcal{I}}_{(1)}$ to the (1, 1) cell, the next three highest-risk individuals ${\mathcal{I}}_{(N-1)}$, ${\mathcal{I}}_{(N-2)}$, and ${\mathcal{I}}_{(N-3)}$ to cells (2, 1), (2, 2), and (1, 2), respectively, and so on, until the lowest-risk 2K − 1 individuals are placed in the bottom row and right-most column. Figure 1 (right) displays a spiral construction when K = 3. The goal of the spiral design is to isolate positive individuals in a small square, leaving a large majority of the rows and columns to test negative.

3.4 Discussion

Among all two-dimensional array arrangements, our results in Section 4 provide overwhelming evidence that gradient and spiral designs can rarely be beaten in terms of efficiency. However, we do not assert that either construction will minimize E(T) over the N! possible arrangements of ${\mathcal{I}}_{(1)},{\mathcal{I}}_{(2)},\dots ,{\mathcal{I}}_{(N)}$. In fact, because matrices can be rotated and/or reflected (about center columns, center rows, or the diagonal) and because rows/columns can be rearranged, the number of unique values of E(T), for a given set of N = K² individuals with different risk probabilities, is slightly less than N!. Towards finding an “optimal” arrangement, we believe that the necessary optimization and counting techniques would prove to be too difficult to implement in practice and would likely be at most marginally more efficient than either a gradient or spiral design. An exhaustive search over all possible arrangements could be used if K is very small; such an exercise would be computationally infeasible otherwise. It is also important to note that both gradient and spiral arrangements are simple to construct. This may be the most important consideration if lab technicians are filling the arrays manually.

4. Comparisons

We first compare our gradient (GA) and spiral (SA) designs to “uninformative” array testing (A); i.e., where individuals are assigned to cells at random. We then compare the most efficient informative array design to two other recently proposed informative hierarchical algorithms.

4.1 Array Comparisons

Let p denote the mean prevalence in the population. To acknowledge heterogeneity, we specify that true probabilities p_i follow a beta distribution with parameters α and β = β(α, p) = α(1 − p)/p. It is easy to show that this distribution has mean p and variance p²(1 − p)/(α + p). Consequently, smaller values of α correspond to more heterogeneity. The performance of our informative designs depends on both the mean prevalence p and the amount of heterogeneity through α. The distribution associated with α = 0 should be viewed as the limiting distribution as α → 0. In Web Appendix C, we prove that this limiting distribution is Bernoulli with mean p. This distribution is not realistic in practice, but it is useful in serving as the distribution with the maximum amount of heterogeneity.

Let X₍₁₎, X₍₂₎, …, X_(N) denote the order statistics of a random sample from a beta(α, β) distribution, where β = α(1 − p)/p, and set $p_{(i)}^{\alpha ,\beta }=E(X_{(i)})$, for i = 1,2, …, N. When α = 0, $E(X_{(i)})=1-{\displaystyle {\sum }_{l=i}^N{(}_l^N){(1-p)}^l{p}^{N-l}}$. When α > 0, E(X_(i)) can be found using standard calculations involving order statistic distributions (which we carry out numerically in R). In this section, we characterize performance using arrays containing $p_{(1)}^{\alpha ,\beta }<p_{(2)}^{\alpha ,\beta }<\cdots <p_{(N)}^{\alpha ,\beta }$. Doing so provides an assessment that does not introduce extra variability from having to simulate the individual probabilities. Define $E(T|\mathcal{Z})$ where $\mathcal{Z}\in \{\mathrm{GA},\mathrm{SA},\mathrm{A}\}$, to be the efficiency when using array procedure $\mathcal{Z}$. Using the expressions in Section 2, we can calculate E(T|GA) and E(T|SA) exactly. Calculating E(T|A) exactly would unfortunately involve averaging over the N! values of E(T), one for each arrangement of $p_{(1)}^{\alpha ,\beta },p_{(2)}^{\alpha ,\beta },\dots ,p_{(N)}^{\alpha ,\beta }$. This is not attempted for the same reasons outlined in Section 3.

In our first investigation, we set S_e = S_p = 1. This removes the effect of imperfect testing and presents an unobscured comparison of GA, SA, and A. We let the mean prevalence p = 0.01, 0.05, 0.10, and 0.20. For each p, we first find the optimal (i.e., most efficient) array dimension K for A using the work of Hudgens and Kim (2011). This same K is then also used for GA and SA (doing this slightly handicaps the performance of GA and SA). To examine different levels of heterogeneity, we let α = 0,0.05,0.10,0.50, and 1. For each (α, p) configuration, we select 10,000 arrangements of $p_{(1)}^{\alpha ,\beta },p_{(2)}^{\alpha ,\beta },\dots ,p_{(N)}^{\alpha ,\beta }$. at random, where N = K², and compute E(T) for each one. In Figure 2, we display box-plots of the 10,000 values of E(T)|N, along with the corresponding values of E(T|GA)|N and E(T|SA)|N. From Figure 2, it is easy to see that both GA and SA can greatly improve efficiency; when compared to the median efficiency of A, the best of the two informative designs confers gains of up to 4%, 10%, 18%, and 25%, when p = 0.01,0.05,0.10, and 0.20, respectively. GA and SA perform better when p is larger and/or when the variability in the population is larger (α is smaller), and GA performs marginally better than SA except occasionally for larger p. It is worth noting that when the efficiency of A is larger than that of individual testing; i.e., when E(T)|N > 1, GA and SA can still provide a sizeable reduction in testing costs.

Figure 2.

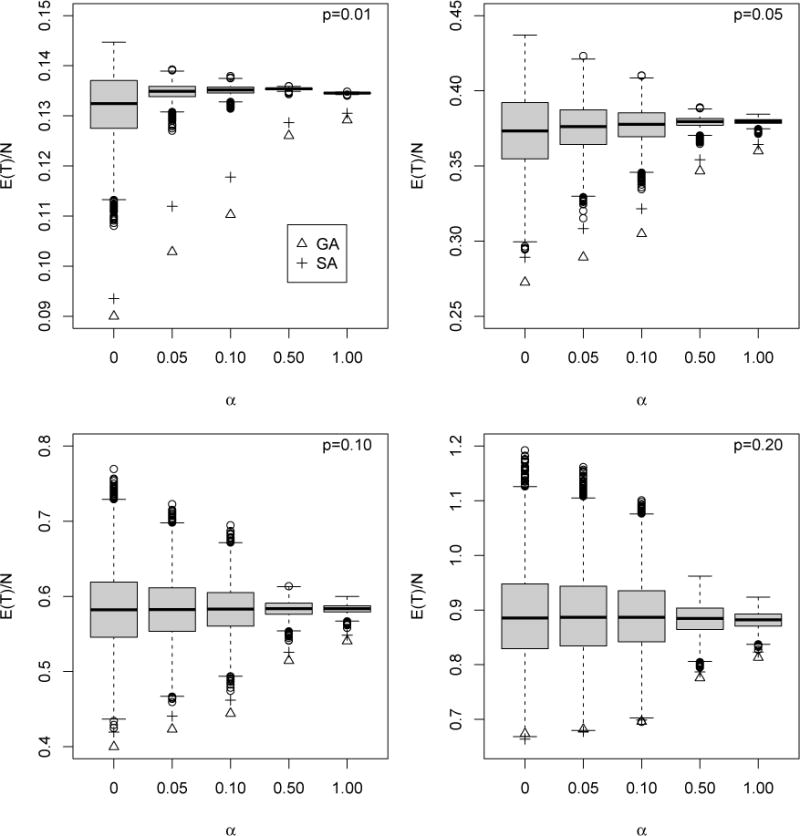
Efficiency comparison with perfect testing. Box-plots of values of E(T)/N for 10, 000 randomly-selected arrangements of A. GA (∆) and SA (+) are also included. The optimal square array size K has been used for each value of p; see Hudgens and Kim (2011). Note that the vertical axis scaling is not uniform across the plots.

In a second investigation, we assess the effect that testing error has on the efficiency, taking S_e ∈ {0.90, 0.95, 0.99} and S_p ∈ {0.90, 0.95, 0.99}. To examine different levels of heterogeneity, we take α ∈ {0.10, 0.50, 1}, and we consider mean prevalence levels p ∈ {0.01, 0.02, …, 0.20}. For each (p, S_e, S_p) combination, we first find the most efficient array size K for A using the work of Kim et al. (2007), which accounts for testing error. We then compute the per-individual efficiencies E(T|GA)/N and E(T|SA)/N for each (α, p, S_e, S_p) combination using the expressions in Section 2; E(T|A)/N is approximated using Equation (13) in Kim et al. (2007) for each specified (p, S_e, S_p) combination. Figure 3 displays the results when α = 0.50; Web Appendix C contains the α = 0.10 and α = 1 figures and an analogous comparison of GA, SA, and A in terms of classification accuracy. From Figure 3, we see that imperfect testing does not alter the main efficiency findings; GA and SA are uniformly more efficient than A, substantially so when p is larger. GA remains marginally more efficient than SA when α = 0.50 and α = 1 (less heterogeneity). When α = 0.10 (more heterogeneity), the opposite can be true when p is larger. Finally, our classification accuracy results in Web Appendix C show that nothing is sacrificed on average by constructing arrays informatively.

Figure 3.

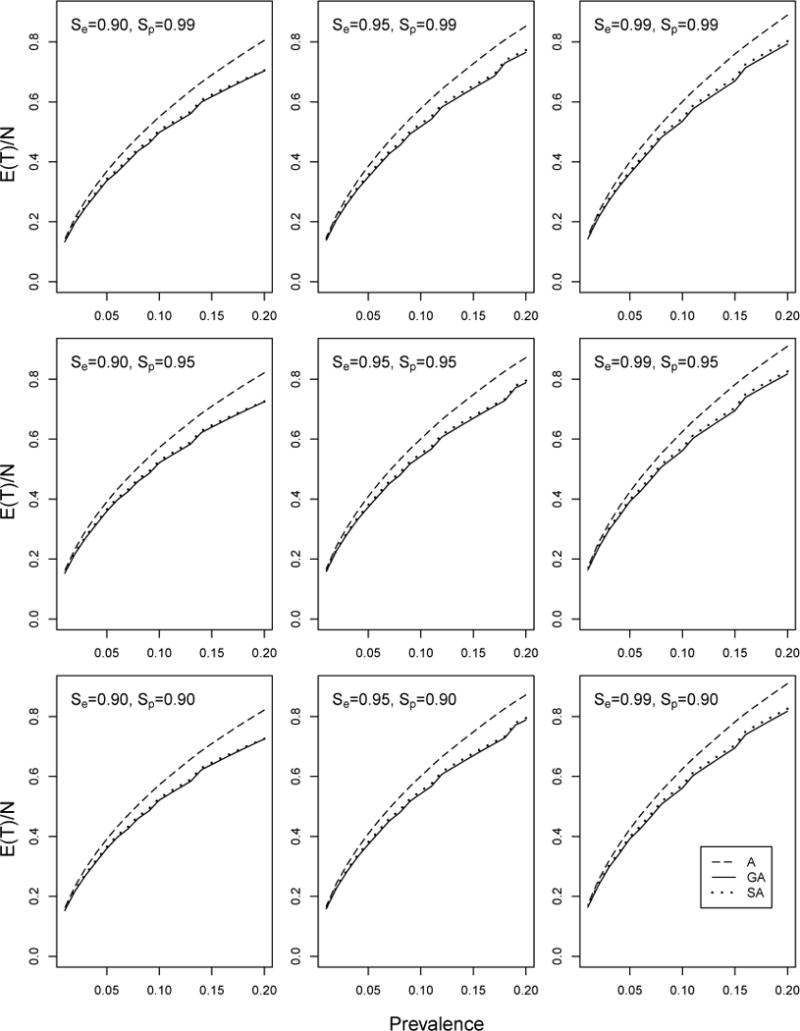
Efficiency comparison with imperfect testing. Per-individual efficiency for GA, SA, and A with α = 0.50. E(T\A) has been approximated using Equation (13) in Kim et al. (2007). The optimal square array size K has been used for each (p, S_e, S_p) configuration.

4.2 Comparisons with other Informative Procedures

We now compare informative array testing to other informative decoding procedures proposed recently in the literature. Specifically, we compare the most efficient array design, GA, to the most efficient Dorfman procedure in McMahan et al. (2011), PSOD, and the most efficient Sterrett procedure in Bilder et al. (2010), FIS. For complete details on PSOD and FIS, see the respective references. Both PSOD and FIS are hierarchial in nature.

PSOD is a Dorfman-type algorithm, so positive pools are decoded using individual testing; that is, like two-dimensional array testing, PSOD is a two-stage procedure. When compared to the Dorfman algorithm which regards the population as homogeneous, PSOD gains efficiency by grouping lower-risk (higher-risk) individuals into larger-sized (smaller-sized) pools. FIS is a Sterrett-type algorithm, so its number of stages is at least three and can be as many as 2(K − 1), where K is the pool size. When compared to two-stage procedures, FIS can gain substantial efficiency because the number of individual tests is often reduced. This phenomenon is commonly seen in the group testing literature; namely, higher-stage procedures almost always increase efficiency. It is important to note that PSOD and FIS require multiple distinct pool sizes to complete the decoding process, so their use may be limited in applications where assays must be calibrated to accommodate differently sized pools. By comparison, array testing uses only the master row/column pool of size K and individual testing.

Using the same values of p, S_e, and S_p as in Figure 3, we provide in Figure 4 a per-individual efficiency comparison of GA, PSOD, and FIS when α = 0.50; Web Appendix D contains the corresponding α = 0.10 and α = 1 figures. The efficiency for each procedure is computed using the order statistic distributions described in Section 4.1. The optimal master pool size is used for FIS at each (p, S_e, S_p) configuration, while for GA, we continue to use the K × K array that is optimally sized for A. PSOD identifies optimal (variable) master pool sizes at each (p, S_e, S_p) configuration using the greedy algorithm outlined in McMahan et al. (2011), which, for purposes here, is implemented within “blocks” of size N = K². As in Section 4.1, we handicap the performance of GA by using the optimal uninformative array size. Therefore, when interpreting the Figure 4/Web Appendix D comparisons, one should keep in mind that optimally sized versions of PSOD and FIS are not subjected to this type of penalty.

Figure 4.

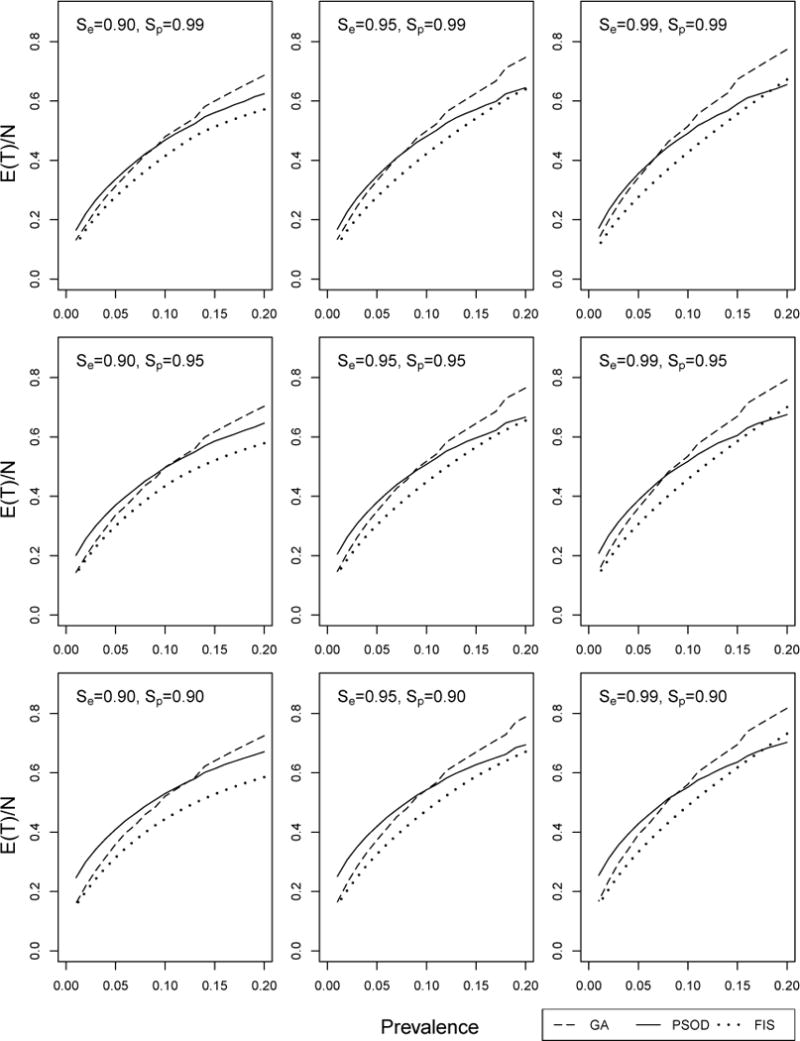
Efficiency comparison with other informative procedures. Per-individual efficiency for GA, PSOD, and FIS with α = 0.50. The optimal pool size has been used for each (p, S_e, S_p) configuration; see Section 4.2.

Between the two-stage procedures when α = 0.50, GA is generally more efficient than PSOD when the mean prevalence is lower, roughly, p < 0.09. This GA/PSOD efficiency “borderline” can be less (p < 0.07) when S_e and S_p are both close to unity, but it can also be greater (p < 0.12) when assay tests are not as accurate. Not surprisingly, FIS is the most efficient among all three procedures, although GA closely rivals FIS when p is small; e.g., p < 0.02. In application, potential users should be aware that while FIS can reduce the number of tests, it is also far more difficult to implement, especially when the decoding process is not automated and when lab technicians must prepare test samples by hand at each decoding stage. For example, when α = 0.50, p = 0.01, and S_e = S_p = 0.95, FIS needs, on average, 6.8 stages to decode positive pools (see Web Appendix D). In this situation, using FIS could dramatically lengthen the expected time needed to dignose each individual. On the other hand, GA reverts to individual testing in its second and final stage.

The corresponding α = 0.10 and α = 1 figures in Web Appendix D display the same general ordering among GA, PSOD, and FIS. When α = 0.10 (more heterogeneity), the region of superiority of GA over PSOD in terms of efficiency is notably smaller; however, when α = 1 (less heterogeneity), it is notably larger. We have found that larger values of α more accurately describe levels of heterogeneity typically seen in application. As expected, optimally sized FIS remains the most efficient regardless of α, but its expected number of stages ranges from 4.7 to as high as 14.4 (see Web Appendix D). In this light, the additional amount of complexity associated with FIS makes the simpler two-stage procedures markedly more attractive.

5. Infertility Prevention Project Data

The Infertility Prevention Project (IPP) is a national program, funded by the CDC, aimed at providing screening and treatment for individuals with chlamydia and/or gonorrhea infection. Chlamydia and gonorrhea are the two most common sexually transmitted diseases (STDs) in the United States. Untreated individuals can experience serious medical conditions, including pelvic inflammatory disease (PID) and ectopic pregnancy in women and sterility in men. Since its origination in 1988, the IPP has been effective at reducing the incidence of chlamydia/gonorrhea infection and enhancing the treatment and follow-up for those infected. The IPP is carried out separately in each of the 50 states; in Nebraska, roughly 20–30 thousand individuals are screened each year at testing sites located throughout the state. Individual specimens (urine or swab) collected at these sites are transported to the Nebraska Public Health Laboratory (NPHL) in Omaha for testing.

At both the regional and state levels, one of the current objectives of the IPP is to expand testing services to screen more individuals for chlamydia and gonorrhea while reducing laboratory costs on a per-individual basis. To accomplish this goal, our medical colleagues at the NPHL have expressed an interest in adopting group testing for chlamydia and gonorrhea surveillance as part of the IPP screening process. In addition to cost considerations, our colleagues are also concerned about being able to correctly identify those individuals infected with these diseases. This is particularly relevant because about 80% (50%) of all chlamydia (gonorrhea) positive individuals are asymptomatic (CDC, 2010). We therefore provide an assessment of the potential use of informative array testing and illustrate how it could be adopted to achieve our colleagues’ goals. Of course, this assessment may be valuable to investigators in other infectious disease contexts.

In Nebraska, there were 23,146 individuals screened in 2008 and 27,551 individuals screened in 2009; all individuals were screened for both infections. At the time of testing, clinicians collected additional covariate information on each individual, including age, race, and other clinical/behavioral risk factors. A complete listing of all covariates is given in Table 1. Acknowledging differences in test kit sensitivities and specificities, we cross-classify each individual according to gender and specimen (urine or swab) creating four strata. Values of S_e and S_p for each stratum, provided to us by the NPHL, are listed in Table 1 for each infection. Our goal is to implement two-dimensional array testing procedures using the 27,551 individuals from 2009. We do so separately within each infection-gender-specimen stratum.

Table 1.

Nebraska IPP data summary. Numbers of individuals screened and overall prevalence levels are provided for years 2008 and 2009. The values of S_e and S_p are provided by the NPHL. The individual covariates available are age, race, clinic type, location of clinic, reason for visit (family planning, prenatal, STD screening), symptoms, clinical observations (cervical friability, PID, cervicitis, urethritis), and risk history (multiple partners in last 90 days, new partner in last 90 days, contact to STD).

					Number screened		Mean prevalence
Infection	Gender	Specimen	Se	Sp	2008	2009	2008	2009
Chlamydia	Female	Urine	0.805	0.96	2338	4972	0.092	0.080
		Swab	0.928	0.96	14441	14530	0.072	0.069
	Male	Urine	0.930	0.95	3541	6139	0.077	0.081
		Swab	0.925	0.95	2826	1910	0.137	0.157
Gonorrhea	Female	Urine	0.849	0.98	2338	4972	0.024	0.017
		Swab	0.966	0.98	14441	14530	0.013	0.013
	Male	Urine	0.970	0.96	3541	6139	0.012	0.021
		Swab	0.985	0.96	2826	1910	0.068	0.070

For each infection, we treat the 2009 diagnoses as the true statuses. For uninformative array testing (A), we assign, by column, the 2009 individuals to optimally sized arrays chronologically based on the specimen’s NPHL arrival date (that is, covariate information is not used in the assignment). Optimal array sizes for A are determined using the 2008 estimated mean prevalence levels; see Equation (2) in Kim et al. (2007). Using the individual diagnoses in 2008 and the corresponding covariates, we fit a first-order logistic regression model within each infection-gender-specimen stratum; for GA and SA, we assign the 2009 individuals to arrays chronologically (as with A), where within-array arrangements are based on the estimated probabilities computed from the 2008 model fits. For GA and SA, we use the same array sizes as those optimally sized for A. As noted in Section 4, doing this penalizes GA/SA, but otherwise ensures the fairest comparison. In each infection-gender-specimen stratum, “leftover” individuals not placed in a full-sized array are decoded using Dorfman retesting; this is done in the same manner for GA, SA, and A. To implement each procedure, we simulate pool (and, if necessary, individual) diagnoses using the S_e and S_p levels in Table 1.

Table 2 displays the mean number of tests and accuracy measures when screening individuals for chlamydia and gonorrhea in 2009. Because the 2009 diagnoses are simulated for each infection, we implement each procedure B = 1000 times for each infection-gender-specimen configuration to average out simulation error; i.e., values in Table 2 are averaged over these 1000 simulations. To assess the merit of other recently proposed informative procedures, and their potential use as part of the IPP, we also include PSOD and FIS in the comparison. PSOD is implemented using blocks of size N = 100 arranged chronologically by arrival date, identically to how PSOD is evaluated using the Nebraska IPP data in McMahan et al. (2011). The FIS master pool size used for 2009 decoding is chosen to be the one that minimizes the number of tests when applying FIS to the 2008 training data.

Table 2.

Nebraska IPP screening results for 2009. Mean number of tests $(\overline{T})$, and accuracy measures, and ( ${\overline{PS}}_e$, ${\overline{PS}}_p$, $\overline{\mathit{PPV}}$, and $\overline{\mathit{NPV}}$), averaged over 1000 implementations, for the 8 strata created by infection, gender, and specimen type. The average number of stages required to decode positive pools and optimal pool sizes are also given. PSOD does not use a common pool size. Gender/specimen individual counts and values of S_e and S_p are in Table 1.

Infection	Gend/Spec	Method	Pool Size	$\overline{T}$	${\overline{PS}}_e$	${\overline{PS}}_p$	$\overline{\mathit{PPV}}$	$\overline{\mathit{NPV}}$	# Stages
Chlamydia	Female/Urine	A	9	2124.4	0.526	0.993	0.874	0.960	2
		SA	9	2131.3	0.526	0.993	0.873	0.960	2
		GA	9	2082.4	0.525	0.994	0.880	0.960	2
		PSOD	–	2533.5	0.650	0.989	0.835	0.970	2
		FIS	13	2051.0	0.581	0.990	0.838	0.964	9.2
	Female/Swab	A	8	6565.3	0.802	0.994	0.907	0.985	2
		SA	8	6472.7	0.802	0.994	0.910	0.985	2
		GA	8	6416.8	0.803	0.994	0.913	0.985	2
		PSOD	–	7029.0	0.862	0.991	0.874	0.990	2
		FIS	8	5909.0	0.842	0.993	0.900	0.988	6.3
	Male/Urine	A	8	3095.2	0.806	0.990	0.876	0.983	2
		SA	8	2973.3	0.807	0.991	0.888	0.983	2
		GA	8	2932.5	0.808	0.991	0.892	0.983	2
		PSOD	–	3243.3	0.869	0.987	0.855	0.988	2
		FIS	8	2690.0	0.843	0.991	0.890	0.986	6.3
	Male/Swab	A	6	1356.4	0.793	0.986	0.911	0.962	2
		SA	6	1344.0	0.794	0.986	0.915	0.963	2
		GA	6	1318.9	0.793	0.987	0.917	0.963	2
		PSOD	–	1278.1	0.870	0.983	0.903	0.976	2
		FIS	7	1213.2	0.823	0.986	0.918	0.968	6.2
Gonorrhea	Female/Urine	A	17	875.3	0.614	0.999	0.921	0.993	2
		SA	17	885.6	0.616	0.999	0.915	0.994	2
		GA	17	876.3	0.617	0.999	0.919	0.994	2
		PSOD	–	1166.4	0.720	0.998	0.845	0.995	2
		FIS	14	862.9	0.697	0.998	0.886	0.995	8.8
	Female/Swab	A	21	2427.1	0.902	0.999	0.909	0.999	2
		SA	21	2333.2	0.903	0.999	0.917	0.999	2
		GA	21	2280.4	0.903	0.999	0.923	0.999	2
		PSOD	–	3046.8	0.935	0.998	0.855	0.999	2
		FIS	21	2112.8	0.926	0.999	0.893	0.999	9.7
	Male/Urine	A	21	1575.8	0.913	0.994	0.775	0.998	2
		SA	21	1325.5	0.913	0.996	0.830	0.998	2
		GA	21	1309.9	0.914	0.996	0.832	0.998	2
		PSOD	–	1676.4	0.942	0.994	0.767	0.999	2
		FIS	22	1300.3	0.927	0.995	0.799	0.998	10.6
	Male/Swab	A	8	929.4	0.956	0.993	0.908	0.997	2
		SA	8	796.7	0.955	0.996	0.943	0.997	2
		GA	8	770.6	0.959	0.996	0.950	0.997	2
		PSOD	–	699.4	0.978	0.993	0.910	0.998	2
		FIS	17	574.8	0.961	0.995	0.942	0.997	7.1

Among the array procedures, GA and SA are often much more efficient than A; for example, when screening 1,910 male subjects for gonorrhea using swabs in 8 × 8 arrays, the mean number of tests expended is 929.4 for A, 796.7 for SA, and 770.6 for GA. However, there is at least one instance where ordering individuals informatively provides little or no benefit (e.g., gonorrhea-female-urine). Further inspection reveals that for this cohort, the adequacy of the first-order logistic regression model for the 2008 data is questionable. With regards to the classification accuracy measures, there are few noticeable differences (beyond what is likely Monte Carlo error) between A and the informative procedures; that is, ordering within the arrays has little or no effect on accuracy. There is moderate evidence that GA and SA can increase the positive predictive value when S_e and S_p are close to unity.

When compared to PSOD, informative array testing often provides substantial savings in the number of tests. For example, when screening 4,972 female subjects for chlamydia using urine samples in 9×9 arrays, the mean number of tests expended is 2082.4 for GA and 2533.5 for PSOD. In this same stratum, FIS is marginally more efficient than GA, needing 2051.0 tests (using master pools of size 13), but FIS requires an average of 9.2 stages to decode master pools which test positive. As we saw in Section 4, the two-stage PSOD procedure can outperform GA and SA when the mean prevalence p is larger (see the male-swab strata). However, in those strata where p is smaller (e.g., gonorrhea-female/male-urine strata), both GA and SA are far more efficient than PSOD and can also nearly outperform FIS. This last finding is especially noteworthy, because FIS requires 8.8–10.6 stages (and multiple distinct pool sizes) to complete the decoding process in these strata.

To illustrate how our informative array procedures produce individual-specific predictive values, we display in Web Appendix E the estimated values of $PP{V}^{{\mathcal{I}}_{\mathit{jk}}}$ ( $NP{V}^{{\mathcal{I}}_{\mathit{jk}}}$) for each female subject who was diagnosed as positive (negative) for chlamydia in the first of our 1000 implementations. Similar figures for the female-gonorrhea and male-chlamydia/gonorrhea cohorts are also included. The information in these figures strongly suggests the possibility of using estimates of $PP{V}^{{\mathcal{I}}_{\mathit{jk}}}$ and $NP{V}^{{\mathcal{I}}_{\mathit{jk}}}$. to “back-end screen” specific individuals who may have been misdiagnosed. One way this could be done is to simply use additional individual testing for those subjects with incongruously low values of $PP{V}^{{\mathcal{I}}_{\mathit{jk}}}$ or $NP{V}^{{\mathcal{I}}_{\mathit{jk}}}$. We plan to investigate this in future research.

Two additional details warrant brief remarks. First, in our implementation of the informative procedures in 2009, we used logistic model fits from 2008 including all of the covariates as first-order terms. We also performed identical analyses in each stratum using first-order models with the “best” subset of covariates (as judged by the Bayesian Information Criterion). Second, we have also reproduced the analyses in Table 2 assuming that the maximum allowable array size (MAAS) is K* × K*, where K* = 10. Current empirical research in chlamydia and gonorrhea screening suggests the choice of K* = 10 to avoid dilution effects (see, e.g., Shipitsyna et al., 2007). The results from each additional analysis provided the same general conclusions regarding the potential advantages of GA and SA. However, using the best subsets models did not always improve the efficiency and using K* = 10 increased the number of tests needed to screen for gonorrhea infection in three of the four strata. Results from the best subsets model fits and those assuming a MAAS of K* = 10 are provided in Web Appendix E.

6. Discussion

We have generalized previous statistical work in two-dimensional array testing to incorporate population heterogeneity. Our work shows that exploiting individual covariate information sensibly can provide large gains in array testing efficiency while maintaining overall classification accuracy. We have also shown how our methodology affords one the flexibility to target potentially misdiagnosed individuals using individual-specific predictive values. Our R programs, which can be downloaded at www.chrisbilder.com/grouptesting/array, calculate the efficiency and the classification accuracy measures described in Section 2.

We have illustrated the implementation of informative array testing using chlamydia and gonorrhea data collected as part of the IPP; however, our methodology is clearly applicable in other infectious disease contexts. Furthermore, we believe this work may be suitably adapted for use in other applications where array testing has been used for classification. For example, to identify lead compounds in drug discovery, high throughput screening via array testing has been shown to be an efficient alternative to individual testing (Warrior et al. 2007). In this and related applications, certain chemical descriptors are known to be good predictors of compound activity; that is, it may be appropriate to treat individual compounds as heterogeneous with different probabilities of positive activity (Remlinger et al., 2006). Further research is needed to assess this potential extension in the light of blocking and synergistic effects which may arise due to pooling (Xie et al., 2001). Our work may also be applicable in screening large DNA libraries (Berger et al., 2000) if individual clone status, for example, whether or not a clone contains a specific DNA sequence, can be modeled appropriately.

Our generalization of (two-dimensional) array testing to heterogeneous populations is driven by an underlying goal to increase efficiency, especially in the current disease screening environment where there is a strong desire to keep overall testing costs low. Extensions of our work could include the use of a master array test (Kim et al., 2007) or the development of procedures using higher-dimensional arrays (Kim and Hudgens, 2009). One might expect the corresponding heterogeneous versions to confer even more efficiency gains than those seen in this paper.